6

Zmienna losowa dwuwymiarowa. Centralne twierdzenie graniczne

Zad. 0 Rzucamy kostką do gry. Zmienna losowa

X

przyjmuje wartość 1 gdy wypadnie

parzysta liczba oczek oraz wartość -1 gdy wypadnie nieparzysta liczba oczek.
Zmienna losowa

Y

przyjmuje wartość 3 gdy wypadnie liczba oczek podzielna przez 3 oraz 2

w przeciwnym przypadku.
Zbadać niezależność zmiennych losowych.

Zad. 1. Dane są niezależne zmienne losowe X, Y o rozkładach:

Znaleźć rozkład, wartość średnią i wariancję następujących zmiennych losowych:
a)

4

2



 X

U

, b)

Y

U

3

2 



, c)

Y

X

U





, d)

Y

X

U

3

2





Zad.2 Zmienna losowa dwuwymiarowa

)

,

(

Y

X

ma następujący rozkład:

3

,

0

)

0

,

1

(





 Y

X

P

,

1

,

0

)

1

,

1

(





 Y

X

P

,

4

,

0

)

0

,

2

(







Y

X

P

,

C

Y

X

P







)

1

,

2

(

a) Znaleźć stałą C

b) Znaleźć dystrybuantę zmiennej losowej X

c) Zbadać, czy zmienne losowe są niezależne.

Zad. 3 Zmienna losowa dwuwymiarowa

)

,

(

Y

X

ma następujący rozkład:

8

1

)

1

,

1

(









Y

X

P

,

4

1

)

2

,

1

(









Y

X

P

,

C

Y

X

P









)

3

,

1

(

,

8

1

)

1

,

1

(





 Y

X

P

,

8

1

)

2

,

1

(





 Y

X

P

,

4

1

)

3

,

1

(





 Y

X

P

.

a) Znaleźć stałą C
b) Znaleźć dystrybuantę zmiennej losowej Y
c) Zbadać, czy zmienne losowe są niezależne.

Zad. 4 20% sztuk pewnego produktu jest wadliwych. Jakie jest prawdopodobieństwo, że w
losowo wybranej próbie 225 sztuk tego produktu :
a) co najwyżej 50 będzie wadliwych
b) więcej niż 35 będzie wadliwych
c) wadliwych będzie więcej niż 35 i mniej niż 50.

Zad. 5 Towarzystwo ubezpieczeniowe posiada 1000 ubezpieczonych od włamania do garażu
w pewnym mieście. Prawdopodobieństwo włamania do garażu w tym mieście w ciągu roku
wynosi 0,1. Znaleźć prawdopodobieństwo, że w ciągu roku co najwyżej 90 ubezpieczonych
zgłosi się do tego towarzystwa po wypłatę odszkodowania z tytułu włamania do garażu.

Zad. 6 Wiadomo, że 80% studentów lubi dodawać ketchup do kanapek. Jakie jest
prawdopodobieństwo, że w losowo wybranej próbie 100 studentów co najwyżej 15 nie lubi
dodawać ketchupu do kanapek.

Zad. 7 10% osób wyraża zgodę na otrzymywanie przesyłek reklamowych na skrzynkę
mailową. Wysłano zapytanie ofertowe do losowo wybranej próby 500 osób.
Jakie jest prawdopodobieństwo, zgodę wyrazi co najwyżej 65 osób.

j

x

-1

0

j

p

4

,

0

0,6

i

y 0

1

2

3

i

p

5

,

0 0,1 0,3 0,1

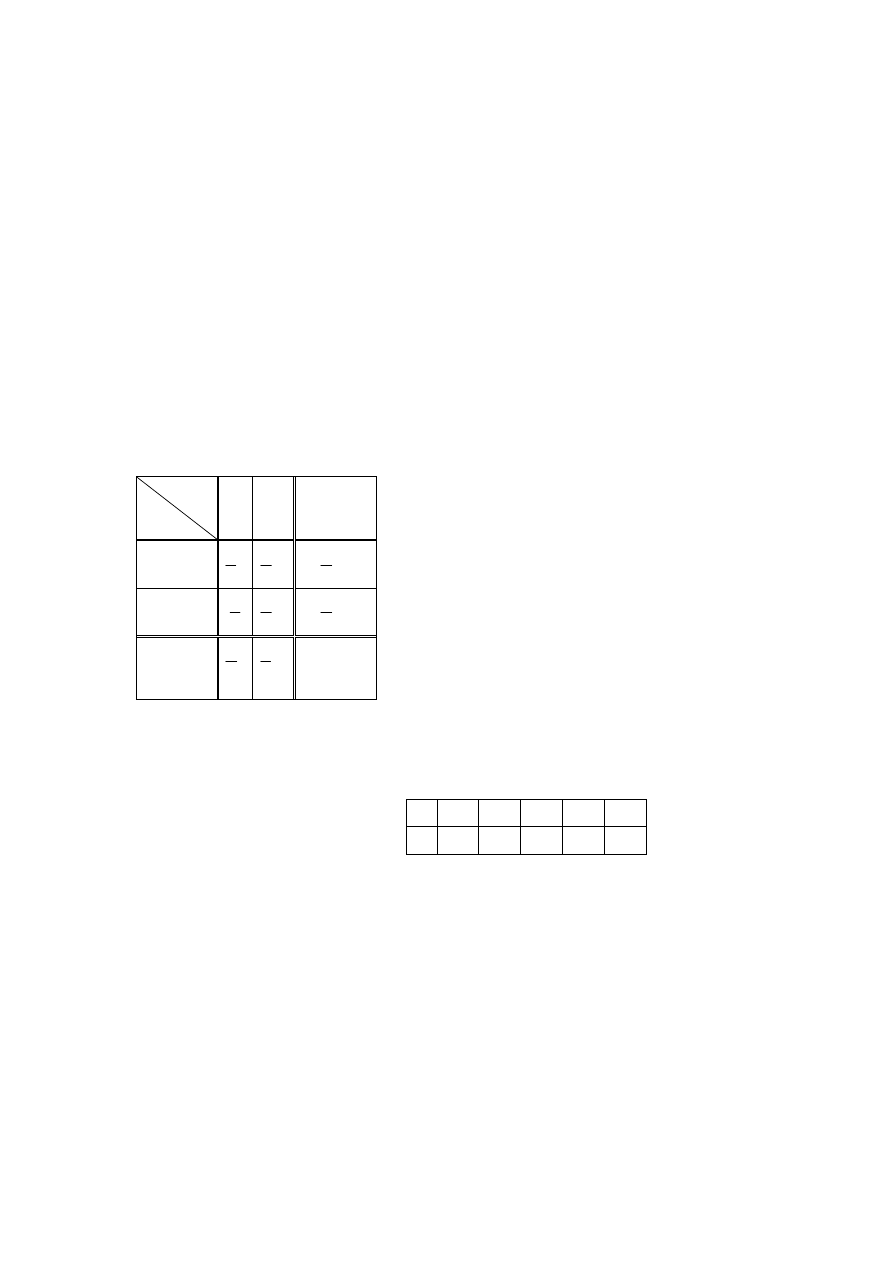
7

Zad. 8 Maszyna licząca dodaje 600 liczb rzeczywistych zaokrąglając każdą z nich do
najbliższej liczby całkowitej. Zakładamy niezależność błędów zaokrągleń i przyjmujemy, że
mają rozkład jednostajny na odcinku <-0,5,0,5>. Obliczyć prawdopodobieństwo, że błąd przy
sumowaniu nie przekroczy 3.

Zad. 9 Mamy ciąg niezależnych zmiennych losowych o jednakowym rozkładzie Poissona z
parametrem

9





.

Obliczyć a)

)

920

(

100

1







i

i

X

P

, b)

)

929

(

100

1







i

i

X

P

, c)

)

884

850

(

100

1









i

i

X

P

Zad. 10 Mamy ciąg niezależnych zmiennych losowych o jednakowym rozkładzie
wykładniczym ze parametrem

4



a

.

Obliczyć

)

90

(

)

400

1







i

i

X

P

a

,

)

100

(

)

400

1







i

i

X

P

b

,

)

115

95

(

)

400

1









i

i

X

P

b

Odpowiedzi:
0) zmienne losowe są niezależne

96

,

0

,

8

,

4

)

)

1

2







u

D

EU

a

8

,

10

,

1

)

)

1

2







u

D

EU

b

44

,

1

,

6

,

0

)

)

1

2





u

D

EU

c

1c)

64

,

14

,

8

,

3

)

)

1

2







u

D

EU

d

nie

c

x

x

x

x

F

b

C

a

)

,

,

2

,

1

2

1

,

4

,

0

1

,

0

)

(

)

,

2

,

0

)

)

2



























nie

c

x

y

y

y

y

F

b

C

a

)

,

,

3

,

1

3

3

,

625

,

0

2

1

,

25

,

0

1

,

0

)

(

)

,

125

,

0

)

)

3



































716

,

0

)

,

94295

,

0

)

,

8212

,

0

)

)

4

c

b

a

,

1587

,

0

)

5

,

1292

,

0

)

6

,

9896

,

0

)

7

,

6628

,

0

)

8

25

,

0

)

,

17

,

0

)

,

7422

,

0

)

)

9

c

b

a

,

84

,

0

)

,

5

,

0

)

,

0228

,

0

)

)

10

c

b

a

Y
X

2

3

rozkład
brzegowy
X

-1

3

1

6

1

2

1

1

3

1

6

1

2

1

Rozkład
brzegowy
Y

3

2

3

1

1

i

u -1

0

1

2

3

i

p 0,2 0,34 0,18 0,22 0,06