Za rozwiàzanie

wszystkich zadaƒ

mo˝na otrzymaç

∏àcznie 50 punktów.

Autor: Anna Jatczak

ARKUSZ I

TEST PRZED PRÓBNÑ MATURÑ 2007

PRZYK¸ADOWY ARKUSZ

EGZAMINACYJNY Z MATEMATYKI

Arkusz I

POZIOM PODSTAWOWY

Czas pracy: 120 minut

Instrukcja dla zdajàcego

1. Prosz´ sprawdziç, czy arkusz egzaminacyjny zawiera 11

stron. Ewentualny brak nale˝y zg∏osiç przewodniczàcemu
zespo∏u nadzorujàcego egzamin.

2. Rozwiàzania zadaƒ i odpowiedzi nale˝y zapisaç w miejscu

na to przeznaczonym.

3. W rozwiàzaniach zadaƒ trzeba przedstawiç tok rozumowa-

nia prowadzàcy do ostatecznego wyniku.

4. Prosz´ pisaç czytelnie; u˝ywaç d∏ugopisu/pióra tylko

z czarnym tuszem/atramentem.

5. Nie wolno u˝ywaç korektora. B∏´dne zapisy trzeba wyraê-

nie przekreÊliç.

6. Zapisy w brudnopisie nie b´dà oceniane.
7. Obok ka˝dego zadania podana jest maksymalna liczba punk-

tów, którà mo˝na uzyskaç za jego poprawne rozwiàzanie.

8. Podczas egzaminu mo˝na korzystaç z zestawu wzorów

matematycznych, cyrkla i linijki oraz kalkulatora.

˚yczymy powodzenia!

Arkusz przygotowany przez Wydawnictwo Pedagogiczne OPERON na wzór oryginalnego arkusza maturalnego.

w w w. o p e r o n . p l

Zadanie 1 (4 pkt)

Dana jest prosta

k o równaniu x

y

3

2

12

0

-

+

= .

a) Wyznacz wspó∏rz´dne punktów P i R przeci´cia prostej k z osiami uk∏adu wspó∏rz´dnych.
b) Oblicz obwód trójkàta OPR, gdzie O jest poczàtkiem uk∏adu wspó∏rz´dnych.
c) Napisz równanie prostej l równoleg∏ej do prostej k, do której nale˝y punkt

;

S

2

1

=

-

^

h.

Matematyka. Arkusz I

2

w w w. o p e r o n . p l

Matematyka. Arkusz I

3

Zadanie 2 (4 pkt)

Funkcja g ka˝dej liczbie n nale˝àcej do zbioru

,

,

,

, , , ,

Z

4

3

2

1 0 1 2 3

= -

-

-

-

"

, przyporzàdkowuje ilo-

czyn tej liczby i liczby o dwa od niej mniejszej.
a) Napisz wzór funkcji g.
b) Sporzàdê wykres funkcji g.
c) Wyznacz zbiór wartoÊci funkcji g.
d) Wyznacz argumenty, dla których zachodzi równoÊç f n

n

=

^ h

.

w w w. o p e r o n . p l

Zadanie 3 (3 pkt)

Trójkàtnà dzia∏k´ o bokach d∏ugoÊci

m

13

,

m

20

,

m

21

podzielono na dwie dzia∏ki o równych polach,

budujàc p∏ot równoleg∏y do najkrótszego boku dzia∏ki. Oblicz d∏ugoÊç tego p∏otu. Wynik zaokràglij
do cz´Êci dziesi´tnych metra.

Matematyka. Arkusz I

4

w w w. o p e r o n . p l

Matematyka. Arkusz I

5

Zadanie 4 (7 pkt)

Do wykresu funkcji f x

x

bx

2

6

2

= -

+

+

^ h

,

x

R

!

nale˝y punkt

;

P

2

10

= -

-

^

h.

a) Wyznacz wartoÊç wspó∏czynnika b we wzorze funkcji f x

^ h.

b) Zapisz funkcj´ f x

^ h w postaci kanonicznej.

c) Wyka˝, ˝e postacià iloczynowà tej funkcji jest wzór f x

x

x

2

1

3

= -

+

-

^

^

^

h

h

h.

d) Sprawdê, czy miejsca zerowe funkcji f x

^ h nale˝à do zbioru rozwiàzaƒ nierównoÊci

<

x

2

3

-

.

w w w. o p e r o n . p l

Zadanie 5 (4 pkt)

Dziadek rozdzieli∏ swoje cukierki pomi´dzy pi´ciu wnuków. Najm∏odszemu Adasiowi da∏ po∏ow´
wszystkich cukierków; Bartkowi da∏ po∏ow´ tego, co Adasiowi; Czarkowi – po∏ow´ tego, co Bartkowi,
Darkowi – po∏ow´ tego, co Czarkowi, zaÊ Erykowi – po∏ow´ tego, co Darkowi. Ostatni cukierek dzia-
dek zatrzyma∏ dla siebie. Oblicz, ile cukierków mia∏ dziadek i ile z nich otrzyma∏ ka˝dy z wnuków.

Matematyka. Arkusz I

6

w w w. o p e r o n . p l

Matematyka. Arkusz I

7

Zadanie 6 (4 pkt)

Dane jest wyra˝enie:

:

x

x

x

x

4

8

5

4

2

5

2

-

-

-

-

^

h

.

a) Wyznacz dziedzin´ wyra˝enia.
b) Wykonaj dzia∏ania i zapisz wyra˝enie w najprostszej postaci.
c) Ustal, dla jakiej wartoÊci x wartoÊç danego wyra˝enia jest równa liczba a, gdzie:

a

36

25

1

3

1

2

2

1

1

2

1

$

=

-

-

-

-

b

b

l

l

R

T

S

SS

V

X

W

WW .

w w w. o p e r o n . p l

Zadanie 7 (6 pkt)

Zawodnik zaplanowa∏, ˝e w ramach przygotowaƒ do zawodów sportowych codziennie przez ca∏y
czerwiec b´dzie trenowa∏ biegi, przy czym ka˝dego dnia b´dzie wyd∏u˝a∏ tras´ o t´ samà liczb´ ki-
lometrów. Po zakoƒczeniu przygotowaƒ stwierdzi∏, ˝e we wszystkie dni nieparzyste miesiàca prze-
bieg∏ ∏àcznie

km

255

, zaÊ we wszystkie dni parzyste przebieg∏ w sumie

km

270

. Oblicz, ile kilometrów

przebieg∏ zawodnik 1 czerwca, a ile 30 czerwca.

Matematyka. Arkusz I

8

w w w. o p e r o n . p l

Matematyka. Arkusz I

9

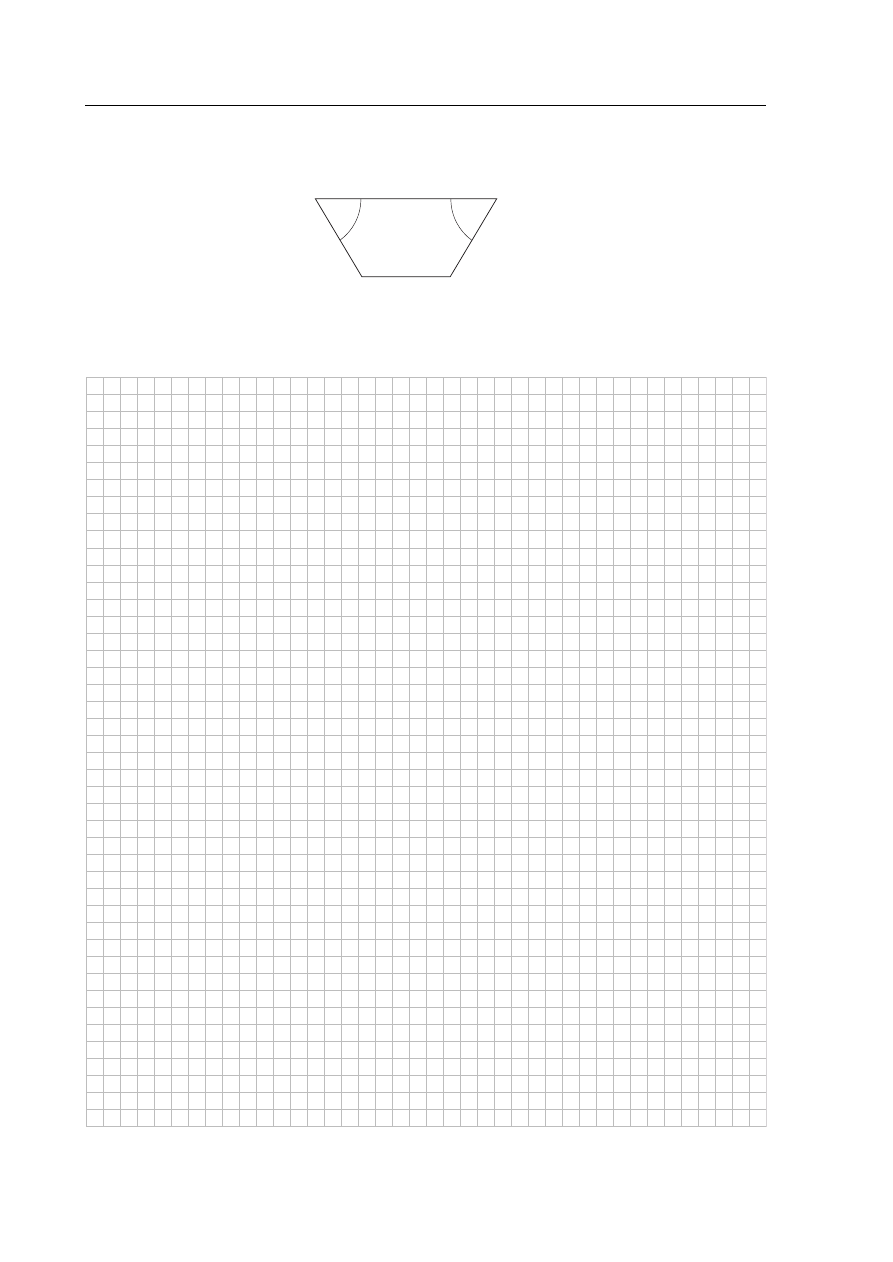
Zadanie 8 (7 pkt)

Kana∏ o d∏ugoÊci km

1

ma kszta∏t graniastos∏upa prostego, którego przekrój jest trapezem o wymiarach

podanych na rysunku.

a) Oblicz, ile litrów wody mo˝e pomieÊciç wype∏niony w ca∏oÊci kana∏.
b) W wyniku zanieczyszczenia na dnie kana∏u utworzy∏a si´ jednolita warstwa osadu o grubo-
Êci 10 cm. Oblicz, o ile procent zmniejszy∏o si´ pole przekroju kana∏u.

0,8 m

0,8 m

1 m

60

°

60

°

w w w. o p e r o n . p l

Zadanie 9 (4 pkt)

Tabela przedstawia liczb´ godzin ponadwymiarowych przepracowanych przez grup´ 20 robotników.

a) Oblicz Êrednià liczb´ godzin ponadwymiarowych przepracowanych przez robotnika z tej grupy.
b) Oblicz, jaki procent grupy stanowià robotnicy, którzy przepracowali mniej godzin ponadwymia-
rowych, ni˝ wynosi Êrednia grupy.
c) Z grupy wybrano w sposób losowy jednego robotnika. Oblicz prawdopodobieƒstwo zdarzenia, ˝e
przepracowa∏ on co najmniej 4 godziny ponadwymiarowe.

Matematyka. Arkusz I

10

liczba godzin ponadwymiarowych

1

2

3

4

5

liczba robotników

3

6

8

2

1

w w w. o p e r o n . p l

Matematyka. Arkusz I

11

Zadanie 10 (7 pkt)

Kraw´dê boczna ostros∏upa prawid∏owego czworokàtnego jest dwa razy d∏u˝sza od kraw´dzi jego
podstawy i nachylona do p∏aszczyzny podstawy pod kàtem

a. Âciana boczna tworzy z podstawà

ostros∏upa kàt

b.

a) Wykonaj rysunek ostros∏upa i zaznacz kàty

a i b.

b) Oblicz wartoÊç wyra˝enia sin

sin

-

a

b .