interferencja

1

INTERFERENCJA FAL

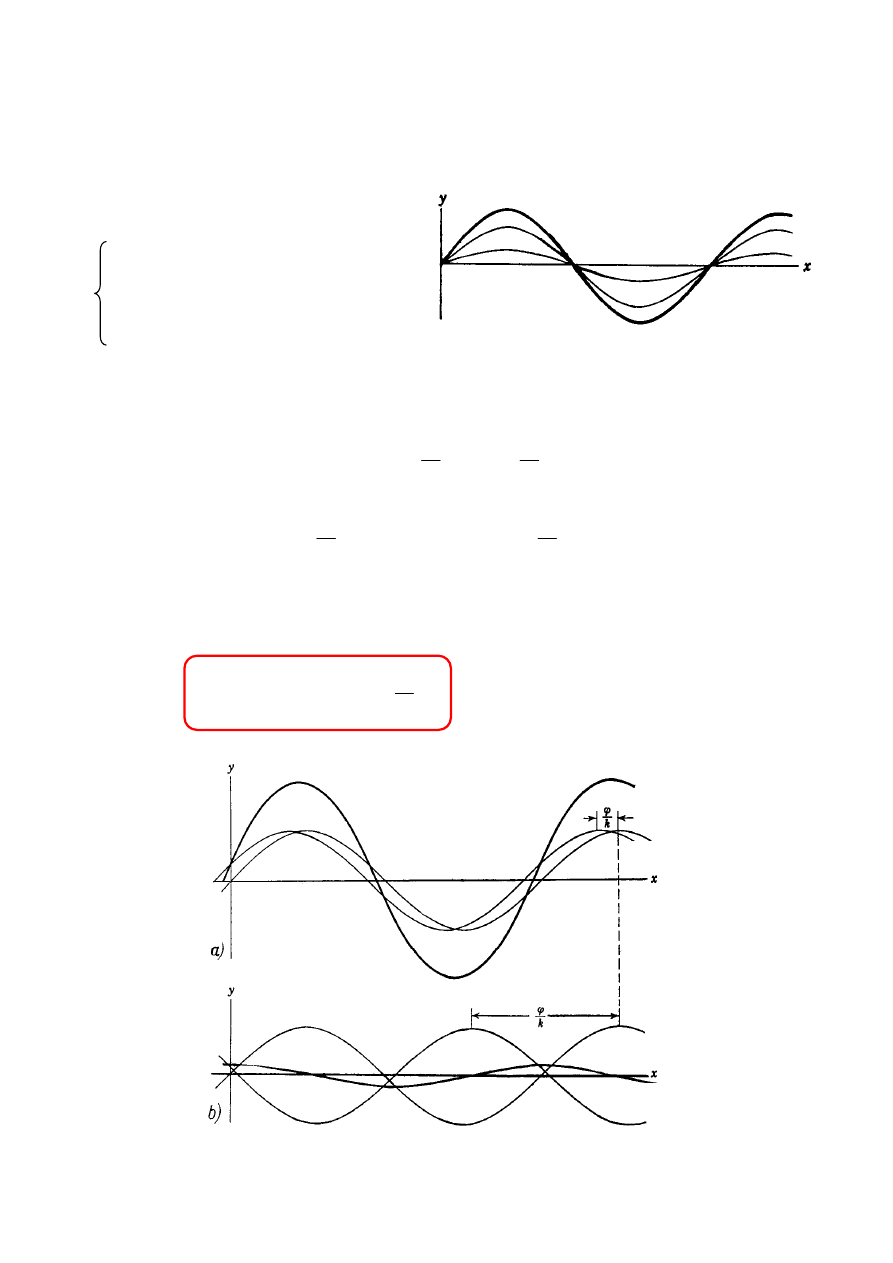
Fale spolaryzowane liniowo,
różnica faz stała w czasie:

)

cos(

1

ϕ

ω

−

−

=

kx

t

E

E

m

)

cos(

2

kx

t

E

E

m

−

=

ω

[

]

)

2

1

cos(

2

1

cos

2

2

1

cos

)

2

1

cos(

2

)

cos(

)

cos(

2

1

ϕ

ω

ϕ

ϕ

ϕ

ω

ω

ϕ

ω

−

−













=

−

−

=

−

+

−

−

=

+

=

kx

t

E

E

kx

t

E

E

kx

t

kx

t

E

E

E

E

m

m

m

Amplituda drgań pola zależy od różnicy faz

ϕ

:

ϕ

ϕ

2

1

cos

2

)

(

0

m

E

E

=

A

∈

( 0 , 2E

m

)

E

1

+ E

2

E

2

E

1

E

1

+ E

2

E

1

E

2

interferencja

2

INTERFERENCJA ŚWIATŁA

1.

Interferują tylko fale o tej samej polaryzacji

2.

Interferują tylko fale o stałej w czasie
różnicy faz, nazywane falami spójnymi lub
koherentnymi.

częstotliwość

ś

wiatła

~10

15

Hz

-->

nie

można

zaobserwować tak szybkich zmian natężenia

FALE SPÓJNE

Atom promieniuje światło w czasie

τ

~ 10

-8

s

ś

wiatło jest więc wysyłane w postaci ciągów falowych

długość ciągu falowego l = c

τ ∼

1- 10m

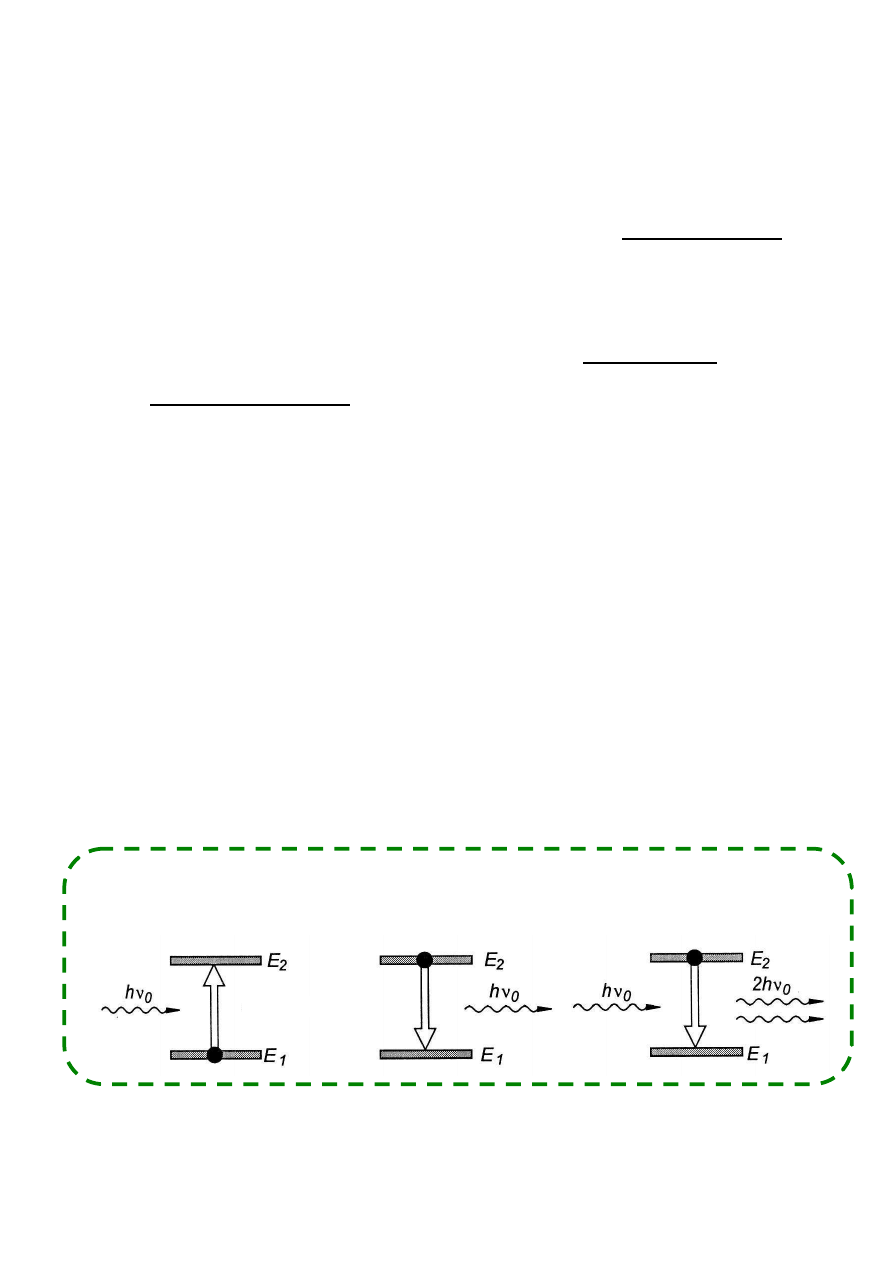
Wysyłanie światła:

emisja emisja

absorpcja spontaniczna wymuszona

Emisja wymuszona umożliwia generację światła spójnego

interferencja

3

INTERFERENCJA DWÓCH FAL

Jeżeli różnica faz jest stała w czasie to:

•

Amplituda zmian pola elektrycznego:

2

cos

2

)

(

0

ϕ

ϕ

∆

=

m

E

E

•

Natężenie światła, dla I

1

= I

2

2

cos

4

2

1

ϕ

∆

⋅

=

I

I

maksimum gdy

2 m

ϕ

π

∆ =

m = 0, 1, 2, 3, ...

minimum gdy

(2

1)

m

ϕ

π

∆ =

+

Obraz się rozmywa gdy m-te maksimum dla fali o długości

λ + ∆λ

pokryje się z (m+1) minimum dla fali o długości

λ

.

Dwie fale spójne:

interferencja

4

INTERFERENCJA DWÓCH FAL

1

1 1

2

2 2

cos(

)

cos(

)

m

m

E

E

t

k l

E

E

t

k l

ω

ω

=

−

=

−

Różnica faz

(

)

(

)

2 2

1 1

2 0 2

1 0 1

2 2

1 1

0

2

1

0

2

2

k l

k l

n k l

n k l

n l

n l

s

s

π

ϕ

λ

π

ϕ

λ

∆ =

−

=

−

=

−

∆ =

−

s = nl

- droga optyczna

0

2

s

π

ϕ

λ

∆ =

∆

Doświadczenie Younga

interferencja

5

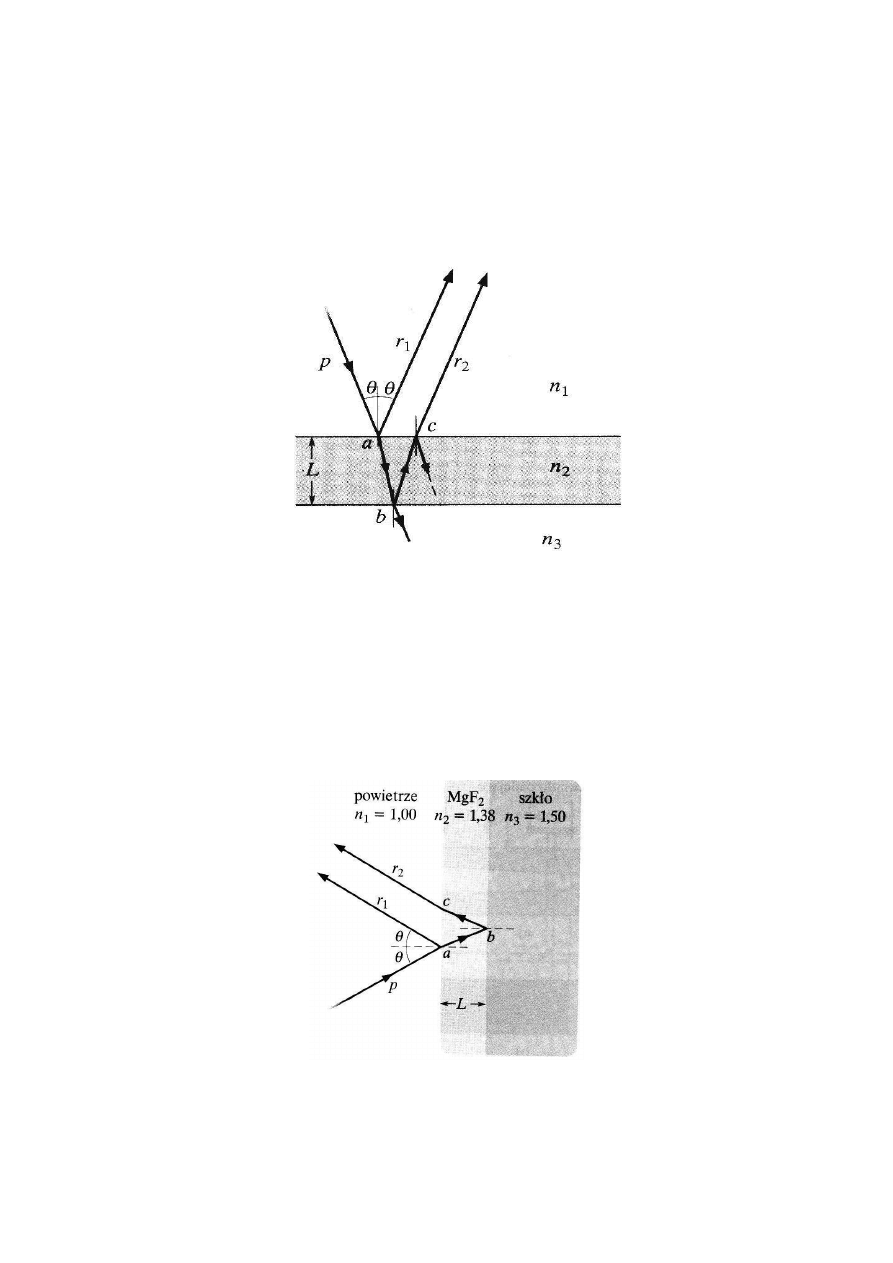
INTERFERENCJA W CIENKIEJ

WARSTWIE

ZASTOSOWANIA CIENKICH WARSTW

warstwa przeciwodblaskowa

interferencja

6

INTERFERENCJA WIELU FAL

Amplituda wypadkowa dla interferencji z N źródeł o
jednakowej amplitudzie A

0

A = A

0

{cos

ω

t + cos (

ω

t +

ϕ

1

) + cos(

ω

t +

ϕ

2

) +.....

+ cos[

ω

t +

ϕ

N

]}

Jeżeli różnice faz pomiędzy sąsiednimi falami są takie same

ϕ

n

-

ϕ

n-1

≡ ϕ

to natężenie światła

2

0

2

sin

2

sin

2

N

I

I

ϕ

ϕ

=

•

Maksima główne

ϕ

=

±

2m

π

m - liczba całkowita

A

max

= NA

0

I

max

= N

2

I

0

•

Minima

ϕ

=

±

2

π

p/N

p – dowolna liczba całkowita dodatnia, która nie jest

wielokrotnością N

interferencja

7

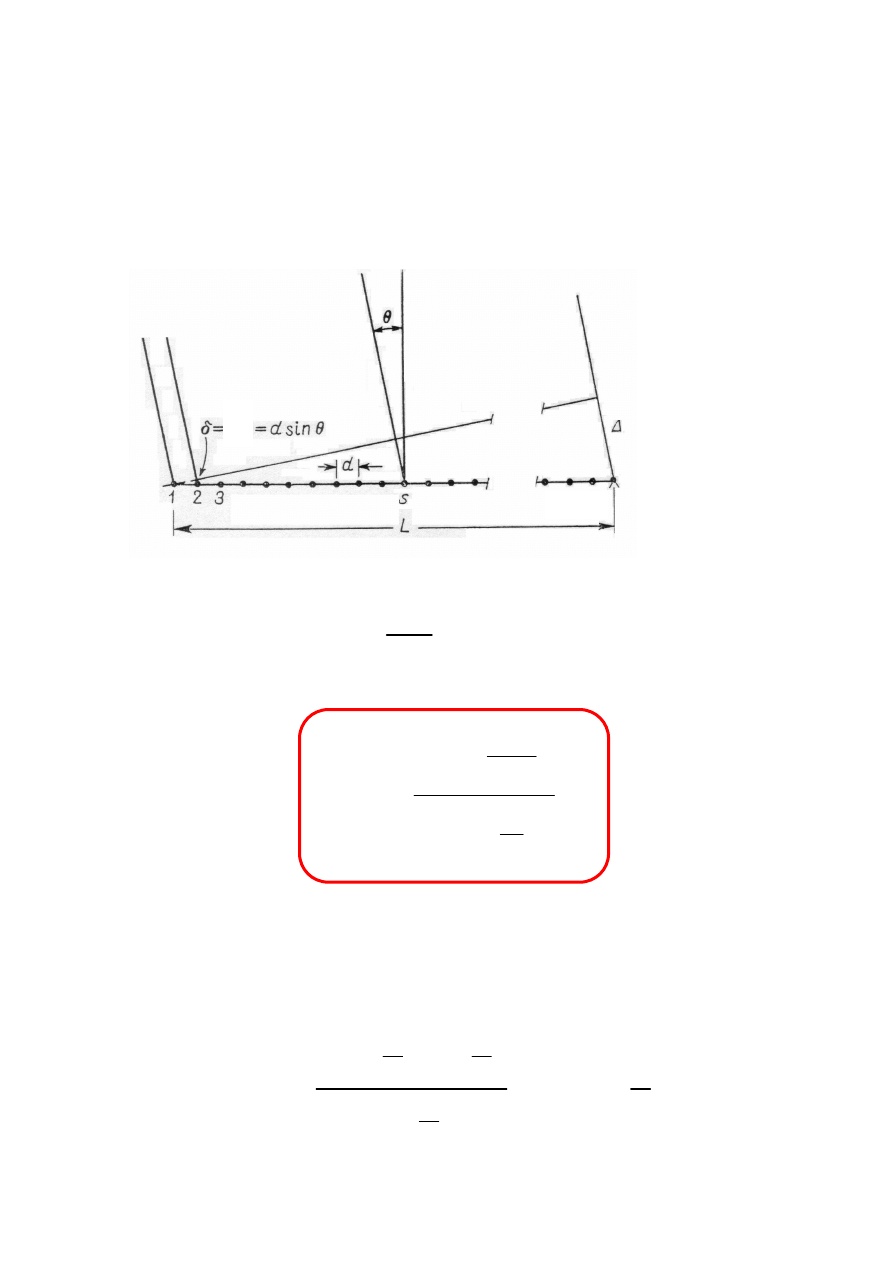
INTERFERENCJA WIELU FAL

N jednakowych źródeł punktowych rozłożonych na
odcinku o długości L

∆

l=dsin

θ

ϕ

θ

λ

π

ϕ

≡

⋅













=

∆

sin

2

0

d

2

0

2

sin

2

sin

2

N

I

I

ϕ

ϕ













=













•

dla N=1 I =I

0

•

dla N=2 sin2

α

= 2sin

α

cos

α

0

0

2 sin

cos

2

2

2

cos

2

sin

2

R

A

A

A

ϕ

ϕ

ϕ

ϕ





























=

=





















N

∆∆∆∆

/N

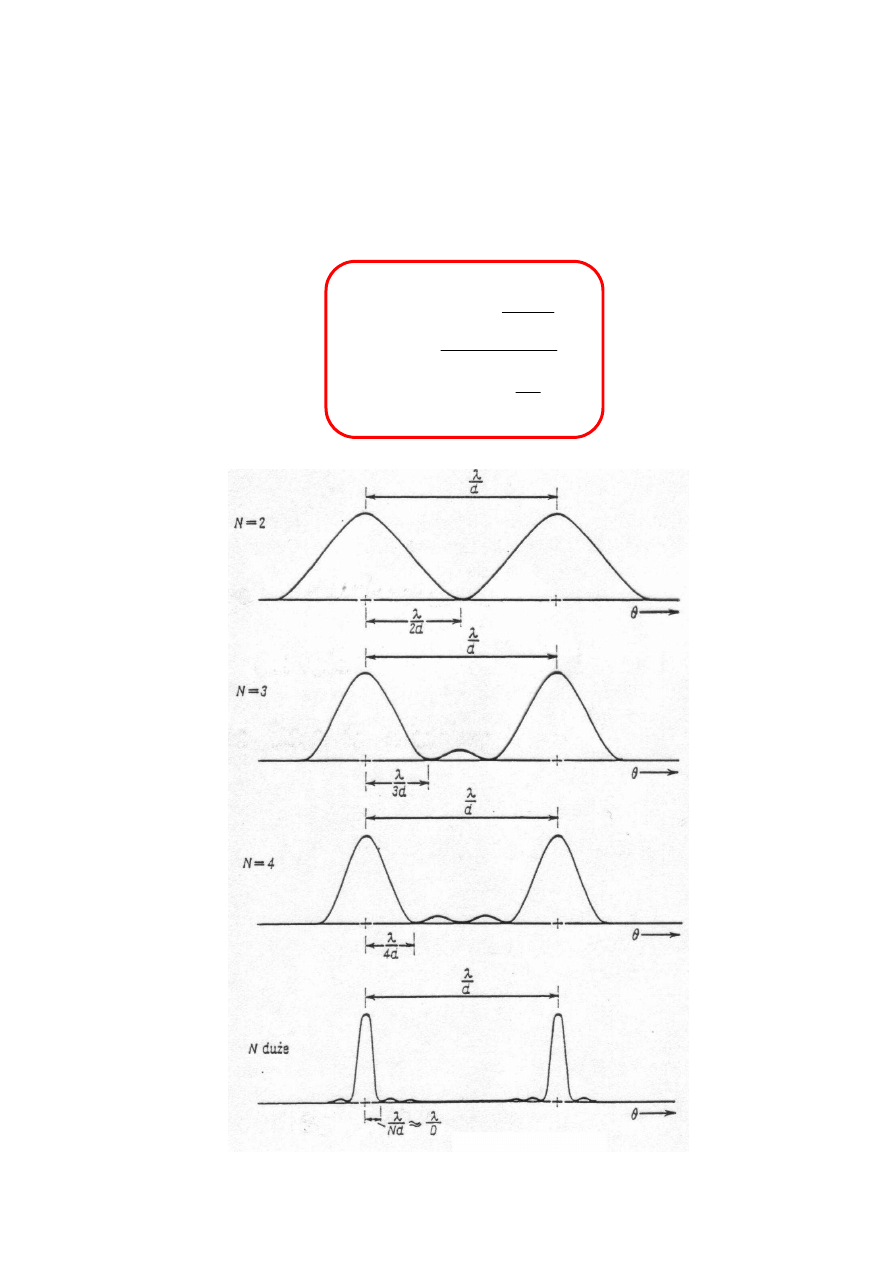
interferencja

8

UKŁAD WIELU SZCZELIN

N jednakowych źródeł:

2

0

2

sin

2

sin

2

N

I

I

ϕ

ϕ

=

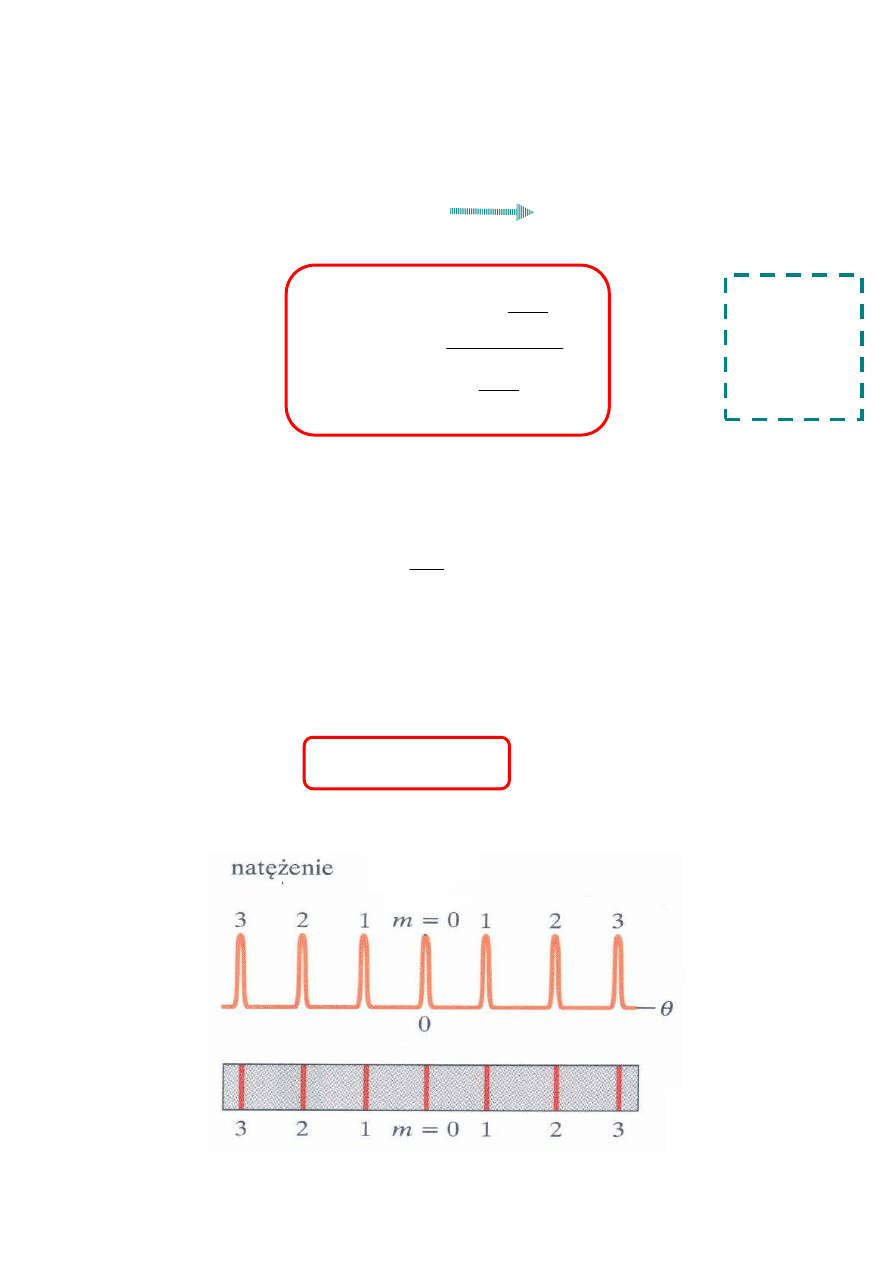
interferencja

9

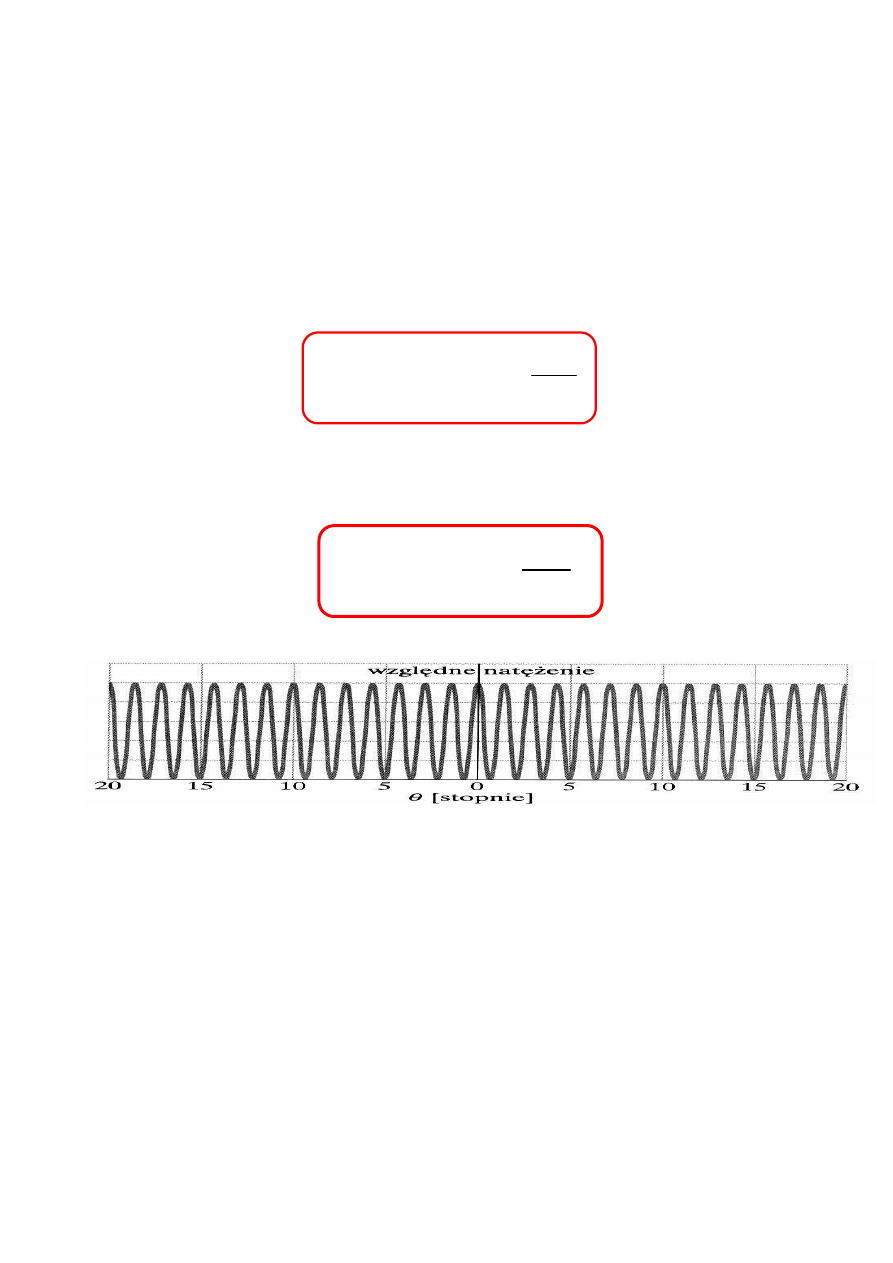
SIATKA DYFRAKCYJNA

Tysiące szczelin na milimetr bardzo małe

ϕ

2

2

0

2

sin

2

2

N

I

N I

N

ϕ

ϕ













=













Maksima główne dla

ϕ

= 2

π

m

θ

λ

π

ϕ

sin

2

d

⋅













=

Warunek występowania maksimum

λ

θ

m

d

=

sin

m – liczba całkowita

bo dla

θ

<< 1

sin

θ

≈

θ

interferencja

10

SIATKA DYFRAKCYJNA

λ

θ

m

d

=

sin

m – liczba całkowita

cz

cz

d

m

λ

θ

=

sin

f

f

d

m

λ

θ

=

sin

Jeżeli na siatkę pada światło białe, to ulega ono
rozszczepieniu. Prążek centralny jest biały, pozostałe
tworzą barwne plamy

θ

cz

>

θ

f

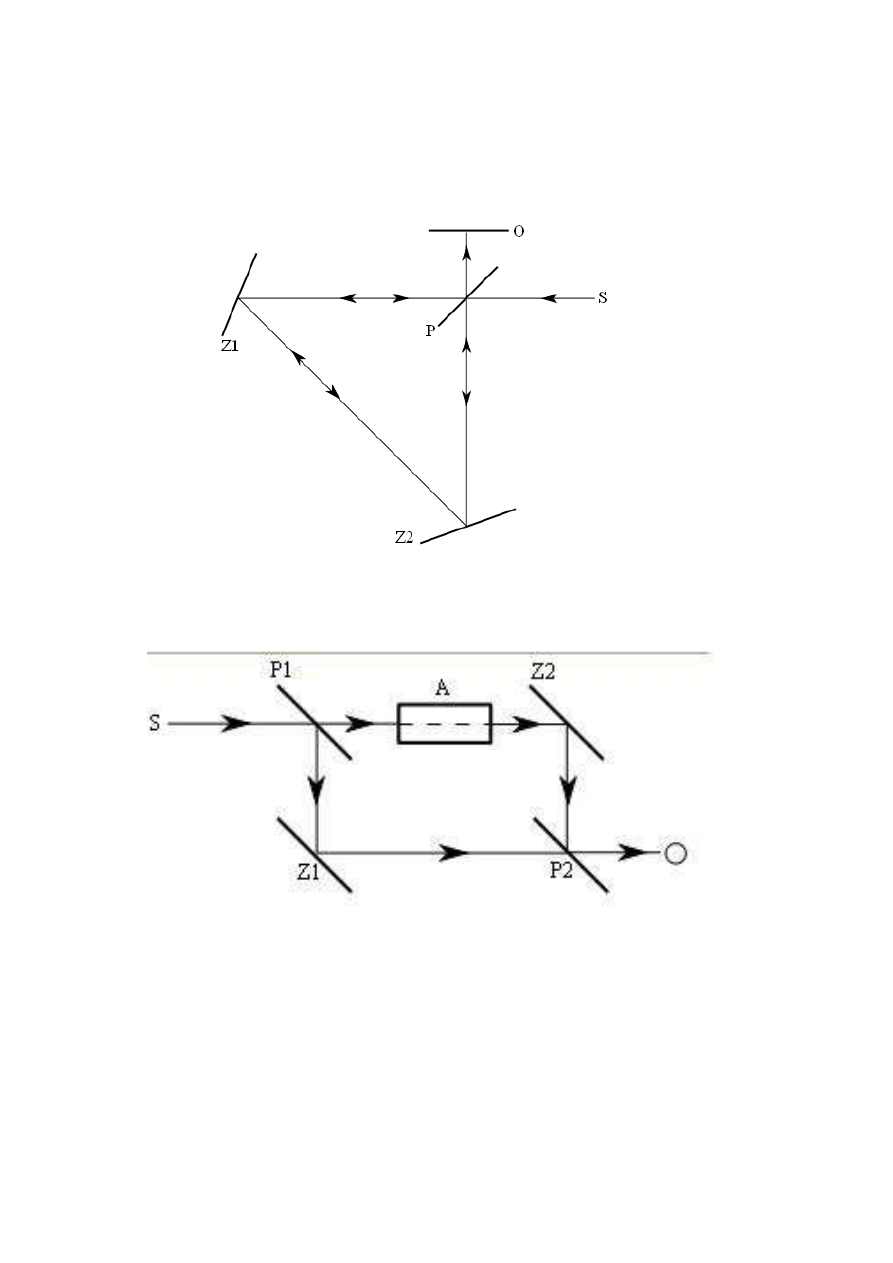
interferencja

11

INTERFEROMETRY