Politechnika Warszawska 

25

 

Wydział Fizyki                                                                                           
Laboratorium Fizyki I 
Kazimierz Blankiewicz 
 

 

BADANIE INTERFERENCJI ŚWIATŁA 

PIERŚCIENIE NEWTONA I PRĄŻKI W KLINIE POWIETRZNYM 

 

1. Podstawy fizyczne 

 
Do najbardziej charakterystycznych zjawisk ruchu falowego należy  interferencja. 

W najogólniejszym sformułowaniu, jest to efekt nakładania się fal. W wyniku tego nałożenia 
może wystąpić wzmocnienie natężenia fali wypadkowej (fale nakładają się w fazach 
zgodnych) lub osłabienie (nakładanie się fal o fazach przeciwnych). Fazą nazywamy 
argument funkcji okresowej opisującej rozchodzącą się falę. Aby można było zaobserwować 
zjawisko interferencji, nakładające się fale (o tej samej częstotliwości) muszą posiadać stałą 
w czasie  różnicę faz, tzn. być spójne. Jeśli ten warunek nie jest spełniony, to w pewnych 
chwilach czasu w danym punkcie przestrzeni fazy są zgodne, powodując wzmocnienie, a w 
innych chwilach przeciwnie, dając osłabienie. Rezultatem tych szybko zmieniających się 
wzmocnień i osłabień jest brak stałego w czasie i dającego się zaobserwować obrazu 
interferencyjnego. 

Większość  źródeł  światła nie jest spójna. Przyczyną tego jest fakt, że każdy atom 

przechodząc z wyższego poziomu energetycznego na niższy, wysyła krótki ciąg falowy, 
niezależnie od innych atomów znajdujących się w stanach wzbudzonych. Nawet światło 
wysłane przez źródło monochromatyczne (o jednej długości fali) stanowi nałożenie krótkich 
ciągów falowych wysyłanych w sposób przypadkowy (nieskorelowanych fazowo), a więc 
źródło jako całość nie jest źródłem spójnym. 

Interferencję możemy zaobserwować stosując niespójne źródło światła, jeśli potrafimy 

zapewnić spójność wzajemną interferujących promieni (promień – strumień światła o bardzo 
małym przekroju). Stosowanym sposobem jest podział promienia biegnącego ze źródła na 
dwa, z których każdy przebywa inną drogę, a następnie spowodowanie ich ponownego 
nałożenia. Formalnie można przyjąć, że te dwa promienie są wysyłane przez dwa wzajemne 
spójne  źródła. Spójność wzajemna tych promieni będzie jednak zachowana tylko wtedy, 
jeżeli różnica przebytych przez nie dróg nie będzie zbyt duża. Jeżeli ten warunek nie zostanie 
spełniony, wówczas promień, który przebył dłuższą drogę może „nie zdążyć” spotkać się ze 
swym macierzystym ciągiem falowym i spójność wzajemna nie będzie już zachowana.  
 
1. Matematyczny opis interferencji. 

W rozdziale tym omówimy warunki otrzymania trwałego obrazu interferencyjnego. 

Rozważania przeprowadzone będą dla układów: soczewka wraz z płytką szklaną (powstały 
obraz nazywamy pierścieniami Newtona) i dwie płytki szklane ustawione wzajemnie pod 
niewielkim kątem tworzące klin powietrzny. Ogólnie można powiedzieć,  że trwały obraz 
interferencyjny  w takich układach otrzymujemy wtedy, kiedy różnica faz fal o tej samej 
częstotliwości będzie stała w każdej chwili obserwacji zjawiska. 

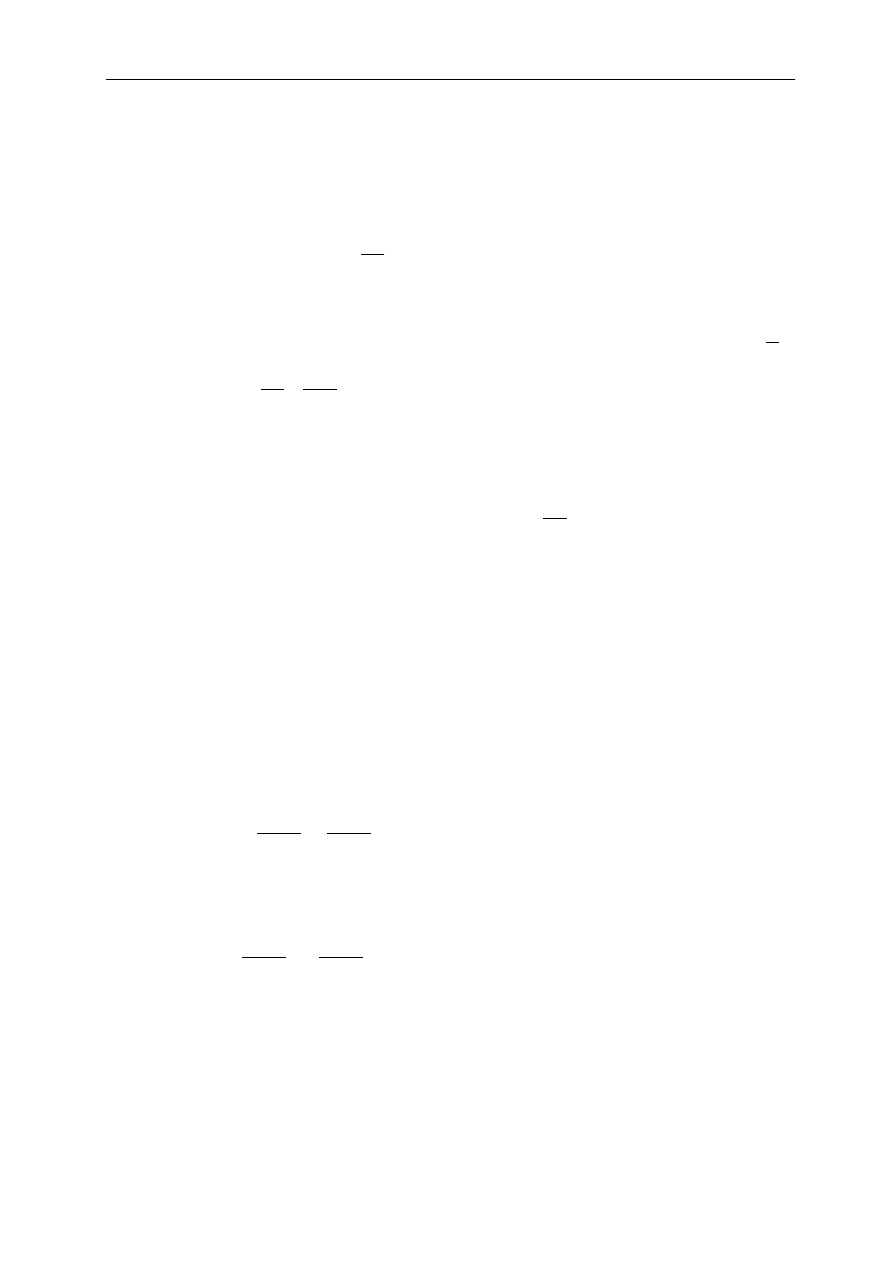
Badanie interferencji światła. Pierścienie Newtona i prążki w klinie powietrznym 

 

2

Załóżmy, że dwie płaskie, harmoniczne fale elektromagnetyczne 1 i 2 (posiadające 

identyczną częstotliwość ω i ten sam kierunek polaryzacji liniowej) rozchodzą się w kierunku 
dodatniego zwrotu osi x. Fale te są opisywane przez wartości natężeń ich pól elektrycznych 
E  i E . 

1

2

Niech fala 2 przebywa dodatkową drogę Δ. Wówczas propagacja fal 1 i 2 może być 

opisana przez wyrażenia: E

1 

= E

01

sin(ωt – kx) oraz E  = E

2

02

sin[ωt – k(x+Δ)] gdzie E i E

01 

02

 

oznaczają amplitudy fal 1 i 2, 

λ

π

2

=

k

  jest liczbą falową a λ – długością fali (w powietrzu). 

Gdy fala 2 przebywa dodatkową drogę Δ w innym ośrodku niż powietrze, wówczas zmienia 
się  długość fali w tym ośrodku, a w konsekwencji i liczba falowa k. Jeżeli współczynnik 

załamania na tym odcinku drogi jest równy n, to długość fali zmaleje do wartości 

n

λ

λ

=

1

, 

a liczba falowa 

λ

π

λ

π

n

k

2

2

1

1

=

=

 wzrośnie i wyniesie nk. Wyrażenie opisujące falę 2 dla tego 

przypadku przyjmie postać: E  = E

2

02

sin(ωt – kx – knΔ ). 

Występujący w argumencie funkcji sinus, iloczyn nΔ – nosi nazwę różnicy dróg optycznych 
(droga optyczna = współczynnik załamania razy droga geometryczna)

. Natomiast iloczyn 

kn

Δ, charakteryzujący zmianę fazy spowodowaną przebyciem dodatkowej drogi optycznej, 

nazywany jest kątem przesunięcia fazowego φ (

Δ

=

Δ

=

n

kn

λ

π

ϕ

2

). 

Policzmy teraz jaki będzie wynik nałożenia się fal 1 i 2. 
 

 + E  = E

E = E

1

2

01

sin(ωt – kx) + E

02

sin(ωt – kx – φ)  

 

 

 

(1a) 

 

Detektory fal elektromagnetycznych (w tym nasze oczy) reagują na natężenie fali I, 

tj. średnią ilość energii padającej na jednostkową powierzchnię w jednostce czasu. 
Energia przenoszona przez falę jest proporcjonalna do kwadratu natężenia pola elektrycznego. 
Dla rozpatrywanego nas przypadku (patrz (1a)) energia będzie więc proporcjonalna do: 
 

E

2

2

 = (E  + E )  =  

1

2

= E

01

2

sin

2

(ωt-kx) + E

02

2

sin

2

(ωt-kx-φ) + 2E

01

E

02

sin(ωt-kx)sin(ωt-kx-φ)  

(1b) 

 

 
Zgodnie ze znanym wzorem trygonometrycznym możemy napisać: 

2

sin

2

sin

2

cos

cos

α

β

β

α

β

α

−

+

=

−

, a ostatni człon wyrażenia na E

2

 możemy przekształcić 

do postaci następującej:  
 

2E

01

E

02

sin(ωt-kx)sin(ωt-kx-φ) = E E {cos(φ) – cos[2(ωt-kx)-φ]} 

01 02

      ←–→       ←––→                        ↔        ←–

−−−−→         

2

β

α

+

2

α

β

−

      

                          

      

α                  

β

   

 
Biorąc pod uwagę ostatni wynik, E

2

możemy wyrazić jako: 

 

E

2

=E

01

2

sin

2

(ωt-kx)+E

02

2

sin

2

(ωt-kx-φ)+E

01

E

02

{cosφ-cos[2(ωt-kx)-φ]}  

(2) 

 
Z równania (2) wynika, że energia przenoszona przez falę zależy od czasu. Jednakże detektor 
rejestruje nie chwilową wartość natężenia fali, ale średnią w czasie wartość strumienia 
energii. Dla rozpatrywanego tu rodzaju fal, można tę średnią policzyć według wzoru:  

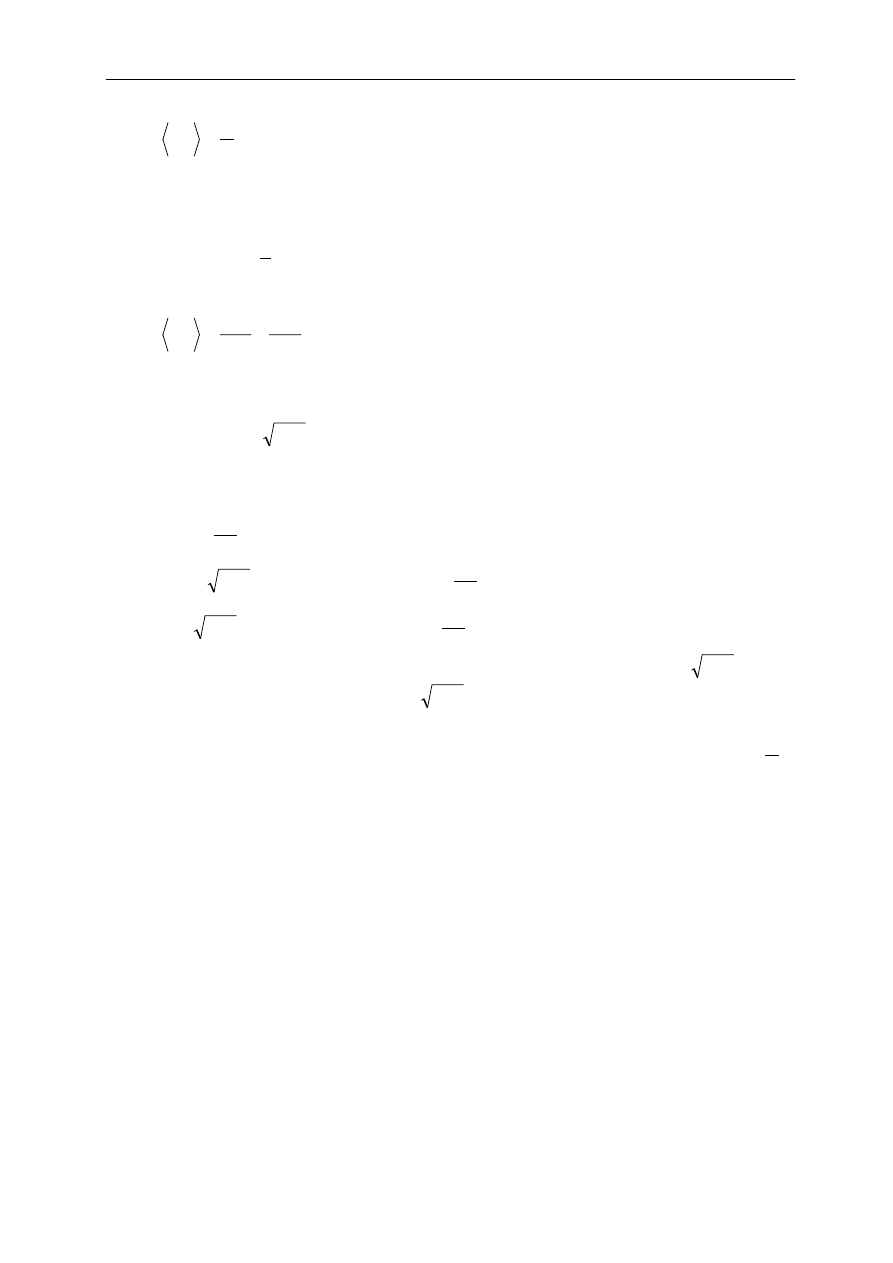
Badanie interferencji światła. Pierścienie Newtona i prążki w klinie powietrznym 

 

3

dt

E

T

E

T

∫

=

0

2

2

1

  

 

 

 

 

 

 

 

 

(3) 

 
Jak wynika z (2) i (3), znalezienie <E

2

> sprowadza się do policzenia średnich wartości  

w okresie funkcji typu sin

2

(ωt + δ) i cos(2ωt + γ). Uśrednienie pierwszej z wymienionych 

funkcji daje wartość 

2

1

 a drugiej 0. Stąd otrzymujemy: 

 

ϕ

cos

2

2

02

01

2

02

2

01

2

E

E

E

E

E

+

+

=

,  

 

 

 

 

 

(4) 

 
czyli: 
 

2

1

2

I

I

I = I

!

 + I  + 

cosφ 

 

 

 

 

 

 

 

 (5) 

2

 
Pierwszy wyraz prawej strony wyrażenia (5) (tj. I

1

) jest natężeniem fali 1, drugi natężeniem 

fali 2, natomiast trzeci opisuje efekt interferencji fali 1 i 2. W zależności od kąta przesunięcia 

fazowego 

Δ

=

n

λ

π

ϕ

2

, wartość tego wyrazu zmienia się w granicach: 

π

λ

π

ϕ

)

1

2

(

2

+

=

Δ

=

m

n

2

1

2

I

I

−

od 

 (wtedy cosφ = -1,    a  

 gdzie m = 0,1,2,... 

do 

2

1

2

I

I

 (wówczas cos

1

=

ϕ

 a  

).

2

2

π

λ

π

ϕ

m

n

=

Δ

=

 

)

2

(

2

1

2

1

I

I

I

I

I

−

+

=

W pierwszym przypadku wystąpi osłabienie natężenia 

, a w 

drugim - jego wzmocnienie 

).

2

(

2

1

2

1

I

I

I

I

I

+

+

=

 Warunek na osłabienie (lub wzmocnienie) 

natężenia najwygodniej jest formułować w odniesieniu do różnicy dróg optycznych nΔ. 

Z powyższych rozważań wynika, że  osłabienie otrzymamy, gdy 

(

)

2

1

2

λ

+

=

Δ

m

n

, 

a wzmocnienie – kiedy nΔ = mλ.

 

 = I  = I

Rozpatrzmy przypadek szczególny, gdy I

1

2

0

. Po podstawieniu tych wartości do 

(5) otrzymamy: I = 2I  + 2I cosφ. Dla wzmocnienia (tj. gdy cosφ = 1) I = 4I

0

0

0

 . Oznacza to, 

że przy nałożeniu fal 1 i 2 wypadkowe natężenie jest aż cztery razy większe od natężenia fali 
składowej, a nie dwa razy jak tego należałoby oczekiwać. Czyżby zasada zachowania energii 
przestała tu obowiązywać? To pozorne naruszenie zasady zachowania energii łatwo 
wyjaśnimy jeżeli zwrócimy uwagę na fakt, że oprócz miejsc gdzie występuje wzmocnienie, 
dla których I = 4I

0

, istnieją takie obszary, gdzie otrzymujemy I = 0 a więc wygaszanie. 

Spotkamy się tu nie z naruszeniem zasady zachowania energii, a tylko z redystrybucją energii 
w przestrzeni. W powyższych rozważaniach przesunięcie fazy było spowodowane 
przebyciem dodatkowej drogi Δ. Nie jest to jedyna przyczyna zmieniająca fazę. Odbicie 
światła w zależności od rodzaju powierzchni odbijającej i kąta padania, może również 
zmienić fazę (w sposób skokowy). I tak na przykład odbicie światła od ośrodka gęstszego 
optycznie i będącego izolatorem powoduje przesunięcie fazy fali o 180

o

. 

Badanie interferencji światła. Pierścienie Newtona i prążki w klinie powietrznym 

 

4

2. Opis ćwiczenia 

 
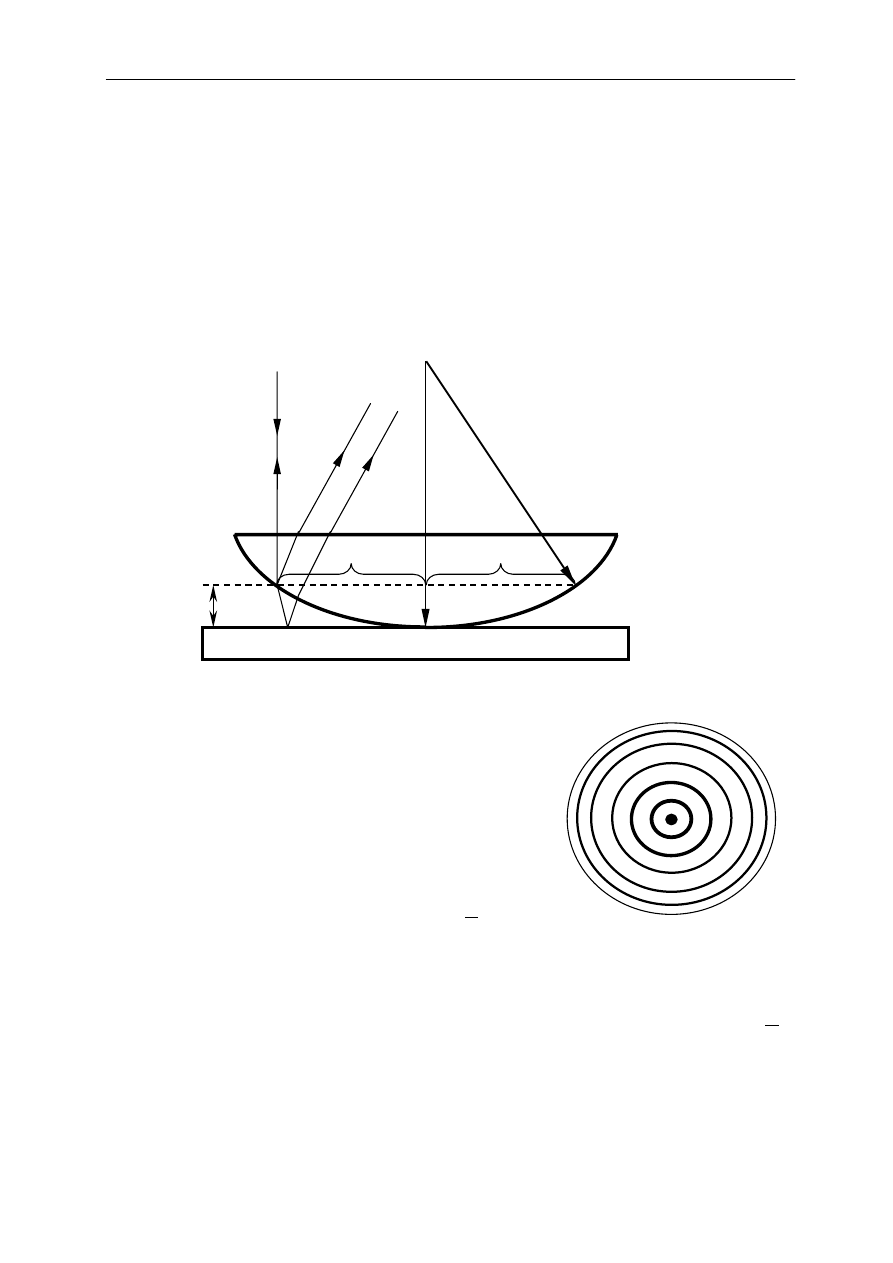
Połóżmy na płaską  płytkę szklaną soczewkę  płasko-wypukłą o dużym promieniu 

krzywizny tak, aby strona wypukła dotykała płytki (rys.1a). Pomiędzy soczewką a płytką 
utworzy się szczelina powietrza o zmiennej grubości. Oświetlmy teraz ten układ  światłem 
monochromatycznym o długości fali λ biegnącym prostopadle do powierzchni płytki. 
Promienie odbite od wypukłej strony soczewki (1’) będą mogły interferować z promieniami 
odbitymi od górnej powierzchni płytki (1”) gdyż  są wzajemnie spójne jako pochodzące 
z podziału tego samego promienia macierzystego (1) a różnica dróg optycznych między nimi 
nie jest duża (∆ <100λ). Inne promienie nie spełniają tych warunków. 
 

 

e 

r

m 

r

m

A

 

B

 

 O

R

R

1 

1' 1''

płytka szklana

soczewka

 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 

Rys.1a. Bieg promieni przy powstawaniu pierścieni Newtona: 

1   - promień macierzysty 

1'  - promień odbity od wypukłej strony soczewki 
1'' - promień odbity od górnej powierzchni płytki 
R - promień krzywizny soczewki 
r

m

 - promień pierścienia Newtona rzędu m 

 
 

Zgodnie z wcześniej przedstawionymi rozważaniami 

wzmocnienie nastąpi gdy: nΔ = mλ  (m=0,1,2,3...)  

a osłabienie (wygaszenie) jeżeli: 

2

)

1

2

(

λ

+

=

Δ

m

n

. Różnicę 

dróg optycznych nΔ w naszym przypadku (rys.1a) stanowi 
odcinek 2e (gdyż n=1 a światło przebywa odcinek e 
dwukrotnie).  Ze względu na zmianę fazy na przeciwną 

przy odbiciu od środka optycznie gęstszego

, należy jeszcze do 2e dodać 

Rys.1b Obraz pierścieni 
Newtona w mikroskopie.

 

2

λ

. 

Eksperymentalnym potwierdzeniem wspomnianego skoku fazy jest powstanie ciemnego 
krążka w punkcie styku soczewki z płytką (prążek zerowego rzędu). Po uwzględnieniu 

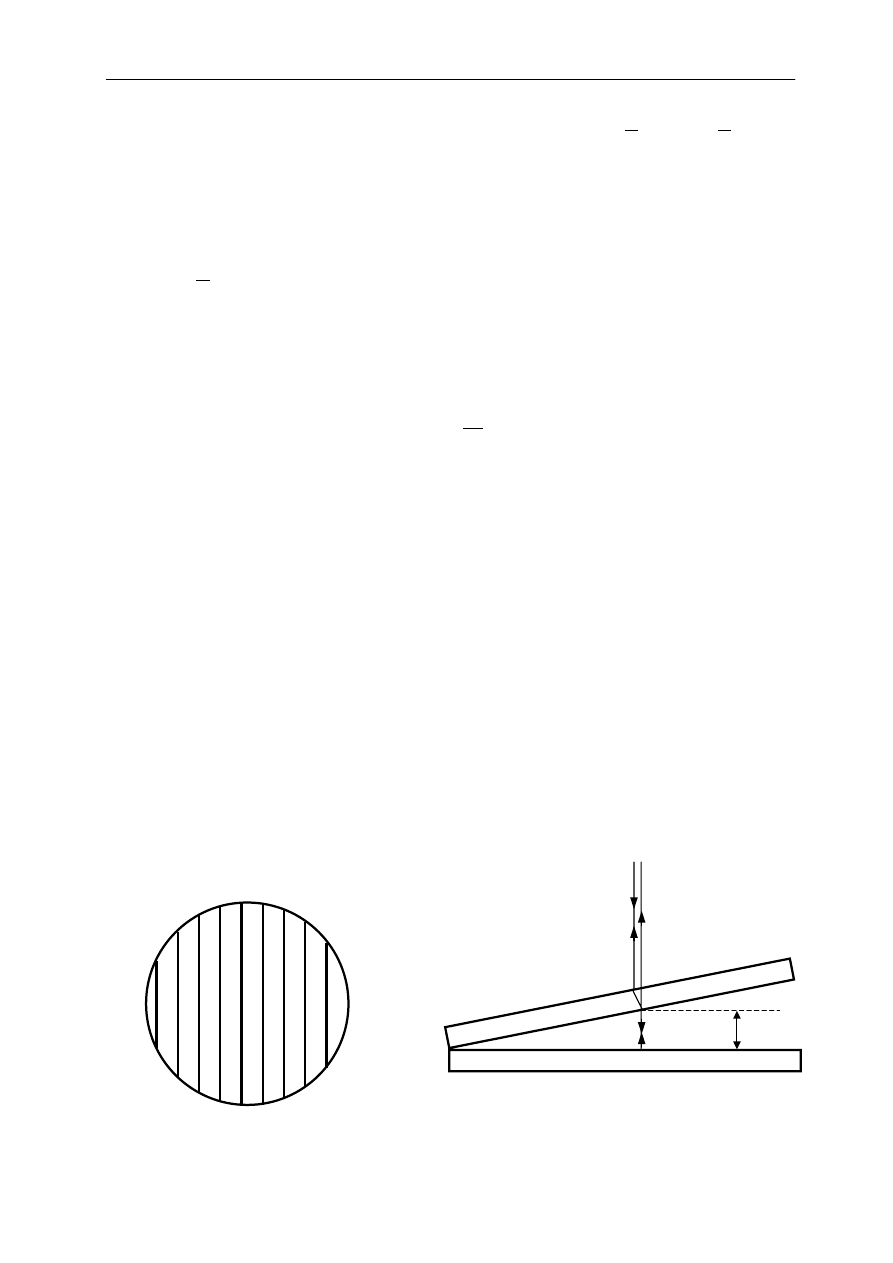
Badanie interferencji światła. Pierścienie Newtona i prążki w klinie powietrznym 

 

5

2

)

1

2

(

2

2

λ

λ

+

=

+

m

e

powyższych uwag warunek na wygaszenie przybierze postać 

, a po 

przekształceniu:  

 
2e = mλ . 

 

 

 

 

 

 

 

 

 

 (6a)  

 
Wzmocnienie otrzymujemy gdy: 

λ

λ

m

e

=

+

2

2

   

 

 

 

 

 

 

 

 

(6b)  

 

Powiążemy teraz e z innymi parametrami, które można stosunkowo łatwo zmierzyć. 

Z trójkąta AOB (rys.1a) mamy związek: 

. Po podniesieniu do kwadratu 

dostajemy: 

. Ponieważ e<<R, to wyraz z e

2

2

2

)

(

e

R

r

R

m

−

+

=

2 

2

2

2

2

Re

2

e

R

r

R

m

+

−

+

=

można pominąć. Po 

wykonaniu redukcji dostajemy ostatecznie: 

R

r

e

m

2

2

=

. Po podstawieniu tego wyrażenia do (6a) 

otrzymujemy związek  łączący promień pierścienia Newtona r

m

 rzędu  m, z promieniem 

krzywizny soczewki R, długością fali λ i rzędem interferencji m: 
 

m

R

r

m

λ

=

2

. 

 

 

 

 

 

 

 

 

 

(7)  

 

Należy zwrócić uwagę,  że związek (7) słuszny jest dla prążków ciemnych, 

w przypadku obserwacji promieni odbitych od układu soczewki i płytki. 

Jeżeli różnica dróg optycznych będzie powstawać nie w przestrzeni pomiędzy 

płaszczyzną a wypukłą stroną soczewki tylko w klinie powietrznym, powstałym przy 
nachyleniu pod małym kątem dwóch podstawowych szkiełek mikroskopowych, to wówczas, 
w polu widzenia (w mikroskopie) zobaczymy ciemne prążki (patrz rys.2). Oznacza to, 
że grubość klina w miejscu powstania danego prążka spełnia warunek zgodny z (6a): 

 
2e = mλ , 

 

 

 

 

 

 

 

 

 

(8)  

 
gdzie 2e jest podwojoną grubością klina (światło biegnie tam i z powrotem – patrz rys.3). 
Grubości klina odpowiadające dwóm kolejnym prążkom, będą się różnić o pół długości fali 
(porównaj wzór (8)). 
 
 

e

1

1''

1' 

1'' 

Rys.3 
Bieg promieni w klinie powietrznym. 

 

Rys.2 
Prążki interferencyjne w klinie powietrznym. 

Badanie interferencji światła. Pierścienie Newtona i prążki w klinie powietrznym 

 

6

 

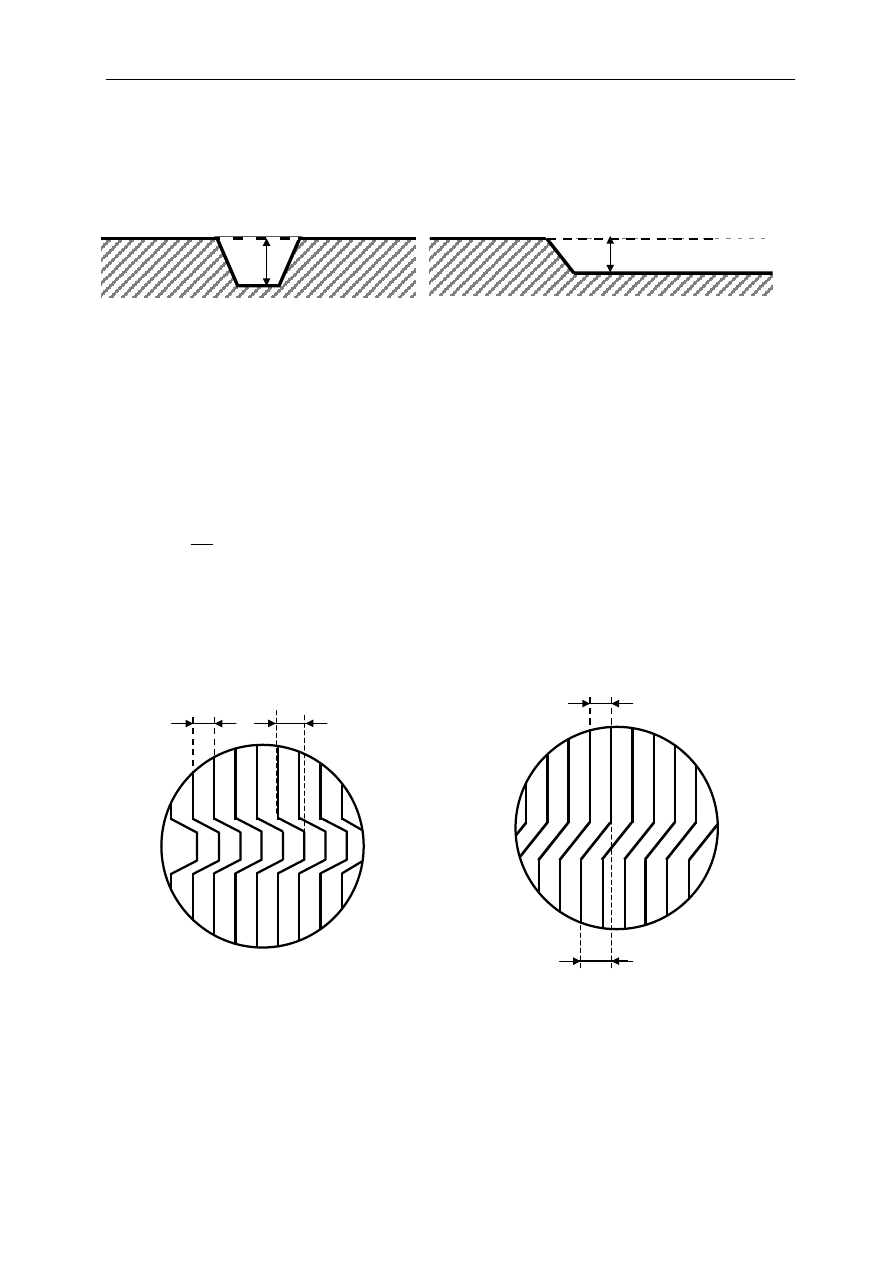
Gdy jedna z powierzchni tworzących klin nie będzie płaszczyzną, a będzie zawierać 

np. rowek o głębokości h (rys.4a), to wtedy obraz prążków ulegnie zmianie i będzie taki jak 
na rys.4b. Oczywiście zawsze ten sam prążek, niezależnie od kształtu, będzie łączył miejsce 
o tej samej grubości klina. Dlatego prążki te noszą nazwę prążków jednakowej grubości.  

 
 
 
 
 
 
 
 
 

h

Rys.4a 
Powierzchnia odbijająca klina 
posiadająca rowek. 

Rys.5a 
Powierzchnia odbijająca klina z uskokiem. 

h 

 
Na podstawie przesunięcia prążka, można wyznaczyć  głębokość rowka. 

Uwzględniając, że wzrost grubości klina o pół długości fali, daje przesunięcie prążka w polu 
widzenia o d, to przesunięcie prążka o x, musi być spowodowane głębokością rowka h, 
zgodnie z równaniem wynikającym z proporcji:  

 

x

d

h

2

λ

=

 

 

 

 

 

 

 

 

 

 

(9)  

 

Efekt przesunięcia prążków może być spowodowany również obecnością uskoku na 

powierzchni odbijającej (rys.5a i 5b). Analizując kierunek przesunięcia prążków można 
ustalić co spowodowało przesunięcie: wgłębienie czy wypukłość, obecne na powierzchni 
odbijającej. Każdy z tych przypadków daje inny (przeciwny) kierunek przesunięcia. 
 

x

d

 

d 

x 

 
 
 
 
 
 
 
 
 
 
 
 
 

Rys.4b 

Rys.5b 

 

Prążki interferencyjne powierzchni  
z rowkiem. 

 

Prążki interferencyjne powierzchni 
 z uskokiem. 

 
 
Przy ustalaniu co spowodowało przesunięcie prążków, wgłębienie czy wypukłość, należy 
wziąć pod uwagę zarówno kierunek klina jak i odwracanie obrazu w mikroskopie użytym 
do obserwacji. 

Badanie interferencji światła. Pierścienie Newtona i prążki w klinie powietrznym 

 

7

3. Wykonanie ćwiczenia 

 

1. Włączyć monochromatyczne źródło światła o znanej długości fali λ. 
2. Połączyć na stoliku krzyżowym płytkę  płasko-równoległą z soczewką i znaleźć ostry 

obraz pierścieni Newtona. 

3. Zmierzyć promienie 10-ciu pierścieni Newtona, r

m

, notując ich rząd interferencji m. 

4.  Z dwóch mikroskopowych szkiełek podstawowych, z których jedno posiada rowek, 

wypukłość lub uskok, sporządzić klin o małym kącie rozwarcia, wkładając na jednym 
końcu kawałek włosa pomiędzy szkiełka lub stosując nacisk na położone na siebie 
szkiełka. 

5. Zaobserwować obraz prążków interferencyjnych i ich przesunięcie w obrębie rowka, 

wypukłości lub uskoku. Obraz prążków korygujemy dociskiem szkiełek. 

6. Po ustaleniu rodzaju deformacji powierzchni odbijającej (rowek czy wzniesienie), 

zmierzyć przesunięcie prążków x i odległość pomiędzy nimi d. Oszacować błędy Δd i Δx. 

7. Używając  źródeł  światła o nieznanej długości fali zmierzyć promienie 10-ciu pierścieni 

Newtona r

m

 (notując m). 

 

4. Opracowanie wyników 

 

1. Sporządzić wykres zależności 

 w funkcji λm dla światła o znanej długości fali.  

2

m

r

2. Stosując metodę najmniejszej sumy kwadratów do wzoru (7), kładąc: 

 oraz x = λm, 

obliczyć R oraz ΔR. 

2

m

r

y

=

3. Sporządzić wykres zależności 

 od Rm (gdzie R - promień krzywizny wyznaczony  

w punkcie 2) dla źródła o nieznanej długości fali oraz stosując metodę najmniejszej sumy 
kwadratów znaleźć nieznaną długość fali λ i jej błąd Δλ.  

2

m

r

4. Na podstawie wzoru (9) wyznaczyć  głębokość rowka (uskoku) h lub wysokość 

wzniesienia oraz obliczyć Δh stosując metodę różniczki zupełnej. 

5. Przeprowadzić dyskusję otrzymanych rezultatów. 
 

5. Pytania kontrolne 

 

1. Jakie warunki muszą być spełnione, aby można było zaobserwować zjawisko 

interferencji? 

2. Jak uzyskać wzajemną spójność promieni? 
3. Jak obliczyć wypadkowe natężenie interferujących fal? 
4. Jakie są warunki uzyskania wzmocnienia (osłabienia) natężenia fali wypadkowej 

w zjawisku interferencji? 

5. Jak otrzymać obraz pierścieni Newtona (ich opis matematyczny)? 
6. Jak wyznaczyć głębokość rowka (wysokość wypukłości)? 
 

6. Literatura 

 

1.  Sz. Szczeniowski, Fizyka Doświadczalna, część IV Optyka, PWN Warszawa 1971, 

str.275 

2.  D. Halliday, R. Resnick, Fizyka, t. 2, PWN Warszawa 1984, str. 418 – 428, 493 - 500