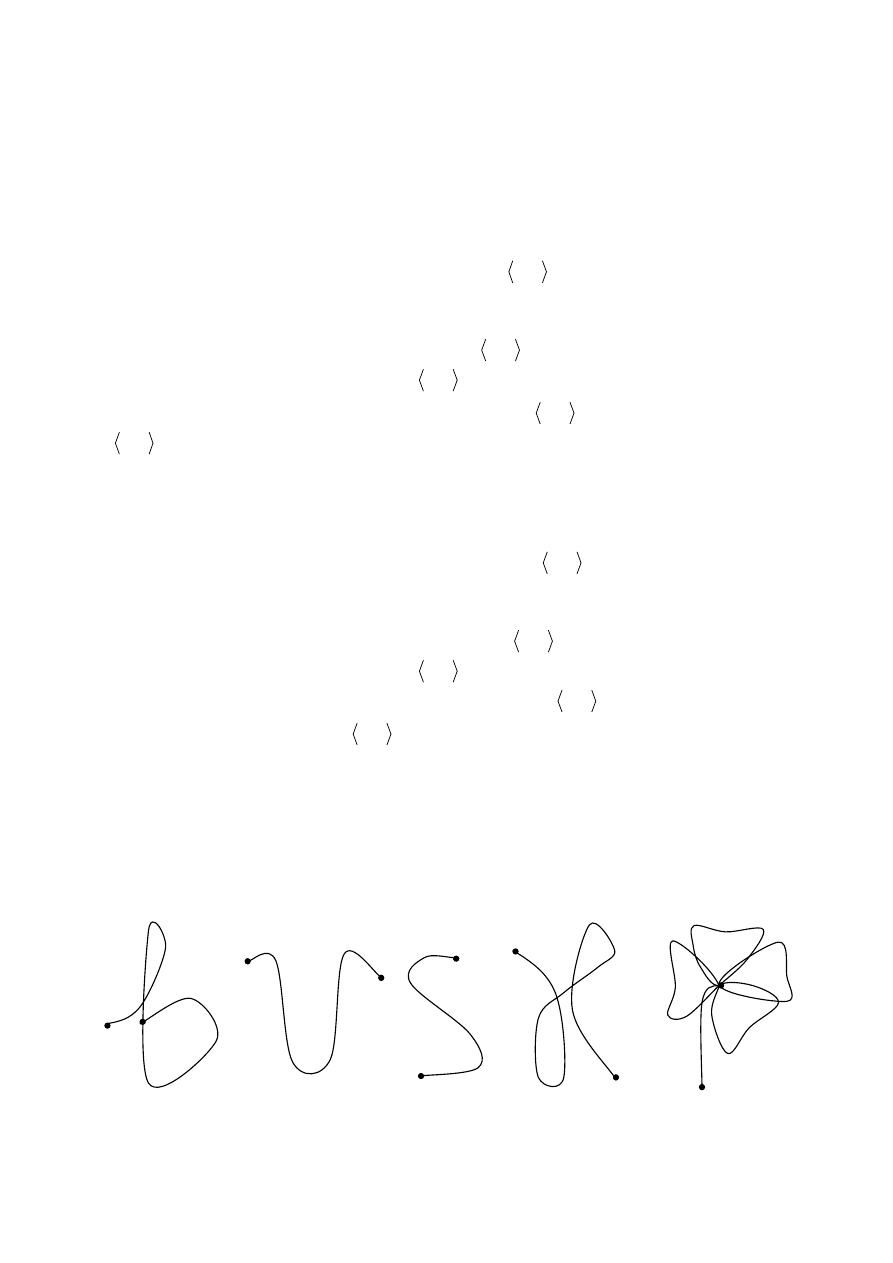
264
WYKŁAD Nr 21
CAŁKI KRZYWOLINIOWE
A) POJĘCIA WSTĘPNE
Def.1.1. (łuk regularny (gładki) na płaszczyźnie)
Łukiem regularnym (gładkim)
na płaszczyźnie nazywamy krzywą o równaniach:
β
α
∈
=
=
,
)
(
),
(
t
t
y
y
t
x
x
spełniającą następujące warunki:
1.
funkcje
)
(
),
(
t
y
t
x
mają ciągłe pochodne w przedziale
β
α,
;
2.
różnym wartościom parametru t z przedziału
β
α,
odpowiadają różne punkty krzywej;
3.
pierwsze pochodne
)
(
),
(
t
y
t
x
′
′
nie znikają jednocześnie w
β
α,
tzn.
[
]
[
]
0
)
(
)
(
2
2
>
′
+
′
t
y
t
x
, gdzie
β
α
∈
,
t
Def.1.2. (łuk regularny (gładki) w przestrzeni)
Łukiem regularnym (gładkim)
w przestrzeni nazywamy krzywą o równaniach:
β
α
∈
=
=
=
,
)
(
),
(
),
(
t
t
z
z
t
y
y
t
x
x
spełniającą następujące warunki:
1.
funkcje
)
(
),
(
),
(
t
z
t
y
t
x
mają ciągłe pochodne w przedziale
β
α,
;
2.
różnym wartościom parametru t z przedziału
β
α,
odpowiadają różne punkty krzywej;
3.
pierwsze pochodne
)
(
),
(
),
(
t
z
t
y
t
x
′
′
′
nie znikają jednocześnie w
β
α,
tzn.
[
]
[
]
[
]
0
)
(
)
(
)
(
2
2
2
>
′
+
′
+
′
t
z
t
y
t
x
,
β
α
∈
,
t
Geometrycznie rzecz biorąc, łuk regularny (gładki) nie przecina się sam z sobą i ma w każdym punkcie
styczną zmieniającą się w sposób ciągły wraz ze zmianą punktu na krzywej.
Uwaga
: Mówiąc obrazowo, łuk gładki (regularny) to taka krzywa, którą można wykreślić bez odrywania
ręki od kartki oraz bez wracania do wcześniej już wykreślonych punktów (patrz Rys.1.) Krzywe b), c) są
łukami gładkimi, natomiast pozostałe nimi nie są.
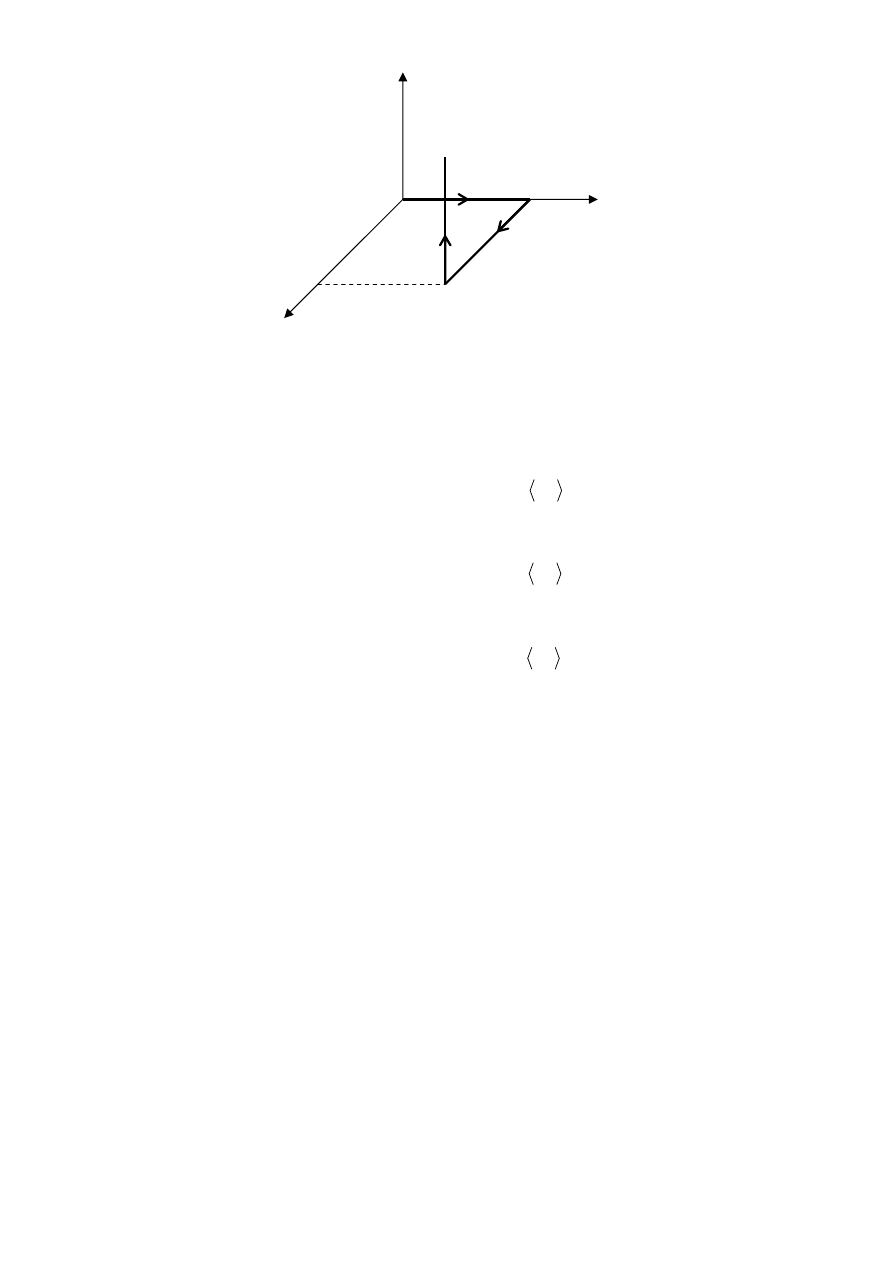
a)
b)
c)
d)
e)
Rys.1
265
Def.1.3. (krzywa regularna)
Krzywą, która daje się podzielić na skończoną ilość łuków regularnych nazywamy krzywą regularną.
Def.1.4. (łuk skierowany)
Łuk L, w którym wyróżniono początek i koniec nazywamy łukiem skierowanym.
Jeśli punkt płaszczyzny
(
)
)
(
),
(
α
α y
x
A
jest początkiem łuku, natomiast punkt
(
)
)
(
),
(
β
β y
x
B
jest końcem
łuku L, to ten łuk oznaczamy przez AB . W przeciwnym przypadku tj., gdy
(
)
)
(
),
(
β
β y
x
B
jest
początkiem, a
(
)
)
(
),
(
α
α y
x
A
końcem – przez BA .
Mówimy, że łuki AB i BA są przeciwnie skierowane.
Analogicznie definiujemy łuk skierowany w przestrzeni. Wówczas punkty A i B mają następujące
współrzędne:
(
)
)
(
),
(
),
(
α
α
α
z
y
x
A
,
(
)
)
(
),
(
),
(
β
β
β
z
y
x
B
.
Def.1.5. (krzywa zamknięta)
Krzywą L nazywamy krzywą zamkniętą, jeśli jej początek pokrywa się z końcem.
Przykłady:
a) Krzywa o równaniach
π
∈
=
=
2
,
0
,
sin
,
cos
t
t
r
y
t
r
x
jest krzywą regularną zamkniętą na
płaszczyźnie. Jest to równanie okręgu o środku w punkcie
(
)
0
,
0
i promieniu r.
b) Linia śrubowa o równaniach:
π
∈
=
=
=
2
,
0
,
,
sin
,
cos
t
ct
z
t
r
y
t
r
x
jest łukiem gładkim w
przestrzeni.
B) CAŁKI KRZYWOLINIOWE NIESKIEROWANE NA PŁASZCZYŹNIE I W PRZESTRZENI
Niech K będzie krzywą regularną na płaszczyźnie OXY,
)
,
( y
x
f
będzie funkcją określoną oraz
ograniczoną wzdłuż punktów tej krzywej.
Krzywą K dzielimy punktami:
B
A
A
A
A
n
=
=
,
...
,
,
1
0
na n dowolnych łuków
n
l
l
l
,
...
,
,
2
1
. Długości tych
łuków częściowych oznaczamy odpowiednio:
n
l
l
l
∆
∆
∆
,
...
,
,
2
1
, przy czym
[
]
[
]
k
k
t
t
k
t
t
dt
t
y
t
x
l
k
k
,
)
(
)
(
1
2
2
1
−
∫
−
′
+
′
=
∆
Na każdym łuku częściowym
)
,
...
,
2
,
1
(
n
k
l
k
=
obieramy dowolny punkt
(
)
k
k
k
y
x
P
,
(Rys.2).
Rys.2
0
A
A
=
1
A
2
A
1
−
k
A
k
A
n
A
B
=
x
y
(
)
k
k
k
y
x
P
,

266
Tworzymy następującą sumę:
( )
∑
=
∆
⋅
=
n
k
k
k
n
l
P
f
S
1
Niech
k
n
k
n
l
∆
=
δ
≤
≤
1
max
. Ciąg podziałów, przy którym średnica
0
→
δ
n
, gdy
∞
→
n
, nazywamy ciągiem
normalnym podziałów
.
Def.1.6. (całka krzywoliniowa na płaszczyźnie)
Jeśli dla każdego normalnego ciągu podziałów krzywej K odpowiadający ciąg sum
n
S
jest zbieżny do tej
samej granicy niezależnie od wyboru punktów
(
)
k
k
k
y
x
P
,
na łukach częściowych
k
l
, to tę granicę
nazywamy całką krzywoliniową nieskierowaną funkcji
)
,
( y
x
f
wzdłuż krzywej
K i oznaczamy
∫
K
dl
y
x
f
)
,
(
W zapisie symbolicznym:
k
n
k
k
K
l
P
f
dl
y
x
f
n
∆
⋅
=
∑
∫
=
→
δ
1
0
)
(
lim
)
,
(
Uwaga: Nazwa „całka nieskierowana” pochodzi stąd, że całka ta nie zmienia znaku przy zmianie
kierunku krzywej
AB
K
=
tzn.
∫
∫
=
BA
AB
dl
y
x
f
dl
y
x
f
)
,
(
)
,
(
Zatem krzywej K nie nadajemy żadnego kierunku.
Analogicznie definiujemy całkę krzywoliniową w przestrzeni, przy czym krzywa K jest krzywą regularną
w przestrzeni, funkcja
)
,
,
(
z
y
x
f
jest określona i ograniczona wzdłuż tej krzywej. Krzywą K dzielimy
punktami:
B
A
A
A
A
n
=
=
,
...
,
,
1
0
na n dowolnych łuków
n
l
l
l
,
...
,
,
2
1
o długościach odpowiednio:
n
l
l
l
∆
∆
∆
,
...
,
,
2
1
, przy czym
[
]
[
]
[
]
k
k
t
t
k
t
t
dt
t
z
t
y
t
x
l
k
k
,
)
(
)
(
)
(
1
2
2
2
1
−
∫
−
′
+
′
+
′
=
∆
Na każdym łuku częściowym
)
,
...
,
2
,
1
(
n
k
l
k
=
obieramy dowolny punkt
(
)
k
k
k
k
z
y
x
P
,
,
. Stąd całka
krzywoliniowa nieskierowana w przestrzeni
k
n
k
k
K
l
P
f
dl
z
y
x
f
n
∆
⋅
=
∑
∫
=
→
δ
1
0
)
(
lim
)
,
,
(
.
WŁASNOŚCI CAŁKI KRZYWOLINIOWEJ NIESKIEROWANEJ
1.
∫
∫
=
⋅
K
K
dl
y
x
f
A
dl
y
x
f
A
)
,
(
)
,
(
, gdzie A jest dowolną stałą;
2.
[
]
∫
∫
∫
±
=
±
K
K
K
dl
y
x
g
dl
y
x
f
dl
y
x
g
y
x
f
)
,
(
)
,
(
)
,
(
)
,
(
3.
∫
∫
∫
+
=
2
1
)
,
(
)
,
(
)
,
(
K
K
K
dl
y
x
f
dl
y
x
f
dl
y
x
f
, gdzie
{ }
P
K
K
K
K
K
=
∩
∪
=
2
1
2
1
,
, przy czym P jest
punktem, który dzieli krzywą K na krzywe
2
1
, K
K
267
Uwaga
: Analogiczne własności posiada całka krzywoliniowa w przestrzeni.
Całkę krzywoliniową nieskierowaną obliczamy zamieniając ją na całkę oznaczoną posługując się
poniższymi twierdzeniami.
Tw.1.1. (o zamianie całki krzywoliniowej nieskierowanej na całkę oznaczoną)
Jeżeli funkcja
)
,
( y
x
f
jest ciągła wzdłuż krzywej regularnej K danej parametrycznie:
β
α
∈
=
=
,
)
(
),
(
t
t
y
y
t
x
x
to
[
] [
]
[
]
∫
∫
β
α
′
+
′
=
dt
t
y
t
x
t
y
t
x
f
dl
y
x
f
K
2
2
)
(
)
(
)
(
),
(
)
,
(
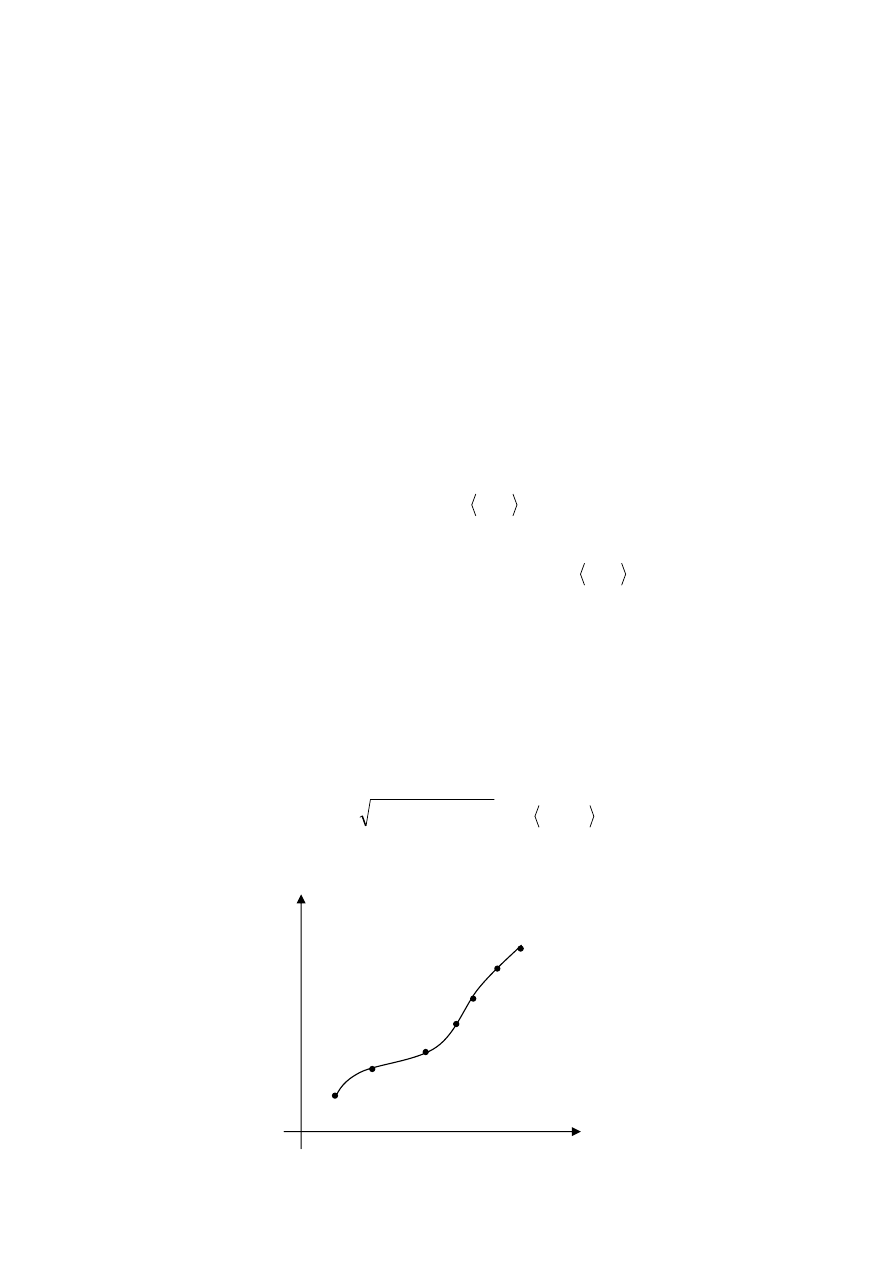
Przykład:
Obliczyć
(
)
∫
+
K
dl
y
x
2
2
2
, gdzie K jest okręgiem o równaniach:
t
a
y
t
a
x
sin
,
cos
=
=
,
π
≤
≤
2
0 t
,
0
>
a
.
Zatem
t
a
t
y
t
a
t
x
sin
)
(
,
cos
)
(
=
=
. Stąd
t
a
t
y
t
a
t
x
cos
)
(
,
sin
)
(
=
′
−
=
′
.
Korzystając z Tw.1.1 mamy:
(
)
(
)
5
2
0
5
2
0
5
2
0
2
2
2
2
2
2
2
2
2
2
2
2
2
cos
sin
sin
cos
a
t
a
dt
a
dt
t
a
t
a
t
a
t
a
dl
y
x
K
π
=
=
=
+
+
=
+
π
π
π
∫
∫
∫
W szczególności, gdy krzywa K nie jest dana w postaci parametrycznej korzystamy z następujących
twierdzeń:
Tw.1.2.
Jeżeli krzywa K dana jest w postaci jawnej:
b
a
x
x
y
y
,
)
(
∈
=
to
[
]
[
]
∫
∫
′
+
=
b
a
K
dx
x
y
x
y
x
f
dl
y
x
f
2
)
(
1
)
(
,
)
,
(
Przykład:
Obliczyć całkę
∫
K
dl
y
, gdzie K – łuk paraboli
px
y
2
2
=
odciętym przez parabolę
py
x
2
2
=
,
(
)
0
>
p
(Rys.3).
Rys.3
x
y
px
y
2
2
=
py
x
2
2
=
)
2
,
2
(
p
p
A
)
0
,
2
( p
A′
0
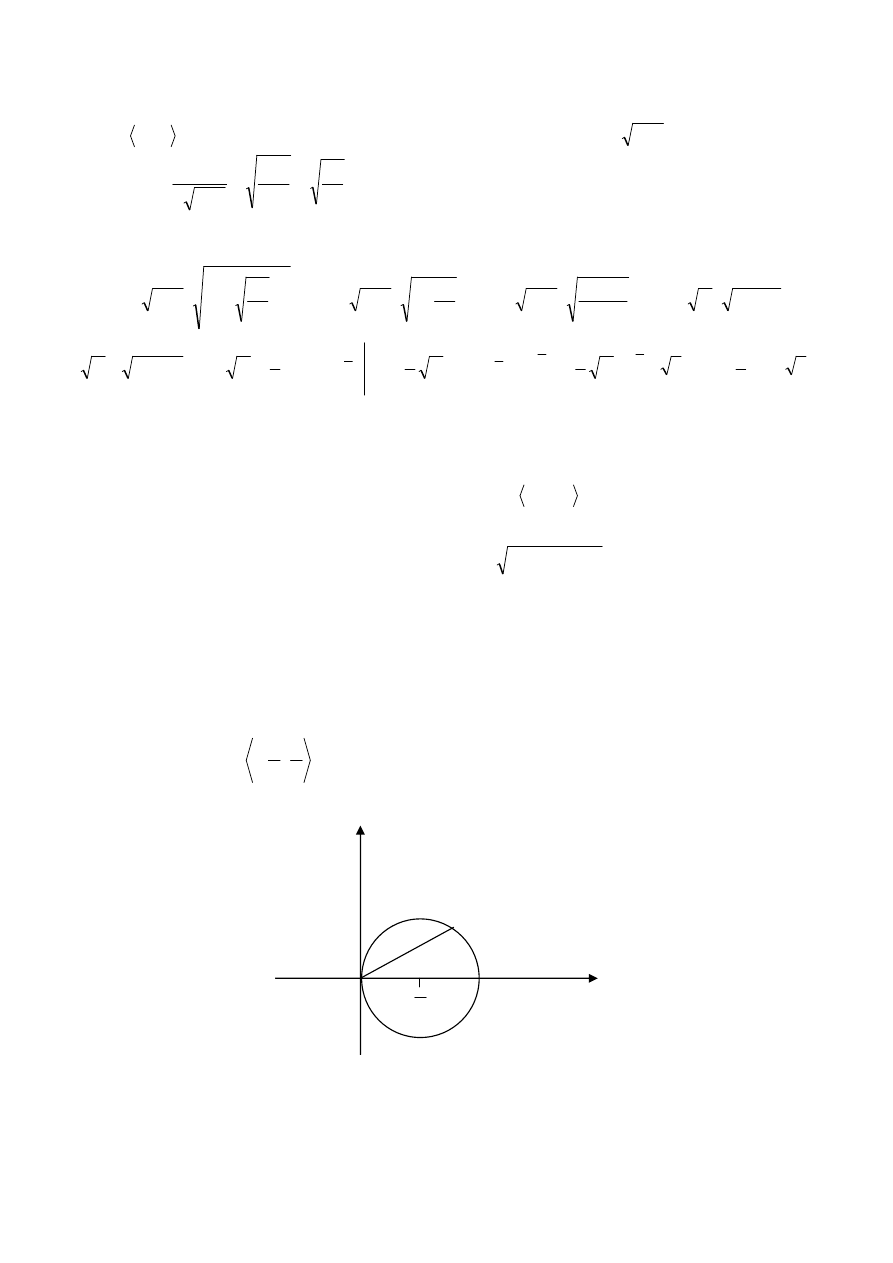
268
Rozwiązując układ równań
px
y
2
2
=
i
py
x
2
2
=
otrzymujemy współrzędne punktów przecięcia
parabol:
)
0
,
0
(
O
i
)
2
,
2
(
p
p
A
.
Stąd
p
x
2
,
0
∈
. Z równania
px
y
2
2
=
(
0
>
y
) wyznaczamy y, czyli
px
x
y
2
)
( =
.
Zatem
x
p
px
p
px
p
x
y
2
2
2
2
2
)
(
2
=
=
=
′
.
Korzystając z Tw.1.2 mamy:
=
+
⋅
=
+
⋅
=
+
⋅
=
+
⋅
=
∫
∫
∫
∫
∫
p
p
p
p
K
dx
p
x
p
dx
x
p
x
px
dx
x
p
px
dx
x
p
px
dl
y
2
0
2
0
2
0
2
0
2
2
2
2
2
2
1
2
2
1
2
(
)
( )
(
)
(
)
1
5
5
3
1
1
5
5
3
1
5
3
1
2
3
1
2
2
2
3
2
3
2
3
2
0
2
3
2
0
−
=
−
=
−
⋅
=
+
⋅
=
+
=
∫
p
p
p
p
p
p
p
x
p
dx
p
x
p
p
p
Tw.1.3.
Jeżeli krzywa K dana jest w postaci biegunowej:
2
1
,
)
(
ϕ
ϕ
∈
ϕ
ϕ
= r
r
to
(
)
[
]
∫
∫
ϕ
ϕ
ϕ
ϕ
′
+
=
2
1
2
2
)
(
sin
,
cos
)
,
(
d
r
r
t
r
t
r
f
dl
y
x
f
K
Przykład:
Obliczyć
(
)
∫
+
K
dl
y
x
2
2
, gdzie K jest okręgiem o równaniu
ax
y
x
=
+
2
2
.
Korzystając ze współrzędnych biegunowych:
ϕ
=
ϕ
=
sin
,
cos
r
y
r
x
otrzymujemy równanie okręgu
ϕ
=
cos
2
ar
r
, gdzie
2
,
2
π
π
−
∈
ϕ
(Rys.4)
Rys.4
Po podzieleniu przez r mamy równanie okręgu w postaci biegunowej:
ϕ
= cos
a
r
.
Stąd
ϕ
=
ϕ
cos
)
(
a
r
,
ϕ
−
=
ϕ
′
sin
)
(
a
r
.
a
2
a
x
y
r
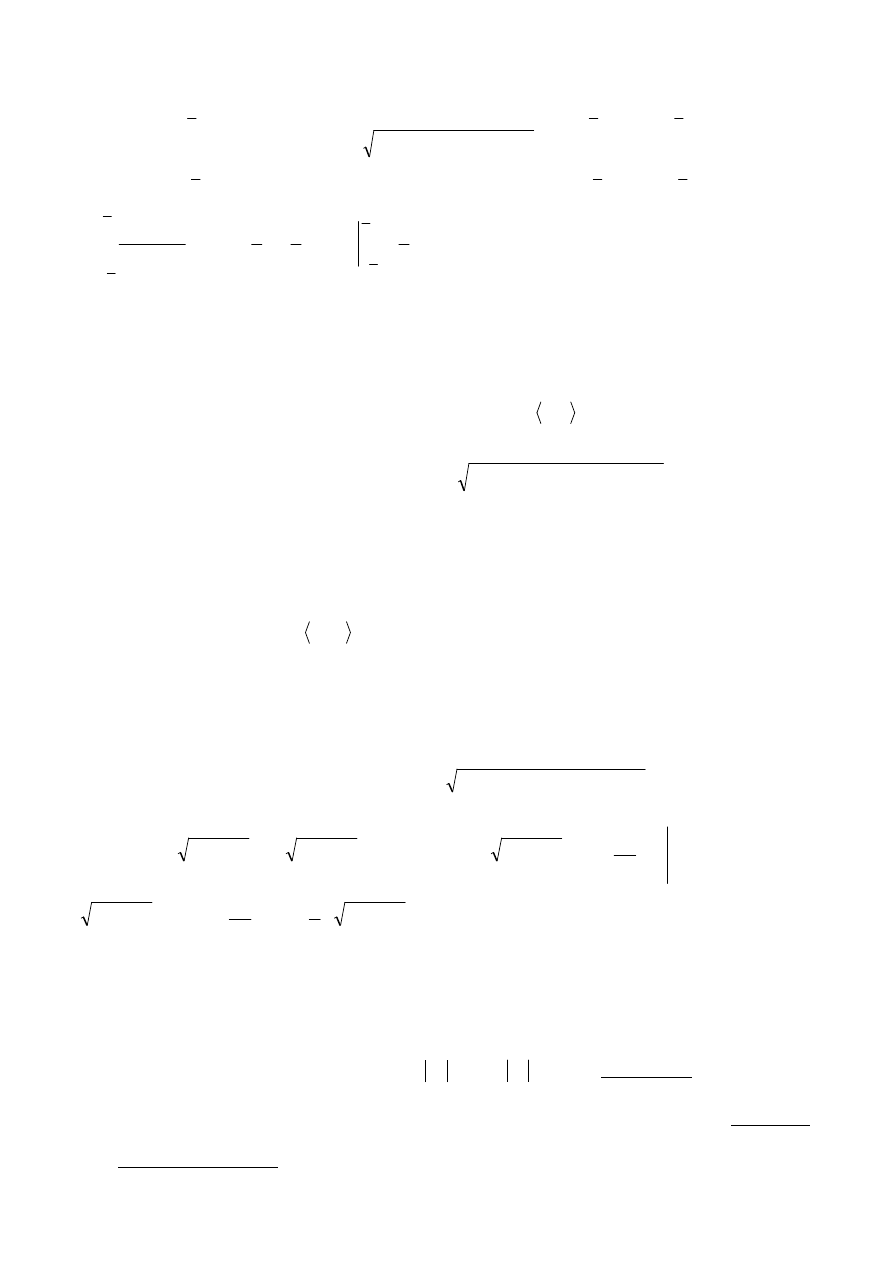
269
Zatem na podstawie Tw.1.3. mamy:
(
)
(
)
=
ϕ
ϕ
=
ϕ
=
ϕ
ϕ
+
ϕ
ϕ
+
ϕ
=
+
∫
∫
∫
∫
π
π
−
π
π
−
π
π
−
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
cos
sin
cos
sin
cos
d
a
a
d
r
a
d
a
a
r
r
dl
y
x
K
3
2
2
3
2
2
3
2
1
2
sin
4
1
2
1
2
2
cos
1
a
a
d
a
π
=
ϕ
+
ϕ
=
ϕ
ϕ
+
=
π
π
−
π
π
−
∫
Tw.1.4.
Jeżeli funkcja
)
,
,
(
z
y
x
f
jest ciągła wzdłuż krzywej regularnej K o równaniach:
β
α
∈
=
=
=
,
)
(
),
(
),
(
t
t
z
z
t
y
y
t
x
x
to
[
] [
]
[
]
[
]
∫
∫
β
α
′
+
′
+
′
=
dt
t
z
t
y
t
x
t
z
t
y
t
x
f
dl
z
y
x
f
K
2
2
2
)
(
)
(
)
(
)
(
),
(
),
(
)
,
,
(
Przykład:
Obliczyć całkę krzywoliniową
(
)
∫
+
+
K
dl
z
y
x
2
2
2
, gdzie K jest linią śrubową o równaniu
π
∈
=
=
=
2
,
0
,
,
sin
,
cos
t
bt
z
t
a
y
t
a
x
.
Zatem
b
t
z
t
a
t
y
t
a
t
x
=
′
=
′
−
=
′
)
(
,
cos
)
(
,
sin
)
(
.
Korzystając z Tw.1.4 otrzymujemy:
(
)
(
)
=
+
+
+
+
=
+
+
∫
∫
π
dt
b
t
a
t
a
t
b
t
a
t
a
dl
z
y
x
K
2
2
2
2
2
2
0
2
2
2
2
2
2
2
2
2
cos
sin
sin
cos
(
)
(
)
=
+
+
=
+
+
=
+
+
=
π
π
π
∫
∫
2
0
3
2
2
2
2
2
0
2
2
2
2
2
2
2
2
0
2
2
2
3
t
b
t
a
b
a
dt
t
b
a
b
a
dt
b
a
t
b
a
(
)
2
2
2
2
2
3
2
2
2
2
4
3
3
2
8
3
2
b
a
b
a
b
a
b
a
π
+
+
π
=
π
+
π
⋅
+
=
INTERPRETACJA GEOMETRYCZNA CAŁKI KRZYWOLINIOWEJ NIESKIEROWANEJ NA
PŁASZCZYŹNIE
1.
Jeżeli
1
)
,
(
≡
y
x
f
dla
(
)
K
y
x
∈
,
to
L
dl
K
=
∫
, gdzie
L
oznacza długość łuku.
2.
Jeżeli funkcja
)
,
( y
x
f
jest ciągła na krzywej K i
0
)
,
(
>
y
x
f
to
∫
K
dl
y
x
f
)
,
(
oznacza pole części
powierzchni walcowej
(Rys.5).
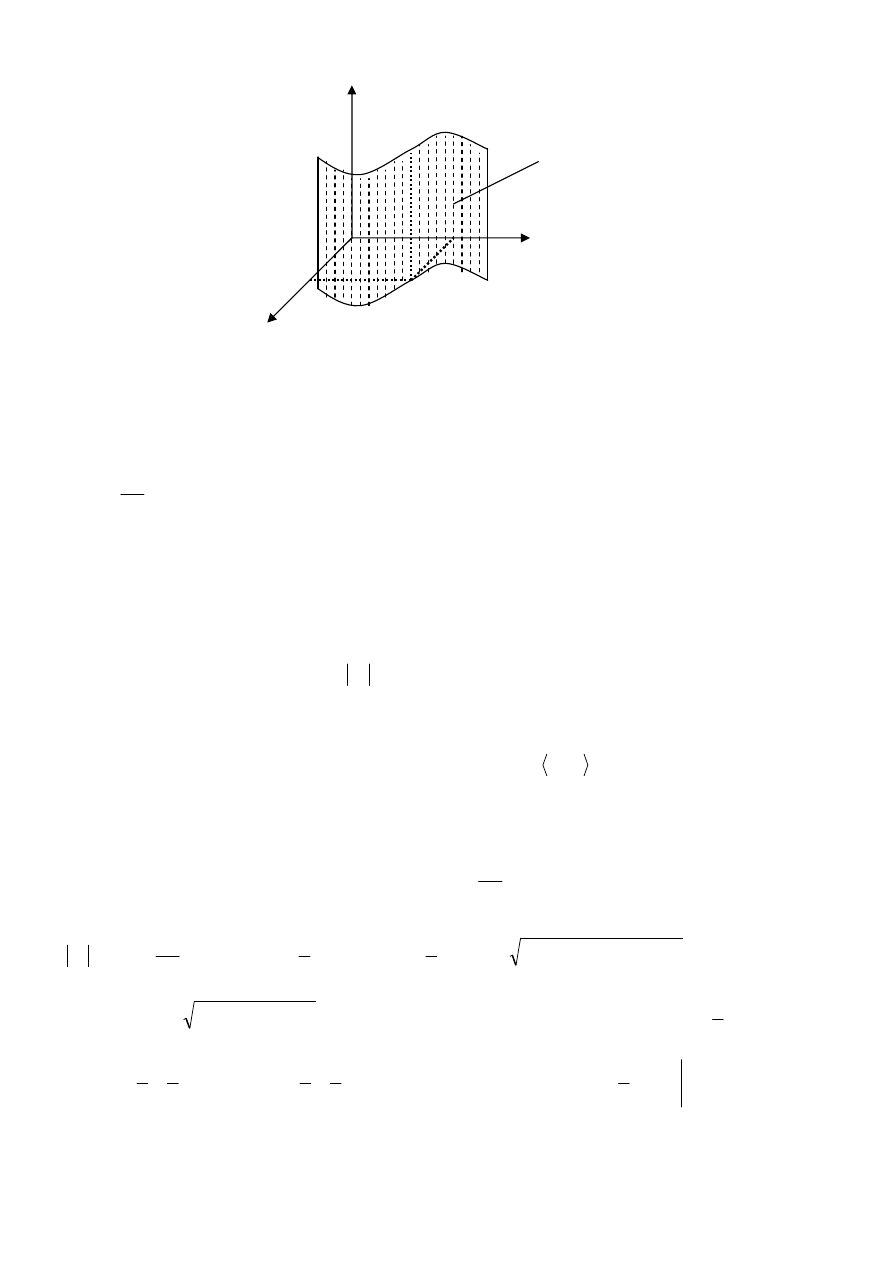
270
Rys.5
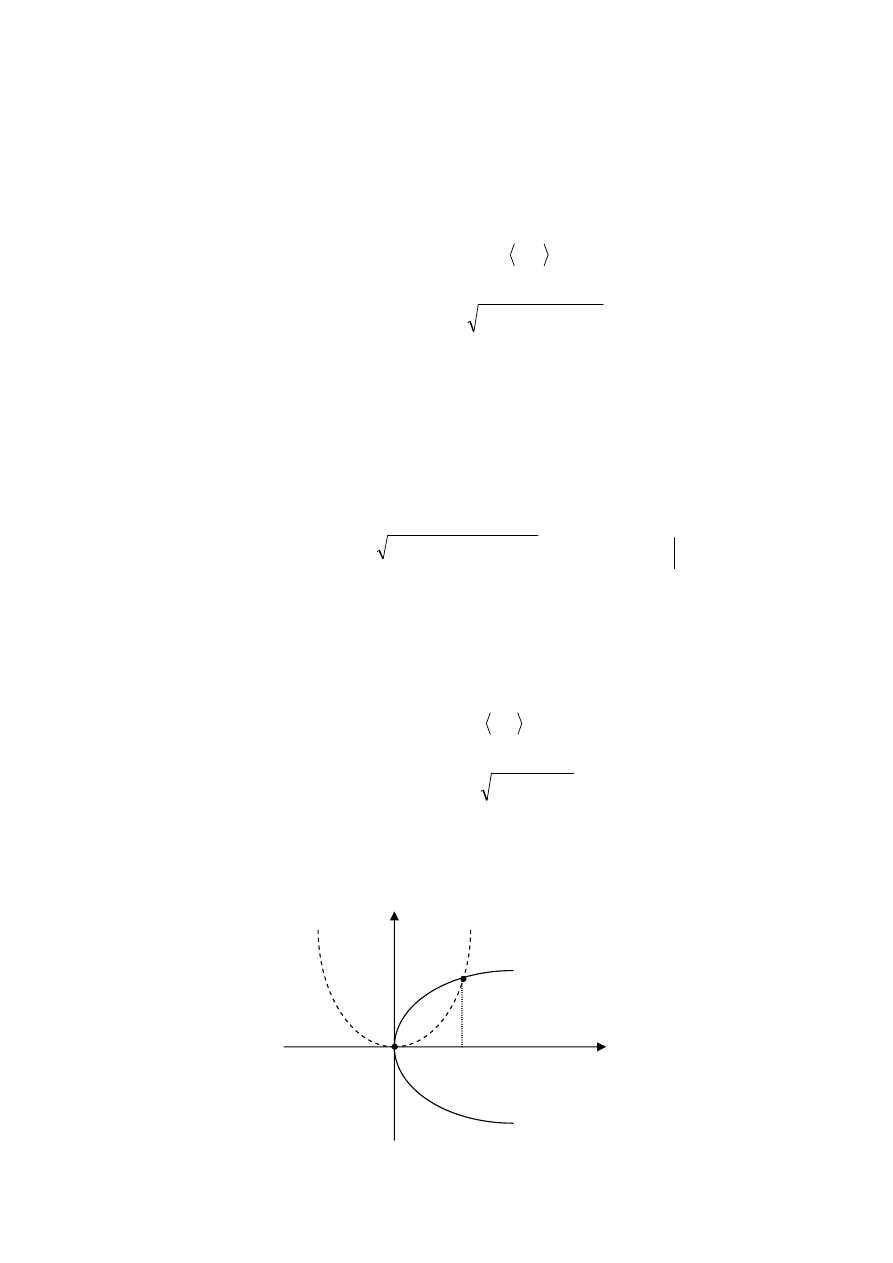
Przykład:
Znaleźć pole powierzchni bocznej walca
4
2
2
=
+ y
x
ograniczonej płaszczyzną OXY oraz powierzchnią
2
2
2
y
z
+
=
.
Jeżeli K jest łukiem na płaszczyźnie OXY to pole powierzchni bocznej walca:
{
}
R
∈
∈
=
z
K
y
x
z
y
x
S
,
)
,
(
:
)
,
,
(
wyciętej z dołu przez powierzchnię
)
,
( y
x
g
z
=
, a z góry przez powierzchnię
)
,
( y
x
h
z
=
wyraża się
wzorem:
[
]
∫
−
=
K
dl
y
x
g
y
x
h
S
)
,
(
)
,
(
Łuk K jest okręgiem o równaniu
4
2
2
=
+ y
x
zatem jego postać parametryczna jest następująca:
π
∈
=
=
2
,
0
,
sin
2
,
cos
2
:
t
t
y
t
x
K
Stąd:
t
t
y
t
t
x
cos
2
)
(
,
sin
2
)
(
=
′
−
=
′
.
Z dołu powierzchnia boczna naszego walca jest ograniczona przez płaszczyznę OXY, czyli powierzchnię
o równaniu
0
=
z
, z góry zaś przez powierzchnię
2
2
2
y
z
+
=
.
Zatem
(
)
(
)
=
+
−
⋅
+
=
+
=
−
+
=
∫
∫
∫
π
dt
t
t
t
dl
y
dl
y
S
K
K
2
2
2
0
2
2
2
cos
2
sin
2
sin
4
2
1
2
2
1
2
0
2
2
(
) (
)
(
)
=
+
=
+
+
=
∫
∫
π
π
dt
t
dt
t
t
t
2
0
2
2
2
2
0
2
sin
1
4
cos
sin
4
sin
2
2
{korzystamy ze wzoru
(
)
t
t
2
cos
1
2
1
sin
2
−
=
}=
(
)
π
=
π
⋅
⋅
=
+
=
+
=
+
=
+
+
=
π
π
π
π
∫
∫
∫
12
2
3
2
2
sin
2
1
3
2
2
cos
3
2
2
cos
2
1
2
3
4
2
cos
2
1
2
1
1
4
2
0
2
0
2
0
2
0
t
t
dt
t
dt
t
dt
t
z
x
y
K
)
,
( y
x
f
∫
K
dl
y
x
f
)
,
(
271
C) CAŁKI KRZYWOLINIOWE SKIEROWANE NA PŁASZCZYŹNIE I W PRZESTRZENI
Rozważmy łuk regularny określony równaniami parametrycznymi:
β
α
∈
=
=
,
)
(
),
(
t
t
y
y
t
x
x
położony na płaszczyźnie OXY.
Wartości α parametru t odpowiada punkt
(
)
)
(
),
(
α
α y
x
A
, natomiast wartości β punkt
(
)
)
(
),
(
β
β y
x
B
. Jak
wiadomo, łukowi temu można nadać kierunek, przyjmując
(
)
)
(
),
(
α
α y
x
A
za początek łuku, natomiast
(
)
)
(
),
(
β
β y
x
B
za koniec (oznaczamy ten łuk przez AB) lub na odwrót (oznaczamy BA).
Def.1.7. (przedstawienie parametryczne zgodne z kierunkiem łuku)
Mówimy, że przedstawienie parametryczne łuku i nadany mu kierunek są zgodne, jeśli kierunek łuku
jest zgodny z kierunkiem wzrostu parametru t (tj. punkt odpowiadający mniejszej wartości parametru t
poprzedza punkt odpowiadający większej wartości).
W przypadku, gdy kierunek łuku jest niezgodny z kierunkiem wzrostu parametru t (tj. punkt
odpowiadający większej wartości parametru t poprzedza punkt odpowiadający mniejszej wartości)
mówimy, że przedstawienie parametryczne łuku i nadany mu kierunek są niezgodne.
Uwaga
: Łuk AB ma przedstawienie parametryczne zgodne z kierunkiem łuku, natomiast łuk BA ma
przedstawienie parametryczne niezgodne z kierunkiem.
Przykład: Niech
2
,
0
,
,
∈
=
=
t
t
y
t
x
.
Jest to przedstawienie parametryczne odcinka łączącego punkty:
)
0
,
0
(
A
i
)
2
,
2
(
B
.
Jest to przedstawienie zgodne z kierunkiem odcinka AB (Rys.6a), natomiast niezgodne z kierunkiem
odcinka BA (Rys.6b).
Uwaga
: Jeśli przedstawienie parametryczne łuku
β
α
∈
=
=
,
,
)
(
),
(
t
t
y
y
t
x
x
jest niezgodne z nadanym
mu kierunkiem to przedstawienie
α
−
β
−
∈
−
=
−
=
,
,
)
(
),
(
t
t
y
y
t
x
x
będzie już zgodne.
Przykład:
Przedstawienie
0
,
2
,
,
−
∈
−
=
−
=
t
t
y
t
x
będzie zgodne z kierunkiem odcinka BA.
A
2
2
x
y
B
Rys.6a.
A
2
2
x
y
B
Rys.6b.

272
Niech będzie dany łuk skierowany AB o przedstawieniu parametrycznym:
,
)
(
),
(
t
y
y
t
x
x
=
=
β
α
∈
,
t
zgodnym z kierunkiem tego łuku oraz wektor
[
]
)
,
(
),
,
(
y
x
Q
y
x
P
W
=
→
zaczepiony w każdym punkcie tego
łuku, gdzie
)
,
(
),
,
(
y
x
Q
y
x
P
są funkcjami określonymi w każdym punkcie łuku AB.
Przedział
β
α,
dzielimy na n podprzedziałów za pomocą punktów:
1
3
2
1
,
...
,
,
,
−
n
t
t
t
t
tzn.
β
=
<
<
<
<
<
<
=
α
−
n
n
t
t
t
t
t
t
1
3
2
1
0
...
Podziałowi temu odpowiada podział łuku AB na n części punktami:
1
3
2
1
,
...
,
,
,
−
n
A
A
A
A
, przy czym punkt
k
A
ma współrzędne
( )
( )
1
,
...
,
2
,
1
,
,
−
=
=
=
n
k
t
y
y
t
x
x
k
k
k
k
.
W każdym podprzedziale
k
k
t
t
,
1
−
n
k
,
...
,
2
,
1
=
wybieramy dowolnie punkt
k
τ , któremu na łuku
odpowiada punkt
( ) ( )
(
)
k
k
k
y
x
C
τ
τ ,
.
Następnie określamy wektory:
[
]
)
(
),
(
k
k
C
Q
C
P
W
=
→
,
[
]
k
k
k
y
x
l
∆
∆
=
∆
→
,
,
gdzie
1
−
−
=
∆
k
k
k
x
x
x
,
1
−
−
=
∆
k
k
k
y
y
y
,
n
k
,
...
,
2
,
1
=
.
Tworzymy sumę iloczynów skalarnych tych wektorów:
∑
=
→
→
∆
⋅
=
n
k
k
k
n
l
W
S
1
czyli
( )
( )
[
]
∑
=
∆
⋅
+
∆
⋅
=
n
k
k
k
k
k
n
y
C
Q
x
C
P
S
1
Rozważmy normalny ciąg podziałów przedziału
β
α,
.
Def.1.8. (całka krzywoliniowa skierowana)
Jeżeli dla każdego normalnego ciągu podziałów przedziału
β
α,
ciąg sum
( )
n
S
jest zbieżny do granicy
właściwej, niezależnej od wyboru punktów
k
τ , to tę granicę nazywamy całką krzywoliniową skierowaną
pary funkcji
[
]
)
,
(
),
,
(
y
x
Q
y
x
P
po łuku AB i oznaczamy:
∫
+
AB
dy
y
x
Q
dx
y
x
P
)
,
(
)
,
(
Uwaga:
Całkę krzywoliniową skierowaną zapisujemy również następująco:
∫
→
→
⋅
AB
dl
W
Analogicznie definiujemy całkę krzywoliniową skierowaną trójki funkcji
[
]
)
,
,
(
),
,
,
(
),
,
,
(
z
y
x
R
z
y
x
Q
z
y
x
P
po łuku AB o równaniach parametrycznych:
β
α
∈
=
=
=
,
;
)
(
),
(
),
(
t
t
z
z
t
y
y
t
x
x
skierowanym od
punktu
(
)
)
(
),
(
),
(
α
α
α
z
y
x
A
do punktu
(
)
)
(
),
(
),
(
β
β
β
z
y
x
B
.
A oznaczamy ją następująco:
dz
z
y
x
R
dy
z
y
x
Q
dx
z
y
x
P
AB
)
,
,
(
)
,
,
(
)
,
,
(
+
+
∫

273
WŁASNOŚCI CAŁKI KRZYWOLINIOWEJ SKIEROWANEJ
1) Jeśli łuki AB i BA są przeciwnie skierowane to
∫
∫
+
−
=
+
BA
AB
dy
y
x
Q
dx
y
x
P
dy
y
x
Q
dx
y
x
P
)
,
(
)
,
(
)
,
(
)
,
(
2) Jeśli krzywa AB jest sumą otwartych gładkich łuków skierowanych:
∑
=
−
=
n
k
k
k
A
A
AB
1
1
, przy czym
przyjmujemy, że:
n
A
B
A
A
=
=
,
0
to
∑ ∫
∫
=
−
+
=
+
n
k
A
A
AB
k
k
dy
y
x
Q
dx
y
x
P
dy
y
x
Q
dx
y
x
P
1
1
)
,
(
)
,
(
)
,
(
)
,
(
Uwaga
: Analogiczne własności posiada całka krzywoliniowa skierowana w przestrzeni.
Tw.1.5. (o zamianie całki krzywoliniowej skierowanej na całkę oznaczoną)
1) W przypadku całki krzywoliniowej skierowanej na płaszczyźnie:
Jeżeli funkcje
)
,
( y
x
P
i
)
,
( y
x
Q
są ciągłe na otwartym łuku regularnym AB o przedstawieniu
parametrycznym
β
α
∈
=
=
,
,
)
(
),
(
t
t
y
y
t
x
x
zgodnym z kierunkiem tego łuku, to całka krzywoliniowa
skierowana na płaszczyźnie istnieje, przy czym
(
)
(
)
[
]
∫
∫
β
α
′
⋅
+
′
⋅
=
+
dt
t
y
t
y
t
x
Q
t
x
t
y
t
x
P
dy
y
x
Q
dx
y
x
P
AB
)
(
)
(
),
(
)
(
)
(
),
(
)
,
(
)
,
(
2) W przypadku całki krzywoliniowej skierowanej w przestrzeni:
Jeżeli funkcje
)
,
,
(
z
y
x
P
,
)
,
,
(
z
y
x
Q
i
)
,
,
(
z
y
x
R
są ciągłe na otwartym łuku regularnym AB o
przedstawieniu parametrycznym
β
α
∈
=
=
=
,
)
(
,
)
(
),
(
t
t
z
z
t
y
y
t
x
x
zgodnym z kierunkiem tego łuku,
to całka krzywoliniowa skierowana w przestrzeni istnieje, przy czym
=
+
+
∫
AB
dy
z
y
x
R
dy
z
y
x
Q
dx
z
y
x
P
)
,
,
(
)
,
,
(
)
,
,
(
(
)
(
)
(
)
[
]
∫
β
α
′
⋅
+
′
⋅
+
′
⋅
=
dt
t
z
t
z
t
y
t
x
R
t
y
t
z
t
y
t
x
Q
t
x
t
z
t
y
t
x
P
)
(
)
(
),
(
),
(
)
(
)
(
),
(
),
(
)
(
)
(
),
(
),
(
Wniosek: Dotyczy Tw.1.5. 1) tj. zamiany całki krzywoliniowej skierowanej na płaszczyźnie na całkę
oznaczoną.
Gdy krzywa dana jest równaniem
b
x
a
x
f
y
≤
≤
=
),
(
{początkiem krzywej jest punkt
))
(
,
(
a
f
a
A
,
a końcem punkt
))
(
,
(
b
f
b
B
} to całka krzywoliniowa skierowana na płaszczyźnie przyjmuje postać:
(
)
(
)
[
]
∫
∫
′
⋅
+
=
+
b
a
AB
dx
x
f
x
f
x
Q
x
f
x
P
dy
y
x
Q
dx
y
x
P
)
(
)
(
,
)
(
,
)
,
(
)
,
(
274
Przykłady:
a) Obliczyć
(
)
(
)
∫
−
+
−
K
dy
xy
y
dx
xy
x
2
2
2
2
, gdzie
AB
K
=
jest łukiem paraboli
2
x
y
=
od punktu
)
1
,
1
(−
A
do punktu
)
1
,
1
(
B
SPOSÓB I
{parametryzacja krzywej}
Parametryzujemy parabolę tak, aby parametryzacja ta była zgodna z kierunkiem krzywej.
Zatem
1
,
1
,
,
2
−
∈
=
=
t
t
y
t
x
(patrz Rys.7).
Stąd
t
t
y
t
x
2
)
(
,
1
)
(
=
′
=
′
.
Rys.7
Zatem na podstawie Tw.1.5. podpunkt 1) mamy:
(
)
(
)
(
) (
)
[
]
[
]
=
−
+
−
=
⋅
⋅
−
+
⋅
⋅
−
=
−
+
−
∫
∫
∫
−
−
dt
t
t
t
t
dt
t
t
t
t
t
t
t
dy
xy
y
dx
xy
x
K
1
1
4
5
3
2
1
1
2
4
2
2
2
2
4
2
2
2
2
1
2
2
2
15
14
5
4
3
1
2
1
3
1
5
4
3
1
2
1
3
1
5
4
3
2
3
1
1
5
6
4
3
−
=
+
+
−
−
−
−
+
−
=
−
+
−
=
−
t
t
t
t
SPOSÓB II {wykorzystanie wniosku z twierdzenia}
Krzywa jest dana w postaci jawnej:
1
1
,
:
2
≤
≤
−
=
x
x
y
K
.
Zatem
x
x
f
2
)
(
=
′
.
(
)
(
)
(
) (
)
[
]
[
]
=
−
+
−
=
⋅
⋅
−
+
⋅
−
=
−
+
−
∫
∫
∫
−
−
dx
x
x
x
x
dx
x
x
x
x
x
x
x
dy
xy
y
dx
xy
x
K
1
1
4
5
3
2
1
1
2
4
2
2
2
2
4
2
2
2
2
2
2
2
15
14
5
4
3
1
2
1
3
1
5
4
3
1
2
1
3
1
5
4
3
2
3
1
1
5
6
4
3
−
=
+
+
−
−
−
−
+
−
=
−
+
−
=
−
x
x
x
x
b) Obliczyć
∫
+
−
K
xdz
zdy
ydx
3
2
, gdzie K jest łamaną o początku
)
0
,
0
,
0
(
O
, końcu
)
1
,
1
,
1
(
C
oraz
wierzchołkach
)
0
,
0
,
1
(
A
i
)
0
,
1
,
1
(
B
.
Krzywa K jest krzywą regularną składającą się z trzech łuków regularnych:
OA
K
=
1
,
AB
K
=
2
oraz
BC
K
=
3
. (patrz Rys.8)
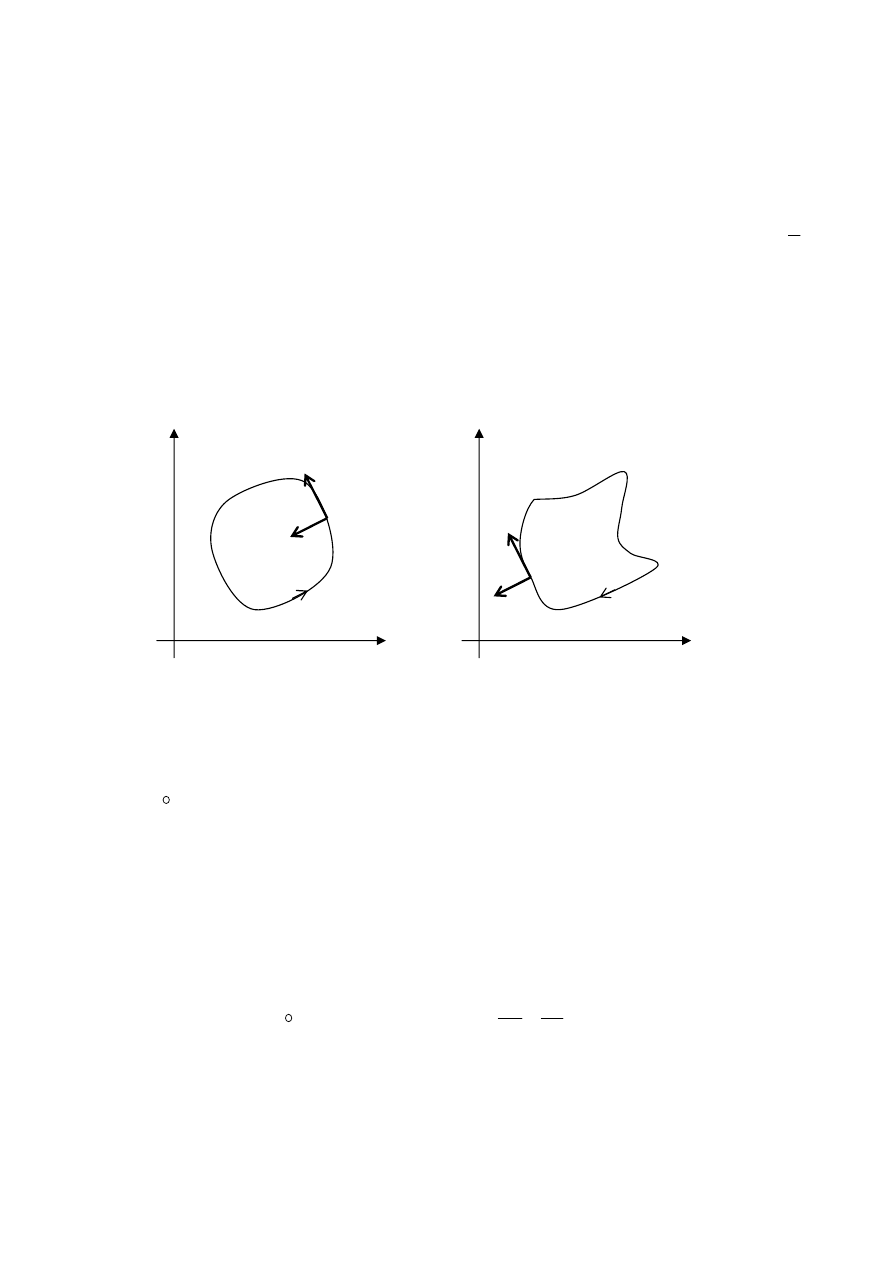
x
y
2
x
y
=
)
1
,
1
(
B
1
0
-1
)
1
,
1
(−
A
275
Rys.8
Wyznaczymy równania parametryczne kolejnych łuków:
1)
1
K
jest odcinkiem o początku
)
0
,
0
,
0
(
O
i końcu
)
0
,
0
,
1
(
A
. Stąd
{
}
1
,
0
0
,
0
,
:
1
∈
=
=
=
t
z
y
t
x
K
2)
2
K
jest odcinkiem o początku
)
0
,
0
,
1
(
A
i końcu
)
0
,
1
,
1
(
B
. Stąd
{
}
1
,
0
0
,
,
1
:
2
∈
=
=
=
t
z
t
y
x
K
3)
3
K
jest odcinkiem o początku
)
0
,
1
,
1
(
B
i końcu
)
1
,
1
,
1
(
C
. Stąd
{
}
1
,
0
,
1
,
1
:
3
∈
=
=
=
t
t
z
y
x
K
Ponieważ
3
2
1
K
K
K
K
∪
∪
=
zatem na podstawie własności 2) otrzymujemy:
∫
∫
∫
∫
+
−
+
+
−
+
+
−
=
+
−
3
2
1
3
2
3
2
3
2
3
2
K
K
K
K
xdz
zdy
ydx
xdz
zdy
ydx
xdz
zdy
ydx
xdz
zdy
ydx
Obliczamy kolejne całki stosując twierdzenie o zamianie całki skierowanej w przestrzeni na całkę
oznaczoną.
(
)
0
0
3
0
0
2
1
0
3
2
1
0
1
=
⋅
⋅
+
⋅
⋅
−
⋅
=
+
−
∫
∫
dt
t
xdz
zdy
ydx
K
(
)
0
0
1
3
1
0
2
0
3
2
1
0
2
=
⋅
⋅
+
⋅
⋅
−
⋅
=
+
−
∫
∫
dt
t
xdz
zdy
ydx
K
(
)
3
3
1
1
3
0
2
0
1
3
2
1
0
1
0
3
=
=
⋅
⋅
+
⋅
⋅
−
⋅
=
+
−
∫
∫
∫
dt
dt
t
xdz
zdy
ydx
K
Ostatecznie:
3
3
0
0
3
2
=
+
+
=
+
−
∫
K
xdz
zdy
ydx
1
K
2
K
3
K
y
x
z
)
1
,
1
,
1
(
C
)
0
,
0
,
1
(
A
)
0
,
1
,
1
(
B
O
276
D) CAŁKA KRZYWOLINIOWA SKIEROWANA PO ŁUKU ZAMKNIĘTYM
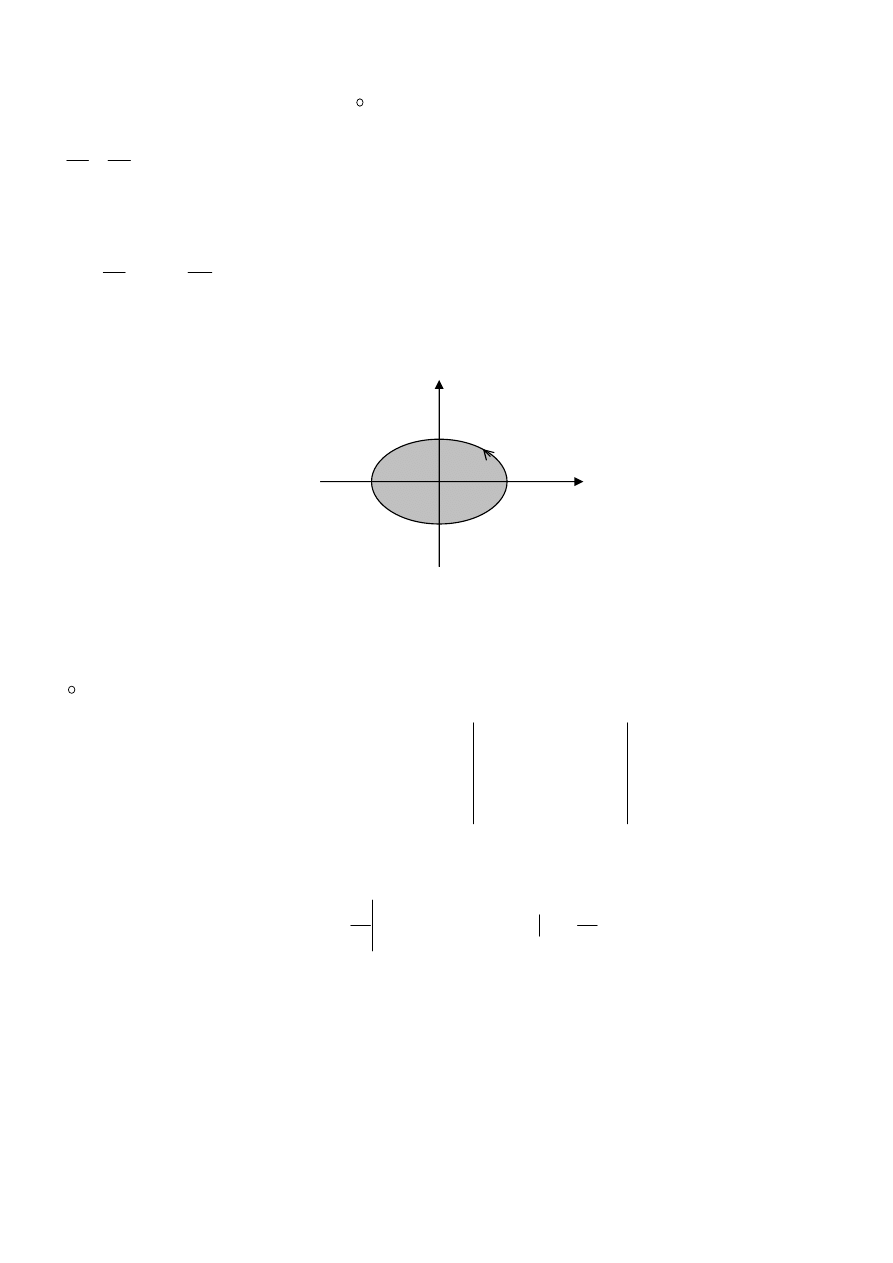
Def.1.9. (krzywa zamknięta skierowana dodatnio (ujemnie) względem swego wnętrza)
Niech K będzie regularną krzywą zamkniętą w przestrzeni
2
R
. Wektor s jest wektorem stycznym do
krzywej K w punkcie
0
P
skierowanym zgodnie z kierunkiem tej krzywej, natomiast wektor n jest
wektorem normalnym powstałym z obrotu wektora s w płaszczyźnie OXY wokół punktu
0
P
o kąt
2
π
+
.
Mówimy, że krzywa jest skierowana dodatnio względem swego wnętrza D, jeśli wektor normalny n jest
skierowany do wnętrza D krzywej K (Rys.9.a).
Jeśli wektor normalny n jest skierowany na zewnątrz obszaru D, to mówimy, że krzywa jest skierowana
ujemnie względem swego wnętrza
(Rys.9.b).
Rys.9.a
Rys.9.b
Uwaga
: Całki krzywoliniowe skierowane
∫
+
K
dy
y
x
Q
dx
y
x
P
)
,
(
)
,
(
po krzywej K zamkniętej oznaczamy
następująco:
∫
+
K
dy
y
x
Q
dx
y
x
P
)
,
(
)
,
(
.
Tw.1.6. (twierdzenie GREENA)
Jeżeli funkcje
)
,
( y
x
P
i
)
,
( y
x
Q
są klasy
1
C
(tzn. są ciągłe wraz z pochodnymi cząstkowymi I – go
rzędu) wewnątrz i na brzegu K obszaru D normalnego względem obu osi współrzędnych oraz brzeg K jest
skierowany dodatnio względem swego wnętrza to
dxdy
y
P
x
Q
dy
y
x
Q
dx
y
x
P
D
K
∫∫
∫
∂
∂
−
∂
∂
=
+
)
,
(
)
,
(
Uwaga:
Twierdzenie Greena dotyczy całki krzywoliniowej skierowanej na płaszczyźnie.
Twierdzenie to pozostaje prawdziwe również dla obszarów, które można podzielić na skończoną ilość
obszarów normalnych względem obu osi współrzędnych.
D
K
s
n
x
y
0
0
P
D
K
s
n
x
y
0
0
P
277
Przykład:
Stosując twierdzenie Greena obliczyć
∫
−
+
+
+
+
K
dy
y
x
xy
dx
y
x
xy
)
(
)
(
, gdzie K jest elipsą o równaniu
1
2
2
2
2
=
+
b
y
a
x
skierowaną dodatnio względem swego wnętrza (tj. przeciwnie do ruchu wskazówek zegara)
(Rys.10).
W naszym przypadku
(
)
(
)
y
x
xy
y
x
Q
y
x
xy
y
x
P
−
+
=
+
+
=
,
,
,
.
Stąd
1
,
1
+
=
∂
∂
+
=
∂
∂
y
x
Q
x
y
P
.
Obszar D jest obszarem normalnym względem obu osi układu współrzędnych, którego brzeg K jest
skierowany dodatnio względem swego wnętrza.
Rys.10
Zatem
(
)
(
)
=
−
=
−
−
+
=
−
+
+
+
+
∫∫
∫∫
∫
D
D
K
dxdy
x
y
dxdy
x
y
dy
y
x
xy
dx
y
x
xy
1
1
)
(
)
(
{wprowadzamy uogólnione współrzędne biegunowe}
=
π
≤
ϕ
≤
≤
≤
=
ϕ
=
ϕ
=
=
2
0
,
1
0
sin
cos
r
abr
J
br
y
ar
x
(
)
(
)
=
ϕ
ϕ
−
ϕ
=
ϕ
⋅
ϕ
−
ϕ
=
∫
∫
∫ ∫
π
π
dr
d
a
b
r
ab
dr
d
abr
ar
br
2
0
1
0
2
1
0
2
0
cos
sin
cos
sin
(
)
(
)
(
)
0
0
0
3
sin
cos
3
cos
sin
2
0
1
0
3
2
0
1
0
2
=
+
+
−
−
=
ϕ
−
ϕ
−
⋅
=
ϕ
ϕ
−
ϕ
=
π
π
∫
∫
b
b
ab
a
b
r
ab
d
a
b
dr
r
ab
NIEZALEŻNOŚĆ CAŁKI KRZYWOLINIOWEJ OD KSZTAŁTU DROGI CAŁKOWANIA
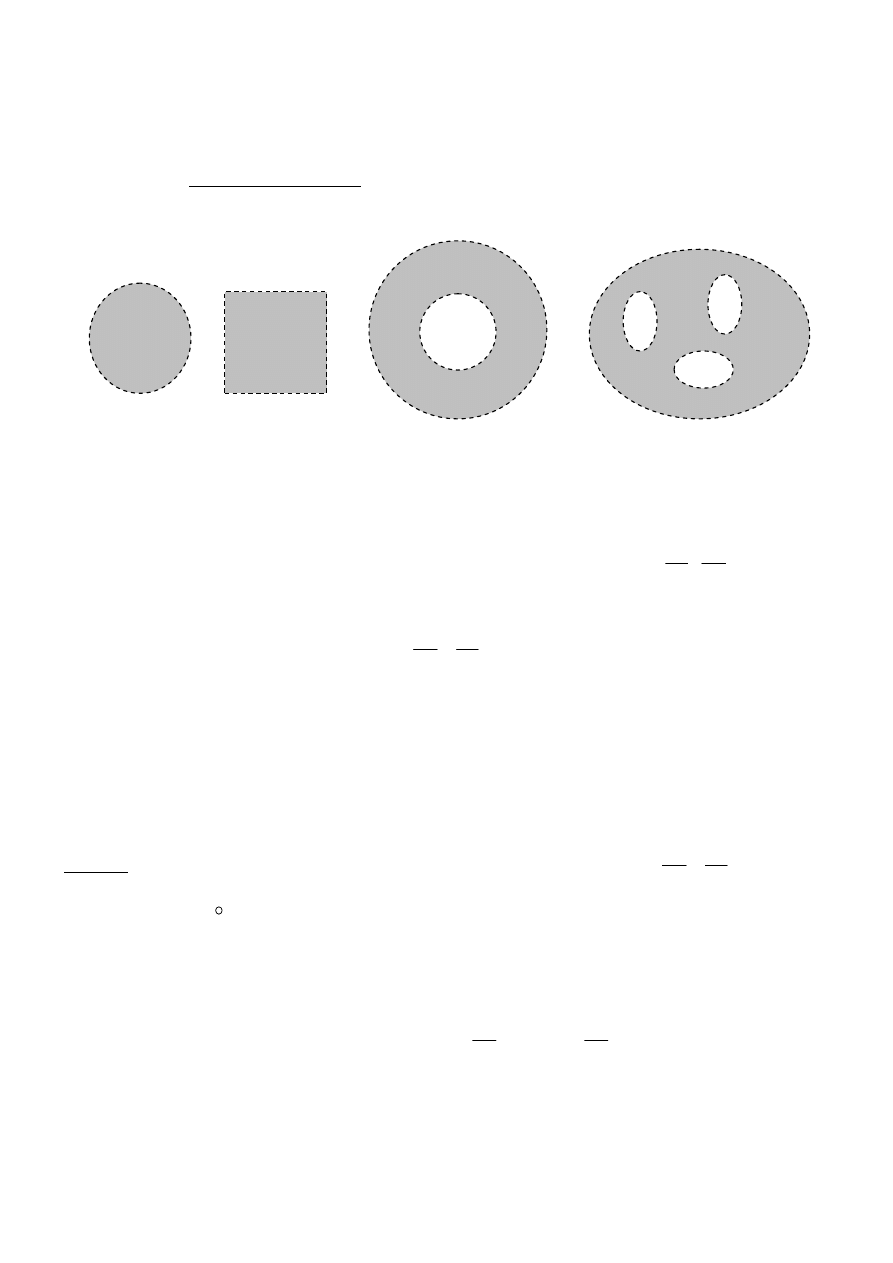
Def.1.10. (obszar jednospójny i wielospójny)
Obszar płaski D nazywamy obszarem jednospójnym, jeśli należy do niego wnętrze każdej regularnej
krzywej zamkniętej.
Obszar, który nie jest jednospójny nazywamy obszarem wielospójnym.
a
-a
-b
b
x
K
D
y
278
Przykład: Patrz Rys.11
a)
Obszarami jednospójnymi są m.in. koło bez brzegu, kwadrat bez brzegu, cała płaszczyzna.
(Rys.11a, b)
b)
Obszarem wielospójnym jest pierścień kołowy bez brzegów. Jest to obszar dwuspójny, gdyż jego
brzeg składa się z dwóch rozłącznych okręgów. (Rys.11c)
c)
Ogólnie: obszarem n – spójnym nazywamy obszar, którego brzeg składa się z n rozłącznych
regularnych krzywych zamkniętych.(Rys.11d)
a)
b)
c)
d)
Rys.11
Tw.1.7. (o niezależności całki krzywoliniowej od kształtu drogi całkowania)
Jeśli funkcje
)
,
( y
x
P
i
)
,
( y
x
Q
są klasy
1
C
(tzn. są ciągłe wraz z pochodnymi
x
Q
y
P
∂
∂
∂
∂
,
) w obszarze
jednospójnym D, to spełnienie równości:
y
P
x
Q
∂
∂
=
∂
∂
w każdym punkcie tego obszaru jest warunkiem koniecznym i wystarczającym na to, żeby całka
∫
+
AB
dy
y
x
Q
dx
y
x
P
)
,
(
)
,
(
na otwartej krzywej
AB
K
=
regularnej (łączącej punkty A i B ) oraz leżącej całkowicie w obszarze D nie
zależała od kształtu tej krzywej, a tylko od punktów A i B.
Wniosek: Jeśli funkcje
)
,
( y
x
P
i
)
,
( y
x
Q
są klasy
1
C
i spełniają warunek
y
P
x
Q
∂
∂
=
∂
∂
w obszarze
jednospójnym D, to
0
)
,
(
)
,
(
=
+
∫
K
dy
y
x
Q
dx
y
x
P
.
Def.1.11. (różniczka zupełna funkcji
)
,
( y
x
F
)
Wyrażenie
dy
y
x
Q
dx
y
x
P
)
,
(
)
,
(
+
jest różniczką zupełną pewnej funkcji
)
,
( y
x
F
w obszarze D, jeśli w
każdym punkcie tego obszaru spełnione są warunki: (*)
)
,
(
),
,
(
y
x
Q
y
F
y
x
P
x
F
=
∂
∂
=
∂
∂
.
Def.1.12. (funkcja pierwotna układu dwóch funkcji, całkowanie różniczki zupełnej)
Funkcję
)
,
( y
x
F
spełniającą warunki (*) w obszarze D nazywamy funkcją pierwotną układu dwóch
funkcji
)
,
( y
x
P
i
)
,
( y
x
Q
w obszarze D.
Wyznaczenie funkcji pierwotnej
)
,
( y
x
F
nazywamy całkowaniem różniczki zupełnej.

279
Tw.1.8.
Warunkiem koniecznym i wystarczającym na to, aby wyrażenie
dy
y
x
Q
dx
y
x
P
)
,
(
)
,
(
+
było różniczką
zupełną pewnej funkcji
)
,
( y
x
F
w obszarze D jest, aby w obszarze D zachodziła równość:
y
P
x
Q
∂
∂
=
∂
∂
.
Wniosek: Warunkiem koniecznym i wystarczającym na to, aby w obszarze jednospójnym D całka
krzywoliniowa
∫
+
AB
dy
y
x
Q
dx
y
x
P
)
,
(
)
,
(
nie zależała od drogi całkowania, jest, aby wyrażenie
dy
y
x
Q
dx
y
x
P
)
,
(
)
,
(
+
było różniczką zupełną.
Tw.1.9.
Jeśli wyrażenie
dy
y
x
Q
dx
y
x
P
)
,
(
)
,
(
+
jest różniczką zupełną pewnej funkcji
)
,
( y
x
F
to
)
(
)
(
)
,
(
)
,
(
A
F
B
F
dy
y
x
Q
dx
y
x
P
AB
−
=
+
∫
gdzie
)
,
( y
x
F
dowolna funkcja pierwotna.
Uwaga:
Zapisujemy również
∫
∫
+
=
+
B
A
AB
dy
y
x
Q
dx
y
x
P
dy
y
x
Q
dx
y
x
P
)
,
(
)
,
(
)
,
(
)
,
(
,
co oznacza całkę krzywoliniową skierowaną od punktu A do punktu B niezależną od drogi całkowania.
Przykład: Obliczyć
(
)
(
)
∫
−
+
+
8
,
6
4
,
3
2
2
y
x
ydy
xdx
wzdłuż drogi przebiegającej w półpłaszczyźnie
0
>
y
.
W zadaniu
2
2
2
2
)
,
(
,
)
,
(
y
x
y
y
x
Q
y
x
x
y
x
P
+
=
+
=
.
Sprawdzamy, czy wyrażenie
dy
y
x
y
dx
y
x
x
2
2
2
2
+
+
+
jest różniczką zupełną?
Obliczamy pochodne cząstkowe:
(
)
(
)
(
)
3
2
2
2
3
2
2
'
2
1
2
2
2
2
1
y
x
xy
y
y
x
x
y
x
x
y
P
y
+
−
=
⋅
+
−
⋅
=
+
⋅
=
∂
∂
−
−
(
)
(
)
(
)
3
2
2
2
3
2
2
'
2
1
2
2
2
2
1
y
x
xy
x
y
x
y
y
x
y
x
Q
x
+
−
=
⋅
+
−
⋅
=
+
⋅
=
∂
∂
−
−
Stąd
0
2
2
>
+
∀
y
x
spełniony jest warunek
y
P
x
Q
∂
∂
=
∂
∂
, zatem powyższe wyrażenie jest różniczką
zupełną pewnej funkcji pierwotnej
)
,
( y
x
F
określonej na zewnątrz okręgu
2
2
2
ρ
=
+ y
x
, gdzie
0
>
ρ
jest dowolną stałą.
Wyznaczając funkcję pierwotną
)
,
( y
x
F
korzystamy z warunków:
)
,
(
),
,
(
y
x
Q
y
F
y
x
P
x
F
=
∂
∂
=
∂
∂
.
280
Wówczas mamy
(1)
2
2
y
x
x
x
F
+
=
∂
∂
(2)
2
2
y
x
y
y
F
+
=
∂
∂
Następnie całkujemy równanie (1) względem zmiennej x i otrzymujemy:
dx
y
x
x
dx
x
F
∫
∫
+
=
∂
∂
2
2
Stąd
dx
y
x
x
y
x
F
∫
+
=
2
2
2
2
1
)
,
(
czyli
)
(
2
2
1
)
,
(
2
2
y
y
x
y
x
F
ϕ
+
+
⋅
=
Zatem
(3)
)
(
)
,
(
2
2
y
y
x
y
x
F
ϕ
+
+
=
gdzie
)
( y
ϕ
jest dowolną funkcją różniczkowalną spełniającą rolę dowolnej stałej.
Równanie (3) różniczkujemy po zmiennej y, więc
)
(
2
2
1
2
2
y
y
y
x
y
F
ϕ′
+
⋅
+
=
∂
∂
Czyli
)
(
2
2
y
y
x
y
y
F
ϕ′
+
+
=
∂
∂
, ale z równania (2)
2
2
y
x
y
y
F
+
=
∂
∂
Przyrównując powyższe równania mamy:
0
)
(
=
ϕ′ y
czyli
C
y
=
ϕ )
(
Ostatecznie funkcja pierwotna ma postać:
C
y
x
y
x
F
+
+
=
2
2
)
,
(
Korzystając z Tw.1.9. obliczamy całkę krzywoliniową:
(
)
(
)
(
)
(
)
5
5
10
16
9
64
36
4
,
3
8
,
6
8
,
6
4
,
3
2
2
=
−
=
+
−
+
=
−
−
=
+
+
∫
−
F
F
y
x
ydy
xdx
Zatem nasza całka nie zależy od drogi całkowania, a jedynie od punktów
(
)
4
,
3
−
A
,
)
8
,
6
(
B
oraz
(
)
(
)
5
8
,
6
4
,
3
2
2
=
+
+
∫
−
y
x
ydy
xdx
Uwaga
: Wyznaczając funkcję pierwotną
)
,
( y
x
F
możemy również całkować równanie (2) względem
zmiennej y i wówczas:
dy
y
x
y
dy
y
F
∫
∫
+
=
∂
∂
2
2
.
Postępując
jak
w
poprzednim
przypadku
otrzymamy
równanie
(3’)
w
postaci:
)
(
)
,
(
2
2
x
y
x
y
x
F
ϕ
+
+
=
, gdzie
)
(x
ϕ
jest dowolną funkcją różniczkowalną spełniającą rolę dowolnej
stałej. Następnie po zróżniczkowaniu (3’) po zmiennej x i przyrównaniu otrzymanej równości do
równania (1) wyznaczymy następujący wzór funkcji pierwotnej
C
y
x
y
x
F
+
+
=
2
2
)
,
(
.
Wyszukiwarka
Podobne podstrony:
Microsoft Word L21 calka krzywolniowa
Microsoft Word W19 Calka podwojna
Microsoft Word W20 Calka potrojna
Microsoft Word L20 calka potrojna
Microsoft Word L19 Calka podwojna
Microsoft Word WE W9 Calka przez czesci, podst i wymierna
Microsoft Word WE W11 Calka oznaczona
Microsoft Word WE L11 Calka oznaczona i zastosowanie
Microsoft Word W14 Szeregi Fouriera
New Microsoft Word Document (2)
Nowy Dokument programu Microsoft Word (5)
Nowy Dokument programu Microsoft Word
Nowy Dokument programu Microsoft Word
Microsoft Word zrodla infor I czesc pprawiona 2 do wydr
Microsoft Word PARAMETRY KOMPUTERÓW mój
więcej podobnych podstron