
DYNAMIKA BUDOWLI
wszystko płynie
wszystko drga
Wszystkie procesy twórcze w przyrodzie dzieją się w stanach dalekich
od równowagi
.
Michał Heller
Szczęście w przestrzeniach Banacha, 1997
Gdańsk, 2007
Dynamika Budowli
Wydział Inżynierii Lądowej i Środowiska
Magdalena Rucka & Krzysztof Wilde
________________________________________________________________________________________________
2007-02-26
2
1. Drgania swobodne nietłumione
Drgania konstrukcji o jednym stopniu swobody:
1. Drgania swobodne:
a) Nietłumione:
0
mu ku
+
=
b) Tłumione:
0
mu cu ku
+
+
=
2. Drgania wymuszone:
( )
mu cu ku
p t
+
+
=
a) Siłą harmoniczną
0
( )
sin( )
p t
p
t
ω
=
b) Impulsem
c) Siłą dowolną
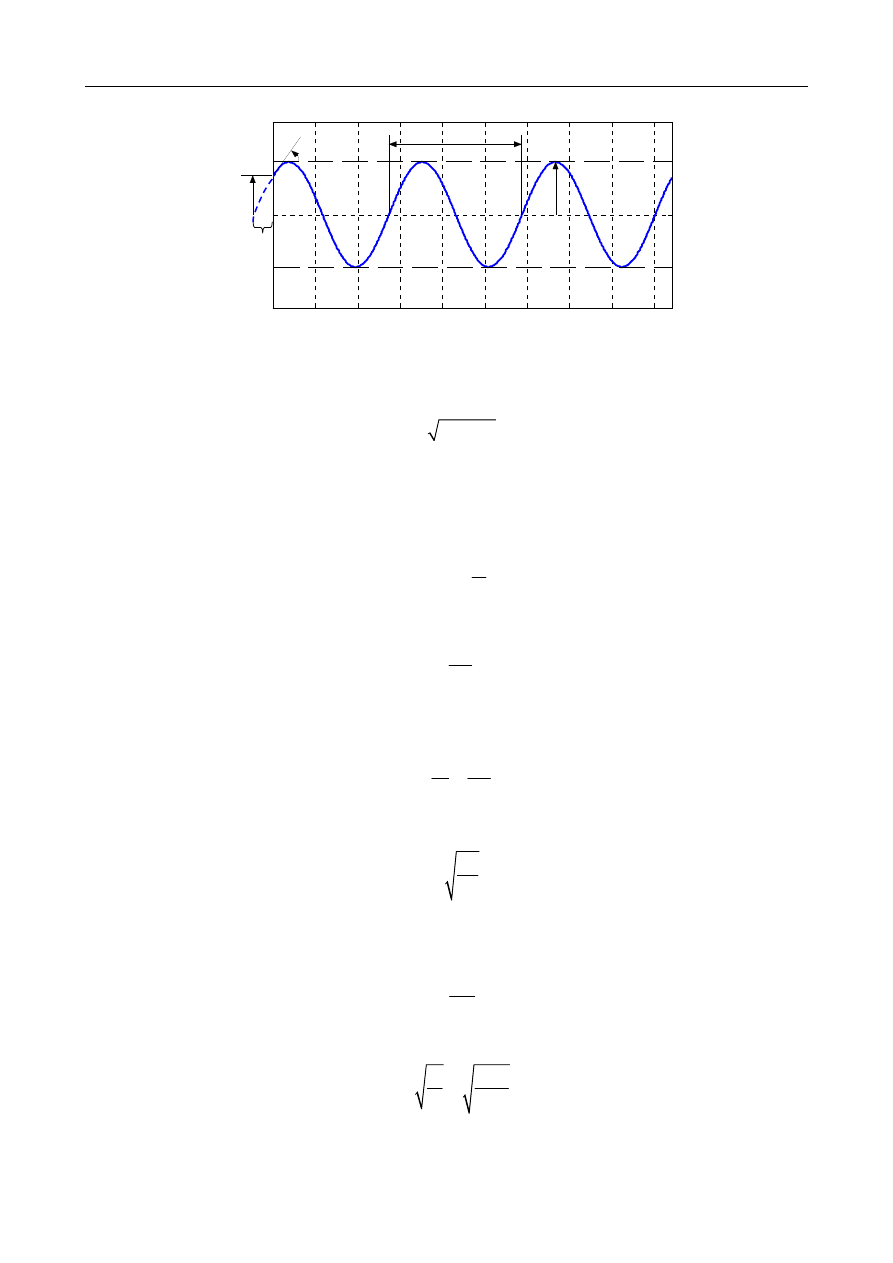
Drgania swobodne nietłumione
Siły sprężystości
s
f i bezwładności
i
f :
( )
( ),
s
f t
ku t
=
(1.1)
( )
( ).
i
f t
mu t
=
(1.2)
0
0.5
1
1.5
2
-3
-2
-1
0
1
2
3
t [s]
s
ila
[
N
]
sila bezwladosci f
i
sila sprezystosci f
s
-0.04
-0.02
0
0.02
0.04
-2
-1
0
1
2
u [m]
s
ila
[
N
]
sila bezwladosci f
i
sila sprezystosci f
s

Dynamika Budowli
Wydział Inżynierii Lądowej i Środowiska
Magdalena Rucka & Krzysztof Wilde
________________________________________________________________________________________________
2007-02-26
3
Drgania swobodne nietłumione opisane są następującym równaniem:
0
mu ku
+
=
, (1.3)
gdzie m oznacza masę, k sztywność. Drgania swobodne zapoczątkowane są poprzez wytrącenie
układu z pozycji równowagi poprzez warunki początkowe, tzn. przyłożenie wychylenia początko-
wego
0
u lub/i prędkości początkowej
0
u w czasie
0
t
=
. Warunki początkowe mają następującą po-
stać:
0
0
(0)
, (0)
u
u
u
u
=
= . (1.4)
Równanie (1.3) wraz z warunkami początkowymi (1.4) tworzy zagadnienie własne. Rozwiązanie
powyższego równania stanowią w dynamice konstrukcji drgania własne nierzeczywistego układu
bez tłumienia.
Równanie charakterystyczne ma postać:
2
0
ms
k
+ = . (1.5)
Jego rozwiązaniem są dwa pierwiastki zespolone:
1
2
s
n
n
s
i
i
ω
ω
=
= −
, (1.6)
gdzie
n
ω
oznacza częstość kołową drgań (naturalną) mierzoną w rad/s wyrażoną wzorem:
n
k
m
ω
=
. (1.7)
Rozwiązaniem ogólnym równania (1.3) jest:
1
2
1
2
1
2
( )
n
n
i t
i t
s t
s t
u t
A e
A e
A e
A e
ω
ω
−
=
+
=
+
. (1.8)
Korzystając z zależności między funkcjami wykładniczymi a trygonometrycznymi:
cos
sin
,
cos
sin
,
n
n
i t
n
n
i t
n
n
e
t i
t
e
t i
t
ω
ω
ω
ω
ω
ω
−
=
+
=
−
(1.9)
równanie (1.8) może być zapisane jako:
( )
cos
sin
n
n
u t
A
t B
t
ω
ω
=
+
. (1.10)
Stałe A oraz B zostaną wyznaczone z warunków brzegowych (1.4):
(0)
(0)
n
u
A u
B
ω
=
=
. (1.11)
Dynamika Budowli
Wydział Inżynierii Lądowej i Środowiska
Magdalena Rucka & Krzysztof Wilde
________________________________________________________________________________________________
2007-02-26
4
0
2
4
6
8
10
12
14
16
18
-0.5
0
0.5
u(0)
u(0)
.
T
n
C
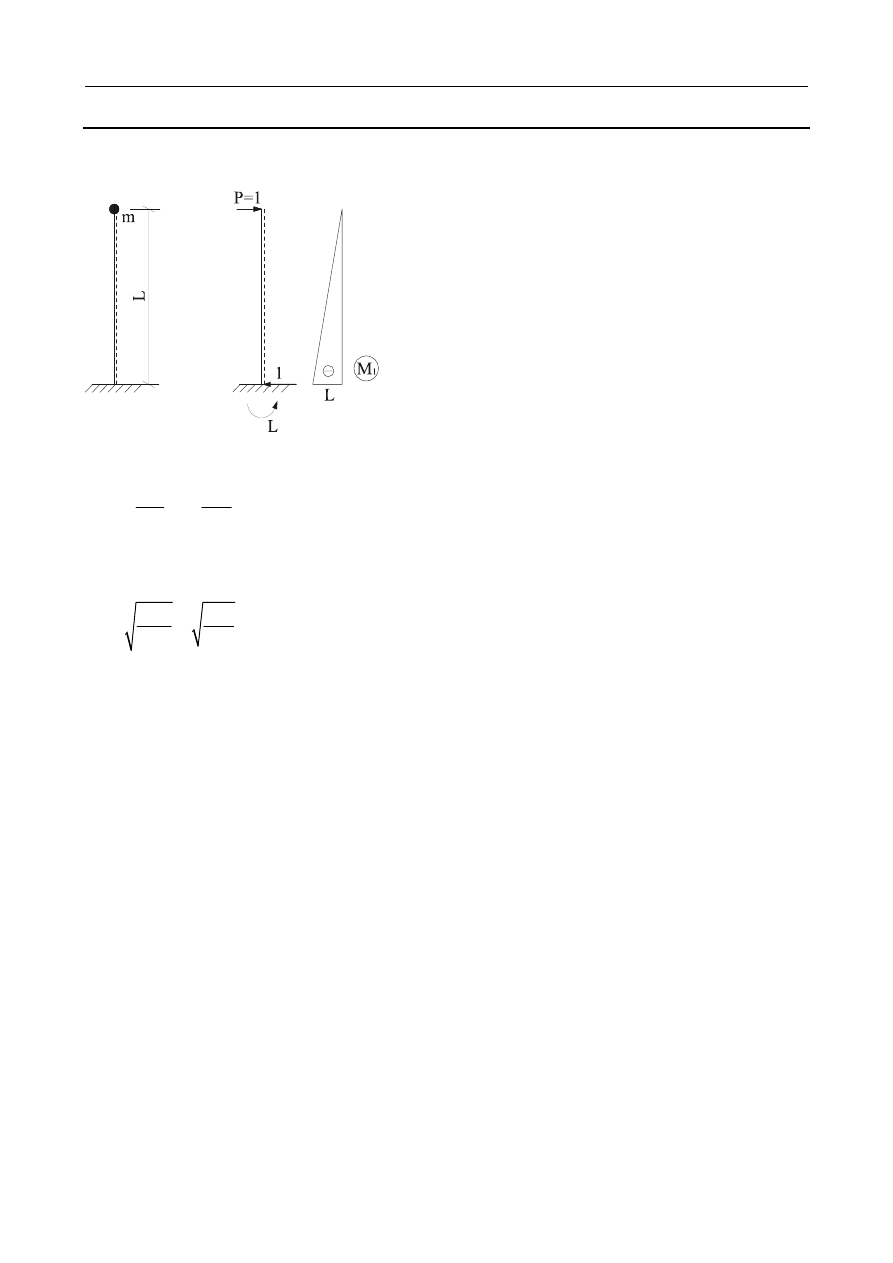
Amplituda drgań zależna od warunków początkowych:
2
2
C
A
B
=
+
(1.12)
pozwala zapisać wzór (1.10) w postaci zwiniętej:
( )
sin(
)
n
u t
C
t
ω
ϕ
=
+
, (1.13)
gdzie:
A
arctg
B
ϕ
=
. (1.14)
Czas potrzebny do wykonania jednego cyklu drgań nazywany jest okresem drgań:
2
n
n
T
π
ω
=
. (1.15)
Częstotliwość mierzona w Hertzach wyraża się następującym wzorem:
1
2
n
n
n
f
T
ω
π
=
=
. (1.16)
Naturalna częstość kołowa drgań może być wyrażona w alternatywnej formie:
n
st
g
ω
δ
=
, (1.17)
gdzie ugięcie statyczne
st
δ
wyraża się wzorem:
st
mg
k
δ
=
. (1.18)
Stąd wzór (1.17) zapisać można jako:
1
n
st
k
m
m
ω
δ
=
=
. (1.19)
Drgania swobodne nietłumione zaprezentowane są w pliku
cw1_01.m
t [s]
u [m]
f
Dynamika Budowli
Wydział Inżynierii Lądowej i Środowiska
Magdalena Rucka & Krzysztof Wilde
________________________________________________________________________________________________
2007-02-26
5
Z
ADANIE
1.1
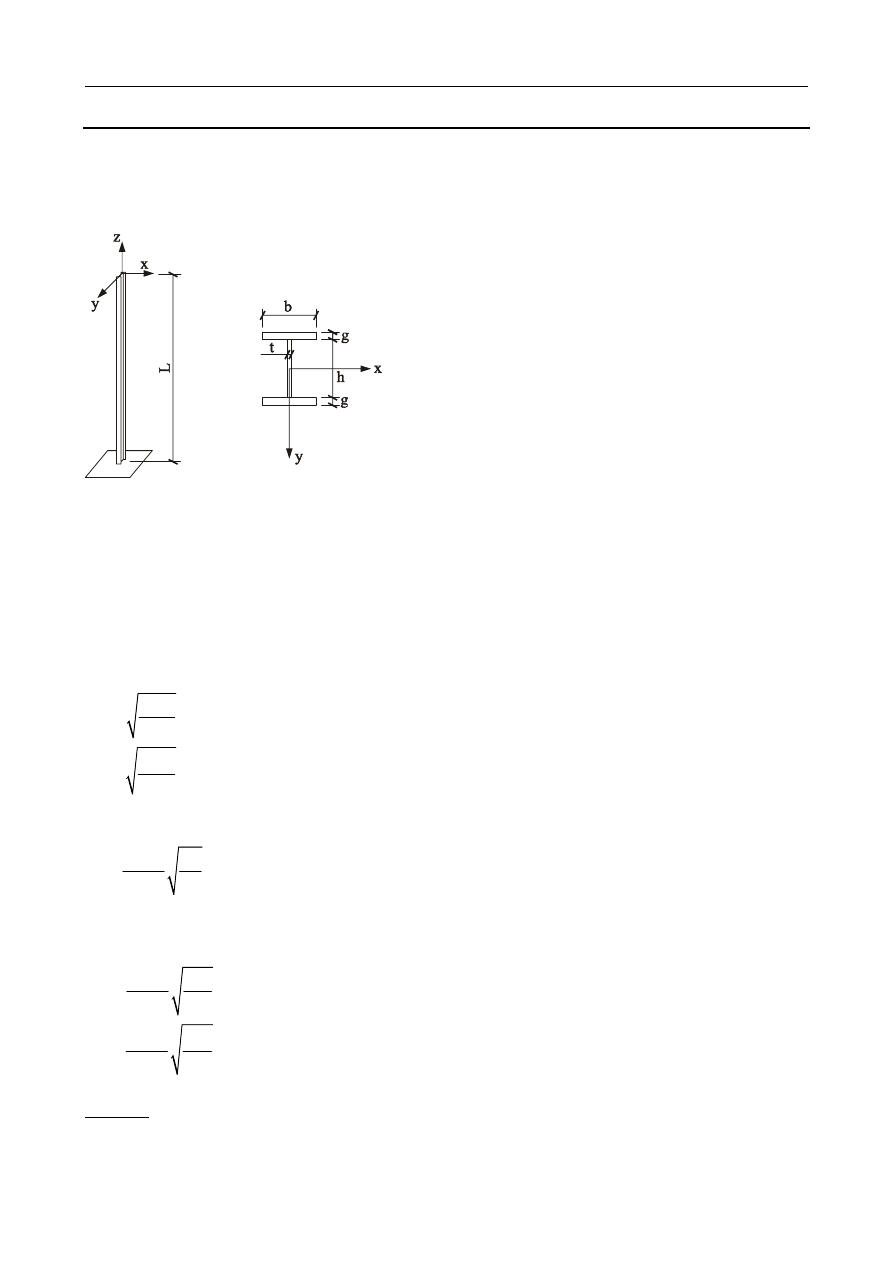
Dany jest wspornik o długości
L, z masą m skupioną na jego końcu, EI = const. Obliczyć częstość
drgań swobodnych nietłumionych.
2
3
1
11
0
3
L
M
L
ds
EI
EI
δ
=
=
∫
3
11
1
3
n
EI
m
mL
ω
δ
=
=
Dynamika Budowli
Wydział Inżynierii Lądowej i Środowiska
Magdalena Rucka & Krzysztof Wilde
________________________________________________________________________________________________
2007-02-26
6
Z
ADANIE
1.2
Dany jest wspornik o długości L = 2 m wykonany ze stali o module sprężystości E = 200GPa i gę-
stości
ρ
= 7850kg/m
3
. Belka ma przekrój dwuteowy o następujących wymiarach: b = 10 cm,
h = 12 cm, g = 2 cm, t = 1 cm. Obliczyć częstotliwości drgań w obu kierunkach. Z jakiej długości
wspornika należy skupić masę, aby otrzymać poprawne wyniki?
Charakterystyki geometryczne przekroju poprzecznego:
Pole powierzchni
2
52 cm
A
=
Momenty bezwładności:
4
4
2117.333 cm
334.333 cm
x
y
I
I
=
=
Masa skupiona z ¼ długości belki
20.41 kg
M
=
3
3
3
278.93 rad/s
44.39 Hz
3
110.84 rad/s
17.64 Hz
y
y
x
n
n
y
x
x
n
n
EI
f
mL
EI
f
mL
ω
ω
=
=
⇒
=
=
=
⇒
=
Porównując z analitycznym wzorem na pierwszą częstość drgań wspornika o masie rozłożonej
μ
:
1
2
3.515 EI
L
ω
μ
=
masa rozłożona po długości belki
40.82 kg/m
μ
=
2
2
3.515
283.03 rad/s
45.05 Hz
3.515
112.47 rad/s
17.90 Hz
y
y
x
n
n
y
x
x
n
n
EI
f
L
EI
f
L
ω
μ
ω
μ
=
=
⇒
=
=
=
⇒
=
Wniosek: skupienie masy z ¼ długości wspornika i wymodelowanie przy użyciu jednego stopnia
swobody dobrze odzwierciedla pierwszą częstość drgań.
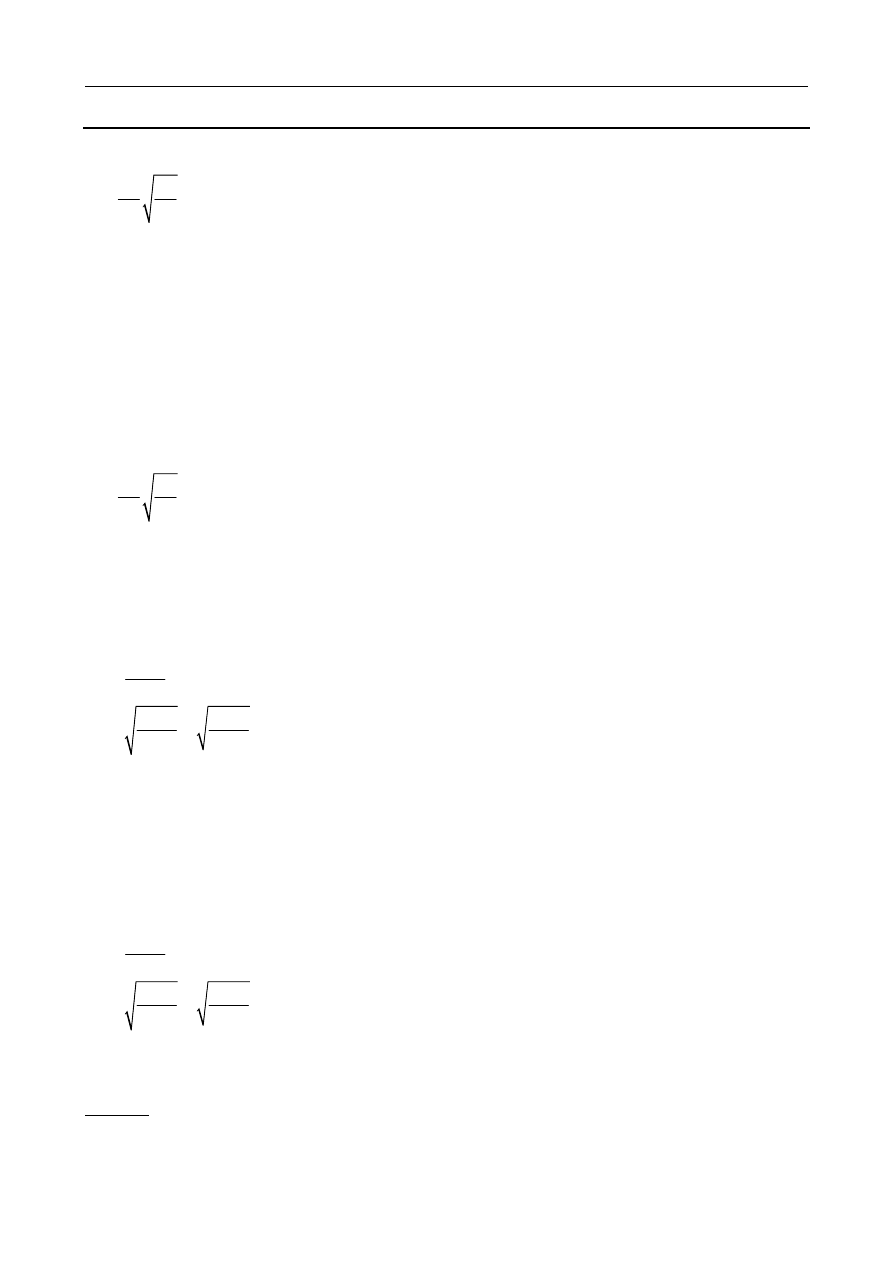
Dynamika Budowli
Wydział Inżynierii Lądowej i Środowiska
Magdalena Rucka & Krzysztof Wilde
________________________________________________________________________________________________
2007-02-26
7
Z
ADANIE
1.3
Pierwsza częstość drgań belki swobodnie podpartej przy uwzględnieniu rzeczywistego ciągłego
rozkładu masy dana jest wzorem:
2
2
EI
L
π
ω
μ
=
.
Z jakiej długości belki swobodnie podpartej należy skupić masę, aby otrzymać poprawną częstość
drgań swobodnych. Przyjąć belkę długości L = 1200 mm, o wysokości przekroju h = 20 i szeroko-
ści b = 60 mm wykonaną z pleksiglasu; gęstość pleksiglasu wynosi r = 1190 kg/m
3
a moduł sprę-
żystości E = 3300 MPa.
8
4
4 10 m
x
I
−
= ⋅
1.428 kg/m
μ
=
Rzeczywista częstość drgań wynosi:
2
2
65.90 rad/s
EI
L
π
ω
μ
=
=
Masa skupiona do środka belki z ½ L:
0.8568 kg
M
=
3
11
48
L
EI
δ
=
3
11
1
48
65.42 rad/s
n
EI
M
ML
ω
δ
=
=
=
Masa skupiona do środka belki z L:
1.7136 kg
M
=
3
11
48
L
EI
δ
=
3
11
1
48
46.26 rad/s
n
EI
M
ML
ω
δ
=
=
=
Wniosek: w przypadku modelowania belki swobodnie podpartej za pomocą jednego stopnia swobo-
dy masę należy zbierać z ½ długości belki.
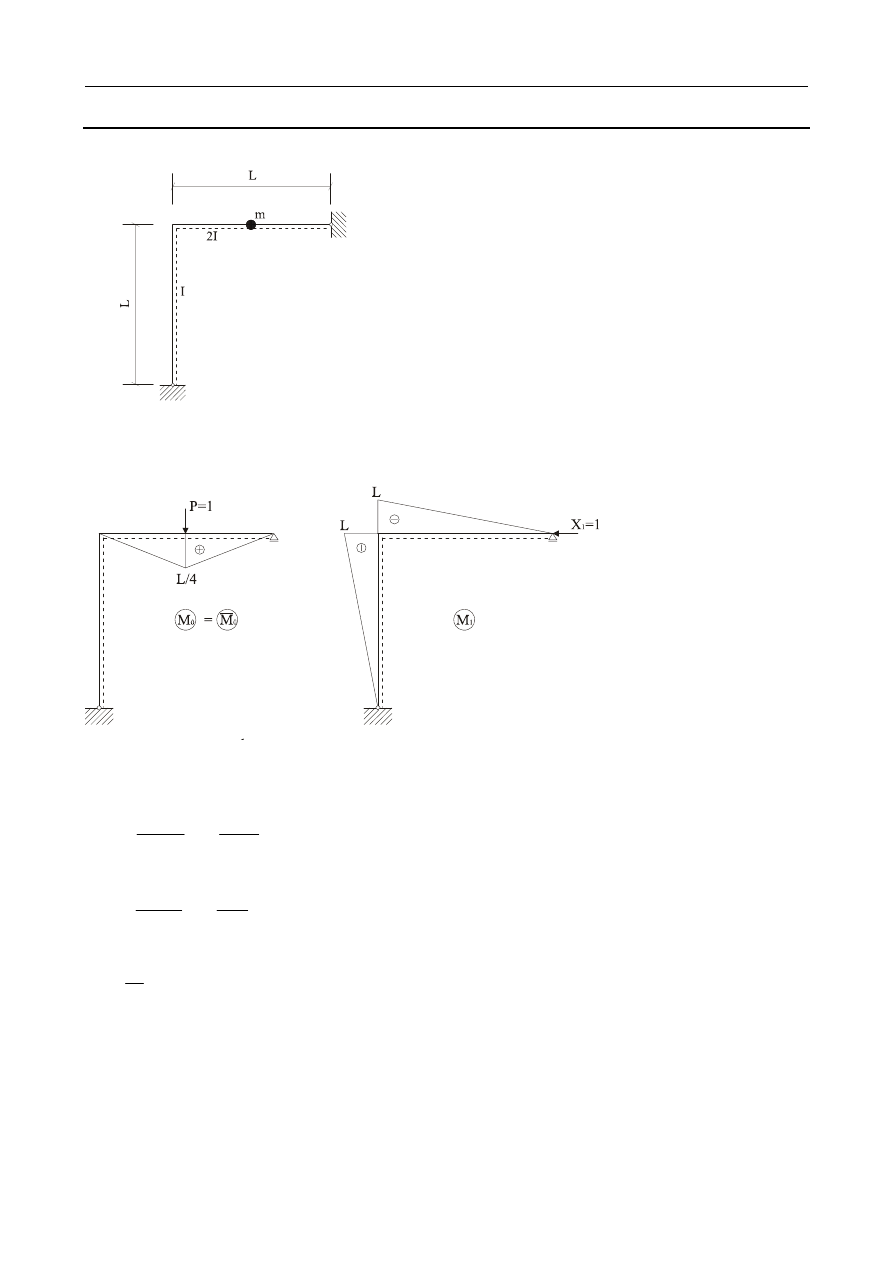
Dynamika Budowli
Wydział Inżynierii Lądowej i Środowiska
Magdalena Rucka & Krzysztof Wilde
________________________________________________________________________________________________
2007-02-26
8
Z
ADANIE
1.4
Dana jest rama jak na rysunku. Obliczyć częstość drgań swobodnych, jeżeli EI = const.
Jest to układ statycznie niewyznaczalny, rozważyć musimy dwa stany: obciążenie obciążeniem ze-
wnętrznym, oraz nadliczbową reakcją:
10
11
1
0
X
δ
δ
+
=
3
1
0
10
0
32
L
M M
L
dx
EI
EI
δ
−
=
=
∫
3
1
1
11
0
2
L
M M
L
dx
EI
EI
δ
=
=
∫
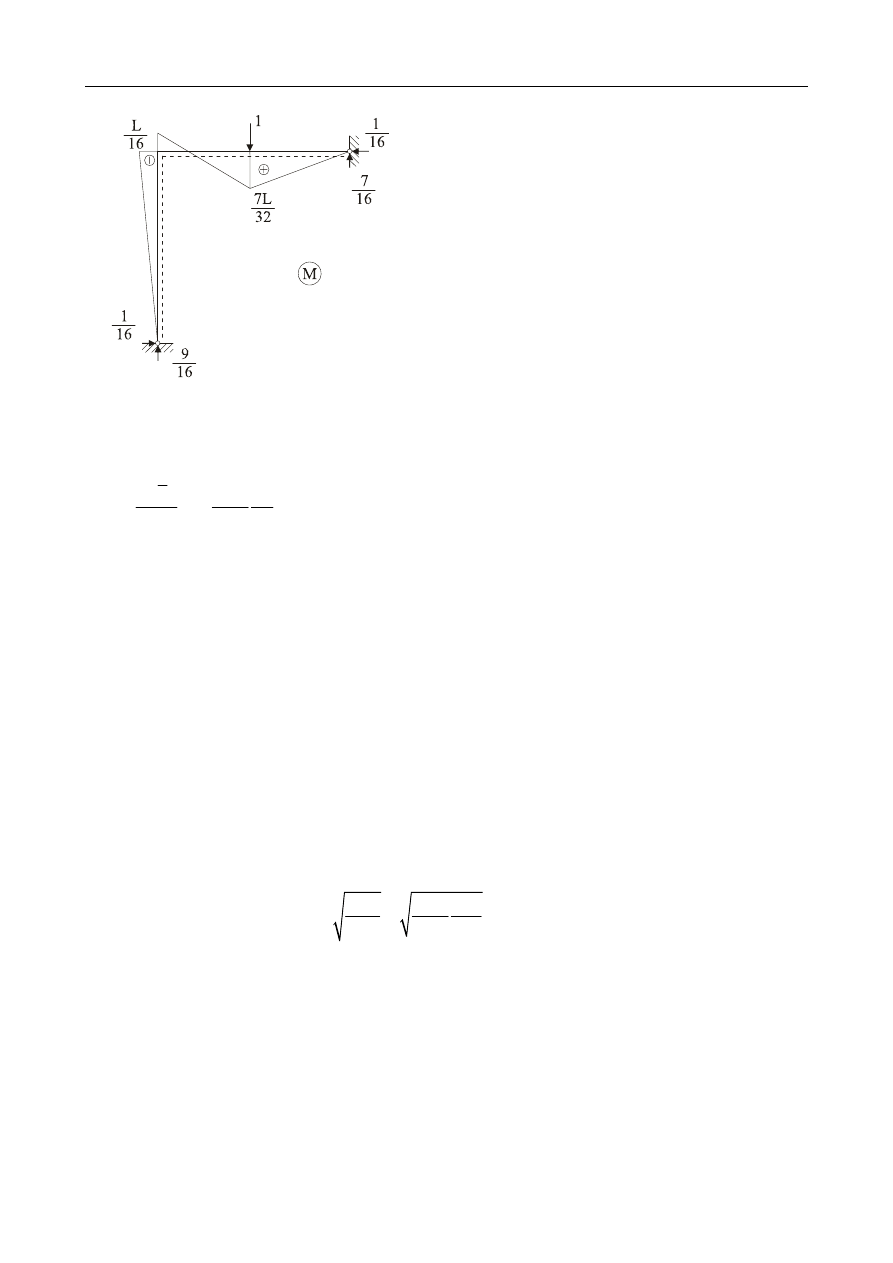
1
1
16
X
=
Dynamika Budowli
Wydział Inżynierii Lądowej i Środowiska
Magdalena Rucka & Krzysztof Wilde
________________________________________________________________________________________________
2007-02-26
9
Aby obliczyć przemieszczenie od siły P = 1 w układzie statycznie niewyznaczalnym możemy sko-
rzystać z twierdzenia redukcyjnego:
3
0
11
0
13
1536
L
MM
L
dx
EI
EI
δ
=
=
∫
Częstość drgań naturalnych:
3
11
1
1536
13
n
EI
m
mL
ω
δ
=
=

Dynamika Budowli
Wydział Inżynierii Lądowej i Środowiska
Magdalena Rucka & Krzysztof Wilde
________________________________________________________________________________________________
2007-02-26
10
Z
ADANIE
1.5
Wyznaczyć boczną sztywność ramy oraz odpowiadającą jej częstość drgań własnych.
a)
b
EI
= ∞ ; b)
0
b
EI
= ; c)
.
b
EI
const
=
Odp. a)
3
24
c
EI
k
h
=
; b)
3
6
c
EI
k
h
=
; c=
3
96
7
c
EI
k
h
=

Dynamika Budowli
Wydział Inżynierii Lądowej i Środowiska
Magdalena Rucka & Krzysztof Wilde
________________________________________________________________________________________________
2007-02-26
11
2. Więzi sprężyście odkształcalne
a) Połączenie szeregowe
Sumaryczne przemieszczenie układu sprężyn:
1
2
n
u u
u
u
= +
+ +
…
. (2.1)
W każdej sprężynie działa stała siła:
1
2
1
2
,
,
,
n
n
P
P
P
u
u
u
k
k
k
=
=
=
…
. (2.2)
Po podstawieniu otrzymujemy:
1
2
1
1
1
n
P
u P
k
k
k
k
⎛
⎞
=
+
+ +
=
⎜
⎟
⎝
⎠
…
, (2.3)
gdzie k oznacza sztywność zastępczą układu szeregowego:
1
1
2
1
1
1
1
1
n
i
n
i
k
k
k
k
k
=
=
+
+ +
=
∑
…
. (2.4)
1
P ku
P
k
u
u
k
P
δ
=
=
= =
1
2
1
1
1
k
k
k
=
+

Dynamika Budowli
Wydział Inżynierii Lądowej i Środowiska
Magdalena Rucka & Krzysztof Wilde
________________________________________________________________________________________________
2007-02-26
12
b) Połączenie równoległe
Siła działająca na układ jest sumą sił występujących we wszystkich sprężynach:
1
2
n
P P P
P
= +
+ +
…
. (2.5)
Przemieszczenie jest jednakowe dla wszystkich sprężyn:
1
1
2
2
n
n
P
k u P
k u
P
k u
=
=
=
…
. (2.6)
Po podstawieniu otrzymujemy:
1
2
(
)
n
P u k
k
k
ku
=
+ + +
=
…
, (2.7)
gdzie k oznacza sztywność zastępczą połączenia równoległego:
1
2
1
n
n
i
i
k k
k
k
k
=
= + + +
=
∑
…
. (2.8)
1
2
k k
k
= +
Dynamika Budowli
Wydział Inżynierii Lądowej i Środowiska
Magdalena Rucka & Krzysztof Wilde
________________________________________________________________________________________________
2007-02-26
13
Z
ADANIE
2.1
Wyznaczyć sztywność układu i częstość drgań swobodnych, jeżeli EI = const,
3
9
B
EI
k
L
=
.
Schemat rozpatrzymy jako superpozycję dwóch stanów:
a) ugięcie punktu 1 przy założeniu, że w punkcie B istnieje podpora stała
2
3
1
1
0
8
L
M
L
dx
EI
EI
δ
=
=
∫
b) ugięcie punktu 1 przy założeniu, że nieskończenie sztywna belka opiera się na podporze spręży-
stej
3
1
6
B
B
B
L
R
k
EI
δ
=
=
3
2
3
2
4
B
L
EI
δ
δ
=
=
3
1
2
3
8
L
EI
δ δ δ
= +
=
3
1
8
3
EI
k
L
δ
= =
3
3
8
L
mEI
ω
=

Dynamika Budowli
Wydział Inżynierii Lądowej i Środowiska
Magdalena Rucka & Krzysztof Wilde
________________________________________________________________________________________________
2007-02-26
14
Z
ADANIE
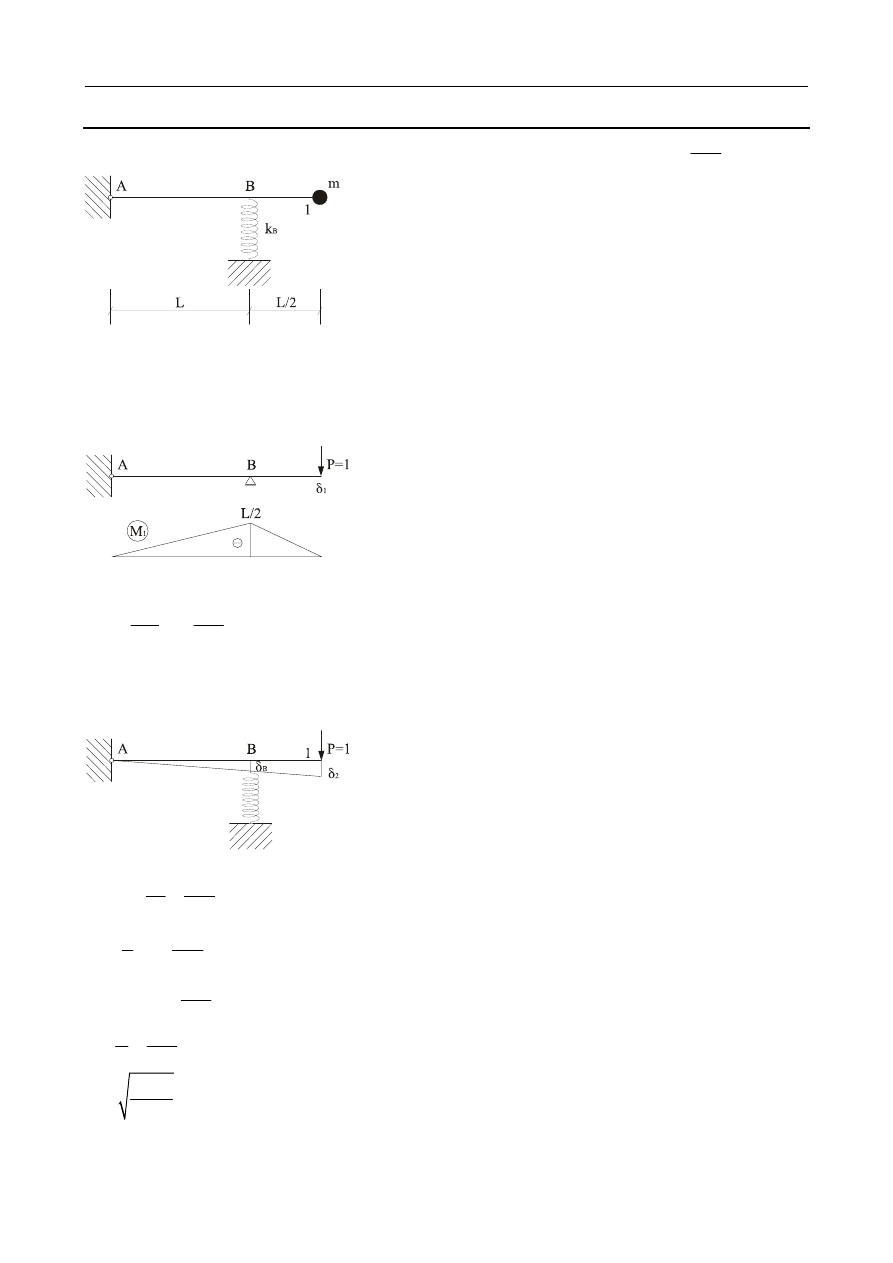
2.2
Wyznaczyć sztywność i częstość drgań układu jak na rysunku:
Sztywność sprężyny łączącej belki wynosi
3
96
s
EI
k
L
=
, EI = const.
Układ składa się z trzech części o ustalonej sztywności:
- belka górna
3
3
48
48
g
g
L
EI
k
EI
L
δ
=
=
- belka dolna
3
3
192
192
d
d
L
EI
k
EI
L
δ
=
=

Dynamika Budowli
Wydział Inżynierii Lądowej i Środowiska
Magdalena Rucka & Krzysztof Wilde
________________________________________________________________________________________________
2007-02-26
15
- sprężyna
3
96
s
EI
k
L
=
Belka dolna i sprężyna łączą się szeregowo w układ, który połączony jest z belką górną równolegle:
3
64
'
d s
d
s
k k
EI
k
k
k
L
=
=
+
Zastępcza sztywność układu:
3
112
'
g
EI
k k
k
L
=
+ =
3
112EI
mL
ω
=
Dynamika Budowli
Wydział Inżynierii Lądowej i Środowiska
Magdalena Rucka & Krzysztof Wilde
________________________________________________________________________________________________
2007-02-26
16
Z
ADANIE
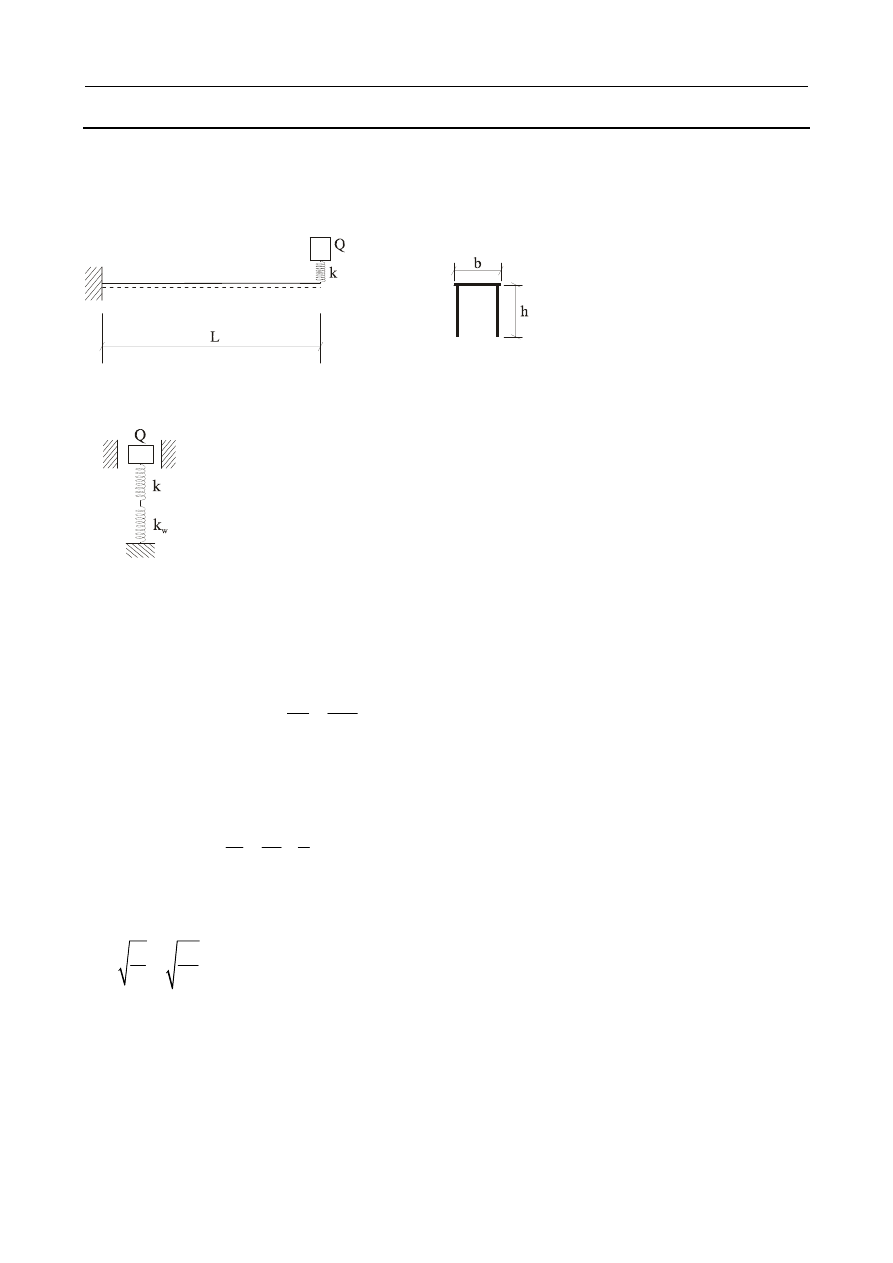
2.3
Obliczyć częstość drgań własnych maszyny o ciężarze Q = 3 kN znajdującej się na końcu belki
wspornikowej długości 3 m, o przekroju jak na rysunku (b = 18 cm, h = 20 cm, grubość ścianki
d = 1 cm, E = 205 GPa), jeżeli pomiędzy belką a maszyną znajduje się podkładka o współczynniku
sprężystości k = 1 MN/m.
4
2574.713 cm
x
I
=
sztywność wspornika:
3
11
1
3
586462.406 N/m
w
EI
k
L
δ
=
=
=
sztywność podkładki: k = 1 MN/m
sztywność układu:
1
1
1
0.000002705
=369666.753 N/m
c
c
w
k
k
k
k
=
+ =
⇒
34.77 rad/s
k
kg
m
Q
ω
=
=
=

Dynamika Budowli
Wydział Inżynierii Lądowej i Środowiska
Magdalena Rucka & Krzysztof Wilde
________________________________________________________________________________________________
2007-02-26
17
Z
ADANIE
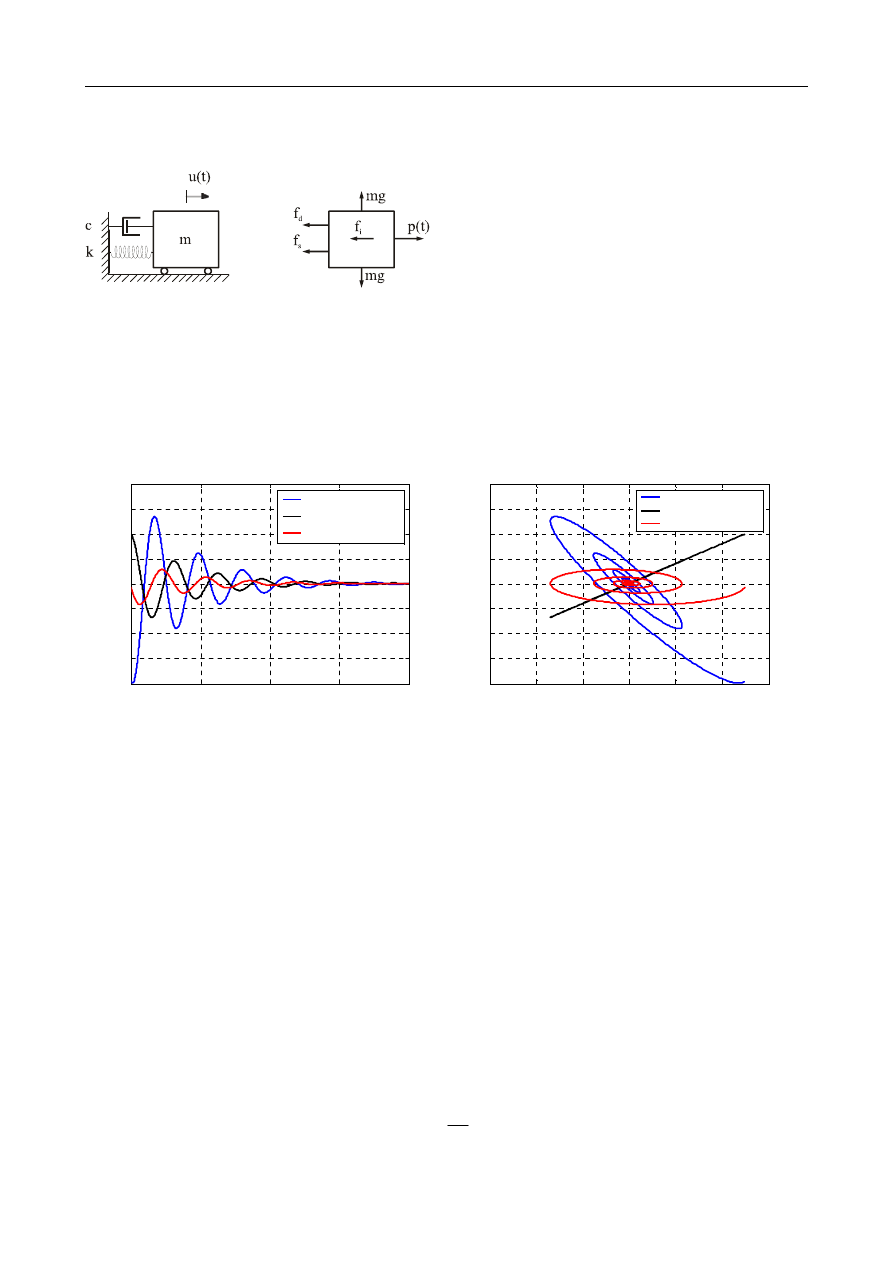
2.4
Znaleźć częstość drgań własnych, okres drgań oraz ilość drgań na minutę fundamentu o ciężarze
Q
= 2000kN. Pole powierzchni podstawy wynosi A = 10 m
2
, a współczynnik sprężystości podłoża
k
z
= 25 MN/m
3
.
Dynamika Budowli
Wydział Inżynierii Lądowej i Środowiska
Magdalena Rucka & Krzysztof Wilde
________________________________________________________________________________________________
2007-02-26
18
3. Drgania swobodne tłumione
Siły sprężystości
s
f
, bezwładności
i
f
dane są wzorami (1.1) i (1.2) natomiast siła tłumienia
d
f
zdefiniowana jest następująco:
( )
( )
d
f t
cu t
=
. (3.1)
0
5
10
15
20
-2
-1.5
-1
-0.5
0
0.5
1
1.5
2
t [s]
si
ly
f
i
f
s
f
d
[N
]
sila bezwladosci f
i
sila sprezystosci f
s
sila tlumienia f
d
-0.4
-0.2
0
0.2
0.4
0.6
-2
-1.5
-1
-0.5
0
0.5
1
1.5
2
u [m]
si
ly
f
i
f
s
f
d
[N
]
sila bezwladosci fi
sila sprezystosci fs
sila tlumienia fd
Drgania swobodne tłumione opisane są następującym równaniem:
0
mu cu ku
+
+
=
(3.2)
gdzie m oznacza masę, k sztywność, c tłumienie. Warunki początkowe, czyli wychylenie początko-
we
0
u
i/lub prędkość początkowa
0
u
, mają następującą postać:
0
0
(0)
(0)
u
u
u
u
=
= . (3.3)
Równanie charakterystyczne jest postaci:
2
0
ms
cs k
+ + = . (3.4)
Jeżeli zdefiniujemy liczbę tłumienia jako:
kr
c
c
ξ
=
, (3.5)
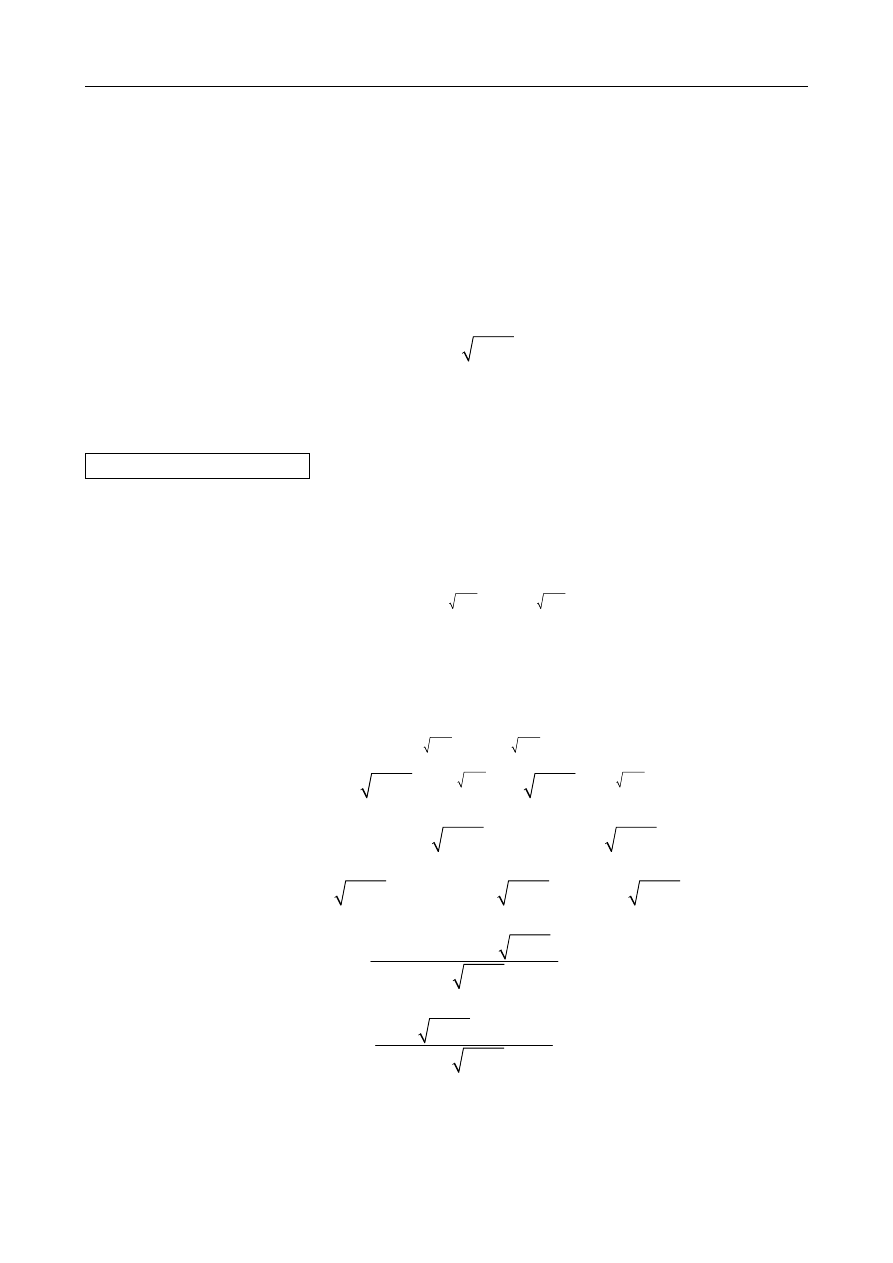
Dynamika Budowli
Wydział Inżynierii Lądowej i Środowiska
Magdalena Rucka & Krzysztof Wilde
________________________________________________________________________________________________
2007-02-26
19
gdzie
kr
c
oznacza tłumienie krytyczne:
2
kr
n
c
m
ω
=
, (3.6)
równanie (3.4) można zapisać w formie:
2
2
2
0
n
n
s
s
ξω
ω
+
+
= . (3.7)
Jego rozwiązaniem są dwa pierwiastki:
2
1,2
1
n
n
s
ξω ω ξ
= −
±
−
. (3.8)
Pierwiastki (3.8) mogą być rzeczywiste lub urojone, w zależności od wartości liczby
ξ
. Rozważy-
my 3 przypadki:
1
ξ
> - tłumienie nadkrytyczne
Pierwiastki (3.8) równania (3.4) są rzeczywiste, a odpowiedź układu opisuje następujące równanie:
1
2
1
2
( )
s t
s t
u t
C e
C e
=
+
(3.9)
czyli:
2
2
1
1
1
2
( )
(
)
n
n
n
t
t
t
u t
e
C e
C e
ω
ξ
ω
ξ
ξω
−
−
−
−
=
+
. (3.10)
Z warunków brzegowych mamy:
0
1
2
1
0
2
(
0)
u t
u
C
C
C
u
C
=
=
=
+
⇒
=
−
(3.11)
2
2
2
2
1
1
1
2
1
1
2
2
1
2
( )
(
)(
)
(
1
1
)
n
n
n
n
n
n
t
t
t
n
t
t
t
n
n
u t
e
C e
C e
e
C e
C e
ω
ξ
ω
ξ
ξω
ω
ξ
ω
ξ
ξω
ξω
ω ξ
ω ξ
−
−
−
−
−
−
−
−
=
−
+
+
+
−
−
+
−
(3.12)
2
2
0
1
2
(
0)
(
1)
(
1)
n
n
n
n
u t
u
C
C
ξω ω ξ
ξω ω ξ
=
=
=
−
−
− +
−
+
− (3.13)
2
2
2
0
0
2
(
1)
(
1
1)
n
n
n
n
n
n
u
u
C
ξω ω ξ
ξω ω ξ
ξω ω ξ
=
−
−
− +
+
− −
+
− (3.14)
2
0
0
2
2
(
1)
2
1
n
n
n
u
u
C
ξω ω ξ
ω ξ
−
−
−
−
=
−
(3.15)
2
0
0
1
2
(
1
)
2
1
n
n
n
u
u
C
ω ξ
ξω
ω ξ
− −
−
=
−
(3.16)
Dynamika Budowli
Wydział Inżynierii Lądowej i Środowiska
Magdalena Rucka & Krzysztof Wilde
________________________________________________________________________________________________
2007-02-26
20
Po uwzględnieniu warunków brzegowych:
2
2
2
2
2
2
2
2
1
1
0
0
0
0
2
2
1
1
1
1
0
0
0
2
(
1
)
(
1)
( )
(
)
2
1
2
1
[ (
)
(
)]
2
2
1
n
n
n
n
n
n
n
n
t
t
t
n
n
n
n
n
n
t
t
t
t
t
n
n
u
u
u
u
u t
e
e
e
u
u
e
e
e
e
e
u
ω
ξ
ω
ξ
ξω
ω
ξ
ω
ξ
ω
ξ
ω
ξ
ξω
ω ξ
ξω
ξω ω ξ
ω ξ
ω ξ
ξω
ω ξ
−
−
−
−
−
−
−
−
−
−
−
− −
−
−
−
−
−
=
+
=
−
−
+
+
−
=
+
−
(3.17)
Ostatecznie:
(
)
(
)
2
2
2
(0)
(0)
( )
(0) cosh
1
sinh
1
1
n
t
n
n
n
n
u
u
u t
e
u
t
t
ξω
ξω
ω
ξ
ω
ξ
ω ξ
−
⎛
⎞
+
⎜
⎟
=
− +
−
⎜
⎟
−
⎝
⎠
(3.18)
1
ξ
= - tłumienie krytyczne
Pierwiastki są rzeczywiste:
1
2
n
s
s
ξω
=
= −
. (3.19)
Odpowiedź układu:
(
)
1
2
( )
n
t
u t
e
C
C t
ω
−
=
+
. (3.20)
Z warunków brzegowych:
0
1
(
0)
u t
u
C
=
=
=
(3.21)
1
2
2
( )
(
)(
)
n
n
t
t
n
u t
e
C
C t
C e
ξω
ξω
ξω
−
−
=
−
+
+
(3.22)
0
1
2
2
0
0
(
0)
n
n
u t
u
C
C
C
u
u
ξω
ξω
=
=
= −
+
⇒
=
+
(3.23)
Po uwzględnieniu warunków brzegowych:
0
0
0
( )
[
(
) ]
n
t
n
u t
e
u
u
u t
ξω
ξω
−
=
+
+
(3.24)
(
)
( )
(0)(1
)
(0)
n
t
n
u t
e
u
t
u
t
ω
ω
−
=
+
+
(3.25)
1
ξ
< - tłumienie podkrytyczne
Pierwiastki są zespolone:
2
1,2
1
n
n
s
i
ξω
ω
ξ
= −
±
−
. (3.26)
Częstość drgań kołowych tłumionych zdefiniujmy jako:
2
1
D
n
ω
ω
ξ
=
−
. (3.27)
Odpowiedź układu:
1
2
1
2
( )
s t
s t
u t
C e
C e
=
+
, (3.28)
Dynamika Budowli
Wydział Inżynierii Lądowej i Środowiska
Magdalena Rucka & Krzysztof Wilde
________________________________________________________________________________________________
2007-02-26
21
czyli:
(
)
1
2
( )
n
D
D
t
i
t
i
t
u t
e
C e
C e
ξω
ω
ω
−
−
=
+
. (3.29)
Zamieniając na postać trygonometryczną:
(
)
( )
cos
sin
n
t
D
D
u t
e
A
t B
t
ξω
ω
ω
−
=
+
(3.30)
Uwzględniając warunki brzegowe:
0
(
0)
u t
u
A
=
=
= (3.31)
(
)
(
)
cos
sin
sin
cos
n
n
t
t
n
D
D
D
D
D
D
u
e
A
t B
t
e
A
t
B
t
ξω
ξω
ξω
ω
ω
ω
ω
ω
ω
−
−
= −
+
+
−
+
(3.32)
0
0
0
(
0)
n
n
D
D
u
u
u t
u
A
B
B
ξω
ξω
ω
ω
+
=
=
= −
+
⇒
=
(3.33)
0
0
0
( )
cos
sin
n
t
n
D
D
D
u
u
u t
e
u
t
t
ξω
ξω
ω
ω
ω
−
⎛
⎞
+
=
+
⎜
⎟
⎝
⎠
(3.34)
gdzie stałe A i B są następujące:
(0)
(0)
(0)
n
D
u
u
A u
B
ξω
ω
+
=
=
(3.35)
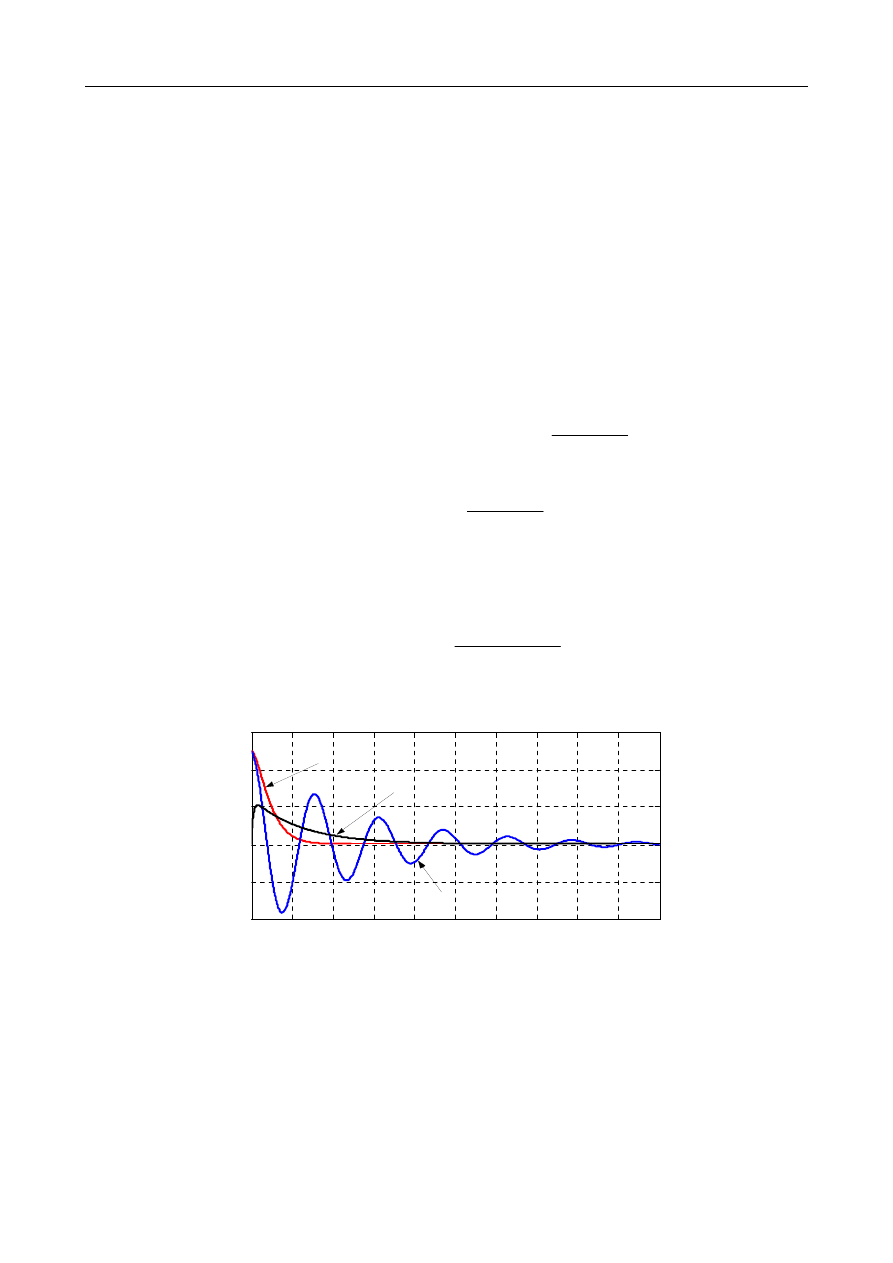
0
2
4
6
8
10
12
14
16
18
20
-0.4
-0.2
0
0.2
0.4
0.6
czas [s]
pr
z
em
ies
z
c
z
eni
e [
m
]
tlumienie krytyczne
ξ
=1
tlumienie podkrytyczne
ξ
<1
tlumienie nadkrytyczne
ξ
>1
Drgania swobodne tłumione zaprezentowane są w pliku cw2_01.m
Dynamika Budowli
Wydział Inżynierii Lądowej i Środowiska
Magdalena Rucka & Krzysztof Wilde
________________________________________________________________________________________________
2007-02-26
22
Logarytmiczny dekrement tłumienia
Liczbę tłumienia
ξ
można wyznaczyć eksperymentalnie poprzez pomiar drgań swobodnych.
W tym celu określić należy iloraz dwóch kolejnych maksymalnych wychyleń:
2
1
( )
2
exp
(
)
1
j
D
j
u
u t
u t T
u
πξ
ξ
+
⎛
⎞
⎜
⎟
=
=
⎜
⎟
+
−
⎝
⎠
(3.36)
Logarytmicznym dekrementem tłumienia
δ określa się wielkość będącą logarytmem naturalnym z
ilorazu dwóch kolejnych wychyleń:
2
1
2
ln
1
j
j
u
u
πξ
δ
ξ
+
=
=
−
(3.37)
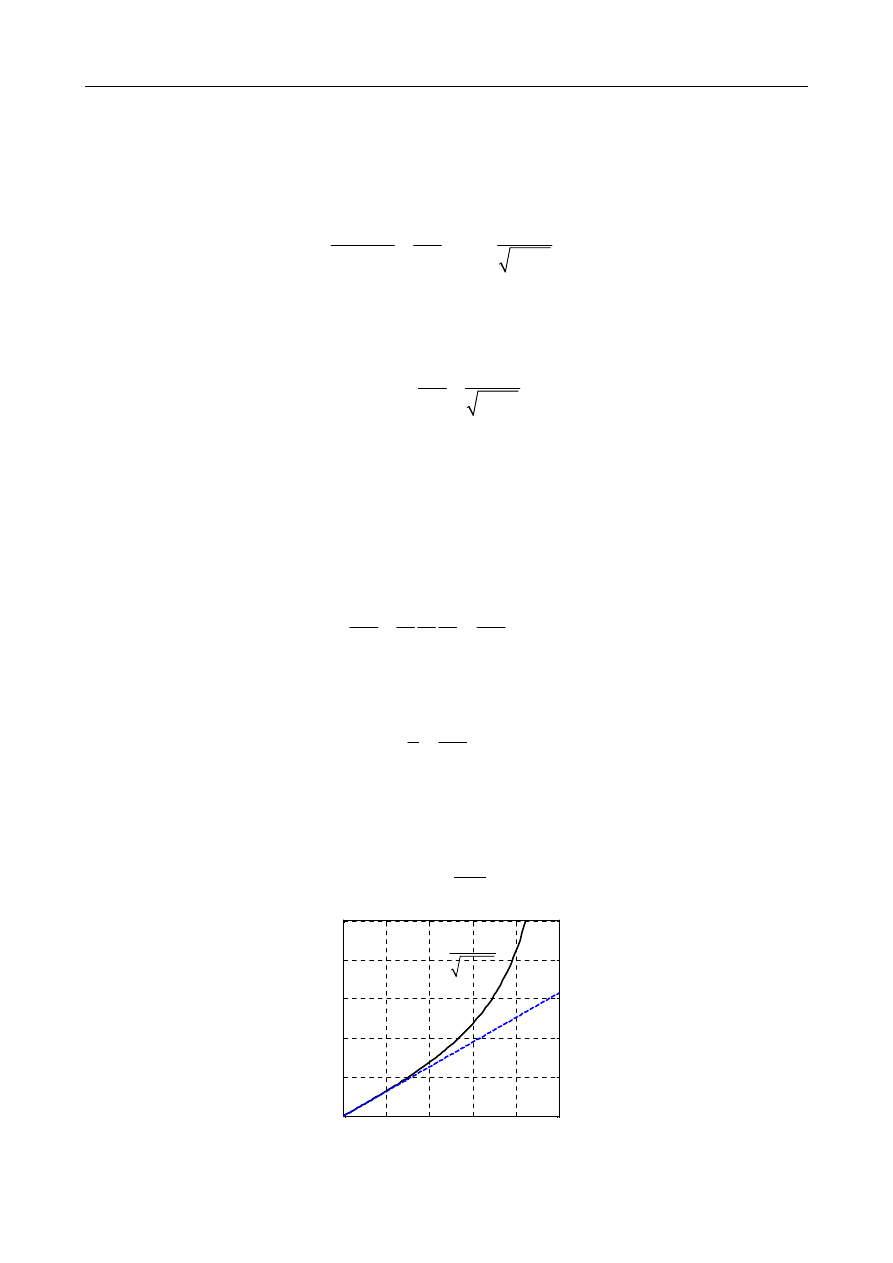
Jeżeli tłumienie
ξ
jest małe (
0.2
ξ
<
), co ma miejsce w rzeczywistych konstrukcjach, logarytmicz-
ny dekrement tłumienia może być uproszczony do postaci:
2
δ
πξ
(3.38)
Aby określić liczbę tłumienia, niekoniecznie trzeba posługiwać się ilorazem dwóch kolejnych am-
plitud. Po j cyklach amplituda zmniejsza wartość z
1
u do
1
j
u
+
:
3
1
1
2
1
2
3
4
1
j
j
j
j
u
u
u
u u
e
u
u u u
u
δ
+
+
=
=
(3.39)
a logarytmiczny dekrement tłumienia przyjmuje postać:
1
1
1
ln
2
j
u
j
u
δ
πξ
+
=
(3.40)
Stąd łatwo wyznaczyć liczbę cykli potrzebną do zmniejszenia amplitudy o zadaną wartość. Na
przykład liczba cykli j potrzebna do zmniejszenia amplitudy o 50 % wynosi:
50%
0.11
j
ξ
(3.41)
0
0.2
0.4
0.6
0.8
1
0
2
4
6
8
10
Liczba tłumienia
ξ
Lo
gar
yt
m
iczn
y de
kre
m
ent
tł
umien
ia
δ
2
2
1
πξ
δ
ξ
=
−
2
δ
πξ
=

Dynamika Budowli
Wydział Inżynierii Lądowej i Środowiska
Magdalena Rucka & Krzysztof Wilde
________________________________________________________________________________________________
2007-02-26
23
Z
ADANIE
3.1
Dany jest układ o znanej liczbie tłumienia
ξ
. Znaleźć liczbę cykli drgań swobodnych potrzebną do
redukcji amplitudy drgań do 10% w stosunku do amplitudy początkowej. Prędkość początkowa jest
równa zeru.
10%
0.366
j
ξ
Z
ADANIE
3.2
Dany jest zbiornik na wodę. Za pomocą kabla przymocowanego do
górnej części zbiornika przyłożono boczną siłę Q = 10 MN
powodując wychylenie zbiornika o 2 m. Kabel przecięto
wprowadzając konstrukcję w drgania. Po upływie 2 sekund, zbiornik
wykonał 4 pełne cykle drgań, a amplituda zmniejszyła się do 1 m.
Obliczyć:
a) liczbę tłumienia
b) okres drgań nietłumionych
c) sztywność
d) masę
e) tłumienie
f) liczbę cykli potrzebną do zmniejszenia amplitudy drgań do 0.2m.
a)
2.76%
ξ
=
b) 0.4998
s
n
T
=
c)
5 MN/m
k
=
d)
31.63955 t
m
=
e) 21955.29
kg/s
c
=
f) 13.28 cykli
j

Dynamika Budowli
Wydział Inżynierii Lądowej i Środowiska
Magdalena Rucka & Krzysztof Wilde
________________________________________________________________________________________________
2007-02-26
24
Z
ADANIE
3.3
Znaleźć częstość naturalną drgań i liczbę tłumienia belki wspornikowej na podstawie eksperymen-
talnie pomierzonego przyspieszenia swobodnego końca belki. Porównać wyznaczoną naturalną
częstość drgań z częstością wyznaczoną analitycznie poprzez skupienie masy belki do jednego
punktu. Wykonana z pleksiglasu belka ma długość L = 480 mm, a jej przekrój jest prostokątny wy-
sokości h = 20 i szerokości b = 60 mm. Gęstość pleksiglasu wynosi r = 1190kg/m
3
a moduł Youn-
ga E = 3300 MPa.
0
0.1
0.2
0.3
0.4
0.5
0.6
0.7
0.8
0.9
1
-80
-60
-40
-20
0
20
40
60
80
czas [s]
p
rz
y
s
pi
es
z
eni
e [
m
/s
2
]
u
5
=5.3293 m/s
2
t
5
=0.3794 s
..
u
11
=1.4088 m/s
2
t
11
=0.6376 s
..
1
ln
2
i
j i
u
j
u
ξ
π
+
=
5
11
1
1
5.3293
ln
ln
0.035 3.5%
2 6
12
1.4088
u
u
ξ
π
π
=
=
=
=
Ponieważ w czasie
0.6376
0.3794
0.2582
t
s
s
s
=
−
=
belka wykonuje 6 cykli drgań to okres drgań
tłumionych
D
T jest równy
0.2582 s
0.0403 s
6
D
T
=
=
Okres drgań naturalnych
2
2
1
0.0403 1 (0.035)
0.0402 s
n
D
T
T
ξ
=
−
=
−
=
Naturalna częstość drgań
2
2
156.298 rad/s
24.875 Hz
0.0402
2
n
n
n
n
f
T
ω
π
π
ω
π
=
=
=
⇒
=
=
Teraz obliczymy częstość drgań skupiając masę z ¼ długości wspornika:
0.17136 kg
M
=
8
4
4 10 m
x
I
−
= ⋅
3
3
144.554 rad/s
23.006 Hz
2
x
n
n
n
EI
f
ML
ω
ω
π
=
=
⇒
=
=
Dynamika Budowli
Wydział Inżynierii Lądowej i Środowiska
Magdalena Rucka & Krzysztof Wilde
________________________________________________________________________________________________
2007-02-26
25
Z
ADANIE
3.4
Maszyna o ciężarze Q = 250 kN zamocowana jest do podłoża za pomocą 4 sprężyn i 4 tłumików.
Pionowe przemieszczenie pod wpływem ciężaru własnego maszyny wynosi 0.8 cm. Tłumiki zapro-
jektowano tak, aby redukowały amplitudę pionowych drgań do 1/8 początkowej amplitudy po 2
cyklach drgań. Obliczyć:
a) częstość drgań nietłumionych;
b) liczbę tłumienia;
c) częstość drgań tłumionych.
Odp. 35.02
rad/s
n
ω
=
,
0.165
ξ
=
, 34.54
rad/s
d
ω
=
Dynamika Budowli
Wydział Inżynierii Lądowej i Środowiska
Magdalena Rucka & Krzysztof Wilde
________________________________________________________________________________________________
2007-02-26
26
4. Drgania
wymuszone
siłą harmoniczną
Drgania wymuszone siłą harmoniczną nietłumione
Drgania wymuszone sinusoidalną siłą harmoniczną nietłumione opisane są następującym równa-
niem:
0
sin
mu ku
p
t
ω
+
=
, (4.1)
gdzie m oznacza masę, k - sztywność,
ω - częstość siły wymuszającej,
0
p amplitudę siły wymu-
szającej. Warunki początkowe, czyli wychylenie początkowe
0
u i/lub prędkość początkowa
0
u ,
mają następującą postać:
0
0
(0)
(0)
u
u
u
u
=
= . (4.2)
Równanie (4.1) jest niejednorodne. Jego rozwiązanie jest sumą całki ogólnej i całki szczególnej:
( )
( )
( )
c
p
u t
u t
u t
=
+
. (4.3)
Całka ogólna równania jednorodnego:
0
mu ku
+
=
. (4.4)
Równanie charakterystyczne ma postać:
2
2
0
n
s
ω
+
= , (4.5)
1,2
n
s
i
ω
= ±
. (4.6)
Całka ogólna ma postać:
( )
cos
sin
c
n
n
u t
A
t B
t
ω
ω
=
+
. (4.7)
Całka szczególna równania niejednorodnego (4.1) ma postać:
( )
sin
cos
p
u t
D
t E
t
ω
ω
=
+
. (4.8)
Wyznaczenie stałych C i D:
cos
sin
p
u
D
t E
t
ω
ω
ω
ω
=
−
, (4.9)
2
2
sin
cos
p
u
D
t E
t
ω
ω
ω
ω
= −
−
. (4.10)
Podstawiając(4.9) i (4.10) do równania (4.1) zapisanego w postaci:
2
sin
o
n
p
u
u
t
m
ω
ω
+
=
, (4.11)
Dynamika Budowli
Wydział Inżynierii Lądowej i Środowiska
Magdalena Rucka & Krzysztof Wilde
________________________________________________________________________________________________
2007-02-26
27
2
2
2
2
sin
cos
sin
cos
sin
o
n
n
p
D
t E
t
D
t
E
t
t
m
ω
ω
ω
ω ω
ω ω
ω
ω
−
−
+
+
=
(4.12)
(
)
(
)
2
2
2
2
cos
sin
sin
o
n
n
p
t E
E
t D
D
t
m
ω
ω
ω
ω
ω
ω
ω
−
+
−
=
(4.13)
2
2
2
2
2
2
0
0
1
n
o
o
n
n
E
E
E
p
p
D
D
D
m
m
ω
ω
ω
ω
ω
ω
⎧
−
=
⇒
=
⎪
⎛
⎞
⎨
−
=
⇒
=
⎜
⎟
⎪
−
⎝
⎠
⎩
(4.14)
(
)
(
)
2
2
1
1
/
o
n
n
p
D
m
ω
ω ω
=
−
(4.15)
(
)
2
1
1
/
o
n
p
D
k
ω ω
=
−
(4.16)
Całka ogólna równania niejednorodnego (4.1):
( )
cos
sin
sin
n
n
u t
A
t B
t D
t
ω
ω
ω
=
+
+
. (4.17)
Wyznaczenie stałych A i B z warunków brzegowych (4.2):
(0)
o
u
A
A u
= ⇒ = (4.18)
( )
sin
cos
cos
n
n
n
n
u t
A
t B
t D
t
ω
ω
ω
ω
ω
ω
= −
+
+
(4.19)
(0)
o
n
n
u
D
u
B
D
B
ω
ω
ω
ω
−
=
+
⇒ =
(4.20)
(
)
(
)
2
/
1
/
o
o
n
n
n
u
p
B
k
ω ω
ω
ω ω
=
−
−
(4.21)
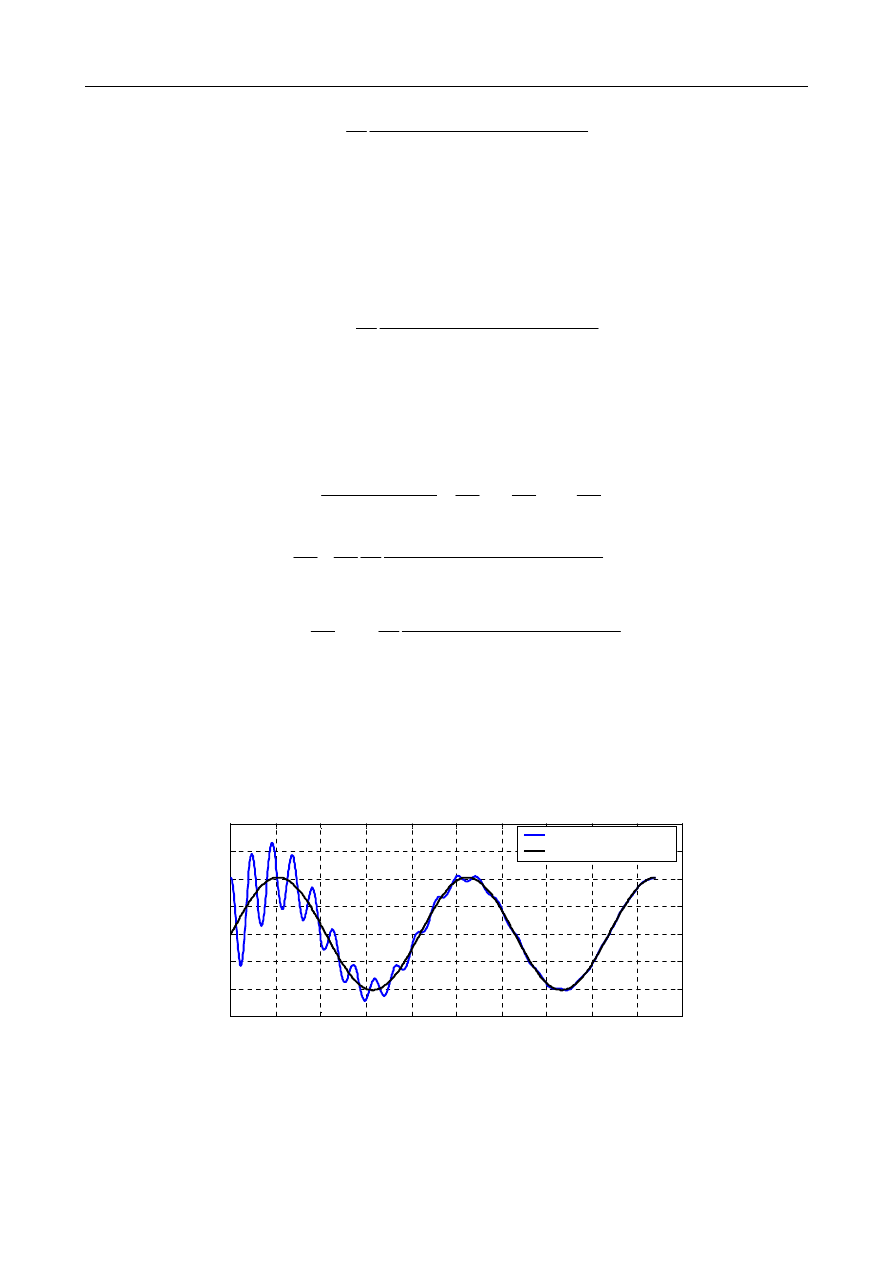
Po podstawieniu stałych A, B, D do równania (4.17) otrzymujemy ostateczną odpowiedź układu:
0
0
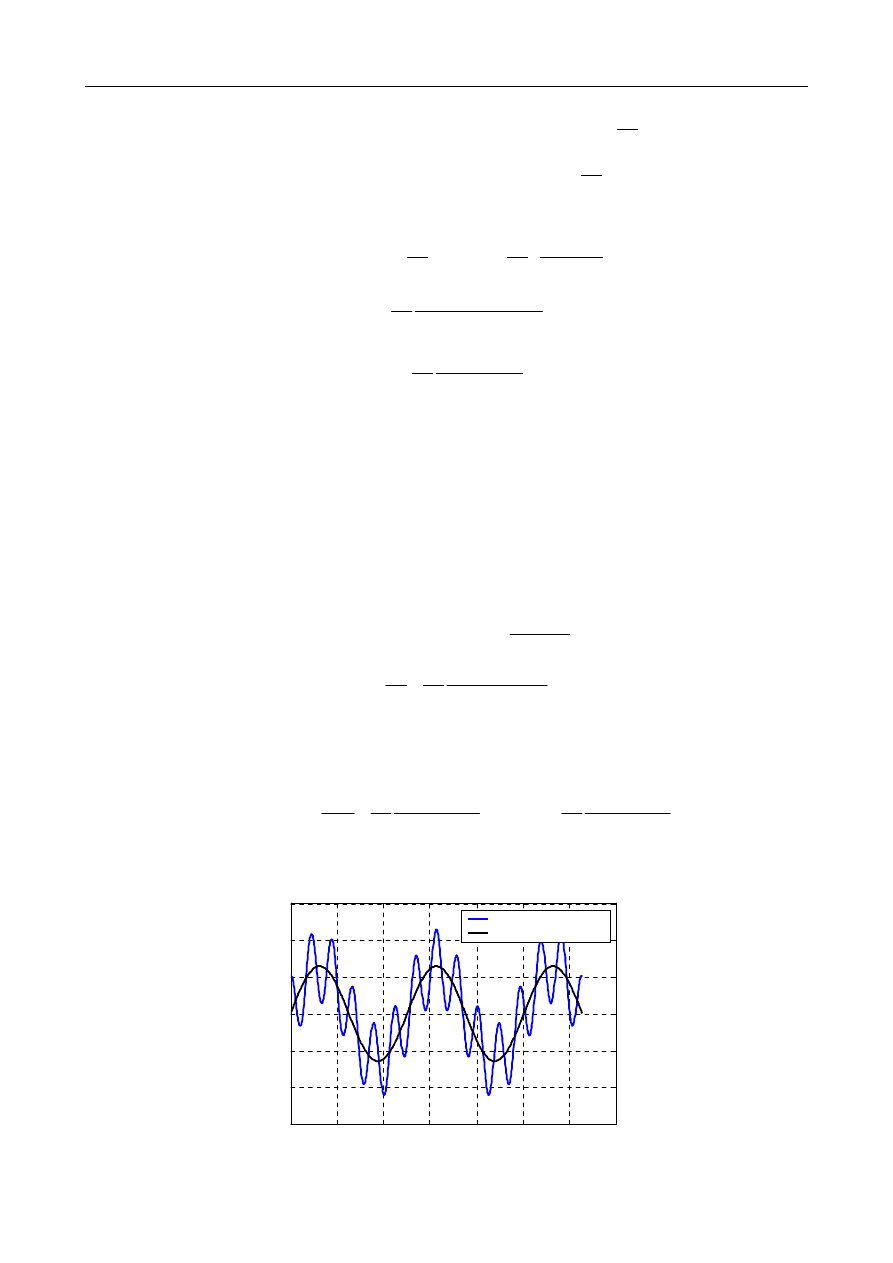
2
2
drgania "zanikające"
drgania ustalone
/
(0)
1
( )
(0) cos
sin
sin
1 ( /
)
1 ( /
)
n
n
n
n
n
n
p
p
u
u t
u
t
t
t
k
k
ω ω
ω
ω
ω
ω
ω ω
ω ω
⎡
⎤
⎡
⎤
=
+
−
+
⎢
⎥
⎢
⎥
−
−
⎣
⎦
⎣
⎦
(4.22)
0
1
2
3
4
5
6
7
-0.03
-0.02
-0.01
0
0.01
0.02
0.03
czas [s]
p
rz
e
m
ie
s
zcze
n
ie
[m
]
odpowiedz calkowita
drgania ustalone
Dynamika Budowli
Wydział Inżynierii Lądowej i Środowiska
Magdalena Rucka & Krzysztof Wilde
________________________________________________________________________________________________
2007-02-26
28
Współczynnik dynamiczny, zjawisko rezonansu:
Rozważmy drgania ustalone o częstości siły wymuszającej
ω :
0
2
1
( )
sin
1 ( /
)
n
p
u t
t
k
ω
ω ω
=
−
(4.23)
Wielkość
0
/
p k może być interpretowana jako ugięcie statyczne układu wywołane przez siłę
0
p
przyłożoną w sposób statyczny:
0
0
( )
st
p
u
k
=
(4.24)
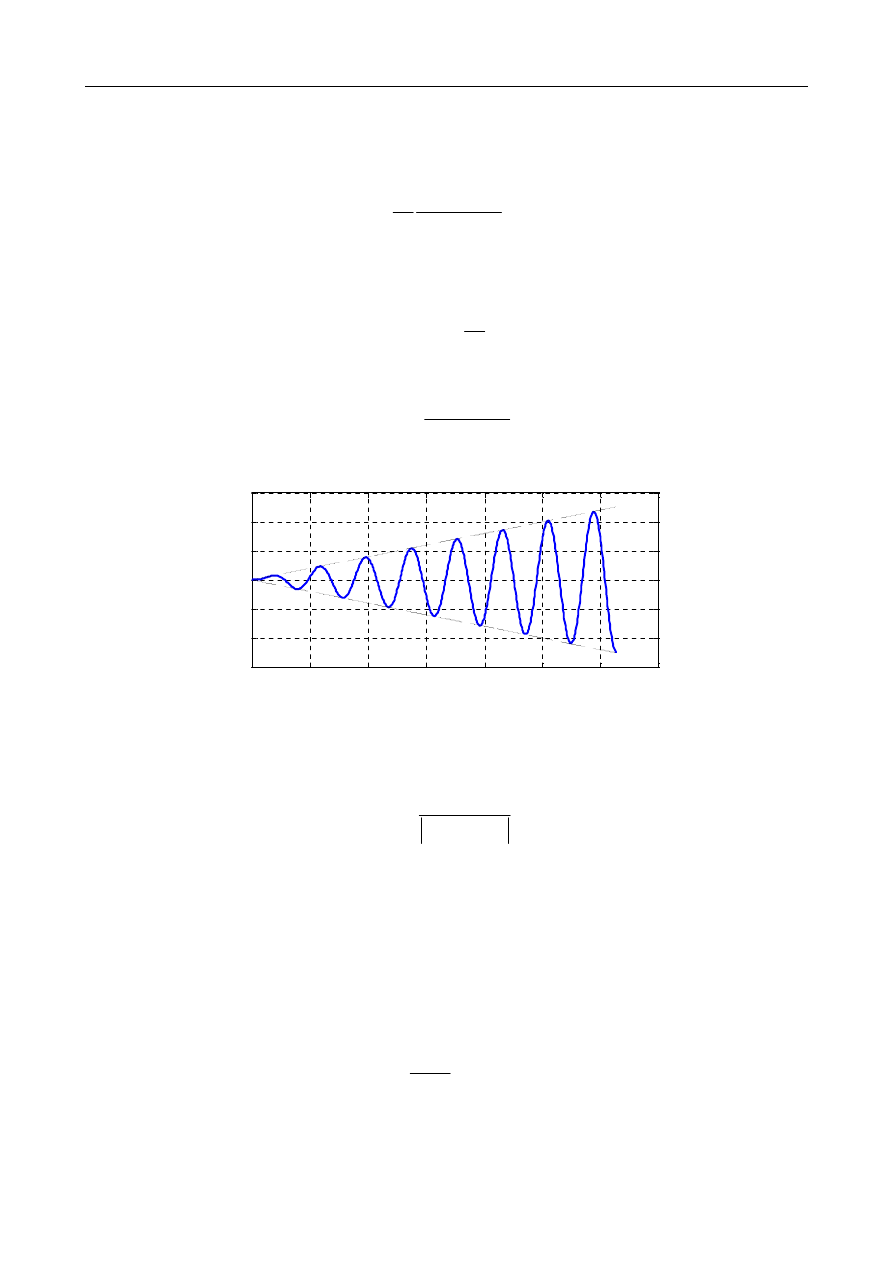
a równanie (4.23) przyjmie postać:
0
2
1
( ) ( )
sin
1 ( /
)
st
n
u t
u
t
ω
ω ω
=
−
(4.25)
0
1
2
3
4
5
6
7
-0.3
-0.2
-0.1
0
0.1
0.2
0.3
t [s]
u [
m
]
odpowiedz rezonansowa ukladu nietlumionego
Współczynnikiem dynamicznym
d
R (zwielokrotnienia amplitudy drgań) nazywamy iloraz amplitu-
dy drgań do amplitudy ugięcia statycznego:
2
1
1 ( /
)
d
n
R
ω ω
=
−
(4.26)
0
( ) ( )
sin
st
d
u t
u
R
t
ω
=
(4.27)
0
0
max ( )
( )
st
d
u t
u
u
R
=
=
(4.28)
Funkcja dynamiczności obciążenia ( )
R t - iloraz odpowiedzi konstrukcji ( )
u t spowodowanej siłą
zmienną w czasie do przemieszczenia statycznego, tzn. przemieszczenia powstałego pod działaniem
siły statycznej równej maksymalnej wartości siły zmiennej w czasie:
0
( )
( )
sin
( )
d
st
u t
R t
R
t
u
ω
=
=
(4.29)
Dynamika Budowli
Wydział Inżynierii Lądowej i Środowiska
Magdalena Rucka & Krzysztof Wilde
________________________________________________________________________________________________
2007-02-26
29
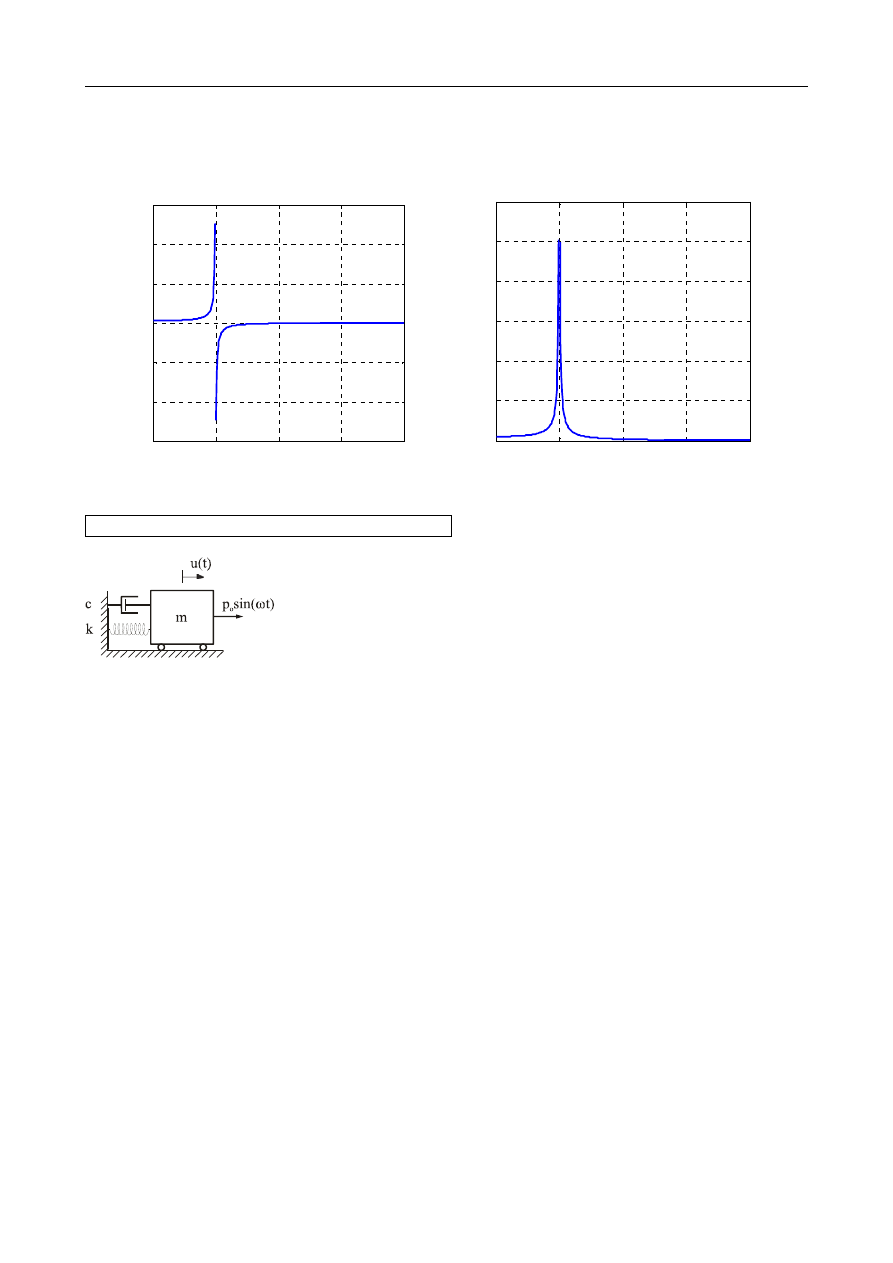
Częstotliwość rezonansowa zdefiniowana jest jako częstotliwość, dla której współczynnik
d
R osią-
ga maksymalną wartość, czyli dla
n
ω
ω
→
.
0
1
2
3
4
-60
-40
-20
0
20
40
60
ω
/
ω
n
[-]
1/
(1-
(
ω
/
ω
n
)
2
) [
-]
0
1
2
3
4
0
10
20
30
40
50
60
ω
/
ω
n
[-]
R
d
[-
]
Drgania wymuszone siłą harmoniczną tłumione
Drgania wymuszone sinusoidalną siłą harmoniczną tłumione opisane są następującym równaniem:
0
sin
mu cu ku
p
t
ω
+
+
=
, (4.30)
gdzie m oznacza masę, k - sztywność, c - tłumienie,
ω - częstość siły wymuszającej,
0
p amplitudę
siły wymuszającej. Warunki początkowe, czyli wychylenie początkowe
0
u i/lub prędkość począt-
kowa
0
u , mają następującą postać:
0
0
(0)
(0)
u
u
u
u
=
= . (4.31)
Równanie (4.30) jest niejednorodne. Jego rozwiązanie jest sumą całki ogólnej i całki szczególnej:
( )
( )
( )
c
p
u t
u t
u t
=
+
(4.32)
Całka ogólna równania (4.30) dla tłumienia podkrytycznego ma postać (3.30):
(
)
( )
cos
sin
n
t
D
D
u t
e
A
t B
t
ξω
ω
ω
−
=
+
, (4.33)
natomiast całka szczególna jest postaci (4.8):
( )
sin
cos
p
u t
D
t E
t
ω
ω
=
+
. (4.34)
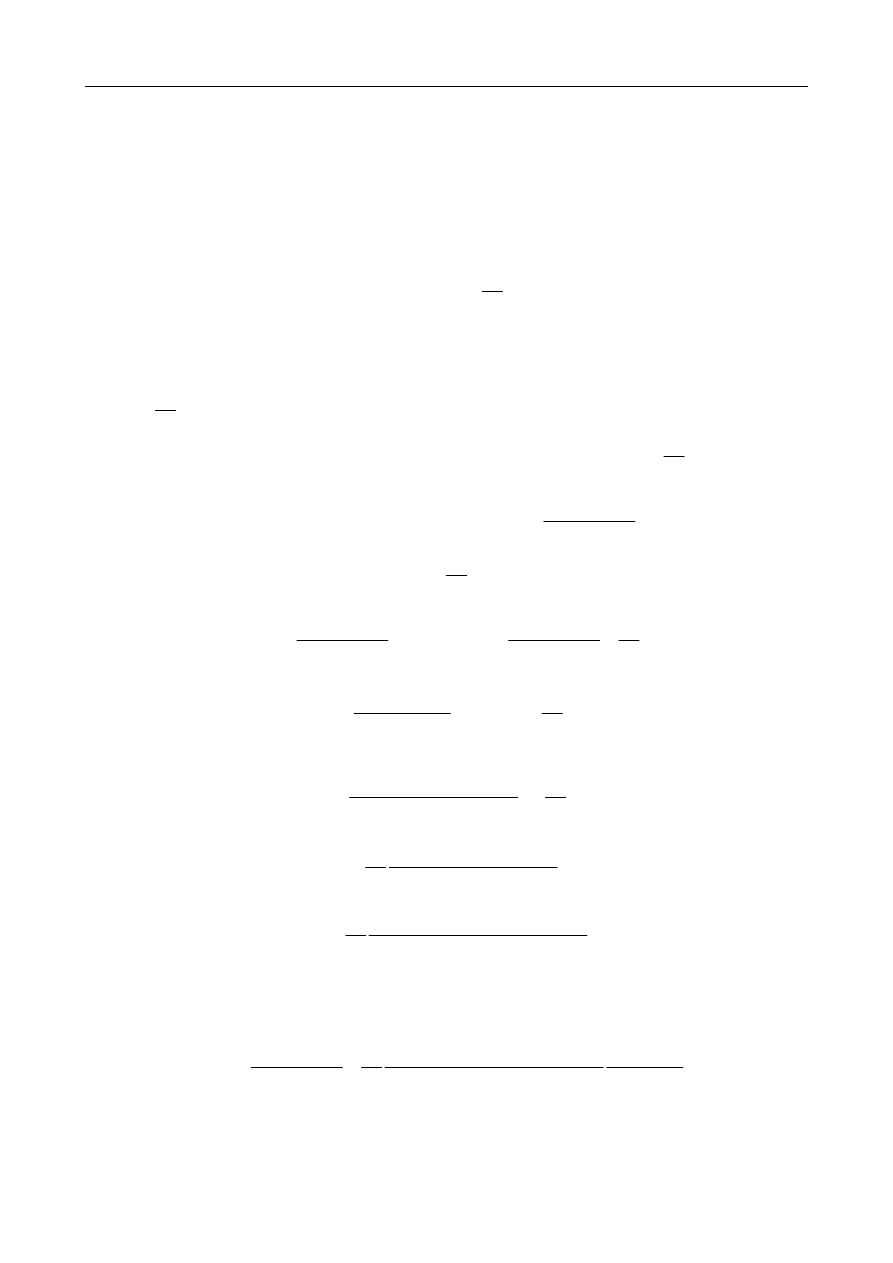
Dynamika Budowli
Wydział Inżynierii Lądowej i Środowiska
Magdalena Rucka & Krzysztof Wilde
________________________________________________________________________________________________
2007-02-26
30
Wyznaczenie stałych D i E:
cos
sin
p
u
D
t E
t
ω
ω
ω
ω
=
−
(4.35)
2
2
sin
cos
p
u
D
t E
t
ω
ω
ω
ω
= −
−
(4.36)
Podstawiając (4.35) i (4.36) do równania (4.30) zapisanego w postaci:
2
2
sin
o
n
n
p
u
u
u
t
m
ω ξ
ω
ω
+
+
=
(4.37)
otrzymujemy związek:
(
)
(
)
2
2
2
sin
cos
2
cos
sin
sin
cos
sin
n
n
o
D
t E
t
D
t E
t
D
t E
t
p
t
m
ω
ω
ω
ω
ξω
ω
ω
ω
ω
ω
ω
ω
ω
−
−
+
−
+
+
=
=
(4.38)
(
)
(
)
2
2
2
2
sin
2
cos
2
sin
o
n
n
n
n
p
t
D
E
D
t
E
D
E
t
m
ω
ω
ξω ω ω
ω
ω
ξω ω ω
ω
−
−
+
+
−
+
+
=
(4.39)
(
)
2
2
2
2
2
2
-
2
0
2
-
- 2
n
n
n
n
o
n
n
E
E
D
E
D
p
D
E
D
m
ω
ω
ω
ξω ω ω
ξω ω
ω
ξω ω ω
⎧
−
⎪
+
+
=
⇒
=
⎪
⎨
⎪
+
=
⎪⎩
(4.40)
(
)
(
)
2
2
2
2
2
2
2
2
2
n
n
o
n
n
n
n
E
E
p
E
m
ω
ω
ω
ω
ω
ξω ω ω
ξω ω
ξω ω
−
−
−
−
+
=
(4.41)
(
)
2
2
2
2
2
n
o
n
n
p
E
m
ω
ω
ξω ω
ξω ω
⎛
⎞
−
−
⎜
⎟
−
=
⎜
⎟
⎝
⎠
(4.42)
(
)
2
2
2
2
(2
)
2
n
n
o
n
p
E
m
ω
ω
ξω ω
ξω ω
⎛
⎞
−
+
⎜
⎟ =
⎜
⎟
−
⎝
⎠
(4.43)
(
)
2
2
2
2
2
(2
)
o
n
n
n
p
E
m
ξω ω
ω
ω
ξω ω
−
=
−
+
(4.44)
[
]
0
2
2
2
2 ( /
)
1 ( /
)
2 ( /
)
n
n
n
p
E
k
ξ ω ω
ω ω
ξ ω ω
−
=
⎡
⎤
−
+
⎣
⎦
(4.45)
Na podstawie zależności (4.40) otrzymujemy stałą D :
(
)
[
]
(
)
2
2
2
2
0
2
2
2
2 ( /
)
2
2
1 ( /
)
2 ( /
)
n
n
n
n
n
n
n
E
p
D
k
ω
ω
ω
ω
ξ ω ω
ξω ω
ξω ω
ω ω
ξ ω ω
−
−
−
=
=
⎡
⎤
−
+
⎣
⎦
(4.46)
Dynamika Budowli
Wydział Inżynierii Lądowej i Środowiska
Magdalena Rucka & Krzysztof Wilde
________________________________________________________________________________________________
2007-02-26
31
[
]
2
0
2
2
2
1 ( /
)
1 ( /
)
2 ( /
)
n
n
n
p
D
k
ω ω
ω ω
ξ ω ω
−
=
⎡
⎤
−
+
⎣
⎦
(4.47)
Wyznaczenie stałych A i B. Całka ogólna równania niejednorodnego (4.33):
(
)
( )
cos
sin
sin
cos
n
t
D
D
u t
e
A
t B
t
D
t E
t
ξω
ω
ω
ω
ω
−
=
+
+
+
(4.48)
(
0)
o
o
u t
A E u
A u
E
=
= + =
⇒ =
− (4.49)
[
]
0
2
2
2
2 ( /
)
1 ( /
)
2 ( /
)
n
o
n
n
p
A u
k
ξ ω ω
ω ω
ξ ω ω
−
=
+
⎡
⎤
−
+
⎣
⎦
(4.50)
(
)
( )
cos
sin
sin
cos
cos
sin
n
t
n
D
D
D
D
D
D
u t
e
A
t B
t
A
t B
t
D
t E
t
ξω
ξω
ω
ω
ω
ω
ω
ω
ω
ω
ω
ω
−
⎡
⎤
=
−
+
−
+
+
⎣
⎦
+
−
(4.51)
(
0)
n
D
o
u t
A B
D
u
ξω
ω
ω
=
= −
+
+
= (4.52)
o
n
o
n
D
D
D
D
u
D
A
u
B
D
A
ω
ξω
ω
ω
ξ
ω
ω
ω
ω
−
+
=
=
−
+
(4.53)
[
]
[
]
2
0
2
2
2
0
2
2
2
1 ( /
)
1 ( /
)
2 ( /
)
2 ( /
)
1 ( /
)
2 ( /
)
o
n
D
D
n
n
n
n
o
D
n
n
u
p
B
k
p
u
k
ω ω
ω
ω
ω
ω ω
ξ ω ω
ω
ξ ω ω
ξ
ω
ω ω
ξ ω ω
−
=
−
+
⎡
⎤
−
+
⎣
⎦
⎛
⎞
−
⎜
⎟
+
+
⎜
⎟
⎡
⎤
−
+
⎣
⎦
⎝
⎠
(4.54)
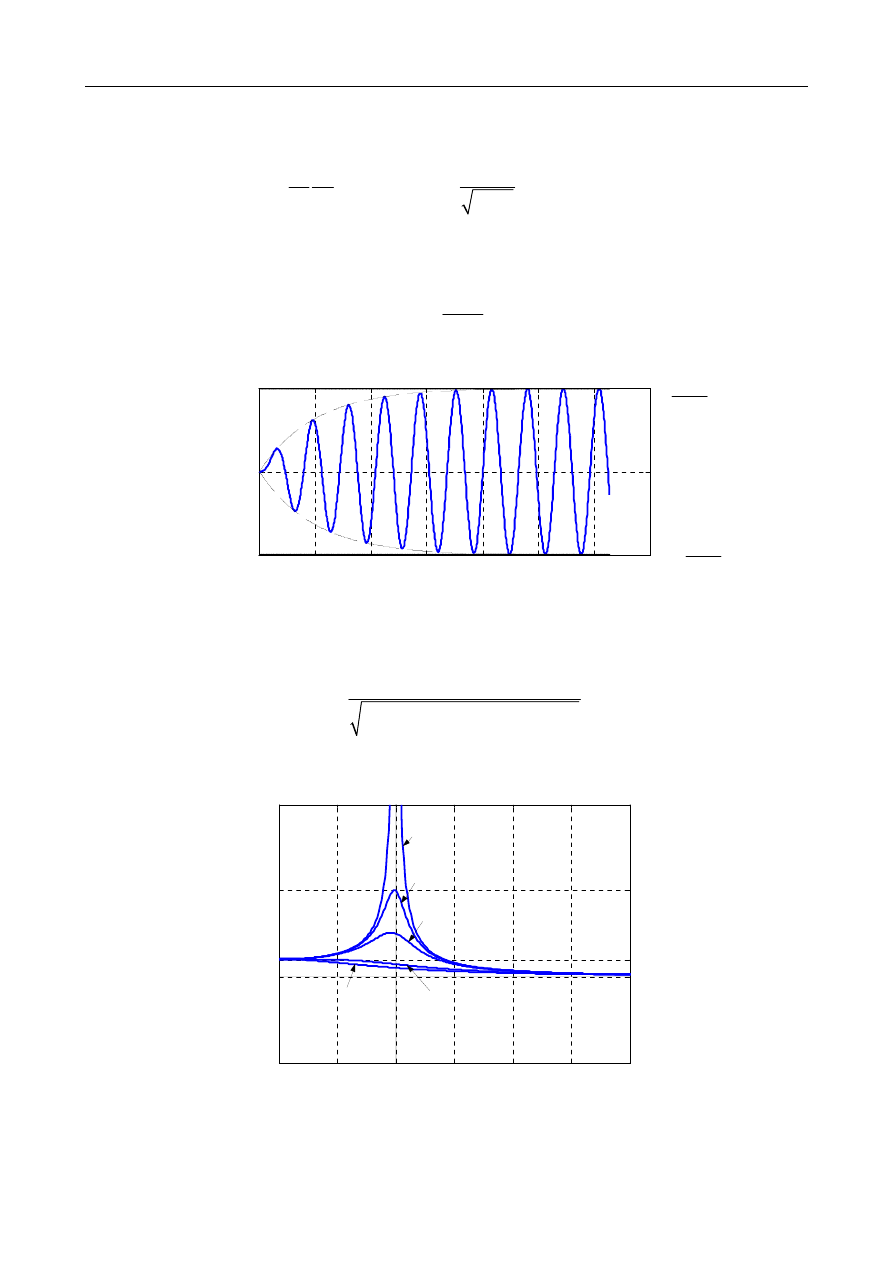
Ostatecznie odpowiedź układu jest wyrażona następująco:
(
)
drgania ustalone
drgania zanikające
( )
cos
sin
sin
cos
n
t
D
D
u t
e
A
t B
t
D
t E
t
ξω
ω
ω
ω
ω
−
=
+
+
+
(4.55)
0
1
2
3
4
5
6
7
8
9
10
-0.015
-0.01
-0.005
0
0.005
0.01
0.015
0.02
czas [s]
pr
z
em
ies
z
c
z
e
ni
e
[m
]
odpowiedz calkowita
drgania ustalone
Dynamika Budowli
Wydział Inżynierii Lądowej i Środowiska
Magdalena Rucka & Krzysztof Wilde
________________________________________________________________________________________________
2007-02-26
32
Dla częstości wymuszenia
n
ω ω
=
odpowiedź układu przyjmuje postać:
0
2
1
( )
cos
sin
cos
2
1
n
t
D
D
n
p
u t
e
t
t
t
k
ξω
ξ
ω
ω
ω
ξ
ξ
−
⎡
⎤
⎛
⎞
⎢
⎥
⎜
⎟
=
+
−
⎜
⎟
⎢
⎥
−
⎝
⎠
⎣
⎦
(4.56)
Odpowiedź układu nie przekracza wartości
0
u :
0
0
( )
2
st
u
u
ξ
=
(4.57)
0
2
4
6
8
10
12
14
-0.05
0
0.05
t [s]
u [
m
]
odpowiedz rezonansowa ukladu tlumionego
Współczynnik dynamiczny:
[
]
2
2
2
1
1 ( /
)
2 ( /
)
d
n
n
R
ω ω
ξ ω ω
=
⎡
⎤
−
+
⎣
⎦
(4.58)
0
0.5
1
1.5
2
2.5
3
-5
0
1
5
10
ω / ω
n
[ - ]
R
d
[ - ]
ξ=0.01
ξ=0.1
ξ=0.2
ξ=1.0
ξ=0.7
( )
0
2
st
u
ξ
( )
0
2
st
u
ξ
−
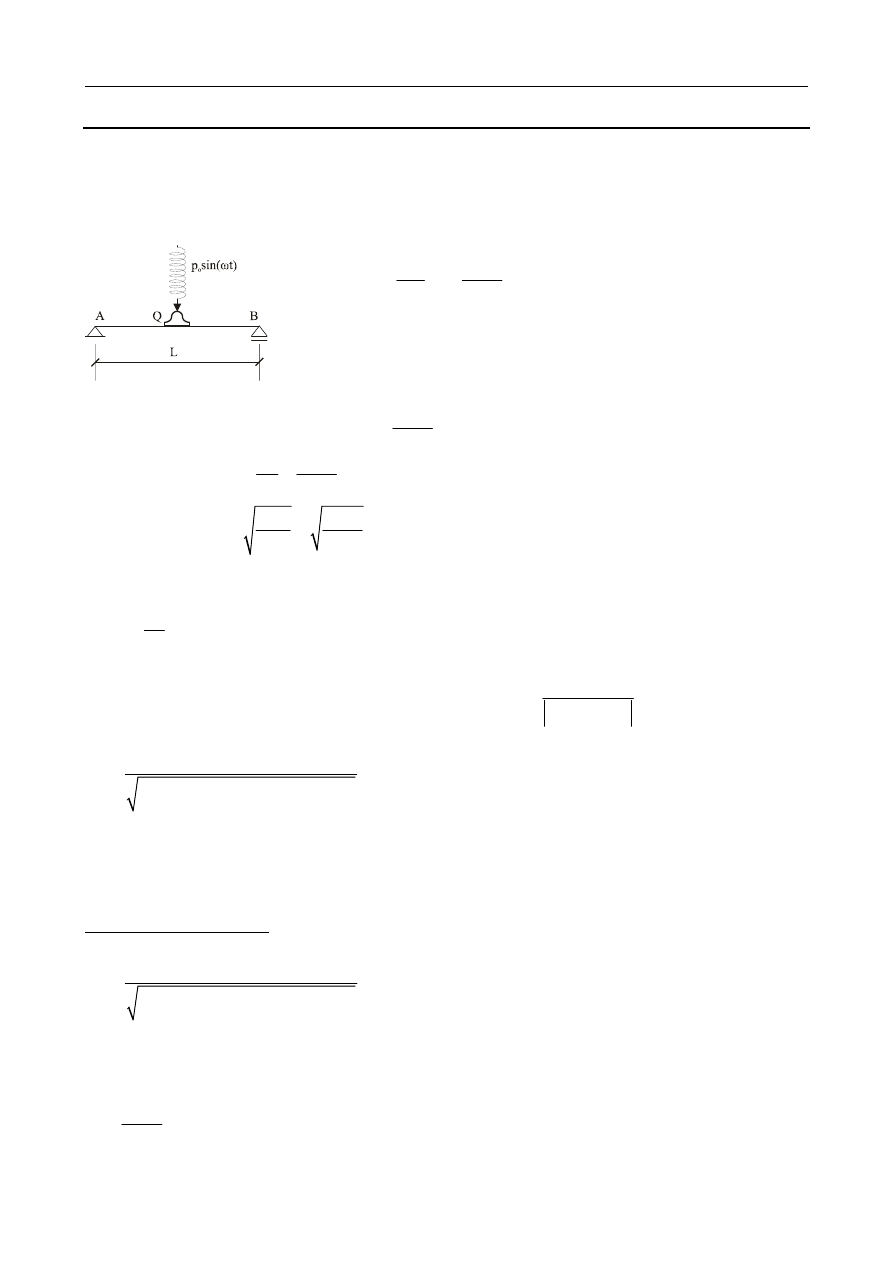
Dynamika Budowli
Wydział Inżynierii Lądowej i Środowiska
Magdalena Rucka & Krzysztof Wilde
________________________________________________________________________________________________
2007-02-26
33
Z
ADANIE
4.1
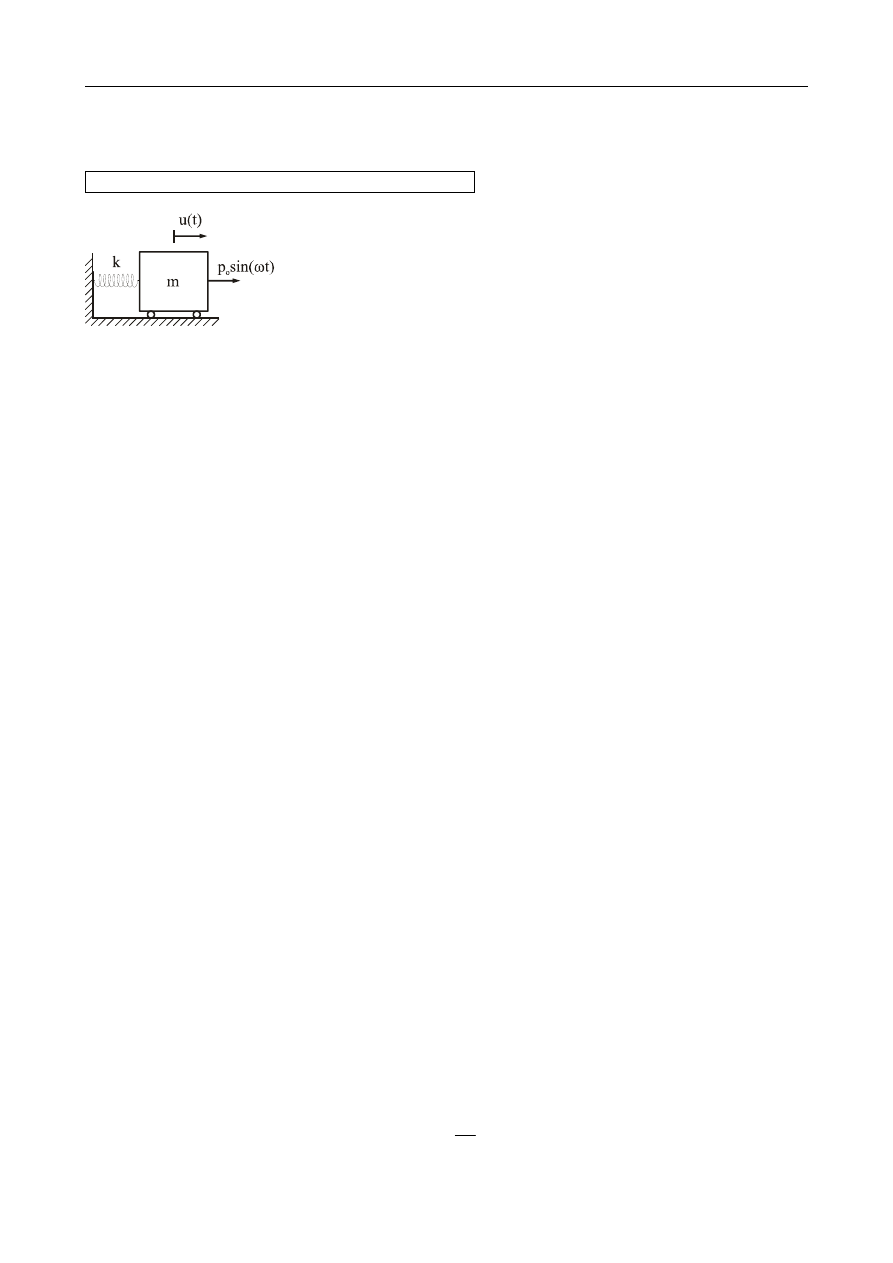
Na belce o długości L = 4 m umieszczony jest silnik o ciężarze Q = 40 kN wywołujący drgania si-
nusoidalne o amplitudzie
0
p = 2 kN i częstości wymuszenia 500 obrotów na minutę. Obliczyć
amplitudę drgań nietłumionych oraz tłumionych dla
5%
ξ
=
. Zbadać przypadek rezonansu dla
drgań tłumionych. EI = 24150 kNm
2
.
Ugięcie statyczne od ciężaru silnika:
3
0.2208 cm
48
Q
QL
EI
δ
=
=
Sztywność układu:
3
11
1
48
1811250 N/m
EI
k
L
δ
=
=
=
Częstość drgań:
3
11
1
48
66.65 rad/s
n
EI
m
mL
ω
δ
=
=
=
Ugięcie statyczne układu wywołane przez siłę
0
p przyłożoną w sposób statyczny:
0
0
( )
0.01104 cm
st
p
u
k
=
=
Częstość wymuszenia:
52.36 rad/s
ω
=
Współczynnik dynamiczny bez uwzględnienia tłumienia:
2
1
2.61
1 ( /
)
d
n
R
ω ω
=
=
−
Współczynnik dynamiczny z uwzględnieniem tłumienia:
[
]
2
2
2
1
2.557
1 ( /
)
2 ( /
)
t
d
n
n
R
ω ω
ξ ω ω
=
=
⎡
⎤
−
+
⎣
⎦
Amplituda drgań nietłumionych:
0
0
( ) 0.0288
cm
st
d
u
u
R
=
=
Amplituda drgań tłumionych:
0
0
( ) 0.0282
cm
t
st
d
u
u
R
=
=
W przypadku rezonansu:
66.65 rad/s
n
ω ω
=
=
Współczynnik dynamiczny:
[
]
2
2
2
1
10
1 ( /
)
2 ( /
)
t
d
n
n
R
ω ω
ξ ω ω
=
=
⎡
⎤
−
+
⎣
⎦
Amplituda drgań tłumionych:
0
0
( ) 0.1104
cm
t
st
d
u
u
R
=
=
Odpowiedź układu nie przekracza wartości
0
u :
0
0
( )
0.1104 cm
2
st
u
u
ξ
=
=
2
3
1
11
0
48
L
M
L
ds
EI
EI
δ
=
=
∫

Dynamika Budowli
Wydział Inżynierii Lądowej i Środowiska
Magdalena Rucka & Krzysztof Wilde
________________________________________________________________________________________________
2007-02-26
34
Z
ADANIE
4.2
Jaka powinna być stała sprężyny
s
k , którą należy wstawić pod silnik o wadze Q = 2 kN, aby
współczynnik dynamiczny
d
R drgań harmonicznych o częstości
10 rad/s
ω
=
spełniał warunek
d
R < 0.5? Belka ma długość L = 2 m, I = 328 cm
4
, E = 200 GPa.
Sztywność belki:
3
11
3
L
EI
δ
=
3
3
b
EI
k
L
=
Sztywność szeregowego połączenia układu belka-sprężyna:
b s
b
s
k k
k
k
k
=
+
Częstość naturalna drgań:
3
2
3
3
3
(
)
s
b s
n
b
s
s
EI
k
k k
k
L
EI
m
m k
k
m
k
L
ω
=
=
=
+
⎛
⎞
+
⎜
⎟
⎝
⎠
(
)
2
1
0.5
1
/
d
n
R
ω ω
=
<
−
czyli
2
2
3
n
ω
ω
>
2
2
3
2 3
2
3
3
m
3
9
9
s
EI
EI
L
k
EI
EI m L
mL
ω
ω
ω
ω
<
=
−
⎛
⎞
−
⎜
⎟
⎝
⎠
s
k
< 6988.85 N/m
Przyjęto:
s
k
=
rad/s
n
ω
=

Dynamika Budowli
Wydział Inżynierii Lądowej i Środowiska
Magdalena Rucka & Krzysztof Wilde
________________________________________________________________________________________________
2007-02-26
35
Z
ADANIE
4.3
Masa m, sztywność k oraz naturalna częstość
n
ω
nietłumionego układu o jednym stopniu swobody
są nieznane. Do wyznaczenia tych wielkości zastosowano test wzbudzenia harmonicznego. Przy
częstotliwości wzbudzenia 4 Hz wystąpił rezonans. Następnie masę zwiększono o 5 kg i wówczas
rezonans wystąpił przy częstotliwości wymuszenia 3 Hz. Wyznaczyć masę i sztywność.
6.43 kg
m
=
,
4061 N/m
k
=
Z
ADANIE
4.4
Układ o jednym stopniu swobody poddano wzbudzeniu siłą sinusoidalną. Przy rezonansie amplitu-
da przemieszczenia została pomierzona i wynosiła 2 m. Przy wzbudzeniu częstością
ω równą 1/10
naturalnej częstości
n
ω
amplitudą wyniosła 0.2 m. Ile wynosi liczba tłumienia?
0.0495
ξ
=
Dynamika Budowli
Wydział Inżynierii Lądowej i Środowiska
Magdalena Rucka & Krzysztof Wilde
________________________________________________________________________________________________
2007-02-26
36
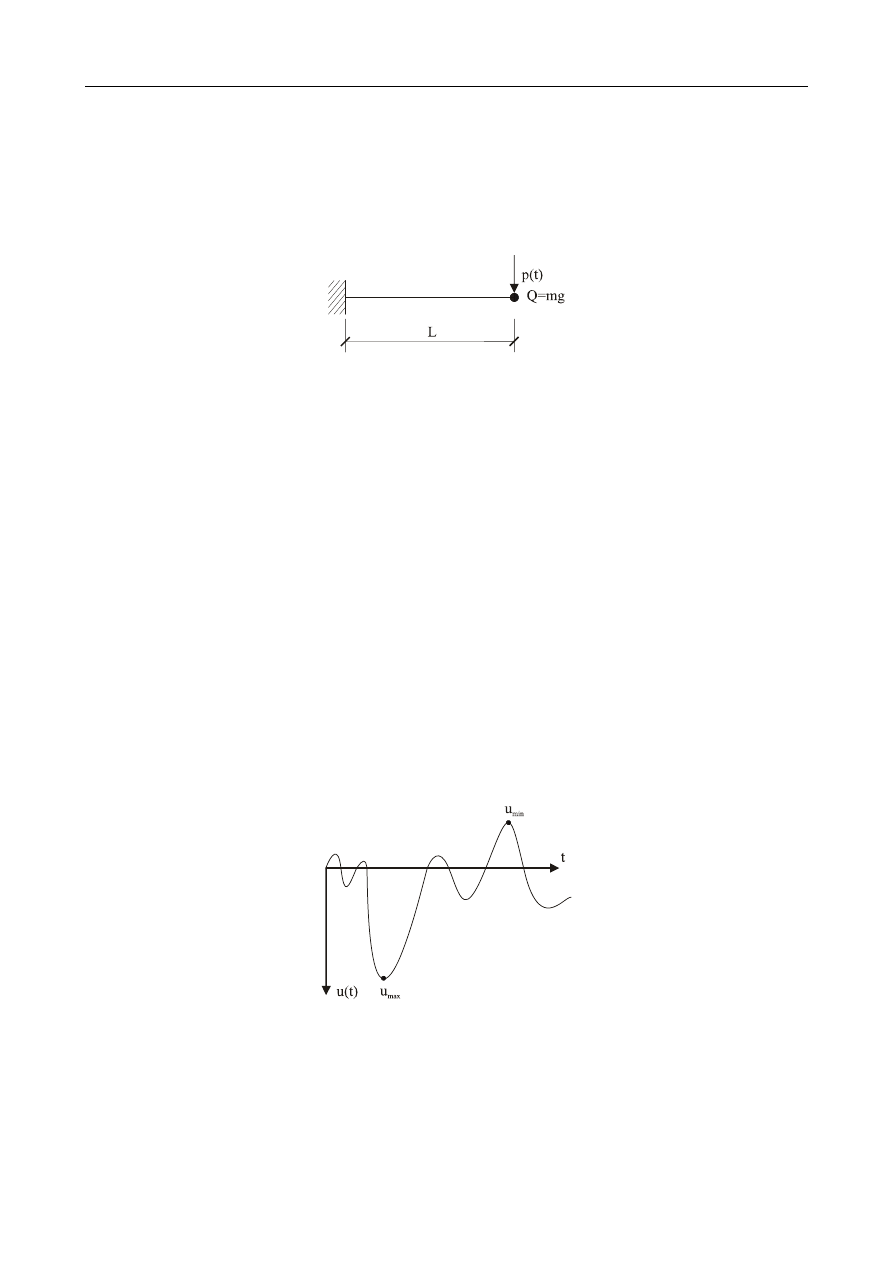
5. Projektowanie
konstrukcji
o jednym stopniu swobody obciążonych dy-
namicznie
Dany jest układ o jednym stopniu swobody (m, k, c) obciążony siłą p(t).
Równanie ruchu:
( )
mu cu ku
p t
+
+
=
(5.1)
Przenosząc wyrazy związane z masą i tłumieniem na prawą stronę otrzymujemy:
( )
z
p
ku
p t
mu cu
=
−
−
(5.2)
gdzie
z
p oznacza zastępczą siłę statyczną.
z
p
ku
=
(5.3)
Siła zastępcza
z
p osiąga wartość minimalna i maksymalną dla minimalnego i maksymalnego prze-
mieszczenia u:
min
min
max
max
z
z
p
ku
p
ku
=
=
(5.4)

Dynamika Budowli
Wydział Inżynierii Lądowej i Środowiska
Magdalena Rucka & Krzysztof Wilde
________________________________________________________________________________________________
2007-02-26
37
Obwiednia momentów jest sumą momentów od obciążenia statycznego oraz dynamicznego:
max
min
obw
=
dyn
Q
dyn
M
M
M
M
±
(5.5)
1 z max
1
1 z min
obw
=
M p
M
M Q
M p
±
(5.6)
Przypadki szczególne:
Drgania swobodne bez tłumienia:
0
mu ku
+
=
( )
sin(
)
n
u t
C
t
ω
ϕ
=
+
2
z
n
p
mu m C kC
ω
= −
=
=
min
max
z
z
p
kC
p
kC
= −
=
Drgania wymuszone harmonicznie:
0
sin
mu cu ku
p
t
ω
+
+
=
min,max
0
( )
st
d
u
u
R
= ∓
min
min
0
max
max
0
z
d
z
d
p
ku
p R
p
ku
p R
= −
= −
=
=
Dynamika Budowli
Wydział Inżynierii Lądowej i Środowiska
Magdalena Rucka & Krzysztof Wilde
________________________________________________________________________________________________
2007-02-26
38
Z
ADANIE
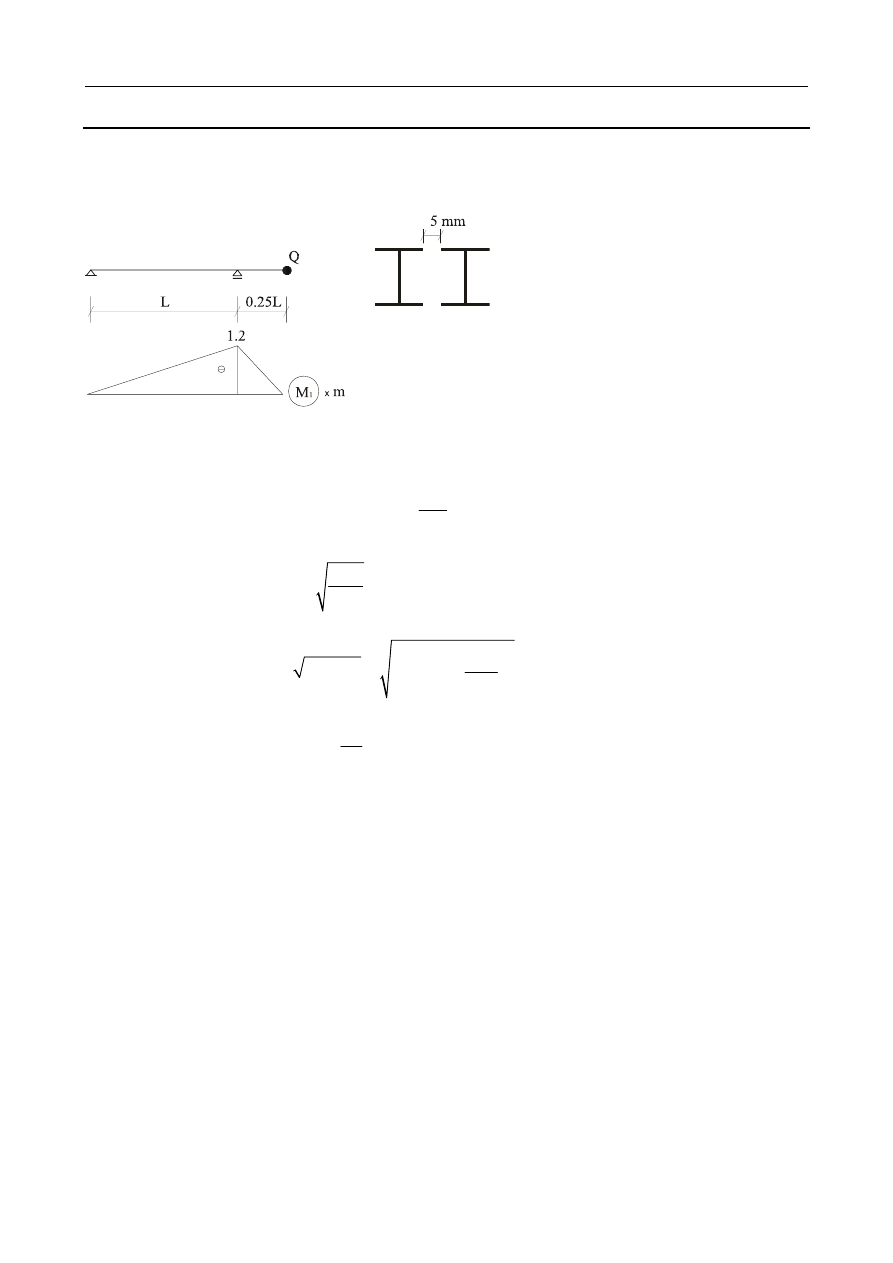
5.1
Wyznaczyć obwiednię momentów zginających odciężaru masy i dynamicznych momentów wywo-
łanych warunkiem początkowym (
0) 0.4
m/s
u t
=
=
. Belka ma długość L = 4.8 m, wykonana jest z
dwóch stalowych dwuteowników I 180 (I
x-x
= 1450 cm
4
). Moduł sprężystości stali E = 200 GPa.
Ciężar Q = 20 kN.
Moment bezwładności przekroju
4
2900 cm
x
I
=
Przemieszczenie od siły jednostkowej:
2
6
1
11
0.496 10 m/N
M
ds
EI
δ
−
=
=
⋅
∫
Częstość drgań własnych:
11
1
31.447 rad/s
n
m
ω
δ
=
=
Amplituda drgań masy:
[
]
2
2
2
2
(0)
(0) +
0.01272 m
n
u
C
A
B
u
ω
⎡
⎤
=
+
=
=
⎢
⎥
⎣
⎦
Zastępcza siła statyczna
11
25645.161 N
z
C
p
kC
δ
=
=
=
1
Q
M
M Q
=
1
dyn
z
M
M p
= ±

Dynamika Budowli
Wydział Inżynierii Lądowej i Środowiska
Magdalena Rucka & Krzysztof Wilde
________________________________________________________________________________________________
2007-02-26
39
Z
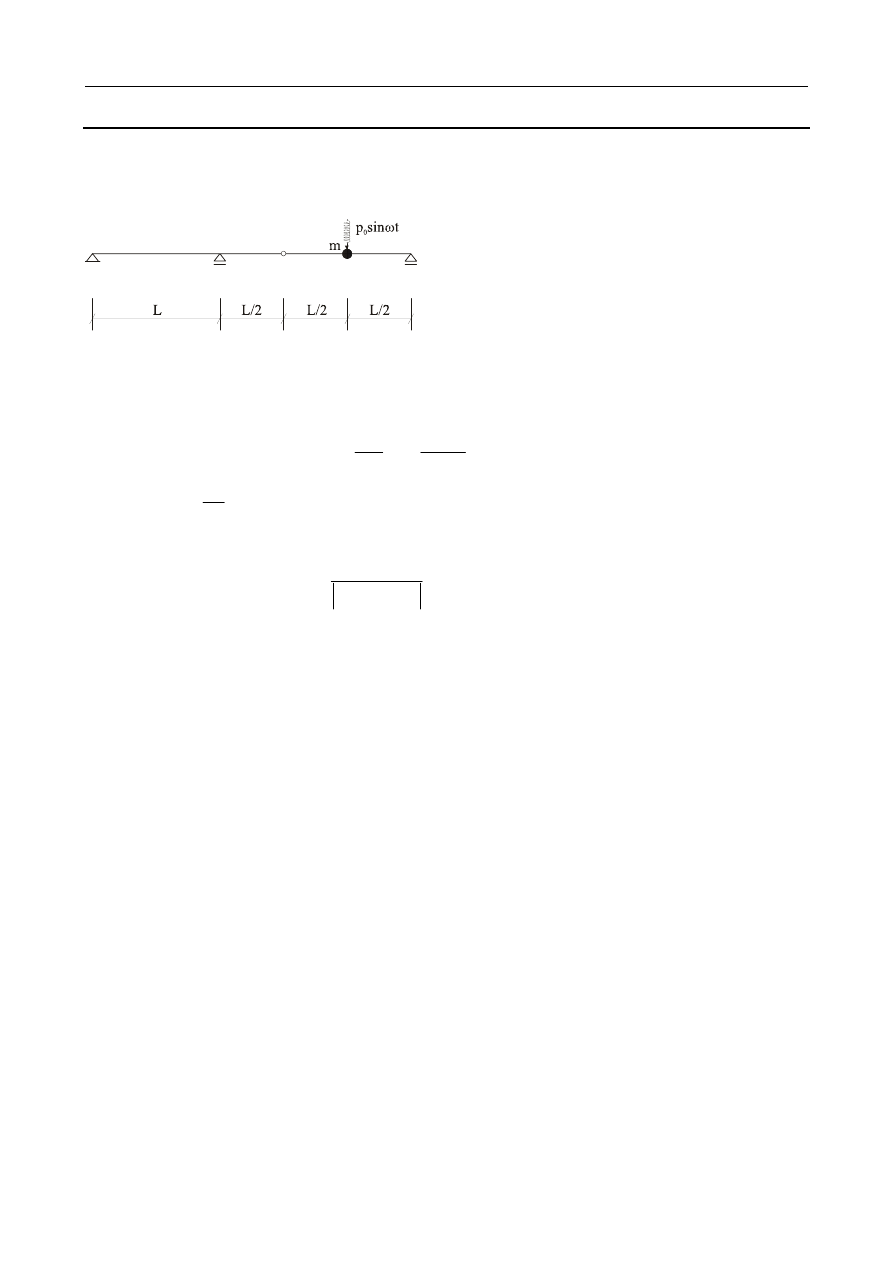
ADANIE
5.2
Na belce (I220, I
x-x
= 3060 cm
4
) znajduje się maszyna o ciężarze Q = 20 kN wywołująca wymusza-
jącą siłę harmoniczną amplitudzie
0
2 kN
p
=
. Liczba obrotów wirnika maszyny wynosi 400 obro-
tów/minutę. Dobrać podkładkę pod maszynę tak, by maksymalne naprężenia przy zginaniu nie
przekraczały 90
MPa
dop
σ
=
. L = 5m.
Przemieszczenie od siły jednostkowej:
2
6
1
11
0.373 10 m/N
M
ds
EI
δ
−
=
=
⋅
∫
Częstość naturalna drgań 36.263
rad/s
n
ω
=
Częstość wymuszenia:
41.888 rad/s
ω
=
Współczynnik dynamiczny:
2
1
2.991
1 ( /
)
d
n
R
ω ω
=
=
−
Zastępcza siła statyczna:
0
5.982 kN
z
d
p
R p
=
=
Moment maksymalny:
max
1
(
)
31.178 kNm
z
M
Q p M
=
+
=
Maksymalne naprężenia:
max
max
112.077 MPa > 90 MPa =
dop
x
M
y
I
σ
σ
=
=
Naprężenia maksymalne przekraczają wartość dopuszczalną, trzeba dobrać podkładkę zmieniającą
częstość drgań własnych układu. Dopuszczalna zastępcza siła statyczna musi wynosić:
0.8636 kN
z
p
≤
0
0.8636 kN
z
d
p
R p
=
=
2
1
0.432
1 ( /
)
d
n
R
ω ω
=
=
−

Dynamika Budowli
Wydział Inżynierii Lądowej i Środowiska
Magdalena Rucka & Krzysztof Wilde
________________________________________________________________________________________________
2007-02-26
40
2
3.315
n
ω
ω
⎛
⎞
=
⎜
⎟
⎝
⎠
2
529.292 rad/s
n
ω
=
1
1
1
b
s
k
k
k
=
+
2
2
2
1
1
1
n
s
n
ω
ω
ω
=
+
Szukana sztywność podkładki wynosi:
1806 kN/m
s
k
=
Dynamika Budowli
Wydział Inżynierii Lądowej i Środowiska
Magdalena Rucka & Krzysztof Wilde
________________________________________________________________________________________________
2007-02-26
41
Z
ADANIE
5.3
Na belkę ciągłą przegubową działa obciążenie harmoniczne. Obliczyć maksymalne wychylenie
masy oraz amplitudy dynamicznych momentów zginających oraz narysować obwiednię momentów,
jeżeli L = 4 m, EI = 40000 kNm
2
,
0
p = 6 kN,
ω = 35 rad/s, m = 4.8 Mg.
Ugięcie od siły jednostkowej:
2
1
11
1
m/kN
12000
M
ds
EI
δ
=
=
∫
Sztywność:
11
1
12000 kN/m
k
δ
=
=
Częstość drgań naturalnych:
50 rad/s
n
ω
=
Współczynnik dynamiczny:
2
1
1.961
1 ( /
)
d
n
R
ω ω
=
=
−
Zastępcza siła statyczna
0
11.8 kN
z
d
p
p R
=
=
Ugięcie maksymalne:
( )
max
11
0
(
) 0.49 cm
Q
st
d
z
u
u
u
R
Q p
δ
=
+
=
+
=
Momenty zginające wywołane statycznym działaniem ciężaru masy:
Amplitudy dynamicznych momentów zginających:
Obwiednia momentów:
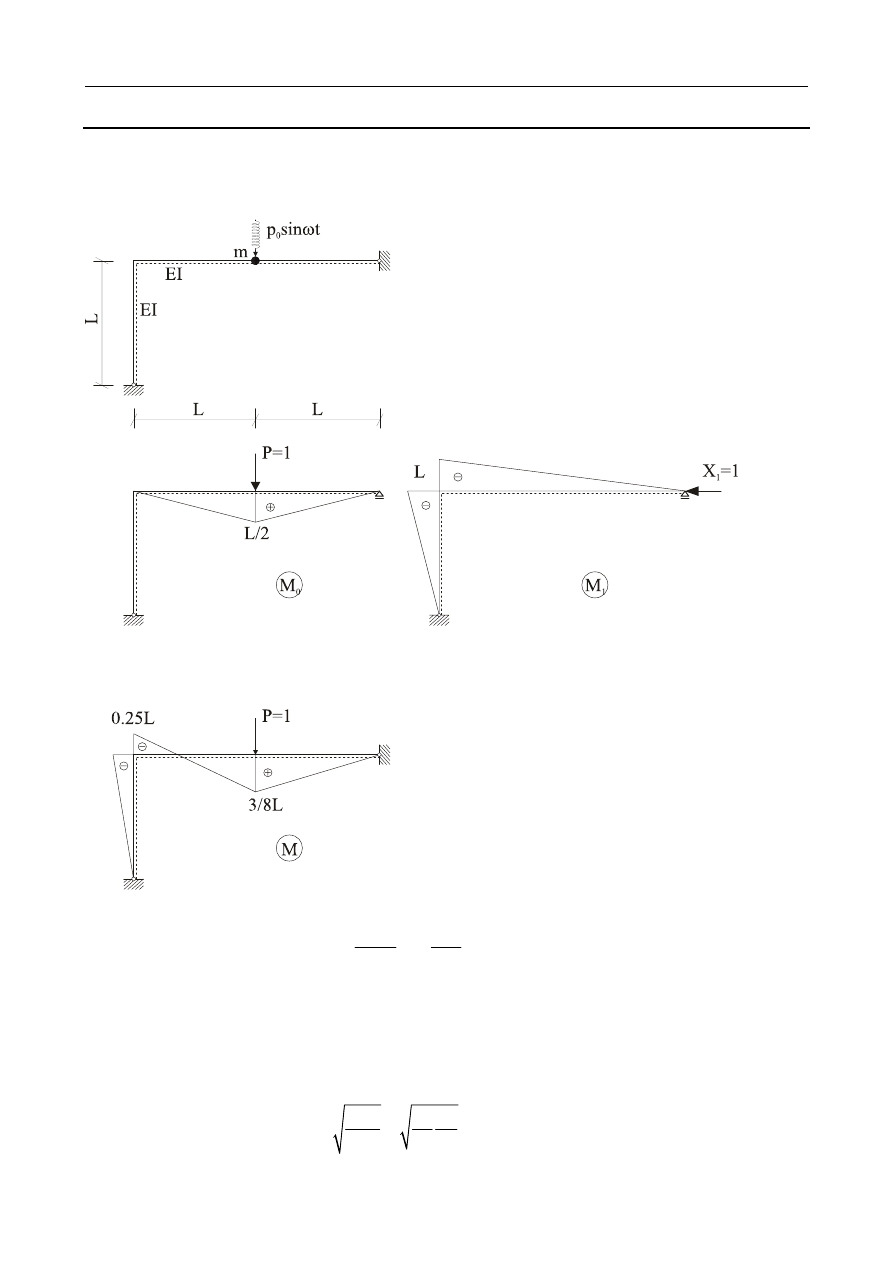
Dynamika Budowli
Wydział Inżynierii Lądowej i Środowiska
Magdalena Rucka & Krzysztof Wilde
________________________________________________________________________________________________
2007-02-26
42
Z
ADANIE
5.4
Rygiel ramy obciążony jest w środku rozpiętości masą skupioną m = 3Mg i siłą harmoniczną o am-
plitudzie
0
p = 6 kN i częstości wymuszenia
ω = 24 rad/s. Narysować obwiednię momentów zgina-
jących, jeżeli L = 4 m, EI = 12500 kNm
2
.
Ugięcie od siły jednostkowej:
0
11
0
20
3
L
MM
dx
EI
EI
δ
=
=
∫
Częstość drgań naturalnych:
11
1
3
25 rad/s
20
n
EI
m
m
ω
δ
=
=
=

Dynamika Budowli
Wydział Inżynierii Lądowej i Środowiska
Magdalena Rucka & Krzysztof Wilde
________________________________________________________________________________________________
2007-02-26
43
Współczynnik dynamiczny:
2
1
12.755
1 ( /
)
d
n
R
ω ω
=
=
−
Zastępcza siła statyczna
0
76.531 kN
z
d
p
R p
=
=
29.43
Q
M
MQ
M
=
=
76.531
dyn
z
M
Mp
M
= ±
= ±
(29.43 76.531)
obwM
M
=
±
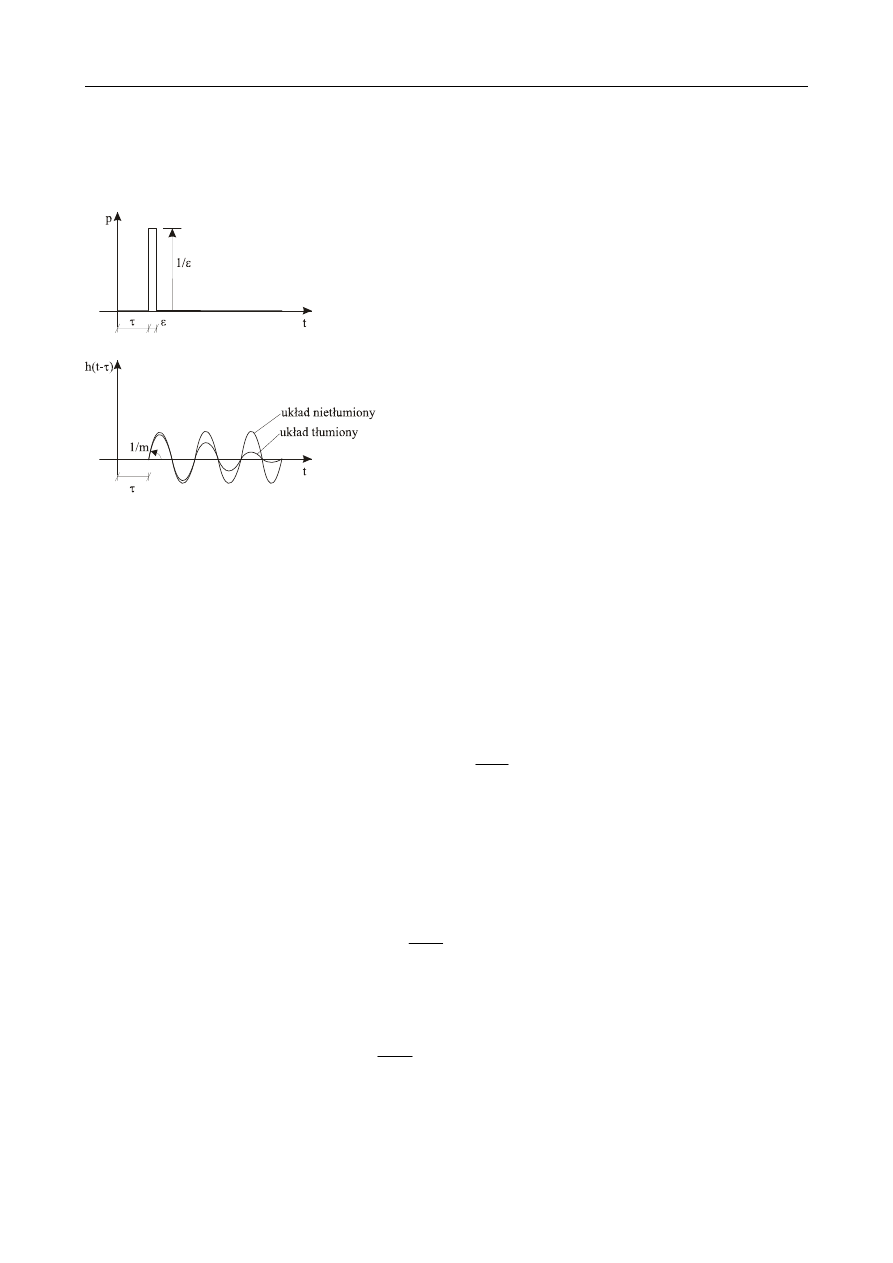
Dynamika Budowli
Wydział Inżynierii Lądowej i Środowiska
Magdalena Rucka & Krzysztof Wilde
________________________________________________________________________________________________
2007-02-26
44
6. Drgania
wywołane dowolnym obciążeniem wymuszającym
6.1. Działanie impulsu jednostkowego
p mu
=
2
1
2
1
(
)
impuls
t
t
pdt m u
u
m u
=
−
= Δ
←
∫
Drgania swobodne układu o jednym stopniu swobody (bez tłumienia) opisane są równaniem:
(0)
( )
(0) cos
(
)
sin
(
).
n
n
n
u
u t
u
t
t
ω
τ
ω
τ
ω
=
− +
−
(6.1)
Wstawiając warunki brzegowe:
(0) 0 i (0)
1/
u
u
u
m
=
= Δ =
, (6.2)
do równania (6.1) otrzymujemy odpowiedź układu:
[
]
1
(
)
( )
sin
(
)
n
n
h t
u t
t
t
m
τ
ω
τ
τ
ω
− ≡
=
−
≥ . (6.3)
Dla układu tłumionego odpowiedź jest następująca:
[
]
(
)
1
(
)
( )
sin
(
)
n
t
d
d
h t
u t
e
t
t
m
ξω
τ
τ
ω
τ
τ
ω
−
−
− ≡
=
−
≥ . (6.4)
impuls jednostkowy gdy
0
ε
→

Dynamika Budowli
Wydział Inżynierii Lądowej i Środowiska
Magdalena Rucka & Krzysztof Wilde
________________________________________________________________________________________________
2007-02-26
45
6.2. Impuls prostokątny
Równanie ruchu:
0
( )
0
d
d
p
t t
mu ku
p t
t t
≤
⎧
+
=
= ⎨
≥
⎩
(6.5)
z warunkami brzegowymi (0) 0 i (0) 0
u
u
=
= . Ruch układu przebiega w 2 fazach:
a) faza działania impulsu
d
t t
≤ , podczas której układ poddany jest działaniu siły
0
( )
p t
p
=
(„step
force”). Odpowiedź układu:
( )
cos
sin
n
n
p
u t
A
t B
t u
ω
ω
=
+
+ ,
0
p
p
u
k
=
(6.6)
Z warunków brzegowych :
(0) 0 i
(0) 0
u
u
=
= otrzymujemy
0
i
0
p
A
B
k
−
=
=
0
( )
(1 cos
),
n
d
p
u t
t
t t
k
ω
=
−
≤ (6.7)
( )
0
( )
(1 cos
),
st
n
d
u t
u
t
t t
ω
=
−
≤
(6.8)
b) faza drgań swobodnych
d
t t
≥
(
)
(
)
( )
( )
( ) cos
sin
d
d
n
d
n
d
n
u t
u t
u t
t t
t t
ω
ω
ω
=
−
+
−
(6.9)
Drgania swobodne zapoczątkowane są prędkością i przemieszczeniem masy w czasie
d
t t
= , wy-
znaczonymi z równania (6.7):
( )
( )
0
0
( )
(1 cos
),
( )
sin
.
d
st
n d
d
st
n
n d
u t
u
t
u t
u
t
ω
ω
ω
=
−
=
(6.10)
Podstawiając (6.10) do równania (6.9) otrzymujemy:
( )
(
) ( )
(
)
0
0
sin
( )
(1 cos
) cos
sin
,
st
n
n d
st
n d
n
d
n
d
d
n
u
t
u t
u
t
t t
t t
t t
ω
ω
ω
ω
ω
ω
=
−
−
+
−
≥ (6.11)
( )
(
)
(
)
0
( )
(1 cos
) cos
sin
sin
,
st
n d
n
d
n d
n
d
d
u t
u
t
t t
t
t t
t t
ω
ω
ω
ω
=
−
−
+
−
≥
⎡
⎤
⎣
⎦
(6.12)
( )
(
)
0
( )
cos
cos
,
st
n
d
n d
d
u t
u
t t
t
t t
ω
ω
=
−
−
≥
⎡
⎤
⎣
⎦
(6.13)
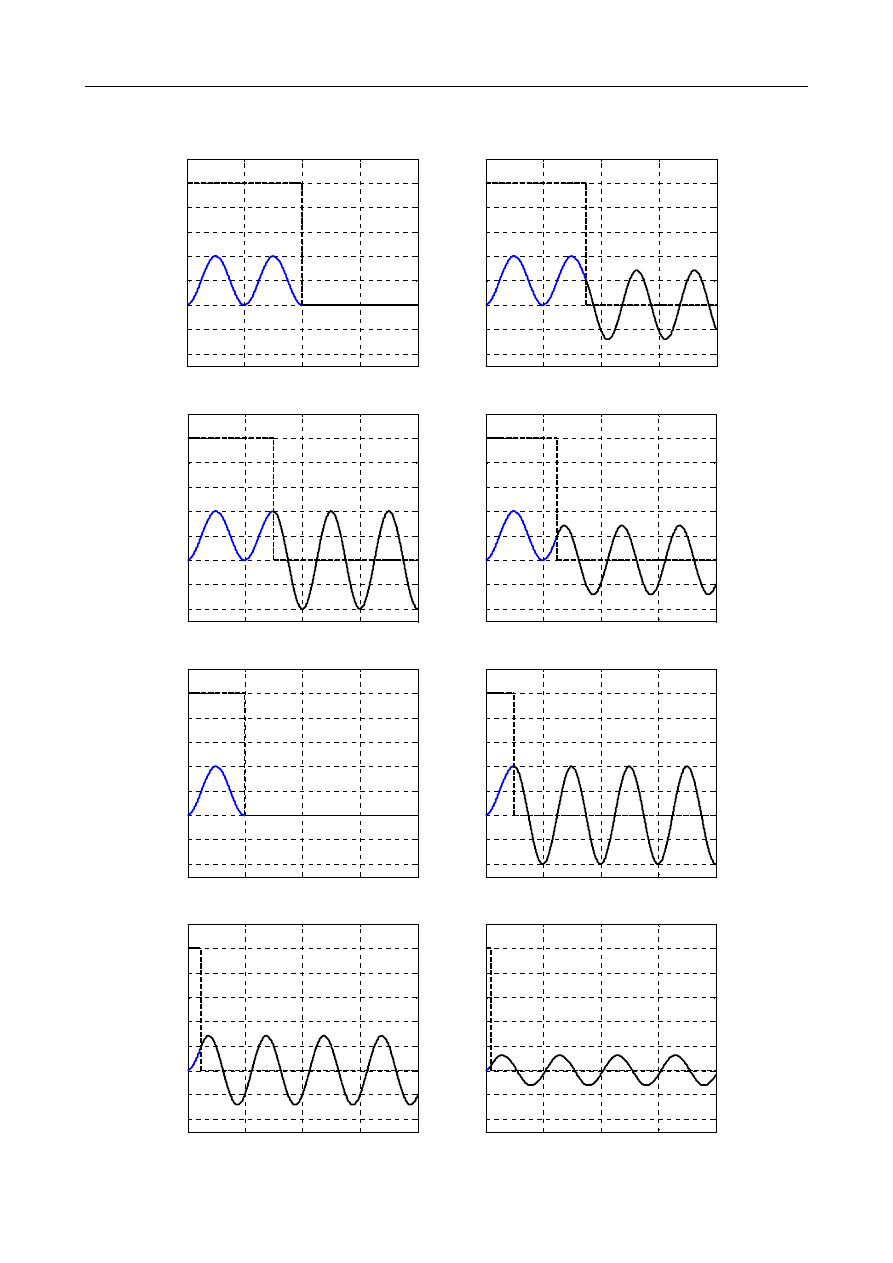
Dynamika Budowli
Wydział Inżynierii Lądowej i Środowiska
Magdalena Rucka & Krzysztof Wilde
________________________________________________________________________________________________
2007-02-26
46
Odpowiedź układu nietłumionego o jednym stopniu swobody na impuls prostokątny:
0
1
2
3
4
-4
-2
0
2
4
6
8
10
12
t [s]
u [
m
]
T
n
/t
d
=2
0
1
2
3
4
-4
-2
0
2
4
6
8
10
12
t [s]
u [
m
]
T
n
/t
d
=1.75
0
1
2
3
4
-4
-2
0
2
4
6
8
10
12
t [s]
u [
m
]
T
n
/t
d
=1.5
0
1
2
3
4
-4
-2
0
2
4
6
8
10
12
t [s]
u [
m
]
T
n
/t
d
=1.25
0
1
2
3
4
-4
-2
0
2
4
6
8
10
12
t [s]
u [
m
]
T
n
/t
d
=1
0
1
2
3
4
-4
-2
0
2
4
6
8
10
12
t [s]
u [
m
]
T
n
/t
d
=0.5
0
1
2
3
4
-4
-2
0
2
4
6
8
10
12
t [s]
u [
m
]
T
n
/t
d
=0.25
0
1
2
3
4
-4
-2
0
2
4
6
8
10
12
t [s]
u [
m
]
T
n
/t
d
=0.1
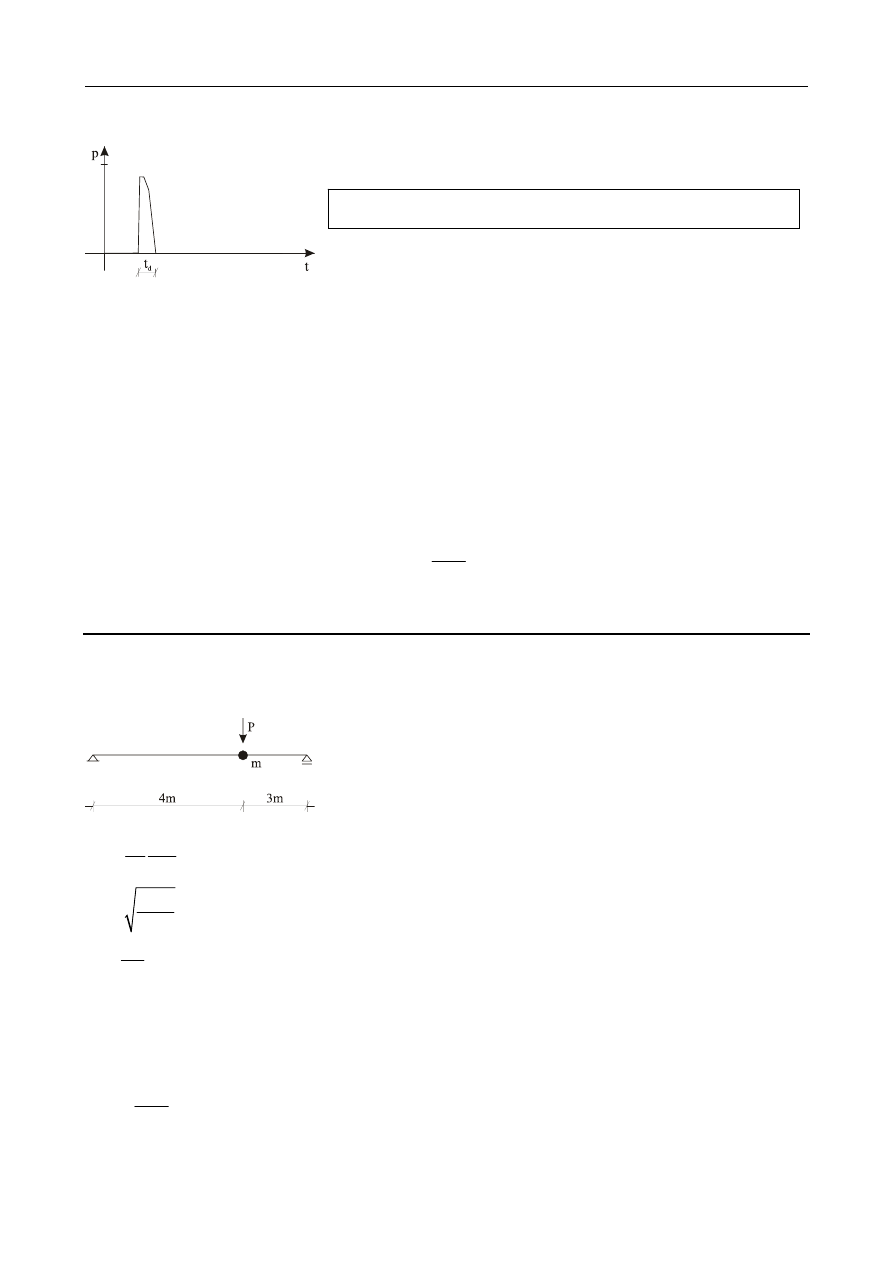
Dynamika Budowli
Wydział Inżynierii Lądowej i Środowiska
Magdalena Rucka & Krzysztof Wilde
________________________________________________________________________________________________
2007-02-26
47
6.3. Przybliżona odpowiedź układu o jednym stopniu swobody dla „krótkich” impulsów:
Jeżeli czas trwania impulsu
d
t jest krótszy od
/ 2
n
T
, wówczas maksymalne przemieszczenie nie
występuje w trakcie trwania impulsu, lecz w fazie drgań swobodnych, a impuls może być traktowa-
ny jako czysty impuls amplitudzie J:
0
( )
d
t
J
p t dt
=
∫
Odpowiedź układu na impuls J o czasie trwania
d
t spełniającym warunek /
0.5
d
n
t T
<
jest odpo-
wiedzią układu na impuls jednostkowy zgodnie z równaniem (6.3):
1
( )
sin
n
n
u t
J
t
m
ω
ω
⎛
⎞
= ⎜
⎟
⎝
⎠
. (6.14)
Z
ADANIE
6.1
Na belce o rozpiętości L = 7 m znajduje się masa m = 1800 kg. Do masy przyłożono nagle impuls
prostokątny o amplitudzie P = 9 kN działający przez czas 0.01 s. Wyznaczyć amplitudę drgań belki
jeżeli E = 210 GPa, I
x
= 4000 cm
4
.
11
48 1
7
x
EI
δ
=
7
26.087 rad/s
48
x
n
EI
m
ω
=
=
2
0.241
n
n
T
π
ω
=
=
/
0.041
d
n
t T
=
impuls :
90 Ns
d
J
P t
= ⋅ =
amplituda:
3
max
1.917 10 m
n
J
u
m
ω
−
=
=
⋅
Impuls „krótki” = impuls spełniający warunek /
0.5
d
n
t T
<
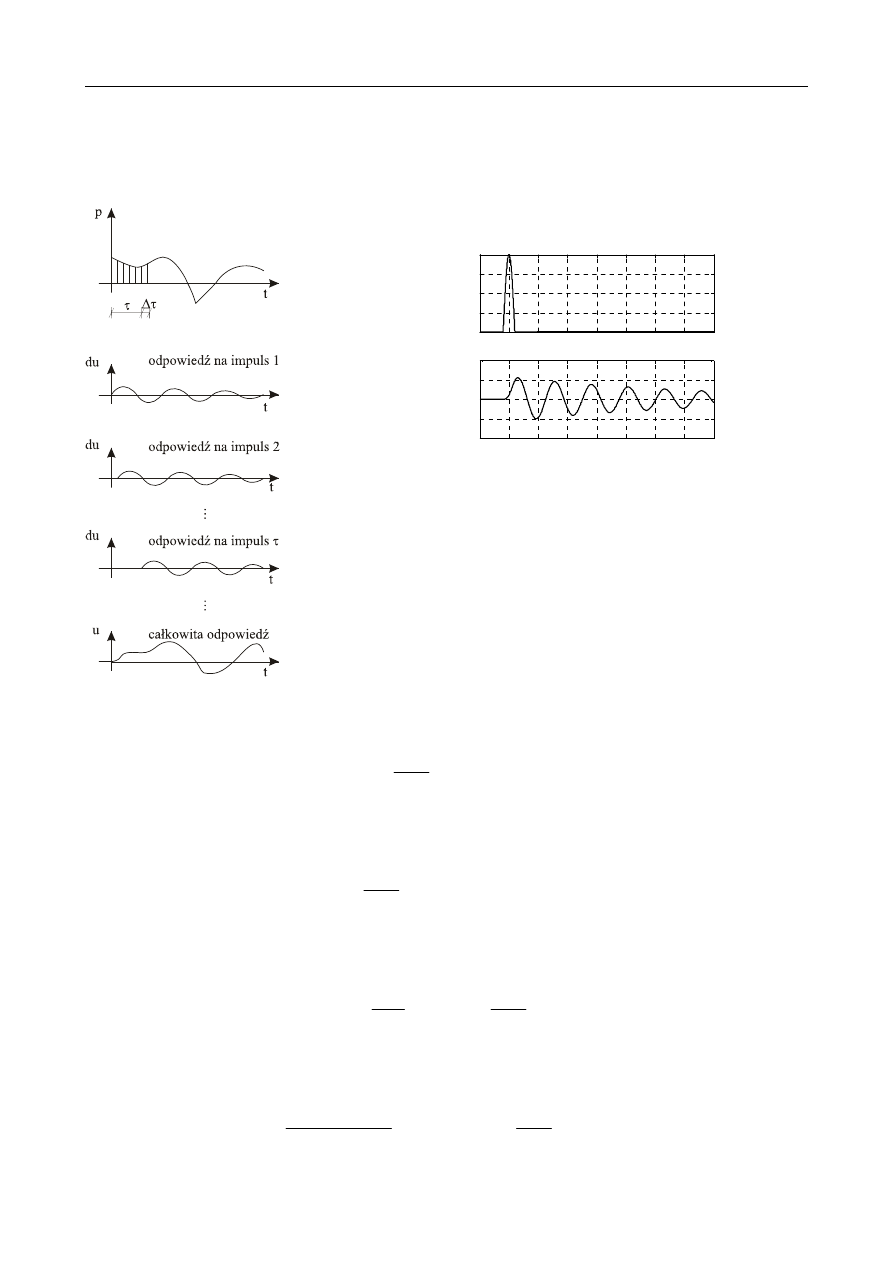
Dynamika Budowli
Wydział Inżynierii Lądowej i Środowiska
Magdalena Rucka & Krzysztof Wilde
________________________________________________________________________________________________
2007-02-26
48
6.4. Działanie dowolnej siły wymuszającej – wybrane sposoby rozwiązania równania ruchu o
jednym stopniu swobody:
a) całka Duhamela
Całka Duhamela dla układu nietłumionego:
[
]
0
( )
( )
sin
(
t
n
n
p
u t
t
d
m
τ
ω
τ
τ
ω
=
− )
∫
. (6.15)
Całka Duhamela dla układu tłumionego:
[
]
(1
)
0
( )
( )
sin
(
n
t
d
d
p
u t
e
t
d
m
ξω
τ
τ
ω
τ
τ
ω
−
−
=
− )
∫
. (6.16)
Całka Duhamela z uwzględnieniem warunków brzegowych dla układu nietłumionego:
[
]
0
(0)
( )
( )
(0) cos
sin
sin
(
) d
t
n
d
n
n
n
u
p
u t
u
t
t
t
m
τ
ω
ω
ω
τ
τ
ω
ω
⎛
⎞
=
+
+
−
⎜
⎟
⎝
⎠
∫
. (6.17)
Całka Duhamela z uwzględnieniem warunków brzegowych dla układu tłumionego:
[
]
(
)
0
(0)
(0)
( )
( )
(0) cos
sin
sin
(
) d
n
n
t
t
t
n
d
d
d
d
d
u
u
p
u t
u
t
t e
e
t
m
ξω
ξω
τ
ξω
τ
ω
ω
ω
τ
τ
ω
ω
−
−
−
⎛
⎞
+
=
+
+
−
⎜
⎟
⎝
⎠
∫
. (6.18)
function [u]=duhamel(m,wn,wd,ksi,p,t)
0
0.5
1
1.5
2
2.5
3
3.5
4
0
5
10
15
20
t [s]
p
(t)
[N
]
0
0.5
1
1.5
2
2.5
3
3.5
4
-0.4
-0.2
0
0.2
0.4
t [s]
u
(t)
[m
]
Dynamika Budowli
Wydział Inżynierii Lądowej i Środowiska
Magdalena Rucka & Krzysztof Wilde
________________________________________________________________________________________________
2007-02-26
49
b) równanie ruchu w przestrzeni stanów
Równanie ruchu układu tłumionego:
( )
mu cu ku
p t
+
+
=
(6.19)
gdzie: ( )
p t - dowolna siła wymuszająca
Proces dynamiczny może byś opisany zmiennymi x
i
definiującymi stan zjawiska. Zmienne x
i
nazy-
wamy zmiennymi przestrzeni stanu (lub prościej stanami). Do jednoznacznego opisu procesu dy-
namicznego o jednej zmiennej niezbędne są dwa stany. Na przykład przemieszczenie u i przyspie-
szenie
u
.
Załóżmy, że:
1
x
u
= - stan nr 1
2
x
u
= - stan nr 2
Przekształcając równanie (6.19) otrzymujemy:
1
( )
c
k
u
u
u
p t
m
m
m
+
+
=
oraz
1
( )
c
k
u
u
u
p t
m
m
m
= −
−
+
zapisując równanie poprzez stany uzyskujemy:
2
2
1
1
( )
c
k
x
x
x
p t
m
m
m
= −
−
+
(6.20)
dodatkowo zależność między stanami można zapisać jako:
1
2
x
x
= (6.21)
Równania (6.20) i (6.21) zapisane wektorowo przyjmują postać:
( )
p t
x = Ax + B
(state space equation of motion)
gdzie:
1
2
x
x
⎡ ⎤
⎢ ⎥
⎣ ⎦
x =
, wektor stanów,
0
1
/
/
k m
c m
⎡
⎤
⎢
⎥
−
−
⎣
⎦
A =
- macierz układu
0
1/ m
⎡
⎤
⎢
⎥
⎣
⎦
B =
Drugim równaniem uogólniającym procesy dynamiczne jest równanie wyjścia:
( )
p t
y = Cx + D
(output
equation)
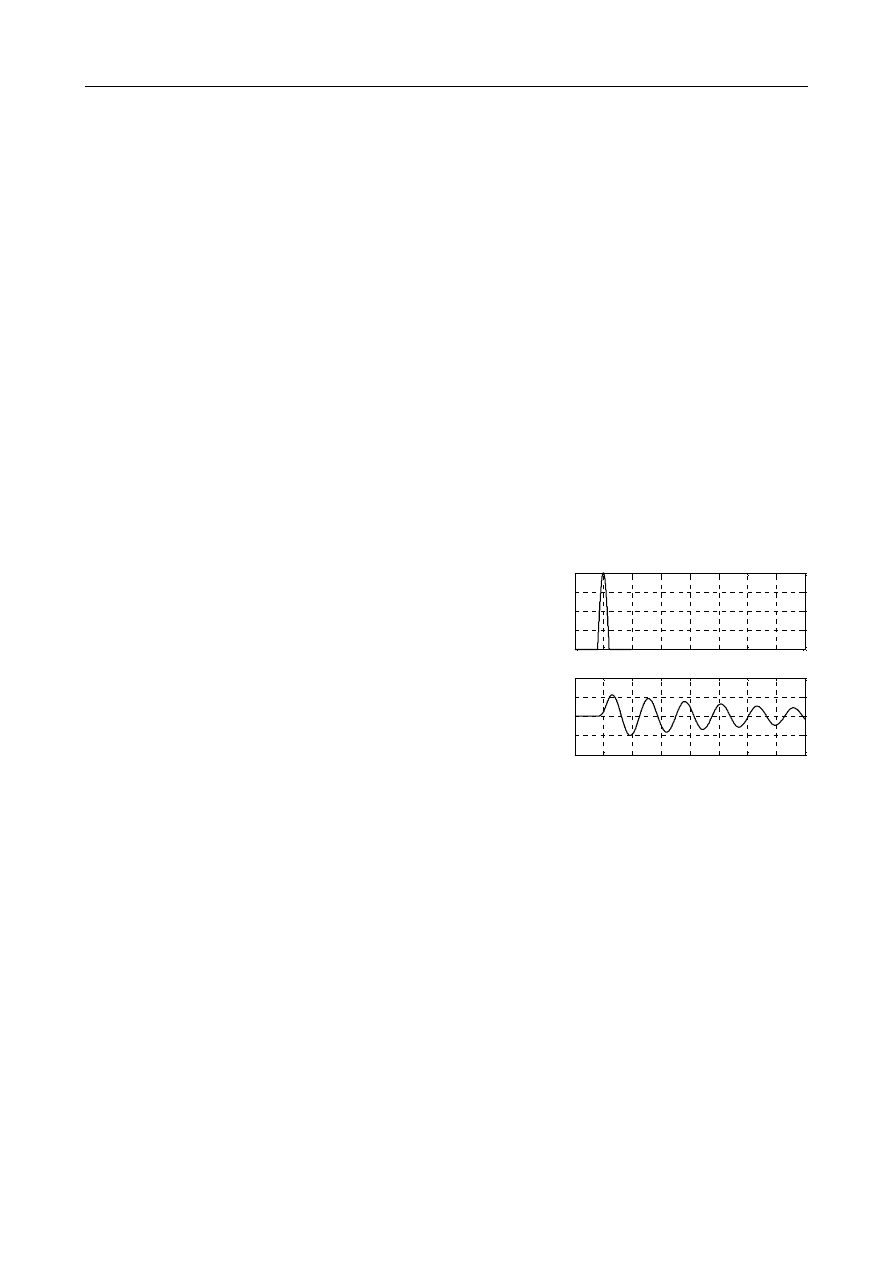
Dynamika Budowli
Wydział Inżynierii Lądowej i Środowiska
Magdalena Rucka & Krzysztof Wilde
________________________________________________________________________________________________
2007-02-26
50
Jeżeli jako decydujące dla opisu dynamiki wybierzemy stan związany z przemieszczeniem, x
i,
to
macierze C i D przyjmą postać:
[
]
1 0
C =
[ ]
0
D =
Macierze A, B, C i D definiują układ dynamiczny w przestrzeni stanów.
Wyjaśnienie użycia funkcji lsim w programie Matlab.
Format funkcji:
[Y, X] = lsim(A,B,C,D, p, t, X0);
Wynik całkowania funkcją lsim
Y - wektor odpowiedzi wybranych stanów
X – wektory odpowiedzi układu wszystkich stanów
Dane
wejściowe do funkcji lsim
A, B, C, D – macierze stanu układu dynamicznego
p – wektory wymuszeń zewnętrznych
t – wektor czasu
X0 – wektor warunków początkowych (przemieszczenia i prędkości),
np. X0=[0 0]
m=1 %kg
k=100 %N/m
c=0.6 %Ns/m
tk = 4; % czas końcowy [s]
fs = 1000; % częstotliwość próbkowania [Hz]
dt=1/fs ; % krok czasowy
N = tk*fs; % liczba próbek
t = linspace(0, tk, N); % wektor czasu
p = [ utworzyć żądany wektor obciążenia];
XO = [0 0]; % warunki początkowe X0= [uo, vo]
A = [ 0 1
-inv(m)*k -inv(m)*c ];
B= [ 0 ; inv(m)];
C = eye(2);
D= [0;0];
[Y,X] = lsim(A,B,C,D,p,t,XO);
przem=Y(:,1);
predk=Y(:,2);
przysp = -inv(m)*c*predk-inv(m)*k*przem+inv(m)*p';
0
0.5
1
1.5
2
2.5
3
3.5
4
0
5
10
15
20
t [s]
p
(t)
[N
]
0
0.5
1
1.5
2
2.5
3
3.5
4
-0.4
-0.2
0
0.2
0.4
t [s]
u
(t)
[m
]

Dynamika Budowli
Wydział Inżynierii Lądowej i Środowiska
Magdalena Rucka & Krzysztof Wilde
________________________________________________________________________________________________
2007-02-26
51
c) metoda różnic centralnych
Siła wymuszająca jest dana w postaci zbioru dyskretnych wartości ( )
i
i
p
p t
=
w punktach czaso-
wych
i
t . Przedział czasu
1
i
i
i
t
t
t
+
Δ =
− zwykle przyjmowany jest jako stały. Odpowiedź układu okre-
ślona jest w dyskretnych chwilach czasu
i
t : Równanie ruchu w chwili
i
t jest następującej postaci:
i
i
i
i
mu
cu
ku
p
+
+
= (6.22)
Podstawą metody jest zastąpienie pochodnych (prędkości i przyspieszeń) centralnymi ilorazami
różnicowymi. Dla stałego kroku czasowego
t
Δ
różnice centralne przyjmują postać:
( )
1
1
1
1
2
2
,
2
i
i
i
i
i
i
i
u
u
u
u
u
u
u
t
t
+
−
+
−
−
−
+
=
=
Δ
Δ
. (6.23)
Podstawiając przybliżone wartości (6.23) do równania (6.22) otrzymujemy:
( )
1
1
1
1
2
2
2
i
i
i
i
i
i
i
u
u
u
u
u
m
c
ku
p
t
t
+
−
+
−
−
+
−
+
+
=
Δ
Δ
(6.24)
Równanie (6.24) można przekształcić do postaci:
do obliczenia znane znane znane
( )
( )
( )
1
1
2
2
2
2
2
2
i
i
i
i
i
m
c
m
c
m
u
p
u
k
u
t
t
t
t
t
k
p
+
−
⎡
⎤
⎡
⎤
⎡
⎤
+
=
−
−
−
−
⎢
⎥
⎢
⎥
⎢
⎥
Δ
Δ
Δ
Δ
Δ
⎢
⎥
⎢
⎥
⎢
⎥
⎣
⎦
⎣
⎦
⎣
⎦
(6.25)
lub:
1
i
i
ku
p
+
=
(6.26)
Nieznana wartość przemieszczenia w chwili
1
i
t
+
można obliczyć ze wzoru:
1
i
i
p
u
k
+
=
(6.27)
Rozwiązanie
1
i
u
+
w chwili
1
i
t
+
jest określone z równania ruchu w chwili
i
t bez korzystania z rów-
nania ruchu w chwili
1
i
t
+
). Stąd metodę różnic centralnych nazywamy metodą bezpośrednią (jaw-
ną). Do określenia
1
i
u
+
wymagane są wartości
i
u oraz
1
i
u
−
.

Dynamika Budowli
Wydział Inżynierii Lądowej i Środowiska
Magdalena Rucka & Krzysztof Wilde
________________________________________________________________________________________________
2007-02-26
52
Do określenia przemieszczenia
1
u wymagane są wartości
0
u oraz
1
u
−
. Wartość
0
u znana jest z wa-
runków początkowych. Aby wyznaczyć wartość
1
u
−
korzystamy z zależności (6.23) dla czasu i=0:
( )
1
0
1
1
1
0
0
2
2
,
2
u
u
u
u
u
u
u
t
t
−
−
−
+
−
=
=
Δ
Δ
, (6.28)
Z równań (6.28) wyznaczamy:
( ) ( )
2
1
0
0
0
2
t
u
u
t u
u
−
Δ
=
− Δ
+
. (6.29)
Przyspieszenie
0
u można określić z równania ruchu (6.22) dla czasu
0
t :
0
0
0
0
mu
cu
ku
p
+
+
=
(6.30)
0
0
0
0
p
cu
ku
u
m
−
−
=
(6.31)
Metoda różnic skończonych wymaga, aby krok czasowy
t
Δ
spełniał warunek:
1
n
t
T
π
Δ
< (6.32)
W praktyce, aby wynik obliczeń były bardziej dokładne przyjmuje się
/
0.1
n
t T
Δ
≤
.
Algorytm metody różnic skończonych:
1. Obliczenia początkowe
1.1.
0
0
0
0
p
cu
ku
u
m
−
−
=
1.2.
( ) ( )
2
1
0
0
0
2
t
u
u
t u
u
−
Δ
=
− Δ
+
1.3.
( )
2
2
m
c
k
t
t
=
+
Δ
Δ
1.4.
( )
2
2
m
c
a
t
t
=
−
Δ
Δ
1.5.
( )
2
2m
b k
t
= −
Δ
2. Obliczenia dla kroku czasowego i
2.1.
1
i
i
i
i
p
p
au
bu
−
=
−
−
2.2.
1
i
i
p
u
k
+
=
2.3. jeżeli wymagane:
( )
1
1
1
1
2
2
,
2
i
i
i
i
i
i
i
u
u
u
u
u
u
u
t
t
+
−
+
−
−
−
+
=
=
Δ
Δ
3. Powtórzenie dla następnego kroku czasowego – zamień i na i+1, powtórz 2.1, 2.2, 2.3 dla
następnego kroku czasowego (i = 0,1,2,…)
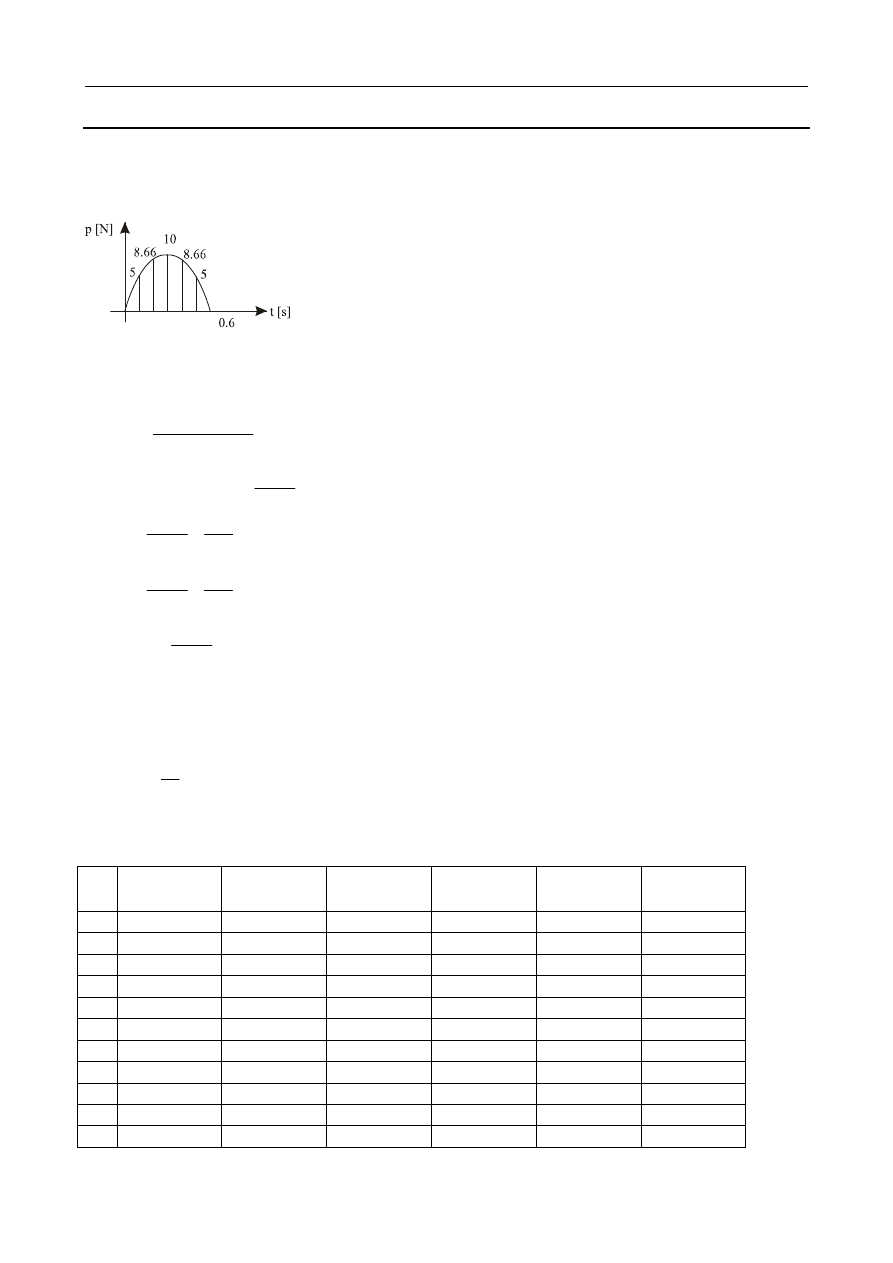
Dynamika Budowli
Wydział Inżynierii Lądowej i Środowiska
Magdalena Rucka & Krzysztof Wilde
________________________________________________________________________________________________
2007-02-26
53
Z
ADANIE
6.2
Układ o jednym stopniu swobody (m = 0.2533 kg, k = 10 N/m,
n
T = 1 s.,
0.05
ξ
=
) poddany jest
działaniu siły wymuszającej jak na rysunku. Obliczyć metodą różnic centralnych przemieszczenie
układu. Krok czasowy
0.1
t
Δ =
s., czas końcowy 1 s, (0) 0, (0) 0
u
u
=
= .
1. Obliczenia początkowe
1.1.
0
0
0
0
p
cu
ku
u
m
−
−
=
1.2.
( ) ( )
2
1
0
0
0
2
t
u
u
t u
u
−
Δ
=
− Δ
+
1.3.
( )
2
2
m
c
k
t
t
=
+
Δ
Δ
1.4.
( )
2
2
m
c
a
t
t
=
−
Δ
Δ
1.5.
( )
2
2m
b k
t
= −
Δ
2. Obliczenia dla kroku czasowego i
2.1.
1
i
i
i
i
p
p
au
bu
−
=
−
−
2.2.
1
i
i
p
u
k
+
=
i
t
i
p
1
i
u
−
i
u
i
p
(2.1)
1
i
u
+
(2.2)
teoretycznie
1
i
u
+
0.0328
0.2332
0.6487
1.1605
1.5241
1.4814
0.9245
0.0599
-0.7751
-1.2718
-1.2674
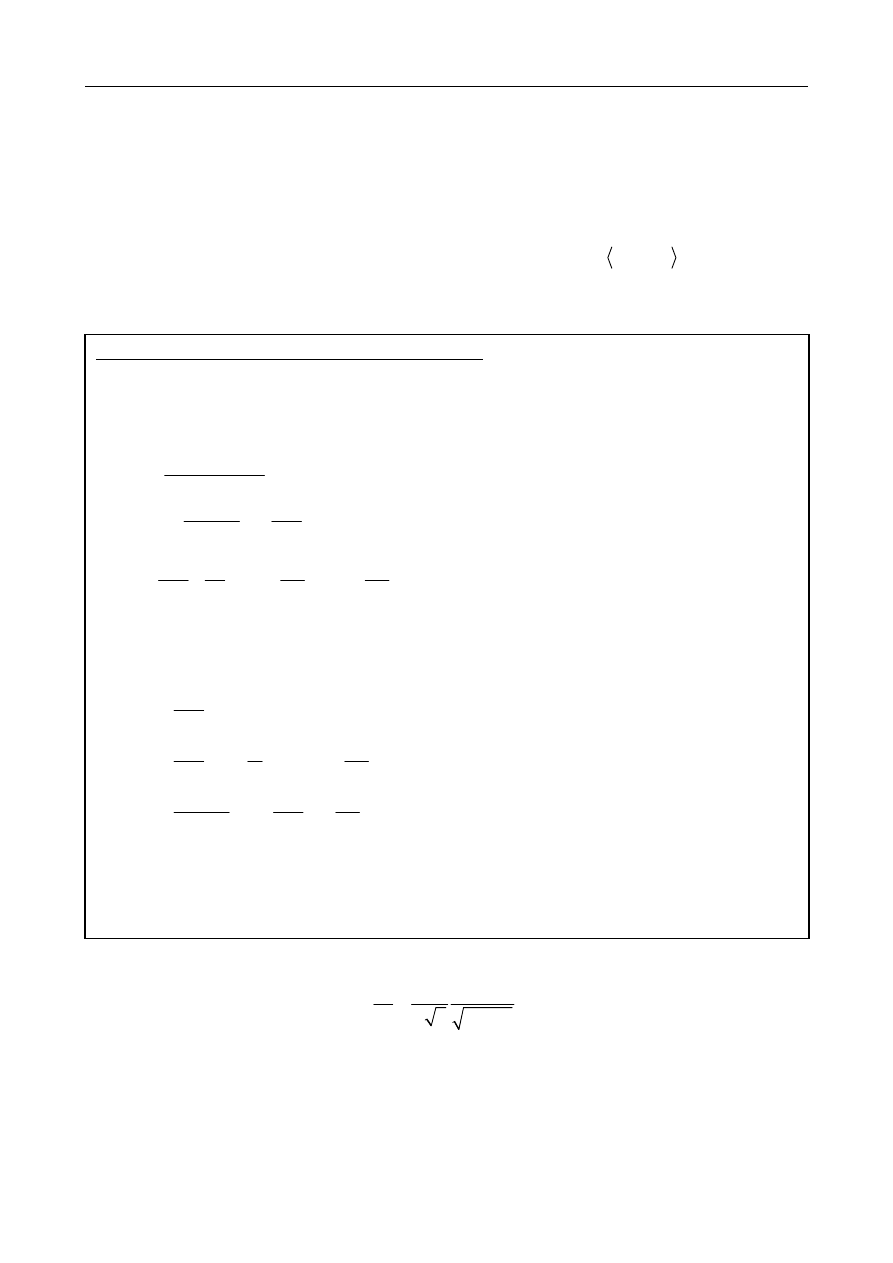
Dynamika Budowli
Wydział Inżynierii Lądowej i Środowiska
Magdalena Rucka & Krzysztof Wilde
________________________________________________________________________________________________
2007-02-26
54
d) metoda Newmarka
W 1959r. Newmark opublikował zbiór metod bazujących na następujących równaniach:
(
)
( )
( )
(
)( )
( )
1
1
2
2
1
1
1
0.5
i
i
i
i
i
i
i
i
i
u
u
t u
t u
u
u
t u
t
u
t
u
γ
γ
β
β
+
+
+
+
= +
+
Δ
+ Δ
⎡
⎤
⎣
⎦
⎡
⎤
⎡
⎤
= + Δ
+
−
Δ
+
Δ
⎣
⎦
⎣
⎦
(6.33)
Parametry
i
β γ
określają zmianę przyspieszenia w jednym kroku czasowym oraz charakteryzują
dokładność i stabilność metody. Następujący wybór parametrów:
1/ 6,1/ 4 ,
1/ 2
β
γ
∈
=
jest sa-
tysfakcjonujący ze wszystkich punktów widzenia metod numerycznych, włączając dokładność obli-
czeń.
Metoda Newmarka jest stabilna, jeżeli:
1
1
2
2
n
t
T
π
γ
β
Δ
≤
−
. (6.34)
Dla parametrów
1/ 4,
1/ 2
β
γ
=
=
warunek ma postać: /
n
t T
Δ
≤ ∞
natomiast dla parametrów
1/ 6,
1/ 2
β
γ
=
=
:
/
0.551
n
t T
Δ
≤
Aby obliczenia były dokładne, należy przyjąć przedział czasowy znacznie mniejszy niż wynika to z
warunku (6.34).
Algorytm metody Newmarka dla układów liniowych:
Przypadki specjalne: (a) metoda średniego przyspieszenia (
1/ 4,
1/ 2
β
γ
=
=
)
(b) metoda liniowego przyspieszenia (
1/ 6,
1/ 2
β
γ
=
=
)
1. Obliczenia początkowe
1.1.
0
0
0
0
p
cu
ku
u
m
−
−
=
1.2.
( )
2
1
k k
m
c
t
t
γ
β
β
= +
+
Δ
Δ
1.3.
m
c
a
t
γ
β
β
=
+
Δ
,
1
1
2
2
b
m
t
c
γ
β
β
⎛
⎞
=
+ Δ
−
⎜
⎟
⎝
⎠
2. Obliczenia dla kroku czasowego i
2.1.
i
i
i
i
p
p
au
bu
Δ = Δ +
+
2.2.
i
i
p
u
k
Δ
Δ =
2.3.
1
2
i
i
i
i
u
u
u
t
u
t
γ
γ
γ
β
β
β
⎛
⎞
Δ =
Δ −
+ Δ
−
⎜
⎟
Δ
⎝
⎠
2.4.
( )
2
1
1
1
2
i
i
i
i
u
u
u
u
t
t
β
β
β
Δ =
Δ −
−
Δ
Δ
2.5.
1
1
1
,
,
i
i
i
i
i
i
i
i
i
u
u
u
u
u
u
u
u
u
+
+
+
= + Δ
= + Δ
= + Δ
3. Powtórzenie dla następnego kroku czasowego – zamień i na i+1, powtórz 2.1 do 2.5 dla
następnego kroku czasowego
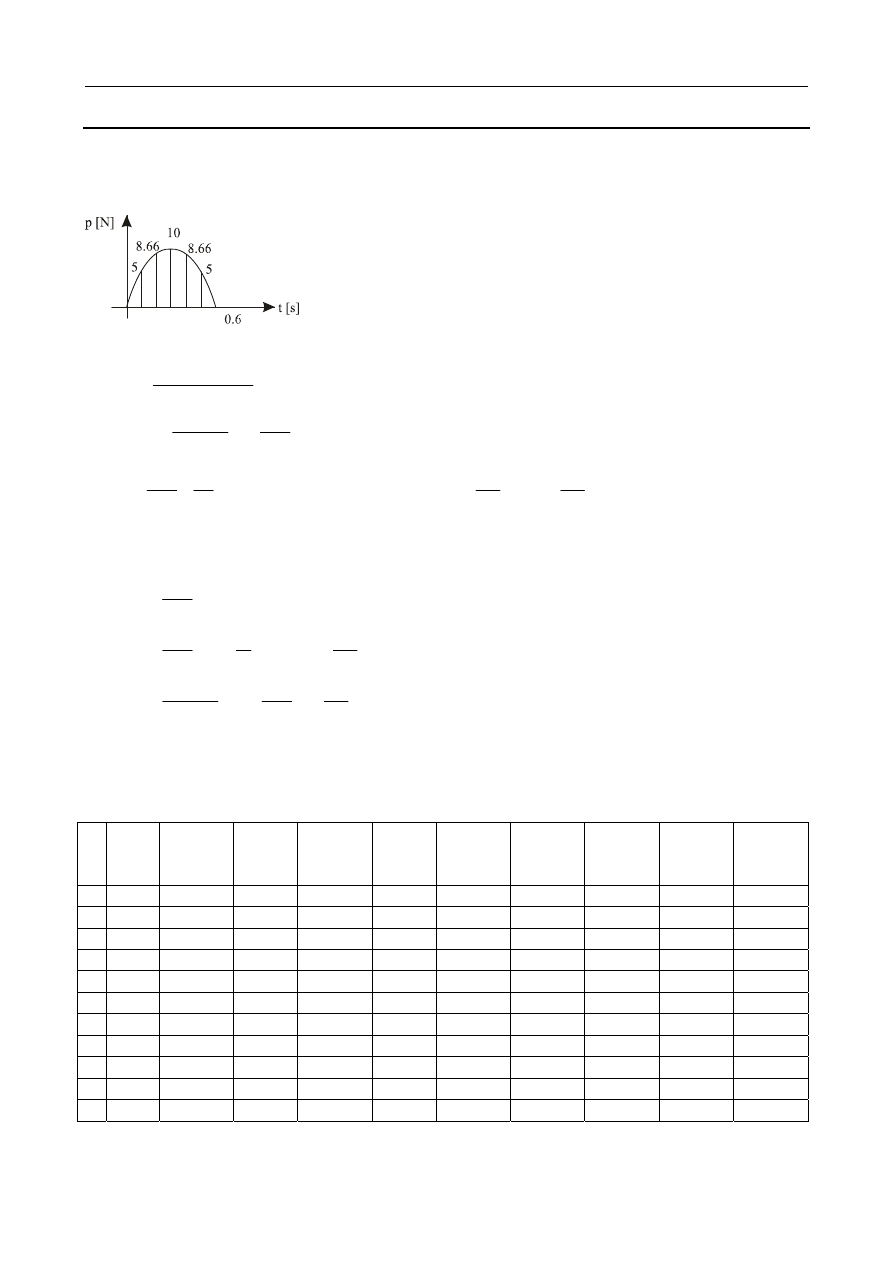
Dynamika Budowli
Wydział Inżynierii Lądowej i Środowiska
Magdalena Rucka & Krzysztof Wilde
________________________________________________________________________________________________
2007-02-26
55
Z
ADANIE
6.3
Układ o jednym stopniu swobody (m = 0.2533 kg, k = 10 N/m,
n
T = 1 s.,
0.05
ξ
=
) poddany jest
działaniu siły wymuszającej jak na rysunku. Obliczyć metodą Newmarka (średniego przyspiesze-
nia) przemieszczenie układu. Krok czasowy
0.1
t
Δ =
s., czas końcowy 1 s., (0) 0, (0) 0
u
u
=
= .
1. Obliczenia początkowe
1.1.
0
0
0
0
p
cu
ku
u
m
−
−
=
1.2.
( )
2
1
k k
m
c
t
t
γ
β
β
= +
+
Δ
Δ
1.3.
m
c
a
t
γ
β
β
=
+
Δ
1
1
2
2
b
m
t
c
γ
β
β
⎛
⎞
=
+ Δ
−
⎜
⎟
⎝
⎠
2. Obliczenia dla kroku czasowego i
2.1.
i
i
i
i
p
p
au
bu
Δ = Δ +
+
2.2.
i
i
p
u
k
Δ
Δ =
2.3.
1
2
i
i
i
i
u
u
u
t
u
t
γ
γ
γ
β
β
β
⎛
⎞
Δ =
Δ −
+ Δ
−
⎜
⎟
Δ
⎝
⎠
2.4.
( )
2
1
1
1
2
i
i
i
i
u
u
u
u
t
t
β
β
β
Δ =
Δ −
−
Δ
Δ
2.5.
1
1
1
,
,
i
i
i
i
i
i
i
i
i
u
u
u
u
u
u
u
u
u
+
+
+
= + Δ
= + Δ
= + Δ
3. Powtórzenie dla następnego kroku czasowego
i
t
i
p
i
u
(2.5)
i
p
Δ
i
p
Δ
(2.1)
i
u
Δ
(2.2)
i
u
Δ
(2.3)
i
u
Δ
(2.4)
i
u
(2.5)
i
u
(2.5)
teore-
tycznie
1
i
u
+
0.0328
0.2332
0.6487
1.1605
1.5241
1.4814
0.9245
0.0599
-0.7751
-1.2718
-1.2674

Dynamika Budowli
Wydział Inżynierii Lądowej i Środowiska
Magdalena Rucka & Krzysztof Wilde
________________________________________________________________________________________________
2007-02-26
56
7. Drgania swobodne układów dyskretnych o n stopniach swobody.
Równanie macierzowe ruchu:
( )
t
+
+
=
Mu Cu Ku P
(7.1)
Rozpatrywać będziemy drgania swobodne bez tłumienia:
+
=
Mu Ku 0
(7.2)
Rozwiązanie ( )
t
u
będzie w formie:
( )
( )
n
n
t
q t
φ
=
u
(7.3)
gdzie:
( )
cos
sin
n
n
n
n
n
q t
A
t B
t
ω
ω
=
+
(7.4)
Wektor
n
φ
odpowiada za kształt odpowiedzi a ( )
n
q t są współrzędnymi modalnymi. Po podstawie-
niu (7.3) i (7.4) do (7.2) otrzymujemy:
(
)
2
n
n
ω
φ
−
=
K
M
0 (7.5)
Równanie (7.5) posiada nietrywialnie rozwiązanie, jeżeli
(
)
2
det
0
n
ω
−
=
K
M
(7.6)
N pierwiastków
2
n
ω
równania (7.6) określa N naturalnych częstości układu
n
ω
(n = 1,2,…N). Każ-
dej częstości
n
ω
odpowiada wektor własny
n
φ
obliczony z dokładnością do stałego mnożnika.
Wektor dany przez relatywne wartości N przemieszczeń
jn
φ
(j = 1,2,…N) określa postać drgań.
N wartości własnych i N wektorów własnych (postaci drgań) można złożyć w macierze. Macierz,
której kolumny składają się z N wektorów własnych nazywa się macierzą modalną:
11
12
1
12
22
2
1
2
N
N
jn
N
N
NN
φ
φ
φ
φ
φ
φ
φ
φ
φ
φ
⎡
⎤
⎢
⎥
⎢
⎥
⎡ ⎤
=
=
⎣ ⎦ ⎢
⎥
⎢
⎥
⎣
⎦
Φ
(7.7)
N wartości własnych
2
n
ω
może być złożonych w diagonalną macierz widmową układu:
2
1
2
2
2
2
0
0
0
0
0
0
N
ω
ω
ω
⎡
⎤
⎢
⎥
⎢
⎥
=
⎢
⎥
⎢
⎥
⎢
⎥
⎣
⎦
Ω
(7.8)

Dynamika Budowli
Wydział Inżynierii Lądowej i Środowiska
Magdalena Rucka & Krzysztof Wilde
________________________________________________________________________________________________
2007-02-26
57
Każda wartość własna
2
n
ω
i każdy wektor własny
n
φ
spełnia równanie:
2
n
n
n
φ
φ ω
=
K
M
(7.9)
Użycie macierzy modalnej i macierzy widmowej pozwala na zapisanie N równań (7.9) w postaci
jednego równania macierzowego:
2
=
KΦ MΦΩ (7.10)
Wektory własne obliczone z dokładnością do stałego mnożnika można znormalizować tak, aby
największa współrzędna wektora była 1:
max
n
n
jn
φ
φ
φ
=
(7.11)
Jeżeli wszystkie wartości własne
2
n
ω
ą rzeczywiste to wektory własne odpowiadające różnym
częstościom
n
k
ω
ω
≠
są ortogonalne:
0
T
n
r
φ φ
=
K
(7.12)
0
T
n
r
φ
φ
=
M
(7.13)
Ortogonalność postaci drgań zapewnia, że następujące macierze są diagonalne:
T
=
K Φ KΦ (7.14)
T
M = Φ MΦ
(7.15)
Elementy leżące na diagonali:
T
n
n
n
K
φ
φ
=
K
(7.16)
T
n
n
n
M
φ
φ
=
M
(7.17)
Możliwe jest również takie znormalizowanie wektorów własnych:
n
n
T
n
n
φ
φ
φ
φ
=
M
(7.18)
że macierz modalna będzie diagonalizować macierz mas do macierzy jednostkowej, a macierz
sztywności do macierzy widmowej:
2
T
=
Φ KΦ Ω
(7.19)
T
=
Φ MΦ I
(7.20)

Dynamika Budowli
Wydział Inżynierii Lądowej i Środowiska
Magdalena Rucka & Krzysztof Wilde
________________________________________________________________________________________________
2007-02-26
58
Wektor przemieszczenia może być wyrażony we współrzędnych modalnych:
1
N
r r
r
q
φ
=
=
=
∑
u
Φq
(7.21)
gdzie
1
2
[ ... ]
T
n
q q
q
=
q
oznacza współrzędne modalne. Mnożąc (7.21) przez
T
n
φ
M
:
1
N
T
T
n
n
r r
r
q
φ
φ
φ
=
=
∑
Mu
M
(7.22)
Wykorzystując właściwość ortogonalności:
T
T
n
n
n n
q
φ
φ
φ
=
Mu
M
(7.23)
T
T
n
n
n
T
n
n
n
q
M
φ
φ
φ
φ
=
=
Mu
Mu
M
(7.24)
W przypadku obliczeń ręcznych niejednokrotnie łatwiej jest posłużyć się macierzą podatności F,
gdzie
1
−
=
F K
(7.25)
Przekształcając równanie (7.2) poprzez lewostronne pomnożenie przez macierz
1
−
K
otrzymujemy:
0
+ =
FMu u
(7.26)
Podstawiając (7.4) do równania (7.26) otrzymamy
(
)
2
0
n
n
ω
φ
−
=
I
FM
(7.27)
Równanie (7.27) ma nietrywialnie rozwiązanie, jeżeli:
(
)
2
det
0
n
ω
−
=
I
FM
(7.28)
N pierwiastków
2
n
ω
równania (7.28) określa N naturalnych częstości układu
n
ω
(n = 1,2,…N). Każ-
dej częstości
n
ω
odpowiada wektor własny
n
φ
.
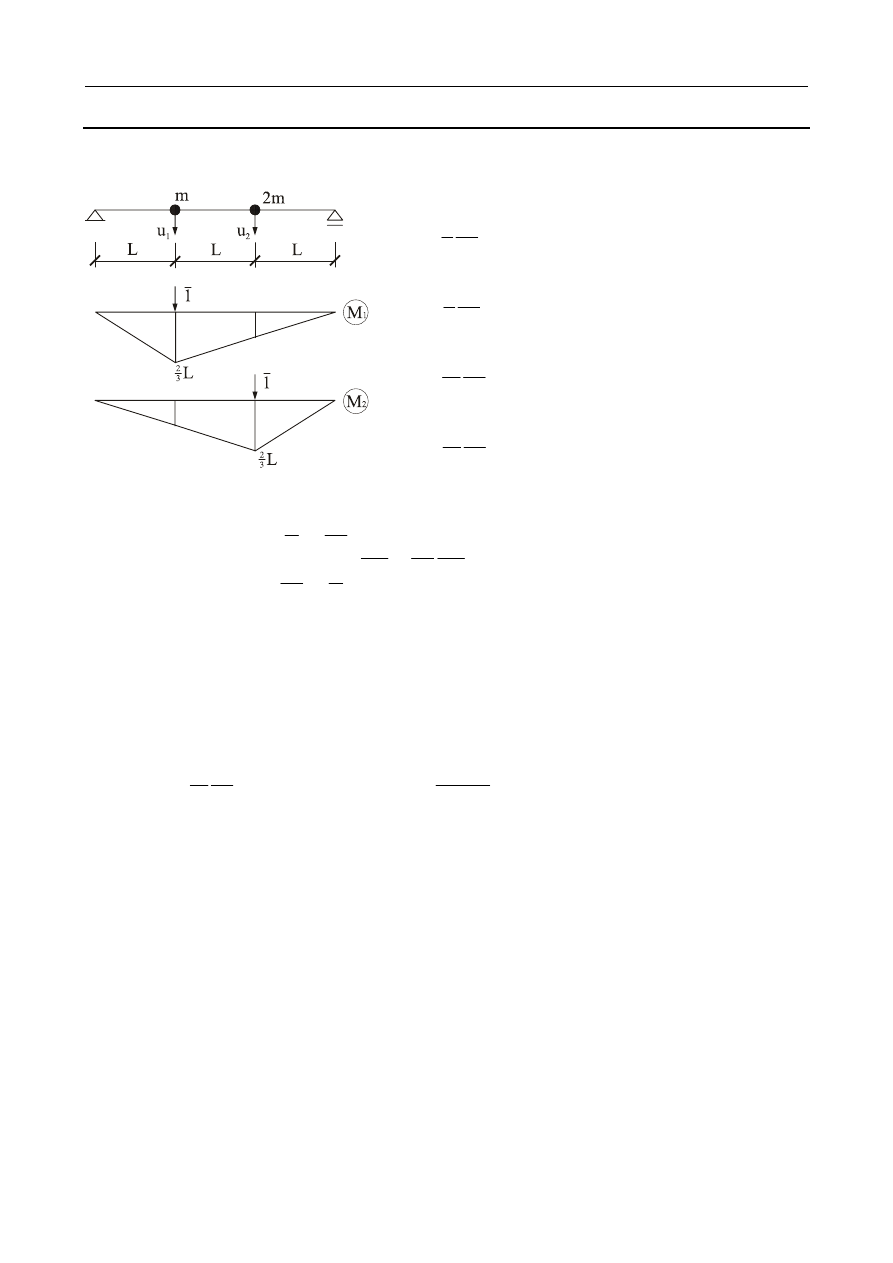
Dynamika Budowli
Wydział Inżynierii Lądowej i Środowiska
Magdalena Rucka & Krzysztof Wilde
________________________________________________________________________________________________
2007-02-26
59
Z
ADANIE
7.1
Obliczyć częstości i postacie drgań swobodnych układu belkowego z dwiema masami skupionymi.
Sprawdzić ortogonalność postaci drgań.
Macierz podatności
3
3
4
7
8
7
1
9
1 8
7
4
7
8
1 8
1 8
9
L
L
E I
E I
⎡
⎤
⎢
⎥
⎡
⎤
=
=
⎢
⎥
⎢
⎥
⎣
⎦
⎢
⎥
⎢
⎥
⎣
⎦
F
Macierz mas
0
1
0
0
2
0
2
m
m
m
⎡
⎤
⎡
⎤
=
=
⎢
⎥
⎢
⎥
⎣
⎦
⎣
⎦
M
(
)
2
n
n
ω
φ
=
I -
FM
0
3
2
1 0
8 14
0 1
7 16
18
n
n
m L
EI
ω
φ
⎛
⎞
⎡
⎤
⎡
⎤
−
=
⎜
⎟
⎢
⎥
⎢
⎥
⎣
⎦
⎣
⎦
⎝
⎠
0
2
3
18
n
mL
EI
ω
λ
=
1 8
14
det
0
7
1 16
λ
λ
λ
λ
−
−
⎡
⎤
=
⎢
⎥
−
−
⎣
⎦
1
0.0441
λ
=
2
0.7559
λ
=
3
11
4
9
L
EI
δ
=
3
22
4
9
L
EI
δ
=
3
12
7
18
L
EI
δ
=
3
21
7
18
L
EI
δ
=
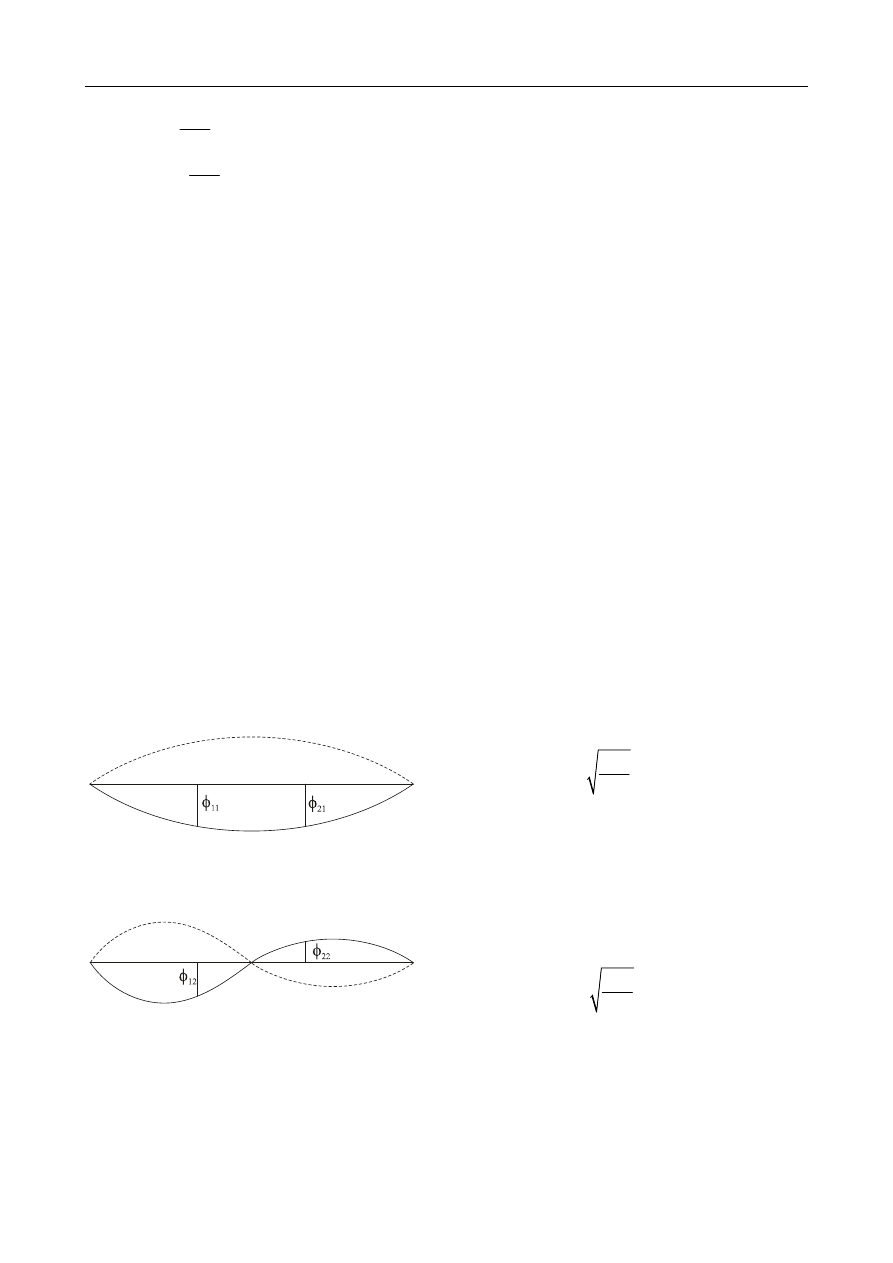
Dynamika Budowli
Wydział Inżynierii Lądowej i Środowiska
Magdalena Rucka & Krzysztof Wilde
________________________________________________________________________________________________
2007-02-26
60
2
1
3
0.7938
EI
mL
ω
=
2
2
3
13.6062
EI
mL
ω
=
1 0
8 14
0
0 1
7 16
0
n
n
λ
φ
⎛
⎞
⎡
⎤
⎡
⎤
⎡ ⎤
−
=
⎜
⎟
⎢
⎥
⎢
⎥
⎢ ⎥
⎣
⎦
⎣
⎦
⎣ ⎦
⎝
⎠
1
0.0441
λ
=
2
0.7559
λ
=
11
21
1 8 0.0441
14 0.0441
0
7 0.0441 1 16 0.0441
0
φ
φ
− ⋅
− ⋅
⎡ ⎤
⎡
⎤
⎡ ⎤
=
⎢ ⎥
⎢
⎥
⎢ ⎥
− ⋅
− ⋅
⎣
⎦
⎣ ⎦
⎣ ⎦
12
22
1 8 0.7559
14 0.7559
0
7 0.7559
1 16 0.7559
0
φ
φ
− ⋅
− ⋅
⎡ ⎤
⎡
⎤
⎡ ⎤
=
⎢ ⎥
⎢
⎥
⎢ ⎥
− ⋅
− ⋅
⎣
⎦
⎣ ⎦
⎣ ⎦
21
1
φ
=
12
1
φ
=
11
0.954
φ
=
22
0.477
φ
= −
1
0.954
1
φ
⎡
⎤
= ⎢
⎥
⎣
⎦
2
1
0.477
φ
⎡
⎤
= ⎢
⎥
−
⎣
⎦
1
3
0.891
EI
mL
ω
=
2
3
3.689
EI
mL
ω
=

Dynamika Budowli
Wydział Inżynierii Lądowej i Środowiska
Magdalena Rucka & Krzysztof Wilde
________________________________________________________________________________________________
2007-02-26
61
Z
ADANIE
7.2
Obliczyć częstości oraz postacie drgań własnych układu dwóch prętów kratowych obciążonych
masą skupioną m. E = 210 GPa, Q = 10kN. Sprawdzić ortogonalność postaci drgań.
(
)
1
k m
n
i
i
mk
i
i
i
z z
l
EA
δ
=
=
∑
7
11
m
1.33862 10
N
δ
−
=
⋅
7
12
m
0.50791 10
N
δ
−
=
⋅
7
22
m
0.38095 10
N
δ
−
=
⋅
7
1.33862 0.50794
10
0.50794 0.38095
−
⎡
⎤
=
⋅
⎢
⎥
⎣
⎦
F
1019.368
0
0
1019.368
⎡
⎤
= ⎢
⎥
⎣
⎦
M
(
)
2
n
n
ω
φ
−
=
I
FM
0
7
7
2
7
7
1 0
1364.54638 10
517.77778 10
0 1
517.77778 10
388.32823 10
n
n
ω
φ
−
−
−
−
⎛
⎞
⎡
⎤
⋅
⋅
⎡
⎤
−
=
⎜
⎟
⎢
⎥
⎢
⎥
⎜
⎟
⋅
⋅
⎣
⎦
⎣
⎦
⎝
⎠
0
1
6297.1656
λ
=
2
60658.0517
λ
=

Dynamika Budowli
Wydział Inżynierii Lądowej i Środowiska
Magdalena Rucka & Krzysztof Wilde
________________________________________________________________________________________________
2007-02-26
62
1
rad
79.35
s
ω
=
2
rad
246.29
s
ω
=
1
6297.1656
λ
=
2
60658.0517
λ
=
11
21
1 0.85928
0.32605
0
0.32605
1 0.24454
0
φ
φ
−
−
⎡ ⎤
⎡
⎤
⎡ ⎤
=
⎢ ⎥
⎢
⎥
⎢ ⎥
−
−
⎣
⎦
⎣ ⎦
⎣ ⎦
12
22
1 8.27707
3.14074
0
3.14074
1 2.35552
0
φ
φ
−
−
⎡ ⎤
⎡
⎤
⎡ ⎤
=
⎢ ⎥
⎢
⎥
⎢ ⎥
−
−
⎣
⎦
⎣ ⎦
⎣ ⎦
11
1
φ
=
12
0.43
φ
= −
21
0.43
φ
=
22
1
φ
=
1
1
0.43
φ
⎡
⎤
= ⎢
⎥
⎣
⎦
2
0.43
1
φ
−
⎡
⎤
= ⎢
⎥
⎣
⎦
1
79.35
rad
s
ω
=
2
246.29
rad
s
ω
=

Dynamika Budowli
Wydział Inżynierii Lądowej i Środowiska
Magdalena Rucka & Krzysztof Wilde
________________________________________________________________________________________________
2007-02-26
63
Z
ADANIE
7.3
Dla 2-kondygnacyjnej ramy obliczyć częstotliwości i postacie drgań własnych.
2h
h
h
m
1
m
2
u
2
u
1
EI
c
EI
b
=
∝
EI
b
=
∝
EI
c
EI
c
EI
c
1
3
2
3
24
24
c
c
EI
k
h
EI
k
h
=
=
1
2
2
2
2
k
k
k
k
k
+
−
⎡
⎤
⎢
⎥
−
⎣
⎦
K=
1
2
0
0
m
m
⎡
⎤
= ⎢
⎥
⎣
⎦
M
[mode,vale]=eig(K,M);
val=diag(vale);
omega=sqrt(val);
f=omega/2/pi
f =
5.7423
13.8631
mode =
-0.7071 -0.7071
-1.0000 1.0000
200 GPa
E
=
3 m
h
=
8
4
2500 10 m
c
I
−
=
⋅
1
2000 kg
m
=
2
1000 kg
m
=
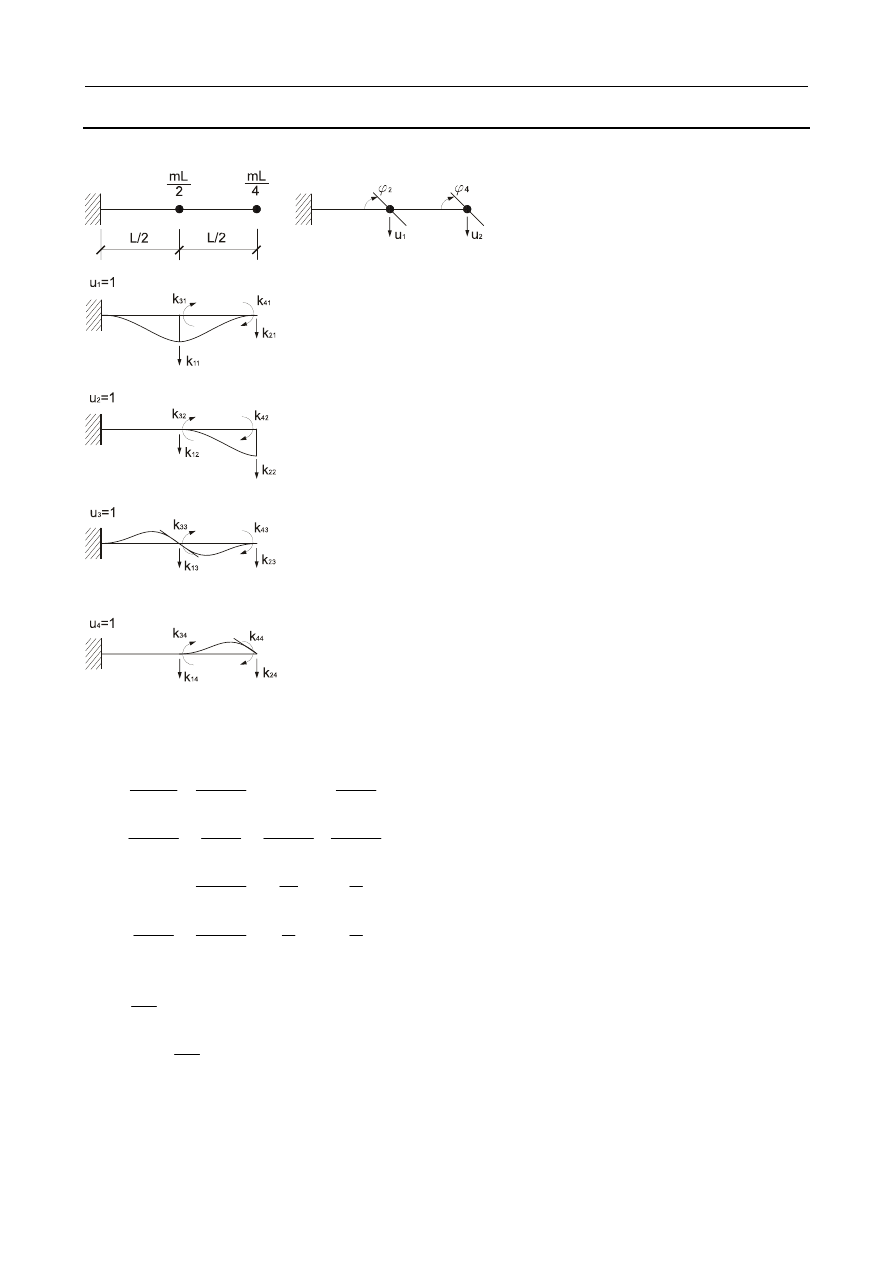
Dynamika Budowli
Wydział Inżynierii Lądowej i Środowiska
Magdalena Rucka & Krzysztof Wilde
________________________________________________________________________________________________
2007-02-26
64
Z
ADANIE
7.4
Obliczyć częstości drgań wspornika; m = 40 kg, L = 3 m, E = 205 GPa, I = 250 cm
4
.
3
3
2
3
3
2
2
2
2
2
192
96
24
0
96
96
24
24
24
16
4
0
24
24
4
8
EI
EI
EI
L
L
L
EI
EI
EI
EI
L
L
L
L
EI
L
L
L
EI
EI
L
L
L
L
−
⎡
⎤
⎢
⎥
⎢
⎥
−
−
−
⎢
⎥
⎢
⎥
= ⎢
⎥
−
⎢
⎥
⎢
⎥
⎢
⎥
−
⎢
⎥
⎣
⎦
K
0
0 0
2
0
0 0
4
0
0
0 0
0
0
0 0
mL
mL
⎡
⎤
⎢
⎥
⎢
⎥
⎢
⎥
= ⎢
⎥
⎢
⎥
⎢
⎥
⎢
⎥
⎣
⎦
M

Dynamika Budowli
Wydział Inżynierii Lądowej i Środowiska
Magdalena Rucka & Krzysztof Wilde
________________________________________________________________________________________________
2007-02-26
65
Sposoby postępowania:
1) uzupełnienie bezmasowych stopni swobody “małymi” masami
przyjęto M(3,3)=M(4,4)=m*10
-6
[mode,vale]=eig(K,M)
val=diag(vale)
omega=sqrt(val)
mode =
0.3274 1.0000 0.0000 0.0000
1.0000 -0.6547 -0.0000 -0.0000
0.3792 0.0987 -0.4142 1.0000
0.4830 -1.7041 1.0000 0.4142
omega =
39.6957
204.4760
164592.101
274607.936
2) kondensacja względem bezmasowych stopni swobody:
3
768
240
7
7
'
240
96
7
7
EI
L
−
⎡
⎤
⎢
⎥
= ⎢
⎥
−
⎢
⎥
⎢
⎥
⎣
⎦
K
0
2
0
4
mL
mL
⎡
⎤
⎢
⎥
= ⎢
⎥
⎢
⎥
⎢
⎥
⎣
⎦
M
mode =
-0.3274 1.0000
-1.0000 -0.6547
omega =
39.6957
204.4761

Dynamika Budowli
Wydział Inżynierii Lądowej i Środowiska
Magdalena Rucka & Krzysztof Wilde
________________________________________________________________________________________________
2007-02-26
66
Z
ADANIE
7.5
Dla wspornika z zadania 7.4 przedstawić na rysunku rozkład modalny wektora przemieszczeń
[1 1]
T
=
u
.
1
0.3274
1
φ
⎡
⎤
= ⎢
⎥
⎣
⎦
2
1
0.6547
φ
⎡
⎤
= ⎢
⎥
−
⎣
⎦
0
2
0
4
mL
mL
⎡
⎤
⎢
⎥
= ⎢
⎥
⎢
⎥
⎢
⎥
⎣
⎦
M
[
]
[
]
1
0
1
2
0.3274 1
1
0
4
0
0.3274
2
0.3274 1
1
0
4
mL
mL
q
mL
mL
⎡
⎤
⎢
⎥ ⎡ ⎤
⎢
⎥ ⎢ ⎥
⎣ ⎦
⎢
⎥
⎢
⎥
⎣
⎦
=
=
⎡
⎤
⎢
⎥ ⎡
⎤
⎢
⎥ ⎢
⎥
⎣
⎦
⎢
⎥
⎢
⎥
⎣
⎦
[
]
[
]
2
0
1
2
1
0.6547
1
0
4
0
1
2
1
0.6547
0.6547
0
4
mL
mL
q
mL
mL
⎡
⎤
⎢
⎥ ⎡ ⎤
−
⎢
⎥ ⎢ ⎥
⎣ ⎦
⎢
⎥
⎢
⎥
⎣
⎦
=
=
⎡
⎤
⎢
⎥ ⎡
⎤
−
⎢
⎥ ⎢
⎥
−
⎣
⎦
⎢
⎥
⎢
⎥
⎣
⎦
1 1
2 2
q
q
φ
φ
=
+
u
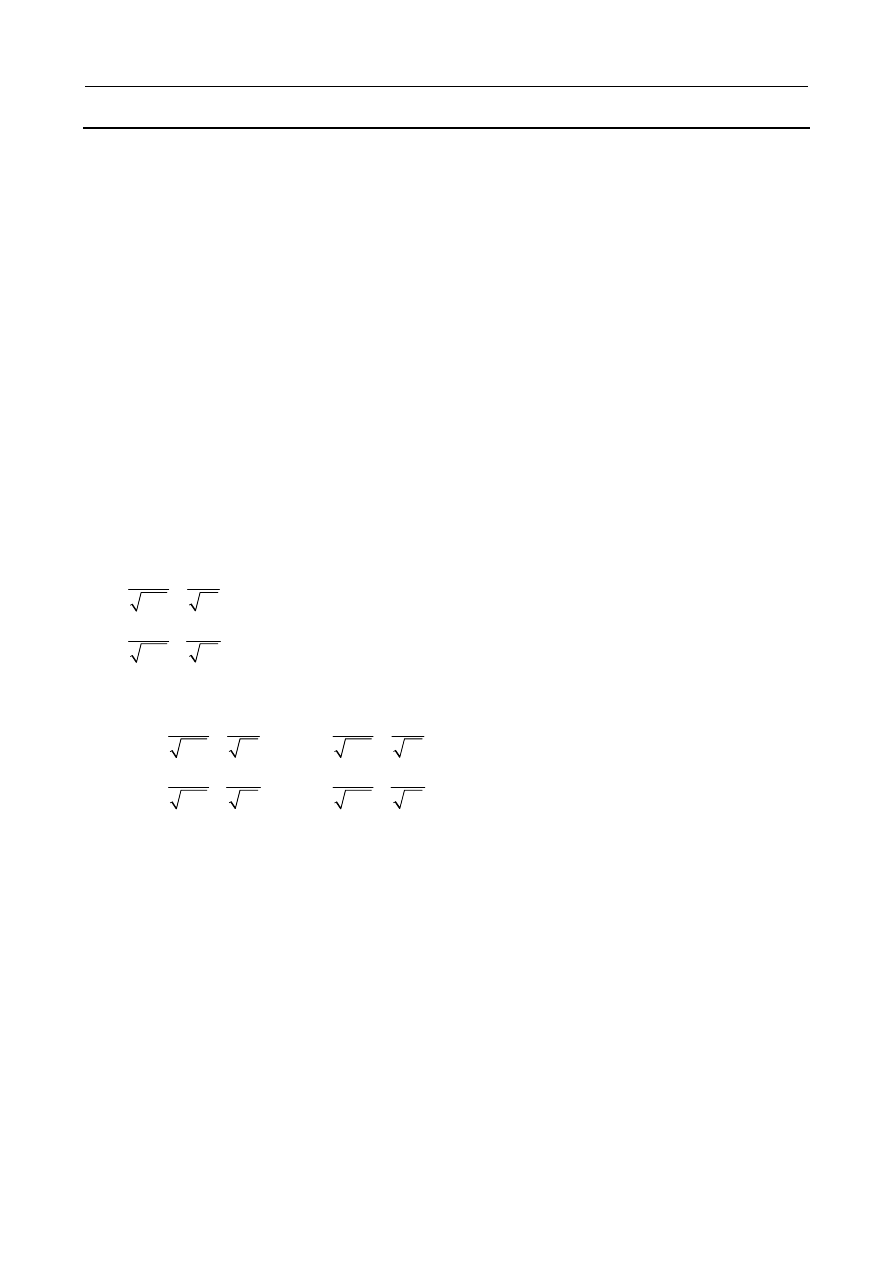
Dynamika Budowli
Wydział Inżynierii Lądowej i Środowiska
Magdalena Rucka & Krzysztof Wilde
________________________________________________________________________________________________
2007-02-26
67
Z
ADANIE
7.6
Unormować wektory własne tak, by diagonalizowały macierz mas do macierzy jednostkowej.
3 0
0 4
⎡
⎤
= ⎢
⎥
⎣
⎦
M
1
5
5
φ
⎡ ⎤
= ⎢ ⎥
⎣ ⎦
2
2
1.5
φ
⎡
⎤
= ⎢
⎥
−
⎣
⎦
Sprawdzenie ortogonalności wektorów własnych:
[
]
3 0
2
5 5
0
0 4
1.5
⎡
⎤ ⎡
⎤
=
⎢
⎥ ⎢
⎥
−
⎣
⎦ ⎣
⎦
1
1
175
T
φ
φ
=
M
2
2
21
T
φ
φ
=
M
5
2
175
21
5
1.5
175
21
⎡
⎤
⎢
⎥
⎢
⎥
=
−
⎢
⎥
⎢
⎥
⎣
⎦
Φ
5
2
5
2
3 0
175
21
175
21
5
1.5 0 4
5
1.5
175
21
175
21
T
⎡
⎤
⎡
⎤
⎢
⎥
⎢
⎥
⎡
⎤
⎢
⎥
⎢
⎥
=
=
⎢
⎥
−
−
⎢
⎥
⎢
⎥
⎣
⎦
⎢
⎥
⎢
⎥
⎣
⎦
⎣
⎦
Φ MΦ
…
…
1 0
0 1
⎡
⎤
= ⎢
⎥
⎣
⎦

Dynamika Budowli
Wydział Inżynierii Lądowej i Środowiska
Magdalena Rucka & Krzysztof Wilde
________________________________________________________________________________________________
2007-02-26
68
8. Drgania wymuszone harmonicznie układów dyskretnych o n stopniach
swobody.
Drgania wymuszone harmonicznie układów dyskretnych o n stopniach swobody.
Równanie macierzowe ruchu:
( )
t
+
+
=
Mu Cu Ku P
(8.1)
Rozpatrywać będziemy drgania bez tłumienia:
0
sin t
ω
+
=
Mu Ku P
(8.2)
Rozwiązanie ( )
t
u
będzie w formie:
( )
sin
t
t
φ
ω
=
u
(8.3)
Po podstawieniu (7.3) do (7.2) otrzymujemy:
(
)
2
0
d
ω
φ
−
=
K
K
M
P (8.4)
2
0
z
P
φ
ω
φ
=
+
K
P
M (8.5)
gdzie
z
P jest zastępczą siłą statyczną, a
d
K dynamiczną macierzą sztywności.
Amplitudy drgań obliczymy z równania:
1
0
d
φ
−
= K P (8.6)

Dynamika Budowli
Wydział Inżynierii Lądowej i Środowiska
Magdalena Rucka & Krzysztof Wilde
________________________________________________________________________________________________
2007-02-26
69
Z
ADANIE
8.1
Obliczyć amplitudy drgań
φ
dla
39 rad/s
ω
=
oraz dla
40 rad/s
ω
=
, E = 205GPa, I = 250cm
4
,
m
= 100kg, L = 3m, p
0
= 1 kN.
3
11
24
L
EI
δ
=
3
22
3
L
EI
δ
=
3
12
5
48
L
EI
δ
=
macierz podatności :
macierz mas :
3
2
5
5
1 6
4 8
L
E I
⎡
⎤
⎢
⎥
⎣
⎦
F =
4
0
0
1
4
m ⎡
⎤
=
⎢
⎥
⎣
⎦
M
0
0
1
0
p
⎡ ⎤
=
⋅
⎢ ⎥
⎣ ⎦
P
macierz sztywności:
3
1 6
5
4 8
5
2
7
E I
L
−
⎡
⎤
=
⎢
⎥
−
⎣
⎦
K
(
)
(
)
1
2
2
1
0
0
0
d
ω
φ
φ
ω
−
−
−
=
⇒
=
−
=
K
M
P
K
M
P
K P
2
3
16
5
4 0
48
5
2
0 1
7
4
d
EI
m
L
ω
−
⎡
⎤
⎡
⎤
=
−
⎢
⎥
⎢
⎥
−
⎣
⎦
⎣
⎦
K

Dynamika Budowli
Wydział Inżynierii Lądowej i Środowiska
Magdalena Rucka & Krzysztof Wilde
________________________________________________________________________________________________
2007-02-26
70
rad
39
s
ω
=
6
1.9304
0.6508
N
10
0.6508
0.2223
m
d
−
⎡
⎤
=
⋅
⎢
⎥
−
⎣
⎦
K
1
0
0.0398
m
0.1164
d
φ
−
⎡
⎤
=
= ⎢
⎥
⎣
⎦
K P
rad
40
s
ω
=
6
1.9225
0.6508
N
10
0.6508
0.2203
m
d
−
⎡
⎤
=
⋅
⎢
⎥
−
⎣
⎦
K
1
0
6.0058
m
17.7404
d
φ
−
⎡
⎤
=
= ⎢
⎥
⎣
⎦
K P

Dynamika Budowli
Wydział Inżynierii Lądowej i Środowiska
Magdalena Rucka & Krzysztof Wilde
________________________________________________________________________________________________
2007-02-26
71
Z
ADANIE
8.2
Wyznaczyć amplitudy drgań
φ
oraz narysować wykres momentów dynamicznych.
EI
= 16000kNm
2
, m
1
= 4Mg, m
2
= 1.2Mg, ω = 31 rad/s, L = 1 m.
3
11
8
3
L
EI
δ
=
3
22
26
3
L
EI
δ
=
3
12
4
3
L
EI
δ
= −
3
8
4
3
3
4
2 6
3
3
L
E I
⎡
⎤
−
⎢
⎥
=
⎢
⎥
⎢
⎥
−
⎢
⎥
⎣
⎦
F
3
3
2 6
4
0 .4 0 6 2 5
0 .0 6 2 5
3
3
3
4
8
0 .0 6 2 5
0 .1 2 5
6 4
3
3
E I
E I
L
L
⎡
⎤
⎢
⎥
⎡
⎤
=
=
⎢
⎥
⎢
⎥
⎣
⎦
⎢
⎥
⎢
⎥
⎣
⎦
K
4 0 0 0
0
0
1 2 0 0
⎡
⎤
= ⎢
⎥
⎣
⎦
M
0
1600
0
⎡
⎤
= ⎢
⎥
⎣
⎦
P
(
)
2
0
ω
φ
−
=
K
M
P
2
2656000 1000000
1000000
846800
ω
⎡
⎤
−
= ⎢
⎥
⎣
⎦
K
M
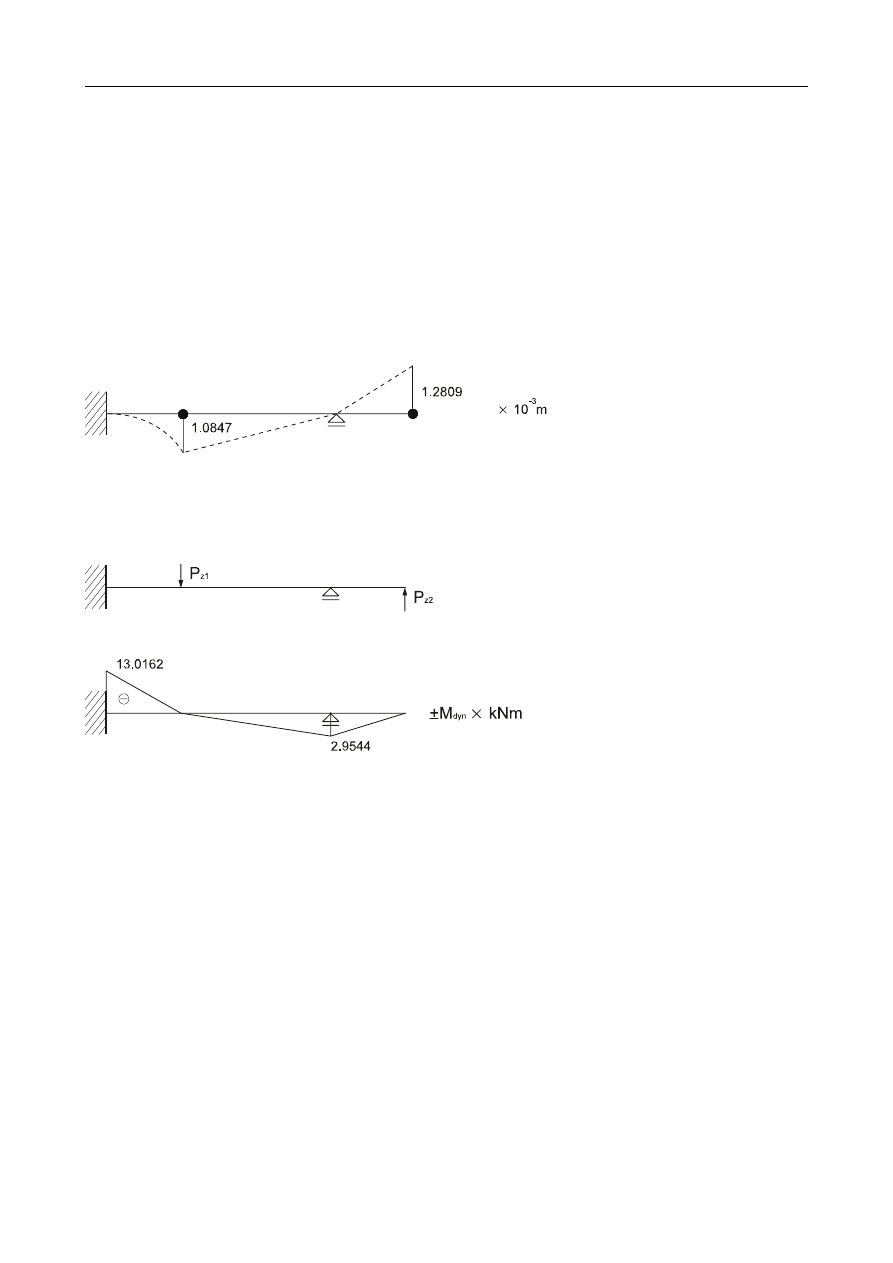
Dynamika Budowli
Wydział Inżynierii Lądowej i Środowiska
Magdalena Rucka & Krzysztof Wilde
________________________________________________________________________________________________
2007-02-26
72
3
1.0847
10 m
1.2809
φ
−
⎡
⎤
=
⋅
⎢
⎥
−
⎣
⎦
Zastępcze siły statyczne
2
0
z
ω
φ
=
+
P
P
M
5.7695
1.4772
z
⎡
⎤
= ⎢
⎥
−
⎣
⎦
P
kN
1
1
2
2
dyn
z
z
M
P M
P M
=
⋅
+
⋅

Dynamika Budowli
Wydział Inżynierii Lądowej i Środowiska
Magdalena Rucka & Krzysztof Wilde
________________________________________________________________________________________________
2007-02-26
73
9. Drgania swobodne tłumione układów dyskretnych o n stopniach swobo-
dy.
Tłumienie:
o
Klasyczne (proporcjonalne) - np. tłumienie Rayleigh’a
0
1
a
a
=
+
C
M
K (9.1)
gdzie
0
1
,
a a
są stałymi.
o
Nieklasyczne (nieproporcjonalne)
Drgania swobodne tłumione w układach n-stopni swobody.
Równanie macierzowe ruchu:
+
+
=
Mu Cu Ku 0
(9.2)
Wektor przemieszczenia wyrażony we współrzędnych modalnych:
1
N
r r
r
q
φ
=
=
=
∑
u
Φq (9.3)
Jeżeli macierz C jest macierzą tłumienia proporcjonalnego to macierz modalna Φ (wyznaczona dla
układu bez tłumienia) diagonalizuje ją:
T
C = Φ CΦ
(9.4)
Równanie (9.2) we współrzędnych modalnych:
+
+
=
Mq Cq Kq 0 (9.5)
Otrzymujemy N równań różniczkowych
0
n n
n n
n n
M q
C q
K q
+
+
=
(9.6)
Liczba tłumienia każdej postaci:
2
n
n
n
n
C
M
ξ
ω
=
(9.7)
Równanie (9.6) można przekształcić do postaci:
2
2
0
n
n
n n
n n
q
q
q
ξ ω
ω
+
+
= (9.8)
Równanie (9.8) jest takie samo jak rówanie dla jednego stopnia swobody. Rozwiązanie jest nastę-
pujące:

Dynamika Budowli
Wydział Inżynierii Lądowej i Środowiska
Magdalena Rucka & Krzysztof Wilde
________________________________________________________________________________________________
2007-02-26
74
(0)
(0)
( )
(0) cos
sin
n n
t
n
n
n
n
n
n
n D
n D
n D
q
q
q t
e
q
t
t
ξ ω
ξ ω
ω
ω
ω
−
⎛
⎞
+
=
+
⎜
⎟
⎝
⎠
(9.9)
Przemieszczenie:
1
1
(0)
(0)
(0) cos
sin
n n
N
N
t
n
n
n
n
n n
n
n
n D
n D
n
n
n D
q
q
q
e
q
t
t
ξ ω
ξ ω
φ
φ
ω
ω
ω
−
=
=
⎛
⎞
+
=
=
+
⎜
⎟
⎝
⎠
∑
∑
u
(9.10)
Rozwiązanie problemu własnego z uwzględnieniem tłumienia.
Rozwiązanie problemu własnego z tłumieniem nastąpi po zamianie równanie różniczkowego dru-
giego stopnia:
1
1
−
−
+
+
=
u M Cu M Ku 0 (9.11)
na równanie pierwszego stopnia:
x = Ax (9.12)
gdzie:
⎡ ⎤
= ⎢ ⎥
⎣ ⎦
u
x
u
(9.13)
Rówanie (9.12) można przedstawić jako:
⎡ ⎤ ⎡
⎤ ⎡ ⎤
=
⎢ ⎥ ⎢
⎥ ⎢ ⎥
−
−
⎣ ⎦ ⎣
⎦ ⎣ ⎦
-1
-1
u
0
I
u
u
M K
M C u
(9.14)
Dynamika Budowli
Wydział Inżynierii Lądowej i Środowiska
Magdalena Rucka & Krzysztof Wilde
________________________________________________________________________________________________
2007-02-26
75
Z
ADANIE
9.1
Wyprowadzić macierze tłumienia proporcjanalnego:
400
0
0
1
0
400
0
386
0
0
200
M
⎡
⎤
⎢
⎥
=
⎢
⎥
⎢
⎥
⎣
⎦
1
1
2
1
3
1
12.57
5%
s
1
39.33
5%
s
1
46.89
s
ω
ξ
ω
ξ
ω
=
=
=
=
=
2
1 0
610
1 2
1
0
1 1
K
−
⎡
⎤
⎢
⎥
=
−
−
⎢
⎥
⎢
⎥
−
⎣
⎦
2
3
0.401
0.803
0.401
0.695
0
0.695
0.803
0.803
0.803
φ
φ
φ
1
⎧
⎫
⎧
⎫
⎧
⎫
⎪
⎪
⎪
⎪
⎪
⎪
=
=
= −
⎨
⎬
⎨
⎬
⎨
⎬
⎪
⎪
⎪
⎪
⎪
⎪
−
⎩
⎭
⎩
⎭
⎩
⎭
Rozwiązanie:
0
1
a
a
=
=
C
M
C
K
2
0
1
1
n
n
n
n
n
n
C
a M
C
a K
a
M
ω
=
=
=
2
2
n
n
n
n
n
n
n
n
C
C
M
M
ξ
ξ
ω
ω
=
=
0
1
1
2
2
n
n
n
n
a
a
ξ
ξ
ω
ω
=
⋅
=
0
1
1
2
2
n
n
n
a
a
ξ
ω
ω
=
⋅
+
Współczynniki
0
a
i
1
a
określimy dla dwóch znanych liczb tłumienia
i
i
j
ξ
ξ
odpowiadających po-
staciom drgań oraz
i
j
0
1
1
2
2
n
i
i
a
a
ξ
ω
ω
=
⋅
+
0
0
1
2
2
n
j
j
a
a
ξ
ω
ω
=
⋅
+

Dynamika Budowli
Wydział Inżynierii Lądowej i Środowiska
Magdalena Rucka & Krzysztof Wilde
________________________________________________________________________________________________
2007-02-26
76
0
1
1
1
1
2
i
i
i
j
j
j
a
a
ω
ω
ξ
ξ
ω
ω
⎡
⎤
⎢
⎥
⎧ ⎫
⎡ ⎤
⎢
⎥
= ⎨ ⎬
⎢ ⎥
⎢
⎥ ⎣ ⎦ ⎩ ⎭
⎢
⎥
⎣
⎦
0
1
1
12.57
0.05
12.57
1
0.05
39.33
39.33
a
a
⎡
⎤
⎢
⎥ ⎡ ⎤ ⎧
⎫
=
⎢
⎥
⎨
⎬
⎢ ⎥
⎩
⎭
⎣ ⎦
⎢
⎥
⎢
⎥
⎣
⎦
0
0.9198
a
=
1
0.0021
a
=
0
1
3.35
1.3
0
1.3 3.55
1.3
0
1.3 1.78
a
a
−
⎡
⎤
⎢
⎥
=
+
= −
−
⎢
⎥
⎢
⎥
−
⎣
⎦
C
M
K
0
1
3
3
3
1
0.0593
2
2
a
a
ξ
ω
ω
=
+
=

Dynamika Budowli
Wydział Inżynierii Lądowej i Środowiska
Magdalena Rucka & Krzysztof Wilde
________________________________________________________________________________________________
2007-02-26
77
Z
ADANIE
9.2
Wyznaczyć postacie i częstości drgań z uwzględnieniem tłumienia – proporcjonalnego i niepropor-
cjonalnego
2
1
2 0
0.4
0.1
0.4
0.1
1 1
0 3
0.1 0.4
0.1
0.1
−
−
−
⎡
⎤
⎡
⎤
⎡
⎤
⎡
⎤
=
=
=
=
⎢
⎥
⎢
⎥
⎢
⎥
⎢
⎥
−
−
−
⎣
⎦
⎣
⎦
⎣
⎦
⎣
⎦
p
n
K
M
C
C
algorytm:
[mode,ome]=eig(K,M)
omega_nietlum=sqrt(ome)
A=zeros(4,4);
O=zeros(2,2);
I=eye(2,2);
A=[O I;-inv(M)*K -inv(M)*Cp];
[mode_t,ome_t]=eig(A)
ome_t=diag(ome_t)
czestosc_kolowa_nietlum=abs(ome_t)
czestosc_kolowa_tlum=imag(ome_t)
wyniki
mode =
-0.3031 -0.6388
-0.5216 0.2475
omega_nietlum =
0.3737 0
0 1.0926
mode_t =
0.0632 + 0.6264i 0.0632 - 0.6264i -0.4707 -0.4707
-0.0245 - 0.2427i -0.0245 + 0.2427i -0.8099 -0.8099
-0.6878 -0.6878 0.0268 - 0.1738i 0.0268 + 0.1738i
0.2665 - 0.0000i 0.2665 + 0.0000i 0.0461 - 0.2991i 0.0461 + 0.2991i
ome_t =
-0.1097 + 1.0871i
-0.1097 - 1.0871i
-0.0570 + 0.3693i
-0.0570 - 0.3693i
czestosc_kolowa_nietlum =
1.0926
1.0926
0.3737
0.3737
czestosc_kolowa_tlum =
1.0871
-1.0871
0.3693
-0.3693

Dynamika Budowli
Wydział Inżynierii Lądowej i Środowiska
Magdalena Rucka & Krzysztof Wilde
________________________________________________________________________________________________
2007-02-26
78
algorytm:
[mode,ome]=eig(K,M)
omega_nietlum=sqrt(ome)
A=zeros(4,4);
O=zeros(2,2);
I=eye(2,2);
A=[O I;-inv(M)*K -inv(M)*Cn];
[mode_t,ome_t]=eig(A)
ome_t=diag(ome_t)
czestosc_kolowa_nietlum=abs(ome_t)
czestosc_kolowa_tlum=imag(ome_t)
wyniki
mode =
-0.3031 -0.6388
-0.5216 0.2475
omega_nietlum =
0.3737 0
0 1.0926
mode_t =
0.0580 + 0.6276i 0.0580 - 0.6276i 0.4703 - 0.0167i 0.4703 + 0.0167i
-0.0473 - 0.2382i -0.0473 + 0.2382i 0.8099 0.8099
-0.6881 -0.6881 -0.0014 + 0.1759i -0.0014 - 0.1759i
0.2638 - 0.0275i 0.2638 + 0.0275i -0.0131 + 0.3026i -0.0131 - 0.3026i
ome_t =
-0.1005 + 1.0872i
-0.1005 - 1.0872i
-0.0162 + 0.3736i
-0.0162 - 0.3736i
czestosc_kolowa_nietlum =
1.0918
1.0918
0.3739
0.3739
czestosc_kolowa_tlum =
1.0872
-1.0872
0.3736
-0.3736

Dynamika Budowli
Wydział Inżynierii Lądowej i Środowiska
Magdalena Rucka & Krzysztof Wilde
________________________________________________________________________________________________
2007-02-26
79
10. Układy dyskretne o n stopniach swobody – dowolne wymusznie.
Równanie ruchu w przestrzeni stanów dla układu o n stopniach swobody
Równanie ruchu układu tłumionego:
Mu + Cu + Ku = p
gdzie:
[
]
1
2
T
n
u
u
u
=
u
- wektor n przemieszczeń opisujących ruch
M- macierz mas układu
C - macierz tłumienia
K – macierz sztywności
p – wektor obciążeń zewnętrznych
Równanie ruchu (4) w przestrzenie stanu przyjmuje postać:
x = Ax + Bp (state space equation of motion)
gdzie:
⎡ ⎤
⎢ ⎥
⎣ ⎦
u
x =
u
, wektor stanów,
⎡
⎤
⎢
⎥
⎣
⎦
-1
-1
0
I
A =
-M K -M C
- macierz układu
I – macierz jednostkowa (n x n)
0 – macierz zerowa (n x n)
0
⎡
⎤
⎢
⎥
⎣
⎦
-1
B =
M
Równanie wyjścia:
y = Cx + Dp (output equation)
Macierze
A, B, C i D opisują proces dynamiczny.
Uwagi:
1. Wektory własne (także dla układów o proporcjonalnym tłumienie) wyznaczone przy pomocy
macierzy stanu są wektorami zespolonymi.
2. Sformułowanie w przestrzeni stanów jest uogólnieniem klasycznego sformułowanie równania
ruchu.
3. Rozwiązanie układu w czasie można uzyskać stosując w Matlabie funkcję lsim.
4. Dla proporcjonalnych macierzy tłumień wektory własne układu są rzeczywiste.
5. Wyznaczenie wektorów własnych układu wymaga użycia funkcji eig(A) w programie Matlab.

Dynamika Budowli
Wydział Inżynierii Lądowej i Środowiska
Magdalena Rucka & Krzysztof Wilde
________________________________________________________________________________________________
2007-02-26
80
Macierz tłumienia
C jest proporcjonalna, jeżeli wyznaczamy ją według wzoru:
α
β
=
C
K + M
gdzie:
α i β to współczynniki proporcjonalności względem K i M
Wszystkie programy komercyjne (dla konstrukcji budowlanych) rozwiązują wyłącznie problemy z
tłumieniem proporcjonalnym.
Wyjaśnienie użycia funkcji lsim w programie Matlab.
Format funkcji
[Yres, Xres] = lsim(A,B,C,D, U, t, X0);
Wynik całkowania funkcją lsim
Yres - wektor odpowiedzi wybranych stanów
Xres – wektory odpowiedzi układu wszystkich stanów
Dane
wejściowe do funkcji lsim
A, B, C, D – macierze stanu układu dynamicznego
U – wektory wymuszeń zewnętrznych
t – wektor czasu
X0 – wektor warunków początkowych (przemieszczenia i prędkości)
Przykład użycia jest podane w programie st_swobo3_w10.m. Wspornik ustawiony pionowo mode-
lowany jest 3 stopniami swobody. Pierwsza masa skupiona znajduje się przy utwierdzeniu. Prze-
mieszczenie 2 opisuje ruch środka wspornika, zaś współrzędna x
3
znajduje się na końcu wspornika.
Animację wykonuje podprogram dof3_ani

Dynamika Budowli
Wydział Inżynierii Lądowej i Środowiska
Magdalena Rucka & Krzysztof Wilde
________________________________________________________________________________________________
2007-02-26
81
11. Transformata Fouriera.
Jean Baptiste Joseph Fourier (1768-1830), francuski matematyk w 1807 roku udowodnił, że każda
okresowa funkcja może zostać rozłożona na sumę sinusów i cosinusów.
0
1
2
3
4
5
-4
-2
0
2
4
t [s]
u(
t)
0
1
2
3
4
0
0.5
1
1.5
2
f [Hz]
u(
t)
0
2
4
-2
-1
0
1
2
t [s]
u(
t)
0
2
4
-2
-1
0
1
2
t [s]
0
2
4
-2
-1
0
1
2
t [s]
0
1
2
3
4
5
0
1
2
3
-2
0
2
t [s]
f [Hz]
u(
t)
Szeregi Fouriera
Funkcję p(t) nazywamy funkcją okresową z okresem T jeżeli spełnia ona następujący warunek:
(
)
( ),
,..., 2, 1,0,1, 2,...,
p t nT
p t
n
+
=
= −∞
− −
∞ (11.1)
gdzie n jest liczbą całkowitą. Przykładowe funkcje okresowe pokazane są na poniższym rysunku.
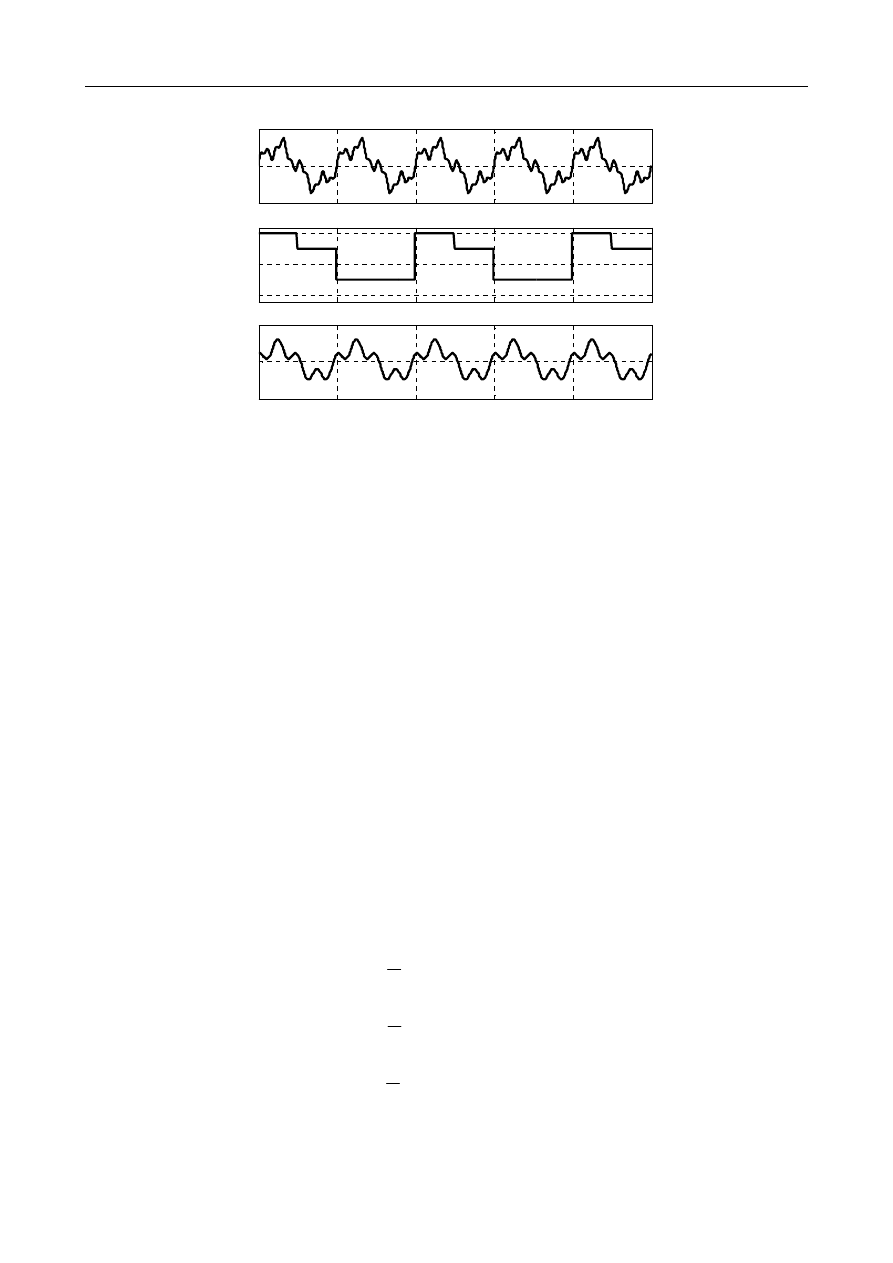
Dynamika Budowli
Wydział Inżynierii Lądowej i Środowiska
Magdalena Rucka & Krzysztof Wilde
________________________________________________________________________________________________
2007-02-26
82
0
2
4
6
8
10
-10
0
10
0
2
4
6
8
10
-1
0
1
0
2
4
6
8
10
-5
0
5
Funkcje okresowe
Okresową funkcję można rozłożyć w nieskończony szereg Fouriera będący sumą sinusów i cosinu-
sów różnej częstotliwości:
0
1
1
( )
cos(2
)
sin(2
)
n
n
n
n
n
n
p t
a
a
f t
b
f t
π
π
∞
∞
=
=
=
+
+
∑
∑
(11.2)
gdzie p(t) jest funkcją w dziedzinie czasu, a
0
, a
n
, b
n
są współczynnikami szeregu Fouriera, f
n
ozna-
cza częstotliwość fali. Zależność pomiędzy częstotliwością f
n
mierzoną w Hertzach a częstością
kołową
ω
n
mierzoną w rad/s opisana jest następująco:
2
n
n
f
ω
π
=
(11.3)
Za pomocą szeregu Fouriera można rozłożyć sygnał na składniki o częstotliwościach będących cał-
kowitymi wielokrotnościami częstotliwości podstawowej (fundamentalnej) f (lub
ω
):
,
n
n
f
nf
n
ω
ω
=
=
(11.4)
Częstotliwość będąca całkowitą wielokrotnością częstotliwości podstawowej nazywana jest często-
tliwością harmoniczną.
Ostatecznie współczynniki szeregu Fouriera wyrażone są następująco:
0
0
0
0
1
( )
2
( ) cos(2
)
2
( )sin(2
)
T
T
n
n
T
n
n
a
p t dt
T
a
p t
f t dt
T
b
p t
f t dt
T
π
π
=
=
=
∫
∫
∫
(11.5)
Dynamika Budowli
Wydział Inżynierii Lądowej i Środowiska
Magdalena Rucka & Krzysztof Wilde
________________________________________________________________________________________________
2007-02-26
83
Z
ADANIE
11.1
Daną funkcję
1 dla
0
( )
3 dla 0
t
p t
t
π
π
− ≤ <
⎧
= ⎨
− ≤ <
⎩
rozwinąć w szereg Fouriera.
-5
0
5
0
1
2
3
4
Rozwinięcie okresowe funkcji p(t).
0
0
0
0
0
1
1
1
( )
3
3
2
2
2
2
a
p t dt
dt
dt
t
t
π
π
π
π
π
π
π
π
π
−
−
−
⎛
⎞
⎡
⎤
⎜
⎟
=
=
+
=
+
=
⎢
⎥
⎜
⎟
⎣
⎦
⎝
⎠
∫
∫
∫
0
0
0
0
1
1
1
( ) cos( )
cos( ) 3 cos( )
sin( )
3sin( )
0
n
a
p t
nt dt
nt
nt
nt
nt
n
π
π
π
π
π
π
π
π
π
−
−
−
⎡
⎤
⎡
⎤
⎢
⎥
=
=
+
=
+
=
⎢
⎥
⎢
⎥
⎣
⎦
⎣
⎦
∫
∫
∫
(
)
(
)
0
0
0
0
1
1
1
( )sin( )
sin( ) 3 sin( )
cos( )
3cos( )
2
2
1 cos(
)
1 ( 1)
n
n
b
p t
nt dt
nt
nt
nt
nt
n
n
n
n
π
π
π
π
π
π
π
π
π
π
π
π
−
−
−
⎡
⎤
⎡
⎤ −
⎢
⎥
=
=
+
=
+
=
⎢
⎥
⎢
⎥
⎣
⎦
⎣
⎦
=
−
=
− −
∫
∫
∫
Ostatecznie szereg Fouriera przyjmuje postać:
1
2
( ) 2
(1 ( 1) )sin( )
n
n
p t
nt
n
π
∞
=
= +
− −
∑
Przeanalizujmy, ile wyrazów nieskończonego szeregu Fouriera potrzebnych jest do opisania zada-
nej funkcji. W tym celu obliczymy sumę szeregu dla różnych wartości n.
1
2
( ) 2
(1 ( 1) )sin( )
N
n
N
n
S t
nt
n
π
=
= +
− −
∑
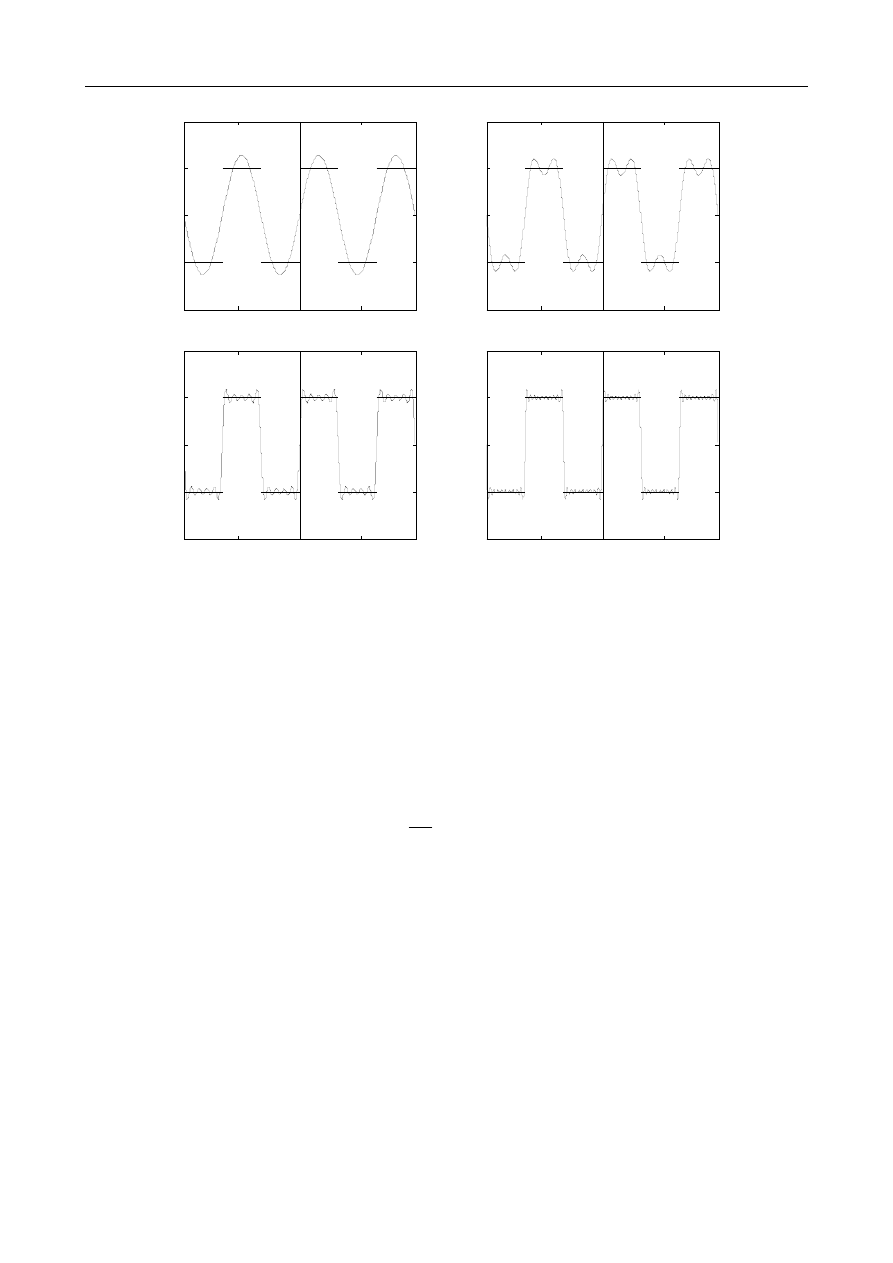
Dynamika Budowli
Wydział Inżynierii Lądowej i Środowiska
Magdalena Rucka & Krzysztof Wilde
________________________________________________________________________________________________
2007-02-26
84
-5
0
5
0
1
2
3
4
N=2
-5
0
5
0
1
2
3
4
N=3
-5
0
5
0
1
2
3
4
N=10
-5
0
5
0
1
2
3
4
N=20
Sumy szeregu dla N=2,3,10,20.
Ciągła transformata Fouriera.
Ciągłe przekształcenie Fouriera opisują zależności:
( )
( )
i t
P
p t e
dt
ω
ω
∞
−
−∞
=
∫
(11.6)
1
( )
( )
2
i t
p t
P
e d
ω
ω
ω
π
∞
−∞
=
∫
(11.7)
Współczynnik Fouriera P(
ω
)
otrzymuje się poprzez korelację rozpatrywanej funkcji p(t) z falą sinu-
soidalną e
i
ω
t
. Jeżeli sygnał zawiera składnik częstotliwościowy
ω
wówczas osiąga duże wartości, w
przeciwnym razie równa się zeru. Informacją, jakiej dostarcza nam transformata Fouriera jest, jakie
składniki częstotliwościowe zawarte są w sygnale. Nic więcej, nic mniej.

Dynamika Budowli
Wydział Inżynierii Lądowej i Środowiska
Magdalena Rucka & Krzysztof Wilde
________________________________________________________________________________________________
2007-02-26
85
Z
ADANIE
11.2
Obliczyć transformatę Fouriera funkcji p(t):
1 dla
( )
0 dla
t
p t
t
π
π
π
π
− ≤ ≤
⎧
= ⎨
− > >
⎩
-4
-2
0
2
4
-1
-0.5
0
0.5
1
1.5
2
Impuls prostokątny.
Wykorzystując zależność oraz wzór obliczamy całkę Fouriera:
(
)
( )
( )
( ) cos( )
sin( )
cos( )
sin( )
sin(
)
2sin(
)
i t
P
p t e dt
p t
t
i
t dt
t dt i
t dt
x
π
π
ω
π
π
π
π
ω
ω
ω
ω
ω
ω
ωπ
ω
ω
∞
∞
−∞
−∞
−
−
−
=
=
−
=
−
=
=
=
∫
∫
∫
∫
Ponieważ transformata Fouriera mierzy częstotliwości, jakie zawarte są w funkcji, a rozważana jest
funkcja stała, stąd największa wartość P(
ω
)
występuje przy zerowej częstotliwości.
-10
-5
0
5
10
-2
0
2
4
6
8
Całka Fouriera impulsu prostokątnego.
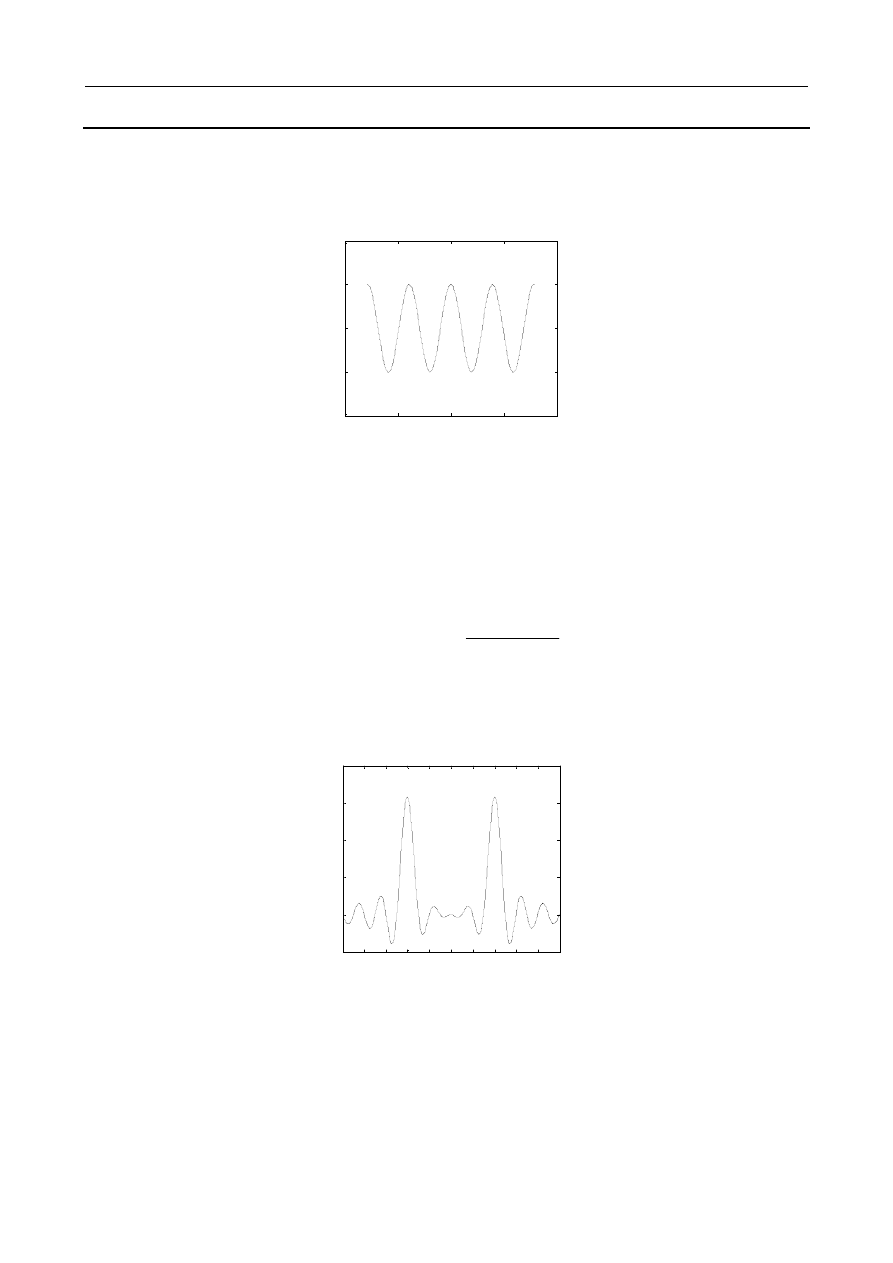
Dynamika Budowli
Wydział Inżynierii Lądowej i Środowiska
Magdalena Rucka & Krzysztof Wilde
________________________________________________________________________________________________
2007-02-26
86
Z
ADANIE
11.3
Obliczyć transformatę Fouriera funkcji p(t):
cos(4 ) dla
( )
0 dla
t
x
p t
x
π
π
π
π
− ≤ ≤
⎧
= ⎨
− > >
⎩
-4
-2
0
2
4
-2
-1
0
1
2
Wykres funkcji p(t).
Wykorzystując zależność oraz wzór obliczamy całkę Fouriera:
(
)
2
( )
( )
( ) cos( )
sin( )
2 sin(
)
cos(4 ) cos( )
cos(4 )sin( )
16
i t
P
p t e
dt
p t
t
i
t dt
t
t dt i
t
t dt
ω
π
π
π
π
ω
ω
ω
ω
ωπ
ω
ω
ω
∞
∞
−
−∞
−∞
−
−
=
=
−
=
−
=
−
=
−
∫
∫
∫
∫
Największe wartości przekształcenia Fouriera występują dla
ω
= 4 i
ω
= - 4 czyli dla częstości
funkcji p(t).
-10 -8
-6
-4
-2
0
2
4
6
8
10
-1
0
1
2
3
4
Całka Fouriera funkcji p(t)

Dynamika Budowli
Wydział Inżynierii Lądowej i Środowiska
Magdalena Rucka & Krzysztof Wilde
________________________________________________________________________________________________
2007-02-26
87
Dyskretna transformata Fouriera i jej realizacja w postaci FFT
Szeregi Fouriera mają zastosowanie w analizie sygnałów okresowych, zaś transformata
(całka)Fouriera stosowana jest w analizie sygnałów nieokresowych. Dyskretne przekształcenie Fo-
uriera DFT (Discrete Fourier Transform) rozwijano w latach 40. i 50. XX wieku. Szeregi Fouriera
zastąpiono postacią dyskretną, aby możliwe było użycie cyfrowych technik obliczeniowych.
Ciągły przebieg p(t) można spróbkować za pomocą przetwornika analogowo-cyfrowego co
t
s
sekund otrzymując N próbek. Częstotliwość próbkowania f
s
mierzy jak często poszukujemy war-
tości funkcji dyskretnej:
1
s
s
f
t
= (11.8)
Zakładamy, że sygnał jest okresowy z okresem T, który otrzymujemy mnożąc liczbę próbek N
przez przedział czasowy pomiędzy poszczególnymi próbkami t
s
:
s
T
Nt
=
(11.9)
Zakładamy również, że częstotliwość podstawowa wyrażona jest wzorem:
0
1
1
s
f
f
T
N t
N
=
=
=
Δ
(11.10)
Widać zatem, że od liczby przyjętych próbek zależy rozdzielczość analizy.
Dyskretna transformata Fouriera DFT wywodzi się z całki Fouriera:
12
( )
( )
ft
X f
x t e
dt
π
∞
−
−∞
=
∫
(11.11)
i ma postać:
2
1
0
( )
( )
i
mn
N
N
n
X m
x n e
π
−
−
=
=
∑
(11.12)
gdzie:
n
– indeks próbek wejściowych w dziedzinie czasu, n = 0,1,...,N-1
m
– indeks próbek wyjściowych w dziedzinie częstotliwości, m = 0,1,...,N-1
x
(n) – ciąg próbek wejściowych, x(0), x(1),...
X
(m) – ciąg próbek wyjściowych DFT, X(0), X(1),...
N
– liczba próbek ciągu wejściowego i wyjściowego
Realizacja DWT – używając algorytmu FFT (Fast Fourier Transform)
t % wektor czasu
a % rozpatrywany sygnał
fs=1/dt % czestotliwosc probkowania
N=length(t)
fo=fs/N % czestotliwosc podstawowa
fa=fft(a); % szybka transformata
base=fo*(0:N/2-1); % wyznaczenie osi czestotliwosci
mag=abs(fa(1:N/2)); % wyznaczenie widma
A=2*mag./N; % normalizacja odpowiedzi
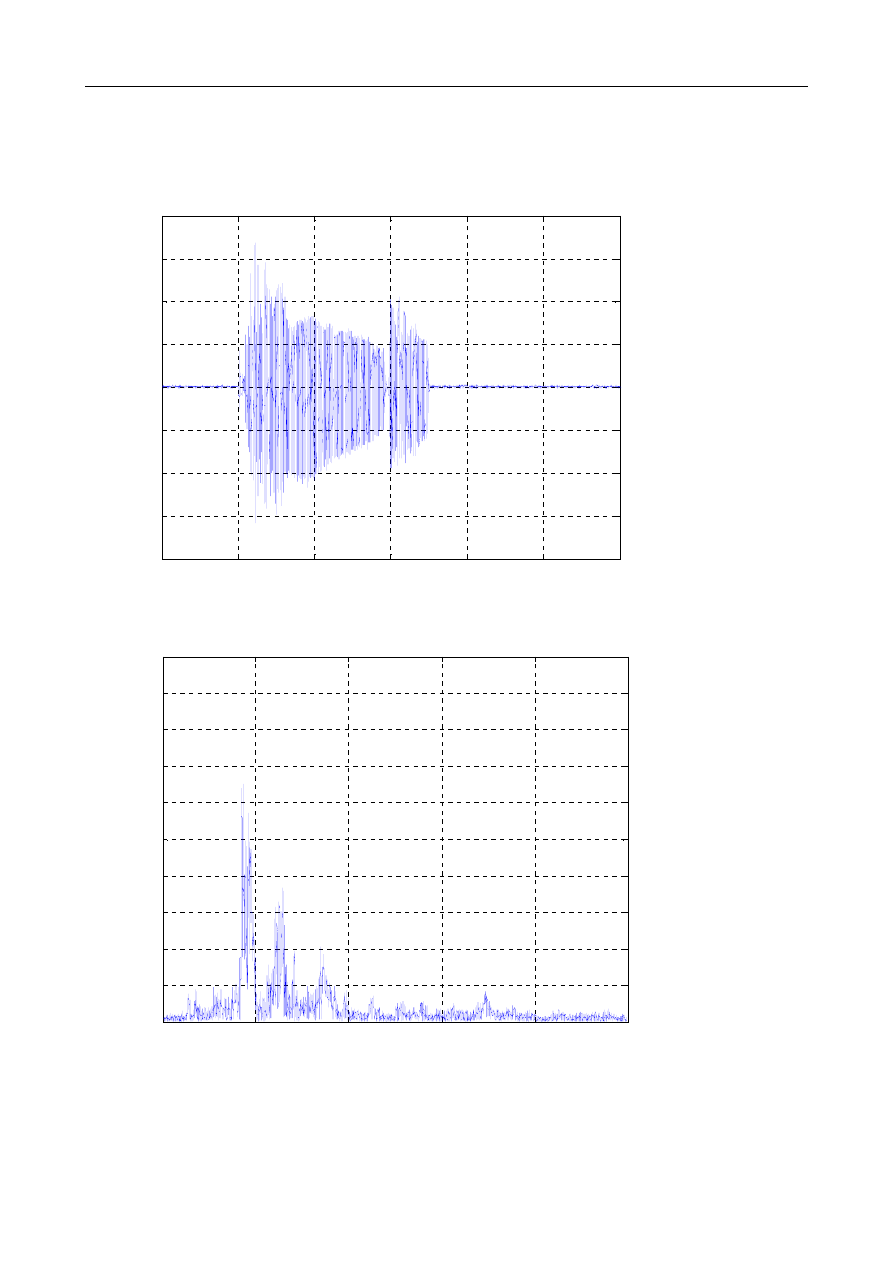
Dynamika Budowli
Wydział Inżynierii Lądowej i Środowiska
Magdalena Rucka & Krzysztof Wilde
________________________________________________________________________________________________
2007-02-26
88
Przykłady:
Drgania silosu podczas wypływu materiału sypkiego:
0
5
10
15
20
25
30
-40
-30
-20
-10
0
10
20
30
40
time [s]
a
v
[m
/s
2
]
0
50
100
150
200
250
0
0.1
0.2
0.3
0.4
0.5
0.6
0.7
0.8
0.9
1
f [Hz]
norm
al
iz
ed
am
pi
tude
F
F
T
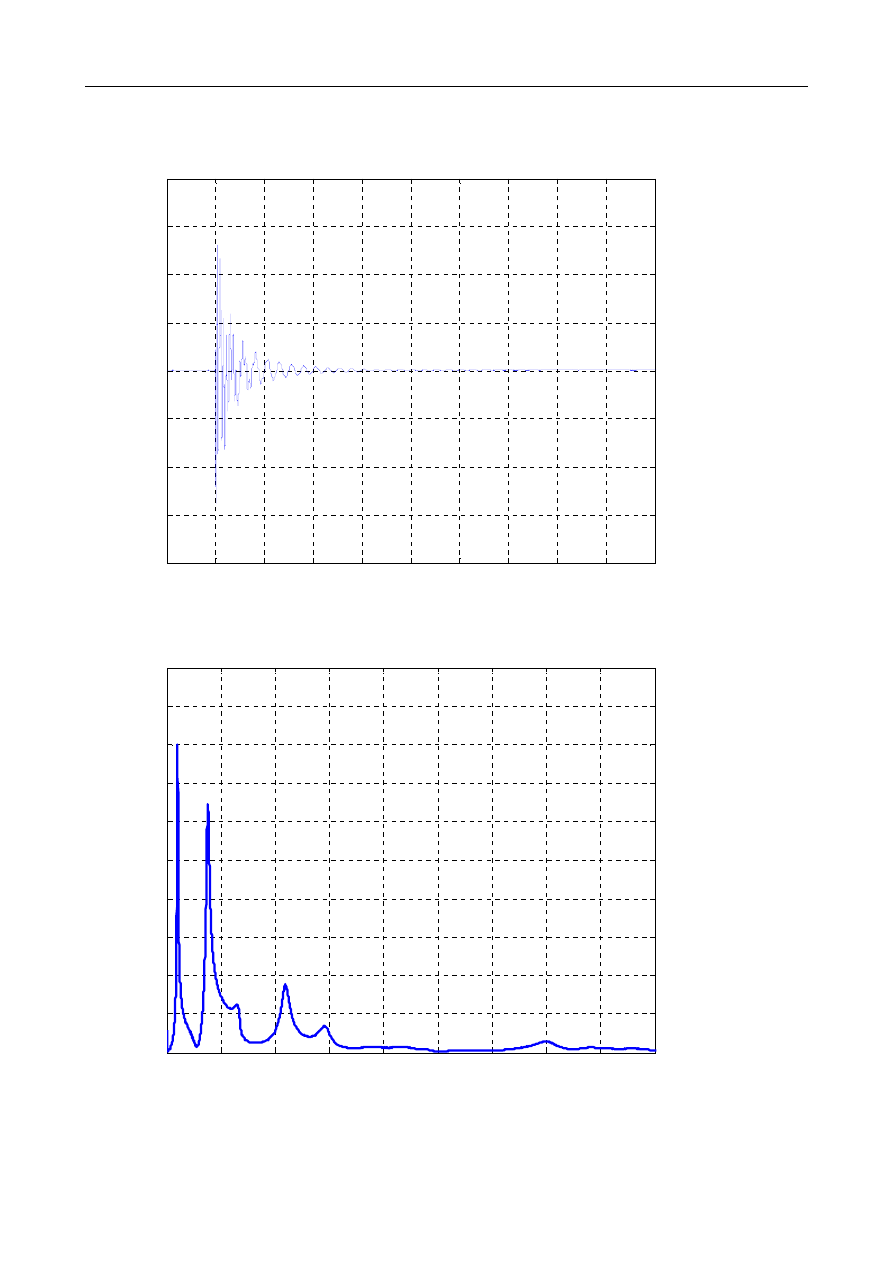
Dynamika Budowli
Wydział Inżynierii Lądowej i Środowiska
Magdalena Rucka & Krzysztof Wilde
________________________________________________________________________________________________
2007-02-26
89
Drgania płyty z pleksi wywołane uderzeniem za pomocą młotka modalnego:
0
0.2
0.4
0.6
0.8
1
1.2
1.4
1.6
1.8
2
-40
-30
-20
-10
0
10
20
30
40
time [s]
a
v
[m
/s
2
]
0
100
200
300
400
500
600
700
800
900
0
0.02
0.04
0.06
0.08
0.1
0.12
0.14
0.16
0.18
0.2
f [Hz]
n
or
m
al
iz
ed
am
pi
tu
de
F
F
T
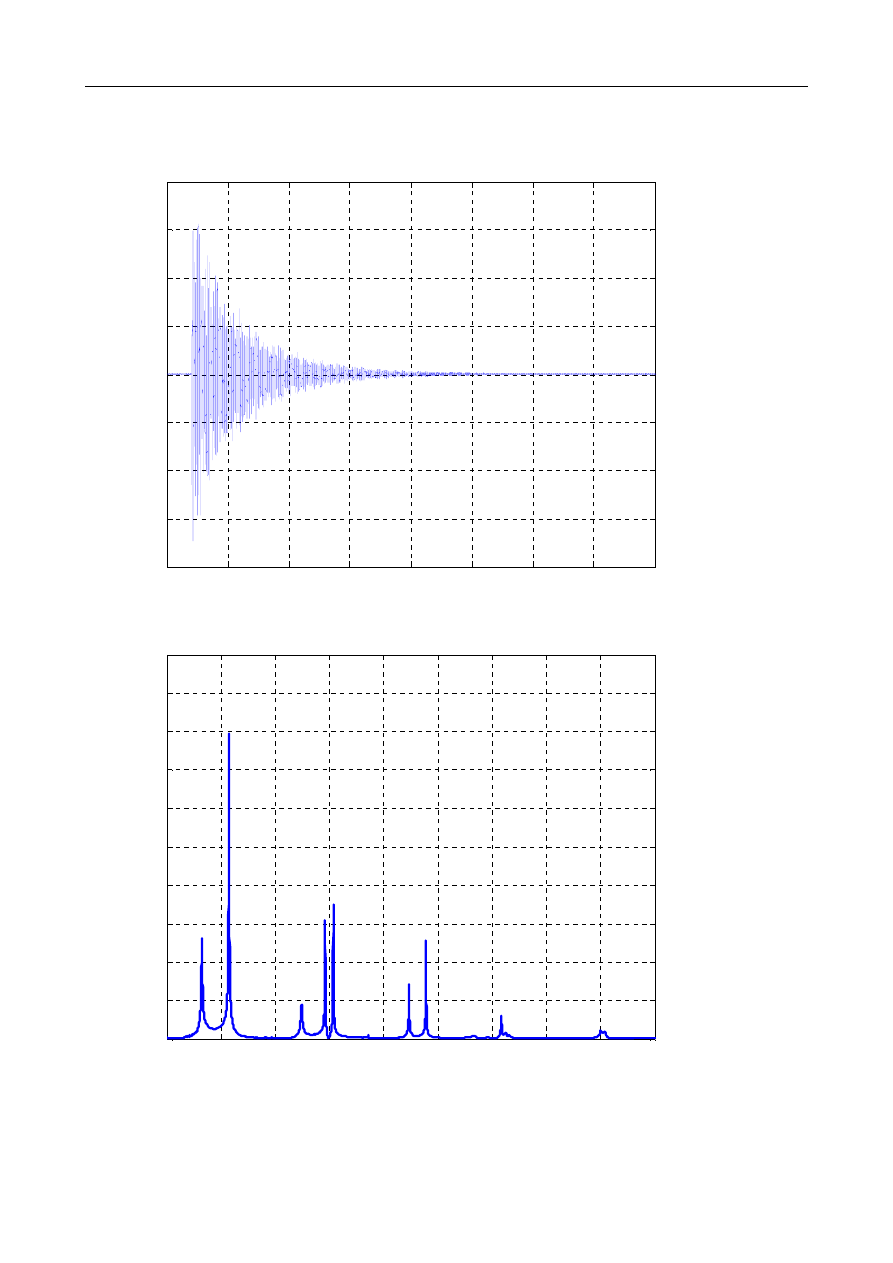
Dynamika Budowli
Wydział Inżynierii Lądowej i Środowiska
Magdalena Rucka & Krzysztof Wilde
________________________________________________________________________________________________
2007-02-26
90
Drgania płyty stalowej wywołane uderzeniem za pomocą młotka modalnego:
0
0.5
1
1.5
2
2.5
3
3.5
4
-40
-30
-20
-10
0
10
20
30
40
time [s]
a
v
[m
/s
2
]
0
100
200
300
400
500
600
700
800
900
0
0.1
0.2
0.3
0.4
0.5
0.6
0.7
0.8
0.9
1
f [Hz]
n
or
m
al
iz
ed
am
pi
tu
de
F
F
T
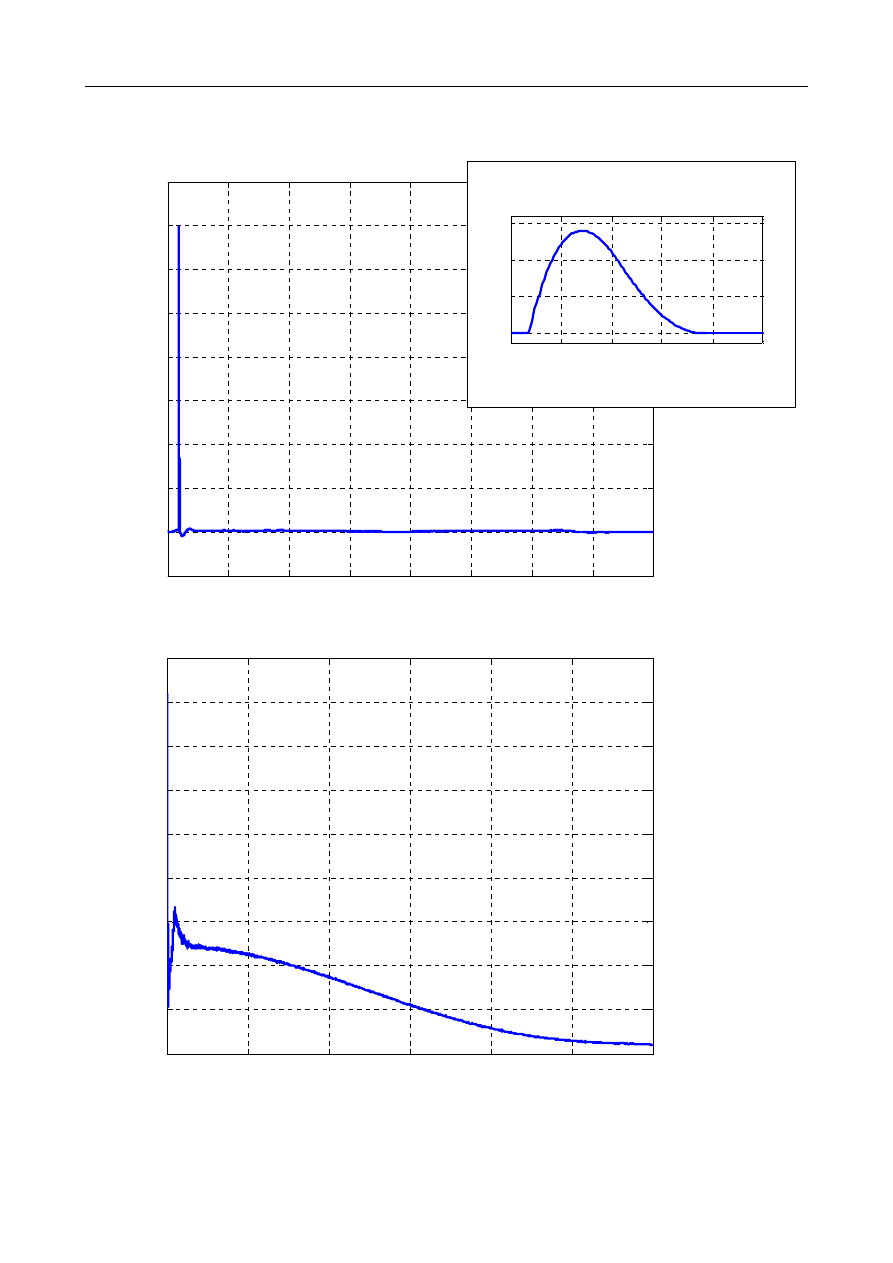
Dynamika Budowli
Wydział Inżynierii Lądowej i Środowiska
Magdalena Rucka & Krzysztof Wilde
________________________________________________________________________________________________
2007-02-26
91
0
1
2
3
4
5
6
7
-2
0
2
4
6
8
10
12
14
16
fo
rc
e
[N
]
time [s]
Siła pochodząca z młotka modalnego (uderzenie w płytę stalową):
0
50
100
150
200
250
300
0
0.005
0.01
0.015
0.02
0.025
0.03
0.035
0.04
0.045
frequency [Hz]
n
or
m
al
iz
ed
am
pl
it
u
de
F
F
T
0.198
0.2
0.202 0.204
0.206 0.208
0
5
10
15
time [s]
fo
rc
e
[N
]

Dynamika Budowli
Wydział Inżynierii Lądowej i Środowiska
Magdalena Rucka & Krzysztof Wilde
________________________________________________________________________________________________
2007-02-26
92
Załącznik A – całkowanie graficzne
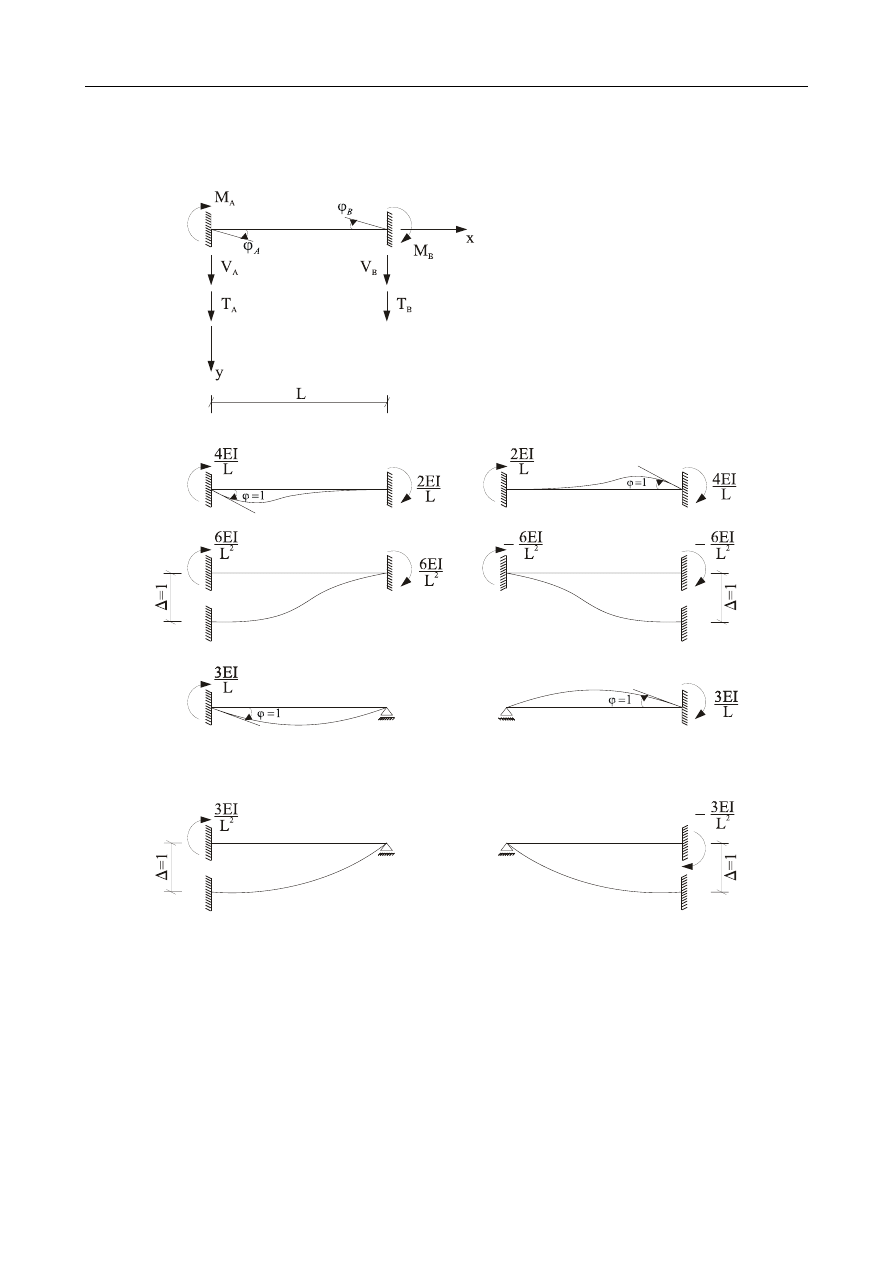
Dynamika Budowli
Wydział Inżynierii Lądowej i Środowiska
Magdalena Rucka & Krzysztof Wilde
________________________________________________________________________________________________
2007-02-26
93
Załącznik B – wyjściowe siły przywęzłowe
Dynamika Budowli
Wydział Inżynierii Lądowej i Środowiska
Magdalena Rucka & Krzysztof Wilde
________________________________________________________________________________________________
2007-02-26
94
Załącznik C – element belkowy
Kondensacja – eliminuje nieistotne, niezerowe przemieszczenia, którym odpowiadają zerowe war-
tości sił przywęzłowych.
Kondensacja układu Kq = P względem podwektora
0
q zawartego w wektorze
q .
11
12
1
0
21
22
2
'
⎡ ⎤
⎡
⎤
⎡
⎤
=
=
⎢ ⎥
⎢
⎥
⎢
⎥
⎣
⎦
⎣
⎦
⎣ ⎦
q
K
K
R
Kq
q
K
K
R
(1)
Rozpisując (1) na 2 równania otrzymujemy:
11
12 0
1
1
21
22 0
2
0
22
2
21
'
'
(
')
−
+
=
+
=
⇒
=
−
K q K q
R
K q K q
R
q
K
R
K q
(2)
A następnie:
1
1
11
12
22
2
12
22
21
1
1
1
11
12
22
21
1
12
22
2
'
'
'
'
(
) '
−
−
−
−
+
−
=
−
=
−
K
P
K q K K R
K K K q
R
K
K K K q
R
K K R (3)
Macierz skondensowana
'
K ostatecznie przyjmuje postać:
1
11
12
22
21
'
−
=
−
K
K
K K K (4)
Przykłady:
a)Kondensacja względem f
a
v
a
a
v
b
b
K
22
K
12
K
21
K
11
v
a
a
v
b
b
Kondensacja względem f
a
oraz
f
b
b
v
b
a
K
22
K
11
K
12
K
21
v
b
a
b
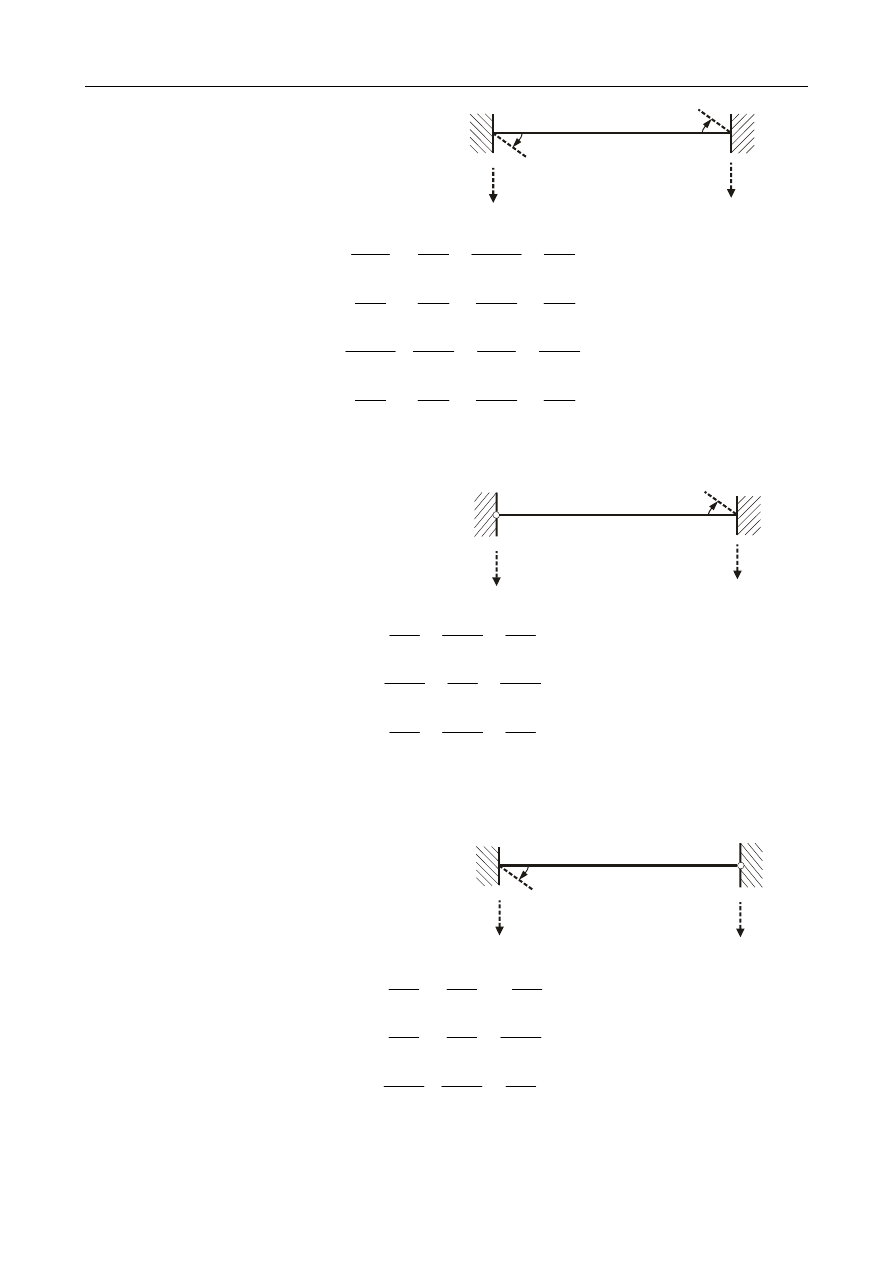
Dynamika Budowli
Wydział Inżynierii Lądowej i Środowiska
Magdalena Rucka & Krzysztof Wilde
________________________________________________________________________________________________
2007-02-26
95
v
k
f
i
v
i
v
k
f
k
v
i
Macierz sztywności elementu belkowego:
3
2
3
2
2
2
3
2
3
2
2
2
12
6
12
6
6
4
6
2
12
6
12
6
6
2
6
4
EI
EI
EI
EI
l
l
l
l
EI
EI
EI
EI
l
l
l
l
EI
EI
EI
EI
l
l
l
l
EI
EI
EI
EI
l
l
l
l
−
⎡
⎤
⎢
⎥
⎢
⎥
−
⎢
⎥
⎢
⎥
= ⎢
⎥
−
−
−
⎢
⎥
⎢
⎥
⎢
⎥
−
⎢
⎥
⎣
⎦
K
(5)
Macierz skondensowana elementu belkowego:
3
3
2
3
3
2
2
2
3
3
3
3
3
3
3
3
3
EI
EI
EI
l
l
l
EI
EI
EI
l
l
l
EI
EI
EI
l
l
l
−
⎡
⎤
⎢
⎥
⎢
⎥
−
−
⎢
⎥
= ⎢
⎥
⎢
⎥
−
⎢
⎥
⎢
⎥
⎣
⎦
K
(6)
Macierz skondensowana elementu belkowego:
3
2
3
2
2
3
2
3
3
3
3
3
3
3
3
3
3
EI
EI
EI
l
l
l
EI
EI
EI
l
l
l
EI
EI
EI
l
l
l
⎡
⎤
−
⎢
⎥
⎢
⎥
−
⎢
⎥
= ⎢
⎥
⎢
⎥
−
−
⎢
⎥
⎢
⎥
⎣
⎦
K
(7)
v
k
f
k
f
i
v
i
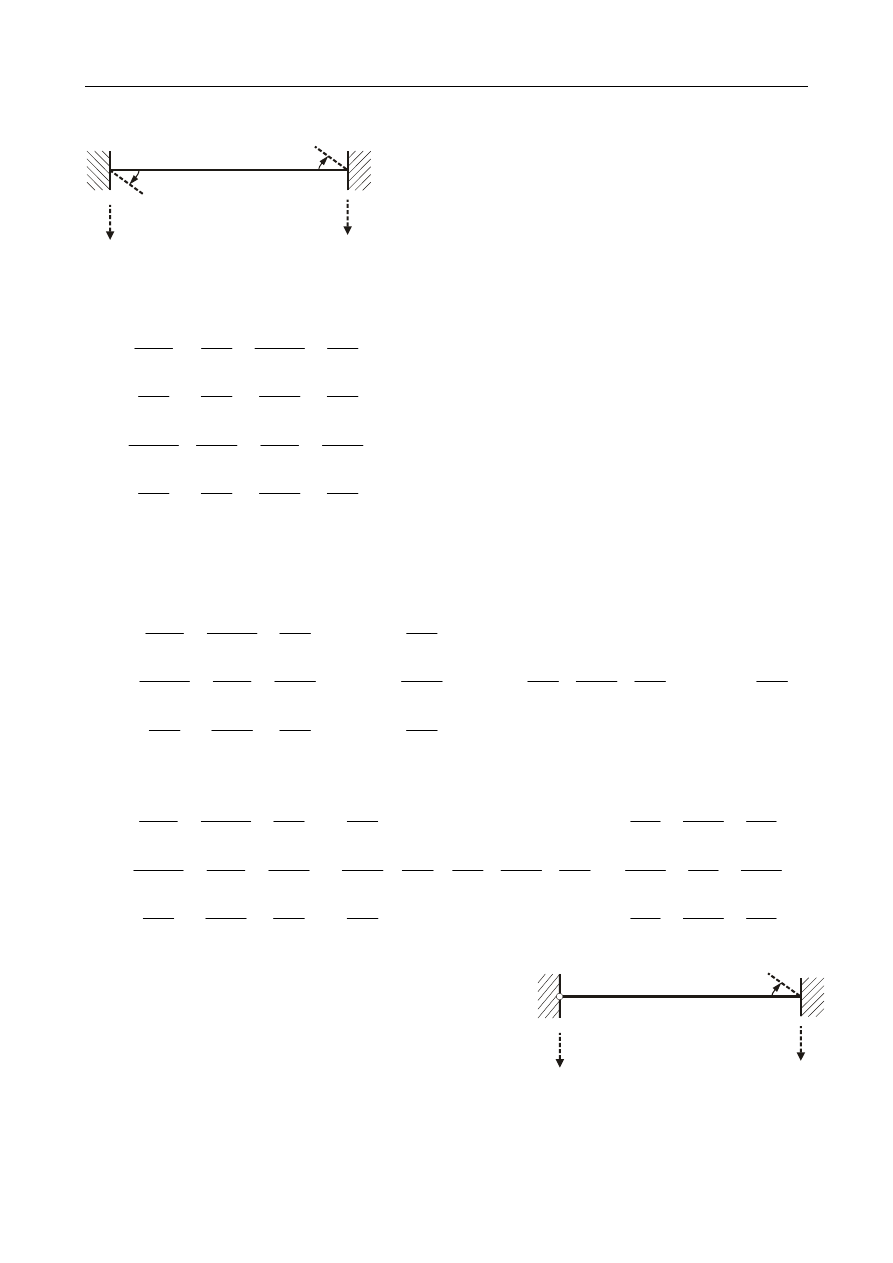
Dynamika Budowli
Wydział Inżynierii Lądowej i Środowiska
Magdalena Rucka & Krzysztof Wilde
________________________________________________________________________________________________
2007-02-26
96
v
k
f
k
v
i
Kondensacja względem
i
ϕ
:
v
k
f
k
f
i
v
i
3
2
3
2
2
2
3
2
3
2
2
2
12
6
12
6
6
4
6
2
12
6
12
6
6
2
6
4
EI
EI
EI
EI
l
l
l
l
EI
EI
EI
EI
l
l
l
l
EI
EI
EI
EI
l
l
l
l
EI
EI
EI
EI
l
l
l
l
−
⎡
⎤
⎢
⎥
⎢
⎥
−
⎢
⎥
⎢
⎥
= ⎢
⎥
−
−
−
⎢
⎥
⎢
⎥
⎢
⎥
−
⎢
⎥
⎣
⎦
K
1
11
12
22
21
'
−
=
−
K
K
K K K
3
3
2
11
3
3
2
2
2
12
12
6
12
12
6
6
6
4
EI
EI
EI
l
l
l
EI
EI
EI
l
l
l
EI
EI
EI
l
l
l
−
⎡
⎤
⎢
⎥
⎢
⎥
−
−
⎢
⎥
= ⎢
⎥
⎢
⎥
−
⎢
⎥
⎢
⎥
⎣
⎦
K
2
12
2
6
6
2
EI
l
EI
l
EI
l
⎡
⎤
⎢
⎥
⎢
⎥
−
⎢
⎥
= ⎢
⎥
⎢
⎥
⎢
⎥
⎢
⎥
⎣
⎦
K
21
2
2
6
6
2
EI
EI
EI
l
l
l
−
⎡
⎤
= ⎢
⎥
⎣
⎦
K
22
4EI
l
⎡
⎤
= ⎢
⎥
⎣
⎦
K
3
3
2
2
3
3
2
3
3
2
2
2
2
3
3
2
2
2
2
2
12
12
6
6
3
3
3
12
12
6
6
6
6
2
3
3
3
'
4
6
6
4
2
3
3
3
EI
EI
EI
EI
EI
EI
EI
l
l
l
l
l
l
l
EI
EI
EI
EI
l
EI
EI
EI
EI
EI
EI
l
l
l
l
EI
l
l
l
l
l
l
EI
EI
EI
EI
EI
EI
EI
l
l
l
l
l
l
l
−
−
⎡
⎤ ⎡
⎤
⎡
⎤
⎢
⎥ ⎢
⎥
⎢
⎥
⎢
⎥ ⎢
⎥
⎢
⎥
−
−
−
−
−
−
⎡
⎤ ⎡
⎤
⎢
⎥ ⎢
⎥
⎢
=
−
=
⎢
⎥ ⎢
⎥
⎢
⎥ ⎢
⎥
⎢
⎣
⎦ ⎣
⎦
⎢
⎥ ⎢
⎥
⎢
−
−
⎢
⎥ ⎢
⎥
⎢
⎢
⎥ ⎢
⎥
⎢
⎣
⎦ ⎣
⎦
⎣
⎦
K
⎥
⎥
⎥
⎥
⎥
i
i
k
k
v
v
ϕ
ϕ
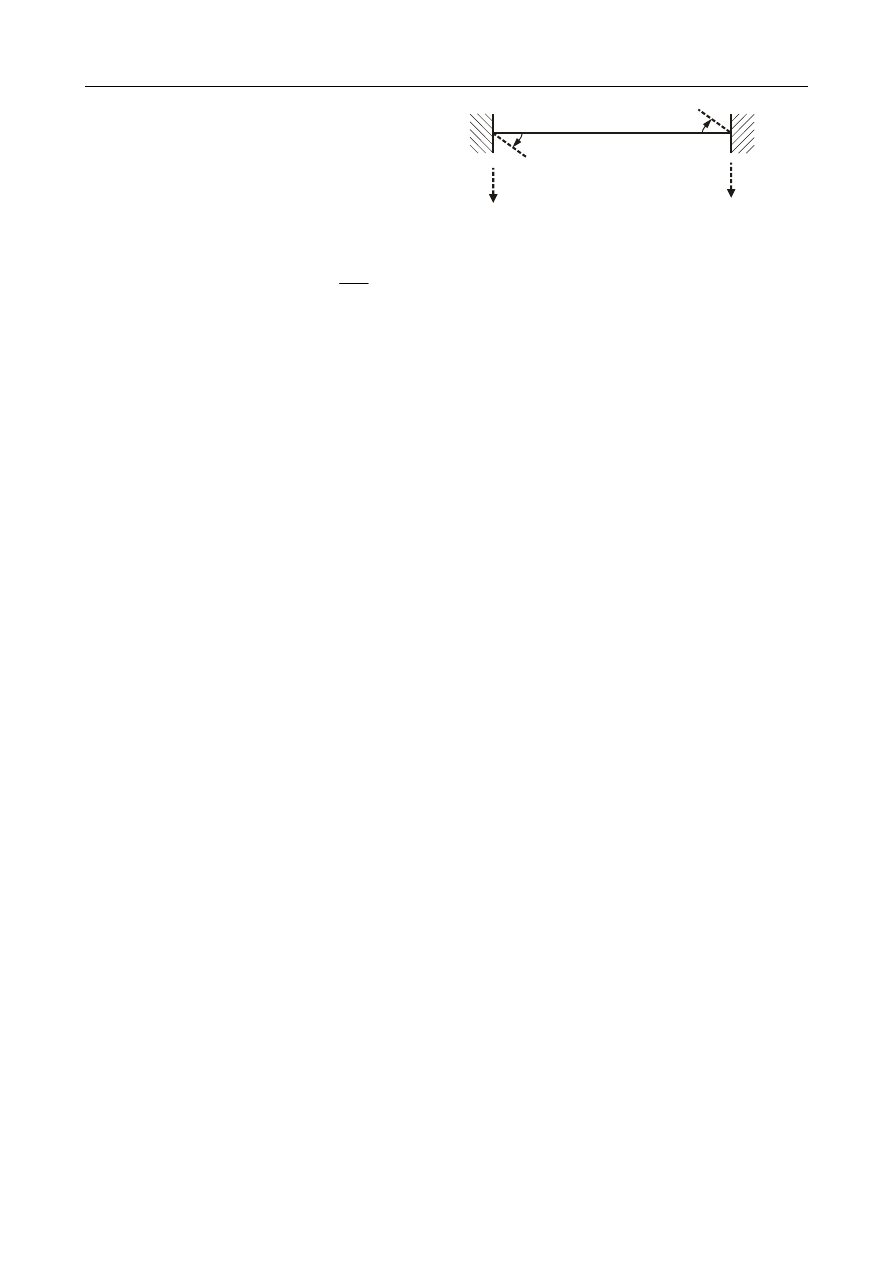
Dynamika Budowli
Wydział Inżynierii Lądowej i Środowiska
Magdalena Rucka & Krzysztof Wilde
________________________________________________________________________________________________
2007-02-26
97
Macierz bezwładności elementu belkowego:
2
2
2
2
156
22
54
13
22
4
13
3
54
13
156
22
420
13
3
22
4
L
L
L
L
L
L
L
L
L
L
L
L
L
μ
−
⎡
⎤
⎢
⎥
−
⎢
⎥
=
⎢
⎥
−
⎢
⎥
−
−
−
⎣
⎦
M
(8)
gdzie
μ
jest masą elementu na jednostkę długości.
v
k
f
k
f
i
v
i
Wyszukiwarka
Podobne podstrony:
Przykłady wyniki2, BUDOWNICTWO PG, III rok, V semestr, dynamika budowli
Pytania z Dynamiki, wszystko, sem. V, Dynamika budowli, Egzaminy
Dynamika Budowli wyklad 4 2011 12
SKRYPT Z PG
PROJEKT U MONIKI, Dynamika budowli
Bryja, dynamika budowli, opracowane zagadnienia
dynamika budowli lista zadan pdb cw6
dynamika budowli lista zadan pdb cw7
dynamika budowli lista zadan pdb cw4
dynamika budowli lista zadan pdb cw3
Lit, Elektronika, Elektronika Dla Mechaników Skrypt PG
skrypt PG cw, Politologia UMCS - materiały, V Semestr zimowy, V Semestr zimowy, Polityka Gospodarcza
0spistr, Elektronika, Elektronika Dla Mechaników Skrypt PG
Dynamika Budowli wyklad 2 2011 Nieznany
00stronatyt, Elektronika, Elektronika Dla Mechaników Skrypt PG
dynamika budowli lista zadan pdb cw5
dynamika budowli notatki do wykładów[1] (1)
Prawo budowlane skrypt wersja 1
więcej podobnych podstron