2009-11-29

1

Geodezja podstawowa 

i astronomia geodezyjna

Ćwiczenie 4

Systemy czasów

Systemy czasów

Rachuba lat (kalendarze) – wykład

SYSTEMY CZASÓW W ASTRONOMII

Czas efemeryd ET (Ephemeris Time) – skala czasu newtonowskiego opartego na
ruchu orbitalnym Ziemi (1954 r. – X Generalna Konferencja Miar i Wag)
Podstawowa jednostka wynikająca z długości okresu obiegu Ziemi wokół Słońca na
epokę 1900 – sekunda efemerydalna (sekunda czasu średniego słonecznego –

p ę

y

(

g

g

1/86400 część doby słonecznej)

2009-11-29

2

Efemerydy – określają położenie danego ciała dla konkretnego momentu 
czasu (tabele)

UT0 ‐ czas uniwersalny prawdziwy
UT1 – czas uniwersalny średni

GMST – średni czas gwiazdowy Greenwich

GST – prawdziwy czas gwiazdowy Greenwich

CZASY ATOMOWE 

Oscylacje elektromagnetyczne atomów

Jednostka podstawowa to sekunda atomowa (1967 r. ‐ XIII Generalna Konferencja
Miar i Wag) ‐ jednostka czasu równa 9 192 631 770 okresom przejścia pomiędzy
podpoziomami f = 3 i f = 4 struktury nadsubtelnej poziomu podstawowego 2s1/2

podpoziomami f = 3 i f = 4 struktury nadsubtelnej poziomu podstawowego 2s1/2
atomu 133Cs znajdującego się na poziomie morza.

Definicja sekundy atomowej oparta jest o zjawisko emisji światła (dokładniej
promieniowania elektromagnetycznego). Światło jest rodzajem drgań pola
elektromagnetycznego, a każde takie drganie trwa określoną ilość czasu. Jeśli więc
weźmiemy odpowiednią ilość takich drgań to dostaniemy w rezultacie niemal
dowolny odstęp czasu (byle nie krótszy niż pojedyncze drganie)

dowolny odstęp czasu (byle nie krótszy niż pojedyncze drganie).

Światło emitowane przez pierwiastek cez jest bardzo jednorodne i stabilne, dzięki
czemu dobrze nadaje się na wzorzec. Żeby zaś ta nowa definicja sekundy dobrze
zgadzała się ze starą, opartą na średniej dobie słonecznej trzeba wziąć właśnie 9 192
631 770 takich drgań.

2009-11-29

3

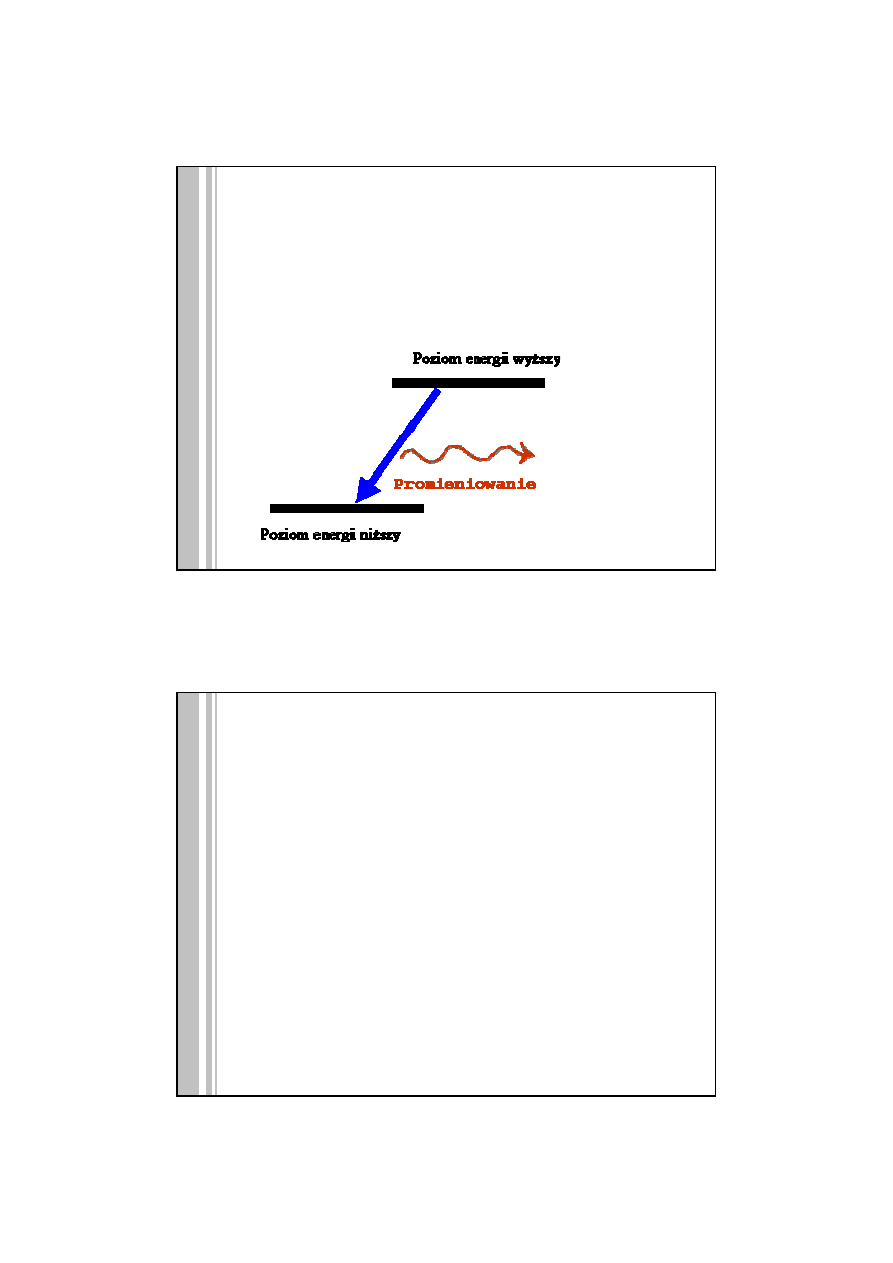
Część definicji traktująca o podpoziomach struktury nadsubtelnej precyzuje
po prostu o które promieniowanie atomu cezu chodzi. Ponieważ cez może
wytwarzać różne rodzaje promieniowania (czyli różne barwy światła
różniącego się czasem drgań), a każdy rodzaj promieniowania odpowiada
przejściom pomiędzy różnymi poziomami energetycznymi, to należy uściślić,
że chodzi o ten jeden konkretny rodzaj przejścia ‐ czyli przejście z podpoziomu

że chodzi o ten jeden konkretny rodzaj przejścia ‐ czyli przejście z podpoziomu
energetycznego o f = 3 na poziom o f = 4

(źródło http://www.fizykon.org/wlk_podstawowe/sekunda.htm)

CZAS ATOMOWY TAI (International Atomic Time) –

UTC (Universal Time Coordinated, Zulu Time) –

CZASY ATOMOWE 

http://www.astro.uni.torun.pl/~kb/Artykuly/U‐PA/Czas1.htm

http://www.astro.uni.torun.pl/~kb/Artykuly/U‐PA/Czas2.htm

http://www.astro.uni.torun.pl/~kb/Artykuly/U‐PA/Czas3.htm

2009-11-29

4

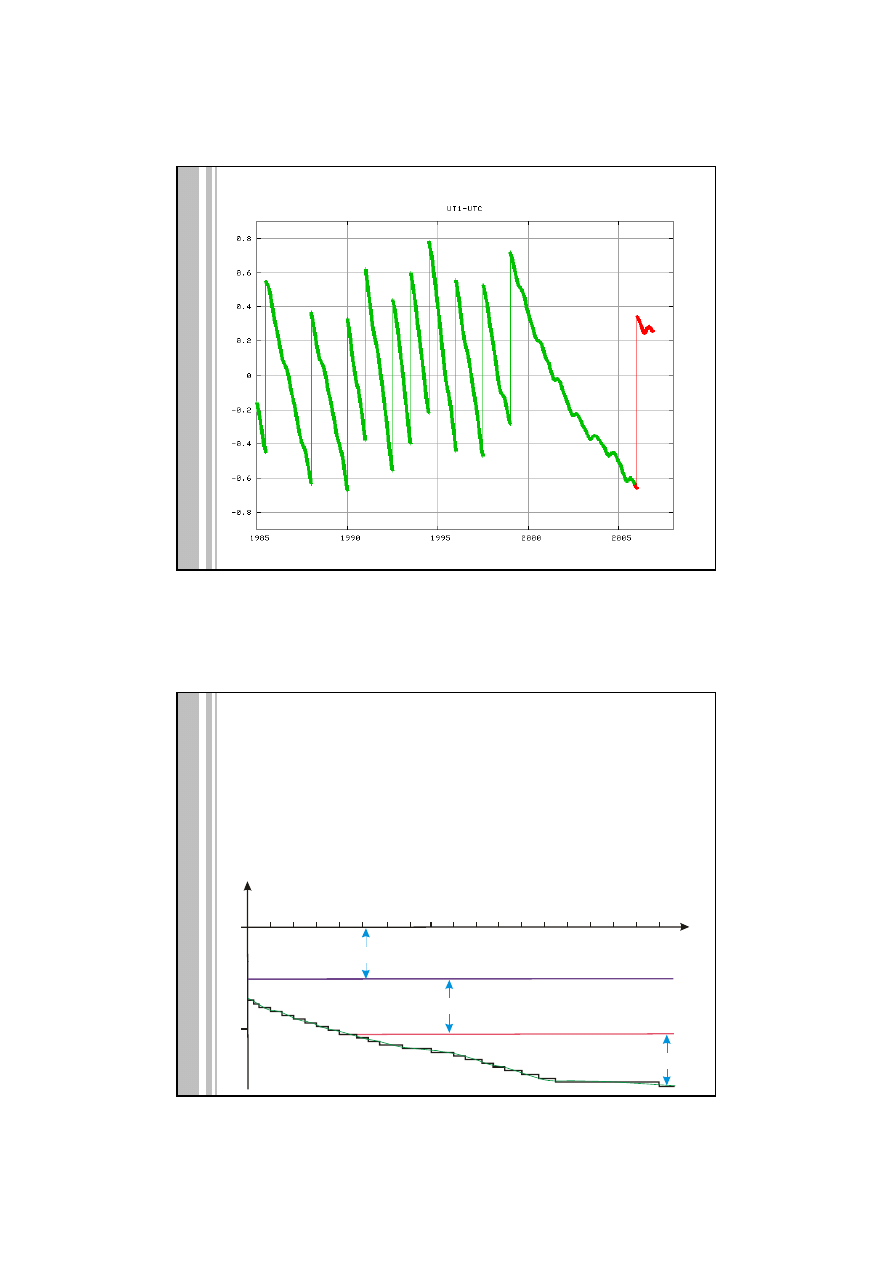
Różnica UT1‐UTC

www.wikipedia.com

TT – Terrestial Time (wykorzystywany w praktyce);

TT jest atomowym przybliżeniem dynamicznego czasu efemeryd

TT = TAI +32.184 s (historyczne różnice pomiędzy TAI i ET kiedy wprowadzano czas 

TT)

GPST – system czasu GPS (na podstawie zegarów na satelitach)‐ różni się o około  

19 s od TAI

19 s od TAI

0

1976

1980

1984

TT

1988

1992

1996

2000

t [s]

2004

2006

32.184

s

-50

UT1

UTC

GPST

TAI

14

s

19

s

2009-11-29

5

SYSTEMY CZASÓW W ASTRONOMII

CZAS GWIAZDOWY 

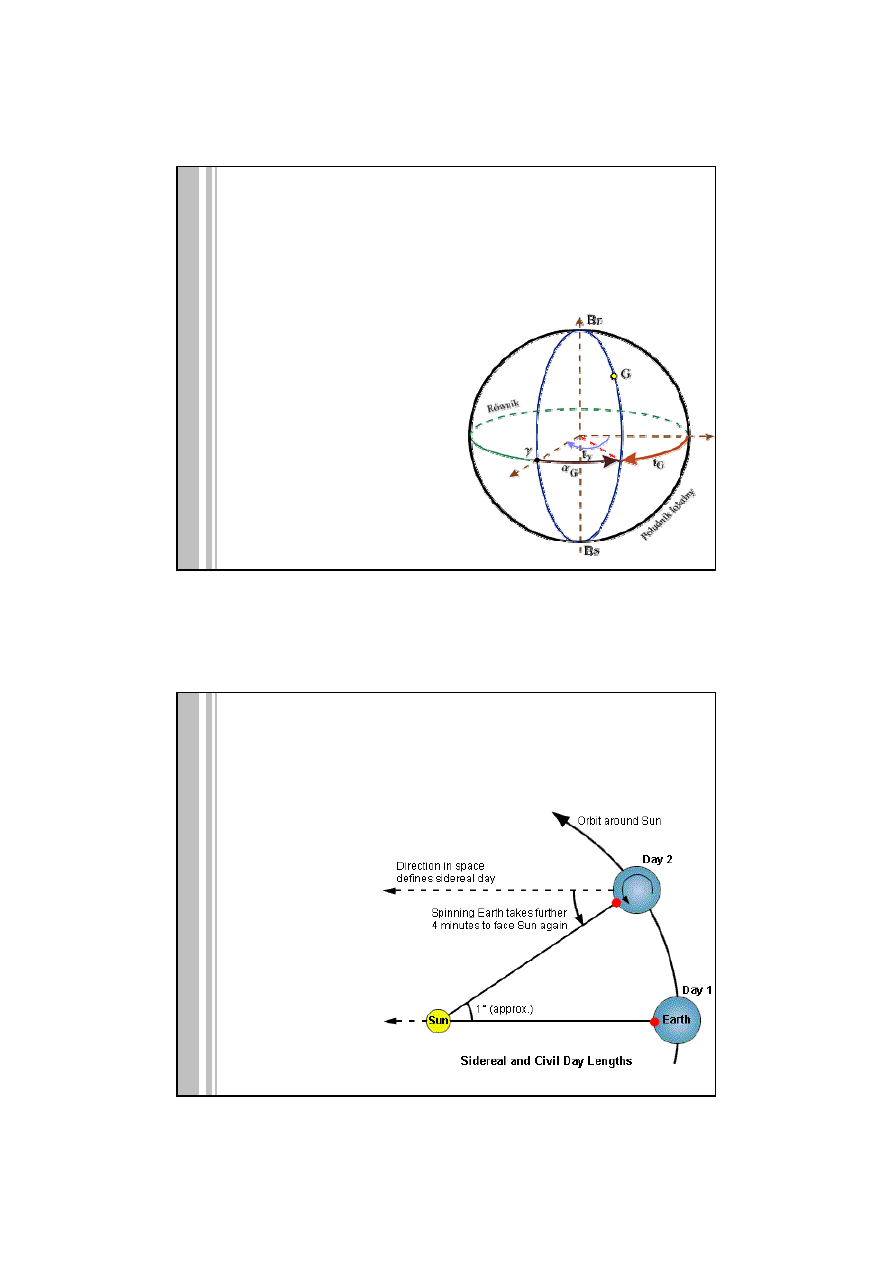
doba gwiazdowa ‐ odstęp pomiędzy kolejnymi górowaniami punktu Barana 

Czas gwiazdowy T* to kąt godzinny punktu Barana 

T*=Tγ

Punktu Barana nie widać więc w praktyce

Punktu Barana nie widać, więc w praktyce 

mierzy się kąt godzinny gwiazdy i znanej 

rektascensji ‐ kąt godzinny punktu Barana                       

równy jest bowiem sumie rektascensji 

i kąta godzinnego tego obiektu  

T* = Tγ = α

G 

+ t

G

http://www.nauticalissues.com/astronomy3.html

DOBA SŁONECZNA A DOBA GWIAZDOWA

Doba gwiazdowa trwa 23h 56m 04s

Doba słoneczna trwa 24h

http://burro.astr.cwru.edu/Academics/Astr306/Coords/coords.html

2009-11-29

6

Stosuje się go ze względów praktycznych – cykl związany z ruchem Słońca; 

Doba słoneczna ‐ odstęp czasu pomiędzy                                                                        
dwoma kolejnymi górowaniami Słońca

Miarą czasu słonecznego T



jest kąt

CZAS SŁONECZNY S

v

Miarą czasu słonecznego T



jest kąt                                                                            

godzinny środka tarczy Słońca. 

Aby mierzyć go od północy, a nie od środka                                                                           
dnia, kiedy to Słońce góruje na południku,                                                                            
definiujemy go jako kąt godzinny środka                                                                        
tarczy Słońca t



plus 12h: 

S = T = t +12h

S

v

= T



= t



+12h

http://www.nauticalissues.com/astronomy3.html

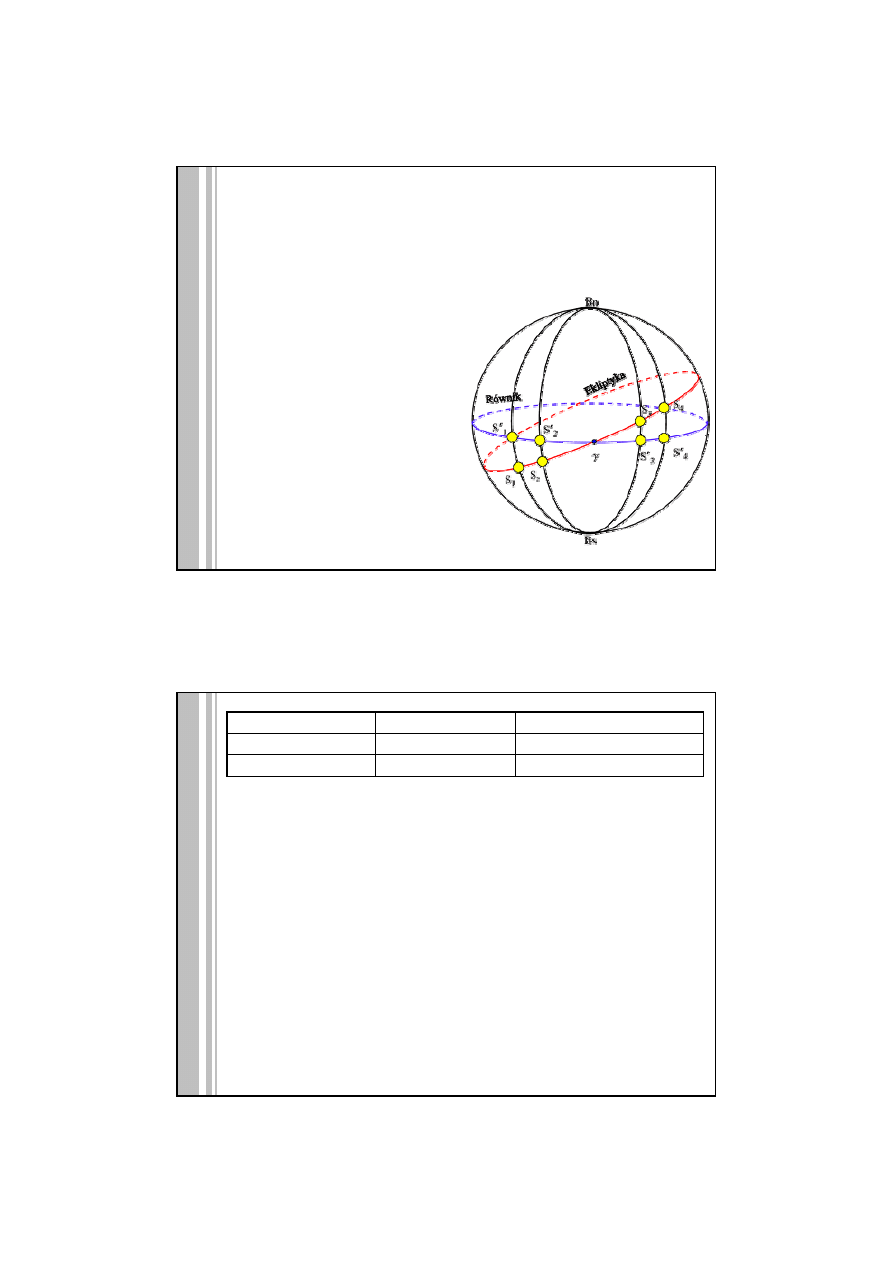
RÓWNANIE CZASU – różnica pomiędzy czasem słonecznym prawdziwym T



ł

ś d i

T

s

d

i

Słońce prawdziwe

Słońce średnie (punkt fikcyjny)

Porusza się po:

ekliptyce

równiku

Prędkość kątowa d/dt

zmienia się

nie zmienia się – stała wartość

a słonecznym średnim T



s

w danym momencie:

T



‐ T

 s

=t 

 s 

‐ t 

 s

Na podstawie definicji czasu gwiazdowego można zapisać:

T* = t 



+ α 



i    T* = t 

 s

+ α 

 s

Ró

i

ż

i

i ć j k

óż i

kt

ji Sł ń

ś d i

Równanie czasu można więc zapisać jako różnicę rektascensji Słońca średniego
i prawdziwego:

T



‐ T

 s

= t



‐ t 

 s

= α 

 s

‐ α 



= ‐7.7*sin(79° + l) + 9.5*sin(2*l)

gdzie l oznacza długość ekliptyczną Słońca prawdziwego, a dwa współczynniki
(‐7,7 i 9,5) są wyrażone w minutach czasu .

2009-11-29

7

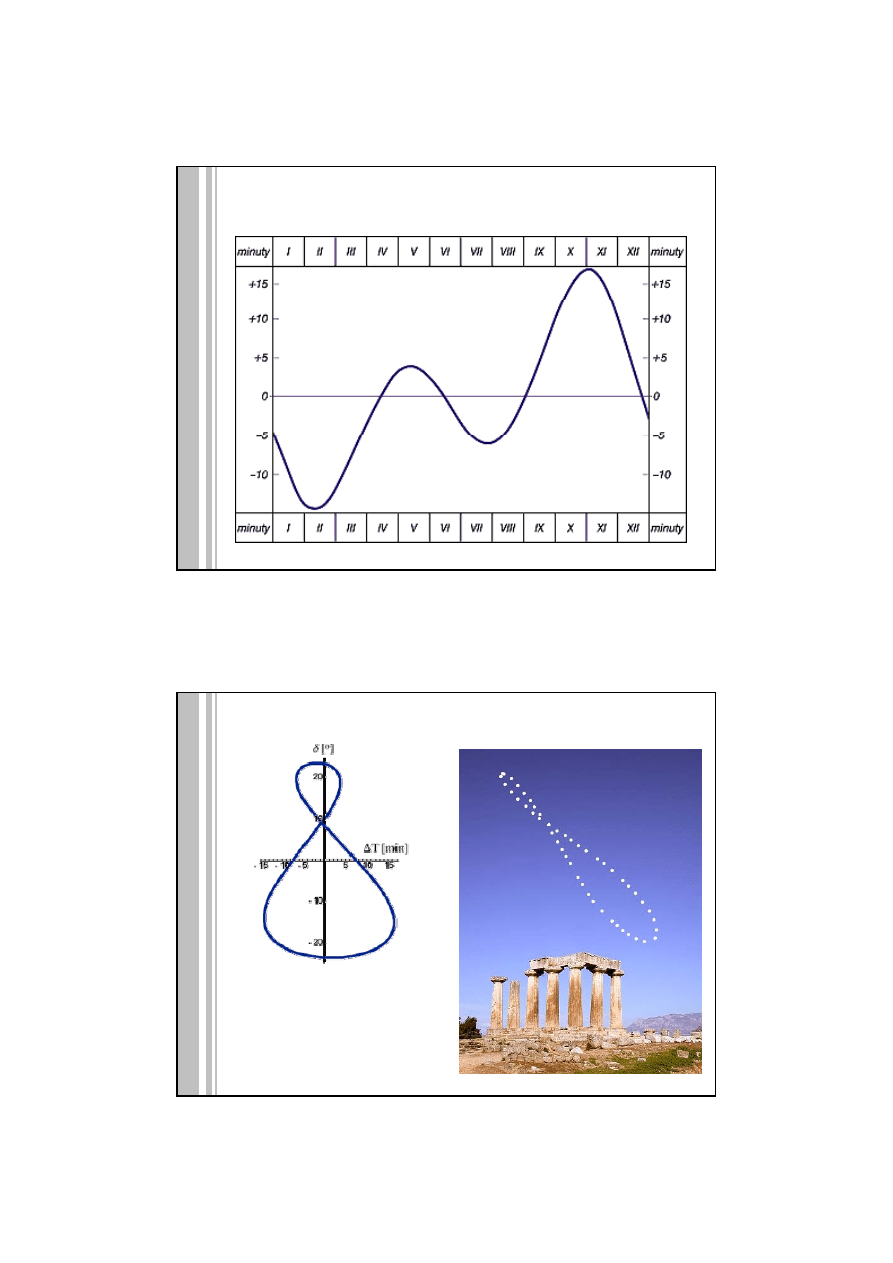
RÓWNANIE CZASU T ‐Ts  

(różnica pomiędzy prawdziwym a średnim czasem słonecznym 

http://www.wiw.pl/astronomia/0302‐czas.asp

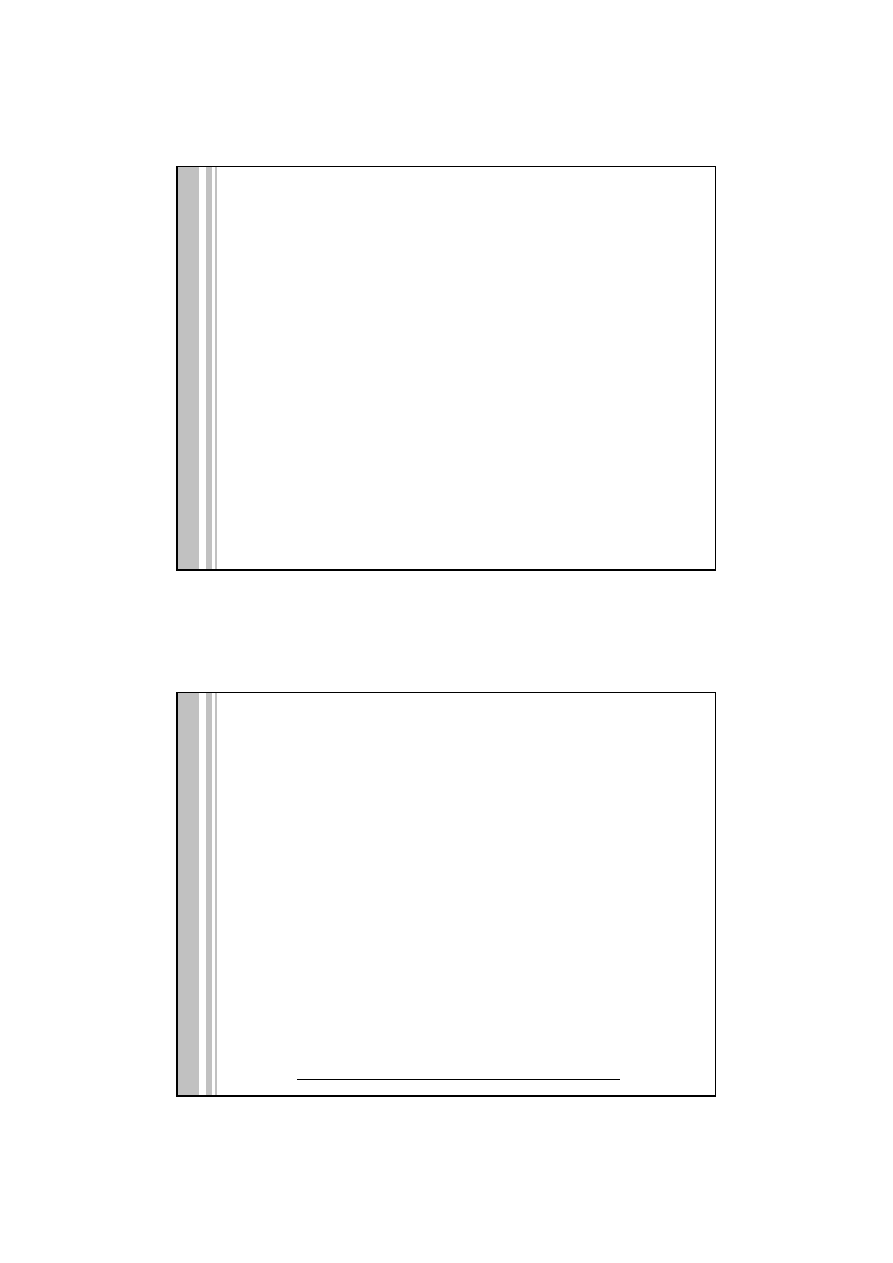
Analemma ‐ krzywa przedstawiająca zmiany różnicy między prawdziwym a średnim 

czasem słonecznym w zależności od położenia Słońca na ekliptyce 

Punkt Raka

P

kt K i

ż

http://www.perseus.gr/Astro‐Solar‐Analemma.htm

Punkt Koziorożca

2009-11-29

8

CZAS MIEJSCOWY (LOKALNY) – wyznaczony w danym miejscu obserwacji,
czyli na południku miejscowym zawierającym miejsce obserwacji

Wszystkie miejsca ma Ziemi położone na tym samym południku mają w
danym momencie jednakowy czas miejscowy (gwiazdowy

słoneczny

danym momencie jednakowy czas miejscowy (gwiazdowy, słoneczny
prawdziwy, słoneczny średni). Różnica czasów miejscowych w dwóch
miejscach równa jest różnicy ich długości geograficznych wyrażonej w mierze
czasowej:

T*

A 

‐ T*

B

= λ

A 

– λ

B

T

A 

‐ T

B

= λ

A 

– λ

B         

(*)

T

sA 

‐ T

sA 

= λ

A 

‐ λ

B

POMIAR DŁUGOŚCI GEOGRAFICZNEJ

1)   Jeden z południków (znana λA ) obieramy jako południk odniesienia i 

‘wozimy’   ze sobą czas gwiazdowy T*A lub średni słoneczny T



sA  tego 

południka. 

2) Obserwujemy moment górowania Słońca na południku o nieznanej długości

geograficznej (w momencie górowania w południku miejscowym jest

dokładnie godzina 12 czasu słonecznego prawdziwego TB=12h.

3) Na podstawie odczytu ‘przewożonego’ czasu z południka λA wyznaczamy czas

prawdziwy słoneczny λA Długość południka miejscowego λB otrzymujemy

prawdziwy słoneczny λA . Długość południka miejscowego λB otrzymujemy

wstawiając te informacje do równania (*):

λB= λA +TA – 12h

Południk odniesienia to przeważnie południk Greenwich

2009-11-29

9

CZAS UNIWERSALNY 

– średni czas słoneczny południka Greenwich

UT= T

s

Greenwich 

Różnica pomiędzy lokalnym (miejscowym) średnim czasem słonecznym na długości λ

A

a średnim słonecznym czasem południka Greenwich o λ

B

=0 (czasem uniwersalnym)

wynosi:

λ

T

sA

‐UT= λ

A

Średni słoneczny czas miejscowy w dowolnym miejscu na Ziemi równy jest czasowi 
uniwersalnemu i długości geograficznej tego miejsca wyrażonej w mierze czasowej
i jest liczony dodatnio na wschód od Greenwich:

T

sA

= UT+λ

A

PODZIAŁ ŚWIATA NA STREFY CZASOWE

W praktyce strefy nie leżą wzdłuż południków, ale wzdłuż granic państw.

2009-11-29

10

CZAS URZĘDOWY

W części krajów (w tym w Polsce) wprowadza się czas letni – do 
właściwego czasu strefowego dodaje się jedną godzinę (dla 
Polski czas właściwy dla południka 30°):

T

λA

letni 

= T

λA

+ 1h

‐ 1 dzień

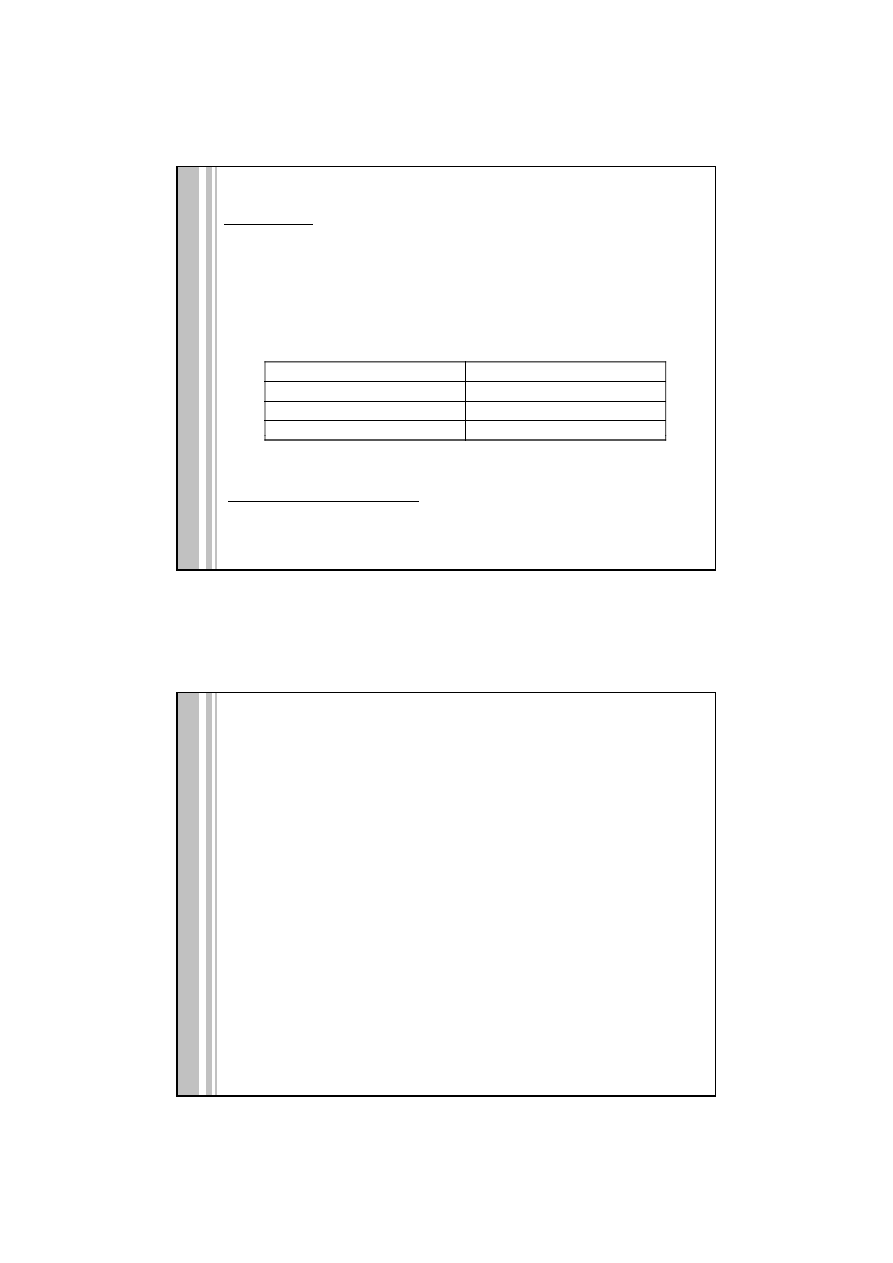
LINIA ZMIANY DATY

.

www.wikipedia.com

+ 1 dzień

1 dzień

LINIA ZMIANY DATY

2009-11-29

11

DATA JULIAŃSKA – ASTRONOMICZNA CIĄGŁA RACHUBA DNI

Data juliańska JD – ciągła rachuba dni wprowadzona w XVI wieku.

Oznacza liczbę dni od momentu 1 stycznia 12

h

(południe) 4713 r. p. n. e.

Odniesienie do określonej skali czasu – dzień juliański w skali UT1 odpowiada
86 400 sekundom UT1, dzień juliański odniesiony do ET odpowiada 86 400

k

d

ET

1 styczeń 1900 12

00

UT1

2 415 021.0

1 styczeń 1977   0

00

UT1

2 443 144.5

1 styczeń 2000 12

00

UT1

2 451 545.0

3 grudzień 2006 12

00

UT1

2454073.00

sekundom ET.

rok juliański = 365.25 dni juliańskich

stulecie juliańskie = 36 525 dni juliańskich

g

Porę dnia określa ułamek dziesiętny numeru dnia (nie godziny).

Zmodyfikowana data juliańska MJD ‐ różnicą jest początek dnia przypadający 
na północ, a momentem zerowym jest 17 listopada 1858 r. 

MJD = JD − 2400000,5

Zadanie 1

W obserwatorium o długości geograficznej λ1=21°30’E zaobserwowano górującą gwiazdę. 
Jaki jest jej kąt godzinny w danym momencie w obserwatoriach λ2=3°10’E  i λ3=7°45’W ?

Zadanie 2

W obserwatorium λ1=15°E gwiazda góruje. Jaka jest długość geograficzna obserwatorium, 
w którym dana gwiazda ma w tym momencie kat godzinny a) t2=22h  b) t2=3h?

Zadanie 3

Jaki jest prawdziwy czas słoneczny w obserwatorium λ1=37°30’E, gdy Słonce góruje w 
obserwatorium λ2=15°E?