2009-12-17

1

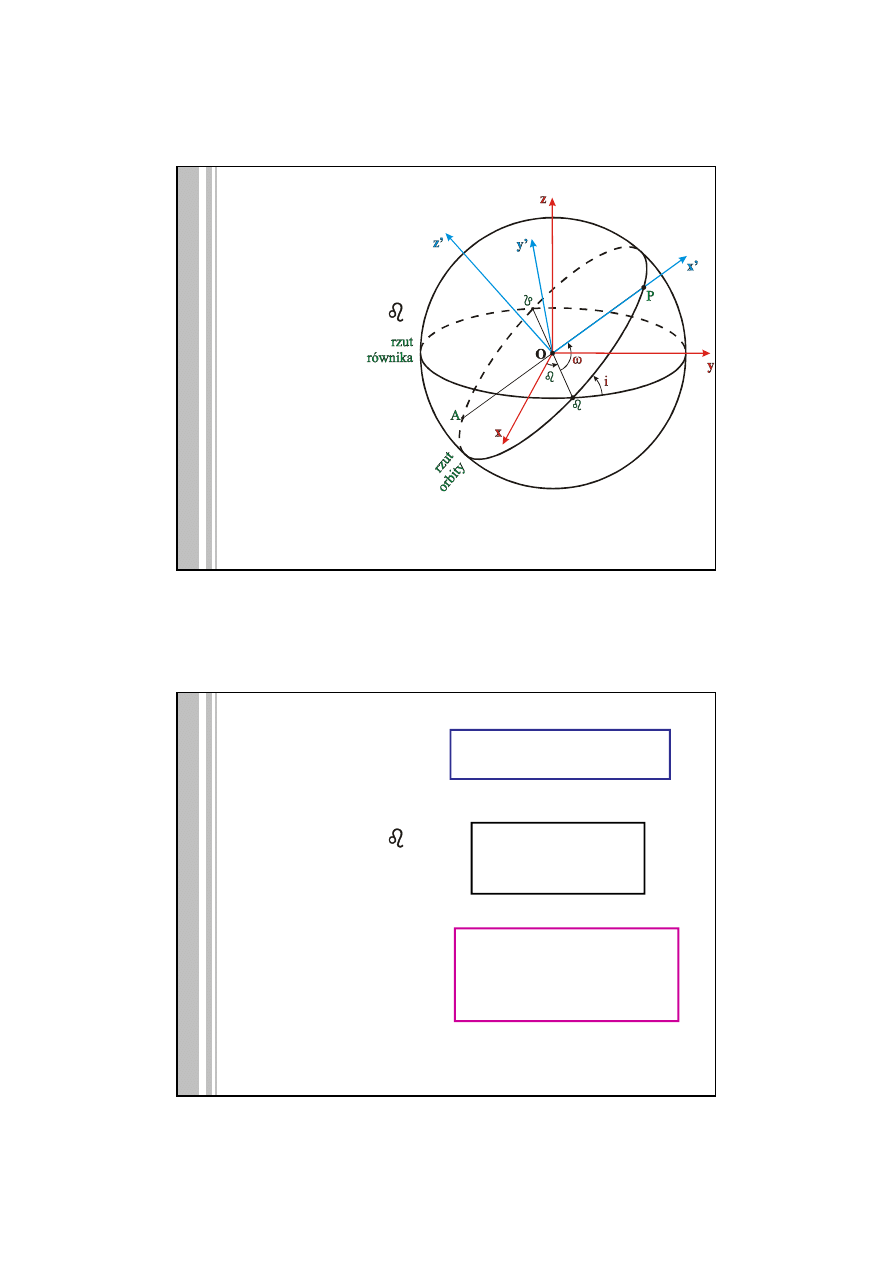
ELEMENTY ORBITY KEPLEROWSKIEJ

Dane dodatkowe: współrzędne elipsoidalne obserwatora – B, L, H

duża półoś orbity – a

mimośród orbity – e

rektascensja węzła
wstępującego orbity –

nachylenie orbity
do równika – i

argument perygeum -

ω

ωω

ω

moment przejścia przez
perycentrum (UTC) – t

p

moment na który
wyznaczamy pozycję (UTC) – t

(anomalia średnia M – łączy t

p

i t)

ELEMENTY ORBITY KEPLEROWSKIEJ

duża półoś orbity – a

mimośród orbity – e

rektascensja węzła
wstępującego orbity –

nachylenie orbity
do równika – i

argument perygeum -

ω

ωω

ω

moment przejścia przez
perycentrum (UTC) – t

p

moment na który
wyznaczamy pozycję (UTC) – t

elementy opisujące kształt

elipsy orbitalnej

elementy opisujące

położenie płaszczyzny

orbity w przestrzeni

elementy opisujące

orientację orbity w tej

płaszczyźnie i położenie ciała

na orbicie dla danej epoki

(anomalia średnia M – łączy t

p

i t)

Dane dodatkowe: współrzędne elipsoidalne obserwatora – B, L, H

2009-12-17

2

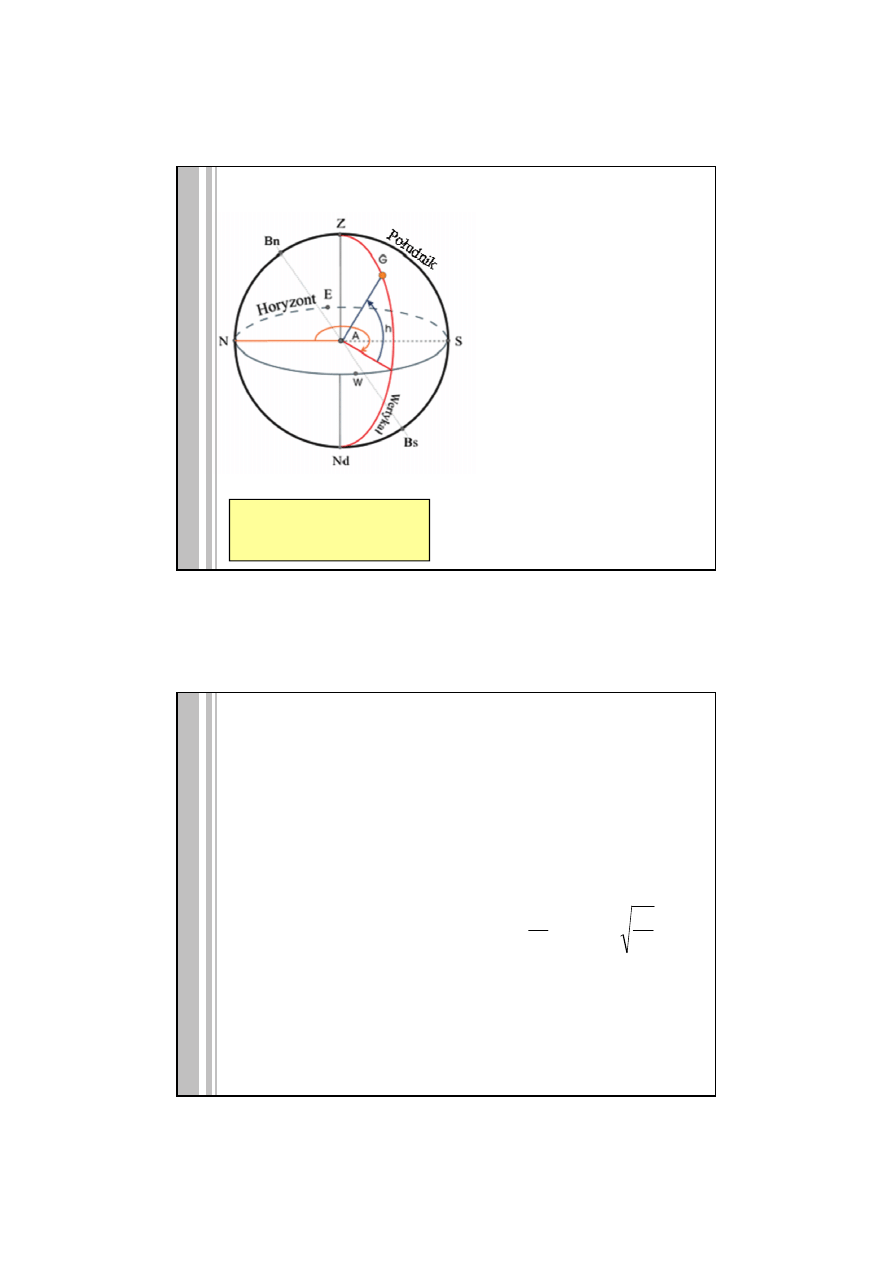
UKŁAD HORYZONTALNY

Wysokość h to kąt środkowy pomiędzy

wektorem wodzącym do danego

obiektu, a płaszczyzną horyzontu

(odległość zenitalna z to dopełnienie

wysokości do 90

°

). Wysokość zawiera

się w granicach <-90

°

, 90

°

>. Oś układu

zdefiniowana jest kierunkiem linii

pionu w miejscu obserwacji.

Azymut A to kąt dwuścienny utworzony

przez płaszczyznę południka

przechodzącego przez punkt północy N

oraz płaszczyznę południka

przechodzącego przez dany obiekt (kąt

mierzony w płaszczyźnie horyzontu na

wschód – zgodnie z ruchem wskazówek

zegara ). Azymut zawiera się

w granicach <0

°

, 360

°

>.

Azymut i wysokość zmieniają się

na skutek ruchu obrotowego

Ziemi.

WYZNACZENIE WSPÓŁRZĘDNYCH HORYZONTALNYCH NA

PODSTAWIE ELEMENTÓW ORBITY

1) Obliczenie anomalii średniej (odległość kątowa od

perycentrum do fikcyjnego punktu poruszającego się po
orbicie ze średnią prędkością kątową n):

( )

p

t

t

n

M

−

⋅

=









°

sek

3

a

n

µ

=

GM

=

µ

gdzie:

n – średnia prędkość kątowa satelity

;

- parametr grawitacyjny.

2009-12-17

3

WYZNACZENIE WSPÓŁRZĘDNYCH HORYZONTALNYCH NA

PODSTAWIE ELEMENTÓW ORBITY

2) Obliczenie anomalii mimośrodowej z równania Keplera:

;

E

e

M

E

sin

⋅

+

=

Metoda iteracyjna:

M

E

=

0

i

i

E

e

M

E

sin

1

⋅

+

=

+

WYZNACZENIE WSPÓŁRZĘDNYCH HORYZONTALNYCH NA

PODSTAWIE ELEMENTÓW ORBITY

3) Obliczenie współrzędnych ciała niebieskiego w układzie

związanym z orbitą:

;

(

)

0

'

sin

'

cos

'

=

=

−

=

z

E

b

y

e

E

a

x

2

1 e

a

b

−

=

Układ orbitalny jest układem kartezjańskim prawoskrętnym
(wnętrze obracającej się prawej dłoni zakreśla łuk od osi OX
do OY, a kciuk wyznacza kierunek osi OZ), oś X jest
skierowana do perycentrum, oś Z jest prostopadła do
płaszczyzny orbity.

Perycentrum – punkt na orbicie ciała niebieskiego okrążającego
dany obiekt, znajdujący się w miejscu największego zbliżenia ciała
do tego obiektu.

2009-12-17

4

WYZNACZENIE WSPÓŁRZĘDNYCH HORYZONTALNYCH NA

PODSTAWIE ELEMENTÓW ORBITY

4) Transformacja układu orbitalnego do układu niebieskiego:





















=

⇒





















=

z

y

x

z

y

x

x

x

'

'

'

'





















⋅

−

⋅

−

⋅

−

=





















'

'

'

)

(

)

(

)

(

z

y

x

i

z

y

x

z

x

z

ω

R

R

R

układ orbitalny układ równikowy (

αααα

,

δδδδ

)

Macierze obrotów:





















−

=

−





















−

=

−





















−

=

−

1

0

0

0

cos

sin

0

sin

cos

)

(

cos

sin

0

sin

cos

0

0

0

1

)

(

1

0

0

0

cos

sin

0

sin

cos

)

(

ω

ω

ω

ω

ω

z

x

z

i

i

i

i

i

R

R

R

WYZNACZENIE WSPÓŁRZĘDNYCH HORYZONTALNYCH NA

PODSTAWIE ELEMENTÓW ORBITY

4) Transformacja układu orbitalnego do układu niebieskiego:

Współrzędne równikowe:

2

2

tan

tan

y

x

z

x

y

+

=

=

δ

α

Układ równikowy równonocny jest
układem kartezjańskim prawoskrętnym
(wnętrze obracającej się prawej dłoni
zakreśla łuk od osi OX do OY, a kciuk
wyznacza kierunek osi OZ), oś X jest
skierowana do punktu Barana.

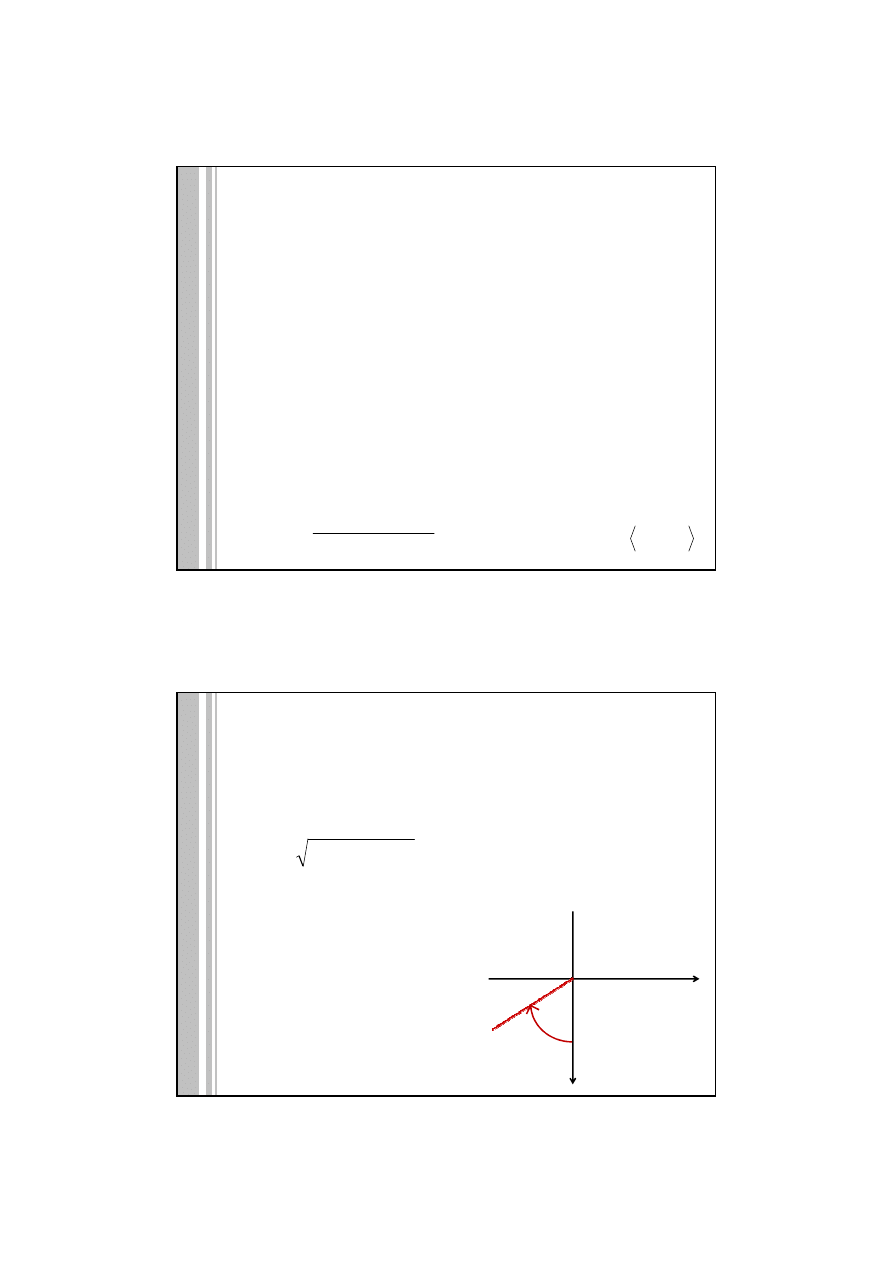
Rektascenzja jest mierzona przeciwnie
do ruchu wskazówek zegara od osi X,

na podstawie analizy znaku X i Y należy

określić prawidłową jej wielkość.

X

Y

αααα

X>0 Y>0

X<0 Y>0

X<0 Y<0

X>0 Y<0

2009-12-17

5

WYZNACZENIE WSPÓŁRZĘDNYCH HORYZONTALNYCH NA

PODSTAWIE ELEMENTÓW ORBITY

5) Transformacja układu równikowego do geocentrycznego

układu godzinnego:

α

−

=

S

t

S

L

S

S

S

UTC

GR

GR

+

=

⇒

Współrzędne godzinne:

S

– czas gwiazdowy średni

αααα

– rektascensja

-

przybliżone

przeliczenie

czasów

(z pominięciem różnicy UT1-UTC oraz
założeniem, że

)

L

≅

λ

α

−

+

+

+

=

L

S

t

t

t

TU

UTC

UTC

S

0

79

365,242198

Uproszczone ćwiczenie nr 5:

h

t

S

24

,

0

∈

WYZNACZENIE WSPÓŁRZĘDNYCH HORYZONTALNYCH NA

PODSTAWIE ELEMENTÓW ORBITY

6) Obliczenie ortokartezjańskich geocentrycznych

współrzędnych godzinnych:

δ

δ

δ

sin

'

sin

cos

'

cos

cos

'

⋅

=

⋅

⋅

−

=

⋅

⋅

=

r

Z

t

r

Y

t

r

X

S

S

r – wektor wodzący ciała niebieskiego w układzie równikowym

(

)

2

2

2

z

y

x

r

+

+

=

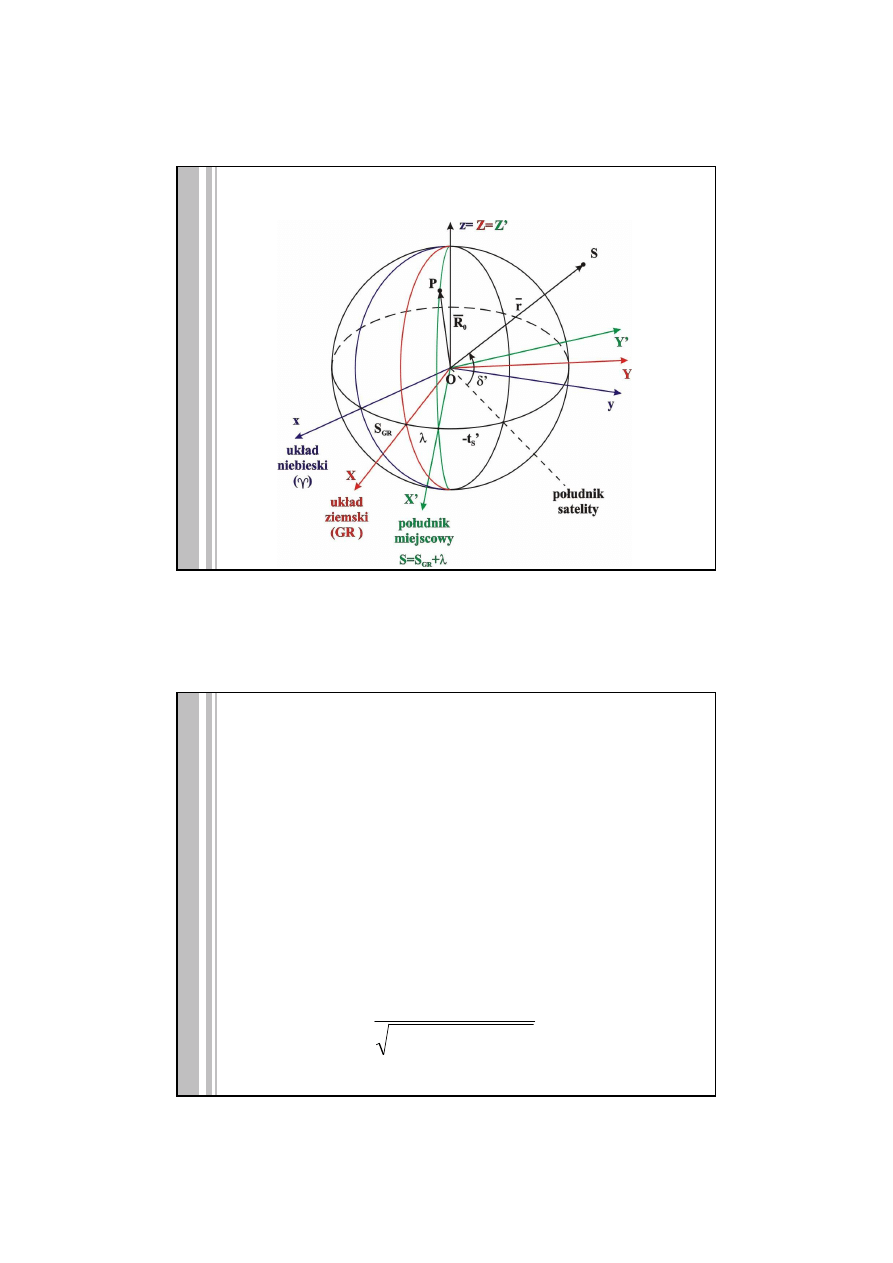
Układ równikowy godzinny także jest
układem kartezjańskim prawoskrętnym.

Kat godzinny jest mierzony zgodnie z
ruchem wskazówek zegara od osi X
wskazującej południk miejscowy – stąd
znak minus przy współrzędnej Y’.

X

Y

t

X>0 Y>0

X<0 Y>0

X<0 Y<0

X>0 Y<0

2009-12-17

6

WYZNACZENIE WSPÓŁRZĘDNYCH HORYZONTALNYCH NA

PODSTAWIE ELEMENTÓW ORBITY

WYZNACZENIE WSPÓŁRZĘDNYCH HORYZONTALNYCH NA

PODSTAWIE ELEMENTÓW ORBITY

7) Obliczenie ortokartezjańskich topocentrycznych

współrzędnych godzinnych:

(

)

(

)

[

]

B

H

e

N

Z

Z

Y

Y

B

H

N

X

X

GRS

T

T

T

sin

1

'

'

cos

'

2

'

'

'

80

⋅

+

−

⋅

−

=

=

⋅

+

−

=

N – promień krzywizny przekroju poprzecznego

B

e

a

N

GRS

GRS

2

2

80

80

sin

1

⋅

−

=

2009-12-17

7

WYZNACZENIE WSPÓŁRZĘDNYCH HORYZONTALNYCH NA

PODSTAWIE ELEMENTÓW ORBITY

8) Obliczenie topocentrycznych współrzędnych godzinnych:

( ) ( )

2

'

2

'

'

'

'

'

'

tan

tan

T

T

T

T

T

S

Y

X

Z

X

Y

t

+

=

−

=

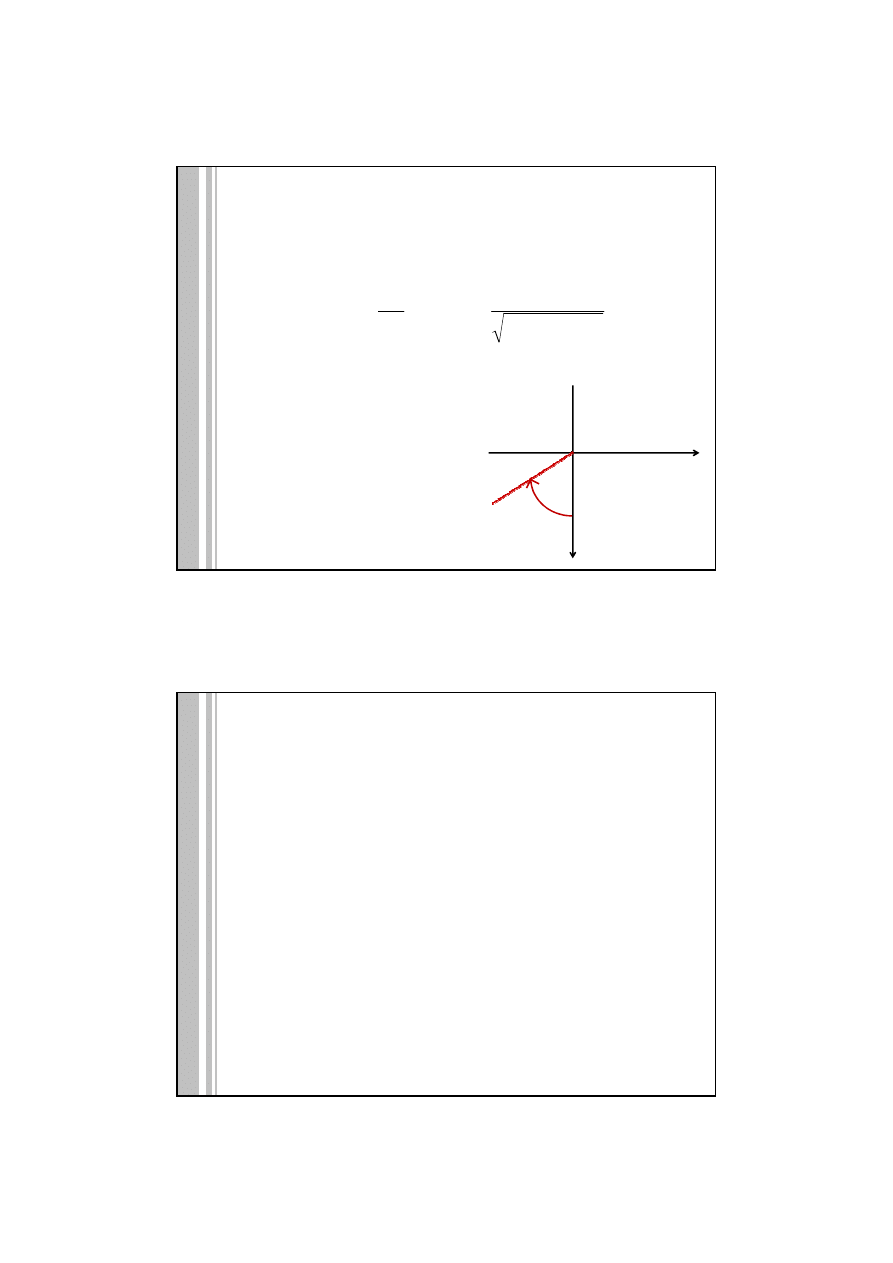
δ

X

Y

t

X>0 Y>0

X<0 Y>0

X<0 Y<0

X>0 Y<0

Układ równikowy godzinny także
jest układem kartezjańskim
prawoskrętnym.

Kat godzinny jest mierzony
zgodnie z ruchem wskazówek
zegara od osi X wskazującej
południk miejscowy, na podstawie
analizy znaku X i Y należy określić
prawidłową wielkość t.

WYZNACZENIE WSPÓŁRZĘDNYCH HORYZONTALNYCH NA

PODSTAWIE ELEMENTÓW ORBITY

9) Obliczenie topocentrycznych współrzędnych

horyzontalnych:

h

A

t

S

,

'

,

'

⇒

δ

(np. trójkąt paralaktyczny)

Należy narysować ten trójkąt i zastanowić się jak on wygląda
(czy t>12h) i w zależności od tego wyznaczyć wartość azymutu
i odległości zenitalnej (wysokości).