Mateusz

Franckowiak

Fizyka metali – laboratorium

14.06.2013

Rok 1 magisterski

Odlewnictwo 1

Wyznaczanie modułu sztywności metodą wahadła

torsyjnego

Ocena:

L 6

1. Cel ćwiczenia

Celem ćwiczenia jest zapoznanie się z metodą wyznaczenia modułu sztywności dla

metali i stopów, metodą wahadła torsyjnego.

2. Wstęp teoretyczny

Odkształcenie sprężyste - odkształcenie, które ustępuje po usunięciu siły, która je

spowodowała. Siła, która powoduje, że odkształcenie jest sprężystym nosi nazwę siły

sprężystości. Odkształcenie sprężyste metali zachodzi poprzez przemieszczanie się atomów na

odległości nie większe niż odległości sieciowe, dzięki czemu nie następują zasadnicze zmiany

w ułożeniu atomów w sieci.

Oscylator harmoniczny - model teoretyczny w naukach ścisłych opisujący układ

w parabolicznym potencjale — potencjał oscylatora harmonicznego, bądź krócej potencjał

harmoniczny, czyli kwadratowa zależność potencjału od odległości , gdzie r jest odległością

w N-wymiarowej przestrzeni, N zależy od konkretnej realizacji modelu. Ze względu na skalę

modelowanych zjawisk wyróżnia się klasyczny oscylator harmoniczny oraz kwantowy

oscylator harmoniczny.

Sprężystość – właściwość fizyczna ciał odzyskiwania pierwotnego kształtu i wymiarów

po usunięciu sił zewnętrznych wywołujących zniekształcenie – czyli zmianie tensora naprężeń

towarzyszy zmiana tensora odkształceń i odwrotnie, przy czym zmiany te są w pełni

odwracalne. Istotną cechą sprężystości jest zachowanie energii.

Ścinanie – odkształcenie ciała spowodowane naprężeniem stycznym do jego

powierzchni. W wytrzymałości materiałów, ścinanie traktuje się również jako stan obciążenia

spowodowany takimi naprężeniami. Naprężenie styczne do powierzchni ciała nazywane jest

naprężeniem ścinającym.

Ściskanie osiowe - w wytrzymałości materiałów definiujemy dwa podstawowe przypadki

ściskania osiowego:

• Ściskanie czyste pręta, w którym do ścianek poprzecznych jednorodnego

i izotropowego pręta pryzmatycznego przyłożone jest obciążenie o stałej gęstości o zwrocie

przeciwnym do wektora normalnego powierzchni ścianki poprzecznej (prostopadłym do

ścianki, skierowanym do wewnątrz). Dla tego przypadku wytrzymałościowego znane jest

rzeczywiste rozwiązanie zagadnienia brzegowego liniowej teorii sprężystości.

• Ściskanie proste pręta, które różni się od ściskania "czystego" tym, że obciążenie

zastępujemy dwójką przeciwnie skierowanych, równych co do wartości i współliniowych sił

skupionych, działających w osi tego pręta. Analityczne rozwiązanie tego przypadku jest

praktycznie niemożliwe, dlatego stosujemy zgodnie z zasadą de Saint-Venanta rozwiązanie

zagadnienia czystego ściskania przyjmując, że

gdzie A oznacza pole przekroju poprzecznego pręta.

Rozciąganie osiowe - w wytrzymałości materiałów definiujemy dwa podstawowe

przypadki rozciągania osiowego:

• Rozciąganie czyste pręta, w którym do ścianek poprzecznych jednorodnego

i izotropowego pręta pryzmatycznego przyłożone jest obciążenie o stałej gęstości o zwrocie

zgodnym z wektorem normalnym powierzchni ścianki poprzecznej (prostopadłym do ścianki,

skierowanym na zewnątrz). Dla tego przypadku wytrzymałościowego znane jest rzeczywiste

rozwiązanie zagadnienia brzegowego liniowej teorii sprężystości.

• Rozciąganie proste pręta, które różni się od rozciągania "czystego" tym, że obciążenie

zastępujemy dwójką przeciwnie skierowanych, równych co do wartości i współliniowych sił

skupionych, działających w osi tego pręta. Analityczne rozwiązanie tego przypadku jest

praktycznie niemożliwe, dlatego stosujemy zgodnie z zasadą de Saint-Venanta rozwiązanie

zagadnienia czystego rozciągania przyjmując, że

gdzie A oznacza pole przekroju poprzecznego pręta.

Prawo Hooke’a – prawo mechaniki określające zależność odkształcenia od naprężenia.

Głosi ono, że odkształcenie ciała pod wpływem działającej na nie siły jest wprost

proporcjonalne do tej siły. Współczynnik między siłą a odkształceniem jest często nazywany

współczynnikiem (modułem) sprężystości.

Najprostszym przykładem zastosowania prawa Hooke’a jest rozciąganie statyczne pręta.

Bezwzględne wydłużenie takiego pręta jest wprost proporcjonalne do siły przyłożonej do pręta,

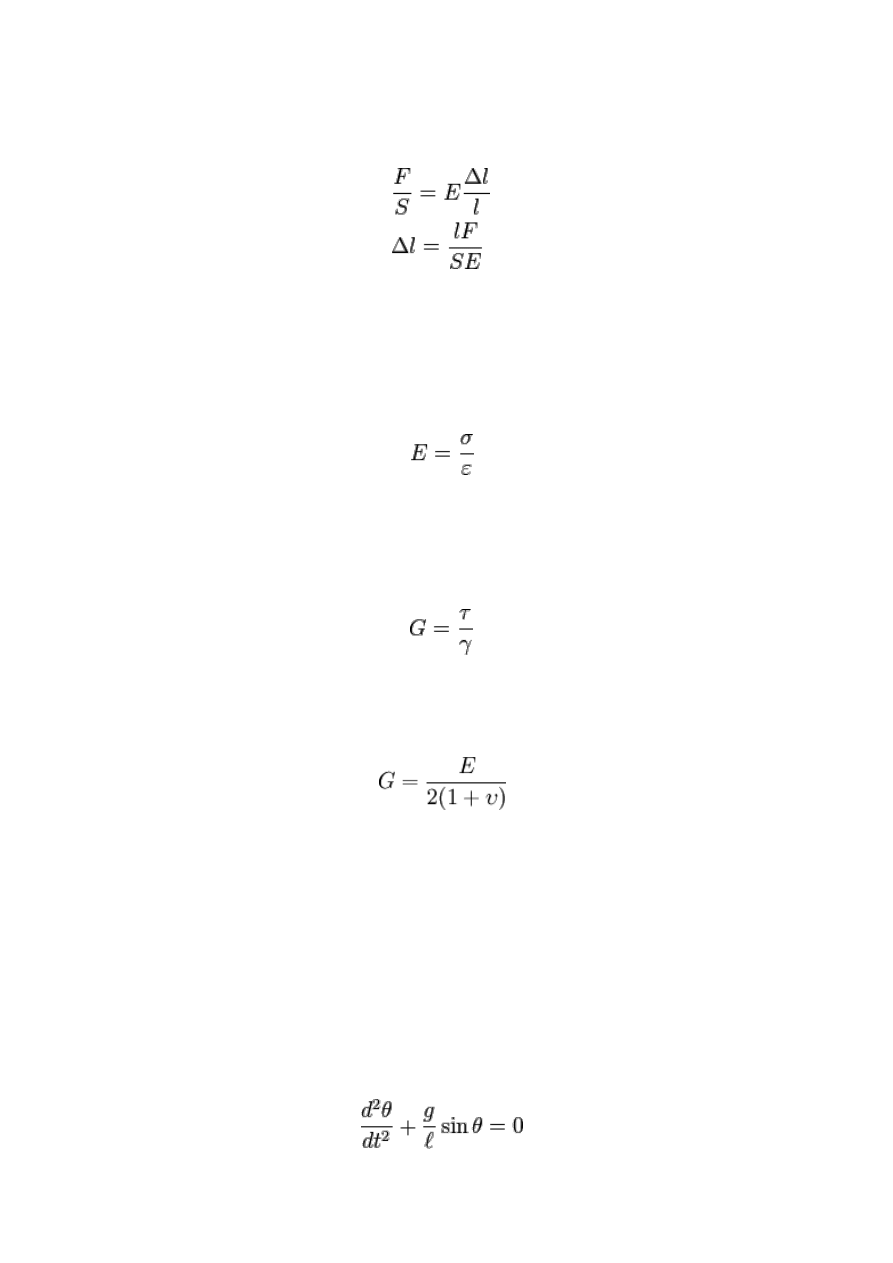
do jego długości i odwrotnie proporcjonalne do pola przekroju poprzecznego pręta.

Współczynnikiem proporcjonalności jest moduł Younga E.

gdzie:

F – siła rozciągająca, S – pole przekroju, Δl – wydłużenie pręta, l – długość początkowa.

Moduł Younga - wielkość określająca sprężystość materiału. Wyraża ona,

charakterystyczną dla danego materiału, zależność względnego odkształcenia liniowego ε

materiału od naprężenia σ, jakie w nim występuje w zakresie odkształceń sprężystych.

Jednostką modułu Younga jest paskal, czyli N/m².

Moduł Kirchhoffa - współczynnik uzależniający odkształcenie postaciowe materiału od

naprężenia, jakie w nim występuje. Jednostką modułu Kirchhoffa jest paskal. Jest to wielkość

określająca sprężystość materiału.

gdzie τ - naprężenia ścinające, γ - odkształcenie postaciowe

Moduł Kirchhoffa dla materiałów izotropowych bezpośrednio zależy od modułu Younga

i współczynnika Poissona:

gdzie υ - współczynnik Poissona, E - moduł Younga

Wahadło – ciało zawieszone lub zamocowane ponad swoim środkiem ciężkości

wykonujące w pionowej płaszczyźnie drgania pod wpływem siły grawitacji. W teorii

mechaniki rozróżnia się dwa podstawowe rodzaje wahadeł:

• matematyczne

• fizyczne

W wahadle matematycznym poruszające się ciało jest punktem materialnym,

zawieszonym na nieważkiej, nierozciągliwej nici o długościl. Ruch ciała ograniczony nicią jest

ruchem po okręgu. Równanie ruchu wahadła określa wzór:

Wahadło fizyczne

Bryła sztywna, która może wykonywać obroty dookoła poziomej osi przechodzącej

ponad środkiem ciężkości tej bryły.

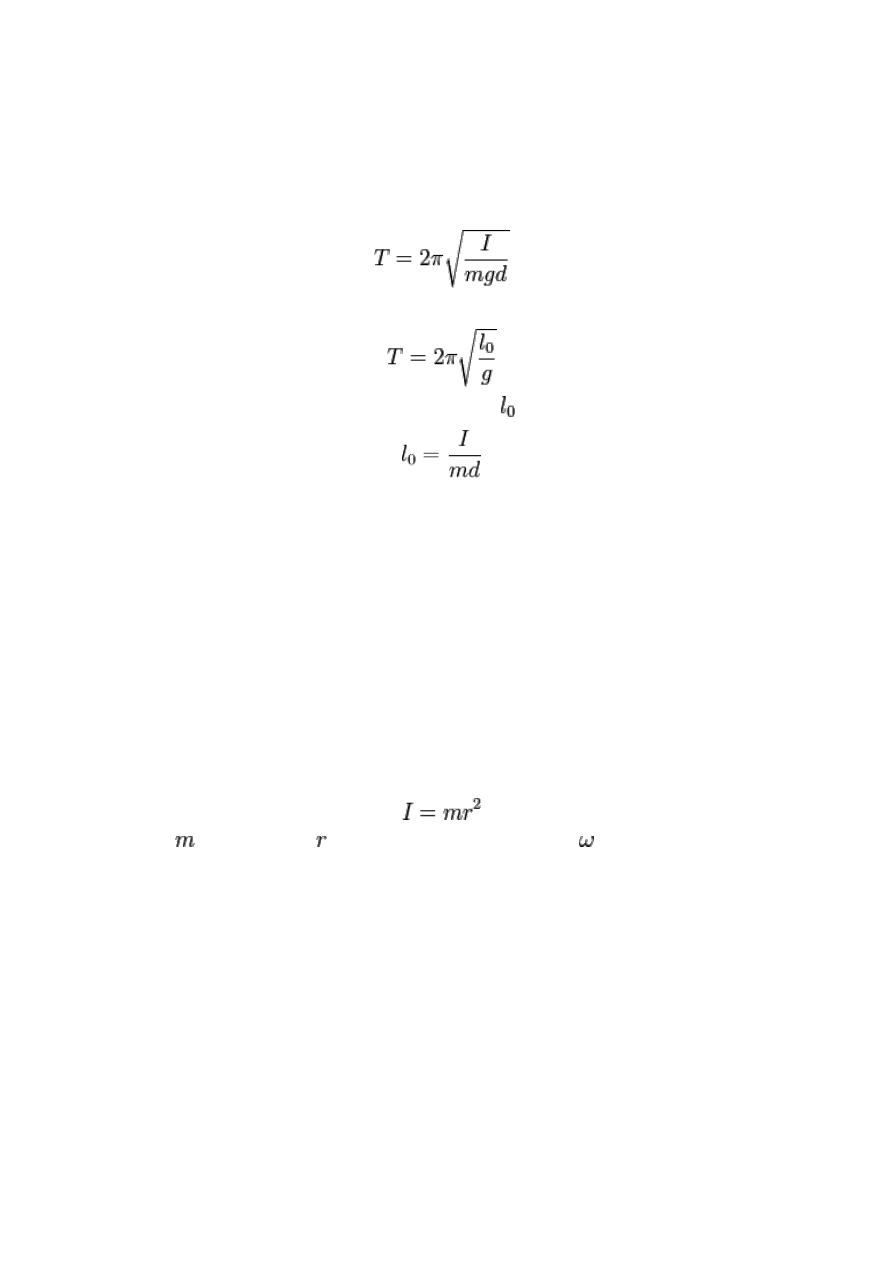
Wzór na okres drgań wahadła fizycznego dla małych wychyleń:

Przez analogię do wahadła matematycznego wzór ten zapisuje się jako:

wprowadzając wielkość długość zredukowana wahadła

gdzie:

d - odległość od punktu zawieszenia do środka ciężkości, g - przyspieszenie ziemskie, I -

moment bezwładności ciała względem osi obrotu, m - masa ciała.

Moment bezwładności – miara bezwładności ciała w ruchu obrotowym względem

określonej, ustalonej osi obrotu. Im większy moment, tym trudniej zmienić ruch obrotowy

ciała, np. rozkręcić dane ciało lub zmniejszyć jego prędkość kątową. Moment bezwładności

odgrywa prawie taką samą rolę w dynamice ruchu obrotowego jak masa w dynamice ruchu

postępowego, opisując relacje między momentem pędu, energią kinetyczną a prędkością

kątową jak masa między pędem, energią kinetyczną a prędkością. Moment bezwładności

zależy od osi obrotu ciała, a w ogólnym przypadku jest tensorem.

gdzie:

– masa punktu, – odległość punktu od osi obrotu, - prędkość kątowa.

3. Przebieg ćwiczenia

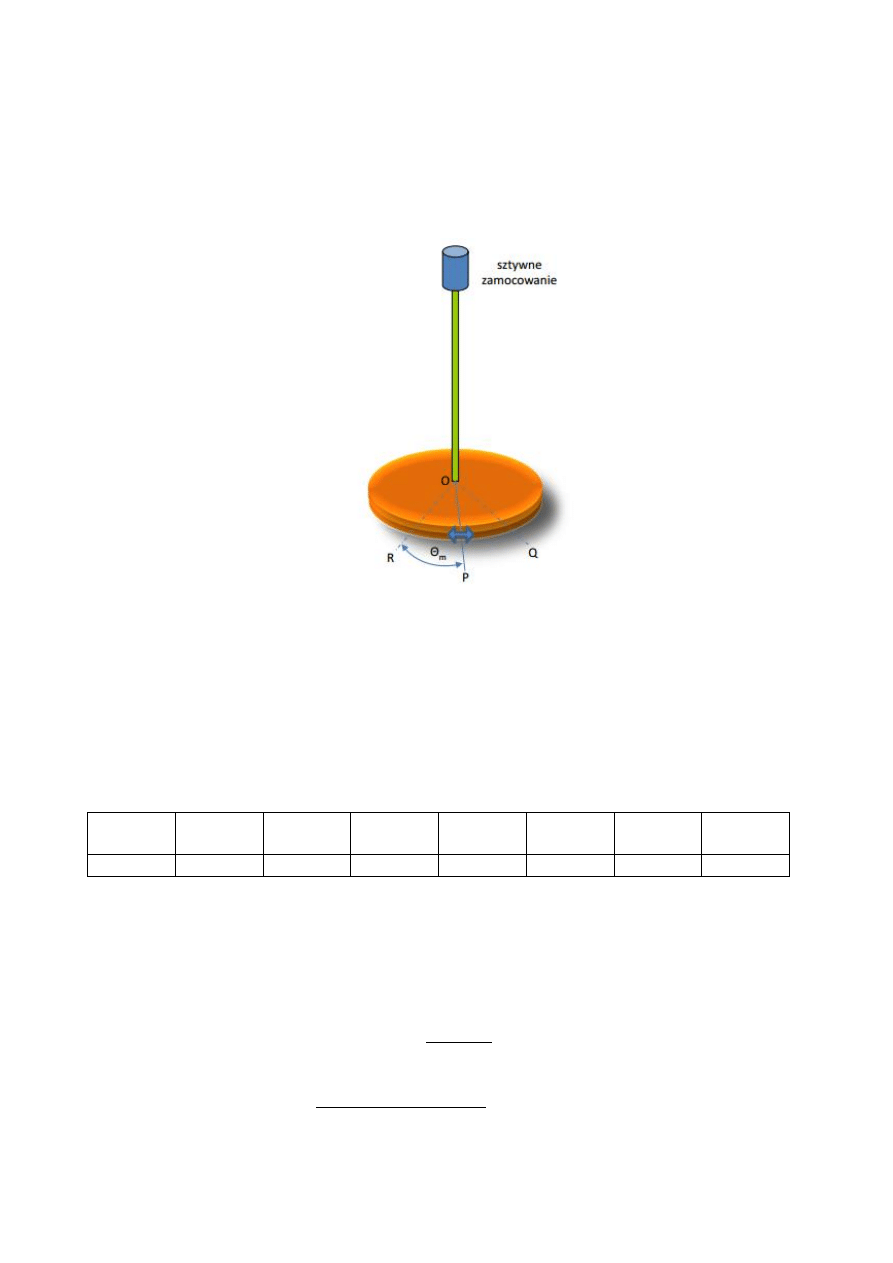
Podczas zajęć laboratoryjnych, wyznaczenie modułu sztywności przeprowadzono za

pomocą wahadła torsyjnego (rys.1.)

Rys.1. Wahadło torsyjne

Badaniu poddano próbkę pręt stalowy i przeprowadzono je zgodnie z wytycznymi

zawartymi w instrukcji do przeprowadzenia laboratorium. Uzyskane wartości umieszczono
w tabeli 1.

Tabela 1.

Badany

materiał

m [kg]

R [m]

r [m]

L [m]

t [s]

N [cykl]

T

n

[s/cykl]

stal

2,1

0,13

0,001

0,85

300

160

1,875

gdzie: t – czas drgań wahadła, N – liczba cykli, m – masa wahadła, R – promień krążka, L –
długość pręta, r – promień pręta.

Moduł sztywności wyliczono ze wzoru:

4. Wnioski

Na podstawie przeprowadzonych badań można sformułować następujące wnioski:

1. Przy użyciu wahadła torsyjnego możliwe jest w prosty sposób określenie modułu

sztywności badanego stopu.

2. Wadą tej metody jest ograniczenie co do wielkości badanej próbki (dla odlewu potrzeba

by próbki o długości kilku pięter, aby ramię, a tym samym i moment siły pozostał stały

mimo skręcania się dolnego końca pręta).