Edukacja 2013, 1(121), 73-88

ISSN 0239-6858

Pomiar kompetencji nauczycieli matematyki

Monika Czajkowska*

W ostatnich latach w wielu krajach, również Polsce, w centrum uwagi znalazło się kształcenie przyszłych

kadr nauczycielskich i kompetencje czynnych nauczycieli zajmujących się edukacją matematyczną. Zaczęto

prowadzić badania, których celem było m.in. określenie związku między kompetencjami nauczyciela a wie-

dzą i umiejętnościami uczniów. Niniejszy artykuł stanowi przegląd badań w tym zakresie, prowadzonych

w różnych krajach europejskich.
Słowa kluczowe: nauczyciel matematyki, kompetencje nauczyciela

Artykuł powstał w wyniku kwerendy bibliotecznej

przeprowadzonej przed rozpoczęciem Badania potrzeb

nauczycieli edukacji wczesnoszkolnej i matematyki w za-

kresie rozwoju zawodowego prowadzonego w Instytucie

Badań Edukacyjnych. Badanie jest finansowane ze środ-

ków Europejskiego Funduszu Społecznego w ramach

Programu Operacyjnego Kapitał Ludzki, Piorytet III:

Wysoka jakość systemu oświaty, Poddziałanie 3.1.1 Two-

rzenie warunków i narzędzi do monitorowania, ewalua-

cji i badań systemu oświaty
* Pracowania Matematyki Instytutu Badań Edukacyj-

nych. E-mail: [e-mail]

Kompetencje nauczycieli

a jakość nauczania

N

a efektywność nauczania ma wpływ

wiele czynników. Do najważniejszych

należą: motywacja uczniów do uczenia się,

szeroko rozumiana organizacja procesu

nauczania – uczenia się, postawy rodziców,

kompetencje nauczyciela. W  ciągu ostat-

nich lat zaczęto poszukiwać odpowiedzi na

pytania, jakie kompetencje powinien mieć

nauczyciel zajmujący się edukacją matema-

tyczną, czy istnieje związek między kom-

petencjami nauczyciela a umiejętnościami

uczniów, jakie kompetencje nauczycie-

la mają wpływ na umiejętności uczniów

i  w jaki sposób mierzyć kompetencje na-

uczycieli (Ball, Thames i  Phelps, 2008;

Baumert i  in., 2010; Davis, 2011; Hill,

Schilling i  Ball, 2004; Kersting, 2008;

Krauss i in., 2008; Niss, 2004). Wśród ba-

daczy tego tematu nie ma zgodności co do

tego, które kompetencje nauczyciela mają

największy wpływ na jakość jego pracy.

Zdaniem Deborah Loewenberg Ball (2008)

i  współpracowników wiedza merytorycz-

na nauczyciela z  przedmiotu, którego na-

ucza, w  szczególności z  matematyki, jest

warunkiem koniecznym i  fundamentem

skutecznego nauczania. Nie jest bowiem

możliwe, aby nauczyciel, który sam nie po-

siada wiedzy i umiejętności z nauczanego

przedmiotu, mógł pomóc uczniom w  ich

opanowaniu. Mierzenie kompetencji mate-

matycznych jest możliwe za pomocą obser-

wacji, rozmów, tekstów kompetencyjnych

w powiązaniu z analizą programów kształ-

cenia nauczycieli. Pytania testowe powin-

ny być tak skonstruowane, aby sprawdzały

specjalistyczną wiedzę nauczycieli, a  nie

tylko znajomość szkolnej matematyki,

którą powinien posiadać każdy absolwent

szkoły średniej. W przykładzie 1 zamiesz-

Czajkowska

74

czono przykłady pytań, zaczerpniętych

z jej artykułu (Ball i  in., 2008), które nie

badają tej unikalnej wiedzy, ponieważ

może na nie odpowiedzieć każdy, kto zna

matematykę.

Przykład 1

a) Jaka liczba jest większa od 1,1 i mniejsza

od 1,11?

b) Czy każdy kwadrat jest prostokątem?

c) Czy prawdą jest, że 0 : 7 = 0?

d) Pani Dominguez pracowała z  nowym

podręcznikiem i  zauważyła, że poświę-

cono w  nim więcej uwagi liczbie 0, niż

w  podręcznikach, z  którymi wcześniej

pracowała. Znalazła stronę, na której

proszono uczniów o stwierdzenie, które

z poniższych zdań są prawdziwe, a które

fałszywe. Które zdania są prawdziwe?

Zdanie

Tak

Nie

0 jest liczbą parzystą.





0 nie jest liczbą. Jest to znak

pozwalający zapisywać duże

liczby.





Liczba 8 może być zapisana

w postaci 008.





Pytania w podpunktach a, b i c są sformu-

łowane w  takiej samej konwencji jak pyta-

nia do uczniów. Mogłyby zostać użyte do

sprawdzania ich wiedzy. Nie wystarczy jed-

nak osadzenie pytań w szkolnym kontekście

(podpunkt d). Jeżeli zadanie, w którym nale-

ży ocenić prawdziwość zdań pochodzi z pod-

ręcznika szkolnego, to nie może sprawdzać

specjalistycznej wiedzy nauczycielskiej. Aby

odpowiedzieć na powyższe pytania, nie jest

potrzebna wiedza i  umiejętności z  zakresu

metodyki nauczania matematyki, czy spoj-

rzenie na matematykę szkolną z punktu wi-

dzenia matematyki wyższej.

Jednym z najważniejszych ustaleń badań ja-

kościowych dotyczących kompetencji nauczy-

cieli matematyki jest to, że repertuar zabiegów

dydaktycznych i sposobów wyjaśniania kon-

kretnych treści matematycznych w  dużym

stopniu zależy od tego, jak głęboko i szeroko

zna je i rozumie sam nauczyciel. Ball (1990)

wykazała tę zależność dla mnożenia, zespół

Hildy Borko (1992) i Martin A. Simon (1993)

dla dzielenia, Ruhama Even (1993), Mary Kay

Stein i współpracownicy (Stein, Baxter i Le-

inhardt, 1990) dla funkcji, a  Ralph Putnam

i inni (Putnam, Heaton, Prawat i Remillard,

1992) dla treści geometrycznych. Badania

prowadzone w tym zakresie ujawniły, że defi-

cyt kompetencji matematycznych nauczyciela

nie może być rekompensowany przez umie-

jętności dydaktyczne i pedagogiczne.

Z drugiej strony same tylko kompetencje

matematyczne nie są warunkiem dostatecz-

nym efektywnego nauczania. Co więcej, co-

raz częściej pojawiają się pytania, jak głęboko

i  jak szeroko nauczyciel powinien znać za-

gadnienia z  matematyki wyższej. Naukowcy

zajmujący się tym problemem nie są zgodni,

w jakim stopniu wiedza matematyczna zdo-

byta na studiach, czy znajomość najnowszych

wyników badań w  zakresie czystej matema-

tyki, jest użyteczna dla nauczycieli szkół pod-

stawowych i  średnich (Baumert i  in., 2010).

Brent Davis (2011) w przeciwieństwie do Ball

twierdzi, że największy wpływ na jakość na-

uczania mają predyspozycje do wykonywania

zawodu nauczyciela matematyki i  talent pe-

dagogiczny, a także kompetencje dydaktycz-

ne. Do nich zalicza takie umiejętności, jak:

stosowanie analogii, metafor, poszukiwanie

praktycznych zastosowań, konkretyzowanie

pojęć i  twierdzeń, tworzenie obrazów pojęć

matematycznych. Efektywne nauczanie ma-

tematyki wymaga bowiem od nauczyciela

umiejętnego przedstawiania treści matema-

tycznych, posługiwania się językiem (mówio-

nym, symbolicznym, graficznym) dostosowa-

nym do poziomu rozwojowego i możliwości

uczniów, doboru właściwych przykładów

ukazujących praktyczne wykorzystanie ma-

Pomiar kompetencji nauczycieli matematyki

75

tematyki w rozwiązywaniu problemów życia

codziennego. Istotne jest tu też dostrzeganie

przez nauczyciela powiązań między treściami

(struktury treści matematycznych), właściwe

organizowanie pracy uczniów tak, aby byli oni

zaangażowani intelektualnie i  emocjonalnie

w proces poznawczy, modyfikowanie i dosto-

sowywanie zadań (łatwiejsze, trudniejsze) do

możliwości uczących się, właściwe reagowanie

na pytania i wątpliwości uczniów, rozumienie

toku ich myślenia (często odbiegającego od

toku myślenia nauczyciela), a  także szybka

ocena ich wypowiedzi, krytyczna ocena pod-

ręczników i  innych pomocy dydaktycznych.

Tę specjalistyczną wiedzę, z której nauczyciele

korzystają, ale która nie zawsze jest dostępna

ich świadomości, nazywa wiedzą ukrytą (tacit

knowledge).

Dotychczas uwaga polskich naukowców

zajmujących się problemem kompetencji

nauczycieli była skoncentrowana prze-

de wszystkim na klasyfikacji kompetencji

nauczycieli lub badaniu kompetencji na-

uczycielskich niezwiązanych bezpośrednio

z matematyką. Na przykład Hanna Hamer

(1994) wyróżnia kompetencje specjalistycz-

ne, dydaktyczne, psychologiczne; Stefan

Dylak (1995) wymienia kompetencje ba-

zowe, konieczne, pożądane; Wacław Stry-

kowski (2003) pisze o  kompetencjach me-

rytorycznych, dydaktyczno-metodycznych

i wychowawczych; Robert Kwaśnica (2003)

wyodrębnia dwie grupy kompetencji: prak-

tyczno-moralne (interpretacyjne, moralne

i komunikacyjne) i techniczne (postulacyj-

ne, metodyczne i realizacyjne). Na posiedze-

niu Komitetu Nauk Pedagogicznych PAN

w dniu 13 listopada 1997 roku, poświęcone-

mu wymaganiom w zakresie wykształcenia

zawodowego nauczycieli, wydzielono kom-

petencje: prakseologiczne, komunikacyjne,

współdziałania, kreatywne, informatyczne,

moralne; Zespół Przygotowania Pedago-

gicznego Nauczycieli przy Radzie ds. Kształ-

cenia Nauczycieli w  MEN (na podstawie:

Szempruch, 2000) podzielił kompetencje

nauczycielskie na interpretacyjno-komuni-

kacyjne, kreatywne, współdziałania, prag-

matyczne i informatyczno-medialne.

Chociaż badania umiejętności nauczyciel-

skich są skupione wokół innych kompe-

tencji niż merytoryczne i  dydaktyczne, to

w licznych artykułach autorzy badań pod-

kreślają wagę tych kompetencji w kształce-

niu przedmiotowym.

Kształcenie przyszłych nauczycieli

– przygotowanie do zawodu

Różnice w kształceniu nauczycieli w różnych

państwach wynikają m.in. z  uwarunkowań

historyczno-społeczno-gospodarczych, syste-

mu szkolnictwa, odmiennych systemów edu-

kacyjnych, sposobu finansowania edukacji,

a także prestiżu zawodu nauczyciela w społe-

czeństwie. Uprawnienia do nauczania można

uzyskać w uniwersytetach, kolegiach nauczy-

cielskich lub specjalnych instytucjach. W nie-

których państwach przyszli nauczyciele szkół

podstawowych przygotowywani są do na-

uczania wszystkich przedmiotów. W  innych

tylko w klasach początkowych (1–3 lub 1–4)

wszystkie lub prawie wszystkie przedmioty są

nauczane przez jednego nauczyciela, a w kla-

sach wyższych szkoły podstawowej i w szko-

łach średnich każdy przedmiot jest prowa-

dzony przez specjalistę. W niektórych krajach

obowiązuje zasada specjalizacji nauczyciel-

skiej w zakresie dwóch lub trzech przedmio-

tów. Przyszli nauczyciele muszą odbywać

praktyki, lecz czas ich trwania i organizacja są

różne. Studenci, aby uzyskać uprawnienia do

nauczania, muszą zdać egzaminy praktyczne

lub teoretyczne. Mogą być one wewnętrzne

lub zewnętrzne, przeprowadzane przez nieza-

leżne instytucje. Na przykład na Tajwanie, aby

uzyskać uprawnienia do nauczania, należy

zdać egzamin państwowy (Teacher Qualifi-

cation Assessment). Składa się on z zagadnień

kontrolujących kompetencje merytoryczne

Czajkowska

76

z zakresu specjalności wybranej przez kandy-

data na nauczyciela i  zagadnień sprawdzają-

cych jego kompetencje pedagogiczne i dydak-

tyczne (Tatto i in., 2012).

Różne rodzaje systemów i programów kształ-

cenia nauczycieli mogą być powodem różnic

w kompetencjach dydaktycznych i matema-

tycznych nauczycieli matematyki. Pierwszym

międzynarodowym badaniem, którego ce-

lem było porównanie kompetencji studentów

będących u progu wejścia do zawodu nauczy-

ciela było Badanie kształcenia i doskonalenia

zawodowego nauczycieli – Matematyka 2008

(Teacher Education and Development Sur-

vey – Mathematics 2008, w skrócie TEDS-M

2008) (Tatto i  in., 2012). Zostało ono prze-

prowadzone z inicjatywy Międzynarodowe-

go Stowarzyszenia na rzecz Badań Osiągnięć

Edukacyjnych (International Association for

the Evaluation of Educational Achievement,

IEA) i  zrealizowane przez Michigan State

University (Stany Zjednoczone), Australian

Council for Educational Research (Australia)

oraz Data Processing Center (DPC) (Niem-

cy). W Polsce za jego realizację odpowiadał

Instytut Filozofii i Socjologii PAN (Sitek i in.,

2010). Badaniem zostało objętych 21 185

studentów ostatniego roku studiów

1

uczelni

i innych instytucji przygotowujących do pra-

cy w  zawodzie nauczyciela edukacji wczes-

noszkolnej lub matematyki z  17 państw:

Botswany, Chile, Filipin, Gruzji, Hiszpanii,

Kanady

2

, Malezji, Niemiec, Norwegii, Oma-

nu, Polski, Rosji, Singapuru, Stanów Zjedno-

czonych, Szwajcarii, Tajlandii i Tajwanu.

1

Badaniem zostali objęci studenci również tych pro-

gramów studiów, na które nabór nie był już prowadzony.

Dlatego w Polsce w badaniu uczestniczyli studenci III roku

studiów pierwszego stopnia, II roku studiów drugiego stop-

nia oraz V roku „wygasających” studiów jednolitych magi-

sterskich. Jednak ze względu na fakt, że studenci studiów

drugiego stopnia posiadają już kwalifikacje pedagogiczne,

zostali oni wykluczeni z analiz międzynarodowych.

2

Kanada nie jest uwzględniana w niektórych raportach,

ponieważ w badaniu wzięli udział studenci tylko z czte-

rech prowincji.

Badanie objęło bardzo zróżnicowane syste-

my edukacyjne i  zróżnicowane programy

kształcenia nauczycieli. Aby ułatwić po-

równania międzynarodowe, poszczególne

programy występujące w  krajach uczest-

niczących w  badaniu podzielono na sześć

grup. Podstawowym kryterium selekcji

był etap, na którym miał nauczać przy-

szły nauczyciel oraz to, czy będzie on uczył

kilku przedmiotów, czy też będzie jedynie

specjalistą z  matematyki. Polscy studenci

znaleźli się w czerech grupach (Sitek i in.,

2010; Tatto i in., 2012). Podstawowym na-

rzędziem badawczym były dwa testy kom-

petencyjne (Sitek i in., 2010; Tatto in., 2008;

2012). Jeden z nich rozwiązywali studenci

– przyszli nauczyciele szkół podstawo-

wych, drugi – przyszli nauczyciele szkół

średnich. Każdy z  zeszytów testowych

zawierał około 25 wiązek zadań mierzą-

cych umiejętności z  zakresu matematyki

i dydaktyki matematyki. Zadania mierzą-

ce kompetencje matematyczne studenta

zostały scharakteryzowane w  trzech ob-

szarach: treści matematycznych (algebra,

geometria, nauka o  liczbie, podstawy ra-

chunku prawdopodobieństwa i statystyki),

kompetencji matematycznych (posiadanie

wiedzy, stosowanie wiedzy, rozumowanie)

i stopnia trudności zadania (niski, średni,

wysoki). Zadania mierzące wiedzę i umie-

jętności z  zakresu dydaktyki matematyki

uporządkowano pod względem kompeten-

cji dydaktycznych (znajomość powiązań

treści programowych, planowanie naucza-

nia, przekazywanie wiedzy i odbieranie jej

od uczniów) oraz stopnia trudności (niski,

średni, wysoki).

Poniżej zamieszczono przykłady zadań

badających kompetencje studentów wraz

z kluczem kodowym zadań otwartych. Za-

dania w Przykładzie 2 pochodzą z testu dla

przyszłych nauczycieli szkół podstawowych,

w Przykładzie 3 – dla przyszłych nauczycieli

szkół średnich.

Pomiar kompetencji nauczycieli matematyki

77

Przykład 2

Jarek zauważył, że kiedy wykonuje na kal-

kulatorze działanie 0,2 · 6, otrzymuje wynik

mniejszy niż 6, a kiedy wykonuje działanie

6 : 0,2, otrzymuje liczbę większą niż 6. Jest

tym zdezorientowany i  prosi nauczyciela

o nowy kalkulator!

a) Jakim błędnym przekonaniem najpraw-

dopodobniej kieruje się Jarek?

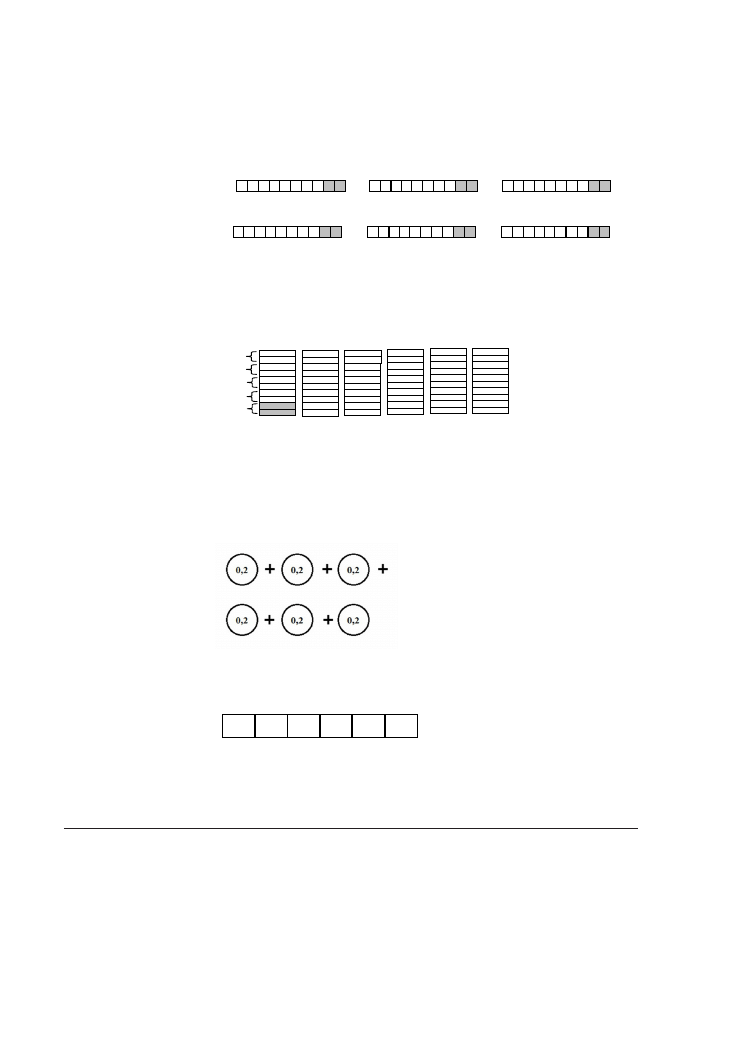
b) Sporządź rysunek obrazujący działanie

0,2 ∙ 6 w taki sposób, by pomógł on Jar-

kowi zrozumieć, dlaczego wynik tego

działania jest właśnie taki, jaki otrzymał.

Tabela 1

Klucz odpowiedzi do przykładu 2

Część a

Poprawność odpowiedzi
Poprawna

Odpowiedzi, które sugerują, że uczeń sądzi, że iloczyn jest zawsze większy

od każdego czynnika oraz że iloraz jest zawsze mniejszy od dzielnej, np.:

Myśli, że przy mnożeniu wynik powinien być większy, a jak się dzieli wynik

powinien być mniejszy.

Częściowo poprawna

Odpowiedzi, które sugerują, że uczeń sądzi, że iloczyn jest zawsze większy

od każdego czynnika albo że iloraz jest zawsze mniejszy od dzielnej, np.:

• Myśli, że przy mnożeniu wynik powinien być większy niż każda z liczb.

• Myśli, że wynik dzielenia powinien być mniejszy niż dzielna.
Odpowiedzi, które sugerują, że Jarek traktuje 0,2 jako liczbę naturalną.

• Myśli, że mnoży i dzieli przez 2, a nie przez 0,2.

Niepoprawna

Odpowiedzi związane ze zrozumieniem liczb dziesiętnych, mnożeniem

i dzieleniem przez liczby dziesiętne lub użyciem kalkulatora.

• On nie rozumie mnożenia (lub dzielenia) przez liczby dziesiętne.

• On nie rozumie, jak używa się kalkulatora.

Część b

Poprawność odpowiedzi
Poprawna

Odpowiedni rysunek, który przejrzyście przedstawia, w jaki sposób

0,2 ∙ 6 daje wynik 1,2; np.:

7

Poprawna

Odpowiedni rysunek, który przejrzyście przedstawia, w jaki sposób 0,2 ∙ 6 daje wynik

1,2; np.:

Częściowo

poprawna

Rysunek, który przedstawia 6 części po 0,2, ale nie wyjaśnia dlaczego 0,2 ∙ 6 daje

wynik 1,2:

Rysunek, który przedstawia, jak 5 części po 0,2 tworzą całość, nie wyjaśnia, w jaki

sposób 6 części po 0,2 równa się 1,2:

Graficzne przedstawienie równości 0,2 ∙ 6 = 1,2 bez wyjaśnienia, dlaczego ona

zachodzi:

0,2

0

0,2

1

1,2

0,2

0,2

0,2

0,4

0,2

0,6

0,2

0,8

0,2

0,2

0,2

0,2

0,2

0,2

W jednej całości mamy pięć części 0,2.

0,2

0,2

0,2

0,2

0,2

0,2

0,2

5 części 0,2 daje 1

+

więc 6 części 0,2 daje 1,2

0,2

0,2

0,2

5 ∙ 0,2 = 1

0,2

0,2

0,2

Czajkowska

78

Częściowo poprawna

Rysunek, który przedstawia 6 części po 0,2, ale nie wyjaśnia dlaczego 0,2 ∙

6 daje wynik 1,2:

Rysunek, który przedstawia, jak 5 części po 0,2 tworzą całość, ale nie

wyjaśnia, w jaki sposób 6 części po 0,2 równa się 1,2:

Graficzne przedstawienie równości 0,2 ∙ 6 = 1,2 bez wyjaśnienia, dlaczego

ona zachodzi:

Niepoprawna

Graficzne przedstawienie 6 części po 0,2 bez wyjaśnień:

Przykład słowny, sugerujący liczenie części po 0,2, np.: „Policz 6 części po

0,2 w następujący sposób: 0,2, 0,4, 0,6, 0,8, 1,0, 1,2.”

*

Źródło: opracowanie własne na podstawie: Teacher Education Study in Mathematics (TEDS-M) 2008. Released items

future teacher Mathematics Content Knowledge (MCK) and Mathematics Pedagogical Content Knowledge (MPCK)

– Primary 2009.
* Autorzy testu w uwagach podają, że sam sposób wyjaśnienia jest dobry, ale niezgodny z poleceniem w zadaniu

„Sporządź rysunek”.

7

Poprawna

Odpowiedni rysunek, który przejrzyście przedstawia, w jaki sposób 0,2 ∙ 6 daje wynik

1,2; np.:

Częściowo

poprawna

Rysunek, który przedstawia 6 części po 0,2, ale nie wyjaśnia dlaczego 0,2 ∙ 6 daje

wynik 1,2:

Rysunek, który przedstawia, jak 5 części po 0,2 tworzą całość, nie wyjaśnia, w jaki

sposób 6 części po 0,2 równa się 1,2:

Graficzne przedstawienie równości 0,2 ∙ 6 = 1,2 bez wyjaśnienia, dlaczego ona

zachodzi:

0,2

0

0,2

1

1,2

0,2

0,2

0,2

0,4

0,2

0,6

0,2

0,8

0,2

0,2

0,2

0,2

0,2

0,2

W jednej całości mamy pięć części 0,2.

0,2

0,2

0,2

0,2

0,2

0,2

0,2

5 części 0,2 daje 1

+

więc 6 części 0,2 daje 1,2

0,2

0,2

0,2

5 ∙ 0,2 = 1

0,2

0,2

0,2

7

Poprawna

Odpowiedni rysunek, który przejrzyście przedstawia, w jaki sposób 0,2 ∙ 6 daje wynik

1,2; np.:

Częściowo

poprawna

Rysunek, który przedstawia 6 części po 0,2, ale nie wyjaśnia dlaczego 0,2 ∙ 6 daje

wynik 1,2:

Rysunek, który przedstawia, jak 5 części po 0,2 tworzą całość, nie wyjaśnia, w jaki

sposób 6 części po 0,2 równa się 1,2:

Graficzne przedstawienie równości 0,2 ∙ 6 = 1,2 bez wyjaśnienia, dlaczego ona

zachodzi:

0,2

0

0,2

1

1,2

0,2

0,2

0,2

0,4

0,2

0,6

0,2

0,8

0,2

0,2

0,2

0,2

0,2

0,2

W jednej całości mamy pięć części 0,2.

0,2

0,2

0,2

0,2

0,2

0,2

0,2

5 części 0,2 daje 1

+

więc 6 części 0,2 daje 1,2

0,2

0,2

0,2

5 ∙ 0,2 = 1

0,2

0,2

0,2

8

Źródło: Opracowanie własne na podstawie: Teacher Education Study in Mathematics (TEDS-M) 2008. Released

items future teacher Mathematics Content Knowledge (MCK) and Mathematics Pedagogical Content

Knowledge (MPCK) – Primary 2009.

*

Autorzy testu w uwagach podają, że sam sposób wyjaśnienia jest dobry, ale niezgodny z poleceniem w

zadaniu „Sporządź rysunek”.

Przykład 3
Masz udowodnić następujące twierdzenie:
Jeśli kwadrat dowolnej liczby naturalnej podzielimy przez 3, wtedy resztą może być tylko 0 lub 1.
Dla każdego z poniższych rozumowań ustal, czy opisuje matematycznie poprawny dowód.

Wariant

rozwiązania

Uzasadnienie podane przez ucznia

Zaznacz jedną

odpowiedź w

każdym wierszu

Tak

Nie

A.

Używam następującej tabeli:

n

1 2 3

4

5

6

7

8

9

10

n

2

1 4 9 16 25 36 49 64 81 100

Reszta przy

dzieleniu przez 3

1 1 0

1

1

0

1

1

0

1

�

�

B.

Pokazuję, że (3n)

2

jest podzielne przez 3 i dla wszystkich innych liczb,

(3n ±1)

2

= 9n

2

± 6n + 1, co zawsze daje resztę 1 po podzieleniu przez 3.

�

�

C.

Wybieram liczbę naturalną n, znajduję jej kwadrat n

2

, a następnie

sprawdzam, czy twierdzenie jest prawdziwe, czy nie.

�

�

D.

Sprawdzam twierdzenie dla kilku początkowych liczb pierwszych, a

następnie wyciągam wniosek oparty na podstawowym twierdzeniu

arytmetyki.

�

�

Źródło: Opracowanie własne na podstawie Teacher Education Study in Mathematics (TEDS-M) 2008. Released

items future teacher Mathematics Content Knowledge (MCK) and Mathematics Pedagogical Content

Knowledge (MPCK) – Secondary 2009.

Wyniki testu skalibrowano, wykorzystując metodę Item Response Theory (IRT), tak aby
średnia była równa 500 punktów i odpowiadała średniej wszystkich krajów, które spełniły

Niepoprawna

Graficzne przedstawienie 6 części po 0,2 bez wyjaśnień:

Przykład słowny, sugerujący liczenie części po 0,2, np.: „Policz 6 części po 0,2 w

następujący sposób: 0,2, 0,4, 0,6, 0,8, 1,0, 1,2.”

*

0,2

0,2

0,2

0,2

0,2

0,2

8

Źródło: Opracowanie własne na podstawie: Teacher Education Study in Mathematics (TEDS-M) 2008. Released

items future teacher Mathematics Content Knowledge (MCK) and Mathematics Pedagogical Content

Knowledge (MPCK) – Primary 2009.

*

Autorzy testu w uwagach podają, że sam sposób wyjaśnienia jest dobry, ale niezgodny z poleceniem w

zadaniu „Sporządź rysunek”.

Przykład 3
Masz udowodnić następujące twierdzenie:
Jeśli kwadrat dowolnej liczby naturalnej podzielimy przez 3, wtedy resztą może być tylko 0 lub 1.
Dla każdego z poniższych rozumowań ustal, czy opisuje matematycznie poprawny dowód.

Wariant

rozwiązania

Uzasadnienie podane przez ucznia

Zaznacz jedną

odpowiedź w

każdym wierszu

Tak

Nie

A.

Używam następującej tabeli:

n

1 2 3

4

5

6

7

8

9

10

n

2

1 4 9 16 25 36 49 64 81 100

Reszta przy

dzieleniu przez 3

1 1 0

1

1

0

1

1

0

1

�

�

B.

Pokazuję, że (3n)

2

jest podzielne przez 3 i dla wszystkich innych liczb,

(3n ±1)

2

= 9n

2

± 6n + 1, co zawsze daje resztę 1 po podzieleniu przez 3.

�

�

C.

Wybieram liczbę naturalną n, znajduję jej kwadrat n

2

, a następnie

sprawdzam, czy twierdzenie jest prawdziwe, czy nie.

�

�

D.

Sprawdzam twierdzenie dla kilku początkowych liczb pierwszych, a

następnie wyciągam wniosek oparty na podstawowym twierdzeniu

arytmetyki.

�

�

Źródło: Opracowanie własne na podstawie Teacher Education Study in Mathematics (TEDS-M) 2008. Released

items future teacher Mathematics Content Knowledge (MCK) and Mathematics Pedagogical Content

Knowledge (MPCK) – Secondary 2009.

Wyniki testu skalibrowano, wykorzystując metodę Item Response Theory (IRT), tak aby
średnia była równa 500 punktów i odpowiadała średniej wszystkich krajów, które spełniły

Niepoprawna

Graficzne przedstawienie 6 części po 0,2 bez wyjaśnień:

Przykład słowny, sugerujący liczenie części po 0,2, np.: „Policz 6 części po 0,2 w

następujący sposób: 0,2, 0,4, 0,6, 0,8, 1,0, 1,2.”

*

0,2

0,2

0,2

0,2

0,2

0,2

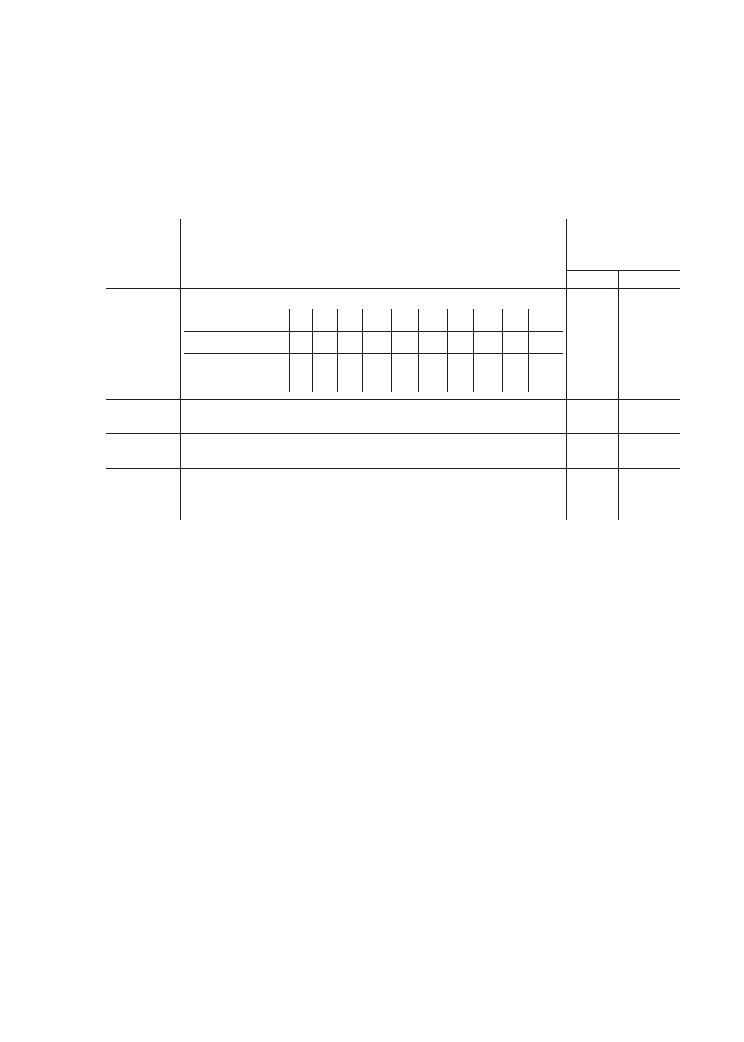
Pomiar kompetencji nauczycieli matematyki

79

Przykład 3

Masz udowodnić następujące twierdzenie:

Jeśli kwadrat dowolnej liczby naturalnej podzie-

limy przez 3, wtedy resztą może być tylko 0 lub 1.

Dla każdego z  poniższych rozumowań

ustal, czy opisuje matematycznie poprawny

dowód.

Wariant

rozwiązania

Uzasadnienie podane przez ucznia

Zaznacz jedną

odpowiedź

w każdym wierszu

Tak

Nie

A.

Używam następującej tabeli:

n

1

2

3

4

5

6

7

8

9

10

n

2

1

4

9 16 25 36 49 64 81 100

Reszta przy

dzieleniu przez 3

1

1

0

1

1

0

1

1

0

1





B.

Pokazuję, że (3n)

2

jest podzielne przez 3 i dla wszystkich innych liczb,

(3n ±1)

2

= 9n

2

± 6n + 1, co zawsze daje resztę 1 po podzieleniu przez 3.





C.

Wybieram liczbę naturalną n, znajduję jej kwadrat n

2

, a następnie

sprawdzam, czy twierdzenie jest prawdziwe, czy nie.





D.

Sprawdzam twierdzenie dla kilku początkowych liczb pierwszych,

a następnie wyciągam wniosek oparty na podstawowym

twierdzeniu arytmetyki.





Źródło: opracowanie własne na podstawie Teacher Education Study in Mathematics (TEDS-M) 2008. Released items

future teacher Mathematics Content Knowledge (MCK) and Mathematics Pedagogical Content Knowledge (MPCK)

– Secondary 2009.

Wyniki testu skalibrowano, wykorzystując

metodę Item Response Theory (IRT), tak

aby średnia była równa 500 punktów i od-

powiadała średniej wszystkich krajów, które

spełniły wymogi dotyczące poziomu reali-

zacji badania, a 100 punktów odpowiadało

wartości odchylenia standardowego.

Wśród przyszłych nauczycieli nauczania

wczesnoszkolnego najlepsze wyniki osiągnęli

studenci z  Rosji i  Szwajcarii, natomiast wy-

niki polskich przyszłych nauczycieli klas 1–3,

zarówno w zakresie matematyki, jak i dydak-

tyki matematyki należały do najniższych spo-

śród wszystkich badanych państw. W grupie

przyszłych nauczycieli szkół podstawowych,

specjalistów z  matematyki, najlepsze wyniki

osiągnęli studenci z  Polski i  Singapuru. Na-

tomiast polscy studenci matematyki, którzy

pisali test dla przyszłych nauczycieli szkół

średnich, mimo że osiągnęli wyższe wyniki

niż średnia międzynarodowa, to ich umiejęt-

ności były znacznie niższe niż umiejętności

studentów wiodących krajów: Rosji, Tajwanu

i Singapuru. Wyniki polskich studentów nale-

żały też do najbardziej zróżnicowanych; część

badanych osiągnęła bardzo wysokie wyniki,

ale co czwarty student posiadał umiejętności

poniżej średniej międzynarodowej.

Warto nadmienić, że w  ramach kontynu-

owania badań TEDS-M, przeprowadzono

w Niemczech badania pod nazwą TEDS-FU,

których celem było określenie skuteczności

kształcenia nauczycieli. Badaniem zostały ob-

jęte osoby, które uczestniczyły w  badaniach

TEDS-M i  po ukończeniu studiów podjęły

pracę w  szkole. Dążono m.in. do uzyskania

Czajkowska

80

odpowiedzi na następujące pytania badawcze:

Czy kompetencje nauczycieli ujawnione w ba-

daniu TEDS-M są trwałe? Jakie uwarunkowa-

nia szkolne sprzyjają rozwojowi kompetencji

młodych nauczycieli? W jaki sposób zmierzyć

sukcesy zawodowe nauczycieli po trzech la-

tach pracy? Czy istnieje związek między wy-

nikami w badaniu TEDS-M a sukcesami za-

wodowymi nauczycieli?

Badania kompetencyjne czynnych

nauczycieli matematyki

Badania dotyczące kompetencji nauczycieli

matematyki prowadzone na świecie w  ubie-

głym stuleciu miały najczęściej formę stu-

dium przypadku. Uzyskanych wyników nie

można było uogólniać, ani wnioskować z nich

o  kompetencjach tej grupy zawodowej. Nie

prowadzono natomiast badań ilościowych,

których celem byłoby zdiagnozowanie kom-

petencji czynnych nauczycieli matematyki.

Zasadniczym powodem był brak narzędzia,

które pozwoliłoby na rzetelną ocenę tych

kompetencji. Jednak wzrost zainteresowania

jakością edukacji matematycznej w ostatnim

dziesięcioleciu i czynników wpływających na

tę jakość spowodował podjęcie pionierskich

prób zbadania kompetencji matematycznych

i  dydaktycznych ogółu nauczycieli matema-

tyki. Najczęściej badania te były przeprowa-

dzane w  kontekście wpływu kompetencji

nauczycieli na osiągnięcia uczniów (Ball, Tha-

mes i Phelps, 2008; Baumert i in., 2010; Hill,

Schilling i Ball, 2004; Hill i Lubienski, 2007).

Jednym z pierwszych badań kompetencyj-

nych nauczycieli matematyki było badanie

przeprowadzone w Kalifornii (Hill, Schil-

ling i Ball, 2004). Każde z użytych w nim

zadań zostało scharakteryzowane w dwóch

obszarach. Pierwszy dotyczył dziedziny

matematyki (content area): liczb, działań,

wzorów, funkcji, algebry, drugi – znajo-

mości treści matematycznych (knowledge

of content) lub wiedzy o typowych błędach

uczniowskich i  ich przyczynach, a  także

sposobach rozumowania i tworzenia stra-

tegii rozwiązywania zadań przez uczniów

(knowledge of students and content). Za-

dania zostały zamieszczone w  trzech ro-

dzajach zeszytów testowych, przy czym

autorzy starali się, aby w  każdym z  nich

znalazła się porównywalna liczba zadań

każdego typu, a testy nie różniły się mię-

dzy sobą stopniem trudności. Każdy ro-

dzaj zeszytu testowego składał się z około

siedmiu tematów i 11–15 zadań. Przykła-

dowe zadania zamieszczono poniżej (Hill,

Schilling i Ball, 2004, s. 29).

Przykład 4

1. Pewnego poranka Allen, kiedy przygoto-

wywał się do prowadzenia lekcji, poczuł

się nieco zdezorientowany. Kiedy zdał so-

bie sprawę, że dziesięć do potęgi drugiej

jest równe sto (10

2

= 100), wtedy zaczął się

zastanawiać, do której potęgi należy pod-

nieść liczbę 10, aby otrzymać 1. Zapytał

Berry mieszkającą obok. Co powinna mu

odpowiedzieć? Proszę zaznaczyć znakiem

(X) jedną odpowiedź.

a) 0

b) 1

c) Nie można podnieść liczby dziesięć do

żadnej potęgi, tak aby wynik był równy 1.

d) -1

e) Nie jestem pewna.

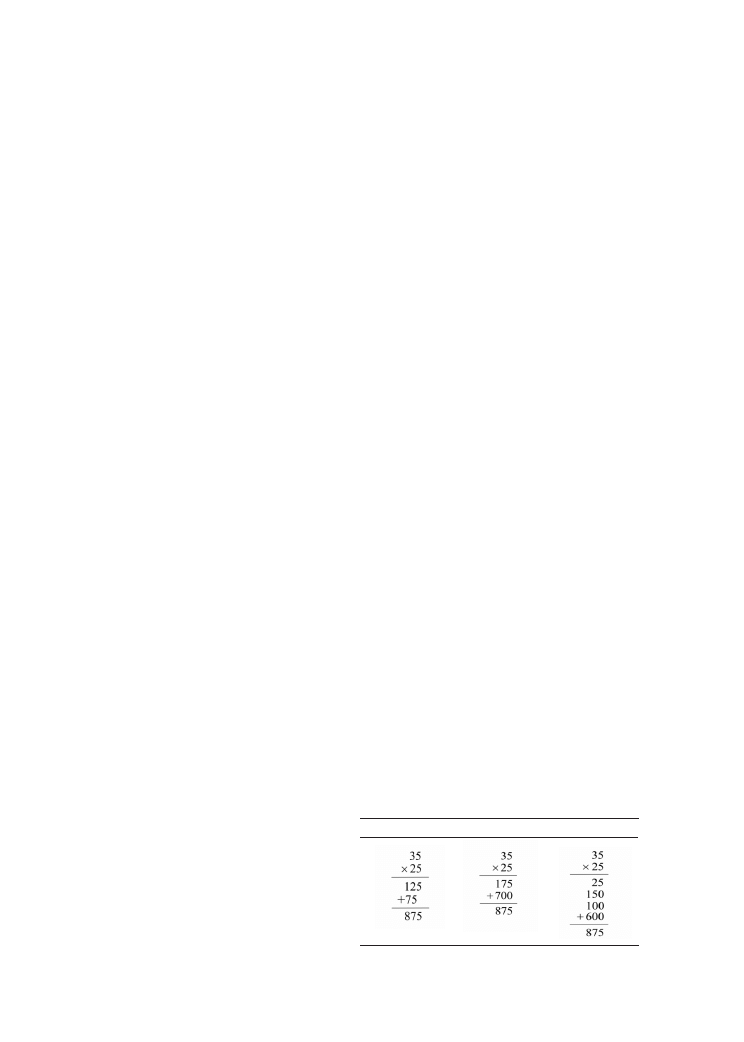
2. Wyobraź sobie, że pracujesz ze swoją kla-

są nad mnożeniem dużych liczb. Zauwa-

żasz, że niektórzy uczniowie wykonali

mnożenie następująco:

Uczeń A

Uczeń B

Uczeń C

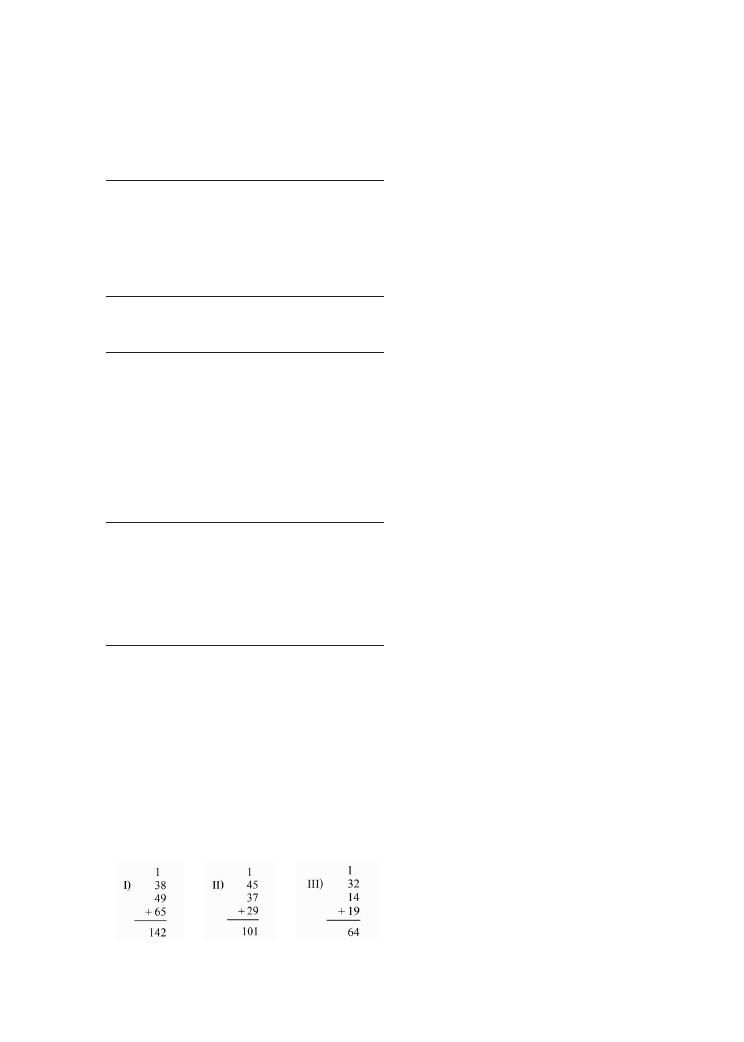
Pomiar kompetencji nauczycieli matematyki

81

Którzy uczniowie, Twoim zdaniem, zasto-

sowali metodę, która może zostać użyta do

mnożenia każdych dwóch liczb całkowitych?

Metoda

Metoda

może zostać

użyta do

mnożenia

każdych

dwóch liczb

całkowitych

Metoda nie

może zostać

użyta do

mnożenia

każdych

dwóch liczb

całkowitych

Nie jestem

pewien/

pewna

A







B







C







3. Pan Fitzgerald pomaga swoim uczniom

porównywać ułamki dziesiętne. Obec-

nie stara się wymyśleć zadanie, które

pozwoli mu sprawdzić, czy jego ucznio-

wie potrafią poprawnie ustawić ułamki

w  kolejności rosnącej. Który z  poniż-

szych zestawów liczb będzie najlepszy

w tym celu?

A

0,5

7

0,01

11,4

B

0,60

2,53

3,14

0,45

C

0,6

4,25

0,565

2,5

D

Każdy z tych zestawów jest dobry w tym

celu. Wszystkie wymagają od uczniów

odczytywania i rozumienia ułamków

dziesiętnych.

4. Pani Jackson przygotowuje się do egzami-

nu i  planuje minilekcje skoncentrowane

na trudnościach, które uczniowie mają

z  dodawaniem liczb sposobem pisem-

nym. Aby jej wskazówki były bardziej

efektywne, zamierza pracować z grupami

uczniów, którzy popełniają ten sam rodzaj

błędu. Przegląda więc ostatni sprawdzian,

aby zobaczyć, z czym mają oni trudności.

Zobaczyła następujące trzy błędy ucz-

niowskie:

Którzy uczniowie popełniają ten sam rodzaj

błędu? Zaznacz jedną odpowiedź.

a) I i II;

b) I i III;

c) II i III;

d) I, II i III.

Badanie przeprowadzono we współpracy

z California’s Mathematics Professional Deve-

lopment Institutes (MPDIs), który organizo-

wał letnie zajęcia mające na celu podniesienie

wiedzy matematycznej nauczycieli. Badani

zostali wybrani spośród nauczycieli szkół

podstawowych, słuchaczy MPDIs, zgodnie

z kryterium, jakim był udział w określonych

zajęciach. Do analizy wyników użyto metody

IRT. Badanie wykazało, że na kompetencje

nauczycieli matematyki ma wpływ znajomość

specjalistycznej wiedzy, a nie tylko ogólna in-

teligencja, zdolności matematyczne czy zdol-

ności pedagogiczne. Na tę specjalistyczną

wiedzę składa się kilka elementów, m.in. zna-

jomość konkretnych treści matematycznych,

ich reprezentacji, umiejętność analizowania

nietypowych rozwiązań zadań i algorytmów,

umiejętność wyjaśniania, prezentowania tre-

ści matematycznych. Sama znajomość szkol-

nej matematyki nie jest wystarczająca. Nie

wystarczy również rozległa wiedza matema-

tyczna. Badanie ujawniło, że na kompetencje

nauczycieli ma wpływ dobra znajomość ma-

tematyki, przy czym nie ma wpływu to, jak

dużo dana osoba wie, tylko jak korzysta z po-

siadanej wiedzy matematycznej, czy rozumie

jej sens, czy potrafi stworzyć jej praktyczną

reprezentację. Badanie jednak miało charak-

ter pilotażowy, próba nie była losowa, więc, jak

piszą sami autorzy (Hill, Schilling i Ball, 2004),

jego wyniki należy traktować jako wstępne,

które wymagają dalszego sprawdzania.

Innym badaniem kompetencji nauczycieli

matematyki, przeprowadzonym na dużą

skalę, było badanie COACTIV (Professional

Competence of Teachers, Cognitively Activating

Instruction, and the Development of Students’

Czajkowska

82

Mathematical Literacy). Zostało przeprowa-

Zostało przeprowa-

dzone w latach 2003–2004 z inicjatywy Ger-

man Research Foundation w Niemczech jako

rozszerzenie badania PISA (Baumert i  in.,

2010; Krauss i in., 2008). Jego celem było okre-

ślenie, w jakim stopniu kompetencje meryto-

ryczne (matematyczne) i dydaktyczne nauczy-

cieli mają wpływ na wyniki procesu uczenia

się – nauczania. Badaniem została objęta re-

prezentatywna próba klas uczniów piętnasto-

letnich (klasy 10) i ich nauczycieli matematy-

ki. Do badania kompetencji matematycznych

i dydaktycznych nauczycieli użyto specjalnie

skonstruowanego testu. Każde z zadań zostało

najpierw przetestowane w wywiadach indywi-

dualnych i w pilotażu. Badaniu poddano rów-

nież cały test pod kątem jego właściwości psy-

chometrycznych i czasu potrzebnego na jego

rozwiązanie. Aby mieć pewność, że zadania

mierzą specjalistyczną wiedzę nauczycieli ma-

tematyki, narzędzie przetestowano także na

grupie uczniów szkół średnich, pobierających

zaawansowany kurs matematyki i  na gru-

pie nauczycieli nauk przyrodniczych, którzy

nie studiowali matematyki. W obu tych gru-

pach test był praktycznie nierozwiązywalny

(Baumert i  in., 2010). Część testu dotycząca

wiedzy i  umiejętności matematycznych na-

uczycieli składała się z 13 zadań obejmujących

arytmetykę, algebrę, geometrię, funkcje i  ra-

chunek prawdopodobieństwa. Natomiast każ-

de z  zadań mierzących kompetencje dydak-

tyczne nauczycieli zostało zakwalifikowane do

jednego z trzech obszarów: zadania, uczniowie,

nauczanie. Zadania pierwszej grupy dotyczyły

różnych sposobów rozwiązywania zadań ma-

tematycznych. Zadania z obszaru „uczniowie”

kontrolowały umiejętności rozpoznawania ro-

zumowania i myślenia uczniów, przewidywa-

nia trudności, jakie mogą oni napotkać, a także

przewidywania typowych błędów uczniow-

skich. Ostatnią grupę („nauczanie”) tworzyły

zadania mierzące umiejętności przedstawia-

nia, reprezentowania i  wyjaśniania określo-

nych treści matematycznych. Wszystkie zada-

nia były zadaniami otwartymi. W trakcie ich

rozwiązywania zabronione było korzystanie

z kalkulatora (Baumert i in., 2010). Poniżej po-

dano przykłady zadań występujących w teście

wraz z przykładami poprawnych odpowiedzi.

Rodzaj

badanych

kompetencji

Zadanie

Przykłady poprawnych odpowiedzi

Kompetencje

matematyczne

Czy prawdą jest, że:

0,999999 . . . = 1?

Odpowiedź proszę uzasadnić.

Niech 0,999…=a.

Wtedy 10a=9,99…, stąd

Zatem a=1, czyli stwierdzenie jest prawdziwe.

Kompetencje

dydaktyczne:

zadania

Jak zmieni się pole kwadratu,

jeśli długość boku zwiększymy

trzykrotnie? Przedstaw swoje

rozumowanie.
Proszę przedstawić kilka możliwych

sposobów rozwiązania tego

problemu (i różne rozumowania).

Rozwiązanie algebraiczne:

Pole wyjściowego kwadratu: a

2

.

Pole nowego kwadratu jest zatem równe:

(3a)

2

= 9a

2

, tzn. ma pole 9 razy większe od pola

wyjściowego kwadratu.

Rozwiązanie geometryczne:

Dziewięć razy większe od pola wyjściowego

kwadratu:

14

Przykład 5

Rodzaj badanych
kompetencji

Zadanie

Przykłady poprawnych odpowiedzi

Kompetencje

matematyczne

Czy prawdą jest, że:

0,999999 . . . = 1?

Odpowiedź proszę uzasadnić.

Niech 0,999…=a.

Wtedy 10a=9,99…, stąd

10𝑎 − 𝑎

�����

��

= 9,99 … − 0,999 …

�����������

�

Zatem a=1, czyli stwierdzenie jest

prawdziwe.

Kompetencje

dydaktyczne:

zadania

Jak zmieni się pole kwadratu, jeśli

długość boku zwiększymy

trzykrotnie? Przedstaw swoje

rozumowanie.
Proszę przedstawić kilka

możliwych sposobów rozwiązania

tego problemu (i różne

rozumowania).

Rozwiązanie algebraiczne:

Pole wyjściowego kwadratu: 𝑎

�

.

Pole nowego kwadratu jest zatem równe:

(3𝑎)

�

= 9𝑎

�

, tzn. ma pole 9 razy większe

od pola wyjściowego kwadratu.

Rozwiązanie geometryczne:

Dziewięć razy większe od pola

wyjściowego kwadratu:

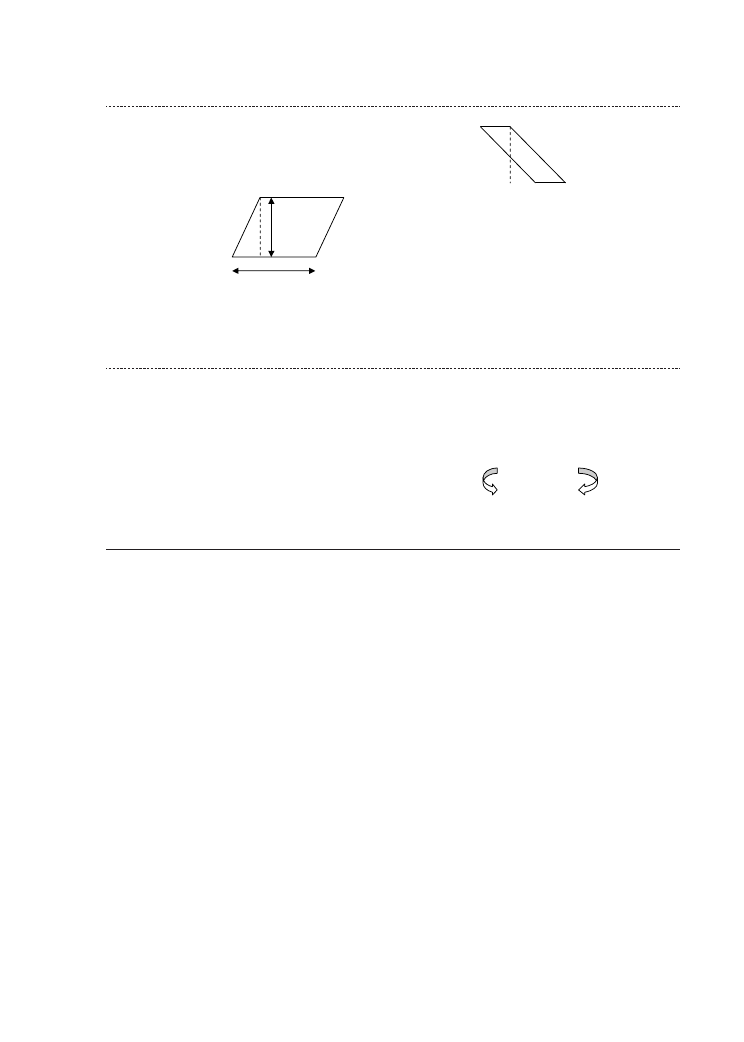
Kompetencje

dydaktyczne:

uczniowie

Pole równoległoboku można

obliczyć, mnożąc długość

podstawy przez jego wysokość.

Proszę podać przykład

równoległoboku, w którym

uczniowie mogą napotkać

trudności z zastosowaniem tej

formuły.

Uwaga: w odpowiedzi nauczyciela

kluczowe jest to, aby wysokość

„wychodziła” poza narysowany

równoległobok.

Kompetencje

dydaktyczne:

nauczanie

Uczeń mówi: nie rozumiem

dlaczego (-1) ∙ (-1) = 1

Proszę podać kilka różnych

sposobów wyjaśnienia tego faktu

swoim uczniom.

Chociaż „stałość zasady” nie jest dowodem

tego faktu, to może być wykorzystana do

logicznego wyjaśnienia mnożenia liczb

ujemnych, a tym samym sprzyjać jego

rozumieniu:

podstawa

wysokość

3 ∙ (–1) = –3

2 ∙ (–1) = –2

1 ∙ (–1) = –1

0 ∙ (–1) = 0

(–1) ∙ (–1) = 1

(–2) ∙ (–1) = 2

+

1

-1

a

3a

14

Przykład 5

Rodzaj badanych
kompetencji

Zadanie

Przykłady poprawnych odpowiedzi

Kompetencje

matematyczne

Czy prawdą jest, że:

0,999999 . . . = 1?

Odpowiedź proszę uzasadnić.

Niech 0,999…=a.

Wtedy 10a=9,99…, stąd

10𝑎 − 𝑎

�����

��

= 9,99 … − 0,999 …

�����������

�

Zatem a=1, czyli stwierdzenie jest

prawdziwe.

Kompetencje

dydaktyczne:

zadania

Jak zmieni się pole kwadratu, jeśli

długość boku zwiększymy

trzykrotnie? Przedstaw swoje

rozumowanie.
Proszę przedstawić kilka

możliwych sposobów rozwiązania

tego problemu (i różne

rozumowania).

Rozwiązanie algebraiczne:

Pole wyjściowego kwadratu: 𝑎

�

.

Pole nowego kwadratu jest zatem równe:

(3𝑎)

�

= 9𝑎

�

, tzn. ma pole 9 razy większe

od pola wyjściowego kwadratu.

Rozwiązanie geometryczne:

Dziewięć razy większe od pola

wyjściowego kwadratu:

Kompetencje

dydaktyczne:

uczniowie

Pole równoległoboku można

obliczyć, mnożąc długość

podstawy przez jego wysokość.

Proszę podać przykład

równoległoboku, w którym

uczniowie mogą napotkać

trudności z zastosowaniem tej

formuły.

Uwaga: w odpowiedzi nauczyciela

kluczowe jest to, aby wysokość

„wychodziła” poza narysowany

równoległobok.

Kompetencje

dydaktyczne:

nauczanie

Uczeń mówi: nie rozumiem

dlaczego (-1) ∙ (-1) = 1

Proszę podać kilka różnych

sposobów wyjaśnienia tego faktu

swoim uczniom.

Chociaż „stałość zasady” nie jest dowodem

tego faktu, to może być wykorzystana do

logicznego wyjaśnienia mnożenia liczb

ujemnych, a tym samym sprzyjać jego

rozumieniu:

podstawa

wysokość

3 ∙ (–1) = –3

2 ∙ (–1) = –2

1 ∙ (–1) = –1

0 ∙ (–1) = 0

(–1) ∙ (–1) = 1

(–2) ∙ (–1) = 2

+

1

-1

a

3a

Przykład 5

Pomiar kompetencji nauczycieli matematyki

83

Rozwiązanie każdego z  zadań było oce-

niane niezależnie przez dwóch, specjalnie

wyszkolonych koderów. Podobnie jak w ba-

daniach TEDS-M i PISA do oceny zadań za-

stosowano kodowanie dwucyfrowe. Pierw-

sza cyfra kodu wskazywała na poprawność

rozwiązania (całkowicie poprawne, częścio-

wo poprawne, niepoprawne), druga na spo-

sób rozwiązania zadania. Analizie poddano

też zadania, które nauczyciele samodziel-

nie przygotowali do kontrolowania wiedzy

i  umiejętności swoich uczniów. Średnio

każdy z badanych przygotował 53 zadania.

Badanie ujawniło duże zróżnicowanie na-

uczycieli pod względem posiadanych kom-

petencji matematycznych. Wysokie wyniki

uzyskali nauczyciele, którzy odebrali aka-

demickie wykształcenie i byli specjalistami

w  zakresie matematyki. Natomiast wyni-

ki nauczycieli, którzy nie legitymowali się

wyższym wykształceniem lub ukończyli

kurs nauczania zintegrowanego w byłej Nie-

mieckiej Republice Demokratycznej, były

znacznie niższe. Również w obszarze kom-

petencji dydaktycznych nauczyciele posia-

dający wyższe matematyczne wykształcenie

okazali się lepsi od nauczycieli dwóch pozo-

stałych grup, jednak tu różnice nie były aż

tak znaczące, jak w przypadku kompetencji

matematycznych.

Celem badania COACTIV było również usta-

lenie, które kompetencje: matematyczne czy

dydaktyczne mają większy wpływ na umiejęt-

ności matematyczne uczniów. Przyjęto założe-

Kompetencje

dydaktyczne:

uczniowie

Pole równoległoboku można

obliczyć, mnożąc długość jego

podstawy i wysokość opuszczoną

na tę podstawę.

Proszę podać przykład

równoległoboku, w którym

uczniowie mogą napotkać trudności

z zastosowaniem tej formuły.

Uwaga: w odpowiedzi nauczyciela kluczowe

jest to, aby wysokość „wychodziła” poza

narysowany równoległobok.

Kompetencje

dydaktyczne:

nauczanie

Uczeń mówi: nie rozumiem

dlaczego (-1) ∙ (-1) = 1

Proszę podać kilka różnych

sposobów wyjaśnienia tego faktu

swoim uczniom.

Chociaż „stałość zasady” nie jest dowodem tego

faktu, to może być wykorzystana do logicznego

wyjaśnienia mnożenia liczb ujemnych, a tym

samym sprzyjać jego rozumieniu:

14

Przykład 5

Rodzaj badanych
kompetencji

Zadanie

Przykłady poprawnych odpowiedzi

Kompetencje

matematyczne

Czy prawdą jest, że:

0,999999 . . . = 1?

Odpowiedź proszę uzasadnić.

Niech 0,999…=a.

Wtedy 10a=9,99…, stąd

10𝑎 − 𝑎

�����

��

= 9,99 … − 0,999 …

�����������

�

Zatem a=1, czyli stwierdzenie jest

prawdziwe.

Kompetencje

dydaktyczne:

zadania

Jak zmieni się pole kwadratu, jeśli

długość boku zwiększymy

trzykrotnie? Przedstaw swoje

rozumowanie.
Proszę przedstawić kilka

możliwych sposobów rozwiązania

tego problemu (i różne

rozumowania).

Rozwiązanie algebraiczne:

Pole wyjściowego kwadratu: 𝑎

�

.

Pole nowego kwadratu jest zatem równe:

(3𝑎)

�

= 9𝑎

�

, tzn. ma pole 9 razy większe

od pola wyjściowego kwadratu.

Rozwiązanie geometryczne:

Dziewięć razy większe od pola

wyjściowego kwadratu:

Kompetencje

dydaktyczne:

uczniowie

Pole równoległoboku można

obliczyć, mnożąc długość

podstawy przez jego wysokość.

Proszę podać przykład

równoległoboku, w którym

uczniowie mogą napotkać

trudności z zastosowaniem tej

formuły.

Uwaga: w odpowiedzi nauczyciela

kluczowe jest to, aby wysokość

„wychodziła” poza narysowany

równoległobok.

Kompetencje

dydaktyczne:

nauczanie

Uczeń mówi: nie rozumiem

dlaczego (-1) ∙ (-1) = 1

Proszę podać kilka różnych

sposobów wyjaśnienia tego faktu

swoim uczniom.

Chociaż „stałość zasady” nie jest dowodem

tego faktu, to może być wykorzystana do

logicznego wyjaśnienia mnożenia liczb

ujemnych, a tym samym sprzyjać jego

rozumieniu:

podstawa

wysokość

3 ∙ (–1) = –3

2 ∙ (–1) = –2

1 ∙ (–1) = –1

0 ∙ (–1) = 0

(–1) ∙ (–1) = 1

(–2) ∙ (–1) = 2

+

1

-1

a

3a

14

Przykład 5

Rodzaj badanych
kompetencji

Zadanie

Przykłady poprawnych odpowiedzi

Kompetencje

matematyczne

Czy prawdą jest, że:

0,999999 . . . = 1?

Odpowiedź proszę uzasadnić.

Niech 0,999…=a.

Wtedy 10a=9,99…, stąd

10𝑎 − 𝑎

�����

��

= 9,99 … − 0,999 …

�����������

�

Zatem a=1, czyli stwierdzenie jest

prawdziwe.

Kompetencje

dydaktyczne:

zadania

Jak zmieni się pole kwadratu, jeśli

długość boku zwiększymy

trzykrotnie? Przedstaw swoje

rozumowanie.
Proszę przedstawić kilka

możliwych sposobów rozwiązania

tego problemu (i różne

rozumowania).

Rozwiązanie algebraiczne:

Pole wyjściowego kwadratu: 𝑎

�

.

Pole nowego kwadratu jest zatem równe:

(3𝑎)

�

= 9𝑎

�

, tzn. ma pole 9 razy większe

od pola wyjściowego kwadratu.

Rozwiązanie geometryczne:

Dziewięć razy większe od pola

wyjściowego kwadratu:

Kompetencje

dydaktyczne:

uczniowie

Pole równoległoboku można

obliczyć, mnożąc długość

podstawy przez jego wysokość.

Proszę podać przykład

równoległoboku, w którym

uczniowie mogą napotkać

trudności z zastosowaniem tej

formuły.

Uwaga: w odpowiedzi nauczyciela

kluczowe jest to, aby wysokość

„wychodziła” poza narysowany

równoległobok.

Kompetencje

dydaktyczne:

nauczanie

Uczeń mówi: nie rozumiem

dlaczego (-1) ∙ (-1) = 1

Proszę podać kilka różnych

sposobów wyjaśnienia tego faktu

swoim uczniom.

Chociaż „stałość zasady” nie jest dowodem

tego faktu, to może być wykorzystana do

logicznego wyjaśnienia mnożenia liczb

ujemnych, a tym samym sprzyjać jego

rozumieniu:

podstawa

wysokość

3 ∙ (–1) = –3

2 ∙ (–1) = –2

1 ∙ (–1) = –1

0 ∙ (–1) = 0

(–1) ∙ (–1) = 1

(–2) ∙ (–1) = 2

+

1

-1

a

3a

14

Przykład 5

Rodzaj badanych
kompetencji

Zadanie

Przykłady poprawnych odpowiedzi

Kompetencje

matematyczne

Czy prawdą jest, że:

0,999999 . . . = 1?

Odpowiedź proszę uzasadnić.

Niech 0,999…=a.

Wtedy 10a=9,99…, stąd

10𝑎 − 𝑎

�����

��

= 9,99 … − 0,999 …

�����������

�

Zatem a=1, czyli stwierdzenie jest

prawdziwe.

Kompetencje

dydaktyczne:

zadania

Jak zmieni się pole kwadratu, jeśli

długość boku zwiększymy

trzykrotnie? Przedstaw swoje

rozumowanie.
Proszę przedstawić kilka

możliwych sposobów rozwiązania

tego problemu (i różne

rozumowania).

Rozwiązanie algebraiczne:

Pole wyjściowego kwadratu: 𝑎

�

.

Pole nowego kwadratu jest zatem równe:

(3𝑎)

�

= 9𝑎

�

, tzn. ma pole 9 razy większe

od pola wyjściowego kwadratu.

Rozwiązanie geometryczne:

Dziewięć razy większe od pola

wyjściowego kwadratu:

Kompetencje

dydaktyczne:

uczniowie

Pole równoległoboku można

obliczyć, mnożąc długość

podstawy przez jego wysokość.

Proszę podać przykład

równoległoboku, w którym

uczniowie mogą napotkać

trudności z zastosowaniem tej

formuły.

Uwaga: w odpowiedzi nauczyciela

kluczowe jest to, aby wysokość

„wychodziła” poza narysowany

równoległobok.

Kompetencje

dydaktyczne:

nauczanie

Uczeń mówi: nie rozumiem

dlaczego (-1) ∙ (-1) = 1

Proszę podać kilka różnych

sposobów wyjaśnienia tego faktu

swoim uczniom.

Chociaż „stałość zasady” nie jest dowodem

tego faktu, to może być wykorzystana do

logicznego wyjaśnienia mnożenia liczb

ujemnych, a tym samym sprzyjać jego

rozumieniu:

podstawa

wysokość

3 ∙ (–1) = –3

2 ∙ (–1) = –2

1 ∙ (–1) = –1

0 ∙ (–1) = 0

(–1) ∙ (–1) = 1

(–2) ∙ (–1) = 2

+

1

-1

a

3a

Źródło: opracowanie i tłumaczenie własne na podstawie Baumert i in. (2010), s. 169.

Czajkowska

84

nie, że nie jest możliwe posiadanie kompeten-

cji dydaktycznych bez posiadania kompetencji

matematycznych na odpowiednim poziomie,

ale kompetencje matematyczne nie mogą za-

stąpić kompetencji dydaktycznych i  sama

wiedza matematyczna nie jest wystarczająca,

aby właściwie planować i  realizować proces

nauczania. Badanie wykazało, że istnieje li-

niowa zależność pomiędzy kompetencjami

dydaktycznymi nauczycieli a  osiągnięciami

piętnastolatków. Poziom kompetencji dydak-

tycznych nauczycieli w  znacznym stopniu

wyjaśnia poziom wiedzy i umiejętności ucz-

niów. Wysokie kompetencje dydaktyczne są

szczególnie ważne w pracy z uczniami mają-

cymi trudności w  nauce matematyki. Nato-

miast kompetencje matematyczne nauczycieli

nie mają znaczącego wpływu na osiągnięcia

uczniów. Nauczyciele o  wysokich wynikach

w obszarze kompetencji matematycznych nie

potrafili udzielać właściwego wsparcia ucz-

niom mającym trudności w nauce i aktywi-

zować ich do nauki matematyki. Nie oznacza

to jednak, że kompetencje matematyczne nie

mają żadnego znaczenia dla nauczania. Oso-

by o  wysokich kompetencjach matematycz-

nych lepiej dostrzegały powiązania między

treściami i  dobierały materiał nauczania

(w tym zadania) pod kątem realizacji pro-

gramu i stawianych celów edukacyjnych. Co

więcej, badanie ujawniło, że deficyty w wie-

dzy i  umiejętnościach matematycznych na-

uczycieli hamują i blokują rozwój ich umie-

jętności dydaktycznych (Baumert i in., 2010;

Krauss i in., 2008).

Inne interesujące badanie, w którym jednak

nie sprawdzano bezpośrednio kompetencji

nauczycieli, tylko narzędzia do mierzenia

kompetencji nauczycieli matematyki, opi-

sano w  artykule Nicole Kersting (2008).

Wzięło w  nich udział 62 nauczycieli ma-

tematyki o  różnym stażu pracy i  różnych

kwalifikacjach nauczycielskich. Autorzy

badań wyszli z  założenia, że dotychcza-

sowe narzędzia badawcze w  postaci pytań

ankietowych nie uwzględniają kontekstu

i  złożoności sytuacji pojawiających się na

lekcjach matematyki. Dlatego do badań

użyto dziesięciu nagrań, które badani mogli

oglądać za pomocą interaktywnej platfor-

my w internecie. Każdy film trwał od 1 do

3 minut i dotyczył albo indywidualnej pracy

z uczniem, albo sytuacji w klasie w trakcie

lekcji matematyki. Pliki wideo były zróż-

nicowane pod względem pojawiających się

na nich treści matematycznych (geometria,

algebra) i  stopnia ich złożoności, a  także

złożoności interakcji nauczyciel – uczeń. Do

każdego filmu były dołączone informacje

dodatkowe o  lekcji. Zadaniem nauczycieli

było obejrzenie wszystkich filmów, a  na-

stępnie udzielenie odpowiedzi na pytania

dotyczące obserwowanych lekcji i napisanie

własnego komentarza. Odpowiedzi zostały

przeanalizowane pod kątem umiejętności

nauczycielskich, takich jak rozpoznawanie

kluczowych momentów lekcji, treści ma-

tematycznych, oceny działań nauczyciela.

Do badania kompetencji matematycznych

nauczycieli zastosowano test składający się

z 32 pytań wielokrotnego wyboru. Ich treść

matematyczna była ściśle powiązana ze

szkolną matematyką. Odpowiedzi nauczy-

cieli zostały ocenione przez specjalistów

– wykładowców uniwersyteckich. Uzupeł-

nieniem tych metod była ankieta, w której

pytano nauczycieli o ich wykształcenie, roz-

wój zawodowy, doświadczenie zawodowe,

a także o to, jak często w swojej pracy np.

zachęcają uczniów do rozwiązywania zadań

nietypowymi, nieznanymi metodami. In-

teresującym, a  jednocześnie zaskakującym

wynikiem opisanych badań jest to, że często

stosowane wskaźniki kompetencji nauczy-

cieli, takie jak: staż pracy, stopień awansu

zawodowego czy stopień ukończonych

studiów (licencjat, magisterium) nie miały

istotnego związku z wynikami nauczycieli,

uzyskanymi z  oceny sytuacji dydaktycz-

nych przedstawionych na filmach, ani te-

stu mierzącego wiedzę matematyczną.

Pomiar kompetencji nauczycieli matematyki

85

W 2008 roku z  inicjatywy OECD po raz

pierwszy przeprowadzono międzynaro-

dowe badanie nauczycieli TALIS (Tea-

ching and Learning International Survey).

Chociaż nie było to badanie sprawdzają-

ce kompetencje i  obejmowało nauczycieli

różnych przedmiotów, warto o nim wspo-

mnieć, ponieważ pozwoliło na porównanie

warunków pracy i  poglądów nauczycieli

o  szeroko pojętym środowisku szkolnym

w  różnych państwach. Głównym jego ce-

lem było dostarczenie informacji społecz-

no-demograficznych o  badanych nauczy-

cielach, a  także informacji dotyczących

m.in. rozwoju zawodowego nauczycieli, ich

przekonań o nauczaniu, praktyce pedago-

gicznej, roli i  mechanizmie funkcjonowa-

nia przywództwa szkolnego. Uczestniczyło

w nim około 73 500 nauczycieli gimnazjów

i uczniów klas 7–9 (w Polsce 3100) z 24 kra-

jów (Piwowarski i Krawczyk, 2009). Należy

jednak podkreślić, że TALIS było bada-

niem ankietowym, a  zatem jego wyniki

prezentują jedynie opinie, poglądy i prze-

konania nauczycieli.

Badania w Polsce

W Polsce przeprowadzono bardzo niewiele

badań dotyczących kompetencji nauczy-

cieli, a  w  szczególności nauczycieli mate-

matyki. Zazwyczaj były to badania sonda-

żowe, których celem było poznanie opinii

nauczycieli na temat własnych umiejętno-

ści. Badani odpowiadali na wiele pytań an-

kietowych, dokonując samooceny. Wyniki

miały zatem charakter deklaratywny i nie

świadczyły o  rzeczywistych kompeten-

cjach nauczycieli. Dotychczasowe badania

koncentrowały się głównie na rozpoznaniu

poziomu kwalifikacji i  kompetencji diag-

nostycznych, organizacyjnych, metodycz-

nych i  informatycznych ogółu nauczycieli

lub nauczycieli określonych przedmiotów

(Raport…, 2010; Sałata, 2007), znacznie

rzadziej merytorycznych (Grzęda, 2009).

Czasami były częścią szerszych badań

dotyczących różnych aspektów pracy na-

uczycieli (Grzęda, 2009). Poniżej zostaną

krótko omówione dwa badania. Pierwsze

przeprowadzone zostało w  ramach pro-

jektu TEDS-M. Drugie objęło nauczycieli

wychowania przedszkolnego i  edukacji

wczesnoszkolnej, którzy również zajmują

się edukacją matematyczną.

Badanie w  ramach projektu TEDS-M ob-

jęło 1076 nauczycieli matematyki uczących

w  szkołach podstawowych (39%) i  w gim-

nazjach (61%) (Grzęda, 2009). Głównym

celem była wszechstronna charakterystyka

tej grupy zawodowej poprzez opisanie jej

kluczowych aspektów, takich jak: droga do

zawodu nauczyciela, czas poświęcany na

obowiązki zawodowe, ścieżki awansu, spo-

soby prowadzenia lekcji, warunki pracy.

Zwrócono w nim uwagę na poznanie moty-

wów wyboru zawodu, ocenę merytoryczną

przygotowania do wykonywania zawodu,

poznanie metod prowadzenia lekcji i  ich

skuteczności, problemów w  pracy z  ucz-

niami, poznanie poglądów na temat istoty

matematyki i  zdolności matematycznych

uczniów. W  opinii badanych nauczycieli

zdecydowanie najlepiej byli oni przygoto-

wani do wykonywania zawodu nauczyciela

matematyki pod względem wiedzy mate-

matycznej, umiejętności rozwijania rozu-

mowania matematycznego uczniów oraz

umiejętności planowania lekcji. Natomiast

czuli się znacznie gorzej przygotowani pod

względem kompetencji interpersonalnych

(umiejętności komunikowania się z  rodzi-

cami i wciągania ich do współpracy, umie-

jętności kierowania klasą i  rozwiązywania

problemów związanych z zachowaniem ucz-

niów) i pracy z uczniem mającym trudności

w nauce. Mimo że nauczyciele nie odczuwa-

li większych trudności z nauczaniem treści

występujących w  programach nauczania,

to jednak zauważali, że rozwijanie takich

umiejętności, jak: rozumienie i  interpreta-

Czajkowska

86

cja pojęć matematycznych, modelowanie

matematyczne oraz wyciąganie wniosków

z  kilku informacji podanych w  różnej po-

staci, jest stosunkowo trudne. Należy zwró-

cić uwagę, że na te problemy dydaktyczne

zwracali uwagę nauczyciele starsi i o więk-

szym stażu zawodowym (Grzęda, 2009).

W 2010 r. Mazowiecki Zespół ds. Systemowe-

go Badania Potrzeb Doskonalenia Nauczycieli

na zlecenie Mazowieckiego Kuratora Oświaty

przeprowadził badanie kompetencji nauczy-

cieli wychowania przedszkolnego i  edukacji

wczesnoszkolnej. Jego celem było rozpozna-

nie poziomu kwalifikacji i kompetencji diag-

nostycznych, organizacyjnych, metodycznych

i  informatycznych nauczycieli wychowania

przedszkolnego i  edukacji wczesnoszkolnej,

niezbędnych do wykonywania zadań wy-

nikających z  nowej podstawy programowej,

a także warunków, w jakich odbywa się rea-

lizacja nowej podstawy programowej oraz zi-

dentyfikowanie potrzeb tej grupy nauczycieli

w  zakresie rozwoju zawodowego. Badaniem

zostało objętych 588 nauczycieli i 174 dyrekto-

rów przedszkoli i szkół podstawowych na Ma-

zowszu. Główną metodą badawczą był sondaż

diagnostyczny. Podstawową techniką była

interaktywna ankieta wypełniana przez na-

uczycieli. Składała się z 25 pytań (w większo-

ści zamkniętych), które zostały pogrupowane

w  bloki tematyczne. Uzupełniającą techniką

badawczą był wywiad grupowy prowadzony

z dyrektorami wylosowanych placówek.

Z badań tych wynika, że w opinii nauczy-

cieli najbardziej potrzebują oni wsparcia

w zakresie organizacji współpracy z rodzi-

cami, a  także rozwoju umiejętności orga-

nizacyjnych i związanych z posługiwaniem

się technologiami informacyjno-komuni-

kacyjnymi. Odczuwają potrzebę dalszego

doskonalenia umiejętności poznawania

oraz zbierania informacji o  dziecku, jego

rodzinie i  środowisku, w  szczególności

w zakresie tworzenia narzędzi do diagnozy,

formułowania wniosków i zaleceń do dal-

szej pracy, komunikowania wyników diag-

nozy, identyfikowania deficytów rozwojo-

wych i  przyczyn trudności w  uczeniu się.

Badani potrzebują wsparcia w  nabywaniu

umiejętności rozwiązywania konfliktów

z rodzicami, opracowania indywidualnego

planu pracy z dzieckiem oraz modyfikacji

programu opiekuńczo-wychowawczego.

W  opinii nauczycieli posiadają oni wyso-

kie kompetencje metodyczne i  doskonale

radzą sobie z planowaniem procesu kształ-

cenia (wybór programu nauczania, w tym

podręcznika i kart pracy), przygotowaniem

się do zajęć (analiza materiału kształcenia,

operacjonalizacja celów kształcenia, różni-

cowanie poziomów wymagań, dobór metod

nauczania, wybór środków dydaktycznych)

oraz realizacją procesu dydaktycznego

wybranymi metodami, z  wykorzystaniem

odpowiednich środków dydaktycznych.

Deklarują natomiast potrzebę wsparcia

w  zakresie konstruowania i  modyfikowa-

nia programów nauczania, a  także oceny

strategii, metod i technik kształcenia oraz

środków dydaktycznych według kryteriów

ich przydatności i skuteczności w przygoto-

waniu dziecka do przejścia od wychowania

przedszkolnego do nauczania szkolnego,

a następnie przedmiotowego.

Należy jednak ponownie zwrócić uwagę, że

badanie miało charakter sondażowy, a  za-

tem jego wyniki odnoszą się jedynie do de-

klaracji i przekonań nauczycielskich o włas-

nych kompetencjach, co może, ale nie musi,

być odzwierciedleniem faktycznych kompe-

tencji nauczycielskich.

Podsumowanie

W ostatnim dwudziestoleciu w  wielu pań-

stwach edukacja stała się przedmiotem

szczególnej troski. Przeprowadzone dotych-

czas badania wyraźnie wskazywały, że na

osiągnięcia uczniów mają wpływ kompeten-

Pomiar kompetencji nauczycieli matematyki

87

cje nauczycieli. Jednak badań, których celem

byłaby diagnoza kompetencji nauczycieli,

przeprowadzono niewiele. Jedną z przyczyn

jest to, że nie wypracowano takich narzędzi,

które w  jednoznaczny sposób pozwalałyby

wnioskować o  kompetencjach nauczycie-

li. Ankiety i testy tylko w pewnym stopniu

umożliwiają określenie ich poziomu wie-

dzy i umiejętności, nie uwzględniają jednak

kontekstu i  złożoności sytuacji pojawiają-

cych się na lekcjach. Ponadto kompetencje

nauczycieli dotyczą bardzo wielu obszarów.

W badaniach zazwyczaj nie mierzono ogółu

kompetencji nauczycielskich, tylko wybrane.

Dlatego przedstawiając wyniki tych badań,

nie należy mówić o ogólnych kompetencjach

nauczycieli, ale o ich kompetencjach z dane-

go obszaru. Należy również uwzględnić fakt,

że kompetencje z różnych obszarów łączą się

ze sobą i wzajemnie przenikają, zatem poja-

wia się problem zbadania ich wzajemnych

powiązań i wpływu na proces nauczania. Na

przykład z dotychczasowych ustaleń wynika

jednoznacznie, że kompetencje matematycz-

ne i dydaktyczne są ze sobą powiązane, ale

już nie ma wśród badaczy zgodności co do

tego, które z  nich mają większy wpływ na

osiągnięcia uczniów. Kolejną przyczyną nie-

wielu badań jest to, że diagnoza kompetencji

nauczycieli jest sprawą „drażliwą”. Czasami

nauczyciele traktują tego typu badania jako

podważanie ich kompetencji. Niektórzy, jak

pokazuje pilotaż Badania potrzeb nauczycieli

edukacji wczesnoszkolnej i matematyki w za-

kresie rozwoju zawodowego

3

, obawiają się

wskazania niedostatków ich wiedzy i  obni-

żenia samooceny. Blokady do udziału w tego

typu przedsięwzięciach są tym większe, im

nauczyciel odczuwa większy lęk przed perso-

nalnym ujawnieniem jego wyników i wyni-

kającymi z tego konsekwencjami.

3

W kwietniu 2012 r. Instytut Badań Edukacyjnych uru-

chomił pilotaż projektu Badanie potrzeb nauczycieli edu-

kacji wczesnoszkolnej i matematyki w zakresie rozwoju za-

wodowego. Wyniki pilotażu są obecnie w opracowywaniu.

Literatura

Ball, D. L. (1990). The mathematical understan-

dings that prospective teachers bring to teacher

education. The Elementary School Journal, 90(4),

449–466.

Ball, D. L., Thames, M. H. i Phelps, G. (2008). Con-

tent knowledge for teaching. Journal of Teacher

Education, 59(5), 389–407.

Baumert, J., Kunter, M., Blum, W., Brunner, M.,

Voss, T., Jordan, A., Klusmann, U., Krauss, S.,

Neubrand M. i  Tsai, Y. (2010). Teachers’ math-

ematical knowledge, cognitive activation in the

classroom and student progress. American Edu-

cational Research Journal, 47(1), 133–180.

Borko, H., Eisenhart, M., Brown, C., Under-

hill, R., Jones, D. i  Agard, P. (1992). Learning

to teach hard mathematics: do novice teachers

and their instructors give up too easily? Jour-

nal for Research in Mathematics Education,

23(3), 194–222.

Davis, B. (2011). Mathematics teachers’ subtle, com-

plex disciplinary knowledge. Educationforum. Po-

brano z: www.sciencemag.org

Dylak, S. (1995). Wizualizacja w kształceniu nauczy-

cieli. Poznań: Wydawnictwo Naukowe UAM.

Even, R. (1993). Subject-matter knowledge and

pedagogical content knowledge: prospective

secondary teachers and the function concept.

Journal for Research in Mathematics Education,

24(2), 94–116.

Hamer, H. (1994). Klucz do efektywności nauczania.

Poradnik dla nauczycieli. Wydawnictwo Veda.

Hill, H. C., Schilling, S. G. i Ball, D. L. (2004). Develo-

ping measures of teachers’ mathematics knowl-

edge for teaching. The Elementary School Journal,

105(1), 11–30.

Hill, H. C. i Lubienski S. T. (2007). Teachers’ mathe-

matics knowledge for teaching and school context.

a study of California teachers. Educational Policy,

21(5), 747–768.

Grzęda, M. (2009). Nauczyciele matematyki w Polsce

– raport z badania TEDS-M. Warszawa: Instytut

Filozofii i Socjologii PAN. Pobrano z: http://www.

ifispan.waw.pl/pliki/raport_z_badania_nauczy-

cieli.pdf

Czajkowska

88

Kersting, N. (2008). Using video clips of mathema-

tics classroom instruction as item prompts to me-

asure teachers’ knowledge of teaching mathema-

tics. Educational and Psychological Measurement,

68(5), 845–861.

Krauss, S., Brunner, M., Kunter, M., Baumert, J.,

Blum, W., Neubrand, M. i Jordan, A. (2008). Peda-

gogical content knowledge and content knowl-

edge of secondary mathematics teachers. Journal

of Educational Psychology, 100(3), 716–725.

Kwaśnica, R. (2003). Wprowadzenie do myślenia

o  nauczycielu. W: Z. Kwieciński, B. Śliwerski

(red.), Pedagogika. Podręcznik akademicki. T. II,

PWN, Warszawa 2003.

Niss, M. (2004). The Danish „KOM” project and

possible consequences for teacher education.

W: R. Strässer, G. Brandell, B. Grevholm i O. He-

lenius (red.), Educating for the future. Proceedings

of an international symposium on mathematics

teacher education: preparation of mathematics

teachers for the future (s. 179–190). Stockholm:

Royal Swedish Academy of Science.

Piwowarski, R. i  Krawczyk, M. (2009). TALIS Na-

uczanie – wyniki badań 2008. Polska na tle mię-

dzynarodowym, Warszawa: Ministerstwo Edukacji

Narodowej, Instytut Badań Edukacyjnych. Pobra-

no z: http://eduentuzjasci.pl/images/stories/bada-

nia/talis/raport_talis.pdf

Putnam, R. T., Heaton, R. M., Prawat, R. S. i Remi-

llard, J. (1992). Teaching mathematics for under-

standing: discussing case studies of four fifth-

-grade teachers. The Elementary School Journal,

93(2), 213–228.

Raport z diagnozy potrzeb doskonalenia zawodowego

nauczycieli w  województwie mazowieckim Kom-

petencje nauczycieli wychowania przedszkolnego

i edukacji wczesnoszkolnej (2010). Warszawa: Ma-

zowiecki Zespół ds. Systemowego Badania Potrzeb

Doskonalenia Nauczycieli. Pobrano z: http://www.

kuratorium.waw.pl/files/f-1969-2-kompetencje_

nauczycieli_wych_przedszkolnego.pdf

Sałata, E. (2007). Realizacja kompetencji nauczyciel-

skich w opinii badanych nauczycieli. W: J. Pavelka

(red.), III. InEduTech 2007 Kl’účové kompetencie

a  technickié vzdelávanie. Presov, 75–80. Pobrano

z: http://www.pulib.sk/elpub2/FHPV/Pavelka2/

index.html

Sitek, M., Czajkowska, M., Hauzer, M., Jasińska,

A., Laskowska, D. i Sikorska J. (2010). Kształcenie

nauczycieli w  Polsce. Wyniki międzynarodowego

badania TEDS-M 2008. Warszawa: Instytut Filo-

zofii i Socjologii PAN. Pobrano z: http://www.ifi-

span.waw.pl/pliki/raport_z_badania_teds-m.pdf

Simon, M. A. (1993). Prospective elementary teachers’

knowledge of division. Journal of Research in Math-

ematics Education, 24(3), 233–254.

Stein, M. K., Baxter, J. A., Leinhardt, G. (1990).

Subject-matter knowledge and elementary in-

struction: a  case from functions and graphing.

American Educational Research Journal, 27(4),

639–663.

Strykowski, W. (2003). Szkoła współczesna i zacho-

dzące w niej procesy. W: W. Strykowski, J. Stry-

kowska i J. Pielachowski (red.), Kompetencje na-

uczyciela szkoły współczesnej. Poznań: eMPi

2

.

Szempruch, J. (2000). Pedagogiczne kształcenie na-

uczycieli wobec reformy edukacji w  Polsce. Rze-

szów: WSP.

Tatto, M. T., Bankov, K., Peck, R., Schwille, J., Senk,

S. L., Rodriguez, M., Ingvarson, L., Reckase,

M. i Rowley, G. (2012). Policy, practice, and readi-

ness to teach primary and secondary mathematics

in 17 countries. Pobrano z: http://www.iea.nl/fi le-

Pobrano z: http://www.iea.nl/file-

admin/user_upload/Publications/Electronic_ver-

sions/TEDS-M_International_Report.pdf

Tatto, M. T., Schwille, J., Senk, S., Ingvarson, L., Peck,

R. i Rowley G. (2008). Teacher education and de-

velopment study in mathematics (TEDS-M): policy,

practice, and readiness to teach primary and sec-

ondary mathematics. Conceptual framework. Po-

brano z: http://tedsm.hu-berlin.de/publik/Down-

loads/framework_juli08.pdf