11. Zjawiska korpuskularno-falowe

11.1. Promieniowanie termiczne

Podstawowe źródła światła: - ogrzane ciała stałe lub gazy, w których zachodzi
wyładowanie elektryczne.

Emisja

↔ absorpcja

R

- widmowa zdolność emisyjna promieniowania

R

d

λ

- szybkość z jaką jednostkowy obszar

powierzchni wypromieniowuje energię z zakresu
długości fal

λ

,

λ

+d

λ

.

Całkowita zdolność emisyjna promieniowania –
szybkość z jaką jednostka powierzchni
wypromieniowuje energię do przedniej półkuli:

∫

∞

=

0

R

edynie

tefana-

λ

λ

d

R

(analogia

do

rozkładu Maxwella dla prędkości!)

Własności widma termicznego:

- nie zależy ani od rodzaju substancji ani od kształtu, a j
od temperatury ciała;

- widmo jest ciągłe;

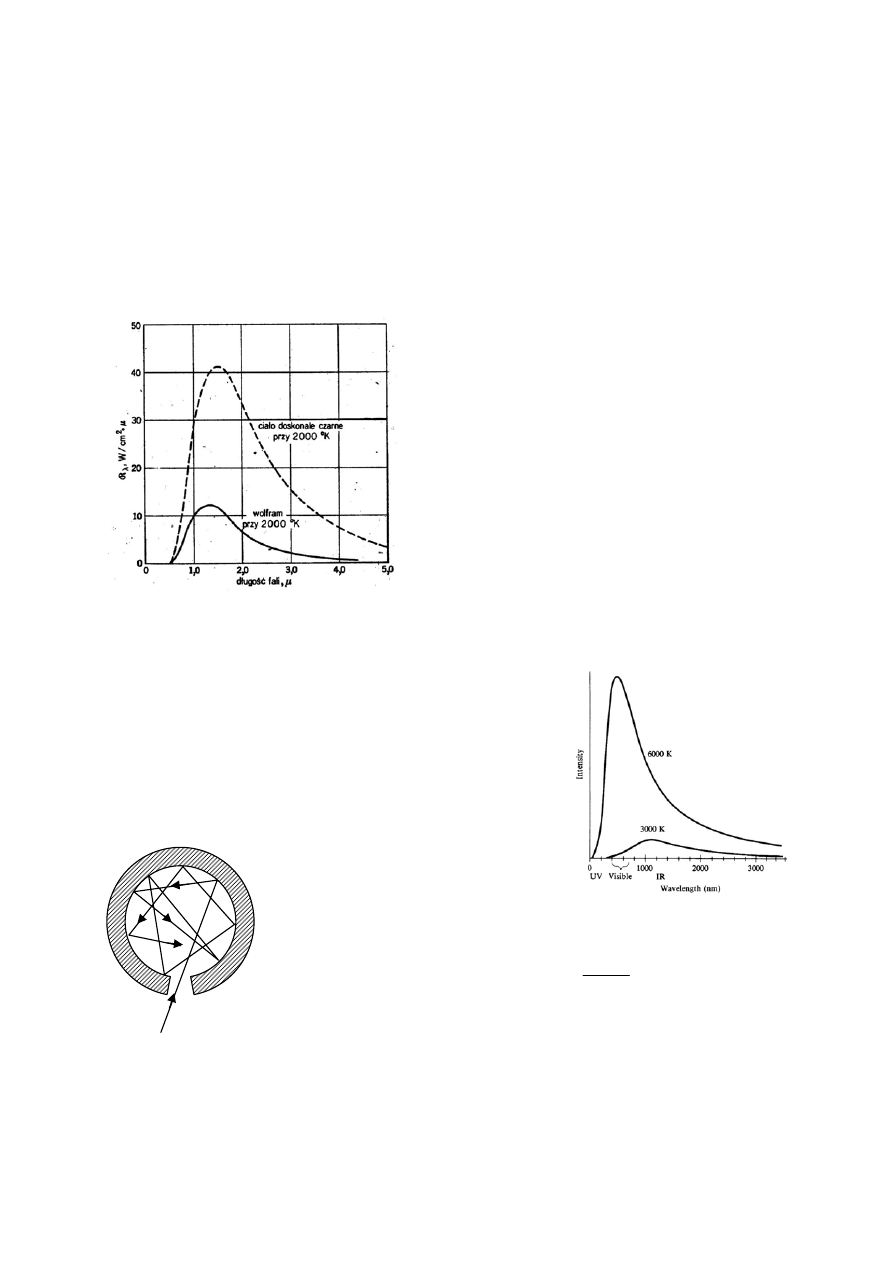
- opisane jest dla ciała doskonale czarnego (ciała, którego
powierzchnia absorbuje całe promieniowanie termiczne).

Emisja energetyczna promieniowania
ciała doskonale czarnego zmienia się z
temperaturą zgodnie z prawem S
Boltzmana:

R

=

σ⋅

T

4

gdzie

σ

=

⎥⎦

⎤

4

K

W

⎢⎣

⎡

⋅

−

2

8

10

67

,

5

m

Zauważmy, że maksima natężenia promieniowania dla różnych temperatur przypadają na
różne długości fal. Tzn. można to zapisać:

λ

1

T

1

=

λ

2

T

2

=

λ

3

T

3

=…. Ogólnie

λ⋅

T = const - prawo Wiena

Zastosowanie: pomiar temperatury gwiazd na podstawie analizy widmowej. Mierzymy

λ

⇒

λ⋅

T = 2,898

⋅10

-3

[m

⋅K] i stąd obliczmy temperaturę gwiazdy.

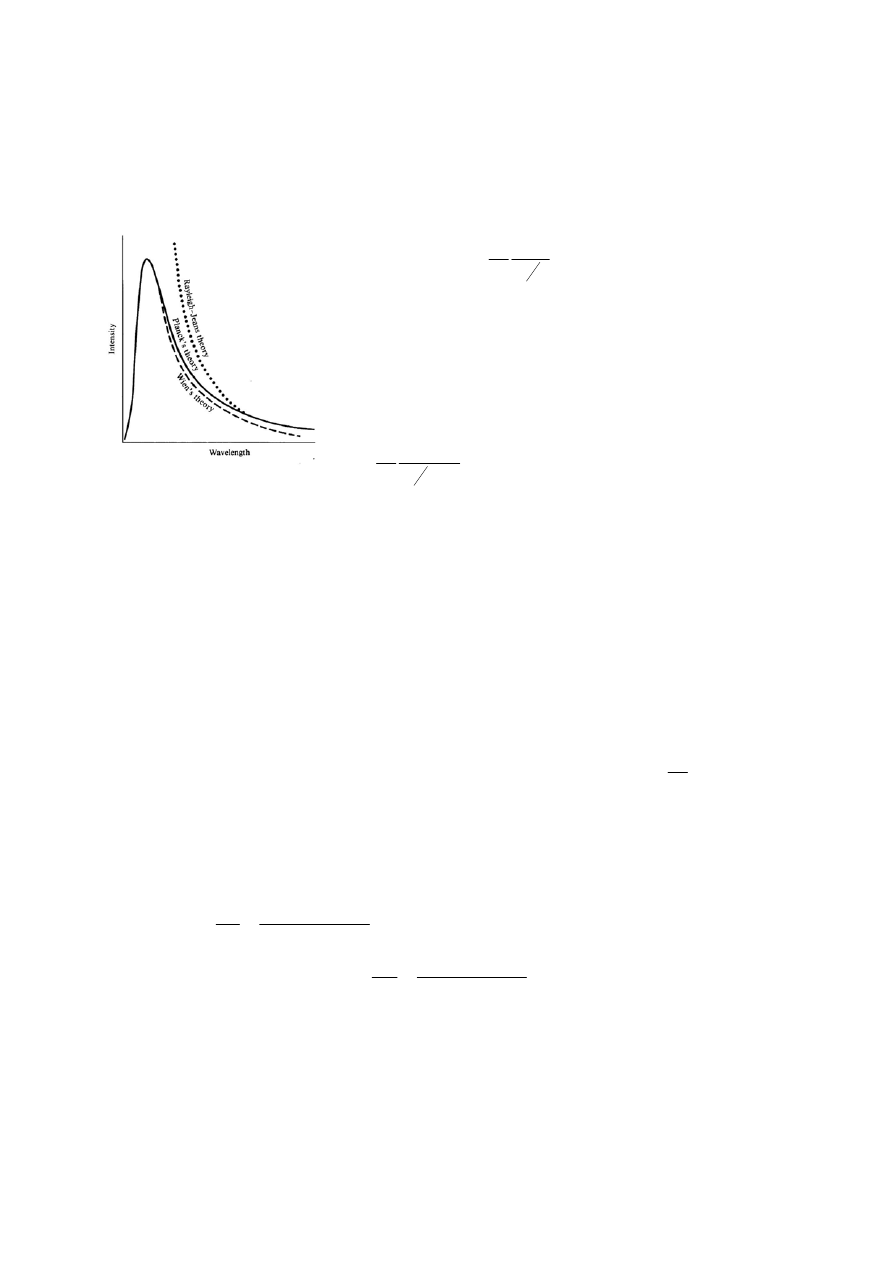
Podejmowano różne próby oparte na fizyce klasycznej, wyjaśnienia rozkładu promieniowania
ciała doskonale czarnego.

Teoria Wiena:

T

c

e

c

R

λ

λ

λ

2

1

5

1

=

gdzie c

1

, c

2

to stałe

wyznaczane doświadczalnie. Pokrywała się ona z wynikami
doświadczalnymi jedynie dla małych długości fal. Z kolei
teoria Rayleigh’a była zgodna z doświadczeniem tylko dla
dużych

λ

.

Dopiero Max Planck (1900) zmodyfikował wzór Wiena:

1

1

2

5

1

+

=

T

c

e

c

R

λ

λ

λ

otrzymując pełną zgodność z wynikami

doświadczalnymi.

Chcąc zbudować teorię wyjaśniającą otrzymaną zależność założył, że atomy ciała doskonale
czarnego zachowują się jak oscylatory harmoniczne o charakterystycznych częstościach
drgań:

1. Energia oscylatora jest kwantowana i dana wzorem: E = nh

ν

gdzie n = 1, 2, 3… -

liczba kwantowa, h = 6,63

⋅10

-34

- stała Plancka.

2. Oscylatory nie wypromieniowują energii w sposób ciągły, ale kwantowany, tzn.

wypromieniowana ilość energii

Δ

E = h

ν

. Oscylator znajdujący się w stanie

stacjonarnym (jeden ze stanów kwantowych) nie emituje ani ni absorbuje energii.

Planck wyznaczył wówczas na drodze teoretycznej stałe:

,

h

c

c

2

1

2

⋅

=

π

k

hc

c

=

2

gdzie c –

prędkość światła, k – stała Boltzmana. (1918 – nagroda Nobla)

Przykład:

Klasyczny oscylator o częstotliwości

ν

= 0,5 Hz i energii E = 0,1 J. Liczba kwantowa takiego

oscylatora

32

34

10

01

,

3

5

,

0

10

63

,

6

1

,

0

⋅

=

⋅

⋅

=

=

−

ν

h

E

n

(!) Jeżeli n zmienia się o jedność, to

względna zmiana energii oscylatora

33

34

10

3

,

3

1

,

0

5

,

0

10

63

,

6

−

−

⋅

=

⋅

⋅

=

Δ

E

E

co jest praktycznie

niemierzalne, czyli kwantowa natura drgań obiektów makroskopowych jest niewidoczna.

11.2. Zjawisko fotoelektryczne

U

h

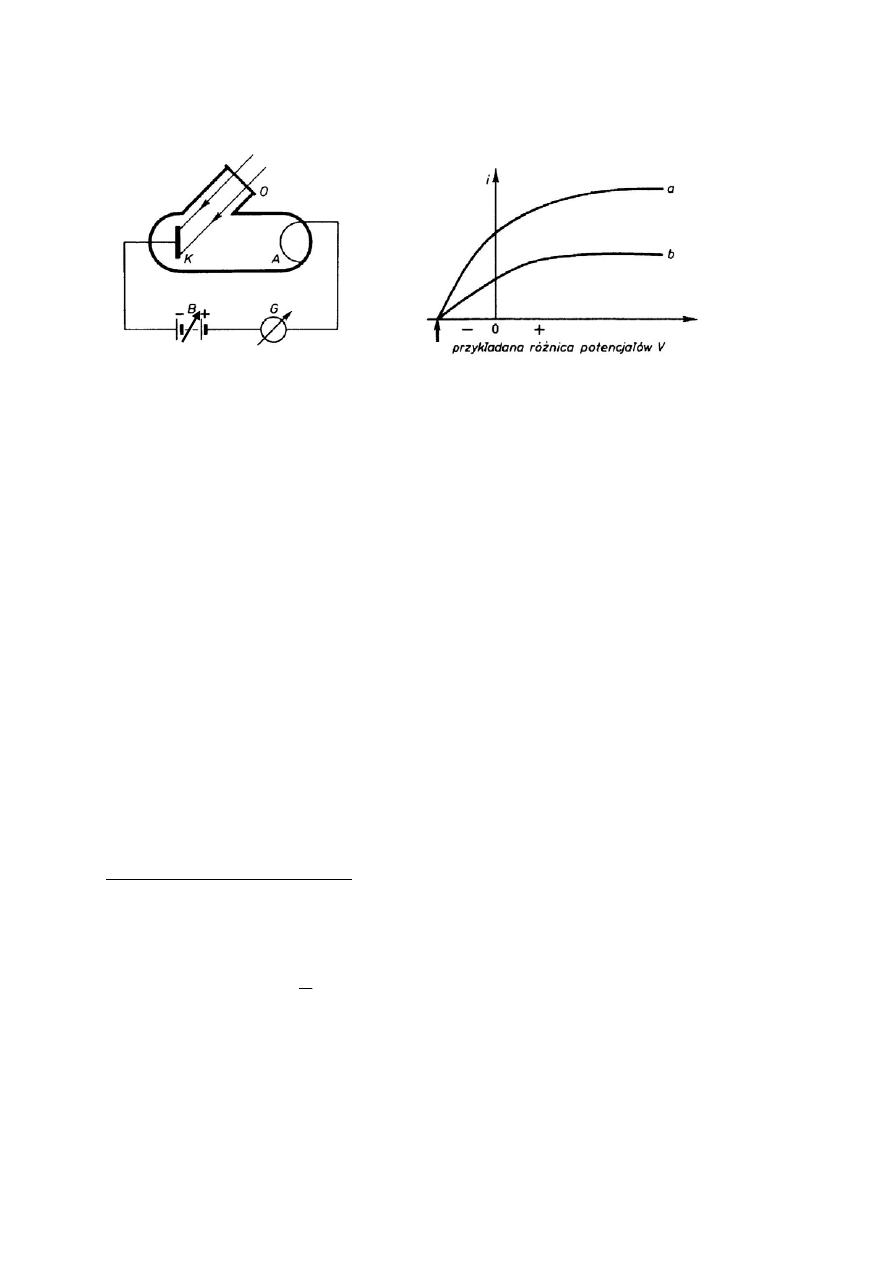
Fotoelektrony wybijane z katody, przyspieszane przez pole elektryczne, tworzą prąd
elektryczny, który płynie miedzy katodą a anodą nawet po przyłożeniu przeciwnego
potencjału do anody. Natężenie prądu fotoelektrycznego spada do zera przy potencjale anody
równym U

h

– potencjał (napięcie) hamujące. E

kmax

= e

⋅

U

h

Na wykresie natężenia fotoprądu od przyłożonego napięcia, krzywą b otrzymano przy
dwukrotnym zmniejszeniu natężenia światła.

Stosowane katody: Li, Cs, Rb

Wyjaśnienie zjawiska:

Planck: światło to fala elektromagnetyczna, rozchodząca się w postaci kwantów energii.

Jednakże wówczas, zgodnie z teorią falową:

1. energia kinetyczna fotoelektronów powinna wzrastać wraz z natężeniem światła,
2. efekt ten powinien występować dla dowolnej częstotliwości światła (o odpowiednio

dużym natężeniu),

3. przy małym natężeniu światła, fotoelektrony powinny wykazywać opóźnienie wybicia

w stosunku do czasu rozpoczęcia naświetlania, aby zmagazynować energię.

Tych efektów się nie obserwuje !!

Einstein: światło rozchodzi się w postaci cząsteczek – fotonów, z których każdy unosi kwant

energii:

λ

ν

c

h

h

E

=

=

A zatem w zjawisku fotoelektrycznym spełniona jest zasada zachowania energii:

h

ν

= W + E

k

gdzie

W – praca wyjścia elektronu, charakterystyczna dla danego

metalu katody.

Jeżeli E

k

= 0 to

W

hc

W

hc

h

gr

gr

gr

=

⇒

=

=

λ

λ

ν

jest to graniczna długość światła, przy

której zachodzi zjawisko fotoelektryczne.

Z zasady zachowania energii:

e

W

e

h

U

h

−

=

ν

ν

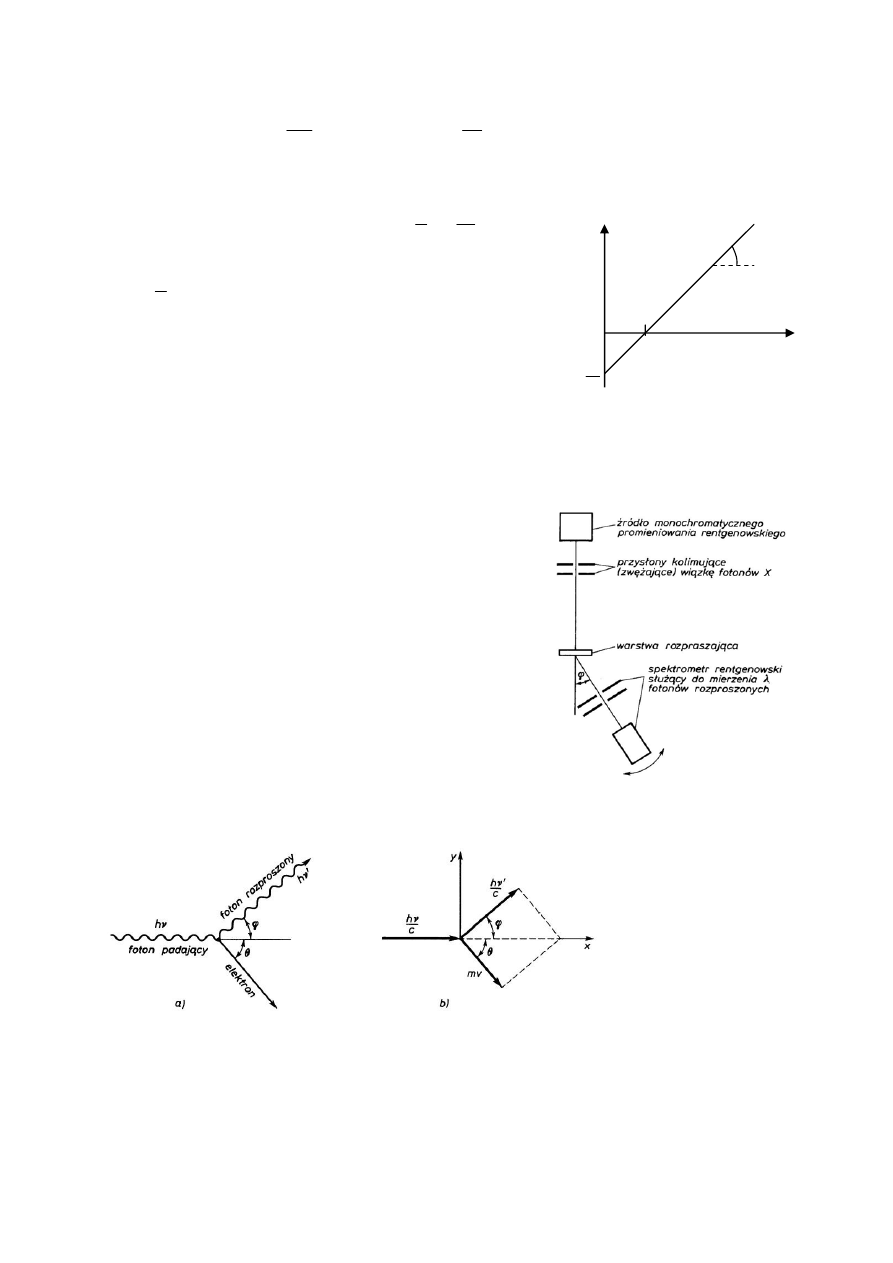
U

h

ν

o

e

W

−

α

α

α

tg

e

h

e

h

tg

⋅

=

⇒

=

Jest to więc sposób wyznaczenia pracy wyjścia

oraz wartości stałej Plancka.

11.3. Zjawisko Comptona

Jest to drugi efekt wskazujący na korpuskularna naturę
światła. Compton (1923) zaobserwował rozproszone
promienie X o zmienionej długości fali. Klasyczna teoria
fal elektromagnetycznych zjawisko rozproszenia
tłumaczyła jako pobudzenie do drgań elektronów ośrodka
rozpraszającego, które staja się wtórnym źródłem fal – ale
bez zmiany długości !

Według teorii kwantowej zjawisko polega na zderzeniu
padającego fotonu z elektronem swobodnym. Podczas
zderzenia foton oddaje elektronowi jedynie część energii.

Zasada zachowania energii:

Zasada zachowania pędu:

Zasada zachowania energii:

Zasada zachowania pędu dla osi OX:

( )

2

2

0

2

0

1

'

c

v

c

m

hc

c

m

hc

−

+

=

+

λ

λ

( )

4

4 3

4

4 2

1

4

3

42

1

elektron

foton

c

v

v

m

h

h

ϕ

ϕ

λ

λ

cos

1

cos

'

2

0

−

+

=

Zasada

zachowania

pędu dla osi OY:

( )

4

4 3

4

4 2

1

3

2

1

elektron

foton

c

v

v

m

h

ϕ

ϕ

λ

sin

1

sin

'

0

2

0

−

−

=

Po wyeliminowaniu z równań v oraz

ϕ

otrzymujemy:

)

cos

1

(

'

0

ϕ

λ

λ

λ

−

=

−

=

Δ

c

m

h

W zjawisku Cmptona zmiana długości fali nie zależy od energii fotonu
padającego, a zależy jedynie od kata jego rozproszenia.

Dla

ϕ

= 0

0

Δλ = 0; dla

ϕ

= 180

0

Δλ = 2

Λ

(rozproszenie wsteczne), a dla

ϕ

= 90

0

Δλ =

Λ

Oba opisy światła: falowy i korpuskularny są poprawne: w pewnych przypadkach
promieniowanie elektromagnetyczne zachowuje się jak fala o określonej długości i
częstotliwości, a w innych jak zbiór fotonów o określonym pędzie i zerowej masie
spoczynkowej. Przejście od obrazu falowego do korpuskularnego opisują wzory:

mv

h

h

p

h

E

=

=

=

λ

λ

ν

Dokładniej omówiony ten problem będzie w rozdz.12.

11.4. Model atomu Bohra

Postulaty Bohra:

I.

Atom wodoru może znajdować się jedynie w ściśle określonych stanach

stacjonarnych, w których nie promieniuje energii.

II.

Elektron atomu w stanie stacjonarnym porusza się tylko po takich orbitach kołowych,

dla których moment pędu jest skwantowany, tzn. spełnia zależność:

π

2

h

n

L

n

=

gdzie

n = 1, 2, ..

III.

Warunkiem wypromieniowania energii jest przejście atomu ze stanu o energii wyższej

E

k

do stanu o energii niższej E

j

: h

ν

= E

k

- E

j

Skoro elektron porusza się po orbicie kołowej pod wpływem siły kulombowskiej będącej siłą
dośrodkową, to z tego warunku można obliczyć prędkość elektronu. A zatem pęd p elektronu
i jego moment pędu L można zapisać:

0

2

0

2

4

4

πε

πε

r

me

pr

L

r

me

mv

p

=

=

=

=

Uwzględniając warunek kwantyzacji momentu pędu otrzymujemy wyrażenia na promień
orbity i energię kinetyczną elektronu.

2

2

0

4

2

0

2

2

8

n

h

me

E

me

h

n

r

n

n

ε

π

ε

−

=

=

A zatem promień orbity rośnie jak n

2

, a energia całkowita rośnie (do zera) jak 1/n

2

. Jonizacji

atomu odpowiada n =

∝. Wówczas całkowita energia atomu E = 0, a r = ∝.

Energia atomu w stanie podstawowym n = 1 :

E

1

= -13,6 eV

Na podstawie powyższych wzorów otrzymujemy wzór na częstość linii widmowych atomu
wodoru:

⎟⎟

⎠

⎞

⎜⎜

⎝

⎛

−

⋅

=

⎟⎟

⎠

⎞

⎜⎜

⎝

⎛

−

=

2

2

2

2

3

2

0

4

1

1

1

1

8

k

j

c

R

k

j

h

me

ε

ν

gdzie

R jest stałą Rydberga.

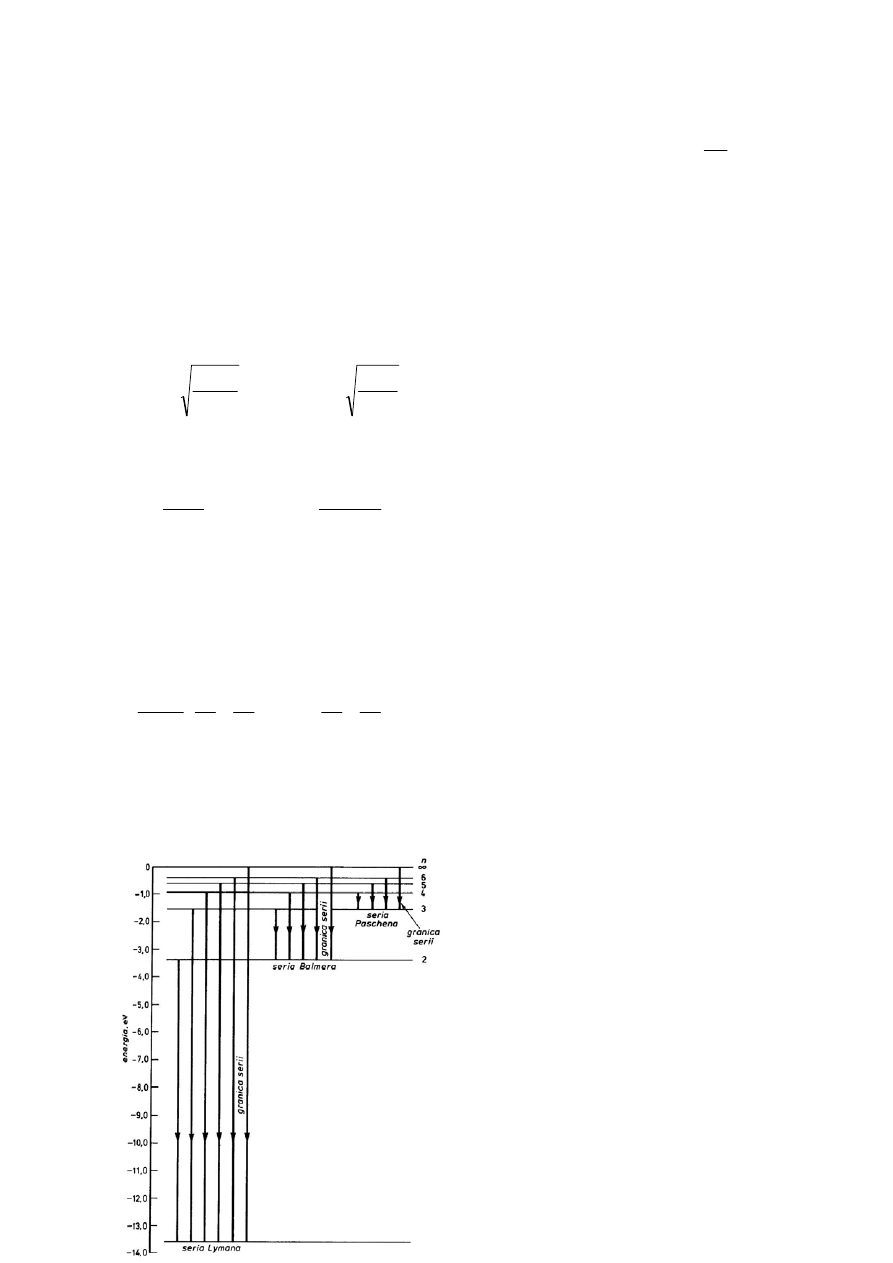
Przejścia elektronu miedzy kwantowanymi poziomami energetycznymi można przedstawić w
postaci tzw. serii widmowych.

Linie serii zagęszczają się w kierunku fal krótkich, a każdą serię ogranicza linia

odpowiadająca najmniejszej długości fali
danej serii.

Przykład:
Obliczyć długość fali emitowanej przy przejściu elektronu z orbity 3 na pierwszą.

31

31

1

3

λ

ν

hc

h

E

E

=

=

−

9

1

3

1

1

2

1

2

1

31

E

E

E

E

hc

−

=

⎟

⎠

⎞

⎜

⎝

⎛−

−

⎟

⎠

⎞

⎜

⎝

⎛−

=

λ

1

31

1

31

8

9

9

8

E

hc

E

hc

=

⇒

=

λ

λ