1

Wszelkie prawa do zada

ń

, plików i instrukcji s

ą

zastrze

ż

one, nikt poza prowadz

ą

cymi zaj

ę

cia i studentami IA na AGH nie ma prawa ich

wykorzystywa

ć

. A tych co maj

ą

takie prawa, prosz

ę

, aby nie umieszczali ich w innym miejscu w sieci.

Grafika 3D

Prosz

ę

, aby ka

ż

de zadanie było rozwi

ą

zane w innym skrypcie.

Wszystkie skrypty i funkcje maj

ą

by

ć

zapisane w dowolnym folderze nale

żą

cym

do Pa

ń

stwa.

cz

ęść

I – funkcja plot3

plot3(x,y,z) rysuje funkcje np. w postaci parametrycznej, przy czym x, y, z – s

ą

to wektory o takim

samym rozmiarze (wszystkie wektory maj

ą

mie

ć

tyle samo elementów).

Zad1. Prosz

ę

przekopiowa

ć

tre

ść

poni

ż

szego skryptu na swój komputer.

figure(1)
t=0:.1:12; x=t; y=sin(t); z=cos(t);
plot3(x,y,z)
grid

on

;

W drugim oknie prosz

ę

narysowa

ć

ten sam wykres, ale dla zrównanych jednostek

na osiach, za pomoc

ą

powy

ż

szych polece

ń

oraz polecenia

axis equal
Wykorzystuj

ą

c edytor wła

ś

ciwo

ś

ci oraz przegl

ą

dark

ę

obiektów

prosz

ę

opisa

ć

osie „x”, ”y” i „z”.

Zad 2. Oto współrz

ę

dne punktów: x = [1 1 -1 1]; y = [4 4 4 4]; z = [-1 1 1 -1];

Prosz

ę

narysowa

ć

trójk

ą

t, który powstanie z powy

ż

szych punktów, czerwon

ą

lini

ą

o grubo

ś

ci 6

(…'LineWidth',6).

cz

ęść

II – wykresy 3D

siatki powierzchni
i powierzchnie

2.1

Funkcja meshgrid i mesh

Funkcja meshgrid

[X , Y] = meshgrid (x, y) przekształca wektory x i y w macierze X i Y, po to, aby powstała
siatka punktów, które u

ż

ywamy do znajdowania warto

ś

ci funkcji dwóch zmiennych

i generowania trójwymiarowych wykresów. Wiersze wynikowej macierzy X s

ą

kopiami wektora

x, kolumny wynikowej macierzy Y s

ą

kopiami wektora y.

Funkcja mesh

mesh (X, Y, Z) rysuje szkielet siatki

2

Zad 3. Prosz

ę

stworzy

ć

skrypt, który zawiera poni

ż

sze polecenia:

clear

all

x=-5:5;
y=-10:10;
[X, Y]=meshgrid(x,y)

Prosz

ę

sprawdzi

ć

jak została wygenerowana siatka X i Y, a potem wstawi

ć

; po poleceniu

[X, Y]=meshgrid(x,y);

I wykorzystuj

ą

c powy

ż

sz

ą

siatk

ę

punktów prosz

ę

narysowa

ć

wykres funkcji:

݂ሺݔ, ݕሻ = ܺ

ଷ

+ 3ܻܺ

ଶ

+ 12ܻܺ

W drugim oknie dla tych samych danych prosz

ę

narysowa

ć

powierzchni

ę

za pomoc

ą

polecenia surf(X,Y,Z). Prosz

ę

doło

ż

y

ć

wska

ź

nik colorbar do obu okien.

Funkcja surf(X,Y,Z) – rysuje powierzchni

ę

kolorow

ą

opisan

ą

przez macierze X,Y,Z.

2.2. Rysowanie siatki powierzchni za pomoc

ą

: mesh(x,y,z), meshc(x,y,z) - meshz(x,y,z)

i waterfall(x,y,z)

Zad 4. Dla nast

ę

puj

ą

cych danych: x=0:0.5:10;y=0:.5:5; z=sin(y)'*cos(x);

w jednym oknie i na 4 wykresach prosz

ę

narysowa

ć

funkcje

mesh(x,y,z), meshc(x,y,z) -

meshz(x,y,z) i waterfall(x,y,z). Korzystaj

ą

c z poni

ż

szej tabelki prosz

ę

opisa

ć

wykresy poprzez

dodanie tytułów.

mesh

Wykres siatkowy

meshc Wykres siatkowy + poziomice

meshz Wykres siatkowy + zasłony na ko

ń

cach

ribbon Wykres wst

ąż

kowy

surf

Wykres powierzchniowy

surfc

Wykres powierzchniowy + poziomice

surfl

Wykres powierzchniowy + cieniowanie

waterfall

funkcja waterfall(x, y, z, c) działa podobnie jak meshz z ta ró

ż

nic

ą

,

ż

e nie

rysuje linii odpowiadaj

ą

cych kolumnom macierzy

2.2. Rysowanie powierzchni za pomoc

ą

: surf, surfc, surfl

Zad 5. Dla nast

ę

puj

ą

cych danych: x=0:0.5:10;y=0:.5:5; z=sin(y)'*cos(x);

a)

w pierwszym oknie na 3 wykresach prosz

ę

narysowa

ć

funkcje surf, surfc, surfl

b)

w dugim oknie na trzech wykresach dla surf prosz

ę

sprawdzi

ć

jak działa przejrzysto

ść

alpha

3

ustawiaj

ą

c w kolejnych oknach alpha(0) alpha(0.5) i alpha(1). Prosz

ę

sprawdzi

ć

te

ż

ukrywanie kraw

ę

dzi:

hidden on

Wyświetlanie ukrytych krawędzi

hidden off

Domyślny, ukrywa niewidoczne krawędzie

c)

w trzecim oknie sterujemy kolorem i wy

ś

wietlaniem siatki oraz kolorem powierzchni

za pomoc

ą

instrukcji:

surf(x,y,z,'FaceColor',[0.5 0.5 0.5], 'EdgeColor','red')
surf(x,y,z,'FaceColor','blue', 'EdgeColor','none')

–prosz

ę

sprawdzi

ć

jak działa dodatkowo

camlight left ( mo

ż

e zamiast left lepiej b

ę

dzie:

headlight, left, right

lighting phong (phong, flat, gouraud, none)

je

ś

li nie wida

ć

zmian, prosz

ę

zmieni

ć

kolor siatki i powierzchni

d)

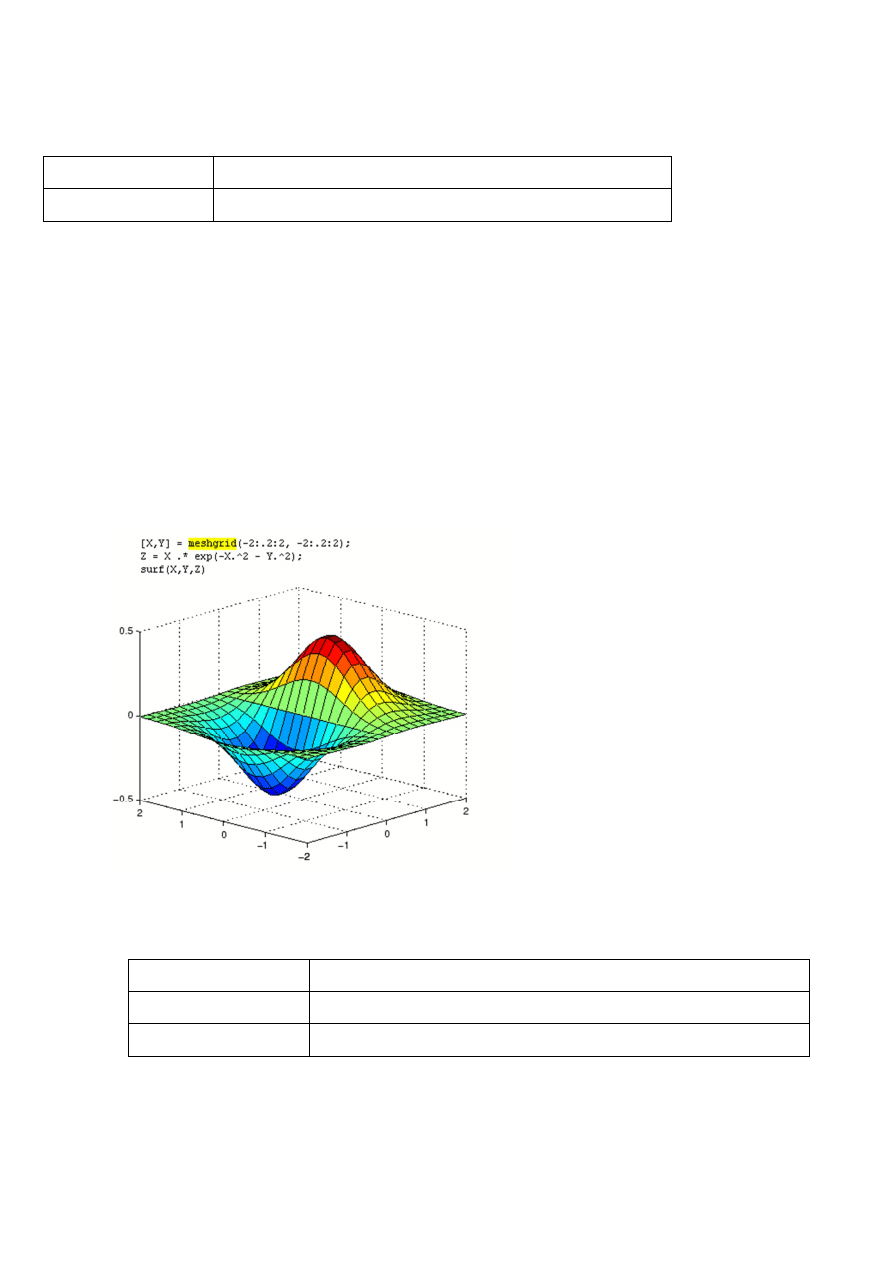
w czwartym oknie

ć

wiczymy cienie - potrzebujemy do tego trzy wykresy funkcji

z=x*exp(-x

2

-y

2

), pierwszy jest na rysunku poni

ż

ej:

drugi wykres powinien by

ć

narysowany za pomoc

ą

funkcji:

surfl(x,y,z), a trzeci mie

ć

dodatkowo doło

ż

on

ą

do surfl(x,y,z) funkcj

ę

shading interp;

shading flat

Powierzchnia z dyskretnymi kolorami

shading interp

Powierzchnia z wypełnieniem kolorami interpolowanymi

shading faceted

Powierzchnia z dyskretnymi kolorami i siatka

e)

w pi

ą

tym oknie zobaczymy jakie s

ą

mo

ż

liwo

ś

ci wy

ś

wietlania poziomic. Znowu podzielimy

okno na 4 wykresy. Bazowym wykresem niech b

ę

dzie

:

x=0:0.1:10;y=0:.1:5; z=sin(y)'*cos(x); meshc(x,y,z)

4

Korzystaj

ą

c z polecenia:

contour(x,y,z,n) – kre

ś

lenie poziomic (wykres konturowy), gdzie n – liczba poziomic

prosz

ę

wykre

ś

li

ć

3 poziomice

i w kolejnym okienku trzy poziomice opisane:

[c,h]=contour(x,y,z,n)
clabel(c,h);

Prosz

ę

sprawdzi

ć

jak działa polecenie contourf(x,y,z,5), w ostatnim, czwartym wykresie.

cz

ęść

IV – dodatkowe wykresy w grafice 3D

bar3, ribbon

Zad 6. Dowoln

ą

funkcj

ę

3D prosz

ę

przedstawi

ć

za pomoc

ą

polecenia

ribbon(Y,Z)

Zad 7. Dla wylosowanych danych Y=round(rand(10,4)*100) na trzech ró

ż

nych wykresach prosz

ę

sprawdzi

ć

jak działa:

bar3(Y,

'detached'

)

bar3(Y,

'grouped'

)

bar3(Y,

'stacked'

) W ka

ż

dym wykresie prosz

ę

zmieni

ć

domy

ś

lny punkt obserwacji

view

Zmiana domy

ś

lnego punktu obserwacji

view(azymut, elewacja)

Okre

ś

la punkt obserwacyjny za pomoc

ą

azymutu i

elewacji

view([x,y,z])

Okre

ś

la punkt obserwacji w układzie kartezja

ń

skim

view(2)

Obserwacja azymut=0, elewacja=90

view(3)

Domy

ś

lny punkt obserwacji: azymut=-37.5 ,

elewacja= 30

cz

ęść

V – animacje

funkcja comet(x,y); - to animacja ruchu komety. x,y – to współrz

ę

dne poło

ż

enia.

Zad 8. Prosz

ę

napisa

ć

skrypt, w którym za pomoc

ą

animacji mo

ż

emy zobaczy

ć

ruch

komety po torze, który jest elips

ą

.

Funkcje getframe i movie, to kolejny przykład animacji. Ka

ż

de polecenie plot generuje

nowe okno, zawarto

ść

tego okna mo

ż

na przy pomocy polecenie getframe zapisa

ć

np.: w tablicy.

Utworzone tablice odtwarzamy wykorzystuj

ą

c polecenie movie. Jako przykład wykorzystania tych

funkcji podaje si

ę

poni

ż

szy skrypt :

for k = 1:16

5

plot(fft(eye(k+16)))
axis equal
M(k) = getframe;
end
movie(M,30)

Zad 9. Prosz

ę

napisa

ć

skrypt, w którym za pomoc

ą

animacji mo

ż

emy zobaczy

ć

kolejne

etapy rysowania funkcji sinus.

Przy braku pomysłu na rozwi

ą

zanie prosz

ę

przej

ś

c do

kolejnego zadania, jest tam ukryta podpowied

ź

.

drawnow – aktualizacja okna

Zad 10. Oto przykład rysowania funkcji przy pomocy polecenia drawnow

x = -2*pi:pi/20:2*pi;
for i=1:8
plot(x(1:i*10),cos(x(1:i*10)))
axis([-2*pi 2*pi -1 1])
drawnow
pause(0.1)
end;

Prosz

ę

wykorzystuj

ą

c dranow narysowa

ć

dowolny wykres funkcji oraz dowoln

ą

powierzchni

ę

.

cz

ęść

VI – walec, kula, wielok

ą

t, elipsoida

cylinder

Generacja walca

elipsoid

Generacja elipsoidy

(nie działa w pracowni)

fill3

Generacja wielok

ą

ta

( nie działa w pracowni)

sphere

Generacja kuli

Zad 11. Prosz

ę

wygenerowa

ć

figury podane w powy

ż

szej tabeli i za pomoc

ą

polecenia slice

przeci

ąć

dwie z tych figur dowoln

ą

płaszczyzn

ą

.