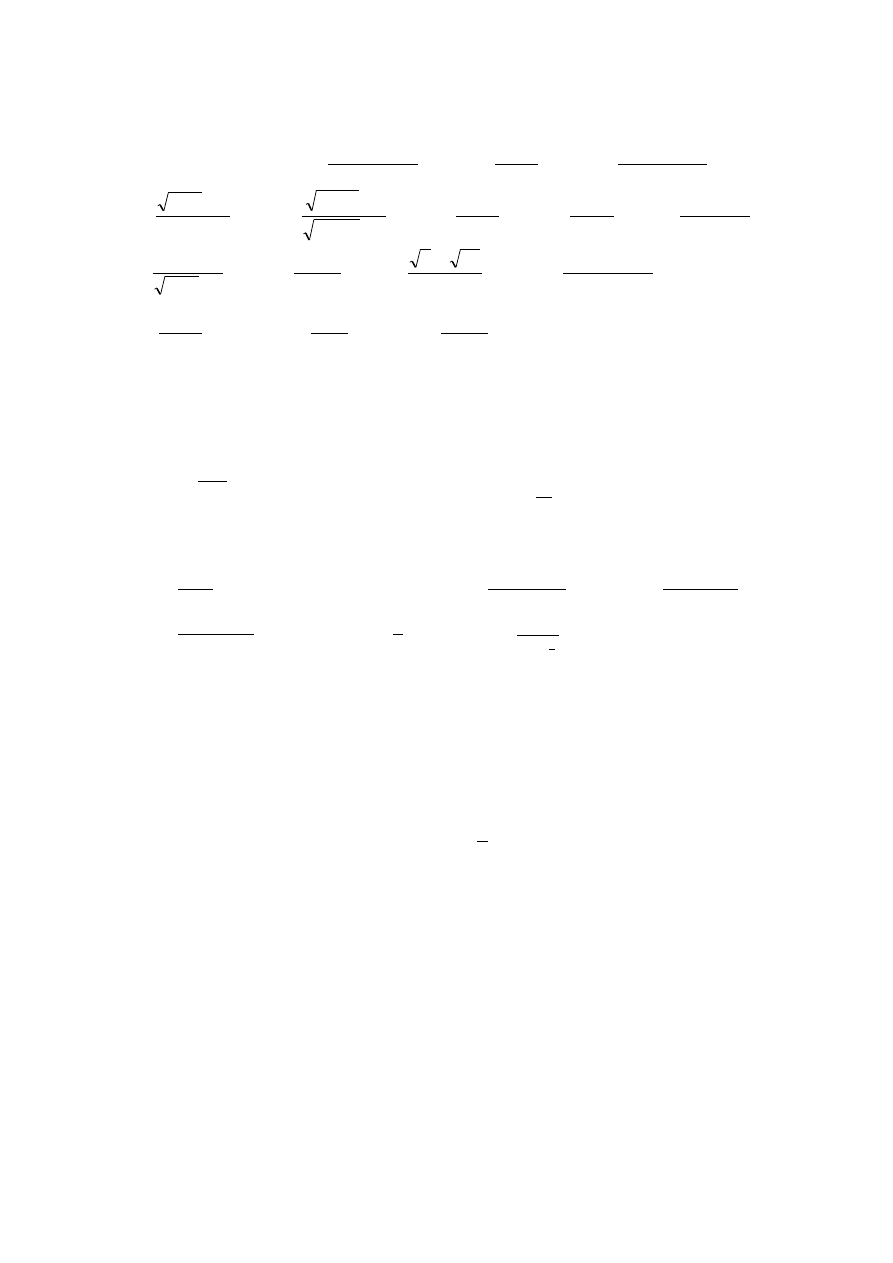
GRANICE I CIĄGŁOŚĆ FUNKCJI
1. Obliczyć granice:
a)
)
6
7
2
(
lim
2
3
x
x
x
, b)
4
6
3
2
5
4
lim
2
2
2
x
x
x
x
x
, c)
1
1
lim
2
1
x
x
x
, d)
2
3
2
3
2
lim
2
2
2
x
x
x
x
x
,
e)
5
2
1
lim
5
x
x
x
, f)
3
9
1
1
lim
2
2
0
x
x
x
, g)
x
tg
x
x
3
5
sin
lim
0
, h)
2
2
0
sin
lim
x
x
x
, i)
2
0
3
2
cos
1
lim
x
x
x
,
j)
1
1
7
sin
lim
0
x
x
x
, k)
4
3
2
lim
2
x
x
x
, l)
1
2
5
lim
x
x
x
x
, m)
4
6
3
2
5
4
lim
2
3
x
x
x
x
x
,
n)
1
2
2
2
1
lim
x
x
x
x
, o)
x
x
x
x
2
5
lim
, p)
2
7
3
lim
2
2
x
x
x
x
.
2. Obliczyć granice jednostronne funkcji
f
w punkcie
0
x
jeżeli:
a)
1
1
1
3
2
2
)
(
0
x
x
x
dla
dla
x
x
x
f
, b)
3
3
3
6
)
(
0
2
x
x
x
dla
dla
x
x
x
f
,
c)
1
2
)
(
0
1
1
2
x
x
f
x
, d)
6
)
(
0
3
x
e
x
f
x
tg
.
3. Obliczyć wszystkie granice funkcji
f
w końcach przedziałów jej dziedziny jeżeli:
a)
1
3
)
(
x
x
x
f
, b)
5
3
)
(
2
3
x
x
x
f
, c)
2
2
4
7
2
)
(
x
x
x
x
f
, d)
2
1
)
(
2
2
3
x
x
x
x
x
f
,
e)
1
2
5
3
)
(
2
x
x
x
x
f
, f)
x
arctg
x
f
1
)
(
, g)
x
e
x
f
1
1
1
)
(
, h)
2
2
ln
)
(
x
x
x
f
,
i)
4
3
ln
)
(
2
x
x
x
f
.
4. Dla jakiej wartości parametru
p
funkcja
f
jest ciągła? Naszkicować wykres funkcji dla tej
wartości parametru.
a)
1
1
1
2
)
(
2
x
x
dla
dla
p
x
x
f
x
, b)
0
0
1
)
(
2
x
x
dla
dla
p
x
x
x
f
,
c)
1
1
3
3
)
(
2
x
x
dla
dla
px
x
x
f
, d)
2
2
2
)
(
2
x
dla
p
x
x
dla
x
x
f
.