Granica i ciągłość funkcji
Pojęcie funkcji. Dane są zbiory X oraz Y.
Jeżeli każdemu elementowi zbioru X zostanie
przyporządkowany dokładnie jeden element zbioru Y, to
mówimy, że została określona funkcja ze zbioru X w zbiór
Y.
Oznaczmy tę funkcję literą f. Piszemy:
Y
X
f
:
Zbiór X nazywamy dziedziną funkcji.
Każdy element zbioru X nazywamy argumentem funkcji f.
Element
Y
y
przyporządkowany argumentowi
X
x
nazywamy wartością funkcji f dla argumentu x. Piszemy:
)
(x
f
y
.
W dalszym ciągu będziemy zajmować się funkcjami, dla
których zbiory X oraz Y są podzbiorami zbioru liczb
rzeczywistych R.
Są to funkcje liczbowe jednej zmiennej rzeczywistej.
Mówiąc: „funkcja” będziemy mieli na myśli takie funkcje.
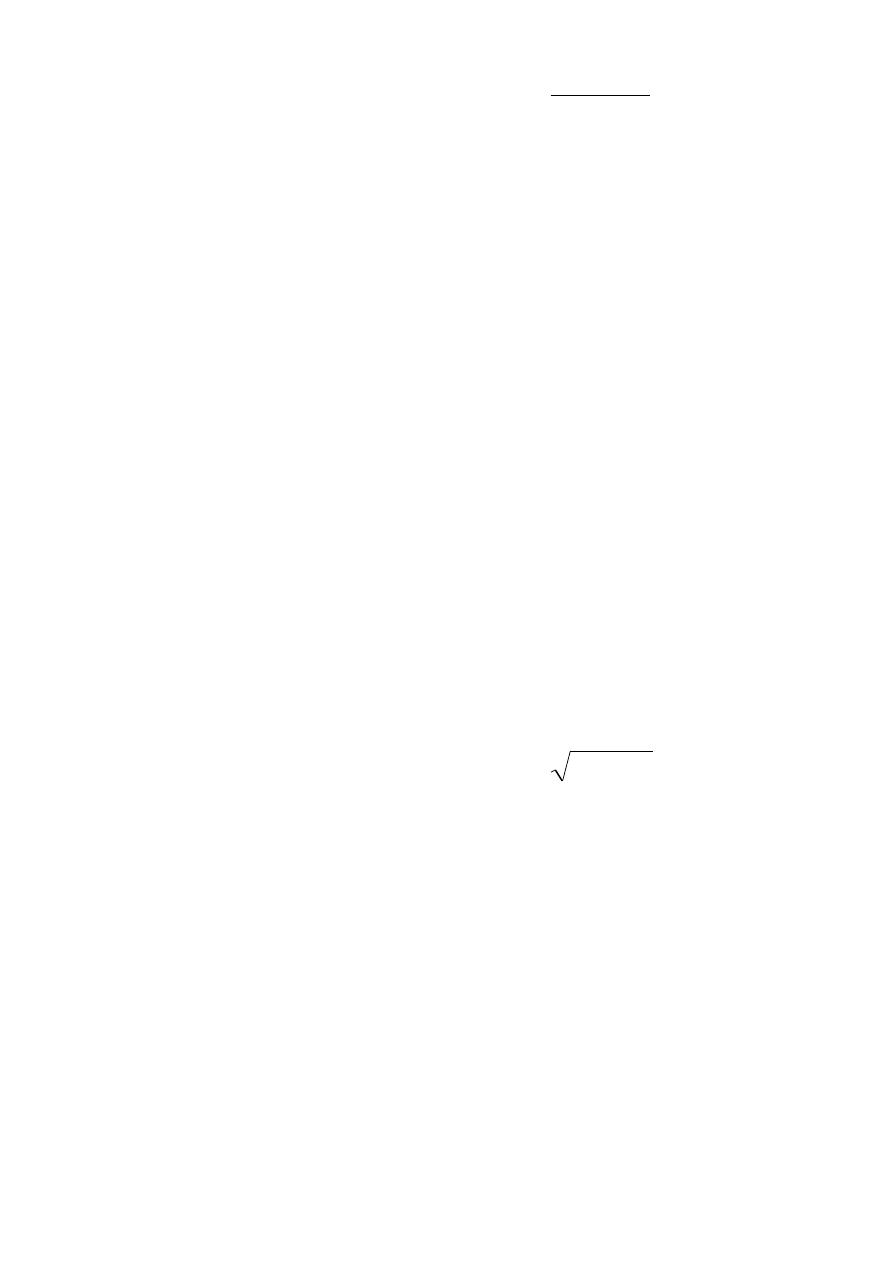
Przykład 1. Dana jest funkcja
x
x
x
x
f
2
3
)
(
2
. Wyznaczmy
dziedzinę tej funkcji.
Funkcja ta nie jest określona, gdy mianownik ma wartość
zero. Zatem:
0
2
2
x
x
Stąd:
0
)
2
(
x
x
Czyli:
2
0
x
i
x
dziedzina funkcji f.
Uwaga: Powyższy warunek możemy zapisać na kilka
sposobów, np.
}
2
,
0
{
R
x
albo
)
;
2
(
)
2
;
0
(
)
0
;
(
x
. Często oznaczamy dziedzinę
literą D, wtedy możemy też napisać np.
}
2
,
0
{
R
D
albo
)
;
2
(
)
2
;
0
(
)
0
;
(
D
.
Przykład 2. Dana jest funkcja
6
2
)
(
x
x
f
. Wyznaczmy
dziedzinę tej funkcji.
Funkcja ta nie jest określona, gdy wyrażenie
podpierwiastkowe jest ujemne. Zatem:
0
6
2
x
. Stąd:
6
2
x
, czyli:
3
x
.
Uwaga: Powyższy warunek możemy zapisać inaczej, np.
)
;
3
x
albo
)
;
3
D
.
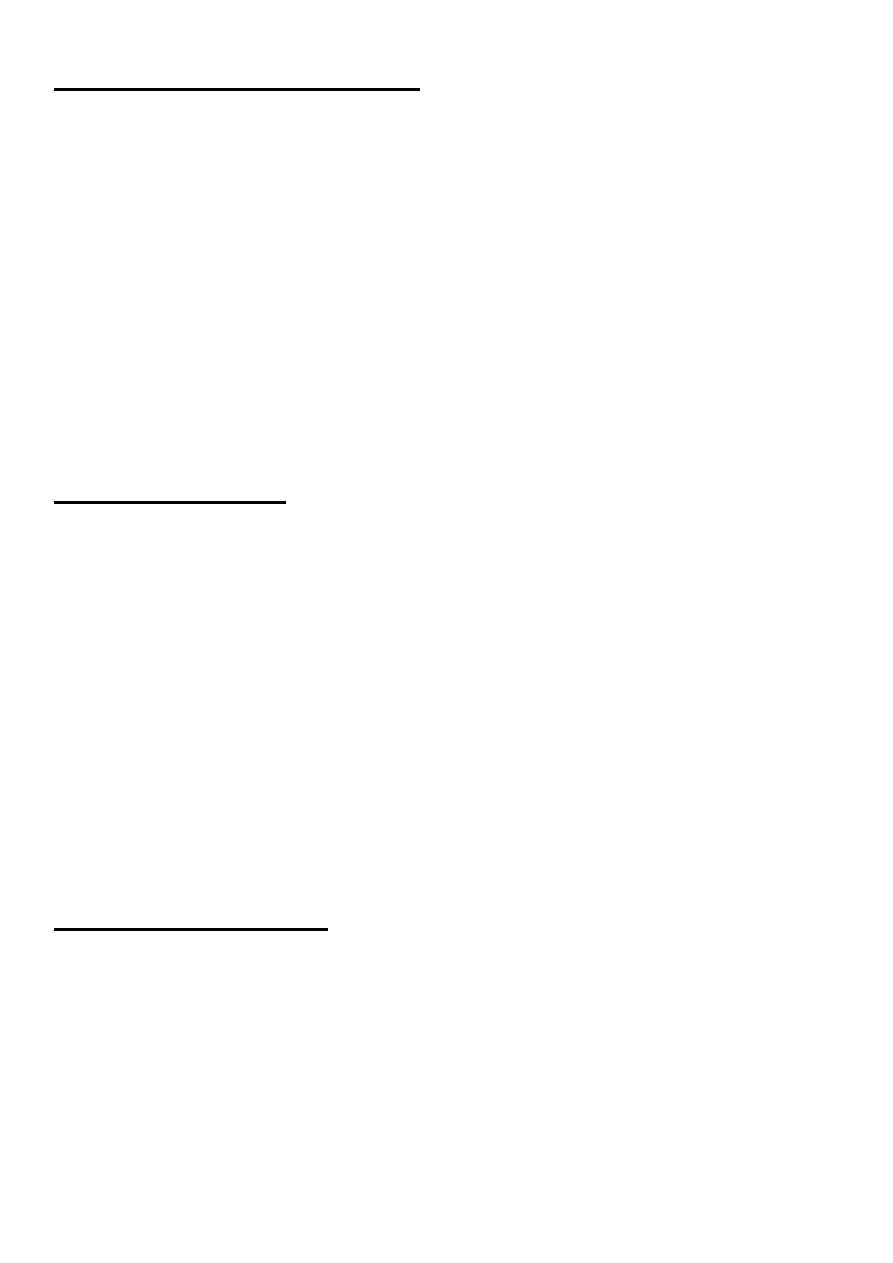
Funkcje różnowartościowe
Mówimy, że funkcja f jest różnowartościowa, gdy
różnym argumentom są przyporządkowane różne wartości
funkcji.
Wykres funkcji różnowartościowej ma własność: każda
prosta równoległa do osi OX przecina wykres w co
najwyżej jednym punkcie.
Funkcje parzyste
Mówimy, że funkcja f jest parzysta, gdy dla dowolnego
argumentu x liczba
x
też jest argumentem i zachodzi
równość:
)
(
)
(
x
f
x
f
Wykres funkcji parzystej jest symetryczny względem osi
OY.
Funkcje nieparzyste
Mówimy, że funkcja f jest nieparzysta, gdy dla
dowolnego argumentu x liczba
x
też jest argumentem i
zachodzi równość:
)
(
)
(
x
f
x
f
Wykres funkcji nieparzystej jest symetryczny względem
początku układu współrzędnych.
Otoczenie i sąsiedztwo liczby (punktu na osi)
Przypomnienie: Otoczeniem liczby g (punktu g – na osi) o
promieniu
nazywamy przedział
)
;
(
g
g
.
Sąsiedztwem liczby g (punktu g – na osi) o promieniu
nazywamy zbiór
}
{
)
;
(
g
g
g
.
Granica funkcji w punkcie
Niech
R
x
0
i niech f będzie funkcją określoną w
sąsiedztwie
0
x
.
Mówimy, że granica funkcji f w punkcie
0
x
jest równa g
jeżeli dla każdego ciągu
)
(
n
x
argumentów funkcji,
zbieżnego do
0
x
, o wyrazach różnych od
0
x
, ciąg
))
(
(
n
x
f
ma granicę g.
Piszemy:
g
x
f
x
x
)
(
lim
0
Uwaga: g może być liczbą lub
lub
.
Granica funkcji w plus nieskończoności
Niech f będzie funkcją określoną w przedziale
)
;
(
a
.
Mówimy, że granica funkcji f w plus nieskończoności
jest równa g jeżeli dla każdego ciągu
)
(
n
x
argumentów
funkcji, rozbieżnego do
, ciąg
))
(
(
n
x
f
ma granicę g.
Piszemy:
g
x
f
x
)
(
lim
Uwaga: g może być liczbą lub
lub
.
Granica funkcji w minus nieskończoności
Niech f będzie funkcją określoną w przedziale
)
;
(
a
.
Mówimy, że granica funkcji f w minus nieskończoności
jest równa g jeżeli dla każdego ciągu
)
(
n
x
argumentów
funkcji, rozbieżnego do
, ciąg
))
(
(
n
x
f
ma granicę g.
Piszemy:
g
x
f
x
)
(
lim
Uwaga: g może być liczbą lub
lub
.
Rachunek granic
Dla granic funkcji prawdziwe są twierdzenia analogiczne
do twierdzeń – rachunku granic dla ciągów.
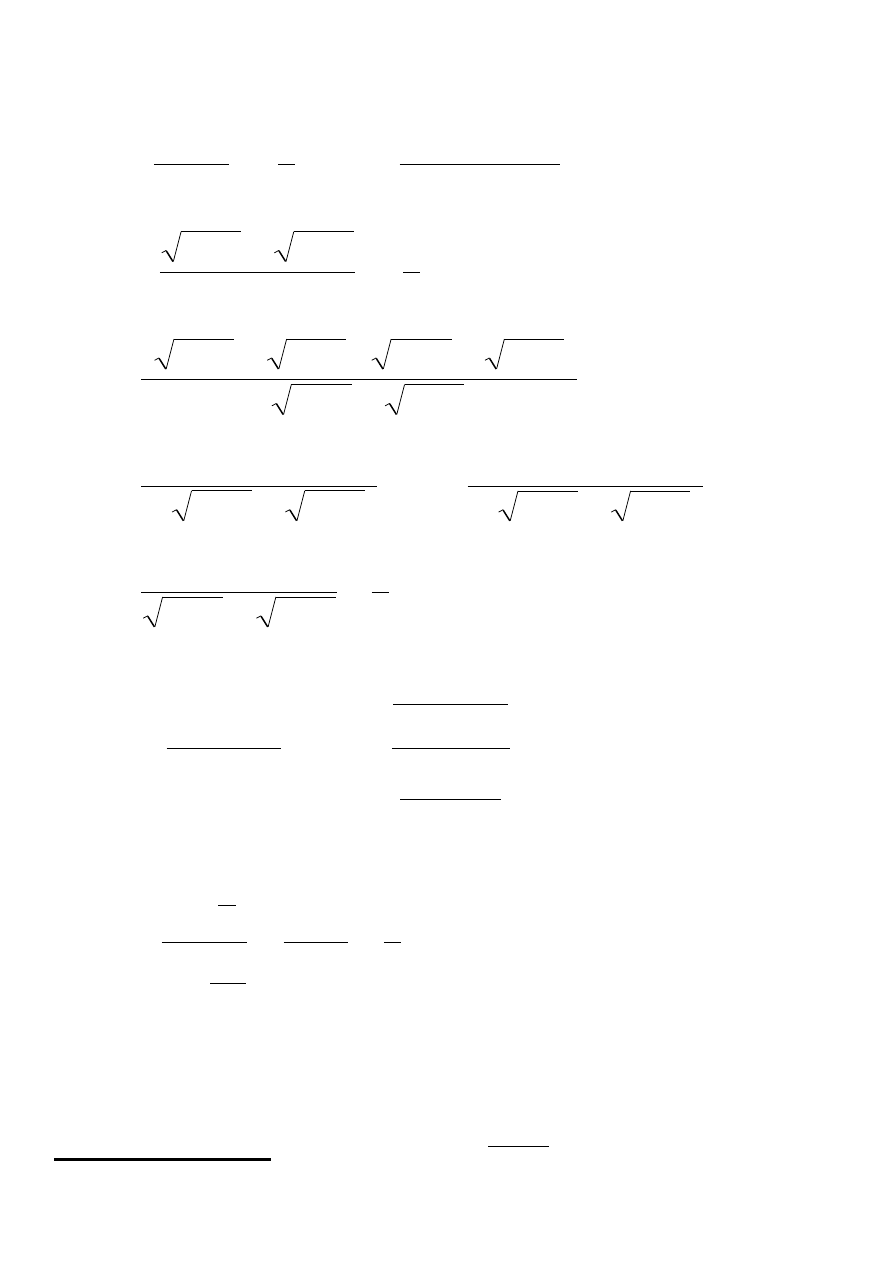
Przykład 1.
a)
1
)
1
)(
1
(
lim
0
0
1
1
lim
1
2
1
x
x
x
x
x
x
x
2
)
1
(
lim
1
x
x
b)
0
0
1
1
lim
0
x
x
x
x
)
1
1
(
)
1
1
)(
1
1
(
lim
0
x
x
x
x
x
x
x
x
)
1
1
(
)
1
(
1
lim
0
x
x
x
x
x
x
)
1
1
(
2
lim
0
x
x
x
x
x
1
2
2
1
1
2
lim
0
x
x
x
c)
2
2
2
2
2
2
4
7
5
3
lim
4
7
5
3
lim
x
x
x
x
x
x
x
x
x
x
7
3
0
7
0
3
4
7
5
3
lim
2
x
x
x
Ważna granica:
1
sin
lim
0
x
x
x
Przykład 1. c.d.
d)
x
x
x
x
x
x
3
3
sin
5
3
lim
0
0
5
3
sin
lim
0
0
5
3
1
5
3
sin
5
3
lim
)
3
.
(
0
y
y
y
x
podst
y
e)
3
2
3
3
sin
3
2
2
sin
2
lim
0
0
3
sin
2
sin
lim
0
0
x
x
x
x
x
x
x
x
x
x
Granice jednostronne
Mówimy, że lewostronna granica funkcji f w punkcie
0
x
jest równa g jeżeli dla każdego ciągu
)
(
n
x
argumentów
funkcji o wartościach mniejszych od
0
x
, zbieżnego do
0
x
,
o wyrazach różnych od
0
x
, ciąg
))
(
(
n
x
f
ma granicę g.
Piszemy:
g
x
f
x
x
)
(
lim
0
0
Mówimy, że prawostronna granica funkcji f w punkcie
0
x
jest równa g jeżeli dla każdego ciągu
)
(
n
x
argumentów
funkcji o wartościach większych od
0
x
, zbieżnego do
0
x
, o
wyrazach różnych od
0
x
, ciąg
))
(
(
n
x
f
ma granicę g.
Piszemy:
g
x
f
x
x
)
(
lim
0
0
Twierdzenie. Funkcja f ma w punkcie
0
x
granicę g
wtedy i tylko wtedy gdy istnieją granice lewo- i
prawostronna funkcji f w tym punkcie i obie te granice są
równe g.
Przykład 2. Obliczmy granice jednostronne funkcji
2
5
3
)
(
x
x
x
f
w punkcie
2
x
:
0
11
2
5
3
lim
0
2
x
x
x
0
11
2
5
3
lim
0
2
x
x
x
Ponieważ te granice nie są sobie równe, więc
2
5
3
lim
2
x
x
x
nie istnieje.
Przykład 3. Obliczmy granice jednostronne funkcji
2
3
)
1
(
1
)
(
x
x
x
f
w punkcie
1
x
:
0
2
)
1
(
1
lim
2
3
0
1
x
x
x
0
2
)
1
(
1
lim
2
3
0
1
x
x
x
Ponieważ obie te granice są sobie równe, więc:
2
3
1
)
1
(
1
lim
x
x
x
Ciągłość funkcji w punkcie
Funkcję f określoną w otoczeniu punktu
0
x
nazywamy
funkcją ciągłą w punkcie
0
x
gdy istnieje granica
)
(
lim
0
x
f
x
x
i jest równa wartości funkcji w tym punkcie:
)
(
)
(
lim
0
0
x
f
x
f
x
x
Przykład 3. Zbadamy ciągłość funkcji
1
1
1
1
)
(
2
x
dla
x
dla
x
x
x
x
f
w punkcie
1
x
.
Rozwiązanie. Obliczmy najpierw granicę:
1
lim
1
)
1
(
lim
0
0
1
lim
1
1
2
1
x
x
x
x
x
x
x
x
x
x
Ze wzoru funkcji:
1
)
1
(
f
.
Ponieważ
)
1
(
1
lim
2
1
f
x
x
x
x
, więc dana funkcja jest
ciągła w punkcie
1
x
.
Uwaga. Ta funkcja jest ciągła także w każdym innym
punkcie – wielomiany, funkcje trygonometryczne, funkcja
wykładnicza i logarytmiczna oraz funkcje utworzone z
nich przez działania arytmetyczne są funkcjami ciągłymi.
Ciągłość funkcji w przedziale
Niech f będzie funkcją określoną w przedziale E.
Funkcję f nazywamy funkcją ciągłą w przedziale E gdy
ta funkcja jest ciągła w każdym punkcie przedziału E.