Kinetyczna teoria gazów

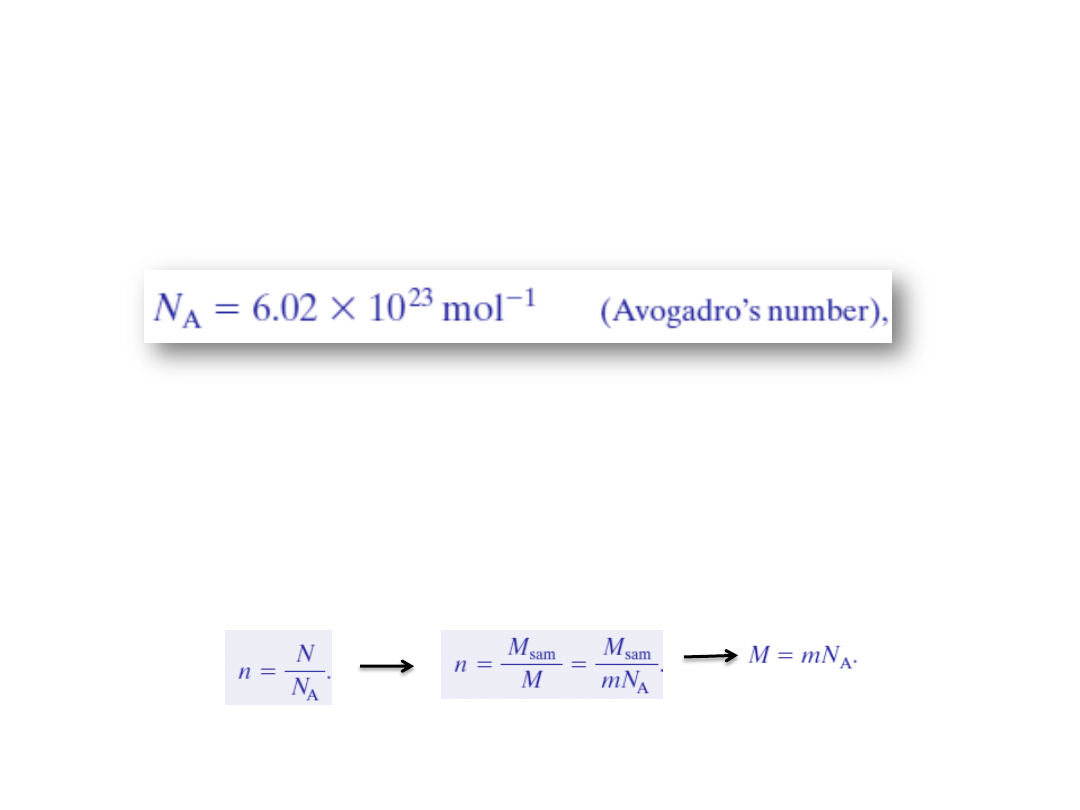
1. Liczba Avogadra

Jeden mol to liczba atomów w próbce węgla-12 o masie 12 g.

Liczba atomów lub cząstek w jednym molu jest nazywana
liczbą Avogadra, N

A

.

Jeśli:
n – liczba moli zawarta w próbce dowolnej substancji,
N – liczba cząsteczek,
M

sam

–masa próbki,

M – masa molowa,
wówczas:

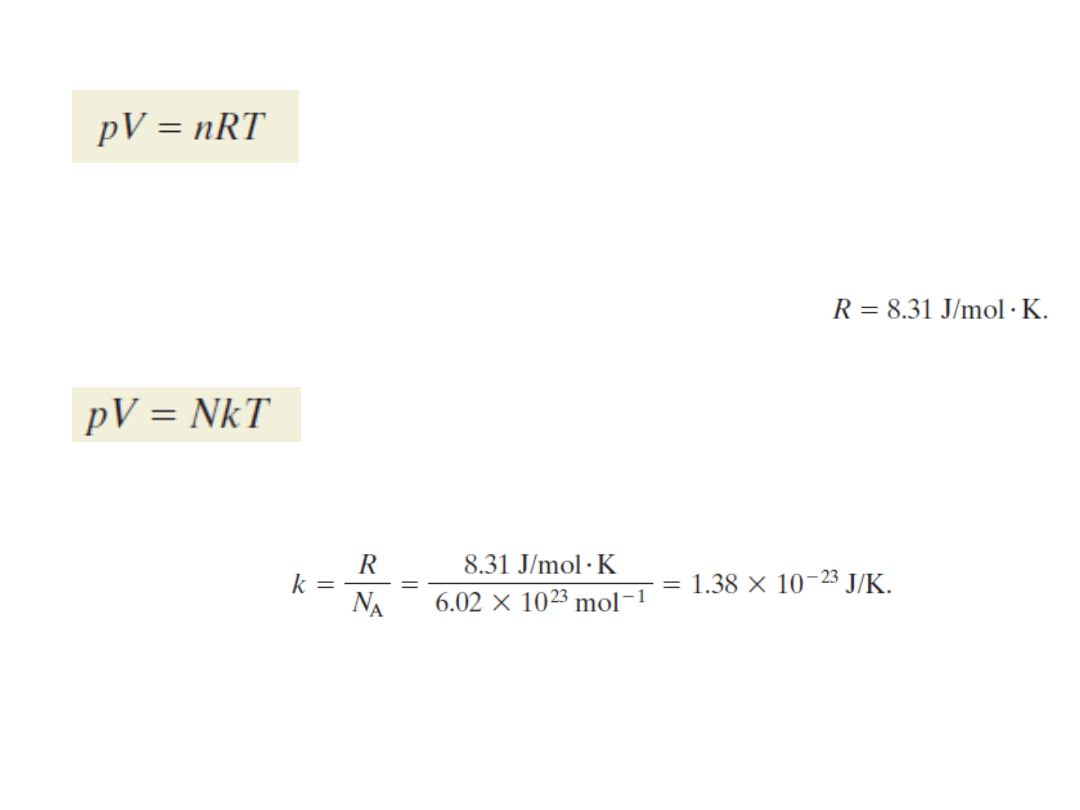
2.

Gazy doskonałe

p – bezwzględna wartość ciśnienia,
n – liczba moli gazu w próbce,
T – temperatura bezwzględna gazu (w kelwinach),
R – stała gazowa, która ma tę samą wartość dla wszystkich gazów:




k – stała Boltzmanna,
N – liczba cząsteczek

(równanie stanu gazu doskonałego)

(równanie stanu gazu doskonałego)

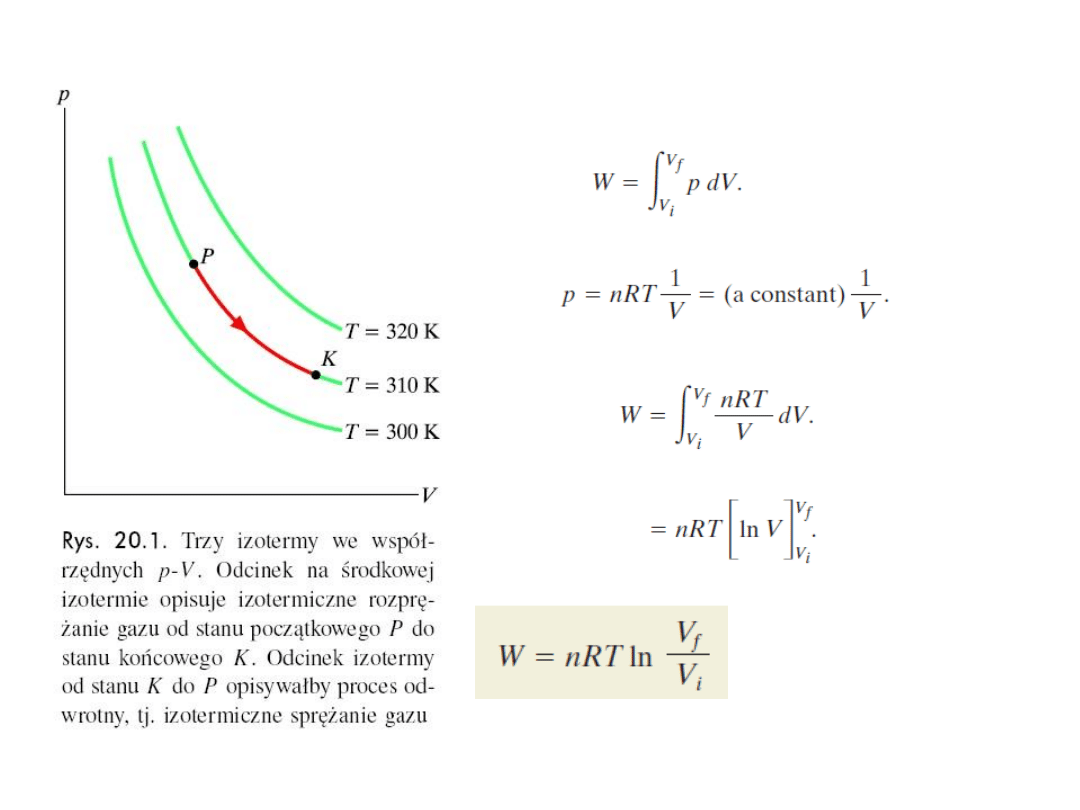
3.

Praca wykonywana przez gaz doskonały w stałej temperaturze

(gaz doskonały,
przemiana izotermiczna)

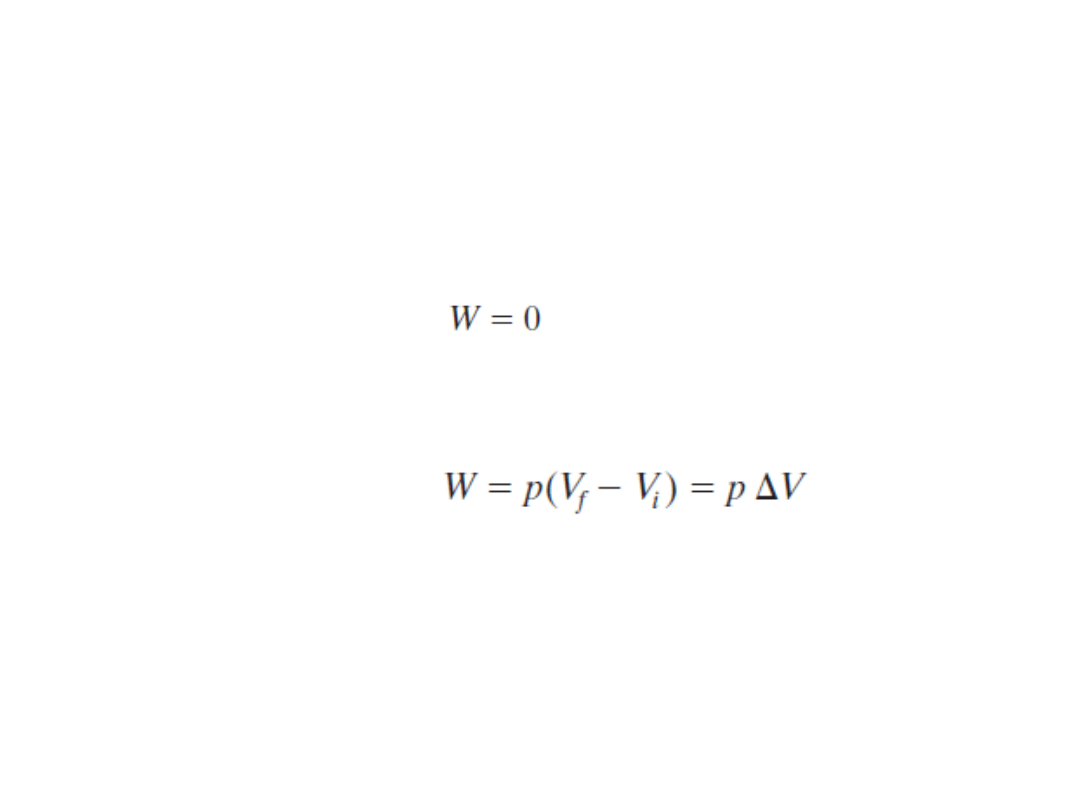
4.

Praca wykonywana przez gaz doskonały przy stałej objętości

i przy stałym ciśnieniu

Praca W wykonywana przez gaz doskonały (lub dowolny inny gaz) podczas przemian
przy stałej objętości i przy stałym ciśnieniu:

Jeżeli objętość gazu jest stała, to




Jeżeli zmienia się objętość, a ciśnienie p jest stałe, to

(przemiana przy stałej objętości)

(przemiana przy stałym ciśnieniu)

Example, Ideal Gas Processes

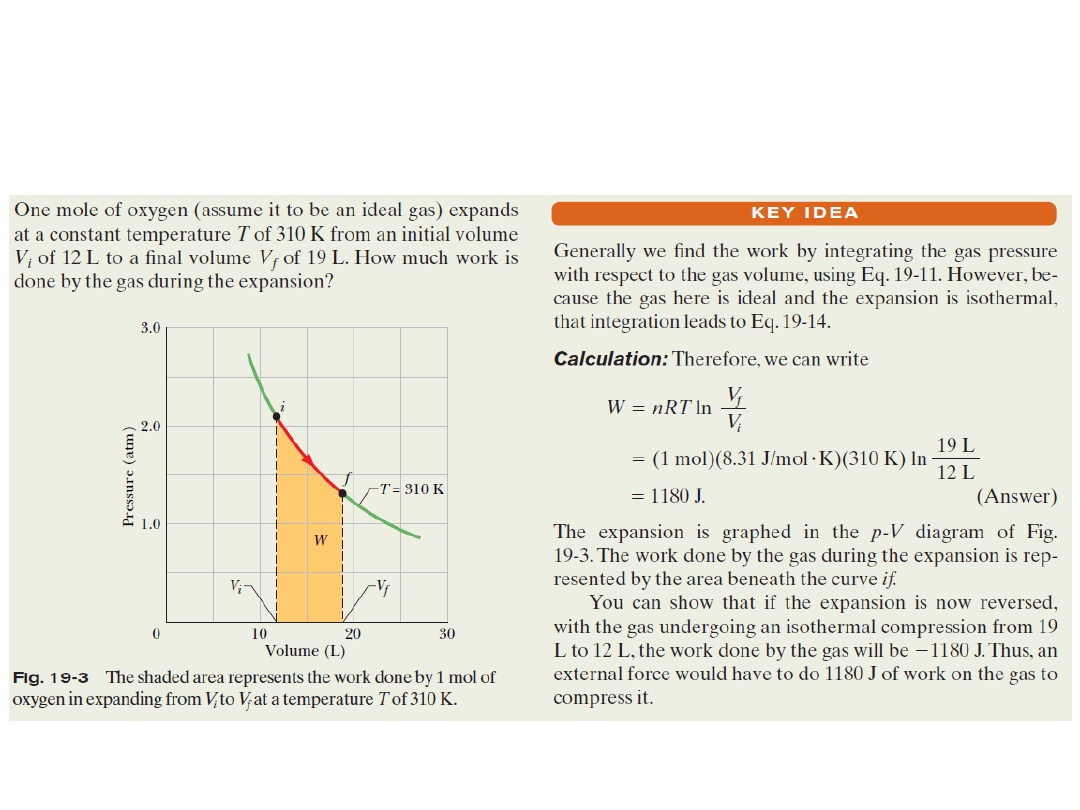
Example, Work done by an Ideal Gas

.

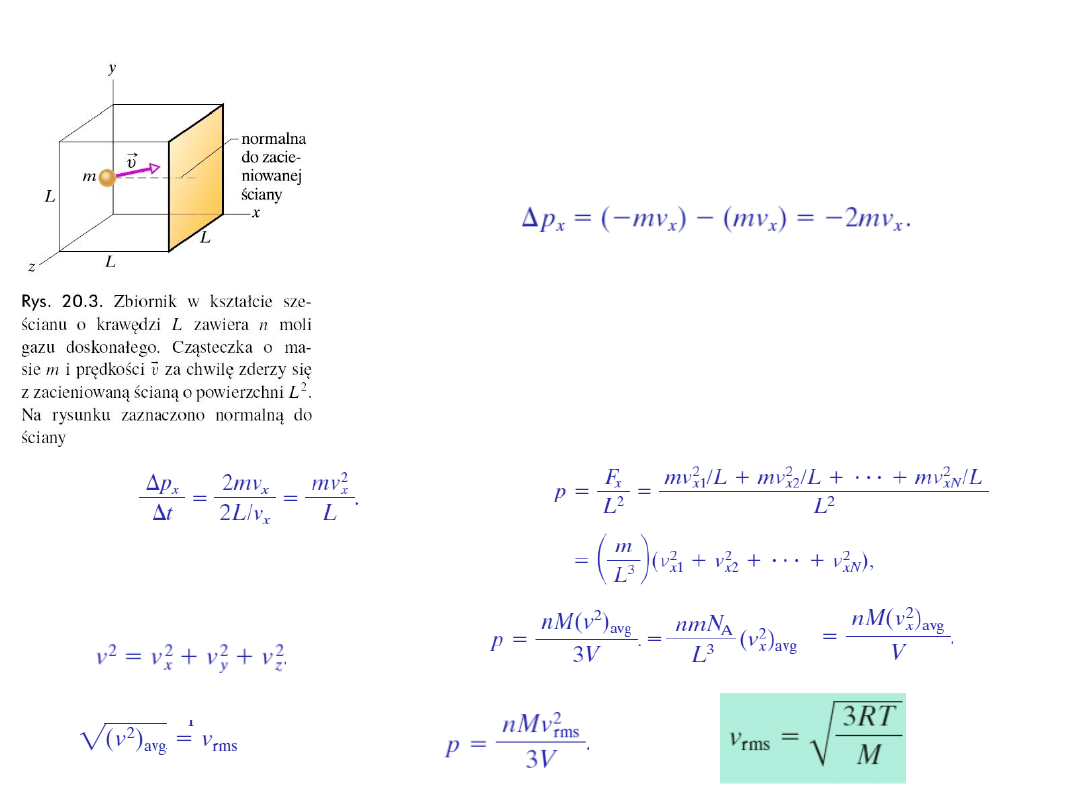
Zatem

Ciśnienie:

But,

Zatem

Z

otrzymujemy

oraz

5. Ciśnienie, temperatura i prędkość średnia kwadratowa

Dla cząsteczki gazu o masie m i prędkości v, która za chwilę
zderzy się z zacieniowaną ścianką zbiornika (rys. 20.3), jeśli
zderzenie jest sprężyste, zmieni się tylko składowa prędkości w
kierunku osi x. Zatem zmieni się jedynie składowa pędu
cząsteczki w kierunku osi x:


Zatem pęd

D

p

x

, który otrzymuje ściana w wyniku zderzenia jest

równy +2mv

x

.

Czas

D

t pomiędzy zderzeniami jest czasem potrzebnym

cząsteczce poruszającej się z prędkością v

x.

na przebycie drogi do

przeciwnej ściany i z powrotem (2L).
Czas

D

t jest więc równy 2L/v

x

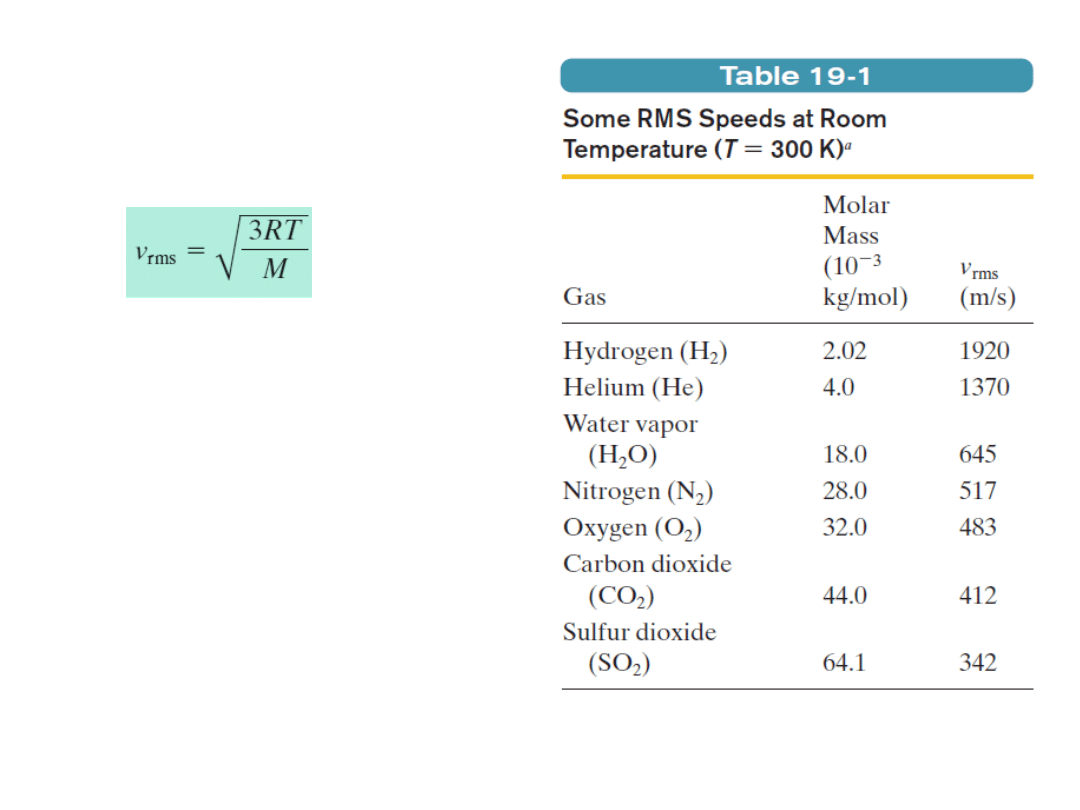
Prędkość średnia kwadratowa:

Przykładowa wartości prędkości
średniej kwadratowej cząsteczek
obliczone na podstawie równania

Example:

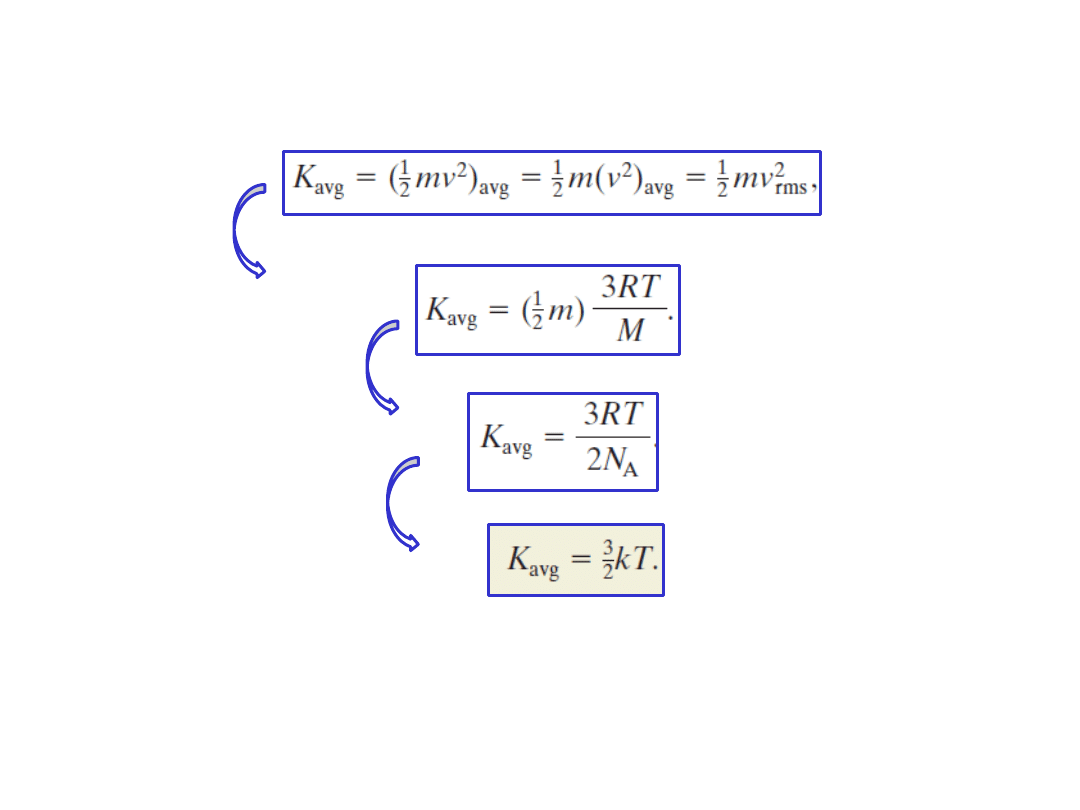
6. Energia kinetyczna ruchu postępowego

– w danej temperaturze T wszystkie cząsteczki gazu doskonałego
(niezależnie od swojej masy) mają taką samą energie kinetyczną ruchu postępowego

– mierząc temperaturę gazu, wyznaczamy jednocześnie średnią energię kinetyczną
ruchu postępowego jego cząsteczek

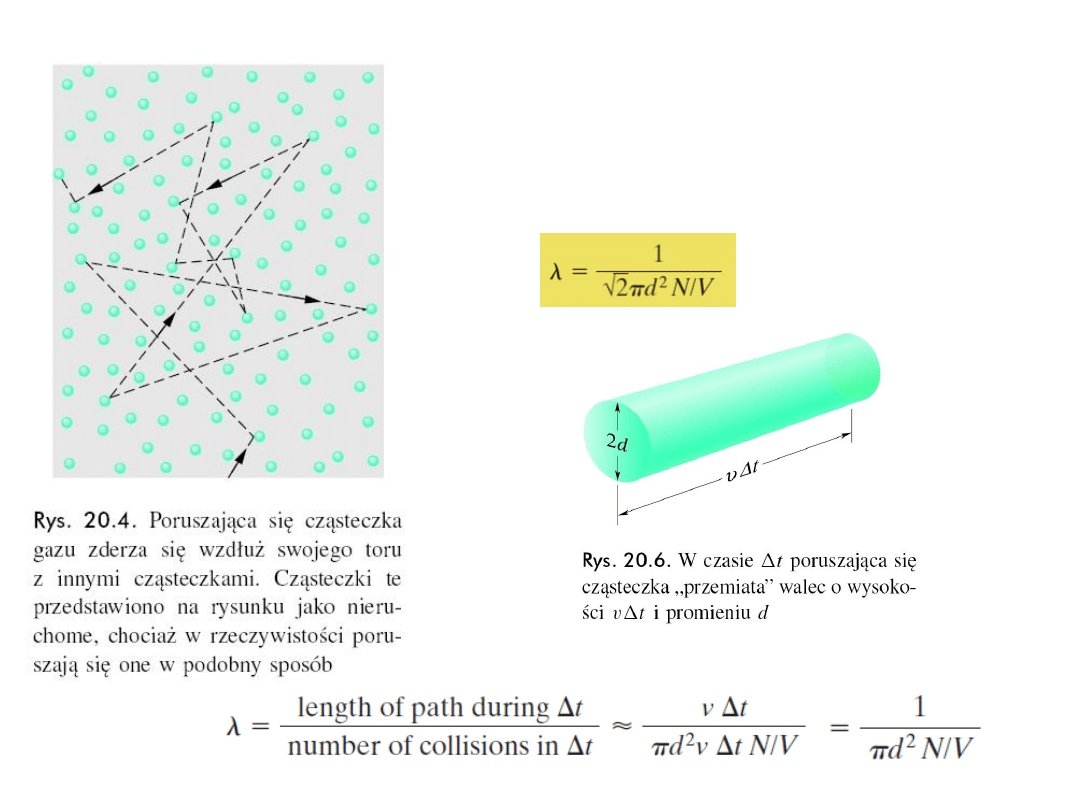
7. Średnia droga swobodna

Średnia droga swobodna

l -

droga, jaką pokonuje średnio

cząsteczka między swoimi kolejnymi zderzeniami.

Wzór opisujący średnią drogę swobodną cząsteczki:

(średnia droga swobodna)

Example, Mean Free Path, Average Speed, Collision Frequency:

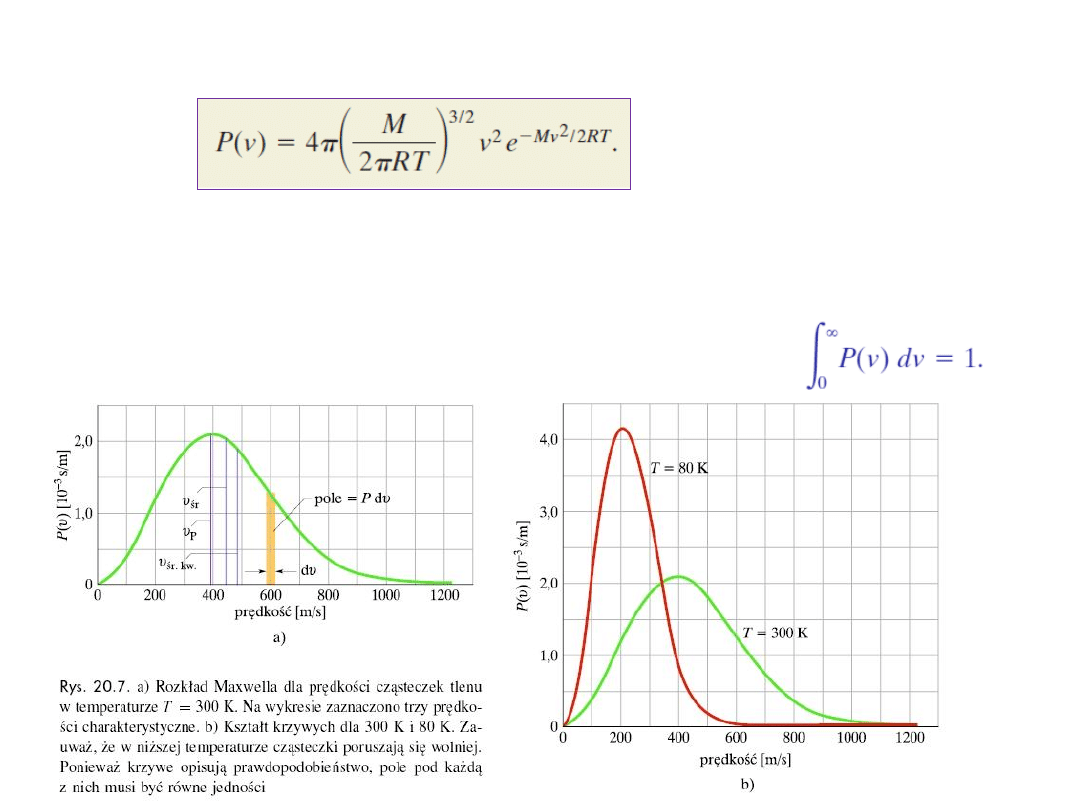
Rozkład Maxwella prędkości cząsteczek gazu: M – masa molowa gazu,
R – stała gazowa,
T – temperatura gazu,
v – prędkość cząsteczek.

Wielkość P(v) jest funkcją rozkładu prawdopodobieństwa: dla dowolnej prędkości v
iloczyn P(v)dv wskazuje, jaki ułamek cząsteczek ma prędkości z przedziału o szerokości dv
i środku w punkcie v.

Całkowite pole powierzchni pod krzywą rozkładu określa, jaka część
cząsteczek ma prędkości z przedziału od zera do nieskończoności:

8. Rozkład prędkości cząsteczek

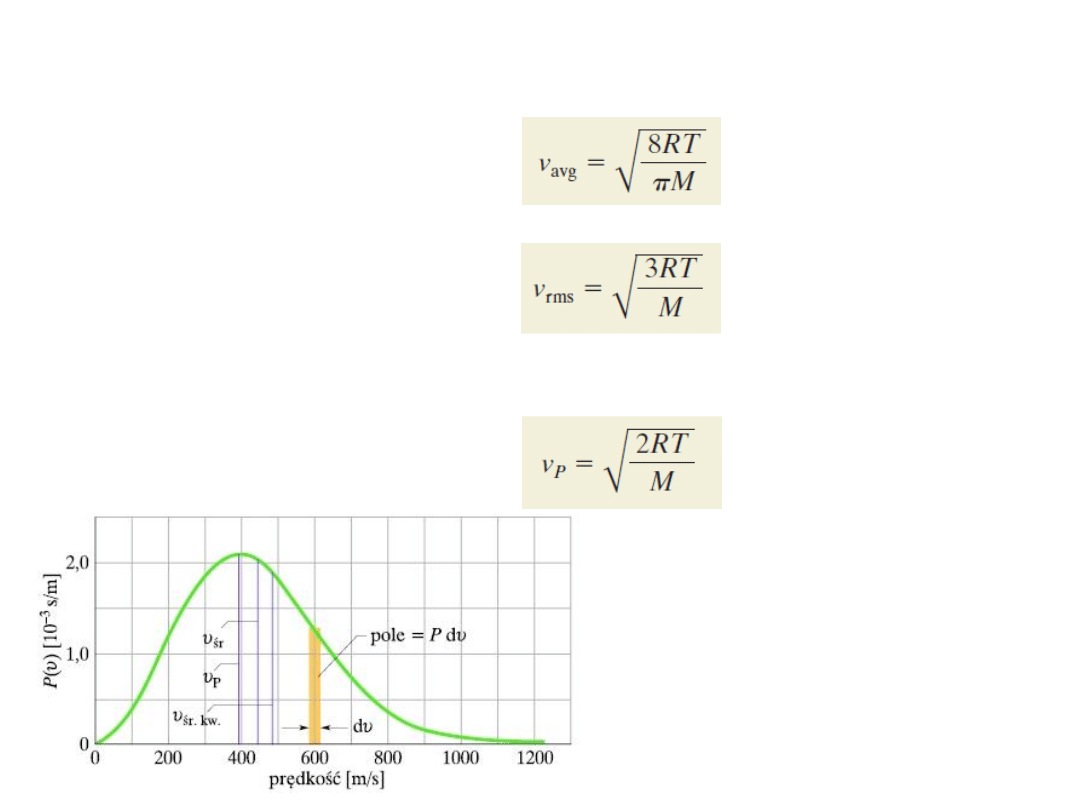
9. Prędkość średnia, prędkość średnia kwadratowa

i prędkość najbardziej prawdopodobna

Prędkość średnia v

avg

cząsteczek gazu:

Prędkość średnia kwadratowa v

rms

:

Prędkość najbardziej prawdopodobna v

P

(prędkość, dla której funkcja rozkładu P(v)

osiąga maksimum:

Example, Speed Distribution in a Gas:

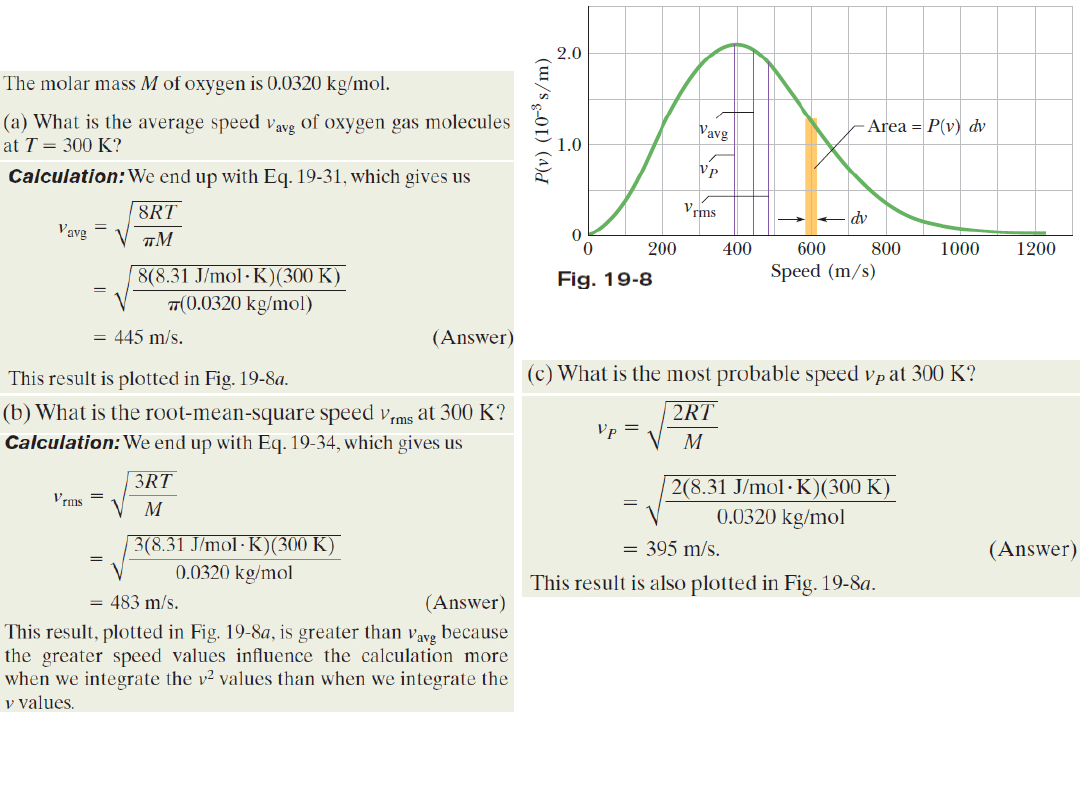
Example, Different Speeds

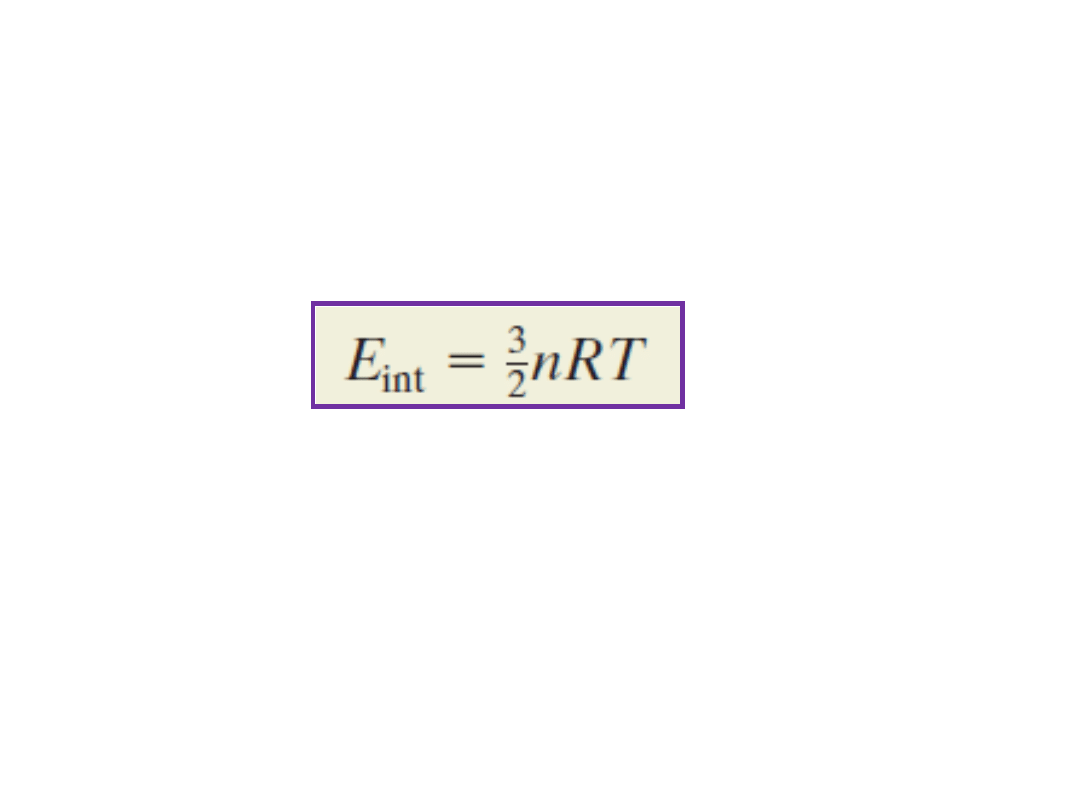
10. Molowe ciepła właściwe gazu doskonałego

Energia wewnętrzna E

int

gazu doskonałego zależy tylko

od temperatury gazu; nie zależy od żadnej innej wielkości
opisującej jego stan:

(jednoatomowy gaz doskonały)

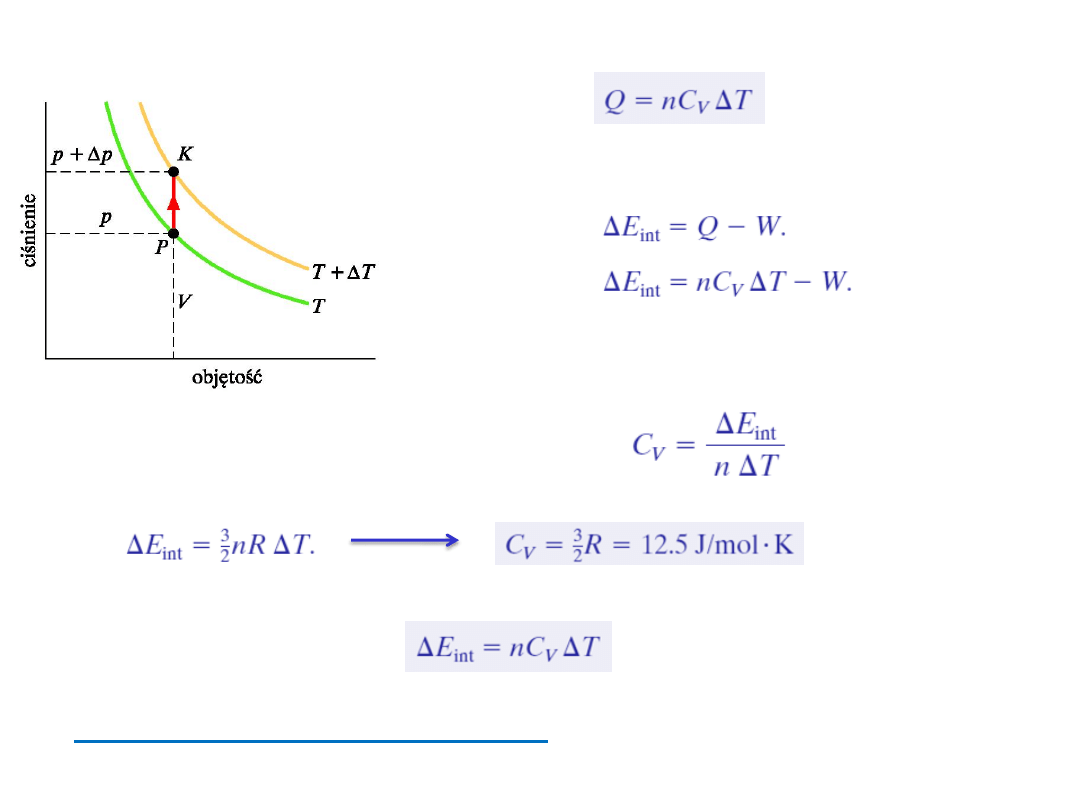
11. Molowe ciepło właściwe przy stałym ciśnieniu

C

V

– molowe ciepło właściwe gazu przy stałej objętości.

Ale

Stąd:

Przy zachowaniu stałej objętości gaz nie może się rozprężać
i dlatego nie wykonuje on pracy (W=0 ). Stąd:

Jeśli gaz doskonały zamknięty w zbiorniku podlega zmianie temperatury

D

T, zmienia

się jego energia wewnętrzna:

Zmiana energii wewnętrznej E

int

gazu doskonałego zamkniętego w zbiorniku

zależy tylko od zmiany temperatury gazu, nie zależy od typu procesu, w wyniku
którego nastąpiła zmiana temperatury.

(stała objętość)

(gaz jednoatomowy)

(gaz doskonały, dowolny proces)

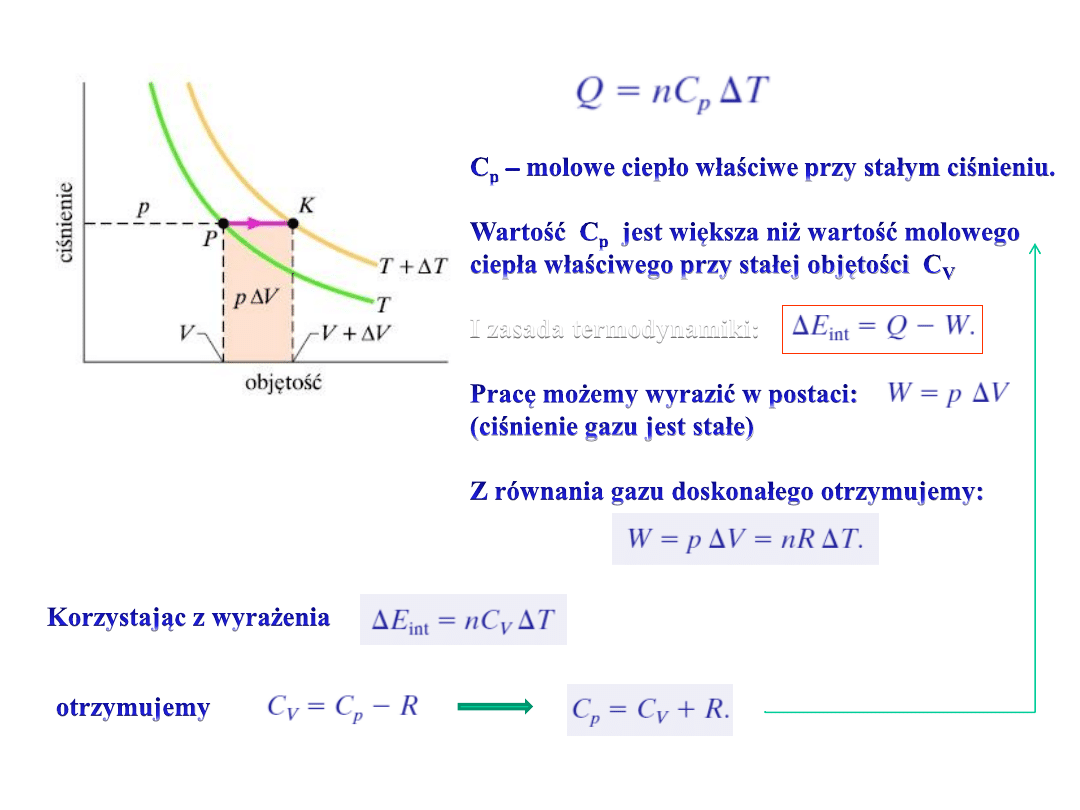
12. Molowe ciepło właściwe przy stałym ciśnieniu

I zasada termodynamiki:

(stałe ciśnienie)

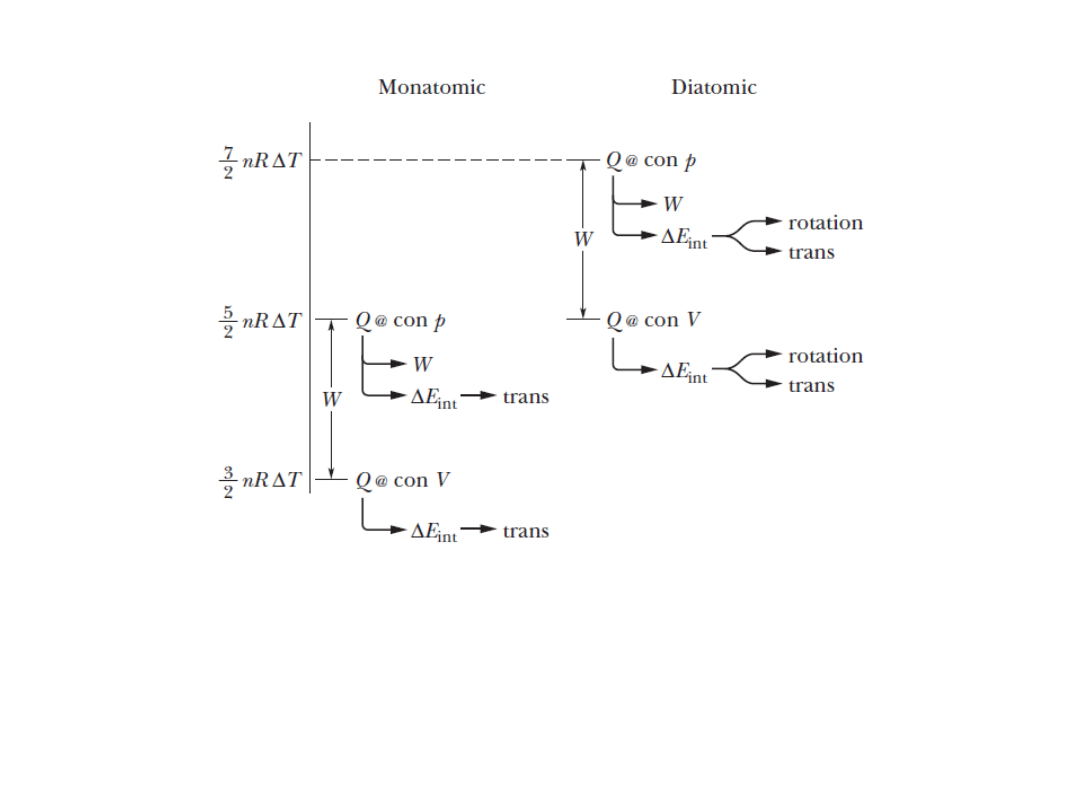
19.8: Molar Specific Heats

Fig. 19-12 The relative values of Q for a monatomic gas (left side) and a diatomic
gas undergoing a constant-volume process (labeled “con V”) and a constant-
pressure process (labeled “con p”). The transfer of the energy into work W and
internal energy (E

int

) is noted.

Example, Monatomic Gas:

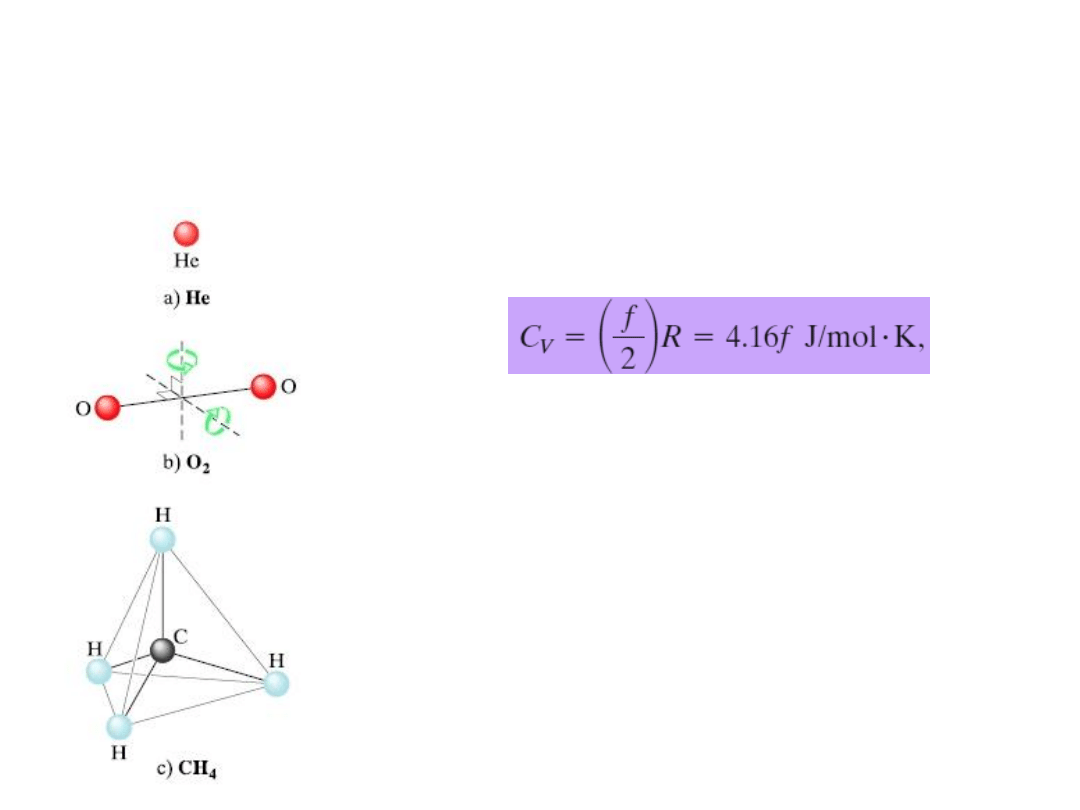
13. Stopnie swobody a molowe ciepła właściwe

Każdy rodzaj cząsteczek charakteryzuje pewna liczba stopni
swobody f, które dają cząsteczce niezależne sposoby
przechowywania energii.
Na każdy stopień swobody przypada – średnio – energia równa
½ kT na cząsteczkę (lub ½ RT na mol).

Rys. 20.11. Modele cząsteczek występujących w teorii kinetycznej:
a)

Hel – przykład cząsteczki jednoatomowej,

b) Tlen – przykład cząsteczki dwuatomowej,
c)

Metan – przykład cząsteczki wieloatomowej.

Kule oznaczają atomy, a linie – wiązania.
Dla cząsteczki tlenu zaznaczono dwie osie obrotu.

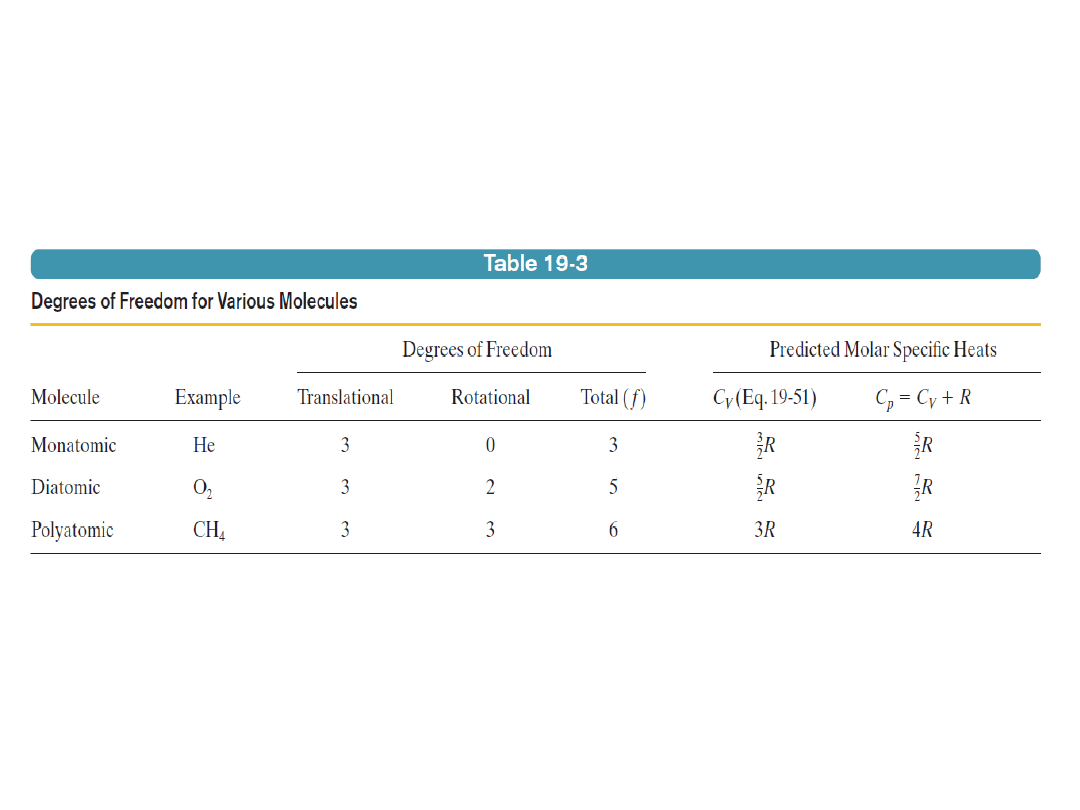
13. Stopnie swobody a molowe ciepła właściwe

Example, Diatomic Gas:

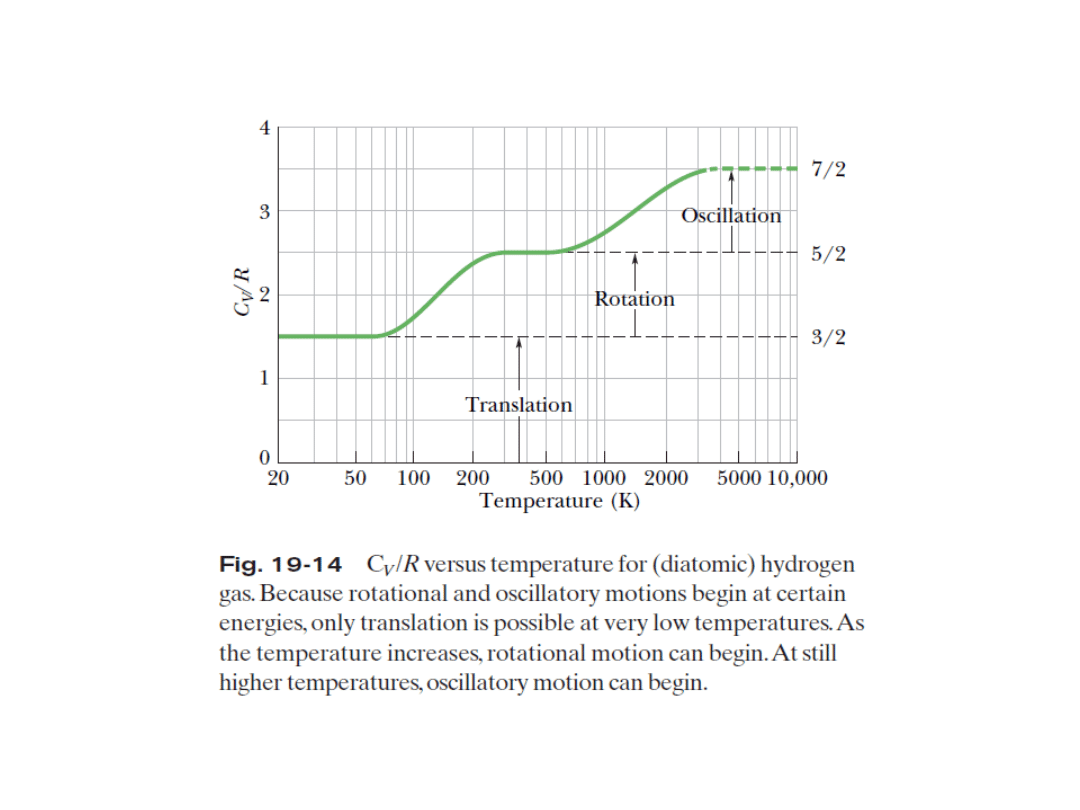
19.10: A Hint of Quantum Theory

I zasada termodynamiki:

Ponieważ Q=0 (rozprężanie adiabatyczne),
korzystając ze wzoru na E

int

, otrzymujemy:

Różniczkując równanie stanu gazu doskonałego

Ponieważ C

P

–

C

V

= R, więc

Korzystając z powyższych równań otrzymujemy:


Zastępująć

g

= C

P

/C

V

i całkując powyższe równanie otrzymujemy:

Ostatecznie:

14. Rozprężania adiabatyczne gazu doskonałego

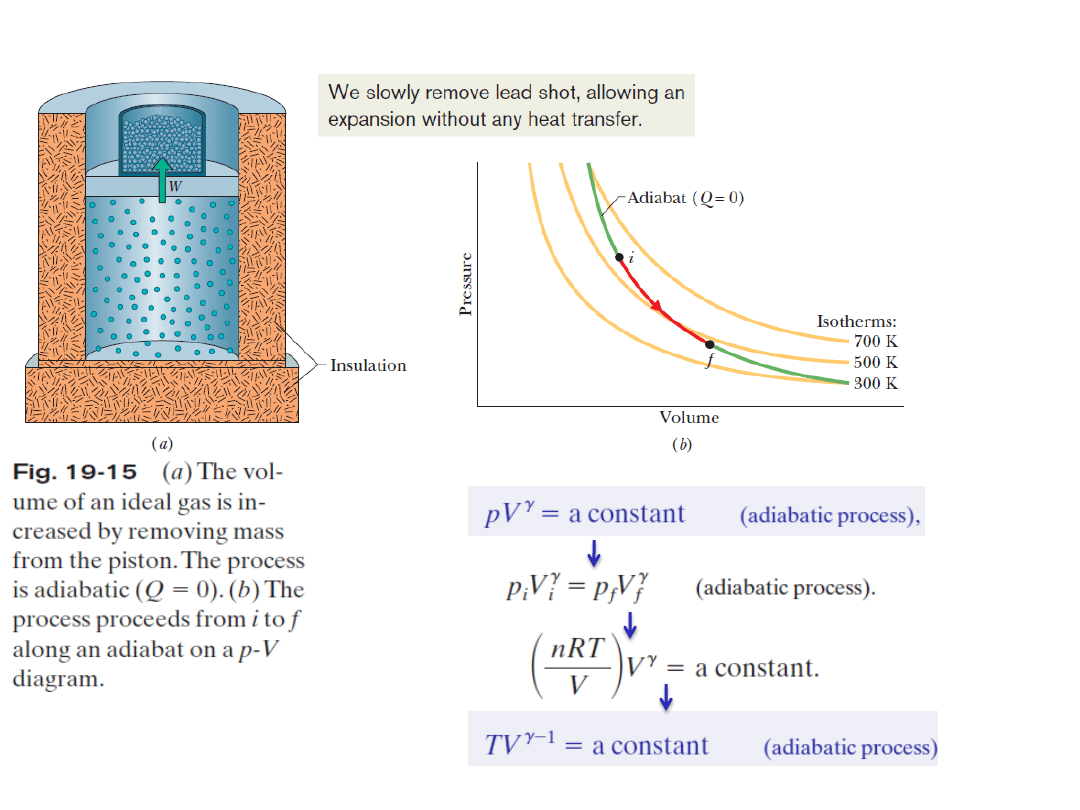
14. Rozprężania adiabatyczne gazu doskonałego

15. Rozprężanie adiabatyczne gazu doskonałego, rozprężanie swobodne

Rozprężanie swobodne – przemiana adiabatyczna, w której gaz nie wykonuje żadnej
pracy, ani żadna praca nie jest wykonywana nad gazem – nie zmienia się energia
wewnętrzna gazu. Rozprężanie swobodne jest więc całkowicie odmiennym procesem
niż przemiana adiabatyczna, w której gaz wykonuje pracę, a więc zmienia swoją
energię wewnętrzną.

W trakcie rozprężania swobodnego gaz znajduje się w równowadze termodynamicznej
tylko w stanie początkowym i końcowym – na wykresie możemy więc przedstawić
tylko te dwa punkty, ale nie możemy wykreślić łączącej ich linii.

Ponieważ E

int

=0, temperatura w stanie końcowym musi być równa temperaturze w

stanie początkowym. Dlatego na wykresie stan początkowy i końcowy muszą
znajdować się na tej samej izotermie oraz


Zatem dla gazu doskonałego:

(rozprężanie swobodne)

(rozprężanie swobodne)

Example, Adiabatic Expansion:

Four Gas Processes for an Ideal Gas