Strona 1 z 3

Metoda Ritza

w zastosowaniu do belek na sprężystych podporach

Przykład liczbowy

Leszek Chodor

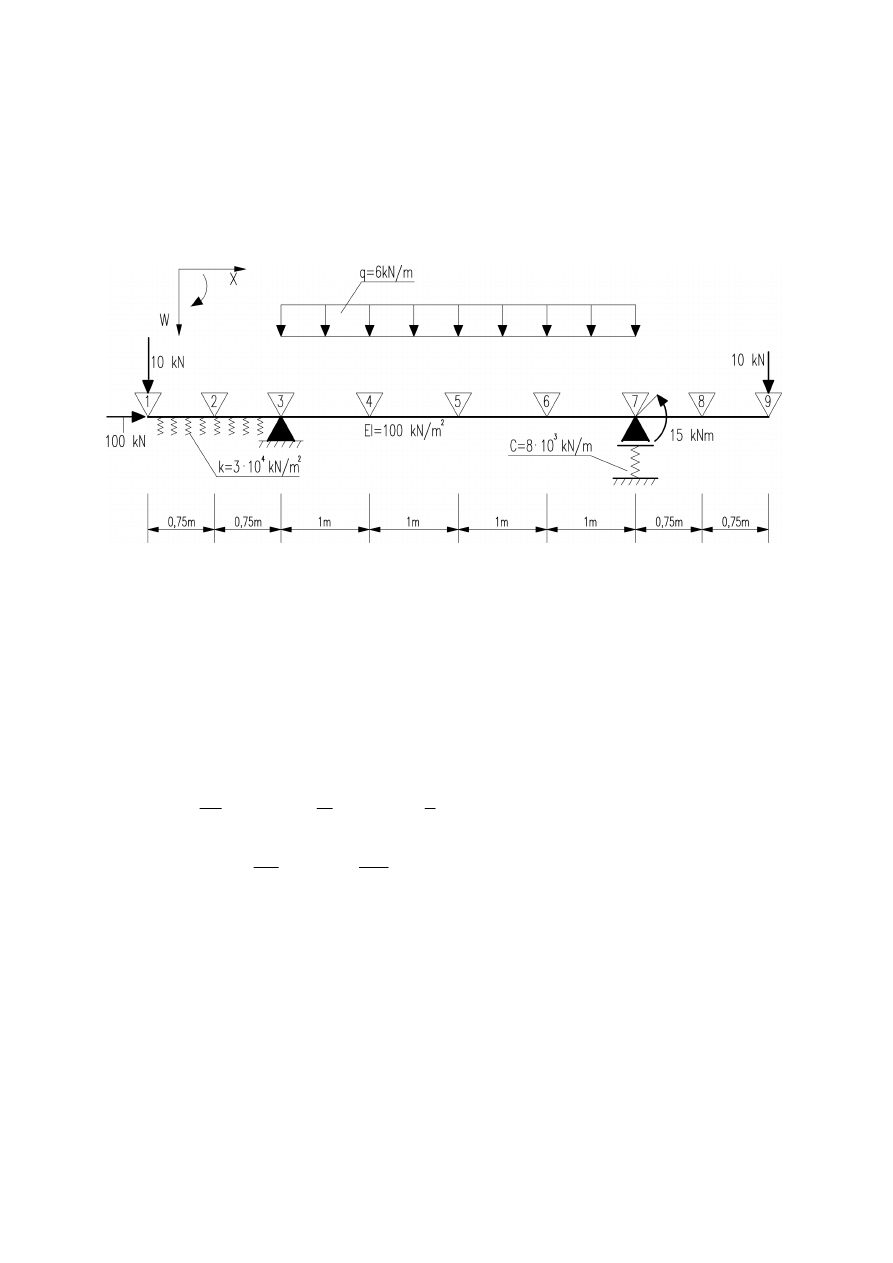
Dla belki pokazanej na rys. 1 wyznaczyć przybliżoną linię ugięcia metodą Lagrange’a-Ritza
Ograniczyć się do II przybliżenia.

1. Funkcjonał energii potencjalnej Lagrange’a

Funkcjonał energii potencjalnej Lagrange’a

Π

dla belki pryzmatycznej na podłożu sprężystym

ze stałą sprężystości

)

(x

k

, obciążonej rozłożonym obciążeniem

)

(x

q

i ściskanej siłą

)

(x

N

,

ze sprężystymi podporami skupionymi ze stałymi sprężystości [pionowa,

obrotowa]=

)

](

,

[

k

M

V

x

C

C

]oraz z obciążeniem skupionym

)

](

,

[

k

x

M

V

zlokalizowanym w

punkcie o współrzędnej

k

x

, można zapisać w postaci:

{

}

∫

+

−

+

−

=

Π

l

k

N

EJ

dx

x

w

x

q

x

w

x

w

x

w

0

2

2

2

2

2

2

)

(

)

(

)]

(

'

[

)]

(

'

[

)]

(

"

[

(1)

{

}

∑

−

−

+

k

k

k

k

k

k

C

k

C

x

w

M

x

w

V

x

w

x

w

M

V

)

(

'

)

(

)]

(

'

[

)]

(

[

2

2

2

2

,

gdzie w(x)- funkcja ugięcia belki, EJ –sztywność giętna belki względem głównej osi zginania.

Uwaga: W przyjętym układzie współrzędnych pokazany na rys.1, oś w skierowana jest do dołu, więc kąty obrotu
i momentu zginające są dodatnie, jeśli są zgodne z ruchem wskazówek zegara (ogólnie z ruchem od osi x do w).

2. Metoda Ritza minimalizacji funkcjonału

W metodzie Ritza poszukuje się funkcji realizującej minimum funkcjonału w klasie
wielomianów:

∑

+

=

=

n

i

i

i

x

a

x

w

1

0

)

(

)

(

ϕ

ϕ

(2)

Rys.1. Rozwiązywana belka

Strona 2 z 3

Funkcje aproksymujące muszą być dopuszczalne, czyli spełniać warunki brzegowe.
Warunkiem koniecznym stacjonarności funkcjonału

Π

jest zerowanie się jego pochodnych

funkcjonału podług stałych w funkcjach Ritza:

,

0

...

1

=

=

=

∂

Π

∂

∂

Π

∂

i

a

a

(3)

który prowadzi do układu równań , z których wyznacza się stałe funkcji aproksymujących.

3. Metodologia podej

ś

cia w zadaniu

Warunek stacjonarności (3) zastosowany do funkcji podcałkowych (1) z podstawioną
aproksymacją (2), doprowadzi do układu równań Ritza ze współczynnikami wyrażonymi
stosownymi całkami.
W niniejszym zadaniu, w celu zwiększenia przejrzystości metody – stosuje się podejście
bezpośrednie bez przygotowania ogólnych formuł.

3.1. Przypuszczenie funkcji aproksymuj

ą

cej Ritza

W danych zadania, warunki brzegowe, które powinna spełniać funkcja Ritza, to:

0

)

5

,

1

(

:

)

1

3

3

=

→

=

=

→

w

m

x

x

dla

,

2) innych stabilnych warunków brzegowych nie ustalimy, ponieważ nie są znane reakcje na
podporach sprężystych, w tym podłoża sprężystego. Dlatego w węzłach tych pozostawiamy
swobodę.
Uwaga:
Jeśliby reakcje na podporach sprężystych można było ustalić, to wówczas, znając stałe
sprężystości podpór wyznaczymy również stabilne przemieszczenia i mielibyśmy dodatkowe
warunki brzegowe. Jednym zdaniem zamienilibyśmy statyczne warunki brzegowe na warunki
kinematyczne. W ten sposób, ograniczając ilość możliwych funkcji rozwiązujących ,
zwiększylibyśmy dokładność rozwiązania przybliżonego

Przy zadanych wyżej warunkach brzegowych, przypuszczamy następujące funkcje Ritza:
1)

,

0

0

=

ϕ

2),

2

3

1

)

(

)

(

x

x

x

−

=

ϕ

,

3)

3

3

2

)

(

)

(

x

x

x

−

=

ϕ

,

4) pozostałe człony rozwinięcia pomija się (w myśl zlecenia zadania)
Przypuszczona funkcja ugięcia Ritza ma więc postać:

.

)

(

)

(

)

(

3

3

2

2

3

1

x

x

a

x

x

a

x

w

−

+

−

=

3.2. Wyznaczenie funkcjonału

Π

dla przyj

ę

tej funkcji Ritza

Pochodne funkcji ugięcia, występujące w funkcjonale , wynoszą:

).

(

6

2

)

(

"

,

)

(

3

)

(

2

)

(

'

3

2

1

2

3

2

3

1

x

x

a

a

x

w

x

x

a

x

x

a

x

w

−

+

=

−

+

−

=

Na poszczególnych odcinkach belki mamy:

1) na całej długości belki (x

0

=0x

l

=7m)

),

2037

336

28

(

50

)]

(

"

[

2

2

2

1

2

1

2

2

)

1

0

a

a

a

a

dx

x

w

l

x

x

EJ

+

+

⋅

∫

=

=

Π

na dwóch pierwszych elementach (x

0

=0; x

l

=1,5m)

Strona 3 z 3

{

}

).

6688

,

13

1875

,

15

5

,

4

(

14950

)]

(

'

[

)]

(

'

[

2

2

2

1

2

1

2

2

2

2

)

2

0

a

a

a

a

dx

x

w

x

w

l

x

x

k

N

+

−

⋅

∫

=

+

−

=

Π

3

) na czterech środkowych elementach (x

0

=1,5m; x

l

=5,5m)

{

}

),

64

333

.

21

(

6

)

(

)

(

2

1

)

3

0

a

a

dx

x

w

x

q

l

x

x

+

−

=

∫

−

=

Π

4) w punktach przyłożenia sił i sprężystych podpór kupionych(x

C

=5,5m;x

V

=0m i 7m,

x

M

=5,5m)

)

a

36.75

+

a

15(7

)

163a

5

,

32

(

10

)

64

16

(

4000

)

5

,

5

(

'

)

7

(

)

0

(

(

)]

5

,

5

(

[

2

1

2

1

2

1

2

2

)

4

+

+

−

+

=

=

+

+

−

=

Π

a

a

a

Mw

w

w

V

w

C

3.2. Wyznaczenie punktu stacjonarno

ś

ci funkcjonału

Π

0,

)

64

16

(

128000

)

336

56

(

50

)

15,1875a

-

4950(9a

1

33

3

2

1

2

1

2

1

1

=

+

+

+

+

+

−

=

∂

Π

∂

a

a

a

a

a

0

)

64

512000(16a

)

4074a

a

(336

0

5

27.3375a

(-15.1875a

4950

1

1294

2

1

2

1

2

1

2

=

+

+

+

+

+

+

−

=

∂

Π

∂

a

a

Rozwiązanie tego układu równań, daje

.

0000183906

,

0

,

0000852087

,

0

2

1

=

=

a

a

Linię ugięcia aproksymowano więc funkcją:

3

2

)

5

,

1

(

06

0.00001839

)

5

,

1

(

87

0.00008520

)

(

−

+

−

=

x

x

x

w

3.3. Wykres linii ugi

ę

cia

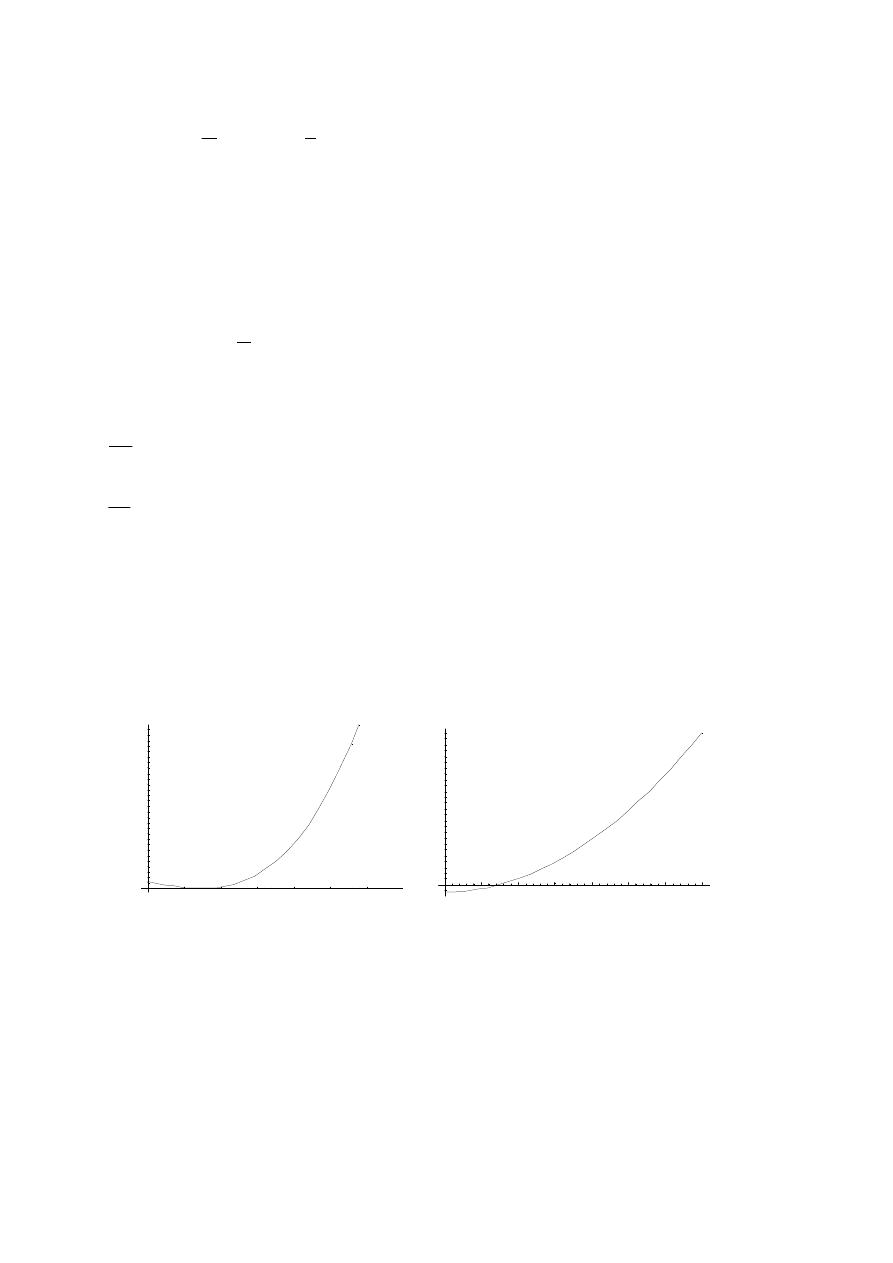
Na rys.2 pokazano wykres aproksymowanej linii ugięcia oraz kątów obrotu.

1

2

3

4

5

6

7

0.0005

0.001

0.0015

0.002

0.0025

1

2

3

4

5

6

7

0.0005

0.001

0.0015

0.002

0.0025

Rys.2. Wykres linii ugięcia i kątów obrotu