E. Michlowicz: IMiU – ćwiczenia 2 – model dwumasowy
1
Ćwiczenia 2 – IMiU
Obliczanie parametrów równań dla modelu dwumasowego
E. Michlowicz: IMiU – ćwiczenia 2 – model dwumasowy
1
Ćwiczenia 2 – IMiU
Obliczanie parametrów równań dla modelu dwumasowego
E. Michlowicz: IMiU – ćwiczenia 2 – model dwumasowy
2
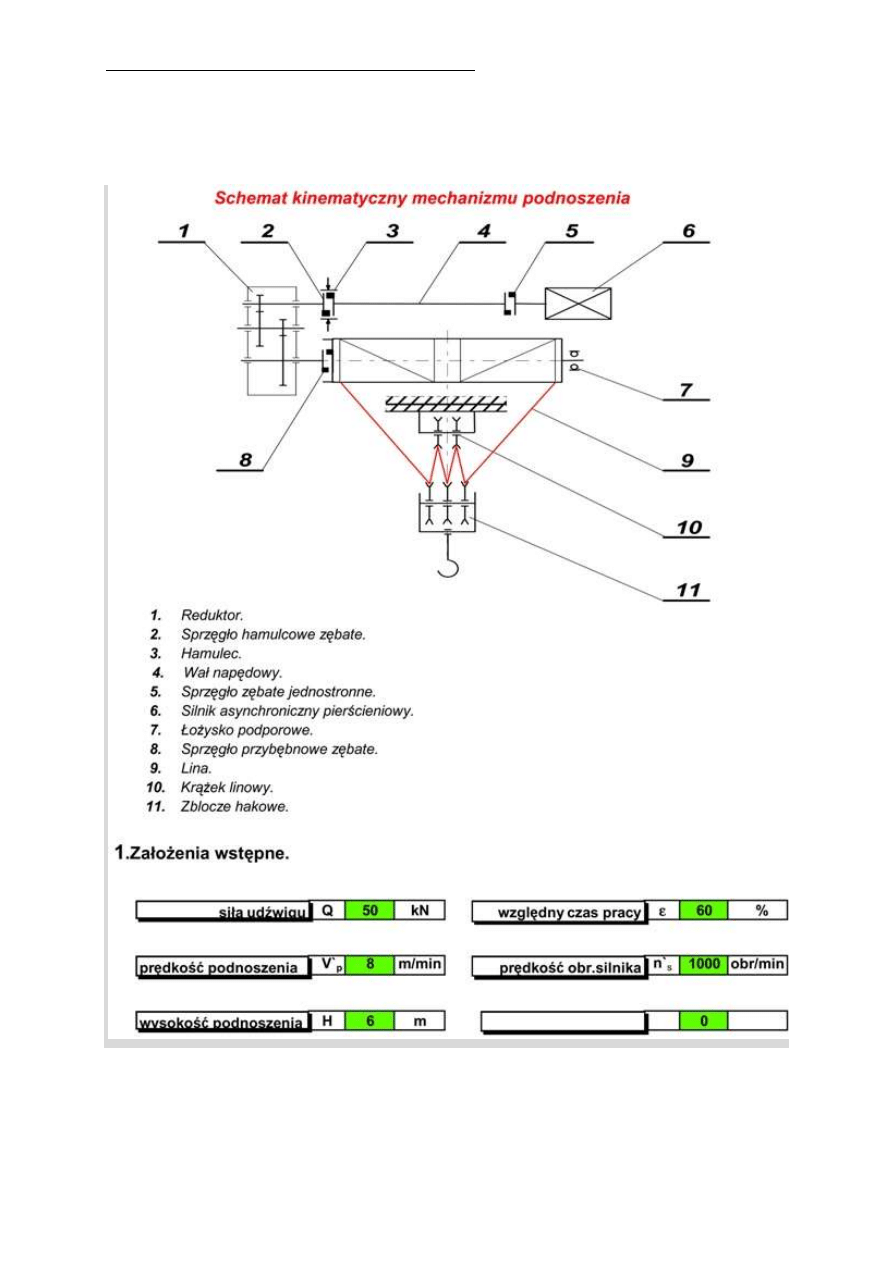
Analiza dynamiczna mechanizmu podnoszenia
Tab. 1. Zestawienie parametrów niezbędnych do przeprowadzenia analizy
dynamicznej mechanizmu podnoszenia
Parametr
Wartość
Jednostka
Masa podnoszona
5000
[kg]
Masa zblocza
203
[kg]
Wysokość podnoszenia
6
[m]
Przełożenie wielokrążka
2
-
Sprawność wielokrążka
0,99
-
Średnica liny
12
[mm]
Średnica bębna
340
[mm]
Moc silnika
8,5
[kW]
Prędkość obrotowa silnika - nominalna
950
[obr/min]
Przeciążalność silnika
2,5
-
Moment bezwładności silnika
0,105
[kg·m
2
]
Moment bezwładności sprzęgła hamulcowego
0,069
[kg·m
2
]
Moment bezwładności koła z
1
0,003
[kg·m
2
]
Moment bezwładności koła z
2
0,014
[kg·m
2
]
Moment bezwładności koła z
3
0,016
[kg·m
2
]
Moment bezwładności koła z
4
0,119
[kg·m
2
]
Moment bezwładności sprzęgła przybębnowego
0,105
[kg·m
2
]
Moment bezwładności bębna
1,97
[kg·m
2
]
Przełożenie 1-st
7,86
-
Przełożenie 2-st
8,14
-
Sprawność 1-st
0,975
-
Sprawność 2-st
0,975
-
Sprawność bębna
0,95
-
Moment hamowania
110
[Nm]
Luz
0,1
[m]
Przekrój metaliczny drutów w linie
54,5
[mm
2
]
E. Michlowicz: IMiU – ćwiczenia 2 – model dwumasowy
3
1. ROZRUCH
Redukcja na liny nabiegające na bęben
1. Obliczenie zredukowanego momentu bezwładności „I
zr1
” przy rozruchu:
𝐼
𝑧𝑟1
= (𝐼
𝑠
+ 𝐼
𝑠ℎ
+ 𝐼
𝑧1
) ∙ 𝑖
𝑐
2
∙ 𝜂
𝑐
+ (𝐼
𝑧2
+ 𝐼
𝑧3
) ∙ 𝑖
2
2
∙ 𝜂
𝑏
∙ 𝜂
2
+ (𝐼
𝑧4
+ 𝐼
𝑠𝑏
+ 𝐼
𝑏
)𝜂
𝑏
𝐼
𝑧𝑟1
= 692,70[𝑘𝑔𝑚
2
]
2. Obliczenie masy „m
1
” zredukowanej na bęben przy rozruchu:
𝑚
1
=
4∙𝐼
𝑧𝑟1
𝐷
𝑏
2
= 23968,82[𝑘𝑔]
3. Obliczenie masy „m
2
” zredukowanej na bęben przy rozruchu:
𝑚
2
= [
𝑚
𝑄
+𝑚
𝑄0
𝑖
𝑤𝑘
2
∙𝜂
𝑤
] = 1313,89[𝑘𝑔]
4. Wyznaczanie siły czynnej „S
1
”:
𝑆
1
=
2∙1,5∙9550∙𝑃
𝑛
𝑠
∙𝐷
𝑏
∙ 𝑖
1
∙ 𝑖
2
∙ 𝜂
𝑐
= 43563,30[𝑁]
5. Wyznaczenie siły biernej „S
2
”:
𝑆
2
=
(𝑚
𝑄
+𝑚
𝑄0
)∙9,81
𝑖
𝑤
∙𝜂
𝑤
= 25778,50[𝑁]
6. Obliczenie współczynnika sprężystości i tłumienia liny:
𝑘 =
2
𝑖
𝑤
∙
𝐸𝐹
𝐿
= 713041,67 [
𝑁
𝑚
]
ℎ = 0,01 ∙ 𝑘 = 7130,42 [
𝑁∙𝑠
𝑚
]
Obliczenie nadwyżki dynamicznej
𝑆
𝑢𝑠𝑡
= 25800[𝑁]
𝑆
𝑚𝑎𝑥
= 32634,39[𝑁]
𝐹
𝑑𝑦𝑛
=
𝑆
𝑚𝑎𝑥
𝑆
𝑢𝑠𝑡
=
32634,39
25800
= 1,265
E. Michlowicz: IMiU – ćwiczenia 2 – model dwumasowy
4
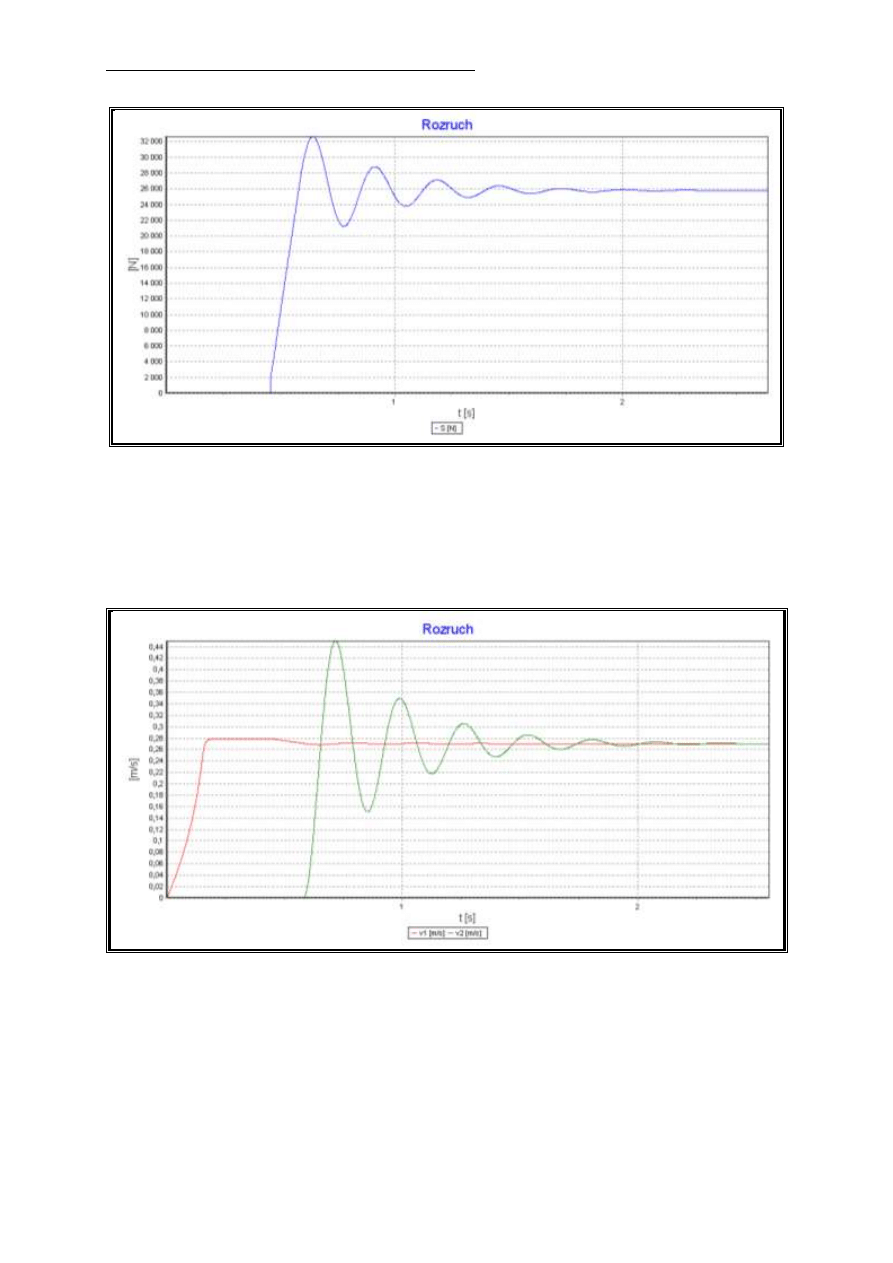
Rys. 1. Wykres siły w więzi sprężystej podczas rozruchu
Rys. 2. Wykres prędkości pierwszej i drugiej masy podczas rozruchu
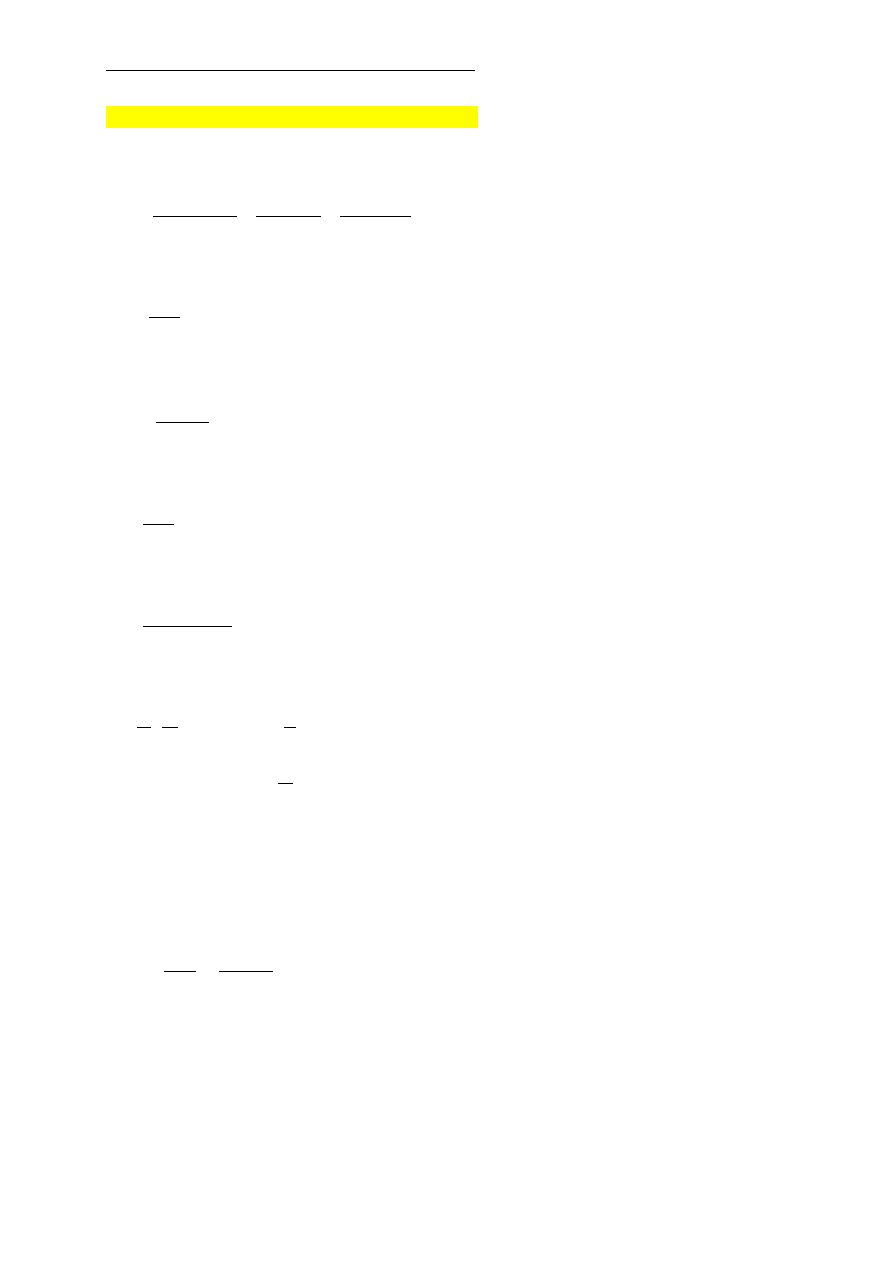
E. Michlowicz: IMiU – ćwiczenia 2 – model dwumasowy
5
2. HAMOWANIE PRZY OPUSZCZANIU
1. Obliczanie zredukowanego momentu bezwładności „I
zr1
” dla hamowania:
𝐼
𝑧𝑟1
=
(𝐼
𝑠
+𝐼
𝑠ℎ
+𝐼
𝑧1
)∙𝑖
𝑐
2
𝜂
𝑐
+
(𝐼
𝑧2
+𝐼
𝑧3
)∙𝑖
2
2
𝜂
𝑏
∙𝜂
2
+
(𝐼
𝑧4
+𝐼
𝑠𝑏
+𝐼
𝑏
)
𝜂
𝑏
= 766,64[𝑘𝑔𝑚
2
]
2. Obliczanie masy „m
1
” zredukowanej na bęben dla hamowania:
𝑚
1
=
4∙𝐼
𝑧𝑟1
𝐷
𝑏
2
= 26527,20[𝑘𝑔]
3. Obliczenie masy „m
2
” zredukowanej na bęben:
𝑚
2
= [
𝑚
𝑄
+𝑚
𝑄0
𝑖
𝑤𝑘
2
∙ 𝜂
𝑤
] = 1287,74[𝑘𝑔]
4. Wyznaczanie siły czynnej „S
1
” przy hamowaniu:
𝑆
1
=
2𝑀
ℎ
𝜂
𝑐
∙𝐷
𝑏
∙ 𝑖
1
∙ 𝑖
2
= 43549,33[𝑁]
5. Wyznaczenie siły biernej „S
2
”:
𝑆
2
=
(𝑚
𝑄
+𝑚
𝑄0
)∙9,81
𝑖
𝑤
∙𝜂
𝑤
= 25778,50[𝑁]
6. Obliczenie współczynnika sprężystości i tłumienia liny :
𝑘 =
2
𝑖
𝑤
∙
𝐸𝐹
𝐿
= 713041,67 [
𝑁
𝑚
]
ℎ = 0,01 ∙ 𝑘 = 7130,42 [
𝑁𝑠
𝑚
]
Obliczenie nadwyżki dynamicznej
𝑆
𝑢𝑠𝑡
= 25790[𝑁]
𝑆
𝑚𝑎𝑥
= 27166,39[𝑁]
𝐹
𝑑𝑦𝑛
=
𝑆
𝑚𝑎𝑥
𝑆
𝑢𝑠𝑡
=
27166,39
25790
= 1,053
E. Michlowicz: IMiU – ćwiczenia 2 – model dwumasowy
6
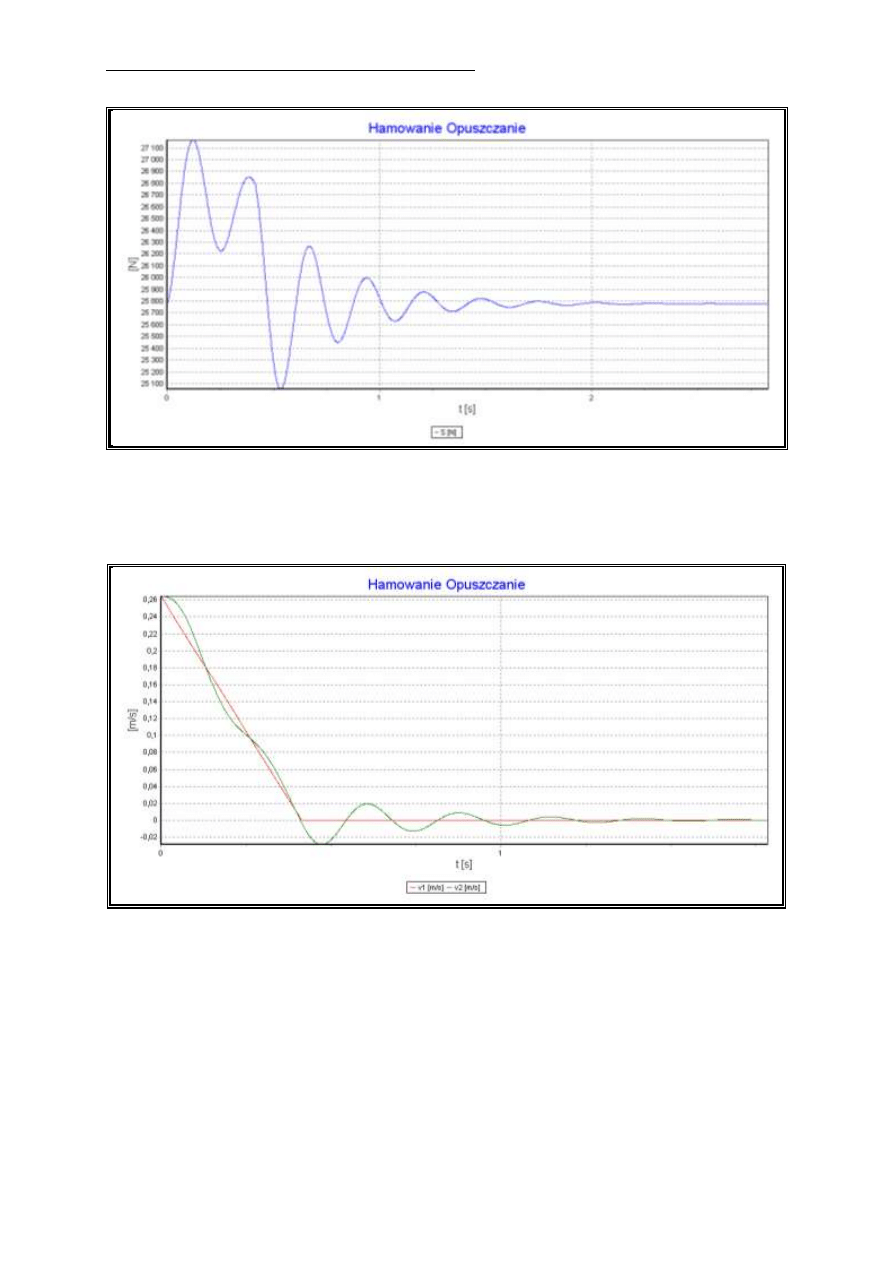
Rys. 3. Wykres siły w więzi sprężystej podczas hamowania przy opuszczaniu
Rys. 4. Wykres prędkości pierwszej i drugiej masy podczas hamowania przy opuszczaniu
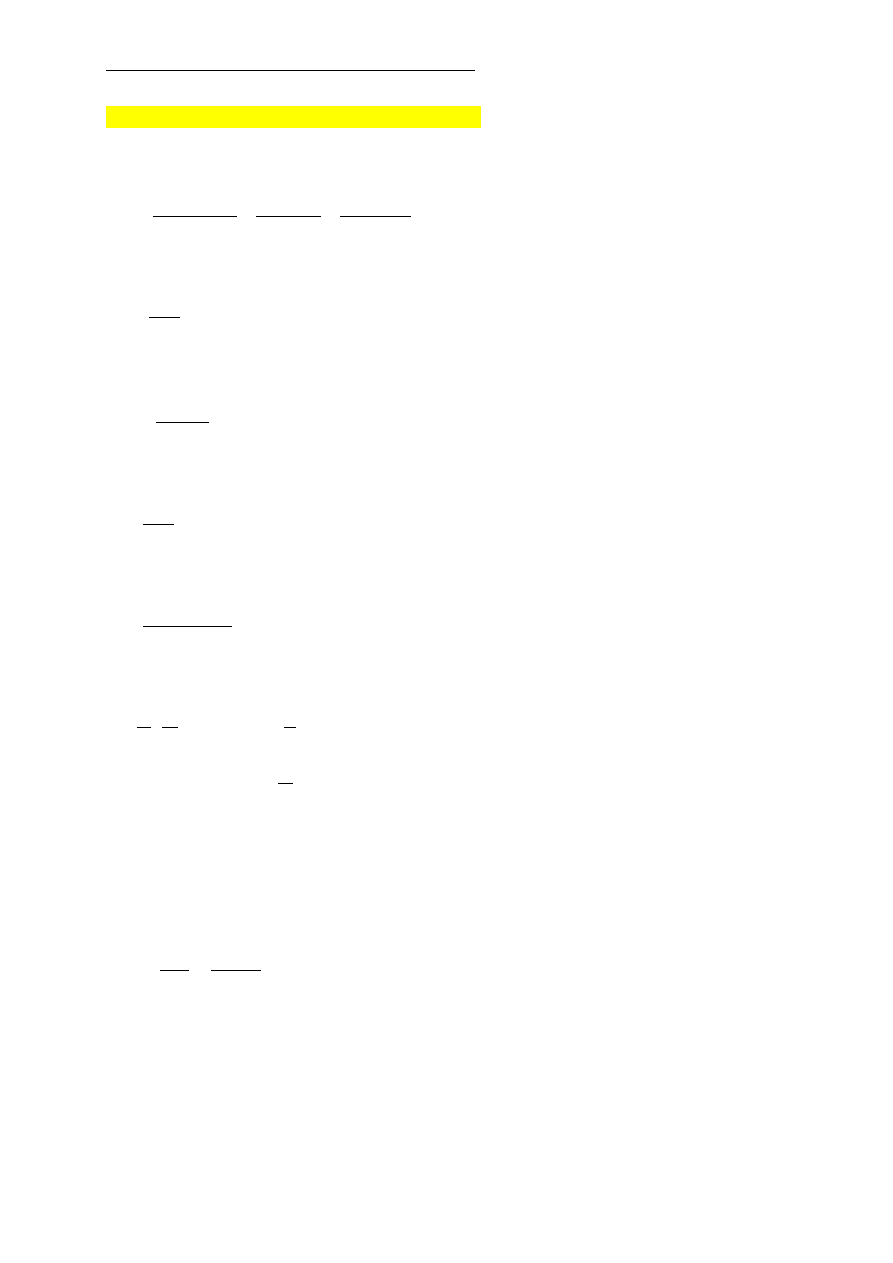
E. Michlowicz: IMiU – ćwiczenia 2 – model dwumasowy
7
3. HAMOWANIE PRZY PODNOSZENIU
1. Obliczanie zredukowanego momentu bezwładności „I
zr1
” przy podnoszeniu:
𝐼
𝑧𝑟1
=
(𝐼
𝑠
+𝐼
𝑠ℎ
+𝐼
𝑧1
)∙𝑖
𝑐
2
𝜂
𝑐
+
(𝐼
𝑧2
+𝐼
𝑧3
)∙𝑖
2
2
𝜂
𝑏
∙𝜂
2
+
(𝐼
𝑧4
+𝐼
𝑠𝑏
+𝐼
𝑏
)
𝜂
𝑏
= 766,64[𝑘𝑔𝑚
2
]
2. Obliczanie masy „m
1
” zredukowanej na bęben przy podnoszeniu:
𝑚
1
=
4∙𝐼
𝑧𝑟1
𝐷
𝑏
2
= 26527,20[𝑘𝑔]
3. Obliczenie masy „m
2
” zredukowanej na bęben przy podnoszeniu:
𝑚
2
= [
𝑚
𝑄
+𝑚
𝑄0
𝑖
𝑤𝑘
2
∙ 𝜂
𝑤
] = 1287,74[𝑘𝑔]
4. Wyznaczanie siły czynnej „S
1
” przy hamowaniu podczas podnoszenia:
𝑆
1
=
2𝑀
ℎ
𝜂
𝑐
∙𝐷
𝑏
∙ 𝑖
1
∙ 𝑖
2
= 43549,33[𝑁]
5. Wyznaczenie siły biernej „S
2
” przy hamowaniu podczas podnoszenia:
𝑆
2
=
(𝑚
𝑄
+𝑚
𝑄0
)∙9,81
𝑖
𝑤
∙𝜂
𝑤
= 25778,50[𝑁]
Obliczenie współczynnika sprężystości i tłumienia liny
𝑘 =
2
𝑖
𝑤
∙
𝐸𝐹
𝐿
= 713041,67 [
𝑁
𝑚
]
ℎ = 0,01 ∙ 𝑘 = 7130,42 [
𝑁𝑠
𝑚
]
Obliczenie nadwyżki dynamicznej
𝑆
𝑢𝑠𝑡
= 25550[𝑁]
𝑆
𝑚𝑎𝑥
= 29318,33[𝑁]
𝐹
𝑑𝑦𝑛
=
𝑆
𝑚𝑎𝑥
𝑆
𝑢𝑠𝑡
=
29318,33
25550
= 1,147
E. Michlowicz: IMiU – ćwiczenia 2 – model dwumasowy
8
Rys. 5. Wykres wartości siły w więzi sprężystej podczas hamowania przy podnoszeniu
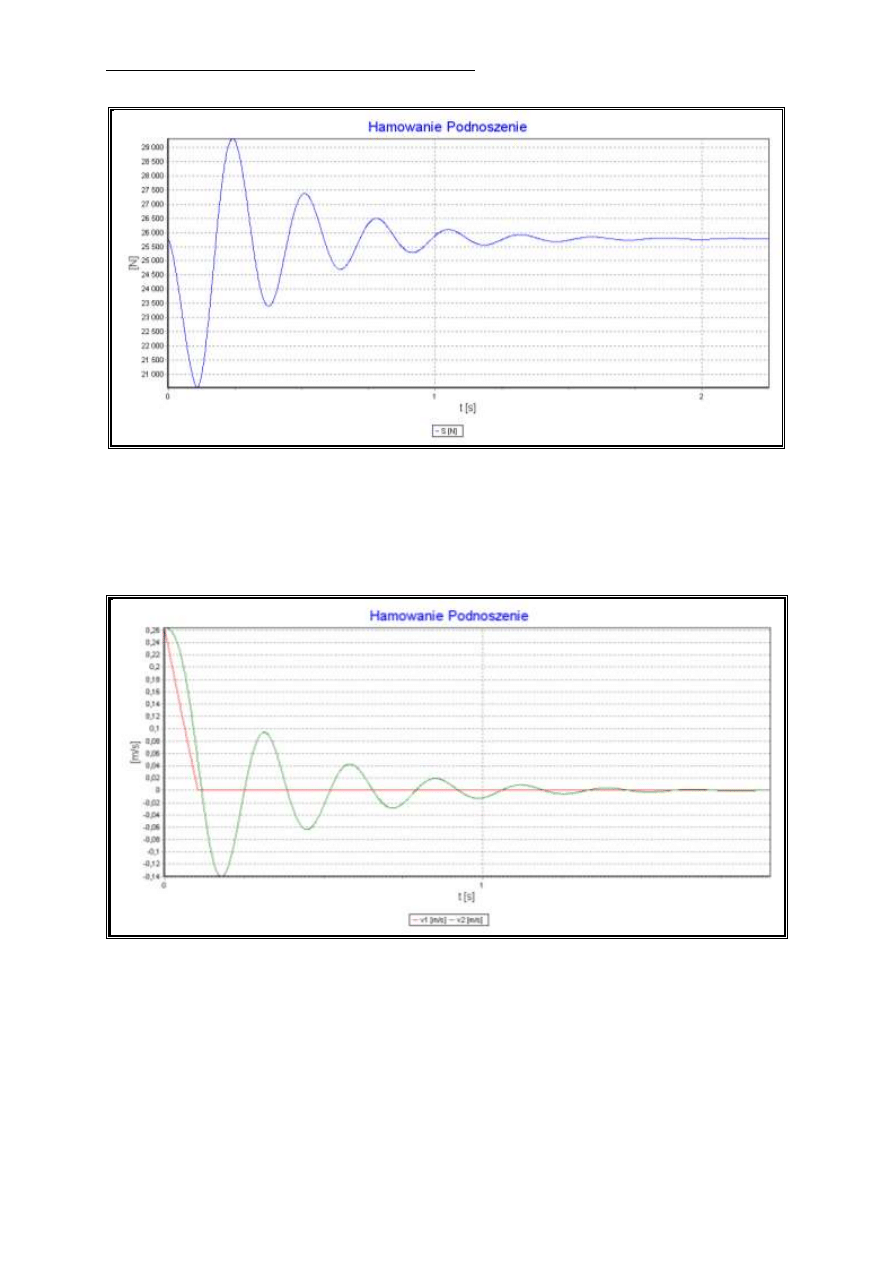
Rys. 6. Wykres prędkości pierwszej i drugiej masy podczas hamowania przy podnoszeniu