Zagadnienia

Podstawy technologii chemicznej

Semestr letni 2011/2012

1. Bilans materiałowy układów bez reakcji chemicznej i z reakcją chemiczną, obliczenia
2. Stopień przemiany w stechiometrycznej i niestechiometrycznej mieszaninie reagentów

BILANS MATERIAŁOWY

[Masowe natężenie przepływu strumieni

dopływających] – [Masowe natężenie przepływu

strumieni odpływających] = [szybkość akumulacji

wewnątrz aparatu]

BILANS MATERIAŁOWY –

podstawa obliczeń w technologii chemicznej

przy braku akumulacji masy wewnątrz aparatu

(STAN USTALONY):

ΣF

i zasil.

= ΣF

i prod.

[masowe natężenie przepływu strumieni

dopływających]

= [masowe natężenie przepływu

strumieni odpływających]

3. Bilans energetyczny:
-

Zasada zachowania energii

-

Składowe energii układów

-

Obliczanie pracy sprężania i ekspansji gazów

-

Entalpia: obliczanie zmian entalpii, pojemność cieplna

-

Entalpia reakcji: obliczanie zmian entalpii w stanie standardowym i
w temperaturze innej niż standardowa

Praca jest dodatnia, gdy tłok jest naszym układem
termodynamicznym.

Jeśli naszym układem będzie gaz, to praca dostarczona temu
układowi będzie ujemna.

Wtedy;

∫

⋅

−

=

2

1

v

v

v

dv

p

W

Z powyższych rozważań wynika, że znak pracy zależy od
wyboru układu termodynamicznego.

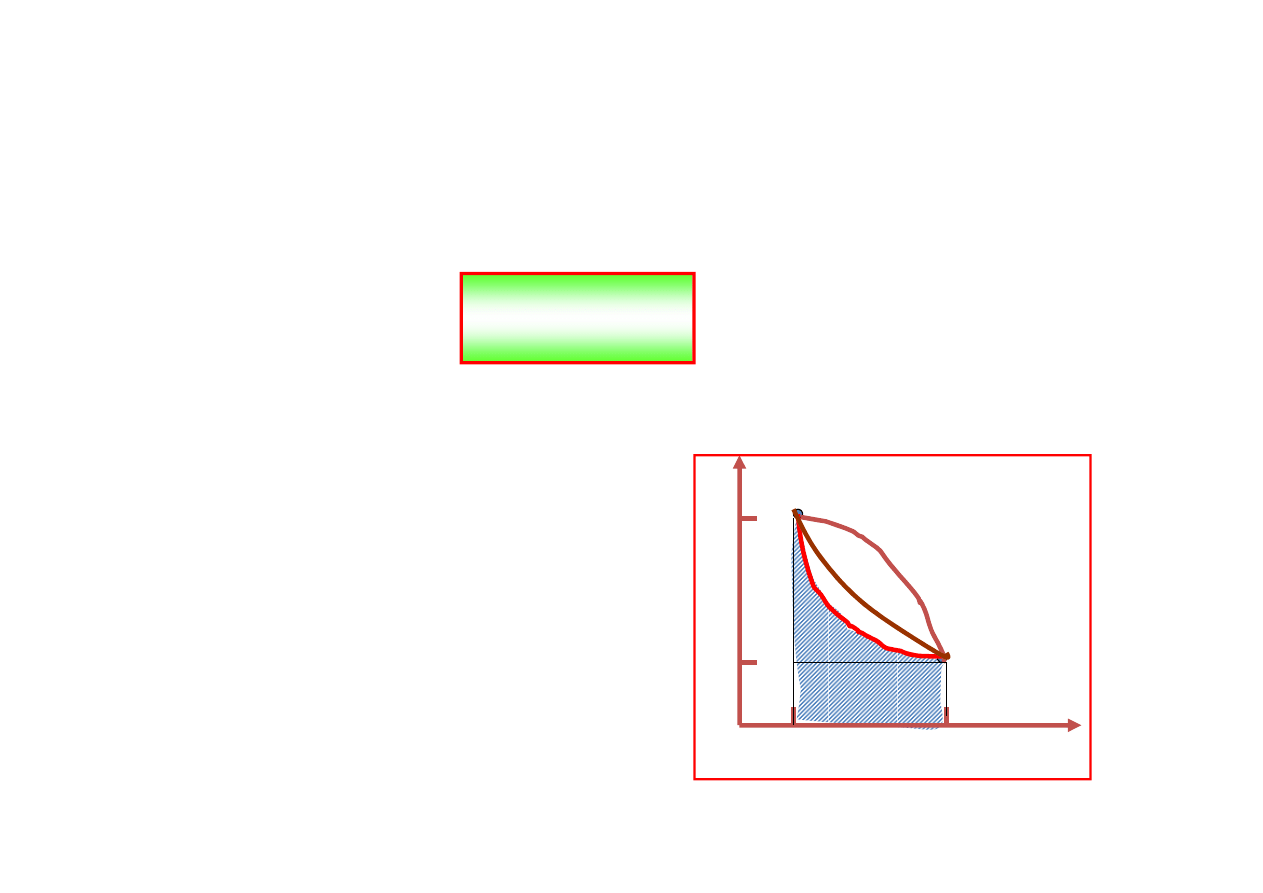
Graficzne przedstawienie pracy
wykonanej przez rozprężający
się gaz jest pokazane obok.
Drogi od punktu 1 do punktu 2
mogą być różne (

różne

przemiany gazowe

)

1

2

V

1

V

2

p

V

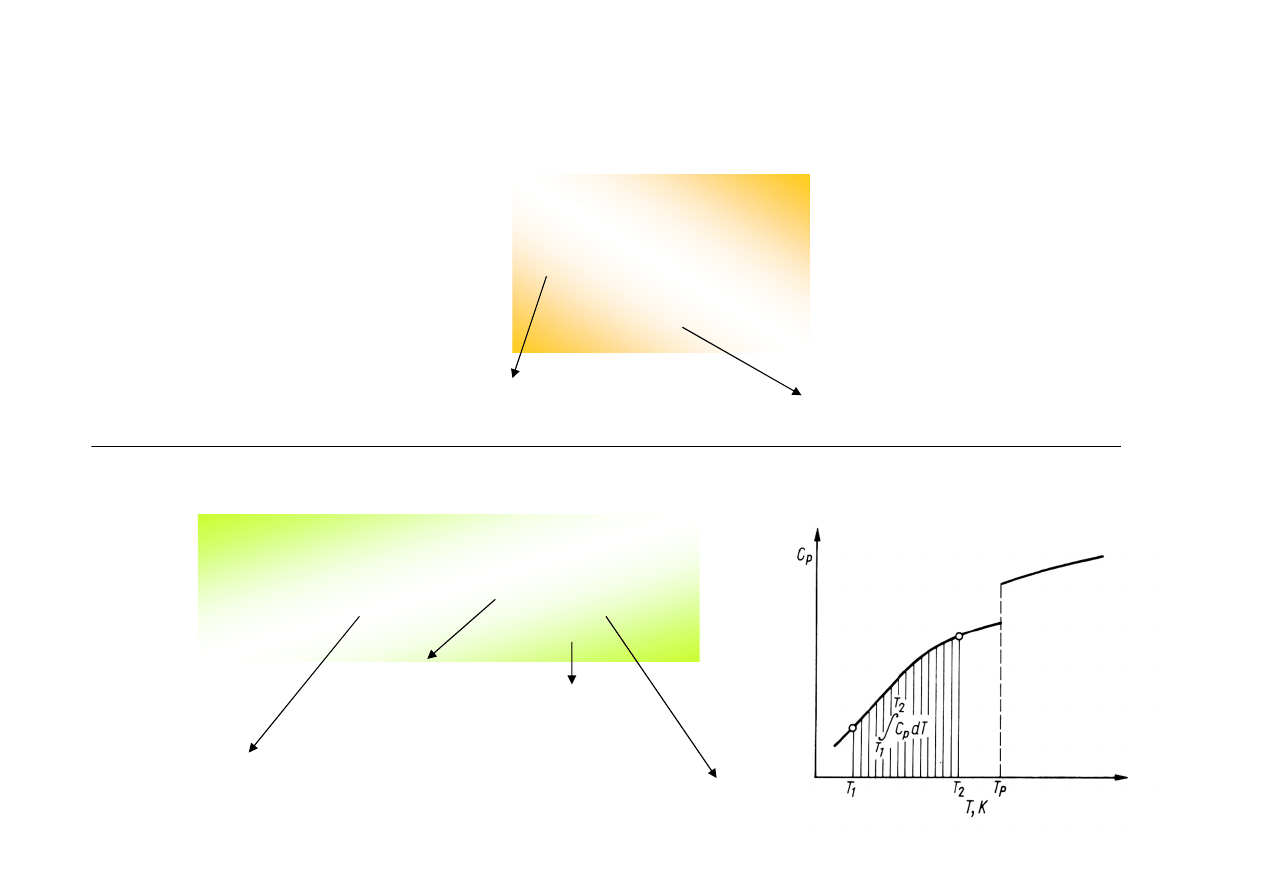
OBLICZANIE ZMIAN ENTALPII

∫

=

−

2

1

1

2

T

T

p

dT

c

H

H

∫

=

T

T

p

T

o

dT

c

H

entalpia molowa

w temperaturze T

temperatura odniesienia

Obliczania entalpii

w przedziale temperatur,

w którym nie ma

przejścia fazowego

*

∫

∫

+

+

=

T

T

p

T

T

f

p

T

f

f

o

dT

c

H

dT

c

H

2

1

Jeżeli w rozważanym zakresie temperatur występuje przemiana fazowa:

temperatura

przejścia fazowego

pojemność cieplna

w fazie 1

pojemność cieplna

w fazie 2

entalpia

przemiany

fazowej

**

Sposób obliczania entalpii reakcji w temperaturze innej niż 298 K

Przyjmujemy, że równanie stechiometryczne reakcji można opisać równaniem:

0 = –

νννν

A

A –

νννν

B

B +

νννν

C

C +

νννν

D

D

w którym A i B są substratami, a C i D – produktami reakcji

Wyrażenia oznaczające zależność molowej pojemności cieplnej od

temperatury mają znaną już postać szeregu potęgowego.

3

2

T

d

T

c

T

b

a

c

i

i

i

i

pi

+

+

+

=

o

dla wszystkich

czterech reagentów!

Po uwzględnieniu współczynników stechiometrycznych reakcji otrzymamy udziały
poszczególnych reagentów:

(

)

3

2

,

T

d

T

c

T

b

a

c

A

A

A

A

A

A

p

A

+

+

+

=

ν

ν

o

(

)

3

2

,

T

d

T

c

T

b

a

c

B

B

B

B

B

B

p

B

+

+

+

=

ν

ν

o

(

)

3

2

,

T

d

T

c

T

b

a

c

C

C

C

C

C

C

p

C

+

+

+

=

ν

ν

o

(

)

3

2

,

T

d

T

c

T

b

a

c

D

D

D

D

D

D

p

D

+

+

+

=

ν

ν

o

Zdefiniujemy teraz wielkość

o

p

c

∆

jako:

∑

=

∆

i

i

,

p

i

p

c

c

o

o

ν

oraz zmiany współczynników:

∑

=

∆

i

i

i

a

a

ν

∑

=

∆

i

i

i

b

b

ν

∑

=

∆

i

i

i

c

c

ν

∑

=

∆

i

i

i

d

d

ν

Po podstawieniu otrzymujemy uproszczone wyrażenie przedstawiające
różnicę pojemności cieplnej produktów i substratów reakcji:

3

2

dT

cT

bT

α

c

p

∆

+

∆

+

∆

+

∆

=

∆

o

Jeżeli znamy standardową entalpię reakcji w jednej temperaturze, np. 298 K,

obliczyć standardową entalpię reakcji

o

T

r

H

,

∆

w innej temperaturze:

(

)

∫

∫

∆

+

∆

+

∆

+

∆

+

∆

=

∆

+

∆

=

∆

T

r

T

p

r

T

r

dT

dT

cT

bT

a

H

dT

c

H

H

298

3

2

298

,

298

298

,

,

o

o

o

o

Jeżeli w przedziale całkowania występują przemiany fazowe substratów lub produktów reakcji,

należy to uwzględnić.

Zakładając, że w temperaturze T

f

występuje przemiana fazowa któregoś z reagentów, wówczas:

∫

∫

∆

+

∆

+

∆

+

∆

=

∆

298

Τ

T

f

p

f

i

Τ

i

p

r

T

r

f

dT

c

H

dT

c

H

H

,

,

298

,

,

o

o

o

o

o

ν

4. Gaz doskonały
-

Właściwości

-

Równanie stanu

-

przemiany: adiabatyczna, politropowa, izotermiczna

-

Obliczanie pracy sprężania i rozprężania gazu doskonałego

PRZEMIANA POLITROPOWA

W urządzeniach przemysłowych sprężanie lub rozprężanie jest przemianą

politropową, opisaną wyrażeniem

const

=

n

PV

( )

( )















−













−

=















−













−

=

−

−

1

1

1

1

1

1

2

1

1

1

2

1

1

n

n

n

n

P

P

n

n

M

ZRT

P

P

n

n

V

ZP

W

Z jest współczynnikiem ściśliwości,

R – stałą gazową,

M – masą cząsteczkową gazu.

Wartość n zależy od rodzaju i sposobu pracy urządzenia

Zasada zachowania energii dla jednostki procesowej

w stanie ustalonym ma postać:

∑

∑

∑

=

+

+

∆

=

0

1

dt

dW

dt

dQ

H

F

i

i

N

i

i

i

s

strumień

wyrażony

w molach (kilomolach)

na jednostkę czasu

entalpia molowa

natężenie przepływu

ciepła przez granicę

jednostki procesowej

- od jednostki procesowej

do otoczenia

natężenie przepływu

energii w postaci pracy

+ praca wykonana

na jednostce procesowej

Właściwości substancji chemicznych:
-

Zasada stanów odpowiadających sobie

-

Wyznaczanie gęstości: metoda Watsona, metoda Bensona, w obszarze krytycznym

-

Lepkość, równanie Soundersa

-

Metoda inkrementów grupowych lub atomowych, na czym polega

METODA BENSONA
•

wzór empiryczny, umo

ż

liwia obliczenie g

ę

sto

ś

ci cieczy nasyconej

w temperaturze wrzenia

403

,

2

lg

4221

,

0

+

=

=

c

c

w

w

c

p

V

V

ρ

ρ

gdzie: V

w

– objętość molowa cieczy nasyconej (wrzącej)

ρ

w

– gestość cieczy w temperaturze wrzenia

p

c

–ciśnienie krytyczne, w MPa

LEPKOŚĆ CIECZY c.d.

Równanie empiryczne Soudersa:

(

)

9

2

log

log

,

M

I

−

10

⋅

=

−3

ρ

η

w którym

η

– lepkość, mPa·s,

ρ

– gęstość w danej temperaturze, kg/m3,

M – masa cząsteczkowa,

I – współczynnik Soudersa, obliczony addytywnie według tabeli inkrementów

grupowych.

Odchylenia od stanu doskonałego:
-współczynnik ściśliwości: definicja, zależność od ciśnienia i temperatury
-

właściwości gazów rzeczywistych-

-

Równanie stanu gazów rzeczywistych: Redlicha-Kwonga, wirialne

-

Współczynnik acentryczny, obliczanie współczynnika acentrycznego

-

Wyznaczanie objętości molowej gazów i cieczy na podstawie
współczynników ściśliwości

WSPÓŁCZYNNIK ŚCIŚLIWOŚCI

RT

PV

Z

=

Dla gazu idealnego: Z=1

Dla gazów rzeczywistych przedstawiany
w postaci tabelaryczne, graficznej
lub matematycznej jako funkcja T

r

, P

r

Równanie Redlicha–Kwonga

(

)

b

V

V

T

a

b

V

RT

P

,

+

−

−

=

5

0

c

,

c

P

T

R

,

a

5

2

2

42748

0

=

c

c

P

T

R

b

0867

,

0

=

Jest ono stosowane do wartości P

r

= 0,8

Równanie Redlicha–Kwonga c.d.

Postać wielomianowa:

0

)

(

2

2

3

=

−

−

−

+

−

AB

Z

B

B

A

Z

Z

Ma trzy rozwiązania względem Z.
Największą otrzymaną wartość Z przypisuje się fazie gazowej, najmniejszą – fazie ciekłej,
pośrednia zaś nie jest brana pod uwagę

5

2

5

2

2

42748

0

,

r

r

,

T

P

,

T

R

aP

A

=

=

r

r

T

P

,

RT

bP

B

08664

0

=

=

Współczynnik acentryczny

P

vp,r

jest zredukowanym ciśnieniem pary nasyconej wyznaczonym dla T

r

= 0,7.

Współczynnik acentryczny obliczono i stabelaryzowano dla kilkuset płynów

(

)

7

0

log

,

T

r

,

vp

r

P

=

+

1

−

=

ω

Współczynnik acentryczny w razie potrzeby można obliczyć ze wzoru:

1

3

,

101

log

1

−

























−

7

3

=

c

br

br

P

T

T

ω

T

br

jest zredukowaną temperaturą

wrzenia,

P

c

– ciśnieniem krytycznym wyrażonym w

kPa.

Wirialne równanie stanu

( )

( )

K

+

+

+

=

2

1

V

T

C

V

T

B

Z

( )

( )

K

+

+

+

=

2

1

V

T

C

V

T

B

RT

PV

Wyznaczanie wielkości cząstkowych molowych mieszaniny

Lotność
-

lotność (aktywność ciśnieniowa)

-

Współczynnik lotności

-

reguła Lewisa-Randalla, wyznaczanie wartości współczynnika
aktywności ciśnieniowej składnika mieszaniny gazowej

-

Wyznaczanie aktywności ciśnieniowej na podstawie podanego
równania stanu

-

Metody UNIFAC i UNIQUAC

-

Równowaga fazowa, kryterium równowagi, opis równowagi ciecz-para

-

Mieszaniny gazów (płynów), sposób uśredniania współczynników w
równaniach stanu

LOTNOŚĆ GAZÓW I CIECZY

Znajomość lotności (aktywności ciśnieniowej) gazów i ich mieszanin jest

potrzebna do obliczania funkcji termodynamicznych, takich jak entalpia i

entropia w stanie nieidealnym oraz do wyznaczania równowag fazowych.

Dla czystych gazów lotność jest zdefiniowana następująco:

∫

=

P

VdP

RT

f

0

1

ln

*

W praktyce częściej oblicza się współczynnik lotności (fugatywności)

φ

,

który dla czystego gazu jest stosunkiem jego lotności do ciśnienia:

P

f

=

φ

LOTNOŚĆ GAZÓW I CIECZY c.d.

Dla składnika i w mieszaninie stosunkiem lotności tego składnika do jego
ciśnienia parcjalnego

P

y

f

i

i

i

=

φ

LOTNOŚĆ CIECZY

Lotność

składnika i w fazie ciekłej jest odniesiona do

zawartości tego składnika w cieczy (ułamka molowego) przez

następujące korelacje:

L

i

f

i

i

i

x

a

=

γ

oL

i

i

i

L

i

f

x

f

γ

=

w których:

a

i

oznacza aktywność składnika i,

γγγγ

i

jego współczynnik aktywności,

f

i

oL

jest lotnością składnika i w stanie standardowym w temperaturze mieszaniny dla

arbitralnie wybranego ciśnienia i składu.

RÓWNOWAGI FAZOWE

RÓWNOWAGA CIECZ-PARA

Kryterium równowagi termodynamicznej między fazą ciekłą a gazową w

mieszaninie wieloskładnikowej jest równość obowiązująca dla wszystkich

składników i tej mieszaniny:

L

i

v

i

f

f

=

RÓWNOWAGA CIECZ-PARA

Dla fazy gazowej możemy napisać:

dla fazy ciekłej zaś

P

y

f

i

v

i

i

=

φ

oL

i

i

i

L

i

f

x

f

γ

=

f oznacza lotność,

γ

– współczynnik aktywności,

indeksy v i L odnoszą się do pary (fazy gazowej) oraz cieczy,

f

i

oL

oznacza lotność składnika i w stanie standardowym,

x

i

jest ułamkiem molowym składnika i w fazie ciekłej,

y

i

– w fazie gazowej.

Współczynnik lotności

φφφφ

i

zależy od temperatury i ciśnienia, a w przypadku

mieszaniny

wieloskładnikowej

także

od

ułamków

molowych

innych

składników fazy parowej. Współczynnik lotności jest tak zdefiniowany, że gdy

P

→

0,

φ

i

→

1 dla wszystkich składników. Dlatego dla małych ciśnień często

przyjmuje się, że współczynnik lotności jest równy jedności.

RÓWNOWAGA CIECZ-PARA