Termodynami

ka



teoria kinetyczno –

molekularna,



zasady termodynamiki

TERMODYNAMIKA

TERMODYNAMIKA

Kinetyczna teoria gazów

Kinetyczna teoria gazów

Problem: opis ruchu układów

wielocząsteczkowych

→

10

19

równań !

1 cm

3

około 10

19

cząsteczek
powietrza !

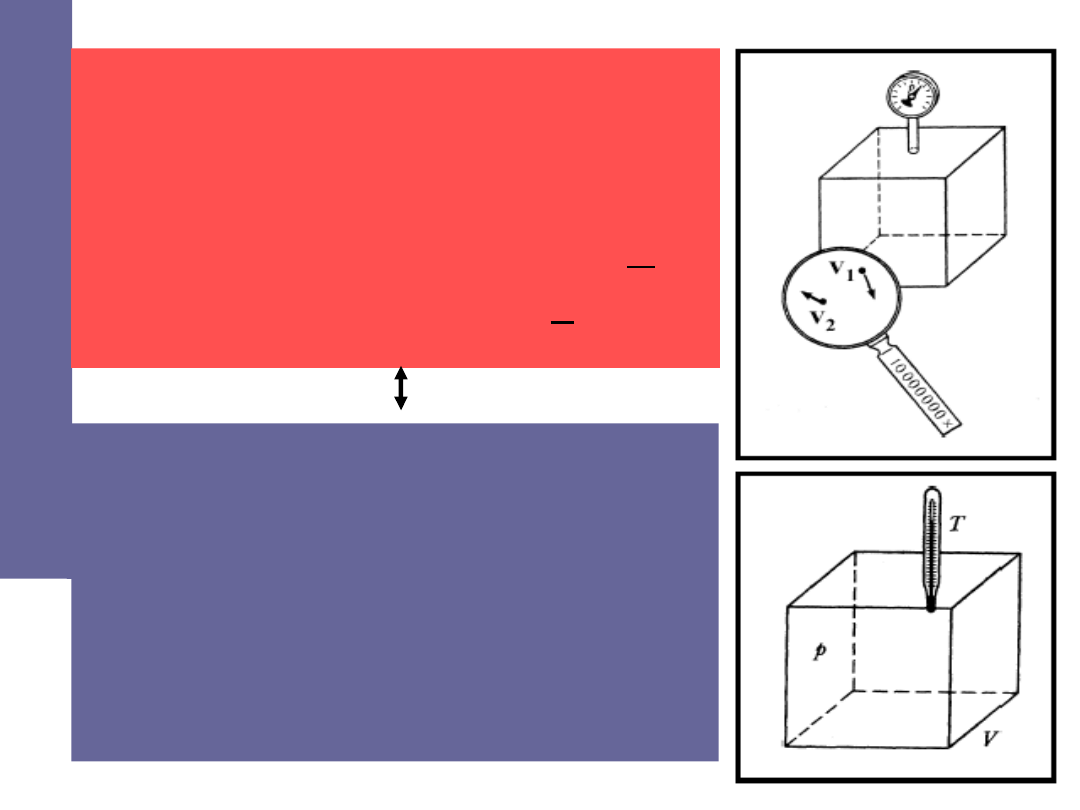
Opis makroskopowy

→

termodynamika

Parametry:

• temperatura

• ciśnienie

• objętość

Opis mikroskopowy

→

fizyka statystyczna

Parametry:

• masa cząsteczki

• średnia energia kinetyczna

• średnia prędkość

k

E

v

m

T

p

V

Prawo gazów

Prawo gazów

dos kona ych

ł

dos kona ych

ł

Gaz doskona

Gaz doskona

ł

ł

y

y

- założenia:

•

Objętość cząsteczek

gazu jest

o wiele mniejsza niż objętość
zajmowana przez gaz (cząsteczki gazu
– punkty materialne)

•

Zasięg sił

działających między

dwiema cząstkami jest
o wiele mniejszy niż średnia odległość
międzycząsteczkowa
(oddziaływania międzycząsteczkowe –
pomijane)

•

Zderzenia

cząsteczek są idealnie

sprężyste

Prawo gazów

Prawo gazów

dos kona ych

ł

dos kona ych

ł

Warunki normalne

Warunki normalne

- założenia:

           

K

C

T

dm

V

hPa

Pa

atm

p

o

15

,

273

0

415

,

22

1013

101325

1

0

3

0

0

=

=

=

=

=

=

Prawo Avogadra

Prawo Avogadra

Jednakowe objętości różnych gazów
znajdujących się pod tym samym
ciśnieniem i w tej samej temperaturze
zawierają jednakową liczbę cząsteczek.

3

0

23

415

,

22

1

6.023·10

dm

V

mol

N

A

=

=

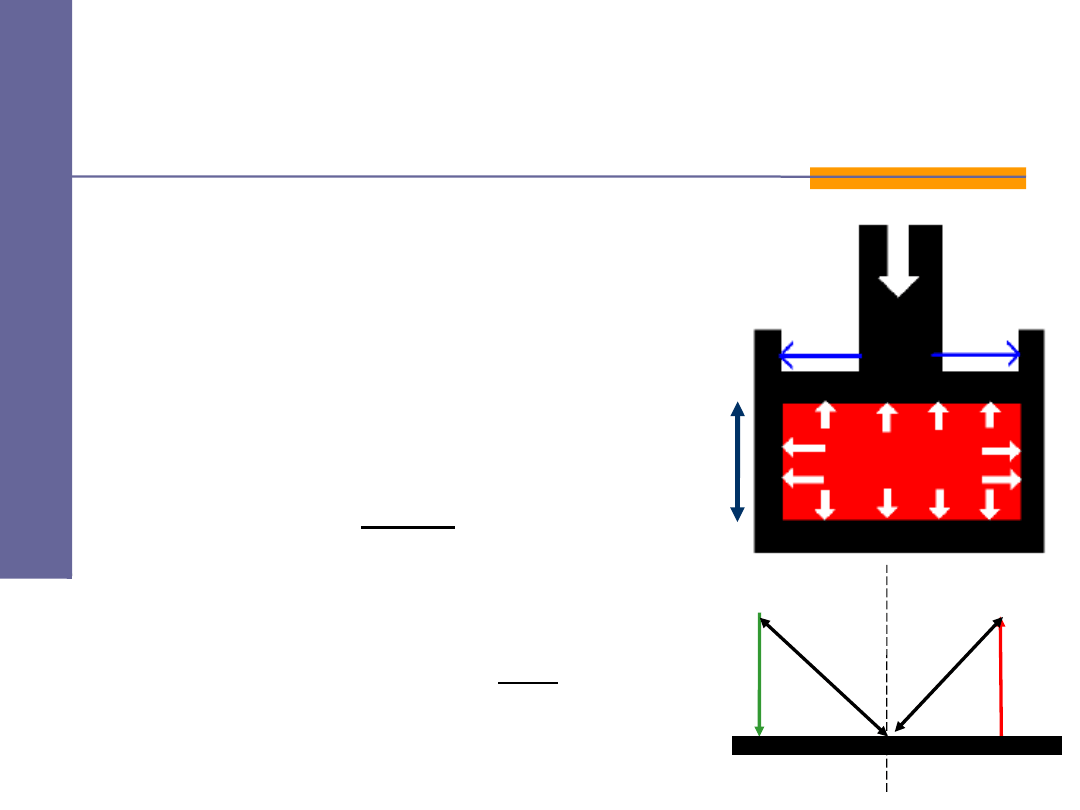
Ci

Ci

ś

ś

nieniem

nieniem

p

p

nazywamy wielkość

fizyczną liczbowo równą sile działającej
na powierzchnię ciała wzdłuż normalnej
do tej powierzchni:

Jednostka:

paskal

1

v



1

v



x

v

1



x

v

1



−

m

m

Ci nienie

ś

Ci nienie

ś

S

F

p

n

∆

=



2

m

N

Pa

=

ciśnienie

siła

powierzchnia

l

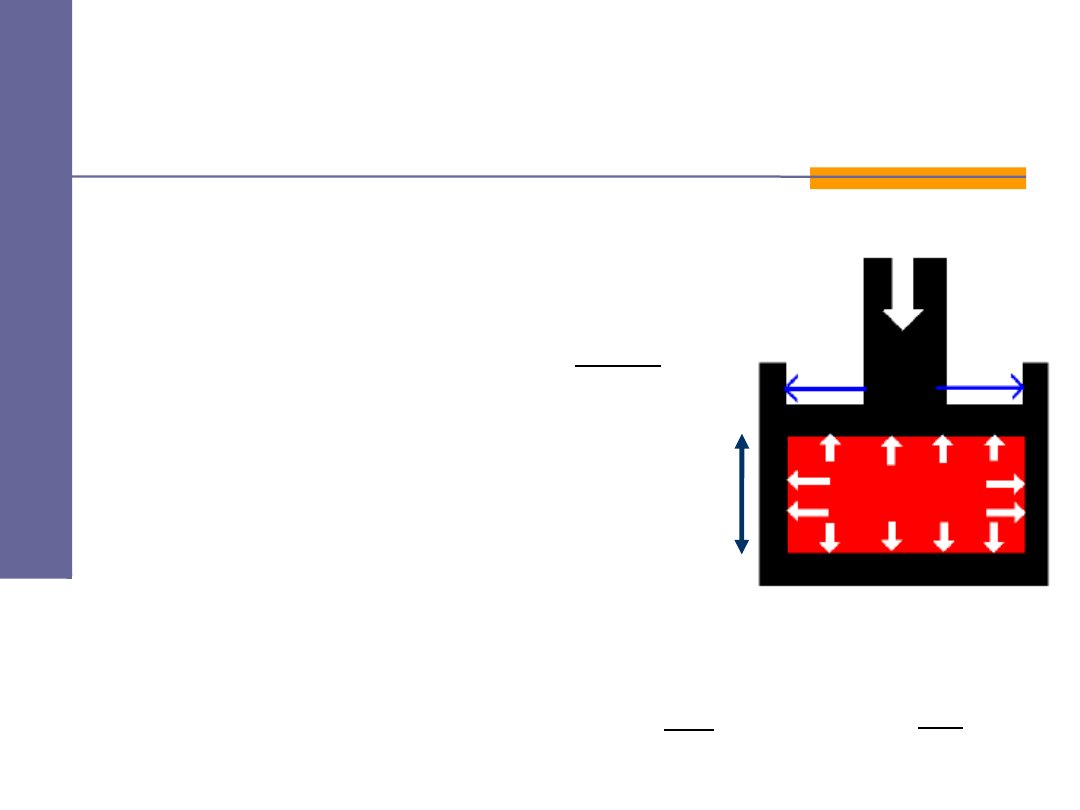
Średnia siła

jaką cząsteczka wywiera na ściankę

w czasie

∆

t wynosi:

t

p

F

x

n

∆

∆

=

⇒





Zmiana pędu

cząsteczki:

Czas

pomiędzy kolejnymi

zderzeniami z tą samą ścianką:

Ci nienie

ś

Ci nienie

ś

x

n

p

t

F





∆

=

∆

⋅

x

x

x

x

v

m

v

m

v

m

p









⋅

⋅

=

⋅

−

−

⋅

=

∆

2

)

(

x

v

l

t

2

=

∆

⇒

t

l

v

x

∆

=

2

ciśnienie

siła

powierzchnia

l

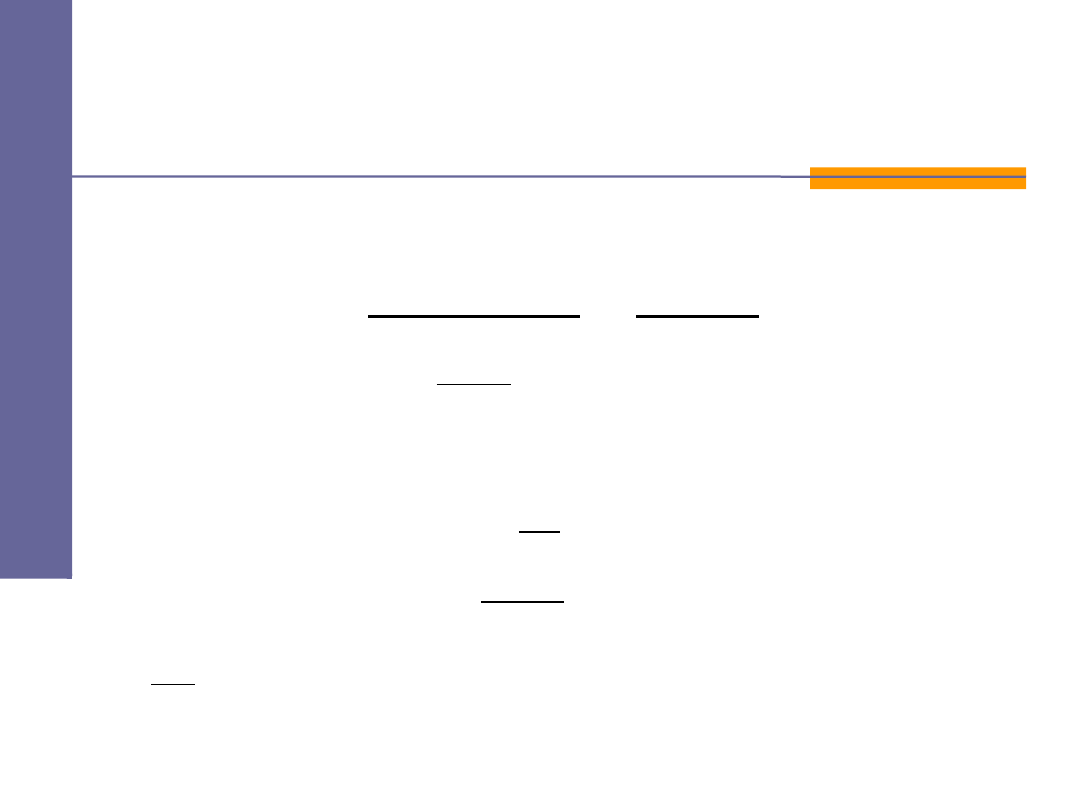
Całkowita siła działająca na ściankę od N cząsteczek:

l

m

N

F

x

n

2

v

=



gdzie jest to uśrednione po wszystkich
cząsteczkach (średnia kwadratu prędkości).

2

x

v

2

x

v

l

m

l

m

F

x

x

x

n

2

v

v

2

)

v

2

(









⋅

=

⋅

⋅

⋅

=

Stąd:

Ci nienie

ś

Ci nienie

ś

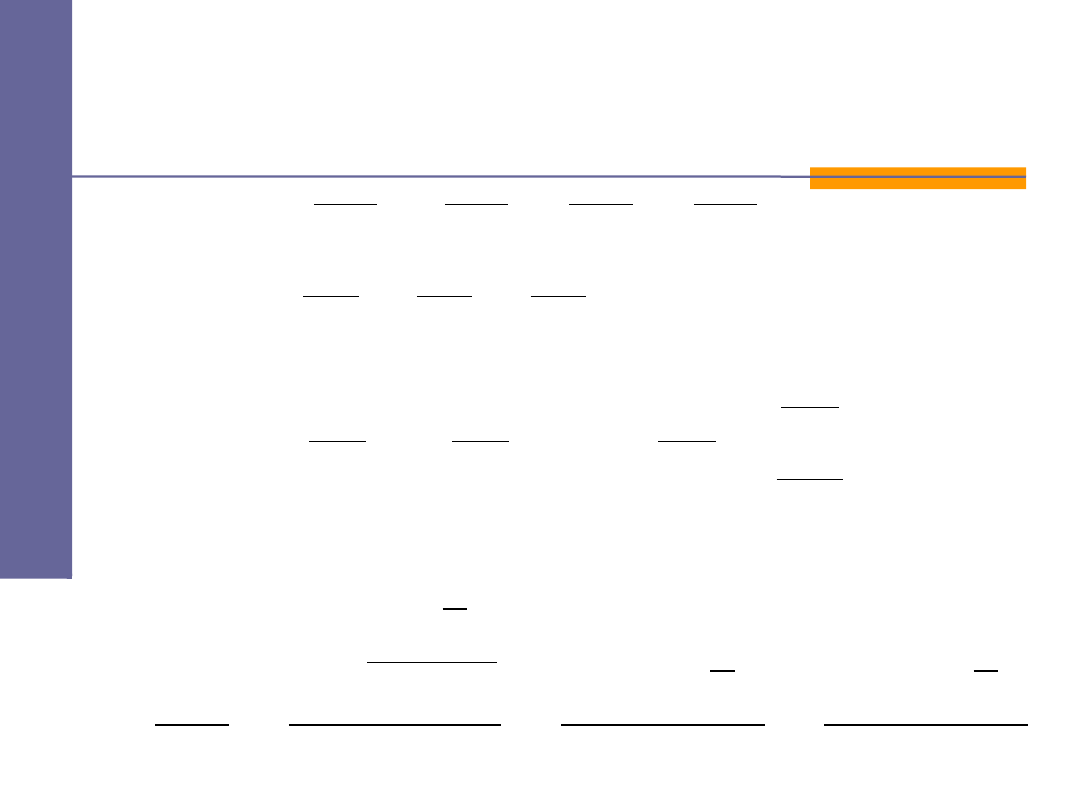
2

2

2

2

z

y

x

v

v

v

v

+

+

=

2

2

2

z

y

x

v

v

v

=

=

ponieważ

oraz

więc

3

,

3

2

2

2

2

v

v

v

v

=

=

x

x

czyli

ostatecznie

Ci

Ci

ś

nienie

nienie

V

v

m

N

S

l

v

m

N

S

l

v

m

N

S

F

p

n

⋅

⋅

⋅

=

⋅

⋅

⋅

⋅

=

⋅

⋅

⋅

=

∆

=

3

3

3

2

2

2



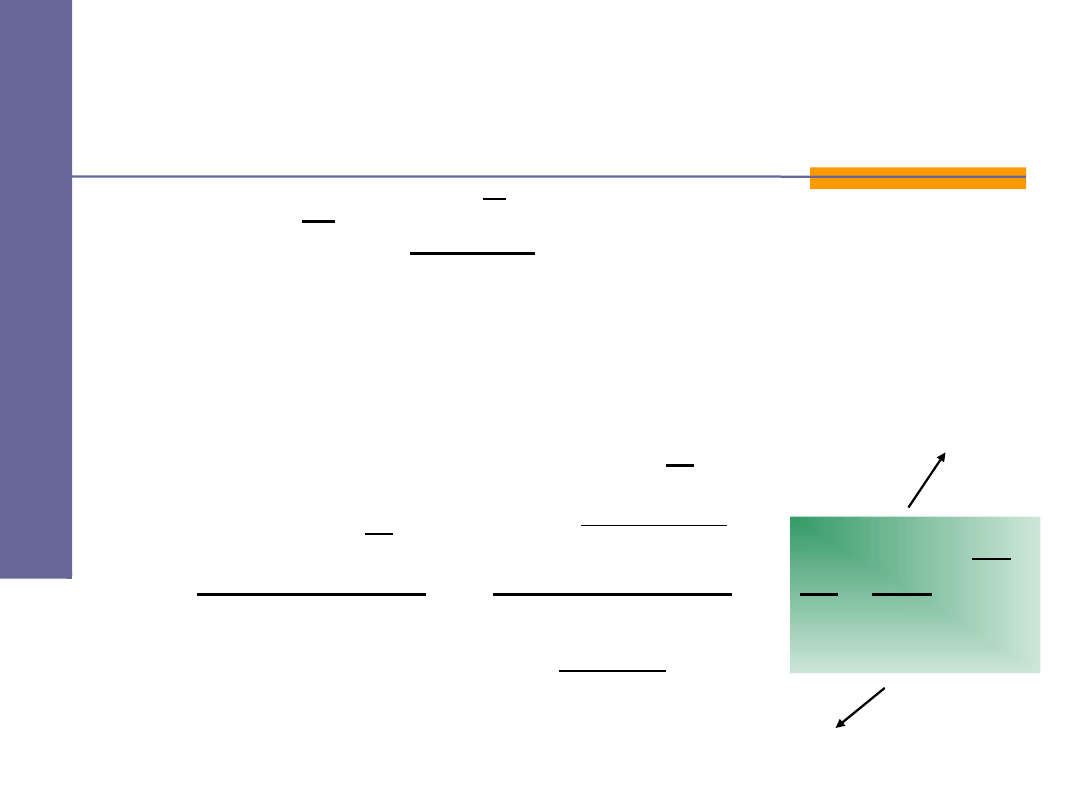
ponieważ

Ostatecznie możemy napisać:

Ci nienie

ś

Ci nienie

ś

k

E

V

N

V

v

m

N

V

v

m

N

p

⋅

⋅

=

⋅

⋅

⋅

=

⋅

⋅

⋅

=

3

2

2

3

2

3

2

2

2

2

v

m

E

k

⋅

=

obj to naczynia

ę ść

ilo cz stek

ść

ą

gazu w naczyniu

- energia kinetyczna

k

E

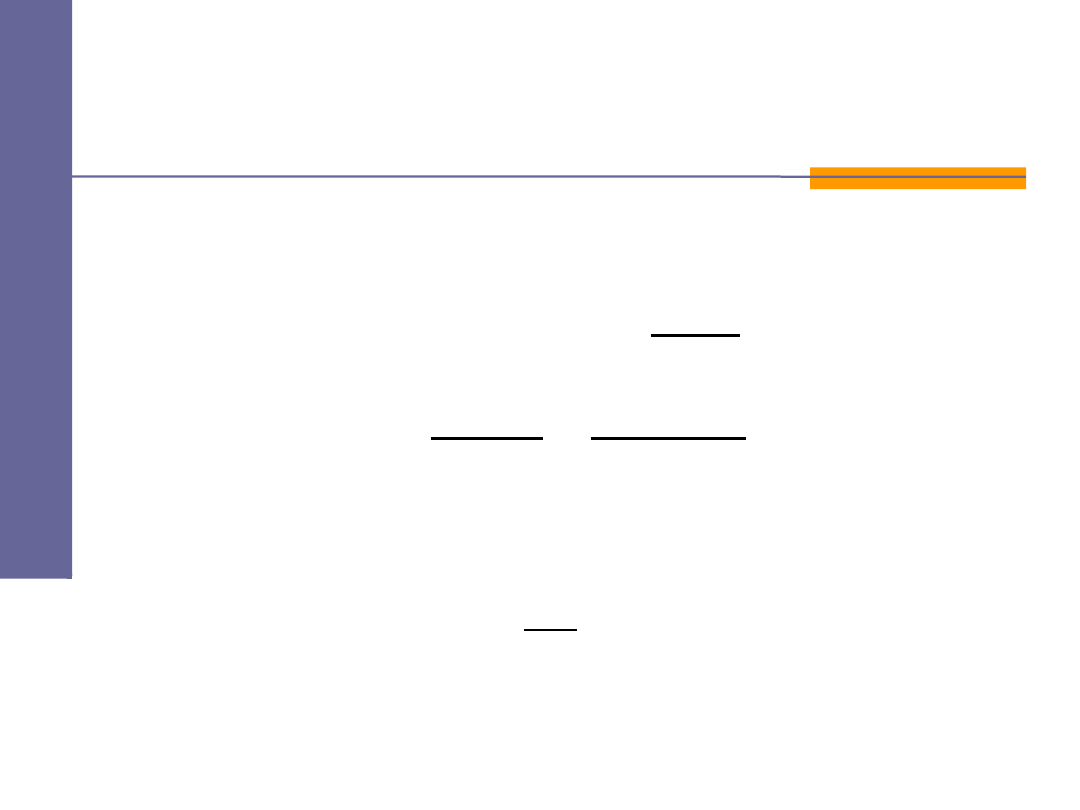
T

T

emperatura

emperatura

2

v

3

2

2

⋅













⋅

=

m

k

T

- s ta a

ł Boltzmanna

Je dno s tka:

ke lvin - K

Temperaturę bezwzględną

definiujemy jako wielkość

wprost proporcjonalną do średniej energii kinetycznej
cząsteczek:

K

J

k

23

10

38

.

1

−

⋅

=

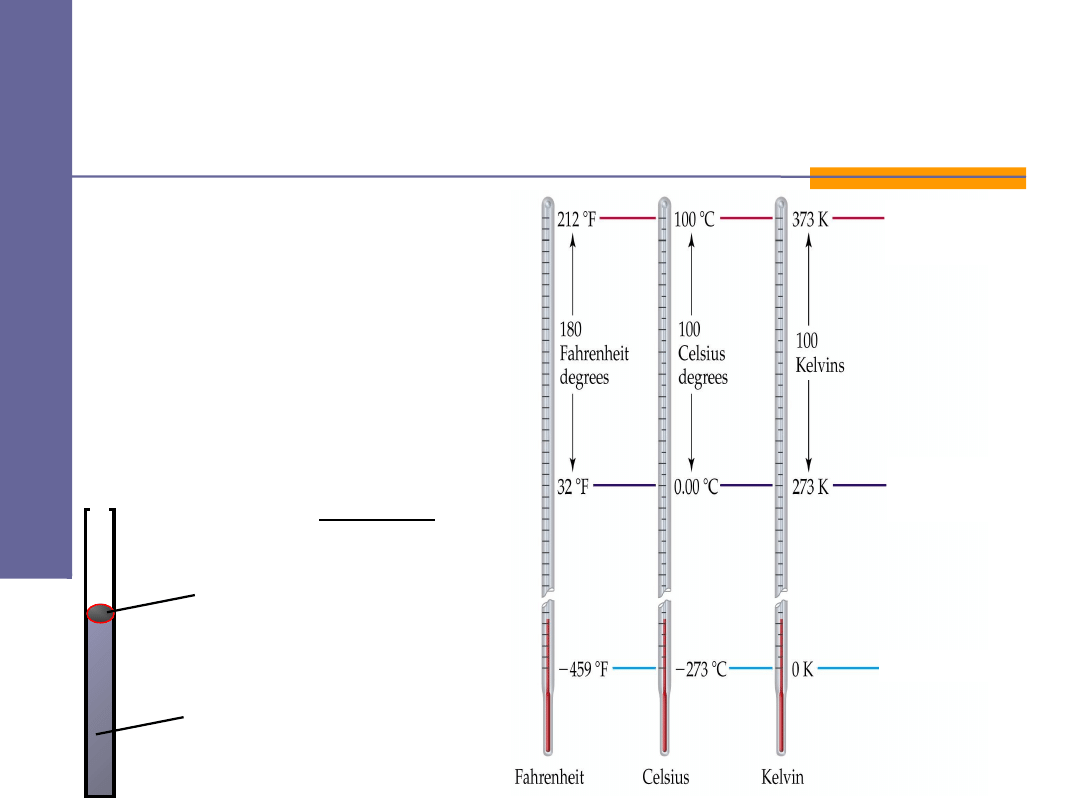
Pomiar

temperatury T

poprzez pomiar

p

i

V

gaz doskona y

ł

rtęć

zero bezwzględne

punkt zamarzania

wody

punkt wrzenia

wody

T

T

emperatura

emperatura

V

T

T

E

V

E

p

k

k

~

~

,

~

T

p

k

N

V

⋅

⋅

=

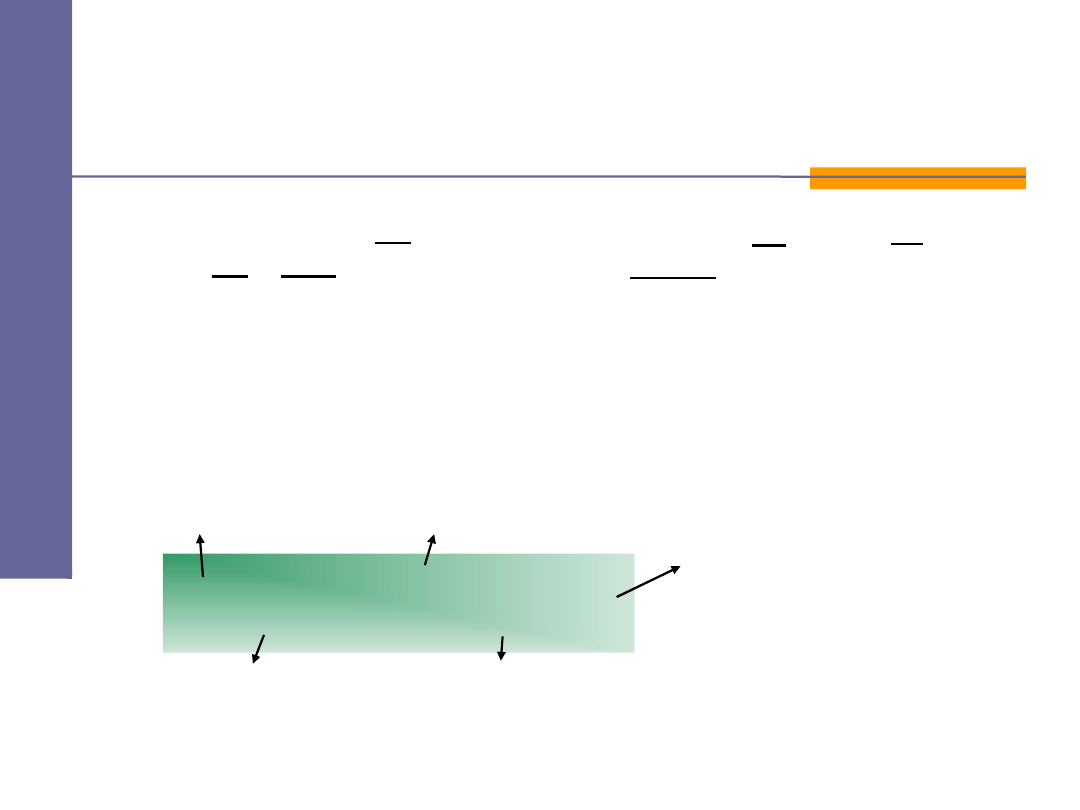
Równanie s tanu gazu dos kona ego

ł

Równanie s tanu gazu dos kona ego

ł

Clapeyro

Clapeyro

n -

n -

XIX w

XIX w

.

.

k

E

V

N

p

⋅

⋅

=

3

2

k

E

k

T













⋅

=

3

2

i

po przekształceniach:

k

E

⇒

T

k

N

V

p

⋅

⋅

=

⋅

ci nienie

ś

obj to

ę ść

liczba cz steczek gazu

ą

sta a Boltzmanna

ł

temperatura w kelwinach - K

wprowadźmy stałą gazowa R:

T

R

n

V

p

T

N

R

N

V

p

A

⋅

⋅

=

⋅

⇒

⋅

⋅

=

⋅

ci nienie

ś

obj to

ę ść

sta a gazowa

ł

temperatura w kelwinach - K

K

mol

J

R

⋅

=

31

.

8

k

N

R

A

⋅

=

Mol

- jednostka liczności

materii w układzie SI.
Jeden

mol

jest to liczność

materii, mającej taką samą
liczbę cząstek ile jest
atomów zawartych w 12
gramach izotopu węgla

12

C.

liczba moli gazu

µ

M

N

N

n

A

=

=

liczba moli gazu

masa molowa – 1 mola

Równanie s tanu gazu dos kona ego

ł

Równanie s tanu gazu dos kona ego

ł

Clapeyro

Clapeyro

n -

n -

XIX w

XIX w

.

.

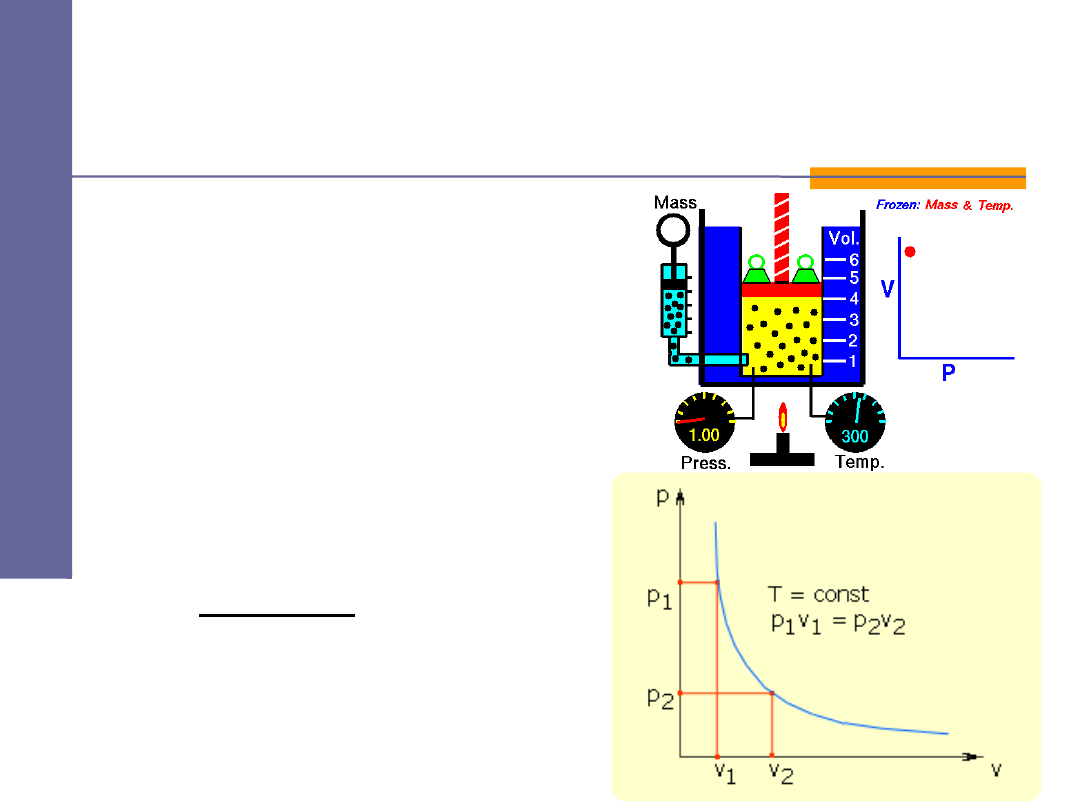
Przemiany gazowe -

Przemiany gazowe -

izotermiczna

izotermiczna

prawo Boyle'a Mariotte'a:

‑

T

R

n

V

p

⋅

⋅

=

⋅

lub

jeżeli

const

T

=

⇓

const

V

p

=

⋅

2

2

1

1

V

p

V

p

⋅

=

⋅

V

const

p

=

lub

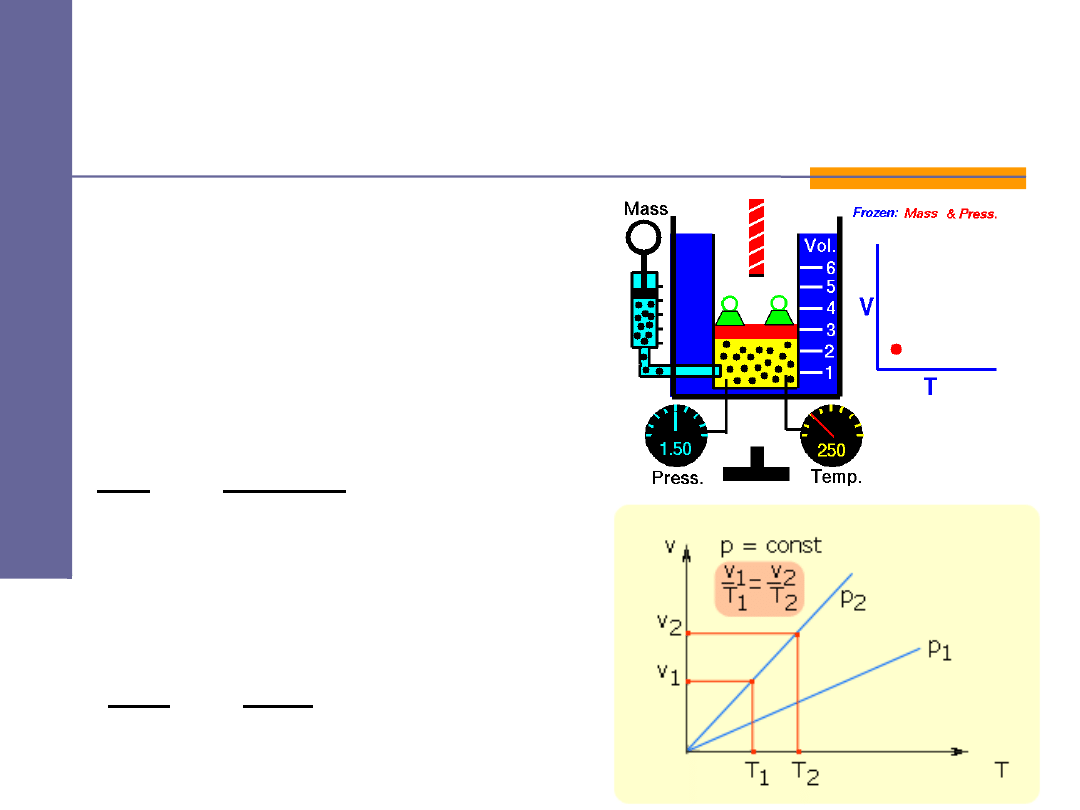
Przemiany gazowe -

Przemiany gazowe -

izobaryczna

izobaryczna

prawo Gay – Lussaca:

T

R

n

V

p

⋅

⋅

=

⋅

lub

jeżeli

const

p

=

⇓

const

R

n

p

T

V

=

⋅

=

2

2

1

1

T

V

T

V

=

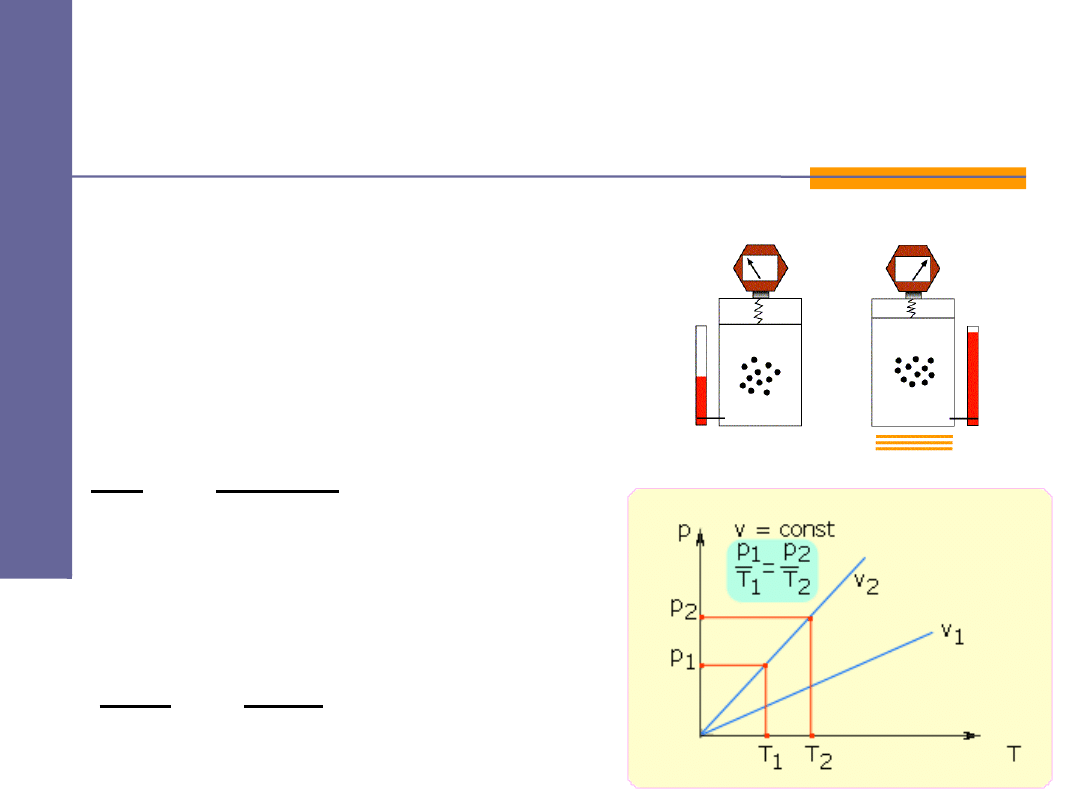
Przemiany gazowe -

Przemiany gazowe -

izochoryczna

izochoryczna

prawo Charlesa :

T

R

n

V

p

⋅

⋅

=

⋅

lub

jeżeli

const

V

=

⇓

const

V

R

n

T

p

=

⋅

=

2

2

1

1

T

p

T

p

=

niskie

ci nienie

ś

wysokie

niska

wysoka

temp.

temp.

Zas ady termodynamiki

Zas ady termodynamiki

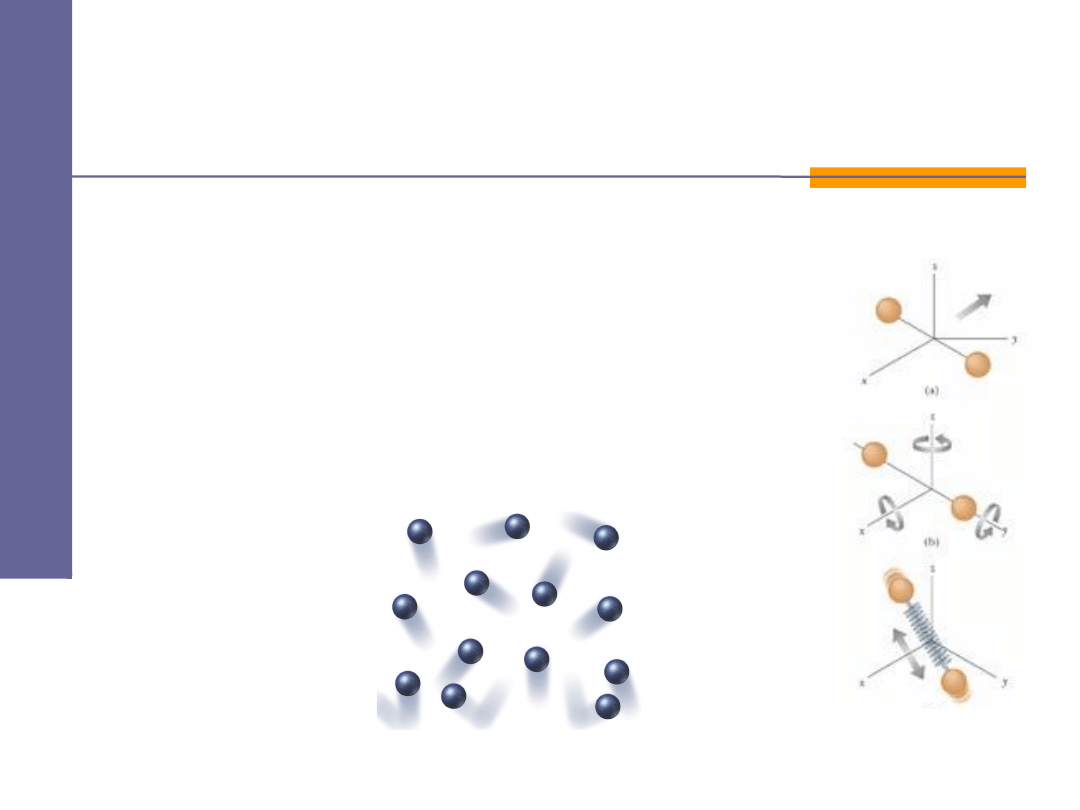
Energia wewnętrzna U

Energia wewnętrzna U

to część energii układu

zależna tylko od jego stanu wewnętrznego, stanowi
ona sumę energii oddziaływań międzycząsteczkowych
i wewnątrzcząsteczkowych układu oraz energii ruchu
cieplnego cząsteczek. Dla gazu doskonałego jest to
suma energii kinetycznej bezładnego ruchu
cząsteczek gazu.

Zas ady termodynamiki

Zas ady termodynamiki

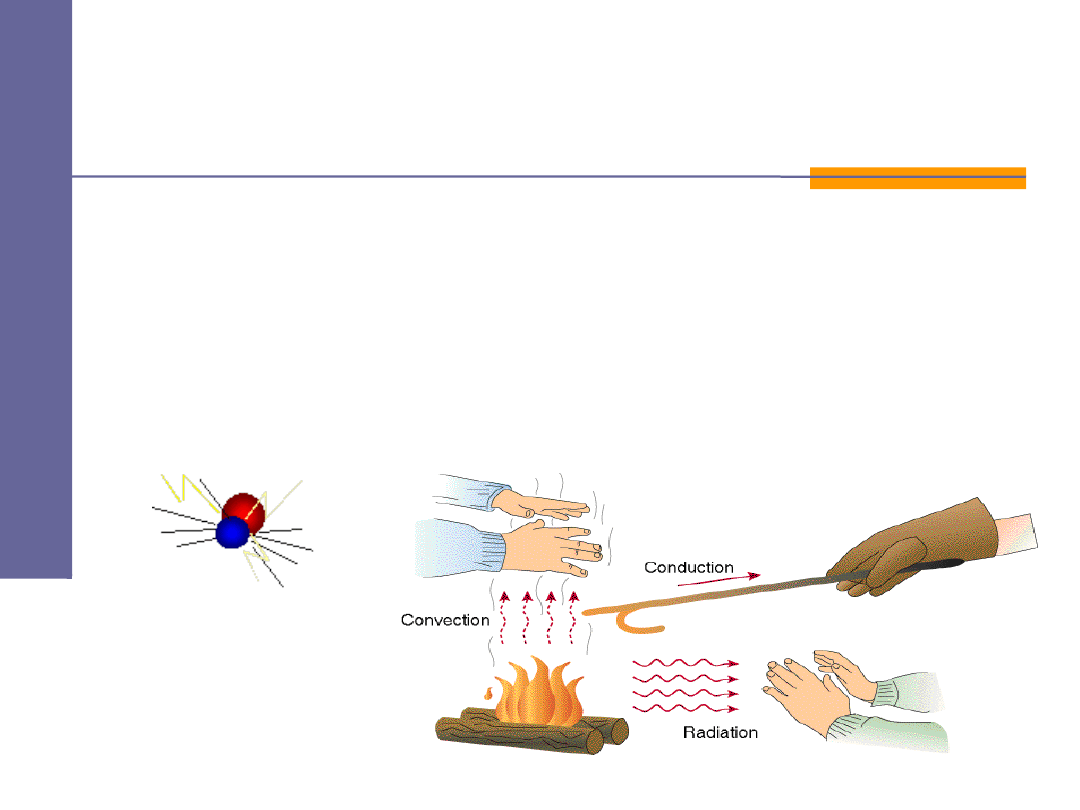
Ciepło

Ciepło

∆

∆

Q

Q

to sposób przekazu energii wewnętrznej od ciała o

wyższej temperaturze do ciała o niższej temperaturze - bez
wykonywania pracy. Ciepło w sensie fizycznym można

wyłącznie

oddać lub przyjąć

, ale nie można go

"mieć"!

Ciepło jest tą częścią

energii przekazywanej, która zachodzi w wyniku

zderzeń

między cząsteczkami

ciał,

konwekcji

,

przewodzenia

lub

wypromieniowania

∆

Q > 0

gdy my dostarczamy

energię,

∆

Q < 0

gdy gaz oddaje energie.

Zas ady termodynamiki

Zas ady termodynamiki

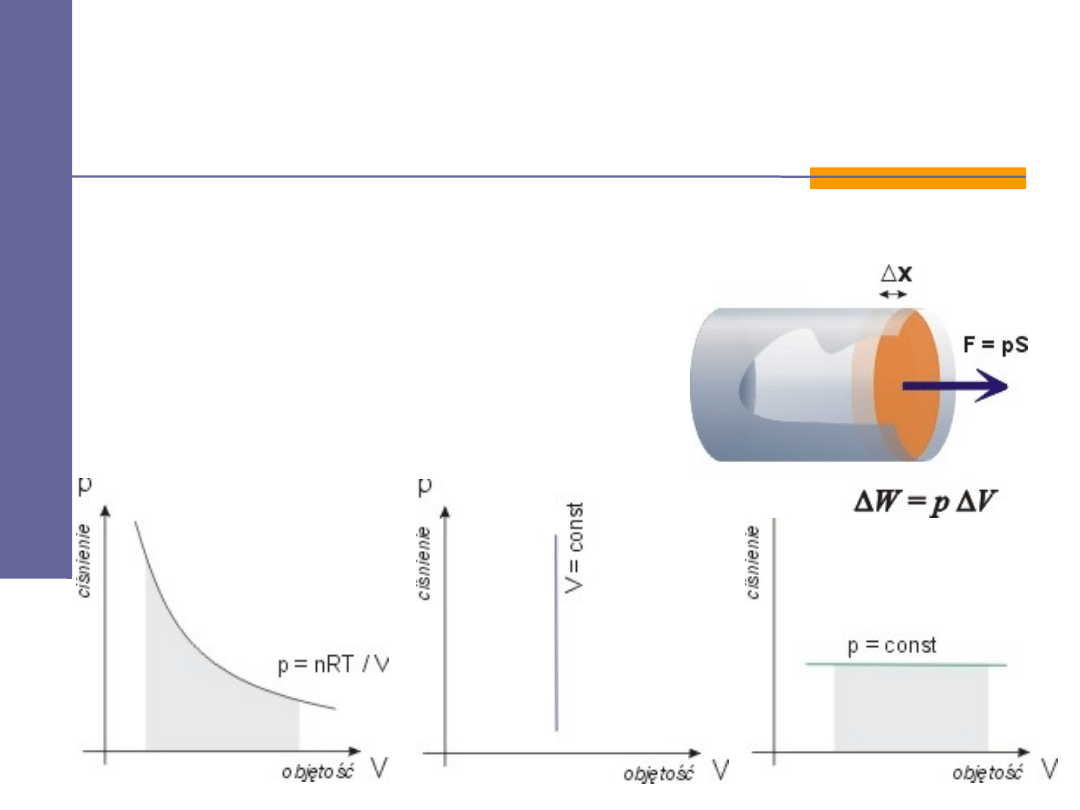
Praca W

jest w termodynamice rozumiana na sposób mechaniczny.

Jest funkcja procesu fizycznego, w którym charakteryzujące układ
parametry ulegają zmianie.

W > 0

gdy my wykonujemy pracę nad gazem,

W < 0

gdy gaz wykonuje pracę.

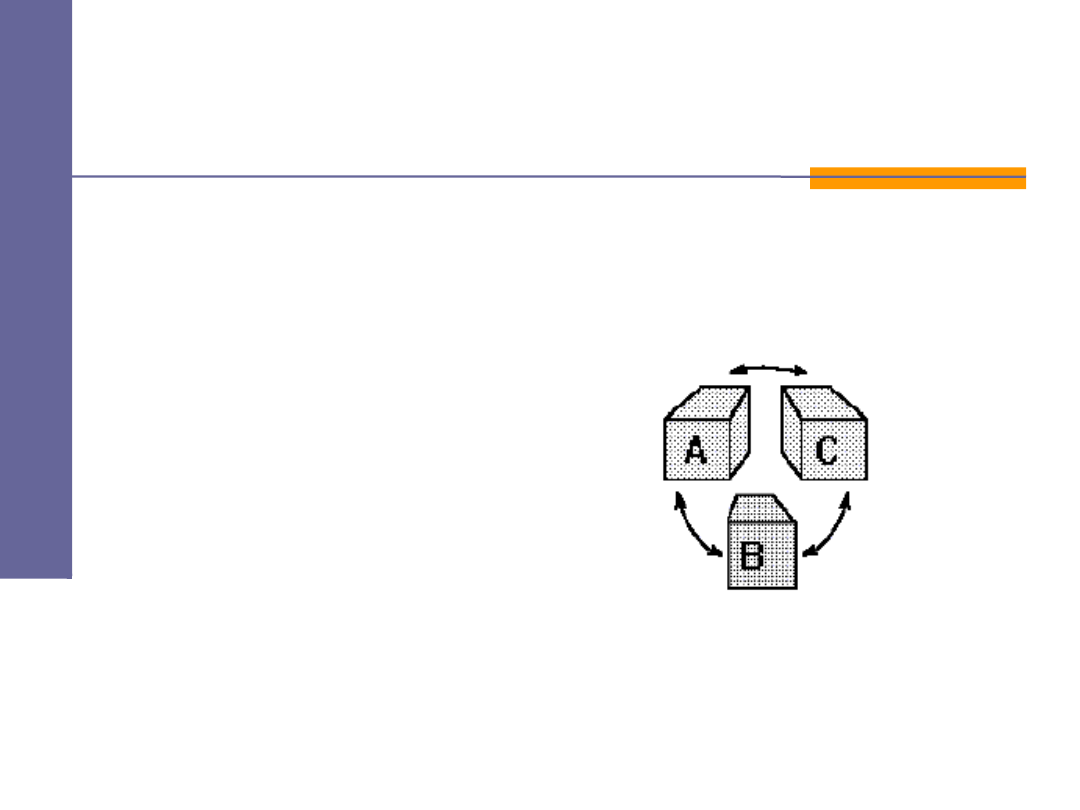
Jeżeli dwa ciała

A

i

B

są  w równowadze termicznej z

ciałem

C

, to ciała

A

i

B

są w równowadze termicznej ze sobą.

Mówimy
o nich, że mają tą samą temperaturę.

średnie energie kinetyczne ruchu postępowego
(na cząsteczkę) dla dwu kontaktujących się gazów są równe

Zerowa zas ada termodynamiki

Zerowa zas ada termodynamiki

Pierws za zas ada termodynamiki

Pierws za zas ada termodynamiki

Zmiana energii wewnętrznej układu równa jest

algebraicznej sumie ciepła wymienionego miedzy

ciałem (układem) a otoczeniem i pracy wykonanej

przez to ciało (układ) lub przez siłę zewnętrzna.

W

Q

U

+

∆

=

∆

Ka da z wielko ci wys t puj ca w tym wzorze

ż

ś

ę

ą

mo e by dodatnia, ujemne lub równa zeru.

ż

ć

 

 

Energię wewnętrzną ciała można zmieniać na dwa sposoby:

niewidoczny dla oka (mikroskopowy) – poprzez dostarczenie

ciepła,

dający się zaobserwować makroskopowo - za pomocą pracy.

 

 

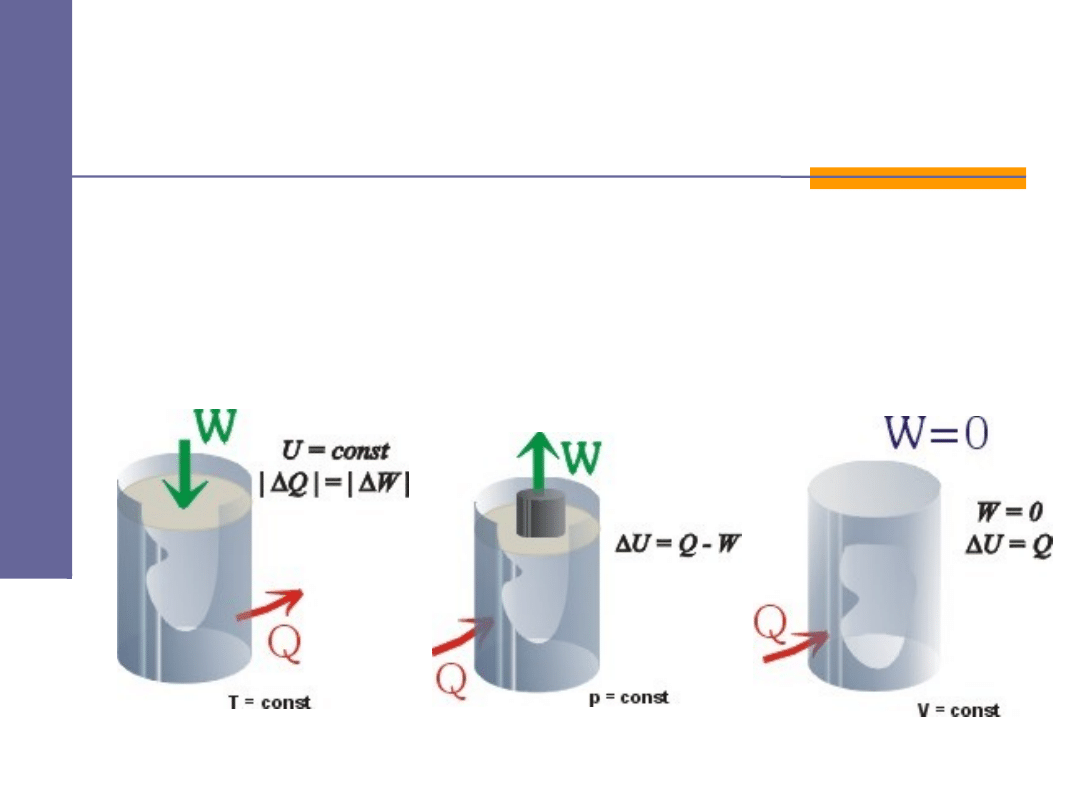
Pierws za zas ada termodynamiki

Pierws za zas ada termodynamiki

W

Q

U

+

∆

=

∆