MIMOŚRODOWE POMIARY

KĄTOWE

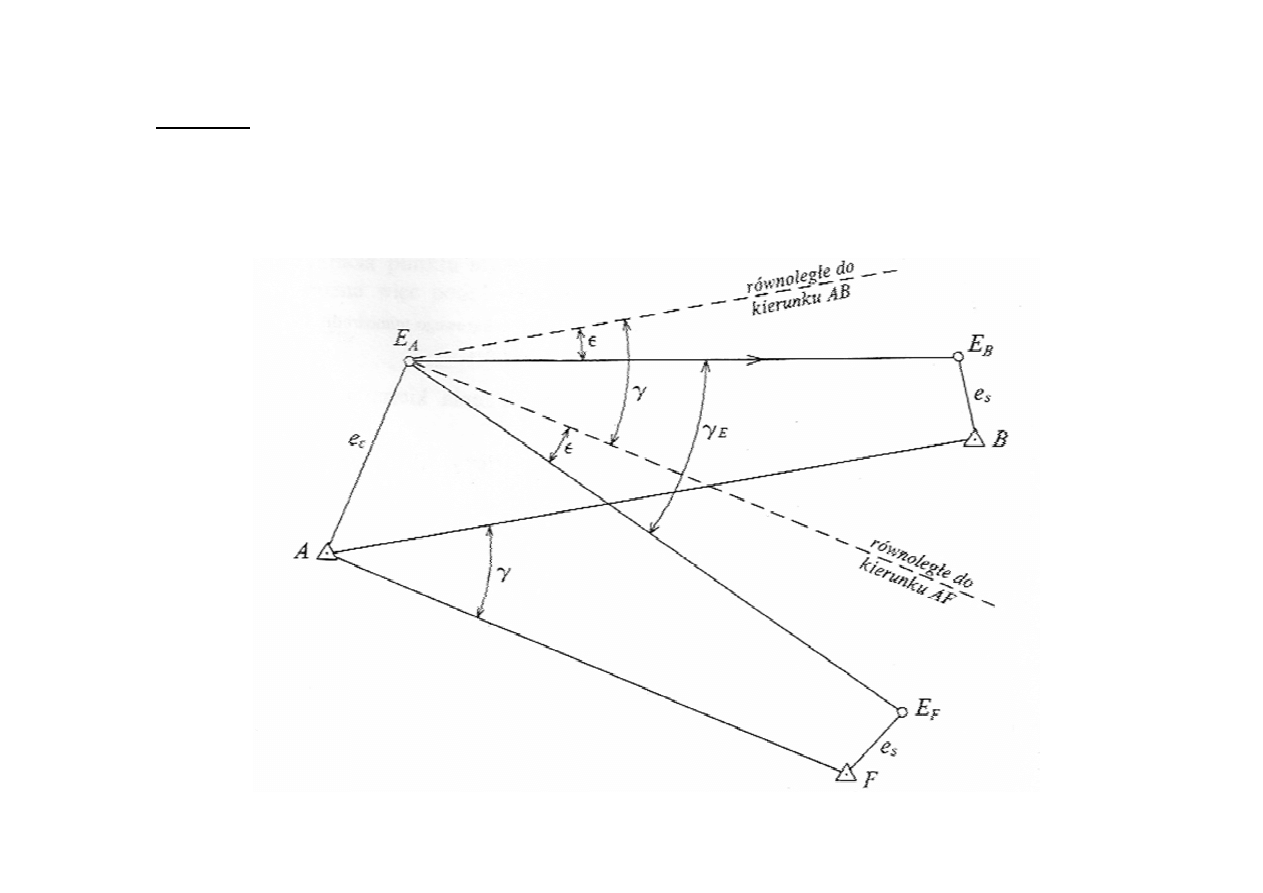
- Mimośrodowe pomiary kątowe -

Definicja – pomiar mimośrodowy jest pomiarem elementu geometrycznego osnowy
poziomej: kierunku, kąta lub odległości, gdy instrument lub (i) sygnał jest ustawiony
ekscentrycznie, czyli w miejscu przesuniętym poza właściwy punkt. Z tego względu
rozróżniamy dwa rodzaje mimośrodu: stanowiska i celu

Elementami mimośrodu stanowiska są:

1.

Mimośród liniowy stanowiska e

c

– długość pozioma odcinka AE wyznaczonego przez

mimośrodowe stanowisko teodolitu E i centr punktu A osnowy

2.

Kąt dyrekcyjny czyli kąt o wierzchołku w punkcie E, liczony zawsze w prawo od
kierunku mimośrodu liniowego do kierunku na wybrany sąsiedni punkt danej sieci

- Mimośrodowe pomiary kątowe -

E

A

– mimośrodowe stanowisko instrumentu (ekscentr punktu A)

E

B

– mimośrodowe stanowisko sygnału (ekscentr punktu B)

e

c

– mimośród liniowy stanowiska ( na punkcie A)

e

s

– mimośród liniowy celu ( na punkcie B)

Θ

– kąt dyrekcyjny mimośrodu stanowiska na punkcie A

ψ

– kąt dyrekcyjny mimośrodu celu na punkcie B

d

0

– odległość między punktami mimośrodowymi

– kierunek pomierzony mimośrodowo

K

AB

– kierunek między punktami geodezyjnymi (centrycznymi)

b

A

E

E

k

- Mimośrodowe pomiary kątowe -

Dośrodkowanie obserwacji mimośrodowych – polega na wykonaniu redukcji
wartości elementów geometrycznych (kierunków, kątów, odległości) pomierzonych na
punktach mimośrodowych poprzez wyliczenie odpowiednich poprawek redukcyjnych
i doprowadzeniu wyników pomiaru do takich wartości, które byłyby uzyskane
podczas przeprowadzania obserwacji na stanowiskach i celach centrycznych

Wyznaczenie poprawek do pomierzonych mimośrodowo kierunków

1.

Bezpośredni pomiar elementów mimośrodu przy dostępnych punktach stanowiska i
ekscentru

2.

Pośredni pomiar elementów mimośrodu przy niedostępnych punktach stanowiska i
ekscentru

Bezpośredni pomiar elementów mimośrodu przy dostępnych punktach stanowiska i ekscentru

•Element liniowy mierzony dalmierzem z błędem nie przekraczającym +/- 0.01m

•Kąt dyrekcyjny względem celowej wyjściowej (kierunek zredukowany do 0-00-00) teodolitem

jednosekundowym w 3 seriach

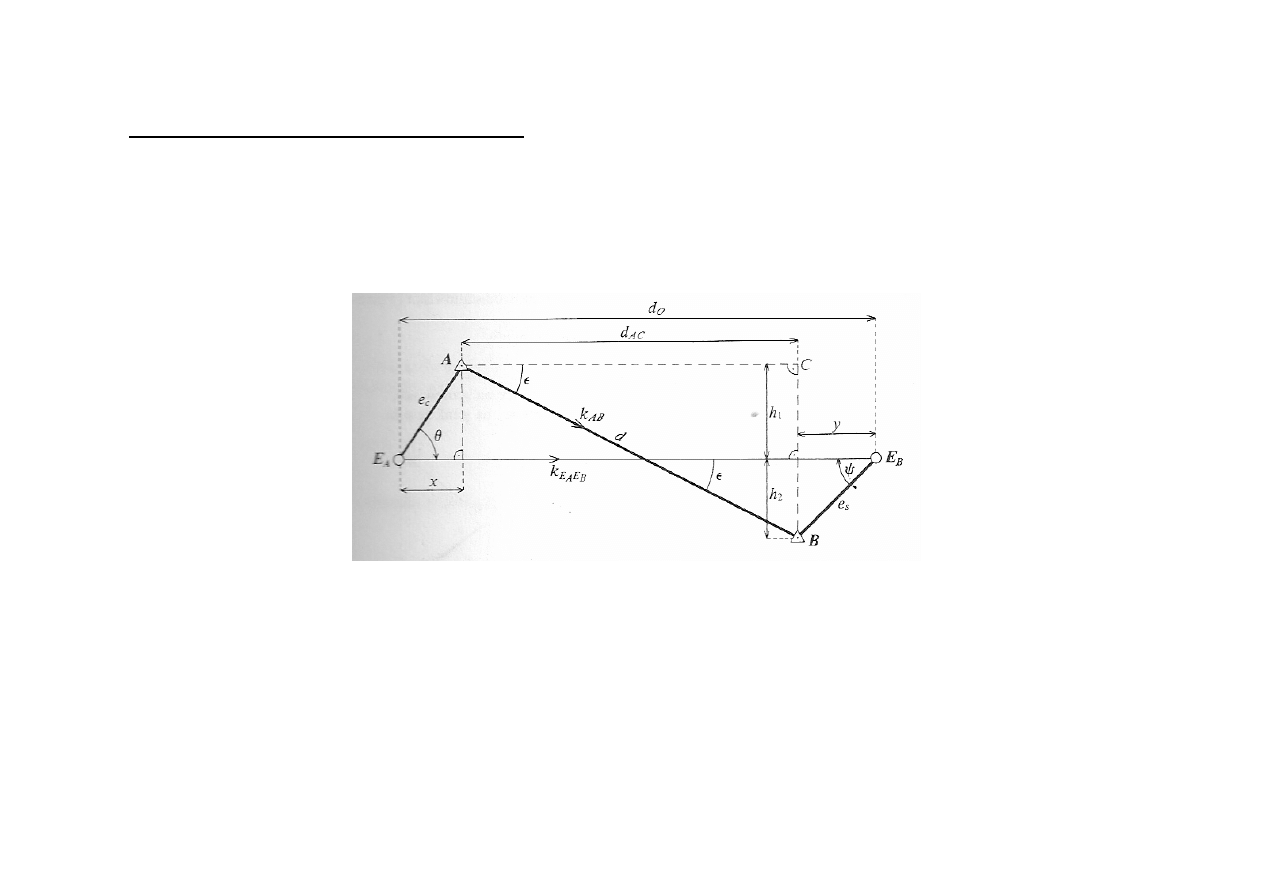
- Mimośrodowe pomiary kątowe -

ψ

θ

ψ

θ

cos

;

cos

sin

;

sin

2

1

s

c

s

c

e

y

e

x

e

h

e

h

=

=

=

=

ψ

θ

ψ

θ

sin

sin

cos

cos

2

1

s

c

s

c

e

e

h

h

b

e

e

y

x

a

+

=

+

=

+

=

+

=

d

b

a

d

b

d

b

tg

AC

=

−

=

=

ε

ε

sin

lub

0

(

)

ψ

θ

ψ

θ

ε

cos

cos

sin

sin

0

0

s

c

s

c

e

e

d

e

e

arctg

a

d

b

arctg

+

−

+

=

−

=

d

e

e

d

b

s

c

ψ

θ

ε

sin

sin

arcsin

arcsin

+

=

=

(

)

(

)

ψ

θ

ρ

ψ

θ

ε

cos

cos

sin

sin

0

''

''

s

c

s

c

e

e

d

e

e

+

−

+

=

(

)

d

e

e

s

c

''

''

sin

sin

ρ

ψ

θ

ε

+

=

Z rysunku mamy:

więc:

Z rysunku mamy:

Gdy znamy odległość między punktami
mimośrodowymi - ekscentrycznymi

Gdy znamy odległość między punktami geodezyjnymi -
centrycznymi

Gdy znamy odległość między punktami
mimośrodowymi - ekscentrycznymi

Gdy znamy odległość między punktami geodezyjnymi -
centrycznymi

Gdy mimośród mały e

c

+e

s

<5m to

0

0

1

≤

ε

więc stosujemy wzory przybliżone. Błąd wyznaczenia poprawki < 0.1

’’

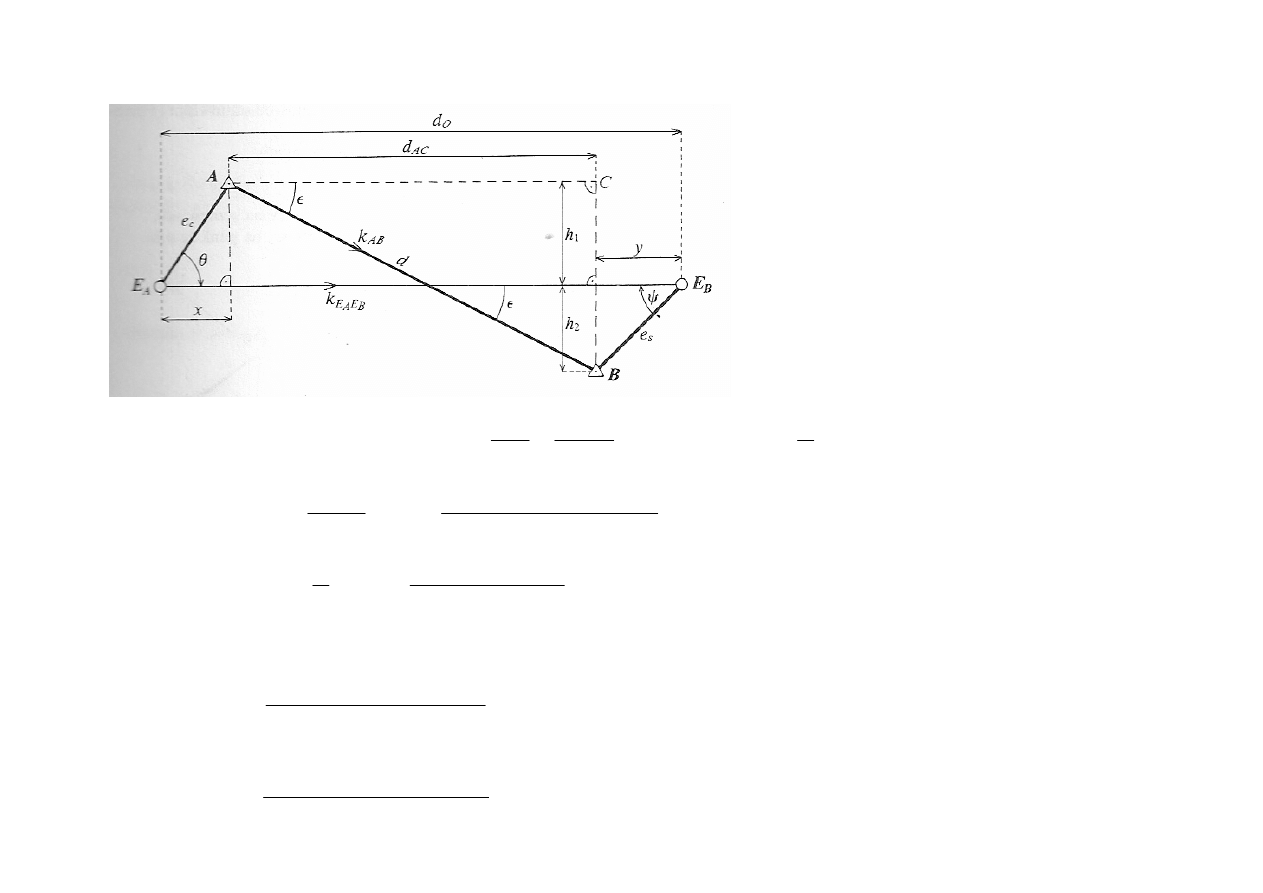
- Mimośrodowe pomiary kątowe -

Jeżeli pomierzone kierunki zredukujemy do zera limbusa (k

1

=0-00-00) oraz przy wyznaczaniu

elementów mimośrodu określimy kąty dyrekcyjne stanowiska i celu dla kierunków przyjętych jako
pierwsze na danym stanowisku, to można przyjąć ostatni wzór pod postacią bardziej dogodną do
obliczeń

(

)

(

)

ρ

ψ

θ

ε

′′

′

+

+

+

=

′′

i

j

s

i

c

d

k

e

k

e

1

1

sin

sin

Łączny wzór na poprawkę do kierunku ze względu
na mimośród stanowiska i celu

(

)

(

)

ρ

ψ

ε

ρ

θ

ε

′′

+

=

′′

′′

+

=

′′

i

j

s

s

i

i

c

c

d

k

e

d

k

e

i

i

1

1

sin

sin

wzór na poprawkę do kierunku ze względu na mimośród stanowiska

wzór na poprawkę do kierunku ze względu na mimośród celu

- Mimośrodowe pomiary kątowe -

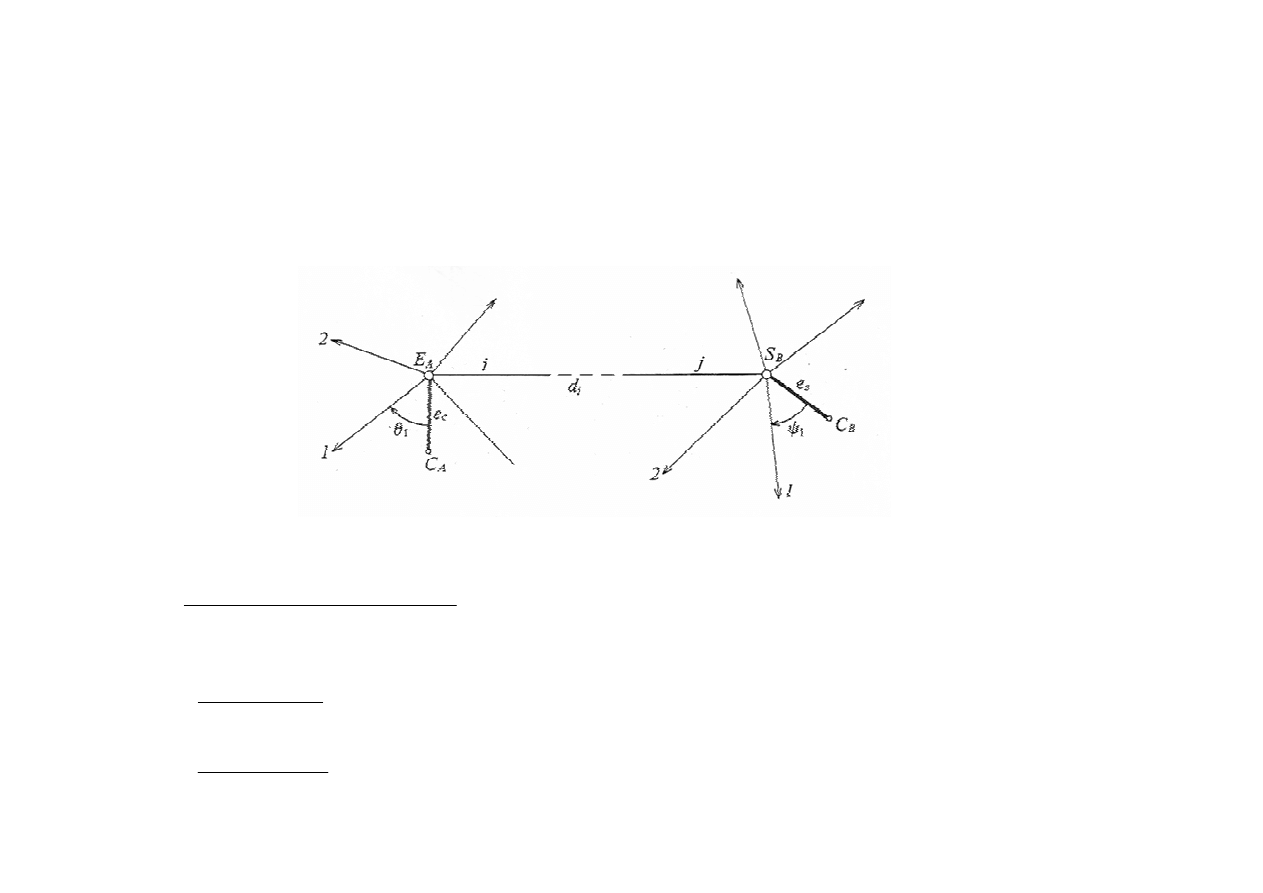
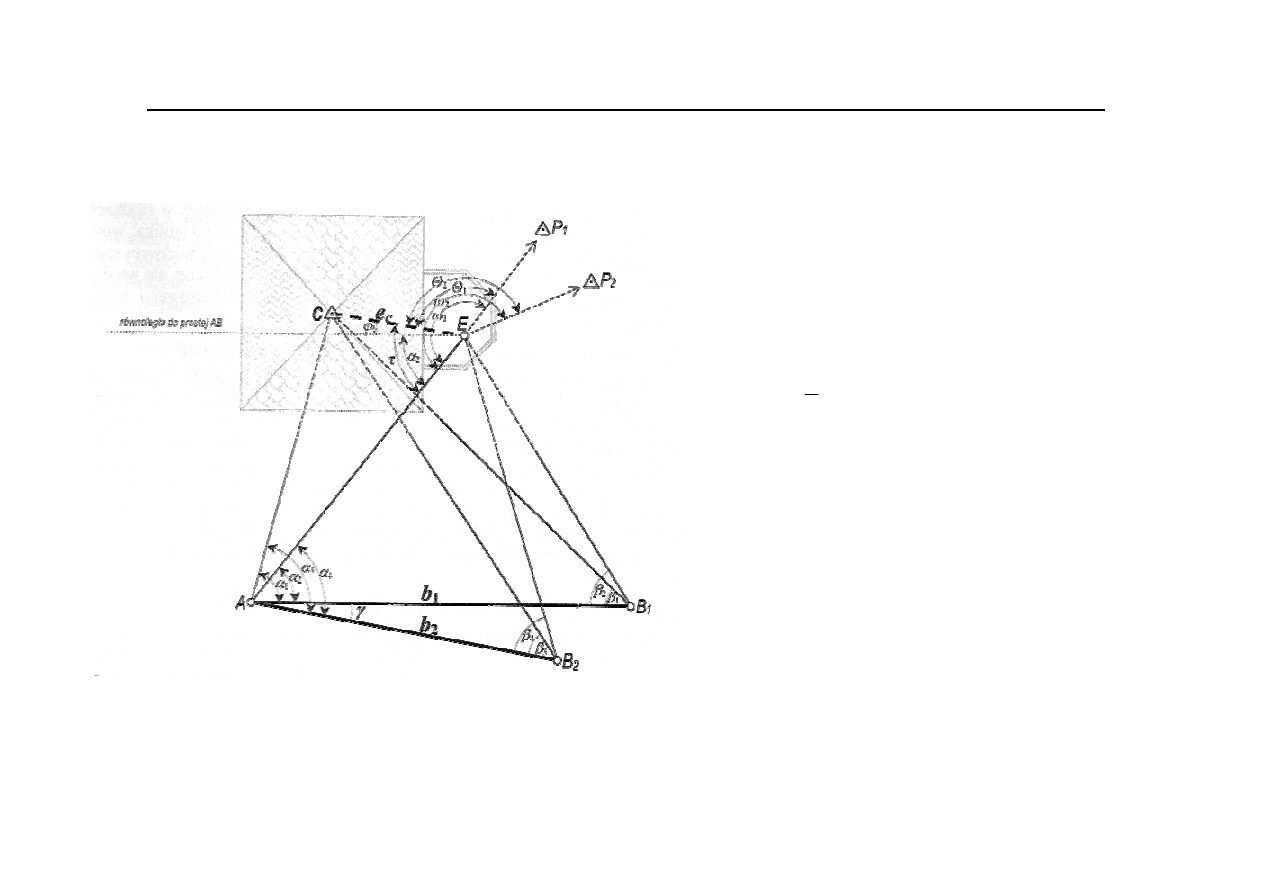
Pośredni pomiar elementów mimośrodu przy niedostępnych punktach stanowiska i ekscentru

1.

Przyjmujemy

lokalny

układ

współrzędnych,

zakładając dowolnie współrzędne punktu A np. x =
y = 100,00 oraz azymut boku np.

)

90

(

100

0

1

g

AB

A

=

2.

Określamy w tym układzie współrzędne punktów:
B

1

, B

2

. Zgodnie z wcześniejszymi założeniami

współrzędne punktu B

1

wyniosą: x

1

= 100,00;

1

1

00

,

100

b

y

+

=

zaś współrzędne punktu B

2

:

(

)

(

)

γ

γ

+

⋅

+

=

+

⋅

+

=

1

1

sin

00

,

100

;

cos

00

,

100

2

2

2

2

AB

AB

A

b

y

A

b

x

)

(

2

1

2

4

1

3

α

α

α

α

γ

−

+

−

=

a kąt:

3.

Dwukrotnie obliczamy współrzędne punktów C, E
na podstawie kątowych wcięć w przód i po
porównaniu

wyników

tworzymy

ś

rednie

arytmetyczne

z

jednoimiennych

par

współrzędnych: punktu C obliczamy dwukrotnie z
trójkątów AB

1

C, AB

2

C oraz punktu E obliczonych

z trójkątów AB

1

E, AB

2

E.

4.

Obliczmy mimośród e

c

liniowy z obliczonych

współrzędnych punktów E, C.

5.

Obliczamy kąty dyrekcyjne:

Θ

1

,

Θ

2

,…

Θ

n,do

punktów celu P

1

, P

2

, …P

n

. Kąty te otrzymamy na

podstawie

różnić

kątów:

ω

1

,

ω

2,

...,

ω

n

pomierzonych na stanowisku E oraz kąta

τ

obliczonego ze współrzędnych punktów: A, E, C:

Θ

1

=

ω

1

-

τ

;

Θ

2

=

ω

2

-

τ

; …

Θ

n

=

ω

n

-

τ

;