Mechanika

Mechanika

Zajmuje się badaniem stanu równowagi
lub ruchem ciał materialnych.

y

Skł d

i

Składa się:

– kinematyki

y

– kinetyki (statyka i dynamika)

Kinematyka

Kinematyka

Dział mechaniki zajmujący się
matematycznym opisem ruch układu

y

y

p

materialnego, bez wnikania w przyczyny,
które ten ruch wywołały lub zakłóciły

które ten ruch wywołały lub zakłóciły.

Przez ruch rozumie się zmiany położenia
rozważanego obiektu materialnego

rozważanego obiektu materialnego
względem przyjętego układu odniesienia.

Dynamika

Dynamika

Zajmuje się opisem metod wyznaczania

Zajmuje się opisem metod wyznaczania
ruchu układu materialnego pod wpływem
przyłożonego obciążenia

przyłożonego obciążenia.

Statyka

Statyka

Dział mechaniki zajmujący się badaniem

Dział mechaniki zajmujący się badaniem
warunków koniecznych i wystarczających
na to aby układ materialny nie zmieniał

na to, aby układ materialny nie zmieniał
swojego położenia w przyjętym układzie
odniesienia.

Ciało materialne

Ciało materialne

Przez ciało materialne rozumie się
jakikolwiek przedmiot fizyczny dostrzegany

j

p

y

y

g y

naszymi zmysłami.
W mechanice wykorzystujemy przybliżone

W mechanice wykorzystujemy przybliżone
modele ciał rzeczywistych:

– Punkt materialny
– Układ punktów materialnych

p

y

– Ciało sztywne

Punkt materialny

Punkt materialny

Przez punkt materialny rozumie się ciało

Przez punkt materialny rozumie się ciało
materialne, którego rozmiary i kształt nie
są istotne w analizowanym problemie

są istotne w analizowanym problemie.

Układ punktów materialnych

Układ punktów materialnych

Ciało materialne może być traktowane

Ciało materialne może być traktowane
jako układ punktów materialnych
(cząsteczek) o rozmiarach znikomo

(cząsteczek) o rozmiarach znikomo
małych w stosunku do rozmiaru
rozważanego ciała.

Ciało sztywne

Ciało sztywne

Ciało sztywne jest to ciało materialne

Ciało sztywne jest to ciało materialne,
którym odległości każdych dwóch jego
punktów są stałe w czasie

punktów są stałe w czasie.
Wymiary i kształt ciała nie zmieniają się w
czasie ruchu ciała.

Siła

Siła

Siła jest miarą wzajemnego oddziaływania
ciał przejawiającą się przez zmianę ich

p

j

ją ą ę p

ę

położenia lub utrzymania w położeniu
równowagi

równowagi.
Oddziaływanie to charakteryzuje się:

– linią działania
– Wartościąą
– Zwrotem

Graficznym obrazem siły jest wektor

Graficznym obrazem siły jest wektor

Masa punktu materialnego

Masa punktu materialnego

Masa punktu materialnego jest wielkością
skalarną, określona przez iloraz miary siły

ą,

p

y

y

ciężkości i miary przyspieszenia
ziemskiego

ziemskiego

0





Q

m

df

g

Pęd punktu materialnego

Pęd punktu materialnego

Pęd punktu materialnego jest iloczynem
masy i prędkości

y p ę

df

v

m

p

f



Aksjomaty mechaniki:

Aksjomaty mechaniki:

• Aksjomat bezwładności
• Aksjomat ruchu (prawo ruchu)

Aksjomat ruchu (prawo ruchu)

• Aksjomat wzajemnego oddziaływania

(

k ji i

k ji)

(prawo akcji i reakcji)

1 Aksjomat bezwładności

1. Aksjomat bezwładności

Jeśli na punkt materialny nie działa żadna

Jeś

a pu

a e a y e d a a ad a

siła, to pęd punktu jest stały:

Przy stałym pędzie punkt

0

p

const

p

v

m

p







Przy stałym pędzie punkt
porusza się ruchem
jednostajnym prostoliniowym

0

)

(

const

m

p

r

v





 

jednostajnym prostoliniowym
v

o

≠ 0

lub jest w spoczynku

0

0

)

(

r

t

v

t

r





v

o

= 0

Bezwładność – ciało bez
udziału innych sił nie może

udziału innych sił nie może
zmienić położenia

2. Aksjomat ruchu (prawo ruchu).

Jeśli na punkt materialny działa siła, to

2. Aksjomat ruchu (prawo ruchu).

zmienia jego pęd według prawa:

 

d

 

F

p

dt

d



dt

df

J

li

ł

t t

h

j

j

t ć

v

m

p

f



Jeżeli założymy ze m=const to prawo ruchu przyjmuje postać

F

a

m

 F

a

m



3. Aksjomat wzajemnego oddziaływania
(

k ji i

k ji)

(prawo akcji i reakcji).

Dwa punkty materialne działają na siebie
zawsze wzajemnie z siłami równymi,

zawsze wzajemnie z siłami równymi,
przeciwnie skierowanymi i leżącymi na
jednej prostej:

jednej prostej:

F

B

m

B

AB

F

BA

F

A

m

A

0





BA

AB

F

F

Konwencja sumacyjna Einsteina

Konwencja sumacyjna Einsteina

Jeżeli w wyrażeniu będącym jednomianem
wskaźniki powtarzają się to należy

p

ją ę

y

dokonać sumowania po powtarzających
się wskaźnikach do odpowiedniej

się wskaźnikach do odpowiedniej
wymiarowości obiektu

n

n

n

i

i

i

i

x

a

x

a

x

a

x

a

x

a













...

2

2

1

1

i



1

n

a

a

a

a

a













nn

i

ii

ii

a

a

a

a

a















...

22

11

1

Konwencja sumacyjna Einsteina

Konwencja sumacyjna Einsteina

k

k

k

k

n

m

mn

n

m

mn

x

x

a

x

x

a







k

k

m

n

x

x

a

x

x

a

x

x

a

x

x

a















...

1

1

3

1

13

2

1

12

1

1

11

1

1

k

k

k

k

x

x

a

x

x

a

x

x

a

x

x

a











...

2

2

3

2

23

2

2

22

1

2

21

1

1

3

1

13

2

1

12

1

1

11

...

k

k

kk

k

k

k

k

k

k

x

x

a

x

x

a

x

x

a

x

x

a









...

3

3

2

2

1

1

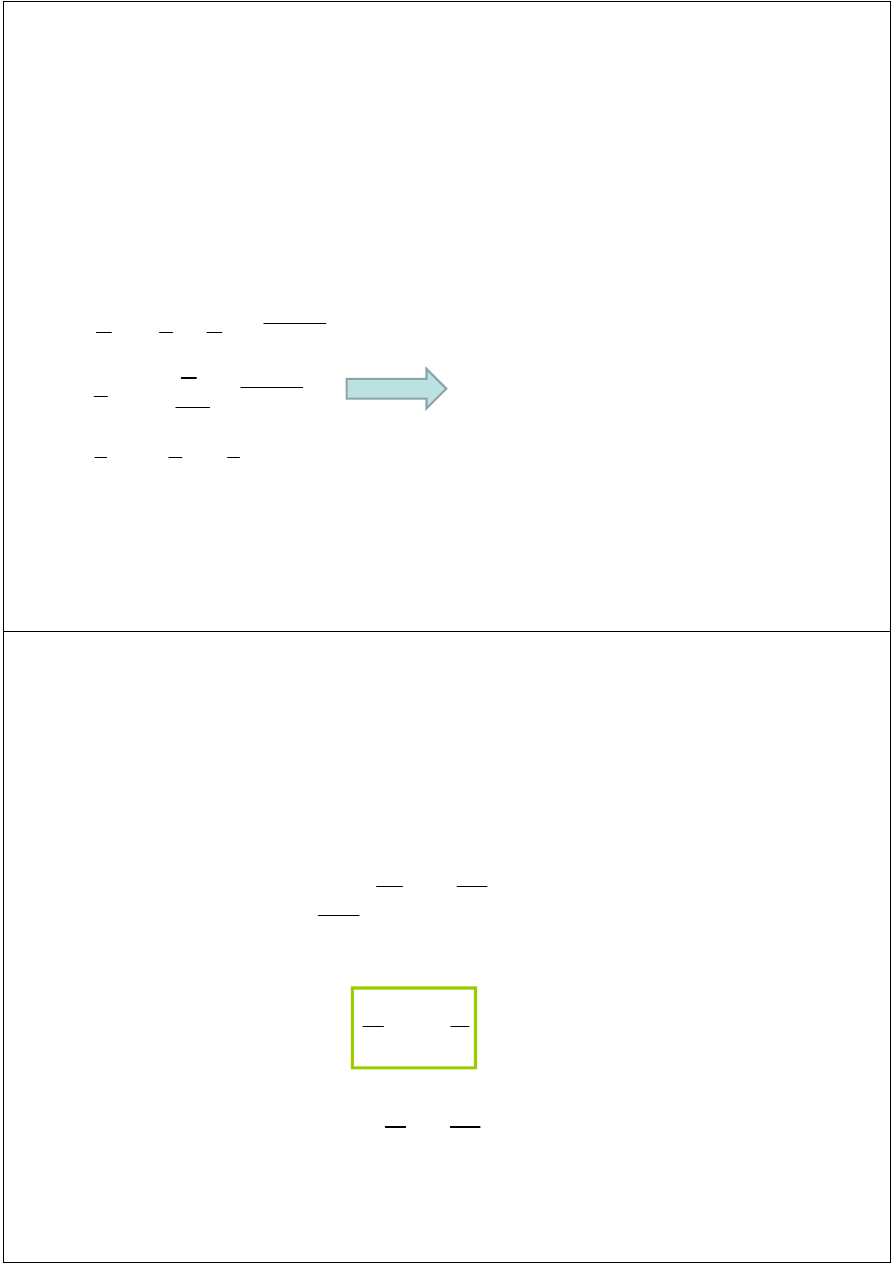
Operacje na wektorach - dodawanie

b

c

b

a





b

c

i

i

i

c

b

a





aa

b

c

b

aa

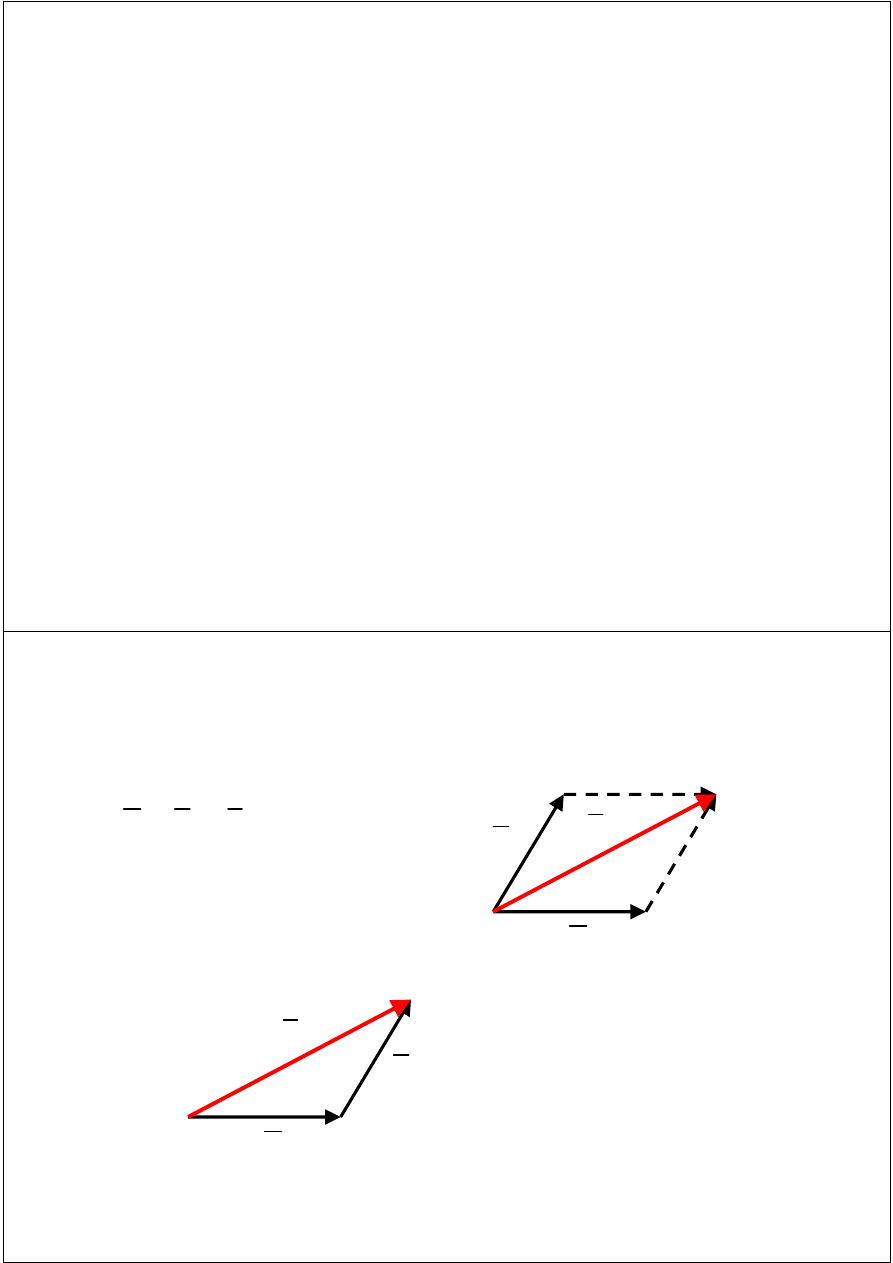
Operacje na wektorach -

odejmowanie

 

b

c

b

a





 

c

b

a







b



c

a

b

a

b

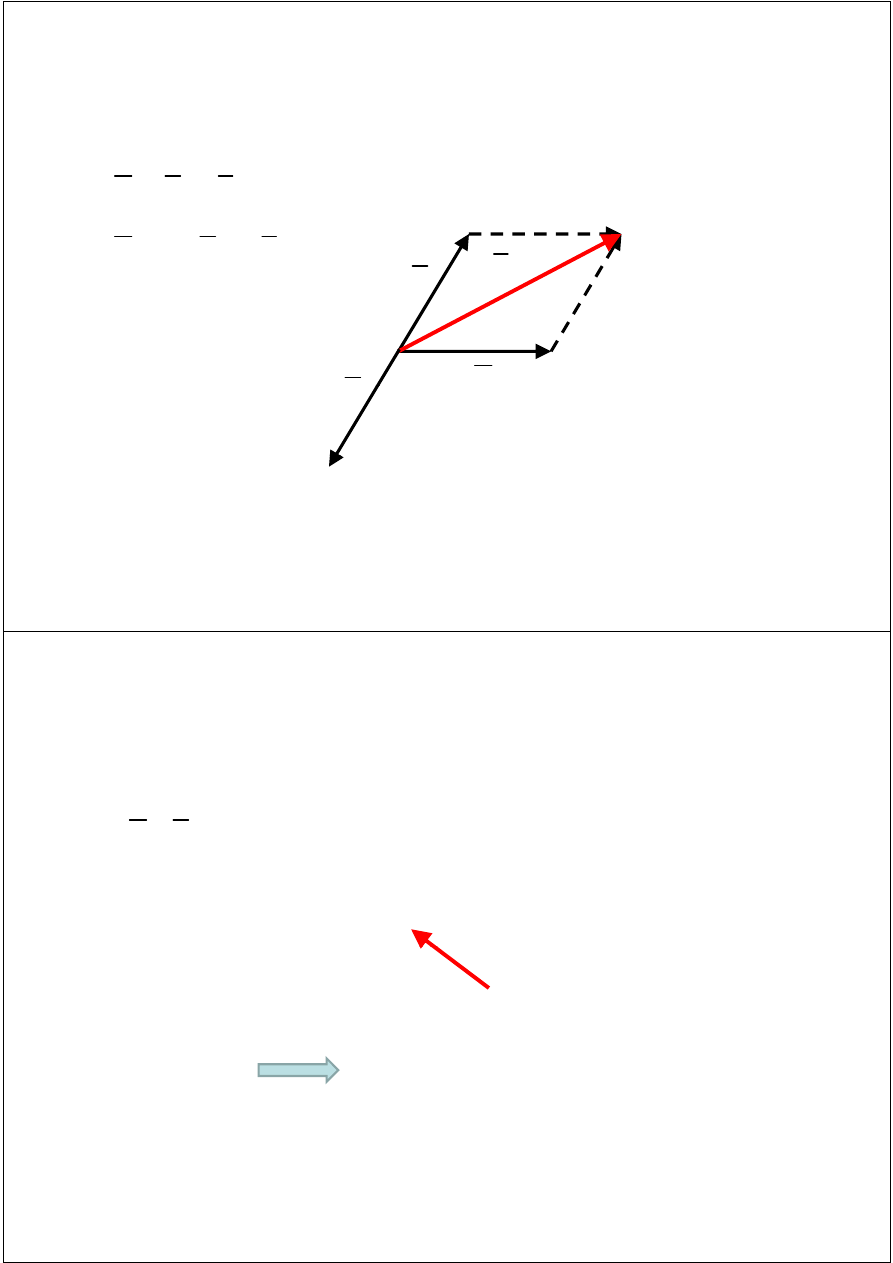
Operacje na wektorach –

iloczyn skalarny

c

b

a





i

i

n

i

i

b

a

b

a

c











i

1

sumacja

j

c

= 0

Wektory są do siebie prostopadłe

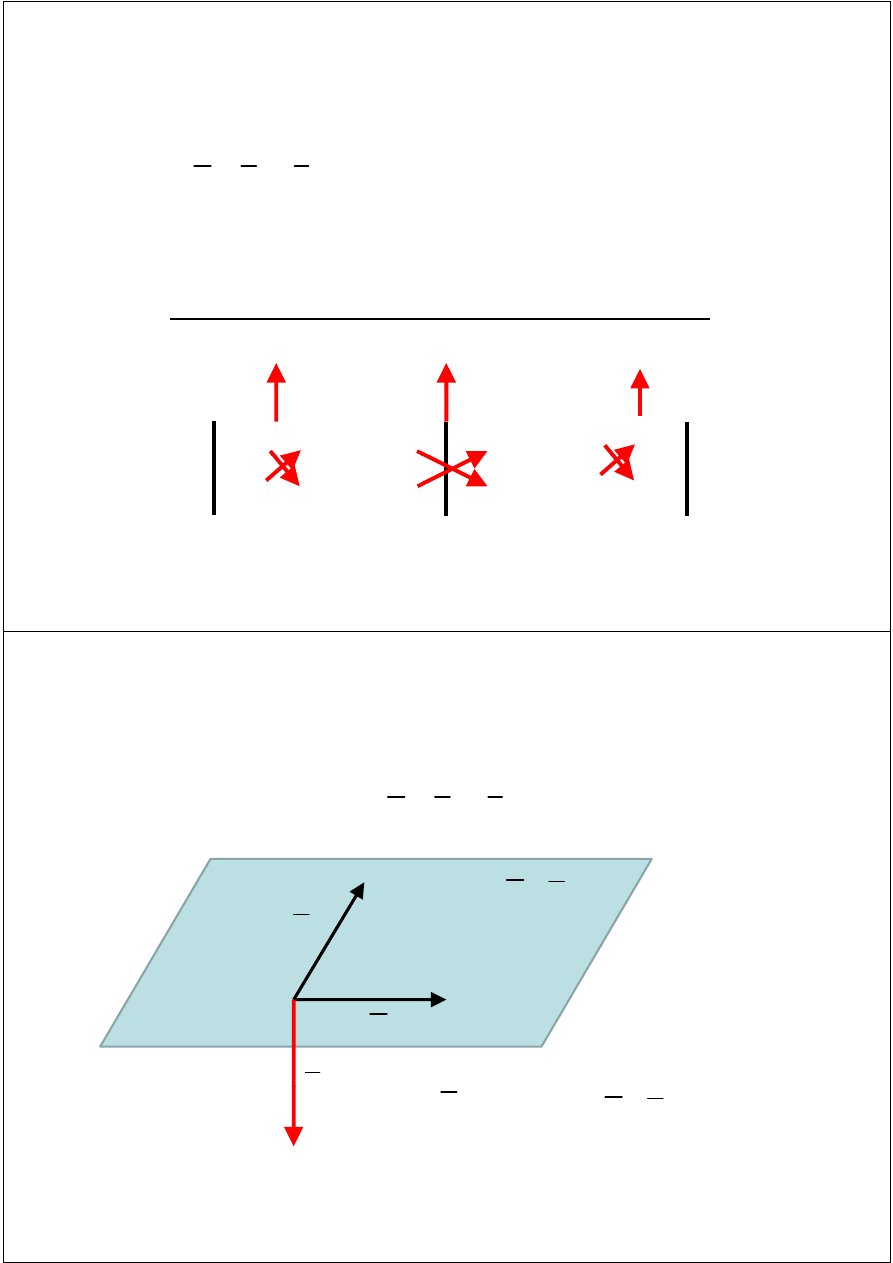
Operacje na wektorach –

iloczyn wektorowy

b c

b

a









a

a

a









3

2

1

3

2

1

,

,

,

,

b

b

b

a

a

a











2

1

2

1

3

1

3

1

3

2

3

2

,

,

a

b

b

a

a

b

b

a

a

b

b

a















3

2

1

,

,

a

a

a





3

2

1

,

,

a

a

a





3

2

1

,

,

a

a

a









3

2

1

3

2

1

,

,

b

b

b









3

2

1

3

2

1

,

,

b

b

b





3

2

1

,

,

b

b

b

Obliczamy wartości podwyznaczników

Dla środkowego wyrazu zmieniamy znak !!!

Operacje na wektorach –

iloczyn wektorowy

b c

b

a





 

b

a



b

b

a

c

a



b



c

Wersor – wektor jednostkowy

(unormowany)





1

,

1

,

1



e

Wersor to wektor o długości jeden, wskazujący kierunek i
zwrot pewnego wektora początkowego, któremu ten wersor
przypisujemy.

AB

e

AB



AB

e

AB

Wersor – wektor jednostkowy

(unormowany)





3

4

5



AB





3

,

4

,

5







AB























3

,

4

,

5

3

,

4

,

5

AB

AB

e









3

4

1

2

5

3

4

5

2

2

2

AB

AB

e















2

5

3

,

2

5

4

,

2

1

AB

e

Mnożenie wersora przez długość początkowego wektora
odtwarza początkowy wektor

odtwarza początkowy wektor.





3

4

5

2

5

3

4

1









AB

AB





3

,

4

,

5

2

5

2

5

,

2

5

,

2





















AB

e

AB

AB

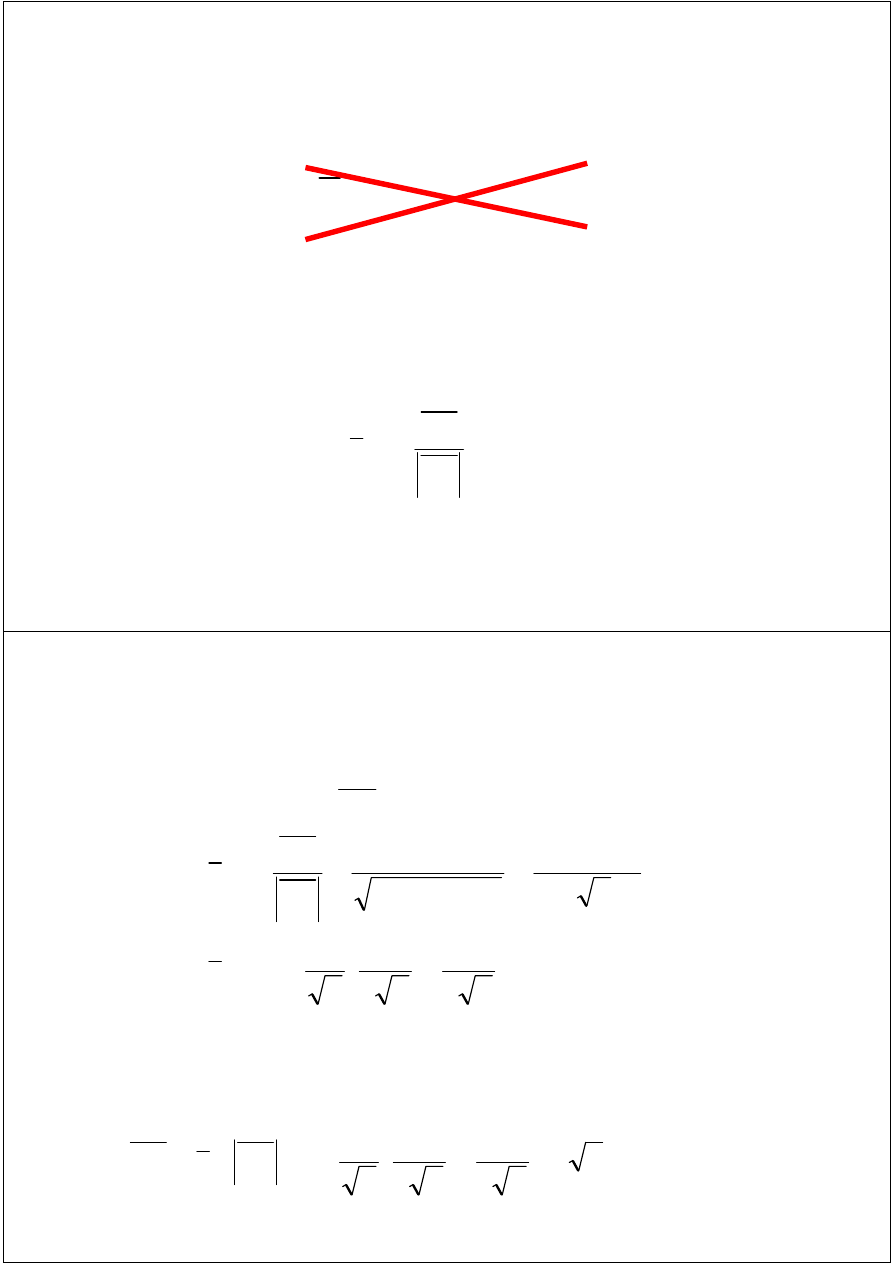
Miara rzutu wektora na prostą

(na kierunek)

a

Szukamy miary rzutu wektora F na kierunek a

a

a

F

e

F

d

a









F

F

F

F

d<0

d>0

d=0

a

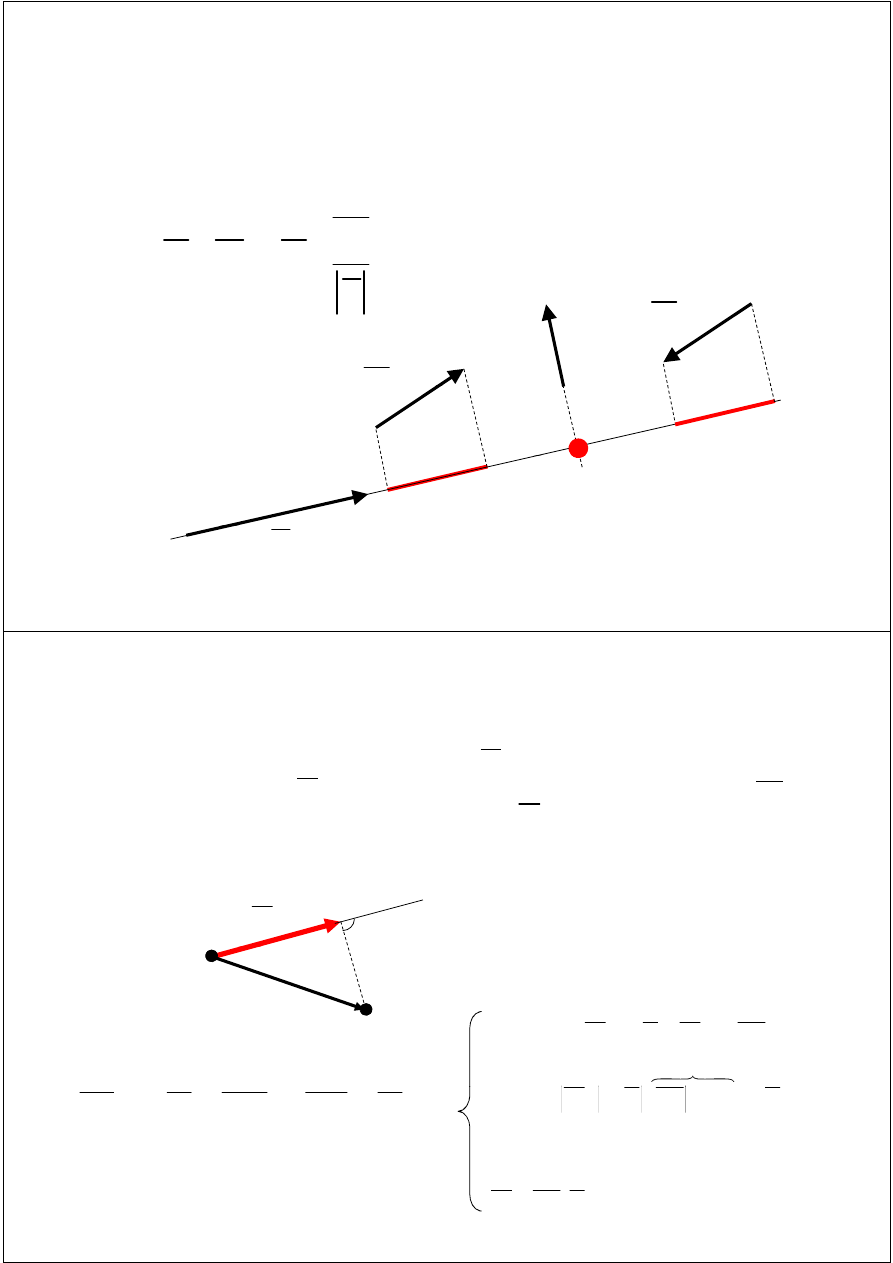
Moment siły względem punktu

Obierzmy dowolny punkt B i siłę zaczepioną w punkcie A.
Momentem siły względem punktu B nazywamy wektor

F

F

B

M

równy iloczynowi wektorowemu siły i wektora łączącego
punkt zaczepienia siły z punktem, względem którego liczymy

t

F

moment:

A

F

.

A

B



r

df

kierunek

AB

M

F

M

B

B







r

B











F

BA

AB

F

M

df

B

moduł

r

F

AB

F

M

B













sin

t t ójk

kt ó

zwrot: trójka wektorów

F

AB

M

B

,

,

jest prawoskrętna

Moment siły względem punktu jest równy zeru, gdy siła
lub jej ramię jest równe zeru

lub jej ramię jest równe zeru.

Gdy siłę lub jej ramię przesuniemy wzdłuż prostej jej

y

ę

j j

ę p

y

p

j j j

działania to moment liczony względem tego samego
punktu nie ulegnie zmianie

F

F

F

A

B

R





const

BR

F

BR

AB

F

AR

F

M













const

BR

F

BR

AB

F

AR

F

M

R

















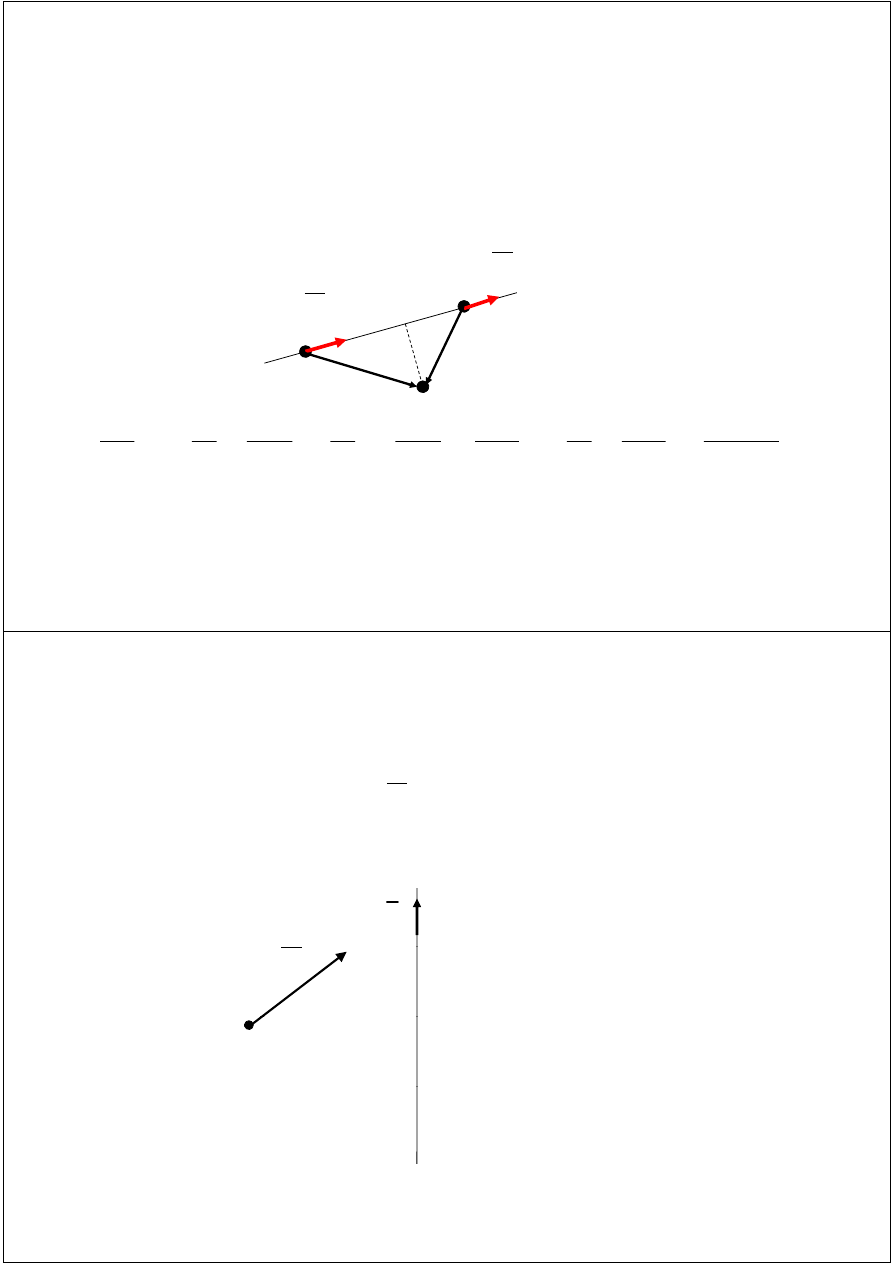
Moment siły względem prostej

Moment siły względem prostej

Niech zadana będzie siła zaczepiona w punkcie A i prosta l.

F

ę

p

p

p

l

l

e

A

F

A

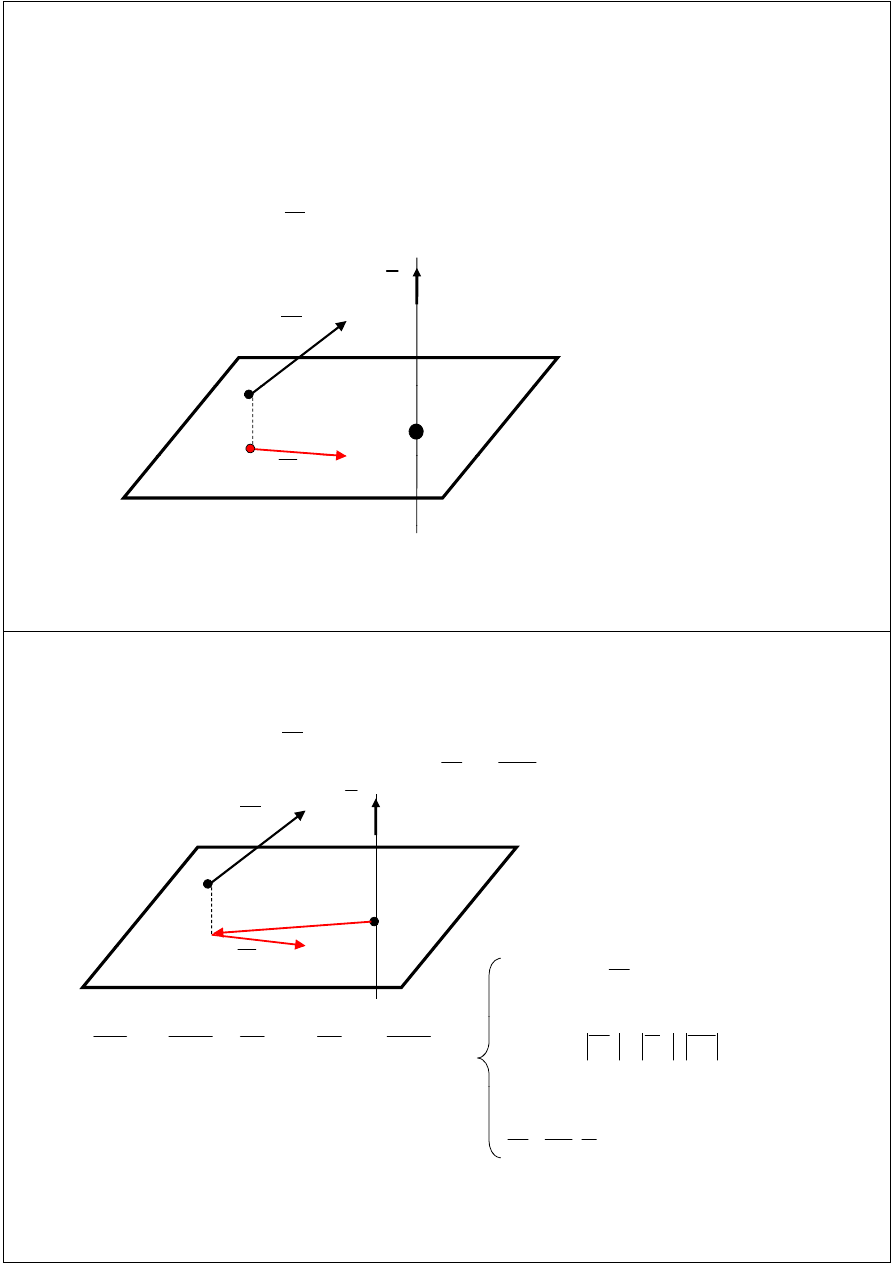
Moment siły względem prostej

Moment siły względem prostej

Na prostej l obierzmy dowolny punkt 0, przez który prowadzimy

p

j

y

y p

, p

y p

y

płaszczyznę prostopadłą do prostej l. Wyznaczmy rzut
prostokątny siły i punktu A na płaszczyznę .

F



l

l

e

A

F



A

A’



O



F

Moment siły względem prostej

F

l

e

Momentem siły zaczepionej w punkcie A względem prostej l
Nazywamy iloczyn wektorowy i .

F



F

0

'

A

l

A

l

e

F



A

A’

O

kierunek

l

M

l

||



F











0

'

'

0

A

F

F

A

M

df

l





moduł





sin

0

'

A

F

M

l





zwrot: wektory



F

A

M

l

,

0

'

,

stanowią trójkę

Moment siły względem prostej
jest równy zeru, gdy prosta wraz



l

,

,

ą

j ę

prawoskrętną

j

y

g y p

z kierunkiem działania siły
leżą w jednej płaszczyźnie.

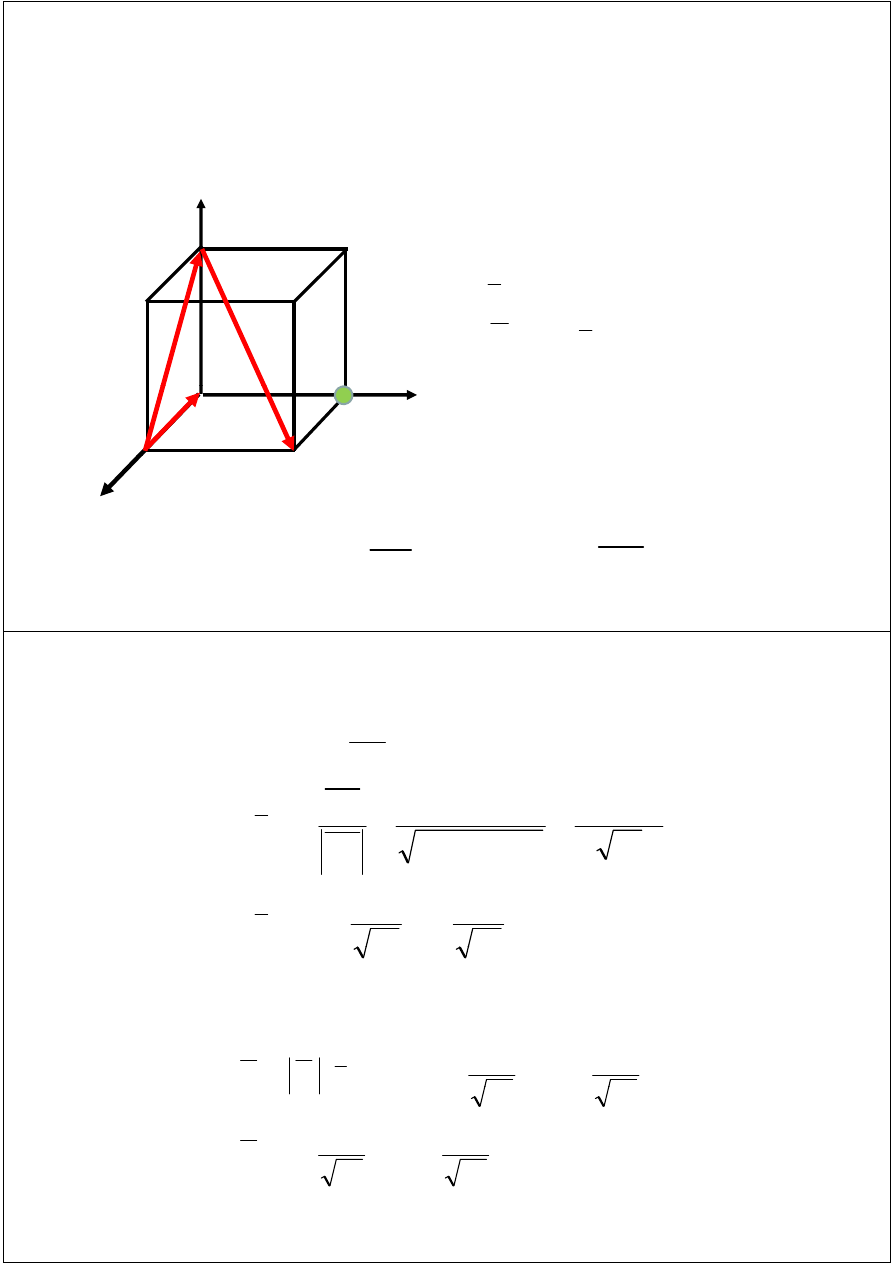
Przykład 1.
a) Oblicz współrzędne wektorów

a) Oblicz współrzędne wektorów
b) Oblicz sumę
c) Oblicz moment względem bieguna A

)

g ę

g

Z

B

4





0

,

0

,

1

e

CO





3

_

F

Y

A

3F

2F

2

_

F

4 m

O





0

,

0

,

1

1

F

e

F

F

CO









X

2F

F

1

_

F

1 m

O





0

0

1

C





4

0

0

B

X

C

D

2 m









4

,

0

,

0

0

,

0

,

1

B

C









0

,

2

,

1

4

,

0

,

0

D

B









4

,

0

,

1





CB





4

,

2

,

1





BD

Wyznaczenie wersora kierunku CB





4

,

0

,

1





CB









4

0

1

4

0

1

CB























17

4

,

0

,

1

4

0

1

4

,

0

,

1

2

2

2

CB

CB

CB

e















17

4

,

0

,

17

1

CB

e





17

17

Wyznaczenie wektora siły F

2

















4

,

0

,

1

2

2

2

F

e

F

F

CB

y

y

2















8

0

2

17

,

,

17

2

2

F

F

F

CB







17

,

0

,

17

2

F

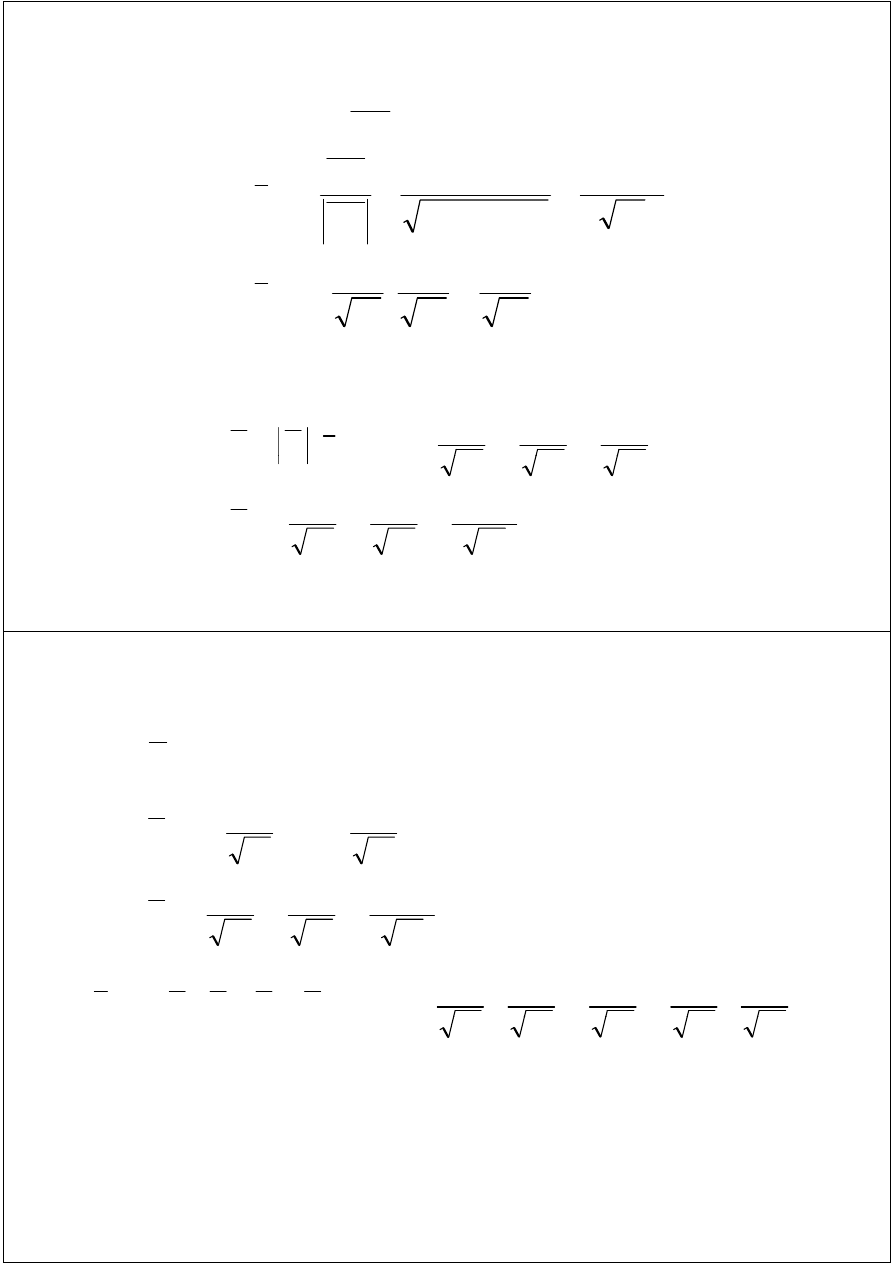
Wyznaczenie wersora kierunku CB





4

,

2

,

1





BD









4

2

1

4

2

1

BD























21

4

,

2

,

1

4

2

1

4

,

2

,

1

2

2

2

BD

BD

BD

e













21

4

,

21

2

,

21

1

BD

e





21

21

21

Wyznaczenie wektora siły F

3



















4

,

2

,

1

3

3

3

F

e

F

F

BD

y

y

3

















12

6

3

21

,

21

,

21

3

3

F

F

F

F

BD







21

,

21

,

21

3

F

Obliczenie sumy





0

,

0

,

2

1

F

F









8

2

F

F











17

8

,

0

,

17

2

2

F

F

F













21

12

,

21

6

,

21

3

3

F

F

F

F

































12

8

,

6

,

3

2

2

3

2

1

3

F

F

F

F

F

F

F

F

F

F

S

i









21

17

,

21

,

21

17

3

2

1

1

i

i

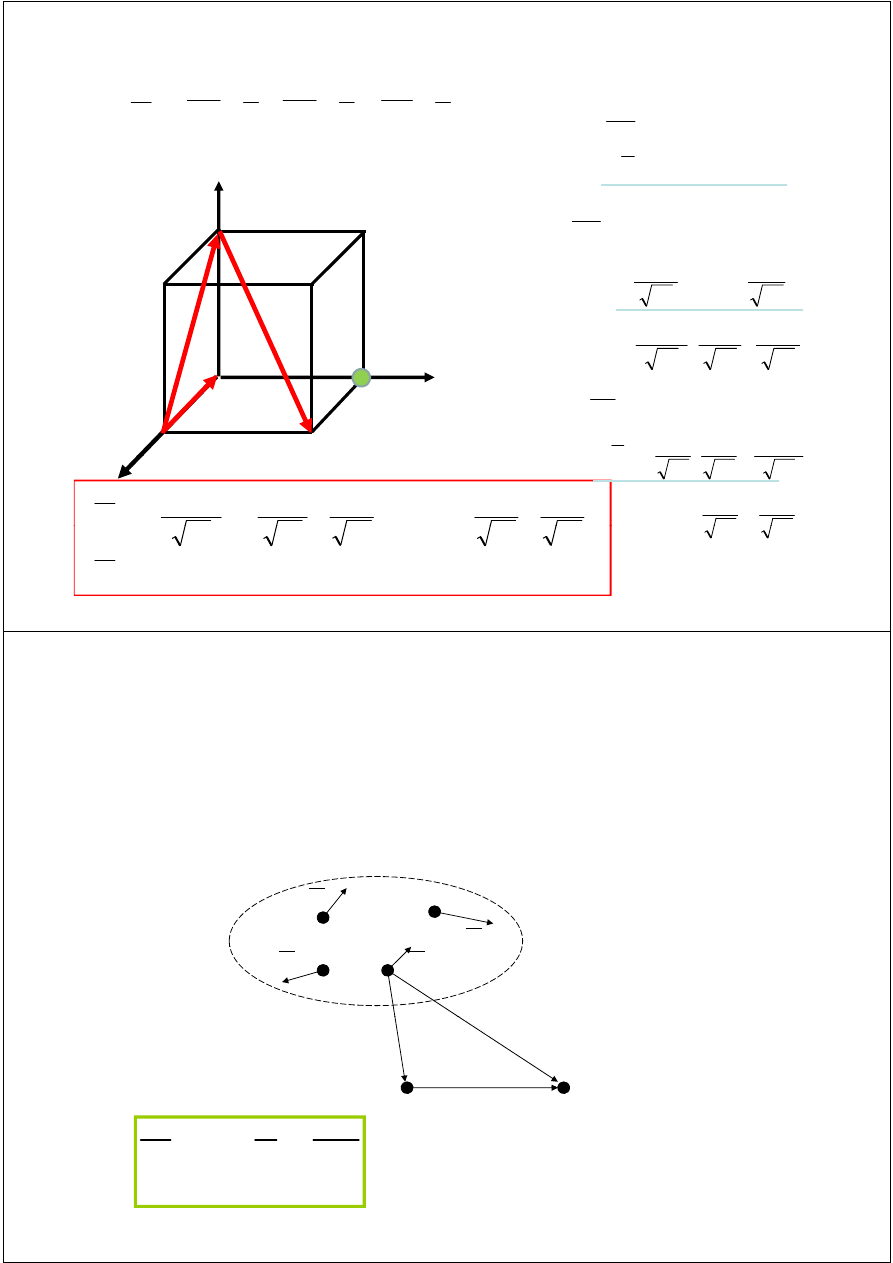
A

AC

AC

Wyznaczenie momentu względem punktu A

3

2

1

F

AB

F

AC

F

AC

M

A





















F

F

AC

0

0

2

0

2

1

1













 







4

0

0

0

0

1

0

2

0

B

C

A









F

4

0

0

1













0

2

1

AC



 







4

,

0

,

0

0

,

0

,

1

0

,

2

,

0

B

C

A

Z

B













17

8

0

17

2

2

F

F

F

_

F

2

_

F

4 m

















17

4

17

8

17

16

F

F

F

3

F

Y

A

3F

2F

2

F

O























12

6

3

4

2

0

F

F

F

F

AB

X

C

D

F

1

_

F

2 m

1 m



















21

6

21

12

0

21

21

21

3

F

F

F

6

4

4

,

12

8

,

16























F

F

F

F

F

F

M

A

2 m





21

21





661

.

3

,

678

.

0

,

492

.

0

21

17

,

21

17

,

17












F

M

A

A

Twierdzenie o zmianie bieguna

g

Dla układu złożonego z n sił obliczmy moment względem

Dla układu złożonego z n sił obliczmy moment względem
Punktu (bieguna) B i nowego punktu (bieguna) R.

A

n

A

1

A

1

F

n

F

2

A

i

A

2

F

i

F

n

B

R





n

df

B

A

F

M









i

i

i

B

B

A

F

M

1

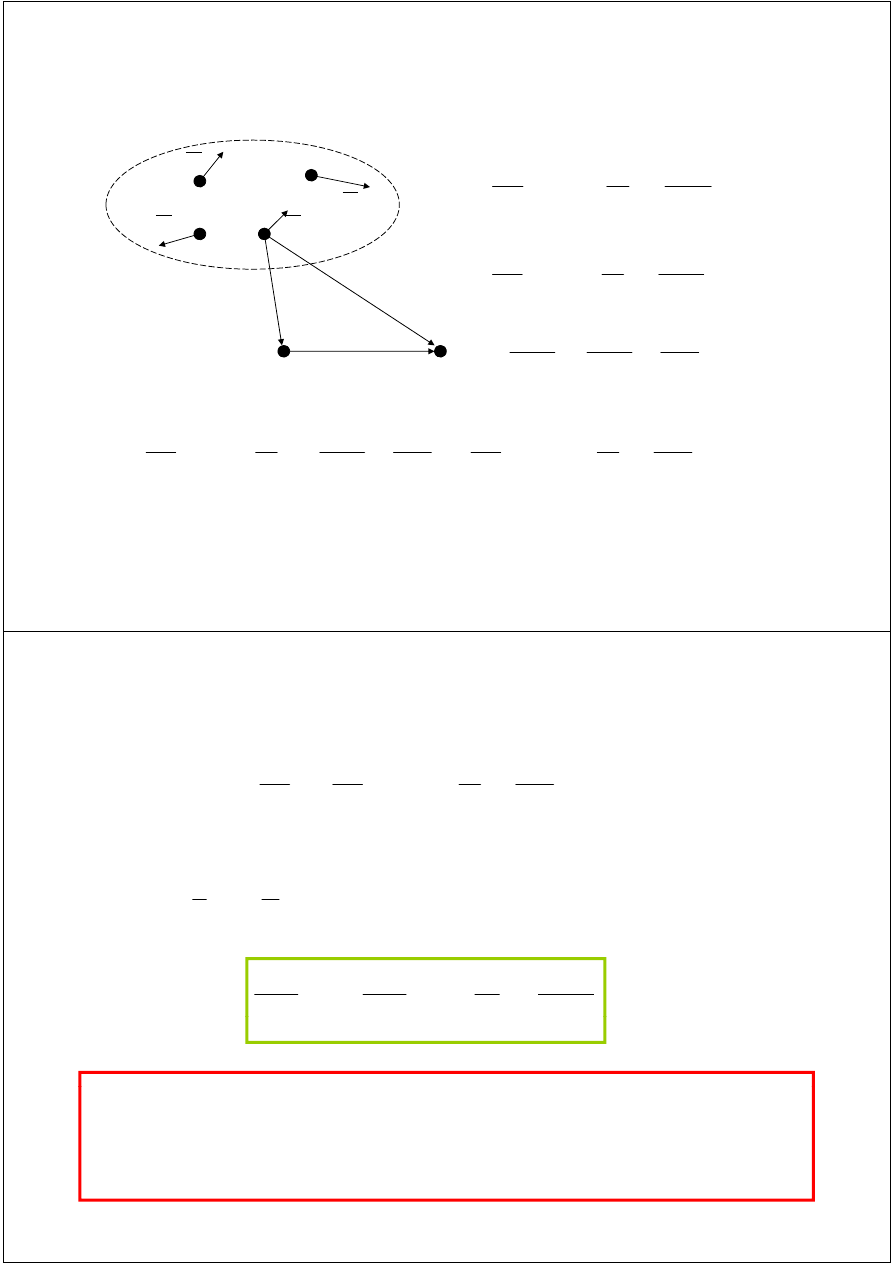
Twierdzenie o zmianie bieguna

g

n

A

A

1

F

n

df

A

i

A

1

A

2

F

i

F

n

F









n

i

i

i

df

B

B

A

F

M

1

2

A

i 1







n

i

i

R

R

A

F

M

B

R



i 1

BR

B

A

R

A

i

i





















n

n

i

i





































i

i

B

i

i

i

R

BR

F

M

BR

B

A

F

M

1

1

Twierdzenie o zmianie bieguna

















n

i

B

R

BR

F

M

M

g



















i

i

B

R

BR

F

M

M

1

Wektor nazywamy sumą układu. Mamy zatem:







n

i

i

df

F

S

1

BR

S

M

M

B

tw

R







BR

S

M

M

B

R







M

t kł d

ił li

l d

bi

j t

Moment układu sił liczony względem bieguna nowego jest
równy momentowi układu względem bieguna starego
powiększonemu o iloczyn wektorowy sumy układu i wektora

powiększonemu o iloczyn wektorowy sumy układu i wektora
łączącego biegun stary z nowym

Wnioski z twierdzenia o zmianie

bieguna

Jeżeli , to moment układu jest stały (niezależny od
wyboru bieguna, względem którego jest liczony).

0



S

y

g

,

g ę

g j

y)

BR

S

M

M

B

R







BR

S

M

M

B

R







0



S

B

R

M

M



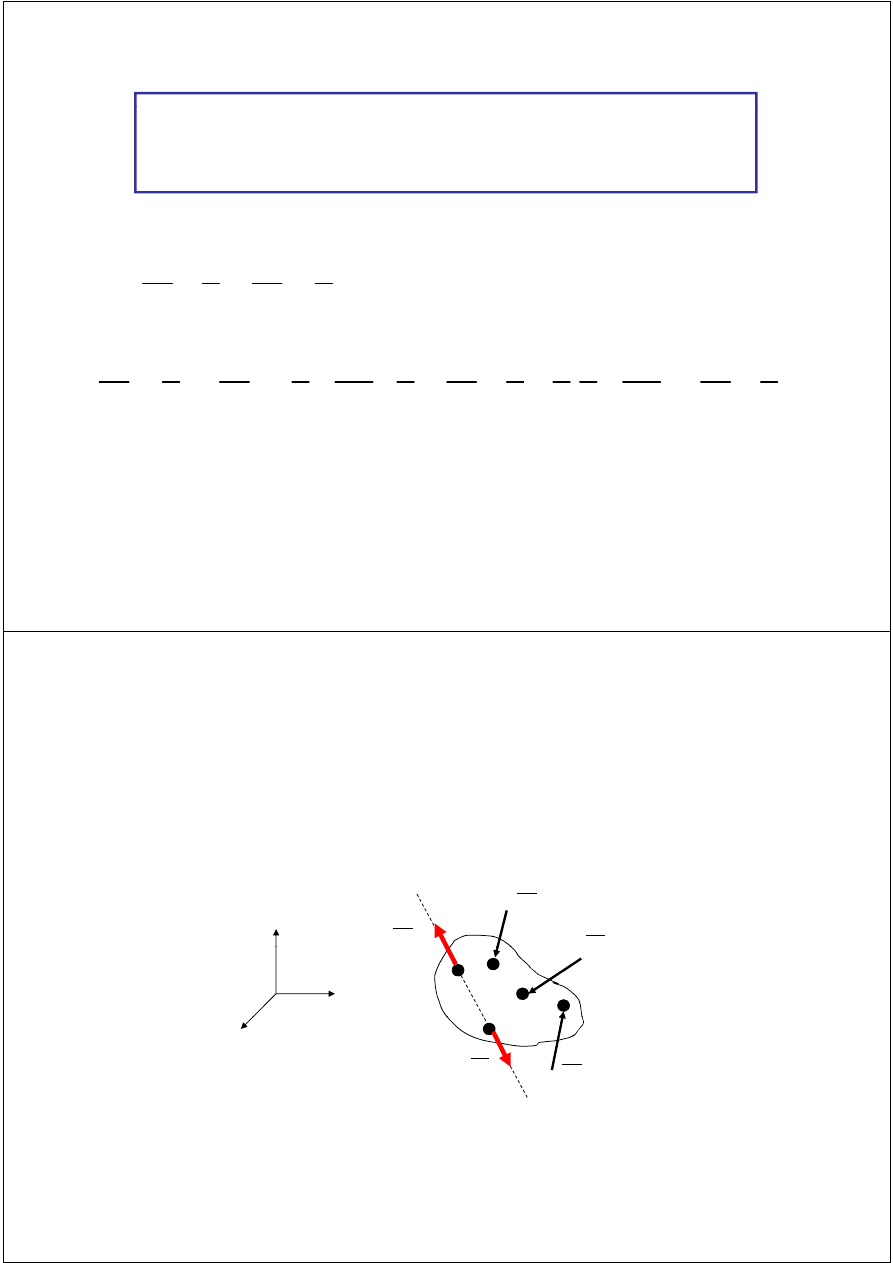
Jeżeli momenty układu liczone względem trzech

y

g ę

niewspółliniowych punktów są równe, to suma układu jest
równa zeru.

Aby wykazać prawdziwość tego wniosku, należy dwukrotnie

Z: punkty A B C są niewspółliniowe:

y y

p

g

,

y

zastosować twierdzenie o zmianie bieguna.

Z: punkty A, B, C są niewspółliniowe:

C

B

A

M

M

M

AC

AB









0

oraz

S

T

 0

:

Suma nie może być
równoległa do AB i AC

AB

S

M

M

D

A

B







:

0



S

0



 AB

S

równoległa do AB i AC

AC

S

M

M

A

C







0



S

0



 AC

S

Il

k l

i

t li

l d

Iloczyn skalarny sumy i momentu liczonego względem
dowolnego punktu jest dla układu sił wielkością stałą
i nazywamy ją parametrem układu:

i nazywamy ją parametrem układu:

const

S

M

S

M

k

A

df











0









D :









S

M

OA

S

S

S

M

S

OA

S

M

S

M

A























0

0

0

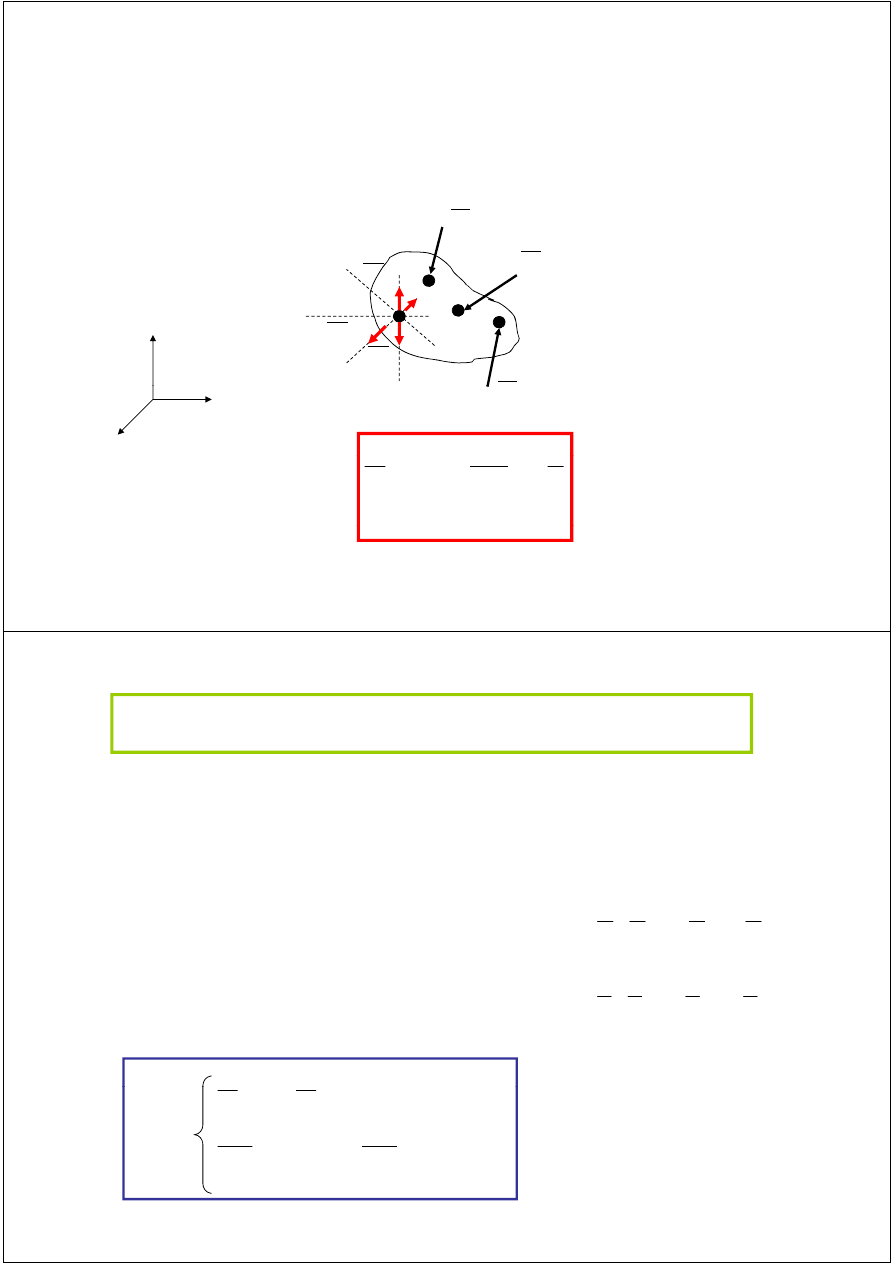
Przekształcenia elementarne

Przekształcenie elementarne I rodzaju- dodanie (lub odjęcie)
do układu sił dwóch sił przeciwnych leżących na jednej prostej

do układu sił dwóch sił przeciwnych, leżących na jednej prostej.

z

F

1

F

F

1

A

y

F

i

F

1

A

i

A

x

F



n

F

n

A

n

Przekształcenia elementarne

Przekształcenie elementarne II rodzaju- dodanie (lub odjęcie)
zbieżnego układu sił o sumie równej zeru

zbieżnego układu sił o sumie równej zeru.

1

F

A

i

F

1

A

A

i

N

z

F

n

A

i

A

A

1

N

k

N

x

y

n

F

k

0

1









k

i

i

N

S

1



i

Równoważność układu sił

Równoważność układu sił

Dwa układy sił nazywamy równoważnymi, jeżeli wykonując

j d

i h k ń

il ść

k t ł ń l

t

h

na jednym z nich skończoną ilość przekształceń elementarnych
I i II rodzaju otrzymamy drugi układ. Z definicji przekształceń
elementarnych wynika że nie zmieniają one sumy i momentu

elementarnych wynika, że nie zmieniają one sumy i momentu
układu.









n

i

F

F

F

F

A

2

1

,

...

,

,

...

,

,

Zatem równoważne układy sił A i B



















k

j

n

i

R

R

R

R

A

A

A

A

A

2

1

2

1

,

...

,

,

...

,

,

Zatem równoważne układy sił A i B
to takie, które mają równe sumy
i równe momenty liczone względem

















k

j

k

j

B

B

B

B

R

R

R

R

B

2

1

2

1

,

...

,

,

...

,

,

dowolnego (każdego) punktu.

)

(

)

(

B

M

A

M

S

S

B

A



df

)

(

)

(

B

M

A

M

Q

Q



Q- dowolny punkt

Twierdzenia o równoważności

kł dó

ił

układów sił:

1 Dwa układy sił A i B są równoważne gdy mają równe sumy

1. Dwa układy sił A i B są równoważne, gdy mają równe sumy

i równe momenty liczone względem jednego (ustalonego) punktu.



:

S

S

Z

B

A

 

 







:

,

:

B

A

T

punkt

ustalony

O

B

M

A

M

S

S

O

O

B

A




'

:

:

O

D

B

A

T

dowolny punkt

Należy wykazać że

 

 

B

M

A

M

Należy wykazać, że

 

 

B

M

A

M

O

O

'

'



 

 

OO

S

A

M

A

M

A

O

O

'

'

'







Stąd po odjęciu stronami

 

 

 

 

 

 

 

 

B

M

A

M

B

M

A

M

OO

S

B

M

B

M

OO

S

A

M

A

M

B

O

O

A

O

O

'

'

l b

0

'











Stąd po odjęciu stronami
otrzymujemy

 

 

 

 

B

M

A

M

B

M

A

M

O

O

O

O

'

'

'

'

lub

0







2. Dwa układy sił A i B są równoważne, gdy mają (odpowiednio)

równe momenty liczone względem trzech niewspółliniowych

równe momenty liczone względem trzech niewspółliniowych
punktów.

Z: O O’ O’’ punkty niewspółliniowe

Z: O, O , O – punkty niewspółliniowe

 

 

 

 

B

M

A

M

O

O



 

 

 

 

B

M

A

M

B

M

A

M

O

O

O

O

''

''

'

'





 

 

 

 

B

A

bieguna

zmianie

o

e

twierdzeni

my

wykorzysta

dowodzie

w

D

B

A

czyli

S

S

T





:

:

:

 

 

 

 

 

 

 

 

B

O

O

A

O

O

B

O

O

A

O

O

OO

S

B

M

B

M

OO

S

A

M

A

M

OO

S

B

M

B

M

OO

S

A

M

A

M





























''

''

'

'

''

''

'

'









B

A

B

A

OO

S

S

OO

S

S















0

''

0

'

Na postawie założenia można napisać:

B

A

B

A

S

S

czyli

S

S







0

''

'

OO

do

równoległ

jest

nie

OO

wektor

Ponieważ

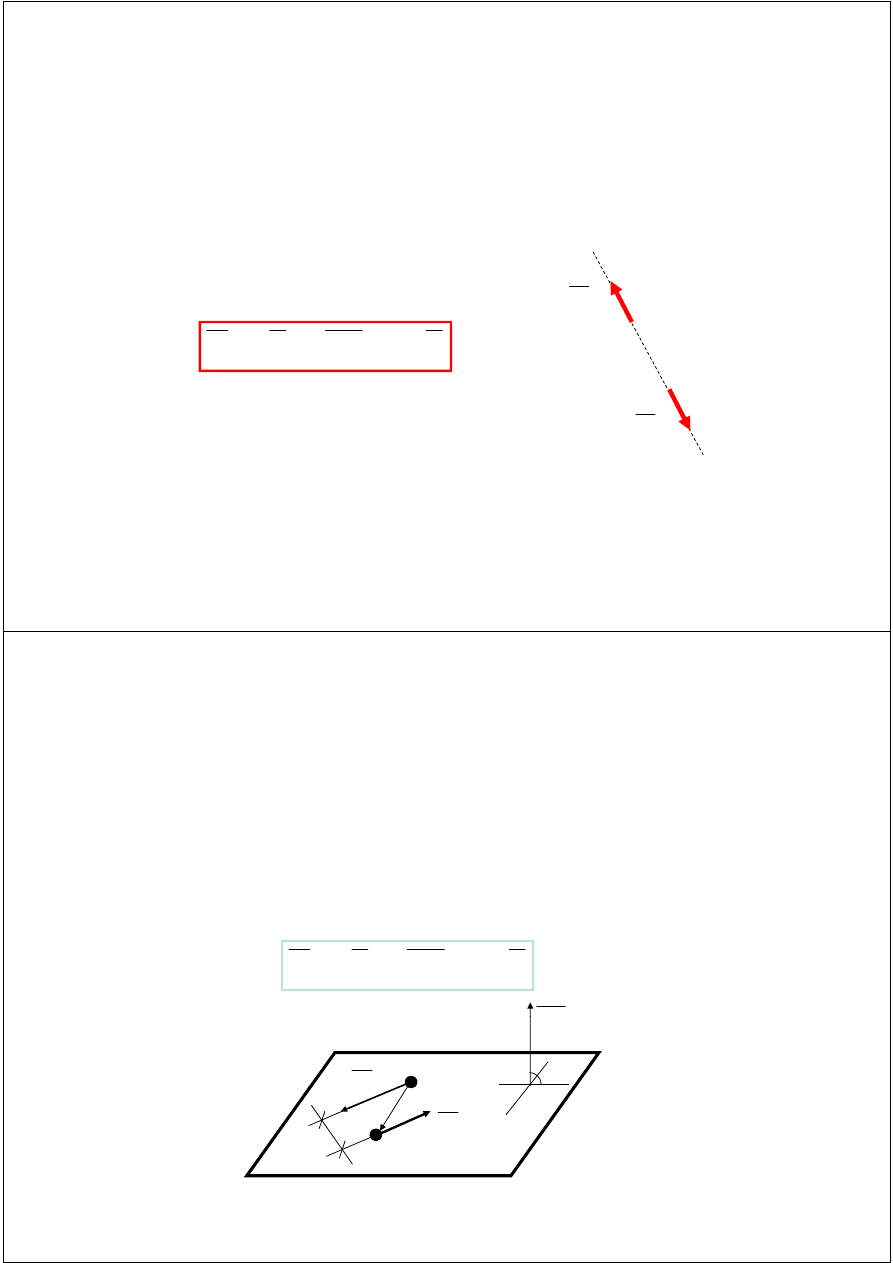
Zerowy układ sił

y

Układ sił, dla którego suma jest wektorem zerowym i moment
li

l d

d

l

kt

ó

i

liczony względem dowolnego punktu równa się zeru,
nazywamy zerowym układem sił:

F

0

0







O

M

S

F

Jako przykład takiego układu można podać układ złożony
z dwu sił przeciwnych leżących na jednej prostej lub układ

z dwu sił przeciwnych leżących na jednej prostej lub układ
zbieżnych sił o sumie równej zeru.

Para sił

Parę sił stanowią dwie siły niezerowe, przeciwne,
nie leżące na jednej prostej.

ą

j

j p

j

Z definicji pary sił wynika, że jej suma jest równa zeru,

ś

li

l d

d

l

k j

ł

zaś moment liczony względem dowolnego punktu jest stały:

0

0







O

M

S

M

O

M

.

A

F



B

F



F



0



d



B

Płaszczyznę wyznaczoną przez parę sił nazywamy
płaszczyzną działania pary:









AB

F

M

M

B

O

d

F

AB

F

M

M

O

O

















sin

kierunek
moduł



 AB

F

M

M

B

O

zwrot wektory stanowią

trójkę prawoskrętną

AB

F

M

O

,

,

Pary sił leżące w jednej płaszczyźnie i mające ten sam moment
stanowią zbiór równoważnych par A zatem parę sił można

stanowią zbiór równoważnych par. A zatem parę sił można
dowolnie przesuwać, obracać w płaszczyźnie jej działania.

F

F

F

F

F

F

Redukcja układu sił - redukcja w punkcie

Redukcja układu sił redukcja w punkcie

Przez redukcję rozumieć będziemy przekształcenie
polegające na zastąpieniu danego układu układem
równoważnym

równoważnym.

Redukcja układu sił w punkcie R (biegunie) polega na

Redukcja układu sił w punkcie R (biegunie) polega na
zastąpieniu danego układu układem równoważnym, złożonym
z wektora równego sumie układu (gdy ) zaczepionego

0



S

w biegunie redukcji i pary sił o momencie równym momentowi
układu liczonego względem bieguna redukcji (gdy ).

0



R

M

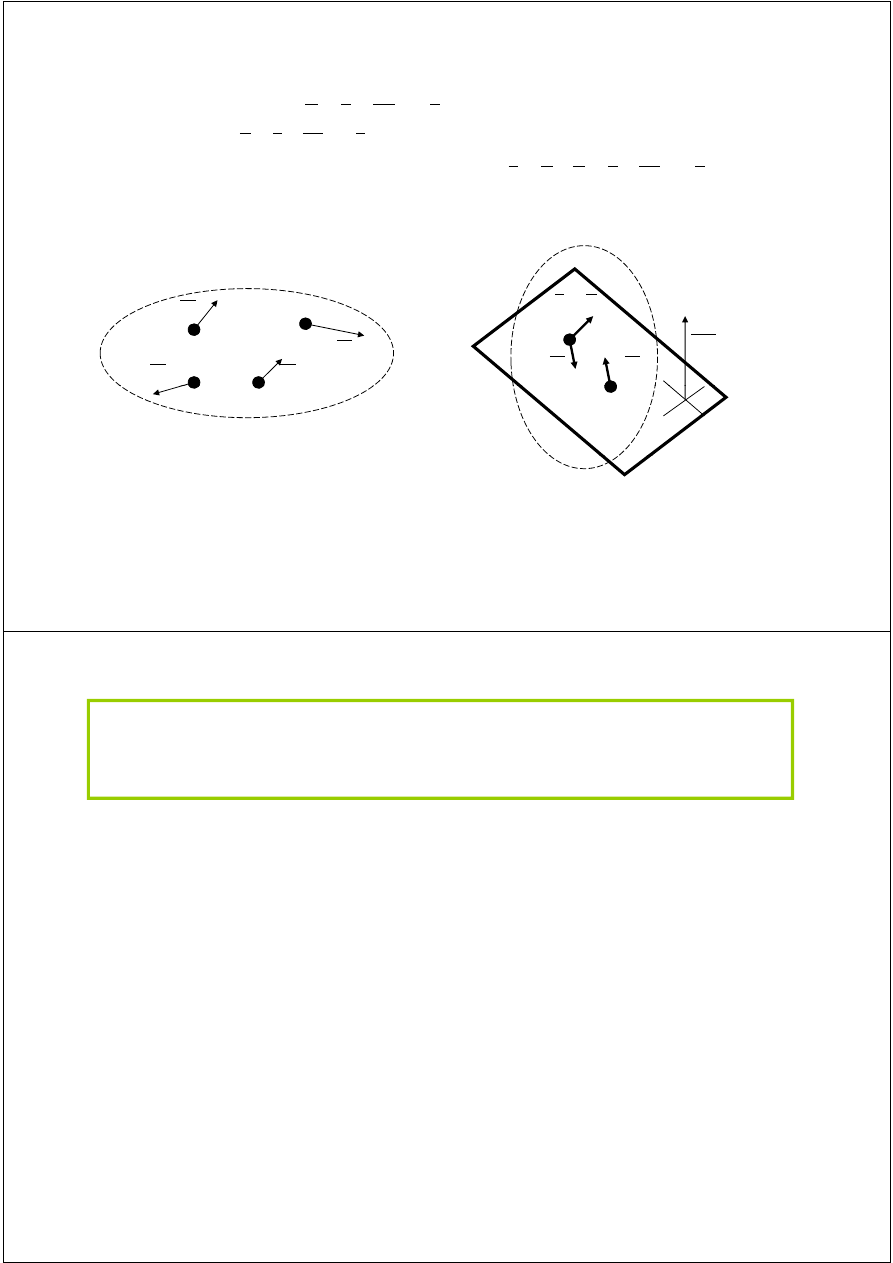
Mogą tutaj wystąpić następujące przypadki:

1) kł d

)

0

0

(S

)

0

0

(









R

M

S

S

b

1) układ zerowy
2) para sił
3) układ złożony z jednego wektora

),

0

0

(







R

M

S

),

0

0

(







R

M

S

)

0

0

(









R

M

S

S

b

3) układ złożony z jednego wektora
4) układ złożony z trzech wektorów

n

A

1

F

A

S

b



i

A

n

1

A

1

F

2

F

i

F

n

F



R

M

F

R

B

F



A

2

A

B

B

B

A



Redukcja układu sił - redukcja do

Redukcja układu sił redukcja do
najprostszej postaci

Przez redukcję rozumieć będziemy przekształcenie

Przez redukcję rozumieć będziemy przekształcenie
polegające na zastąpieniu danego układu równoważnym,
możliwie prostszym (złożonym z mniejszej liczby sił).

Układ sił, którego suma jest równa zeru, redukuje się do

kład

ero ego gd jego moment jest ero

a do par

układu zerowego, gdy jego moment jest zerowy, a do pary
sił, gdy ma moment niezerowy.

Układ sił równoważny danemu układowi, a złożony

y

,

y

z najmniejszej liczby sił, nazywamy

najprostszym układem

sił

. Jest nim:

1. Układ zerowy, gdy
2. para sił, gdy
3 wypadkowa układu sił gdy

,

0

0







O

M

S

,

0

0







O

M

S

0

0

K

S

3. wypadkowa układu sił, gdy
4. układ złożony z dwu sił skośnych, gdy

,

0

0







K

S

.

0



K

Układy te wzajemnie się wykluczają.

Wypadkowa układu

yp

Układ równoważny danemu układowi, złożony z jednej
niezerowej siły równej sumie układu.

Ma ściśle określoną prostą działania o tej własności, że
moment układu liczony względem jej punktów jest równy zeru

moment układu liczony względem jej punktów jest równy zeru,
zaś liczony względem punktów nie należących do tej prostej-
różny od zerai prostopadły do sumy układu.

y

p

p

y

y

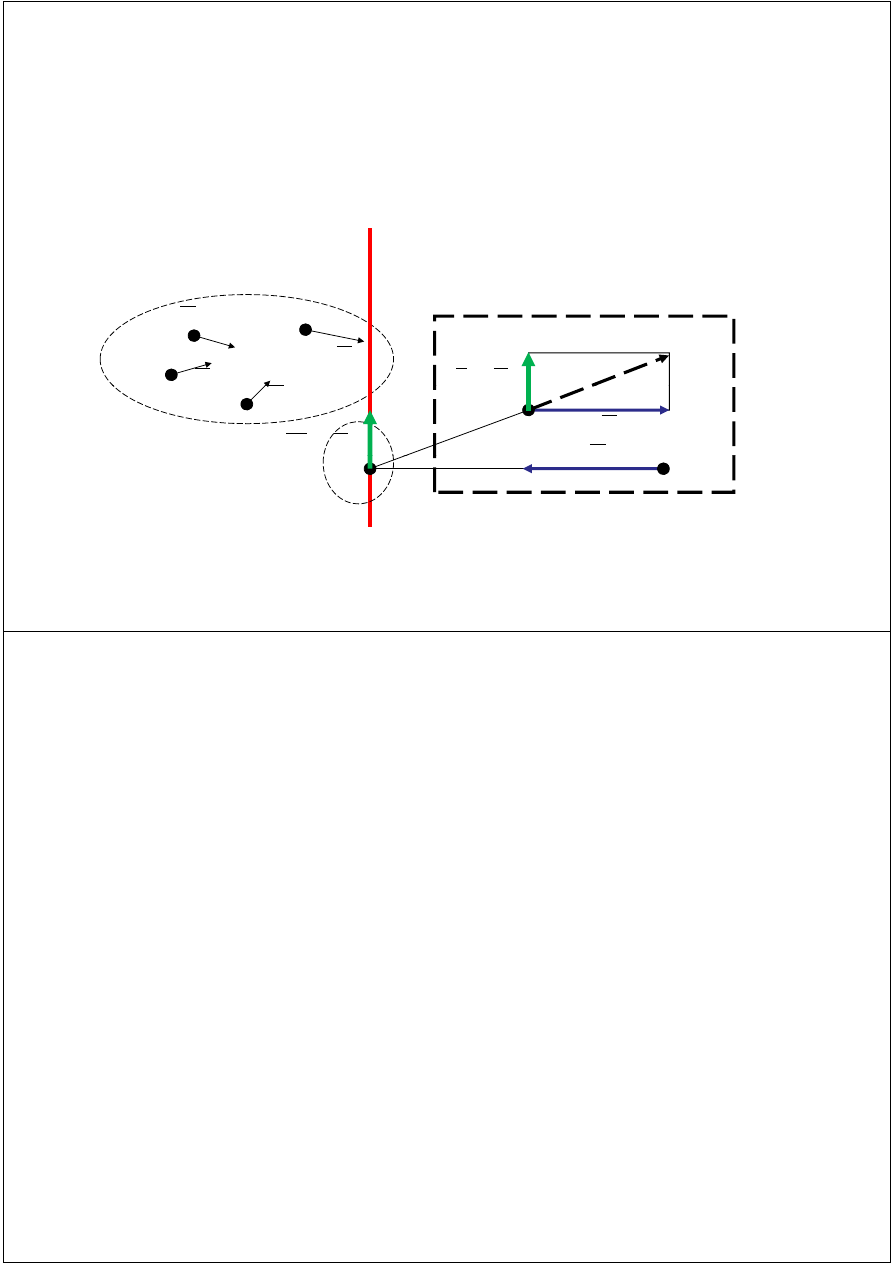
Układ sił o sumie niezerowej i parametrze układu równym

d k j

i d

dk

j (

kt h l ż

h

zeru redukuje się do wypadkowej (w punktach leżących na
prostej działania wypadkowej), zaś w punktach poza prostą,
na której leży wypadkowa otrzymujemy układ równoważny

na której leży wypadkowa, otrzymujemy układ równoważny,
złożony z trzech sił leżących w jednej płaszczyźnie.

L

t d i ł i

dk

j

A

F

L- prosta działania wypadkowej

A

A

n

A

1

A

1

F

2

F

n

F

D

A

S

b



A

2

A

i

A

2

i

F

F

F



B

A

S

W



A

S

b

F



A

B

C

D

B

A





Różnica między sumą sił a

wypadkową

Suma jest to wektor swobodny (nie ma ustalonego punktu
zaczepienia), który może być wektorem zerowym.

Wypadkowa, jako układ równoważny danemu, jest wektorem
niezerowym o ściśle określonej prostej działania

niezerowym, o ściśle określonej prostej działania.

Suma nie może być równoważna układowi sił, gdyż nie jest

y

g y

j

układem.

2

/

10kN

2

/

10

m

kN

25

kN





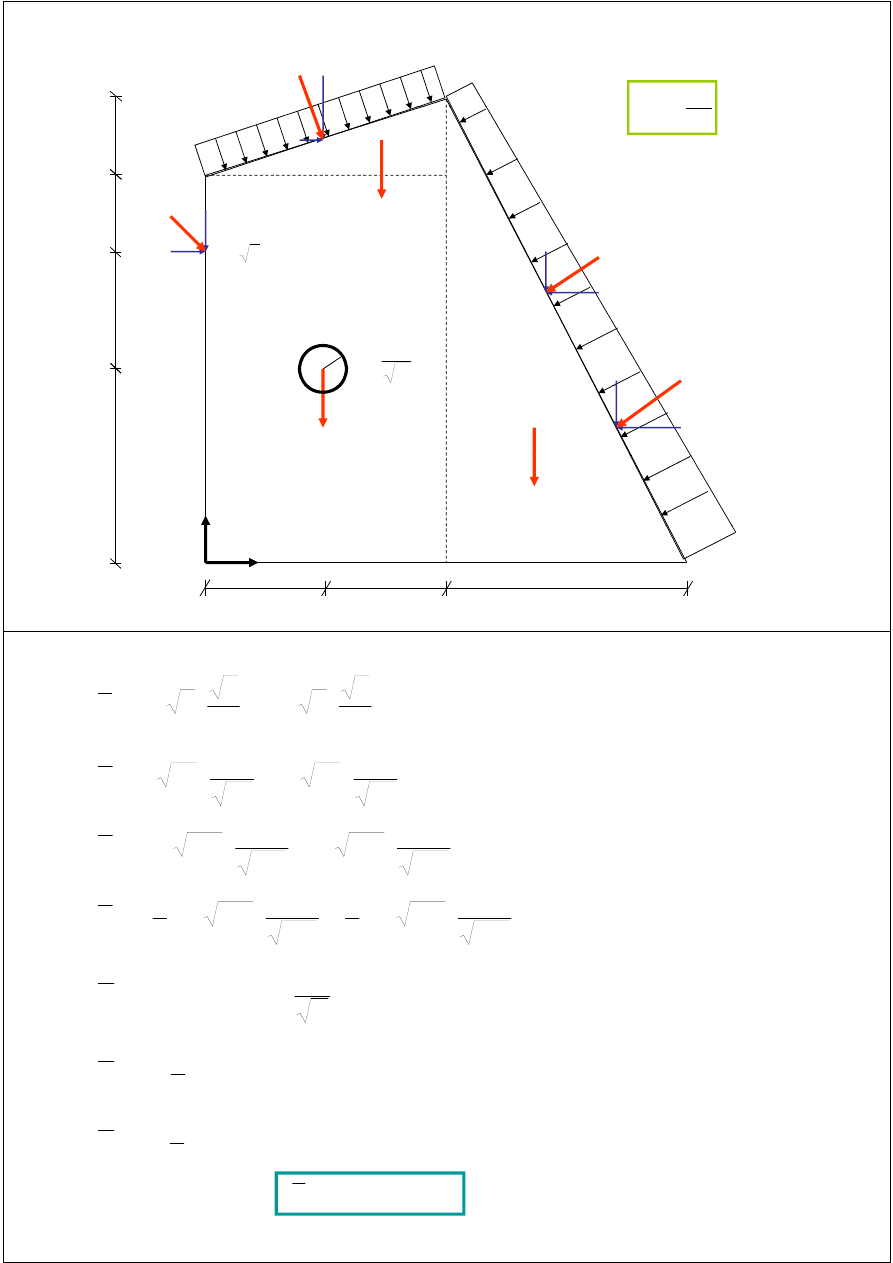
Zredukować podany układ sił do najprostszej postaci.

2

2

/

10

m

kN

/

10

m

kN

2

P

3

G

3

25

m





2

1

P

P



45

3

3

P

45

2

100

3



4



R

4

P

2

G

1

G

5

y

2



3

3

6

x

y



2

/

30

m

kN





0

,

100

,

100

0

,

2

2

2

100

,

2

2

2

100

1























P





0

,

60

,

20

0

,

40

6

40

10

,

40

2

40

10

2



























P





0

,

60

,

120

0

,

180

6

180

10

,

180

2

180

10

3































P





0

,

60

,

120

0

,

180

6

180

20

2

1

,

180

12

180

20

2

1

4



































P





0

,

1100

,

0

25

4

10

6

,

0

,

0

2

1

























































G









0

,

900

,

0

0

,

25

12

6

2

1

,

0

2









































G







0

,

150

,

0

0

,

25

2

6

2

1

,

0

2

3





























G





0

,

2430

,

120

2









S





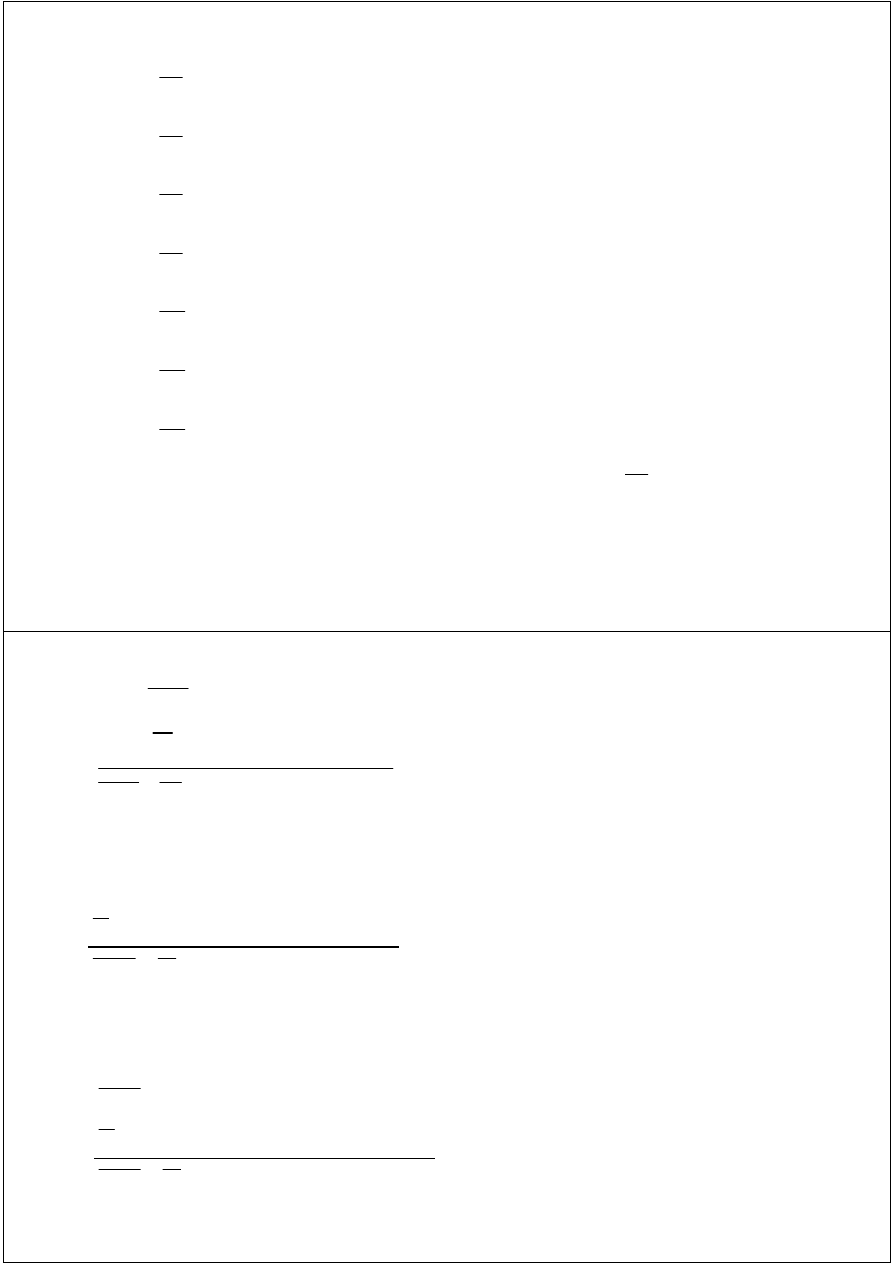
0

,

100

,

100

1



P





0

,

8

,

0

1

A









0

,

60

,

20

0

,

100

,

100

2

1



P

P









0

,

11

,

3

0

,

8

,

0

2

1

A

A









0

,

60

,

120

3





P





0

,

6

,

9

3

A









0

1100

0

0

,

60

,

120

4





G

P









0

5

3

0

,

4

,

10

4

A

A









0

900

0

0

,

1100

,

0

1



G

G









0

4

8

0

,

5

,

3

5

A

A









0

,

150

,

0

0

,

900

,

0

3

2





G

G













2

0

,

4

,

8

6

A





0

,

150

,

0

3

G













0

,

3

2

10

,

4

7

A









0

,

8

,

0

1

O

A









800

,

0

,

0

0

,

100

,

100

1

1

1









F

O

A

P





800

,

0

,

0

1

1

F

O

A













0

,

60

,

20

0

,

11

,

3

2

2



P

O

A





400

,

0

,

0

2

2





 F

O

A













0

,

60

,

120

0

,

6

,

9

3

3





P

O

A









180

,

0

,

0

3

3



 F

O

A









0

,

4

,

10

4

O

A









120

,

0

,

0

0

,

60

,

120

4

4

4











F

O

A

P





0

5

3

O

A

2





















0

,

1100

,

0

0

,

5

,

3

5

5



P

O

A





0

150

0

0

,

3

2

10

,

4

7













P

O

A





0

4

8

O

A





3300

,

0

,

0

5

5





 F

O

A









600

,

0

,

0

0

,

150

,

0

7

7

7









F

O

A

P













0

,

900

,

0

0

,

4

,

8

6

6



P

O

A





7200

,

0

,

0

6

6





 F

O

A









12240

0

0





O

M

12240

4

150

8

900

3

1100

4

120

10

60

6

120

9

60

3

60

11

20

8

100





























O

M

12240

4

150

8

900

3

1100

4

120

10

60

























Układ redukuje się po wypadkowej

0

0









S

S

M

k

O



Wyznaczenie prostej działanie wypadkowej (osi środkowej)

K

t

t

i

i bi

i

k j

t ki





S

0

,

2430

,

120





Korzystamy z tw. o zmianie bieguna i poszukujemy takiego
punktu X(x,y,0) aby Mx = 0





x

y

y

x

OX

2430

120

,

0

,

0

0

,

,





OX

S

M

M

O

X







x

y 2430

120

,

0

,

0















0

0

0

12240

2430

120

12240

0









x

y





















































0

0

0

0

0

0

12240

102

120

12240

0













y

x





























x

y 2430

120

12240

0

04

,

5

2430

12240

0









x

y

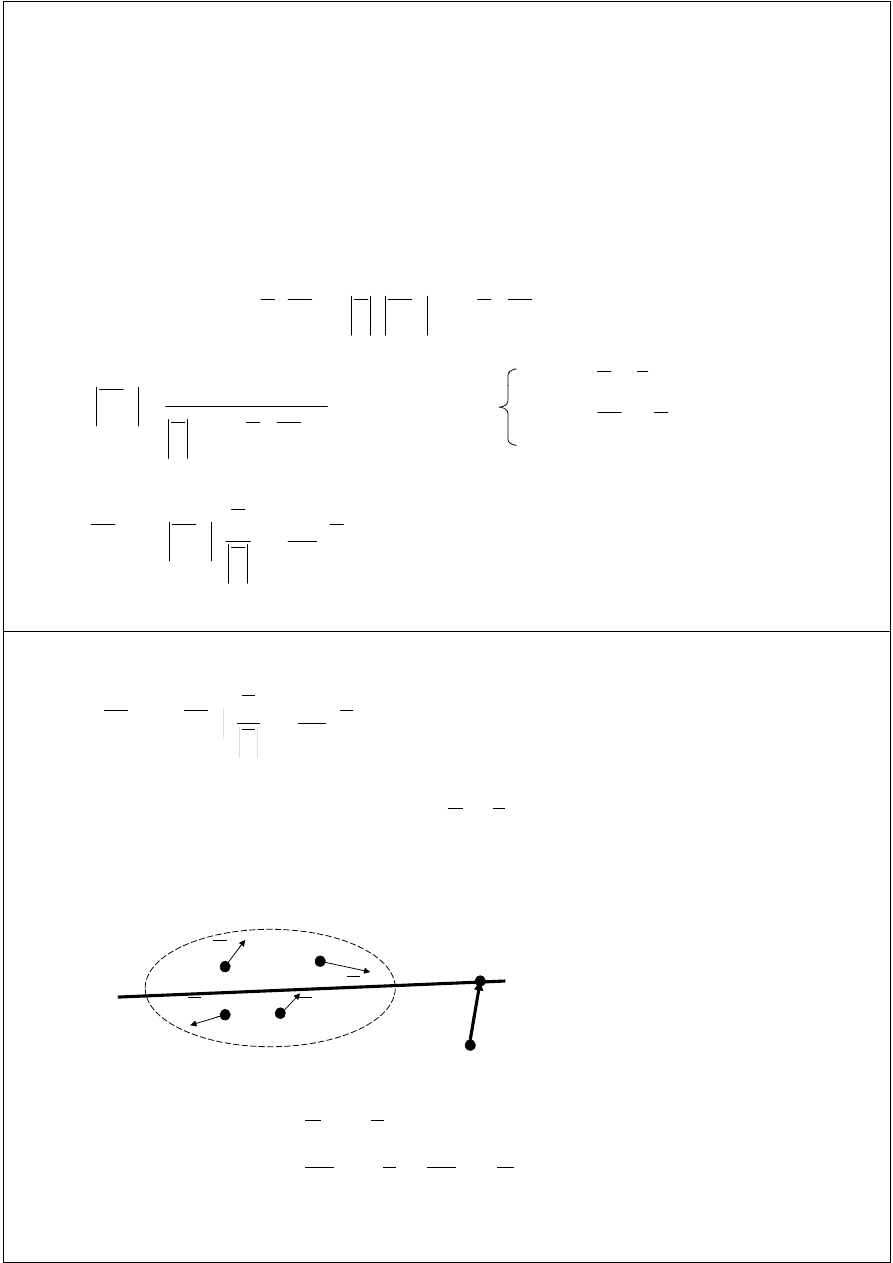
Oś środkowa układu sił, skrętnik

Jest to miejsce geometryczne punktów o tej własności,
że moment układu liczony względem tych punktów jest

że moment układu liczony względem tych punktów jest
równy zeru (K=0), lub jest równoległy do sumy układu
Punkty osi środkowej mają jeszcze jedną własność wynikającą





.

0



K

Punkty osi środkowej mają jeszcze jedną własność wynikającą
z parametru układu:

const

M

S

M

S

M

S

k

A

A

A





















cos

const

M

S

M

S

M

S

k

A

A

A



















,

cos

Stąd otrzymujemy:

k

S

k

0

0







min

,

cos





















A

A

M

S

S

k

M

gdy

S

M

k

S

k

A

||

0

0

0











A zatem mamy:





k

S





S

S

k

S

S

M

M

A

A





















2

S

S

K

S

S

M

M

A

A





















2

S

S





2

Własność tę można ująć następująco:
Moduł momentu (układu sił o ) liczonego względem
punktów osi środkowej jest minimalny.

0



S

A

F

i

A

n

A

1

A

1

F

2

F

i

F

n

F

A

oś środkowa

A

2

A

O (stały punkt odniesienia)

A

S

0



A

A

A

S

M

M

||

0





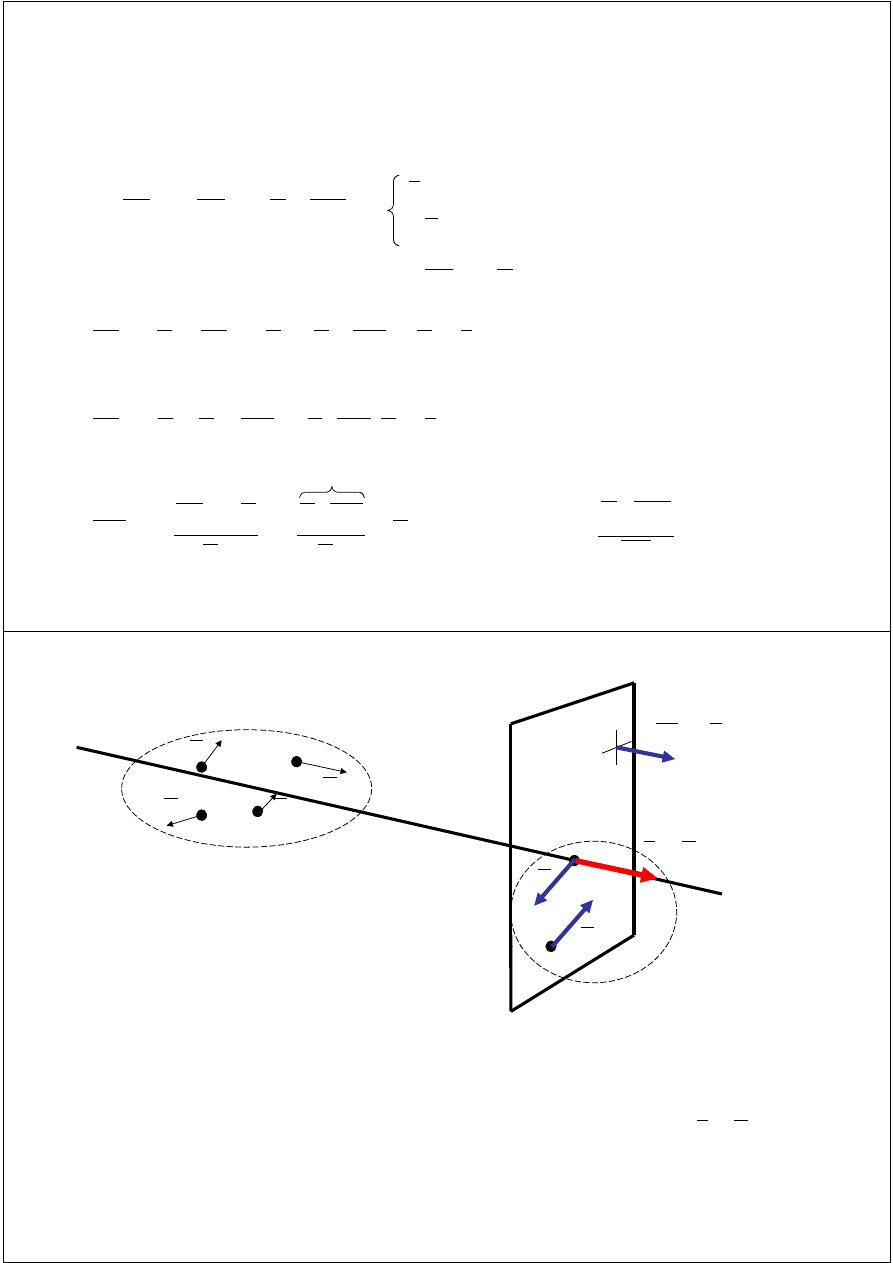
Znajdujemy punkty, które należą do osi środkowej, a więc
jej równanie. Do równania osi środkowej możemy również
dojść z definicji. Z twierdzenia o zmianie do bieguna mamy:

0

0

0





K

gdy

S

K

gdy











OA

S

M

M

O

A

Mnożymy wektorowo wektory

:

S

i

M

A





S

OA

S

S

M

S

M

O

A















0

Powyższe wyrażenie zapisujemy następująco:





S

OA

S

OA

S

S

M

O













2

0

Powyższe wyrażenie zapisujemy następująco:

S

OA

S

S

M

OA

O







 



Stąd otrzymamy:



OA

S





S

S

S

OA

O





















2

2

gdzie

2

S

O

S





0



k

S

M

A

||

i

A

n

A

1

A

1

F

F

F

n

F

S

M

A

||

A

2

A

i

2

F

i

F

F

S

b



A

F

F



oś środkowa

B- skrętnik

A

ę

W przypadku układu o parametrze wprowadza się

0



k

pojęcie skrętnika, to jest układu zredukowanego w dowolnym
punkcie osi środkowej. Układ taki składa się z wektora
l ż

i ś dk

j i

ił

i

ó

l

ł

S

b



leżącego na osi środkowej i pary sił o momencie równoległym
do sumy układu.

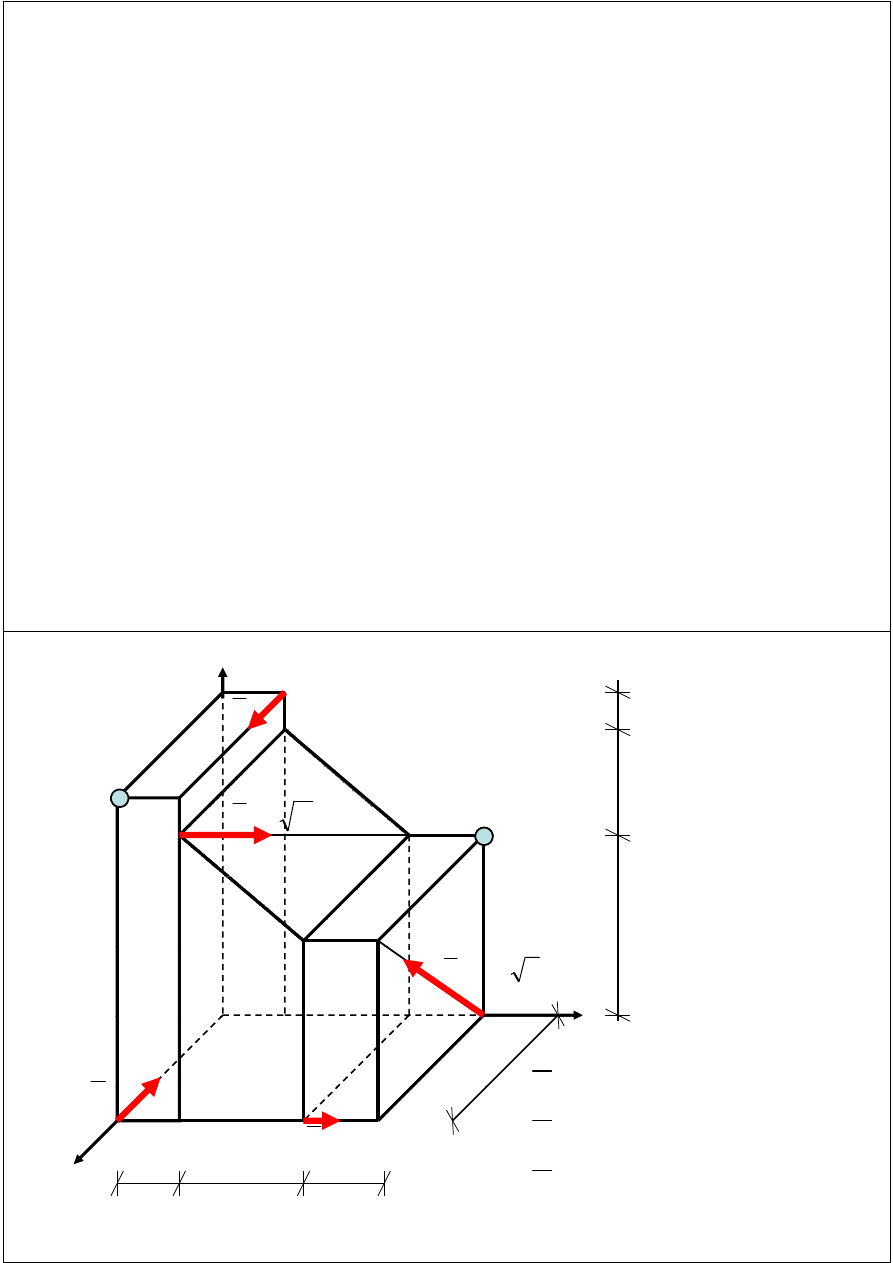
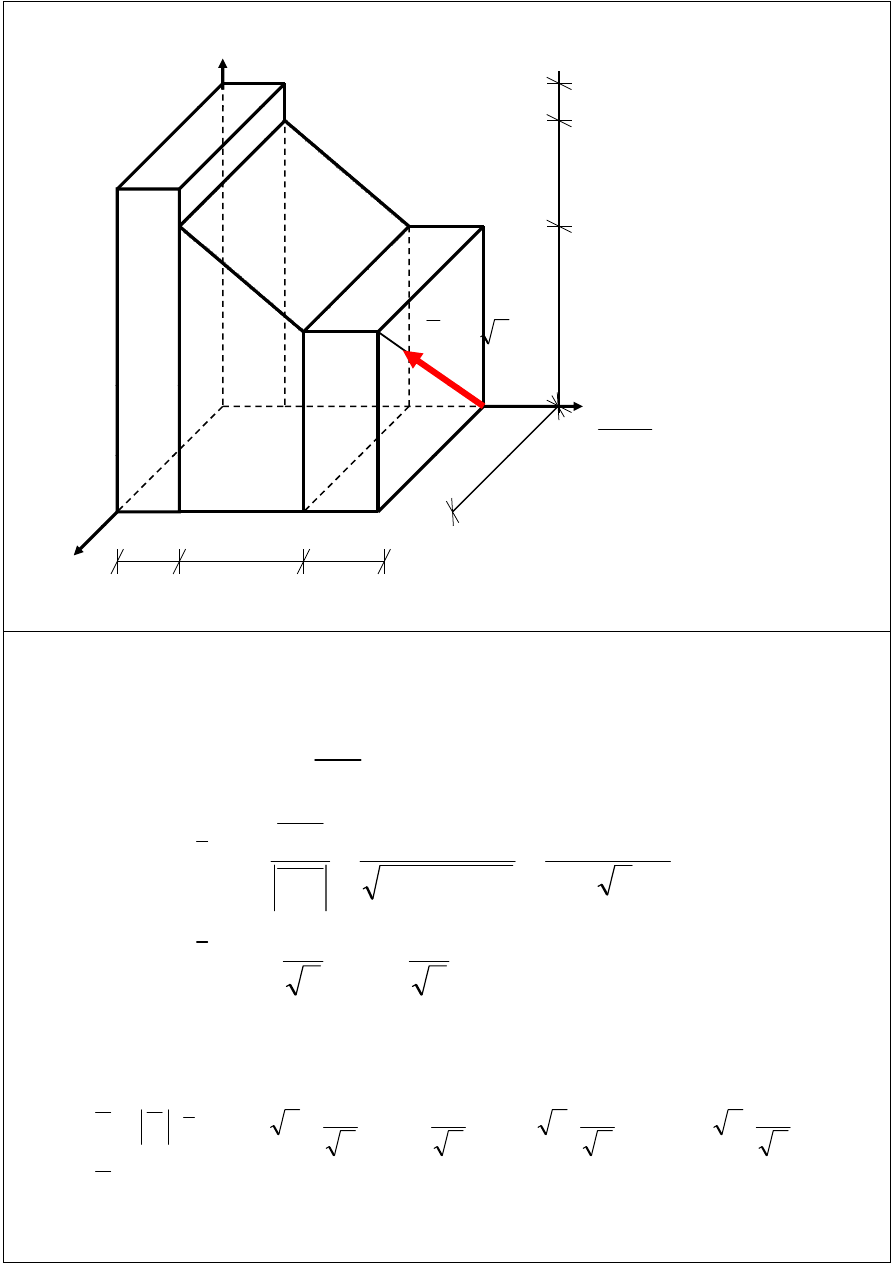
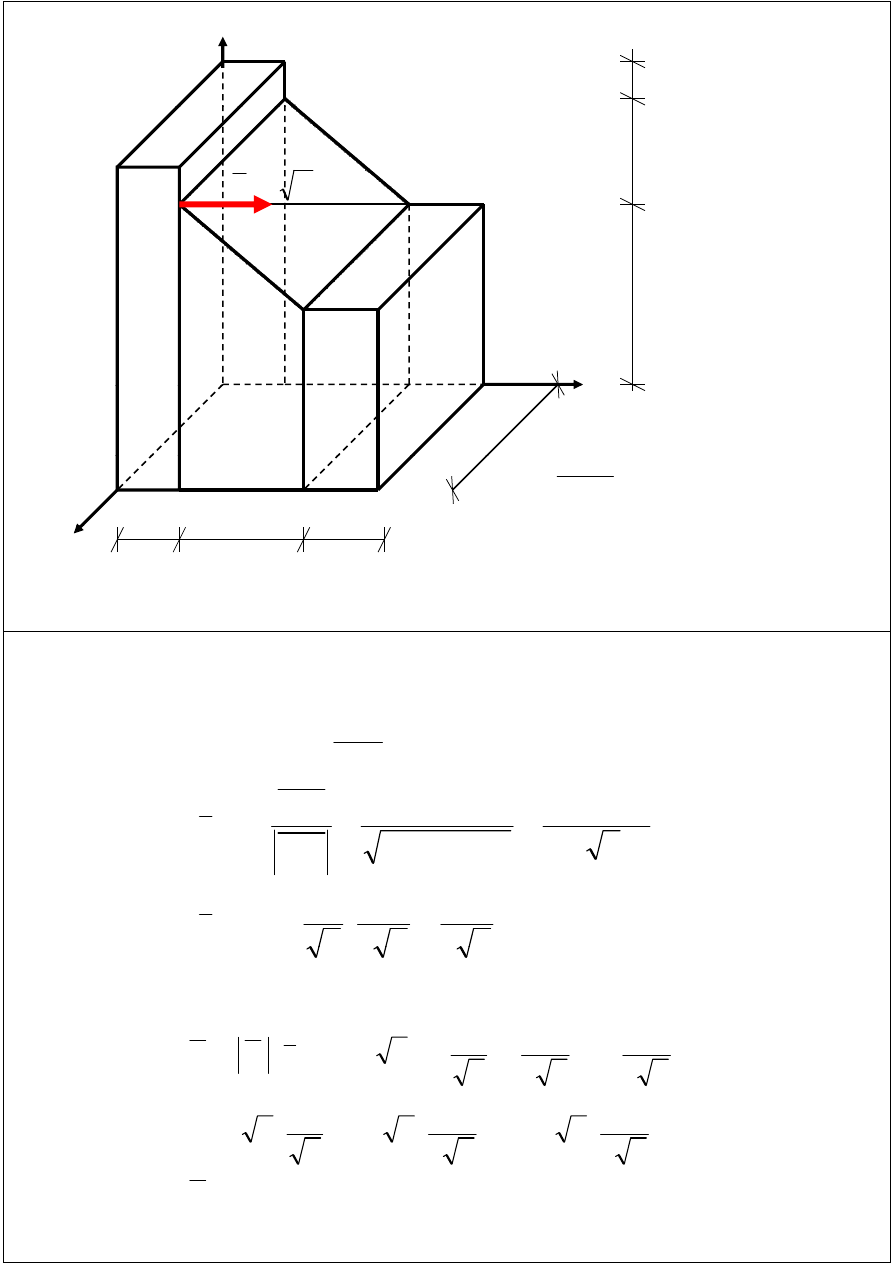
PRZYKŁAD

Dla podanego układu sił obliczyć:

PRZYKŁAD

Dla podanego układu sił obliczyć:
- sumę układu,

moment układu sił względem punktu A (z definicji)

- moment układu sił względem punktu A (z definicji)
- moment układu sił względem punktu B (z definicji
oraz z twierdzenia o zmianie bieguna)

oraz z twierdzenia o zmianie bieguna).

Zredukować podany układ do najprostszej postaci

Zredukować podany układ do najprostszej postaci.

z

5

F

10kN

5

A

1





9

,

0

,

5

A

G

3













5

,

7

,

0

,

,

B

A

4

F

kN

2

30

4

A

F

B









0

5

5

0

,

0

,

5

1

A

A

A

E

5









0

,

7

,

0

0

,

5

,

5

3

2

A

A

y

3

F

kN

2

25

3

A









9

1

0

8

,

1

,

5

4

A

A

20kN

5

C





9

,

1

,

0

5

A

F





0

0

20



F

1

A

2

F

15kN

2

A

D

1

F









0

,

15

,

0

0

,

0

,

20

2

1







F

F

x

4

1

2





0

,

0

,

10

5



F

z

11

33

A

E

5









5

7

5

0

,

7

,

0

3

E

A

3

F

kN

2

25

E

5





5

,

7

,

5

E

y

5





5

0

5



E

A

A

3

5





5

,

0

,

5

3



E

A

x

4

1

2

Wyznaczenie wersora kierunku A

3

E





5

,

0

,

5

3



E

A

y

3



 









2

5

5

,

0

,

5

5

,

0

,

5

3

2

2

2

3

E

A

E

A

E

A

e









1

1

2

5

5

0

5

2

2

2

3

E

A











2

1

,

0

,

2

1

3

E

A

e

Wyznaczenie wektora siły F

3

2

1

2

25

,

0

,

2

1

2

25

2

1

,

0

,

2

1

2

25

3

3

3































e

F

F

E

A





25

,

0

,

25

3











F

z

1

3

A

4

F

kN

2

30

F

B

 





8

,

1

,

5

4

A

A

A

4

5





5

,

5

,

0

F

yy

5

4

1

2





3

,

4

,

5

4







F

A

x

4

1

2

Wyznaczenie wersora kierunku A

4

F





3

,

4

,

5

4







F

A









3

4

5

3

4

5

F

A



























2

5

3

,

4

,

5

3

4

5

3

,

4

,

5

4

2

2

2

4

4

F

A

F

A

F

A

e















2

5

3

,

2

5

4

,

2

1

4

F

A

e





2

5

2

5

2

Wyznaczenie wektora siły F

4

2

5

3

,

2

5

4

,

2

1

2

30

4

4

4























e

F

F

F

A

y

y

4

2

5

3

2

30

,

2

5

4

2

30

,

2

1

2

30



























18

,

24

,

30

2

5

2

5

2

4










F

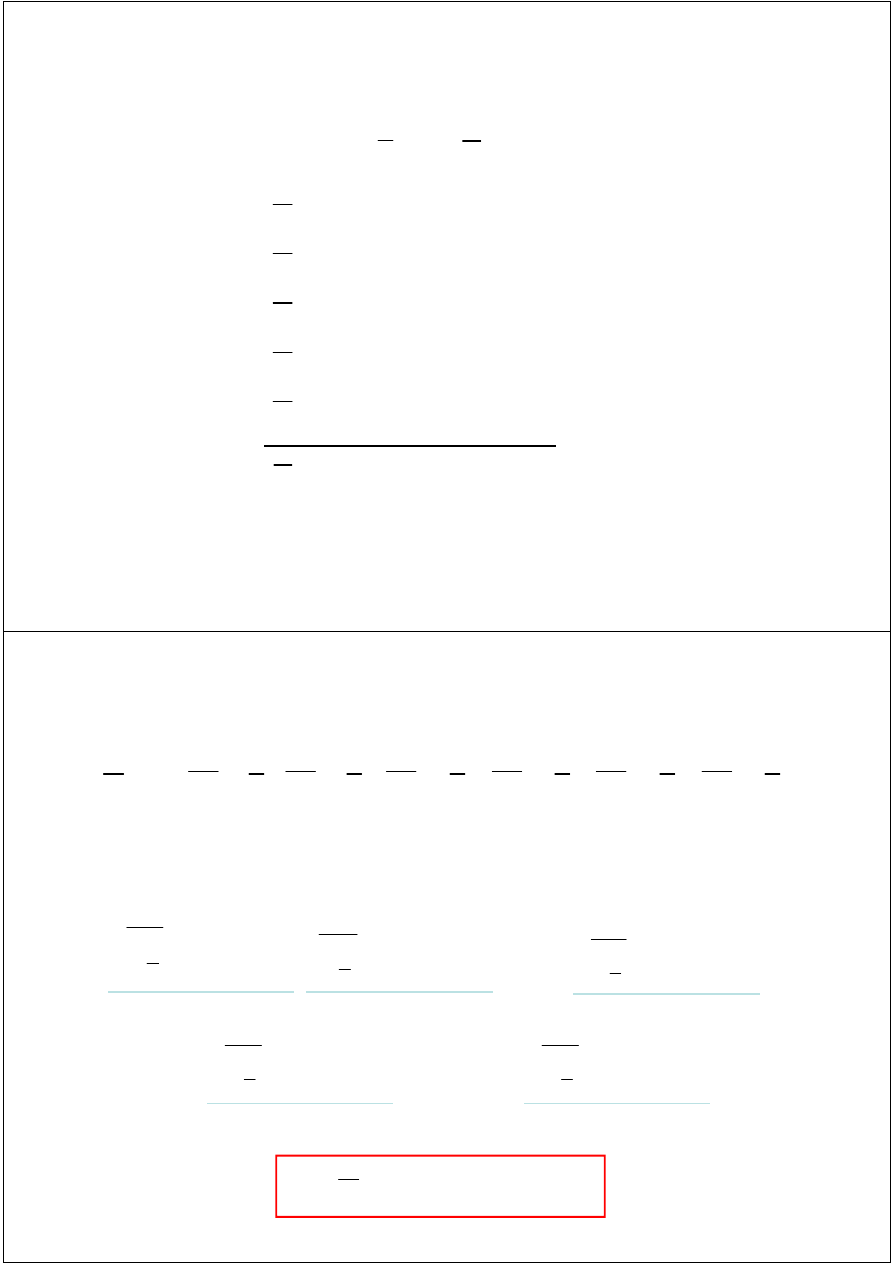
Wyznaczenie sumy układu





5

i

F

S

y

y





0

,

0

,

20

1





F



1

i









25

0

25

0

,

15

,

0

2



F

F









18

,

24

,

30

25

,

0

,

25

4

3









F

F









0

,

0

,

10

5



F





7

,

39

,

15





S

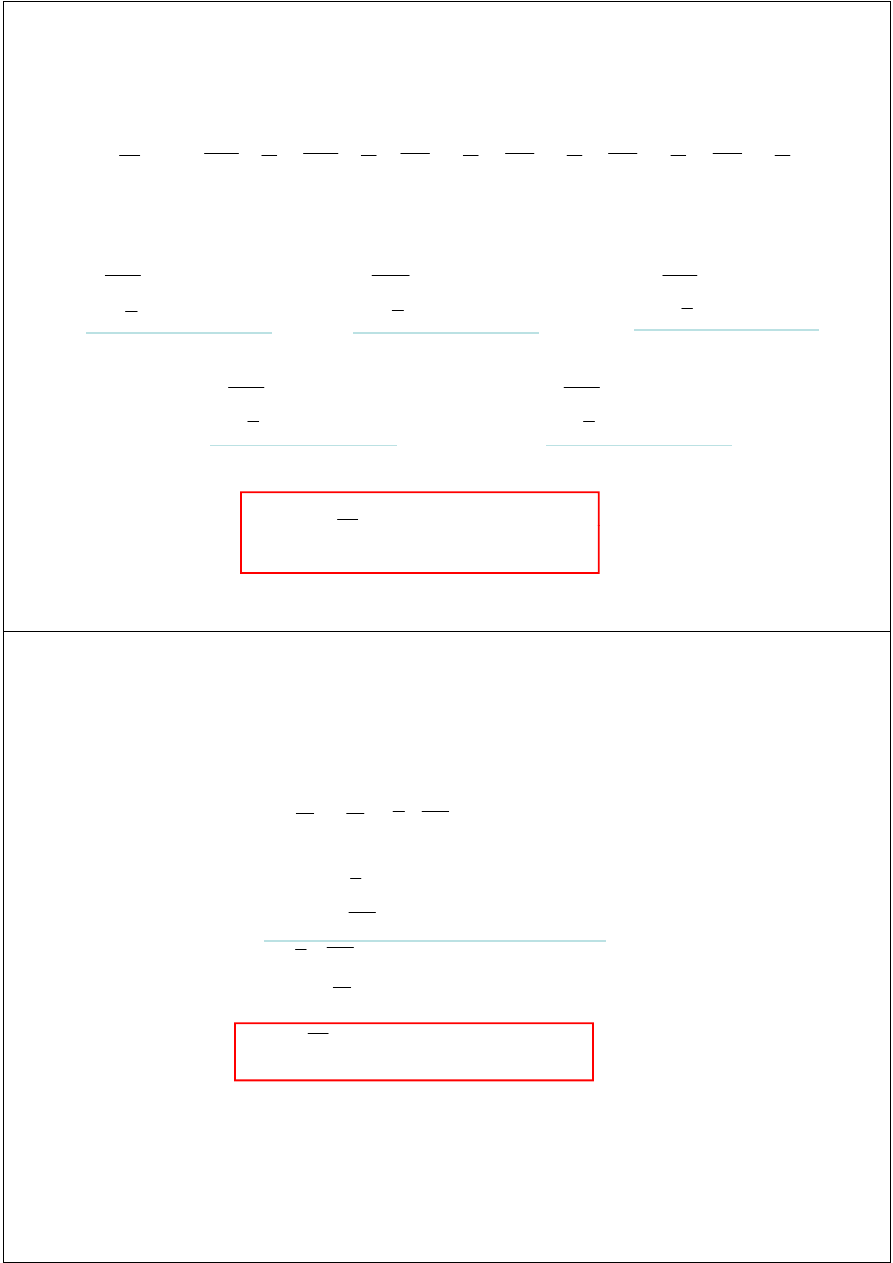
Wyznaczenie momentu względem punktu A

5

5

4

4

3

3

2

2

1

1

5

F

AA

F

AA

F

AA

F

AA

F

AA

F

AA

M

i

i

A



























y

g ę

1

i













 











9

,

1

,

0

8

,

1

,

5

0

,

7

,

0

0

,

5

,

5

0

,

0

,

5

9

,

0

,

5

5

4

3

2

1

A

A

A

A

A

A





9

;

0

;

0

AA

1









9

;

5

;

0

AA







9

7

5

AA











 























0

;

180

;

0

0

;

0

;

20

F

9

;

0

;

0

AA

1

1





















0

;

0

;

135

0

;

15

;

0

F

9

;

5

;

0

AA

2

2























175

;

100

;

175

25

;

0

;

25

F

9

;

7

;

5

AA

3

3

























0

;

0

;

135









18

24

30

F

1

;

1

;

0

AA

4









175

;

100

;

175









0

0

10

F

0

;

1

;

5

AA

5













30

;

30

;

6

18

;

24

;

30

F

4



















10

;

0

;

0

0

;

0

;

10

F

5













155

,

110

,

316





A

M

Wyznaczenie momentu względem punktu B

5

5

4

4

3

3

2

2

1

1

5

F

BA

F

BA

F

BA

F

BA

F

BA

F

BA

M

i

i

B



























y

g ę

5

5

4

4

3

3

2

2

1

1

1

i

i

i

B















 











9

1

0

8

1

5

0

7

0

0

5

5

0

0

5

5

7

0

5

4

3

2

1

A

A

A

A

A

B









0

0

20

F

5

;

7

;

5

BA

1















0

15

0

F

5

;

2

;

5

BA

2















25

;

0

;

25

F

5

;

0

;

0

BA

3

















 











9

,

1

,

0

8

,

1

,

5

0

,

7

,

0

0

,

5

,

5

0

,

0

,

5

5

,

7

,

0

5

4

3

2

1

A

A

A

A

A

B









140

;

100

;

0

0

;

0

;

20

F

1



















75

;

0

;

75

0

;

15

;

0

F

2















0

;

125

;

0

25

;

0

;

25

F

3





















60

0

36

18

;

24

;

30

F

3

;

6

;

5

BA

4

4

























60

40

0

0

;

0

;

10

F

4

;

6

;

0

BA

5

5













60

;

0

;

36









60

;

40

;

0







65

15

111

M





65

,

15

,

111





B

M

Wyznaczenie momentu względem

tw

punktu B z twierdzenia o zmianie bieguna





.







AB

S

M

M

A

tw

B









4

,

7

,

5

7

,

39

,

15









AB

S





90

,

95

,

205







 AB

S





155

110

316







A

M





65

,

15

,

111





B

M

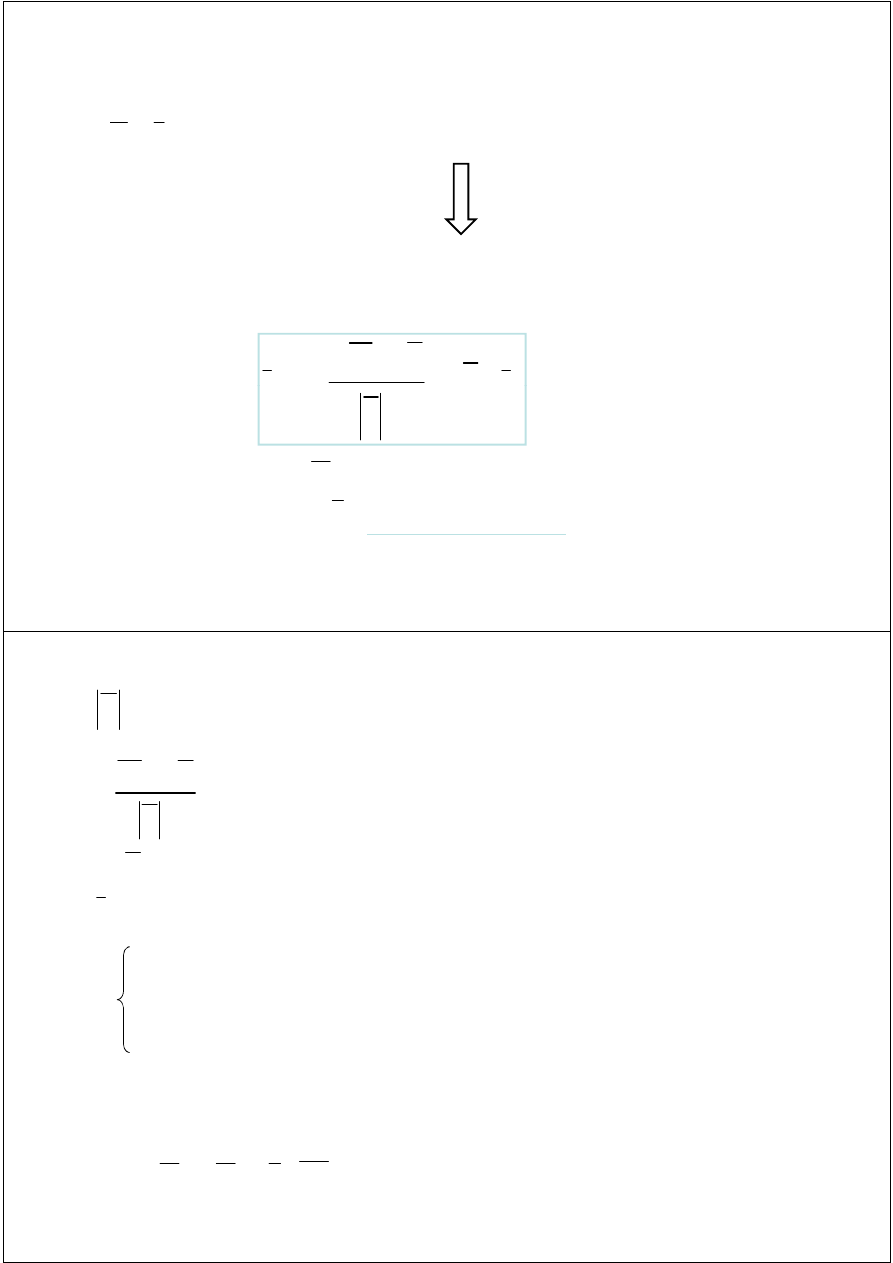
Wyznaczenie parametru układu

y

p



 



 





0

1535

7

155

39

110

15

316

7

;

39

;

15

155

;

110

;

316

































S

M

k

A

Równanie osi środkowej

Redukcja do skrętnika

 

A

r

S

S

M

r















j

 

A

2

r

S

S

r



















7

;

39

;

15

155

;

110

;

316










S

M

A









13974

;

113

;

6815



1795

7

39

15

S

2

2

2

2













785

,

7

;

063

,

0

;

797

,

3

S

M

2

A

















7

;

39

;

15

S

S

2





























9

;

0

;

5

r

;

;

A













































39

063

,

0

0

39

063

,

0

y

15

203

,

1

5

15

797

,

3

x

l:





















7

215

,

1

9

7

785

,

7

z





środkowej

osi

l

prostej

R

pkt





)

(

215

,

1

;

063

,

0

;

203

,

1

.

AR

S

M

M

A

R







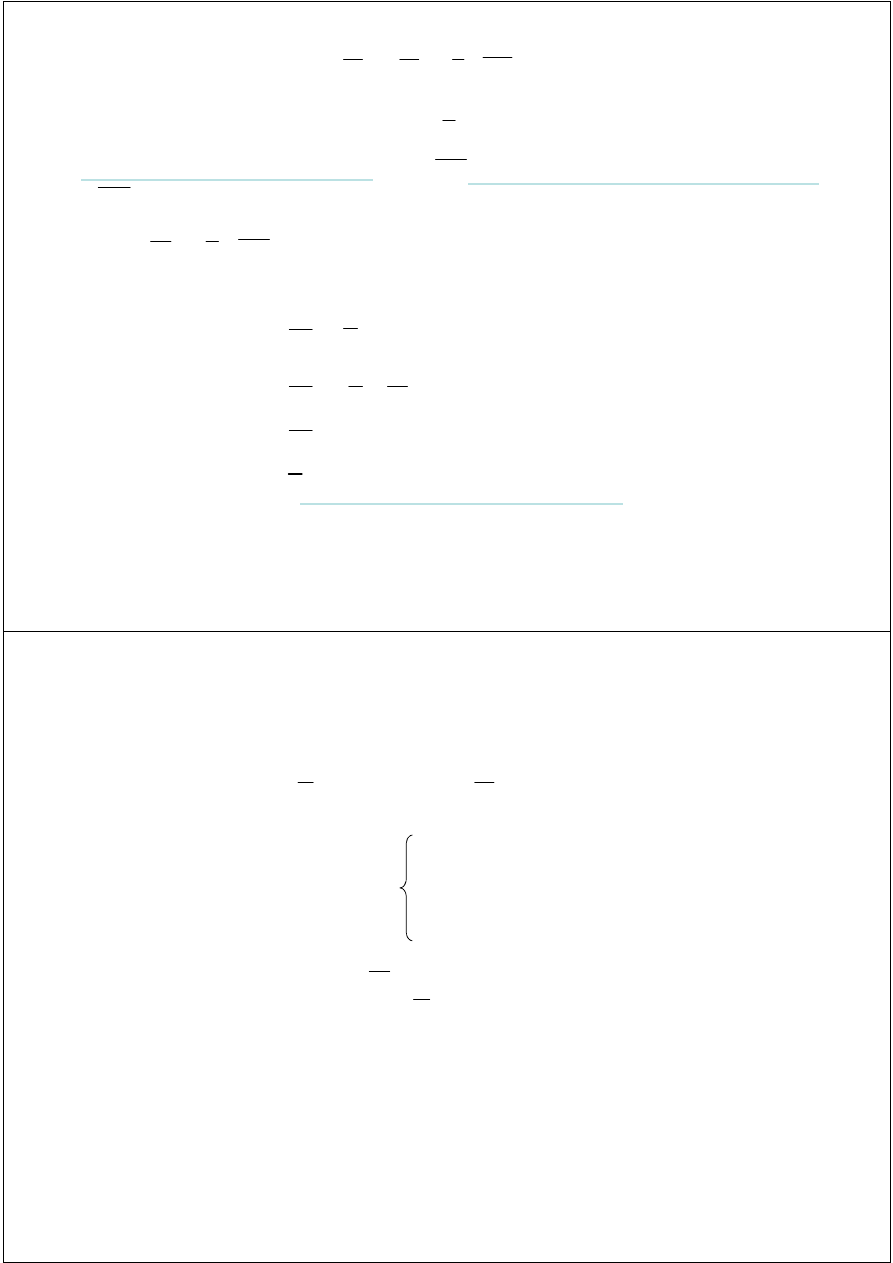
AR

S

M

M

A

R















785

7

;

063

0

;

797

3

7

;

39

;

15













AR

S











9

;

0

;

5

215

,

1

;

063

,

0

;

203

,

1



A

R









014

,

149

;

354

,

143

;

174

,

303

785

,

7

;

063

,

0

;

797

,

3









AR







785

,

7

;

063

,

0

;

797

,

3







AR



 



014

149

354

143

174

303

155

110

316

AR

S

M



 







972

,

5

;

354

.

33

;

826

,

12

014

,

149

;

354

,

143

;

174

,

303

155

;

110

;

316





















AR

S

M

A

Sprawdzenie

||

?

?

S

M

R





972

,

5

;

354

,

33

;

826

,

12









M

O

S

M

R

R













096

0

;

202

0

;

57

0

7

;

39

;

15

,

;

,

;

,



S

R







096

,

0

;

202

,

0

;

57

,

0







0



0



0



Odpowiedź:

Podany układ sił redukuje się do skrętnika złożonego z
wektora sumy





O

7

;

39

;

15

S















15

203

,

1

x

l





;

;

leżącego na osi środkowej



















7

215

,

1

39

063

,

0

z

y

l:

i pary sił o momencie
równoległym do wektora sumy





972

,

5

;

354

,

33

;

826

,

12

M

R







S

równoległym do wektora sumy

S

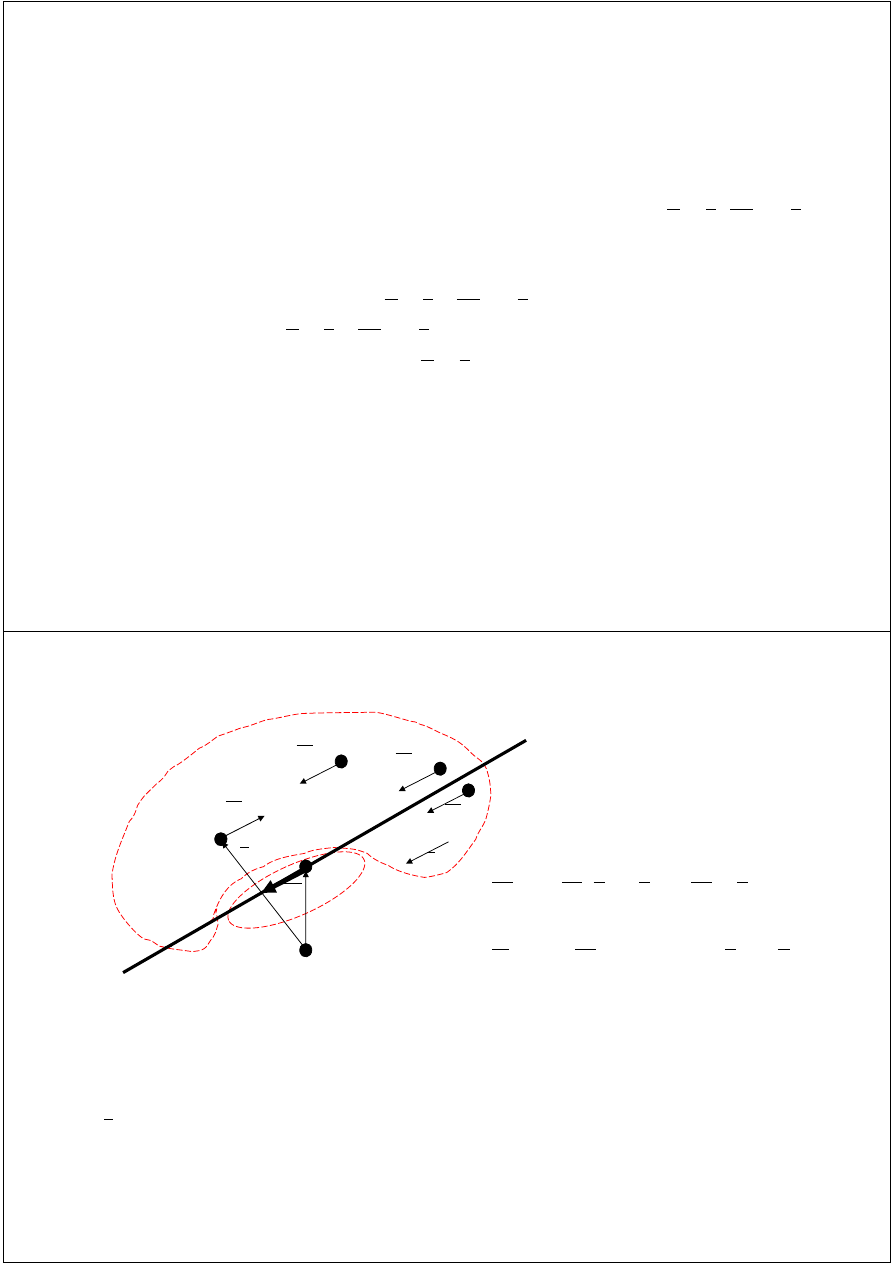
Równoległy układ sił,

ś d k ó

l

ł

kł d

ił

środek równoległego układu sił

Układ sił, w którym siły są równoległe do stałego kierunku,
nazywamy równoległym układem sił. Parametr takiego układu
jest zawsze równy zeru, co wynika z faktu, że przy
moment jest prostopadły do sumy A zatem równoległy układ sił

0

0





A

M

i

S

moment jest prostopadły do sumy. A zatem równoległy układ sił
redukuje się do:
1. układu zerowego, gdy

,

0

0







A

M

S

1. układu zerowego, gdy
2. pary sił, gdy
3. wypadkowej układu, gdy

,

0

0



A

M

S

,

0

0







A

M

S

.

0



S

A

A

prosta działania

2

A

n

A

1

A

1

F

2

F

F

F

prosta działania
wypadkowej

A

i

A

i

F

n

F

L

e

i

r

*

O





W

B

O





















n

n

l

i

l

l

i

i

e

F

e

e

F

F

B

O

0

1

1



























l

i

i

i

i

e

F

F

S

O- stały punkt odniesienia

- wersor osi l

L

e

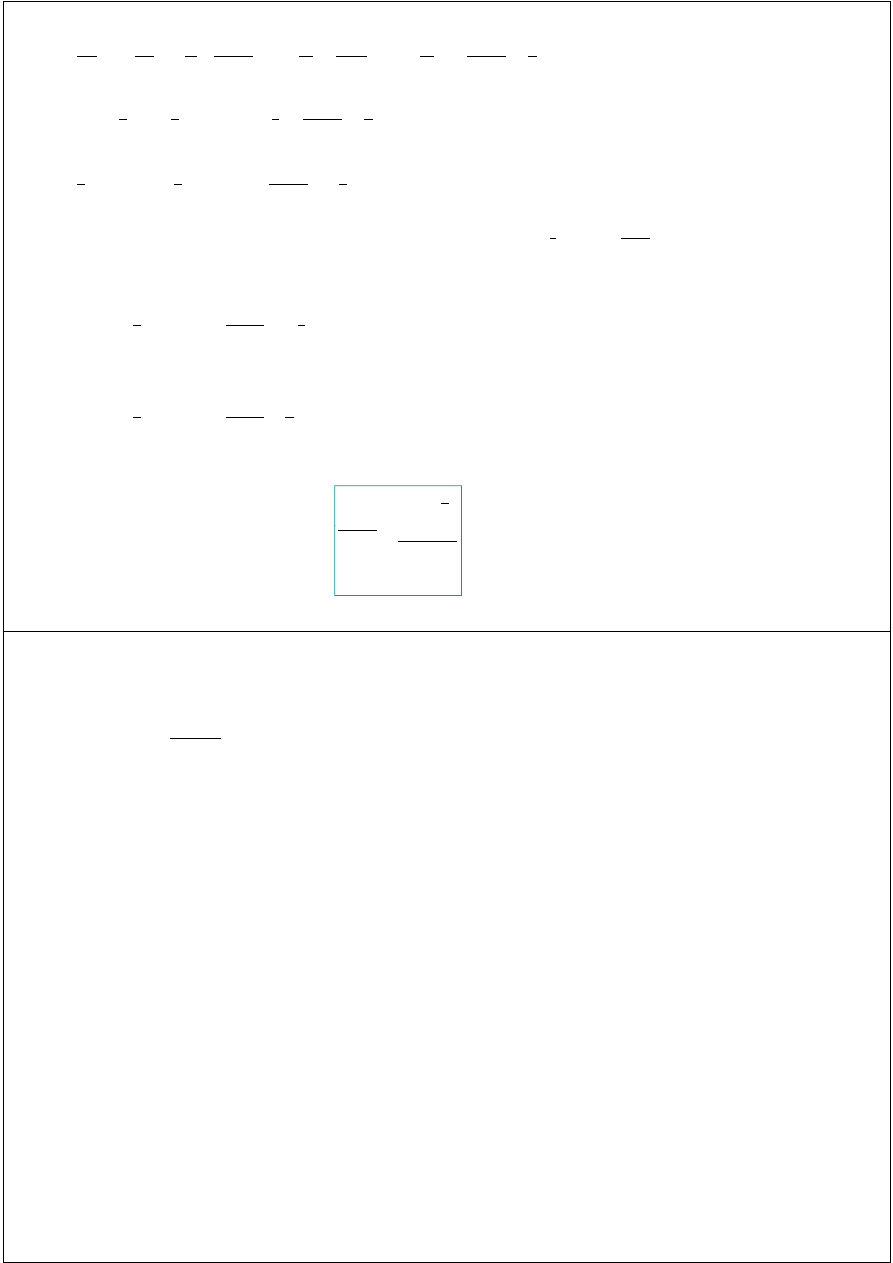
0

*

*

1

1

*









































OO

F

O

A

F

OO

S

M

M

n

i

i

i

n

i

i

O

O

 

0

*

1

1







































OO

e

F

r

e

F

n

n

l

n

i

i

i

l

n

i

i

0

*

1

1









































OO

F

r

F

e

n

i

n

i

i

i

i

l

Z tego związku wynika że wektor

























*

OO

F

r

F

n

n

i

Z tego związku wynika, że wektor
jest równoległy do prostej l, co można zapisać następująco

:





























1

1

OO

F

r

F

i

i

i

i

i





n

n

*

1

1



























e

OO

F

r

F

l

n

i

n

i

i

i

i



(równanie prostej l),

lub jest równy zeru:

0

*

1

1



























OO

F

r

F

n

i

n

i

i

i

i

lub jest równy zeru:

(nie zależy od kierunku l).

Stąd mamy:



n

i

i

r

F











n

i

i

i

F

OO

1

1

*

Wektor określa położenie punktu zwanego środkiem
równoległego układu sił. Środek ten ma następujące właściwości:

układ posiadający środek redukuje się w tym punkcie

*

OO

- układ posiadający środek redukuje się w tym punkcie

do wypadkowej,

- moment układu względem środka jest równy zeru,

o e t u adu

g ęde

ś od a jest ó

y e u,

- jeżeli w równoległym układzie sił posiadającym środek obrócimy

siły wokół punktów ich zaczepienia o ten sam kąt, to środek
układu nie zmieni swojego położenia.

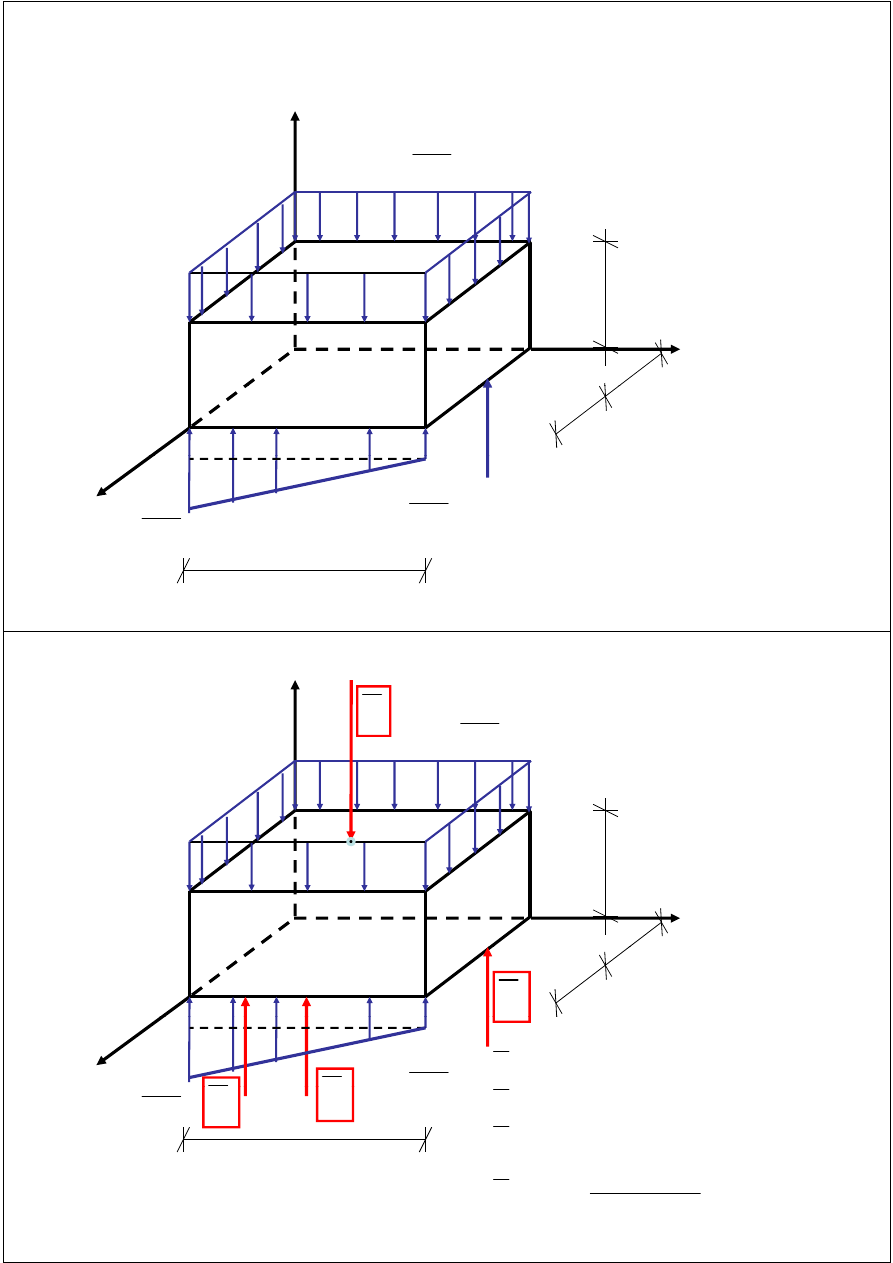
PRZYKŁAD: Wyznaczyć położenie środka zadanego układu
wektorów równoległych

z

2

20

m

kN

m

3

O

y

2

2

x

kN

200

kN

30

mb

kN

10

6

mb

30

mb

1

P

z





3

,

3

,

2

A

1

2

20

kN









0

3

4

A

0

,

6

,

2

A

2

2

m

1

A

3









0

,

2

,

4

A

0

,

3

,

4

A

4

3

O

2

A

1

y

2

kN

200

2

P

3

A

2

4

A

2

kN

200

P

x

b

kN

10



 



480

,

0

,

0

4

6

20

,

0

,

0

1













P

kN

30

3

P

4

P

6

mb









6

10

,

0

,

0

200

,

0

,

0

3

2







P

P

mb

30









60

,

0

,

0

2

6

10

30

,

0

,

0

4





















P

,

4

,

3

,

2

,

1

P

P

P

P

F



4

3

2

1

A

,

A

,

A

,

A





3

,

3

,

2

A

1



 



480

,

0

,

0

4

6

20

,

0

,

0

1













P













0

3

4

A

0

,

6

,

2

A

3

,

3

,

2

A

2

1



 











6

10

0

0

200

,

0

,

0

,

,

,

,

2

1



P

P









0

,

2

,

4

A

0

,

3

,

4

A

4

3













60

,

0

,

0

6

10

30

,

0

,

0

6

10

,

0

,

0

4

3





















P

P





4





60

,

0

,

0

2

,

0

,

0

4









P





0

160

0

0

P

S

4













:

A

O

r

0

160

,

0

,

0

P

S

i

i

i

1

i



















3

,

3

,

2

A

O

r

1

1













0

3

4

A

O

r

0

,

6

,

2

A

O

r

2

2

















0

,

2

,

4

A

O

r

0

,

3

,

4

A

O

r

4

4

3

3









i

P

i







1

,

0

,

0

e



:

F

F



 



:

e

F

F

i

i







 





 



200

1

,

0

,

0

200

,

0

,

0

F

480

1

,

0

,

0

480

,

0

,

0

F

2

1



















 





 



60

1

,

0

,

0

60

,

0

,

0

F

60

1

,

0

,

0

60

,

0

,

0

F

4

3













4



 



4

:

r

F

160

F

i

4

1

i











 



1440

1440

960

3

3

2

480

r

F

:

r

F

i

i



 





 





 



0

,

1200

,

400

0

,

6

,

2

200

r

F

1440

,

1440

,

960

3

,

3

,

2

480

r

F

2

2

1

1























 





 



0

,

120

,

240

0

,

2

,

4

60

r

F

0

,

180

,

240

0

,

3

,

4

60

r

F

4

4

3

3













4





1440

,

60

,

80

r

F

i

i

4

1

i











3

1

1

r

F

i

i

4















9

;

375

,

0

;

5

,

0

9

,

8

3

,

2

1

1440

,

60

,

80

160

1

F

r

F

O

O

i

4

1

i

i

i

1

i

*















 



















