Katedra Elektrotechniki Teoretycznej i Informatyki 

 

 

 

Przedmiot: Elektrotechnika teoretyczna 

 

Numer ćwiczenia: 

6 

 
Temat: Wyznaczanie parametrów czwórnika, 
połączenia czwórników 

 

 

 

I. Wprowadzenie 

Czwórnikiem  jest  element  o  czterech  zaciskach  posiadający  parę  zacisków  nazywanych 

wejściem i oznaczanych jako  I

1

  i  I

1

’  oraz  parę zacisków nazywanych wyjściem i oznaczanych 

jako I

2

 i I

2

’. Pomiędzy prądami zachodzą zależności: 

I

1

 = I

1

’ i I

2 

= I

2

’ 

Czwórniki możemy sklasyfikować na: 

a)  liniowe i nieliniowe 
b)  stacjonarne i niestacjonarne, 
c)  symetryczne i niesymetryczne, 
d)  odwracalne i nieodwracalne, 
e)  pasywne i aktywne. 

Związek pomiędzy wielkościami wejściowymi i wyjściowymi napięć U

1

 i U

2

 oraz prądu I

1

 

i  I

2 

dla  dowolnego  czwórnika  można  przedstawić  w  różny  sposób  za  pomocą  równań 

nazywanych równaniami czwórnika. Rozróżniamy sześć zasadniczych równań czwórnika: 

a)  impedancyjne: U

1

 i U

2

 są wyrażone w zależności od I

1

 i I

2

, 

b)  admitancyjne: I

1

 i I

2

 są wyrażone w zależności od U

1

 i U

2

, 

c)  łańcuchowe prosta: U

1

 i I

1

 są wyrażone w zależności od U

2

 i I

2

, 

d)  łańcuchowe odwrotne: U

2

 i I

2

 są wyrażone w zależności od U

1

 i I

1

, 

e)  hybrydowe: U

1

 i I

2

 są wyrażone w zależności od I

1

 i U

2

, 

f)  hybrydowe odwrotne: I

1

 i U

2

 są wyrażone w zależności od U

1

 i I

2

. 

 

Równania łańcuchowe 
Ogólna postać równań łańcuchowych dla dowolnego czwórnika jest postaci: 

2

2

1

1

I

U

D

C

B

A

I

U

, 

gdzie:  A,  B,  C  i  D  nazywane  są  parametrami  łańcuchowymi,  a  macierz 

D

C

B

A

A

macierzą parametrów łańcuchowych. 

W zależności od typu czwórników (T, Π, Γ

-1

) można napisać szczegółową postać macierzy 

łańcuchowej uwzględniającej wartości impedancji i admitancji danego czwórnika.  

 
Warunki symetrii czwórnika 
Czwórnik  nazywamy  symetrycznym  jeśli  przy  zmianie  miejscami  zacisków  wejścia  i 

wyjścia  nie  ulegnie  zmienię  rozpływ  prądów  i  rozkład  napięć  w  obwodzie  dołączonym  do 
czwórnika. 

Na podstawie równań łańcuchowych czwórnik spełnia warunki symetrii jeżeli: 

det A = 1 oraz A = D. 

 

Impedancja charakterystyczna (impedancja falowa) 
Impedancja  charakterystyczną  lub  falową  czwórnika  symetrycznego  nazywamy  taką 

impedancję Z

c

, która dołączona do zacisków wyjściowych czwórnika powoduje, że impedancja 

wejściowa jest jej równa: 

k

k

c

Z

Z

Z

Z

C

B

Z

2

20

1

10

, 

gdzie: Z

10

 i Z

20

 to impedancje w stanie jałowym odpowiednio wejściowa i wyjściowa, a Z

1k

 

i Z

2k

 to impedancje w stanie zwarcia odpowiednio wejściowa i wyjściowa. 

 

 

 II. Przebieg ćwiczenia 

Celem  ćwiczenia  jest  poznanie  metod  wyznaczania  parametrów  i  wielkości 

charakteryzujących liniowe czwórniki pasywne. 

 

 

 

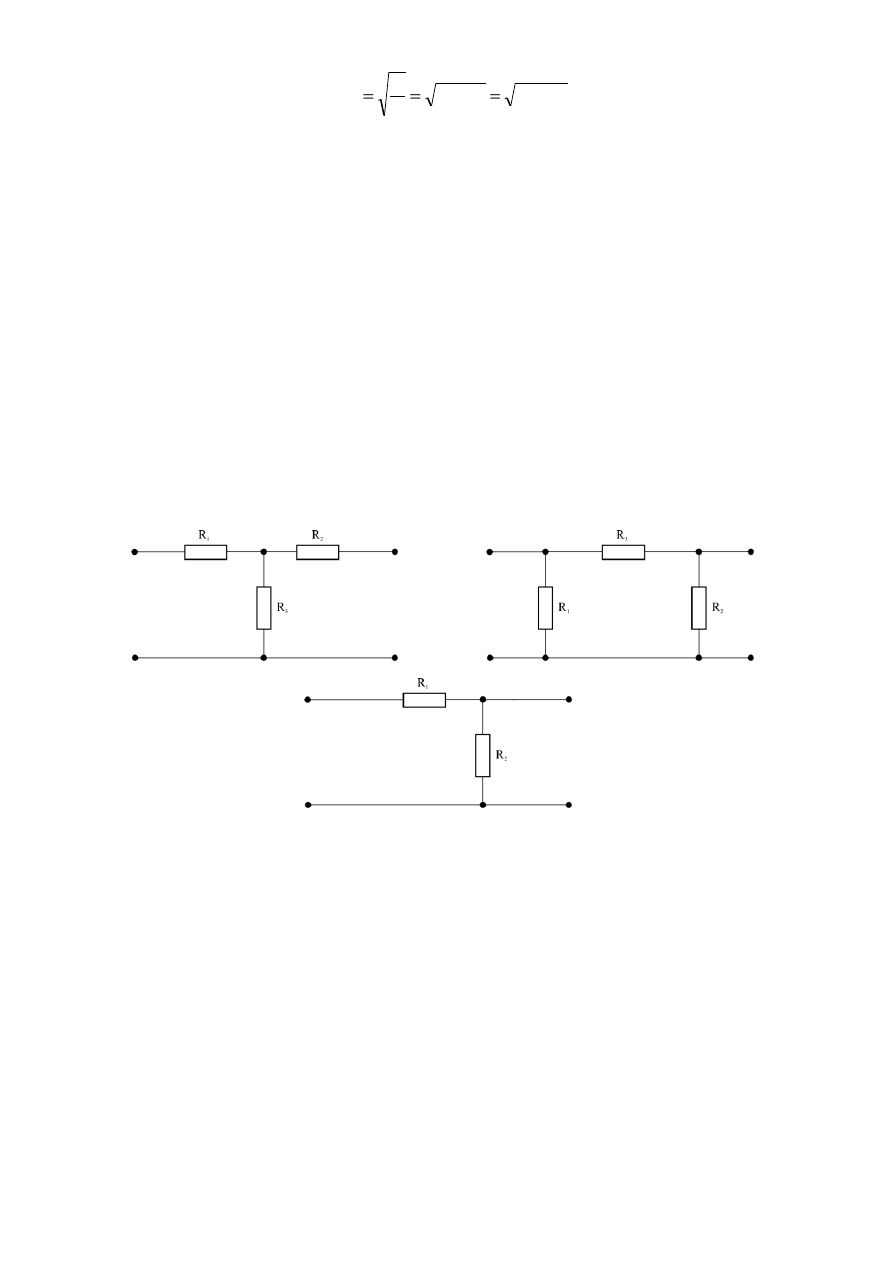
Zadanie I.   Wyznaczanie parametrów łańcuchowych czwórników typu T, Π oraz 

odwrócone Γ (rysunek 1).  

1.  Zmierzyć wartości poszczególnych elementów dla wszystkich typów czwórników. 
2.  Obliczyć parametry łańcuchowe wszystkich czwórników na podstawie wartości 

rezystancji zmierzonych w pkt. 1. 

3.  Wyniki dla poszczególnych czwórników zapisać w tabeli 1. w pola „obliczone”. 
4.  Na podstawie pomiarów obserwacji wielkości elektrycznych w różnych stanach pracy 

czwórników (rysunek 2.) określić ponownie ich parametry łańcuchowe i wpisać do 
tabeli 1. w pola „zmierzone”. 

5.  Uzyskane wartości porównać i zapisać wnioski. 

 
 
 

 

 
 
 
 
 
 

Zadanie II.   Analiza pracy czwórników. 

1.  Określić,  który  czwórnik  jest  symetryczny.  Dla  czwórników  symetrycznych  obliczyć 

impedancję  wejściową  w  stanie  jałowym  i  w  stanie  zwarcia  oraz  impedancję 
charakterystyczną czwórnika. 

2.  Obciążyć  czwórnik  impedancją  charakterystyczną.  Narysować  układ  pomiarowy 

pozwalający  zmierzyć  impedancję  wejściową  czwórnika,  połączyć  układ,  wykonać 
pomiary i zapisać wyniki w tabeli 2. 

3.  Przedstawić wnioski. 

 
 
 
 
 

a) 

b) 

c) 

Rysunek 1 Schematy czwórników wykorzystanych podczas realizacji ćwiczenia: a) typu T, b) typu Π c) typu 
odwrócone Γ.

 

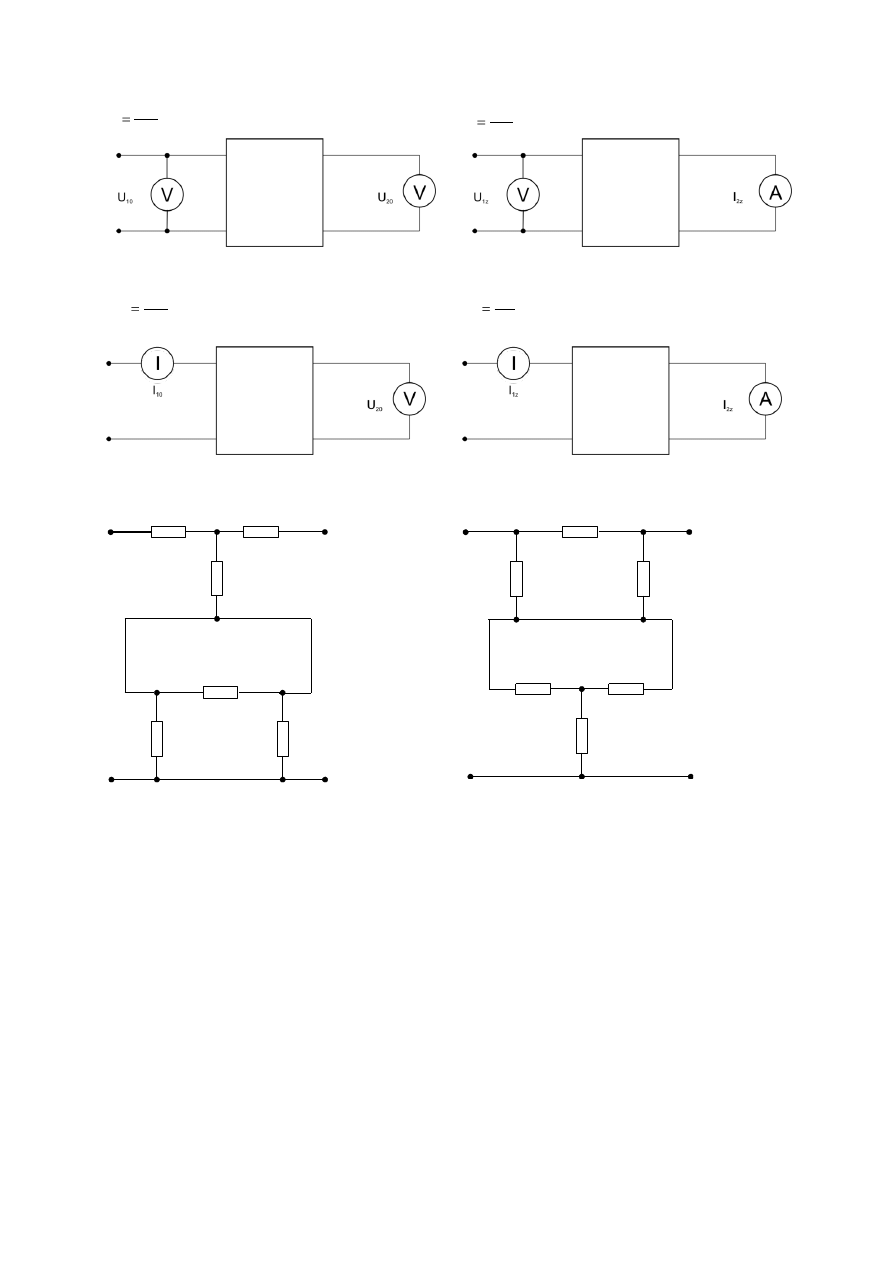
- układ do pomiaru parametru A 

 

 

 

 

- układ do pomiaru parametru B 

 
 

 

- układ do pomiaru parametru C 

 
 
 

 

- układ do pomiaru parametru D 

 
 
 

 

 

 

a) 

 

b) 

 

 

 

 

 

 

 
 

Zadanie III.   Łączenie czwórników 
1.  Połączyć czwórniki typu T i Π (o parametrach wyznaczonych na poprzednich 

ćwiczeniach) w następujący sposób: 

a)  kaskadowo (na wejściu czwórnik typu T), 
b)  kaskadowo (na wejściu czwórnik typu Π), 
c)  szeregowo (zgodnie z rysunek. 3a), 
d)  szeregowo  (zgodnie z rysunek 3b), 
e)  równolegle. 

2.  Dla wszystkich połączeń zmierzyć i obliczyć parametry łańcuchowe czwórników 

zastępczych. 

3.  Wyniki pomiarów i obliczeń przedstawić w tabeli 3. 

 

I.  Uwagi do sprawozdania 

Na  podstawie  przeprowadzonych  pomiarów  należy  wykonać  sprawozdanie  z  wykonanego 

ćwiczenia. W sprawozdaniu należy zawrzeć: 

1. Cel i metodykę ćwiczenia. 

1

2

z

z

U

B

I

10

20

I

C

U

1

2

z

z

I

D

I

10

20

U

A

U

Rysunek 2 Schematy układów pomiarowych umożliwiających określenie parametrów łańcuchowych czwórnika.

 

Rysunek 3 Połączenia szeregowe czwórników T i Π.

 

2. Schematy  układów  pomiarowych  wraz  z  dokładnym  opisem  elementów  układu  i 

parametrami urządzeń pomiarowych. 

3. Przedstawić wyniki pomiarowe w tabelach. 
4. Przeprowadzić  analizę  analityczną  układów  pomiarowych,  a  następnie  porównać 

wyniki obliczeń z wynikami uzyskanymi podczas pomiarów. 

5. Przeprowadzić dyskusję wyników pomiarowych i przedstawić wnioski. 

 

II.  Zagadnienia teoretyczne 

1. Omówić przebieg ćwiczenia: 

a. cel ćwiczenia, 
b. układy pomiarowe i sposób przeprowadzenia pomiarów. 

2. Równania czwórników typu T, Π oraz Γ.  
3. Parametry łańcuchowe czwórników T, Π oraz odwrócone Γ. 
4. Symetryczność i odwracalność czwórników. 
5. Impedancja charakterystyczna czwórników. 
6. Sposoby łączenia czwórników oraz metody określania parametrów wypadkowych. 
 

III. Literatura 

1.  M. Krakowski, Elektrotechnika teoretyczna, tom I Obwody liniowe i nieliniowe, 

PWN. 

2.  S. Bolkowski, Teoria obwodów elektrycznych, Wydawnictwa Naukowo-Techniczne, 

Warszawa, Wydanie V 

 

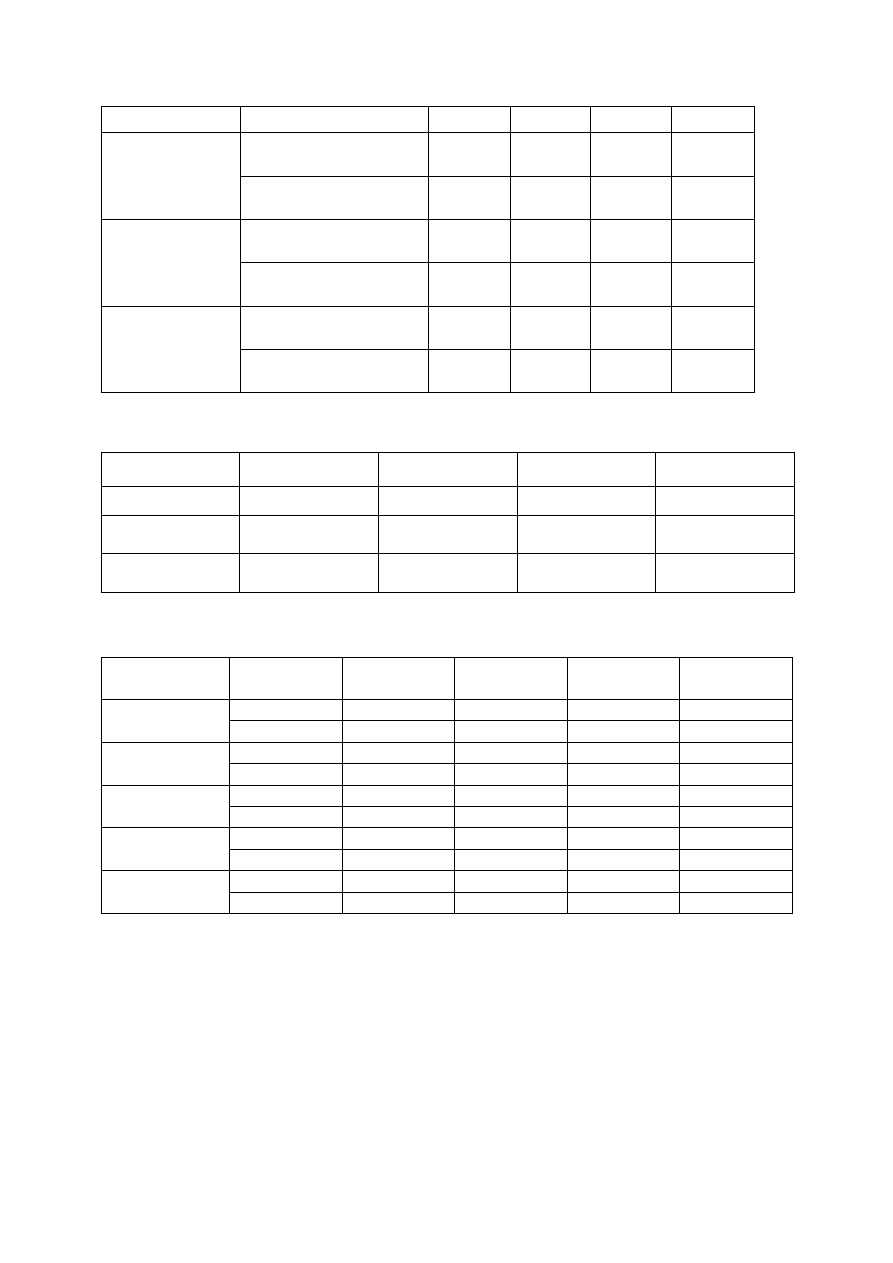
Tabela 1 Parametry łańcuchowe czwórników określone podczas pomiarów. 

typ czwórnika 

parametry łańcuchowe 

A 

B 

C 

D 

 

T 

obliczone 

 

 

 

 

zmierzone 

 

 

 

 

 

П 

obliczone 

 

 

 

 

zmierzone 

 

 

 

 

 

Γ

 

obliczone 

 

 

 

 

zmierzone 

 

 

 

 

 

 

Tabela 2 Określenie impedancji wejściowej czwórników symetrycznych  

typ czwórnika 

U

1

[V] 

I

1

 [mA] 

Z

zmierzone

 

Z

obliczone

 

T 

 

 

 

 

П 

 

 

 

 

Γ 

 

 

 

 

 
 

Tabela 3 Parametry łańcuchowe połączenia czwórników T i Π 

 

 
 
Podpis prowadzącego: 
 

Typ połączenia 

parametry 

łańcuchowe 

A 

B 

C 

D 

a 

zmierzone 

 

 

 

 

obliczone 

 

 

 

 

b 

zmierzone 

 

 

 

 

obliczone 

 

 

 

 

c 

zmierzone 

 

 

 

 

obliczone 

 

 

 

 

d 

zmierzone 

 

 

 

 

obliczone 

 

 

 

 

e 

zmierzone 

 

 

 

 

obliczone