Definicje i tolerancje odchy³ek kszta³tu i po³o¿enia
Uwagi ogólne do odchy³ek kszta³tu i po³o¿enia
T o l e r a n c j a k s z t a ³ t u i p o ³ o ¿ e n i a e l e m e n t u g e o m e -
t r y c z n e g o ( p o w i e r z c h n i a , o œ , p u n k t l u b p ³ a s z c z y z -
n a s y m e t r i i ) d e f i n i u j e przedzia³, w k t ó r y m m u s i s i ê
m i e œ c i æ k a ¿ d y p u n k t t e g o e l e m e n t u . W z a l e ¿ n o œ c i
o d t o l e r o w a n e j w ³ a œ c i w o œ c i i s p o s o b u w y m i a r o w a -
n i a przedzia³em tolerancji m o ¿ e b y æ :
•
p o w i e r z c h n i a o g r a n i c z o n a o k r ê g i e m ,
•
p o w i e r z c h n i a m i ê d z y d w o m a w s p ó ³ œ r o d k o w y m i
o k r ê g a m i ,
•
p o w i e r z c h n i a m i ê d z y d w o m a p r o s t y m i r ó w n o -
l e g ³ y m i ,
•
p o w i e r z c h n i a m i ê d z y d w o m a l i n i a m i r ó w n o o d -
l e g ³ y m i ,
•
p r z e s t r z e ñ m i ê d z y d w o m a p ³ a s z c z y z n a m i r ó w -
n o l e g ³ y m i ,
•
p r z e s t r z e ñ m i ê d z y d w o m a p ³ a s z c z y z n a m i r ó w -
n o o d l e g ³ y m i ,
•
p r z e s t r z e ñ m i ê d z y d w o m a p ³ a s z c z y z n a m i r ó w -
n o o d l e g ³ y m i ,
•
p r z e s t r z e ñ o g r a n i c z o n a w a l c e m ,
•
p r z e s t r z e ñ m i ê d z y d w o m a w s p ó ³ o s i o w y m i w a l -
c a m i ,
•
p r z e s t r z e ñ o g r a n i c z o n a p r o s t o p a d ³ o œ c i a n e m .
D l a tolerancji po³o¿enia w y m a g a n e j e s t p o d a n i e
odniesienia, k t ó r e p o d a j e d o k ³ a d n e p o ³ o ¿ e n i e
p r z e d z i a ³ u t o l e r a n c j i . O d n i e s i e n i e m j e s t t e o r e -
t y c z n i e d o k ³ a d n y e l e m e n t g e o m e t r y c z n y ( n p . o œ ,
p ³ a s z c z y z n a , l i n i a p r o s t a i t d . ) . O d n i e s i e n i e m o ¿ e
b a z o w a æ n a j e d n y m l u b k i l k u e l e m e n t a c h o d n i e -
s i e n i a .
Element tolerowany m o ¿ e w p r z e d z i a l e t o l e r a n c j i
p r z y j m o w a æ d o w o l n y k s z t a ³ t , d o w o l n e p o ³ o ¿ e n i e
o r a z d o w o l n y k i e r u n e k , c h y b a ¿ e z o s t a n ¹ p o d a n e
d o d a t k o w e o g r a n i c z e n i a .
D l a wartoœci tolerancji
t
o b o w i ¹ z u j e t a s a m a j e d -
n o s t k a , j a k d l a w y m i a r u d ³ u g o œ c i . J e œ l i n i e p o -
d a n o i n a c z e j t o l e r a n c j a o b o w i ¹ z u j e n a c a ³ e j
d ³ u g o œ c i l u b p o w i e r z c h n i t o l e r o w a n e g o e l e m e n t u .
žžžžž
•••
žžžžž
œœœ
žžžžž
PROSTOLINIOWOή
I S O 1 1 0 1
P£ASKOŒÆ
I S O 1 1 0 1
t
0 , 1
0 , 1 / 2 0 0
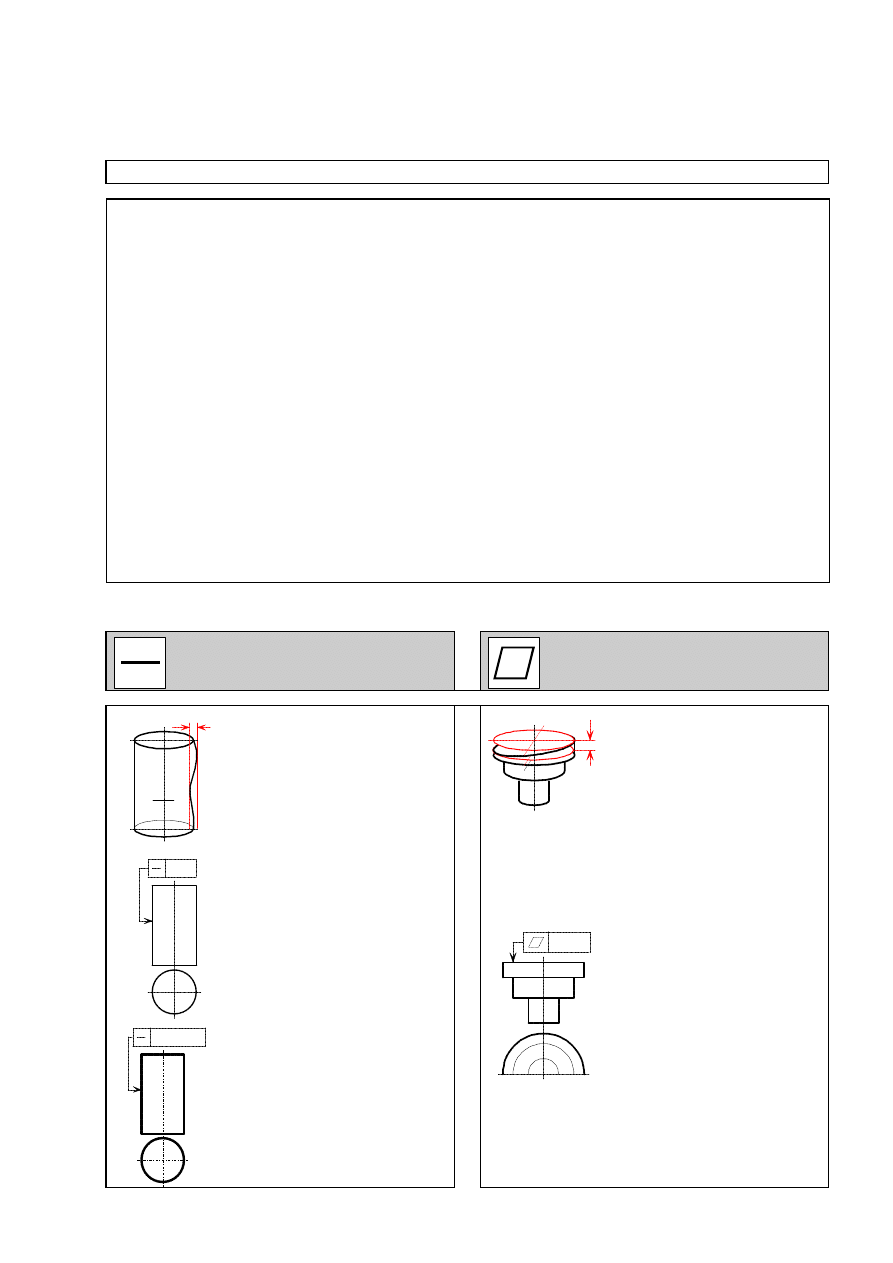
Definicja
P r z e d z i a ³ t o l e r a n c j i j e s t o g r a -
n i c z o n y w p ³ a s z c z y Ÿ n i e p o -
m i a r u d w o m a r ó w n o l e g ³ y m i l i -
n i a m i p r o s t y m i l e ¿ ¹ c y m i w o d -
l e g ³ o œ c i
t
o d s i e b i e .
Przyk³ady
K a ¿ d a t w o r z ¹ c a t o l e r o w a n e j
p o w i e r z c h n i w a l c o w e j m u s i l e -
¿ e æ p o m i ê d z y d w o m a p r o s t y -
m i o d l e g ³ y m i o d s i e b i e o 0 , 1 .
D o w o l n y o d c i n e k d ³ u g o œ c i 2 0 0
d o w o l n e j t w o r z ¹ c e j t o l e r o w a -
n e j p o w i e r z c h n i w a l c o w e j m u s i
l e ¿ e æ p o m i ê d z y d w o m a r ó w -
n o l e g ³ y m i p r o s t y m i o d l e g ³ y m i
o d s i e b i e o 0 , 1 .
Wskazówka:
D a l s z e t o l e r a n c j e p r o s t o l i n i o -
w o œ c i p a t r z D I N I S O 1 1 0 1 .
t
0 , 0 8
Definicja
P r z e d z i a ³ t o l e r a n c j i j e s t o g r a -
n i c z o n y d w o m a r ó w n o l e g ³ y m i
p l a s z c z y z n a m i l e ¿ ¹ c y m i o d
s i e b i e w o d l e g ³ o œ c i
t.
Przyk³ad
T o l e r o w a n a p o w i e r z c h n i a m u -
s i l e ¿ e æ p o m i ê d z y d w o m a r ó w -
n o l e g ³ y m i p ³ a s z c z y z n a m i o d -
l e g ³ y m i o d s i e b i e o 0 , 0 8 .
−
2
−
OKR¥G£OŒÆ
I S O 1 1 0 1
WALCOWOή
I S O 1 1 0 1
t
0 , 1
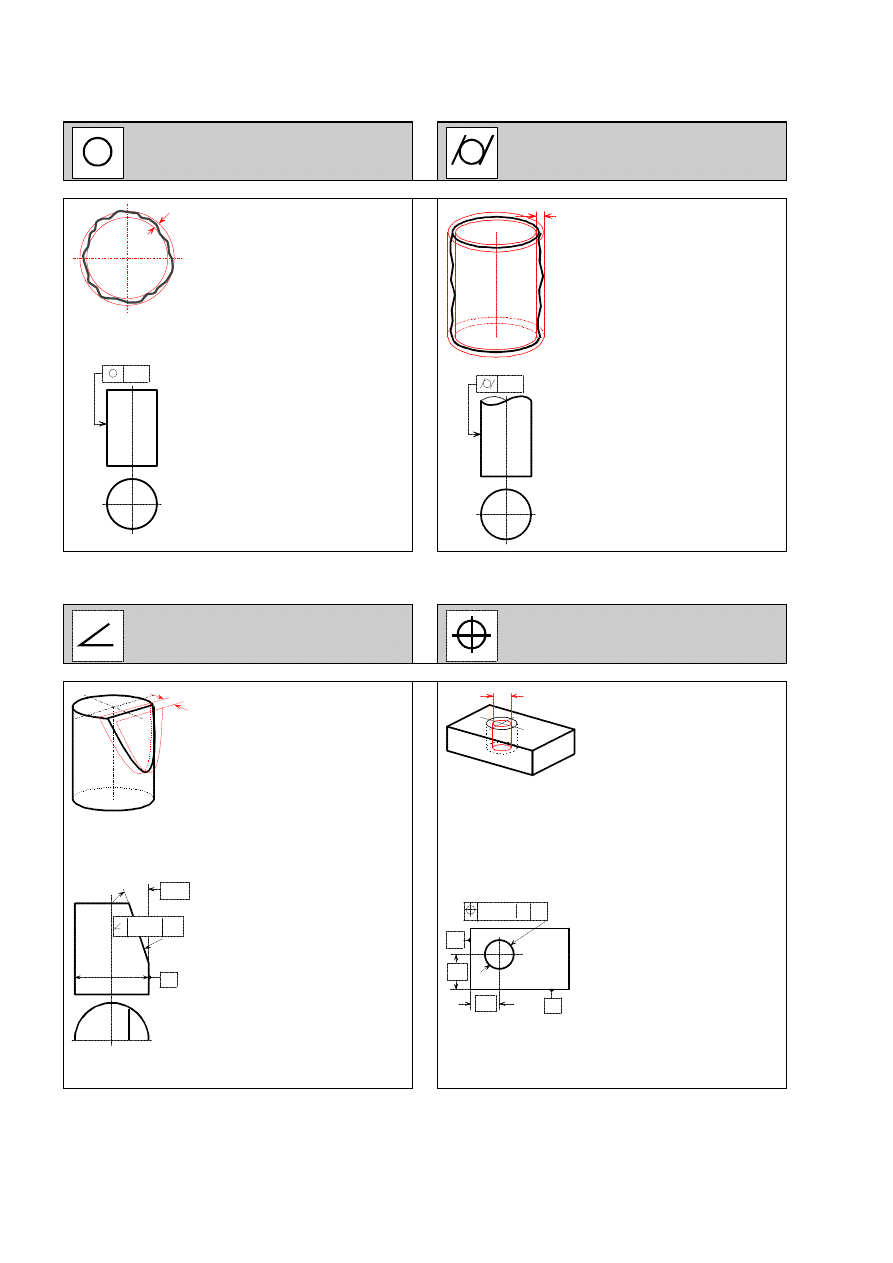
Definicja
P r z e d z i a ³ t o l e r a n c j i j e s t w p ³ a -
s z c z y Ÿ n i e p o m i a r u p r o s t o p a -
d ³ e j d o o s i o g r a n i c z o n y d w o -
m a o k r ê g a m i w s p ó ³ œ r o d k o w y -
m i l e ¿ ¹ c y m i w o d l e g ³ o œ c i
t
o d
s i e b i e .
Przyk³ad
Linia obwodu w dowolnym
przekroju tolerowanej powierz-
chni walcowej musi lezec po-
miedzy dwoma wspólsrodko-
wymi okregami odleglymi od
siebie o 0,1.
t
0 , 1
Definicja
P r z e d z i a ³ t o l e r a n c j i j e s t o g r a -
n i c z o n y d w o m a w s p ó ³ o s i o w y -
m i w a l c a m i o k r ê g a m i l e ¿ ¹ c y -
m i w o d l e g ³ o œ c i
t
o d s i e b i e .
Przyk³ad
T o l e r o w a n a p o w i e r z c h n i a w a l -
c o w a m u s i l e ¿ e æ p o m i ê d z y
d w o m a w s p ó ³ o s i o w y m i w a l c a -
m i o d l e g ³ y m i o d s i e b i e o 0 , 1 .
NACHYLENIE
I S O 1 1 0 1
POZYCJA
I S O 1 1 0 1
t
12 °
A
0,05 A
Definicja
P r z e d z i a ³ t o l e r a n c j i j e s t o g r a -
n i c z o n y d w o m a r ó w n o l e g ³ y m i
p ³ a s z c z y z n a m i l e ¿ ¹ c y m i w o d -
l e g ³ o œ c i
t
o d s i e b i e i n a c h y l o -
n y m i d o p ³ a s z c z y z n y o d n i e s i e -
n i a p o d w y z n a c z o n y m k ¹ t e m .
Przyk³ad
T o l e r o w a n a p o w i e r z c h n i a m u -
s i l e ¿ e æ p o m i ê d z y d w o m a r ó w -
n o l e g ³ y m i p ³ a s z c z y z n a m i o d l e -
g ³ y m i o 0 , 0 5 o d s i e b i e , k t ó r e
s ¹ n a c h y l o n e p o d k ¹ t e m 1 2
°
d o o s i o d n i e s i e n i a A.
t
1 0
2 0
A
A
B
B
0,02
∅
Definicja
J e ¿ e l i w a r t o œ æ t o l e r a n c j i j e s t
p o p r z e d z o n a z n a k i e m
∅
,
w ó w c z a s p r z e d z i a ³ t o l e r a n c j i
j e s t o g r a n i c z o n y p o w i e r z -
c h n i ¹ w a l c a o œ r e d n i c y
t
,
k t ó r e g o o œ p o k r y w a s i ê z t e -
o r e t y c z n i e d o k ³ a d n y m p o ³ o -
¿ e n i e m l i n i i t o l e r o w a n e j .
Przyk³ad
O œ t o l e r o w a n e g o o t w o r u
m u s i l e ¿ e æ w e w n ¹ t r z w a l c a
o œ r e d n i c y 0 , 0 2 , k t ó r e g o o œ
p o k r y w a s i ê z t e o r e t y c z n i e
d o k ³ a d n y m p o ³ o ¿ e n i e m l i n i i
t o l e r o w a n e j w z g l ê d e m p o -
w i e r z c h n i A i B.
Uwaga:
T o l e r a n c j a s y m e t r i i l i n i i l u b
o s i p a t r z D I N I S O 1 1 0 1 .
−
3
−
PROFIL LINII
I S O 1 1 0 1
PROFIL POWIERZCHNI
I S O 1 1 0 1
t
0 , 0 4
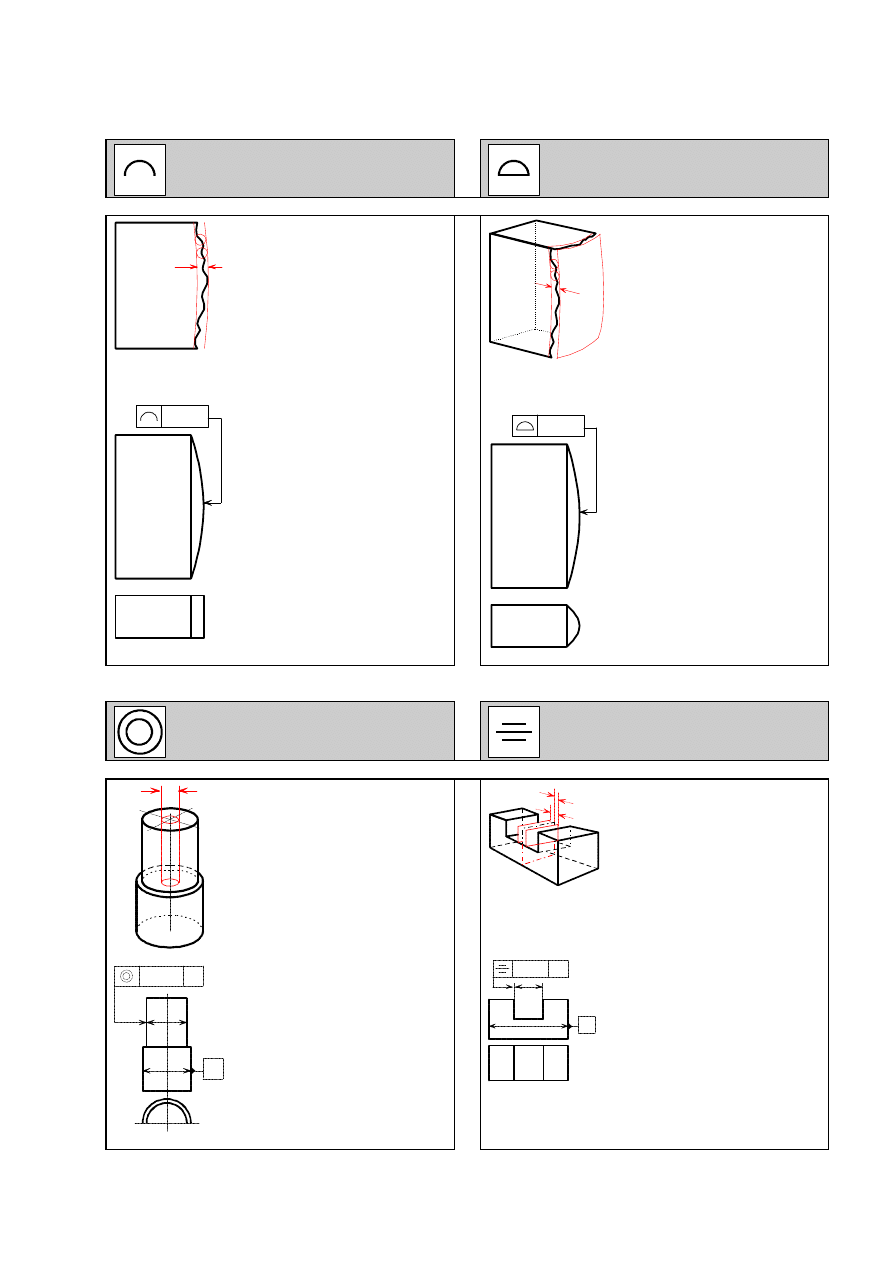
Definicja
P r z e d z i a ³ t o l e r a n c j i j e s t o g r a -
n i c z o n y p r z e z d w i e l i n i e , s t y -
c z n e d o o k r ê g ó w o œ r e d n i c y
t
,
k t ó r y c h œ r o d k i l e ¿ ¹ n a l i n i i o
i d e a l n y m k s z t a ³ c i e
g e o m e -
t r y c z n y m
Przyk³ad
W k a ¿ d y m p r z e k r o j u r ó w n o -
l e g ³ y m d o p ³ a s z c z y z n y r y s u n -
k u t o l e r o w a n y p r o f i l m u s i l e -
¿ e æ p o m i ê d z y d w o m a l i n i a m i
s t y c z n y m i d o o k r ê g ó w o œ r e d -
n i c y 0 , 0 4 , k t ó r y c h œ r o d k i l e ¿ ¹
n a l i n i i o i d e a l n y m k s z t a ³ c i e
g e o m e t r y c z n y m .
t
0 , 0 2
Definicja
P r z e d z i a ³ t o l e r a n c j i j e s t o g r a -
n i c z o n y p r z e z d w i e p o w i e r z -
c h n i e , s t y c z n e d o k u l o œ r e d -
n i c y
t
, k t ó r y c h œ r o d k i l e ¿ ¹ n a
p o w i e r z c h n i o i d e a l n y m k s z t a ³ -
c i e g e o m e t r y c z n y m .
Przyk³ad
R o z p a t r y w a n a p o w i e r z c h n i a
m u s i l e ¿ e æ p o m i ê d z y d w o m a
p o w i e r z c h n i a m i s t y c z n y m i d o
k u l o œ r e d n i c y
t
, k t ó r y c h œ r o d k i
l e ¿ ¹ n a p o w i e r z c h n i o i d e a l -
n y m k s z t a ³ c i e
g e o m e t r y c z -
n y m .
WSPÓ£ŒRODKOWOŒÆ
WSPÓ£OSIOWOŒÆ
I S O 1 1 0 1
SYMETRIA
I S O 1 1 0 1
t
A
A
0,08
∅
Definicja
P r z e d z i a ³ t o l e r a n c j i s t a n o w i
w a l e c o œ r e d n i c y
t
, k t ó r e g o o œ
p o k r y w a s i ê z l i n i ¹ o d n i e s i e -
n i a .
Przyk³ad ( w s p ó ³ o s i o w o œ æ )
O œ t o l e r o w a n e g o w a l c a m u s i
l e ¿ e æ w e w n ¹ t r z w a l c a o œ r e d -
n i c y 0 , 0 8 k t ó r e g o o œ p o k r y w a
s i ê z o s i ¹ o d n i e s i e n i a A.
Uwaga:
T o l e r a n c j a w s p ó ³ œ r o d k o w o œ c i
p a t r z D I N I S O 1 1 0 1 .
t
t/2
A
A
0,08
Definicja
P r z e d z i a ³ t o l e r a n c j i j e s t o g r a -
n i c z o n y d w o m a p ³ a s z c z y z n a -
m i o d l e g ³ y m i o
t
, l e ¿ ¹ c y m i
s y m e t r y c z n i e w z g l ê d e m o s i
l u b p ³ a s z c z y z n y o d n i e s i e n i a .
Przyklad
P ³ a s z c z y z n a œ r o d k o w a r o w k a
m u s i l e ¿ e æ p o m i ê d z y d w o m a
r ó w n o l e g ³ y m i p ³ a s z c z y z n a m i
o d l e g ³ y m i o 0 , 0 8 , k t ó r e s ¹ s y -
m e t r y c z n e w z g l ê d e m œ r o d k o -
w e j p ³ a s z c z y z n y e l e m e n t u o d -
n i e s i e n i a A.
Uwaga:
T o l e r a n c j a s y m e t r i i l i n i i l u b o s i
p a t r z D I N I S O 1 1 0 1 .
−
4
−
RÓWNOLEG£OŒÆ
I S O 1 1 0 1
PROSTOPAD£OŒÆ
I S O 1 1 0 1
t
0 , 1
A
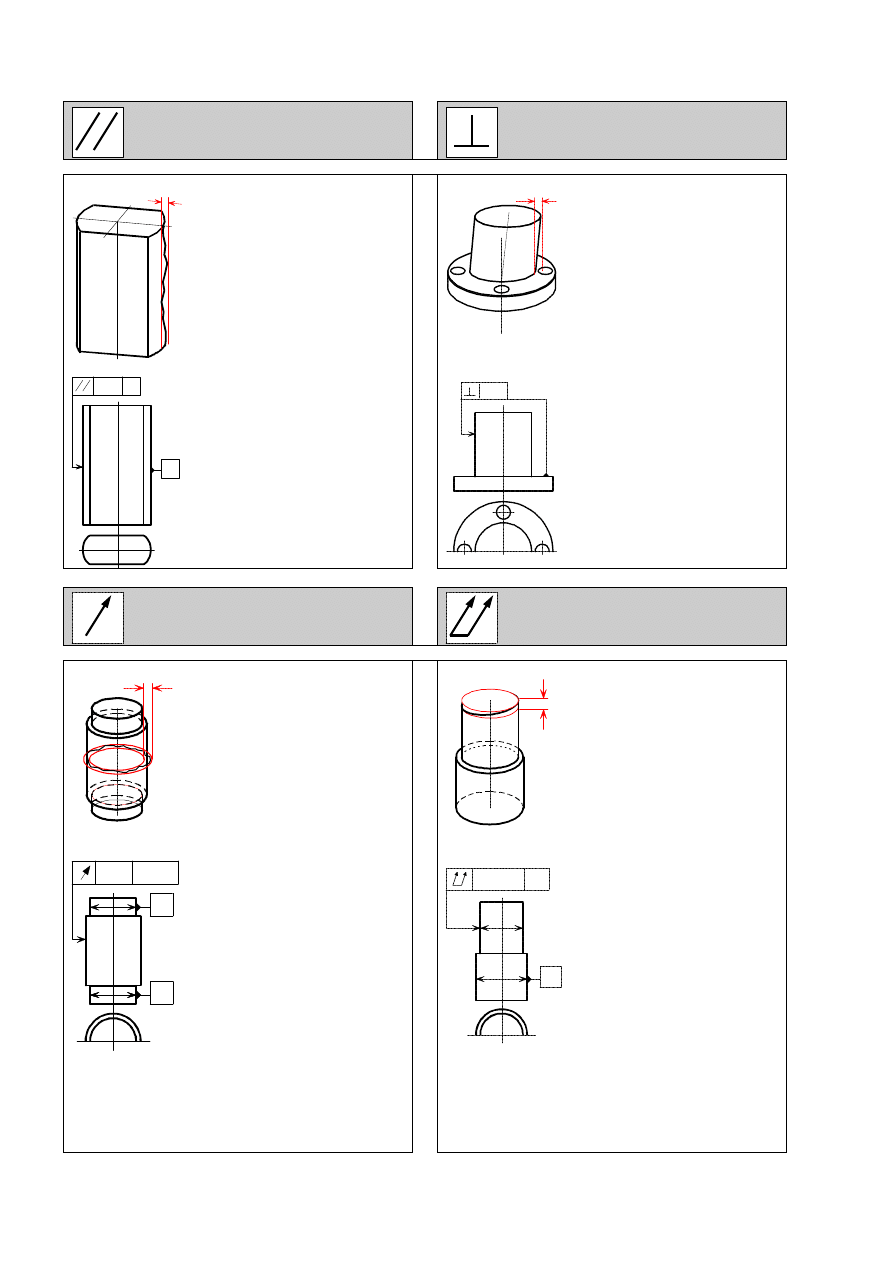
Definicja
P r z e d z i a ³ t o l e r a n c j i j e s t w p ³ a -
s z c z y Ÿ n i e p o m i a r u o g r a n i c z o -
n y p r z e z d w i e l i n i e p r o s t e o d -
l e g ³ e o
t
, r ó w n o l e g ³ e d o o d n i e -
s i e n i a .
Przyk³ad
K a ¿ d a l i n i a t w o r z ¹ c a t o l e r o w a -
n e j p o w i e r z c h n i m u s i l e ¿ e æ
p o m i ê d z y d w o m a
r ó w n o l e -
g ³ y m i l i n i a m i o d l e g ³ y m i o 0 , 1 ,
k t ó r e s ¹ r ó w n o l e g ³ e d o p ³ a s z -
c z y z n y o d n i e s i e n i a A.
Uwaga:
T o l e r a n c j a s y m e t r i i l i n i i l u b o s i
p a t r z D I N I S O 1 1 0 1 .
t
0 , 1
Definicja
P r z e d z i a ³ t o l e r a n c j i j e s t w p ³ a -
s z c z y Ÿ n i e p o m i a r u o g r a n i c z o -
n y p r z e z d w i e r ó w n o l e g ³ e l i n i e
p r o s t e o d l e g ³ e o
t
, p r o s t o p a d ³ e
d o o d n i e s i e n i a .
Przyk³ad
K a ¿ d a l i n i a t w o r z ¹ c a t o l e r o w a -
n e j p o w i e r z c h n i w a l c o w e j m u s i
l e ¿ e æ p o m i ê d z y d w o m a r ó w -
n o l e g ³ y m i l i n i a m i o d l e g ³ y m i o
0 , 1 , k t ó r e s ¹ r ó w n o l e g ³ e d o
p ³ a s z c z y z n y o d n i e s i e n i a .
Uwaga:
T o l e r a n c j a s y m e t r i i l i n i i l u b o s i
p a t r z D I N I S O 1 1 0 1 .
BICIE LOKALNE
( t u p o p r z e c z n e ) I S O 1 1 0 1
BICIE CA£KOWITE
I S O 1 1 0 1
t
A
A B
0,1
B
Definicja
P r z e d z i a ³ t o l e r a n c j i j e s t w p ³ a -
s z c z y Ÿ n i e p o m i a r u p r o s t o p a -
d ³ e j d o o s i o g r a n i c z o n y p r z e z
d w a w s p ó ³ œ r o d k o w e o k r ê g i
o d l e g ³ e o d s i e b i e o
t
, k t ó r y c h
w s p ó l n y œ r o d e k l e ¿ y n a o s i
o d n i e s i e n i a .
Przyk³ad
L i n i a o b w o d o w a d o w o l n e g o
p r z e k r o j u t o l e r o w a n e j p o w i e r z -
c h n i w a l c o w e j m u s i l e ¿ e æ p o -
m i ê d z y d w o m a w s p ó ³ œ r o d k o -
w y m i o k r ê g a m i o d l e g ³ y m i o
0 , 1 , k t ó r y c h w s p ó l n y œ r o d e k
l e ¿ y n a o s i o d n i e s i e n i a u t w o -
r z o n e j z A i B.
Wskazówki:
P r z y p o m i a r z e o b i e k t m i e r z o -
n y n a l e ¿ y o b r a c a æ w o k ó ³ o s i
o d n i e s i e n i a .
T o l e r a n c j a b i c i a w z d ³ u ¿ n e g o
i t o l e r a n c j e b i c i a w d o w o l n y m
l u b z a d a n y m k i e r u n k u p a t r z
D I N I S O 1 1 0 1 .
t
D
D
0,08
∅
Definicja
P r z e d z i a ³ t o l e r a n c j i j e s t o g r a -
n i c z o n y p r z e z d w i e p ³ a s z -
c z y z n y r ó w n o l e g ³ e o d l e g ³ e o
t
,
p r o s t o p a d ³ e d o o s i o d n i e s i e -
n i a .
Przyk³ad
( c a ³ k o w i t e b i c i e
w z d ³ u ¿ n e )
T o l e r o w a n a p o w i e r z c h n i a m u -
s i l e ¿ e æ p o m i ê d z y d w o m a r ó w -
n o l e g ³ y m i p o w i e r z c h n i a m i o d -
l e g ³ y m i o 0 , 1 , p r o s t o p a d ³ y m i
d o o s i o d n i e s i e n i a D.
Wskazówki:
P r z y p o m i a r z e o b i e k t m i e -
r z o n y n a l e ¿ y k i l k a k r o t n i e o b r ó -
c i æ w o k ó ³ o s i o d n i e s i e n i a .
O b i e k t m i e r z o n y i u r z ¹ d z e n i e
p o m i a r o w e p r z e s u w a æ w z g l ê -
d e m s i e b i e p r o m i e n i o w o .
T o l e r a n c j a c a ³ k o w i t e g o b i c i a
p o p r z e c z n e g o p a t r z D I N I S O
1 1 0 1 .
−
5
−
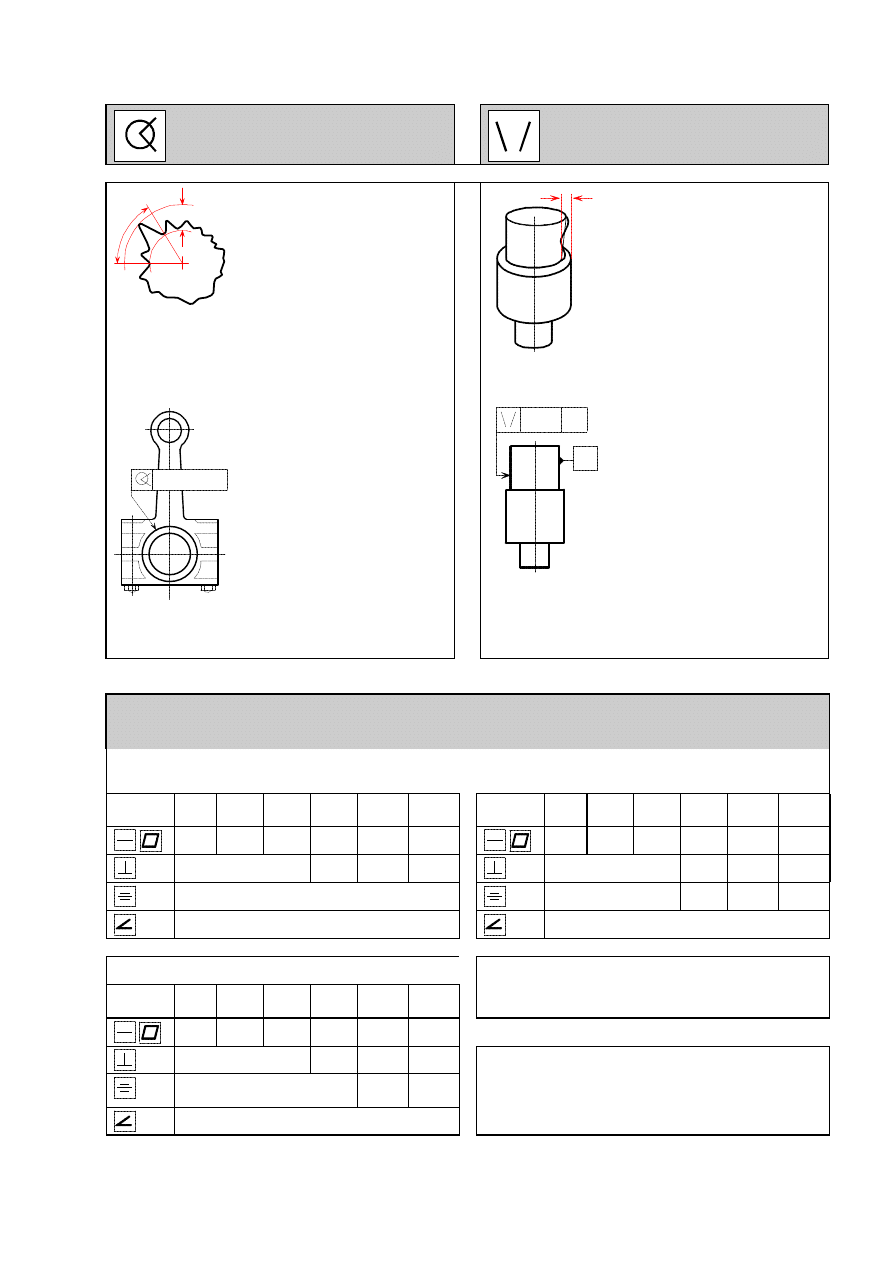
OKR¥G£OŒÆ
W SEKTORZE K¥TOWYM
I S O 1 1 0 1
STO¯KOWOŒÆ
I S O 1 1 0 1
α
t
0,012/15
o
Definicja
P r z e d z i a ³ t o l e r a n c j i j e s t w p ³ a -
s z c z y Ÿ n i e p o m i a r u p r o s t o p a -
d ³ e j d o o s i o g r a n i c z o n a p r z e z
d w a w s p ó ³ œ r o d k o w e o k r ê g i o d -
l e g ³ e o d s i e b i e o
t
. M i e r z o n a
l i - n i a o b w o d u m u s i l e ¿ e æ w
p r z e - d z i a l e t o l e r a n c j i d o w o l -
n e g o s e k t o r a k ¹ t o w e g o w y -
z n a c z o - n e g o o d œ r o d k a p r o f i -
l u .
Przyk³ad
W d o w o l n y m s e k t o r z e k ¹ t o -
w y m o s z e r o k o œ c i 1 5
°
, w y z n a -
c z o n y m o d œ r o d k a p r o f i l u , " l o -
k a l n a " o d c h y ³ k a o k r ¹ g ³ o œ c i
m u s i b y æ m n i e j s z a n i ¿ 0 , 0 1 2 .
Wskazówka:
O d c h y ³ k a o k r ¹ g ³ o œ c i w g D I N
I S O 1 1 0 1 m o ¿ e b y æ w i ê k s z a
i w r a z i e p o t r z e b y t o l e r o w a n a
s p e c j a l n i e .
t
A
A
0,04
Definicja
P r z e d z i a ³ t o l e r a n c j i j e s t w p ³ a -
s z c z y Ÿ n i e p o m i a r u o g r a n i c z o -
n a p r z e z d w i e l i n i e r ó w n o l e g ³ e
d o o d n i e s i e n i a , o d l e g ³ e o d s i e -
b i e o
t
. N i e z m i e r z o n y p r o f i l ,
l e c z o g r a n i c z o n y d o o d c i n k a
p o m i a r o w e g o s e g m e n t p r o s t e j
o d n i e s i e n i a w y z n a c z o n e j m e -
t o d ¹ LSS m u s i l e ¿ e æ w p r z e -
d z i a l e t o l e r a n c j i .
Przyk³ad
K a ¿ d y , z m i e r z o n y n a t o l e r o -
w a n e j p o w i e r z c h n i w a l c o w e j ,
s e g m e n t p r o s t e j r e f e r e n c y j n e j
o b l i c z o n e j m e t o d ¹ L S S m u s i
l e ¿ e æ p o m i ê d z y d w o m a l i n i a m i
p r o s t y m i o d l e g ³ y m i o 0 , 0 4 ,
r ó w n o l e g ³ y m i d o p r z e c i w l e g ³ e j
l i n i i t w o r z ¹ c e j .
Wskazówki:
O d c h y ³ k a r ó w n o l e g ³ o œ c i m o ¿ e
b y æ w i ê k s z a i w r a z i e p o t r z e b y
t o l e r o w a n a s p e c j a l n i e .
TOLERANCJE OGÓLNE ODCHY£EK KSZTA£TU I PO£O¯ENIA
I S O 2 7 6 8
Klasa tolerancji H
Klasa tolerancji L
W y m .
n o m i n .
÷
10
> 10
÷
30
> 30
÷
100
> 100
÷
300
> 300
÷
1000
>1000
÷
3000
W y m .
n o m i n .
÷
10
> 10
÷
30
> 30
÷
100
> 100
÷
300
> 300
÷
1000
>1000
÷
3000
0,02
0,05
0,1
0,2
0,3
0,4
0,1
0,2
0,4
0,8
1,2
1,6
0,2
0,3
0,4
0,5
0,6
1
1,5
2
0,5
0,6
1
1,5
2
0,1
0,5
Klasa tolerancji K
Okr¹g³oœæ
W y m .
n o m i n .
÷
10
> 10
÷
30
> 30
÷
100
> 100
÷
300
> 300
÷
1000
>1000
÷
3000
O g ó l n ¹ t o l e r a n c j ¹ o k r ¹ g ³ o œ c i j e s t Minimum z t o l e r a n c j i
œ r e d n i c y i o g ó l n e j t o l e r a n c j i b i c i a .
0,05
0,1
0,2
0,4
0,6
0,8
0,4
0,3
0,8
1
Równoleg³oœæ
0,6
0,8
1
O g ó l n ¹ t o l e r a n c j ¹ r ó w n o l e g ³ o œ c i j e s t Minimum z t o l e -
r a n c j i w y m i a r u i o g ó l n e j t o l e r a n c j i p r o s t o l i n i o w o œ c i /
0,2
p ³ a s k o œ c i .
−
6
−
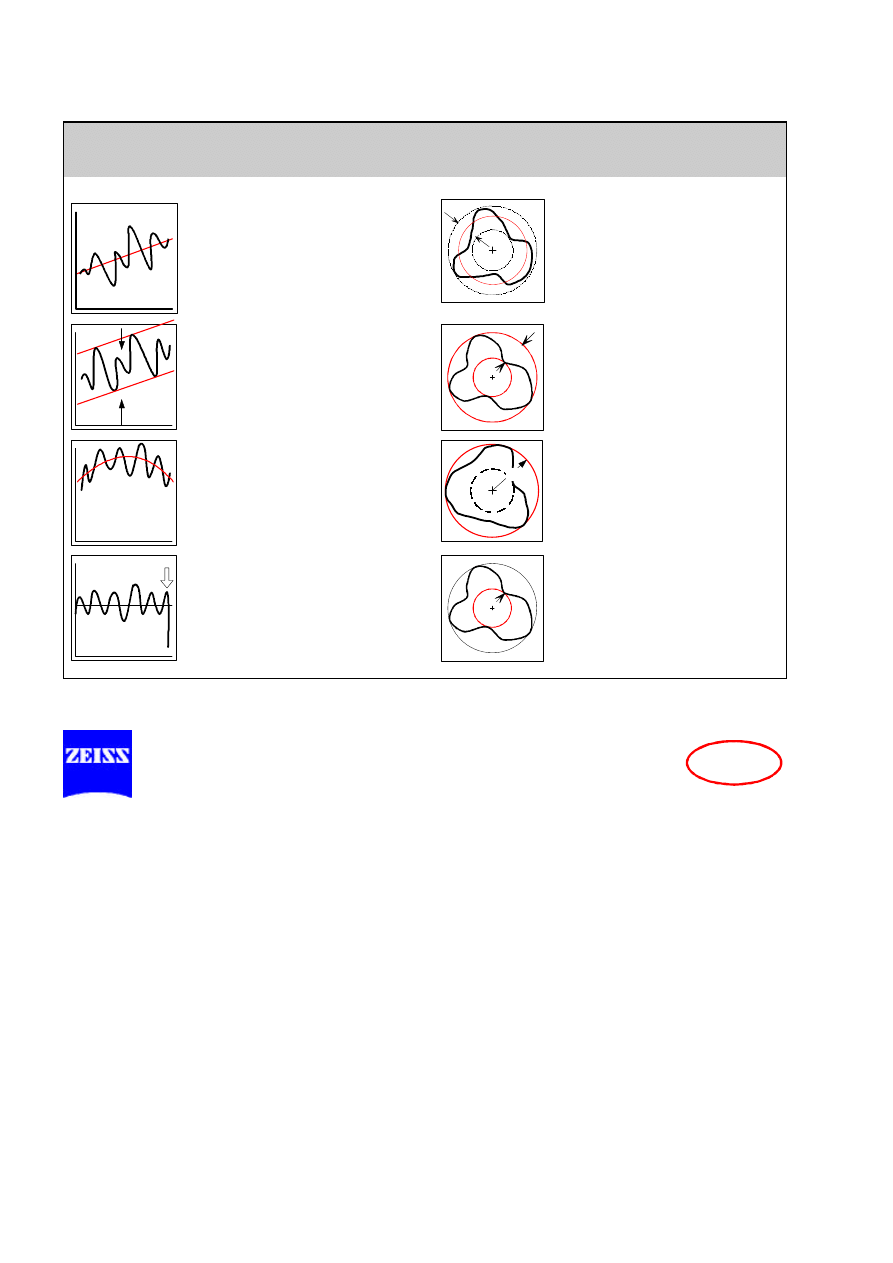
METODY OBLICZENIOWE ELEMENTÓW ODNIESIENIOWYCH
ISO 6318
Linia œrednia
Linia
œrednia przechodz¹ca przez
profil w ten sposób,
¿e suma kwa-
dratów
odchy³ek profilu jest mini-
malna.
LSS
=
L
east
S
quare
S
traights
Okr¹g referencyjny
Okr¹g przechodz¹cy przez profil
okr¹g³oœci w ten sposób, ¿e suma
kwadratów
odchy³ek profilu jest mi-
nimalna.
LSC
=
L
east
S
quare
C
ircle
Minimalne pasmo
Proste
równoleg³e opisane na pro-
filu przy minimalnej ich
odleg³oœci.
MZS
=
M
inimum
Z
one
S
traights
Minimalna odleg³oœæ okregów
Dwa
wspó³œrodkowe okrêgi: opisa-
ny i wpisany, których wzajemna
odleg³oœæ jest minimalna.
MZC
=
M
inimum
Z
one
C
ircles
Parabola regresyjna
Parabola
œrednia (2. rzêdu) prze-
chodz¹ca przez profil w ten sposób,
¿e suma kwadratów odchy³ek pro-
filu jest minimalna.
LSP
=
L
east
S
quare
P
arabola
Rmin
Najmniejszy okr¹g opisany
Najmniejszy
okr¹g opisany na pro-
filu
okr¹g³oœci.
MCC
=
M
inimum
C
ircumscribed
C
ircle
POZYCJA
Rozpoznanie krawêdzi
Wyznaczana jest pozycja
nieci¹-
g³oœci profilu (krawêdŸ). A¿ do kra-
wêdzi profil jest oceniany metod¹
LSS.
KER
=
K
anten
ER
kennung
Rmin
Najwiêkszy okr¹g wpisany
Najwiêkszy okr¹g wpisany w profil
okr¹g³oœci.
MIC
=
M
aximum
I
nscribed
C
ircle
Carl Zeiss
Spó³ka z o.o. - Segment Industrielle Meßtechnik
02-525 Warszawa. ul. Chodkiewicza 8/4
Tel. (022) 881 02 49, 881 02 50, Fax (022) 8482353
Mahr