1

Rozwiązywanie algebraicznych

układów równań liniowych

metodami bezpośrednimi

2

Plan wykładu:

1. Definicje macierzy, norm etc.
2. Metoda eliminacji Gaussa, Jordana
3. Rozkład LU metodą Gaussa
4. Układy równań z macierzą symetryczną. Rozkłady: LDL

T

, LL

T

5. Układy równań z macierzą trójdiagonalną
6. Iteracyjne poprawianie rozwiązań
7. Układy liniowe nadokreślone, układ normalny równań, metody

ortogonalizacji

3

Pojęcia podstawowe

Macierz jest uporządkowanym układem
mxn liczb rzeczywistych lub zespolonych
A=(a

ij

) (i=1,..,m; j=1,...,n)

Jeśli m=n to A jest kwadratowa stopnia n.

Macierz diagonalna D=(



ij

d

ij

)

Macierz jednostkowa I=(



ij

)

A

m

£n

=

2
6

6

4

a

11

a

12

: : :

a

1n

a

21

a

22

: : :

a

2n

: : :

: : :

: : :

: : :

a

m1

a

m2

: : :

a

mn

3
7

7

5

D =

2
6

6

4

d

1

0

: : :

0

0

d

2

: : :

0

: : :

: : :

: : :

: : :

0

0

: : :

d

n

3
7

7

5

(A

T

)

T

= A

(®A)

T

= ®A

T

(A + B)

T

= A

T

+ B

T

(AB)

T

= B

T

A

T

(Ax)

T

= x

T

A

T

Transpozycja - A=(a

ij

) to A

T

=(a

ji

)

Ślad macierzy A=A

nxn

tr(A) =

n

X

i=1

a

ii

tr(A

T

) = tr(A)

4

Jeśli

to macierz jest

nieosobliwa

i dla takiej macierzy

istnieje macierz odwrotna A

-1

Macierz symetryczna

Macierz ortogonalna Q=Q

m

x

n

Macierz idempotentna

det(A)

6= 0

AA

¡1

= A

¡1

A = I

(AB)

¡1

= B

¡1

A

¡1

A

T

= A

Q

T

Q = I

Macierz trójkątna lewa (dolna)

Macierz trójkątna prawa (górna)

Sumy, iloczyny i odwrotności macierzy trójkątnych
tego samego rodzaju są macierzami trójkątnymi.

Wyznacznik macierzy trójkątnej

L =

2
6

6

4

l

11

0

: : :

0

l

21

l

22

: : :

0

: : :

: : :

: : :

: : :

l

n1

l

n2

: : :

l

nn

3
7

7

5

R =

2
6

6

4

r

11

r

12

: : :

r

1n

0

r

22

: : :

r

2n

: : :

: : :

: : :

: : :

0

0

: : :

r

nn

3
7

7

5

det(L) = l

11

l

22

: : : l

nn

det(R) = r

11

r

22

: : : r

nn

det(A) = det(A

T

)

det(AB) = det(A)det(B)

Q

¡1

Q = I

Q

T

= Q

¡1

A

2

= A

5

Macierzą hermitowską nazywamy macierz, która
po transpozycji i sprzężeniu zespolonemu jej
elementów jest równa macierzy pierwotnej

Elementy diagonalne macierzy hermitowskiej są
rzeczywiste (pozostałe mogą być zespolone lub
rzeczywiste).

Macierzą dodatniookreśloną nazywamy macierz
rzeczywistą lub hermitowską o własności:

Macierz dodatnio określona jest zawsze odwracalna.
Macierz odwrotna jest
również dodatnio określona.

Przestrzenią liniową (wektorową) nad ciałem
liczb rzeczywistych (zespolonych) nazywamy zbiór
obiektów (wektorów) z określonym działaniem
dodawania elementów przestrzeni oraz mnożenia ich
przez liczbę i oznaczamy R

N

(C

N

).

Aksjomaty: łączność, przemienność, element
neutralny, element odwrotny,....

A

H

=

¡

A

T

¢

¤

x

T

Ax > 0;

x

2 R

n

;

x

6= 0

Uporządkowany zbiór liczb rzeczywistych
(zespolonych) tworzy wektor

Przestrzeń wektorowa będąca zbiorem takich
obiektów ma wymiar n.
Dowolny zbiór n wektorów liniowo niezależnych w
R

N

tworzy bazę przestrzeni. Każdy element
przestrzeni można zapisać jako kombinację
liniową elementów bazy

Podprzestrzeń linową R w R

N

tworzy zbiór

wszystkich wektorów

Macierz możemy traktować jako obiekt
zbudowany z wektorów ( wektory wierszowe lub
kolumnowe).
Rzędem macierzy A=A

mxn

r=rank(A)
nazywamy największą liczbę niezależnych liniowo
wektorów wierszowych lub kolumnowych. Jeśli
r=m=n to macierz jest nieosobliwa.

x = (x

1

; x

2

; x

3

; : : : ; x

n

)

y

1

; y

2

; : : : ; y

n

x = ®

1

y

1

+ ®

2

y

2

+ : : : + ®

n

y

n

y

1

; y

2

; : : : ; y

k

;

k

· n

6

Normy wektorów i macierzy
Normy wprowadza się w celu ilościowego
określania własności wektorów i macierzy.
Normą wektora nazywamy funkcję, która
każdemu elementowi w R

N

przyporządkowuje liczbę

rzeczywistą. Dla dowolnych

norma wektora musi spełniać następujące
aksjomaty:

Dla n-wymiarowego wektora

najczęściej stosowane są normy z rodziny L

P

:

- norma pierwsza

- norma druga (euklidesowa)

- norma maksymalna

Dla dowolnego wektora x w przestrzeni R

n

prawdziwe są poniższe relacje pomiędzy normami:

Normy macierzy
Własności norm macierzy

Normy zgodne

– norma macierzy indukowana

przez normę wektora

x = [x

1

; x

2

; : : : ; x

n

]

T

jjxjj

p

= (

jx

1

j

p

+

jx

2

j

p

+ : : :

jx

n

j

p

)

1

p

p =

1;

kxk

1

= max

fjx

1

j; jx

2

j; : : : ; jx

n

jg

x; y

2 R

n

®

2 R

jjxjj ¸ 0;

jjxjj = 0 () x = 0

jj®xjj = j®j ¢ jjxjj
jjx + yjj · jjxjj + jjyjj

kxk

1

· kxk

2

· kxk

1

·

p

n

kxk

2

· nkxk

1

p = 2;

kxk

2

= (x

2

1

+ x

2

2

+ : : : + x

2

n

)

1=2

p = 1;

kxk

1

=

jx

1

j + jx

2

j + : : : + jx

n

j

jjAjj ¸ 0;

jjAjj = 0 () A = 0

jj®Aj = j®j ¢ jjAjj

jjA + Bjj · jjAjj + jjBjj

jjABjj · jjAjj ¢ jjBjj

jjAxjj · jjAjj ¢ jjxjj(normy zgodne)

7

Macierz o m wierszach i n kolumnach można
traktować jako operator liniowy przekształcający
przestrzeń R

m

w R

n

. Normę takiej macierzy można

określić przy użyciu wektorów:

gdzie: p i q oznaczają normy wektorów w
przestrzeniach R

n

i w R

m

. Mówimy, że norma ||A||

pq

jest normą indukowaną przez normy ||.||

p

oraz ||.||

q

.

Dla p=q oznaczając

możemy określić następujące normy macierzy

- maksymalna suma modułów w kolumnie

- norma spektralna

kAk

p

=

kAk

pq

kAk

1

=

max

j=1;2;:::;n

m

X

i=1

ja

ij

j

kAk

2

= ( max

i=1;:::;n

¸

i

(AA

T

))

1=2

kAk

1

=

max

i=1;2;:::;n

n

X

j=1

ja

ij

j

kAk

1

1

= max

i;j

ja

ij

j

- maksymalna suma modułów w wierszu

- maksymalny moduł elementu

W przestrzeniach z normą ||

⋅||

2

często używa się

euklidesowej (Frobeniusa)

normy macierzy:

która nie jest indukowana żadną normą ale spełnia
ona z normą ||

⋅||

2

warunek zgodności:

Normy macierzy mają istotne znaczenie w analizie
błędów (np. błędów rozwiązania układów równań
liniowych).

kAk

E

=

v

u

u

t

m

X

i=1

n

X

j=1

a

2

ij

kAk

2

· kAk

E

kxk

2

;

x

2 R

n

kAk

pq

= sup

x

2Rn

x

6=0

kAxk

q

kxk

p

8

Szukamy rozwiązania układu równań liniowych w
postaci:

Powyższy układ równań można zapisać w postaci
macierzowej:

gdzie:
- macierz współczynników układu

- szukany wektor - wektor wyrazów
rozwiązań wolnych

a

11

x

1

+ a

12

x

2

+ : : : + a

1n

x

n

=

b

1

a

21

x

1

+ a

22

x

2

+ : : : + a

2n

x

n

=

b

2

: : : : : : : : : : : : : : : : : : : : : : : : : : :

=

: : :

a

n1

x

1

+ a

n2

x

2

+ : : : + a

nn

x

n

=

b

n

Ax = b

A =

2
6

6

4

a

11

a

12

: : :

a

1n

a

21

a

22

: : :

a

2n

: : :

: : :

: : :

: : :

a

n1

a

n2

: : :

a

nn

3
7

7

5

x =

2

6

6

6

4

x

1

x

2

..

.

x

n

3

7

7

7

5

b =

2

6

6

6

4

b

1

b

2

..

.

b

n

3

7

7

7

5

Warunek rozwiązywalności układu niejednorodnego:

R(A) – podprzestrzeń liniowa rozpięta na wektorach
kolumnowych macierzy A

Dla

warunek rozwiązywalności układu jest spełniony dla
każdego b i rozwiązanie ma postać

Jeśli rank(A)=r<n to rozwiązania tworzą rozmaitość
(n-r) wymiarową.

b

2 R(A)

R(A) = R

n

x = A

¡1

b

9

Układ równań z macierzą trójkątną

Zakładamy, że elementy leżące na diagonali są niezerowe.
Rozwiązanie układu można znaleźć posługując się wzorem
rekurencyjnym, zaczynając od elementu x

n

:

W celu wyznaczenia wszystkich składowych wektora rozwiązania
x należy wykonać:

- M operacji mnożenia i dzielenia

- D operacji dodawania i odejmowania

a

11

x

1

+ a

12

x

2

+ : : : + a

1n

x

n

=

b

1

a

22

x

2

+ : : : + a

2n

x

n

=

b

2

: : : : : : : : : : : :

: : :

: : :

a

nn

x

n

=

b

n

M =

1
2

n

2

+

1
2

n

D =

1
2

n

2

¡

1
2

n

x

n

=

b

n

a

nn

x

i

=

b

i

¡ a

ii+1

x

i+1

¡ : : : ¡ a

in

x

n

a

ii

10

Uwarunkowanie zadania - rozwiązania
układu równań

Wpływ błędów zaokrągleń na wynik można
oszacować analizując zaburzenia danych: A,b

a) zaburzamy wektor b:

b) zaburzamy elementy macierzy A:

ostatnią nierówność zapisujemy w postaci

A(x + ±x)

=

b + ±b

±x

=

A

¡1

±b

jj±xjj · jjA

¡1

jj ¢ jj±bjj

(A + ±A)(x + ±x) = b
A±x + ±A(x + ±x) = 0
±x =

¡A

¡1

±A(x + ±x)

jj±xjj · jjA

¡1

jj ¢ jj±Ajj ¢ jjx + ±xjj

jj±xjj

jjx + ±xjj

· ·(A)

jj±Ajj

jjAjj

·(A) =

jjAjj ¢ jjA

¡1

jj

gdzie

jest

wskaźnikiem uwarunkowania macierzy

Korzystając z wyniku (a) oraz nierówności

dostajemy oszacowanie na błąd względny
rozwiązania:

Wniosek - duży wskaźnik uwarunkowania macierzy
może powodować duże względne zaburzenia
rozwiązania nawet dla małych zaburzeń wektora
danych. Zadanie jest wówczas

źle uwarunkowane

.

jjbjj = jjAxjj · jjAjj ¢ jjxjj

jj±xjj

jjxjj

· ·(A)

jj±bjj

jjbjj

11

Metoda eliminacji Gaussa rozwiązania układu
równań liniowych. Metoda jest dwuetapowa:

1) Eliminacja zmiennych. Układ pierwotny:

Odejmujemy od i-tego wiersza (i=2,3,...,n) wiersz
pierwszy pomnożony przez współczynnik

Z równań i=2,3,..,n wyeliminowana została
zmienna x

1

.

a

(1)
11

x

1

+ a

(1)
12

x

2

+ : : : + a

(1)
1n

x

n

=

b

(1)
1

a

(1)
21

x

1

+ a

(1)
22

x

2

+ : : : + a

(1)
2n

x

n

=

b

(1)
2

: : : : : : : : : : : : : : : : : : : : : : : : : : :

=

: : :

a

(1)
n1

x

1

+ a

(1)
n2

x

2

+ : : : + a

(1)

nn

x

n

=

b

(1)

n

A

(1)

x = b

(1)

l

i1

=

a

(1)
i1

a

(1)
11

A

(2)

x = b

(2)

a

(2)
11

x

1

+ a

(2)
12

x

2

+ : : : + a

(2)
1n

x

n

=

b

(2)
1

a

(2)
22

x

2

+ : : : + a

(2)
2n

x

n

=

b

(2)
2

: : : : : : : : : : : : : : : : : : : : :

=

: : :

a

(2)
n2

x

2

+ : : : + a

(2)

nn

x

n

=

b

(2)

n

Powtarzamy operację, ale odejmujemy od i-tego
wiersza (i=3,4,...,n) wiersz drugi pomnożony przez
współczynnik

Postępując dalej w ten sposób eliminujemy z
każdego następnego równania jedną zmienną.
Eliminację kończymy po (n-1) krokach, gdy
uzyskamy trójkątny układ równań w postaci:

l

i2

=

a

(2)
i2

a

(2)
22

A

(n)

x = b

(n)

a

(n)
11

x

1

+ a

(n)
12

x

2

+ : : : + a

(n)
1n

x

n

=

b

(n)
1

a

(n)
22

x

2

+ : : : + a

(n)
2n

x

n

=

b

(n)
2

: : : : : : : : : : : :

=

: : :

a

(n)

nn

x

n

=

b

(n)

n

12

2) Etap drugi nazywany jest
postępowaniem odwrotnym.
Rozwiązanie (kolejne składowe wektora x)
znajdujemy stosując wzór rekurencyjny dla
macierzy trójkątnej. Wyznaczenie rozwiązania
metodą Gaussa wymaga wykonania:

- M op. mnożenia i dzielenia

- D op. dodawania i odejmowania

Metoda eliminacji w tej postaci jest niestabilna
numerycznie – problem dzielenia przez 0 lub
liczbę bliską zeru. Rozwiązanie:

a) częściowy wybór elementów głównych
b) pełny wybór elementów głównych

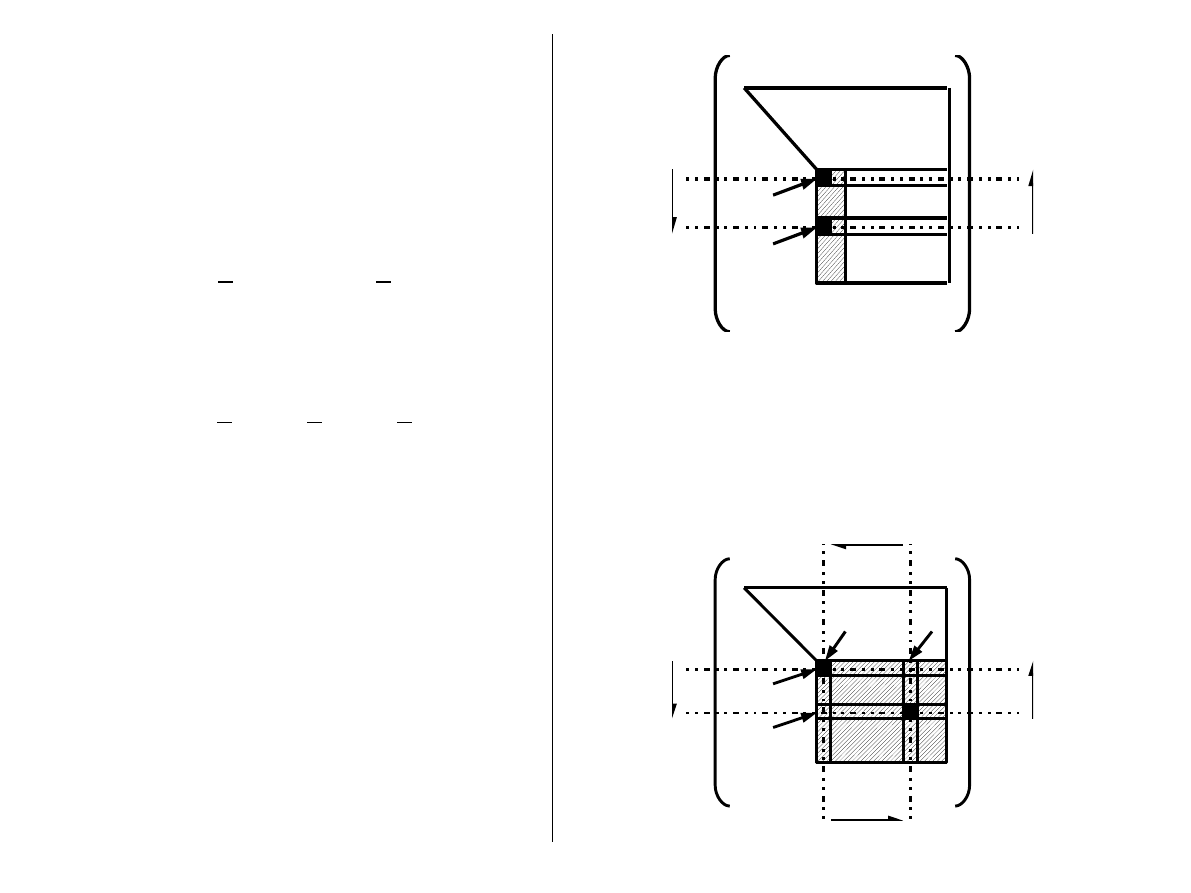
Częściowy wybór elementów głównych
W k-tym kroku szukamy elementu

i przestawiamy wiersze r oraz k.

M =

1
3

n

3

+ n

2

¡

1
3

n

D =

1
3

n

3

+

1
2

n

2

¡

5
6

n

ja

(k)
rk

j = max

k

·i·n

ja

k

ik

j

Pełny wybór elementów głównych
W k-tym kroku szukamy elementu

i przestawiamy wiersze: k i r oraz kolumny: k i s

ja

(k)

rs

j = max

k

·i;j·n;

ja

k

ij

j

r

k

r

k

s

k

13

Stosując wybór elementu głównego
rozwiązanie otrzymujemy zawsze.
W trakcie wyboru elementu głównego należy
zmienić także kolejność w x i b.
Modyfikacji tej można nie stosować dla:

a) macierzy z dominującą przekątną

b) macierzy symetrycznej i jednocześnie
dodatniookreślonej

Metoda eliminacji Jordana
(eliminacji zupełnej)
W układzie równań:

równanie pierwsze dzielimy obustronnie przez
współczynnik:

ja

ii

j ¸

n

X

j=1;j

6=i

ja

i;j

j (i = 1; : : : ; n)

a

(1)
11

x

1

+ a

(1)
12

x

2

+ : : : + a

(1)
1n

x

n

=

b

(1)
1

a

(1)
21

x

1

+ a

(1)
22

x

2

+ : : : + a

(1)
2n

x

n

=

b

(1)
2

: : : : : : : : : : : : : : : : : : : : : : : : : : :

=

: : :

a

(1)
n1

x

1

+ a

(1)
n2

x

2

+ : : : + a

(1)

nn

x

n

=

b

(1)

n

w

1

= a

(1)
11

Następnie odejmujemy od i-tego wiersza (i=2,3,...,n)
wiersz pierwszy przemnożony przez

i otrzymujemy

Podobnie postępujemy z równaniem drugim. Dzielimy
je przez

Następnie od i-tego wiersza (i=1,3,4,...,n)
odejmujemy wiersz drugi pomnożony przez
współczynnik:

w

1i

= a

(1)
i1

x

1

+ a

(2)
12

x

2

+ : : : + a

(2)
1n

x

n

=

b

(2)
1

a

(2)
22

x

2

+ : : : + a

(2)
2n

x

n

=

b

(2)
2

: : : : : : : : : : : : : : : : : : : : :

=

: : :

a

(2)
n2

x

2

+ : : : + a

(2)

nn

x

n

=

b

(2)

n

A

(2)

x = b

(2)

A

(1)

x = b

(1)

w

2

= a

(2)
22

w

2i

= a

(2)
i2

14

Otrzymujemy zmodyfikowany układ równań:

Po przeprowadzeniu (n-1) eliminacji zmiennych

układ równań ma poniższą postać:

czyli gotowe rozwiązanie. Liczba operacji:

A

(3)

x = b

(3)

x

1

+ 0

¢ x

2

+ a

(3)
13

x

3

+ : : : + a

(3)
1n

x

n

=

b

(3)
1

x

2

+ a

(3)
23

x

3

+ : : : + a

(3)
2n

x

n

=

b

(3)
2

: : : : : : : : : : : : : : : : : : : : :

=

: : :

a

(3)
n3

x

3

+ : : : + a

(3)

nn

x

n

=

b

(3)

n

x

1

=

b

(n)
1

x

2

=

b

(n)
2

: : :

=

: : :

x

n

=

b

(n)

n

M =

1
2

n

3

+

1
2

n

2

D =

1
2

n

3

¡

1
2

n

2

Rozkład LU metodą Gaussa-Crouta(GCW)

Metodę Gaussa można użyć do znalezienia takich
macierzy L i U, które z macierzą A związane są
relacją:

Procedura wyznaczania elementów tych

macierzy nosi nazwę

rozkładu LU

.

Sposób postępowania (wykorzystujemy

metodę eliminacji Gaussa):

1) mnożenie wiersza pierwszego przez

czynnik

i odjęcie go od i-tego wiersza (i=2...n),

zastępujemy mnożeniem przez macierz:

co można zapisać macierzowo:

A = L

¢ U

l

i1

=

a

(1)
i1

a

1

11

L

(1)

=

2
6

6

6

6

4

1

0

: : :

: : :

0

¡l

21

1

0

: : :

0

¡l

31

0

1

0

0

: : :

: : :

: : :

1

0

¡l

n1

0

0

: : :

1

3
7

7

7

7

5

n

£n

L

(1)

A

(1)

= A

(2)

L

(1)

b

(1)

= b

(2)

15

Macierze L

(i)

są nieosobliwe (można znaleźć dla każdej

macierz odwrotną). Przemnażając obie strony
powyższych równań przez (L

(n-1)

)

-1

, (L

(n-2)

)

-1

....,

otrzymamy:

wprowadzamy oznaczenia

Jak znaleźć macierze (L

(i)

)

-1

?

Eliminacja zmiennej z równań (i=3,4,...,n)
wygląda podobnie. Mnożymy wiersze
zmodyfikowanego układu równań o indeksach
i=3,4,...,n przez czynnik

i odejmujemy od nich wiersz drugi. Operację tą
można przeprowadzić mnożąc układ równań
obustronnie przez macierz L

(2)

:

Zapis macierzowy operacji:

Po wykonaniu (n-1) takich operacji dostajemy

l

i2

=

a

(2)
i2

a

2

2

L

(2)

A

(2)

=

A

(3)

L

(2)

b

(2)

=

b

(3)

L

(2)

=

2
6

6

6

6

4

1

0

: : :

: : :

0

0

1

0

0

: : :

0

¡l

32

1

0

0

: : :

: : :

: : :

1

0

0

¡l

n2

0

0

1

3
7

7

7

7

5

L

(n

¡1)

L

(n

¡2)

: : : L

(1)

A

(1)

=

A

(n)

L

(n

¡1)

L

(n

¡2)

: : : L

(1)

b

(1)

=

b

(n)

A

(1)

=

³

L

(1)

´

¡1

³

L

(2)

´

¡1

: : :

³

L

(n

¡1)

´

¡1

A

(n)

b

(1)

=

³

L

(1)

´

¡1

³

L

(2)

´

¡1

: : :

³

L

(n

¡1)

´

¡1

b

(n)

L

(1)

=

2

6

6

4

1

0

: : :

0

¡l

21

1

: : :

0

: : :

: : :

1

0

¡l

n1

0

: : :

1

3

7

7

5

³

L

(1)

´

¡1

=

2

6

6

4

1

0

: : :

0

l

21

1

: : :

0

: : :

: : :

1

0

l

n1

0

: : :

1

3

7

7

5

L

=

(L

(1)

)

¡1

(L

(2)

)

¡1

: : : (L

(n

¡1)

)

¡1

U

=

A

(n)

=

µ

L

(n

¡1)

L

(n

¡2)

: : : L

(1)

¶

A

(1)

A

=

L

¢ U

16

Dysponując macierzami L i U można rozwiązać układ
równań:

poprzez rozwiązanie 2 układów równań

Rozwiązanie każdego z równań wiąże się z nakładem
obliczeń jak dla układu z macierzą trójkątną (~1n

2

).

Rozkład LU (eliminacja Gaussa) to nakład rzędu
~0.5n

3

.

Sprawdzenie

macierz L jest macierzą dolną z jedynkami
na diagonali:

macierz U jest macierzą górną z
niezerowymi elementami na diagonali:

L

(i)

³

L

(i)

´

¡1

= I

L

=

(L

(1)

)

¡1

(L

(2)

)

¡1

: : : (L

(n

¡1)

)

¡1

L

=

2
6

6

6

6

4

1

0

: : :

: : :

0

l

21

1

0

: : :

0

l

31

l

32

1

0

0

: : :

: : :

: : :

1

0

l

n1

l

n2

l

n3

: : :

1

3
7

7

7

7

5

Ax = b
LU x = b

Ly = b

U =

2
6

6

6

6

4

u

11

u

12

u

13

: : :

u

1n

0

u

22

u

23

: : :

u

2n

0

0

u

33

: : :

u

nn

: : :

: : :

: : :

: : :

: : :

0

0

0

: : :

u

nn

3
7

7

7

7

5

U x = y

17

Jaki jest

wektor reszt

rozwiązania?

Norma maksymalna wektora reszt może być mała nawet
dla źle uwarunkowanych macierzy.

Zalety:

1) Duża wydajność dla dużej liczby równań. Rozkład LU

opłaca się stosować w przypadku rozwiązywania wielu
układów równań z tą samą macierzą współczynników
układu A. Każdy układ równań różni się wtedy tylko
wektorem wyrazów wolnych. Rozkład LU wykonuje się
w takim przypadku tylko raz (ilość operacji ~n

3

).

Rozwiązanie pojedynczego układu równań można
znaleźć przy zastosowaniu algorytmu postępowania
odwrotnego (ilość operacji ~n

2

).

2) Oszczędność zajmowanej pamięci. Elementy macierzy

L i U mogą zostać zapisane w macierzy A.

3) Jeśli macierz A jest symetryczna i dodatniookreślona

to nie trzeba dokonywać wyboru elementów
podstawowych.

r = b

¡ A~x = (A + ±A)~x ¡ A~x = ±A~x

jjrjj

1

=

jjb ¡ A~xjj

1

· k

2

"

jj±Ajj

1

jj~xjj

1

18

Układy równań z macierzą symetryczną.
Rozkład LDL

T

Oznaczmy rozkład LU jako:

Szukamy rozkładu macierzy A w postaci:

gdzie: L – macierz trójkątna dolna z jedynkami na
diagonali, D – macierz diagonalna z elementami
diagonalnymi macierzy , U – macierz trójkątna
górna z jedynkami na diagonali

Wykorzystujemy symetrię macierzy

co prowadzi do rozkładu dla macierzy
symetrycznych:

Rozwiązanie układu Ax=b:

A = LU

A = LDU

A = LDL

T

Elementy rozkładu wyznaczamy rekurencyjnie

a dla i=2,3,...,n oblicza się na przemian:

Nakład obliczeń:

Zalety:
- nakład obliczeń dwukrotnie mniejszy niż w GCW
- dzięki symetrii macierzy wystarczy zapamiętać

elementów

d

1

= a

11

l

ij

=

a

ij

¡

P

j

¡1

k=1

c

ik

l

jk

d

j

c

ij

= d

j

l

ij

;

j = 1; 2; : : : ; i

¡ 1

d

i

= a

ii

¡

i

¡1

X

k=1

c

ik

l

ik

M =

1
6

n

3

+ n

2

¡

7
6

n

D =

1
6

n

3

¡

1
6

n

¹

U

U

T

DL

T

= A

T

= A

) U = L

T

N =

n(n + 1)

2

Lz = b

Dy = z

L

T

x = y

19

Rozkład LL

T

(Banachiewicza-Cholesky'ego)

Jeśli macierz A jest macierzą symetryczną
dodatnio określoną wówczas można dokonać
następującego rozkładu:

Macierz L jest macierzą trójkątną dolną z
elementami na diagonali mogącymi
się różnić od 1. Macierz

spełnia warunek

więc rozkład ten nie jest jednoznaczny. Jeśli
jednak liczby na diagonali macierzy L są
dodatnie wówczas rozkład jest jednoznaczny, a
elementy macierzy wyznaczamy ze wzorów:

A = LL

T

A = ¹

L ¹

L

T

l

ii

=

v

u

u

ta

ii

¡

i

¡1

X

k=1

l

2

ik

; i = 1; 2; : : : ; n

l

ji

=

a

ji

¡

P

i

¡1

k=1

l

jk

l

ik

l

ii

; j = i + 1; i + 2; : : : ; n

Nakład obliczeń:

Przykład

n

¡ p

D =

1
6

n

3

+

1
2

n

2

+

1
3

n

A =

2

4

4

2

2

2

5

3

2

3

6

3

5

i = 1 :

l

11

= 2;

l

21

= 1;

l

31

= 1

i = 2 :

l

22

= 2;

l

32

= 1

i = 3 :

l

33

= 2

A

=

2

4

4

2

2

2

5

3

2

3

6

3

5

=

2

4

2

0

0

1

2

0

1

1

2

3

5 ¢

2

4

2

1

1

0

2

1

0

0

2

3

5

¹

L =

¡L

M =

1
6

n

3

+

1
2

n

2

¡

2
3

n

20

Inne zastosowania rozkładu LU.

Obliczanie wyznacznika

Aby obliczyć wyznacznik macierzy A możemy

posłużyć się rozkładem

Wyznacznik macierzy U jest iloczynem

elementów stojących na diagonali tej

macierzy (n-1 operacji mnożenia).

Odwracanie macierzy

Aby znaleźć przy pomocy macierzy L i U

macierz odwrotną A

-1

należy rozwiązać

n układów równań:

A = LU

det(L) = 1

det(A + E)

=

det(LU )

=

det(L)det(U ) = det(U )

LU x

(i)

= e

(i)

;

i = 1; 2; : : : ; n

e

(i)

= [0; 0; : : : ; 1; : : : ; 0]

T

Rozwiązania układów równań x

(i)

stanowią

kolumny macierzy odwrotnej A

-1

(po

uwzględnieniu ewentualnych przestawień

wierszy wynikających z wyboru elementu

podstawowego).

Przykład

Znaleźć macierz A

-1

jeśli macierz A jest

zdefiniowana:

A =

2

4

1

0

1

3

3

0

0

2

2

3

5

A

¡1

=

2

4

1
2

1
6

¡

1
4

¡

1
2

1
6

1
4

1
2

¡

1
6

1
4

3

5

P

n

=

2

4

2
3
1

3

5

L =

2

4

1

0

0

0

1

0

1
3

¡

1
2

1

3

5 U =

2

4

3

3

0

0

2

2

0

0

2

3

5

x

(1)

=

2

4

1=6
1=6

¡1=6

3

5 x

(2)

=

2

4

¡1=4

1=4
1=4

3

5

x

(3)

=

2

4

1=2

¡1=2

1=2

3

5

LU X = I

! X = A

¡1

21

Układy równań z macierzą trójdiagonalną

Szukamy rozwiązania układu równań:

Zdarza się że macierz układu równań ma postać (np.
równania z ilorazami różnicowymi):

Można wykonać rozkład LU macierzy T, macierze te
mają postać:

L =

2
6

6

6

6

6

6

6

6

4

1

l

2

1

0

l

3

1

. .. ...

0

. .. ...

l

n

1

3
7

7

7

7

7

7

7

7

5

U =

2
6

6

6

6

6

6

6

6

4

u

1

c

1

u

2

c

2

0

u

3

c

3

. .. ...

0

. ..

c

n

¡1

u

n

3
7

7

7

7

7

7

7

7

5

Elementy macierzy rozkładu obliczamy
rekurencyjnie:

Rozwiązanie układu Tx=b:

l

i

=

a

i

u

i

¡1

U x = y

T x = b

T =

2
6

6

6

6

6

6

6

6

4

d

1

c

1

a

2

d

2

c

2

a

3

d

3

c

3

. .. ... ...

. .. ...

c

n

¡1

a

n

d

n

3
7

7

7

7

7

7

7

7

5

u

1

= d

1

u

i

= d

i

¡ l

i

c

i

¡1

;

i = 2; 3; : : : ; n

Ly = b

22

Rozwiązanie:

nakład obliczeń: M=2n-2, D=n-1
liczba zajętych komórek: P=3n-2

Jeśli macierz jest

dominująca kolumnowo

to

rozkład T=LU jest równoważny rozkładowi z
częściowym wyborem elementu podstawowego
(niezawodność metody).

Iteracyjne poprawianie rozwiązania układu
równań

Błąd rozwiązania można sprawdzić obliczając

wektor reszt

:

Zazwyczaj współrzędne wektora r są różne od
zera. Oznacza to, że nie uzyskaliśmy dokładnego
rozwiązania, ale przybliżone. Rozwiązanie to
chcemy poprawić:

x

n

=

y

n

u

n

gdzie:

x jest poprawką, którą można łatwo

wyznaczyć rozwiązując układ:

Należy jednak pamiętać, że wyznaczona poprawka
do rozwiązania również jest przybliżeniem. Kolejne

poprawione rozwiązanie

, które uzyskamy będzie

miało postać:

Jeżeli wektor reszt r=b-Ax jest obliczony dokładnie,
poprawka

x została wyznaczona metodą Gaussa-

Crouta oraz zachodzi warunek:

wówczas norma wektora reszt obliczona w kolejnych
iteracjach maleje

A±x = r

r = b

¡ A~x

~

x = x

¡ ±x

¹

x = ~

x + ±x + ±(±x)

jjb ¡ A¹xjj

1

·

1
2

jjb ¡ Axjj

1

y

1

= b

1

y

i

= b

i

¡ l

i

y

i

¡1

x

i

=

y

i

¡ c

i

x

i+1

u

i

;

i = n

¡ 1; n ¡ 2; : : : ; 1

1
2

jjrjj

1

¸ "jjAjj

1

W

3

(n)

jj±xjj

1

+

jjAxjj

1

"

W

3

(n) =

9
2

n

3

+

61

2

n

2

¡ 18n ¡ 16

23

Algorytm iteracyjnego poprawiania rozwiązania:

1. Rozwiązujemy układ Ax

(1)

=b metodą Gaussa

2. Obliczamy wektor reszt r

(1)

i sprawdzamy

rozwiązanie

3. Sprawdzamy czy poniższy warunek jest prawdziwy

jeśli nie to przerywamy obliczenia. Jeśli jest

spełniony to kontynuujemy.

4. Obliczamy poprawkę i wyznaczamy

5. Wyznaczamy wektor reszt r

(2)

i sprawdzamy

rozwiązanie. W razie konieczności powtarzamy

kroki 3,4,5 aż do skutku.

jjr

i

jj

1

>

jjAx

(1)

jj

1

"

±x

(1)

x

(2)

= x

(1)

+ ±x

(1)

24

Rozwiązywanie układów liniowych
nadokreślonych

Jak rozwiązać poniższy problem?

dla warunku

Brak dokładnego rozwiązania w większości
przypadków. Można poszukiwać conajwyżej
„najlepszego” przybliżenia rozwiązania w sensie
średniokwadratowym.
Dla

rozwiązaniem średniokwadratowym problemu
nadokreślonego (

least square problem

) jest taki

wektor x, który minimalizuje normę:

2
6

6

6

6

6

6

6

6

4

a

11

: : :

a

1n

a

21

: : :

a

2n

: : :

: : :

: : :

: : :

: : :

: : :

: : :

: : :

: : :

: : :

: : :

: : :

a

m1

: : :

a

mn

3
7

7

7

7

7

7

7

7

5

¢

2

6

6

4

x

1

: : :
: : :

x

n

3

7

7

5 =

2
6

6

6

6

6

6

6

6

4

b

1

b

2

: : :
: : :
: : :
: : :

b

m

3
7

7

7

7

7

7

7

7

5

m > n

r = b

¡ Ax

jjrjj

2

= (r

T

r)

1=2

Jeśli macierz A jest macierzą o rozmiarach mxn i
elementach rzeczywistych, b jest wektorem m-
elementowym, a x wektorem n elementowym
spełniającym równanie

wówczas dla dowolnego n-elementowego wektora y
spełniona jest nierówność

Dla dowolnego wektora otrzymujemy warunek

skąd wynika że wektor r jest ortogonalny do
wszystkich wektorów z przestrzeni R(A) rozpiętej na
wektorach kolumnowych macierzy A.
Ponadto nadokreślony układ równań można
przekształcić do postaci

układu normalnego

Macierz A

T

A jest symetryczna, dlatego układ

normalny można rozwiązać metodą Cholesky'ego.
Jeśli kolumny macierzy A są niezależne liniowo to
macierz jest nieosobliwa.

A

T

(b

¡ Ax) = 0

jjb ¡ Axjj

2

· jjb ¡ Ayjj

2

(Az)

T

(b

¡ Ax) = 0

(A

T

A)x = A

T

b

x

6= 0 ! Ax 6= 0

x

T

(A

T

A)x

=

(Ax)

T

Ax =

jjAxjj

2

2

> 0

! det(A

T

A) > 0

25

Gdy kolumny A są niezależne liniowo, wówczas
rozwiązanie układu jest jednoznaczne

gdzie macierz A

I

:

jest

pseudoodwrotnością

macierzy A.

P

A

jest operatorem rzutu ortogonalnego na

przestrzeń kolumnową macierzy A.

Uwaga: jeśli kolumny A są zależne liniowo
(

bardzo często

) to wówczas istnieje wiele

rozwiązań (średniokwadratowych ) dających ten
sam wektor reszt.

Przykład – wpływ uwarunkowania macierzy na
rozwiązanie układu normalnego

x = A

I

b

A

I

= (A

T

A)

¡1

A

T

r

=

(I

¡ P

A

)b

P

A

=

AA

I

= A(A

T

A)

¡1

A

T

A =

2

6

6

4

1

1

1

"

0

0

0

"

0

0

0

"

3

7

7

5 ; b =

2

6

6

4

1
0
0
0

3

7

7

5 ; j"j ¿ 1

Przekształcamy do układu normalnego

Dla precyzji obliczeń rzędu



i macierz A

T

A staje się osobliwa – układ nie posiada

rozwiązania.

Metody wykorzystujące rozkład QR

Dla macierzy A o rozmiarach mxn, w której kolumny
są niezależne liniowo istnieje jednoznaczny rozkład
w postaci

Q jest macierzą o rozmiarach mxn taką że:

D jest macierzą diagonalną

A

T

A

=

2

4

1 + "

2

1

1

1

1 + "

2

1

1

1

1 + "

2

3

5

A

T

b

=

2

4

1
1
1

3

5

"

2

¼ 0

A = QR

Q

T

Q = D

D = diag(d

1

; d

2

; : : : ; d

n

)

d

k

> 0; k = 1; : : : ; n

26

R jest macierzą trójkątną górną z elementami

Warunek minimalizacji normy wektora reszt w
sensie średniokwadratowym przyjmuje postać

Jak wyznaczyć macierze Q i R?

Zmodyfikowana metoda Grama-Schmidta

Wyznaczamy ciąg macierzy

r

kk

= 1; k = 1; : : : ; n

A = A

(1)

; A

(2)

; : : : ; A

(n+1)

= Q

q

i

=

2

6

6

4

q

1;i

: : :
: : :

q

m;i

3

7

7

5

a

(k)
i

=

2

6

6

6

4

a

(k)
1;i

: : :
: : :

a

(k)
m;i

3

7

7

7

5

A

(k)

=

³

q

1

; : : : ; q

k

¡1

; a

(k)
k

; : : : ; a

(k)

n

´

Założenia

1) k-1 pierwszych kolumn w A

(k)

to także k-1

pierwszych kolumn w Q

2) kolumny

są ortogonalne do kolumn

Proces ortogonalizacji polega na rekurencyjnej
ortogonalizacji kolumn o indeksie od k do n w k-tej
iteracji względem kolumny q

k

w ten sposób wyznaczamy k-tą kolumnę R (elementy
r

kj

) oraz kolumnę k+1 macierzy Q (elementy a

j

(k+1)

).

Klasyczna met. GS:

q

1

; : : : ; q

k

¡1

q

k

= a

(k)
k

;

d

k

= q

T

k

q

k

;

r

kk

= 1

a

(k)
k

; : : : ; a

(k)

n

Ax = b

) A

T

Ax = A

T

b

R

T

Q

T

QRx = R

T

Q

T

b

R

T

DRx = R

T

Q

T

b

DRx = Q

T

b

Rx = D

¡1

Q

T

b = y

a

(k+1)
j

=

a

(k)
j

¡ r

kj

a

(k)
k

r

kj

=

q

T

k

a

(k)
j

d

k

j

=

k + 1; : : : ; n

27

klasyczna met. GS
różni się kolejnością
obliczeń:

Jednocześnie przekształcamy wektor b tj.:

Po n+1 krokach b

(n+1)

jest to część wektora

pierwotnego ortogonalna do R(A) i stanowi wektor
reszt.
Po przeprowadzeniu procesu ortogonalizacji do
końca (kolumny macierzy A są liniowo niezależne)
dostajemy

Wyznaczenie R i y wymaga wykonania mn(n+1)
operacji a rozwiązanie układu n(n+1)/2.

Metoda Grama-Schmidta dla macierzy o
liniowo zależnych kolumnach

S=R

-1

jest macierzą trójkątną górną.

Stąd wynika

Może się okazać że a

1

, a

2

,...,a

k-1

są niezależne

liniowo, ale a

k

jest już ich kombinacją (oraz

wektorów q

1

, q

2

,...). Wtedy

(w macierzy Q)
i powinniśmy przerwać proces ortogonalizacji.
Jeśli jednak

to istnieje wektor

Można więc przestawić kolumny j i k oraz
prowadzić proces ortogonalizacji do momentu
gdy pozostałe wektory a

j

(k)

nie będą liniowo

zależne. Szukamy wektora o największej normie:

a następnie za kolumnę k
podstawiamy kolumnę s.

b = b

(1)

; b

(2)

; : : : ; b

(n+1)

b

(k+1)

= b

(k)

¡ y

k

q

k

;

y

k

=

q

T

k

b

(k)

d

k

Q

=

(q

1

; : : : ; q

n

)

R

=

(r

kj

)

y

=

(y

1

; y

2

; : : : ; y

n

)

T

A

=

QR

b

=

Qy + r

Rx

=

y

A = QR

! AR

¡1

= Q

! Q = AS

q

k

= s

1k

a

1

+ s

2k

a

2

+ : : : + s

kk

a

k

rank(A) > k

a

(k)
j

6= 0;

k

· j · n

jja

k

s

jj

2

= max

k

·j·n

jja

(k)
j

jj

2

q

k

= a

k

¡

k

¡1

X

i=1

r

ik

q

i

r

ik

=

q

T

i

a

k

d

i

; i = 1; 2; : : : ; k

¡ 1

a

(k)
k

= 0

28

Dla rank(A)=r

A

<n rozkład QR ma postać

gdzie: R

rxr

-macierz trójkątna górna (r

kk

=1)

S- macierz o rozmiarach r

A

x

(n-r

A

)

Rozwiązania szukamy rozwiązując układ

gdzie: x

1

- ma r składowych, x

2

– jest dowolnym

wektorem o n-r składowych (np. x

2

=0).

(R; S)x = y

x = (x

1

; x

2

)

T

x

1

= R

¡1

y

¡ R

¡1

Sx

2

Przykład

zakładamy

Q =

2

6

6

4

1

0

0

"

¡" ¡"=2

0

"

¡"=2

0

0

¡"=2

3

7

7

5 ;

r =

¡

1
3

"

2

6

6

4

0
1
1
1

3

7

7

5

R =

2

4

1

1

1

0

1

1=2

0

0

1

3

5 ; y =

2

4

1

1=2
1=3

3

5

x =

2

4

1=3
1=3
1=3

3

5 ; x

dok

=

2

4

1=(3 + "

2

)

1=(3 + "

2

)

1=(3 + "

2

)

3

5

"

¿ 1;

"

2

¼ 0

Q

=

(q

1

; q

2

; : : : ; q

r

A

)

A

=

Q(R; S)

b

=

Qy + r