Cel ćwiczenia:

Celem ćwiczenia jest zapoznanie z podstawowymi algorytmami rozwiązywania układów równań liniowych metodami dokładnymi i iteracyjnymi

Zadanie do zrealizowania:

Rozwiązanie obwodu metodą (Rys.1) przy pomocy programu Scilab

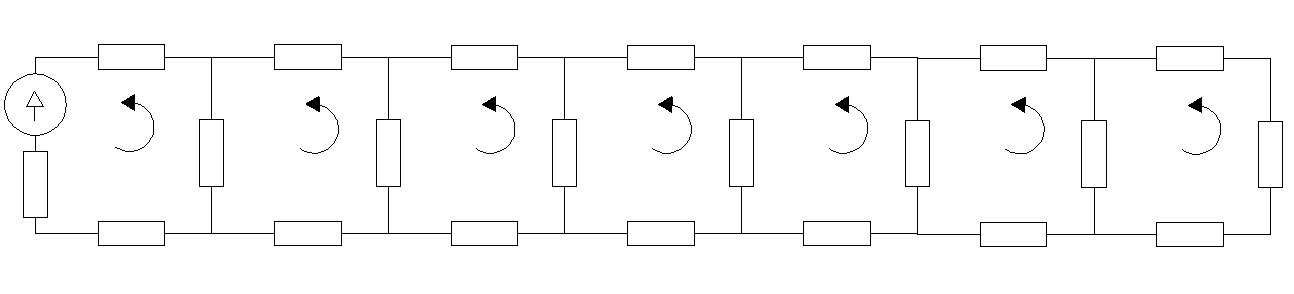
Rys1.Schemat obwodu podanego przez prowadzącego

Przebieg ćwiczenia :

1. Wyznaczenie prądów oczkowych w obwodzie drabinkowych rozwiązując układ równań metodą eliminacji Gaussa

2. Wyznaczenie prądów oczkowych w obwodzie drabinkowych rozwiązując układ równań metodą wbudowanej funkcji linsolve() programu Scilab

3. Wyznaczenie prądów oczkowych w obwodzie drabinkowych rozwiązując układ równań metodą iteracji prostej Jacobiego (dwa eksperymenty dla różnych dokładności)

Wyznaczenie prądów oczkowych w obwodzie drabinkowych rozwiązując układ równań metodą eliminacji Gaussa

R=10;

A=diag(4*R*ones(7,1))+diag(-R*ones(6,1),1)+diag(-R*ones(6,1),-1)//wyznaczenie macierzy A na podstawie schematu elektrycznego

b=[10;0;0;0;0;0;0] // wyznaczenie macierzy b na podstawie schematu elektrycznego

Ab=[A b] // połączenie macierzy A i b

L12=Ab(2,1)/Ab(1,1) // mnożnik eliminacji

Ab(2,:) = Ab(2,:) - L12*Ab(1,:) eliminacja z 2 równania

L13=Ab(3,1)/Ab(1,1) // mnożnik eliminacji

Ab(3,:) =;0;0;0] //Ab(3,:) - L13*Ab(1,:) eliminacja z 3 równania

L23=Ab(3,2)/Ab(2,2))

Ab(3,2:$)=Ab(3,2:$)-L23*Ab(2,2:$)

L24=Ab(4,2)/Ab(2,2))

Ab(4,2:$)=Ab(4,2:$)-L24*Ab(2,2:$)

L34=Ab(4,3)/Ab(3,3))

Ab(4,3:$)=Ab(4,3:$)-L34*Ab(3,3:$)

L35=Ab(5,3)/Ab(3,3))

Ab(5,3:$)=Ab(5,3:$)-L35*Ab(3,3:$)

L45=Ab(5,4)/Ab(4,4

Ab(5,4:$)=Ab(5,4:$)-L45*Ab(4,4:$)

L46=Ab(6,4)/Ab(4,4)) // mnożnik eliminacji

Ab(6,4:$)=Ab(6,4:$)-L46*Ab(4,4:$) // eliminacja 6 równania

L56=Ab(6,5)/Ab(5,5))

Ab(6,5:$)=Ab(6,5:$)-L56*Ab(5,5:$)

L67=Ab(7,6)/Ab(6,6

Ab(7,6:$)=Ab(7,6:$)-L67*Ab(6,6:$)

// obliczanie wyników od końca

x(7)=Ab(7,8)/Ab(7,7) )

x(6)=(Ab(6,8)-Ab(6,7)*x(7))/Ab(6,6)

x(5)=(Ab(5,8)-Ab(5,6)*x(6))/Ab(5,5)

x(4)=(Ab(4,8)-Ab(4,5)*x(5))/Ab(4,4)

x(3)=(Ab(3,8)-Ab(3,4)*x(4))/Ab(3,3)

x(2)=(Ab(2,8)-Ab(2,3)*x(3))/Ab(2,2)

x(1)=(Ab(1,8)-Ab(1,2)*x(2))/Ab(1,1)

Wyniki :

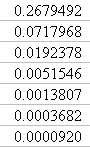
x =

0.2679492

0.0717968

0.0192378

0.0051546

0.0013807

0.0003682

0.0000920

Wyznaczenie prądów oczkowych w obwodzie drabinkowych rozwiązując układ równań metodą wbudowanej funkcji linsolve() programu Scilab

R=10;

A=diag(4*R*ones(7,1))+diag(-R*ones(6,1),1)+diag(-R*ones(6,1),-1)//wyznaczenie macierzy A na podstawie schematu elektrycznego

b=[10;0;0;0;0;0;0] // wyznaczenie macierzy b na podstawie schematu elektrycznego

xtest=linsolve(A,-b) // wybudowana funkcja Scilab'a obliczająca prądy oczkowe

xtest =

0.2679492

0.0717968

0.0192378

0.0051546

0.0013807

0.0003682

0.0000920

Wyznaczenie prądów oczkowych w obwodzie drabinkowych rozwiązując układ równań metodą iteracji prostej Jacobiego (dwa eksperymenty dla różnych dokładności)

1.) Dokładności bezwzględna 1 mA

R=10;

A=diag(4*R*ones(7,1))+diag(-R*ones(6,1),1)+diag(-R*ones(6,1),-1)//wyznaczenie macierzy A na podstawie schematu elektrycznego

b=[10;0;0;0;0;0;0] // wyznaczenie macierzy b na podstawie schematu elektrycznego

L=tril(A,-1) // macierze poddiagonalna

D=diag(diag(A)) // macierze diagonalna

U=triu(A,1) // macierze naddiagonalna

Dinv=inv(D) // macierz odwrotna

//Pętla z instrukcją for dla dokładności bezwzględnej 1 mA

i=1

x(:,1)=b

for i=2:50,x(:,i)=-Dinv*(L+U)*x(:,i-1)+Dinv*b

if sum(abs(x(:,i)-x(:,i-1))) <0.001,

break;

end

end

// ręczne poprawienie uwarunkowania układu równań

TempA=A(7,:);

A(7,:)=A(6,:);

A(6,:)=A(5,:);

A(5,:)=A(4,:);

A(4,:)=A(3,:);

A(3,:)=A(2,:);

A(2,:)=A(1,:);

A(1,:)=TempA;

TempB=b(7);

b(7)=b(6);

b(6)=b(5);

b(5)=b(4);

b(4)=b(3);

b(3)=b(2);

b(2)=b(1);

b(1)=TempB;

plot(1:i, x(:,1:i)); // polecenie do rysowania wykresu

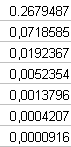
2. Dokładność bezwzględna 1μA

R=10;

A=diag(4*R*ones(7,1))+diag(-R*ones(6,1),1)+diag(-R*ones(6,1),-1)//wyznaczenie macierzy A na podstawie schematu elektrycznego

b=[10;0;0;0;0;0;0] // wyznaczenie macierzy b na podstawie schematu elektrycznego

L=tril(A,-1) // macierze poddiagonalna

D=diag(diag(A)) // macierze diagonalna

U=triu(A,1) // macierze naddiagonalna

Dinv=inv(D) // macierz odwrotna

//Pętla z instrukcją for dla dokładności bezwzględnej 1 mA

i=1

x(:,1)=b

for i=2:50,x(:,i)=-Dinv*(L+U)*x(:,i-1)+Dinv*b

if sum(abs(x(:,i)-x(:,i-1))) <0.00001,

break;

end

end

// ręczne poprawienie uwarunkowania układu równań

TempA=A(7,:);

A(7,:)=A(6,:);

A(6,:)=A(5,:);

A(5,:)=A(4,:);

A(4,:)=A(3,:);

A(3,:)=A(2,:);

A(2,:)=A(1,:);

A(1,:)=TempA;

TempB=b(7);

b(7)=b(6);

b(6)=b(5);

b(5)=b(4);

b(4)=b(3);

b(3)=b(2);

b(2)=b(1);

b(1)=TempB;

plot(1:i, x(:,1:i)); // polecenie do rysowania wykresu

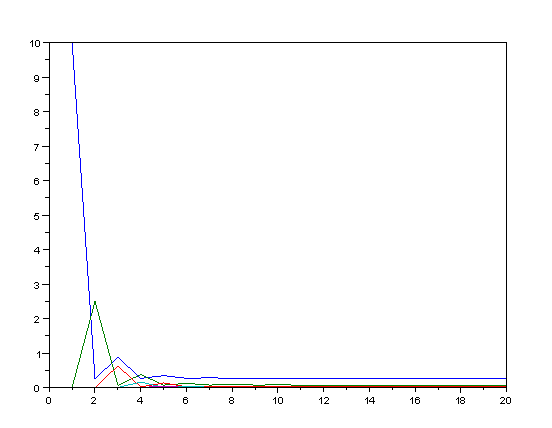
Wnioski :

Sprawdzenie wyników :

Wbudowana funkcja linsolve()	Metoda eliminacji Gaussa	Iteracja prosta Jacobiego 1 mA	Iteracja prosta Jacobiego 1 μA
0.2679492	0.2679492	0.2679487	0.2679492
0.0717968	0.0717968	0,0718585	0.0717968
0.0192378	0.0192378	0,0192367	0.0192378
0.0051546	0.0051546	0,0052354	0.0051546
0.0013807	0.0013807	0,0013796	0.0013807
0.0003682	0.0003682	0,0004207	0.0003682
0.0000920	0.0000920	0,0000916	0.0000920

Powyższych danych wynika , że wbudowana dokładnością bezwzględną Scilab'a jest dokładność rzędu 1μ=0,00001

---