38

ÂWIAT NAUKI PAèDZIERNIK 2004

ATOMOWE

TRZY SPOÂRÓD TEORII stworzonych przez Einsteina okaza∏y si´ szczególnie

inspirujàce dla in˝ynierów na poczàtku obecnego stulecia. Ruchy Browna

– intrygujàce b∏àdzenia mikroskopijnych drobin, których natur´ Einstein

jako pierwszy prawid∏owo wyjaÊni∏ – próbuje si´ wykorzystaç w nowego

rodzaju filtrach. Z kolei w rodzàcej si´ w∏aÊnie spintronice zastosowanie

znajduje szczególna teoria wzgl´dnoÊci, a na bazie kondensatu Bosego–Einsteina,

niezwyk∏ego stanu materii, którego istnienie genialny fizyk przewidzia∏ 80 lat temu,

w rozrzuconych po ca∏ym Êwiecie laboratoriach opracowuje si´ czujniki przyÊpieszenia.

PRZEGLÑD

• Abstrakcyjne idee Einsteina

wcià˝ sà inspiracjà dla in˝y-

nierów. Na przyk∏ad szczegól-

na teoria wzgl´dnoÊci odgry-

wa kluczowà rol´ w uk∏adach,

które pozwalajà manipulowaç

spinami elektronów.

• Opis ruchu czàstek dopro-

wadzi∏ do stworzenia tzw. za-

padek Browna, które pozwa-

lajà szybko sortowaç DNA lub

oddzielaç cia∏a sta∏e od cieczy.

• S∏uszne okaza∏y si´ te˝

przewidywania Einsteina, ˝e

kraƒcowo sch∏odzone atomy

b´dà „kondensowaç” w stan

o w∏aÊciwoÊciach Êwiat∏a la-

serowego. Zjawisko mo˝e ju˝

wkrótce oka˝e si´ przydatne

przy konstrukcji superdok∏ad-

nych czujników pola grawita-

cyjnego, a tak˝e niezwykle

stabilnych ˝yroskopów.

poÊwi´conà rozmiarom czàstek. Aby zarobiç na
˝ycie, pracowa∏ w szwajcarskim biurze patento-
wym, analizujàc cudze wynalazki. Mo˝na by po-
myÊleç, ˝e ta praca powinna zainspirowaç go
do zastanowienia si´ nad praktycznymi aspek-
tami teorii, które w wolnym czasie tworzy∏. Ale
chocia˝ tamtego roku opublikowa∏ a˝ pi´ç naj-
wa˝niejszych w swojej niezwyk∏ej karierze prac
naukowych, nie zdradza∏ przekonania, ˝e jego
nowatorskie poglàdy na temat materii, energii
i czasu kiedykolwiek przyczynià si´ do post´pu
w przemyÊle czy medycynie.

Nie znaczy to jednak, ˝e Einstein in˝ynieri´

lekcewa˝y∏. Po prostu nie by∏a ona jego mocnà
stronà. Jego wynalazki – ch∏odziarka bez rucho-
mych cz´Êci i nieprzeciekajàca pompa – nigdy
nie wesz∏y do masowej produkcji, choç ta ostat-
nia znalaz∏a zastosowanie w reaktorach powie-
lajàcych. To jednak bez znaczenia; opierajàc si´
na niezwyk∏ych spostrze˝eniach Einsteina, ˝e
Êwiat∏o rozchodzi si´ w postaci paczek – foto-
nów, które zawsze biegnà z tà samà i najwi´k-
szà mo˝liwà pr´dkoÊcià c – a materia i energia
zgodnie z równaniem E = mc

2

sà sobie równo-

wa˝ne, naukowcy opracowali w XX wieku po-
t´˝ne techniki [patrz: „Einstein na co dzieƒ”,
strona 32].

Obecnie in˝ynierowie wykorzystujà s∏ynne teo-

rie w nowych sytuacjach, czego najlepszym przy-
k∏adem sà innowacyjne projekty komputerów.
Konstruktorzy znajdujà zastosowania dla niektó-
rych mniej znanych teorii Einsteina. Na przyk∏ad
specjaliÊci od nanotechnologii pracujà nad urzà-
dzeniami, które mogà przyÊpieszyç analiz´ DNA,
dzi´ki wykorzystaniu przypadkowych ruchów czà-

stek – zjawiska, które Einstein poprawnie wyjaÊni∏
w roku 1905. W laboratoriach na ca∏ym Êwiecie
bada si´ nowe formy materii, których istnienie
Einstein przewidzia∏ w roku 1925, w jednym ze
swoich s∏ynnych eksperymentów myÊlowych. Sku-
piska ultrazimnych spójnych atomów, które w
Êwiecie materii sà odpowiednikiem Êwiat∏a lase-
rowego, mogà znaleêç zastosowanie w przenoÊ-
nych zegarach atomowych, superprecyzyjnych
˝yroskopach przeznaczonych do nawigacji i czuj-
nikach pola grawitacyjnego u∏atwiajàcych poszu-
kiwanie pól naftowych i minera∏ów.

W artykule tym b´dzie mowa o trzech nowych

dziedzinach, które narodzi∏y si´ ostatnio w labo-
ratoriach, a ich bazà sà teorie Einsteina, i nie
ulega wàtpliwoÊci, ˝e w przysz∏oÊci pojawià si´
kolejne. Chocia˝ up∏yn´∏o ju˝ niemal sto lat od
chwili, kiedy uczony stworzy∏ narz´dzia matema-
tyczne pozwalajàce lepiej opisaç WszechÊwiat,
inteligentni wynalazcy wcià˝ na ich podstawie
konstruujà nowe urzàdzenia.

Teoria wzgl´dnoÊci a spin

JEDYNYM KOMPUTEREM

, jakiego Einstein u˝ywa∏,

tworzàc w 1905 roku teori´ wzgl´dnoÊci, by∏ jego
w∏asny mózg. Pod wieloma wzgl´dami maszyna
biochemiczna ma znacznie wi´ksze mo˝liwoÊci
ni˝ jakikolwiek komputer elektroniczny – ˝aden
z dotychczas wyprodukowanych pó∏przewodni-
kowych mikroprocesorów nie mo˝e konkurowaç
pod wzgl´dem g´stoÊci upakowania i sprawnoÊci
energetycznej z ludzkim mózgiem, którego kilo-
gram zawiera z grubsza 1000 bln elementów, zu-
˝ywajàcych w dodatku mniej energii i wydziela-
jàcych mniej ciep∏a ni˝ Pentium 4.

PAèDZIERNIK 2004 ÂWIAT NAUKI

39

DA

VID EMMITE

PROPOZYCJE

NA WIEK XXI

W 1905 roku Albert Einstein mia∏ 26 lat i koƒczy∏ rozpraw´ doktorskà

Technologie nowej generacji

pozwalajà zastosowaç teorie Einsteina

w komputerach, urzàdzeniach medycznych,

a nawet okr´tach podwodnych

W. Wayt Gibbs

ALFRED T

. KAMAJIAN

To w∏aÊnie odprowadzanie ciep∏a i rosnàce zapotrzebo-

wanie na energi´ sà dziÊ g∏ównymi przeszkodami w kon-
struowaniu coraz pot´˝niejszych, a mimo tu wcale nie dro˝-
szych mikroprocesorów. W nadchodzàcym dwudziestoleciu
producenci procesorów krzemowych w znanej nam dziÊ po-
staci napotkajà fundamentalne ograniczenia natury ekono-
micznej i fizycznej. Nie b´dà wi´c mieli innego wyboru –
zwrócà si´ w stron´ innych zjawisk fizycznych, na przyk∏ad
zwiàzanych ze szczególnà teorià wzgl´dnoÊci.

Na pozór to doÊç dziwaczny pomys∏. Przecie˝ szczególna

teoria wzgl´dnoÊci opisuje ruch cia∏ z wielkimi pr´dkoÊcia-
mi, Einstein odrzuci∏ w niej koncepcje absolutnego czasu i
absolutnego spoczynku. Jedyna sta∏a, jakà wprowadzi∏, to c

– pr´dkoÊç, z którà Êwiat∏o rozchodzi si´ w pró˝ni. Dla cia-
∏a, które nabiera pr´dkoÊci (wzgl´dem obserwatora), ma to
zdumiewajàce konsekwencje. Jego d∏ugoÊç maleje, a czas w
uk∏adzie z nim zwiàzanym wydaje si´ biec wolniej ni˝ dla
obserwatora. Ponadto jeÊli cia∏o porusza si´ w polu elektro-
statycznym, doÊwiadcza jego dzia∏ania tak, jakby pole to by-
∏o w cz´Êci magnetyczne. Wspomniane efekty relatywistycz-
ne sà pomijalne, jeÊli pr´dkoÊç nie jest znaczàcym u∏amkiem
pr´dkoÊci Êwiat∏a c, wynoszàcej prawie 300 000 km/s.

Nawet przenoÊne komputery nie „poruszajà si´” tak szyb-

ko, aby efekty te mia∏y znaczenie. Inaczej jest jednak z p∏y-
nàcymi w ich wn´trzu elektronami. Na poczàtku tego roku
grupa fizyków kierowana przez Davida D. Awschaloma z
University of California w Santa Barbara pokaza∏a, jak za
pomocà teorii wzgl´dnoÊci zmusiç szybkie elektrony w pó∏-
przewodniku do niezwyk∏ych wyczynów.

Prace sà wcià˝ we wst´pnej fazie, którà mo˝na porównaç

z budowaniem pierwszych bramek logicznych mniej wi´cej
40 lat temu. Ale je˝eli in˝ynierowie wymyÊlà, jak w niewiel-
kim krzemowym chipie zintegrowaç miliony relatywi-
stycznych bramek – a Awschalom nawiàza∏ tym celu wspó∏-
prac´ z zespo∏ami badawczymi z Intela i Hewlett-Packarda

– mogà powstaç procesory znacznie szybsze od dzisiejszych,
zu˝ywajàce mniej energii, a co za tym idzie, wydzielajàce
mniej ciep∏a.

Co wi´cej, dzi´ki uk∏adom relatywistycznym mo˝na by

przejÊç na logik´ bardziej z∏o˝onà ni˝ binarna, b´dàca fun-
damentem wspó∏czesnych komputerów. W zasadzie nowe
maszyny b´dà mog∏y modyfikowaç swojà wewn´trznà ar-
chitektur´, dostosowujàc si´ niemal natychmiast do wykony-
wanych zadaƒ. Wyobraêmy sobie na przyk∏ad telefon ko-
mórkowy, w którym cz´Êç nadawczo-odbiorcza dostosuje
si´ do dowolnego standardu sieci, a naciÊni´cie guzika uru-
chomi program t∏umaczàcy mow´.

Uk∏ady scalone nowego typu wytwarzane b´dà najpraw-

dopodobniej w istniejàcych fabrykach. Nowym elementem nie
jest bowiem sam materia∏, ale wspó∏czesna fizyka – teoria
wzgl´dnoÊci i mechanika kwantowa.

Przyciàganie magnetyczne

DZIA

¸ANIE ZWYK¸YCH

pó∏przewodnikowych uk∏adów scalo-

nych opiera si´ na „klasycznej”, XIX-wiecznej teorii elektro-
magnetyzmu. P∏ytki krzemowe sà domieszkowane jonami,
które skupione w niewielkich wyspach dajà w nich nadmiar
lub niedobór elektronów. Napi´cia przyk∏adane do mikro-
skopijnych elektrod otaczajàcych wyspy wpychajà lub wy-
ciàgajà z nich elektrony, otwierajàc i zamykajàc bramki lo-
giczne oraz sterujàc przep∏ywem pràdu.

Kontrolowanie ruchu du˝ej liczby elektronów nie jest su-

perprecyzyjne – cz´Êç z nich rozbiega si´ w przypadkowych
kierunkach, a energia jest rozpraszana w wielu zderzeniach
w postaci ciep∏a. Ju˝ od przesz∏o 10 lat fizycy poszukujà sub-
telniejszego rozwiàzania – starajà si´ sterowaç elektronami,
wykorzystujàc pole magnetyczne, a nie elektryczne.

Jak wyjaÊnia Michael E. Flatté, fizyk z University of Io-

wa, jest to mo˝liwe, poniewa˝ elektron zachowuje si´ tak,
jakby znajdowa∏ si´ w nim malutki magnes sztabkowy. Ma-
gnesy majà biegun pó∏nocny i po∏udniowy. Podobnie jak Zie-
mia, która wiruje wokó∏ osi ∏àczàcej bieguny, tak elektron
ma orientacj´ magnetycznà opisanà przez wielkoÊç kwan-
towà zwanà spinem. Nazwa ta (z angielskiego „wirowaç”)
sugeruje zwiàzek z ruchem obrotowym. Czàstki w rzeczy-
wistoÊci nie wirujà, chocia˝ zachowujà si´ tak, jakby by∏y

40

ÂWIAT NAUKI PAèDZIERNIK 2004

Relatywistyczne chipy pozwolà wyjÊç

poza stosowanà dziÊ logik´ binarnà.

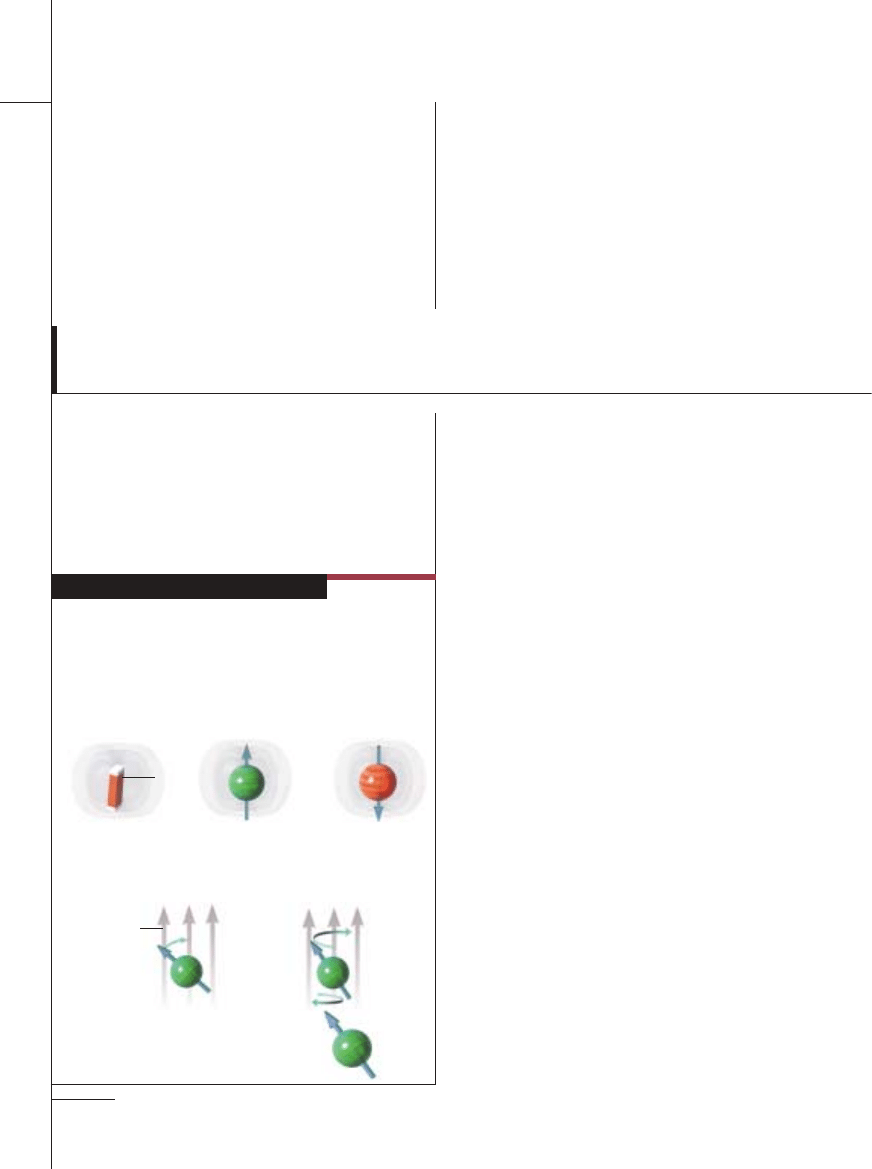
Magnetyczna magia

Elektron ma pewnà w∏aÊciwoÊç kwantowà zwanà spinem, która spra-
wia, ˝e zachowuje si´ on podobnie jak magnes wirujàcy wokó∏ osi ∏à-
czàcej biegun pó∏nocny i po∏udniowy. Spiny elektronów (kulki) mogà
byç ró˝nie zorientowane.

Pole magnetyczne sprawia, ˝e spin elektronu ustawia si´ wzd∏u˝ linii
pola podobnie jak ig∏a kompasu (poni˝ej z lewej). Ale kierunek spinu
mo˝e te˝ wykonywaç precesj´ podobnie jak zataczajàcy si´ bàk (po-
ni˝ej z prawej).

Po wy∏àczeniu pola magnetycznego precesja
elektronu ustaje, a kierunek spinu si´ ustala.

SPINY ELEKTRONÓW

Magnes

N

N

N

N

S

S

S

S

Pole

magnetyczne

ALFRED T

. KAMAJIAN

maleƒkimi wirujàcymi bàkami. Po umieszczeniu elektronu
w polu magnetycznym jego spin ulega precesji – oÊ z nim
zwiàzana kreÊli okràg. Po wy∏àczeniu pola magnetycznego
spin elektronu zachowuje ustalony kierunek [ramka na
poprzedniej stronie]. „Wykorzystujàc to zjawisko, mo˝na od-
wróciç orientacj´ spinu, który raz b´dzie wskazywaç «gó-
r´», a raz «dó∏», a zatem zmieniaç informacj´, którà niesie
elektron, z 1 na 0” – wyjaÊnia Flatté.

Podczas gdy w elektronice informacje sà zakodowane w po-

staci liczby i energii elektronów w obwodzie, w rodzàcej si´
dopiero spintronice dane sà zwiàzane z orientacjà elektronu,
a operacje logiczne polegajà na obracaniu spinów tam i z
powrotem [patrz: David D. Awschalom, Michael E. Flatté i
Nitin Samarth „Spintronika”; Âwiat Nauki, sierpieƒ 2002].
W tym roku Motorola uruchomi∏a produkcj´ spintronicz-
nych chipów pami´ci, tzw. MRAM (magnetycznych RAM).
W odró˝nieniu od tradycyjnych pami´ci komputerowych
koÊci MRAM nie tracà zapisanych danych po od∏àczeniu za-
silania; elektrony zachowujà orientacje spinów a˝ do po-
nownego w∏àczenia pràdu.

Elementy spintroniczne wyÊmienicie nadajà si´ do urzà-

dzeƒ zasilanych z baterii, poniewa˝ odwrócenie spinów nie
wymaga wiele energii, a pràd mi´dzy poszczególnymi ope-
racjami mo˝na wy∏àczaç. Odwrócenie spinu nie wp∏ywa
na energi´ kinetycznà czàstki, a wi´c w uk∏adach praktycz-
nie nie wydziela si´ ciep∏o. Ponadto proces ten jest niezmier-
nie szybki – w uk∏adach eksperymentalnych odwrócenie

spinu trwa∏o nie d∏u˝ej ni˝ kilka pikosekund (bilionowych
cz´Êci sekundy).

Do niedawna jednak wszystkie uk∏ady spintroniczne mu-

sia∏y zawieraç metale ferromagnetyczne, które nie∏atwo
wkomponowaç w uk∏ady scalone z zastosowaniem obecnych
technologii. „Trudno sobie wyobraziç, jak rozmieÊciç malut-
kie magnesy w milionach ró˝nych miejsc chipu, a nast´p-
nie ka˝dym z nich z osobna sterowaç. Nie jest to wprawdzie
niemo˝liwe, ale bardzo trudne – stwierdza Awschalom. –
Znacznie elegantszym rozwiàzaniem by∏oby wykorzystanie
ju˝ istniejàcych, wartych biliony dolarów instalacji produk-
cyjnych i u˝ycie do gry w spiny pola elektrycznego”.

Od cyfr binarnych do fazowych

WRÓ

åMY DO EINSTEINA

i przypomnijmy sobie jego zaskaku-

jàce spostrze˝enie, ˝e z pozycji szybko poruszajàcego si´
elektronu pole elektryczne wyglàda jak magnetyczne. W
pracy opublikowanej w styczniu zespó∏ Awschaloma wyka-
za∏, ˝e na∏o˝enie na siebie dwóch warstw pó∏przewodni-
ków o nieco ró˝nej strukturze wywo∏uje napr´˝enia, któ-
re sà êród∏em wewn´trznego pola elektrycznego. Pole ma
obszary o du˝ym i ma∏ym nat´˝eniu, które odgrywajà rol´
p∏otów na drodze elektronów przez pó∏przewodnik. „Teo-
ria wzgl´dnoÊci mówi, ˝e dla poruszajàcych si´ elektronów
pole elektryczne jest po cz´Êci polem magnetycznym” –
stwierdza badacz. Spiny elektronów rozpoczynajà wi´c pre-
cesj´ jak chyboczàce si´ bàki.

PAèDZIERNIK 2004 ÂWIAT NAUKI

41

RELATYWISTYCZNE MIKROCHIPY

Komputer nie tylko dwójkowy

Szczególna teoria wzgl´dnoÊci podpowiada, jak zbudowaç mikrouk∏ady czu∏e na orientacj´ spinu. Mo˝na by je wytwarzaç, korzystajàc z ist-
niejàcych linii technologicznych. Ze szczególnej teorii wzgl´dnoÊci wynika, ˝e elektrony mknàce przez przyrzàd po cz´Êci odczuwajà statycz-
ne pole elektryczne jako pole magnetyczne. Na skutek oddzia∏ywania magnetycznego spiny elektronów ustawiajà si´ zgodnie z kierunkiem
tego pola. Elektroda zwana bramkà wytwarza pole elektryczne, które mo˝na w∏àczaç i wy∏àczaç. Dla szybko poruszajàcych si´ elektronów tak˝e i
to pole zawiera sk∏adowà magnetycznà, która wywo∏uje precesj´ ich spinów. Zdj´cie napi´cia z bramki wy∏àcza pole, co ustala nowe po∏o˝enie spi-
nu. Dzi´ki zmianom pr´dkoÊci elektronów i nat´˝enia pola elektrycznego wytwarzanego przez bramk´ taki relatywistyczny mikrouk∏ad mo˝e
zapisywaç spintroniczne „bity” nale˝àce do wi´kszego zbioru wartoÊci ni˝ tylko 0 i 1.

Mo˝liwe
wartoÊci
cyfr fazowych

Mo˝liwe wartoÊci

1

cyfr dwójkowych

0

15

14

13

12

11

10

9

8

7

6

5

4

3

2

1

0

Pole magnetyczne,
które elektrony
odbierajà
jako efekt
relatywistyczny

Elektrony
z uporzàdkowanymi
spinami

Bramka

Spiny elektronów ulegajà
precesji, zmieniajàc swà faz´

Arsenek
glinowo-
-galowy

Arsenek
galu

SKALA NIEZACHOWANA

Napr´˝enia w sieci krystalicznej
pó∏przewodnika (linie) sà êród∏em pola
elektrycznego (pomaraƒczowe strza∏ki)

„Mamy dwie metody oddzia∏ywania na elektrony – kon-

tynuuje Awschalom. – Pierwsza to zmiana napi´cia, która
decyduje o ich pr´dkoÊci. Im szybciej poruszajà si´ elektro-
ny, tym silniejsze pole magnetyczne odbierajà”. I tym szyb-
sza jest precesja spinów. Drugi trik polega na wykorzysta-
niu zale˝noÊci napr´˝enia od kierunku. „Mo˝emy te˝ wp∏ywaç
na elektrony, starannie dobierajàc kszta∏t i kierunek kana-
∏u, w którym p∏ynà” – dodaje.

W styczniowym artykule zespó∏ opisuje, jak za pomocà

impulsów Êwiat∏a laserowego zmieniaç orientacj´ spinów –
zapisywaç spintroniczne bity – i jak je odczytywaç, mierzàc
kierunek spinów. „Kolejnym krokiem powinno byç zapisy-
wanie bitów, przesuwanie ich i odczytywanie w jednym przy-

rzàdzie elektronicznym. To bardzo istotny etap i ju˝ uda∏o
nam si´ z tym zadaniem uporaç – mówi Awschalom. – Przy-
rzàd zadowala si´ równie niewielkimi napi´ciami, jak stoso-
wane dziÊ w komputerach uk∏ady CMOS. Spiny elektronów
natychmiast ulegajà polaryzacji, kiedy te docierajà do na-
pr´˝onego obszaru struktury pó∏przewodnikowej. Nast´p-
nie mo˝na spójnie (koherentnie) odwracaç kierunek ich spi-
nu”, w∏àczajàc i wy∏àczajàc napi´cie na elektrodach.

S∏owo „spójne” ma tu podstawowe znaczenie, poniewa˝

wià˝e si´ z nim intrygujàca mo˝liwoÊç wykroczenia w uk∏a-
dach spintronicznych poza tradycyjne bity – zapisywane w
uk∏adzie dwójkowym jako 1 i 0 – i dzia∏ania na cyfrach fa-
zowych (phase digit), które b´dà mog∏y przyjmowaç war-
toÊci z szerszego zbioru. Faza elektronu to kierunek, który
wskazuje jego spin. Wyobraêmy sobie ig∏´ kompasu: je˝eli
uk∏ad b´dzie umia∏ rozró˝niaç elektrony ze spinami o orien-
tacji pó∏nocnej, po∏udniowej, wschodniej i zachodniej, to
ka˝dy fazowy odpowiednik bitu b´dzie móg∏ przyjmowaç
wartoÊci 0, 1, 2 lub 3.

„Im precyzyjniej nauczymy si´ odczytywaç faz´, tym bar-

dziej zag´Êcimy zapis danych – podkreÊla Awschalom. – To,

czy g´stoÊç wzroÊnie 50 czy 10 tys. razy, zale˝y tylko od do-
k∏adnoÊci odczytu kàta”. Po latach badaƒ nad obrazowa-
niem za pomocà rezonansu magnetycznego, dzi´ki któremu
okreÊla si´ spin jàder atomowych, „umiemy mierzyç te kàty
z wielkà dok∏adnoÊcià”.

„Nie uda∏o si´ jeszcze zbudowaç dzia∏ajàcego tranzystora

spinowego” – studzi entuzjazm Flatté. Tranzystorów nie mo˝-
na pominàç, poniewa˝ to one wzmacniajà sygna∏, pozwala-
jàc mu pokonaç wiele bramek w mikroprocesorze. Chocia˝
nie ma jeszcze tranzystorów w wersji spintronicznej, badacze
sà pewni, ˝e si´ pojawià i ju˝ przewidujà ich zastosowania.

W ubieg∏ym roku Reinhold Koch i jego wspó∏pracowni-

cy z berliƒskiego Instytutu Elektroniki Cia∏a Sta∏ego im. Pau-
la Drudego opublikowali projekt spintronicznego elementu
logicznego, którego funkcj´ mo˝na zmieniaç za pomocà
programu. W jednej chwili bramka mo˝e realizowaç funkcj´
AND, a kilka nanosekund póêniej zmieniç si´ w bramk´
OR, NOR lub NAND.

Komputery zdolne do zmiany swojej architektury w czasie

pracy mia∏yby niezwyk∏e mo˝liwoÊci. Koch zaprojektowa∏ nie-
dawno pe∏ny sumator – podstawowà jednostk´ logicznà kom-
putera – zast´pujàc 16 tradycyjnych tranzystorów elektronicz-
nych czterema elementami logiki spinowej. Spintroniczna
wersja uk∏adu zu˝ywa∏aby o 85% mniej energii i zajmowa∏a
o 75% mniej miejsca, a jednoczeÊnie by∏aby równie szybka
jak najlepsze struktury oparte na krzemie.

In˝ynierowie sà wcià˝ dalecy od doskona∏oÊci w wykorzy-

staniu efektów relatywistycznych w projektowaniu mikro-
struktur spintronicznych. Ale technologia oparta na teoriach
Einsteina mo˝e skierowaç na zupe∏nie nowà drog´ przemys∏
komputerowy, w przeciwieƒstwie do dzisiejszej, nienaje˝o-
nà coraz to nowymi przeszkodami. „Jednym z interesujàcych
aspektów tkwiàcej w tym fizyki – t∏umaczy Awschalom – jest
to, ˝e im mniejszy jest przyrzàd, tym lepiej funkcjonuje”.

B∏àdzenie przypadkowe a praca

EINSTEIN ZYSKA

¸ S¸AW¢

g∏ównie dzi´ki swoim ideom odnoszà-

cym si´ do rzeczy wielkich: pr´dkoÊci Êwiat∏a, ewolucji Wszech-
Êwiata, natury czasu. Ale w 1905 roku zwróci∏ uwag´ tak˝e
na mikroskopijne czàstki. W og∏oszonej wtedy rozprawie dok-

42

ÂWIAT NAUKI PAèDZIERNIK 2004

ALFRED T

. KAMAJIAN

Poszturchiwanie

Botanik Robert Brown ku swojemu zaskoczeniu zaobserwowa∏ w 1827
roku, ˝e ziarna py∏ku roÊlin w kropli wody oglàdanej pod mikroskopem
taƒczà, jakby by∏y ˝ywe. Dopiero w 1905 roku Albert Einstein zrozumia∏,
˝e przypadkowe b∏àdzenie drobin jest wywo∏ane bombardowaniem ich
przez czàsteczki wody. Chocia˝ zbyt ma∏e, aby je zobaczyç, poruszajà
si´ tak szybko i wyst´pujà w tak du˝ej liczbie, ˝e uderzajàc w ziarna py∏-
ku, przesuwajà je. Obserwujàc py∏ek przez pewien czas, mo˝na
zauwa˝yç, ˝e porusza si´ on po chaotycznej ∏amanej (b∏àdzenie przy-
padkowe).

CZÑSTKI W RUCHU

CZÑSTKI W RUCHU

Ziarno py∏ku

SKALA NIEZACHOWANA

Czàsteczka wody

Przypadkowy
tor

Chaotyczny ruch czàstek w cieczy

daje si´ zastosowaç do sortowania wirusów.

torskiej uÊciÊli∏ wczeÊniejsze oszacowania ich rozmiarów. W
artykule opublikowanym na ∏amach Annalen der Physik przed-
stawi∏ matematyczny opis ruchów Browna – zjawiska mikro-
skopowego, które nurtowa∏o uczonych od 1827 roku, kiedy
po raz pierwszy zaobserwowa∏ je botanik Robert Brown.

Spostrzeg∏ on, ˝e niewielkie drobiny, na przyk∏ad ziaren-

ka py∏ków roÊlin, wykonujà bez∏adne, zygzakowate ruchy
[ramka na poprzedniej stronie]. Najprostszym wyjaÊnieniem
wydawa∏o si´ stwierdzenie, ˝e sà to organizmy ˝ywe, ale
Brown wykaza∏, ˝e podobnie zachowujà si´ w wodzie drob-
no sproszkowane minera∏y. Na poczàtku XX wieku niektórzy
teoretycy formu∏owali hipotezy, ˝e przyczynà zjawiska sà si-
∏y elektryczne popychajàce drobiny materii, inni odwo∏ywa-
li si´ do skutków parowania, konwekcji, wp∏ywu Êwiat∏a lub
jeszcze innych przyczyn.

Einstein wyrazi∏ przypuszczenie, ˝e drobiny w cieczy wy-

konujà bez∏adne ruchy na skutek zderzeƒ z nadbiegajàcymi
ze wszystkich kierunków czàsteczkami. Zjawisko stanowi
wa˝ki argument za (wtedy kontrowersyjnà) teorià, wyjaÊnia-
jàcà natur´ ciep∏a jako przypadkowego ruchu czàstek. W
swoim artykule Einstein wyprowadzi∏ podstawowe wzory
matematyczne opisujàce ruchy Browna.

Ga∏àê matematyki, która wzi´∏a stàd swój poczàtek, oka-

za∏a si´ niezwykle przydatna do analizy rynków gie∏dowych,
opisu dyfuzji w cieczach i gazach, a ostatnio do budowy tzw.
zapadki Browna. W uk∏adzie takim wykorzystuje si´ fakt,

˝e w przypadku ruchów Browna mniejsze czàstki ulegajà
wi´kszym przemieszczeniom ni˝ du˝e. Dzi´ki zastosowaniu
mikroskopowego odpowiednika zapadki b∏àdzenie czàstek da
si´ wykorzystaç na przyk∏ad do sortowania wirusów wed∏ug
ich rozmiarów lub do oczyszczania wody.

W ubieg∏ym roku in˝ynierowie zbudowali dwa takie urzà-

dzenia, wykorzystujàc technik´ podobnà do stosowanej w
produkcji uk∏adów scalonych. James C. Sturm i jego wspó∏-
pracownicy z Princeton University zbudowali zapadk´ Brow-
na, która przypomina maszyn´ pachinko (japoƒski automat
do gry, nieco podobny do bilardu) wielkoÊci paznokcia. W
p∏ytce krzemowej wytrawili kana∏, zostawiajàc z jego lewej
strony równo rozmieszone rz´dy s∏upków szerokoÊci 6

µ

m i

wysokoÊci 3

µ

m. S∏upki by∏y pochylone pod kàtem 45° i usta-

wione tak, ˝e wszystkie drobiny unoszàce si´ w cieczy prze-
p∏ywajàcej przez kana∏ co chwila w nie uderza∏y i odchyla-
∏y si´ w prawo. Im wi´ksza by∏a drobina, tym silniejszy by∏
efekt zderzenia i wi´ksze jej przesuni´cie.

Podczas testów, których wyniki opublikowano w grudniu

ubieg∏ego roku, Sturm przepuszcza∏ przez swoje urzàdzenie
zawiesin´ wodnà zawierajàcà DNA dwóch ró˝nych wirusów.
W eksperymencie uda∏o si´ oddzieliç ci´˝sze helisy od l˝ej-
szych. Zastosowanie technologii opartej na dorobku Einsteina
mo˝e skróciç czas potrzebny do rozdzielenia du˝ych fragmen-
tów DNA nawet o dwie trzecie w porównaniu z dzisiejszymi
metodami, a urzàdzenie mo˝e byç taƒsze i mniejsze.

PAèDZIERNIK 2004 ÂWIAT NAUKI

43

ALFRED T

. KAMAJIAN

ZAPADKI BROWNA

Skuteczniejsze sita i filtry

Ruchy Browna to gwa∏towne i chaotyczne przesuni´cia drobin. W przypadku zapadek
Browna asymetryczne przeszkody nadajà bez∏adnym skokom okreÊlony kierunek. Jed-
na z takich konstrukcji przypomina miniaturowà maszyn´ pachinko. Kiedy jakaÊ ciecz
– na przyk∏ad kropla osocza krwi – przep∏ywa przez kana∏, unoszàce si´ w niej drobi-
ny takie jak wirusy uderzajà w przechylone s∏upki przypominajàce z´by mechanizmu
zapadkowego (z lewej). W rezultacie wirusy odk∏adajà si´ posortowane wed∏ug roz-
miarów w dolnej cz´Êci aparatu, co umo˝liwia ich rozdzielenie.

Niemieccy in˝ynierowie zbudowali inny rodzaj zapadki Browna, wytrawiajàc w p∏yt-

ce krzemu tysiàce kanalików (poni˝ej z lewej). Woda zanieczyszczona sadzà, materia-
∏em biologicznym lub innymi drobinami jest przepuszczana tam i z powrotem przez po-
rowatà przegrod´. B∏àdzàce w wodzie zanieczyszczenia uderzajà w Êcianki kanalików
przypominajàcych kszta∏tem szyjki butelek, które je odbijajà do przodu, powodujàc, ˝e
w koƒcu wszystkie trafiajà na jednà stron´ p∏ytki. Oczyszczalnia Êcieków (poni˝ej z
prawej) mog∏aby zawieraç wiele sit dzia∏ajàcych na zasadzie zapadki Browna.

Zbiornik

czystej

wody

Instalacja

chlorowania

Osadnik

Sita

z zapadkami

Browna

Mieszalnik

„Zàb” zapadki

Wirus T2

Bakteriofag
lambda

Kierunek
przep∏ywu

Mniejsze drobiny
wykonujà
gwa∏towniejsze
ruchy i mogà
przedostawaç si´
do sàsiednich
kana∏ów

Dop∏yw

reagentów

chemicznych

SKALA NIEZACHOWANA

Sven Matthias i Frank Müller z Max-Planck-Institut für

Mikrostrukturphysik w Weinbergu w Niemczech zbudowa-
li inny mechanizm zapadkowy. Z wyglàdu przypomina on
gàbk´: cieniutkà p∏ytk´ krzemu przenikajà tysiàce równole-
g∏ych kanalików. Ka˝dy z nich wielokrotnie si´ rozszerza i
zw´˝a niczym szyjki butelek.

Matthias i Müller wpasowali swój przyrzàd w naczynie

wype∏nione wodà i mikroskopijnymi plastikowymi kulecz-
kami, rozdzielajàc je na cz´Êç górnà i dolnà. Dno naczynia
porusza∏o si´ w gór´ i w dó∏, sprawiajàc, ˝e woda przep∏y-
wa∏a tam i z powrotem przez p∏ytk´. Koraliki przedostawa-
∏y si´ przez przew´˝enia, ale na skutek ruchów Browna nie
mog∏y si´ cofaç. Stopniowo prawie wszystkie przesz∏y przez

zapadk´ do górnej cz´Êci naczynia, pozostawiajàc w dolnej
niemal czystà wod´. Poniewa˝ skal´ urzàdzenia mo˝na ∏atwo
powi´kszyç, da si´ w nim byç mo˝e oddzielaç sta∏e zanie-
czyszczenia, jak sadza, wirusy czy fragmenty komórek, z
ciàg∏ego strumienia cieczy.

W poszukiwaniu atomowych kropli

EINSTEIN ZMAGA

¸ SI¢

z niezrozumia∏ymi prawami kwantowy-

mi rzàdzàcymi Êwiatem atomów. Fakt, ˝e regu∏y te g∏ównà
rol´ przypisujà przypadkowi i nieoznaczonoÊci, k∏óci∏ si´ ze
zdrowym rozsàdkiem uczonego. Pomimo sceptycyzmu w

odniesieniu do filozoficznych konsekwencji fizyki kwanto-
wej Einstein wniós∏ wa˝ny wk∏ad i w t´ dziedzin´.

W roku 1925 po przeczytaniu artyku∏u, w którym Satyen-

dra Nath Bose opisywa∏ statystyk´ rzàdzàcà fotonami, zda∏
sobie spraw´, ˝e gdyby atomy uda∏o si´ sch∏odziç niemal do
zera bezwzgl´dnego i skupiç, to, co niezwyk∏e, zgodnie z
prawami fizyki kwantowej, powinny one ulec przejÊciowej
kondensacji, tworzàc superatom. Grupa atomów zachowy-
wa∏aby si´ w sposób ca∏kowicie zgodny podobnie jak fotony
w wiàzce laserowej.

Praktyka dowiod∏a niezwyk∏ej u˝ytecznoÊci laserów i sà

te˝ przes∏anki, ˝e podobnie by∏oby w przypadku ich atomo-
wego odpowiednika. Ale kondensat Bosego–Einsteina (tak na-

zywa si´ kropla ultrazimnych atomów) przez przesz∏o 70 lat
pozostawa∏ tylko w sferze przewidywaƒ. Dopiero w czerw-
cu 1995 roku Eric A. Cornell i Carl E. Weimann z JILA w
Boulder w Kolorado doprowadzili 2000 atomów rubidu do
tej niezwyk∏ej jednoÊci, którà przepowiedzia∏ Einstein. SzeÊç
lat póêniej za to osiàgni´cie otrzymali wspólnie z Wolfgan-
giem Ketterlem z Massachusetts Institute of Technology Na-
grod´ Nobla.

DziÊ Cornell i jego studenci z JILA zbli˝ajà si´ do koƒca

prac nad chipem, na którego powierzchni znajdà si´ kana-
∏y dla kondensatu. Uk∏ad mo˝e dzieliç i ∏àczyç jego krople,
co pozwoli mu wykrywaç przyÊpieszenia i obroty z jeszcze
wi´kszà czu∏oÊcià ni˝ uk∏adom laserowym. Twórcy nazwa-
li przyrzàd interferometrem atomowym.

„Instalujàc go pod kad∏ubem samolotu, mo˝na by mie-

rzyç niewielkie zmiany nat´˝enia i kierunku pola grawita-
cyjnego, którego miarà jest przyÊpieszenie – mówi Cornell.
– Takie wahania grawitacji mogà ujawniç obiekty niewidocz-
ne, ukryte g∏´boko pod ziemià lub pod wodà”. Anomalie mo-
gà byç wywo∏ane przez obszary roponoÊne, ˝y∏y zawierajà-
ce rudy metali, jaskinie, a nawet podziemne bunkry i tunele.

„Interferometry atomowe mia∏yby dok∏adnoÊç od 100 do

1000 razy wi´kszà ni˝ najlepsze dziÊ czujniki ruchu obroto-
wego, jakimi sà mechaniczne ˝yroskopy – przewiduje Cor-
nell. – Powodem, dla którego potrzebujemy naprawd´ sku-
tecznych ˝yroskopów, jest precyzyjne obliczanie pozycji.
OczywiÊcie, dysponujàc systemem GPS, niewielu korzysta
jeszcze z ˝yroskopu. Ale jest on nadal niezastàpiony, je˝eli
przez d∏ugi czas siedzi si´ w tytanowej skorupie g∏´boko pod
wodà i nie wolno ha∏asowaç. Nie przypadkiem za badania
p∏aci marynarka wojenna”. Wojsko jest te˝ zainteresowane
systemami nawigacyjnymi, które dzia∏a∏yby nawet w przypad-
ku ca∏kowitego zag∏uszenia sygna∏ów GPS.

Interferometr atomowy zawiera dwie grupy atomów i

mierzy rozk∏ad pojawiajàcy si´ w wyniku ich interferencji.
Podobnie jak wszystkie obiekty kwantowe kondensat Bose-
go–Einsteina wykazuje po cz´Êci w∏aÊciwoÊci falowe, po
cz´Êci czàstkowe. Kiedy kropla kondensatu rozpadnie si´
na dwie, ka˝da z nich jest poczàtkowo opisywana przez fa-
l´ o takiej samej d∏ugoÊci i fazie. Ale je˝eli obydwie cz´Êci

44

ÂWIAT NAUKI PAèDZIERNIK 2004

ALFRED T

. KAMAJIAN

Nowy stan materii

W temperaturze wy˝szej zaledwie o miliardowà cz´Êç kelwina od zera
bezwzgl´dnego powstaje kondensat Bosego–Einsteina – najzimniejszy
obiekt we WszechÊwiecie. Za pomocà pola magnetycznego i Êwiat∏a la-
serowego naukowcy potrafià spowolniç ruch atomów i zbli˝yç je do sie-
bie tak, ˝e efekty kwantowe powodujà synchronizacj´ ich zachowania.
Atomy w kropli kondensatu poruszajà si´ zgodnie niczym jeden gigan-
tyczny superatom.

ATOMOWA KROPLA

SKALA NIEZACHOWANA

Atom

Kondensat
Bosego–Einsteina

Wiàzki laserowe

sch∏adzajà atomy

do temperatury

bliskiej zera

bezwzgl´dnego

Dok∏adny pomiar grawitacji

ujawni

ukryte g∏´boko pod ziemià lub wodà obiekty.

pokonajà ró˝ne drogi, w chwili rekombinacji ich parametry
b´dà ró˝ne. Fale b´dà interferowaç, dajàc prà˝ki o du˝ej
g´stoÊci atomów, podczas gdy inne obszary b´dà niemal
puste.

Ketterle i Mark A. Kasevich ze Stanford University wraz

ze wspó∏pracownikami niedawno zbudowali dzia∏ajàce inter-
ferometry atomowe, ale na razie urzàdzenia te zajmujà ca-
∏y pokój, poniewa˝ podzia∏ i rekombinacja kropelki konden-
satu nast´puje w trakcie jej swobodnego spadku we wn´trzu
olbrzymiej komory pró˝niowej. Cornell i jego wspó∏pracow-
nica z JILA, Dana Anderson, pracujà nad por´czniejszymi
konstrukcjami.

„Prowadzàc atomy w kana∏ach, mo˝emy zmniejszyç in-

terferometr do rozmiarów niewielkiego chipu” – wyjaÊnia
Ying-Ju Wang, jedna z magistrantek Cornella, i pokazuje jed-
noczeÊnie kawa∏ek szk∏a wielkoÊci szkie∏ka mikroskopowe-
go. Przez jego Êrodek niczym tory kolejowe dla muchy bie-
gnà dwa paski z∏ota. Âcie˝kami p∏ynie pràd elektryczny,
wytwarzajàc pola magnetyczne, które znoszà si´ dok∏adnie
poÊrodku. „U˝ywane przez nas atomy rubidu skupiajà si´ w
obszarze, gdzie pole magnetyczne jest najs∏absze – t∏uma-
czy Wang. – Dlatego atomy podà˝à kana∏em, w którym po-
le jest zerowe”.

Z∏ote tory prowadzà do rozga∏´zienia w kszta∏cie litery Y

– podzielnika wiàzki. „Tutaj za pomocà wiàzki laserowej wy-
twarzamy fal´ stojàcà – opowiada Wang. – Pe∏ni ona funkcj´
siatki dyfrakcyjnej, kierujàc po∏ow´ atomów kondensatu w
lewo, a po∏ow´ w prawo. Kropelki oddalajà si´ od siebie na
odleg∏oÊç oko∏o 300

µ

m, a nast´pnie napotykajà kolejne fa-

le stojàce, które dzia∏ajà jak zwierciad∏a i odbijajà atomy do
ty∏u. Tam si´ spotykajà, nak∏adajà na siebie i interferujà”.
Powstajàce prà˝ki rejestruje specjalna kamera.

Chocia˝ w∏aÊciwy interferometr mieÊci si´ na p∏ytce wiel-

koÊci d∏oni, kompletne urzàdzenie nadal zajmuje ca∏à ∏aw´
laboratoryjnà. „Niektóre elementy naszej konstrukcji da si´
∏atwo zmniejszyç – t∏umaczy Cornell. – Z innymi nie jest tak
prosto”. Jak chocia˝by z laserowym systemem ch∏odzàcym,
który spowalnia atomy tak, ˝e ich temperatura spada z po-
kojowej do zaledwie miliardowych cz´Êci kelwina powy˝ej
zera bezwzgl´dnego.

Jak widaç, atomowego ˝yroskopu nie uda si´ zmieÊciç w

zegarku na r´k´ ani w telefonie komórkowym. Ale niewy-
kluczone, ˝e ju˝ nied∏ugo krople kondensatu Bosego–Ein-
steina znajdà si´ w dziobach samolotów lub w kad∏ubach
okr´tów podwodnych. A je˝eli za wskazówk´ przyjàç histo-
ri´ lasera, przyszli wynalazcy znajdà dla nowego stanu ma-
terii nowe zastosowania, o jakich si´ nawet nie Êni dzisiejszym
naukowcom.

n

PAèDZIERNIK 2004 ÂWIAT NAUKI

45

ALFRED T

. KAMAJIAN

ATOMOWY INTERFEROMETR

Asymmetric Pores in a Silicon Membrane Acting as Massively Parallel

Brownian Ratchets. S. Matthias i F. Müller; Nature, tom 424, s. 53-57,
3 VII 2003.

Tilted Brownian Ratchet for DNA Analysis. L. R. Huang i. in.; Analytical

Chemistry, tom 75, s. 6063-6967, 15 XII 2003.

Coherence with Atoms. M. A. Kasevich; Science, tom 298, s. 1363-

-1368; 15 XI 2002.

Coherent Induced Spin Polarization in Strained Semiconductors. Y. Ka-

to i in.; artyku∏ dost´pny w sieci pod adresem:

arXiv.org/abs/cond-mat/0403407

JEÂLI CHCESZ WIEDZIEå WI¢CEJ

Jak zobaczyç niewidoczne

W∏aÊciwoÊci kondensatu Bosego–Einsteina zbli˝one do w∏aÊciwoÊci Êwiat∏a laserowego mo˝-
na wykorzystaç w miernikach pola grawitacyjnego i ˝yroskopach. Krople kondensatu mogà dzie-
liç si´ i ∏àczyç w interferometrze (poni˝ej). Oddzia∏ywania magnetyczne stanowià prowadni-
c´ dla atomów odbijajàcych si´ od podzielnika wiàzki i „zwierciade∏” w postaci fali stojàcej
w promieniu lasera. Zwykle obydwie po∏owy kondensatu podró˝ujà i ∏àczà si´, zachowujàc
zgodnoÊç fazy, co daje okreÊlony rozk∏ad prà˝ków interferencyjnych. Ale jakiekolwiek ró˝ni-
ce w obydwu pokonywanych drogach – z powodu minimalnego gradientu pola grawitacyjne-
go albo nawet niewielkiego obrotu urzàdzenia – spowodujà przesuni´cie prà˝ków. W przysz∏o-
Êci interferometry zainstalowane na pok∏adach samolotów mogà pos∏u˝yç do poszukiwania
grawitacyjnych wskazówek Êwiadczàcych o obecnoÊci g∏´bokich z∏o˝y ropy lub rud metali. Sa-
moloty wojskowe zaÊ mogà wykorzystaç czujniki pola grawitacyjnego z kondensatem Bose-
go–Einsteina do poszukiwania podziemnych bunkrów lub tuneli.

Zwierciad∏a

1

Krople kondensatu
poruszajà si´

mi´dzy Êcie˝kami
ze z∏ota

3

Rekombinujàcy
kondensat

interferuje, dajàc
prà˝ki, które
ujawniajà niewielkie
niejednorodnoÊci
pola grawitacyjnego

Nieco

silniejsze

pole

grawitacyjne

2

Laserowy podzielnik wiàzki rozszczepia
krople na po∏owy; zwierciad∏a laserowe

odbijajà poruszajàcy si´ kondensat

Nieco
s∏absze
pole
grawitacyjne

Pola naftowe

SKALA
NIEZACHOWANA