Fragment książki Jarosława Strzeleckiego Logika z wyobraźnią.

Wszelki uwagi merytoryczne i stylistyczne proszę kierować pod adres jstrzelecki@uwm.edu.pl

PODZIAŁ LOGICZNY

I. DEFINICJA: Podziałem logicznym jakiegoś zbioru  Z  jest układ przynajmniej dwóch (np.  A,  B) 
niepustych podzbiorów zbioru Z, takich że

1. Każdy element zbioru  A  jest elementem zbioru  Z, ale nie każdy element zbioru  Z  jest 

elementem A (inaczej mówiąc zbiór A jest podrzędny względem zbioru Z).

2. Każdy element zbioru  B  jest elementem zbioru  Z, ale nie każdy element zbioru  Z  jest 

elementem B (inaczej mówiąc zbiór B jest podrzędny względem zbioru Z).

3. Żaden element zbioru A nie jest elementem zbioru B oraz żaden element zbioru B nie jest 

elementem zbioru A (inaczej mówiąc A i B nie mają żadnych wspólnych elementów).

4. Zbiory A i B zostały utworzone w oparciu o określoną zasadę podziału.
5. Suma zbiorów A i B jest zbiorem Z.

II. POJĘCIA dodatkowe:

1. Całość dzielona (

 

 totum divisionis

 

 )  : zbiór Z

2. człony podziału (

 

 membra divisonis

 

 )  : zbiory A, B

III. UWAGI:

1. Podział logiczny może być układem  większej ilości  podzbiorów niż tylko dwóch (A, B, 

C,...).

2. Przez pojęcie nazwy możemy rozumieć jej zakres, czyli zbiór wszystkich jej desygnatów. 

Wówczas podział logiczny będzie podziałem logicznym określonego pojęcia - nazwy.

3. Są dwa rodzaje zasad podziału: 

a) według   cech   sprzecznych   (np.   biały   –   niebiały,   parzysta   –   nieparzysta,   polski   – 

niepolski,   śmiertelny   –   nieśmiertelny,   pijany   –   niepijany).   Podział   taki   nazywamy 
dychotomicznym albo dwudzielnym.

b) według modyfikacji wybranej cechy (np. Wybraną cechą niech będzie kolor ludzkiej 

skóry.   Jej   modyfikacjami   są   różne   kolory,   zatem   podział   logiczny   zbioru   ludzi   ze 

względu na kolor skóry jest następujący: biali, czarni, żółci, czerwoni). Podział taki 
nazywamy wieloczłonowym.

Zbiór Z

Zbiór A

Zbiór B

4. Formalnymi warunkami poprawności podziału logicznego są:

a) warunek jedyności zasady – podział posiada tylko jedną zasadę podziału (por. I.4.),
b) warunek rozłączności członów podziału – człony podziału nie mają żadnego wspólnego 

elementu (por. I.3),

c) warunek zupełności – suma członów podziały jest równa całości dzielonej (por. I.5.).

IV. Przykłady. Mamy następujący zbiór przedmiotów o nazwie Żółty Zbiór:

Dokonajmy na nim różnych podziałów logicznych.

IV.I Poprawne podziały logiczne.

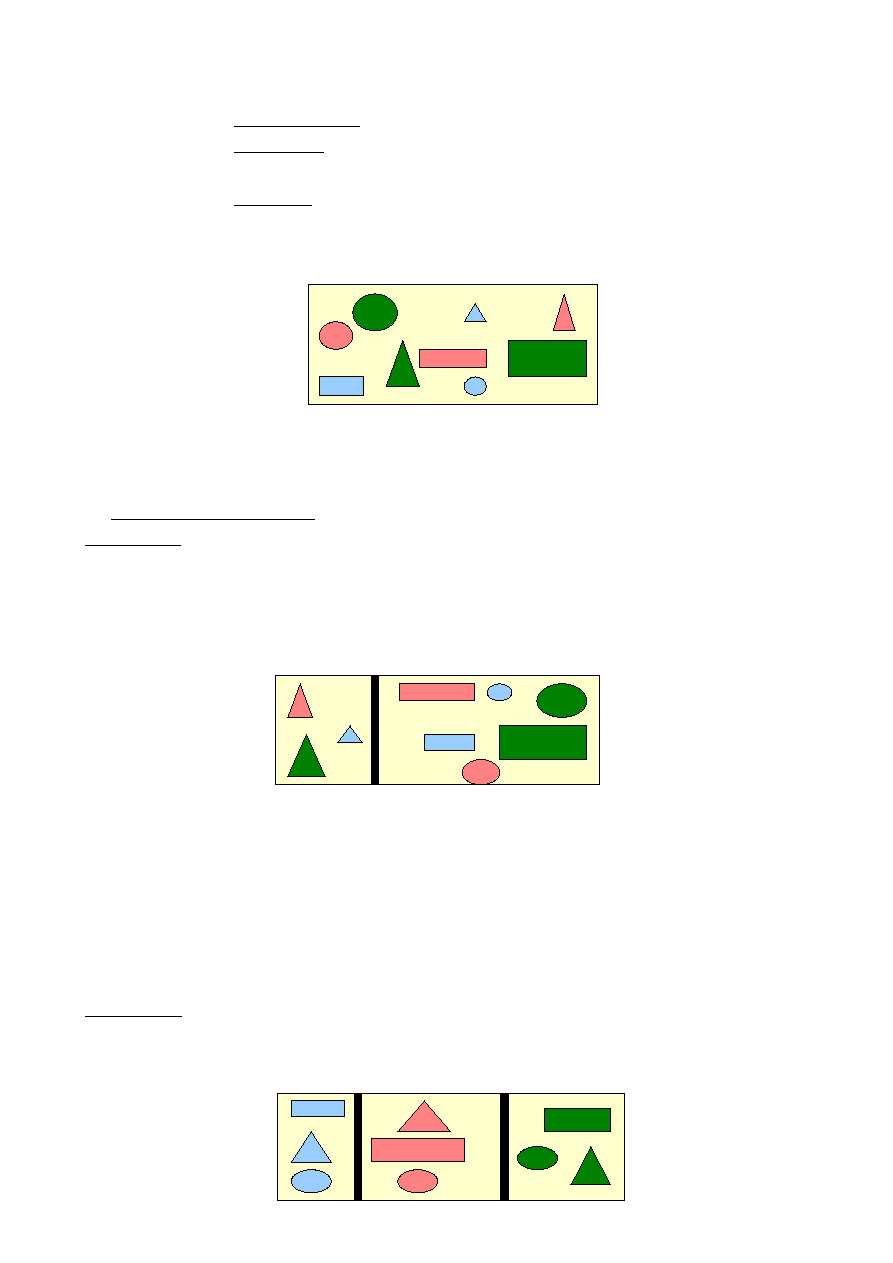
Przypadek   I.  Całością   dzieloną   jest   Żółty   Zbiór.   Zasadą   podziału   niech   będzie   układ   cech 
sprzecznych:   być   trójkątem   –   niebyć   trójkątem.   Wówczas   mamy   do   czynienia   z   podziałem 

dychotomicznym,   czyli   dwudzielnym.  Nasz   Żółty   Zbiór   będzie   posiadał   dwa   podzbiory:   zbiór 
trójkątów oraz zbiór pozostałych figur. Oto graficzne przedstawienie tego podziału:

Sprawdźmy, czy podział taki spełnia formalne warunki poprawności. Czy przyjęliśmy tylko jedną 

zasadę podziału? Tak. Jest nią zasada bycia trójkątem. Czy człony podziału są względem siebie 
rozłączne? Tak. Żaden element zbioru trójkątów nie jest elementem drugiego zbioru i na odwrót. 

Czy suma zbioru trójkątów i zbioru pozostałych figur jest równa Zbiorowi Żółtemu? Tak. Żółty 
Zbiór   składa   się   z   trzech   trójkątów,   trzech   prostokątów,   trzech   okręgów.   Z   tych   samych 

elementów składa się zbiór będący sumą zbiorów trójkątów i pozostałych figur.

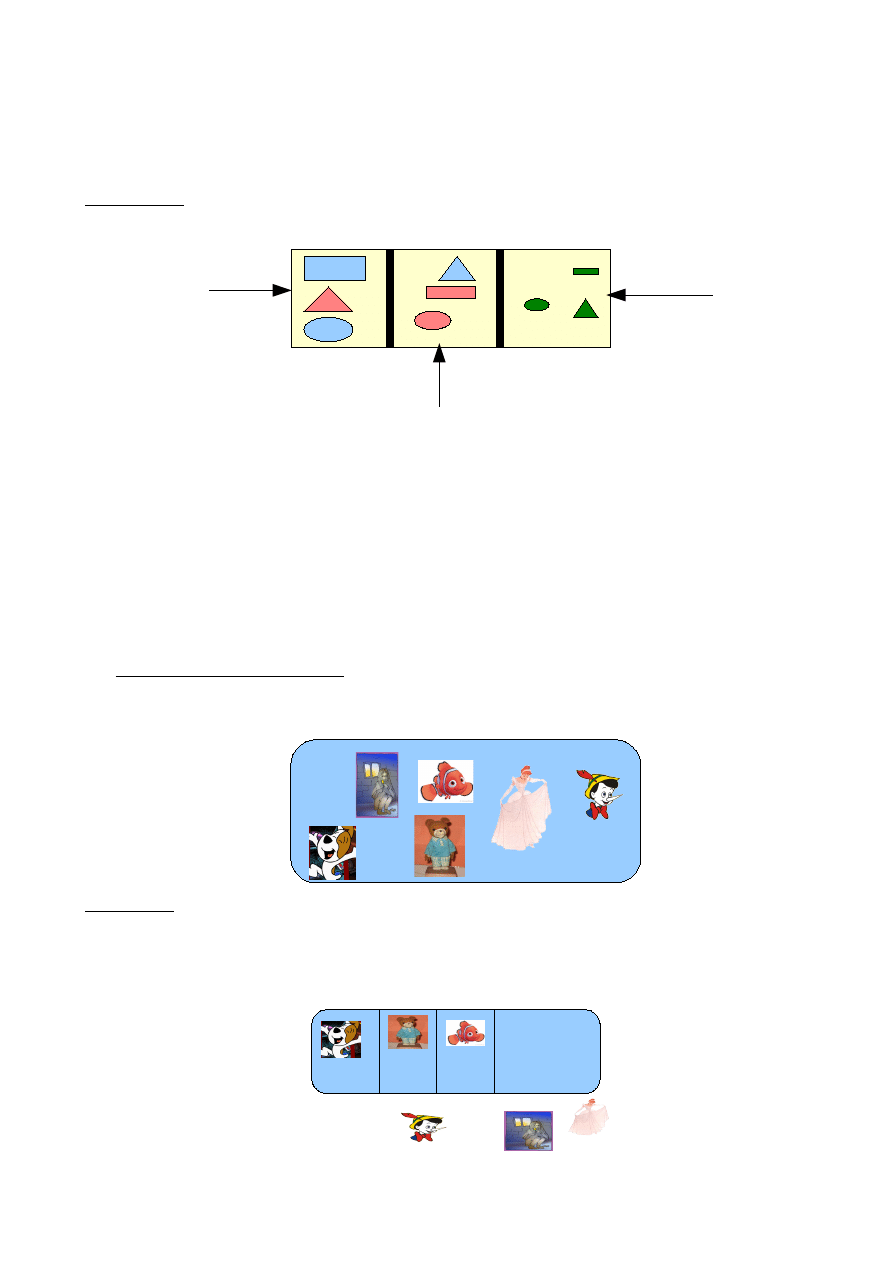
Przypadek II.  Tym razem podzielimy Żółty Zbiór według modyfikacji pewnej cechy. Będzie nią 
kolor.   Powinniśmy   uzyskał   podział   wieloczłonowy.   Członami   podziału   będą   zbiory:   figur 

niebieskich, czerwonych, zielonych. Oto on:

I tym razem podział logiczny jest poprawny formalnie. Został przeprowadzony ze względu na 

jedną tylko zasadę podziału (kolor). Człony podziału nie posiadają wspólnych desygnatów. Suma 
członów podziału równa jest Zbiorowi Żółtemu.

Przypadek III. Oto graficzna reprezentacja logicznego podziału dokonanego na Żółtym Zbiorze

Członami podziału są zbiory A, B, C. Według jakiej zasady przeprowadzono w tym przypadku 

podział logiczny? Z pewnością jest to podział wieloczłonowy, a więc jego fundamentum divisionis 
(zasadą   podziału)   jest   modyfikacja   pewnej   cechy.   Jest   nią,   jak   łatwo   można   się   domyśleć, 

wielkość powierzchni danej figury. Elementami zbioru A są figury o największej powierzchni. Do 
zbioru B należą wszystkie figury o średniej powierzchni, a zbiór C stanowią figury o najmniejszej 

powierzchni. Zbiory A, B, C wykluczają się (spełniony warunek rozłączności). Ich suma jest równa 
Żółtemu Zbiorowi (spełniony warunek zupełności).

IV.II Niepoprawne podziały logiczne.

Tym razem rozpatrzmy przypadki niepoprawnych podziałów logicznych. Stwórzmy zbiór o 

nazwie Bohaterowie Bajek:

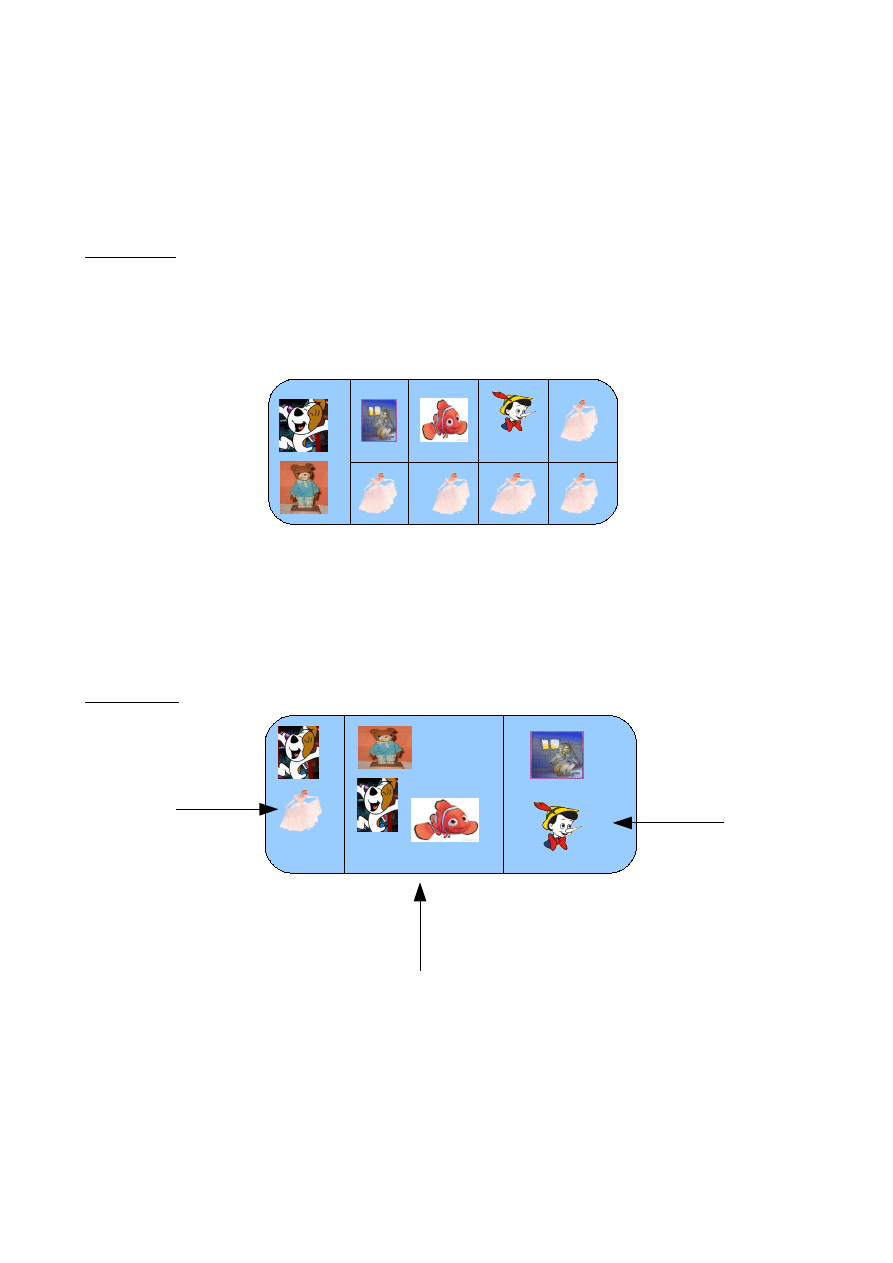
Przypadek  I.  Zasadą   podziału  jest  modyfikacja  cechy  być  zwierzęciem  (być  przedstawicielem 
jakiegoś gatunku zwierzęcia). Chcemy zatem dokonać podziału wieloczłonowego. Przyjmijmy, że 

zakres nazwy człowiek wyklucza się z zakresem nazwy zwierzę, czyli że żaden człowiek nie jest 
zwierzęciem i żadne zwierzę nie jest człowiekiem. Wówczas zbiór wyglądałby następująco:

A

B

C

Spełniliśmy warunek jedyności zasady podziału. Nie naruszyliśmy również zasady rozłączności 

członów   podziału,   ponieważ   żadne   ze   zwierząt   nie   należy   do   przynajmniej   dwóch   różnych 
podzbiorów zbioru Bohaterowie Bajek, czyli że każde zwierze jest przedstawicielem co najwyżej 

jednego   gatunku.   Niestety   suma   członów   podziału   nie   jest   równa   całości   dzielonej,   tzn.   że 
przeprowadzony „podział logiczny” jest niezgodny z warunkiem zupełności.

Przypadek II. Spróbujemy dokonać takiego „podziału logicznego”, aby naruszona została zasada 

rozłączności  członów  podziału.  Musimy  zatem  znaleźć   taką   zasadę  podziału, w wyniku  której 
pewne elementy zbioru Bohaterowie Bajek zostaną przypisani do więcej niż tylko jednego członu 

podziału.   Niech  fundamentum   divisionis  będzie   pochodzenie   (narodowość)   bohatera.   Całość 
dzielona wygląda następująco:

Reksio   i   Miś   Uszatek  należą   do   zbioru   polskich   postaci  bajkowych.   Dziewczynka   z  zapałkami 

wywodzi   się   z   Danii.   Nemo   jest   bohaterem   wymyślonym   przez   Amerykanów.   Pinokio   jest 
narodowości włoskiej. Problematyczna jest postać Kopciuszka. Może ona wywodzić się z Egiptu, 

Grecji, Rzymu, Chin, Francji lub Niemczech.

Przypadek III. Przyjrzyjmy się naszemu zbiorowi Bohaterów Bajek:

Elementami  zbiór  A  są   bohaterowie,   których   przygody   przyniosły   największe   zyski   w   Polsce. 

(Oczywiście  tylko zakładamy,  że  tak  jest!!).  Zbiór  B  składa  się  z ulubionych  bohaterów  Jasia 
Kowalskiego, zaś zbiór C stanowią postaci, których dzieci boją się najbardziej (Nie jest to prawdą, 

ale ze względów dydaktycznych, uznajmy, że faktycznie tak jest). Nie mamy tutaj do czynienia z 
żadnym   podziałem   logicznym,   ponieważ   wszystkie   zbiory   (A,   B,   C)   zostały   wyróżniowe   na 

podstawie innej zasady, a każdy podział logiczny posiada tylko jeden fundamentum divisionis.

A

B

C

KWALIFIKACJA

I. DEFINICJA

KWALIFIKACJA jest to uznanie, że jakiś przedmiot należy do wyróżnionego zbioru.

II. UWAGI
Zakres   nazwy   stanowi   zbiór   jej   wszystkich   desygnatów,   zatem   kwalifikacja   może   być 

utożsamiona z rozstrzygnięciem, czy jakiś przedmiot jest albo nie jest desygnatem danej nazwy.

III. Przykład
Mamy następujący przedmiot:

Naszym zadaniem jest zakwalifikować go do właściwego zbioru zwierząt. Na przykład do takiego:

Tygrysek należy do zbioru tygrysów. Zakresem nazwy jest zbiór jej wszystkich desygnatów, zatem 

dokonując kwalifikacji rozstrzygnęliśmy, że Tygrysek jest desygnatem nazwy tygrys.

ANALIZA PRZEDMIOTU

I. DEFINICJE

ANALIZA PRZEDMOTU jest to wyodrębnienie w przedmiocie jego części.
Składnik jest to samodzielna część przedmiotu.

Własność jest to niesamodzielna część przedmiotu.
PARTYCJA jest to wyodrębnienie w przedmiocie jego składników, czyli części samodzielnych.

STRATYFIKACJA  jest   to   wyodrębnienie   w   przedmiocie   jego   własności,   czyli   części 
niesamodzielnych.

II. UWAGI

1. Partycja

 

   może   być   operacją  realną  (np.   realną   partycją   na   oknie   byłoby   faktyczne 

oddzielenie szyby od ram, wykręcenie klamek, zawiasów)

lub mentalną (np. tylko w myślach oddzielam od siebie szyby, ramę okna, klamki, zawiasy).

2. Stratyfikacja

 

  jest zawsze operacją mentalną.

3. Partycję i stratyfikację można przeprowadzać zarówno na zbiorach jak i na indywiduach.

4. Różnica

 

   między   definicją   nominalną   a   analizą   przedmiotu   jest   taka,   że   w   definicji 

nominalnej podawane jest znaczenie definiowanego wyrażenia (metajęzyk), a w analizie 

przedmiotu wyodrębniane są części przedmiotu (język przedmiotowy).

5. Różnica

 

   między   definicją   realną   a   analizą   przedmiotu   jest   taka,   że   w  definicji   realnej 

podawana jest jednoznaczna charakterystyka przedmiotu (język przedmiotowy), a nie są 
wyodrębniane części przedmiotu (język przedmiotowy).

III. Przykład I

SOKRATES

Mentalną partycją jest wyodrębnienie nosa, oczu, brody, łysiny. Gdybyśmy wzięli młotek i 

stukając   nim   w   nos,   oczy,   brodę,   łysinę,   odłupalibyśmy   te   części,   wówczas   dokonalibyśmy 

partycji realnej.

Stratyfikacja  Sokratesa   (mówiąc   dokładniej   popiersia   Sokratesa)   polegałaby   na 

wyodrębnieniu własności twarzy Sokratesa, a więc: brzydka twarz, jajowata głowa, kartoflany nos 
itp. .