Skok do   

strony tytułowej

  serwisu

 

Z serwisu korzystało już

82201

osób

do strony tytułowej

Ogólne wprowadzenie

Chemia dla Ciebie

download

linki

 

| 

mikro i makro

 | 

wyobraźnia

 |  

nowe spojrzenie

 |  

termodynamika

 |  

nie wszystko na raz

 |  

co los nam zdarzy 

 |  

podsumowanie

 |

Na czym  polega trudność w studiowaniu chemii fizycznej? 
Moim zdaniem, nie na trudności w zrozumieniu fizykochemicznego opisu zjawisk, lecz na niewłaściwym sposobie podania tej
wiedzy. Zrozumienie zjawisk fizykochemicznych, dość często złożonych i wymagających zazwyczaj znajomości matematyki, 
przy  klarownym wywodzie  i  logicznym  powiązaniu przyczyn  i skutków,  co  najwyżej może wymagać większej  ilości czasu
i   zwiększonego   wysiłku   intelektualnego.   Problem   polega   głównie   na   tym,   że   ucząc   chemii   w   XXI   wieku,   wiedząc,   że
prawdziwych przyczyn makroskopowych skutków zjawisk szukać trzeba na poziomie cząsteczkowym (świat mikro), ciągle nie
potrafimy  zerwać z podziałami i podejściem do zjawisk rodem z XIX wieku (głównie opis świata w skali makro). Ponadto
wykładowcy, autorzy podręczników i twórcy programów studiów (tzw. treści programowych) nie mogą się zdecydować, jak
traktować  obiekt  swoich   działań,  czyli  studenta   pierwszych   lat  studiów.  Z  jednej  strony  zakładają  (niestety   dość  słusznie)
poziom wiedzy, każący tłumaczyć budowę materii na poziomie wywodów Daltona, ale za chwilę przechodzą do omawiania
równania Schrödingera w sposób, jakby to było prawo Pitagorasa czy Talesa. Chcąc wyłożyć chemię fizyczną przy założeniu
rzeczywistego poziomu wiedzy studiujących, trzeba by poświecić na to trzy-czterokrotnie więcej czasu niż dotychczas (co jest
mało realne). Sensownym zabiegiem byłoby włączenie fizykochemicznego opisu  zjawisk do  nauki różnych dziedzin  chemii
(ogólnej, organicznej, nieorganicznej itp.) kosztem zredukowania objętości ich części opisowej. Wówczas przedmiot "chemia
fizyczna" należałoby potraktować jako uporządkowanie i pogłębienie wiedzy zdobytej wcześniej w trakcie nauki tych "innych
chemii".   Także   powiązanie   konsekwentnego   tłumaczenia   wszelkich   zjawisk   zasadami   termodynamiki   z   opisem   prostych
modeli "makroskopowych" danych zjawisk, byłoby dla studiujących dużym ułatwieniem w percepcji wykładanego materiału.
Z całym szacunkiem dla przeszłości trzeba stworzyć nowy model wykładu chemii fizycznej, pozwalający uczynić z przedmiotu
rzeczywisty fundament wszelkich dziedzin chemii. A ponieważ prawdopodobieństwo wpływu mojego zdania na decyzje tych,
którzy rzeczywiście kształtują proces dydaktyczny, jest mniejsze od szansy trafienia szóstki w totka, niniejsza witrynka ma być
"protezą"  ułatwiającą  (przynajmniej niektórym)  zrozumienie  chemii fizycznej,  w pewnym  stopniu  bazującą na  powyższych
założeniach. Będzie to swoisty przewodnik po meandrach myślowych autorów podręczników do chemii fizycznej.

A oto dla przykładu krótki cytat z podręcznika akademickiego do chemii fizycznej (jednego z lepszych, moim zdaniem):

 ...   operujemy   często   pojęciem   orbitalu   (rozumiejąc   je   ściśle,   jako   część   kątową   funkcji   falowej
elektronu).
Orbital traktujemy często jako stan określony trzema liczbami kwantowymi n, l, m, który pomieścić może
maksymalnie dwa elektrony z przeciwnymi spinami

Zapamiętałem  więc,   że   orbital  to   funkcja   (tu   już  mam  wątpliwości,   czy   chodzi  o   funkcję   w  pojęciu   ogólnym,   czy
o   funkcję   matematyczną),   stan,   który   może   pomieścić   (niezbyt   to   szczęśliwe   sformułowanie)   elektrony.   A   już
kawałeczek dalej czytam:

 Wszystkie   powłoki   elektronowe,   złożone   z   poszczególnych   orbitali   stanowią   w   atomie   tzw.   osłonę
elektronową.
(...)   Rozpatrzmy   teraz   ważny   przypadek,   gdy   następuje   przeskok   elektronów   z   wyższych   powłok
elektronowych na (...) orbital wewnętrznej powłoki ...
Przeskok elektronu (...) prowadzi do emisji dużego kwantu energii

Teraz  zaczynam wątpić, czy to, co przed chwila zapamiętałem nie kłóci się z następnymi zdaniami, z których wynika,
że     orbitale   to   fizyczne   miejsca,   przestrzeń,   pomiędzy  którymi  mogą   przemieszczać   się   elektrony   i   które   stanowią
składniki większej struktury - powłoki. Ponadto mowa o wyższych powłokach, bez wyjaśnienia co to znaczy (wyższe od
czego?).  W następnym miejscu czytamy:

Zapełnianie orbitali następuje kolejno według wzrastającej energii.

i kawałek dalej:

Elektrony mając do dyspozycji równocenne energetycznie orbitale ...

Czy to orbitale mają energię, czy chodzi o energię elektronów znajdujących się na tych orbitalach?

Tak oto dobry podręcznik "wyjaśnił" mi pojęcie orbitali i ich energii. Jak mam później zrozumieć nakładanie się orbitali,
tworzenie orbitali cząsteczkowych, orbitale wiążące i antywiążące, hybrydyzację itp. A wystarczyłoby parę zdań więcej
by sprawę uczynić łatwiejszą do zrozumienia.

Dla kogoś, kto ma już jakąś wiedzę na temat elektronów, orbitali, kwantowania energii itp. tego typu skróty myślowe
i  brak   precyzji  sformułowań  nie  ma  większego   znaczenia.  Taki styl  wywodu jest  nawet   pożądany,   bowiem  pozwala
uprościć argumentację, dzięki czemu cały wywód staje się bardziej klarowny. Jeśli jednak czyta to ktoś, kto styka się
z  tą   problematyką   po   raz  pierwszy   -   szybko   nabierze   przekonania,   że   chemia   fizyczna   to   wiedza  tak   hermetyczna
i zagmatwana, że "uciec" od niej trzeba jak najszybciej.

A ponieważ  nie da się "uciec" od chemii fizycznej i chemii w ogóle, bo to przecież opis tego, co dzieje się w nas i wokół
nas -  postaram się w  następnych  podrozdziałach  dotyczących  energii  i  materii wyjaśnić,  lub  może  raczej przybliżyć
problem i ułatwić zrozumienie  tych pozornych  niespójności w podręcznikach. Zapewne i mnie nie do  końca  uda się
uciec od niekontrolowanych skrótów myślowych i uproszczeń - przepraszam. Obiecuję jednak, że będę się starał, by
było ich jak najmniej.

 

 

Aby dobrze zrozumieć chemię  (a chemię  fizyczną przede wszystkim) trzeba pamiętać  o kilku zasadniczych sprawach,
które teraz tylko krótko zasygnalizuję, a w kolejnych podrozdziałach postaram się rozwinąć myśli zawarte w poniższych

Zjawiska obserwowane i omawiane w skali makro (czyli w ilościach dostępnych naszym zmysłom: zlewka z roztworem,
kryształek   soli   widzialny   gołym   okiem   itp.)   są   średnią   statystyczną,   wypadkową,   zjawisk  mikro   (dziejących   się   na
poziomie cząsteczek i atomów).  [

rozwinięcie tematu

]

Wielu pojęć dotyczących mikroświata nie da się zrozumieć, wyobrazić, bowiem nie mają one odpowiedników w znanym
nam  makroświecie,  a rzeczy, których nie poznaliśmy zmysłami nie potrafimy sobie wyobrazić. Stosujemy wówczas dość
ułomne porównania (np. elektron jako kuleczka) i branie tych porównań za "dobrą monetę" może prowadzić do wielu
nieporozumień. [

rozwinięcie tematu

]

Starajmy się patrzeć na świat, na zjawiska fizykochemiczne świeżym okiem. Wiele pojęć i określeń przyjęliśmy w szkole
"na  wiarę"   i z  czasem  podświadomie  uznaliśmy  je za  oczywiste  i więcej  się  nad  nimi  nie  zastanawiamy  -  a  szkoda.
Przemyślmy jeszcze raz te "oczywistości" (np. materia i energia czy ładunek elektryczny). [

więcej na ten temat

]

Rozpatrując   różne  zjawiska  zachodzące w przyrodzie  miejmy  ciągle  na  uwadze,  że  w czasie  ich  trwania  ścierają  się
zazwyczaj   dwie   tendencje   -   spadek   energii   wewnętrznej,   któremu   przeciwstawia   się   spadek   wartości   entropii
("uporządkowanie" układu) lub w innym przypadku wzrost entropii (układ dąży do rozproszenia), któremu towarzyszy
zazwyczaj będący w opozycji wzrost energii wewnętrznej [

rozwinięcie tematu

]

Panta rei (wszystko płynie) - tę prawdę znali już starożytni. Nie zapominajmy, że materia nigdy nie trwa w idealnym
bezruchu.  Oznacza  to   między   innymi,   że   w  czasie,  gdy   rozpatrujemy  zjawisko  czy   proces 

A

  dzieją  się   jednocześnie

i wpływają wzajemnie na swój przebieg także zjawiska 

B

, 

C

, 

D

  ... itd. Ta równoległość wzajemnie zależnych zjawisk

powoduje, że ich pełny opis byłby tak skomplikowany (jeśli w ogóle możliwy), że niczego by nie wyjaśniał. Ograniczamy
się   więc   zazwyczaj  do   opisu  interesującego   nas  zjawiska,   abstrahując   od   innych,  dziejących   się  równolegle  zjawisk,
chyba, że wpływają one na   zjawisko obserwowane w stopniu na tyle znacznym, że pominąć ich się nie da. Ponieważ
jednak w różnych warunkach to samo zjawisko współdziała w sposób istotny z różnymi  zjawiskami równoległymi, to co
jest prawidłowym opisem w jednej sytuacji, traci na aktualności w innej (np. dysocjacja substancji w roztworze o bardzo
małym stężeniu i w sytuacji wysokiego stężenia) [

rozwinięcie tematu

]

 To  samo  zjawisko opisywane w skali makro  i w skali  mikro (atom - cząsteczka  - kilka cząsteczek) będzie wyglądać
inaczej, co może sprawiać wrażenie, że są to różne rzeczywistości. Nigdy nie zapominajmy, że rzeczywistość jest jedna,
jest jaka  jest  (w naszym  makroskopowym ujęciu  świata),  a  tylko  nasze  punkty  widzenia  i związane   z tym  opisy  się
różnią. [

więcej na ten temat

]

podpunktach. 

Powyższa wyliczanka ani nie wyczerpuje tematu, ani kolejność tematów nie ma nic wspólnego z ich ciężarem gatunkowym. O istnieniu tych problemów (i innych też) pamiętać 

trzeba zawsze, co nie znaczy, że zawsze wszystkie trzeba brać pod uwagę w rozpatrywaniu konkretnego zjawiska. Szczególnie ważne, by przypominać sobie o tych sprawach 

wtedy, gdy "coś nam nie gra" w opisie zjawiska. Myślowe rozszerzenie zakresu interpretacji powinno pomóc w zrozumieniu odstępstw od reguły czy spodziewanego zachowania.

Innymi słowy, krótko można to ująć, że w przyrodzie  

nie ma  wyjątków

, prawa  są niezmienne, tylko skutki  mogą być różne  w różnych sytuacjach (wpływ innych, równoległych

zjawisk).

Mikro  i makro 

Pierwotnym  poznaniem i opisem zjawiska było poznanie i opis układu makroskopowego, dostępnego  bezpośrednio naszym
zmysłom.  Właściwości  poszczególnych  stanów  skupienia,  przejścia  między nimi  (topnienie,   rozpuszczanie,   parowanie  itp.)
i reakcje chemiczne obserwowaliśmy na poziomie makro i z tych obserwacji powstawały pierwsze sformułowania reguł i praw
rządzących przyrodą. Dopiero później nauka odkryła atomową budowę materii i te same zjawiska zaczęły być rozpatrywane
na poziomie mikrozjawisk, zachodzących w skali mikro - między pojedynczymi cząsteczkami czy atomami. Ten opis zjawiska
na   poziomie   mikro   pokazywał,   jak   złożonym  był  proces,  który   w  skali  makro   wydawał  się   prostym  (np.   parowanie   czy
rozpuszczanie). Pokazywał jednocześnie, że proces w skali makro nie jest sumą  identycznych składowych mikro, lecz średnią
statystyczną, często dość  różnych zjawisk elementarnych. Można powiedzieć, że ludzkość odkryła nie tylko fakt, że z pozoru
ciągły  kawałek  materii zbudowany  jest  z  atomów,   ale   i  że   z  pozoru  proste  zjawisko  fizykochemiczne  "zbudowane"  jest  z
różniących   się   między   sobą   zjawisk   elementarnych.   Tak   więc   chcąc   zrozumieć     np.   dyfuzję,   musimy   sobie   uświadomić
zjawisko bezładnych ruchów termicznych cząsteczek, zjawisko przypadkowości zderzeń tych cząsteczek, rozkładu ich energii
translacji   (szybkości   poruszania   się)   oraz   rolę   przypadku,   rządzącego   w   tym   świecie   mikrozjawisk.   Ze   "statystycznego"
zsumowania tych wszystkich elementów powstaje zjawisko w skali makro, które często daje się opisać dość prostą zależnością
(cząsteczki  z  obszaru  o  większym  stężeniu  samoistnie przesuwają  się do  obszaru  o  stężeniu  mniejszym aż do  wyrównania
stężenia w całej objętości). 

Ponieważ  zjawisko  makro  jest  "statystyczną  sumą"  wielkiej  ilości dość  różnorodnych  zjawisk w  skali mikro,  jego  przebieg
będzie   zależał   od   ilości   i   rodzaju   zjawisk   elementarnych,   a   te   z   kolei   będą   zależeć   od   różnych   parametrów   zjawiska
(np. temperatury, stężenia, ciśnienia itp.). Przypomina to np. zjawisko mieszania barw. Poniżej zmieszano ze sobą kolor żółty z
czerwonym,  uzyskując różne  efekty,  zależne od  ilości jednego  i drugiego  składnika w  mieszaninie.  Pola skrajne  różnią  się
zasadniczo, środkowe są bardziej do siebie zbliżone, ale mało podobne do skrajnych. 

  

  

  

  

  

  

  

  

  

  

  

  

Podobnie   rzecz   wygląda   z   procesem   fizykochemicznym.   Jeżeli   składają   się   na   niego   procesy   "czerwony"   i   "żółty",   to
w warunkach, w których decydującą rolę gra mikroproces "czerwony", proces makro będzie przebiegał zdecydowanie inaczej,
niż gdy przewagę, ze względu na zmianę parametrów, uzyska proces elementarny "żółty". W przypadku prowadzenia procesu
w warunkach, gdy udział "żółtego" i "czerwonego" będą podobne, uzyskamy jeszcze inny przebieg procesu. 
        Jeżeli będziemy uczyć się o tym procesie "na pamięć", jak to ma miejsce w zdecydowanej większości przypadków, trudno
nam  będzie   zapamiętać,  jak  taka  czy   inna   zmiana   któregoś  z  parametrów  procesu  wpływa   na   jego   przebieg.   Szczególne,
że parametrów istotnych dla tego przebiegu jest zazwyczaj kilka. Jeżeli zrozumiemy i zapamiętamy podstawowy mechanizm
procesu - wpływ poszczególnych parametrów będzie logiczny i konsekwencje ich zmian oczywiste. 

do strony

tytułowej

do góry

strony 

Rozpuszczalność a temperatura 

Badając   zależność   rozpuszczalności  od   temperatury,   znajdujemy,   że   ciała  stałe   na   ogół  lepiej  się   rozpuszczają   w  wyższej
temperaturze (ale są wyjątki!), gazy w wyższej temperaturze rozpuszczają się gorzej, za to wpływ na ich rozpuszczalność ma
ciśnienie   (ze   wzrostem   ciśnienia   rozpuszczalność   rośnie),   zaś   rozpuszczalność   cieczy   w   innej   cieczy   czasem   rośnie
z  temperaturą,   czasem  maleje,  a  czasem  najpierw  rośnie  a  potem  maleje.  Niektóre  ciecze  mieszają  się  ze  sobą   w  sposób
niczym nie ograniczony. I jak to wszystko spamiętać, nie pomylić się na egzaminie, skąd wiedzieć czy dana substancja to nie
"wyjątek" - głowa boli, choć problem (w skali całej chemii fizycznej) stosunkowo niewielki. 

zagęszczenia cząsteczek gazu nad cieczą (ciśnienia gazu) - im większe, tym więcej cząsteczek będzie wnikać do wnętrza
roztworu;

powinowactwa   gazu   do   cieczy   (siły   solwatacji)  -   im  silniejsze,   tym  więcej  cząsteczek   gazu  będzie   tworzyć   asocjaty
z cząsteczkami cieczy, co utrudnia opuszczenie roztworu;

ruchliwości cząsteczek gazu (temperatura) - im wyższa temperatura, tym większa ruchliwość cząsteczek gazu (co sprzyja
ruchowi w obu kierunkach), słabsze wiązanie cząsteczek gazu w cieczy (słabsza solwatacja, ułatwia opuszczanie cieczy
przez  gaz)  i  większa  ruchliwość  cząsteczek  cieczy,   co  też  sprzyja  "wyrzucaniu"  gazu   z roztworu.   Ponieważ zmiana
temperatury wpływa jednocześnie na trzy procesy, efekt wypadkowy nie zawsze da się przewidzieć. Ponieważ jednak
siły solwatacji są zazwyczaj niewielkie a "zysk energetyczny" cząsteczek cieczy jest zazwyczaj większy niż cząsteczek
gazu, efekt końcowy to zazwyczaj zmniejszanie rozpuszczalności w miarę podwyższania temperatury.

Zastanówmy się zatem, co to znaczy "rozpuszczać się" i jaki jest mechanizm cząsteczkowy takiego procesu. Przejdźmy od
procesu w skali makro do składowych   mikroprocesów. Rozpatrzmy na początek sytuacje wyjściowe głównych elementów
naszego procesu, czyli cieczy, gazu i ciała stałego w danej temperaturze.
              Cząsteczki  cieczy  (rozpuszczalnika)  poruszają się  bezładnymi ruchami  z różną  prędkością i w  różnych  kierunkach,
przekazując   sobie   nawzajem   energię   kinetyczną   (translacji)   w   procesach   zderzeń.   Ponadto   na   cząsteczki   te   działa   siła
grawitacji (ziemskie pole grawitacyjne) i siły oddziaływań innych cząsteczek, głównie siły elektrostatyczne. Te ostatnie siły
mają bardzo duże znaczenie w cieczach polarnych (woda, alkohole) a minimalne w niepolarnych np. węglowodorach.
O sile grawitacji bardzo często zapominamy przy rozpatrywaniu zjawisk zachodzących z udziałem cieczy, a zawdzięczamy jej
istnienie ciśnienia hydrostatycznego.
        Gaz - tu rodzaje oddziaływań są analogiczne, z tym, że grawitacja nie odgrywa tu większej roli (stosunkowo małe masy
cząsteczek gazu), a także oddziaływania międzycząsteczkowe, ze względu na duże odległości między cząsteczkami, są nikłe
i można nie zwracać na  nie uwagi.  Cząsteczki gazu zderzając się  ze ścianami naczynia,  w  którym  są zamknięte powodują
powstanie zjawiska ciśnienia, jednakowego we wszystkich kierunkach.
              Ciało stałe, to  cząsteczki o  silnych  oddziaływaniach międzycząsteczkowych, drgające w  węzłach sieci krystalicznej
(energia kinetyczna) o rozkładzie energii drgań podobnym do rozkładu szybkości poruszania się cząsteczek cieczy.

Jak   przebiega   proces   przechodzenia   cząsteczek   ciała   stałego   do   roztworu
(to oczywiście bardzo skrócony i uproszczony opis). 
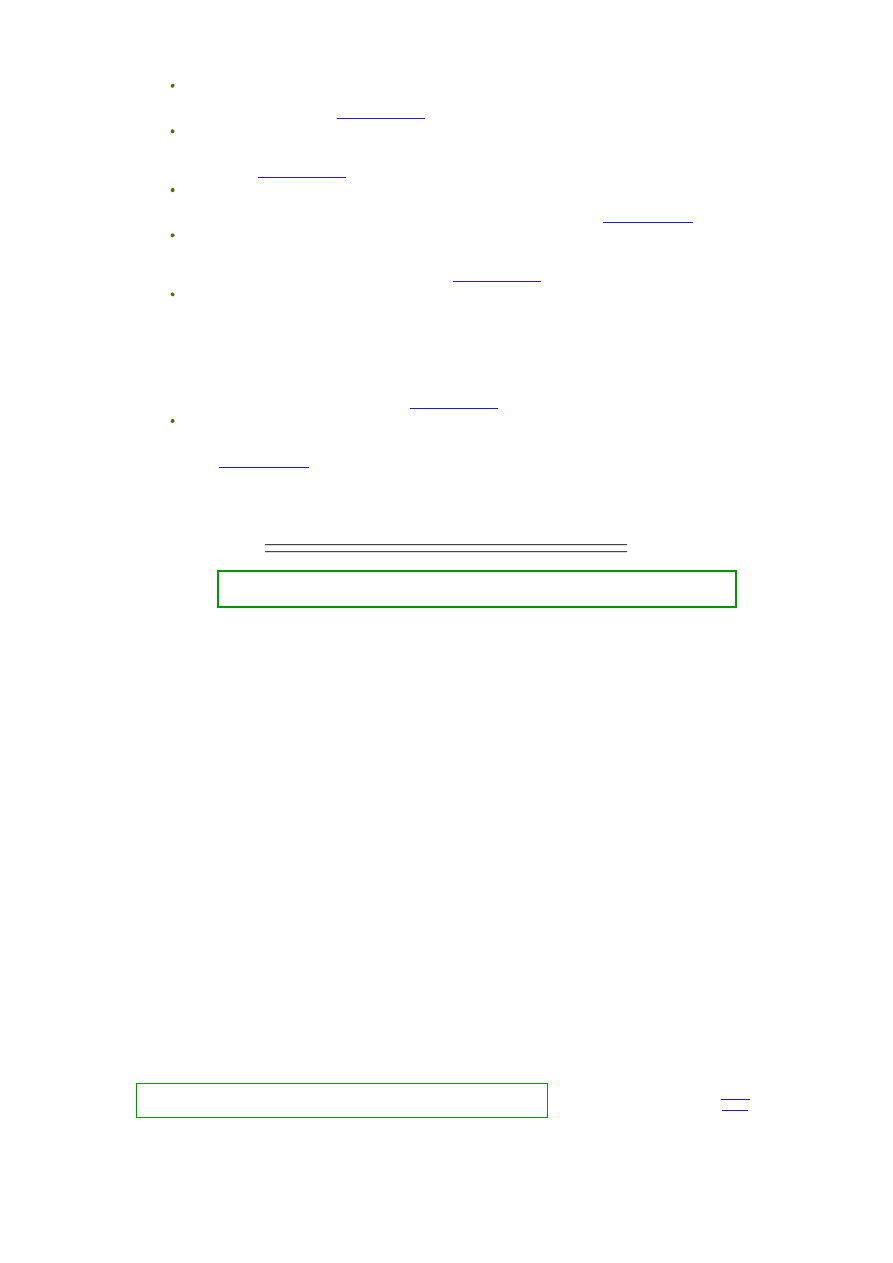
Krystaliczne   ciało   stałe   symbolizują   niebieskie   kółka   powiązane   siłami   sieci
krystalicznej   (przerywane   niebieskie   linie).   Cząsteczki   cieczy   symbolizują
czerwone   punkty,   powiązane   siłami   oddziaływań   międzycząsteczkowych
(przerywane czerwone linie).

Przypadkowe,   co   do   kierunku   i   siły,   drgania   cząsteczek   w   sieci   krystalicznej
(niebieskie  strzałki)  spowodowały  "wypchnięcie"  cząsteczki  ciała  stałego  z  sieci
krystalicznej. Żeby wniknąć pomiędzy cząsteczki cieczy cząsteczka ta musi mieć
energię wystarczającą nie tylko do pokonania sił spójności sieci krystalicznej ale
także  do   pokonania   sił  spójności  cieczy,   a  ponadto,  po   wniknięciu  do   roztworu

musi się w nim utrzymać. To ostatnie będzie możliwe, jeśli siły oddziaływań między cząsteczkami cieczy, siły oddziaływań
cząsteczek cieczy  z cząsteczkami substancji rozpuszczonej oraz  siły przyciągania i  wiązania cząsteczek  w  sieć krystaliczną
będą względem siebie odpowiednio równoważone.

Jeżeli teraz zastanawiamy się, jak zależeć będzie od temperatury proces rozpuszczania w skali makro, to rozważyć musimy, jak
zmienią   się   te   trzy   siły   i   jak   zmienią   się   relacje   ilościowe   między   nimi,   bo   to   od   nich   zależy   makroskopowy   efekt
rozpuszczania. Najczęściej bywa tak, że podwyższenie temperatury zwiększa energie drgań cząsteczek w sieci (łatwiej się od
niej  odrywają),   zmniejsza   siły   oddziaływań   międzycząsteczkowych   cieczy   (łatwiej   wniknąć   pomiędzy   nie)   ale   zmniejsza
również solwatacje. W końcowym efekcie, tam gdzie proces solwatacji nie jest bardzo istotny, wzrost temperatury zwiększa
rozpuszczalność.   Tam  jednak   gdzie   solwatacja   odgrywa   zasadniczą   lub   nawet   główną   rolę   -   wzrost   temperatury   będzie
rozpuszczalność osłabiał.

Na podstawie procesu rozpuszczania ciała stałego w cieczy, dość prostego z pozoru i przedstawionego w uproszczony sposób,
wykazaliśmy,   jak  trudno   przewidzieć  przebieg    procesu   makroskopowego,  jeśli  nie   zna   się  jego  mechanizmu   na   poziomie
mikroświata.  A  trzeba  pamiętać,   że   zazwyczaj  dołączają   tu   zjawiska   dysocjacji,   asocjacji  i  sprawa   komplikuje   się  jeszcze
bardziej.   Uczenie  się  wszystkich  przypadków na  pamięć  jest pozbawione  sensu  i  w  praktyce niewykonalne.  Zapamiętanie
podstawowych   mechanizmów  procesu w  powiązaniu  z  innymi wiadomościami  (solwatacja,  oddziaływania  elektrostatyczne
miedzy   jonami  czy   dipolami   cząsteczkowymi,   energia   sieci  krystalicznej  itp.)   pozwala  nam  dość  swobodnie  przewidywać
przebieg zjawiska w różnych układach, jeśli tylko znamy konieczne do tego parametry układu w którym proces przebiega.

Prześledźmy   teraz  w  podobny   sposób   zjawisko  rozpuszczania  się  gazu w cieczy.
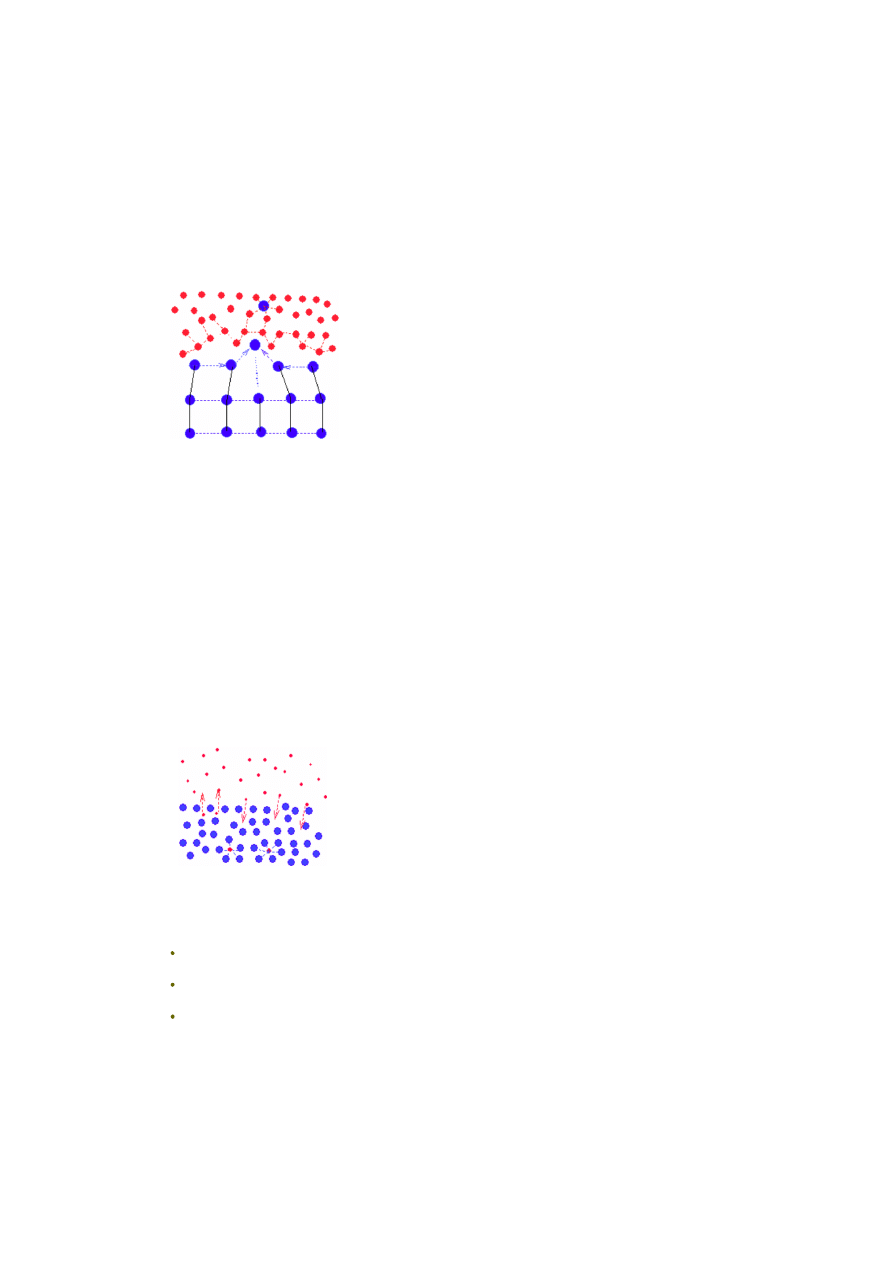
Gaz styka się z cieczą na granicy faz. Cząsteczki gazu (czerwone kropki)   będące
w   pobliżu   tej   granicy   faz   i   zdążające   w   jej   kierunku,   mogą   (jeśli   posiadają
odpowiednią   energię   kinetyczną)   pokonać   siły   napięcia   powierzchniowego
(oddziaływań   wiążących   warstwę   powierzchniową   cząsteczek   cieczy)   i  wniknąć
do   wnętrza   cieczy   (niebieskie   kropki).     Tam,   albo   zostaną   związane   siłami
solwatacji przez cząsteczki cieczy, albo poprzez zderzenia z cząsteczkami ponownie
"wyrzucone" nad  powierzchnię.  Im więcej cząsteczek  gazu w  cieczy, tym więcej
z   nich   będzie     z   niej   usuwanych   (większe   prawdopodobieństwo   zderzeń).   Po
pewnym   czasie   wytworzy   się   równowaga   -   tyle   samo   cząsteczek   będzie   się

rozpuszczać (wnikać do wnętrza cieczy) co opuszczać roztwór. Procesowi opuszczania cieczy przez cząsteczki gazu sprzyja
też ich stosunkowo mała masa, co w połączeniu z ruchliwością powoduje, że siła grawitacji ziemskiej nie ma tu praktycznie
znaczenia. Parametry tego stanu równowagi będą zależały od trzech czynników:

Tak więc najczęściej obserwowany spadek rozpuszczalności gazu w cieczy  pod wpływem zwiększania temperatury nie jest
żadnym   wyjątkiem   od   reguły,   lecz   wynikiem   zmian   w   obrębie   składowych   procesów   zjawiska.   Także   nikła   zazwyczaj
rozpuszczalność gazów w cieczach wynika nie z jakichś ich specjalnych właściwości, a  głównie z ich małej masy. Sprzyja ona
uzyskiwaniu dużych prędkości przez cząsteczki gazu po zderzeniu z "masywną" cząsteczką cieczy i ułatwiania w ten sposób
opuszczanie   roztworu.   Także   niewielka   zazwyczaj   polarność   cząsteczek   gazu   nie   sprzyja   solwatacji,   która   jest   ważnym
czynnikiem utrzymującym gaz w cieczy.  Gaz o dużej polarności (np. HCl) rozpuszcza się w polarnych cieczach bardzo dobrze

(HCl

aq

 

około 35%

 

w wodzie). Warto  też zaznaczyć, że niska polarność gazów, to nie specyficzna ich właściwość, a raczej

odwrotnie - stan gazowy  jest  skutkiem niskiej polarności, bowiem cząsteczki nie wiążąc się ze sobą w  asocjaty nie tworzą
elementów  o   dużej  masie.  Gdyby  cząsteczki  wody   nie   były   polarne,   woda  w warunkach  standardowych  byłaby   gazem  o
właściwościach fizycznych zbliżonych do amoniaku bądź metanu.

Zajmijmy się teraz rozpuszczaniem cieczy, a dokładniej mieszaniem się cieczy, bowiem  wskazać tu, co jest rozpuszczalnikiem
a  co   substancją   rozpuszczoną,   jest  dość  trudno.   Na   tym  przykładzie  można   przy   okazji  zauważyć,   jak  zwodnicze   i  mało
precyzyjne są niektóre używane przez nas pojęcia (rozpuszczalnik, rozpuszczanie A w B itp.).

rys. 1

rys. 2

 

rys. 3

 

Rysunek   po   lewej   symbolizuje   dwie   ciecze   (cząsteczki   "zielone"   i
"czerwone").   Mieszanie   będzie   polegało   na   wnikaniu   cząsteczek
zielonych między czerwone i czerwonych między zielone, aż do uzyskania
jednorodnej mieszaniny (ostatni rysunek). 
Jeżeli   jedna   ciecz   jest   polarna,   z   silnymi   oddziaływaniami
międzycząsteczkowymi, a druga ciecz jest niepolarna, to mieszanie takich
cieczy  jest niemożliwe  lub  bardzo  utrudnione.  Mieszaniu  się cząsteczek
mogą   przeszkadzać   siły   międzycząsteczkowe,   uniemożliwiające
wniknięcie   "obcych"   cząsteczek   pomiędzy   silnie   przyciągające   się
cząsteczki cieczy polarnej (rys. 2). 
Jeżeli   siły   spójności  cieczy   polarnej     pozwolą   nawet   na   wprowadzenie
cieczy   niepolarnej   (np.   przez  silne   wstrząsanie   czy   mieszanie),   to   siły
międzycząsteczkowe   polarnych   cząsteczek   będą   tworzyć   powiązane
struktury  i "wypychać" z nich cząsteczki niepolarne. Polarne cząsteczki,
które   wnikną   pomiędzy   niepolarne,   będą   na   tych   samych   zasadach
odtwarzać powiązane struktury łącząc się w większe agregaty i po chwili
obie ciecze będą znów rozdzielone. 

Przy   niezbyt  silnych   oddziaływaniach   międzycząsteczkowych   niewielka
część cieczy polarnej rozpuści się w niepolarnej i niewielka część cieczy
niepolarnej rozpuści się w cieczy polarnej. Otrzymamy dwie fazy ciekłe -
nasycony   roztwór   cieczy   polarnej   w   niepolarnej   i   nasycony   roztwór
cieczy niepolarnej w polarnej.

Jeżeli polarne będą obie ciecze, to mieszanie nastąpi dość łatwo, bowiem
oddziaływanie   cząsteczek   czerwona-zielona,   czerwona-czerwona   i
zielona-zielona   będą   podobne   i   zastąpienie   w   strukturach   polarnych
cieczy   jednych   cząsteczek   drugimi   nie   będzie   stanowiło   problemu
energetycznego.
Pewną   rolę   w   mieszaniu   się   cieczy   może   odgrywać   także   wielkość
cząsteczek   mieszanych   substancji   (na   podobnej   zasadzie,   jak   to
opisywaliśmy przy rozpuszczaniu gazów w cieczach).

Przy mieszaniu cieczy niepolarnych nie występują silne siły oddziaływań
międzycząsteczkowych   i   wymieszanie   się   cząsteczek   następuje   bez
większych   problemów.   Generalnie   więc,   zgodnie   z   zasadą   "podobne
rozpuszcza  się  w  podobnym",  kłopoty  z rozpuszczalnością pojawiają  się
w miarę zwiększania się różnic między polarnościami mieszanych cieczy.
Wzrost   temperatury,   osłabiając   oddziaływania   międzycząsteczkowe,
zazwyczaj   zwiększa   rozpuszczalność   (mieszalność   cieczy),   o   ile   nie
wpływa jednocześnie na inne zjawiska zachodzące wraz z rozpuszczaniem
(np. hydrolizę, dysocjację, solwatację itp.).

Tak więc zamiast próbować zapamiętać reguły dotyczące zjawiska rozpuszczania w skali makro, które są różne dla różnych
układów i różnie reagują na zmianę parametrów (np. temperatury), lepiej zastanowić się nad mechanizmem zjawiska (czy też,
jak już wiemy - zjawisk) w skali cząsteczkowej i na tej podstawie zbudować wyobrażenie o istocie procesu. Wówczas  dla
każdej konkretnej sytuacji (a w najgorszym razie dla większości sytuacji) będziemy potrafili trafnie przewidzieć efekt makro
na podstawie analizy zjawisk na poziomie cząsteczkowym. Nawet korzystanie z popularnych reguł (np. owe przywołane już
wcześniej   "podobne   w   podobnym")   staje   się   bezpieczniejsze   jeżeli   znamy   mechanizm   (np.   co   rozumieć   pod   pojęciem
"podobne").

"Klasyczna"   chemia   fizyczna   opisuje   poruszany   wyżej   temat   roztworów   o   wiele   bardziej   jednoznacznie   i   precyzyjnie
(termodynamiczne   funkcje   nadmiarowe,   entalpie   procesów   np.   solwatacji   i   rozpuszczania,   entropia,   roztwory   idealne,
regularne, doskonałe, rzeczywiste itp.). Jeśli jednak zaczniemy studiować to "matematycznie doskonałe" ujęcie problematyki
roztworów po wcześniejszym przemyśleniu sprawy w taki uproszczony sposób (jak powyżej), skorzystamy z tego studiowania
o wiele więcej, niż gdy podejdziemy do tego bez "oswojenia" problemu i przygotowania. 

do strony

tytułowej

do góry

strony 

Skręcalność płaszczyzny polaryzacji światła spolaryzowanego 

Izomeria optyczna sprawia zazwyczaj sporo kłopotów. Po pierwsze, dla swobodnego poruszania się wśród zagadnień w niej
omawianych potrzebna jest spora doza wyobraźni przestrzennej, a nie każdy ją posiada, zaś po drugie - nie bardzo wiadomo o
co tam chodzi. Co to za dziwna i tajemnicza cecha tych asymetrycznych cząsteczek, wywołująca skręcenie płaszczyzny drgań
fali światła. Omawianie zjawiska w skali makro sprowadza się do podziału substancji, na takie, które skręcają tę płaszczyznę,
bo mają asymetryczny atom węgla lub same są asymetryczne, oraz na takie, w których są atomy węgla asymetrycznego, ale
płaszczyzny polaryzacji nie skręcają (formy mezo), oraz na takie, które zawierają tyle samo cząsteczek skręcających w lewo
co i w prawo (racematy). Do tego wszystkiego dochodzą rozróżnienia diastereoizomerów i enancjomerów, konfiguracji L i D
oraz  R  i  S,  anomeryczne  formy  α  i  β ...     i  mętlik   w  głowie  pełny   i  obezwładniający.  Te   ostatnie   rozróżnienia,  to  sprawa
umowna, pewien fachowy język i nie ma wyboru - trzeba się go nauczyć. Jednak na samo zjawisko można spojrzeć nieco
inaczej niż to czyni większość podręczników - i może dla niektórych będzie to spojrzenie rozjaśniające sytuację.

Ostrzegam, że zamieszczone tu "wyjaśnienia" nie należą do oficjalnej nauki, są mocno popularno-naukowe (czasem bardziej

popularne niż naukowe) ale mam nadzieję, że ułatwią zrozumienie istoty zjawiska.

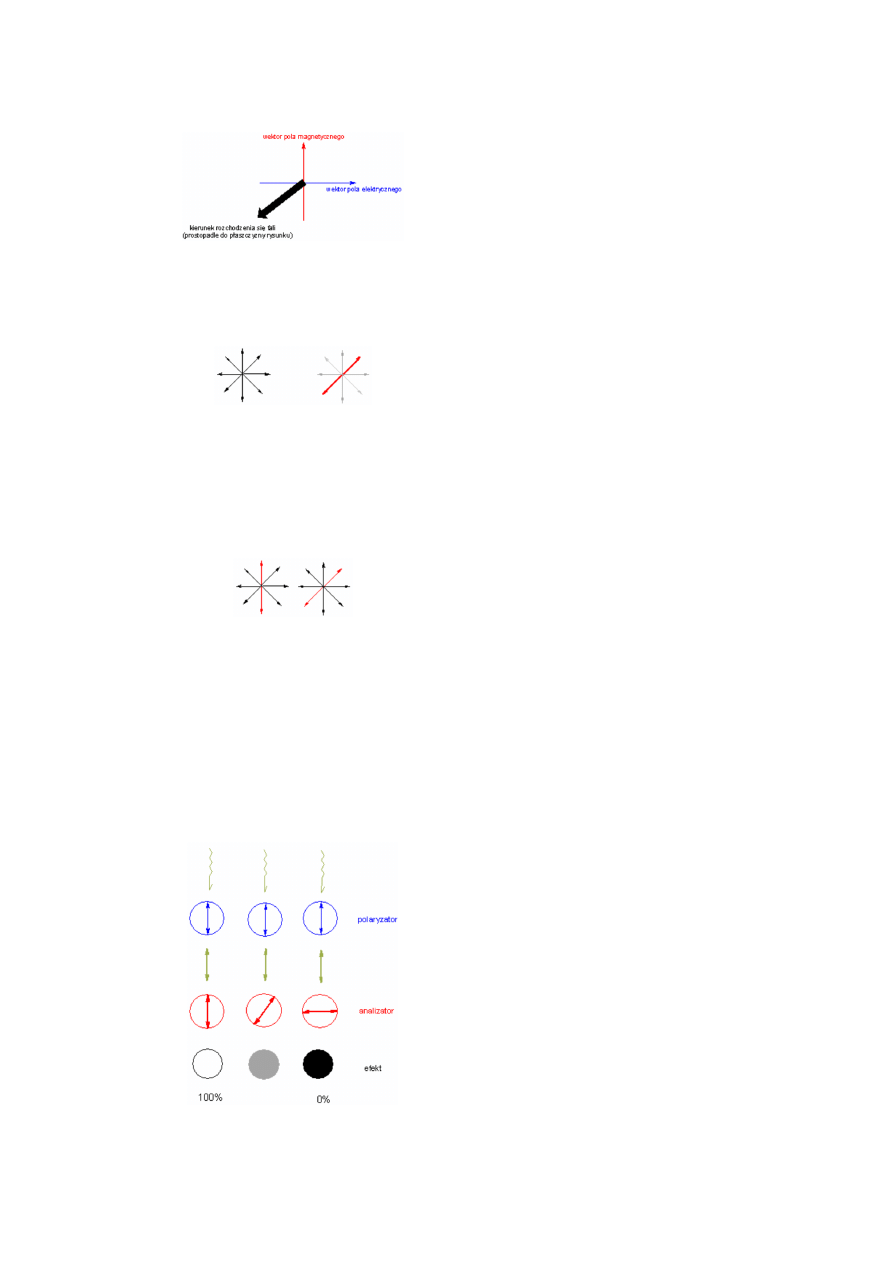
Zacząć trzeba od tego, że fala świetlna to kolejno po sobie
następujące   zmiany   natężenia   pola   elektrycznego   i   pola
magnetycznego   (fala elektromagnetyczna). Wektory tych
pól   (magnetycznego   i   elektrycznego)   są   do   siebie
prostopadłe   i   jednocześnie   prostopadłe   do   kierunku
rozchodzenia się fali. Tak więc patrząc na zbliżającą się do
nas falę  elektromagnetyczną  "widzimy" wektory  tych  pól
jako   prostopadłe   do   siebie   w   płaszczyźnie   naszego
widzenia. Promień   świetlny wytworzony przez termiczne
źródło   światła   jest   wiązką   fal   elektromagnetycznych   o
bardzo   różnych   ułożeniach   płaszczyzn   wektorów
elektrycznych czy magnetycznych. W samej wiązce nie ma
wyróżnionego   któregokolwiek   kierunku   drgań   pola
(ułożenia wektora pola). 

Jeżeli  jednak   taki "nieuporządkowany"   promień  (rysunek
po   lewej)   przepuścimy   przez   odpowiedni   ośrodek,   np.
dwójłomny   kryształ   szpatu   islandzkiego   (CaCO

3

),   pod

odpowiednim kątem w stosunku do osi sieci krystalicznej,
to   promień   zostanie   rozszczepiony   na   dwa   promienie
o   uporządkowanych   kierunkach   drgań.   Każdy   z   tych
nowych promieni będzie składał się z wiązki fal drgających
w   jednej   płaszczyźnie   (rysunek   prawy,   polaryzacja
w płaszczyźnie  oznaczonej na  czerwono,  szare  promienie
ulegają wygaszeniu). Wiązkę tak drgających fal świetlnych
nazywamy

 

światłem

 

spolaryzowanym.

 

Fala

elektromagnetyczna w wiązce spolaryzowanej nie różni się
niczym  od   fali   w   wiązce   nieuporządkowanej,   natomiast
światło   spolaryzowane   (wiązka   fal   o   wyróżnionej
płaszczyźnie   drgań)   uzyskuje   nowe   właściwości,
wynikające z faktu uporządkowania. A właściwie nie tyle
uzyskuje   nowe   właściwości,   co   uzyskuje   cechy
pozwalające   zauważyć   te   właściwości.   Jedną
z   podstawowych   "nowych"   cech   wiązki   światła
spolaryzowanego   jest   wyróżniona   płaszczyzna   drgań.
Istnienie   takiego   wyróżnionego   kierunku   powoduje,   że
wiązka przepuszczana przez ośrodki zawierające elementy
asymetryczności   zmienia   kierunek   (płaszczyznę)   drgań   -
następuje   skręcenie   płaszczyzny   polaryzacji   promienia
spolaryzowanego.   Takiemu   samemu   procesowi   skręcenia
ulegają   płaszczyzny   drgań   w   wiązce   niespolaryzowanej,
tylko wówczas nie ma sposobu by to zjawisko zauważyć.
Właściwości   wiązki   skręconej   niczym   nie   różnią   się   od
właściwości tej wiązki przed skręceniem płaszczyzn drgań.
Gdyby   na   rysunku   obok   nie   wyróżniono   kolorem
czerwonym   jednej   fali,   skręcenie   całej   wiązki   o   45°
w prawo byłoby niezauważalne.

skręcenie  płaszczyzn drgań wszystkich fal w promieniu  w identyczny sposób

nie powoduje praktycznie  żadnej zmiany w postrzeganiu tego promienia (jego

parametrów)

Jeżeli zbudujemy układ, w którym wiązka światła zostanie
najpierw   spolaryzowana   przez   polaryzator   (np.   kryształ
szpatu   islandzkiego)   a   potem   przepuszczona   przez
analizator (taki sam polaryzator jak pierwszy, tylko pełni w
tym   układzie   inną   rolę)   to   ilość   światła,   która   przejdzie
przez   taki   układ   zależy   od   kąta   między   płaszczyznami
polaryzacji   polaryzatora   I   i   polaryzatora   II   (analizatora).
Jeśli   kąt   między  płaszczyznami  jest   0°  -   przechodzi  całe
światło,   jeżeli   kąt   ten   wynosi   90°   -   wiązka   zostaje
całkowicie   wygaszona,   w   przypadkach   pośrednich
ustawienia płaszczyzn efekt wygaszania jest częściowy.
Innymi słowy możemy powiedzieć, że jeśli spolaryzowana
wiązka   światła   pada   na   analizator   w  taki   sposób,   że   jej
płaszczyzna   polaryzacji   jest   zgodna   z   płaszczyzną
polaryzacji   analizatora   -   przechodzi   przez   analizator
praktycznie bez strat. Jeśli wiązka pada tak na analizator,
że   kąt   między  jej   płaszczyzną   polaryzacji   a   płaszczyzną
polaryzacji   analizatora   wynosi   90°   -   wiązka   przez
analizator  nie   przechodzi  (całkowite  wygaszenie).   Jest   to
bardzo   uproszczony   schemat   działania   polarymetru,   czyli
urządzenia pozwalającego określić wielkość kąta skręcenia
płaszczyzny polaryzacji światła spolaryzowanego.

Na   rysunku   poniżej   zamieszczono   schemat   działania
polarymetru.   Zasada   działania  tego   urządzenia  polega   na
zniwelowaniu   efektu   osłabienia   wiązki   światła
spolaryzowanego,   będącego   konsekwencją   skręcenia
płaszczyzny polaryzacji tej wiązki przez badany roztwór.

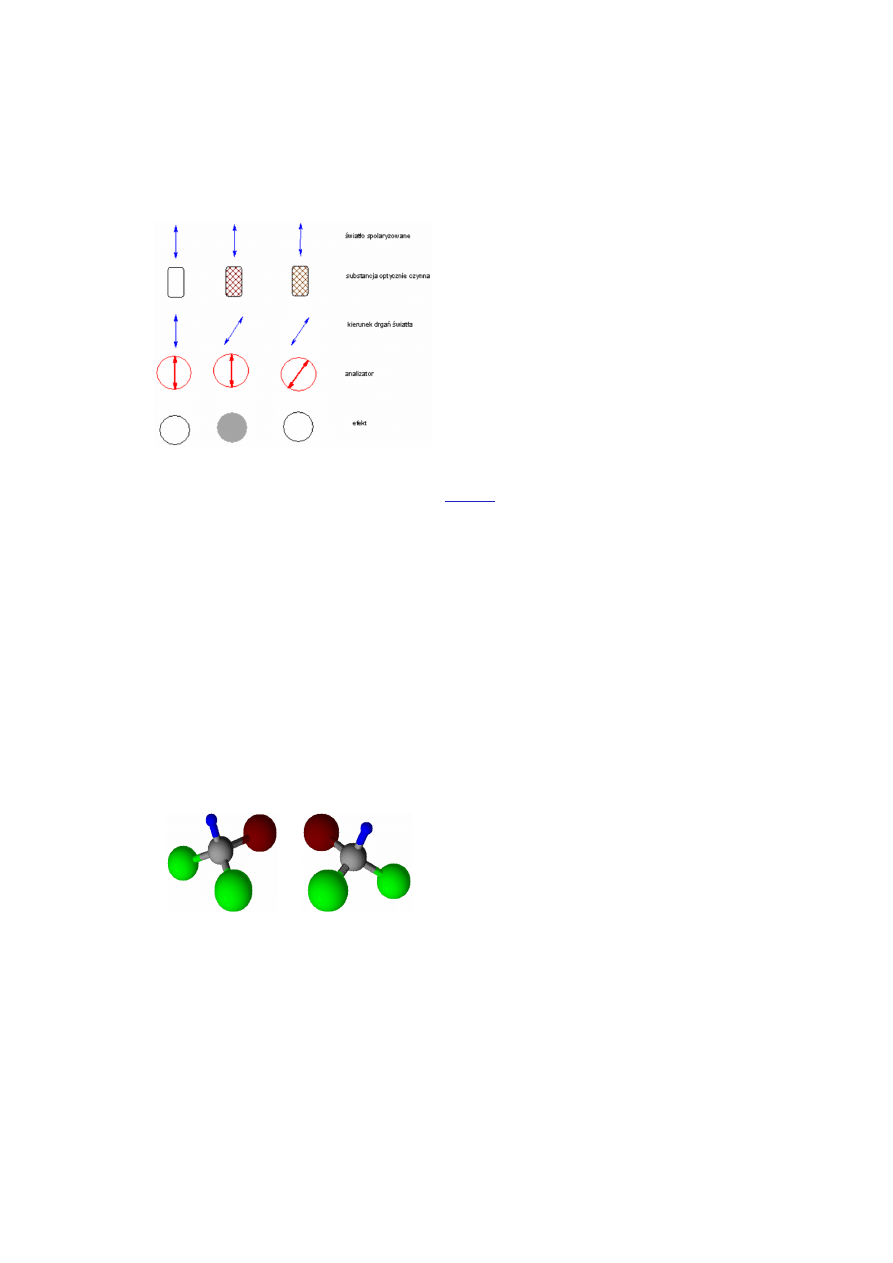
Praktyczne wykorzystanie polarymetru polega  na tym,  że
między   polaryzator   a   analizator   (ruchomy   polaryzator)
wstawiamy naczynie z czystym  rozpuszczalnikiem (woda,
ślepa   próba)   i   ustawienie   analizatora,   przy   którym   nie
następuje   osłabienie   wiązki   spolaryzowanej  uznajemy   za
zero. (Rysunek poniżej, pierwsza kolumna). 

Następnie   między   polaryzator   a   analizator   wstawiamy
naczynie   z   roztworem   substancji   optycznie   aktywnej   -
skręcającej

 

płaszczyznę

 

polaryzacji

 

światła

spolaryzowanego   (kolumna   druga   rysunku   obok).   To
skręcenie powoduje, że światło padające na analizator drga
w   płaszczyźnie   tworzącej   pewien   kąt     z   płaszczyzną
polaryzacji  (przepuszczania) analizatora.  W konsekwencji
powoduje to osłabienie wiązki.

Jeżeli   teraz   przekręcimy   analizator   tak,   żeby   jego
płaszczyzna   polaryzacji   pokryła   się   z   płaszczyzną
polaryzacji światła, które przeszło przez określoną warstwę
roztworu optycznie aktywnego, znów uzyskamy całkowitą
przepuszczalność.   Na   podstawie   kąta,   o   jaki  trzeba   było
obrócić  analizator  dla  uzyskania  pełnej przepuszczalności
światła, wnioskujemy o kącie skręcenia płaszczyzny wiązki
spolaryzowanej przez badany roztwór.

Dla

  światła

  o   określonej   długości   fali

(monochromatycznego)   w   danej   temperaturze   kąt
skręcenia   płaszczyzny   światła   spolaryzowanego   będzie
zależał od grubości warstwy roztworu i stężenia substancji
optycznie czynnej.

(patrz: też)

Tak   mniej  więcej  wygląda   sprawa   z  punktu   widzenia   makroskopowego   opisu  zjawiska.   Nas  jednak,   jak   zwykle,   bardziej
interesuje molekularny aspekt sprawy - on bowiem pozwoli nam (tak przynajmniej przypuszczamy)   na zrozumienie, co tak
naprawdę się dzieje i  dlaczego tak się dzieje.  Cząsteczki, z których zbudowana jest materia, składają się z atomów ułożonych
w  przestrzeni  w  określonej  dla  danej  cząsteczki  konfiguracji  przestrzennej.   Atomy   zawierają   protony   (ładunek   dodatni)   i
elektrony   (ładunek   ujemny),   które   wytwarzają   wokół   cząsteczki   pole   elektryczne,   a   będąc   w  ciągłym   ruchu   (spin,   czyli
wirowanie, niewielkie przemieszczenia w obrębie wiązań - oscylacja, poruszanie się elektronów po orbitalach itp.) wytwarzają
zmienne   pole   elektryczne.   To   zmienne   pole   elektryczne   jest   przyczyną   powstawania   wokół   cząsteczki   zmiennego   pola
magnetycznego.   W   sumie   więc   można   powiedzieć,   że   cząsteczka   generuje   charakterystyczne   dla   siebie   pole
elektromagnetyczne.  Fala  świetlna,  będąc falą  elektromagnetyczną,  przebiegając  obok  cząsteczki  sumuje  się  (wektorowo!)
z jej polem elektromagnetycznym,  dając w efekcie nową jakość, nową falę, która  od pierwotnej będzie różnić się (między
innymi)  płaszczyzną  drgań.  Wielkość   tego   skręcenia  płaszczyzny   drgań  zależeć  będzie  od  składu  i struktury  przestrzennej
cząsteczki,   od   ilości   cząsteczek,   z  którymi  fala   wejdzie   w  oddziaływania   oraz   od   usytuowania   cząsteczki  w  stosunku  do
kierunku rozchodzenia się fali. Ponieważ w układach makroskopowych (a w praktyce te nas interesują) mamy ogromne ilości
cząsteczek   współoddziałujących   z  falą   świetlną,     możemy   uznać,   że   skręcalność   takiego   układu   jest  statystyczną   średnią
wszystkich   możliwych   układów   cząsteczki   wobec   promienia,   a   zatem   jest   charakterystyczna   dla   danego   związku,   jego
struktury. W układzie molekularnym skręcalność zależna  byłaby nie tylko od budowy cząsteczki, ale także od ustawienia jej
w przestrzeni    względem promienia.  Jeżeli każda  cząsteczka  skręca  płaszczyznę  drgań fali  świetlnej,  to  płaszczyzna  drgań
światła spolaryzowanego powinna ulec skręceniu po przejściu przez każdy ośrodek przezroczysty, a w praktyce tak się nie
dzieje - skręcenie powodują tylko niektóre związki o szczególnej budowie cząsteczek.

Jeżeli cząsteczka o budowie i ustawieniu jak obok, po lewej,
skręca płaszczyznę np. o  kąt +α  , to  cząsteczka po prawej
skręci   płaszczyznę   o   kąt     -α,   bowiem   jej   struktura   jest
identyczna,   a   ułożenie   wobec   promienia   jest   dokładnie
lustrzanym   odbiciem   ułożenia   cząsteczki   pierwszej.
Jednocześnie   należy   zauważyć,   że   są   to   identyczne
cząsteczki - wystarczy drugą obrócić w prawo o 120° wokół
osi pionowej aby otrzymać pierwszą. A ponieważ w układzie
makro   występują   praktycznie   wszystkie   możliwe   ułożenia
cząsteczek,   można   uznać,   że   każdemu   położeniu,   które
skręca   płaszczyznę   polaryzacji   o   jakiś   kąt   w   prawo
odpowiada   ułożenie   innej  cząsteczki  na  drodze   promienia,
które   skręci   o   ten   sam   kąt   płaszczyznę   polaryzacji,   ale
w lewo. Suma tych znoszących się na wzajem oddziaływań
spowoduje   w   końcowym   efekcie   brak   zmiany   położenia
płaszczyzny   polaryzacji   promienia   wychodzącego   w
stosunku do padającego. Substancje zawierające cząsteczki z
elementem   symetrii   nie   powodują   (w   układach
makroskopowych) skręcenia płaszczyzny polaryzacji światła
przez nie przechodzącego.

Zestawienia cząsteczek o budowie asymetrycznej

Inaczej   ma   się   sprawa   w   przypadku   cząsteczek
asymetrycznych.   Jeżeli   w   strukturze   cząsteczki   występuje
centrum   asymetrii  (najczęściej   interesuje   nas   atom   węgla

 

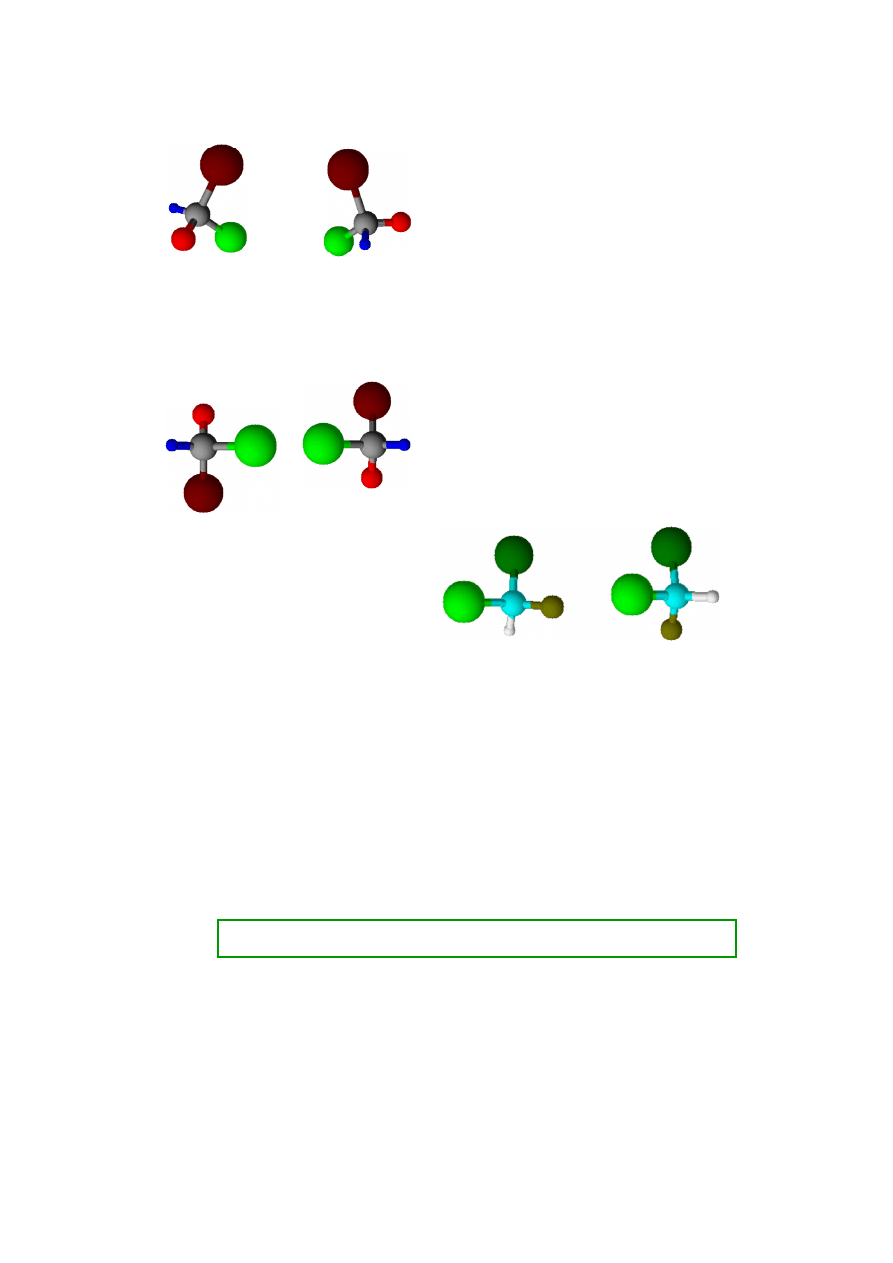
połączony   z   czterema  

różnymi

  podstawnikami)   to   żaden

obrót  czy przesunięcie w przestrzeni nie da ułożenia, które
byłoby   lustrzanym  odbiciem  tej  cząsteczki  (w  przestrzeni
trójwymiarowej!   Na   rysunkach   na   płaszczyźnie   dość
trudno   to   pokazać).   Przykład   (schemat)   takiej   struktury
obok.   Każdy   kolor   czterech   podstawników   centralnego
atomu   symbolizuje   inny   podstawnik.   Jeżeli   ustawimy
cząsteczki  w  stosunku   do   siebie   tak,   że   dwa   podstawniki
będą lustrzanymi odbiciami, to dwa pozostałe będą ułożone
różnie (górne i dolne zestawienie na rysunku obok). Znaczy
to,   że   nawet   w  nieskończenie   dużym  zbiorze     cząsteczek
o   asymetrycznej   strukturze   nigdy   nie   znajdzie   się   para
znosząca   nawzajem   swoje   wpływy   na   promieniowanie
elektromagnetyczne   (światło   spolaryzowane).   Zatem
promień   spolaryzowany   zawsze   zostanie   skręcony   przez
takie cząsteczki o kąt charakterystyczny dla tej substancji.

Każdej   strukturze   cząsteczek   danego   związku   o
asymetrycznej   budowie   odpowiada   struktura   będąca   jej
lustrzanym   odbiciem   i   skręcająca   dokładnie   tak   samo
płaszczyznę polaryzacji światła, tyle tylko, że w przeciwnym
kierunku.   Są   to   jednak   inne   cząsteczki,   izomery,   o   tym
samym   składzie   atomowym   ale  

różnej   strukturze

przestrzennej

. 

Przez żadne  przekształcenie  w  przestrzeni (bez rozrywania
wiązań) nie da się cząsteczki u dołu po lewej, przeprowadzić
w   cząsteczkę   po   prawej.   Takie   dwie   formy   nazywamy
enencjomerami. 
Enancjomery   skręcają   płaszczyznę   polaryzacji   światła
dokładnie   tak   samo,   ale   w   przeciwnych   kierunkach
(oznaczamy tę skręcalność jako + lub -).

 

 

Równomolowa   mieszanina   enancjomerów,   zwana
mieszaniną   racemiczną,   jest   optycznie   nieczynna,
bowiem skręcalność w lewo zostaje zrównoważona
skręcalnością   takiej   samej   ilości   cząsteczek
w   prawo.   Wypadkowa   skręcalność   takiej
mieszaniny wynosi zero.

Jeżeli w cząsteczce związku jest więcej niż jedno centrum asymetrii (chiralności), to sprawy skręcalności nieco się komplikują.
Izomery   optyczne,   które   nie   są   enancjomerami   (lustrzanymi   odbiciami   trójwymiarowej   konfiguracji)   nazywamy
diasteroizomerami.   W   przypadku   cząsteczek   zawierających   dwa   identyczne   co   do   składu   centra   asymetrii  (patrz   -   kwas
winowy)   może   być   układ   (++);   (--)   lub   (+-).   Ta   ostatnia   forma   jest   optycznie   nieczynna   i   nosi  symbol  mezo   (np.   kwas
mezowinowy).  Brak skręcania   płaszczyzny  polaryzacji światła przez formy  mezo wynika z tego,  że skręcenie  przez jedno
centrum asymetrii jest równoważone przez skręcenie w przeciwną stronę przez drugie centrum. Ale to są już sprawy izomerii,
chemii organicznej (szczególnie chemii cukrów) a nam chodziło tylko o mechanizm i zasadę zjawiska skręcalności.

Zatem  w  skali   mikro    każda  cząsteczka   skręca  płaszczyznę   polaryzacji  światła,  a   wielkość   i znak  tego   efektu  zależy  od
usytuowania cząsteczki względem kierunku rozchodzenia się promieniowania i jego płaszczyzny polaryzacji. Skręcalność jest
więc zjawiskiem powszechnym i niecharakterystycznym, jeśli chodzi o wielkość i kierunek zmian. 
Natomiast w skali makro płaszczyznę polaryzacji skręcają tylko substancje posiadające centrum asymetrii, wielkość ta jest
dla danej substancji charakterystyczna, może stanowić nawet jej parametr identyfikacyjny, a także pozwala odróżnić różne
izomery tej samej substancji.

Zrobiło się trochę jaśniej? I o to chodziło. Teraz, mając ogólne wyobrażenie o zasadach zjawiska zabierz się do studiowania
pełnej,   naukowej  prawdy   o   polaryzacji  światła   i  czynności  optycznej  związków.   Zobaczysz  o   ile   łatwiej  Ci  teraz  będzie
zrozumieć wszystkie problemy związane z izomerią optyczną.

Czego wyobrazić się nie da 

Im   lepiej  i   głębiej    poznajemy  świat   cząsteczek,   atomów   i   cząstek   elementarnych,   tym   bardziej  staje   się   on   dla   nas   ...
niezrozumiały. Rzecz w tym, że prawa i zasady obowiązujące w tym mikroświecie   (mechanika kwantowa) nie przystają w
żaden sposób do naszego świata w wymiarze makro. Inaczej mówiąc, nie mamy doświadczeń życiowych, które pozwoliłyby
zjawiska   mechaniki   kwantowej   opisać     przykładami   makroświata   o   mechanice   newtonowskiej.   A   ponieważ   elementów
mikroświata nie możemy obserwować bezpośrednio, za pomocą zmysłów, nie możemy również zrozumieć jak on działa. Dla
doraźnych celów dydaktycznych budujemy uproszczone modele w skali makro, które tłumacząc jedno - zaciemniają drugie.
Jeżeli  w  wyobraźni  ucznia   zaszczepimy   pojęcie   elektronu,   jako   maleńkiej  kulki   obdarzonej  ładunkiem,   trudno   będzie   mu
przyjąć później do wiadomości, że elektron jest falą i w dodatku może być w tym samym czasie w dwóch różnych miejscach.
Jeśli  jednak  nie  podsuniemy   mu  żadnego  rozwiązania,  żadnego   modelu  z  zakresu  znanego  mu  świata  makro,  w  ogóle   nie
pojmie   istoty   elektronu   i  nie   zrozumie  najprostszych   (jak  na  mikroświat)   pojęć   i  zjawisk,  jak   choćby   tworzenie   wiązania
chemicznego.   Dotarłszy   jednak   do   pewnego   poziomu   wiedzy   -   np.   kończąc   naukę   a   zaczynając   studiowanie   -   musimy
odważnie powiedzieć sobie DOŚĆ. Dość oszukiwania się, że elektron to kuleczka a wiązanie chemiczne to sprężynka, dość
oszukiwania   siebie  samego,   że   rozumiemy   co   to   jest   pole   grawitacyjne   czy  elektryczne,   że   pojmujemy   zjawisko  zamiany
energii na masę i że w ogóle rozumiemy co to jest masa i energia. Przyjąwszy sokratesowskie "wiem, że nic nie wiem" (z
całym szacunkiem dla proporcji), zastanówmy się, czy przyznawszy się do niezrozumienia i niezdolności wyobrażenia sobie,
dość przecież podstawowych zjawisk i pojęć, musimy przyjąć niemożność poznania przez nas  tego świata? Odwołajmy się tu

na moment do matematyki, która bazuje na aksjomatach (np. bezwymiarowość punktu czy jeden wymiar prostej, złożonej z
bezwymiarowych punktów - kto to ROZUMIE !?) i pojęciach   też nie dających się wyjaśnić (nieskończoność, zero, wartość
nieskończenie mała ...) uchodzi (i słusznie) za królową nauk, i bez której dochodzenie do prawdy obiektywnej jest niemożliwe
w żadnej dziedzinie wiedzy, . Tak więc przyjmując coś "na wiarę" nie obniżamy rangi naukowego poznania, jeżeli tylko cała
konstrukcja   zbudowana   na  tych   aksjomatach  jest   spójna   i  skuteczna.   Jeśli  przyjmiemy   "na  wiarę"   postulat   fal  materii  de
Broglie'a, to dzięki temu będziemy mogli przewidzieć skutecznie przebieg wielu zjawisk, niewytłumaczalnych bez przyjęcia tej
teorii. Zauważmy, że bez względu na czyją korzyść rozstrzygnie się odwieczny spór materialistów z idealistami (czy pierwsza
była materia czy idea, lub trywializując: co było pierwsze - jajko czy kura) prawa fizyki nie zmienią się na jotę. Innymi słowy,
obojętnie czy przyjmiemy prymat jajka czy kury, opis jednego i drugiego pozostanie identyczny.

Te parę zdań powyżej to tylko wywołanie tematu, z którym każdy musi się sam uporać. Każdy sam musi przemyśleć sprawę
by   zrozumieć   głębie   stwierdzenia   "wiem,   że   nic   nie   wiem"   i  zrozumieć,   że   taka   "niewiedza"   to   wiedza   bardzo   głęboka
i   ułatwiająca   pojmowanie   nawet   bardzo   skomplikowanych   i   trudnych   do   przeniesienia   w   świat   makro-modeli   zjawisk
atomowo-cząsteczkowych. 

Osobiście proponuję następujące podejście do sprawy:
Nie odrzucajmy porównań i przykładów spotykanych w podręcznikach i na wykładach, są to bowiem najczęściej dość dobrze
przemyślane i zazwyczaj "najlepsze z możliwych" makro-schematy mikro-zjawisk. Pamiętajmy jednak, że dotyczą one tylko
tego zjawiska (lub często nawet tylko jego elementu) i nie należy ich przenosić na inne zjawiska. Elektron jako naładowana
kulka   może   być   dobrym  przybliżeniem  w  tłumaczeniu   podstaw   istoty   wiązania   chemicznego   czy   dysocjacji,   nie   nada  się
jednak   zupełnie   do   wyjaśniania   zjawiska   rezonansu   magnetycznego   jąder   (NMR).   Tam   bardziej   przekonującym   będzie
porównywanie elektronów do  mgły czy  chmury  o różnej gęstości  w różnych miejscach cząsteczki -  taki model z kolei  nie
bardzo się przyda przy objaśnianiu wiązań. Zatem nie - elektron jest kulką, czy - elektron jest chmurą, czy - elektron jest falą,
lecz - w zjawisku X możemy sobie przyjąć, że elektron jest kulką, ale w zjawisku Y musimy o tym "zapomnieć" i przyjąć,
że  jest  chmurą  itp.  Zaś  czym  jest  elektron  w rzeczywistości  ?  "Wiem,   że  nic  nie  wiem"   -  ale  reakcje  chemiczne  potrafię
przeprowadzić zgodnie z założeniami i procesy fizykochemiczne wykorzystuję bez kłopotów w praktyce - a więc jednak coś
wiem?...

 

 

Spójrzmy na świat od nowa 

Jak już pisałem na stronie tytułowej, kłopoty z chemią fizyczną biorą się między innymi stąd, że w szkole tego działu chemii
nie ma prawie wcale, a na studiach występuje on od razu w swojej "oficjalnej", precyzyjnej, "matematycznej" postaci. Czasu
na "zbędne" tłumaczenia podstawowych pojęć najczęściej nie ma i do wszystkiego trzeba dochodzić samemu. I tu czyha na
nas spore niebezpieczeństwo.  Tak samo brzmiące  słowa,  pojęcia,  co do znaczenia których w  potocznym użyciu  nie mamy
żadnych wątpliwości, w chemii fizycznej nabierają nowych, precyzyjniejszych znaczeń, których  najczęściej nikt nam w porę
nie wyjaśnił (znów ten brak czasu). Tym sposobem, wykładowca używając terminu z zakresu chemii fizycznej ma co innego na
myśli niż słuchacz i problem z brakiem zrozumienia (lub gorzej - z niewłaściwym zrozumieniem) wykładanego tematu gotowy. 

Dobrym przykładem takich niezgodności są stany skupienia. Od dziecka rozróżniamy ciała stałe, ciecze i gazy i taki podział
stanów materii utrwala nam później  szkoła. W chemii fizycznej te trzy  stany też  występują, ale terminy te oznaczają teraz
trochę coś innego. Przez ciało stałe rozumiemy np. tylko stany krystaliczne, uporządkowane, zmieniające stan skupienia w
ściśle określonej  temperaturze. Niektóre  substancje,  które   uważamy  w życiu  codziennym  za  ciała  stałe,  wykazują  bowiem
podstawowe  cechy - stały  kształt  - dla fizykochemii  są cieczami o  bardzo dużej lepkości (szkło, parafina  stała, wosk itp.).
W potocznym zrozumieniu ciała stałego też spotykaliśmy problemy z zakwalifikowaniem substancji do odpowiedniej grupy
(ciała maziste, gęste smary, plastelina), ale nikt nie robił z tego problemu. W chemii fizycznej, jak we wszystkich naukach
przyrodniczych, staramy się być bardzo precyzyjni i jednoznaczni, stąd o zakwalifikowaniu substancji do odpowiedniej grupy
nie decydują nasze subiektywne, zmysłowe odczucia a precyzyjna definicja (choć i tu pojawiają się czasem kłopoty), związana
z jakimś istotnym parametrem. 

 

do strony

tytułowej

do góry

strony 

Pięć stanów skupienia? 

Przyzwyczailiśmy się do trzech stanów skupienia materii: ciało stałe, ciecz i gaz. W chemii fizycznej za ciało stałe uznajemy
ciała krystaliczne. Ciała stałe (w potocznym rozumieniu), które nie mają budowy regularnej, krystalicznej, zaliczamy do cieczy
o bardzo  dużej lepkości.  Podgrzewając ciała krystaliczne  dochodzimy  w  pewnym momencie  do określonej  temperatury,  w
której   siły   sieci   krystalicznej   nie   są   już   w   stanie   utrzymać   rozedrganych   cząsteczek   w   ustalonym   porządku   i   kryształ
przechodzi w ciecz (temperatura topnienia). Bezpostaciowe, amorficzne ciało stałe, które z punktu widzenia chemii fizycznej
jest   cieczą   o   ogromnej  lepkości,   ogrzewane   zmniejsza   swoją   lepkość,   co   oznacza,   że   energia   kinetyczna   poszczególnych
cząsteczek   zaczyna   być   porównywalna   z  siłami  oddziaływań   międzycząsteczkowych,   i  ciało   stałe  poprzez  stadium   formy
mazistej   przechodzi   w  "klasyczną"   ciecz  (o   ile   wcześniej  nie   ulegnie   pirolizie   -   ale   to   dotyczy  także   krystalicznych   ciał
stałych).  Tak   więc  pojęcia  -   ciało   stałe   i  ciecz, w  chemii  fizycznej  znaczą   co  innego  niż w  języku   potocznym,  kryterium
podziału jest tu struktura cząsteczkowa a nie właściwości fizyczne. 

Przyzwyczailiśmy się także traktować różne podziały i klasyfikacje zbyt formalistycznie, ostro rozgraniczając np. ciecze i gazy
czy ciała stałe i ciecze (w tym codziennym rozumieniu tych pojęć) - bowiem takie podejście "porządkuje" nam świat i daje
poczucie panowania nad mnogością informacji o nim.  O tym, że istnieje niebezpieczeństwo "zgubienia" części świata przy
takim podejściu   do  problemu   przypomina   choćby  wspomniany  wyżej  przypadek  ciał mazistych,   co  do  których   nie  mamy
pewności jak je zakwalifikować - do ciał stałych czy do cieczy. Także pozornie jednoznaczne i precyzyjne definicje potrafią
wprowadzić nas w błąd, jeśli niezbyt krytycznie podejdziemy do ich treści. Dla wygody i jasności sformułowań dość często
stosujemy różne skróty, nie dopowiadamy (np. opuszczamy informację o koniecznych warunkach) i jeśli ktoś potraktuje taką
"skróconą" definicję zbyt serio - kłopot gotowy. Na przykład dość często roztwór nasycony definiowany jest jako roztwór o
maksymalnym stężeniu - z lenistwa nie dodając, że w danej temperaturze. A potem nagle okazuje się, że są także roztwory
przesycone, tzn. takie, których stężenie jest większe niż nasyconych! Większe niż maksymalnie możliwe! I mętlik w głowie
pewny. Dla wyjaśnienia tej pozornej sprzeczności między definicjami szybko dodaje się, że roztwór nasycony to roztwór o

najwyższym  możliwym  stężeniu   w  danej  temperaturze   w  stanie   równowagi  termodynamicznej,   czy   też  termodynamicznie
trwały, czego większość studentów w początkowym okresie nauki i tak nie rozumie. I tak już przy dość prostych zjawiskach
można zacząć się gubić i przestać lubić chemię. Jak się przed tym uchronić? NIC NA PAMIĘĆ - WSZYSTKO NA ROZUM.

Trzy   stany   skupienia,   do   których   już  się   przyzwyczailiśmy,   a   które   w  ujęciu   fizykochemicznym   dają  ową   piękną   ostrość
podziału   (znika  nam problem  ciał  mazistych)   nagle  okazują  się  nie   być  jedynymi  jakie   zna  przyroda.   O  istnieniu    innych
najczęściej nie mieliśmy pojęcia, a trzeba w tym kontekście wspomnieć  o stanie nadkrytycznym (fluid) i ciekłych kryształach.
Pierwszych   w   życiu   codziennym   nie   spotykamy,   bo   występują   w   warunkach   ciśnienia   i   temperatury   na   co   dzień   nie
spotykanych,   te   drugie   zaś   są   stałym   elementem   naszej   rzeczywistości,   ale   spotykamy   się   z   nimi   w   postaci   ekranów
i wyświetlaczy różnych urządzeń i nie mamy większego pojęcia o ich postaci w formie wolnej substancji. A jedne i drugie
łączą w sobie cechy znanych stanów skupienia. Ciekłe kryształy stanowią pomost między ciałami stałymi a cieczami, fluid jest
połączeniem cech gazu i cieczy. I znów, gdy pojawi się taka nowa jakość, wali się nam w gruzy miły porządek świata i ogarnia
nas frustracja. Żeby ustrzec się takich przykrych niespodzianek, pamiętajmy, że materia to cząsteczki zbudowane z  atomów, a
te z kolei z cząstek elementarnych, i tylko to jest pewne, trwałe i stałe (choć i tu uczeni spierają się o detale). Wszystkie cechy
materii  obserwowane  w  skali  makro,   to   wypadkowe   cech   elementarnych  składników  materii  i  oddziaływań   między   nimi.
Trzeba   sobie   zatem   odważnie   powiedzieć   -   żadne   charakterystyczne   cechy   materii   w   skali   makro   nie   istnieją!     To,   co
opisujemy jako cechy materii (np. stany skupienia) to tylko przypadkowa wartość, będąca wypadkową cech składników w
danych warunkach. To, że mimo tego większość otaczającej nas materii potrafimy jakoś skwalifikować i zaszufladkować to i
tak cudowny przypadek. I nie jest to, wbrew pozorom, żadna rewolucyjna zmiana spojrzenia na świat - w wielu przypadkach
taki   ogląd   świata   już   od   dawna   akceptujemy,   tylko   nie   zawsze   zdajemy   sobie   z   tego   sprawę.   Weźmy   przykład   wody.
Spotykamy  ją w postaci oceanów,  mórz, jezior, rzek, strumyków, deszczu  i mgły, śniegu i  lodu, lodowców i zamarzniętych
kałuż, kropli kapiących z kranu czy mokrej plamy na obrusie. I nikogo głowa nie boli o to, jak jednoznacznie odróżnić strumyk
od rzeczki i czym się różni kropla rosy od kropli deszczu. Wiemy, że od kropelki mgły aż po ocean to wszystko tylko zbiór
cząsteczek wody,  a   różne  cechy  różniące  mgłę  od oceanu, to nie jakieś specjalne, charakterystyczne cechy takiej postaci
wody   lecz   jedynie   suma   właściwości,   dość   ściśle   zdefiniowanych,   molekuł   H

2

O.   A   że   możemy   zbiór   cząsteczek   wody

zwiększać   cząsteczka   po   cząsteczce,   to   oczywiste,   że   nie   istnieją   żadne   ścisłe   rozgraniczenia   między   mgłą   a   oceanem,   a
jedynie umowne podziały, zbudowane w oparciu o pewne cechy wynikające z wielkości zbioru cząsteczek wody. Skoro bez
większych zastrzeżeń akceptujemy  takie podejście w  stosunku do  wody -  to  dlaczego  mielibyśmy  inaczej traktować różne
zbiory cząstek elementarnych i atomów? Choć z drugiej strony, dość trudno pozbyć się wręcz podświadomych skojarzeń, że
tlen to gaz, a woda to ciecz. Zatem, żadna postać materii nie jest cieczą, gazem czy ciałem stałym - każda substancja jest tylko
sobą. Może występować w postaci cieczy, ciała stałego bądź gazu, lub pod inną postacią. Musimy zatem myślowo oddzielić
substancję, cechy jej cząsteczek czy atomów, od cech fizycznych układów makroskopowych. Nie ma kropli wody na stole, nie
ma oceanu - są tylko cząsteczki wody tworzące bądź kroplę bądź ocean, albo kałużę, ale to zawsze tylko woda. 

Prześledźmy teraz przemiany fazowe:   ciało stałe - ciecz - gaz z  punktu widzenia cząsteczkowego (oczywiście, jak zwykle
w dużym skrócie i uproszczeniu).
Cząsteczki  dipolowe   siłami   elektrostatycznego   oddziaływania   ładunków   ujemnych   i   dodatnich   w   cząsteczkach   utrzymują
uporządkowaną strukturę sieci krystalicznej. Siły tego oddziaływania są większe niż energia kinetyczna drgań tych cząsteczek.
Wraz ze wzrostem temperatury rośnie energia pojedynczych cząsteczek, aż w pewnym momencie dochodzi do zrównania siły
wiązań  cząsteczek   w  sieć   z  energią   kinetyczną   drgań   i  pękają  wiązania   sieci  krystalicznej.   Uporządkowana   przestrzennie
struktura  rozpada  się  -  następuje  topnienie   substancji.  Energia  translacyjna   cząsteczek   w  powstałej po   stopieniu   kryształu
cieczy jest większa niż siły oddziaływań międzycząsteczkowych, ale jeszcze siły międzycząsteczkowe są na tyle silne, że ciecz
stanowi układ dość spójny (lepkość, ciągłość strugi). Ponadto energia translacji (poruszania się cząsteczek) jest mniejsza od sił
grawitacji ziemskiej działającej na cząsteczki. Cząsteczki w cieczy poruszają się dość niezależnie (bezładnie), ale ciągle ich
zachowanie   determinowane   jest  przez  grawitacje  i  oddziaływania   międzycząsteczkowe,   którym  próbuje   przeciwstawić  się
energia translacyjna cząsteczek. Wypadkowe tych trzech sił determinują główne cechy cieczy.
Podgrzewając   układ   dalej   doprowadzamy   do   stanu,   kiedy   energia   translacji   przekroczy   wartości   potrzebne   do   zerwania
wszelkich oddziaływań międzycząsteczkowych oraz pokona  siły grawitacji - wówczas ciecz przejdzie  w  gaz.  W gazie   siły
oddziaływań   międzycząsteczkowych   oraz  siły   grawitacji  nie   mają   większego   znaczenia  i  można   na   chwilę   o   ich   istnieniu
zapomnieć.   Cząsteczki  gazu   wypełniają   więc  równomiernie   całą   objętość   naczynia   w  którym   się   znajdują   i   na   wszystkie
ścianki wywierają takie samo ciśnienia (w cieczy istnieje w różnej odległości od powierzchni różne co do wielkości ciśnienie
hydrostatyczne).

Z tego co powiedziano powyżej wynika, że stan skupienia zależy głównie od wzajemnych relacji  trzech czynników  - energii
kinetycznej   cząsteczek,   wielkości   siły   grawitacji   (co   związane   jest   z   masą   cząsteczki)   i   wielkości   sił   oddziaływania
międzycząsteczkowego (co  pośrednio  związane jest  ze składem i strukturą cząsteczki). Wyobraźmy sobie zatem substancję
w   stanie   krystalicznym,   w   którym   wiązania   sieci   krystalicznej   są   tak   silne,   że   cząsteczki   nawet   uzyskawszy   energię
wystarczającą   do   pokonania   sił   grawitacji   ciągle   jeszcze   nie   mają   wystarczającej   energii   potrzebnej   do   pokonania   sił
utrzymujących   je   w   sieci   krystalicznej.   W   momencie   osiągnięcia   energii   pozwalającej   wyrwać   się   z   układu   kryształu,
cząsteczki te przechodzą bezpośrednio w stan gazowy, bowiem energię  zdolną pokonać grawitację osiągnęły już dawno. Tak
duża energia translacji powoduje, że cząsteczki te poruszają się na tyle szybko, że oddziaływania międzycząsteczkowe tracą na
znaczeniu. Takie przejścia bezpośrednio z ciała stałego w gaz nazywamy sublimacją.

A teraz przyjrzyjmy się innemu zjawisku. Jeżeli mamy substancję w stanie gazowym, to chcąc przeprowadzić ją w stan ciekły
musimy obniżyć jej energię do stanu, w którym zaczną nabierać znaczenia siły grawitacji. To z kolei spowoduje zbliżenie się 
cząsteczek do siebie na odległości, w których oddziaływania międzycząsteczkowe zaczną być znaczące. Jednym słowem, aby
skroplić gaz (doprowadzić do kondensacji par cieczy) trzeba zbliżyć cząsteczki gazu  do siebie  na odpowiednią odległość i
zadbać o odpowiednio niską energię translacji tych cząsteczek. Najłatwiej dokonać tego obniżając temperaturę (zmniejszenie
energii)  i  zwiększając  ciśnienie  (zbliżenie  cząsteczek).     A  tak  na  marginesie  -  w  "starym"   spojrzeniu   na  świat  nie  zawsze
zauważamy tożsamość zjawiska kondensacji pary i skraplania gazu, często traktujemy je jako różne zjawiska, nie kojarząc, że
np. zwykła destylacja to także proces skraplania gazu!
A  teraz   wyobraźmy   sobie   sytuację,   że   zbliżenia   cząsteczek   gazu   dokonujemy   zwiększając  ciśnienie  i  podgrzewając   gaz,
zamiast go oziębiać. Możemy tym sposobem doprowadzić do sytuacji, w której cząsteczki substancji będą tak blisko siebie
(ciśnienie), że siły oddziaływań międzycząsteczkowych osiągną wartości charakterystyczne  dla cieczy, a   energia translacji
(wysoka temperatura), znacznie przewyższająca siły grawitacji i oddziaływań międzycząsteczkowych, spowoduje utrzymanie
podstawowych  cech gazu. Taki stan  będzie miał  jednocześnie cechy gazu i cieczy i nazywany jest stanem  nadkrytycznym
(fluidalny, płyn w stanie nadkrytycznym).

Ciekły kryształ - stan skupienia makroskopowo wyglądający jak ciecz, a strukturalnie jak ciało stałe, krystaliczne. Zachowuje
się   w   wielu   zjawiskach   fizycznych     jak   kryształ   (wykazuje   np.   zjawisko   anizotropii   charakterystyczne   dla   układów
krystalicznych)   ale   wykazuje   podstawowe   cechy   cieczy   (np.   przyjmuje   kształt   naczynia).   Już   sama   nazwa   wskazuje   na
bezradność uczonych w zakwalifikowaniu go do którejś z "klasycznych" grup substancji.   A sprawa jest stosunkowo prosta.

Niektóre   substancje   o   specyficznej  budowie   cząsteczki   i   polarności,  powodujących   powstawanie   dużych   sił   oddziaływań
międzycząsteczkowych, wykazują dość duży stopień uporządkowania molekuł. Jest on prawie tak regularny jak w kryształach,
skąd biorą się cechy krystaliczne takich substancji. Jednocześnie substancje te wykazują cechy zewnętrzne cieczy, bowiem
siły wiązań międzycząsteczkowych nie są aż tak silne, by unieruchomić wszystkie cząsteczki w sztywnej sieci. Jest to raczej
skupisko mikrokryształów, mogących przesuwać się względem siebie, ale także w dość uporządkowany sposób. Stąd płynięcie
takich substancji.

Czy w świetle powyższego warto upierać się przy trzech (czterech? pięciu?) stanach skupienia? Czy warto uznawać przejścia
fazowe gaz-ciecz-ciało stałe za "normalne", "naturalne" a sublimację za wyjątkowe zjawisko? Czy uczyć się na pamięć, że
gazu nie da się skroplić powyżej temperatury krytycznej, nie rozumiejąc jednocześnie dlaczego tak się dzieje? A może lepiej (i
mądrzej) pomyśleć, przemyśleć i zapamiętać, skąd takie czy inne właściwości się biorą?

do strony

tytułowej

do góry

strony 

Forma substancji a reaktywność

Następne przyzwyczajenie, od którego dobrze jest się wyzwolić, to traktowanie symboli związków i samych związków jako
bytów tożsamych. Bardzo często zapominamy, że  H

2

O to  tylko  symboliczny zapis cząsteczki wody a nie woda jako taka.

Informacje   płynące   z   takiego   zapisu   nic   nam   nie   mówią   o   rzeczywistości   i   na   przykład   niezrozumiałym   jest,   dlaczego
cząsteczki o masie molowej 18 tworzą ciecz a nie gaz, tak jak inne substancje o podobnej masie i strukturze - NH

3

; CO

2

, CH

4

czy   H

2

S.   Bardzo   mało   w   czasie   nauczania   chemii   mówi   się   o   wpływie   formy,   postaci,   w   jakiej   występują   reagenty   na

reaktywność substancji. Wyjątkiem, zazwyczaj jedynym, jest węgiel, na przykładzie którego nieco szerzej omawia się wpływ
struktury   na   reaktywność  i  właściwości  chemiczne   (grafit   i  diament).   Omawia   się     jednak   wówczas  te   różnice   z  punktu
widzenia alotropii pierwiastków i mało kto uogólnia i przenosi te wiadomości na inne pierwiastki i związki chemiczne. Nie
można, z praktycznego punktu widzenia, każdej reakcji opisywać pełną, wyczerpująca informacją, bo zagmatwalibyśmy tak jej
zapis, że stałby się całkowicie nieczytelny - ale trzeba ciągle powtarzać, że na przykład woda w reakcji, to nie H

2

O a skupiska

cząsteczek wody, powiązanych w przestrzenne formy wiązaniami wodorowymi ({H

2

O}

p

), że częściowo są to jony (minimalna

dysocjacja - ale jednak występuje) itp. itd.

Zapominając o złożoności realnej sytuacji reakcji nie zrozumiemy także, dlaczego raz ona zachodzi a innym razem nie, chociaż
w zapisie symbolicznym wygląda to tak samo. Na przykład niełatwo pojąć, dlaczego ketozy są reduktorami, choć ani grupa
alkoholowa ani ketonowa takich właściwości nie wykazuje i dlaczego glukoza jest reduktorem, skoro występując w postaci
cyklicznej też  nie  ma grupy  aldehydowej. Wszelkie, nawet bardzo  daleko  idące uproszczenia w tłumaczeniu i zapisywaniu
chemii są konieczne i zazwyczaj  przydatne -  inaczej zapewne już na samym  początku  nauczania  ucieklibyśmy z krzykiem
przerażenia - nie wolno jednak ani na chwilę zapominać, że są to uproszczenia, że rzeczywistość jest bardziej złożona. Na
nauczycielach   wszelkich   szczebli   nauczania   spoczywa   obowiązek   wyjaśniania,   w   odpowiednim   momencie,   co   jest
uproszczeniem, o czym w danej chwili nie mówimy i co sprawia, że omawiany "wyjątek" jest wyjątkiem (czyli, jak już wiemy,
spełnieniem  innej  reguły,   ważniejszej  w   danych   warunkach).   Zapisywanie   glukozy  we   wszystkich   omawianych   reakcjach
wyłącznie wzorem C

6

H

12

O

6 

trudno nazwać nauczaniem chemii - raczej jest to publiczna egzekucja tej pięknej nauki.

A  dla   uczących   się   uwaga   -   żeby   zbyt   szybko   nie   rozgrzeszali   swojego   intelektualnego   lenistwa   argumentem  kiepskiego
nauczyciela - pamiętajcie, że liczy się tylko WASZA rzetelna wiedza na dany temat. Jeśli trafił wam się kiepski nauczyciel, to
wasz problem i kłopot, ale w niczym to was nie rozgrzesza. Dobry chemik zna dobrze chemię i w momencie kiedy musimy się
tą wiedzą wykazać, poziom naszych nauczycieli nie ma nic do rzeczy. Nauczyciel często nie wspomina o zawiłościach chemii,
bo   go   nikt   o   to   nie   pyta.  Zanim  wydamy   opinię  o   naszym  mistrzu,  sprawdźmy   najpierw  jaki  on   rzeczywiście   jest.  Czyli
najpierw  sami  zacznijmy  zastanawiać się  nad  problemami  poruszanymi  na  wykładzie czy przeczytanymi  w  podręczniku,  a
później  wdajmy się  w dyskusję z  nauczycielem.  Raz jeszcze powtórzmy sobie niepodważalną prawdę -  chemii  nie  da  się
nauczyć   na   pamięć,   bez   zrozumienia   jej   zasad,   reguł     i   wzajemnych   relacji   między   nimi.   Dopiero   widzenie   zjawiska
w kontekście całej chemii i fizyki pozwala zrozumieć jego przebieg i jego istotę.

Podsumowując   niniejszy   podpunkt,   pamiętajmy,   że   każda   przemiana   -   tak   reakcja   chemiczna   jak   i   zjawisko   fizyczne
("fizykochemiczne")   -   odbywa   się   z   pewnym   efektem   energetycznym.   Jedne   wiązania   czy   oddziaływania   muszą   zostać
pokonane,  rozerwane  (potrzeba  energii) by  mogły  powstać  nowe (odzysk  energii).  Zatem,  czy  i  jak    przebiegnie  zjawisko
(reakcja), decydować będą etapy uwalniające lub  pobierające energię. Żeby jakiś etap wymagający energii mógł zaistnieć,
układ musi mieć dostęp do "zapasu" energii. Ten zapas mógł być stworzony w poprzednim etapie, wyzwalającym energię, lub
takiego zapasu nie ma i proces się zatrzymuje. Tak więc o reakcji nie decyduje reguła, np.  tlenki niemetali z wodą dają kwas,
lecz siła wiązań i oddziaływań. Dla CO

2

 ta reguła jest prawdziwa,  dla SiO

2

 -  już nie (siły wiązań tworzących krystaliczną

strukturę krzemionki - kwarcu na to nie pozwolą w "zwykłych" warunkach). 

do strony

tytułowej

do góry

strony 

Stany pośrednie i brzegowe

Wszyscy   jesteśmy   przyzwyczajeni,   że   roztwór   opisujemy,   charakteryzujemy,   przede   wszystkim   jego   stężeniem.   Niekiedy
jednak zamiast stężenia pojawia się aktywność, czasem dla roztworów elektrolitów obliczamy siłę jonową roztworu. Wiemy,
że   aktywność   jest   zawsze   mniejsza   od   stężenia,   zrównuje   się   z  nim   w   przypadku   roztworów   o   hipotetycznym  stężeniu
"nieskończenie   małym".   Z   kolei   przy   stężeniach   dużych   (co   to   konkretnie   znaczy?)   "obowiązkowo"   posługujemy   się
aktywnością zamiast stężenia, bo tu różnice między tymi wartościami są bardzo duże (czyli jakie?). 

Obliczając pH roztworów silnego kwasu np. HCl

aq

, kwasu solnego, obliczamy po prostu logarytm dziesiętny ze stężenia HCl.

Jeśli jednak stężenie  kwasu jest mniejsze niż powiedzmy  10

-5

 mol/dm

3

,  w  obliczeniach musimy  uwzględnić prócz stężenia

kwasu także inne czynniki (np. dysocjację wody), bo inaczej dla stężenia kwasu np. 10

-12

 mol/dm

3

 znajdziemy pH = 12 !!

I tak jest dla wielu zjawisk, procesów i reakcji. W pewnych zakresach parametrów zjawiska układ zachowuje się inaczej niż
w pozostałych. Najczęściej wyróżnić możemy praktycznie trzy takie zakresy - zakres pośrednich wartości, najszerszy (i o nim
głównie uczymy  się w chemii, także fizycznej), oraz dwa zakresy brzegowe - parametrów bardzo dużych i bardzo małych.
W każdym z tych zakresów układ zachowuje się odmiennie, opisują go inne równania. Dzieje się tak z powodów, które już
były poruszane - złożoności każdego zjawiska. W każdym z tych trzech zakresów znaczenia nabierają  inne elementy procesu.
Jak roztwór jest bardzo rozcieńczony, oddziaływania między jonami są na tyle słabe, że nie mają praktycznie żadnego wpływu
na zachowanie się roztworu i w praktyce spełniona jest równość c = a (aktywność jonów a można zastąpić stężeniem jonów
c). W roztworach stężonych, średnia odległość między jonami się zmniejsza, średnia siła oddziaływań jest na tyle duża, że o
zachowaniu roztworu decydować będzie aktywność ("użyteczne" stężenie a nie nominalne). Podobnie gazy rzeczywiste, przy
stosunkowo niskich ciśnieniach (kilku atmosfer) zachowywać się będą w praktyce jak gazy idealne (czyli takie hipotetyczne,

których cząsteczki nie mają objętości i nie oddziałują ze sobą),  jednak przy ciśnieniach wysokich objętość ich cząsteczek jak i
siły  oddziaływań  międzymolekularnych  będą musiały  być  wzięte  pod  uwagę  dla  dokładnego  opisania  zjawiska.    Ponieważ
jednak dążymy zawsze do maksymalnej prostoty w opisie zjawisk (co jest wygodne ale nie zawsze bezpieczne) konstruujemy
wzory,  które  nie  uwzględniają  tych  elementów procesu,  które  z  PRAKTYCZNEGO  punktu widzenia  nie mają znaczenia.
Stąd dla różnych  zakresów różne (pozornie) równania,  które  zazwyczaj dają się sprowadzić do  jednego,  opisującego pełny
zakres zjawiska, ale za cenę znacznego skomplikowania zapisu. 

Konkluzja   taka   jak   w   pozostałych   podpunktach   -   korzystajmy   z   uproszczeń,   skupiajmy   uwagę   na   tym,   co   w   danych
warunkach najistotniejsze, ale ani na chwilę nie zapominajmy, że rzeczywistość jest o wiele bardziej złożona i uproszczeń nie
stosuje. To, że w tej chwili nie mówimy o procesie x, to nie znaczy, że go nie ma. Jest, i jak o nim zapomnimy, to on sam się w
odpowiednim momencie przypomni i może nas niemile zaskoczyć.

do strony

tytułowej

do góry

strony 

Definicje, opisy, prawa, reguły ... 

W świetle tego, o czym mówiliśmy wcześniej, dość oczywistym staje się, że w stosunku do sformułowań definicji, praw, reguł
itp. dotyczących opisu zjawisk i procesów obserwowanych w skali makro powinniśmy wykazywać "ograniczone zaufanie". 
Jeżeli odnoszą się one do skali mikroświata - cząstek elementarnych,  atomów, cząsteczek (choć tu już wzmożona ostrożność),
to owo zaufanie może być duże. Pamiętając o złożoności zjawisk obserwowanych  w skali makro, oczywistym się staje, że
opisujące   je   reguły,   definicje,   ba,   nawet   prawa,   powinny   być   obwarowane   całym   zestawem   warunków   (bo   w   różnych
warunkach suma zjawisk mikro jest różna). Jednak, gdybyśmy w sformułowaniu definicji czy reguły chcieli umieścić wszystkie
konieczne dla jej jednoznaczności warunki - stałaby się nieczytelna i nie do zapamiętania, czyli straciłaby sens. Pamiętajmy
więc,   że   wszystkie   sformułowania   dotyczące   skali   makro,   nawet   jeśli   brzmią   bardzo   kategorycznie,   najpewniej   są   tylko
przybliżeniami  opisującymi  zjawisko  w  warunkach   najbardziej  prawdopodobnych,   najczęściej  spotykanych.   W  warunkach
odbiegających   od   "normalności"   to   samo   formalnie   zjawisko   przebiegać   będzie   zapewne   nieco   inaczej.   Jednocześnie
przestrzegałbym przed dość popularnym podejściem do tego problemu, które zazwyczaj owocuje stwierdzeniem, że w danych
warunkach "substancja  nie stosuje się do  prawa  ...". Takie sformułowania wyrabiają  w nas podświadome przekonanie, że
prawa przyrody nie są absolutne i jedne substancje im podlegają a inne nie, a to nieprawda. Właśnie podleganie wszystkim
prawom przyrody powoduje, że substancja zachowuje się niezgodnie z naszym sformułowaniem prawa, ale nie niezgodnie z
prawem.  Zjawisko  przebiega   zgodnie  z  prawem,   a  dokładniej  zgodnie   ze   wszystkimi  prawami,   które   w  tej  sytuacji  mają
zastosowanie. 

Dość   częstym   sposobem,   stosowanym   w  podręcznikach,   jest   zawarcie   zastrzeżeń   dotyczących   omawianego   zjawiska   we
wstępie  do  rozdziału.   Często  np.  wstęp  do  rozdziału   o  gazach  brzmi  jakoś tak:    Załóżmy,  że  mamy  do  czynienia  z  gazem
idealnym, tzn. takim, który ...   i dalej biegnie długi rozdział o gazach. Już po paru stronach zapominamy, że opisy dotyczą
hipotetycznego   gazu  doskonałego   i   w  pamięci  zakodowują   się   nam  informacje,   jako   dotyczące   gazu   jako   takiego,   czyli
rzeczywistego.  A potem w opisie niektórych  sytuacji dotyczących gazu rzeczywistego (np.  skraplanie czy przejście w stan
nadkrytyczny) pojawiają się sformułowania sprzeczne z poprzednimi i problem gotowy. Tak więc bądźmy czujni i krytyczni
wobec wiedzy podręcznikowej - nie dlatego, że nie ufamy wiedzy jej autorów, ale dlatego, że ci autorzy, nie zawsze potrafią
przekazać   swą   wiedzę   w   sposób   dla   nas   jasny   i   przejrzysty.   Dlatego   tak   dobrym   sposobem   na   rzetelną   wiedzę   jest

studiowanie

,   czyli   korzystanie   z   różnych   źródeł,   różnych   autorów   i   samodzielne   (a   więc   świadome)   zestawianie   tych

informacji w zasób wiedzy na dany temat.

Pamiętajmy też, że sporo różnych określeń, które  w konkretnych przypadkach mają ściśle określone znaczenie, używanych
jest  również w znaczeniu potocznym. W tym drugim przypadku ich znaczenie nie jest ściśle zdefiniowane i ma za zadanie
raczej   wskazać   na   pewne   elementy   zjawiska   niż   precyzyjnie   je   określić,   np.   poziom   energetyczny   czy   oddziaływanie
międzycząsteczkowe.

W opisie zjawisk chemicznych bardzo  często korzystamy z określenia "wiązanie chemiczne".  Mówimy  o energii wiązania,
o jego  długości, oscylacji wiązań, zerwaniu bądź utworzeniu wiązania. Takie częste korzystanie z tego pojęcia wyrabia w nas
podświadome   odbieranie   wiązania   jako   fizycznego   elementu   wiążącego   dwa   atomy,   a   pisanie   wiązań   we   wzorach
strukturalnych   jako   kreski  jeszcze   bardziej  to   podświadome   rozumienie   utwierdza.   Dla   klarowności  wywodu   stosowanie
takiego pojęcia jest bardzo wygodne i nikogo nie namawiam by z niego zrezygnował - pamiętajmy jednak, że za tym pojęciem
nie   kryje   się   żadna   sprężynka   czy   patyczek,   lecz  jest   to   układ  dwóch   atomów   i  dwóch   lub   więcej  elektronów,   których
wzajemne oddziaływania elektrostatyczne i magnetyczne powodują, że tworzą one w pewnej konfiguracji układ dość trwały.
Pamiętajmy również, że jest  to układ dynamiczny - położenie względem siebie poszczególnych elementów tego układu jest
zmienne,   a  jak   "dołożymy"   do   tego   nieokreśloność  pojęcia   elektron   (kulka,   chmura,   fala   ?)   oraz  nieprecyzyjność   pojęcia
"orbital",   to   stanie   się   jasne,   że   pojęcie   wiązania   chemicznego   w  wielu   przypadkach   używane   jest   w  tym  "potocznym",
ogólnym znaczeniu.

Obłaskawiona termodynamika 

Termodynamika - już sam dźwięk tego słowa budzi grozę i przerażenie wśród studentów młodszych lat. Co jest powodem, że
ten dział chemii fizycznej jest uważany za tak trudny? 

Po   pierwsze,  dotyczy   spraw  dość  trudnych  do   wyobrażenia,  bo   traktuje   o  przepływie   energii pomiędzy   różnymi  formami
organizacji materii. Tak więc, bardziej intuicyjnie wyczuwana niż rozumiana energia, pojawia się tu w różnych postaciach -
energii   kinetycznej,   potencjalnej,   chemicznej,   wewnętrznej   układu,   zewnętrznej   otoczenia,   wewnętrznej   cząsteczek,
przekazywana jest w sposób kwantowany lub ciągły, na sposób ciepła lub pracy itp. itd. Nie dość, że nie bardzo wiemy co to
jest ta energia, to jeszcze występuje w tak skomplikowanych kontekstach.

Po drugie, ponieważ opisuje sprawy trudne do wyobrażenia, aby być dokładną i precyzyjną w tych opisach musi posługiwać
się matematyką, czasem dość skomplikowaną - a tego wielu nie lubi. Często tylko poprzez przekształcenia matematycznych
opisów można wykazać i określić powiązania skutkowo-przyczynowe między zjawiskami mikroświata.

Po   trzecie,   pojawia   się   cała   nowa   nomenklatura,   zestaw   pojęć   zazwyczaj   precyzyjnie   definiowanych,   czyli  konieczność
nauczenia   się   dość   specyficznego   i   niełatwego   języka.   Często   podobnie   brzmiące   terminy   oznaczają   dość   różne   pojęcia,
czasem odwrotnie - prawie identyczne pojęcia są opisywane zdecydowanie różnymi terminami. 

Po  czwarte  (tu na szczęście  bywają wyjątki - oby  jak najliczniejsze) wykładowcy i autorzy  podręczników ten  dość trudny
materiał przekazują w literalnej zgodzie z rzeczywistością nie dbając specjalnie o komfort zrozumienia i percepcji słuchaczy i

{4Na + O

2

 + E

s

}  +   

(E

1

 - E

2

)

   =     {2Na

2

O  + E

p

}  

czytelników.  Czyli  innymi słowy,  mówią cała prawdę ale mało  zrozumiale (tu,  jak  w całej chemii  fizycznej  - materiału  do
wyjaśnienia dużo a czasu mało).

Poniżej postaram się w sposób bardzo uproszczony, nie wchodząc w szczegóły, przygotować grunt pod przyszłe zrozumienie
wszystkich zawiłości termodynamiki. Nauczyć się jednak niestety będziecie musieli sami.

do strony

tytułowej

do góry

strony 

Energia wewnetrzna a entalpia 

Cząsteczka  to  materia  (atomy)  i  energia  zawarta  w  wiązaniach  chemicznych  łączących  te  atomy   oraz  w  oddziaływaniach
międzycząsteczkowych. Każda przemiana chemiczna (reakcja) oraz fizyczna ("fizykochemiczna") związana jest z przepływem
energii - energia bowiem nie powstaje i nie znika, zatem musi w odpowiedniej ilości być dostępna w układzie. Jeżeli kawałek
metalicznego  sodu spalimy w tlenie, to dla każdego, początkującego nawet chemika będzie oczywiste, że musimy  mieć  co
najmniej cztery atomy sodu i cząsteczkę tlenu by przeprowadzić taką reakcję:

 4Na + O

2

 = 2Na

2

O

Włączmy do rozważań o przebiegu tej reakcji zmiany energetyczne. Rozbijmy myślowo ten proces na dwa etapy:  rozerwania
wiązań w cząsteczce tlenu oraz rozerwania wiązań między atomami sodu w strukturze metalicznej (kryształ metaliczny),   a
następnie połączenia atomów tlenu i sodu w dwie cząsteczki Na

2

O. 

Tak więc oprócz  materii (sód i tlen) i  energii w niej zawartej (E

s

) potrzebna będzie dodatkowa energia E

1

 (do 

rozerwania

wiązań

 substratów). 

W analogiczny sposób możemy wyobrazić sobie przebieg reakcji odwrotnej, prowadzącej od tlenku sodu do pierwiastkowego
sodu i tlenu:

2Na

2

O  =  4Na + O

2

   

 Tu również najpierw musimy dostarczyć energii potrzebnej do rozerwania wiązań i przejścia w stan atomowy (E

2

). Energię

zawartą w cząsteczkach Na

2

O oznaczmy E

p

. 

Obydwa   te   procesy  prowadzą   do   identycznego   stanu   termodynamicznego,   zawierającego   4   atomy   Na,   dwa   atomy   tlenu
i pewną ilość energii E:

4Na;  O

2   {E

s

} 

    

+     E

1     

——>        

Na, Na, Na, Na, O, O, {E}

<——        E

2   

 +

    2Na

2

O  

 {E

p

}

Energia {E} układu "atomowego"  będzie więc równa:

 E = E

s

 + E

1

    (E

s

 - energia wewnętrzna substratów), 

gdy reakcja biegnie od substratów 4Na i O

2

   dotlenku, lub, rozumując analogicznie dla przejścia od tlenku sodu do "układu

atomowego":

E = E

p

 + E

2    

(E

p

 - energia wewnętrzna produktów). 

Stąd równość:  E

s

 + E

1

 = 

 

E

p

 + E

2

 dająca po prostym przekształceniu:    E

1 

- E

2

 = E

p

 - E

s

 

Rozpatrując zatem reakcję, tak jak ją zapisaliśmy:       4Na + O

2

 = 2Na

2

O ,   ale z uwzględnieniem również energii, możemy

napisać bilans:

{4Na + O

2

 + E

s

} + 

E

1

  =   {2Na

2

O  + E

p

} + 

E

2

Z ilości energii E

1

 pobranej w pierwszym etapie przez cząsteczki substratów została "zwrócona"  ilość E

2

 w czasie tworzenia

się cząsteczek produktów. W czasie reakcji została więc pobrana ilość energii ΔE =  

E

1

- E

2

 

 =   E

p

 - E

s

. 

Możemy to wszystko ująć w następujący schemat:

4 Na;  O

2

{E

s

}

+ E

1

  

——>

Na, Na, Na, Na, O, O, {E}

2Na

2

O{E

p

}

4 Na;  O

2

 {E

s

}

+ E

1

   

——>

Na, Na, Na, Na, O, O, {E}

Na, Na, Na, Na, O, O, {E}

- E

2

   

——>

2Na

2

O {E

p

}

4 Na;  O

2

 

{E

s

}

+ E

1

   

——>

Na, Na, Na, Na, O, O, {E}

- E

2

   

——>

2Na

2

O  {E

p

}

<——

   

E

2

 +

który da się "rozłożyć" na dwa równania:

łącząc te dwa równania otrzymujemy:

Tak   więc   aby   otrzymać   z   sodu   i   tlenu   tlenek   sodu   musimy   najpierw   dostarczyć   substratom,   zawierającym   energię   E

s

,

dodatkową ilość  energii  E

1

,  potrzebną  do  atomizacji substratów.  Następnie część energii układu  zostaje "zmagazynowana"

w postaci energii wewnętrznej produktu (E

p

) i pozostaje nadmiar energii (E

2

). 

Całkowity wydatek energetyczny reakcji będzie zatem: 
E

1

  -   energia   włożona   w   rozbicie   substratów   na   atomy,   minus     E

2

  -   energia   zwrócona   w   czasie   łączenia   się   atomów

w cząsteczki produktu. Tak więc wymieniona z otoczeniem w trakcie reakcji ilość energii  wyniesie:

ΔE=  

E

1

- E

 

2

 

 =  E

p

 - E

s

. 

Teraz zapis równania (pełniej odzwierciedlający rzeczywistość) będzie wyglądał następująco:

4Na + O

2

 = 2Na

2

O + ΔE

 Dlaczego wartość ΔE została zapisana z prawej strony równania? To następny "kłopot" - wiele symboli, punktów odniesienia
itp.,   które   z  logicznego   punktu   widzenia   mogłyby   być  zapisywane  różnie,   w  celu   uniknięcia   niejednoznaczności,   zostało 
przyjęte   jako   obowiązujące   na   zasadzie   ogólnoświatowej  umowy   (podobnie  jak   np.   układ   SI).  Na   takiej  właśnie  zasadzie
wydatek energetyczny reakcji jest zapisywany  po  prawej  stronie  równania  (jako  "produkt",  wynik  reakcji). Oblicza  się  go
zatem jako  E

p

 -  E

s

 (energia  wewnętrzna produktów - energia wewnętrzna substratów). Jeżeli znak wartości tej ΔE będzie

ujemny, tzn. ilość energii wewnętrznej zawarta  w produktach E

p

 jest mniejsza niż ilość energii wewnętrznej substratów E

s

,

reakcja   jest   egzoenergetyczna   (egzotermiczna),   oddaje   energię   do   otoczenia,   jeśli   znak   jest   dodatni   -   reakcja   jest
endoenergetyczna, pobiera energię z otoczenia.

Teraz już chyba pora na przybliżenie terminów - energia wewnętrzna i entalpia.
Jeżeli wyobrazimy sobie zamknięty, izolowany układ, który nie może wymienić z otoczeniem ani materii ani energii, to suma
wszystkich  postaci energii  zawarta   w  składnikach  tego   układu  będzie  jego  energią  wewnętrzną.  W realnym  świecie  takim
praktycznym  odpowiednikiem  układu  izolowanego  może być  bomba  kalorymetryczna lub zwykły,  szczelny  termos. Trzeba
pamiętać, że pojęcie układ może oznaczać każdy element rzeczywistego świata, wyizolowany myślowo z reszty otoczenia.
Może  to  być  zawartość  naczynia  reakcyjnego,  ale  może  również być  to   pojedyncza  cząsteczka   w  tym  naczyniu.   Granice
układu zakreślamy w zależności od potrzeb przeprowadzanych rozważań termodynamicznych czy obliczeń. Granicami układu
mogą być np. ścianki zamkniętego naczynia, ale też mogą to być granice całkowicie umowne, fizycznie nie istniejące. Tak
więc już samo pojęcie układu jest dość rozmyte. Układy dzielimy zazwyczaj na izolowane (jak wyżej), zamknięte, tzn. takie,
które nie mogą wymieniać z otoczeniem materii (zamknięte naczynie), lub najczęściej spotykane układy otwarte, w których
może ulegać wymianie zarówno materia jak i energia (np. zlewka z roztworem). 

Każdy układ materialny "zawiera"  w sobie  parę  "typów",  rodzajów energii.  Mamy tu  zazwyczaj na myśli  energię jądrową
(manifestuje swą obecność podczas przemian jądrowych, na co dzień o  niej pamiętać  nie  musimy), energię elektronów, ze
szczególnym   uwzględnieniem  elektronów  walencyjnych,   wśród   których   rozróżniamy  energię   oscylacji  (zmieniająca   się   w
czasie   oscylacji   wiązań)   i   energię   elektronową   (energię   wiązań),   energię   rotacji   cząsteczek   i   energię   translacji   (ruchu
postępowego cząsteczek). Do tego dochodzą energie oddziaływań międzycząsteczkowych - solwatacji, wiązań wodorowych,
oddziaływań międzyjonowych oraz innych oddziaływań typu dipol-dipol itp. W czasie różnego rodzaju przemian chemicznych
bądź fizycznych  (przemiany  fazowe)   zmieniają  się  wartości  poszczególnych   typów  energii,   ale  jeżeli  układ  jest   izolowany
suma   wszystkich   energii   pozostaje   stała.   Jeśli  np.   suma   energii   zmieniających   się   w  czasie   reakcji   (np.   energia   wiązań,
solwatacji,   wiązań  wodorowych),   po   reakcji  jest  mniejsza   niż  przed   reakcją,   to   "nadmiar"   energii  zamieni  się   na  energię
translacji (wzrośnie temperatura układu).

Zmiany energii wewnętrznej, będące wynikiem procesu (reakcji) mogą zostać przekazane otoczeniu albo na sposób ciepła albo
na sposób pracy, albo na oba te sposoby jednocześnie. Najczęściej spotykanym sposobem prowadzenia reakcji chemicznych
i procesów fizykochemicznych jest proces pod stałym ciśnieniem (atmosferycznym). W takich procesach dochodzi najczęściej
do zmiany objętości układu (np. ze względu na zmianę temperatury), czyli zmiana energii wewnętrznej następująca w czasie
reakcji powoduje zmianę energii translacji (temperatura, przekazanie energii na sposób ciepła, energia pozostająca w układzie)
oraz równolegle zmianę energii na sposób pracy (p·ΔV - wykonanie pracy objętościowej, przekazanie energii do otoczenia na
sposób pracy). Funkcja termodynamiczna, która uwzględnia te dwa sposoby przekazania energii nazywa się entalpią. Czyli
innymi słowy entalpia (oznaczana jako H) ma taki sam sens jak energia wewnętrzna (oznaczana jako U); w przypadkach stałej
objętości układu (p·ΔV=0) jej zmiana jest równa zmianie energii wewnętrznej (ΔH =   ΔU), zaś w warunkach izobarycznych
(p=const) ΔH = ΔU + p·ΔV co oznacza także, że   ΔU = ΔH - p·ΔV. Zatem entalpia (różnica entalpii) oznacza całą energię
wymienioną w danym procesie, a energia wewnętrzna określa tylko energię, która pozostała w układzie.

I żeby się w tym wszystkim nie pogubić, pamiętajmy, że funkcje termodynamiczne pozwalają nam obliczać 

różnice

 między

dwoma stanami układu (np. przed i po reakcji) i mimo, że często mówimy np. entalpia procesu czy entalpia reakcji to na
myśli  mamy  różnice  entalpii stanu  początkowego   i  końcowego  a  nie  bezwzględne  wartości.  Bezwzględne  wartości energii
wewnętrznej czy entalpii nie są możliwe do obliczenia (podobnie jak potencjał czy wysokość mają sens praktyczny tylko w
przypadku określenia jakiegoś konkretnego punktu odniesienia). Tu warto przypomnieć, że umownie przyjmujemy, że entalpie
tworzenia pierwiastków w ich stanach stabilnych w warunkach standardowych (25°C, 1 atm)  wynoszą zero (umowny punkt
odniesienia), co pozwala nam obliczać standardowe entalpie tworzenia związków (ponieważ wartość punktu odniesienia jest
umowna, także te wartości należy traktować jako umowne!). Więcej na ten temat w 

rozdziale o budowie materii

.

do strony

tytułowej

do góry

strony 

Entropia - chaos czy porządek 

Drugie, równie ważne i równie trudne (albo i trudniejsze) do wyjaśnienia pojęcie to entropia. W najprostszym ujęciu entropia
jest funkcją opisującą stan uporządkowania materii. Tu trzeba zwrócić uwagę na dwa podejścia do słowa "uporządkowanie".
Jedni  autorzy   rozumieją   słowo  porządek,   tak   jak   to   ma   miejsce   w     mowie   potocznej  (wszystkie   elementy   o   podobnym
charakterze   w   jednym   miejscu,   blisko   siebie,   ułożone   zgodnie   z   jakąś   regułą),   inni   zaś   podchodzą   do   tematu   bardziej
filozoficznie,   uważając   za   porządek   stan,   do   którego   dąży   samoistnie   natura,   czyli   w   codziennym   pojęciu   "kosmiczny
bałagan", czyli wszystko wszędzie. My będziemy rozumieć porządek w sposób potoczny. Takie podejście powoduje mniejsze
zamieszanie pojęciowe w tym i tak niełatwym temacie.

Jeżeli doprowadzimy do układu energię, to wzrośnie energia wewnętrzna układu i przede wszystkim spowoduje to zwiększenie
ruchliwości cząsteczek (energii translacji).  Taki wzrost ruchliwości to jednocześnie wzrost  nieuporządkowania,  czyli wzrost
entropii.  Trzeba  jednak  zauważyć,  że  taki sam co  do   wielkości bezwzglednej wzrost  nieuporządkowania  (choć  nie  bardzo
wiadomo co to by miało znaczyć) jest względnie duży, jeśli dotyczy "idealnego" porządku, zaś może być uznany za niewielki,
jeśli dotyczy układu o bardzo niskim stopniu uporządkowania. Zamiana miejscami na półce dwóch książek, jeśli te książki są
tam  ustawione  od   największej do  najmniejszej,  daje  poczucie  zabałaganienia  i jest  szybko   zauważalna.  Taka  sama  zmiana
wśród książek, które stoją bez planu, stanowi niewielki wzrost nieuporządkowania (a czasami może wręcz stanowić krok w
kierunku większego porządku). 

Spójrzmy na diagram poniżej. Mamy tam pola białe i czerwone, w górnych wierszach "uporządkowane", w dolnych nastąpiła
zamiana elementu 3 z 24 i 6 z 25. Mamy wiec identyczny wkład energii potrzebnej do zamienienia pól miejscami i różny efekt
końcowy w sytuacjach A, B i C (różną zmianę stopnia uporządkowania, w ostatnim wiersz nie widać żadnej zmiany, choć
zamiana nastąpiła)

1

2

3

4

5

6

7

8

9

10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30

A

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

B

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

C

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Ponieważ w przyrodzie stopień nieuporządkowania wiąże się zazwyczaj z wyższą temperaturą a porządek z niższą, entropią
nazywamy   stosunek   ilości   przeniesionej   energii   na   sposób   ciepła   ("bezwzględna   wartość   stopnia   zabałaganienia")   do
temperatury, w której to przeniesienie zostało dokonane ("standardowy poziom bałaganu"), czyli określamy względny wzrost
nieuporządkowania względem stanu "naturalnego", związanego z daną temperaturą.

Wzrost entropii, którą oznaczamy literą S wyznacza wzór  ΔS = ΔQ/T

Jest to wzór, który  definiuje entropię,  jednak  dotyczy  stanów w przyrodzie niespotykanych,   czyli 

przemiany  odwracalnej

,

zachodzącej w stałej temperaturze (a to oznacza, że układ i otoczenie jest w identycznej temperaturze i wówczas przepływa
energia,  co  jest sprzeczne  z II  zasadą   termodynamiki).  Jeżeli  zastosujemy   pojęcie  entropii  do  stanów  rzeczywistych,  czyli
układu  o  temperaturze  T

1

  i otoczenia  o  temperaturze  niższej T

2

,  to   przepływ  energii na  sposób  ciepła  między  układem  a

otoczeniem  (od   układu   do   otoczenia)   o   wielkości  Q  spowoduje   zmianę   zarówno   entropii  układu   jak   i  otoczenia.   Zmiana
entropii układu będzie równa ΔS

u

 = -Q/T

1

 ,   zaś zmiana entropii otoczenia będzie wynosić ΔS

o

 = +Q/T

2

. Całkowita zmiana

entropii układu i otoczenia będzie sumą tych zmian i wyniesie:

Jak   z   powyższych   wzorów   wynika,   spadek   wartości   entropii  układu   jest   mniejszy   niż   wzrost   entropii   otoczenia.   Zatem
całkowita   zmiana  entropii  układu  i  otoczenia  jest  zawsze  dodatnia.  W   momencie,   gdy   temperatura  otoczenia  i układu
zrównają   się,   następuje   osiągnięcie   stanu   równowagi  (niemożliwy  jest   przepływ  energii)   a   ponieważ  entropia   sumaryczna
rosła, oznacza to, że w stanie równowagi osiągnęła maksimum.

Przepływ   energii   na   sposób   ciepła   powoduje   nie   tylko   prosty   wzrost   temperatury,   ale   przekłada   się   także   na   zrywanie
wszelkich   wiązań,   od   solwatacji   i   wiązań   wodorowych   poczynając   a   na   dysocjacji   i   rozrywaniu   wiązań   w   reakcjach
chemicznych kończąc.

 

Konieczność rozpatrywania  procesów  z punktu  widzenia  skali makro  i skali  mikro  każe  nam również na  pojęcie entropii

popatrzeć z tych dwóch punktów  widzenia. Rozpatrując  entropię  na poziomie cząsteczkowym wiążemy wzrost entropii ze
wzrostem stanu nieuporządkowania, ale zastrzegamy, że to  pojęcie ("nieuporządkowanie") niezdefiniowane. Aby być bliżej
stwierdzeń   naukowych,   ścisłych,   powiążmy   to   intuicyjne   pojęcie   nieuporządkowania   z   matematycznym   pojęciem
prawdopodobieństwa.   Związek   między   wartością   entropii   S   a   tzw.   prawdopodobieństwem   termodynamicznym  W   podał
Boltzmann w postaci równania:

S = k· ln W

gdzie k - stała Boltzmanna.

Prawdopodobieństwo termodynamiczne jest proporcjonalne do prawdopodobieństwa matematycznego (W~P lub W=q·P) i tę
zależność   wykorzystamy   do   wykazania   powiązania   między   stanem  nieuporządkowania   a   wartością   entropii.   Wyjaśnijmy
sprawę na modelu  dyfuzji cząsteczek w roztworze (rysunek poniżej). Załóżmy, że stan początkowy tego układu (1), to 1 mol
cząsteczek znajdujących się w połowie A objętości tego roztworu. Stan końcowy (2) to równomierne rozproszenie wszystkich
cząsteczek w całej objętości roztworu. Ponieważ nie ma żadnych powodów, by dowolna cząsteczka znajdowała się akurat w
tej (A) a nie innej (B) części roztworu, prawdopodobieństwo "matematyczne" wystąpienia dowolnej cząsteczki w połowie A

wynosi 1/2, a jednego mola cząsteczek w jednej połowie roztworu związane jest z prawdopodobieństwem (1/2)

N

, gdzie N -

ilość cząsteczek w 1 molu. Przypominam, że prawdopodobieństwo wystąpienia n zdarzeń pozytywnych jednocześnie (każda z
cząsteczek zawartych w tym molu występuje w tej samej części roztworu) jest iloczynem prawdopodobieństw poszczególnych

zdarzeń, czyli w tym przypadku (1/2)

n

, gdzie n - ilość cząsteczek w molu, czyli N.

stan początkowy

stan końcowy

P = (1/2)

N

P = 1

N

Stan   końcowy   procesu   dyfuzji   to   równomierne   rozproszenie   cząsteczek   w   całej   objętości.   Tu   prawdopodobieństwo
wystąpienia dowolnej cząsteczki w objętości roztworu wynosi 1 (cząsteczka jest tu na pewno), czyli dla N cząsteczek jest to

1

N

 =  1. Zatem stan końcowy jest stanem o wyższym prawdopodobieństwie niż stan  wyjściowy. W trakcie spontanicznych

procesów układ dąży do stanu bardziej prawdopodobnego. Z wcześniej podanego równania i   powyższych rozważań można
wyprowadzić wzór:

ΔS = k·ln q·P

2

 - k·ln q·P

1

 = k·ln (P

2

/P

1

) = k·ln (W

2

/W

1

)

A ponieważ              

W

2

>W

1

      to         

k·ln (W

2

/W

1

)>0

      czyli         

ΔS>0

. 

Uogólniając, prawdopodobieństwo stanu mniej uporządkowanego jest zawsze większe niż bardziej uporządkowanego. 
W trakcie procesów spontanicznych układ dąży do stanu bardziej prawdopodobnego (mniej uporządkowanego), co wiąże się
ze wzrostem entropii.

 

Robiąc pewne uproszczenie można uznać, że przyroda dąży do rozproszenia zarówno energii jak i materii, co przekłada się na

wzrost entropii i spadek energii układu. Tak zachowują się wszystkie układy naturalne w procesach samorzutnych. Pytanie,
jakie    pojawia  się  w  tym  kontekście:  dlaczego  istnieją  trwałe   struktury,   skoro wszystko   samoistnie   dąży do   rozproszenia?
Dzieje się tak dzięki temu, że zazwyczaj rozpraszaniu materii (wzrost entropii) towarzyszyć musi wkład energii, zaś obniżaniu
energii  towarzyszy   zazwyczaj  większe   uporządkowanie   czyli   spadek   entropii.   Zatem  te   dwa   czynniki  działają   najczęściej
antagonistycznie,   wyznaczając   pewne   zakresy   i   pułapy   współdziałania,   powodując   może   nieco   chwiejną   równowagę
w przyrodzie, ale jednak równowagę. Równowagę tę opisuje funkcja zwana entalpią swobodną.

do strony

tytułowej

do góry

strony 

Entalpia swobodna a równowagi 

Zmianę   entalpii  swobodnej  w  danym  procesie   (zwanej  także   potencjałem  termodynamicznym)   oznaczamy   symbolem  ΔG
i wyrażamy wzorem:

ΔG =  ΔH - T·ΔS

Jak z powyższego widać, zmiana entalpii swobodnej bierze pod uwagę zarówno wymianę energii na sposób ciepła, wymianę
energii z  otoczeniem  na  sposób  pracy   (te  dwa   elementy   zawarte   są  w  różnicy   entalpii),   jak   również energię   powodującą
rozproszenie materii (entropia).

Wyobraźmy sobie energetyczne konsekwencje pewnego procesu np. dysocjacji elektrolitycznej słabego elektrolitu (dajmy na
to   kwasu   octowego   CH

3

COOH).   Na   początku   procesu   mamy   w  roztworze   wodnym   jedynie   niezdysocjowane   cząsteczki

CH

3

COOH. Po pewnym czasie, po kolejnych zderzeniach któraś z cząsteczek uzyskała energię pozwalającą na rozerwanie

najsłabszego wiązania, czyli dysocjację na CH

3

COO

-

 i H

+

. Ten miniukład (dwa jony) ma energię wewnętrzną większą niż miał

przed dysocjacją, ale ma też większy stopień nieuporządkowania. Wzrosła zatem i entalpia (ΔH) i entropia (ΔS), zaś znak ΔG
będzie zależał od wzajemnych relacji wielkości zmiany entalpii, zmiany entropii i temperatury, w której toczy się proces. Już
wcześniej  powiedzieliśmy,   że  dowolny   proces  będzie   przebiegał  tak  długo,   aż  "zysk"   z  powodu  zmiany   wartości  jednego
parametru   (np.   wzrostu   entropii)   zrównoważy   "stratę"   np.   z  powodu   zmiany   wartości  drugiego   parametru   (np.   wzrostu
energii).  Tu zysk ze wzrostu entropii  przeważa i cząsteczka pozostanie zdysocjowana. Takie minizjawisko powtórzy się  dla
następnych  cząsteczek,   bowiem  zawsze   zysk  ze   wzrostu  entropii przeważy   stratę  z  powodu  wzrostu   energii.   Jednak  o   ile
nakład energii na rozerwanie wiązania O-H jest w zasadzie zawsze taki sam ("straty" rosną liniowo, proporcjonalnie do ilości
zdysocjowanych cząsteczek w roztworze), to przyrost "zysku" spowodowanego wzrostem entropii jest z każdą zdysocjowaną
cząsteczką  coraz mniejszy,  bowiem  taki  sam  efekt  (rozpad  cząsteczki na  dwa jony) wprowadza  względnie   coraz mniejsze
zmiany w nieuporządkowanie roztworu. Przyrost ilości jonów o dwa, jeśli dotyczy sytuacji gdy ilość jonów rośnie od dwóch
do czterech jest przyrostem o 100%.  Identyczny przyrost  ilości jonów o  dwa,  jeśli dotyczy  sytuacji wzrostu od 98  do 100
jonów,   to   przyrost   tylko   o   około   2%   zaś  przyrost   od   100   000   000   do   100   000   002   jonów  jest   już  tylko   "cieniem"   tego
pierwszego. Tak więc "zyski" przyrastają coraz wolniej a "straty" rosną proporcjonalnie do ilości zdysocjowanych cząsteczek,
co powoduje, że w pewnym momencie, przy określonym stosunku ilości jonów do ilości cząsteczek niezdysocjowanych, te
dwie wartości dla układu makroskopowego (roztworu kwasu octowego o stężeniu c i temperaturze T)  zrównają się. Dojdzie
do sytuacji,  że ΔG  =  ΔH - T·ΔS = 0   i proces się zatrzyma. Uzyskamy stan równowagi termodynamicznej  między jonami

CH

3

COO

-

 i H

+

 

z jednej strony a cząsteczkami CH

3

COOH

 

z drugiej.

Zauważmy teraz, że podniesienie temperatury (ogrzanie roztworu) powoduje wzrost bezwzględnej wartości drugiego składnika
(T·ΔS), czyli ΔG<0 i proces rusza dalej w kierunku dysocjacji kolejnych cząsteczek, aż do uzyskania ponownie ΔG=0. O tym,
że stopień dysocjacji i stała dysocjacji rosną wraz  z temperaturą wiedzieliśmy już  wcześniej - tu jednak mamy wyjaśnienie w
oparciu o termodynamikę, czyli niejako wyjaśnienie rzeczywistego źródła takiego zachowania się słabych elektrolitów. Trzeba
też   w   tym   miejscu   przypomnieć,   że   uzyskana   równowaga   (makroskopowo   opisywana   stopniem   i   stałą   dysocjacji)   jest
równowagą dynamiczną, co oznacza, że na poziomie mikroukładów (pojedynczych cząsteczek) zachodzą procesy dysocjacji,
ale   odbywają   się   one   kosztem   energetycznym   równolegle   przebiegających   procesów   łączenia   się   jonów   w   cząsteczki
niezdysocjowane.   Statystycznie   rzecz   ujmując   wydajność   obu   procesów   (dysocjacji   cząsteczek   i   asocjacji   jonów)     jest
identyczna i żadnych zmian  w skali makro (w roztworze) nie obserwujemy. 

Opisany   powyżej  proces dysocjacji  słabego  elektrolitu  ilustruje  schemat  dolny-lewy.  Przyrost wartości  entropii  układu  jest
coraz   mniejszy   (coraz   mniejsze   są   przyrosty   procesów   elementarnych,   bo   odbywają   się   "na   tle"   coraz   większego
nieuporządkowania), zaś przyrost energii jest liniowy.

Schemat dolny po prawej ilustruje powiększony element lewego schematu, od punktu równowagi. Jasno z niego wynika, że
postęp   w   procesie   makro   (zwiększanie   stopnia   dysocjacji)   jest   niemożliwy,   bowiem   wówczas   "koszt"   (wzrost   energii
wewnętrznej, opisany zmianą entalpii) jest zawsze większy od "zysku" (opisanego wzrostem entropii).

Jeżeli jednak stworzymy sytuację mieszczącą  się w obrębie tego drugiego schematu, musi nastąpić natychmiastowa reakcja

układu. Dzieje się tak, kiedy do roztworu słabego kwasu w stanie równowagi (np. octowego, jak w tym przykładzie) dodamy
kwasu silnego (np. HCl). Kwas silny jest  całkowicie zdysocjowany, tak więc w roztworze będziemy wówczas mieli o wiele
więcej jonów, niż wynika to z układu stanu równowagi kwasu octowego (matematycznie ze stałej równowagi dysocjacji tego
kwasu). Oznacza to z jednej strony wzrost entropii układu, ale z drugiej strony także wzrost energii wewnętrznej (entalpii). Jak
wynika z przebiegu wykresów tych dwu zmian, wzrost entropii będzie słabszy niż wzrost energii i układ dążąc do równowagi
spowoduje, że część anionów octanowych połączy się z protonami w cząsteczki niezdysocjowanego kwasu by obniżyć poziom
energii.   Ponieważ   tworzenie   niezdysocjowanej   cząsteczki   słabego   kwasu   z   jego   anionu   i   protonu   daje   większy   zysk
energetyczny  (mocniej obniża energię)  niż tworzenie  niezdysocjowanej cząsteczki  HCl,  nastąpi  cofnięcie dysocjacji  kwasu
octowego   (słabego)   pod   wpływem   dodatku   kwasu   silnego.     Proces   już   nam   wcześniej   znany,   ale   tu   uzyskał   logiczne
wyjaśnienie.

A   jak   jesteśmy   przy   równowagach,   to   tak   "przy   okazji"   wspomnijmy   i   wyjaśnijmy   sprawę   procesów   równowagowych,
odwracalnych w ujęciu termodynamicznym. Dowolny proces jest odwracalny, jeżeli ilość energii oddana do otoczenia podczas
przejścia  układu od  stanu A do stanu  B  jest  identyczna z  ilością energii potrzebną do przeprowadzenia układu  ze stanu B
z powrotem w stan A. W rzeczywistości takie układy nie istnieją, są niemożliwe do zrealizowania. W praktyce np. dlatego,
że   część   energii  wymieniana   podczas  zmiany   stanu   układu   rozprasza   się   w  otoczeniu.   Najczęściej  przywoływany   proces
rozprężania i sprężania gazu, to nie tylko praca potrzebna do  zmniejszenia objętości gazu,  która  później zostanie "oddana"
przez zwiększenie objętości gazu, ale też praca potrzebna na pokonanie siły tarcia tłoka, która ulega "rozproszeniu" w czasie
zarówno   sprężania   jak   i   rozprężania   gazu.   Innymi   słowy   można   powiedzieć,   że   każdemu   rozpatrywanemu   procesowi
teoretycznie   odwracalnemu   towarzyszy   inny   (inne)   proces,   również   powodujący   wymianę   energii   i   to   w   sposób
nieodwracalny. Wszystkie procesy samorzutne są procesami nieodwracalnymi, a odwracalność realnych procesów, o których
mówią  podręczniki  chemii  fizycznej  są   stanami  wyidealizowanymi,   upraszczającymi rzeczywistość  w  celu   jej  łatwiejszego
zrozumienia (tak jak pojęcie gazu idealnego). Tak więc układy rzeczywiste mogą czasami   praktycznie ulegać przemianom
odwracalnym  (tak   jak  gazy   rzeczywiste   w  pewnych  stanach   zachowują   się  praktycznie   jak   gazy  idealne),   jednak  należy
pamiętać, że to tylko przybliżenie.

Za doskonałe przybliżenia takich odwracalnych  procesów możemy uznawać procesy przebiegające na poziomie cząsteczek
i atomów.

Nie wszystko na raz 

Jak  już  nie raz  wspominaliśmy  w tym  opracowaniu, rozpatrując  dane zjawisko nie  wolno  nam zapominać o  toczących  się
równolegle   innych   procesach,   które   mają   wpływ  na   nasz  rozpatrywany   układ.   Wpływ  jest   raz  większy,   raz   mniejszy,   w
zależności  od   rodzaju   i  wielkości   oddziaływań   między  elementami   jednego   i  drugiego   układu.   Z  pewną   przesadą   można
powiedzieć,   że   w   celu   wyczerpującego   opisu   danego   stanu   czy   procesu   powinniśmy   wziąć   pod   uwagę   wpływ   całego
wszechświata na nasz proces. Takie ortodoksyjne podejście do opisywania pełnej prawdy o układzie, z praktycznego punktu
widzenia   nie   jest   ani  możliwe,   ani   potrzebne,   ani   rozsądne.   Opis   byłby   co   prawda   prawdziwy,   ale   tak   zagmatwany,   że
praktycznie  nic  by  z  niego  nie wynikało.   Z drugiej  strony,  zbytnio  upraszczając  sytuację  możemy    pozbawić  się  ważnych
informacji,   których   brak   powoduje   niezrozumienie   zachowania   się   badanego   układu.   Jak   więc   znaleźć   złoty   środek?  Tu
niestety gotowej recepty nie ma i być nie może. Umiejętności wyboru, co w danej sytuacji jest istotne, a co bez zbytniej straty
dla prawdziwego opisu zjawiska można pominąć, nabiera się z czasem, w trakcie zdobywania coraz głębszej wiedzy. Ktoś, kto
ma już sporą wiedzę o  materii i  prawach nią rządzących  może dokonać  szybkiego przeglądu  i zadecydować,  co w danym
układzie i  w danej sytuacji jest najistotniejsze. Jednocześnie nie  zgubi z pola  widzenia tego, co mniej istotne a może mieć
znaczenie w szczególnych warunkach (warunki brzegowe). Będzie miał też na uwadze czynniki, które na obserwowany układ
wpływ mają tak mały, że w pierwszym przybliżeniu można je całkowicie pominąć, ale nie wolno zapomnieć, że istnieją i jakiś
jednak wpływ  mają!

do strony

tytułowej

do góry

strony 

Przykład pierwszy - dysocjacja 

Rozpatrywaliśmy już przykład dysocjacji w przypadku słabego elektrolitu. Doszliśmy wówczas do wniosku, że nakład energii
na   rozerwanie   wiązań   jonowych   dość   szybko   równoważy   zysk   spowodowany   wzrostem   entropii,   wynikłym   z   procesu
dysocjacji,   co   spowoduje   zatrzymanie   procesu   w   skali   makro,   czyli   ustalenie   się   stanu   dynamicznej   równowagi.   Dla
wyjaśnienia,   czemu   słabe   elektrolity   dysocjują   tylko   częściowo,  taki  uproszczony   opis  zjawiska  zupełnie  nam  wystarczył.
Gdybyśmy   chcieli   jednak   dokładniej   wyjaśnić   zjawiska   związane   ze   słabymi   elektrolitami   -   nie   byłoby   tak   łatwo.   Aby
zrozumieć te bardziej złożone problemy, np. istotę aktywności elektrolitów, zmiany stopnia dysocjacji w zależności od stężenia
roztworu   i   temperatury,   niezależność   stałej   dysocjacji   od   stężenia,   trzeba   włączyć   do   opisu   stanu   układu   (roztworu)
oddziaływania   międzycząsteczkowe.   Musimy   wziąć   pod   uwagę   energetyczne   aspekty   oddziaływań   cząsteczek
rozpuszczalnika,   cząsteczek   związku   rozpuszczonego,   jonów   powstałych   z  dysocjacji   oraz  wszystkich   innych   elementów
składających się na roztwór. Musimy te relacje między wszystkimi składnikami układu rozpatrzyć we wszystkich możliwych
konfiguracjach ("każdy z każdym") i odmianach (dipol-dipol, wiązania wodorowe, solwatacja, elektrostatyczne przyciąganie
i odpychanie itp.) z jednoczesnym uwzględnieniem zmian w wartościach dwóch najistotniejszych funkcji - entalpii i entropii.

Tak   więc   zbytnie   uproszczenie  opisu  zjawiska   powoduje   niejasności  (czemu  stopień   dysocjacji  zależy  od   stężenia  a  stała
dysocjacji nie), zaś wzięcie pod uwagę wszystkich składowych układu i ich wzajemnych relacji tworzy trudną do całościowego
ogarnięcia  sieć powiązań i wzajemnych wpływów. Żeby sobie umieć radzić z tego typu problemami trzeba ćwiczyć, uczyć się 
(poznawać prawa i reguły) i znów ćwiczyć, ćwiczyć. A ćwiczyć radzę na początek na dość prostych przykładach: dokonać
najpierw uproszczonego opisu zjawiska, potem zastanowić się, jakie  jeszcze inne czynniki teoretycznie mogłyby mieć wpływ
na obserwowane zjawisko i po kolei  rozważać  każde z  nich w kontekście zjawiska  głównego. Następnie wybrać  te, co do
których nabraliśmy podejrzenia, że mogą mieć istotny wpływ na zjawisko (dwa, trzy najważniejsze) i jeszcze raz przemyśleć
całość procesu z uwzględnieniem tych wybranych wpływów. Dobrze jest też spróbować wyjaśnić zjawisko zarówno na gruncie
obserwacji makroskopowych (prawa, wzory, reguły) jak i na poziomie cząsteczkowym.

Można na przykład przeprowadzić takie rozważania: 
Żeby konkretna cząsteczka kwasu octowego rozpadła się na jony, musi dojść do zdarzenia, które spowoduje uzyskanie przez
cząsteczkę  takiej  energii,  że  rozerwanie  wiązania  (pokonanie  sił  przyciągania   elektrostatycznego  jonów  reszty   kwasowej i
protonu) będzie możliwe. Można to sobie wyobrazić, jako np. zderzenie dipola cząsteczki wody o odpowiednio dużej energii
translacji  z  atomem  wodoru  ugrupowania  COOH  cząsteczki  kwasu.  W  tym momencie   trzeba  sobie   uświadomić,  że  różne
cząsteczki  wody  w  tym  roztworze   mają   różne   energie   translacji  (temperatura   roztworu   określa   średnią   energię   translacji

cząsteczek),   tak   więc   nie   każde   zderzenie   spowoduje   oderwanie   protonu.   Warto   też   sobie   przypomnieć,   że   wiązanie
chemiczne nie ma ustalonej długości, atomy związane wiązaniem oscylują (przybliżają się do siebie i oddalają) i stan, kiedy
wiązanie będzie wydłużone ułatwi oderwanie protonu. Od temperatury zależy i ilość cząsteczek wody o odpowiedniej energii
translacji, jak również temperatura ma wpływ na oscylacje wiązań. Stąd im wyższa temperatura, tym więcej cząsteczek wody
zdolnych  dokonać  dysocjacji kwasu octowego.  Nie  zapomnijmy  też,  że  cząsteczki  kwasu  są  otoczone  cząsteczkami wody
(solwatacja, hydratacja), szczególnie w okolicy polarnego elementu cząsteczki kwasu czyli grupy -COOH, co stanowi swego
rodzaju "mur obronny" chroniący przed uderzeniami innych cząsteczek. Teraz już widzimy złożoność, prostego w pierwotnym
opisie, aktu dysocjacji. 
Rozważmy drugi ważny element wpływający na dysocjację słabych elektrolitów - stężenie. Wiemy, że w danej temperaturze
stopień dysocjacji jest tym wyższy im stężenie elektrolitu niższe. Przypominając sobie, że stopień dysocjacji to stosunek ilości
cząsteczek,   które   uległy   dysocjacji   do   ilości   cząsteczek   rozpuszczonych   w   roztworze,   dochodzimy   do   konstatacji,   że
dwukrotnie wyższy stopień dysocjacji może oznaczać taką samą ilość zdysocjowanych cząsteczek ale z dwukrotnie mniejszej
ilości cząsteczek rozpuszczonych (mniejsze stężenie). Możemy zatem zbudować sobie myślowy model, w którym bezwzględna
ilość   cząsteczek   zdysocjowanych   zależy   od   rozpuszczalnika   (jego   "wysokoenergetycznej"   części   cząsteczek,   zdolnych
sprowokować dysocjacje), stężenie substancji rozpuszczonej nie ma tu większego znaczenia, a wzrost  stopnia dysocjacji to
wynik definicji tego parametru a nie zmiany właściwości substancji rozpuszczonej. Co  na ten temat mówi doświadczenie? 

Otóż zmieniając dziesięciokrotnie stężenie kwasu od c = 0,05 mol/dm

3

 do c = 0,005 mol/dm

3

 stopień dysocjacji rośnie nam od

2%  do  6%  (trzykrotnie)  a  ilość  zdysocjowanych  cząsteczek  ...  maleje   ponad  trzykrotnie.  Tak  więc  widać,  że  nasz model
zbytnio nie odbiega od rzeczywistości.

Zastanówmy się teraz nad sytuacja "odwrotną". W roztworze są dodatnie protony i ujemne aniony reszty octanowej. Te dwa
odwrotnie naładowane elementy powinny łączyć się ze sobą, tym łatwiej i szybciej, że ich pola elektryczne będą "aktywnie
wyszukiwać" i przyciągać jony przeciwnego znaku. Spotkanie dwóch przeciwnie naładowanych jonów będzie tym łatwiejsze
im  więcej  ich  będzie  w roztworze  (duże  stężenie)  i  im  wyższa  będzie  temperatura   roztworu  (szybko  poruszające  się  jony
częściej będą się ze sobą spotykały). Z drugiej jednak strony, można sobie wyobrazić, że zbyt szybko poruszające się jony będą
zbyt krótko przebywać w polu wzajemnych oddziaływań i mimo spotkania do odtworzenia cząsteczki nie dojdzie. Tu widać, że
stężenie dość jednoznacznie wpływa na rozpatrywany proces łączenia się jonów:  im większe - tym łatwiej się spotykają jony,
tym są bliżej siebie i tym silniej działają, ważne w tym przypadku, siły elektrostatyczne. Natomiast wypadkowy efekt wpływu
temperatury   nie  do   końca  jest  jasny  -  zwiększona  energia  translacji powoduje   częstsze   spotkania  jonów,  ale  też  zwiększa
względna ilość spotkań nieaktywnych.

Ponieważ w stanie równowagi w układzie makroskopowym biegnie zjawisko dysocjacji w jedną stronę a proces łączenia się
jonów w drugą, wydajność tych dwóch procesów musi być równa. Zmiana parametru układu wpływa oczywiście na obydwa
procesy, na ich wydajności i w konsekwencji prowadzi do obserwowanych zmian. Temperatura zmienia i stopień i wartość
stałej dysocjacji, zmiana stężenia zmienia tylko stopień dysocjacji. To wiedzieliśmy już wcześniej, ale teraz wiemy - i to jest w
nauce najważniejsze - DLACZEGO tak się dzieje.

Który model zatem jest lepszy, prawdziwszy - ten wcześniejszy, termodynamiczny czy ten wykoncypowany przez nas przed
chwilą? W tym momencie nie ma to najmniejszego  znaczenia. Jeśli do kogoś  przemawia matematyka, rozumie ten język i
swobodnie się nim posługuje w rozumowaniu, model termodynamiczny będzie lepszy, prawdziwszy, bardziej naukowy. Jeśli z
matematycznych   rozważań   niewiele   rozumiem,   nie   czuję   pojęcia   prawdopodobieństwo   i  nie   rozumiem  dlaczego   wartość
entropii  rośnie najpierw  szybko  a  potem wolniej,  zaś przemawia  do  mnie  obrazowe  zderzanie  się  cząsteczek,  model  drugi
będzie lepszy. Ważne, byśmy zapamiętali o co w tym zjawisku chodzi, dlaczego takie czy inne czynniki mają wpływ i jaki,
byśmy   umieli powiązać   przyczyny   i  skutki  i  na  podstawie  tej  wiedzy   szybko   mogli  ustalić   wpływ  jednych   czynników  na
drugie. Jak osiągniemy taki stan wiedzy na dany temat, to studiowanie i rozumienie tej ścisłej, "oficjalnej" wiedzy będzie o
niebo łatwiejsze i skuteczniejsze. Tak więc wychodząc od wyobrażeń nawet nie całkiem prawdziwych, szybko i skutecznie
będziemy mogli posiąść wiedzę ścisłą i w 100% prawdziwą (jeśli taka gdziekolwiek istnieje, ale to już zadanie dla filozofów).
Będziemy mieli i piątkę w indeksie i, co ważniejsze, rzetelną wiedzę, którą będziemy umieli zastosować w praktyce.

do strony

tytułowej

do góry

strony 

Przykład drugi - rozpuszczanie 

Rozpatrując  sprawy związane  z rozpuszczaniem  substancji  czy  mieszaniem  się  cieczy  -  czyli z pozoru  ze  zjawiskami dość
prostymi - co i raz spotykamy "dziwne" zachowania, wyjątki od reguł. Szybko zaczynamy wątpić w jakiś porządek i istnienie
reguł rządzących tym procesem. Jedne substancje rozpuszczając się powodują ogrzewanie się roztworu a inne ochłodzenie,
a u większości nie zauważamy żadnego efektu cieplnego. Pewne substancje mieszają się ze sobą bez ograniczeń, większość
jednak ma określoną granicę rozpuszczalności tworząc roztwory nasycone. Okazuje się jednak, że można przejść poza zakres
rozpuszczalności,   istnieją   bowiem   roztwory   przesycone.   Substancje   najczęściej   lepiej   rozpuszczają   się   w   wyższych
temperaturach ("wyjątek" gazy) ale np. Ca(OH)

2

 rozpuszcza się w 60°C prawie o 30% gorzej niż w 20°C, a rozpuszczalność

NaCl praktycznie  nie zależy od temperatury. I jak się w tym wszystkim połapać.

Taka "niekonsekwencja" w regułach związanych z procesem rozpuszczania sugeruje istnienie co najmniej paru równoległych
zjawisk, składających się na proces rozpuszczania (czy szerzej - tworzenia roztworu). Zastanówmy się, jakie procesy mogą
brać udział w tym zjawisku. Po pierwsze, energia wiązań kryształu czy silnych oddziaływań międzycząsteczkowych cieczy,
która musi zostać pokonana, żeby pojedyncze cząsteczki mogły wniknąć między cząsteczki rozpuszczalnika. Po drugie, musi
dojść   do   rozluźnienia   oddziaływań   międzycząsteczkowych   rozpuszczalnika   i   następnie   solwatacji   cząsteczek   substancji
rozpuszczonej.   Jeżeli   substancja   jest   elektrolitem,   szczególnie   jeśli   jest   silnym   elektrolitem,   nastąpi   zjawisko   dysocjacji.
Wszystkie te zjawiska powiązane są ze zmianą energii - rozluźnienie sił międzycząsteczkowych z pobraniem energii (rozpad
kryształu,  dysocjacja),     solwatacja  z oddaniem  energii.  I tu  już ktoś, kto  ma choćby  odrobinę  doświadczenia w  "myśleniu
fizykochemicznym"   zauważa,   że   efekt   końcowy   (grzanie   czy   ochładzanie   się   roztworu),   jak   i   wpływ   temperatury   na
zachowanie substancji, zależy od relacji ilościowych efektów energetycznych pobierania i oddawania energii na sposób ciepła.
Jeśli   przeważą   (co   do   wielkości   wymienianej   energii)   procesy   egzotermiczne   (solwatacja)   nad   endotermicznymi
(rozpuszczanie  się  kryształu)  cały  proces  będzie  egzotermiczny.  Jeśli  te  dwa  typy  procesów  się  bilansują,  efekt   termiczny
zjawiska tworzenia roztworu będzie bliski zera i efektu zmiany temperatury roztworu nie zauważymy.

Jeżeli   rozpuszczamy   w   wodzie   tiosiarczan   sodu   bezwodny   (Na

2

S

2

O

3

),   to   roztwór   bardzo   silnie   się   rozgrzewa.   W   tym

przypadku silna solwatacja powoduje wydzielenie takiej ilości ciepła (energii na sposób ciepła), że znacznie przewyższa ona
ilość   energii   pochłoniętej   przez  sieć   krystaliczną   w  celu   uwolnienia   cząsteczek   i   przez   zjawisko   dysocjacji,   a   właściwie
hydrolizy  tiosiarczanu. Jeśli jednak rozpuszczać będziemy  tiosiarczan pięciowodny (Na

2

S

2

O

3

*5H

2

O) to  roztwór się bardzo

silnie   ochłodzi.   W   tym    przypadku   proces  hydratacji  nie   wystąpi,   bowiem  cząsteczki   tiosiarczanu   już  są   uwodnione.   O
wielkości efektu zadecyduje proces zrywania wiązań sieci krystalicznej i wiązań jonowych, proces będzie endotermiczny.

prawdopodobieństwo znalezienia się konkretnej cząsteczki w części objętości A roztworu wynosi 1/4. Dla N cząsteczek

w roztworze, prawdopodobieństwo, że znajdą się wszystkie w tej części roztworu wyniesie (1/4)

N

, a więc będzie bardzo

małe. Stan, w którym cząsteczki skupione są w jednym miejscu jest bardzo mało prawdopodobny. Prawdopodobieństwo,
że   konkretna   cząsteczka   znajdzie   się   w   dowolnym   miejscu   roztworu   wynosi   1,   zatem   prawdopodobieństwo

równomiernego rozłożenia N cząsteczek w roztworze wynosi 1

N

 = 1. Tak więc układ samoistnie będzie dążył do stanu

bardziej prawdopodobnego. (Podobnie tłumaczyć możemy zjawisko wzrostem entropii);

inne tłumaczenie, też związane  z  prawdopodobieństwem zdarzeń  losowych, ale bardziej działające  na  wyobraźnię, to
rozpatrywanie   stanu   roztworu   o   gradiencie   stężenia   (

c

1

>c

2

)   jako   zbioru   cząsteczek   rozpuszczalnika   i   substancji

rozpuszczonej,   zderzających   się   przypadkowo   ze   sobą.   Dla   cząsteczek   substancji   rozpuszczonej   usytuowanych   na
granicy stężenia wysokiego i niskiego ilość zderzeń "od dołu do góry" będzie większa niż odwrotnie i więcej cząsteczek
będzie poruszać się w stronę mniejszego stężenia. Dla pełniejszego opisu takiej sytuacji trzeba by jeszcze rozważyć rolę
sił oddziaływania cząsteczek substancja-substancja oraz substancja-rozpuszczalnik.
W stanie równowagi wydajność procesu przemieszczania się cząsteczek między dwoma dowolnymi obszarami roztworu
jest   identyczna,   zatem   roztwór   makroskopowy   wykazuje   równowagę,   jednakowe   stężenie   w   każdym   elemencie
objętości. 

można również zaproponować podejście do tematu takie, jak w  punkcie powyżej, ale wziąć pod uwagę nie samodzielnie
poruszające się cząsteczki substancji rozpuszczonej a asocjaty, elementy powstałe w zjawisku solwatacji (aktywny udział
cząsteczek rozpuszczalnika w tym procesie ).

Wydawałoby się, że już zapanowaliśmy na procesem rozpuszczania, a tu pojawia się nowy "kłopot". Jeśli proces rozpuszczania
jest egzoenergetyczny to wzrost temperatury powinien hamować i cofać ten proces. Wielu z nas tak by skojarzyło wcześniej
przyswojoną regułę dotycząca np. reakcji endo- i egzotermicznych. W tym przypadku to skojarzenie i zastosowanie takiego
schematu   myślenia   jest   błędem.   W   przypadku   reakcji   chemicznych,   temperatura   decyduje   o   tym   co   jest   bardziej
prawdopodobne   -   zamiana   kompleksu  aktywnego   w  produkt   czy  powrót   ze   stanu   kompleksu   aktywnego   do   substratów.
W   przypadku   procesu   rozpuszczania   temperatura   ma   bezpośredni   dodatni   wpływ   na   główny   etap   procesu   -   odrywanie
cząsteczek  od  sieci krystalicznej  i  ewentualną  jonizację  (dysocjację),   natomiast  wpływ  ujemny  może  mieć  na  następujący
później  proces  solwatacji.   Tak  więc   mimo,   że   proces  całościowo   może  być   egzoenergetyczny,   to   wzrost   temperatury   nie
będzie go osłabiał. Widać tu, jak bardzo zawodne może być korzystanie z ogólnych reguł, bez głębokiej znajomości zasad,
z których dana reguła została wywiedziona i granic, w których można ją  stosować.

Jeżeli   stan   nasycenia   potraktujemy   jako   układ   znajdujący   się   w   warunkach,   w   których   szybkość   (wydajność)   procesu
przechodzenia   cząsteczek   z   ciała   stałego   do   roztworu   zrównuje   się   z   wydajnością   procesu   krystalizacji   (przechodzenia
cząsteczek z roztworu do kryształu ciała stałego), to dla zrozumienia całości sprawy musimy przeanalizować, jak poszczególne
parametry tego stanu (głównie temperatura i związana z nią lepkość oraz translacja cząsteczek, tak rozpuszczalnika jak i ciała
rozpuszczonego)   wpływają   na   wydajność  jednego   i  drugiego   procesu.   Tylko   wówczas   będziemy   w  stanie   ogarnąć   całość
problemu i zrozumieć różne "anomalie" występujące w tych procesach. Ponadto musimy być świadomi, że inaczej parametry
stanu roztworu mogą wpływać na sam proces (szybkość rozpuszczania) a inaczej na moment  osiągnięcia stanu równowagi,
czyli stężenie nasycenia (rozpuszczalność). W ujęciu termodynamiki statystycznej o stanie równowagi (nasyceniu) zdecyduje
zrównanie wzrostu energii (cząsteczki rozpuszczone, a szczególnie jony powstałe z dysocjacji będzie charakteryzować wyższa
energia niż elementy kryształu) ze wzrostem entropii.  Zaś  wielkość zmian energetycznych i zmian uporządkowania układu
(entropii) zależeć będzie od paru czynników (ciepło rozpuszczania i solwatacji, ilość cząsteczek i jonów w stanie nasycenia,
siła wiązań jonowych itp.) co w sumie daje trudny do przewidzenia a priori końcowy efekt makroskopowy.

Tak  więc  rozpuszczalność,  stężenie  stanu  nasycenia,  nie  jest parametrem substancji  rozpuszczanej lecz  zależy  zarówno od
cech  substancji rozpuszczanej jak i rozpuszczalnika,  jest wypadkową wzajemnych relacji między tymi cechami i związanymi
z  tym  zjawiskami.   To   też  przyczynek  do   wcześniej  postulowanego   "nowego   spojrzenia  na  świat".   To,   że   cechy   roztworu
zależeć   muszą   i   od   substancji   rozpuszczonej   i   od   rozpuszczalnika   jest   dla   nas   dość   oczywiste,   ale   ponieważ   tablice
fizykochemiczne   podają   wartości   rozpuszczalności   substancji,   podświadomie   często   gotowi   jesteśmy   traktować
rozpuszczalność jako parametr charakterystyczny dla tej substancji, a nie całego roztworu. 

do strony

tytułowej

do góry

strony 

Przykład trzeci - dyfuzja 

Dyfuzja - zjawisko polegające na samoistnym, równomiernym rozprzestrzenianiu się cząsteczek substancji rozpuszczonej w
całej objętości roztworu. Zjawisko to, jak wiele innych, objaśnić  można na kilka sposobów:

 

Ponieważ  zjawisko  dyfuzji  polega  na   przemieszczaniu   się  cząsteczek   substancji  rozpuszczonej  w  ośrodku   rozpuszczalnika
można  przy  opisie  tego   procesu  wziąć  pod  uwagę  (choć  ostrożnie  -  nie  wszystko  na  raz!)  także   lepkość  rozpuszczalnika,
stosunek   masy   cząsteczki  rozpuszczalnika   i   substancji   rozpuszczonej,   siły   grawitacji,   oddziaływania   międzycząsteczkowe
cząsteczek rozpuszczalnika a także kształty i rozmiary cząsteczek. Wszystkie te czynniki w większy czy mniejszy sposób mogą
wpłynąć na szybkość procesu dyfuzji. Trzeba też uzmysłowić sobie, że pojęcie "szybkość dyfuzji" nie ma żadnego realnego
sensu, dopóki nie zdefiniujemy go w sposób jednoznaczny. Wpływ wszystkich tych elementów jest  zawarty w I i II prawie
Ficka, które pozwalają określić (przewidzieć) stężenie w każdym punkcie roztworu i w każdej dowolnej chwili. Nauczenie się
praw  Ficka   i   zapamiętanie   postaci  matematycznego   zapisu  niewiele   jednak   przyczyni  się   do   zrozumienia   istoty   zjawiska.
Natomiast,   jeśli   ktoś   sprawnie   posługuje   się   aparatem   matematycznym   (szczególnie   rachunkiem   różniczkowym),   to
zrozumienie wyprowadzenia tych wzorów może być dobrym początkiem dla głębokiego zrozumienia problemu.

Mówiąc o uzyskiwaniu przez układ najniższych energii i najwyższych wartości  entropii powinniśmy dodawać (a przynajmniej
o   tym  pamiętać),   że   najniższych   czy  najwyższych  z  możliwych  do   osiągnięcia  w  danej  sytuacji.   Jeżeli  przedzielimy   dwa

roztwory o różnych stężeniach błoną półprzepuszczalną, to układ będzie się starał osiągnąć równe stężenia po obu stronach tej
błony, ale jeżeli anion substancji rozpuszczonej będzie miał rozmiary nie pozwalające przeniknąć przez błonę (np. cząsteczki
białka), to będzie mogło dojść co najwyżej do wyrównania stężeń kationów. Tu pamiętać należy, że roztwór i każda jego część
musi być elektrycznie obojętna, nie może się więc zdarzyć, że na przykład.połowa kationów przejdzie na drugą stronę błony,
pozostawiając aniony. Doprowadziło by to do powstania ogromnego potencjału na granicy faz (po dwóch stronach błony). Ten
potencjał powstając   już znacznie wcześniej zahamuje ruch kationów. To fizyczne ograniczenie możliwości ruchu niektórych
elementów układu  podczas procesu  dyfuzji przez błony  leży  u  podstaw  zjawiska  ciśnienia  osmotycznego  i  tzw.  równowag
Donnana.

Rola przypadku w przyrodzie 

W potocznym rozumieniu pojęcie przypadek kojarzy nam się zazwyczaj nie tylko z czymś nieprzewidywalnym, ale dodatkowo
mało   prawdopodobnym,   niespodziewanym.   W   matematyczno-fizycznym   ujęciu   przez   przypadek,   zdarzenie   losowe,
rozumiemy wszystko to, czego dokładnie nie da się przewidzieć a priori, przewidzieć co do wartości, parametrów, ale   że to
coś nastąpi jesteśmy najczęściej pewni. Warto sobie przemyśleć i uświadomić takie rozumienie przypadku, bo inaczej pojawią
się trudności w zrozumieniu wielu spraw związanych z fizykochemią.

Jeśli chodzi o rolę przypadku w przyrodzie możemy powiedzieć, że występujący w skali mikro przypadek, nieprzewidywalne
zdarzenie, zamienia się w skali makro w ...  pewność, ścisłe prawo. Wyobraźmy sobie dwa naczynia z taką samą ilością gazu
(ilością cząsteczek), przy czym objętość jednego jest dwukrotnie większa od drugiego. Bez trudu wykażemy, że w warunkach
tej   samej   temperatury,   ciśnienie   w  naczyniu   większym   będzie   dwa   razy   mniejsze   niż  w   naczyniu   mniejszym   (równanie
Clapeyrona).  Tu  nie  ma  cienia  wątpliwości  i  o żadnym  przypadku,  żadnej przypadkowej  wartości ciśnienia  nie ma  mowy.
Wiemy również, że ciśnienie to jest identyczne w każdym miejscu ściany naczynia. Wiemy także, że ciśnienie to jest skutkiem
uderzeń  o   ściany  naczynia   poruszających   się  bezładnie   cząsteczek  gazu.   Jeśli więc  wyobrazimy   sobie,   że   śledzimy   jedną
cząsteczkę gazu przez jakiś czas, to nie jesteśmy w stanie w żadnym momencie przewidzieć ani kierunku ruchu, ani szybkości
tej cząsteczki, ani nawet czy w najbliższej przyszłości uderzy ona o ściankę naczynia czy nie. Tak więc zachowanie każdej
z  cząsteczek   tworzących   gaz  jest   nieprzewidywalne   (losowe,   przypadkowe)   natomiast  zachowanie   się   zbioru   cząsteczek,
rozpatrywanych jako całość ("gaz") jest przewidywalne i ściśle określone. Suma przypadków tworzy pewność! To sobie trzeba
dobrze przemyśleć.

Wiemy, że rozpad jąder atomowych naturalnych izotopów promieniotwórczych odbywa się z bardzo dokładnie określonym
czasem półtrwania (czasem rozpadu promieniotwórczego połowy cząsteczek danego izotopu). Natomiast nie jesteśmy w stanie
określić, który atom ulegnie rozpadowi jako następny, ani nawet które atomy będą należały do tej połowy, która rozpadnie się
w tym czasie półtrwania. Każdy rozpad jest czystym przypadkiem, ale bez względu na to, które atomy i ile zgromadzimy w
jednym miejscu, zawsze dokładnie połowa z nich rozpadnie się po tym samym czasie.

Szybkość konkretnej reakcji chemicznej w konkretnych warunkach jest bardzo ściśle określona przez stałą szybkości reakcji k.
Szybkość ta określa ile cząsteczek substratu zamieni się w produkt  w określonym przedziale czasu. Pojedyncze cząsteczki 
substratu   reagując  ze  sobą  tworzą  tzw.  kompleks  aktywny,   twór  pośredni  między  substratem  a  produktem.   Jest  to  twór  o
bardzo   wysokiej  energii   i  po   powstaniu   bardzo   szybko   musi  zamienić  się   w  produkt,   lub   z  powrotem  wrócić   do   postaci
substratu. Jeśli większość kompleksów aktywnych zamienia się w produkt, reakcja biegnie szybko, jeśli większość wraca do
postaci substratu, reakcja biegnie wolno. Tak więc szybkość reakcji określa suma zdarzeń pozytywnych (kompleks aktywny
przechodzi w produkt), natomiast to, czy konkretny kompleks aktywny zamieni się w produkt czy też wróci do stanu substratu
jest   zupełnym  przypadkiem.   Tak   więc   znów  suma   całkowicie   przypadkowych   zdarzeń   zamienia   się   w  precyzyjnie   i   bez
żadnego przypadku określoną pewność.

Wielkość wypadkowego efektu dużej ilości zdarzeń przypadkowych, losowych, daje się wyznaczyć precyzyjnie przy pomocy
rachunku prawdopodobieństwa i podstawowych zasad statystyki. Warto zatem przypomnieć sobie, lub przybliżyć podstawowe
zasady   tych   działów  matematyki.   Bez  podstawowej   choćby   znajomości  matematyki  dość   trudno   poruszać   się   w  gąszczu
dokładnych opisów skomplikowanych zjawisk należących do fizykochemii. 

 

Podsumowanie 

W tym miejscu można już zrobić małe uogólnienie podsumowujące, pamiętając, że jak wszystkie uogólnienia, ma ono na celu
wyłącznie   wstępne   uporządkowanie   wcześniej   omówionych   spraw   a   nie   ogłoszenie   prawdy   niepodważalnej,   jedynej   i
ostatecznej.

Każde   zjawisko   można   rozpatrywać   w   skali   makro,   bezpośrednio   dostępnej  naszym   zmysłom.   Na   podstawie   obserwacji
i  doświadczeń   znajdujemy   uogólnione   zasady   i  prawa  wiążące   poszczególne   elementy   i  parametry   procesu.  Takie   ujęcie,
będące   bardzo   często   podstawowym  ujęciem  w  szybkim  kursie   chemii  fizycznej,     pozwala   przewidywać  skutki,   nie   daje
jednak możliwości poznania prawdziwej istoty zjawiska. Aby zrozumieć zjawisko i móc przewidywać zachowanie się procesu,
bez  względu   na   zakres   zmienności   wartości  parametrów,   musimy   rozpatrzyć   jego   przebieg  w  skali  cząsteczek   i  atomów.
Pamiętając, że najczęściej na rozważane zjawisko składa się kilka równoległych i nawzajem powiązanych procesów, starajmy
się   wyodrębnić   te  najistotniejsze  i   na   nie   zwrócić   przede   wszystkim  uwagę  (nie   wszystko   na   raz).   Procesy  mniej  istotne
włączmy   do   rozważań  później,   gdy  zrozumiemy   działanie  głównych  sił  sprawczych  rozpatrywanego  zjawiska.   Pamiętajmy
jednocześnie, by nie "zapomnieć" o mniej ważnych, ale mających wpływ na rozpatrywane zjawisko, procesach.

Dla zjawisk, w których bierze udział duża ilość cząsteczek czy atomów, mimo losowego, przypadkowego charakteru zdarzeń
elementarnych,   rachunek   prawdopodobieństwa   pozwala   precyzyjnie   i   dokładnie   przewidywać   efekt   końcowy,   będący
statystyczną   średnią   efektów   zdarzeń   elementarnych.   Nie   zapominajmy,   że   wiele   pojęć   typu:   pole   elektromagnetyczne,
energia,   ładunek,   wiązanie   chemiczne,   orbital   itp.   mimo,   że   posługujemy   się   nimi   tak,   jakby   oznaczały   konkretną,
zdefiniowaną   wartość   materialną   (procent   wiązania   jonowego,   odbicie   światła,   energia   orbitala)   są   tylko   pojęciami,
niemożliwymi     do   wyobrażenia   i   bardziej   wyczuwanymi   intuicyjnie   niż   zrozumiałymi.   Z   pokorą   zatem   przyjmijmy,   że
"wyjaśnieniem" niektórych zdarzeń z zakresu mechaniki kwantowej (poziom mikro) może być wyłącznie opis matematyczny.
Jednocześnie pamiętajmy, że ten matematyczny opis zjawiska pozwala obliczyć pewne parametry, przewidzieć zachowanie,
najczęściej jednak nie pozwala zrozumieć dlaczego tak się dzieje. Mówi nam co ale nie mówi dlaczego. 
Tak więc starajmy się o następującą sekwencję poznawczą: ogólny opis zjawiska i powiązanie parametrów, zrozumienie istoty

zjawiska na poziomie cząsteczkowym i dopiero wówczas wzory i matematyka, jako precyzyjny opis. Nauczmy się też czytać
wzory, rozumieć definicje i prawa a szczególnie zdobądźmy umiejętność czytania wykresów i diagramów.

A oprócz tego, a może przede wszystkim, pamiętajmy o podstawowej zasadzie rozpraszania energii i materii - niech entalpia
i entropia, a szczególnie entalpia swobodna ( potencjał termodynamiczny), będą dla nas pojęciami zrozumiałymi, oczywistymi
i włączanymi na początku każdych rozważań.

 

 

Raz  jeszcze  przypominam.   Te   rozważania   to   przykład,   jak   można   się   starać   przybliżyć   zrozumienie,   czasem  rzeczywiście
niełatwych wiadomości z chemii fizycznej. To opracowanie nie ma rangi podręcznika, interpretacje zjawisk tu podawane mogą
czasem nawet znacznie różnić się od "oficjalnego" opisu a nawet mogą niekiedy być nie całkiem prawdziwe. 

Zadaniem tego

opracowania   nie  jest  nauczenie  kogokolwiek  czegokolwiek,  a   jedynie  pokazanie  drogi   do  łatwiejszego,   rozumnego  i
skutecznego sposobu przyswojenia sobie wiedzy z podręczników i wykładów

. Jest to tylko uzupełnienie, wprowadzenie do

tematu,  na  które  zazwyczaj wykładowcom  brakuje czasu. Jest  to  materiał  do  przemyśleń  a nie  szkolna  wiedza  podana do
wierzenia. Im bardziej nie będziesz się ze mną zgadzć - tym lepiej (dla Ciebie). Postaraj się jednak wyraźnie wyartykułować, z
czym  się   nie   zgadzasz  i   dlaczego   uważasz  moje   sugestie   za   gorsze   od   Twoich   przemyśleń.   O  to   tu   chodzi   -   zacznijmy
samodzielnie myśleć! To nie tylko, że nie boli ale daje czasem dużą przyjemność i satysfakcję. Warto spróbować.

Jeżeli Twój opis zjawiska jest skuteczny, tzn. pozwala logicznie kojarzyć przyczyny i skutki, pozwala skutecznie i prawidłowo
przewidywać   konsekwencje   zmian   parametrów   układu,  jest  na  tyle  przejrzysty,   że   łatwy   do   zapamiętania  -   to   już  bardzo
dobrze.  Nawet   jeśli  nie   we  wszystkim  jest   zgodny   z  oficjalną   wiedzą.  Jeśli    w  niczym  nie   kłóci  się  ze   znanymi  prawami
przyrody, to już super. A jeśli dodatkowo jest zgodny z oficjalną wiedzą na dany temat - zostań wykładowcą. Studenci będą
chodzić na Twoje wykłady niczym na najlepsze filmy.

 

do strony tytułowej

do góry strony