GEOMETRIA PRZEKROJU
1
1. CHARAKTERYSTYKI GEOMETRYCZNE FIGUR PŁASKICH
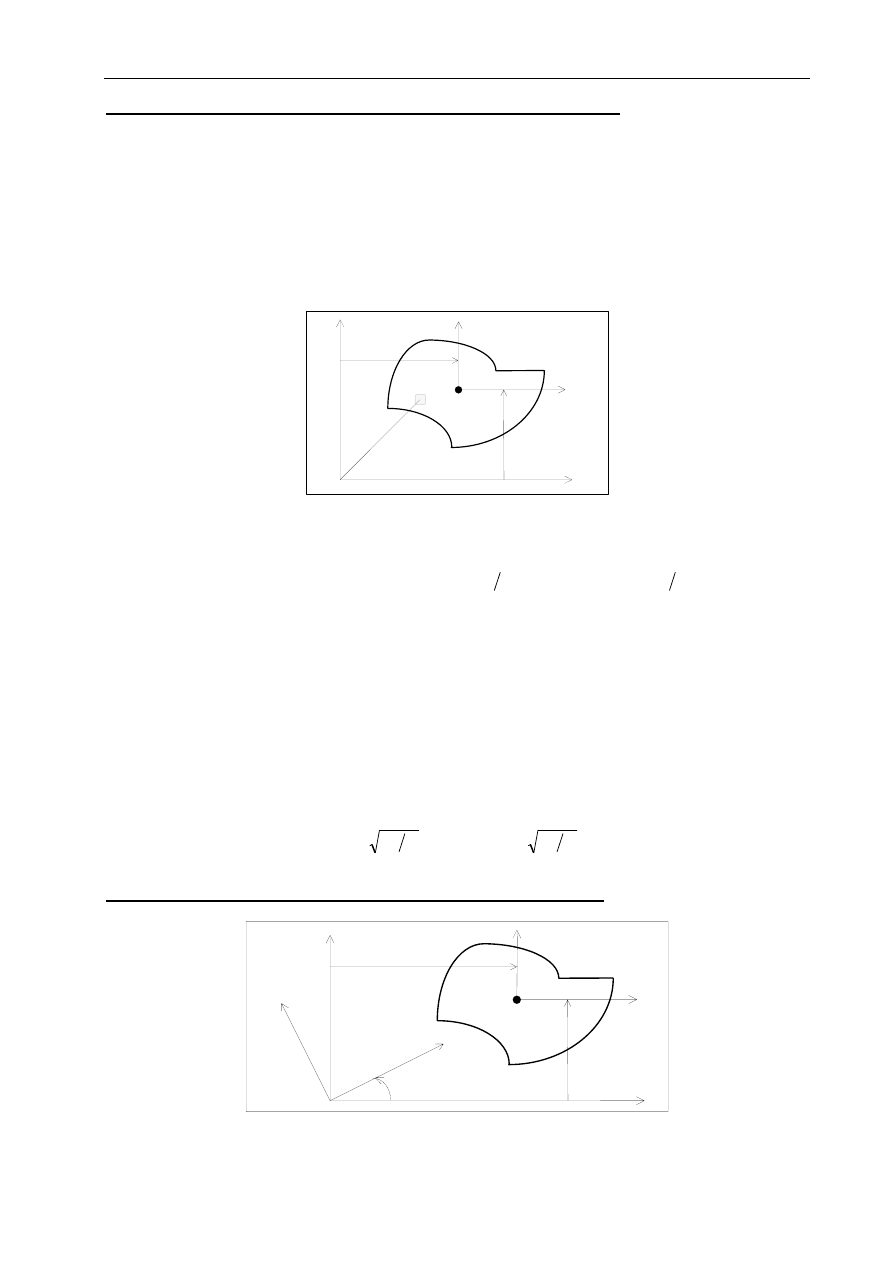
Oznaczenia:
(y, z) - dowolny układ współrzędnych
(y
c
, z
c
) - centralny układ współrzędnych, "równoległy" do układu (y, z)
A - pole powierzchni figury
C
-
środek ciężkości figury
y
s
, z
s
- współrzędne środka ciężk. figury C w dowolnym ukł. współrzędnych (y, z)
C
y
z
y
c
z
c
y
s
z
s
A
dA
ρ
O
1.1. Momenty statyczne
S
z d A
S
y d A
y
A
z
A
=
=
∫∫
∫∫
1.2. Położenie środka ciężkości C
z
S
A
y
S
A
s
y
s
z
=
=
1.3. Momenty bezwładności, moment dewiacji
I
z d A
I
y d A
y
A
z
A
=
>
=
>
∫∫
∫∫
2
2
0
0
(
)
(
)
(
)
I
d A
y
z
d A I
I
o
z
y
A
A
=
=
+
=
+
>
∫∫
∫∫
ρ
2
2
2
0
(
)
I
y z d A
yz
A
=
<=>
∫∫
(
)
0
1.4. Promienie bezwładności
i
I
A
i
I
A
y
y
z
z
=
=
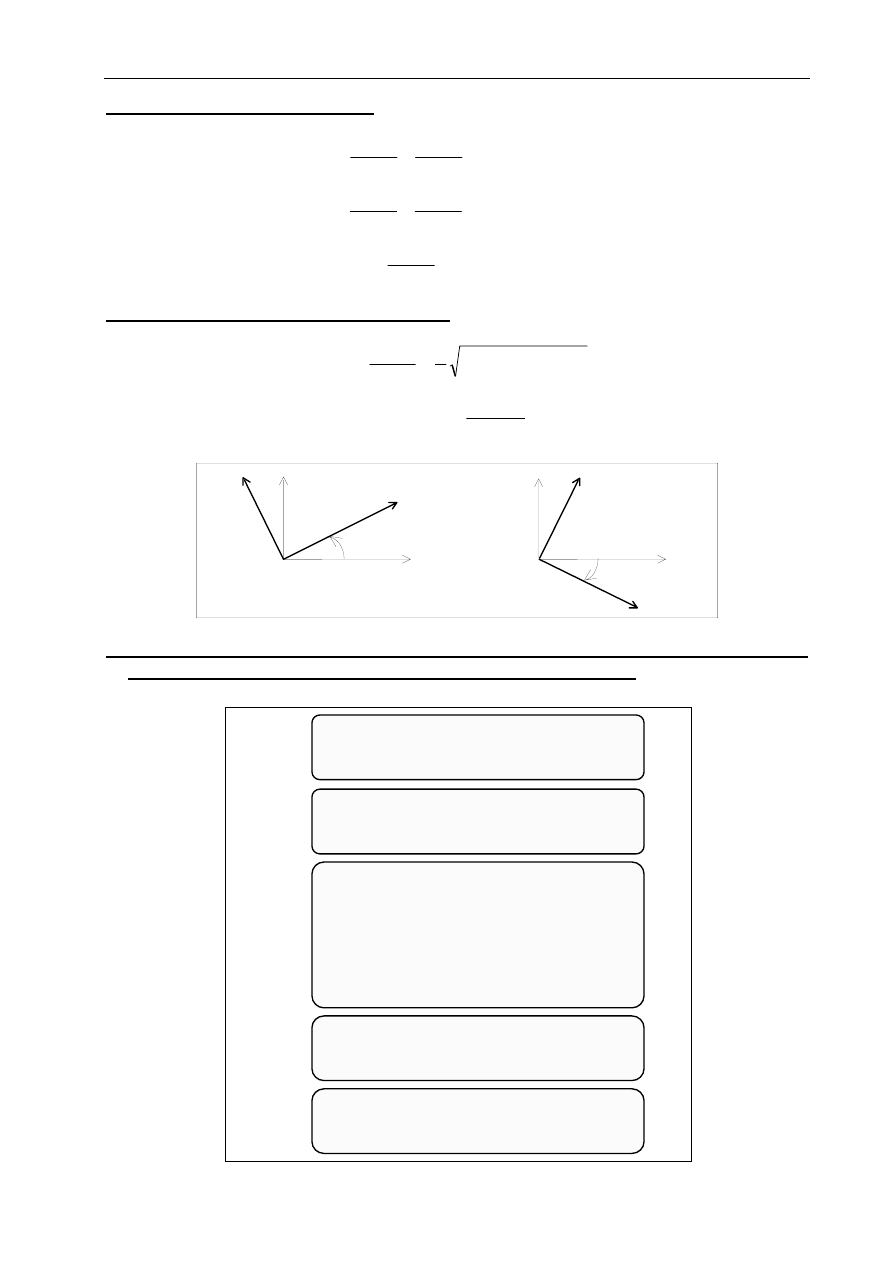
2. Translacja układu współrzędnych - twierdzenie Steinera
C
y
z
y
c
z
c
y
s
z
s
A
O
α
y '
z '
I
I
A z
y
y
s
c
=
+
2
I
I
A y
z
z
s
c
=
+
2
I
I
A y z
yz
y z
s
s
c c
=
+
GEOMETRIA PRZEKROJU
2
3. Obrót układu współrzędnych
I
I
I
I
I
I
y
y
z
y
z
yz
'
cos
sin
=
+
+
−
−
2
2
2
2
α
α
I
I
I
I
I
I
z
y
z
y
z
yz
'
cos
sin
=
+
−
−
+
2
2
2
2
α
α
I
I
I
I
y z
y
z
yz
' '
sin
cos
=
−
+
2
2
2
α
α
4. Główne osie i momenty bezwładności
(
)
I
I
I
I
I
I
y
z
y
z
yz
1 2
2
2
2
1
2
4
,
=
+
±
−
+
tan
,
,
α
1 2
1 2
=
−
I
I
I
yz
z
y
z
1
2
α
1
> 0
z
y
1
α
1
< 0
2
5. Algorytm wyznaczania położenia głównych, centralnych osi bezwładności i
obliczania głównych, centralnych momentów bezwładności
Przyjąć dowolny układ współrzędnych (x, y)
"wygodny" do obliczeń
1
Wyznaczyć położenie środka ciężkości
C ( y , z )
s
s
2
Obliczyć centralne momenty bezwładności
( twierdzenie Steinera )
I
y
c
= I
y
s
- A z
2
I
z
c
= I
z
s
- A y
2
c
= I
yz
s
- A y z
I
z
y
c
s
3
Obliczyć główne centralne
momenty bezwładności
4
Wyznaczyć połóżenie głównych centralnych
osi bezwładności
5
GEOMETRIA PRZEKROJU
3
6. Charakterystyki wybranych przekrojów
I
I
a
I
I
a
I
a
y
z
y
z
y z
=
=
=
=
=
4
4
4
12
3
4
'
'
' '
;
I
bh
I
hb
I
bh
I
hb
I
b h
y
z
y
z
y z
=
=
=
=
=
3
3
3
3
2
2
12
12
3
3
4
;
;
;
'
'
' '
I
bh
I
hb
I
b h
I
bh
I
hb
I
b h
y
z
yz
y
z
y z
=
=
= −
=
=
=
3
3
2
2
3
3
2
2
36
36
72
12
12
24
;
;
;
;
'
'
' '
I
I
R
y
z
=
=
π
4
4
I
R
I
R
y
z
=
=
0 11
8
4
4
.
;
π
I
I
R
I
R
y
z
yz
=
=
= −
0 055
0 0165
4
4
.
.
y
z
z '
y '
a
a
y
z
z '
y '
b
h
z '
y '
b
h
y
z
y
z
R
y
z
4 R
3 π
R
y
z
R
a
a
4 R
3 π
a =