Uniwersytet Kazimierza 

Uniwersytet Kazimierza 

Wielkiego

Wielkiego

Wydział Matematyki, 

Wydział Matematyki, 

Fizyki i Techniki

Fizyki i Techniki

Edukacja Techniczno-

Edukacja Techniczno-

Informatyczna

Informatyczna

CHARAKTERYSTY

CHARAKTERYSTY

KI 

KI 

GEOMETRYCZNE 

GEOMETRYCZNE 

PRZEKROJÓW

PRZEKROJÓW

Cechy przekroju

Cechy przekroju

•

Przekroje mogą być traktowane jako 

Przekroje mogą być traktowane jako 

figury płaskie.

figury płaskie.

•

Figura płaska charakteryzuje się 

Figura płaska charakteryzuje się 

tym,że jeden z jej wymiarów jest 

tym,że jeden z jej wymiarów jest 

nieskończenie mały.

nieskończenie mały.

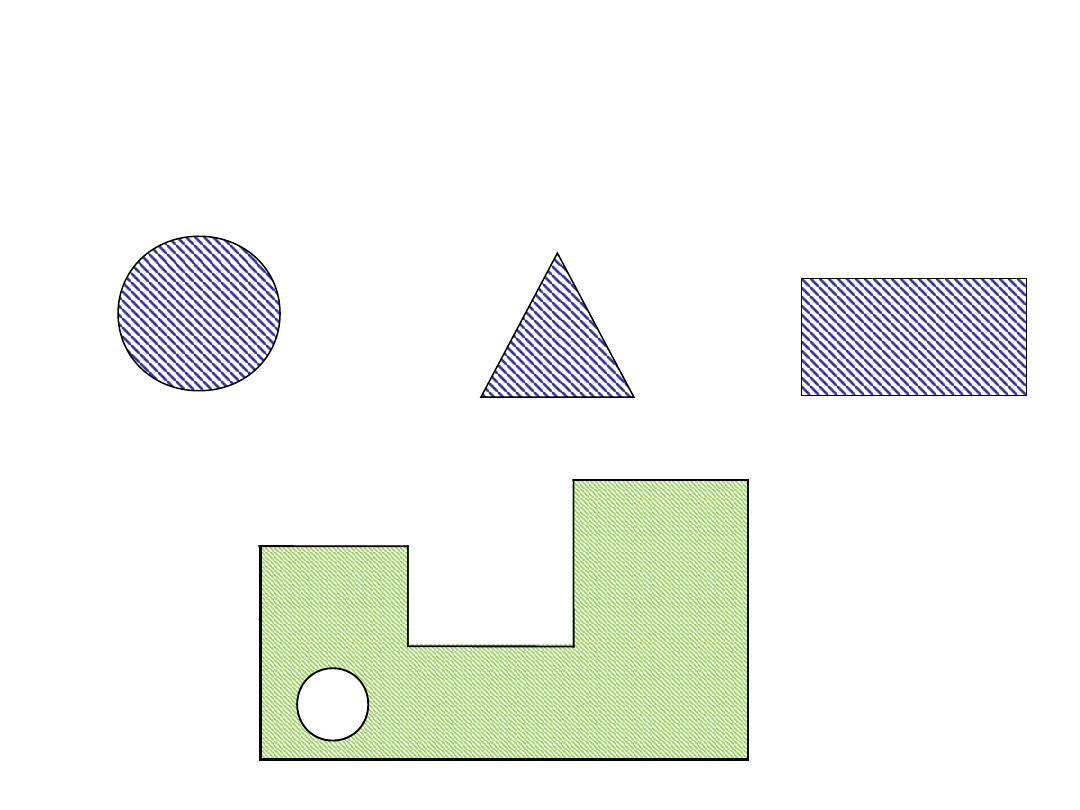
1. KSZTAŁT 

1. KSZTAŁT 

PRZEKROJU

PRZEKROJU

- proste

- złożone

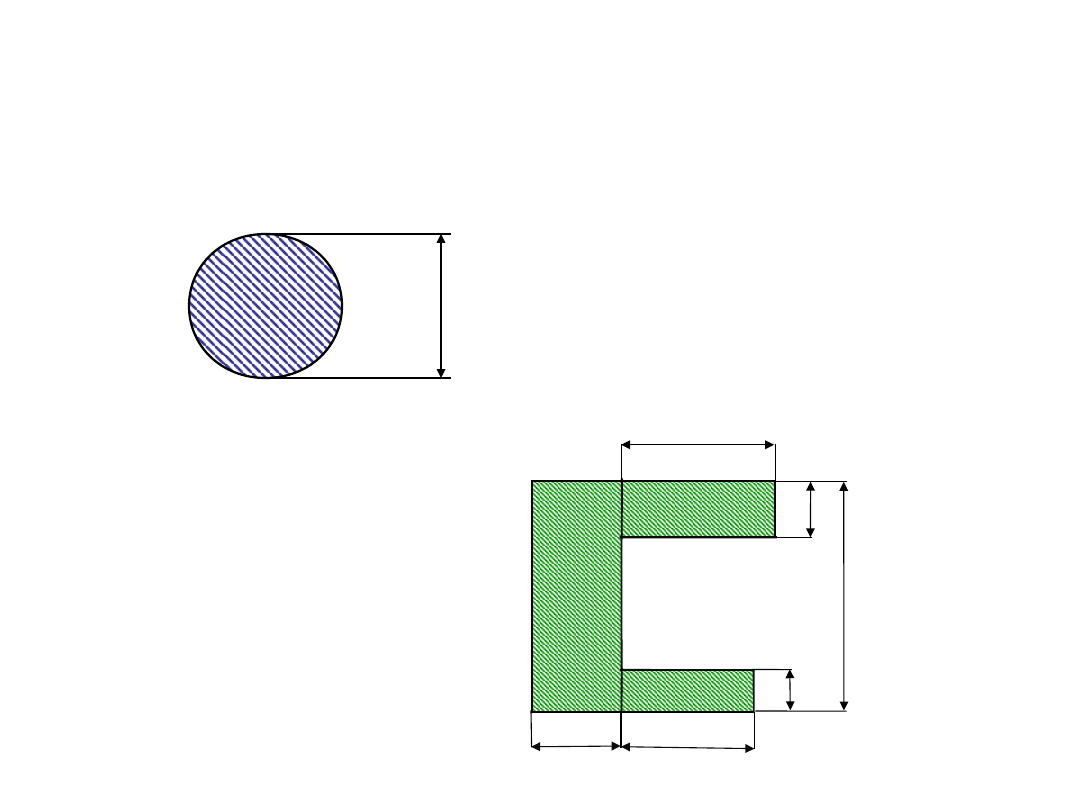
2. WYMIARY PRZEKROJU

2. WYMIARY PRZEKROJU

d

d

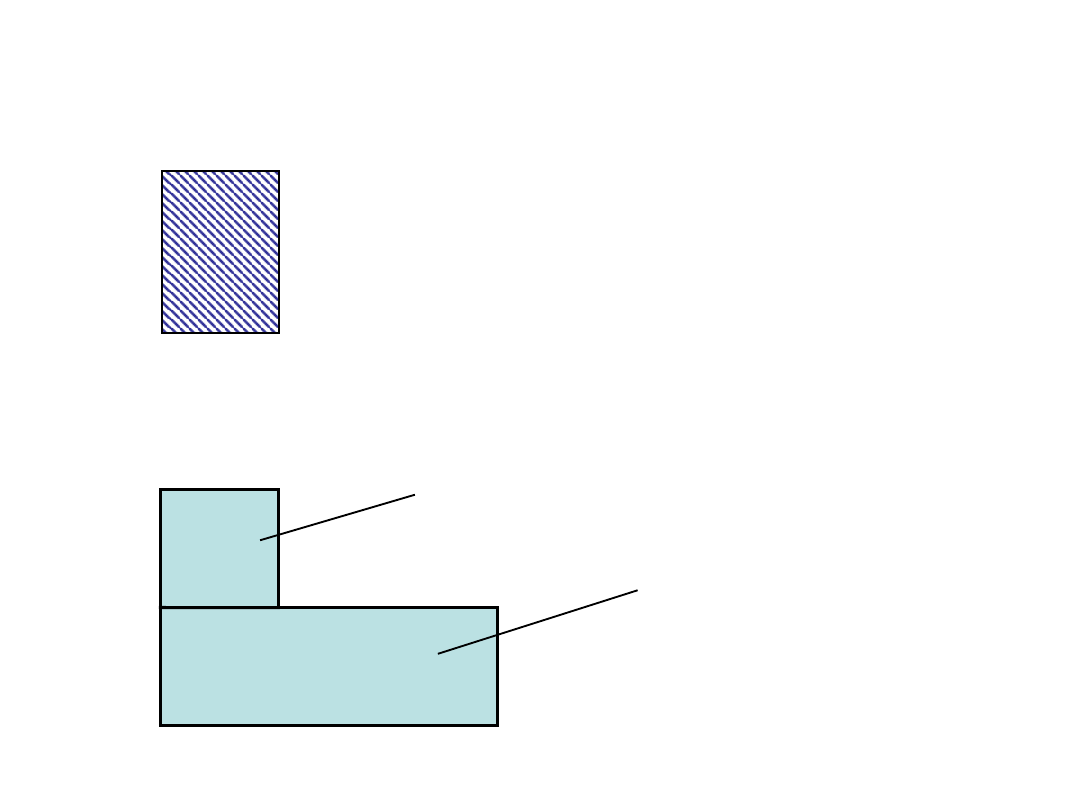
3. POLE PRZEKROJU

3. POLE PRZEKROJU

h

h

b

b

F= h ∙ b

F= h ∙ b

F

F

1

1

F

F

2

2

F= F

F= F

1

1

+F

+F

2

2

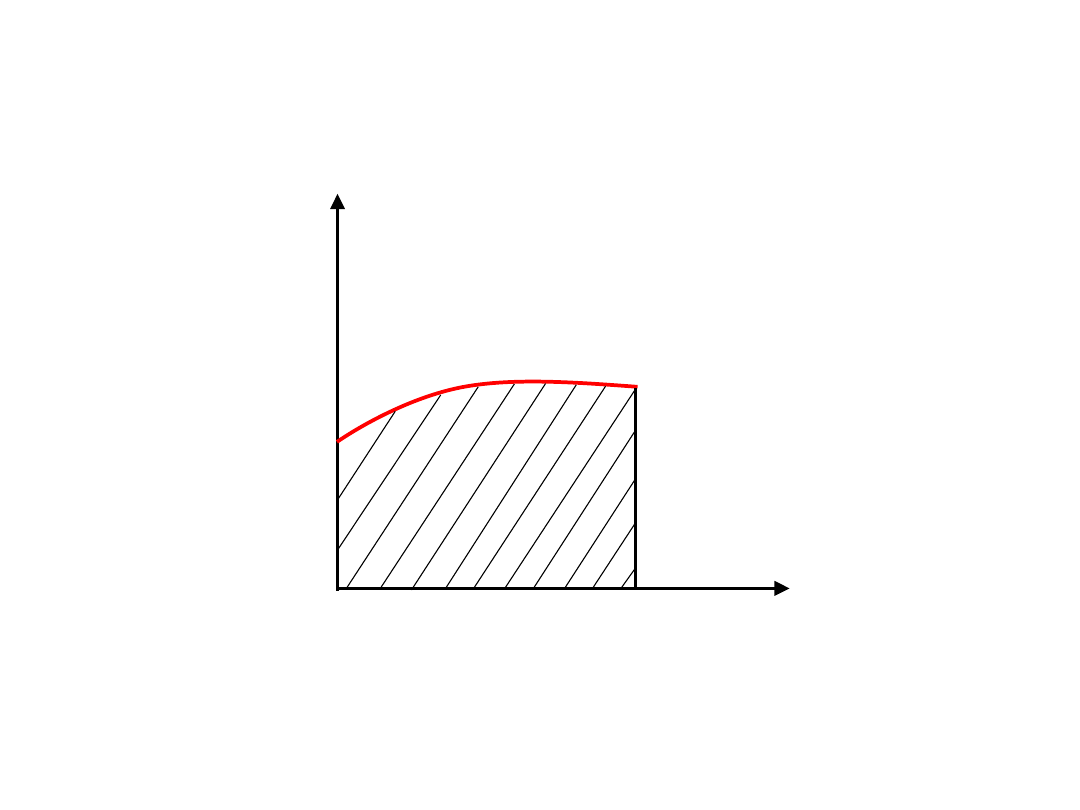
0

0

a

a

x

x

y

y

f(x)

f(x)

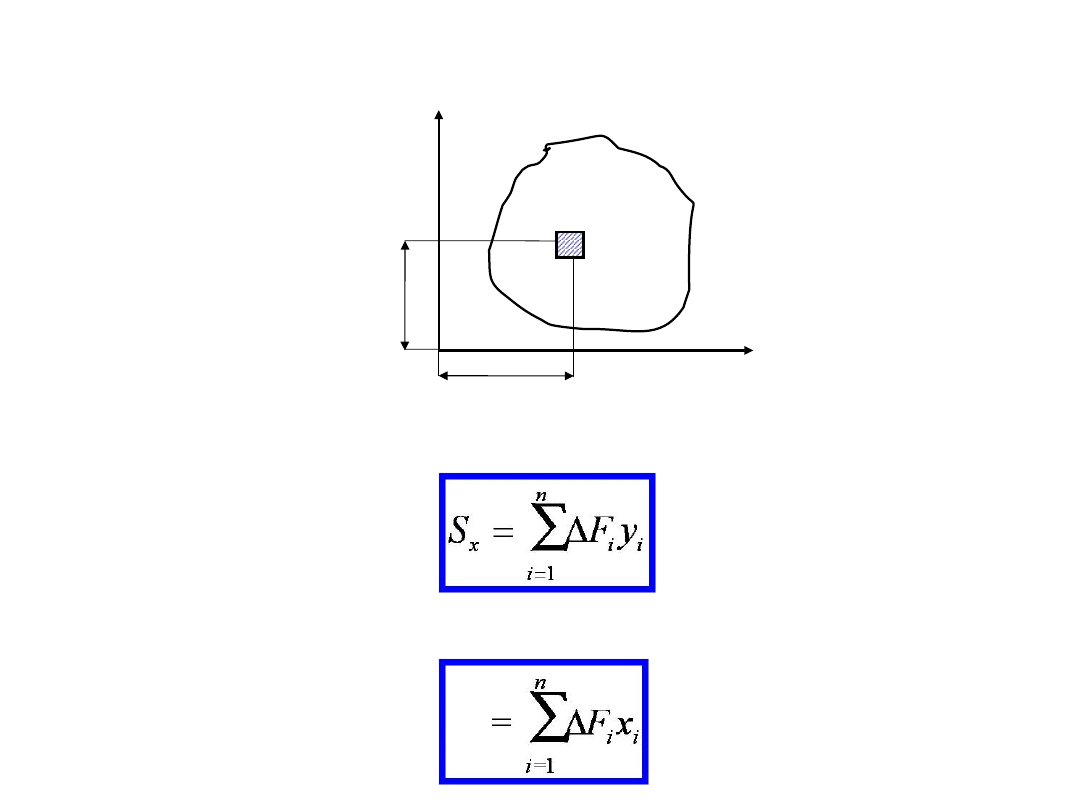
4. MOMENT STATYCZNY 

4. MOMENT STATYCZNY 

PRZEKROJU

PRZEKROJU

ΔF

i

x

x

y

y

y

y

i

i

0

0

x

x

i

i

Moment statyczny przekroju względem osi x:

[mm

3

]

Moment statyczny przekroju względem osi y:

[mm

3

]

S

y

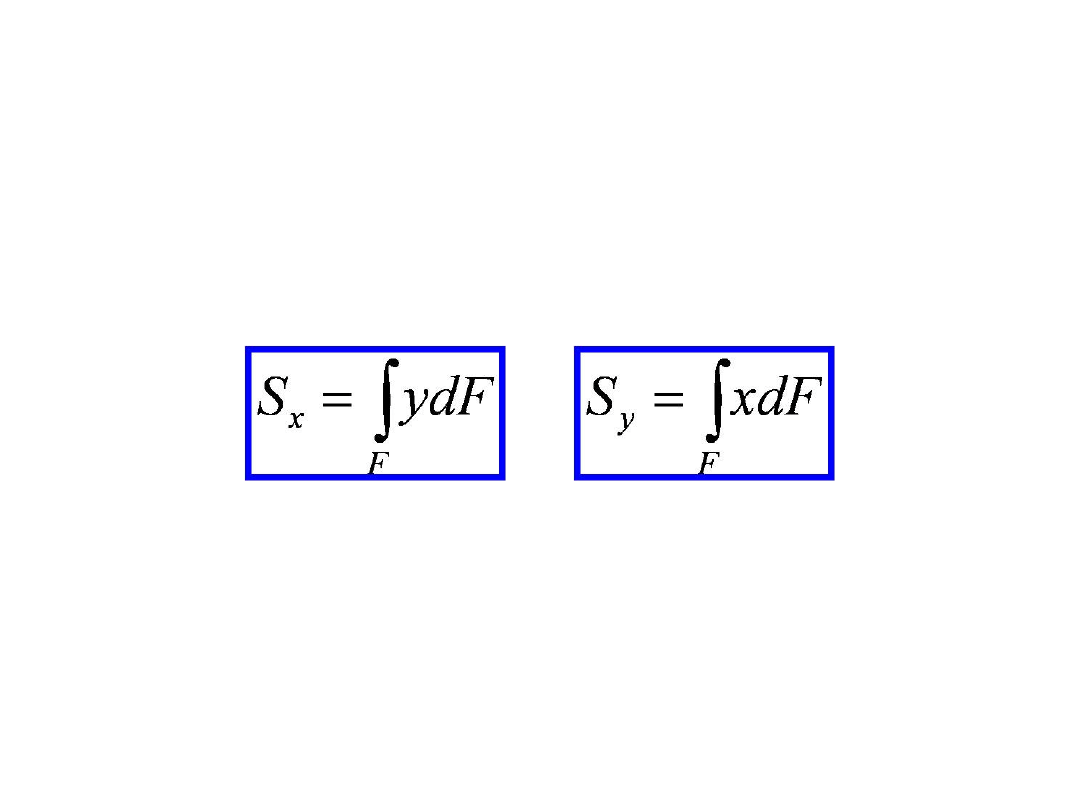
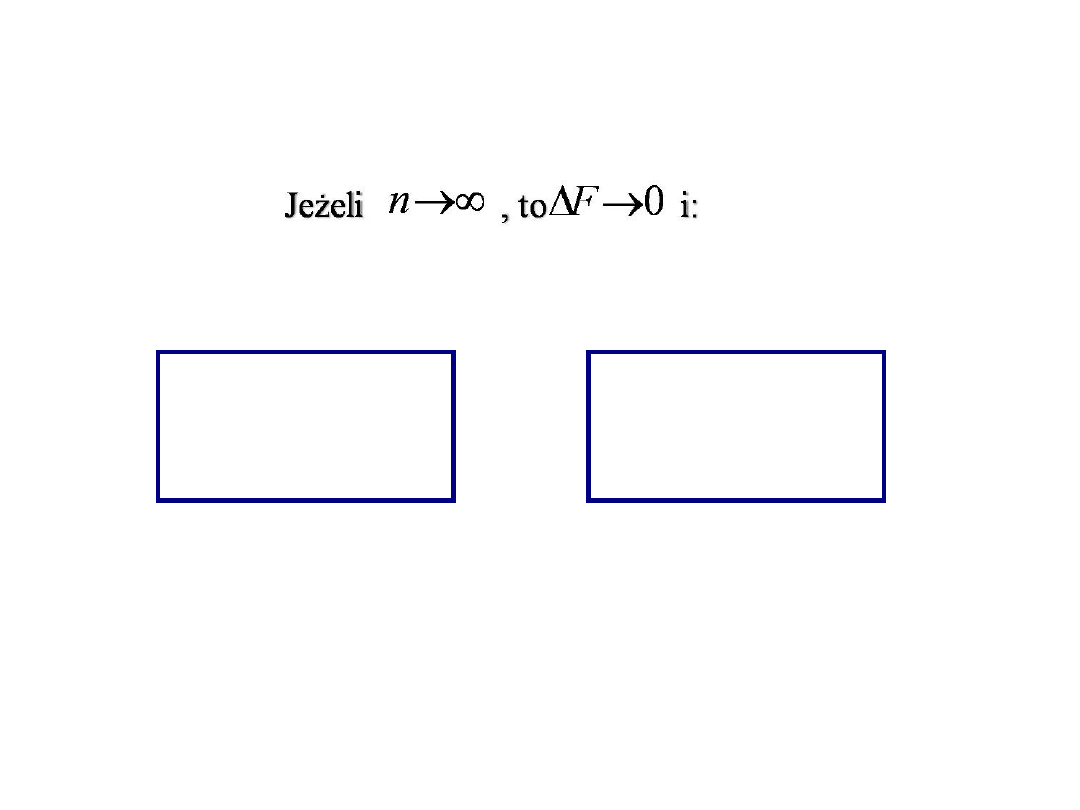
Jeżeli n → ∞,  to   ΔF

i

 → 

0

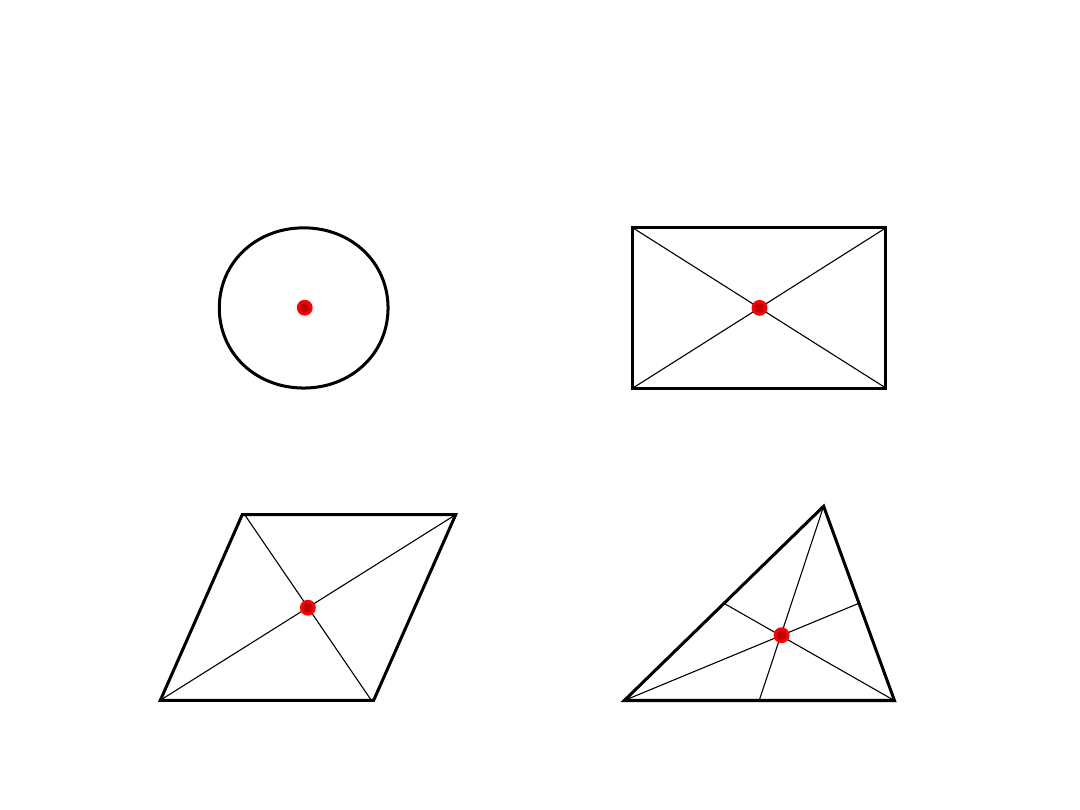
5. ŚRODEK CIĘŻKOŚCI 

5. ŚRODEK CIĘŻKOŚCI 

PRZEKROJU 

PRZEKROJU 

koło

prostokąt

równoległobok

trójkąt

C

C

C

C

C

C

C

C

- przekrój prosty

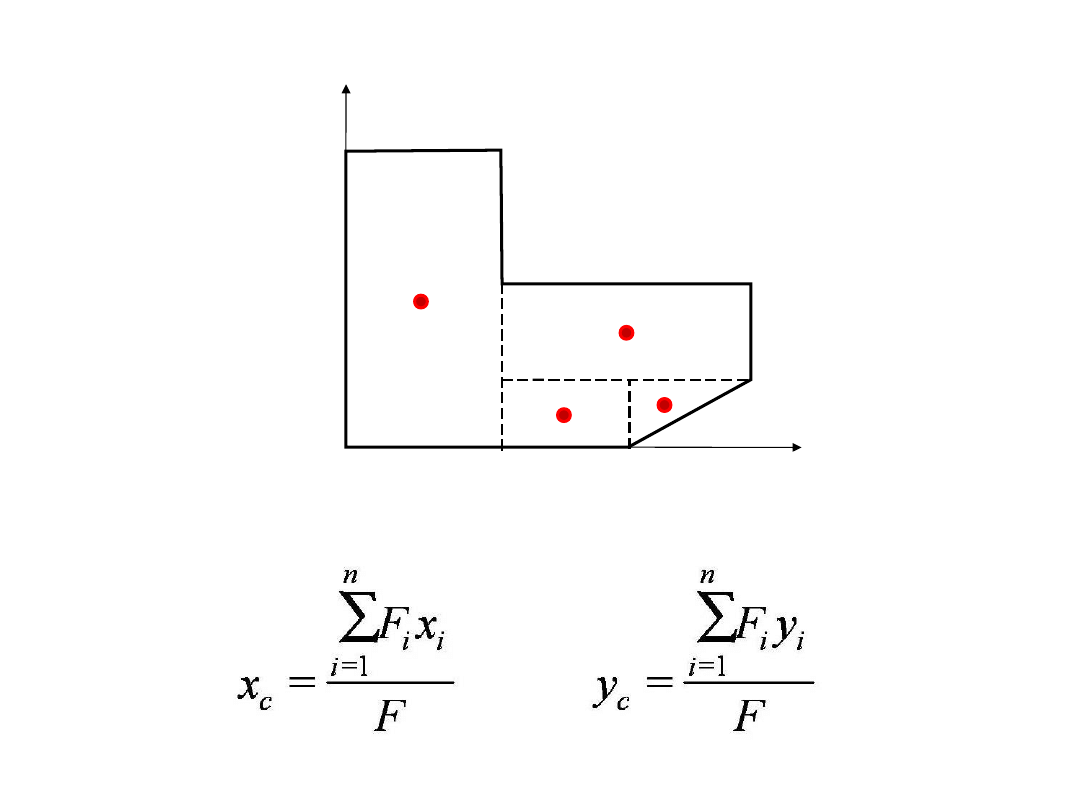
- przekrój złożony

F

1

, C

1 

(x

1

,y

1

);

F

2

, C

2 

(x

2

,y

2

);

F

3

, C

3 

(x

3

,y

3

);

F

4

, C

4 

(x

4

,y

4

).

C

C

1

1

C

C

2

2

C

C

3

3

C

C

4

4

0

x

y

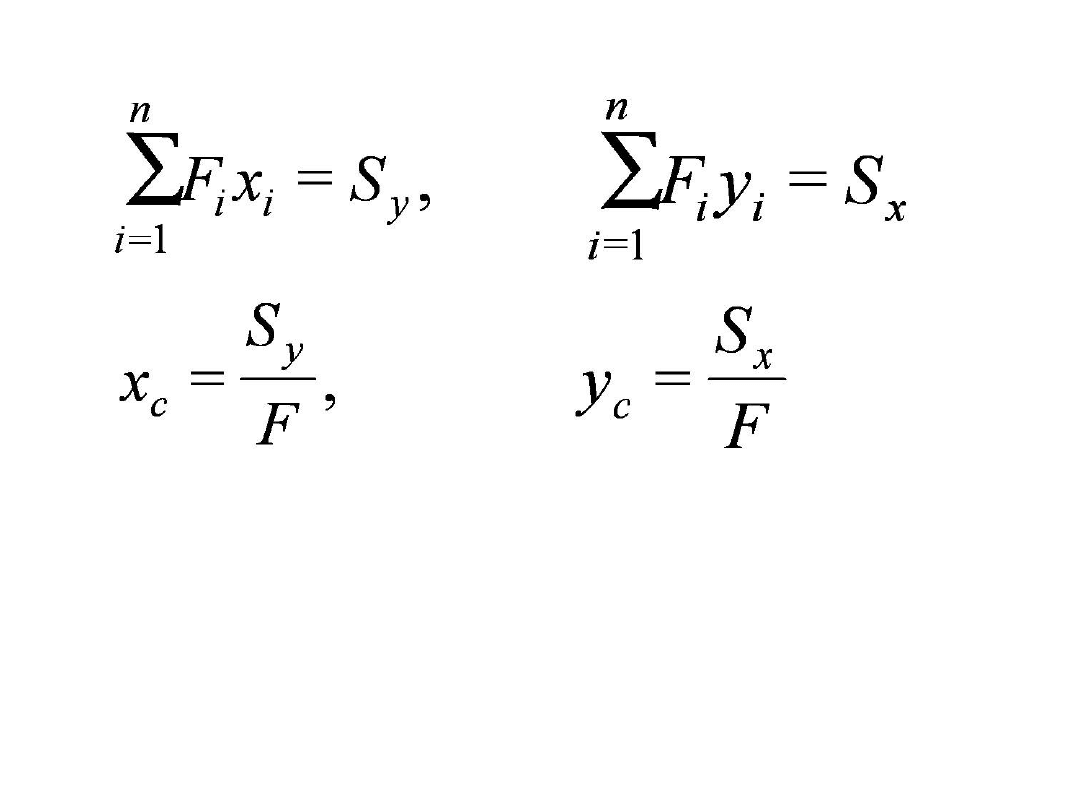
Jeżeli oś x jest osią centralną, to y

c

 = 0 i 

S

x

 = 0

Moment statyczny przekroju względem osi centralnej
 jest równy zeru.

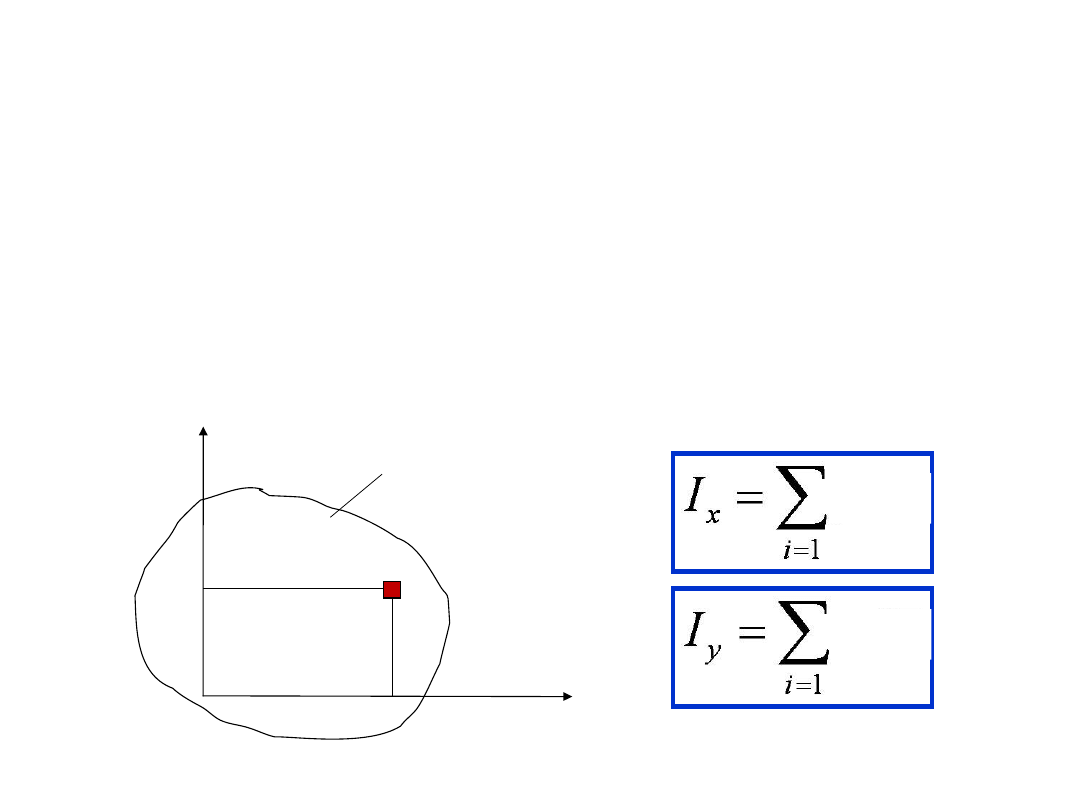
6. MOMENT BEZWŁADNOŚCI PRZEKROJU 

6. MOMENT BEZWŁADNOŚCI PRZEKROJU 

WZGLĘDEM OSI

WZGLĘDEM OSI

( OSIOWY MOMENT BEZWŁADNOŚCI )

( OSIOWY MOMENT BEZWŁADNOŚCI )

 

 

Osiowym momentem bezwładności

Osiowym momentem bezwładności

 przekroju o 

 przekroju o 

powierzchni 

powierzchni 

F

F

 względem dowolnej osi leżącej w 

 względem dowolnej osi leżącej w 

płaszczyźnie przekroju nazywamy sumę iloczynów 

płaszczyźnie przekroju nazywamy sumę iloczynów 

pól elementarnych powierzchni 

pól elementarnych powierzchni 





F

F

 przekroju i 

 przekroju i 

kwadratów ich odległości od osi.

kwadratów ich odległości od osi.

   

   

 

 

x

x

x

x

y

y





F

F

0

0

y

y

F

F

y

y

2

2





F

F

x

x

2

2





F

F





F

y

dF

x

I

2





F

x

dF

y

I

2

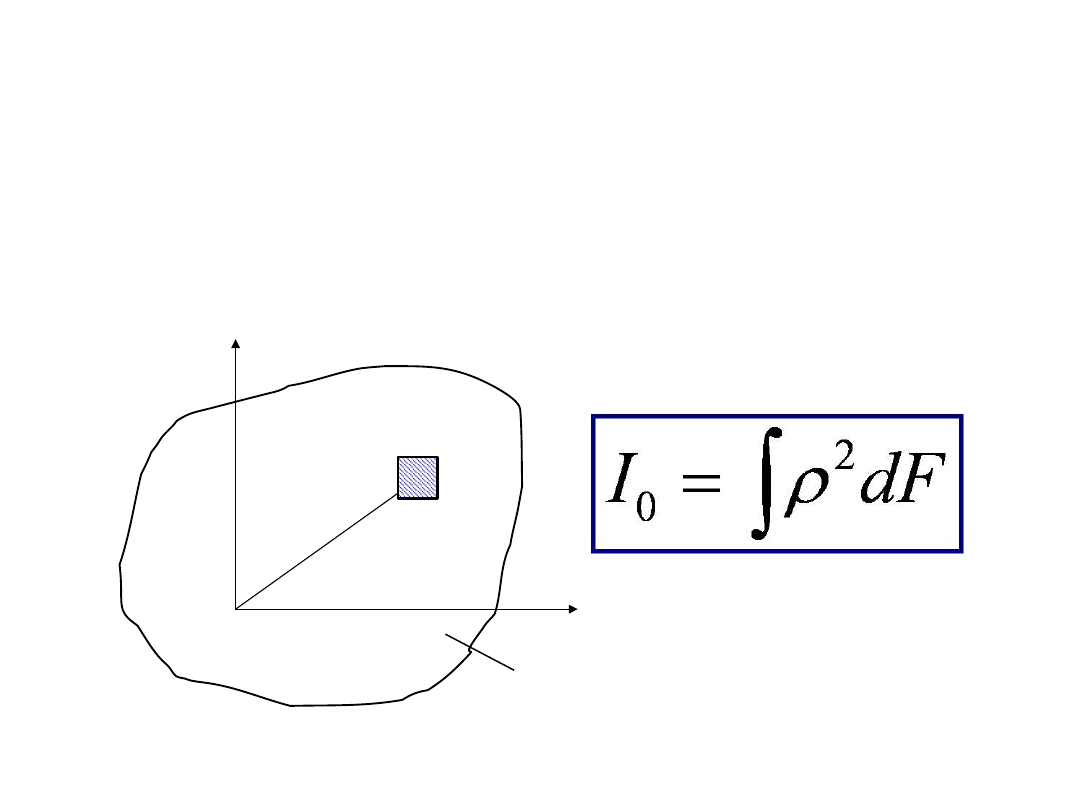
dF

x

y

0

F

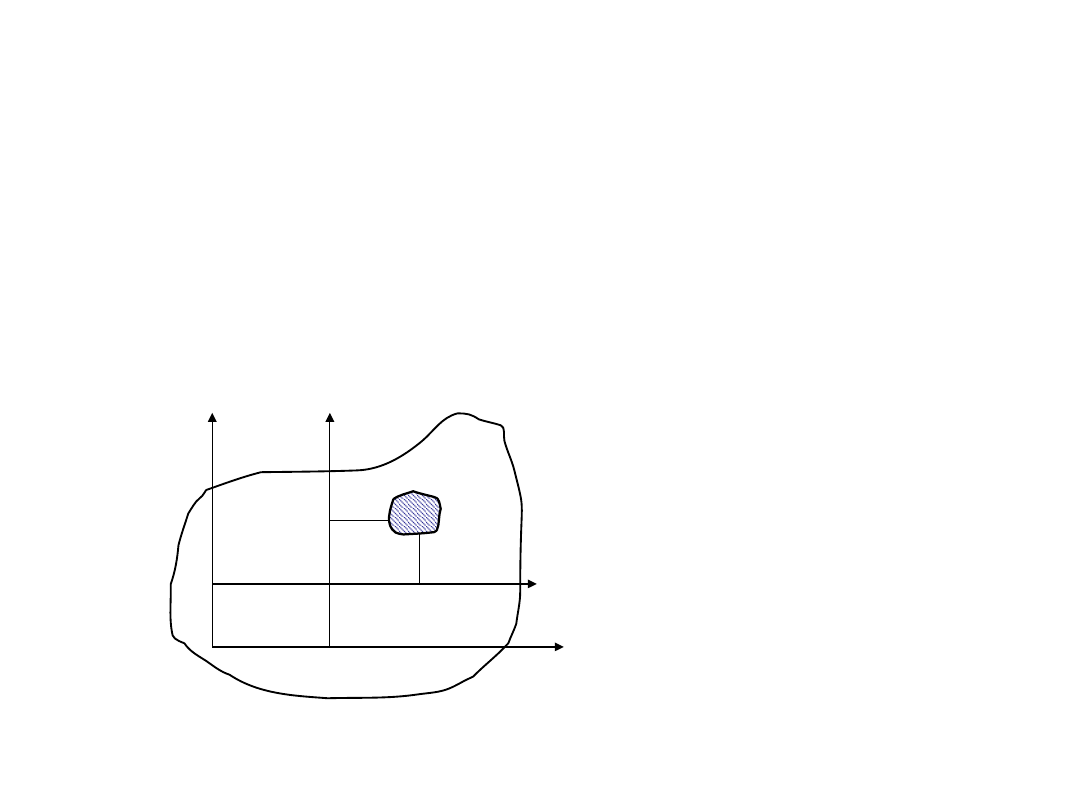
Biegunowym momentem bezwładności przekroju 

Biegunowym momentem bezwładności przekroju 

o 

o 

powierzchni 

powierzchni 

F

F

 względem dowolnego punktu 0 (bieguna) 

 względem dowolnego punktu 0 (bieguna) 

leżącego w płaszczyźnie figury nazywamy sumę iloczynów 

leżącego w płaszczyźnie figury nazywamy sumę iloczynów 

elementarnych powierzchni

elementarnych powierzchni

 dF

 dF

 figury i kwadratów ich 

 figury i kwadratów ich 

odległości od bieguna , czyli:

odległości od bieguna , czyli:



7. BIEGUNOWY MOMENT 

BEZWŁADNOŚCI 

PRZEKROJU

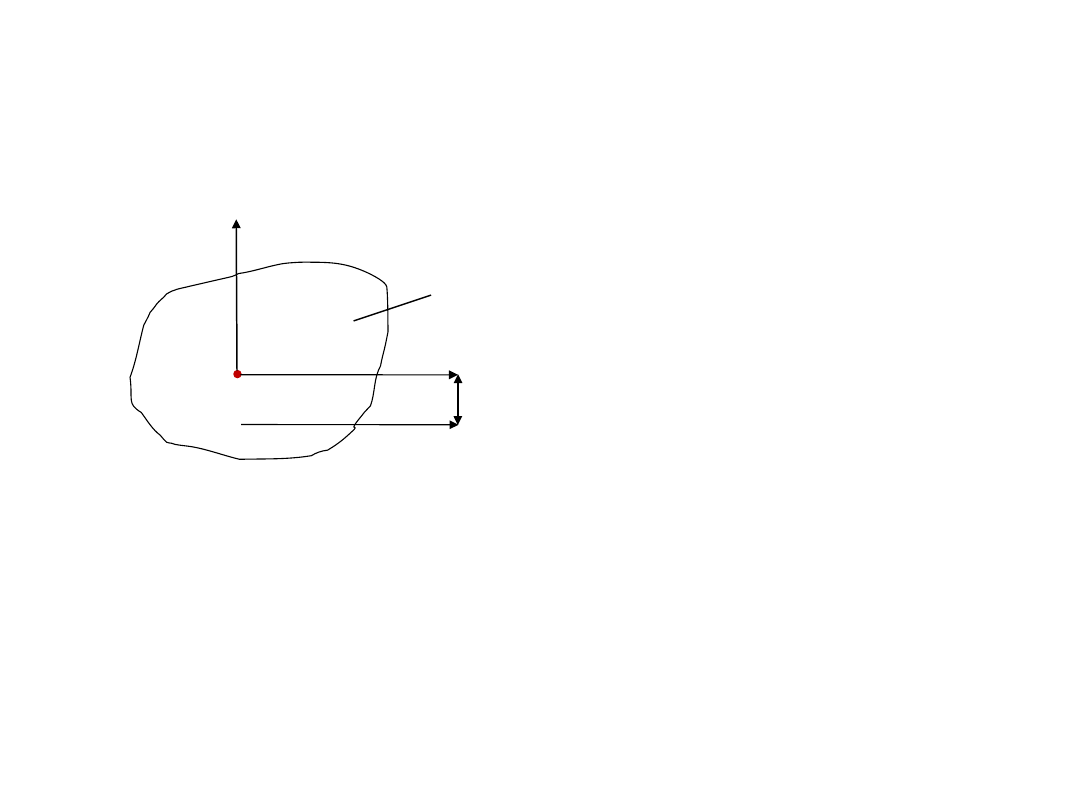
Odśrodkowym momentem bezwładności

Odśrodkowym momentem bezwładności

 

 

figury płaskiej o powierzchni 

figury płaskiej o powierzchni 

F

F

 względem 

 względem 

układu osi prostokątnych leżących w 

układu osi prostokątnych leżących w 

płaszczyźnie figury nazywamy sumę 

płaszczyźnie figury nazywamy sumę 

iloczynów elementarnych powierzchni 

iloczynów elementarnych powierzchni 

dF

dF

 

 

figury i ich odległości od tych osi.

figury i ich odległości od tych osi.

                       

                       

x

x

x

x

1

1

y

y

2

2

d

d

F

F

x

x

1

1

y

y

1

1

y

y

a

a

b

b

0

0

1

1

0

0

F

F





f

xy

xydF

I

F

8. MOMENT BEZWŁADNOŚCI 

8. MOMENT BEZWŁADNOŚCI 

WZGLĘDEM OSI RÓWNOLEGŁYCH 

WZGLĘDEM OSI RÓWNOLEGŁYCH 

(TW. STEINERA)

(TW. STEINERA)

Moment bezwładności przekroju względem osi x

Moment bezwładności przekroju względem osi x

1

1

 jest 

 jest 

równy sumie momentu bezwładności względem osi 

równy sumie momentu bezwładności względem osi 

centralnej x równoległej do x

centralnej x równoległej do x

1

1

 oraz iloczynu pola 

 oraz iloczynu pola 

przekroju i kwadratu odległości miedzi tymi osiami.

przekroju i kwadratu odległości miedzi tymi osiami.

C

y

F

x

x

x

1

1

x , y- osie centralne

x , y- osie centralne

x

x

1 

1 

|| x

|| x

b

b

I

x1

=I

x

+b

2

F

Momenty bezwładności 

Momenty bezwładności 

przekrojów złożonych

przekrojów złożonych

Elementy stosowane w konstrukcjach bardzo często mają 

Elementy stosowane w konstrukcjach bardzo często mają 

przekroje o dowolnie złożonym kształcie, dla których nie 

przekroje o dowolnie złożonym kształcie, dla których nie 

można wyznaczyć momentów bezwładności w prosty 

można wyznaczyć momentów bezwładności w prosty 

sposób. Najczęściej stosowane w praktyce formy 

sposób. Najczęściej stosowane w praktyce formy 

przekrojów złożonych mają kształt teowników, kątowników, 

przekrojów złożonych mają kształt teowników, kątowników, 

ceowników, trapezów, itp. Takie przekroje można zawsze 

ceowników, trapezów, itp. Takie przekroje można zawsze 

podzielić na przekroje prostsze, a mianowicie: prostokąty, 

podzielić na przekroje prostsze, a mianowicie: prostokąty, 

trójkąty, koła, itd.,i można wykazać, że 

trójkąty, koła, itd.,i można wykazać, że 

bezwładności 

bezwładności 

przekroju złożonego

przekroju złożonego

 jest sumą momentów

 jest sumą momentów

bezwładności jego składowych przekrojów prostych.

bezwładności jego składowych przekrojów prostych.

n

Ix

Ix

Ix

Ix









...

2

1

Z podanych wiadomości 

Z podanych wiadomości 

wynikają następujące ważne 

wynikają następujące ważne 

wnioski:

wnioski:

 

 

- każda figura ma nieskończenie dużo 

- każda figura ma nieskończenie dużo 

osiowych i biegunowych momentów 

osiowych i biegunowych momentów 

bezwładności,

bezwładności,

- mówiąc o momencie bezwładności figury 

- mówiąc o momencie bezwładności figury 

trzeba zawsze dodać względem jakiej osi czy 

trzeba zawsze dodać względem jakiej osi czy 

jakiego bieguna jest ten moment obliczony, 

jakiego bieguna jest ten moment obliczony, 

- 

- 

im dalej od środka ciężkości znajduje się oś 

im dalej od środka ciężkości znajduje się oś 

(biegun) momentu, tym większy jest moment 

(biegun) momentu, tym większy jest moment 

bezwładności,

bezwładności,

- moment biegunowy jest najmniejszy, jeśli za 

- moment biegunowy jest najmniejszy, jeśli za 

biegun obieramy środek ciężkości figury

biegun obieramy środek ciężkości figury