
2. Charakterystyki geometryczne przekroju pręta
1
Dr inż. Justyna Grzymisławska
Wytrzymałość materiałów
Dr inż. Justyna Grzymisławska
Temat 2
Charakterystyki geometryczne przekroju
pręta
Poznań
2. Charakterystyki geometryczne przekroju pręta
2
Dr inż. Justyna Grzymisławska
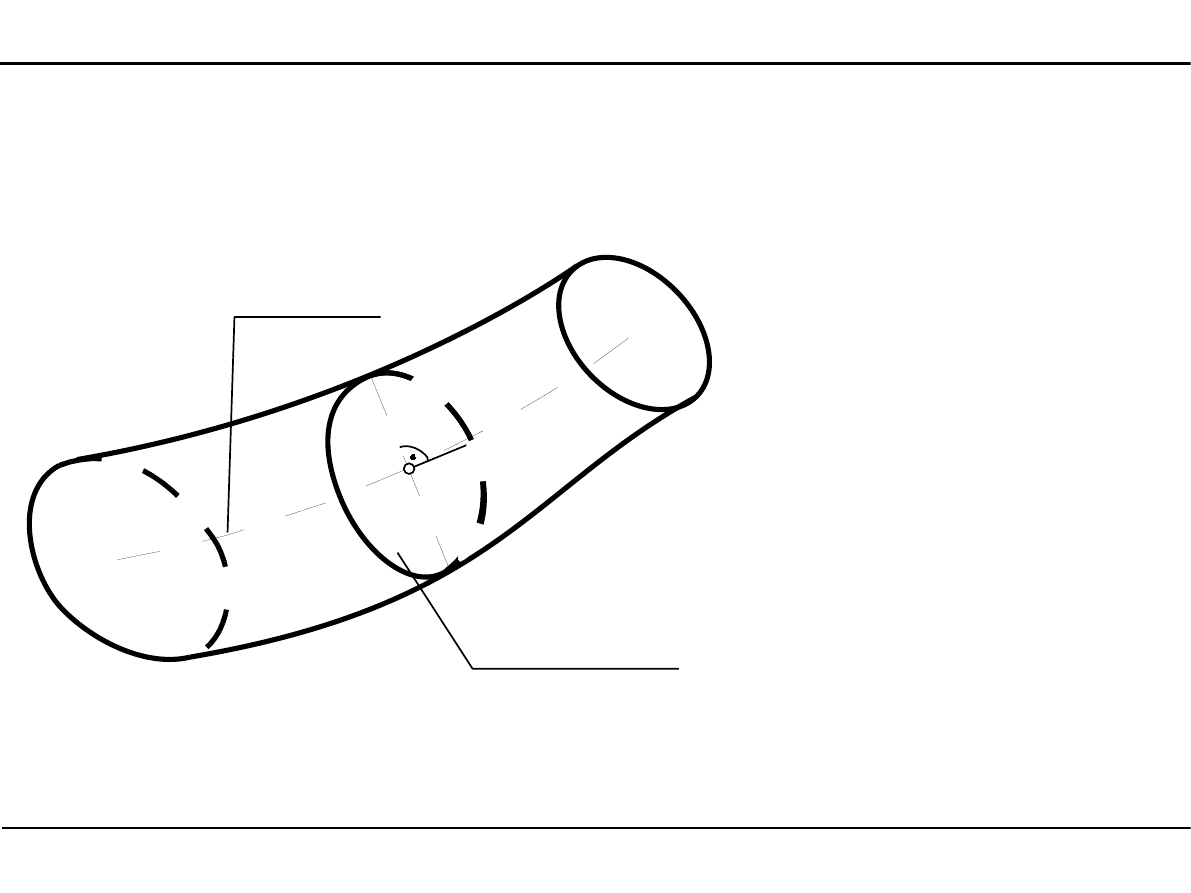
Pręt jest to bryła geometryczna
wypełniona materiałem,
której jeden wymiar,czyli
długość, jest dużo
większa niż dwa pozostałe.
przekrój pręta
A
B
oś pręta
sc
Definicja pręta
Nie ma przy tym znaczenia
jakim materiałem (betonem,
stalą czy drewnem) jest on
wypełniony.
2.1. Pręt
2. Charakterystyki geometryczne przekroju pręta
3
Dr inż. Justyna Grzymisławska
A
B
Z=Z
0
Y=Y
0
X
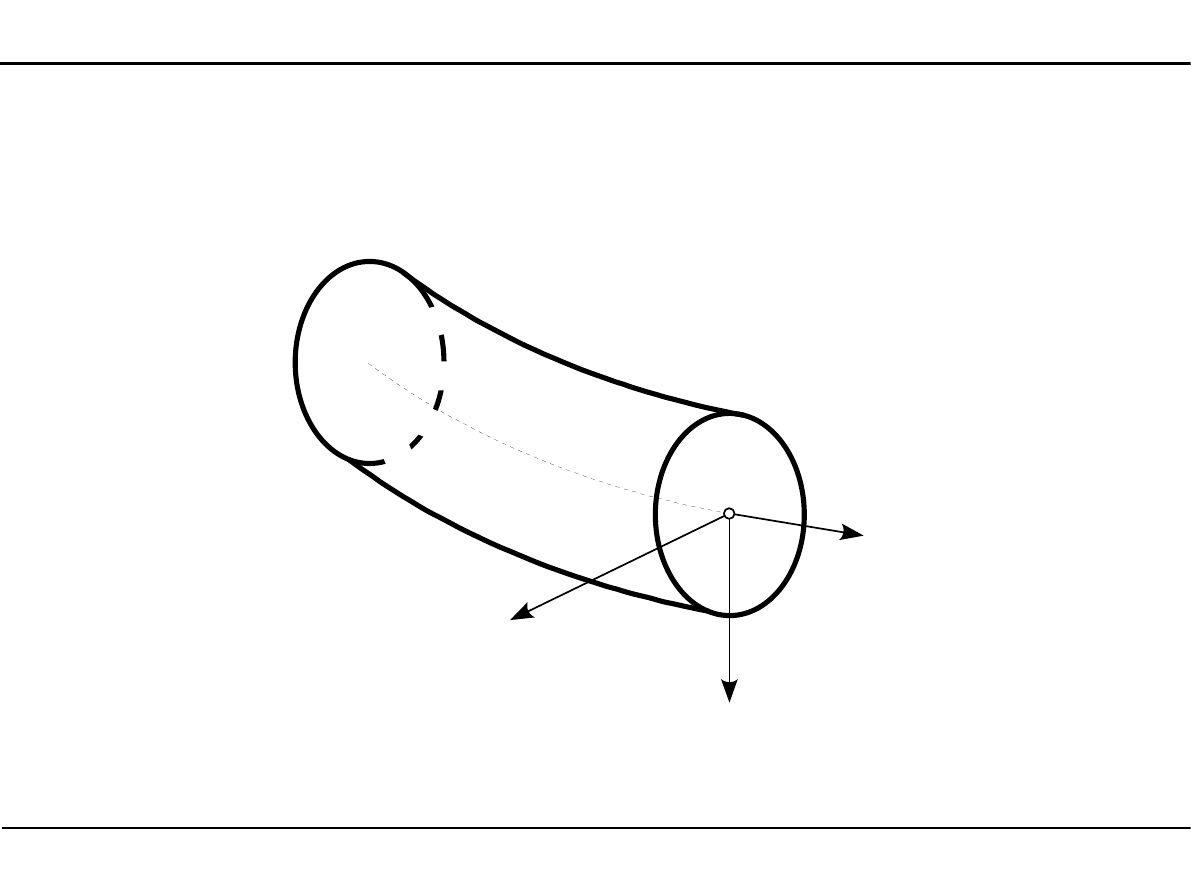
2.1. Pręt
Układ współrzędnych związany z przekrojem pręta
sc
2. Charakterystyki geometryczne przekroju pręta
4
Dr inż. Justyna Grzymisławska
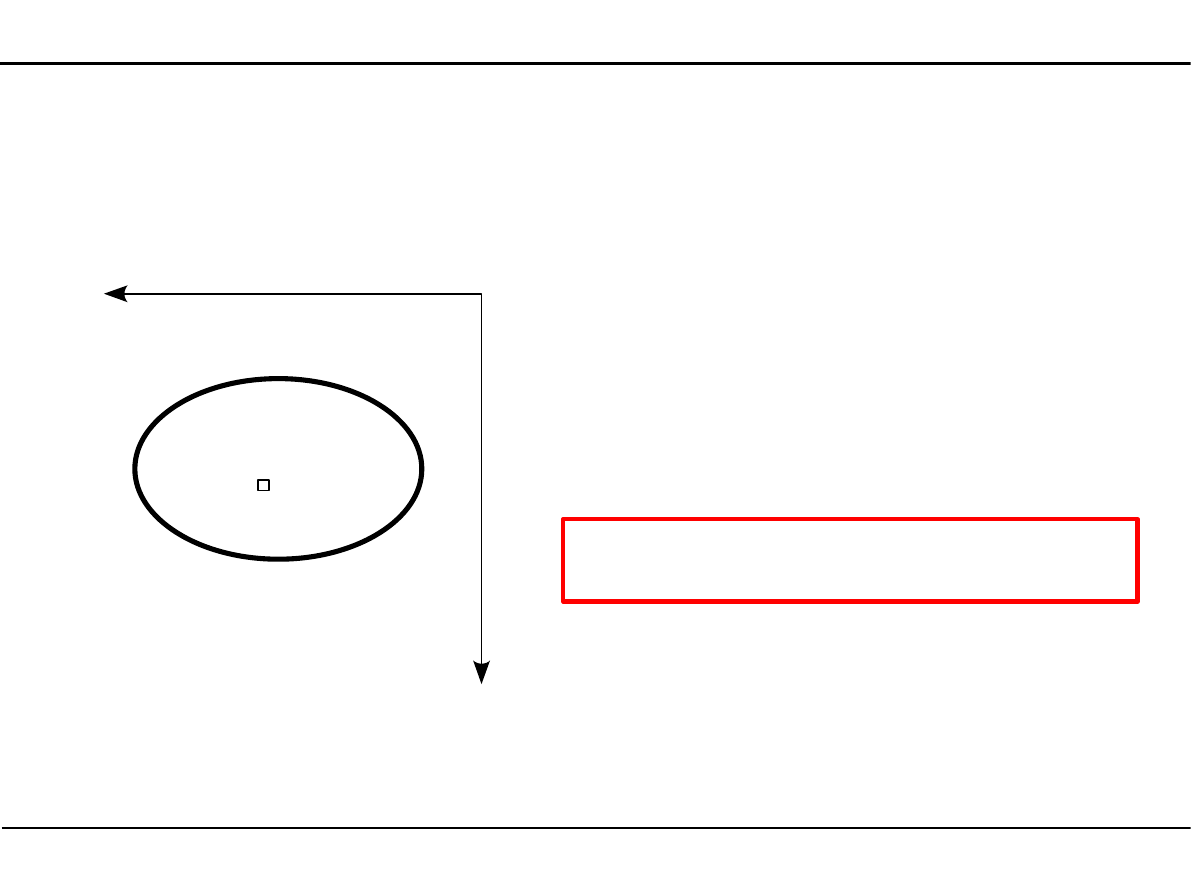
2.2. Definicje charakterystyk geometrycznych przekroju pręta
Pole powierzchni przekroju pręta
Z
Y
dA
A=
∫
A
dA
Jednostką pola powierzchni jest [m
2
].
W naszym kursie najczęściej
będziemy używać [cm
2
].
Pole powierzchni jest zawsze większe od
zera.
2. Charakterystyki geometryczne przekroju pręta
5
Dr inż. Justyna Grzymisławska
2.2. Definicje charakterystyk geometrycznych przekroju pręta
dA
Z
Y
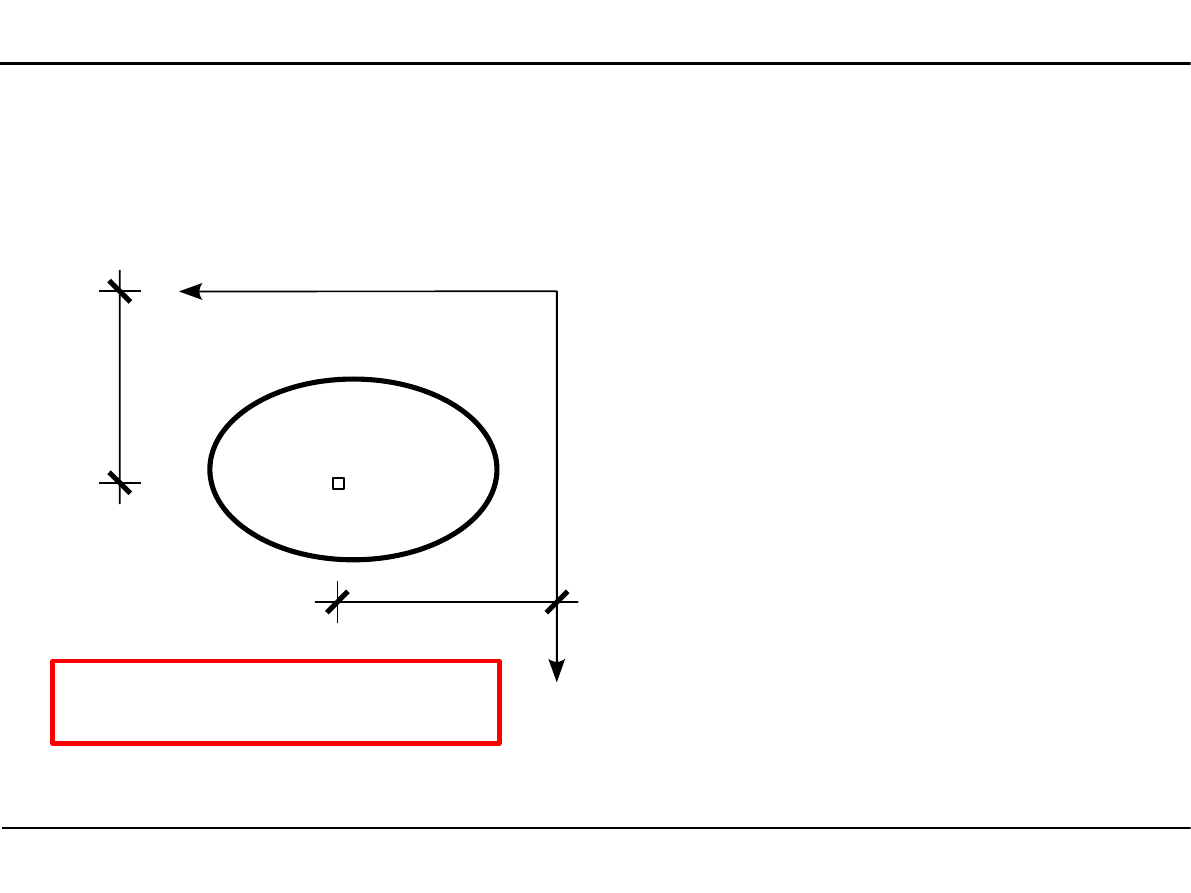
Moment statyczny względem osi Y
S
Y
=
∫
A
z⋅dA
Moment statyczny względem osi Z
S
Z
=
∫
A
y⋅dA
Jednostką momentu statycznego jest [m
3
].
W naszym kursie najczęściej będziemy
używać [cm
3
].
Momenty statyczne przekroju pręta
y
z
2. Charakterystyki geometryczne przekroju pręta
6
Dr inż. Justyna Grzymisławska
dA
Z
Y
y
z
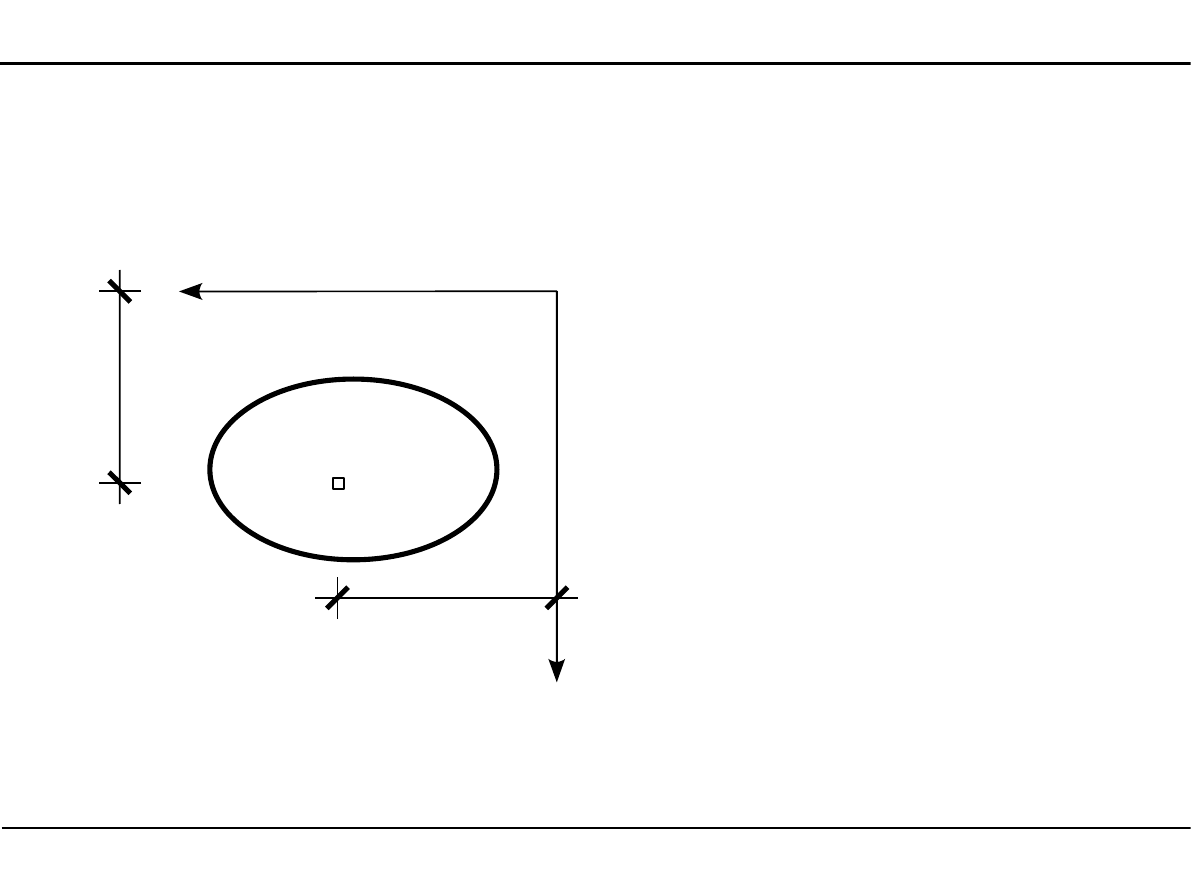
2.2. Definicje charakterystyk geometrycznych przekroju pręta
J
Y
=
∫
A
z
2
⋅
dA
J
Z
=
∫
A
y
2
⋅
dA
Jednostką osiowego momentu
bezwładności jest [m
4
].
W naszym kursie najczęściej
będziemy używać [cm
4
].
Osiowe momenty bezwładności
Osiowe momenty bezwładności
są zawsze większe od zera.
Moment bezwładności względem osi Y
Moment bezwładności względem osi Z
2. Charakterystyki geometryczne przekroju pręta
7
Dr inż. Justyna Grzymisławska
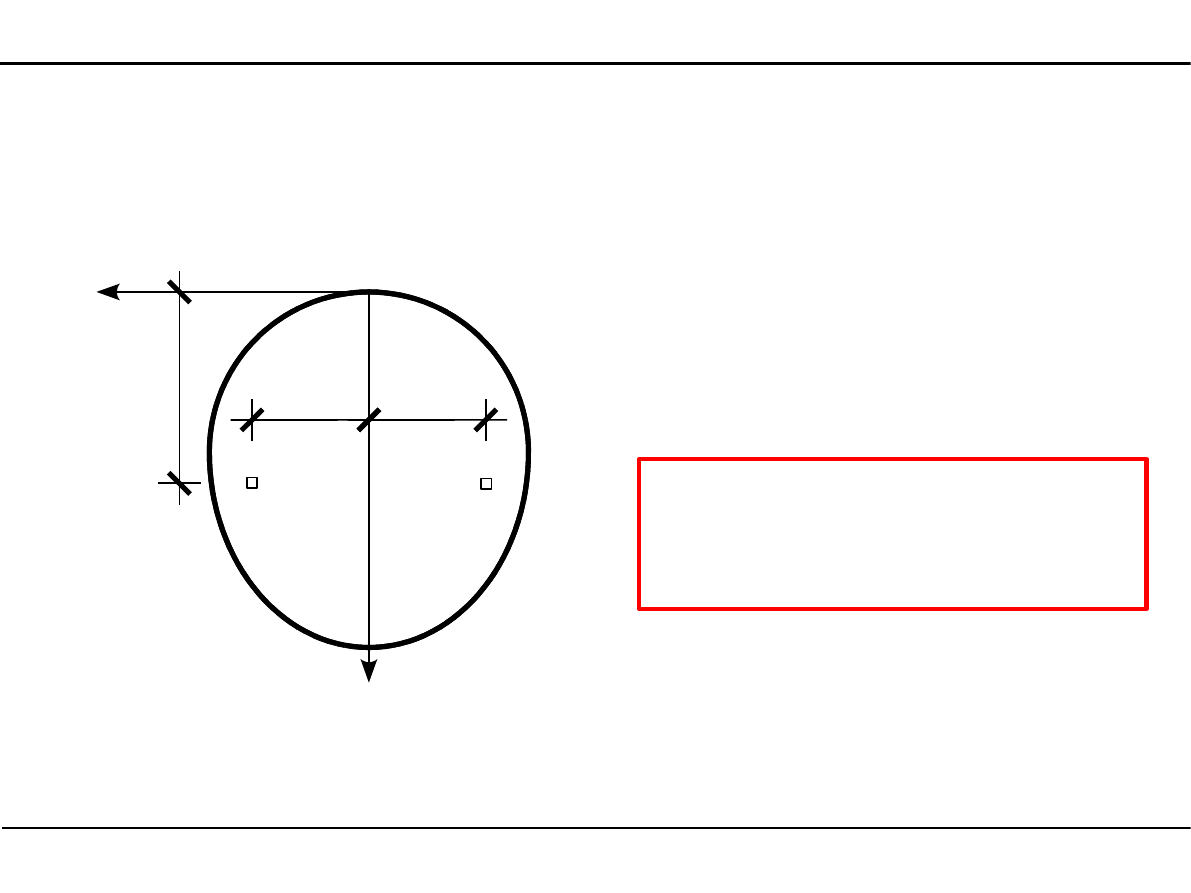
2.2. Definicje charakterystyk geometrycznych przekroju pręta
dA
Z
Y
J
YZ
=
∫
A
y⋅z⋅dA
Jednostką dewiacyjnego momentu
bezwładności jest [m
4
].
W naszym kursie najczęściej
będziemy używać [cm
4
].
Dewiacyjny moment bezwładności
y
z
2. Charakterystyki geometryczne przekroju pręta
8
Dr inż. Justyna Grzymisławska
2.2. Definicje charakterystyk geometrycznych przekroju pręta
Dewiacyjny moment bezwładności
Dewiacyjny moment bezwładności
przekroju symetrycznego.
Z
Y
dA
dA
J
YZ
=
0
Dewiacyjny moment bezwładności
przekroju w układzie, w którym choć
jedna z osi jest osią symetrii
przekroju, wynosi zero.
z
y
-y

2. Charakterystyki geometryczne przekroju pręta
9
Dr inż. Justyna Grzymisławska
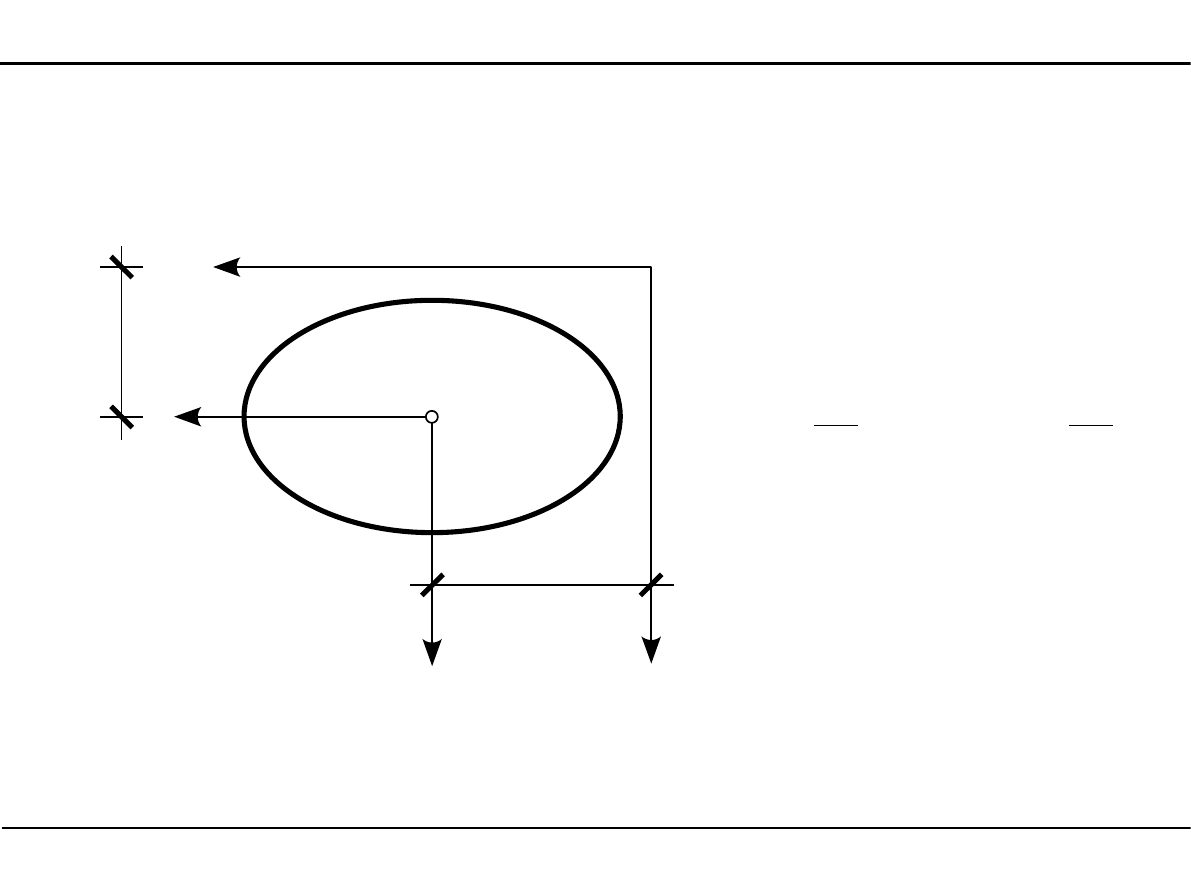
2.3. Środek ciężkości przekroju
Definicja środka ciężkości przekroju
Osią środkową nazywamy taką oś, względem której moment statyczny
wynosi zero.
Środkiem ciężkości nazywamy punkt przecięcia się dwóch osi środkowych.
2. Charakterystyki geometryczne przekroju pręta
10
Dr inż. Justyna Grzymisławska
Y
0
Z
0
2.3. Środek ciężkości przekroju
Wyznaczanie położenia środka ciężkości
sc
Z
P
Y
P
Y
P
Z
P
- początkowy układ
współrzędnych.
y
C
=
S
ZP
A
z
C
=
S
YP
A
Y
0
Z
0
- układ osi środkowych.
y
C
z
C

2. Charakterystyki geometryczne przekroju pręta
11
Dr inż. Justyna Grzymisławska
2.3. Środek ciężkości przekroju
Wyznaczanie położenia środka ciężkości
Praktyczne wzory służące do wyznaczania położenia środka ciężkości.
y
C
=
S
ZP
A
=
∑
i=1
i=n
A
i
⋅
y
i
∑
i=1
i=n
A
i
z
C
=
S
YP
A
=
∑
i=1
i=n
A
i
⋅
z
i
∑
i=1
i=n
A
i
y
i
, z
i
- współrzędne środka ciężkości
i-tej figury w układzie Y
P
Z
P
.
A
i
- pole powierzchni i-tej figury.
2. Charakterystyki geometryczne przekroju pręta
12
Dr inż. Justyna Grzymisławska
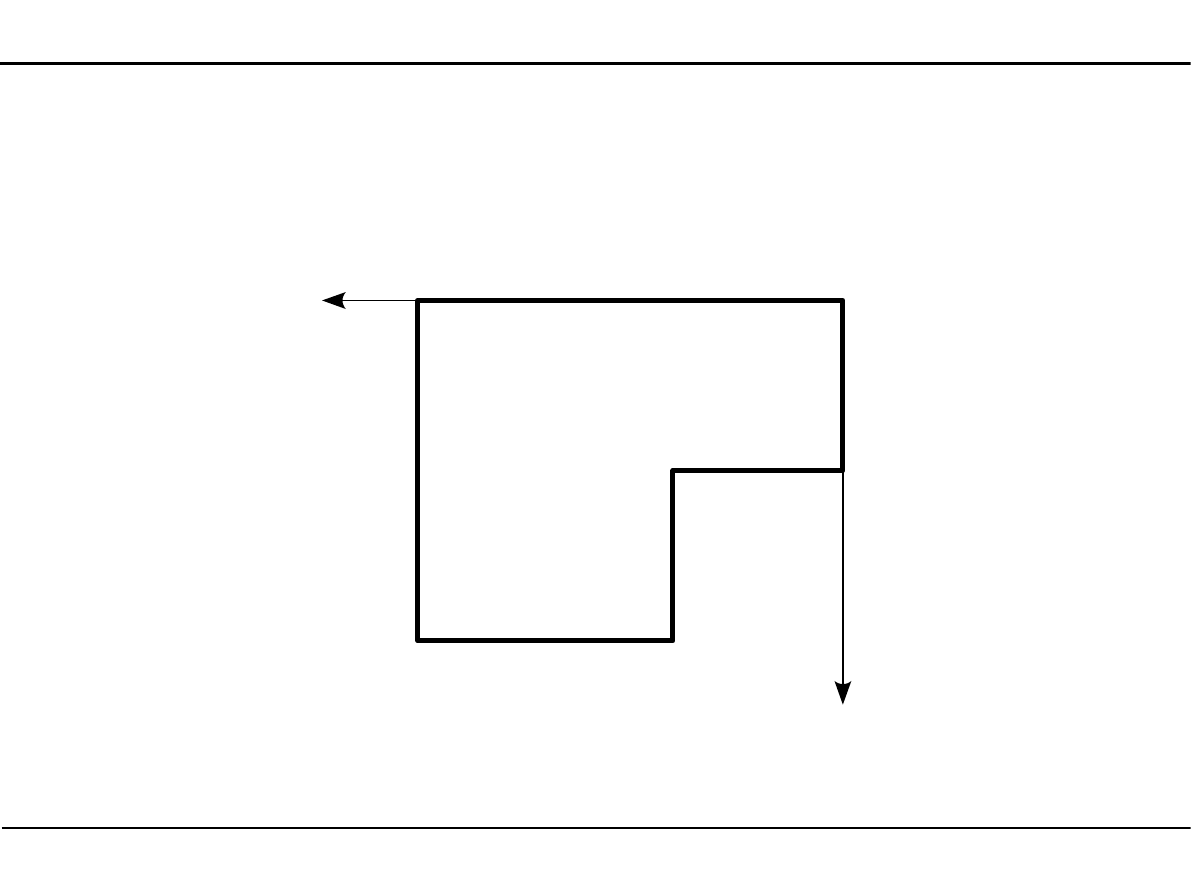
2.3. Środek ciężkości przekroju
Wyznaczanie położenia środka ciężkości
Z
P
Y
P
2. Charakterystyki geometryczne przekroju pręta
13
Dr inż. Justyna Grzymisławska
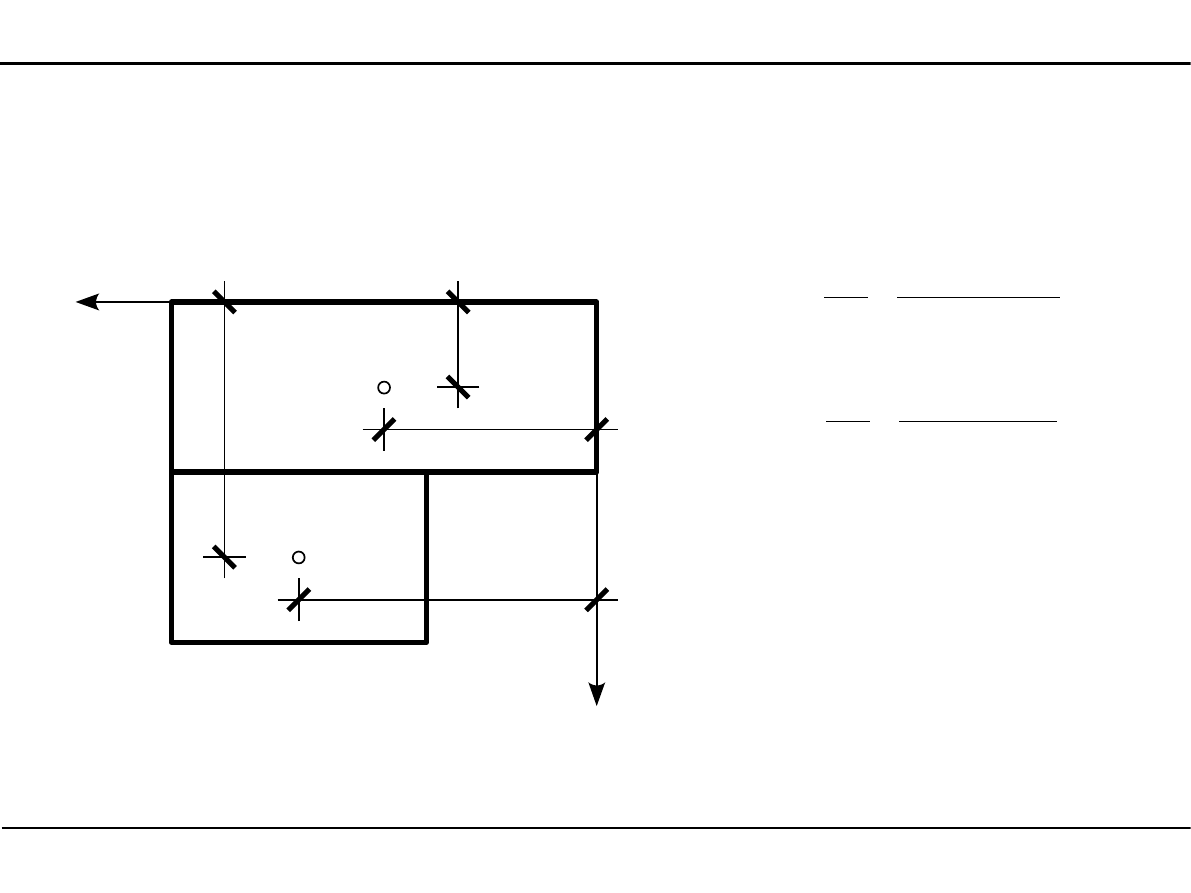
2.3. Środek ciężkości przekroju
Wyznaczanie położenia środka ciężkości
Z
P
Y
P
sc
1
sc
2
y
C
=
S
ZP
A
=
A
1
⋅
y
1
A
2
⋅
y
2
A
1
A
2
z
C
=
S
ZP
A
=
A
1
⋅
z
1
A
2
⋅
z
2
A
1
A
2
y
1
z
1
y
2
z
2
2. Charakterystyki geometryczne przekroju pręta
14
Dr inż. Justyna Grzymisławska
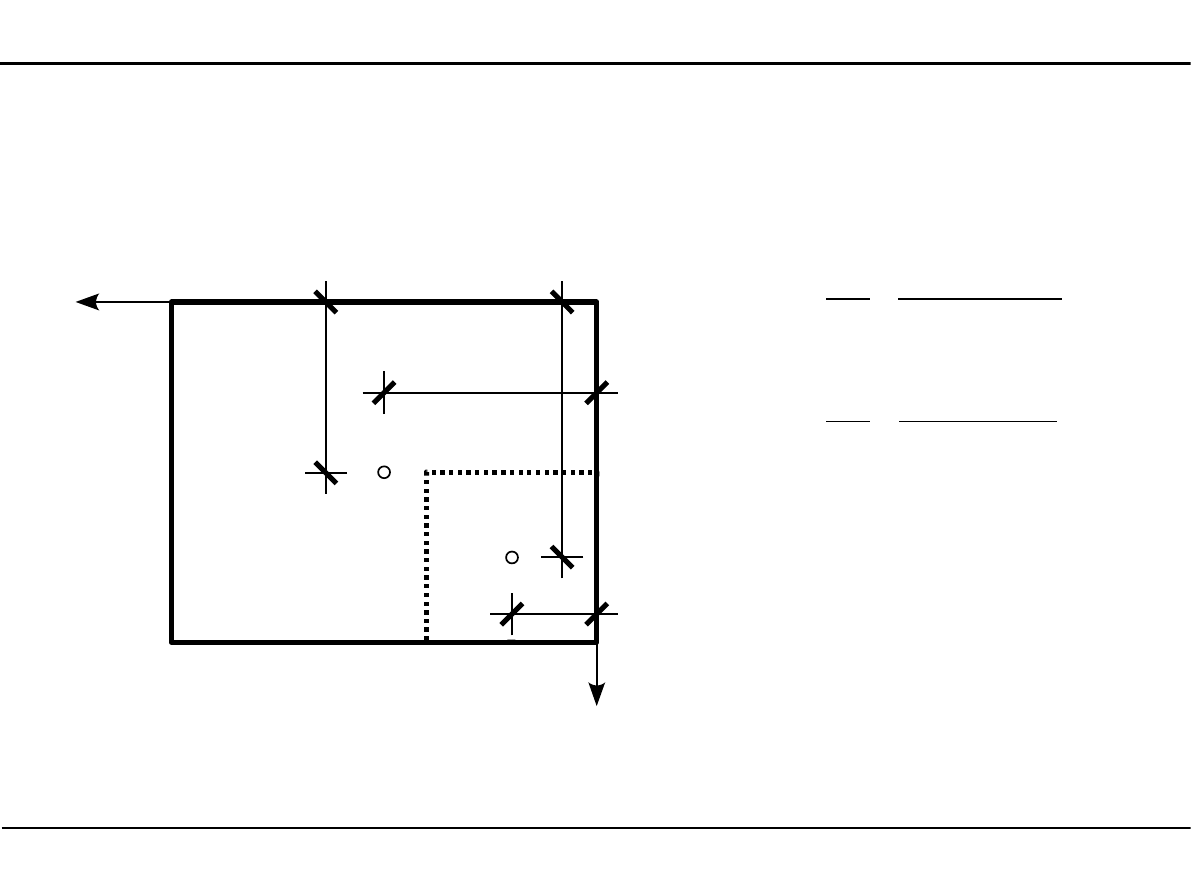
2.3. Środek ciężkości przekroju
Wyznaczanie położenia środka ciężkości
Z
P
Y
P
sc
1
sc
2
y
C
=
S
ZP
A
=
A
1
⋅
y
1
−
A
2
⋅
y
2
A
1
−
A
2
z
C
=
S
ZP
A
=
A
1
⋅
z
1
−
A
2
⋅
z
2
A
1
−
A
2
y
1
z
1
y
2
z
2

2. Charakterystyki geometryczne przekroju pręta
15
Dr inż. Justyna Grzymisławska
2.3. Środek ciężkości przekroju
Właściwości środka ciężkości
W przekroju z jedną osią symetrii środek ciężkości znajduje się na tej osi.
W przekroju z dwiema osiami symetrii środek ciężkości znajduje się w punkcie
przecięcia obu tych osi.
W przekroju z ponad dwoma osiami symetrii wszystkie te osie przecinają się
jednym punkcie, którym jest środek ciężkości.
Środek ciężkości może się znajdować w punkcie nie leżącym w przekroju.
2. Charakterystyki geometryczne przekroju pręta
16
Dr inż. Justyna Grzymisławska
2.3. Środek ciężkości przekroju
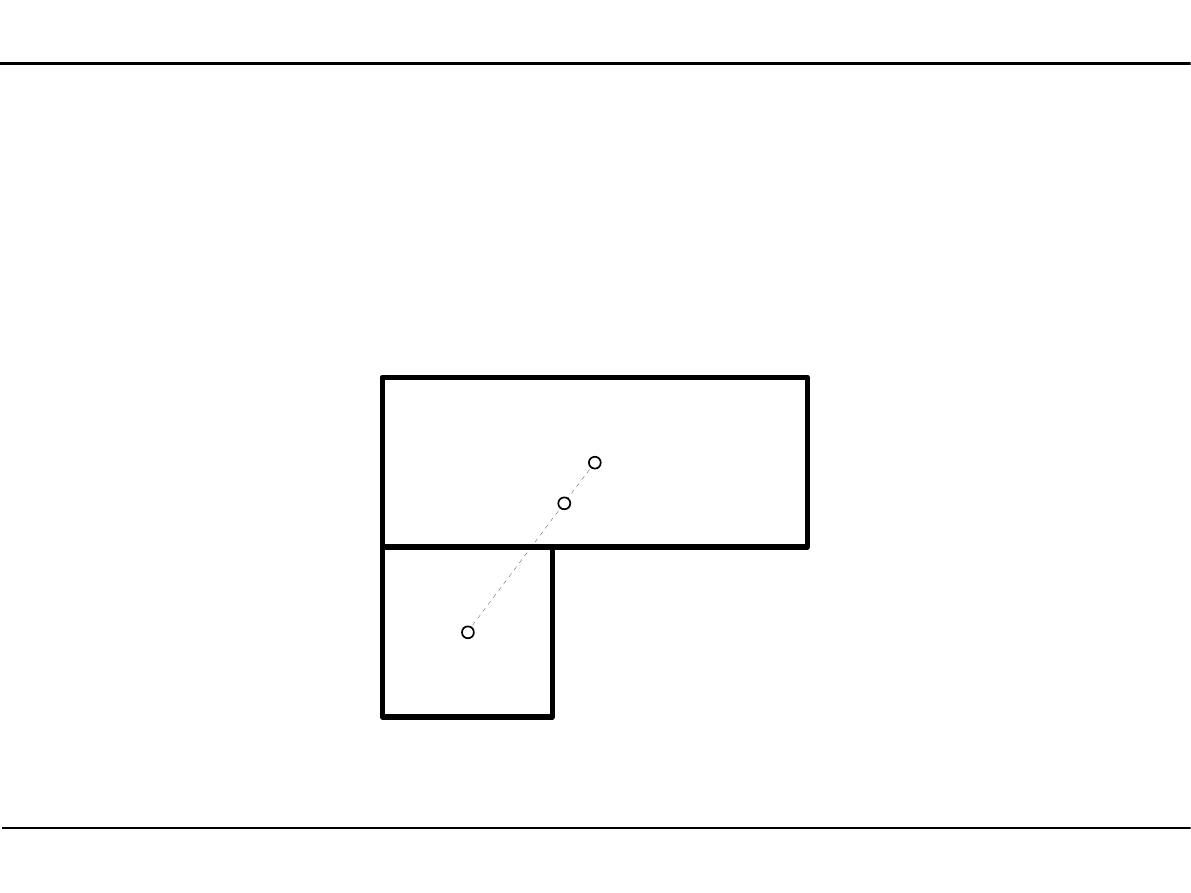
Właściwości środka ciężkości
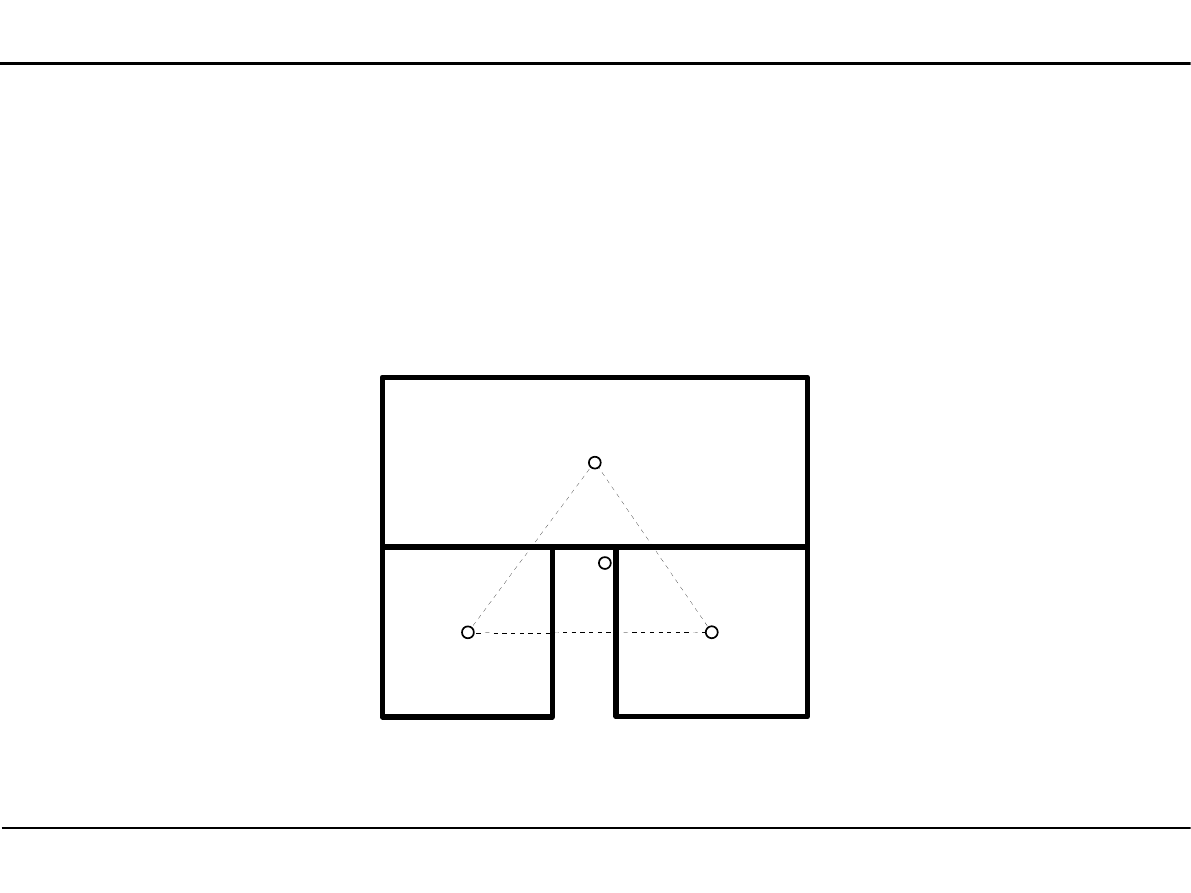
Jeżeli dodajemy do siebie dwie figury, to środek ciężkości znajduje się na odcinku
łączącym środki ciężkości obu figur bliżej figury o większym polu powierzchni.
sc
1
sc
2
sc
2. Charakterystyki geometryczne przekroju pręta
17
Dr inż. Justyna Grzymisławska
2.3. Środek ciężkości przekroju
Właściwości środka ciężkości
sc
1
sc
2
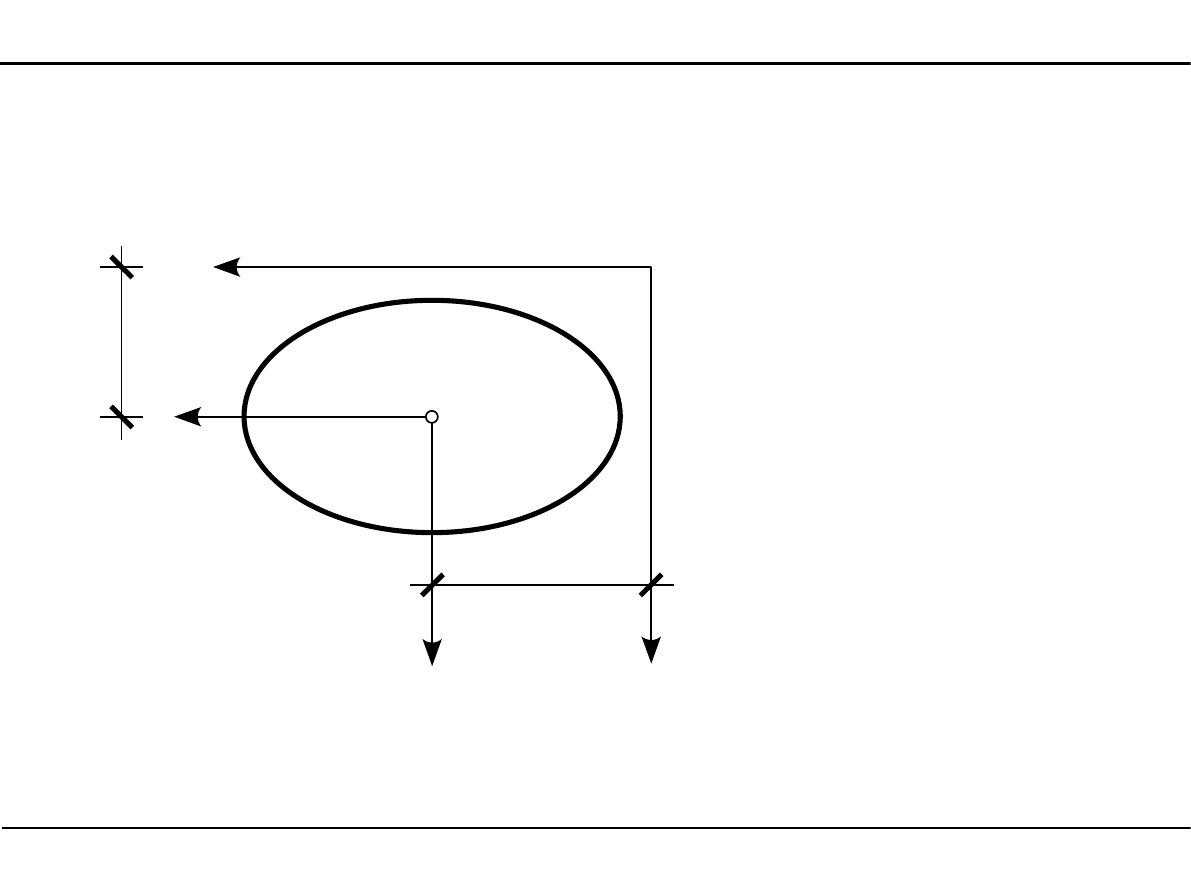
Jeżeli dodajemy do siebie trzy figury, to środek ciężkości znajduje się wewnątrz
trójkąta, którego wierzchołkami są środki ciężkości poszczególnych figur.
sc
3
sc
2. Charakterystyki geometryczne przekroju pręta
18
Dr inż. Justyna Grzymisławska
Y
0
Z
0
sc
2.4. Wyznaczanie momentów bezwładności przekroju
Twierdzenie Steinera
Dane są momenty bezwładności
w układzie osi środkowych
J
Y0
, J
Z0
oraz J
Y0Z0
Szukamy momentów bezwładności
w dowolnym układzie
współrzędnych J
Y
, J
Z
oraz J
YZ
Z
Y
J
Y
=
J
Y0
z
C
2
⋅
A
J
Z
=
J
Z0
y
C
2
⋅
A
J
YZ
=
J
Y0Z0
y
C
⋅
z
C
⋅
A
y
C
z
C

2. Charakterystyki geometryczne przekroju pręta
19
Dr inż. Justyna Grzymisławska
2.4. Wyznaczanie momentów bezwładności przekroju
Wyznaczanie momentów bezwładności przekroju pręta w układzie osi
środkowych
J
Y0
=
∑
i=1
i=n
J
Y0i
z
0i
2
⋅
A
i
J
Z0
=
∑
i=1
i=n
J
Z0i
y
0i
2
⋅
A
i
J
Y0Z0
=
∑
i=1
i=n
J
Y0iZ0i
y
0i
⋅
z
0i
⋅
A
i
J
Y0i
, J
Z0i
, J
Y0iZ0i
- momenty bezwładności
względem osi środkowych i-tej figury.
y
0i
, z
0i
- współrzędne środka ciężkości
i-tej figury w układzie Y
0
Z
0
.
A
i
- pole powierzchni i-tej figury.
2. Charakterystyki geometryczne przekroju pręta
20
Dr inż. Justyna Grzymisławska
Z
0
Y
0
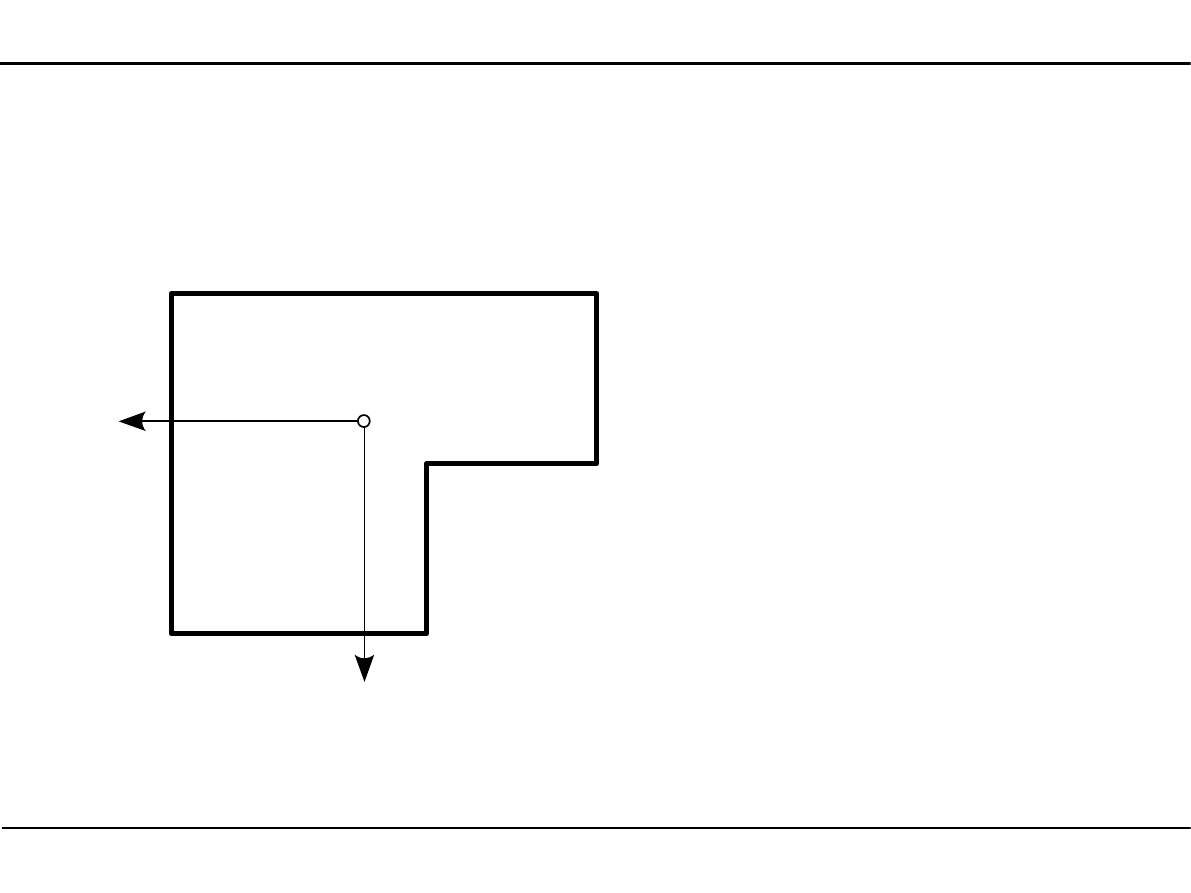
2.4. Wyznaczanie momentów bezwładności przekroju
Wyznaczanie momentów bezwładności przekroju pręta w układzie osi
środkowych
sc
Szukamy momentów bezwładności
przekroju J
Y0
, J
Z0
oraz J
Y0Z0
2. Charakterystyki geometryczne przekroju pręta
21
Dr inż. Justyna Grzymisławska
Z
02
Y
02
Z
01
Y
01
Z
0
Y
0
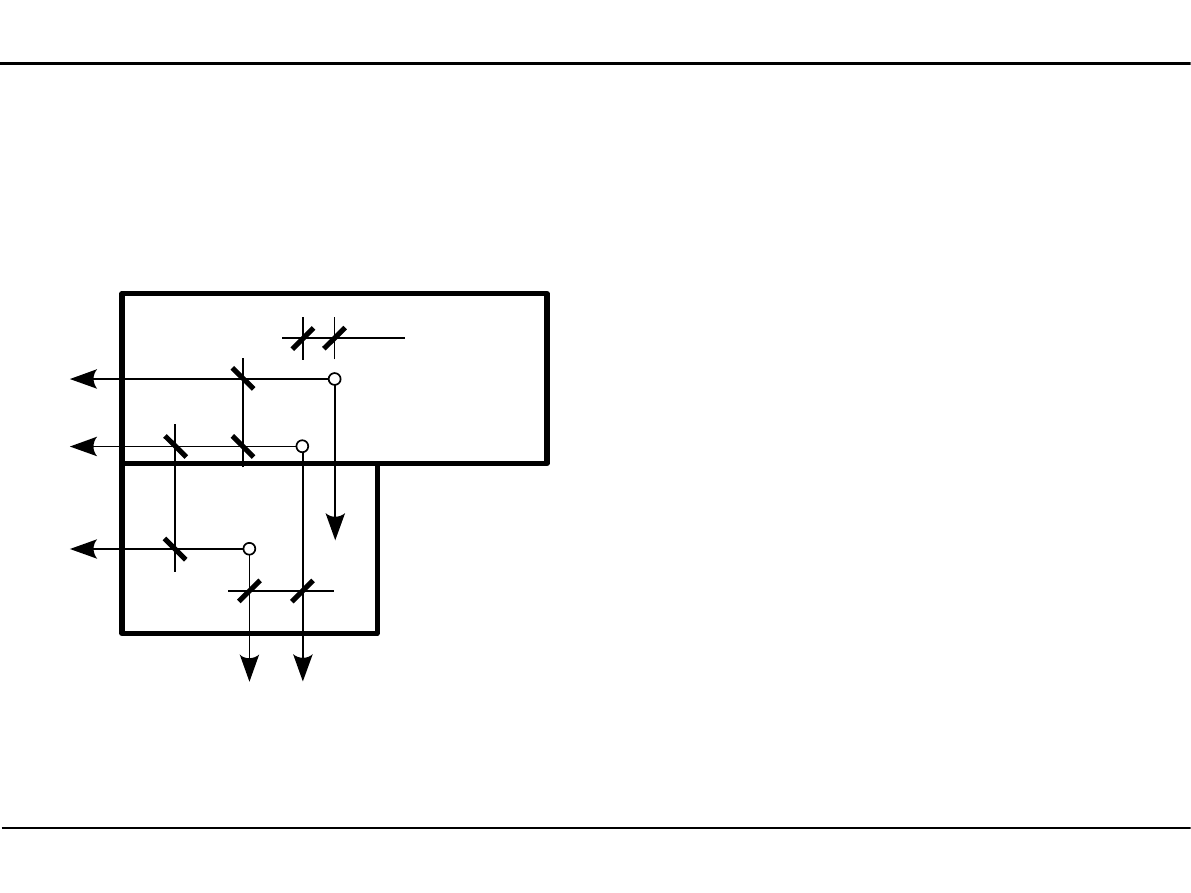
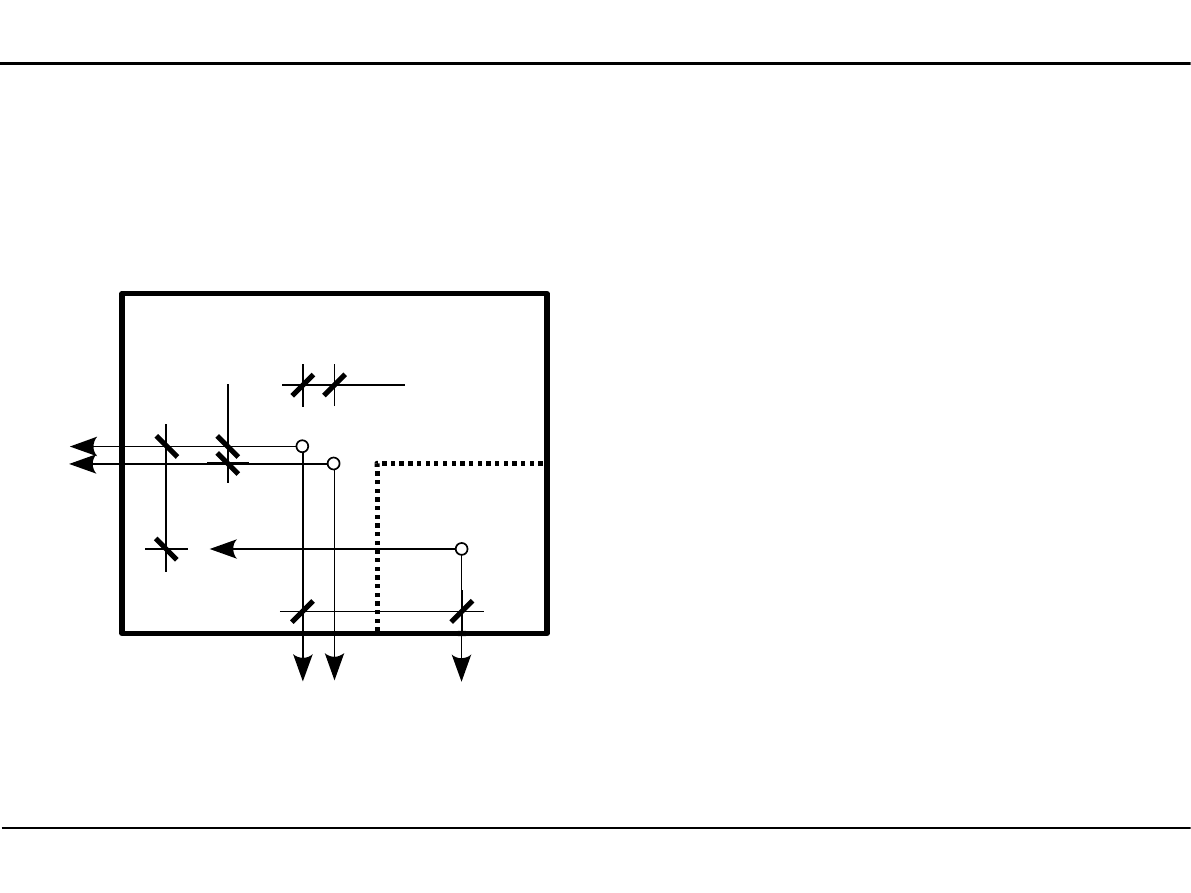
2.4. Wyznaczanie momentów bezwładności przekroju
Wyznaczanie momentów bezwładności przekroju pręta w układzie osi
środkowych
J
Y0
=
J
Y01
z
01
2
⋅
A
1
J
Y02
z
02
2
⋅
A
2
J
Z0
=
J
Z01
y
01
2
⋅
A
1
J
Z02
y
02
2
⋅
A
2
J
Y0Z0
=
J
Y01Z01
y
01
⋅
z
01
⋅
A
1
J
Y02Z02
y
02
⋅
z
02
⋅
A
2
sc
sc
1
sc
2
y
01
z
0
1
y
02
z
0
2
2. Charakterystyki geometryczne przekroju pręta
22
Dr inż. Justyna Grzymisławska
Z
02
Y
02
Z
01
Y
01
Z
0
Y
0
2.4. Wyznaczanie momentów bezwładności przekroju
Wyznaczanie momentów bezwładności przekroju pręta w układzie osi
środkowych
sc
sc
1
sc
2
J
Y0
=
J
Y01
z
01
2
⋅
A
1
−
J
Y02
z
02
2
⋅
A
2
J
Z0
=
J
Z01
y
01
2
⋅
A
1
−
J
Z02
y
02
2
⋅
A
2
J
Y0Z0
=
J
Y01Z01
y
01
⋅
z
01
⋅
A
1
−
J
Y02Z02
y
02
⋅
z
02
⋅
A
2
y
01
z
01
y
02
z
0
2
2. Charakterystyki geometryczne przekroju pręta
23
Dr inż. Justyna Grzymisławska
Y
0'
Z
0'
Y
0'
Z
0'
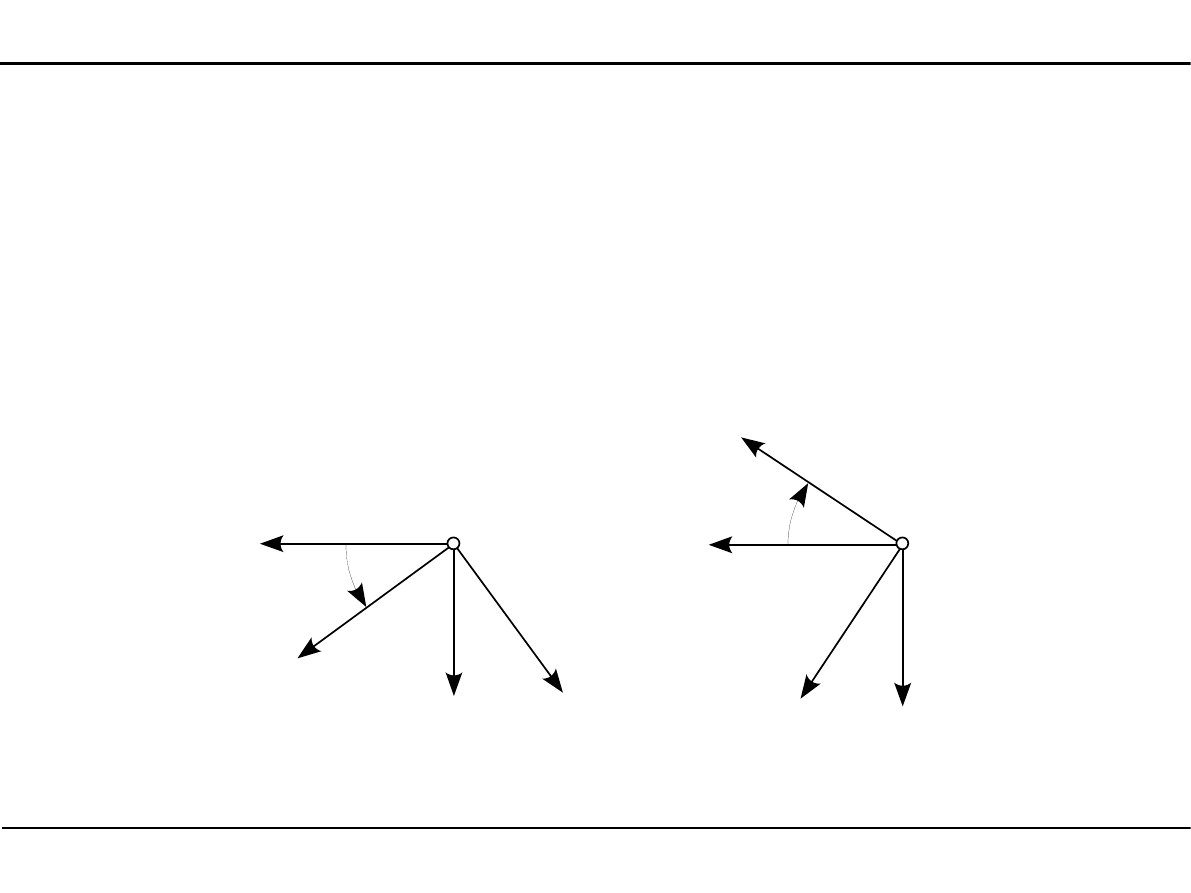
2.4. Wyznaczanie momentów bezwładności przekroju
Transformacja układu współrzędnych
Transformacja jest to obrót układu współrzędnych względem jego początku.
Dodatni kąt
α
kręci od osi Y do osi Z.
Y
0
Z
0
sc
α
>0
Y
0
Z
0
sc
α
<0

2. Charakterystyki geometryczne przekroju pręta
24
Dr inż. Justyna Grzymisławska
2.4. Wyznaczanie momentów bezwładności przekroju
Transformacja układu współrzędnych
Momenty bezwładności w układzie transformowanym wynoszą
J
Y0 '
=
J
Y0
J
Z0
2
J
Y0
−
J
Z0
2
⋅
cos
2⋅
−
J
Y0Z0
⋅
sin
2⋅
J
Z0'
=
J
Y0
J
Z0
2
−
J
Y0
−
J
Z0
2
⋅
cos
2⋅
J
Y0Z0
⋅
sin
2⋅
J
Y0 ' Z0 '
=
J
Y0
−
J
Z0
2
⋅
sin
2⋅
J
Y0Z0
⋅
cos
2⋅

2. Charakterystyki geometryczne przekroju pręta
25
Dr inż. Justyna Grzymisławska
2.4. Wyznaczanie momentów bezwładności przekroju
Główne momenty bezwładności
Istnieje taki układ współrzędnych, którym osiowe momenty bezwładności osiągają
wartości ekstremalne.
Ponadto w układzie tym dewiacyjny moment bezwładności równa się zero.
Układ ten nazywamy układem osi głównych, osiowe momenty bezwładności
- głównymi momentami bezwładności.

2. Charakterystyki geometryczne przekroju pręta
26
Dr inż. Justyna Grzymisławska
2.4. Wyznaczanie momentów bezwładności przekroju
Główne momenty bezwładności
Główne momenty bezwładności wynoszą
J
Ygl
=
J
Y0
J
Z0
2
J
Y0
−
J
Z0
2
⋅
cos
2⋅
gl
−
J
Y0Z0
⋅
sin
2⋅
gl
J
Zgl
=
J
Y0
J
Z0
2
−
J
Y0
−
J
Z0
2
⋅
cos
2⋅
gl
J
Y0Z0
⋅
sin
2⋅
gl
Kąt nachylenia układu współrzędnych, w którym występują główne momenty
bezwładności nazywamy kierunkiem głównym. Wynosi on
tg
2⋅
gl
=
−
2⋅J
Y0Z0
J
Y0
−
J
Z0

2. Charakterystyki geometryczne przekroju pręta
27
Dr inż. Justyna Grzymisławska
2.4. Wyznaczanie momentów bezwładności przekroju
Główne momenty bezwładności
Główne momenty bezwładności możemy także wyznaczyć ze wzoru
J
1/2
=
J
Y0
J
Z0
2
±
J
Y0
−
J
Z0
2
2
J
Y0Z0
2
J
1
=
max
{
J
Ygl
J
Zgl
J
2
=
min
{
J
Ygl
J
Zgl
Główne momenty bezwładności są zawsze większe od zera.

2. Charakterystyki geometryczne przekroju pręta
28
Dr inż. Justyna Grzymisławska
2.4. Wyznaczanie momentów bezwładności przekroju
Główne momenty bezwładności
Jeżeli jedna z osi układu jest osią symetrii przekroju pręta, to dewiacyjny moment
bezwładności w takim układzie wynosi zero.
W układzie osi głównych dewiacyjny moment bezwładności wynosi zero.
Jeżeli przynajmniej jedna z osi środkowych jest osią symetrii przekroju pręta,
to układ ten jest układem osi głównych.

2. Charakterystyki geometryczne przekroju pręta
29
Dr inż. Justyna Grzymisławska
2.4. Wyznaczanie momentów bezwładności przekroju
Niezmienniki
Niezmiennikiem nazywamy wielkość fizyczną, która nie zmienia swojej wartości przy
transformacji układu współrzędnych.
Pierwszy niezmiennik ma wartość
I
1
=
J
Y0
J
Z0
=
J
Y0 '
J
Z0'
=
J
Ygl
J
Zgl
Drugi niezmiennik ma wartość
I
2
=
J
Y0
⋅
J
Z0
−
J
Y0Z0
2
=
J
Y0 '
⋅
J
Z0 '
−
J
Y0 ' Z0 '
2
=
J
Ygl
⋅
J
Zgl
2. Charakterystyki geometryczne przekroju pręta
30
Dr inż. Justyna Grzymisławska
Z
0
=Z
gl
Y
0
=Y
gl
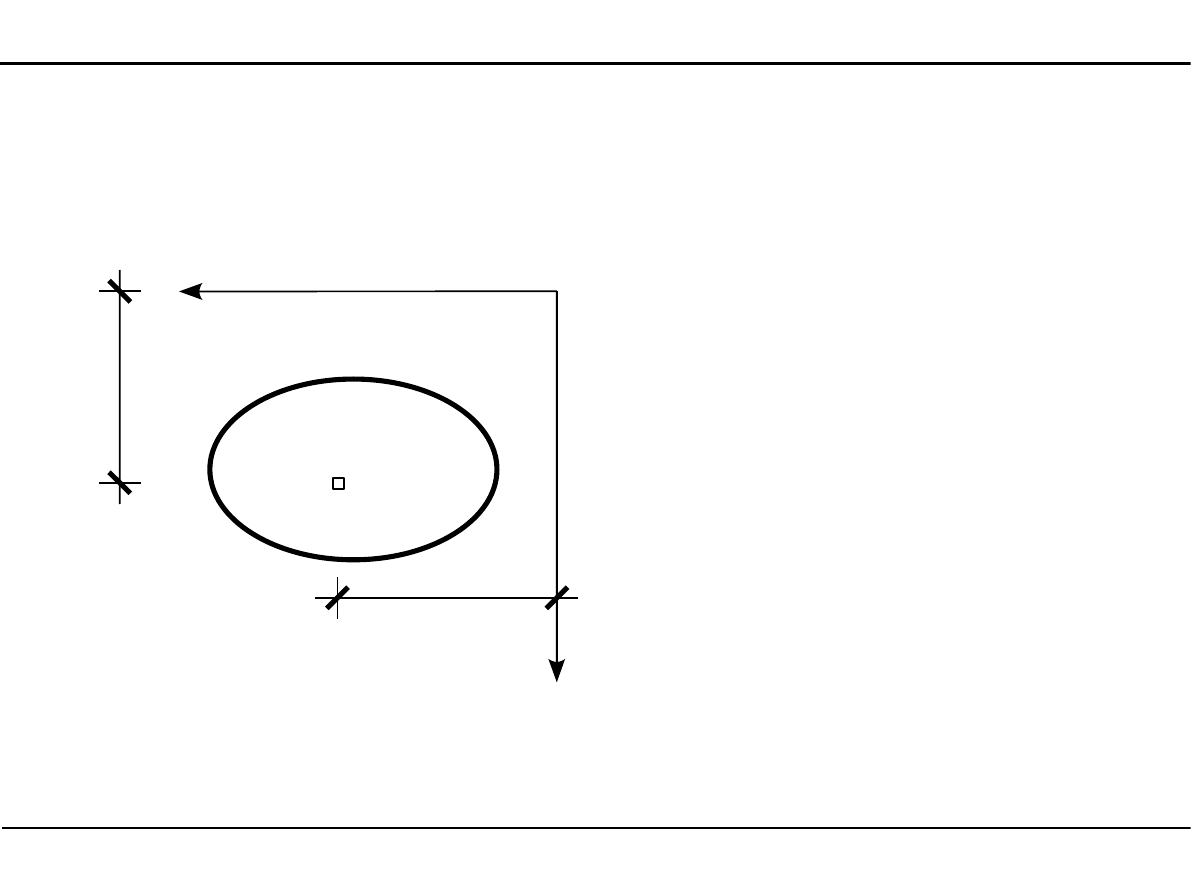
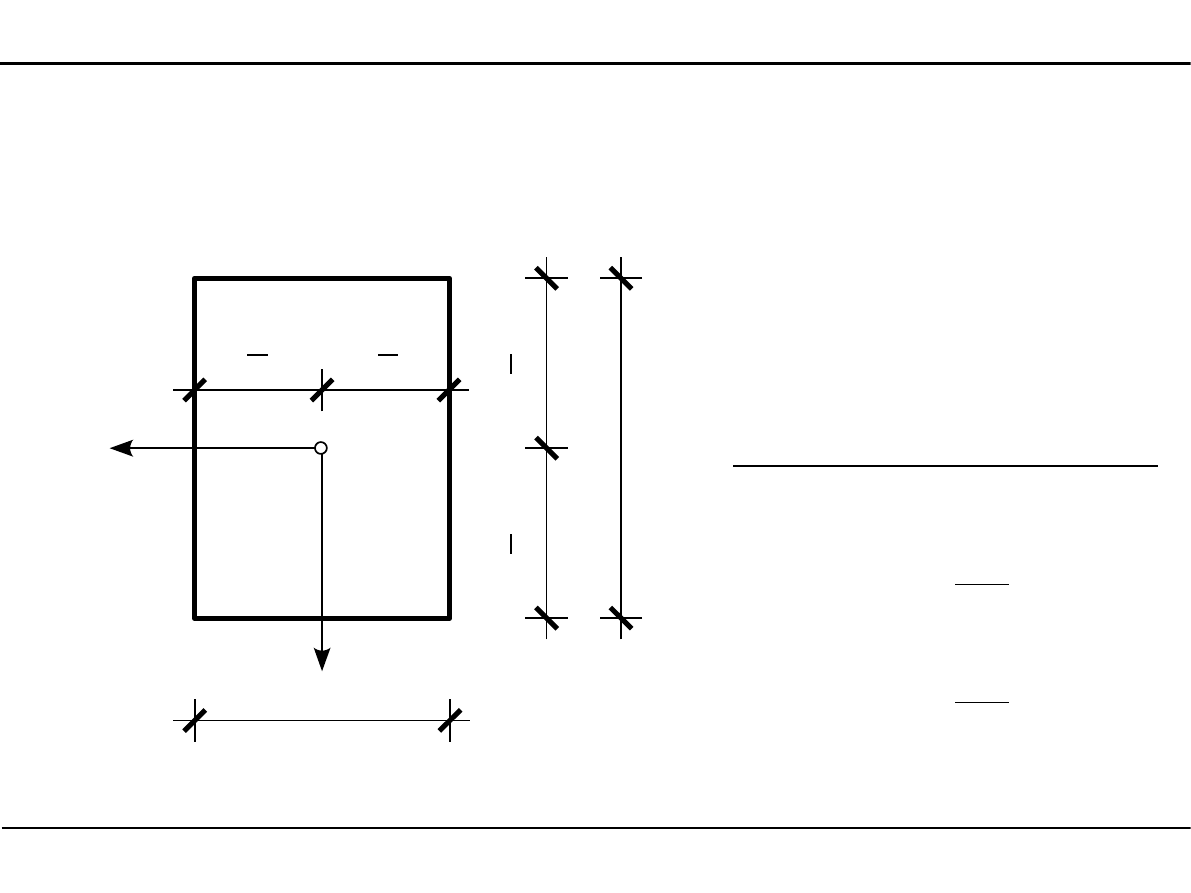
2.5. Charakterystyki geometryczne podstawowych przekrojów
Prostokąt
sc
A=b⋅h
J
oś
=
wymiar∥do osi
⋅
wymiar ⊥ do osi
3
12
Główne momenty bezwładności
J
Y0
=
J
Ygl
=
b⋅h
3
12
J
Z0
=
J
Zgl
=
h⋅b
3
12
b
h
b
2
b
2
h
2
h
2
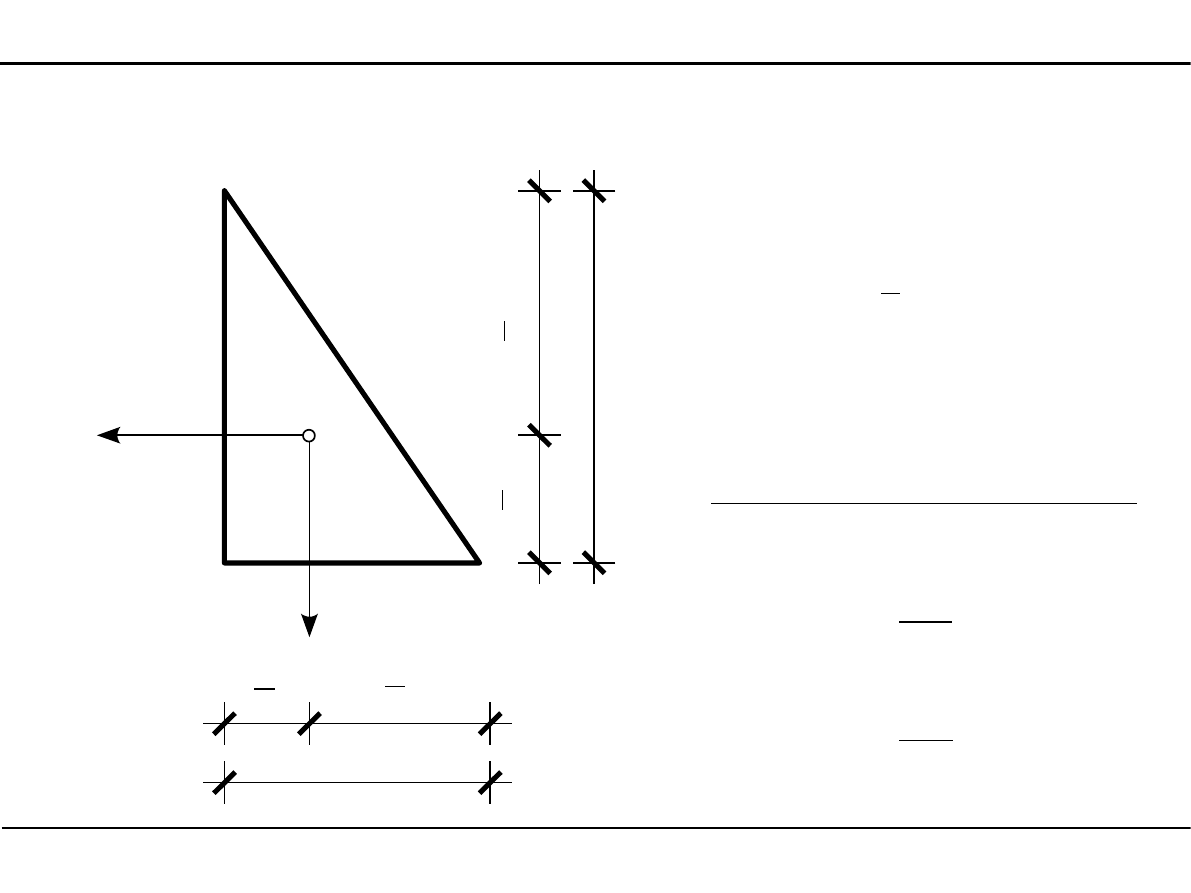
2. Charakterystyki geometryczne przekroju pręta
31
Dr inż. Justyna Grzymisławska
Z
0
Y
0
2.5. Charakterystyki geometryczne podstawowych przekrojów
Trójkąt prostokątny
b
h
sc
b
3
2
3
⋅
b
h
3
2
3
⋅h
A=
1
2
⋅
b⋅h
Osiowe momenty bezwładności
J
oś
=
wymiar∥do osi
⋅
wymiar ⊥do osi
3
36
J
Y0
=
b⋅h
3
36
J
Z0
=
h⋅b
3
36
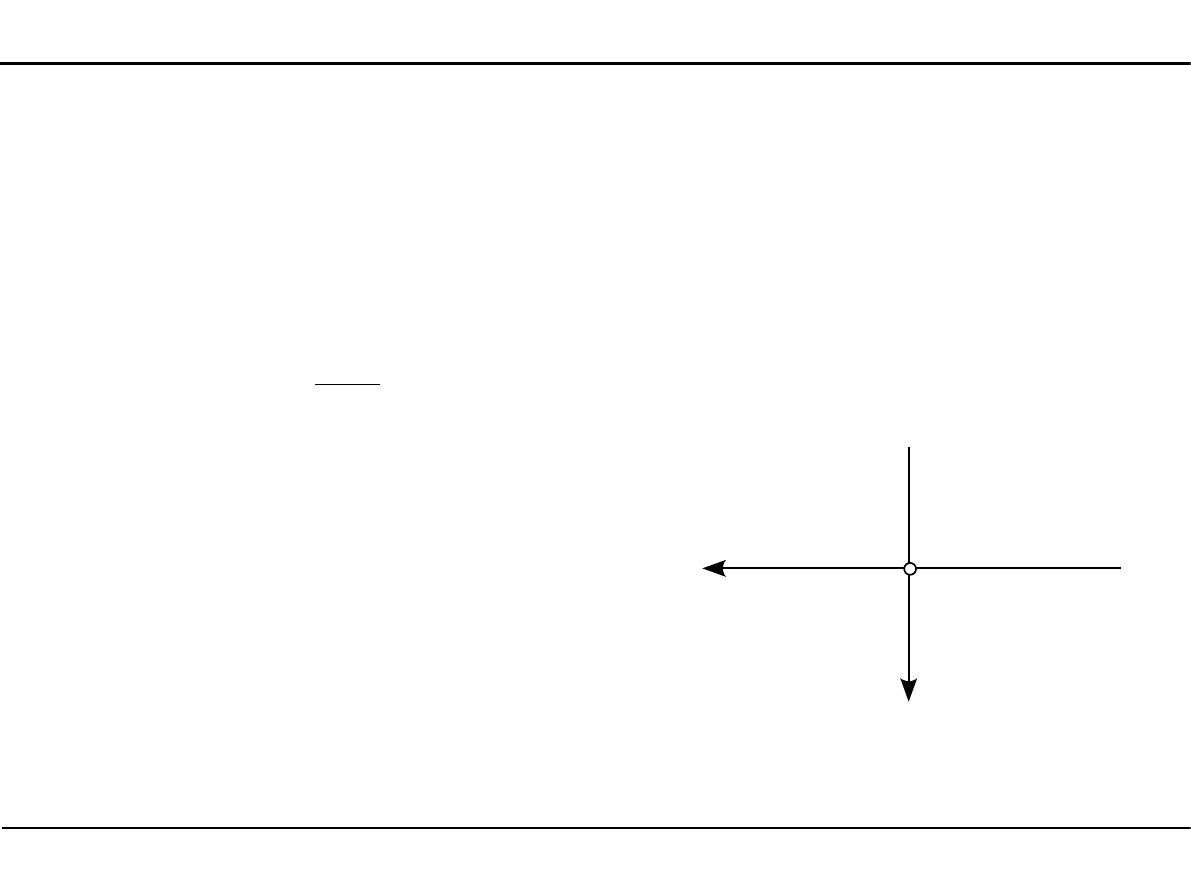
2. Charakterystyki geometryczne przekroju pręta
32
Dr inż. Justyna Grzymisławska
Z
0
Y
0
sc
dodatnia
dodatnia
ujemna
ujemna
2.5. Charakterystyki geometryczne podstawowych przekrojów
Trójkąt prostokątny
Dewiacyjny moment bezwładności
∣
J
Y0Z0
∣
=
b
2
⋅
h
2
72
Ćwiartki dodatnie - y
0
∙z
0
>0
Ćwiartki ujemne - y
0
∙z
0
<0
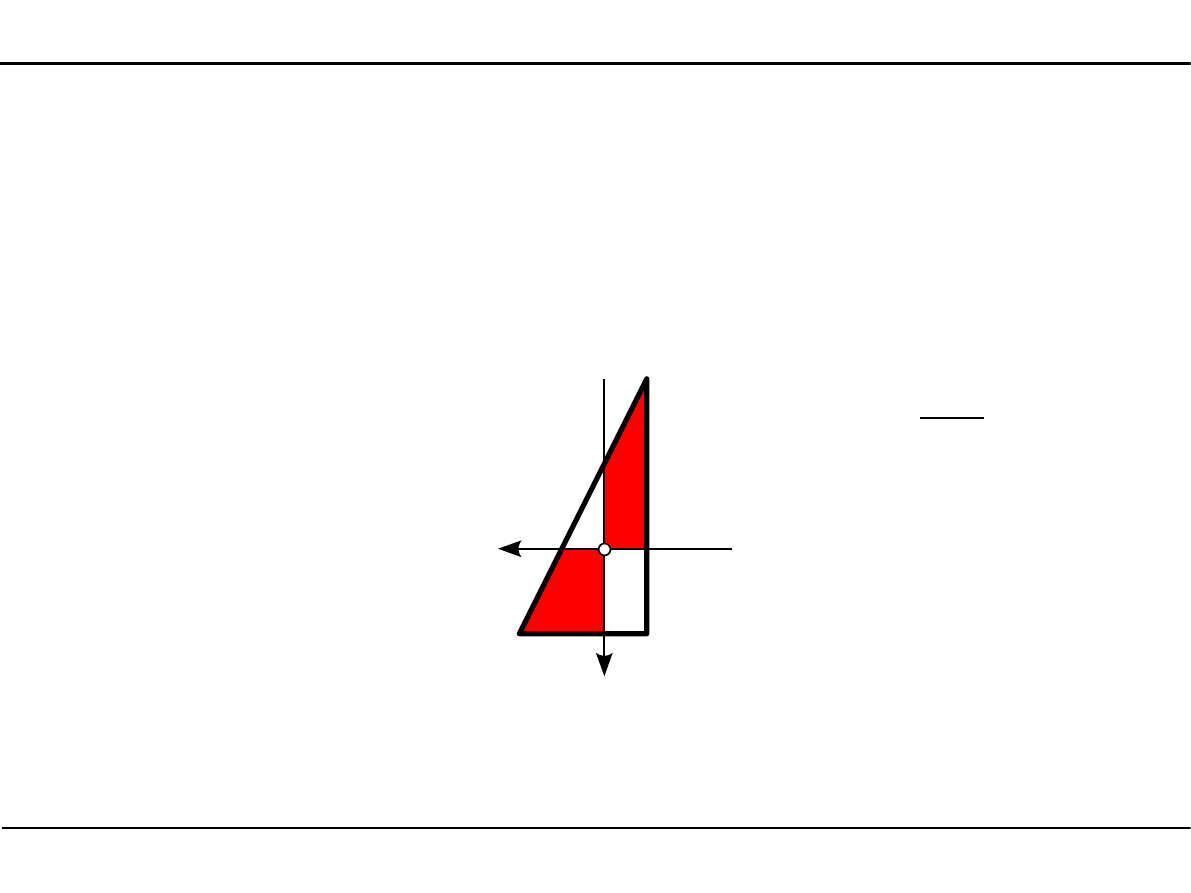
2. Charakterystyki geometryczne przekroju pręta
33
Dr inż. Justyna Grzymisławska
2.5. Charakterystyki geometryczne podstawowych przekrojów
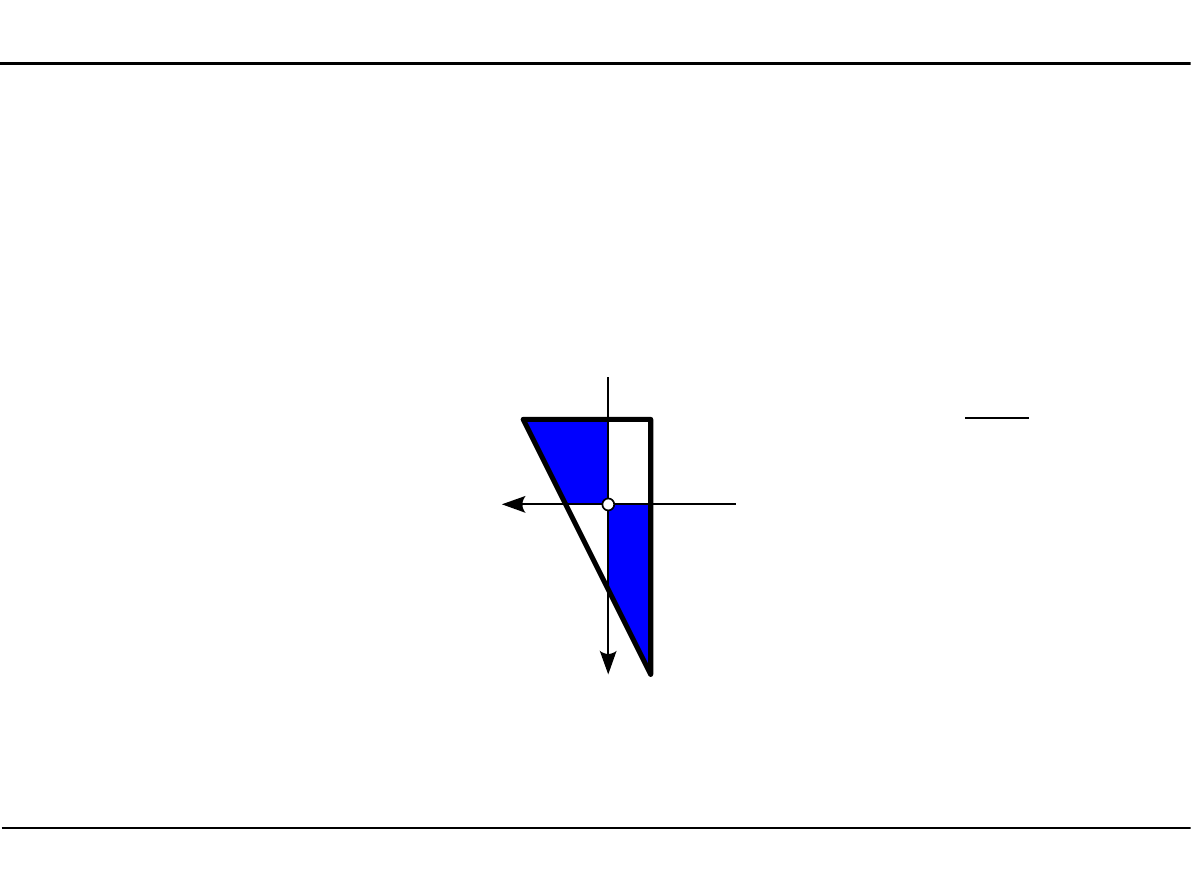
Trójkąt prostokątny
Jeżeli większa część trójkąta leży w ćwiartkach dodatnich, to dewiacyjny moment
bezwładności jest dodatni.
Z
0
Y
0
sc
J
Y0Z0
=
b
2
⋅
h
2
72
2. Charakterystyki geometryczne przekroju pręta
34
Dr inż. Justyna Grzymisławska
2.5. Charakterystyki geometryczne podstawowych przekrojów
Trójkąt prostokątny
Jeżeli większa część trójkąta leży w ćwiartkach ujemnych, to dewiacyjny moment
bezwładności jest ujemny.
Z
0
Y
0
sc
J
Y0Z0
=−
b
2
⋅
h
2
72
2. Charakterystyki geometryczne przekroju pręta
35
Dr inż. Justyna Grzymisławska
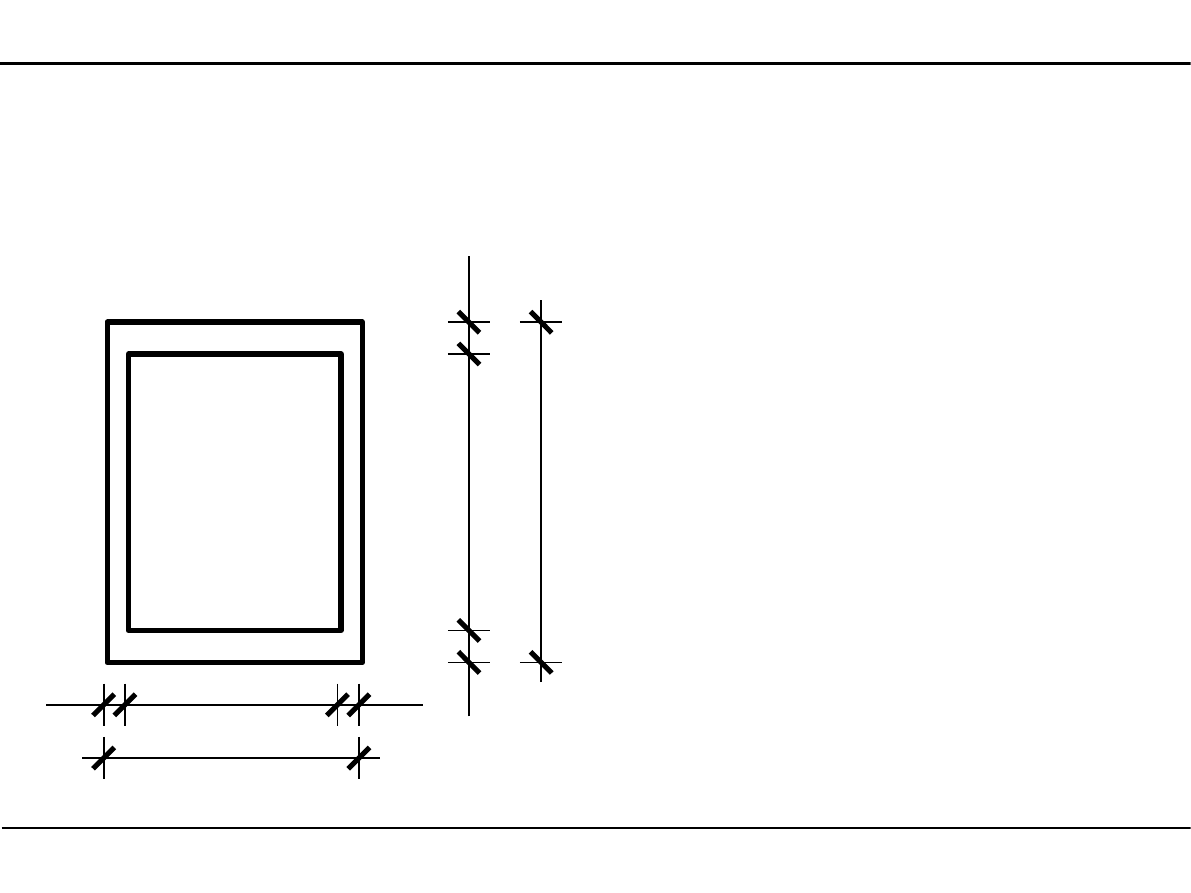
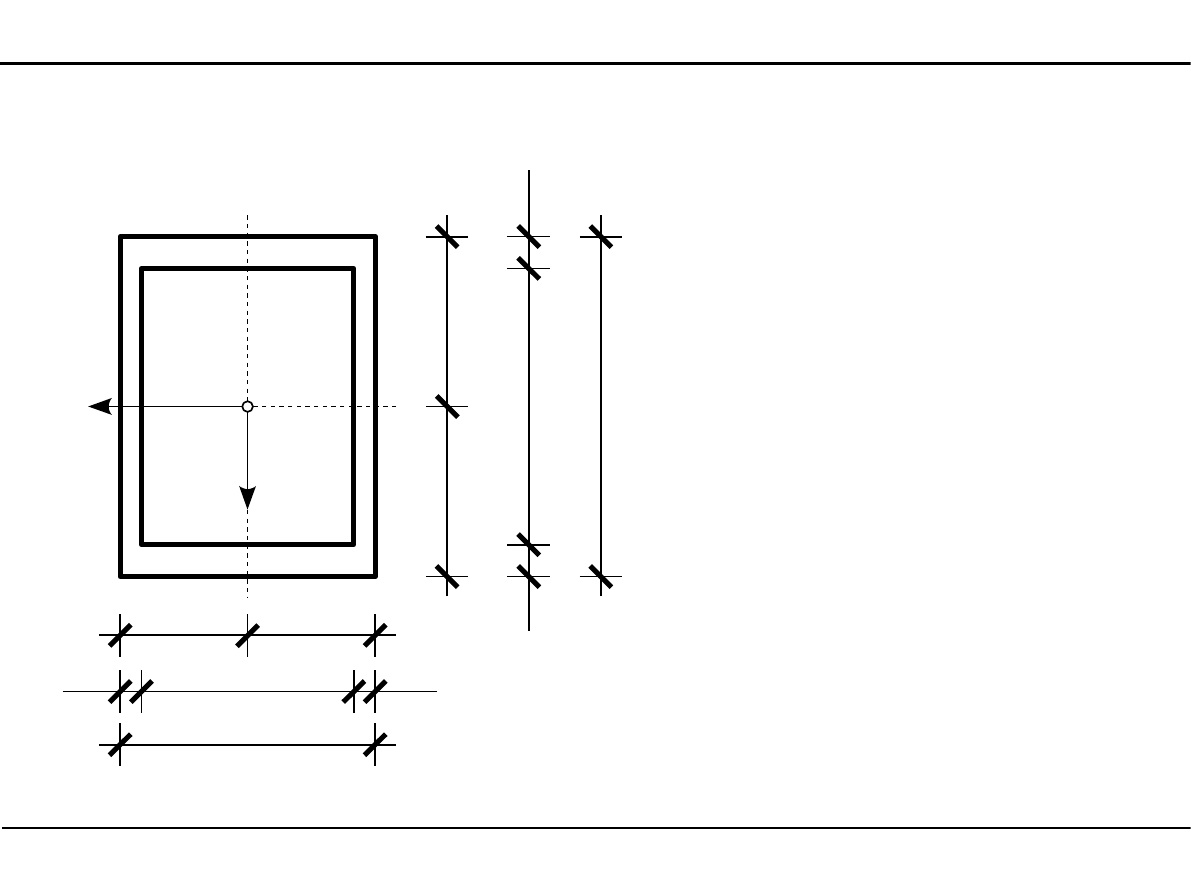
2.6. Charakterystyki geometryczne przekroju skrzynkowego
Wyznaczyć charakterystyki geometryczne
przekroju skrzynkowego przedstawionego
na poniższym rysunku.
Zadanie 1
[cm]
15,0
2,
0
2,
0
17
,0
1,0
1,0
13,0
21
,0
2. Charakterystyki geometryczne przekroju pręta
36
Dr inż. Justyna Grzymisławska
Y
0
=Y
gl
Z
0
=Z
gl
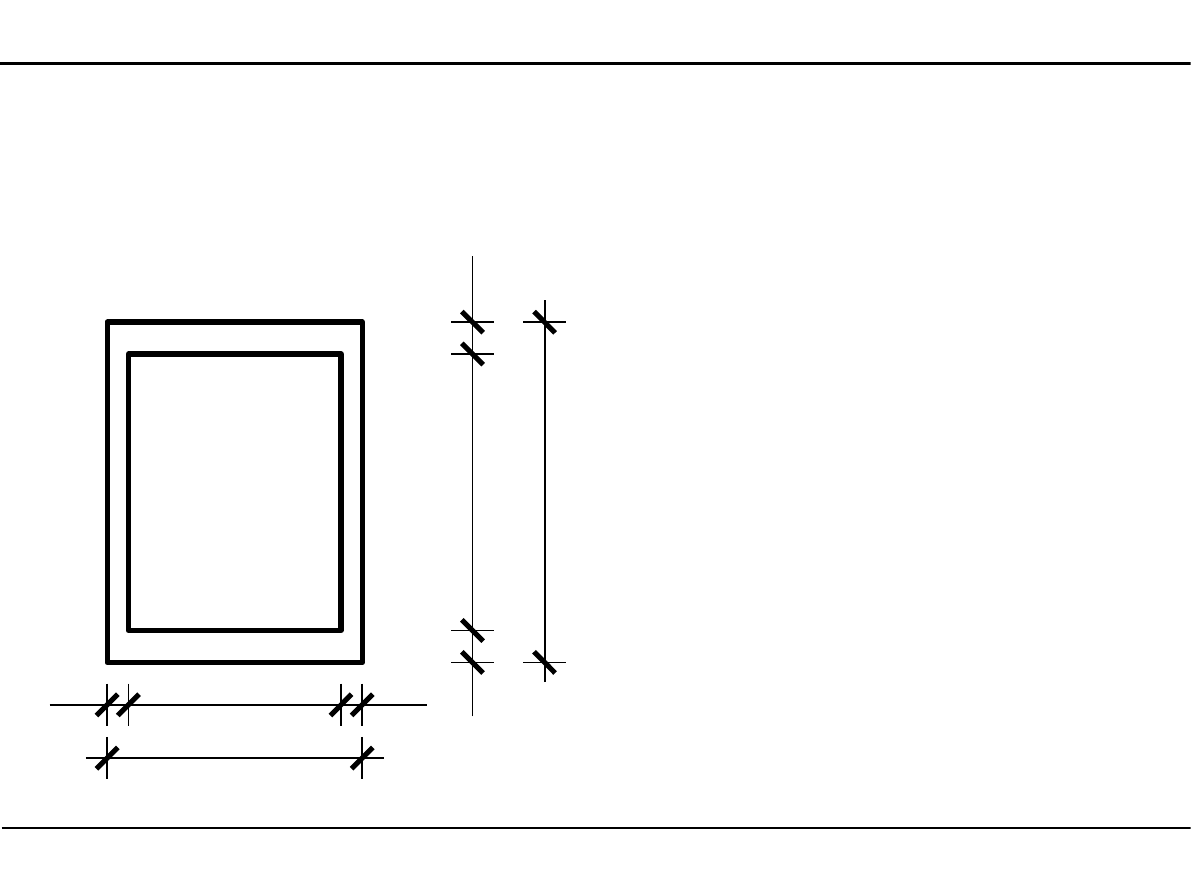
2.6. Charakterystyki geometryczne przekroju skrzynkowego
Położenie środka ciężkości
przekroju skrzynkowego
[cm]
sc
1,0
1,0
13,0
15,0
2,
0
2,
0
17
,0
21
,0
7,50
7,50
10
,5
0
10
,5
0
2. Charakterystyki geometryczne przekroju pręta
37
Dr inż. Justyna Grzymisławska
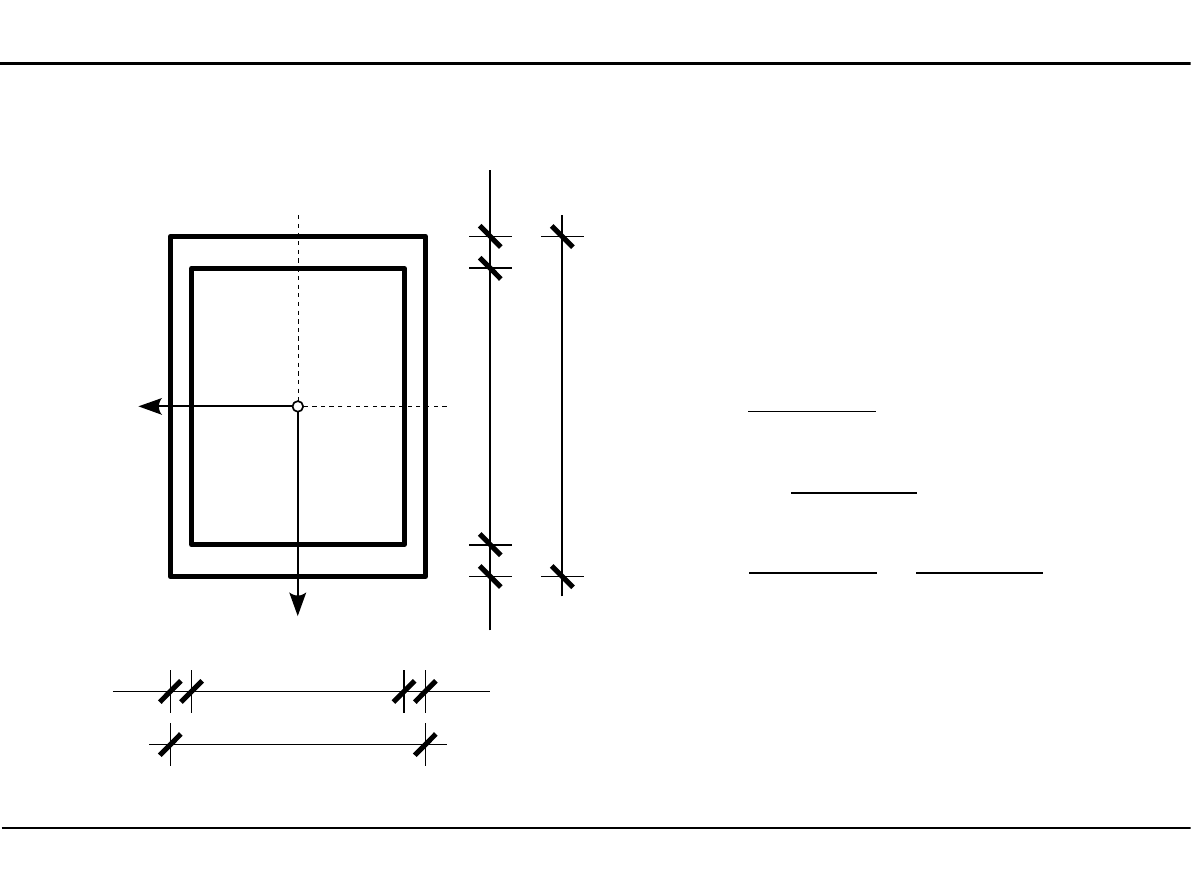
2.6. Charakterystyki geometryczne przekroju skrzynkowego
[cm]
Pole powierzchni przekroju skrzynkowego
A=15,0⋅21,0−13,0⋅17,0=94,0 cm
2
15,0
21
,0
1,0
1,0
13,0
2,
0
2,
0
17
,0
2. Charakterystyki geometryczne przekroju pręta
38
Dr inż. Justyna Grzymisławska
Y
0
=Y
gl
Z
0
=Z
gl
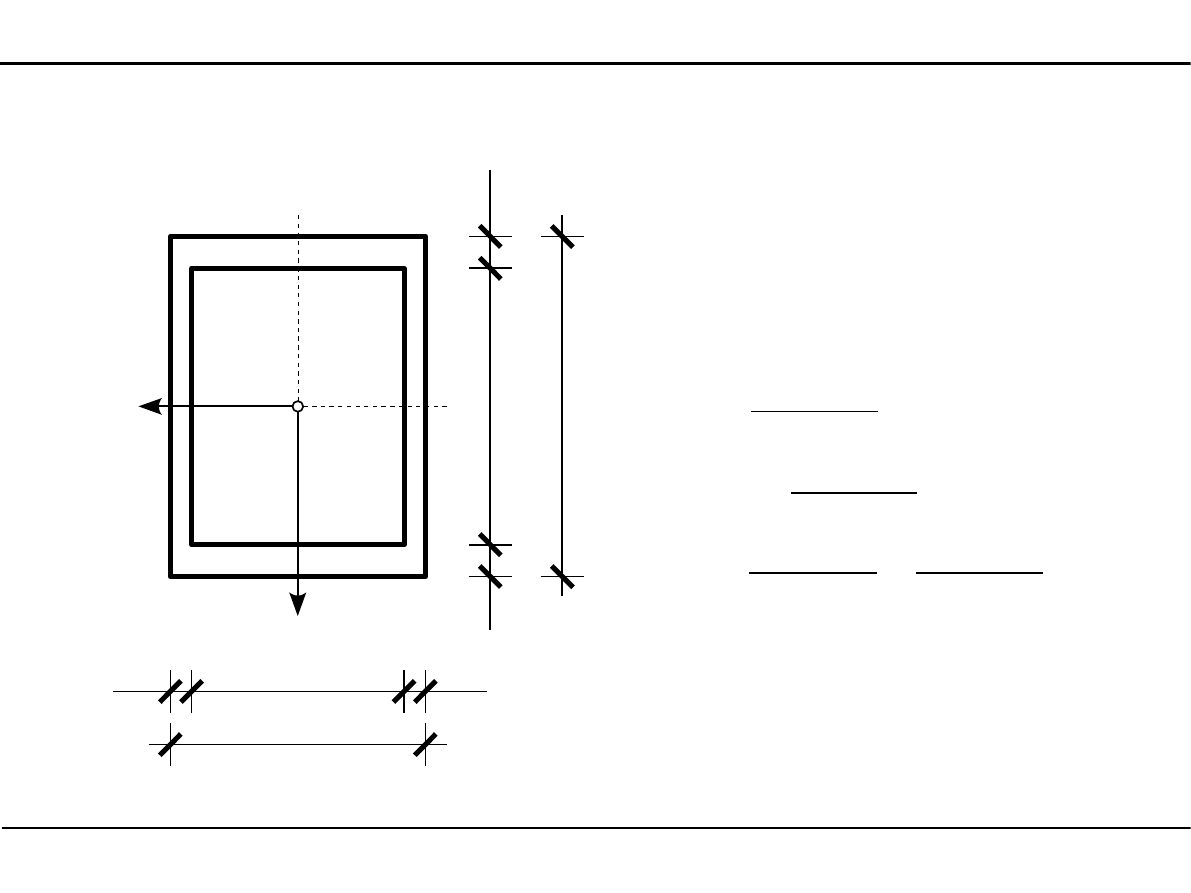
2.6. Charakterystyki geometryczne przekroju skrzynkowego
Główne momenty bezwładności
przekroju skrzynkowego
[cm]
sc
sc
1
=sc
2
Y
01
=Y
02
Z
01
=Z
02
z
01
=
0,0 cm
z
02
=
0,0 cm
J
Y0
=
J
Ygl
=
15,0⋅21,0
3
12
0,0
2
⋅
15,0⋅21,0
−
13,0⋅17,0
3
12
0,0
2
⋅
13,0⋅17,0
=
=
15,0⋅21,0
3
12
−
13,0⋅17,0
3
12
=
6254 cm
4
1,0
1,0
13,0
15,0
2,
0
2,
0
17
,0
21
,0
2. Charakterystyki geometryczne przekroju pręta
39
Dr inż. Justyna Grzymisławska
2.6. Charakterystyki geometryczne przekroju skrzynkowego
Główne momenty bezwładności
przekroju skrzynkowego
y
01
=
0,0 cm
y
02
=
0,0 cm
J
Z0
=
J
Zgl
=
21,0⋅15,0
3
12
0,0
2
⋅
15,0⋅21,0−
−
17,0⋅13,0
3
12
0,0
2
⋅
13,0⋅17,0
=
=
21,0⋅15,0
3
12
−
17,0⋅13,0
3
12
=
2794 cm
4
[cm]
1,0
1,0
13,0
15,0
2,
0
2,
0
17
,0
21
,0
sc
Y
0
=Y
gl
Z
0
=Z
gl
Z
01
=Z
02
Y
01
=Y
02
sc
1
=sc
2
2. Charakterystyki geometryczne przekroju pręta
40
Dr inż. Justyna Grzymisławska
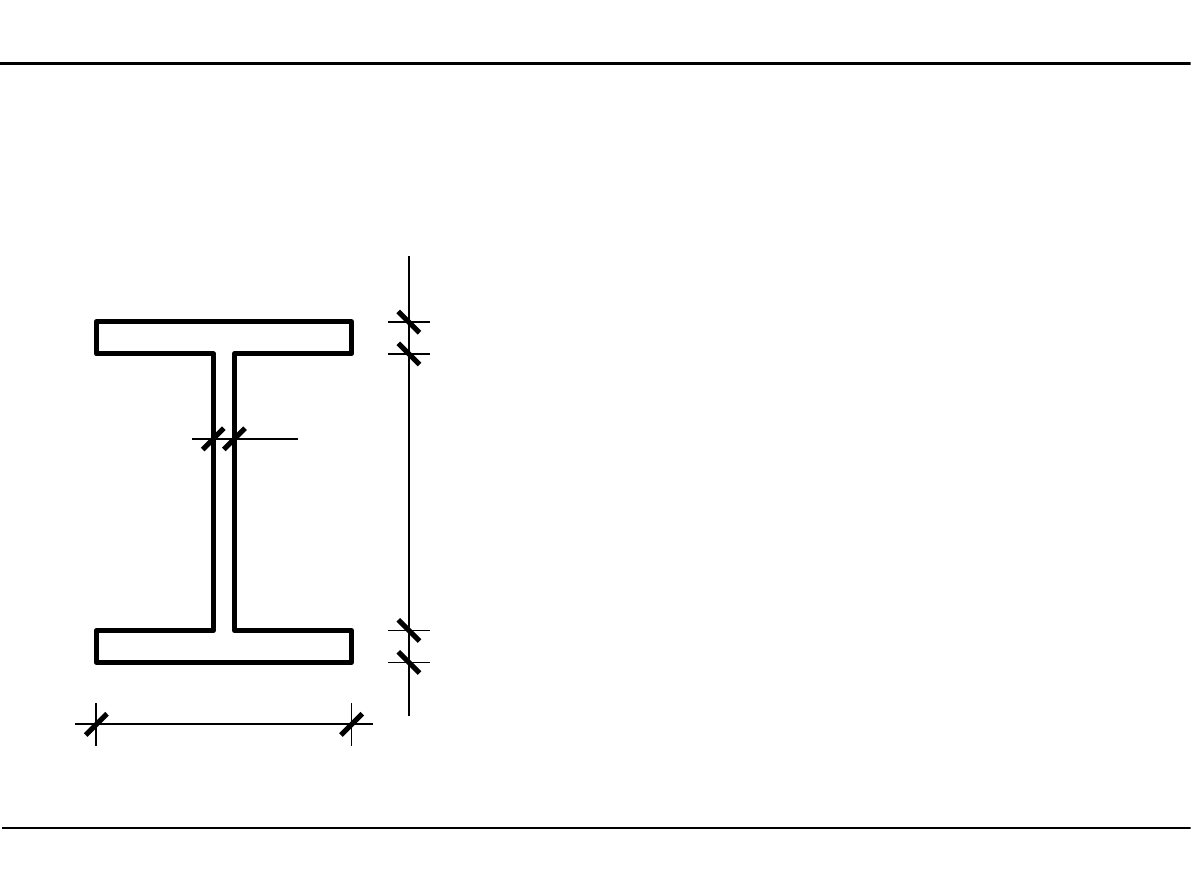
2.7. Charakterystyki geometryczne przekroju dwuteowego
Zadanie 2
Wyznaczyć charakterystyki geometryczne
przekroju dwuteowego przedstawionego
na poniższym rysunku.
[cm]
15,0
2,
0
2,
0
30
,0
1,0
2. Charakterystyki geometryczne przekroju pręta
41
Dr inż. Justyna Grzymisławska
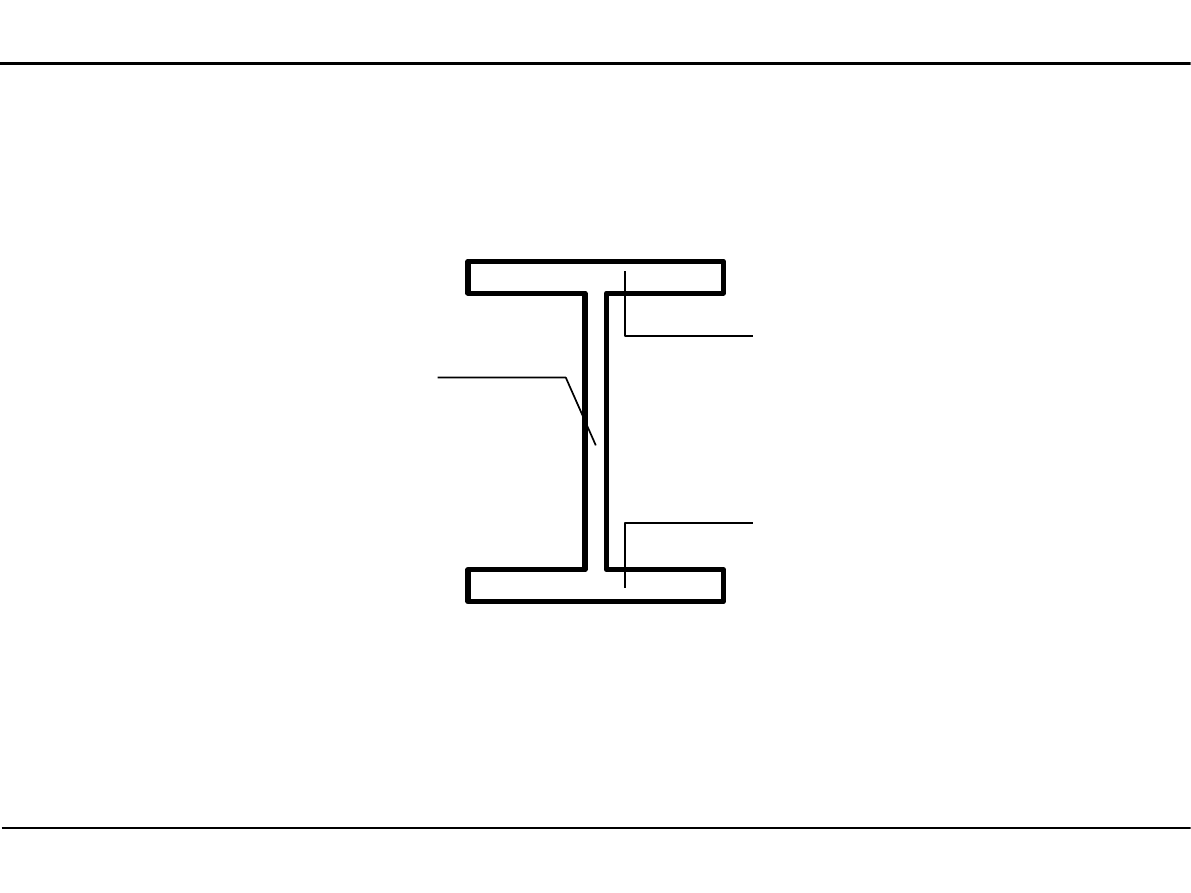
2.7. Charakterystyki geometryczne przekroju dwuteowego
Nazwy poszczególnych elementów przekroju dwuteowego
półka
półka
środnik
2. Charakterystyki geometryczne przekroju pręta
42
Dr inż. Justyna Grzymisławska
Y
0
=Y
gl
Z
0
=Z
gl
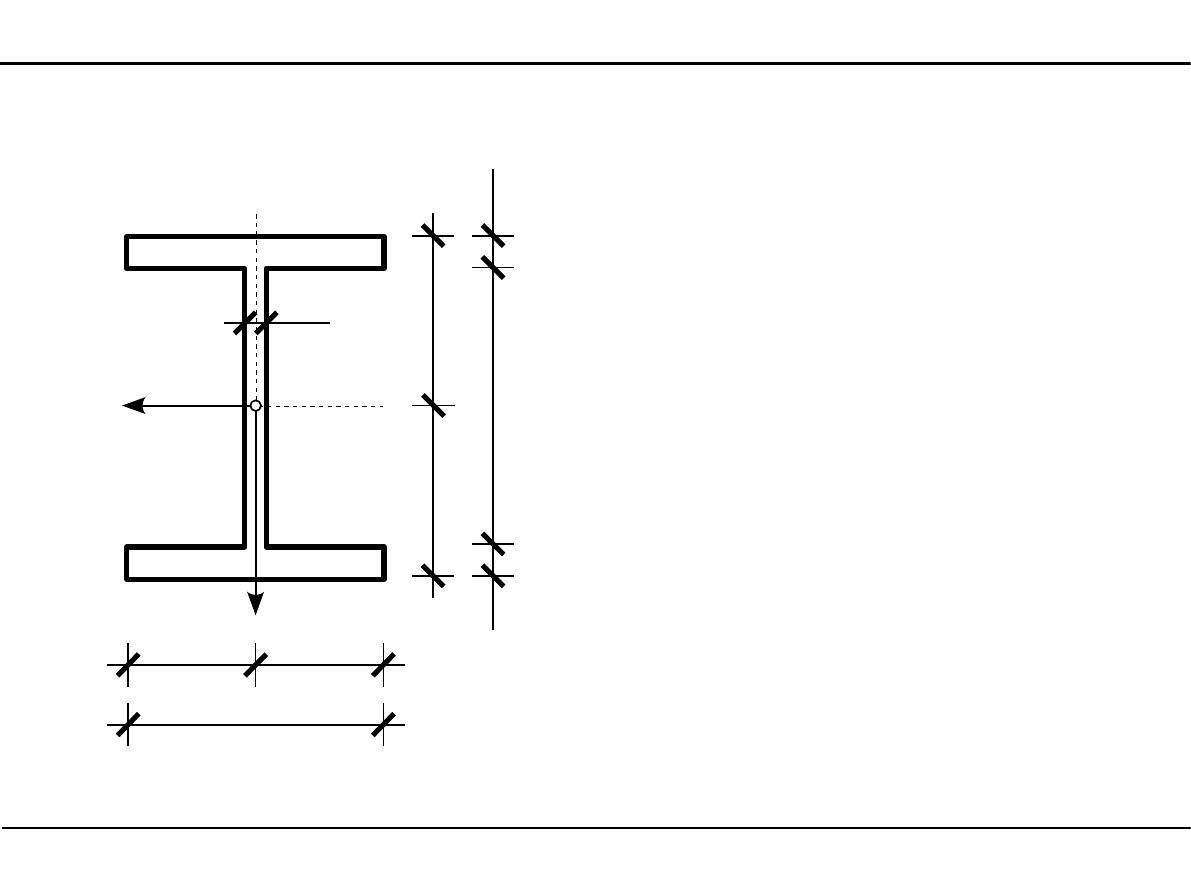
2.7. Charakterystyki geometryczne przekroju dwuteowego
Położenie środka ciężkości
przekroju dwuteowego
[cm]
sc
15,0
2,
0
2,
0
30
,0
1,0
7,50
7,50
17
,0
17
,0
2. Charakterystyki geometryczne przekroju pręta
43
Dr inż. Justyna Grzymisławska
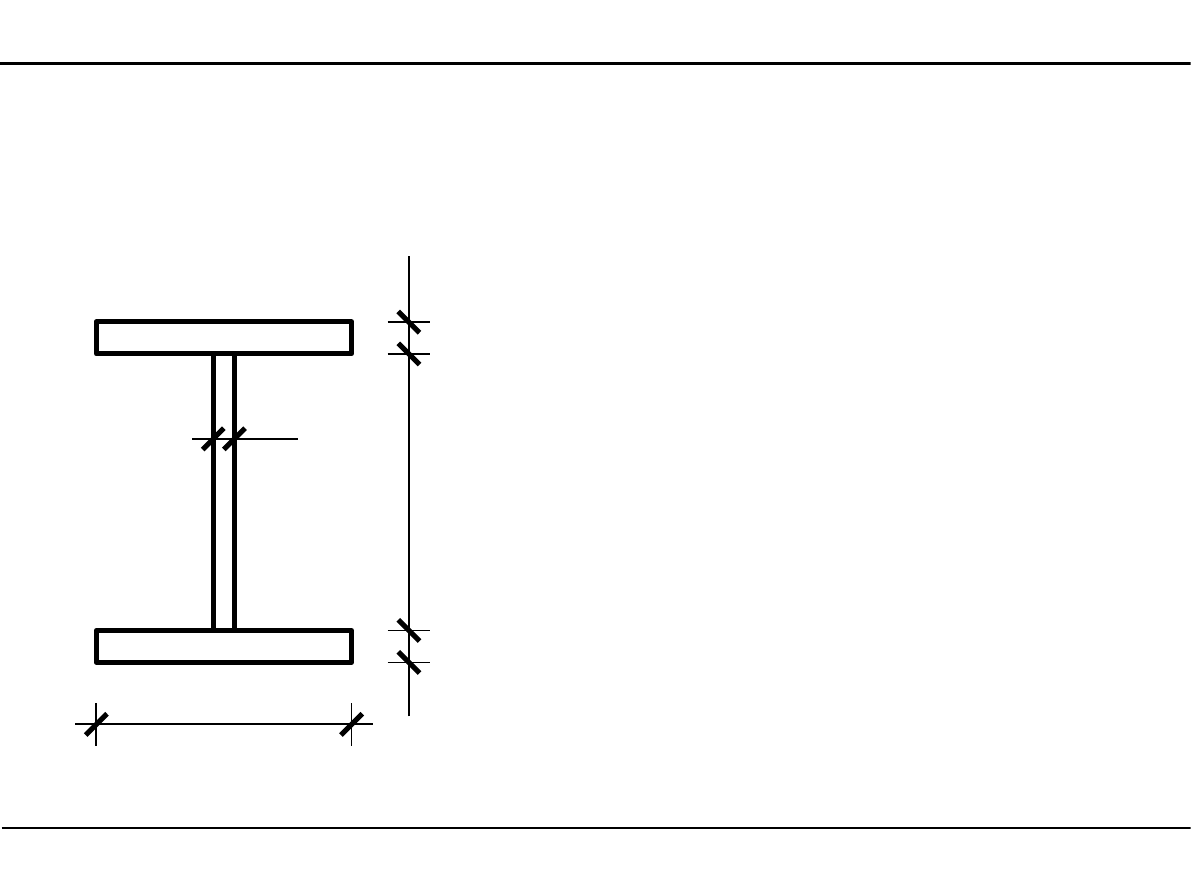
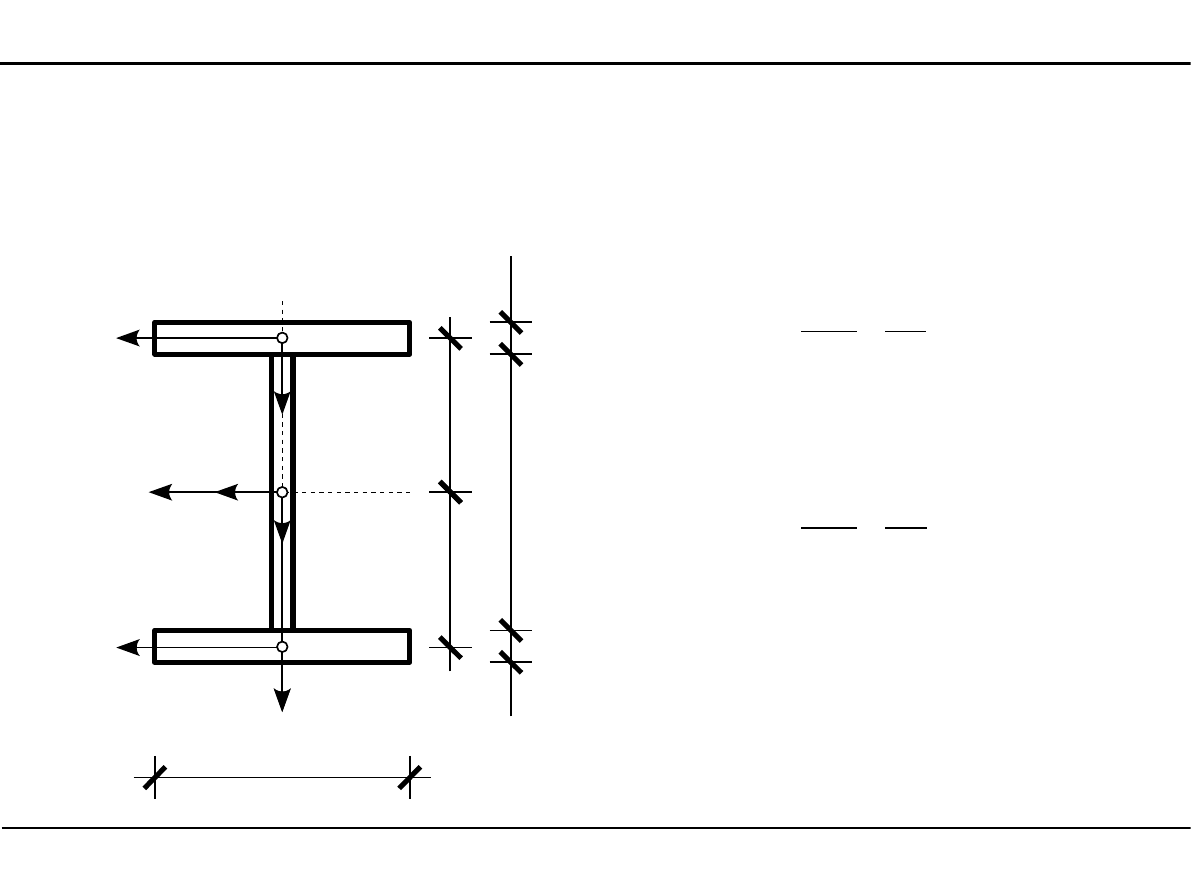
2.7. Charakterystyki geometryczne przekroju dwuteowego
Pole powierzchni przekroju dwuteowego
[cm]
A=2⋅15,0⋅2,030,0⋅1,0=90,0 cm
2
15,0
2,
0
2,
0
30
,0
1,0
2. Charakterystyki geometryczne przekroju pręta
44
Dr inż. Justyna Grzymisławska
Y
03
Z
03
Y
02
Z
02
Y
01
Z
01
Y
0
=Y
gl
Z
0
=Z
gl
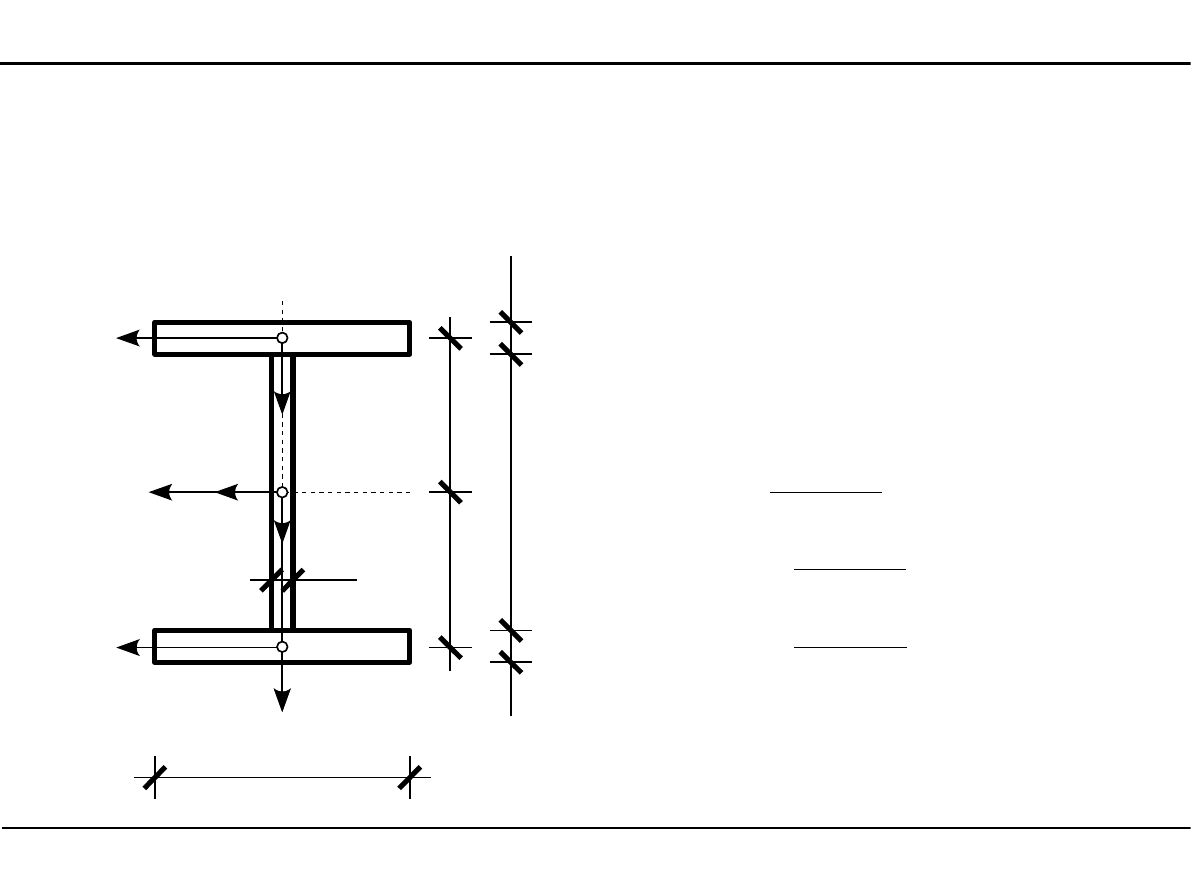
2.7. Charakterystyki geometryczne przekroju dwuteowego
Główne momenty bezwładności
przekroju dwuteowego
sc
[cm]
sc
1
z
01
=−
30,0
2
2,0
2
=−
16,0 cm
sc
2
z
02
=
0,0 cm
sc
3
z
03
=
30,0
2
2,0
2
=
16,0cm
15,0
2,
0
2,
0
30
,0
16
,0
16
,0
2. Charakterystyki geometryczne przekroju pręta
45
Dr inż. Justyna Grzymisławska
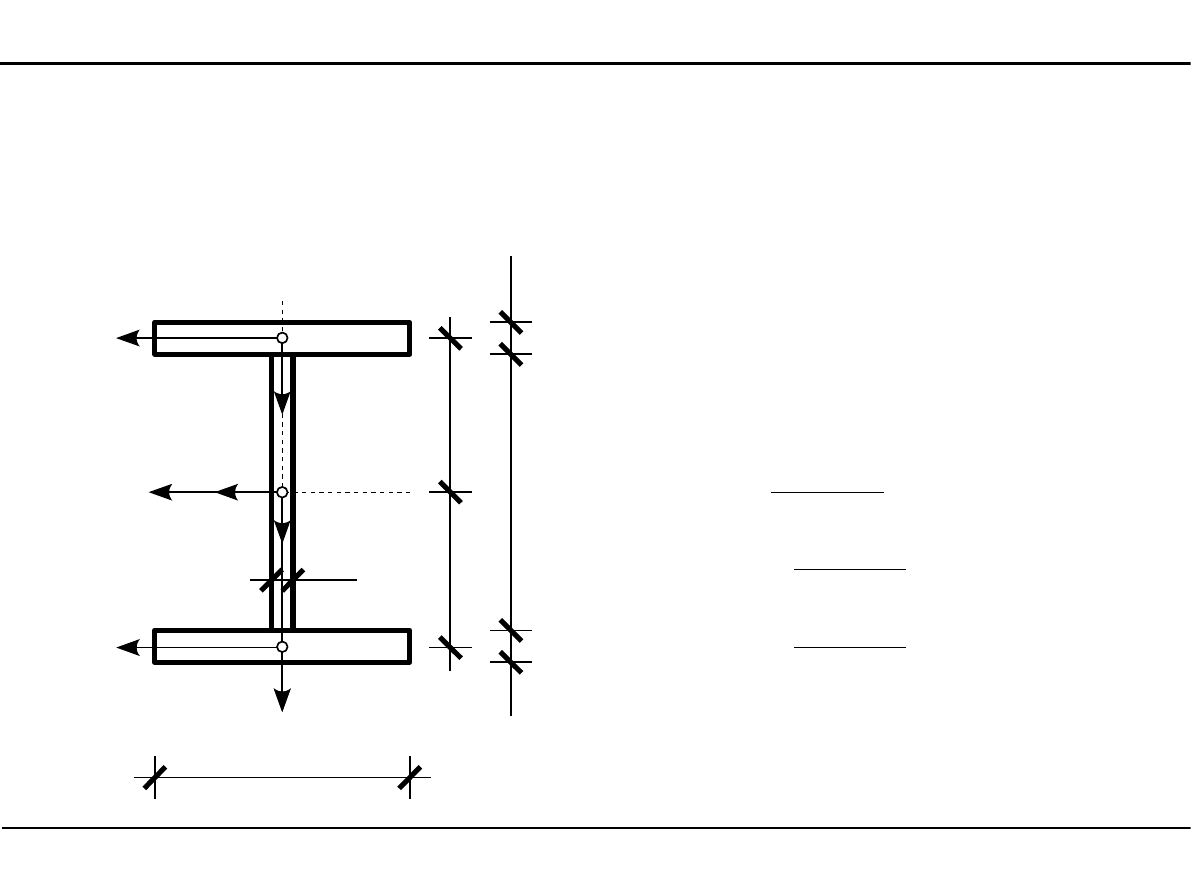
2.7. Charakterystyki geometryczne przekroju dwuteowego
Główne momenty bezwładności
przekroju dwuteowego
z
01
=−
16,0cm
z
02
=
0,0 cm
z
03
=
16,0cm
J
Y0
=
J
Ygl
=
15,0⋅2,0
3
12
−
16,0
2
⋅
15,0⋅2,0
1,0⋅30,0
3
12
0,0
2
⋅
1,0⋅30,0
15,0⋅2,0
3
12
16,0
2
⋅
15,0⋅2,0=
=
17630 cm
4
[cm]
2,
0
2,
0
30
,0
1,0
sc
Y
0
=Y
gl
Z
0
=Z
gl
15,0
16
,0
sc
1
sc
2
sc
3
Y
01
Z
01
Y
02
Z
02
Y
03
Z
03
16
,0
2. Charakterystyki geometryczne przekroju pręta
46
Dr inż. Justyna Grzymisławska
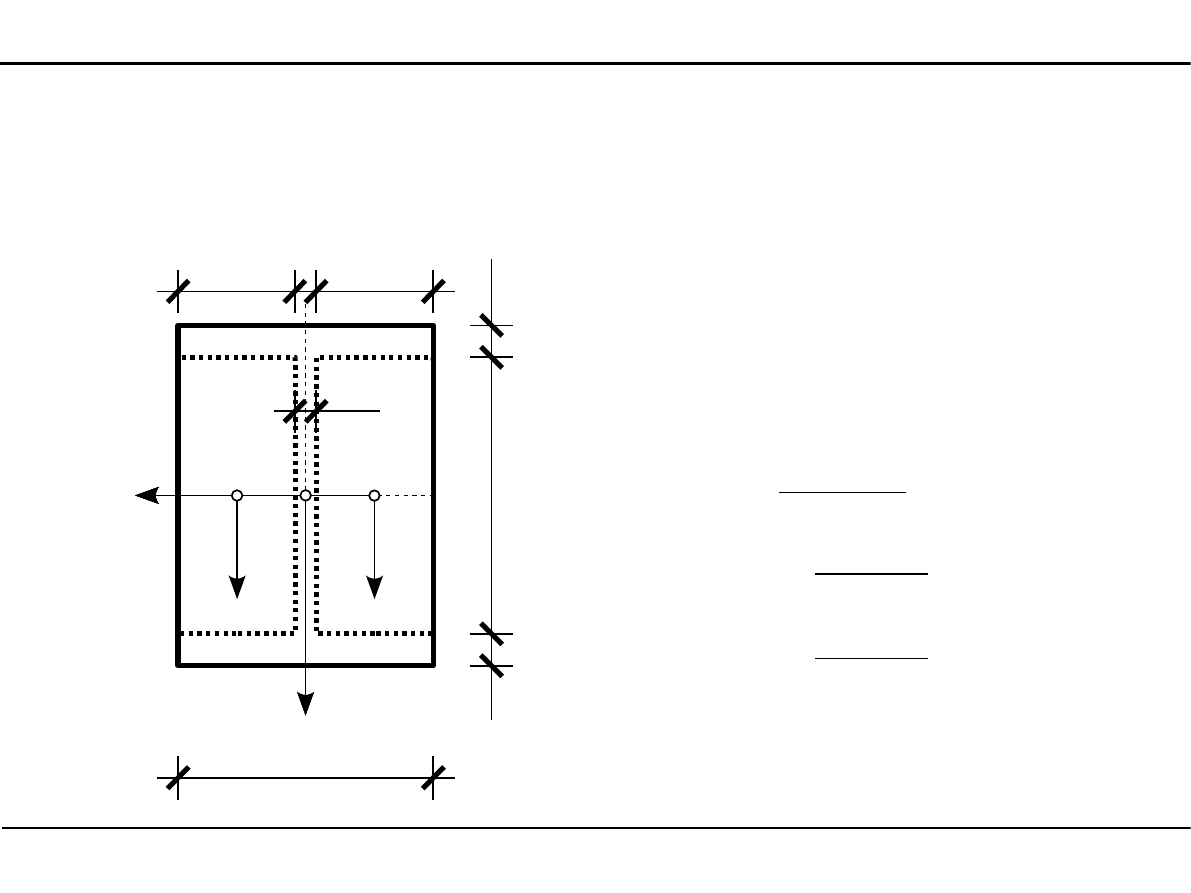
2.7. Charakterystyki geometryczne przekroju dwuteowego
Główne momenty bezwładności
przekroju dwuteowego
y
01
=
0,0 cm
y
02
=
0,0 cm
y
03
=
0,0 cm
J
Z0
=
J
Zgl
=
2,0⋅15,0
3
12
0,0
2
⋅
15,0⋅2,0
30,0⋅1,0
3
12
0,0
2
⋅
1,0⋅30,0
2,0⋅15,0
3
12
0,0
2
⋅
15,0⋅2,0=
=
1128 cm
4
[cm]
2,
0
2,
0
30
,0
1,0
sc
Y
0
=Y
gl
Z
0
=Z
gl
15,0
16
,0
sc
1
sc
2
sc
3
Y
01
Z
01
Y
02
Z
02
Y
03
Z
03
16
,0
2. Charakterystyki geometryczne przekroju pręta
47
Dr inż. Justyna Grzymisławska
Z
03
Y
0
3
=
Z
02
Y
0
2
=
Y
0
1
Z
01
Y
0
=Y
gl
Z
0
=Z
gl
2.7. Charakterystyki geometryczne przekroju dwuteowego
Główne momenty bezwładności
przekroju dwuteowego
sc
[cm]
sc
1
z
01
=
0,0 cm
sc
2
z
02
=
0,0 cm
sc
3
z
03
=
0,0 cm
J
Y0
=
J
Ygl
=
15,0⋅34,0
3
12
0,0
2
⋅
15,0⋅34,0−
−
7,0⋅30,0
3
12
0,0
2
⋅
7,0⋅30,0
−
−
7,0⋅30,0
3
12
0,0
2
⋅
7,0⋅30,0
=
=
17630 cm
4
15,0
2,
0
2,
0
30
,0
1,0
7,0
7,0

2. Charakterystyki geometryczne przekroju pręta
48
Dr inż. Justyna Grzymisławska
2.7. Charakterystyki geometryczne przekroju dwuteowego
Główne momenty bezwładności przekroju dwuteowego
J
Y0
=
J
Ygl
=
15,0⋅34,0
3
12
0,0
2
⋅
15,0⋅34,0−
−
7,0⋅30,0
3
12
0,0
2
⋅
7,0⋅30,0
−
−
7,0⋅30,0
3
12
0,0
2
⋅
7,0⋅30,0
=
=
17630 cm
4
J
Y0
=
J
Ygl
=
15,0⋅34,0
3
12
−
2⋅7,0⋅30,0
3
12
=
17630cm
4
2. Charakterystyki geometryczne przekroju pręta
49
Dr inż. Justyna Grzymisławska
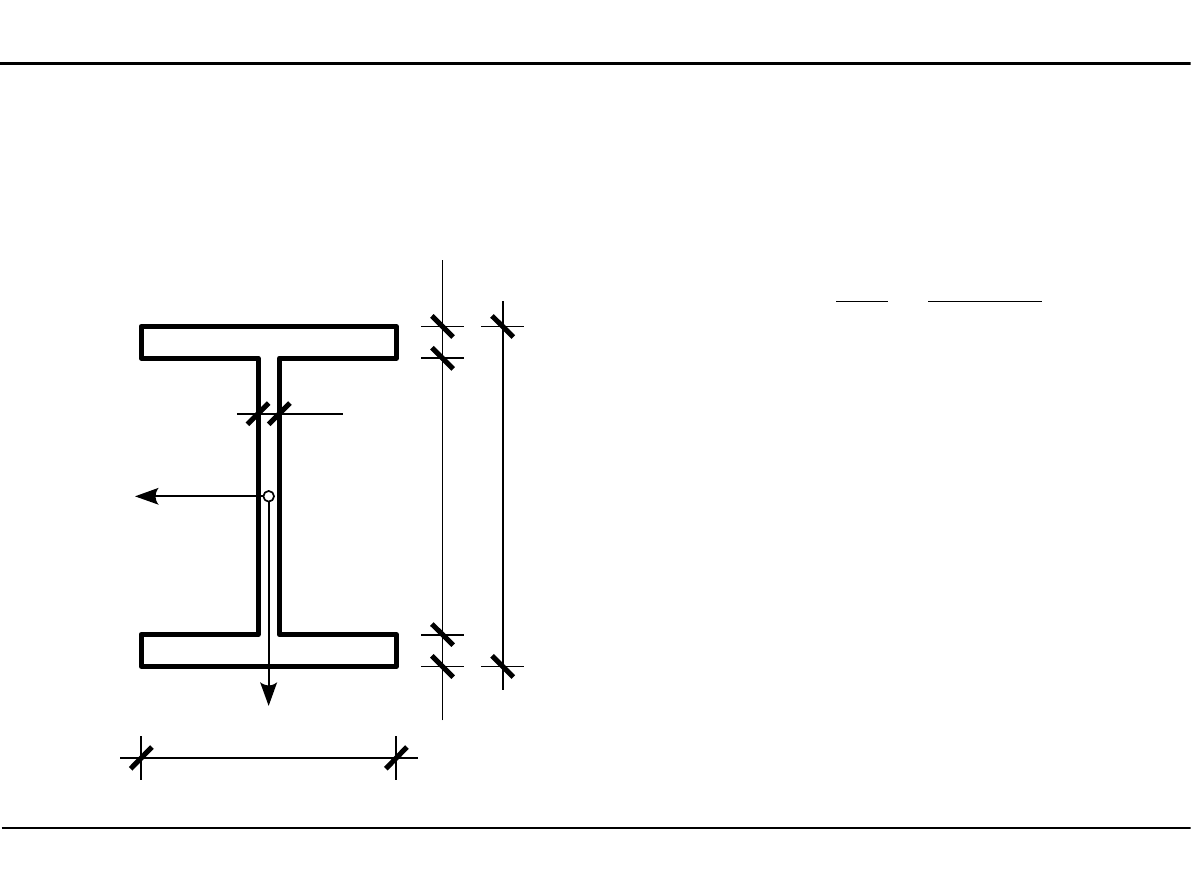
2.7. Charakterystyki geometryczne przekroju dwuteowego
Główne momenty bezwładności przekroju dwuteowego
sc
Y
0
=Y
gl
Z
0
=Z
gl
s
t
h
s
t
h
g
J
Y0
=
J
Ygl
=
s⋅h
3
12
−
s−g
⋅
h
S
3
12
2. Charakterystyki geometryczne przekroju pręta
50
Dr inż. Justyna Grzymisławska
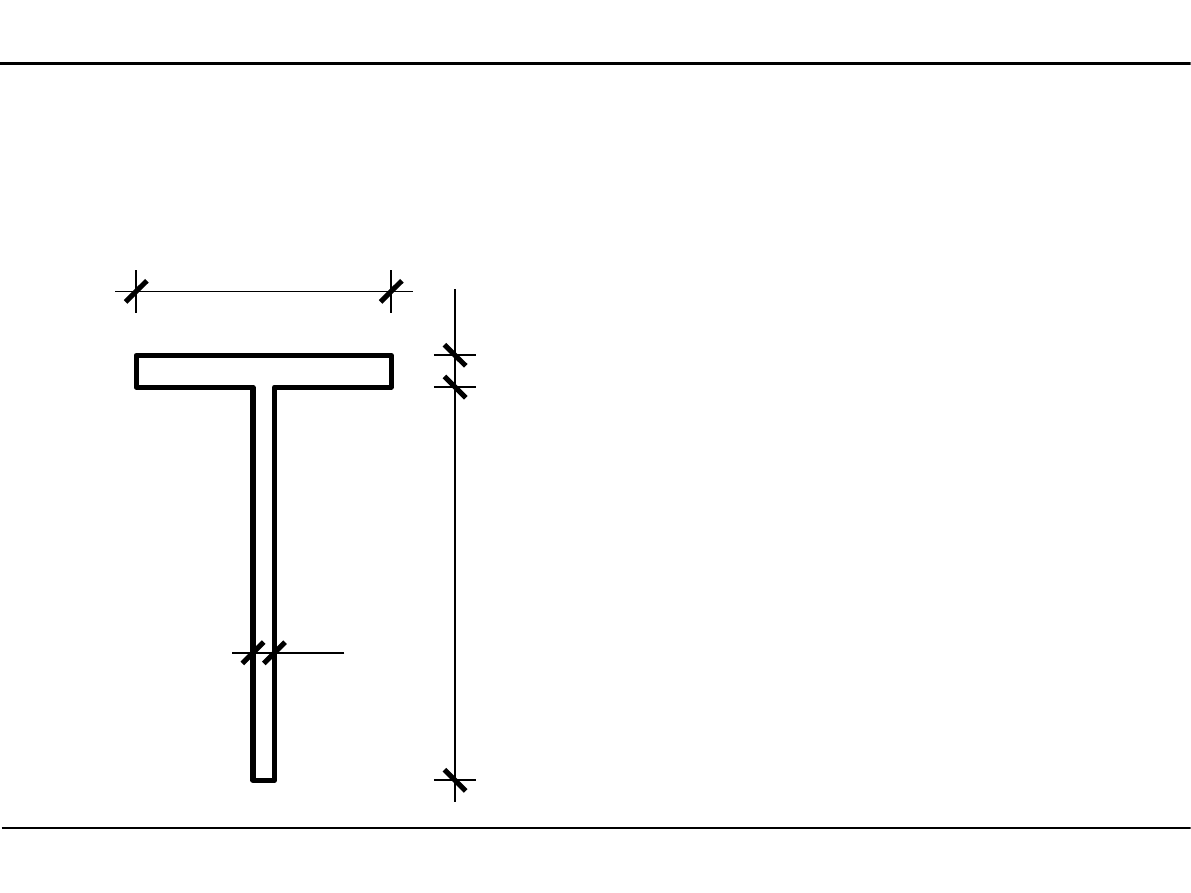
2.7. Charakterystyki geometryczne przekroju teowego
Zadanie 3
Wyznaczyć charakterystyki geometryczne
przekroju teowego przedstawionego na
poniższym rysunku.
[cm]
14,0
2,
0
36
,0
1,0
2. Charakterystyki geometryczne przekroju pręta
51
Dr inż. Justyna Grzymisławska
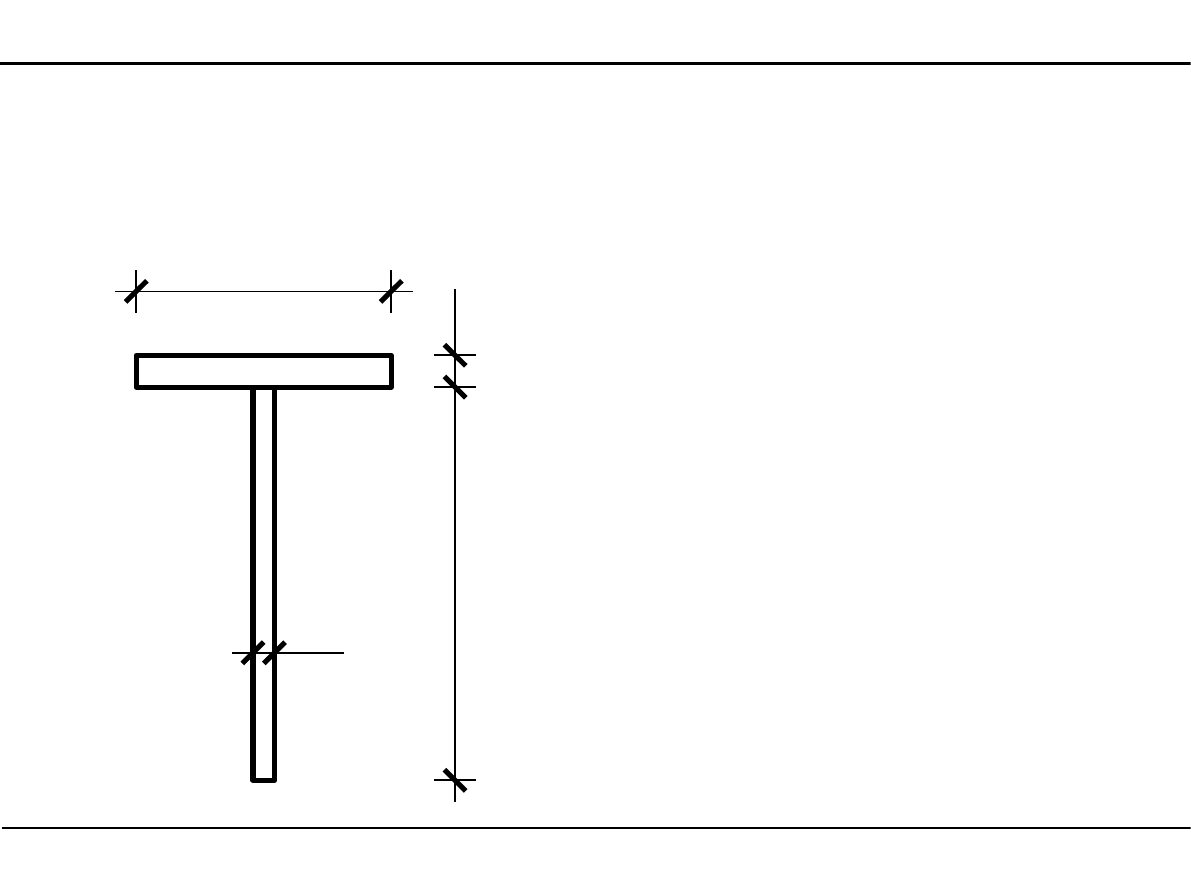
2.7. Charakterystyki geometryczne przekroju teowego
Pole powierzchni przekroju teowego
[cm]
A=14,0⋅2,036,0⋅1,0=64,0cm
2
14,0
2,
0
36
,0
1,0
2. Charakterystyki geometryczne przekroju pręta
52
Dr inż. Justyna Grzymisławska
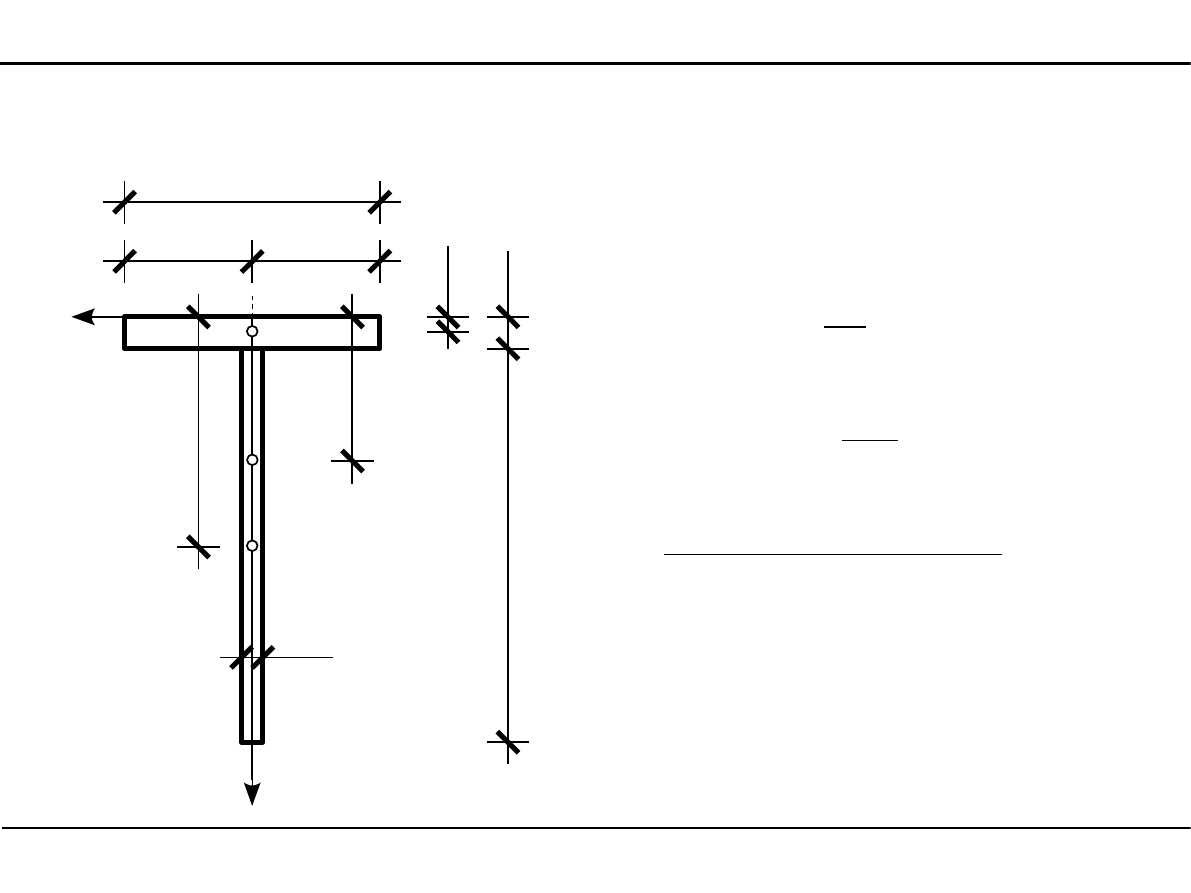
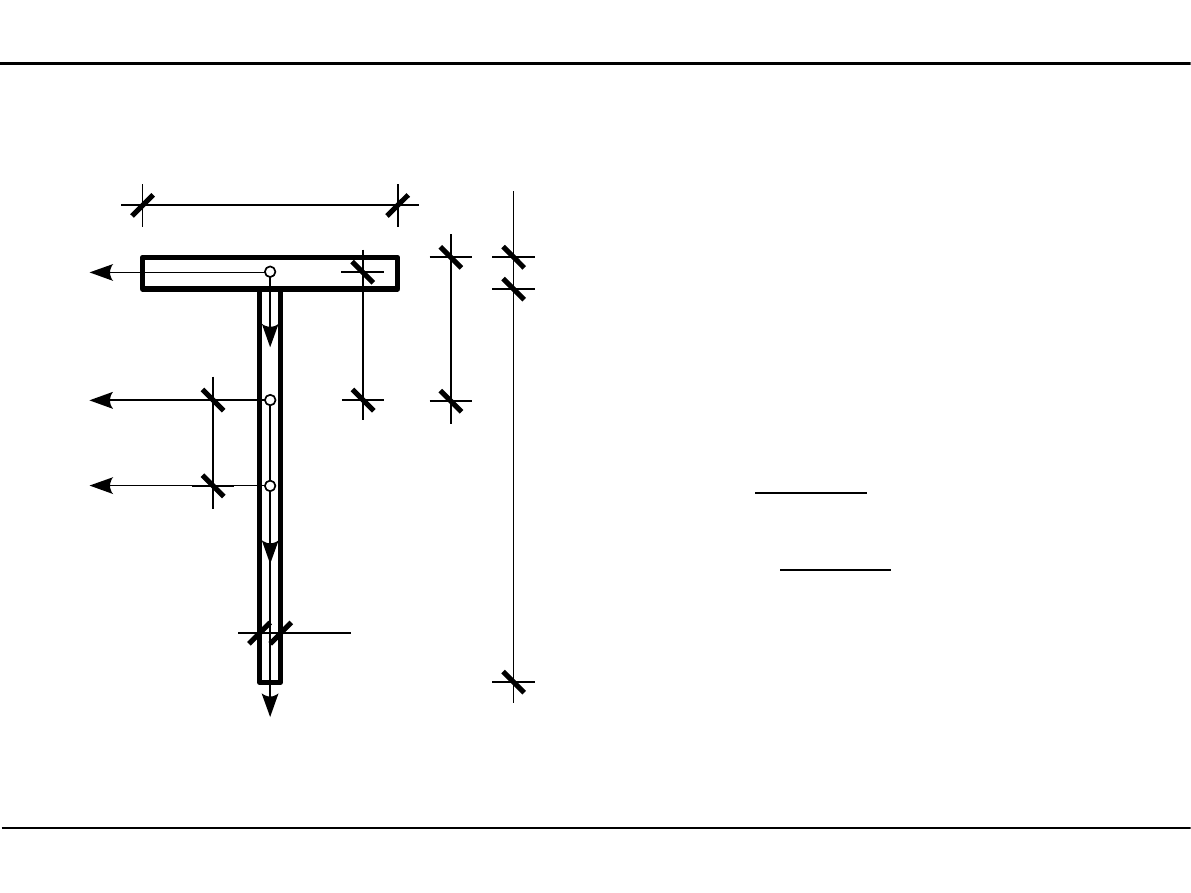
2.7. Charakterystyki geometryczne przekroju teowego
Położenie środka ciężkości
przekroju teowego
[cm]
Y
P
Z
P
sc
1
z
1
=
2,0
2
=
1,0 cm
1,
0
sc
2
z
2
=
2,0
36,0
2
=
20,0cm
z
C
=
14,0⋅2,0⋅1,036,0⋅1,0⋅20,0
14,0⋅2,036,0⋅1,0
=
11,69cm
sc
14,0
2,
0
36
,0
1,0
7,0
7,0
20
,0
11
,6
9
2. Charakterystyki geometryczne przekroju pręta
53
Dr inż. Justyna Grzymisławska
Y
02
Z
02
Y
01
Z
01
Y
0
=Y
gl
Z
0
=Z
gl
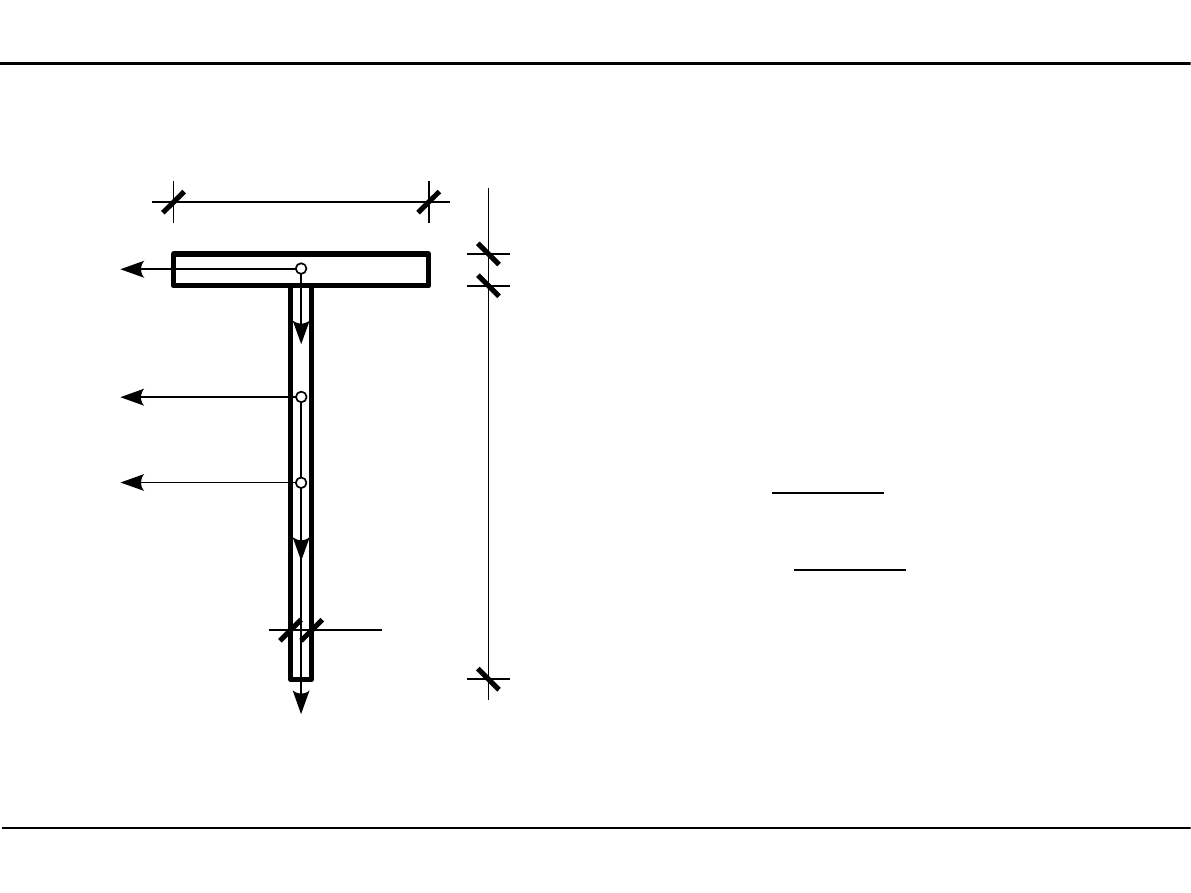
2.7. Charakterystyki geometryczne przekroju teowego
Główne momenty bezwładności
przekroju teowego
[cm]
1,0
sc
sc
1
z
01
=
1,0−11,69=−10,69 cm
sc
2
z
02
=
20,0−11,69=8,310 cm
J
Y0
=
J
Ygl
=
14,0⋅2,0
3
12
−
10,69
2
⋅
14,0⋅2,0
1,0⋅36,0
3
12
8,310
2
⋅
1,0⋅36,0=
=
9583 cm
4
14,0
2,
0
36
,0
11
,6
9
10
,6
9
8,
31
0
2. Charakterystyki geometryczne przekroju pręta
54
Dr inż. Justyna Grzymisławska
2.7. Charakterystyki geometryczne przekroju teowego
Główne momenty bezwładności
przekroju teowego
[cm]
1,0
Y
0
=Y
gl
sc
Z
0
=Z
gl
sc
1
Y
01
Z
01
y
01
=
0,0 cm
sc
2
Y
02
Z
02
y
02
=
0,0 cm
J
Z0
=
J
Zgl
=
2,0⋅14,0
3
12
0,0
2
⋅
14,0⋅2,0
36,0⋅1,0
3
12
0,0
2
⋅
1,0⋅36,0=
=
460,3cm
4
14,0
2,
0
36
,0
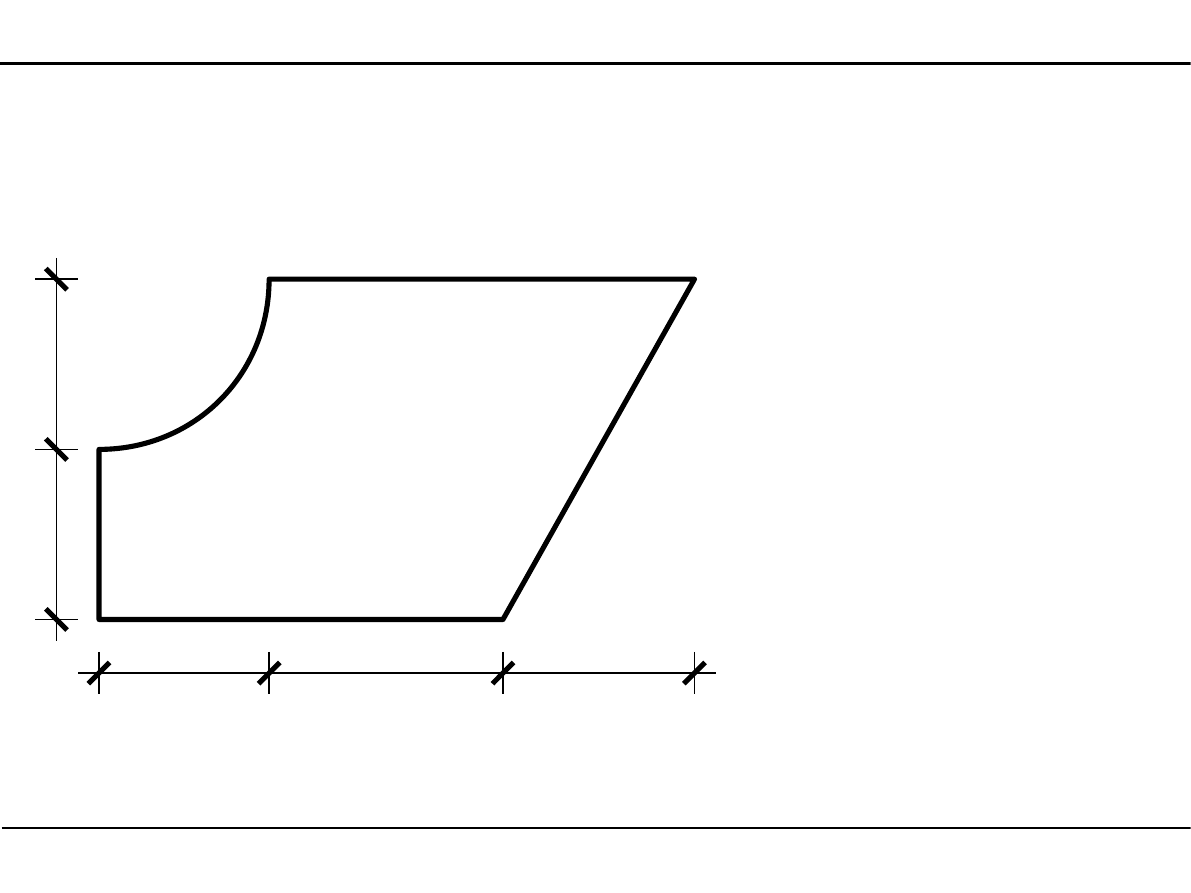
2. Charakterystyki geometryczne przekroju pręta
55
Dr inż. Justyna Grzymisławska
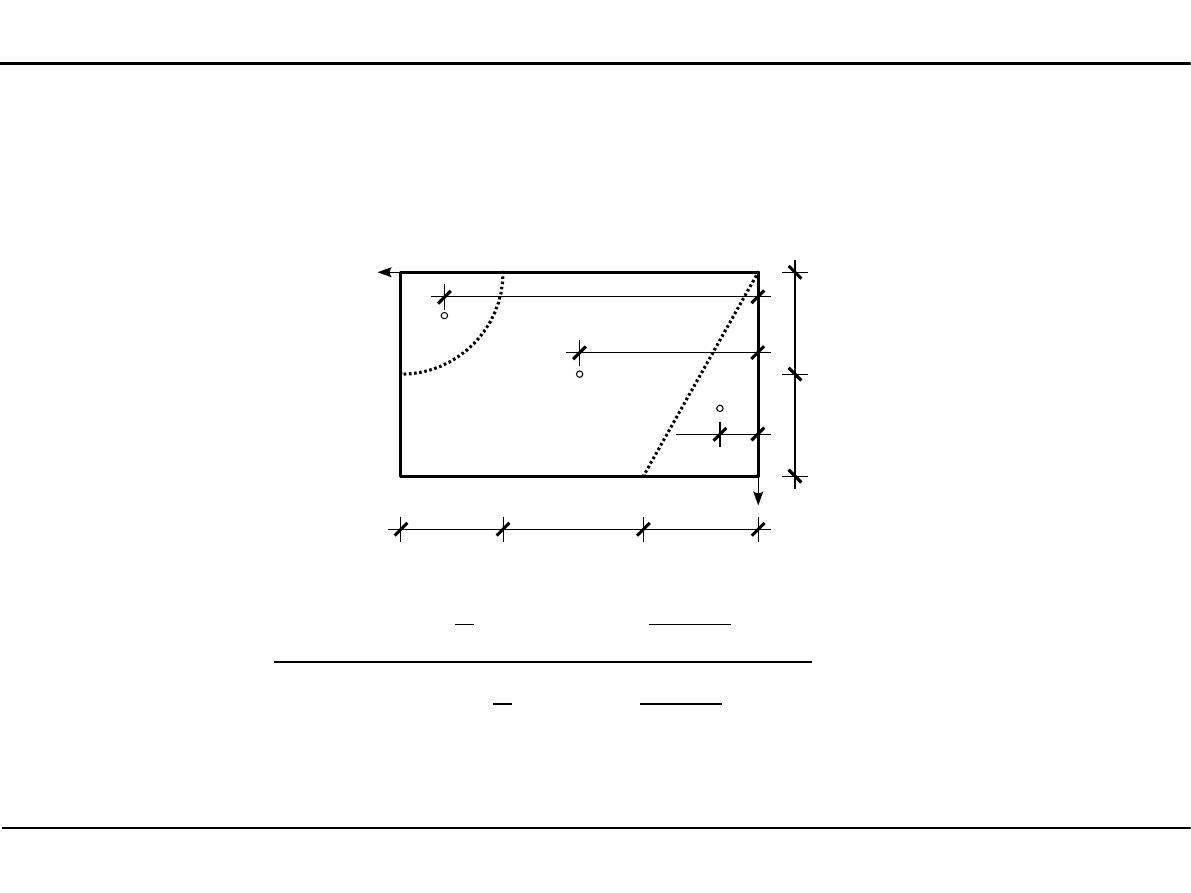
Wyznaczyć główne
momenty bezwładności
przekroju przedstawio-
nego na poniższym
rysunku.
2.8. Charakterystyki geometryczne dowolnego przekroju
Zadanie 4
[cm]
4,0
5,5
4,5
4,
0
4,
0
2. Charakterystyki geometryczne przekroju pręta
56
Dr inż. Justyna Grzymisławska
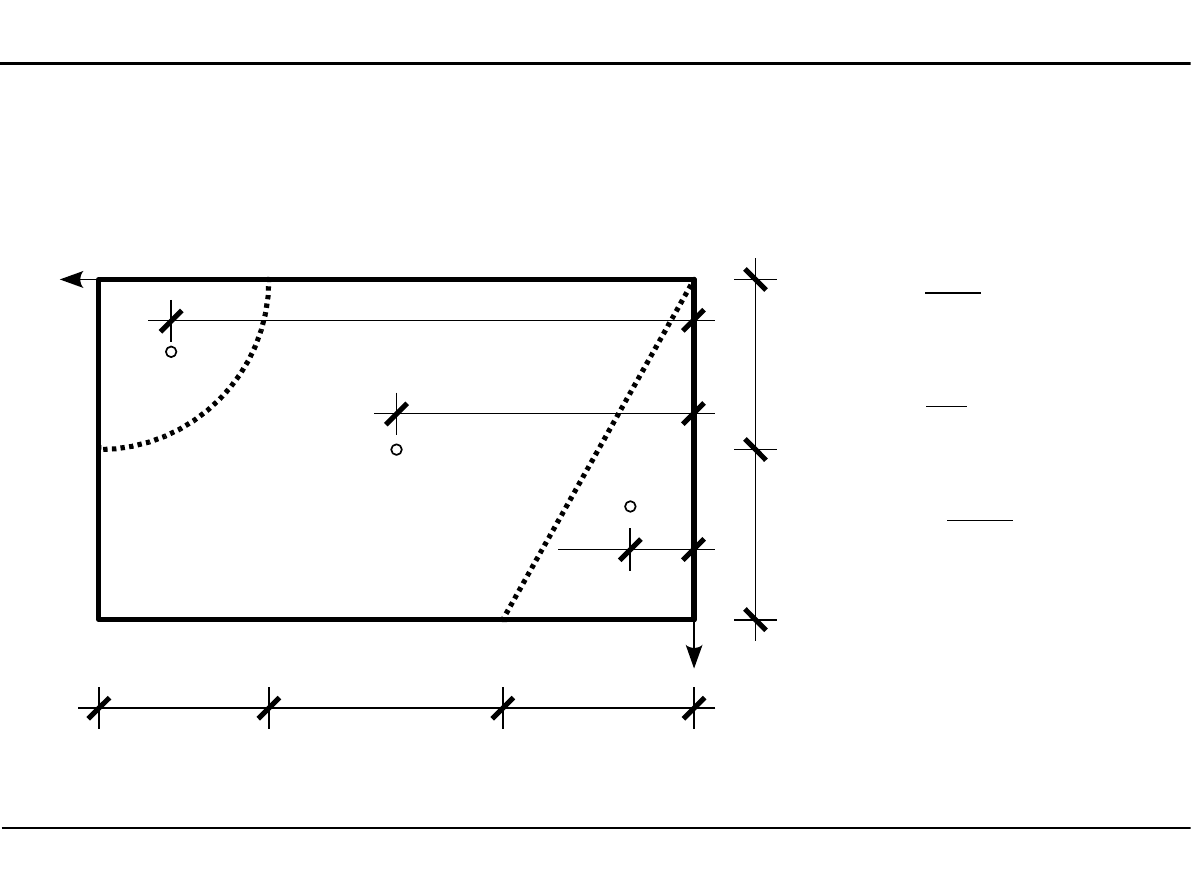
2.8. Charakterystyki geometryczne dowolnego przekroju
Położenie środka ciężkości dowolnego przekroju
y
1
=
14,0
2
=
7,0 cm
y
2
=
4,5
3
=
1,50 cm
y
3
=
14,0−
4⋅4,0
3⋅
=
12,30cm
[cm]
Y
P
Z
P
4,0
5,5
4,5
4,
0
4,
0
sc
1
7,0
sc
2
1,50
sc
3
12,30
2. Charakterystyki geometryczne przekroju pręta
57
Dr inż. Justyna Grzymisławska
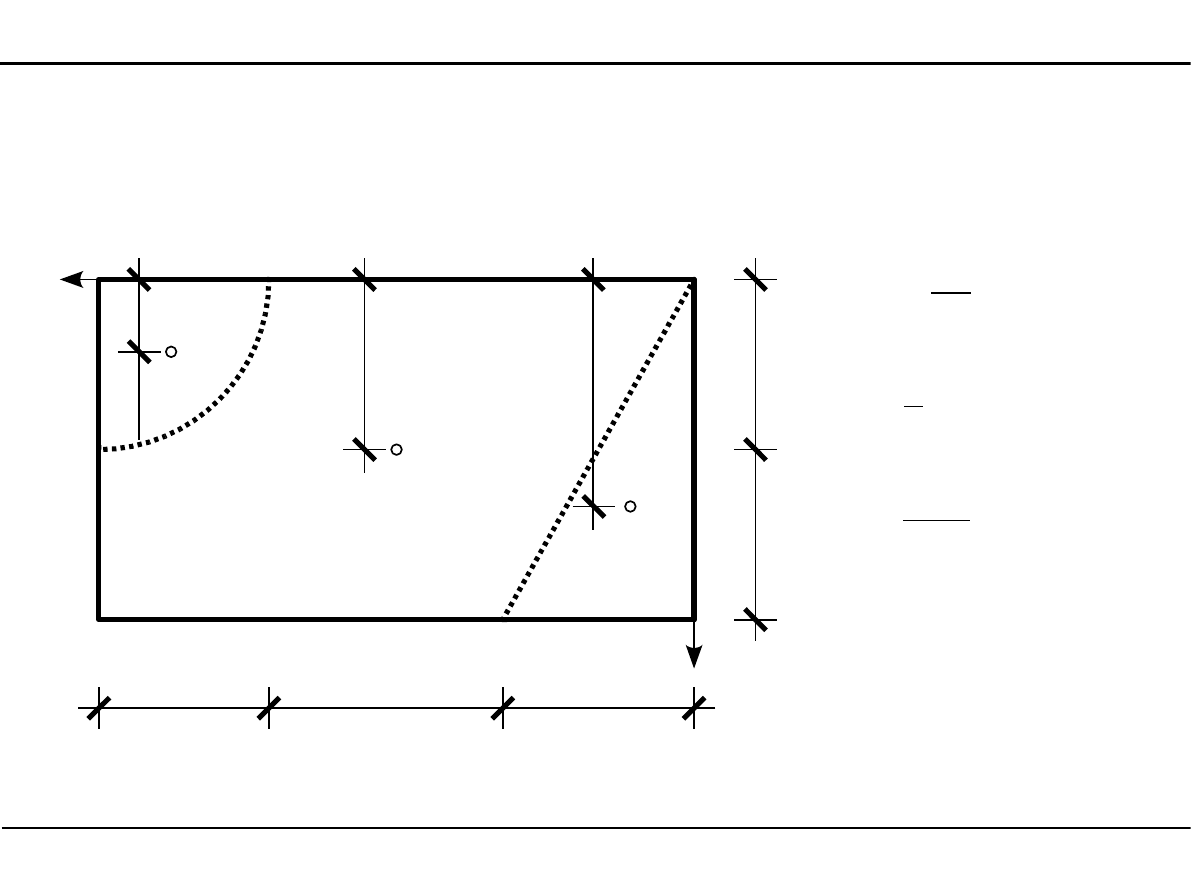
y
C
=
14,0⋅8,0⋅7,0−
1
2
⋅
4,5⋅8,0⋅1,5−
⋅
4,0
2
4
⋅
12,30
14,0⋅8,0−
1
2
⋅
4,5⋅8,0−
⋅
4,0
2
4
=
7,398cm
2.8. Charakterystyki geometryczne dowolnego przekroju
Położenie środka ciężkości dowolnego przekroju
4,0
5,5
4,5
4,
0
[cm]
4,
0
Y
P
Z
P
sc
1
7,0
12,30
1,50
sc
2
sc
3
2. Charakterystyki geometryczne przekroju pręta
58
Dr inż. Justyna Grzymisławska
2.8. Charakterystyki geometryczne dowolnego przekroju
z
1
=
8,0
2
=
4,0 cm
z
2
=
2
3
⋅
8,0=5,333cm
z
3
=
4⋅4,0
3⋅
=
1,698 cm
Położenie środka ciężkości dowolnego przekroju
[cm]
4,0
5,5
4,5
4,
0
4,
0
Y
P
Z
P
sc
1
4,
0
sc
2
5,
33
3
sc
3
1,
69
8
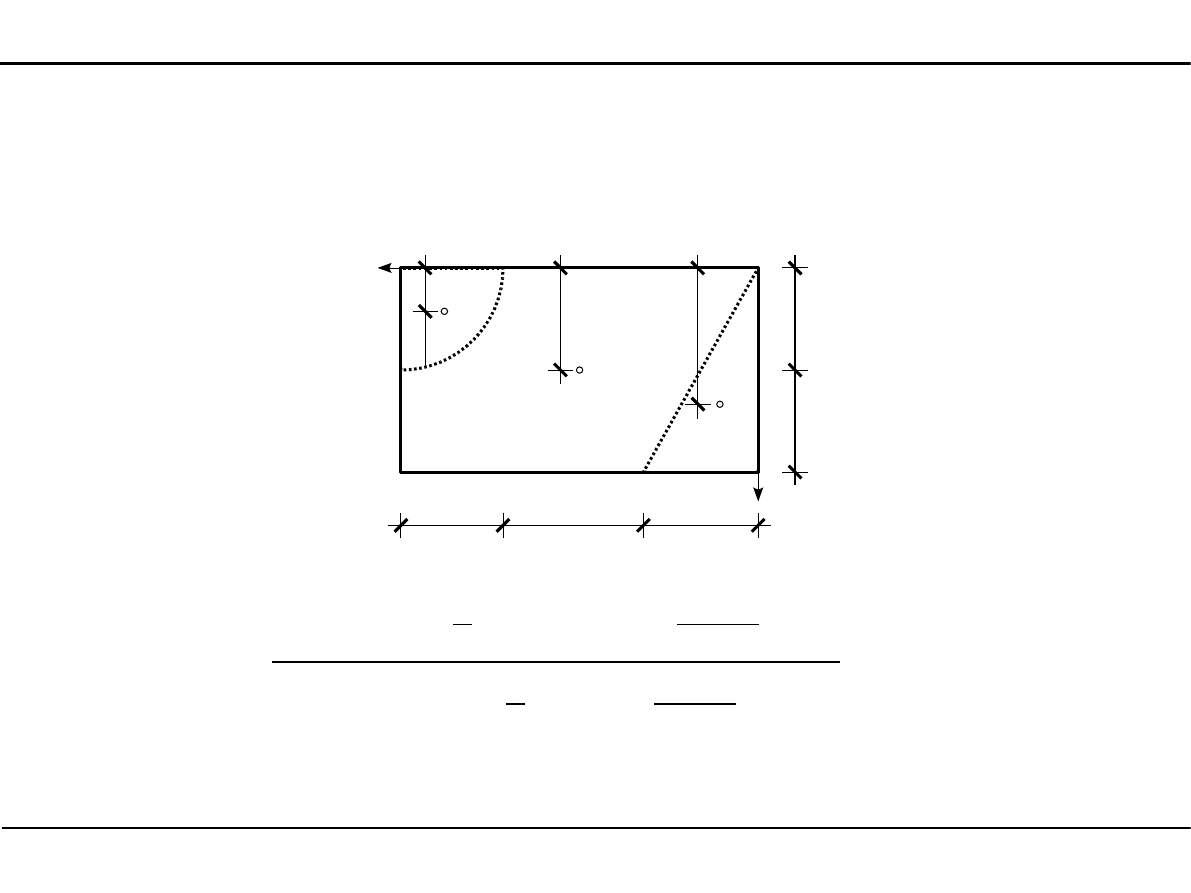
2. Charakterystyki geometryczne przekroju pręta
59
Dr inż. Justyna Grzymisławska
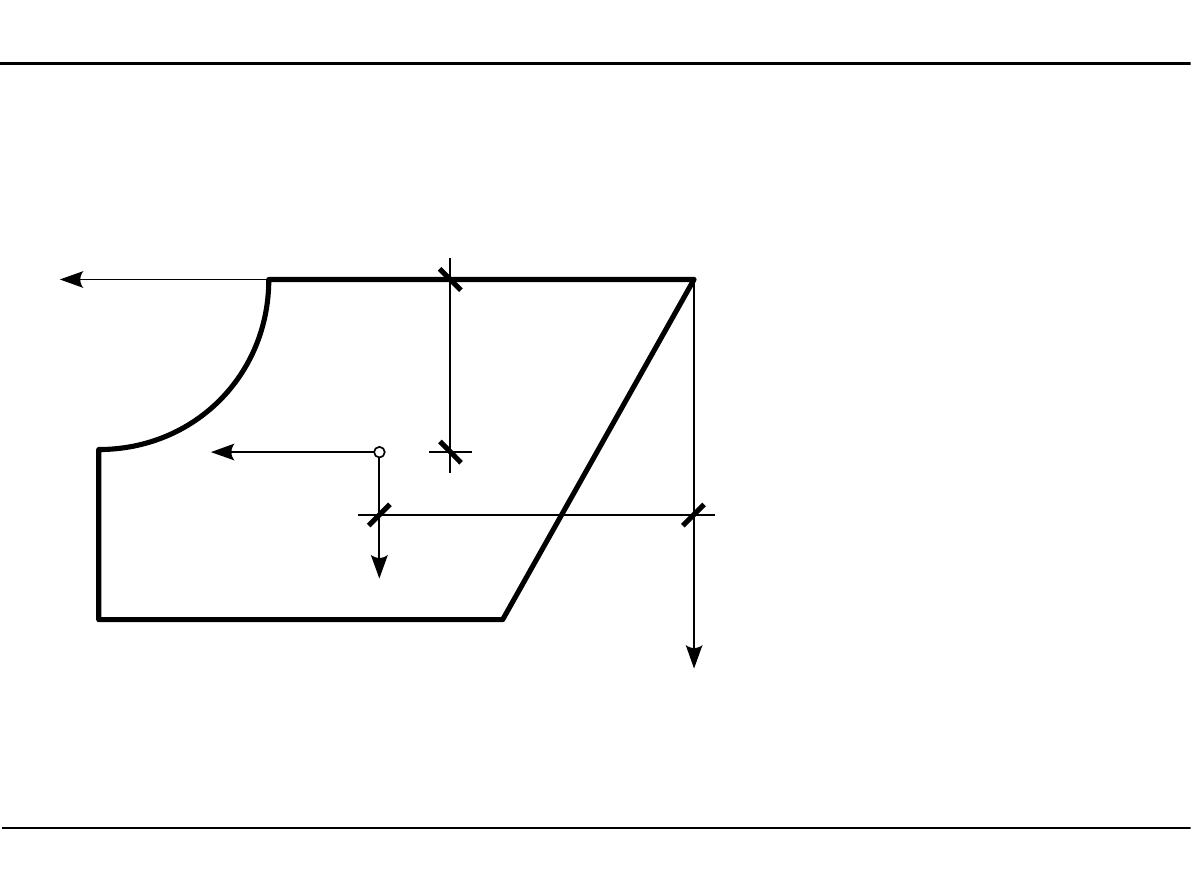
2.8. Charakterystyki geometryczne dowolnego przekroju
Położenie środka ciężkości dowolnego przekroju
z
C
=
14,0⋅8,0⋅4,0−
1
2
⋅
4,5⋅8,0⋅5,333−
⋅
4,0
2
4
⋅
1,698
14,0⋅8,0−
1
2
⋅
4,5⋅8,0−
⋅
4,0
2
4
=
4,061cm
4,0
5,5
4,5
4,
0
[cm]
4,
0
Y
P
Z
P
sc
1
sc
2
sc
3
4
,0
5,
3
33
1
,6
98
2. Charakterystyki geometryczne przekroju pręta
60
Dr inż. Justyna Grzymisławska
Y
0
Z
0
2.8. Charakterystyki geometryczne dowolnego przekroju
Położenie środka ciężkości dowolnego przekroju
y
C
=
7,398cm
z
C
=
4,061 cm
Y
P
Z
P
Z
P
[cm]
7,398
4,
06
1
sc
2. Charakterystyki geometryczne przekroju pręta
61
Dr inż. Justyna Grzymisławska
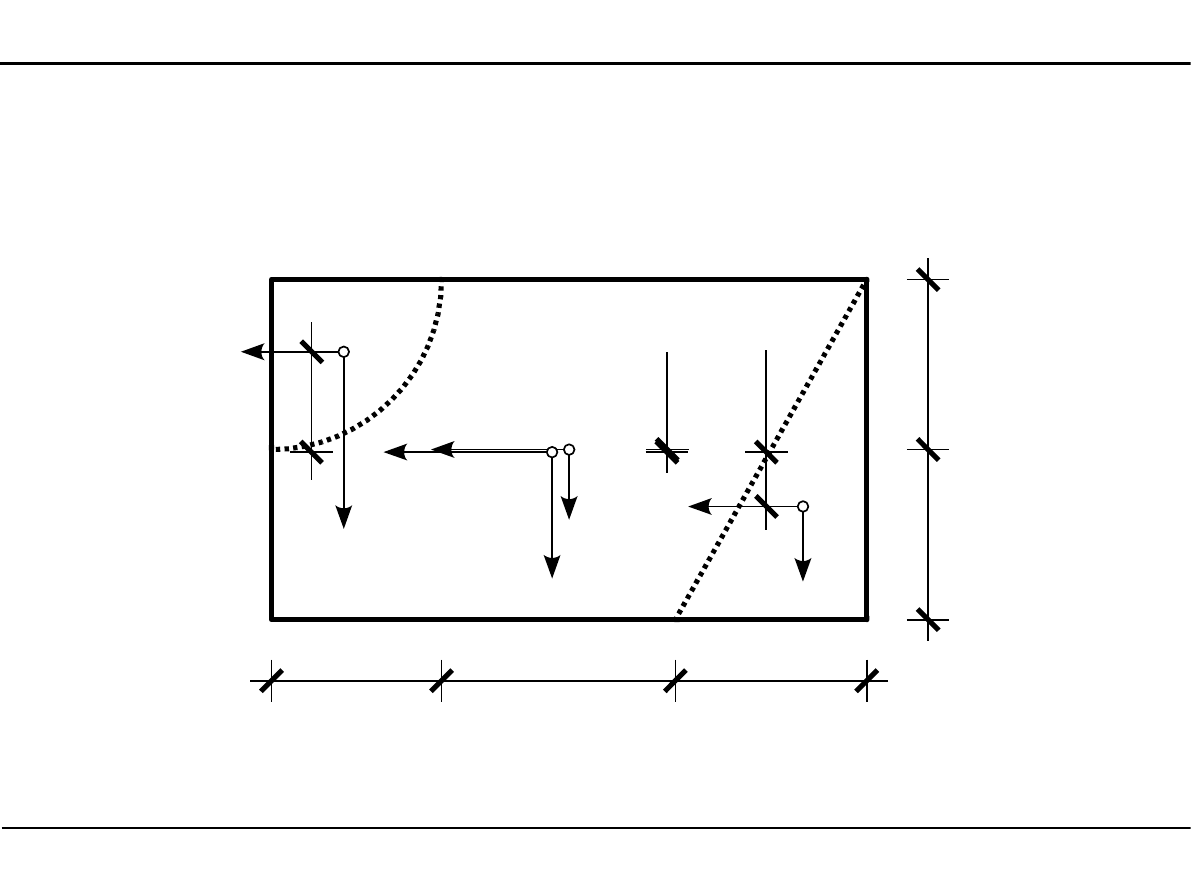
2.8. Charakterystyki geometryczne dowolnego przekroju
Momenty bezwładności dowolnego przekroju w osiach środkowych
z
01
=
4,0−4,061=−0,061cm
z
02
=
5,333−4,061=1,272 cm z
03
=
1,698−4,061=−2,363 cm
[cm]
4,0
5,5
4,5
4,
0
4,
0
sc
1
Z
01
Y
01
sc
Y
0
Z
0
0,
06
1
sc
2
Z
02
Y
02
1,
27
2
sc
3
Y
03
Z
03
2,
36
3
2. Charakterystyki geometryczne przekroju pręta
62
Dr inż. Justyna Grzymisławska
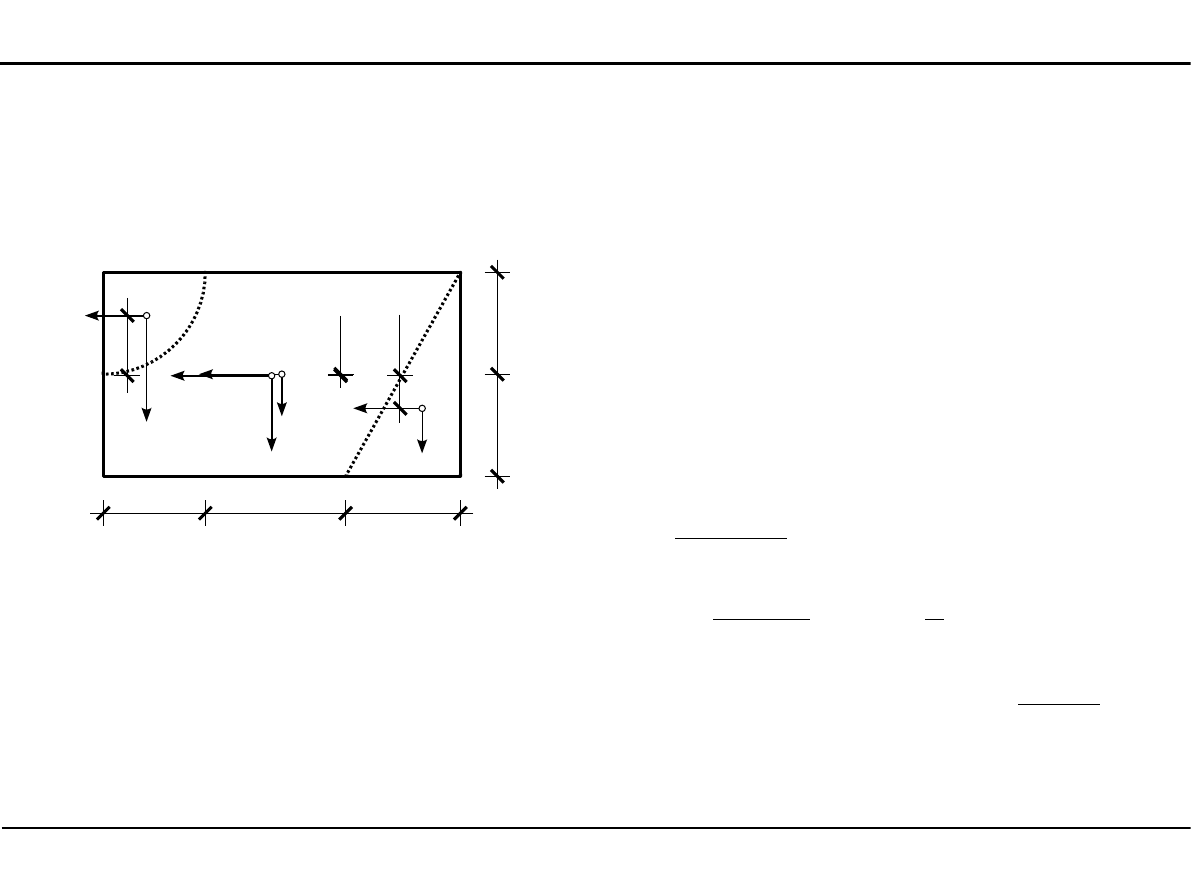
2.8. Charakterystyki geometryczne dowolnego przekroju
Momenty bezwładności dowolnego przekroju w osiach środkowych
z
01
=−
0,061cm
z
02
=
1,272 cm
z
03
=−
2,363 cm
J
Y0
=
14,0⋅8,0
3
12
−
0,061
2
⋅
14,0⋅8,0−
−
4,5⋅8,0
3
36,0
1,272
2
⋅
1
2
⋅
4,5⋅8,0
−
−
0,05488⋅4,0
4
−
2,363
2
⋅
⋅
4,0
2
4
=
=
420,4 cm
4
4,0
5,5
4,5
4,
0
4,
0
sc
1
sc
2
sc
3
0,
06
1
1,
2
72
2
,3
63
sc
Y
0
Z
0
[cm]
Z
01
Y
01
Z
02
Y
02
Y
03
Z
03
2. Charakterystyki geometryczne przekroju pręta
63
Dr inż. Justyna Grzymisławska
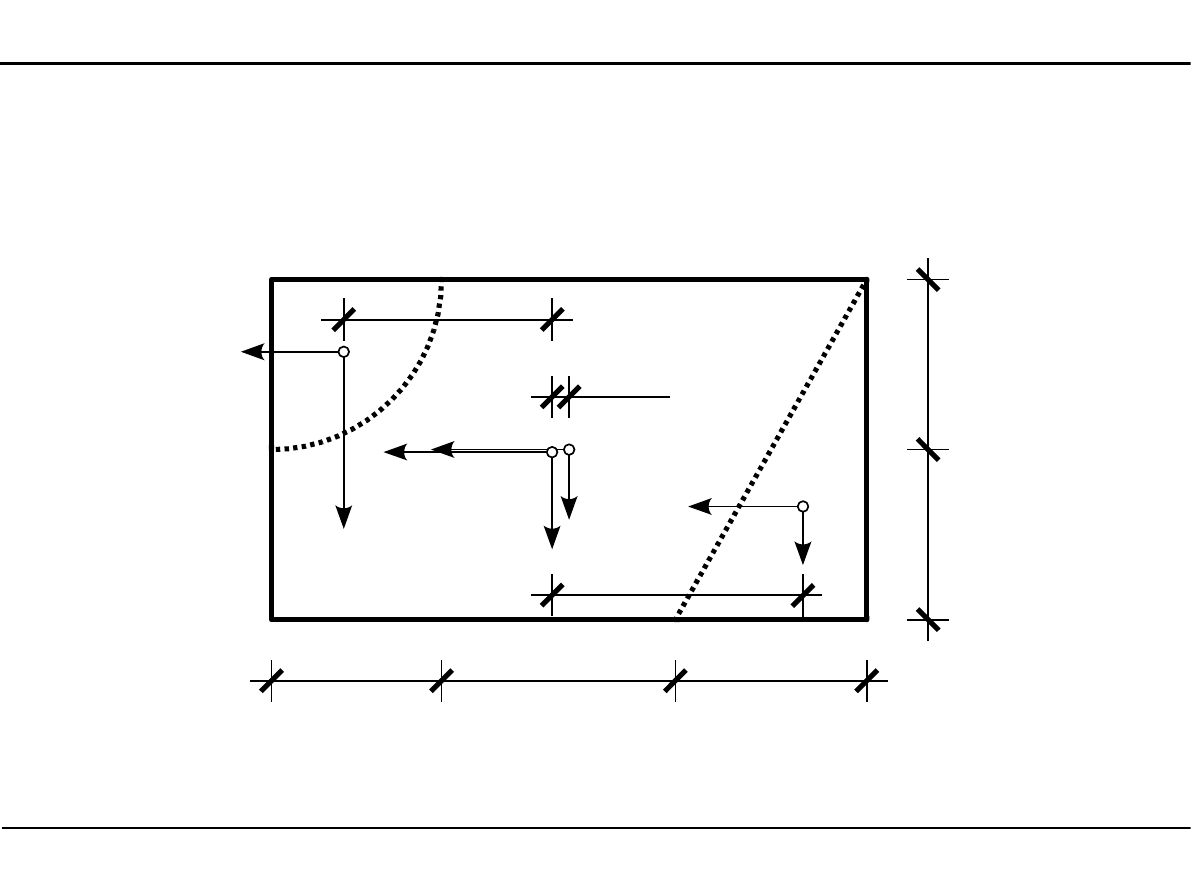
2.8. Charakterystyki geometryczne dowolnego przekroju
Momenty bezwładności dowolnego przekroju w osiach środkowych
y
01
=
7,0−7,398=−0,398cm
y
02
=
1,5−7,398=−5,898 cm y
03
=
12,30−7,398=−4,902 cm
[cm]
4,0
5,5
4,5
4,
0
4,
0
sc
1
Z
01
Y
01
sc
Y
0
Z
0
0,398
sc
2
Z
02
Y
02
5,898
sc
3
Y
03
Z
03
4,902
2. Charakterystyki geometryczne przekroju pręta
64
Dr inż. Justyna Grzymisławska
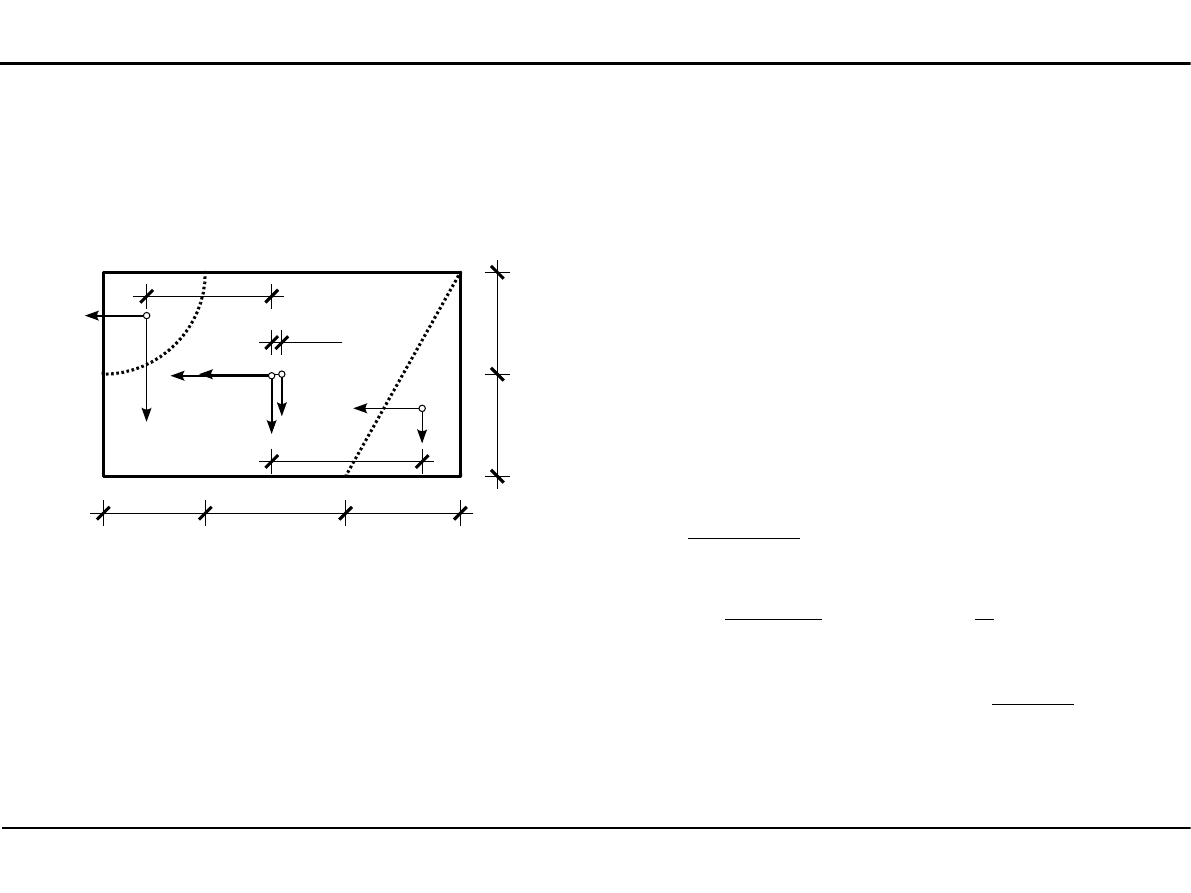
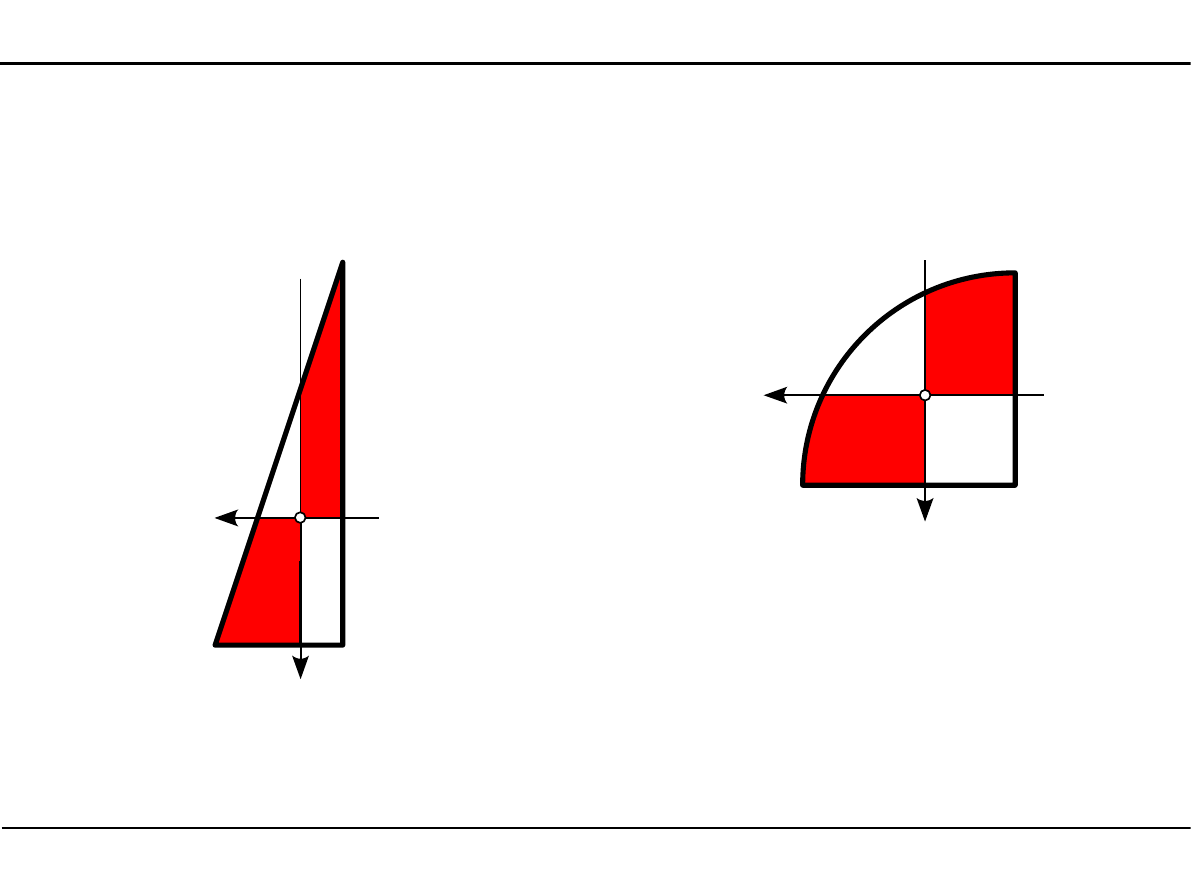
2.8. Charakterystyki geometryczne dowolnego przekroju
Momenty bezwładności dowolnego przekroju w osiach środkowych
y
01
=−
0,398cm
y
02
=−
5,898 cm
y
03
=
4,902cm
J
Z0
=
8,0⋅14,0
3
12
−
0,398
2
⋅
14,0⋅8,0−
−
8,0⋅4,5
3
36,0
−
5,898
2
⋅
1
2
⋅
4,5⋅8,0
−
−
0,05488⋅4,0
4
4,902
2
⋅
⋅
4,0
2
4
=
=
884,4 cm
4
4,0
5,5
4,5
4,
0
4,
0
sc
1
sc
2
sc
3
sc
Y
0
Z
0
[cm]
Z
01
Y
01
Z
02
Y
02
Y
03
Z
03
0,398
5,898
4,902
2. Charakterystyki geometryczne przekroju pręta
65
Dr inż. Justyna Grzymisławska
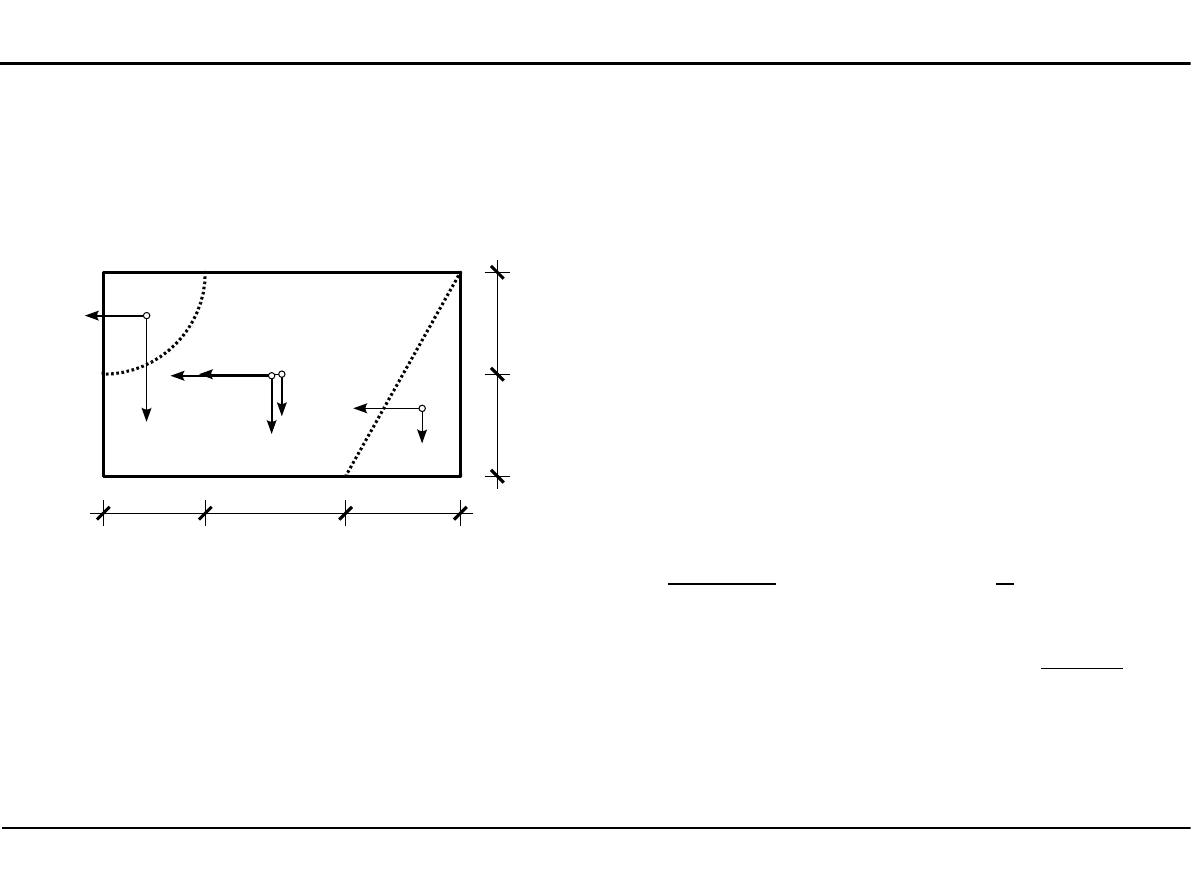
2.8. Charakterystyki geometryczne dowolnego przekroju
Momenty bezwładności dowolnego przekroju w osiach środkowych
sc
3
Y
03
Z
03
sc
2
Y
02
Z
02
2. Charakterystyki geometryczne przekroju pręta
66
Dr inż. Justyna Grzymisławska
2.8. Charakterystyki geometryczne dowolnego przekroju
Momenty bezwładności dowolnego przekroju w osiach środkowych
y
01
=−
0,398cm
y
02
=−
5,898 cm
y
03
=
4,902cm
z
01
=−
0,061cm
z
02
=
1,272 cm
z
03
=−
2,363 cm
J
Y0Z0
=
0,0
−
0,398
⋅
−
0,061
⋅
14,0⋅8,0−
−
8,0
2
⋅
4,5
2
72
1,272⋅
−
5,898
⋅
1
2
⋅
4,5⋅8,0
−
−
0,01647⋅4,0
4
−
2,363
⋅
4,902⋅
⋅
4,0
2
4
=
=
261,2cm
4
4,0
5,5
4,5
4,
0
4,
0
sc
1
sc
2
sc
3
sc
Y
0
Z
0
[cm]
Z
01
Y
01
Z
02
Y
02
Y
03
Z
03

2. Charakterystyki geometryczne przekroju pręta
67
Dr inż. Justyna Grzymisławska
2.8. Charakterystyki geometryczne dowolnego przekroju
Główne momenty bezwładności dowolnego przekroju
J
Y0
=
420,4 cm
4
J
Z0
=
884,4cm
4
J
Y0Z0
=
261,2cm
4
tg
2⋅
gl
=
−
2⋅261,2
420,4−884,4
=
1,126
gl
=
24,19 °
J
Ygl
=
420,4884,4
2
420,4−884,4
2
⋅
cos
2⋅24,19°
−
261,2⋅sin
2⋅24,19 °
=
303,1cm
4
J
Zgl
=
420,4884,4
2
−
420,4−884,4
2
⋅
cos
2⋅24,19 °
261,2⋅sin
2⋅24,19°
=
1002 cm
4

2. Charakterystyki geometryczne przekroju pręta
68
Dr inż. Justyna Grzymisławska
2.8. Charakterystyki geometryczne dowolnego przekroju
Główne momenty bezwładności dowolnego przekroju
J
Ygl
=
J
2
=
303,1 cm
4
J
Zgl
=
J
1
=
1002 cm
4
J
1/2
=
420,4884,4
2
±
420,4−884,4
2
2
261,2
2
=
{
1002 cm
4
303,1 cm
4

2. Charakterystyki geometryczne przekroju pręta
69
Dr inż. Justyna Grzymisławska
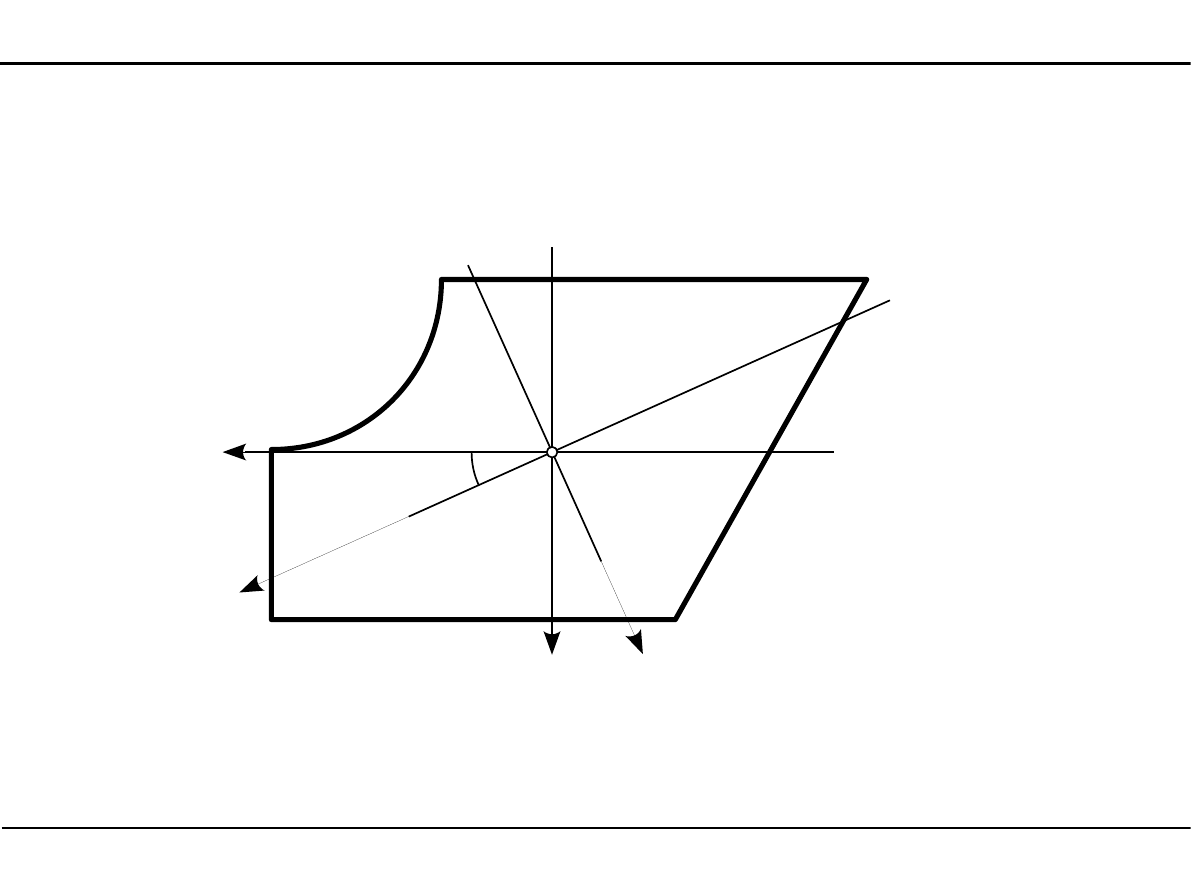
2.8. Charakterystyki geometryczne dowolnego przekroju
Główne momenty bezwładności dowolnego przekroju
J
Y0
=
420,4 cm
4
J
Z0
=
884,4cm
4
J
Y0Z0
=
261,2cm
4
I
1
=
420,4884,2=1305 cm
4
J
Ygl
=
J
2
=
303,1 cm
4
J
Zgl
=
J
1
=
1002 cm
4
I
1
=
303,11002=1305 cm
4
I
2
=
420,4⋅884,4−261,2
2
=
303576cm
4
≈
303600 cm
4
I
2
=
303,1⋅1002=303706 cm
4
≈
303700 cm
4
2. Charakterystyki geometryczne przekroju pręta
70
Dr inż. Justyna Grzymisławska
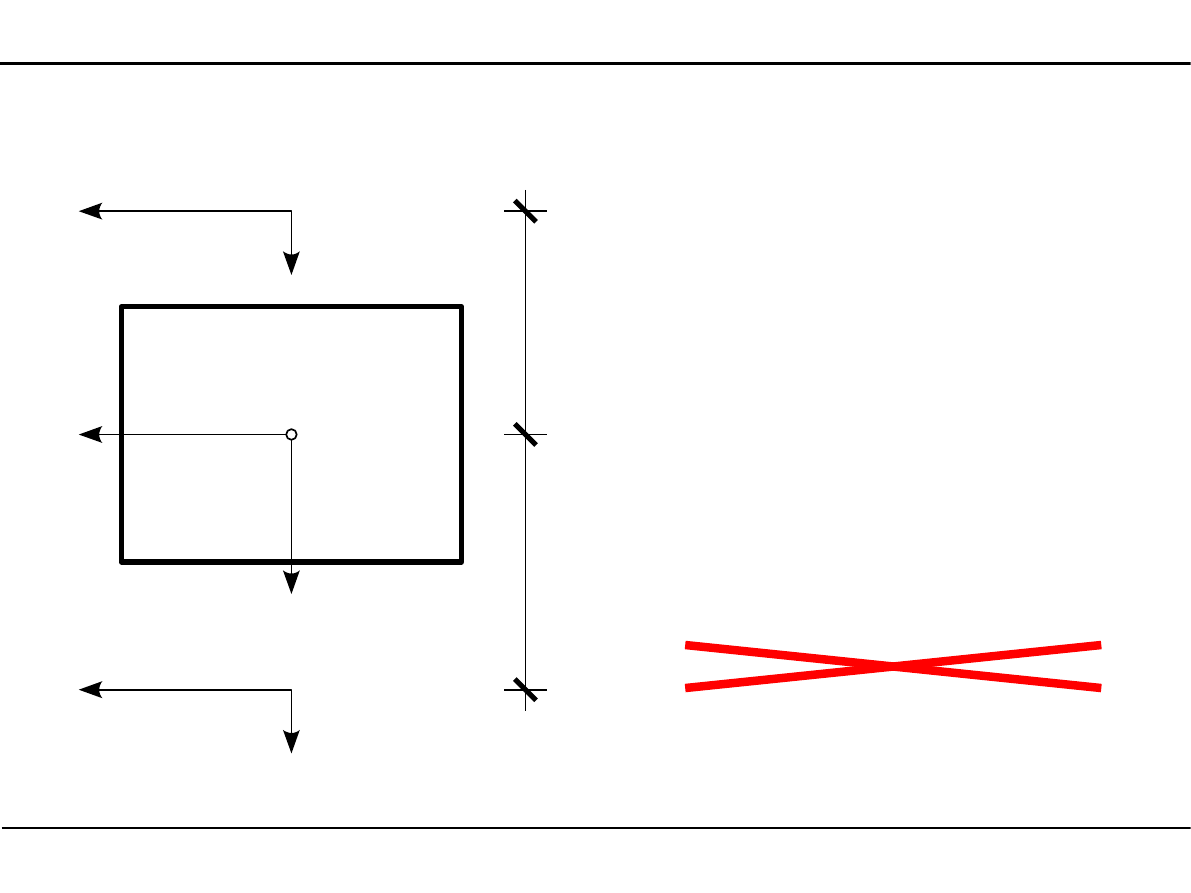
Y
gl
=2
Z
gl
=1
2.8. Charakterystyki geometryczne dowolnego przekroju
Główne momenty bezwładności dowolnego przekroju
Y
0
Z
0
sc
24
,1
9
0
2. Charakterystyki geometryczne przekroju pręta
71
Dr inż. Justyna Grzymisławska
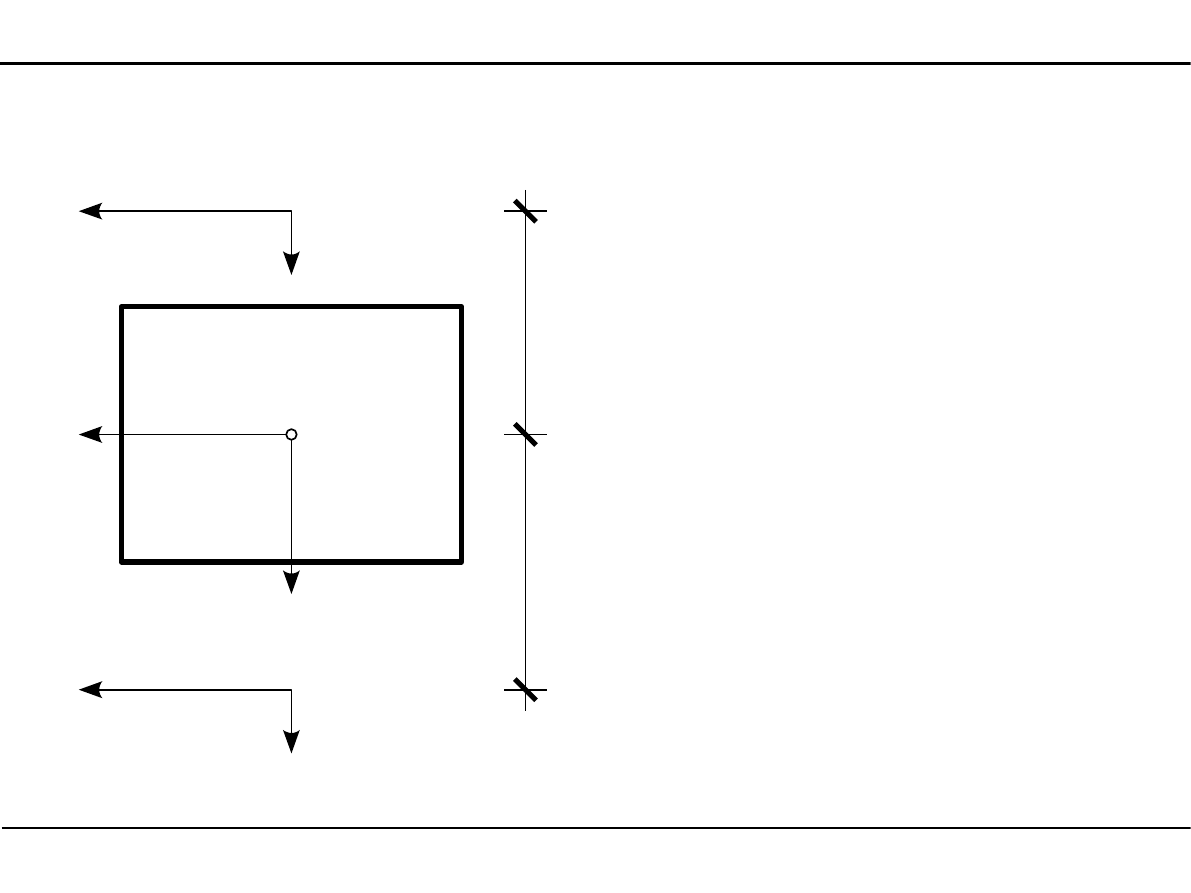
2.9. Zastosowanie twierdzenia Steinera
Zadanie 5
Dany jest przekrój prostokątny
o polu powierzchni równym
60,0 cm
2
oraz moment bezwład-
ności tego przekroju względem
osi Y
1
równy 3120 cm
4
. Wyznaczyć
wartość momentu bezwładności
względem osi Y
2
.
Y
0
Z
0
sc
[cm]
7,
0
5,
0
Y
1
Z
1
J
Y1
=
3120 cm
4
Y
2
Z
2
J
Y2
=
312012,0
2
⋅
60,0=11760 cm
4
A = 60,0 cm
2
2. Charakterystyki geometryczne przekroju pręta
72
Dr inż. Justyna Grzymisławska
2.9. Zastosowanie twierdzenia Steinera
Zadanie 5
J
Y1
=
3120 cm
4
J
Y1
=
J
Y0
z
C1
2
⋅
A
3120=J
Y0
7,0
2
⋅
60,0
J
Y0
=
3120−7,0
2
⋅
60,0=180,0 cm
4
J
Y2
=
J
Y0
z
C2
2
⋅
A
J
Y2
=
180,05,0
2
⋅
60,0=1680 cm
4
Y
0
Z
0
sc
Y
1
Z
1
Y
2
Z
2
[cm]
7,
0
5,
0
A = 60,0 cm
2

2. Charakterystyki geometryczne przekroju pręta
73
Dr inż. Justyna Grzymisławska
2.10. Kształtowniki walcowane
Kształtowniki walcowane są podstawowym asortymentem wyrobów stalowych.
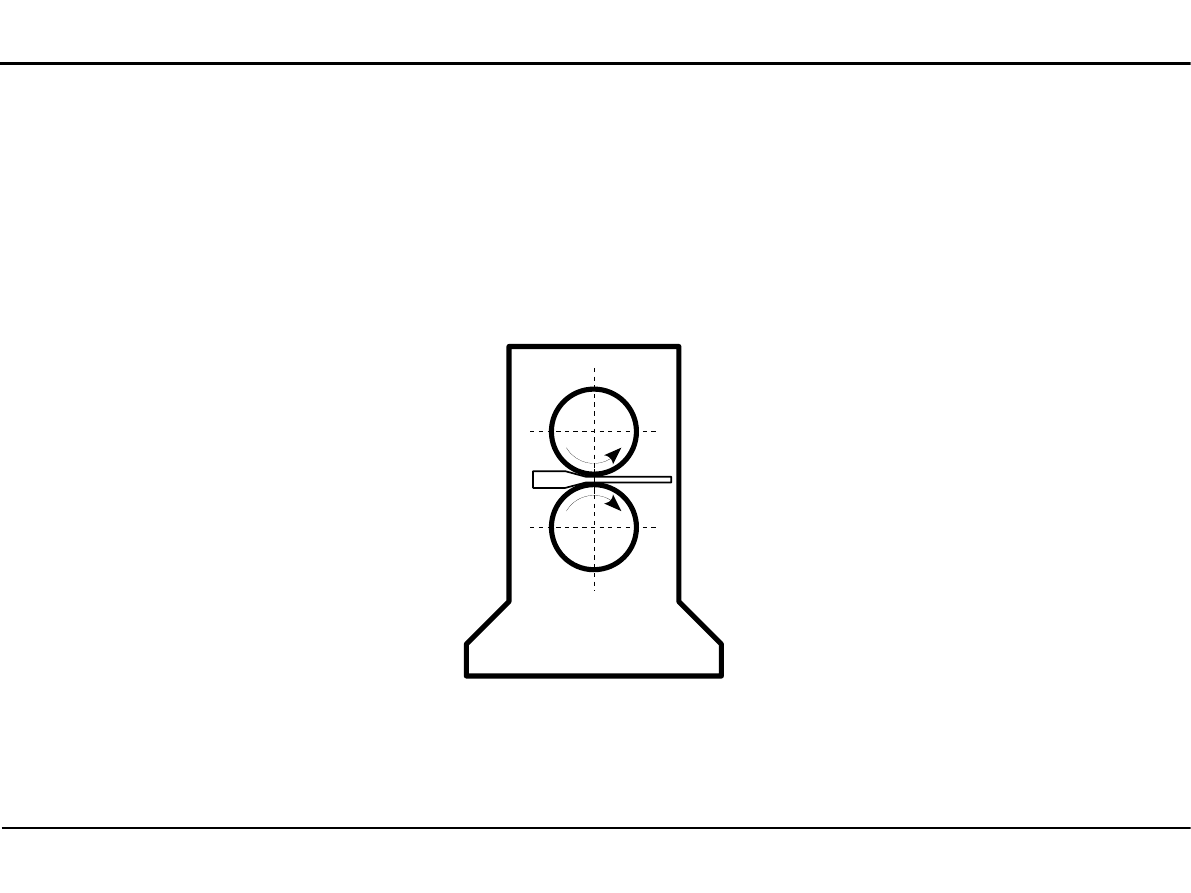
Ogólna charakterystyka kształtowników walcowanych
Walcowanie polega na przepuszczeniu elementu wyjściowego pomiędzy
dwoma walcami obracającymi się w przeciwnych kierunkach.
Odstęp pomiędzy walcami jest regulowany. Na łożyska jednego z walców wywierany
jest nacisk. Jest on potrzebny aby w walcowanym elemencie wywołać
odpowiedni zgniot.
2. Charakterystyki geometryczne przekroju pręta
74
Dr inż. Justyna Grzymisławska
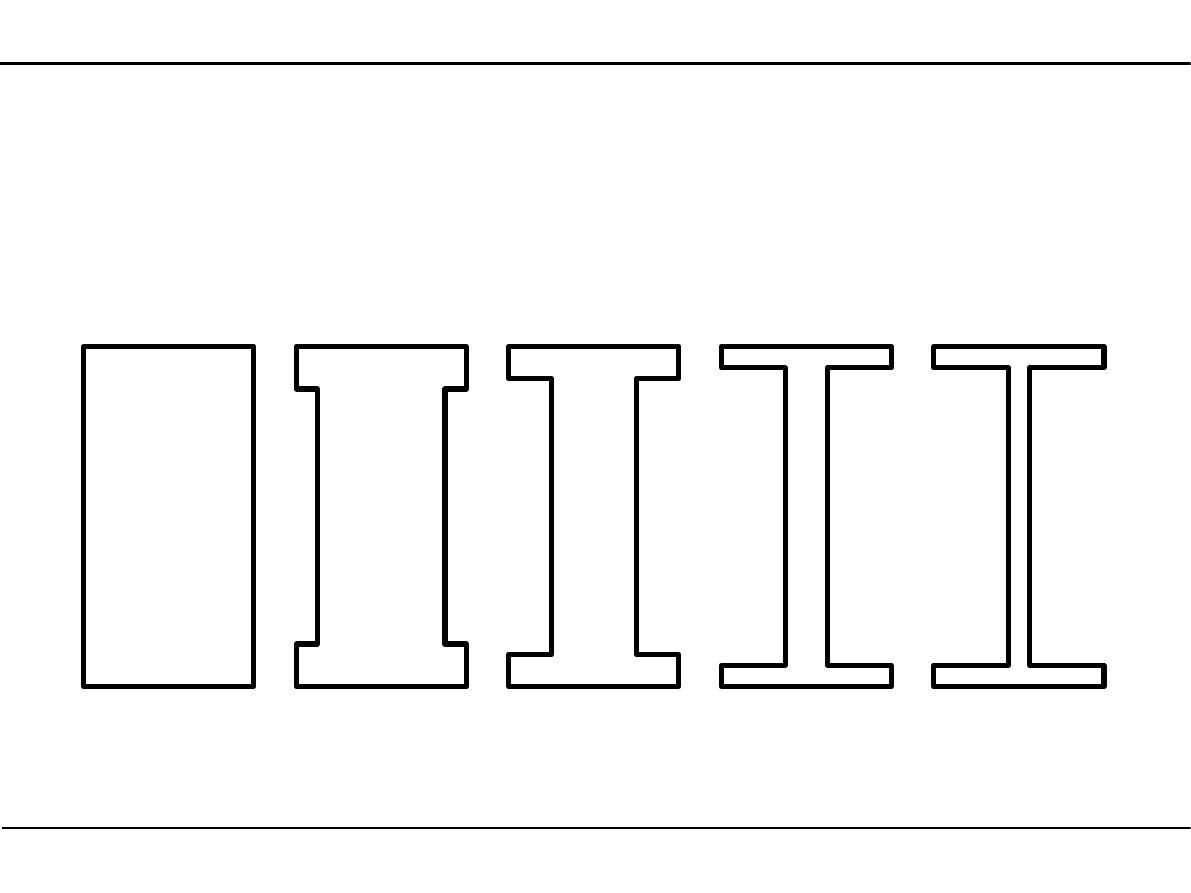
2.10. Kształtowniki walcowane
Ogólna charakterystyka kształtowników walcowanych
Budowa walcarki typu duo.
2. Charakterystyki geometryczne przekroju pręta
75
Dr inż. Justyna Grzymisławska
2.10. Kształtowniki walcowane
Ogólna charakterystyka kształtowników walcowanych
Kolejne etapy walcowania.

2. Charakterystyki geometryczne przekroju pręta
76
Dr inż. Justyna Grzymisławska
2.10. Kształtowniki walcowane
Ogólna charakterystyka kształtowników walcowanych
Charakterystyki geometryczne kształtowników walcowanych odczytujemy z

2. Charakterystyki geometryczne przekroju pręta
77
Dr inż. Justyna Grzymisławska
2.10. Kształtowniki walcowane
Dwuteowniki
Typy dwuteowników:
1. normalne
2. szerokostopowe - HEB
3. równoległościenne - IPE
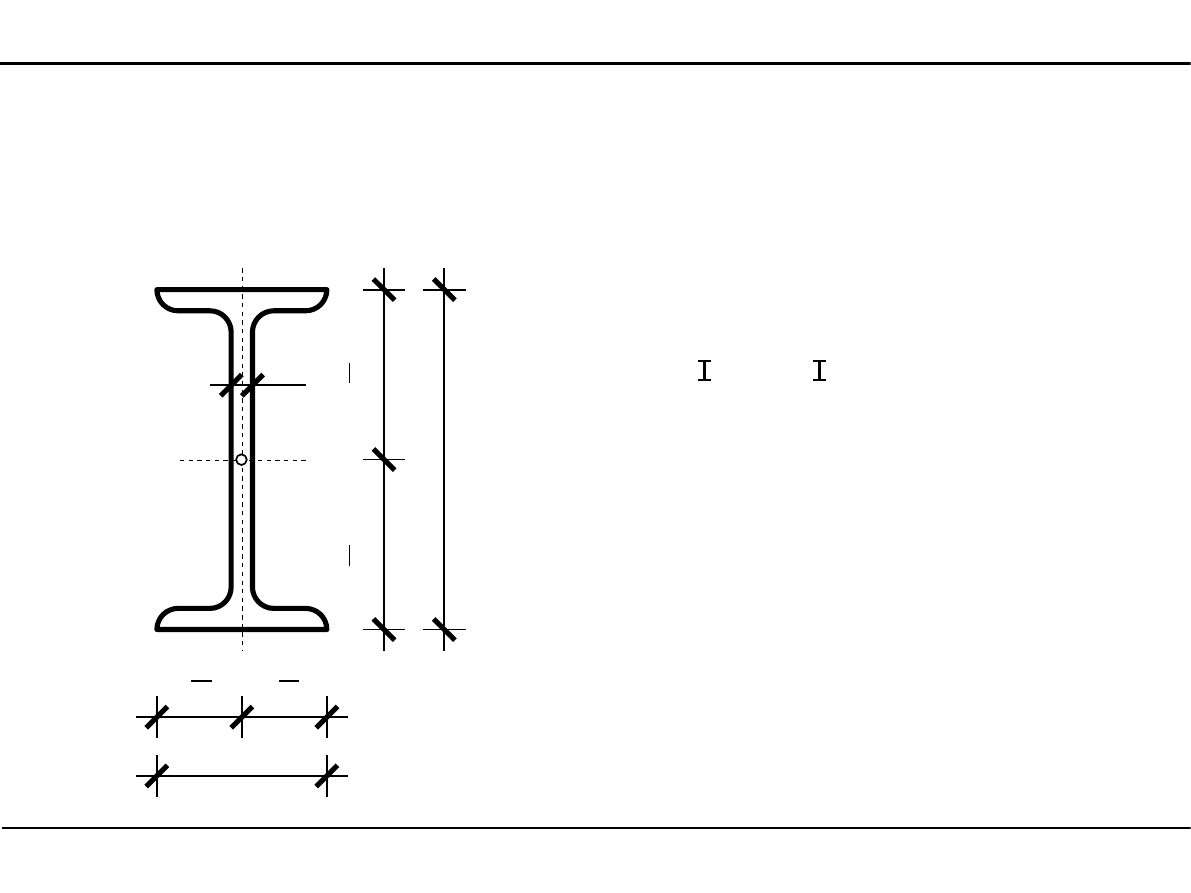
2. Charakterystyki geometryczne przekroju pręta
78
Dr inż. Justyna Grzymisławska
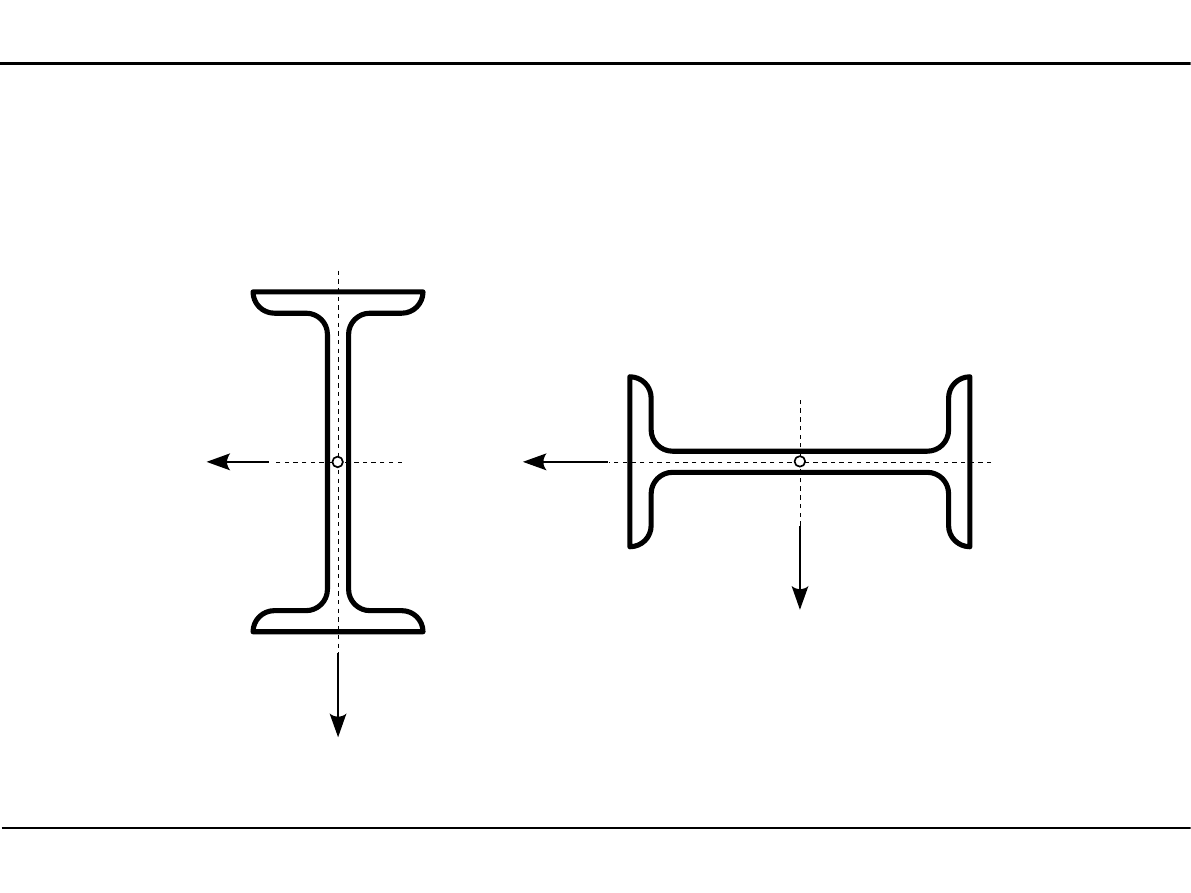
2.10. Kształtowniki walcowane
Dwuteowniki
Wymiary dwuteownika
s
h
g
X
X
Y
Y
sc
s
2
s
2
h
2
h
2
A - pole powierzchni
J
X
, J
Y
- momenty bezwładności
Oznaczenie dwuteownika
200
200PE
HEB200
2. Charakterystyki geometryczne przekroju pręta
79
Dr inż. Justyna Grzymisławska
2.10. Kształtowniki walcowane
Dwuteowniki
Y
0
Z
0
X
X
Y
Y
sc
J
Y0
= J
X
(T)
J
Z0
= J
Y
(T)
Y
0
Z
0
X
X
Y
Y
sc
J
Y0
= J
Y
(T)
J
Z0
= J
X
(T)

2. Charakterystyki geometryczne przekroju pręta
80
Dr inż. Justyna Grzymisławska
2.10. Kształtowniki walcowane
Dwuteowniki
2. Charakterystyki geometryczne przekroju pręta
81
Dr inż. Justyna Grzymisławska
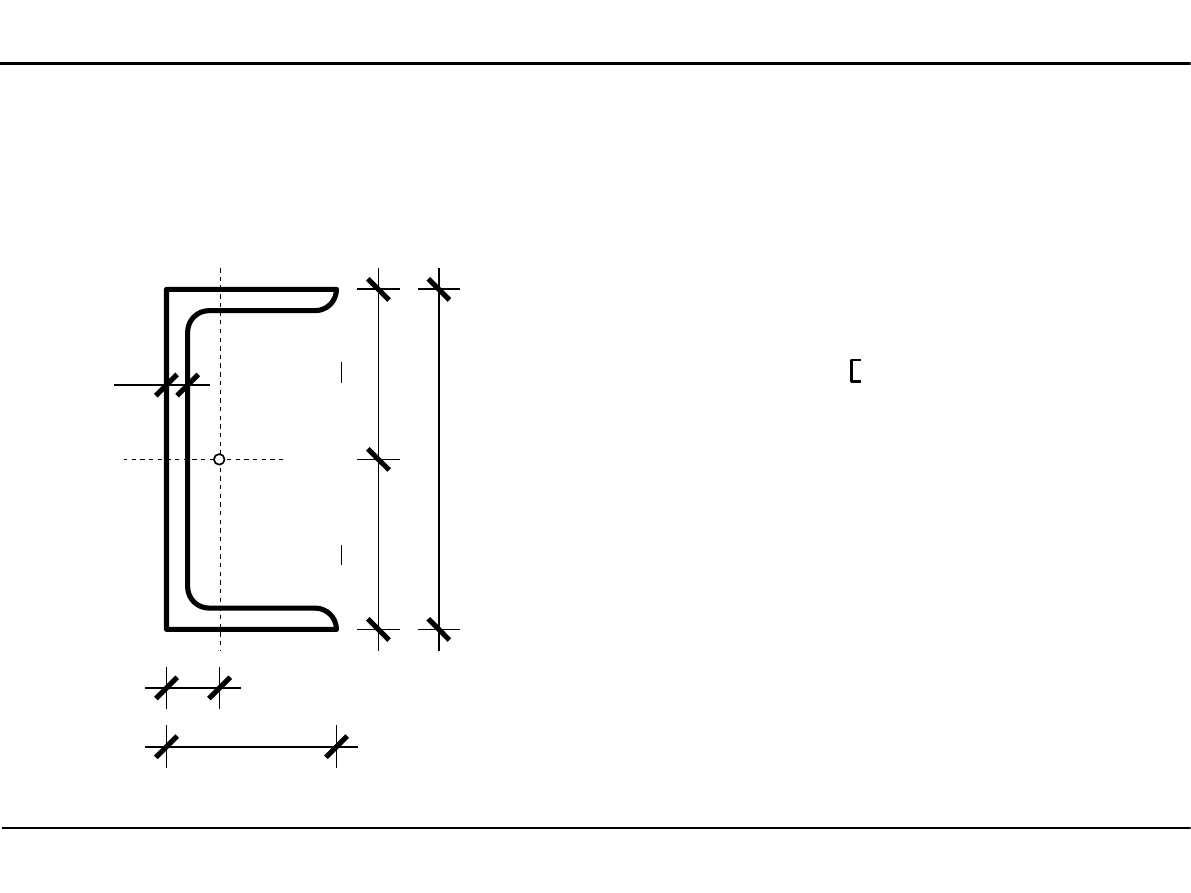
2.10. Kształtowniki walcowane
Ceowniki
s
h
g
X
X
Y
Y
sc
h
2
h
2
e
Wymiary ceownika
A - pole powierzchni
J
X
, J
Y
- momenty bezwładności
Oznaczenie ceownika
200

2. Charakterystyki geometryczne przekroju pręta
82
Dr inż. Justyna Grzymisławska
2.10. Kształtowniki walcowane
Ceowniki
2. Charakterystyki geometryczne przekroju pręta
83
Dr inż. Justyna Grzymisławska
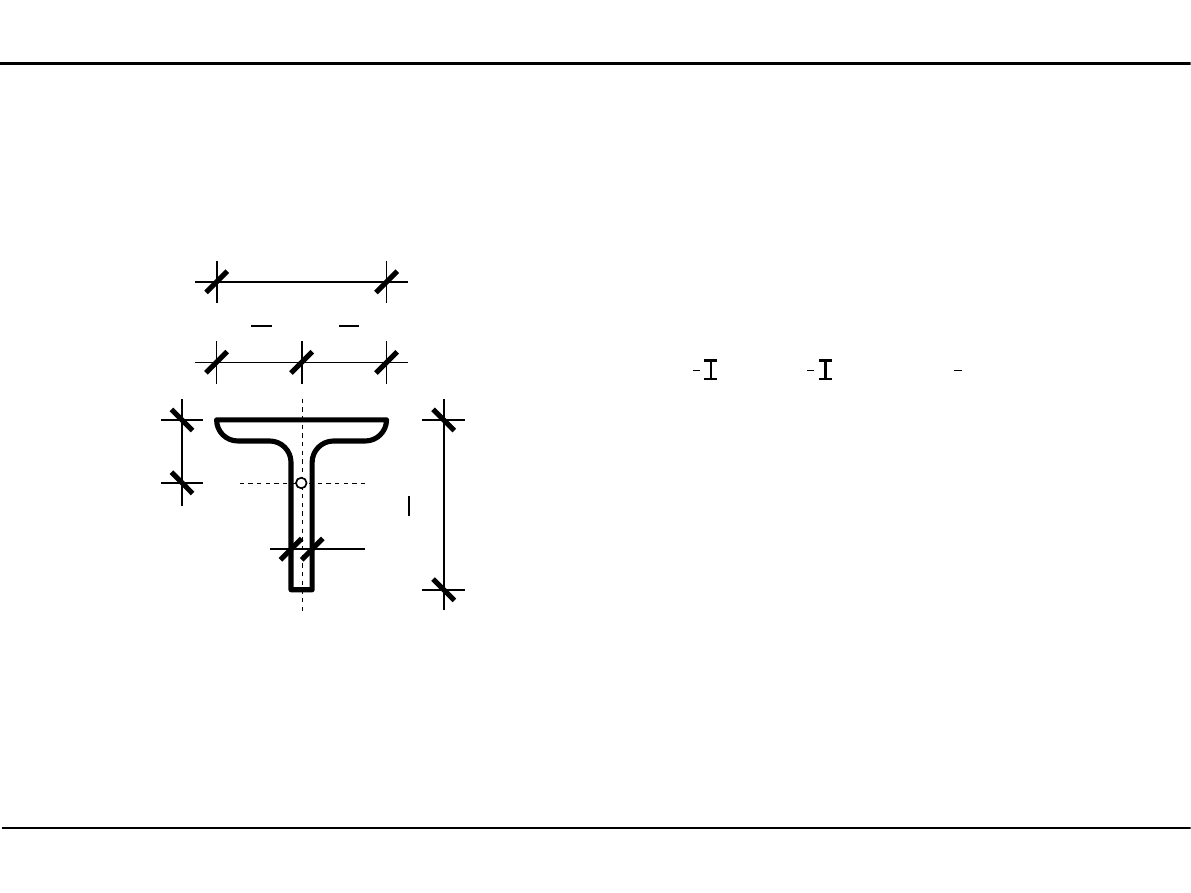
2.10. Kształtowniki walcowane
Teownik
Wymiary teownika
A - pole powierzchni
J
X
, J
Y
- momenty bezwładności
Oznaczenie teownika
200
200PE
HEB200
1
2
1
2
1
2
s
h
2
g
X
X
Y
Y
sc
s
2
s
2
e
2. Charakterystyki geometryczne przekroju pręta
84
Dr inż. Justyna Grzymisławska
1
1
2
2
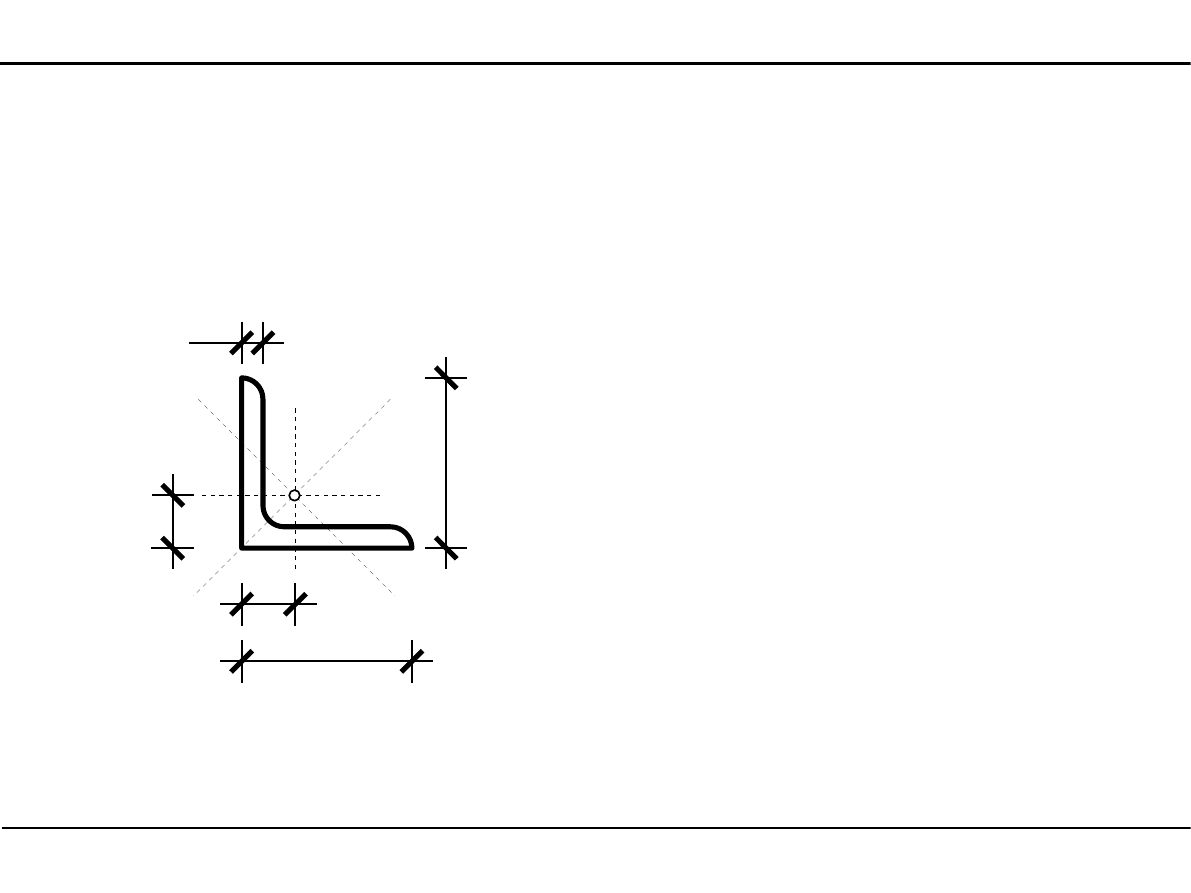
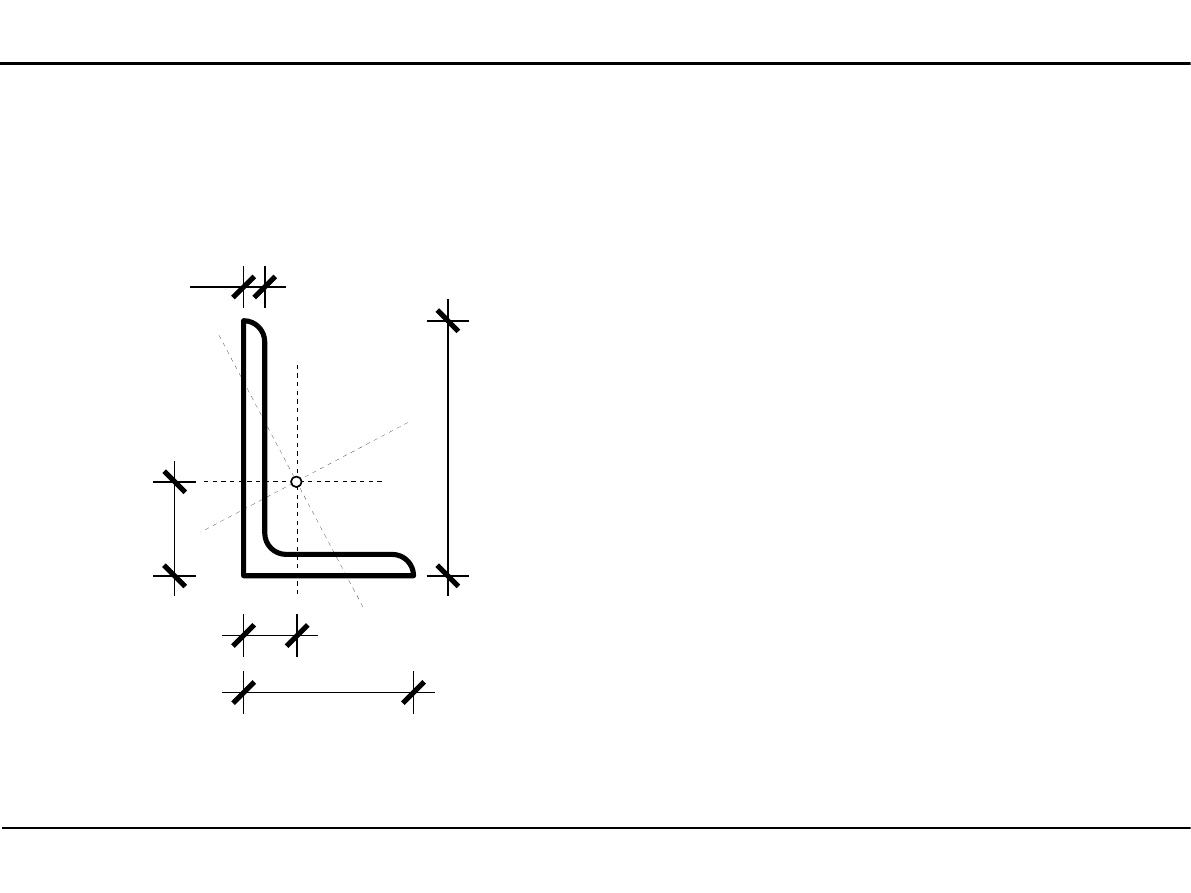
2.10. Kształtowniki walcowane
Kątownik równoramienny
Oznaczenie kątownika równoramiennego
L a×g
a
a
g
X
X
Y
Y
sc
e
e
Wymiary kątownika równoramiennego
A - pole powierzchni
J
X
, J
Y
- momenty bezwładności
J
1
, J
2
- główne momenty bezwładności

2. Charakterystyki geometryczne przekroju pręta
85
Dr inż. Justyna Grzymisławska
2.10. Kształtowniki walcowane
Kątownik równoramienny
2. Charakterystyki geometryczne przekroju pręta
86
Dr inż. Justyna Grzymisławska
1
1
2
2
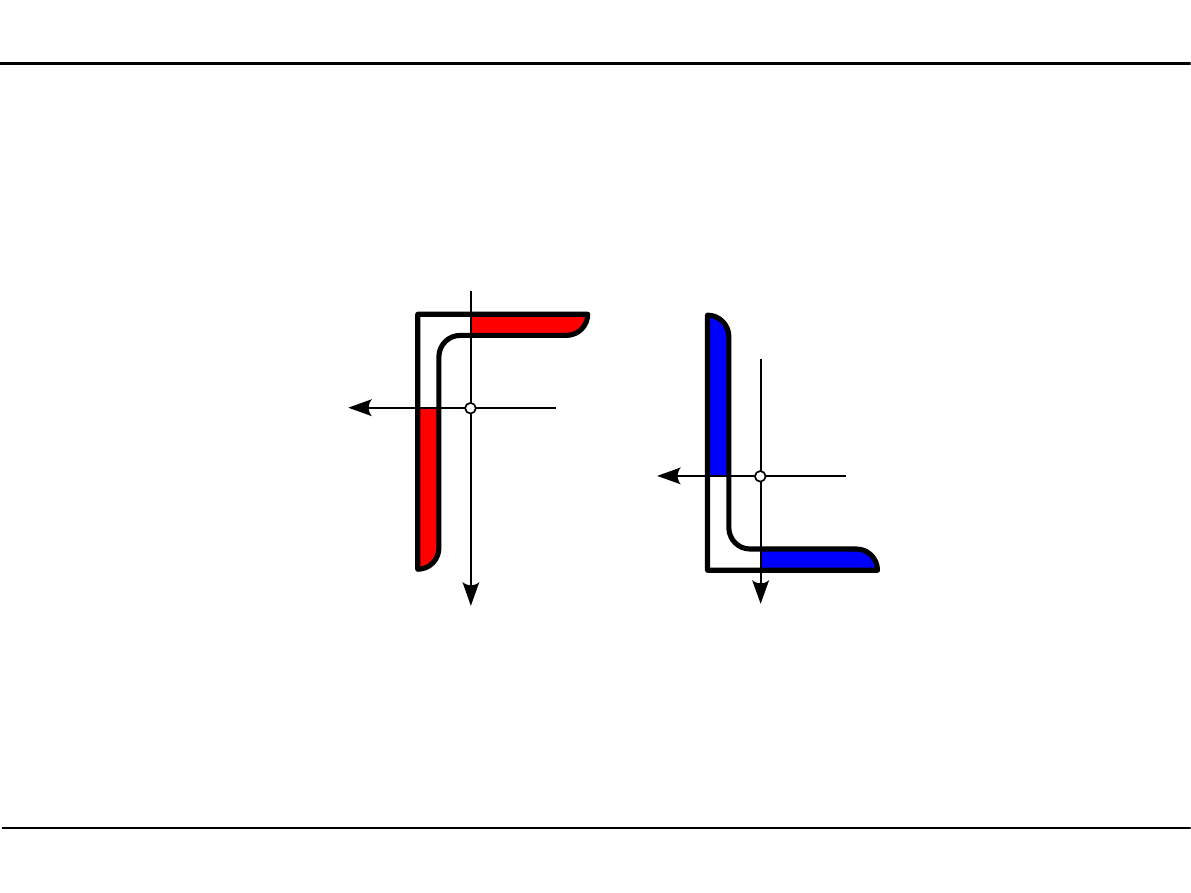
2.10. Kształtowniki walcowane
Kątownik nierównoramienny
Oznaczenie kątownika nierównoramiennego
L b×a×g
Wymiary kątownika nierównoramiennego
a
b
g
X
X
Y
Y
sc
e
X
e
Y
A - pole powierzchni
J
X
, J
Y
- momenty bezwładności
J
2
- główny moment bezwładności
2. Charakterystyki geometryczne przekroju pręta
87
Dr inż. Justyna Grzymisławska
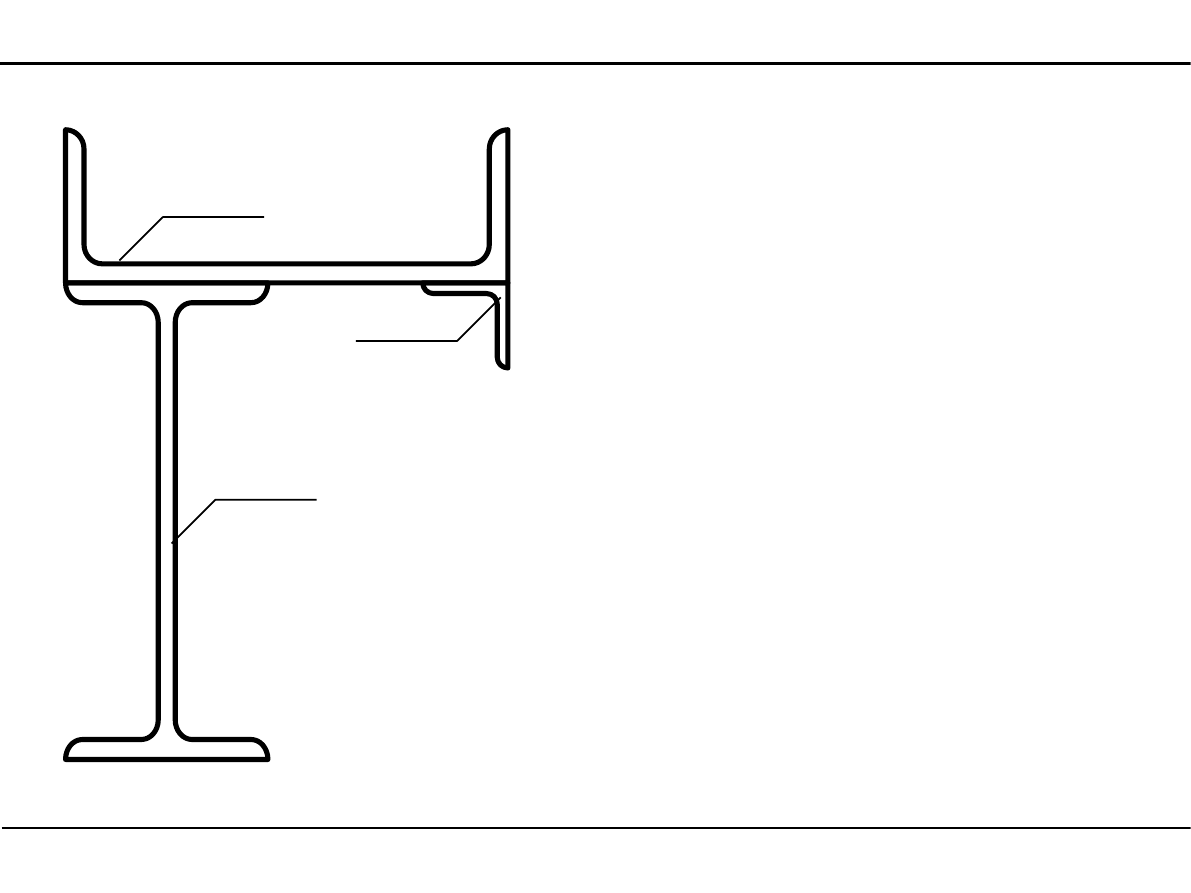
2.10. Kształtowniki walcowane
Dewiacyjny moment bezwładności kątownika
sc
Y
0
Z
0
J
Y0Z0
0
sc
Y
0
Z
0
J
Y0Z0
0
2. Charakterystyki geometryczne przekroju pręta
88
Dr inż. Justyna Grzymisławska
2.11. Charakterystyki geometryczne
kształtowników walcowanych
Zadanie 1
Wyznaczyć główne momenty
bezwładności przekroju
przedstawionego na
poniższym rysunku.
260
280
50
×
5

2. Charakterystyki geometryczne przekroju pręta
89
Dr inż. Justyna Grzymisławska
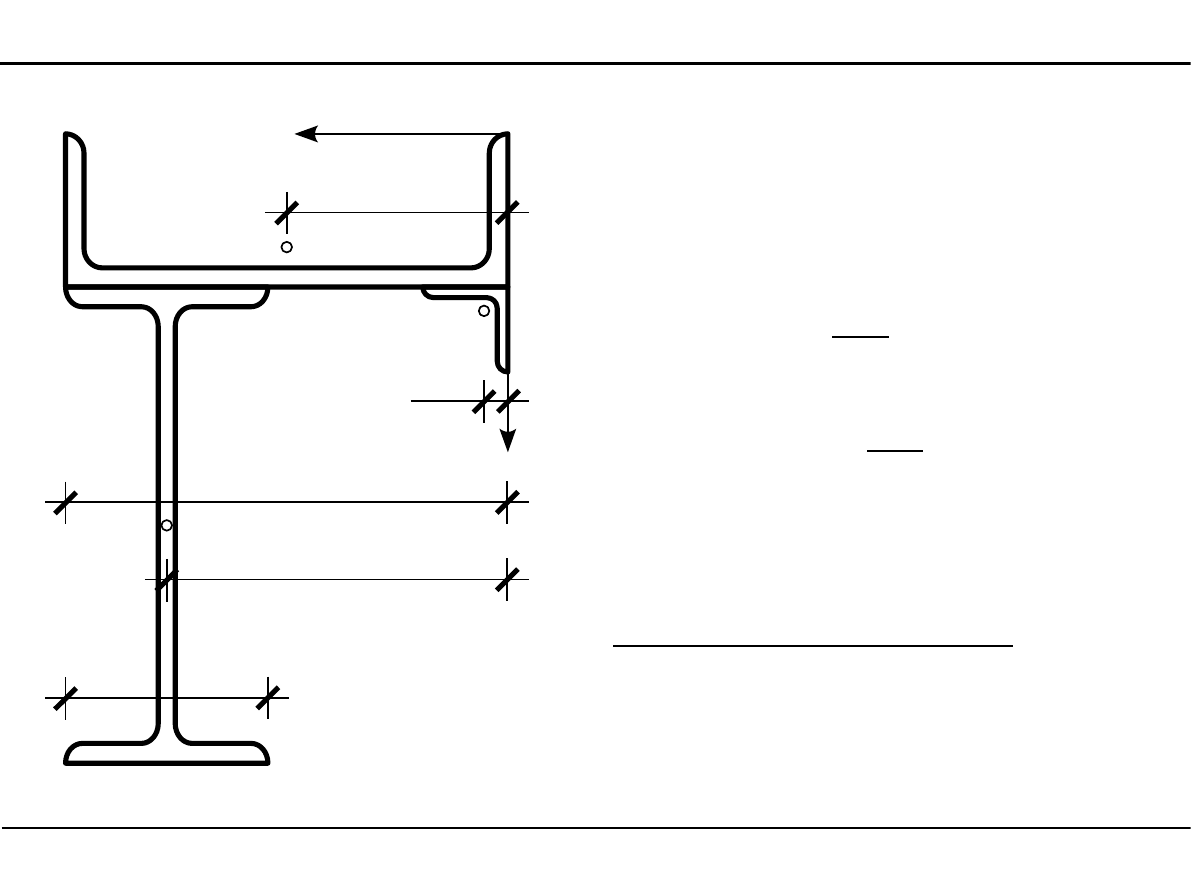
2.11. Charakterystyki geometryczne kształtowników walcowanych
Pola powierzchni kształtowników walcowanych
Ceownik - A
1
= 48,3 cm
2
Dwuteownik - A
2
= 61,1 cm
2
Kątownik - A
3
= 4,80 cm
2
2. Charakterystyki geometryczne przekroju pręta
90
Dr inż. Justyna Grzymisławska
2.11. Charakterystyki geometryczne
kształtowników walcowanych
Położenie środka ciężkości przekroju
y
1
=
26,0
2
=
13,0 cm
y
2
=
26,0−
11,9
2
=
20,05 cm
y
3
=
1,40cm
y
C
=
48,3⋅13,061,1⋅20,054,8⋅1,40
48,361,14,8
=
16,28 cm
[cm]
Y
P
Z
P
sc
1
26,0
13,0
sc
2
11,9
20,05
sc
3
1,40
2. Charakterystyki geometryczne przekroju pręta
91
Dr inż. Justyna Grzymisławska
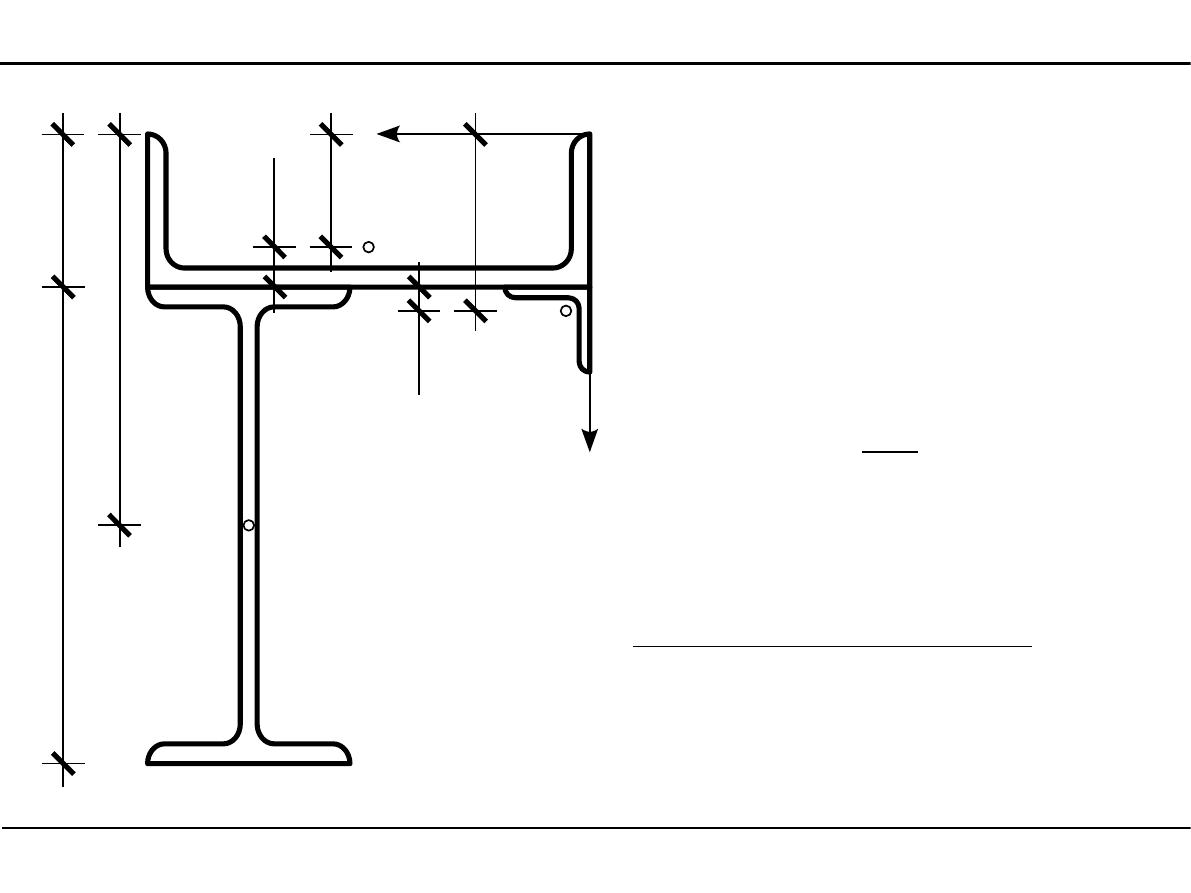
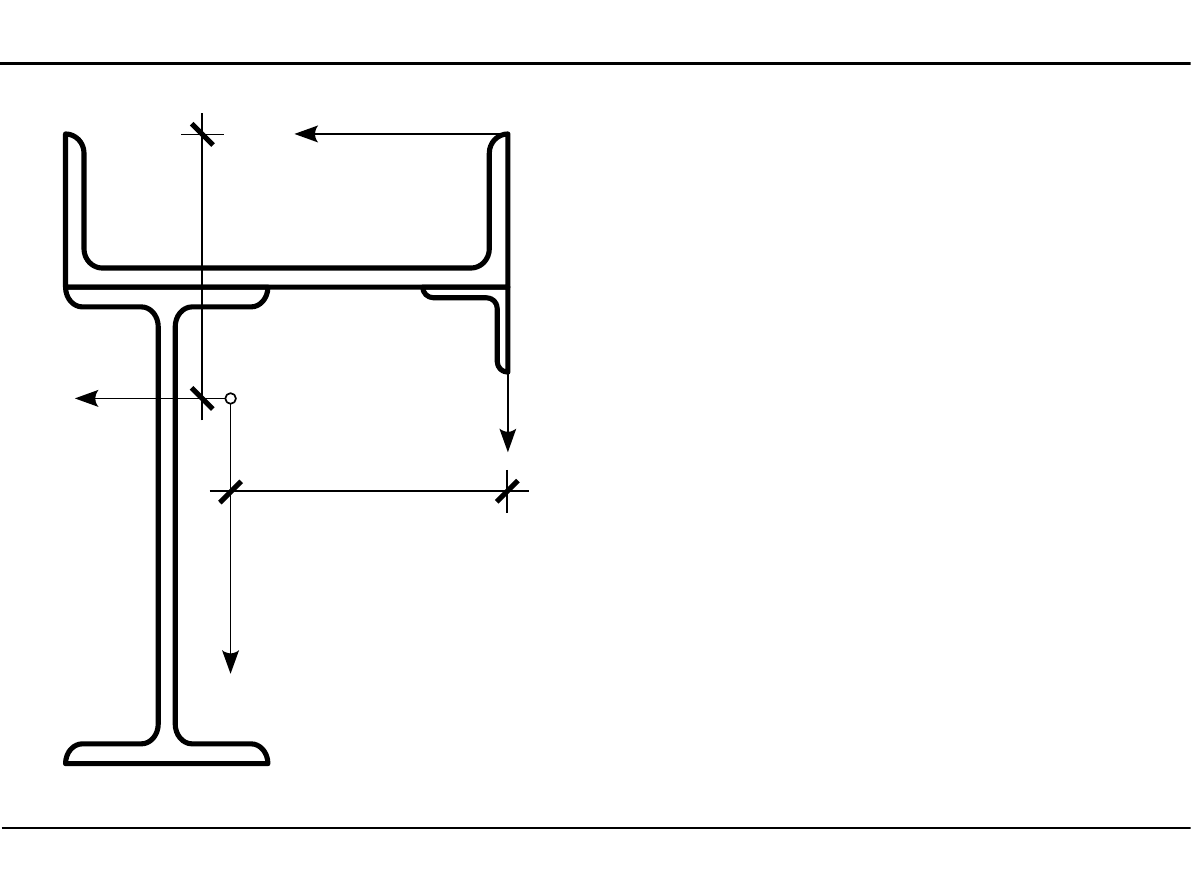
2.11. Charakterystyki geometryczne
kształtowników walcowanych
Położenie środka
ciężkości przekroju
z
1
=
9,0−2,36=6,64cm
z
2
=
9,0
28,0
2
=
23,0cm
z
3
=
9,01,40=10,40 cm
z
C
=
48,3⋅6,6461,1⋅23,04,8⋅10,40
48,361,14,8
=
16,56cm
[cm]
Y
P
Z
P
sc
1
2,
36
6,
64
sc
2
9,
0
28
,0
23
,0
sc
3
1,
40
10
,4
0
2. Charakterystyki geometryczne przekroju pręta
92
Dr inż. Justyna Grzymisławska
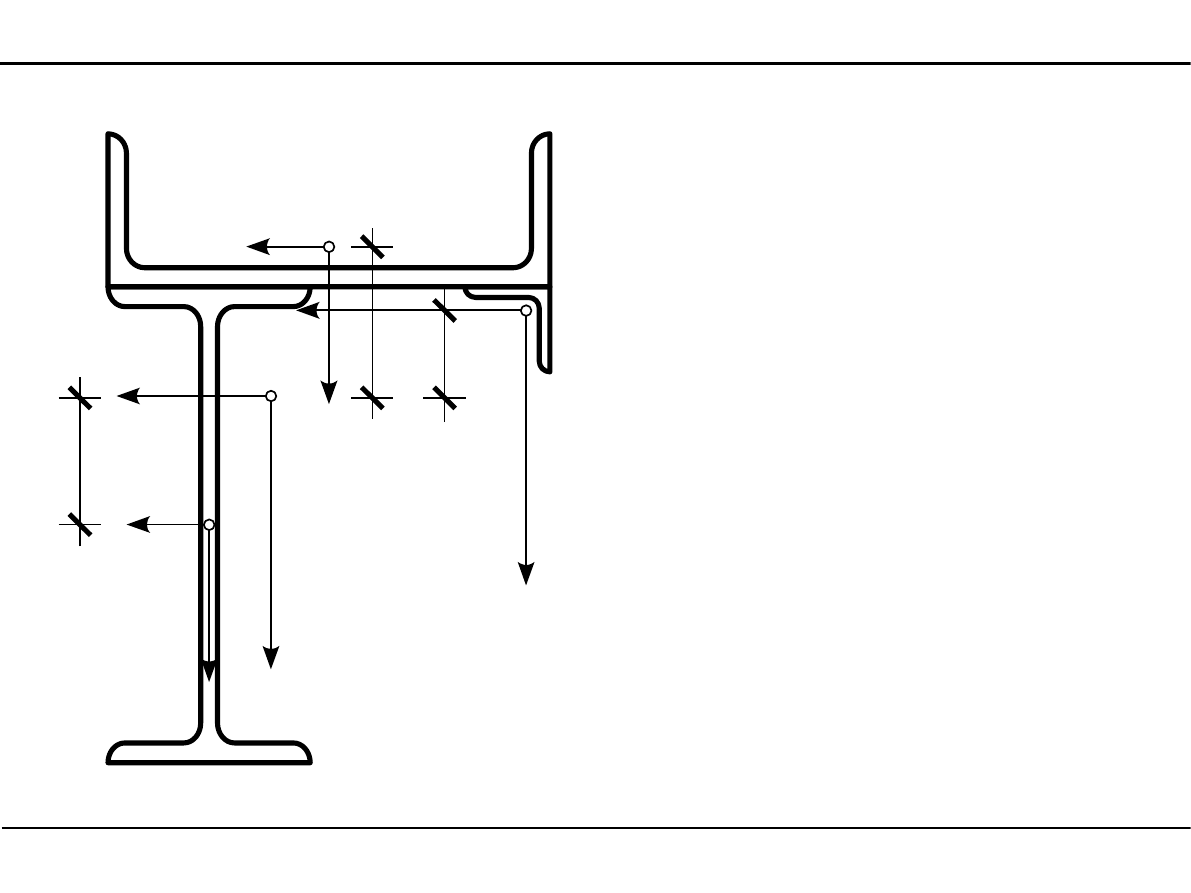
2.11. Charakterystyki geometryczne
kształtowników walcowanych
Położenie środka
ciężkości przekroju
[cm]
Y
P
Z
P
y
C
=
16,28cm
16,28
z
C
=
15,55cm
15
,5
5
Y
0
Z
0
sc
2. Charakterystyki geometryczne przekroju pręta
93
Dr inż. Justyna Grzymisławska
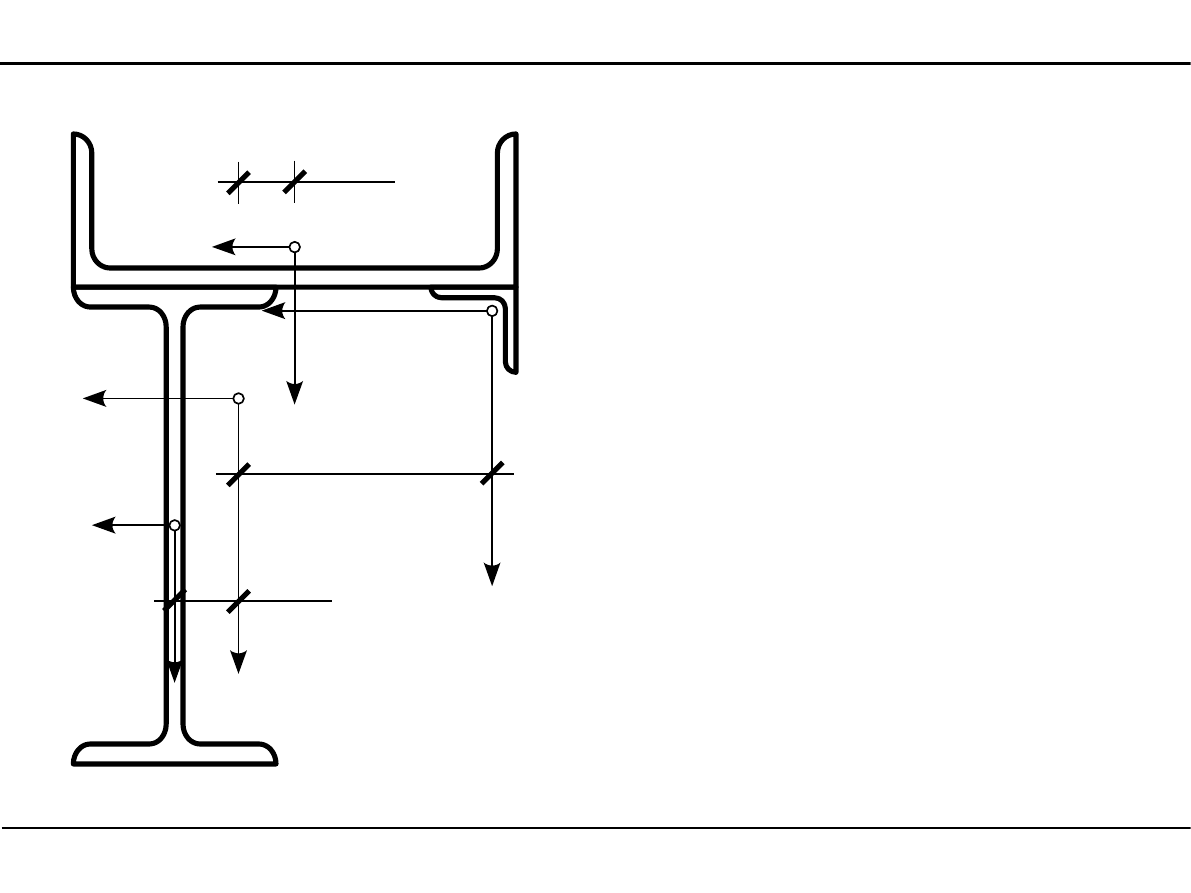
2.11. Charakterystyki geometryczne
kształtowników walcowanych
Momenty bezwładności względem
osi środkowych
z
01
=
6,64−15,55=−8,910 cm
z
02
=
23,0−15,55=7,450 cm
z
03
=
10,40−15,55=−5,150 cm
J
Y0
=
317,0
−
8,910
2
⋅
48,375907,450
2
⋅
61,1
11,0
−
5,150
2
⋅
4,80=15270cm
4
[cm]
sc
Y
0
Z
0
sc
1
Y
01
Z
01
8,
91
0
sc
2
Y
02
Z
02
7,
45
0
sc
3
Y
03
Z
03
5,
15
0
2. Charakterystyki geometryczne przekroju pręta
94
Dr inż. Justyna Grzymisławska
2.11. Charakterystyki geometryczne
kształtowników walcowanych
Momenty bezwładności względem
osi środkowych
y
01
=
13,0−16,28=−3,280 cm
y
02
=
20,05−16,28=3,770cm
z
03
=
1,40−16,28=−14,88cm
J
Z0
=
4820
−
3,280
2
⋅
48,3364,03,770
2
⋅
61,1
11,0
−
14,88
2
⋅
4,80=7646 cm
4
[cm]
sc
Y
0
Z
0
sc
1
Y
01
Z
01
3,280
sc
2
Y
02
Z
02
3,770
sc
3
Y
03
Z
03
14,88
2. Charakterystyki geometryczne przekroju pręta
95
Dr inż. Justyna Grzymisławska
1
2
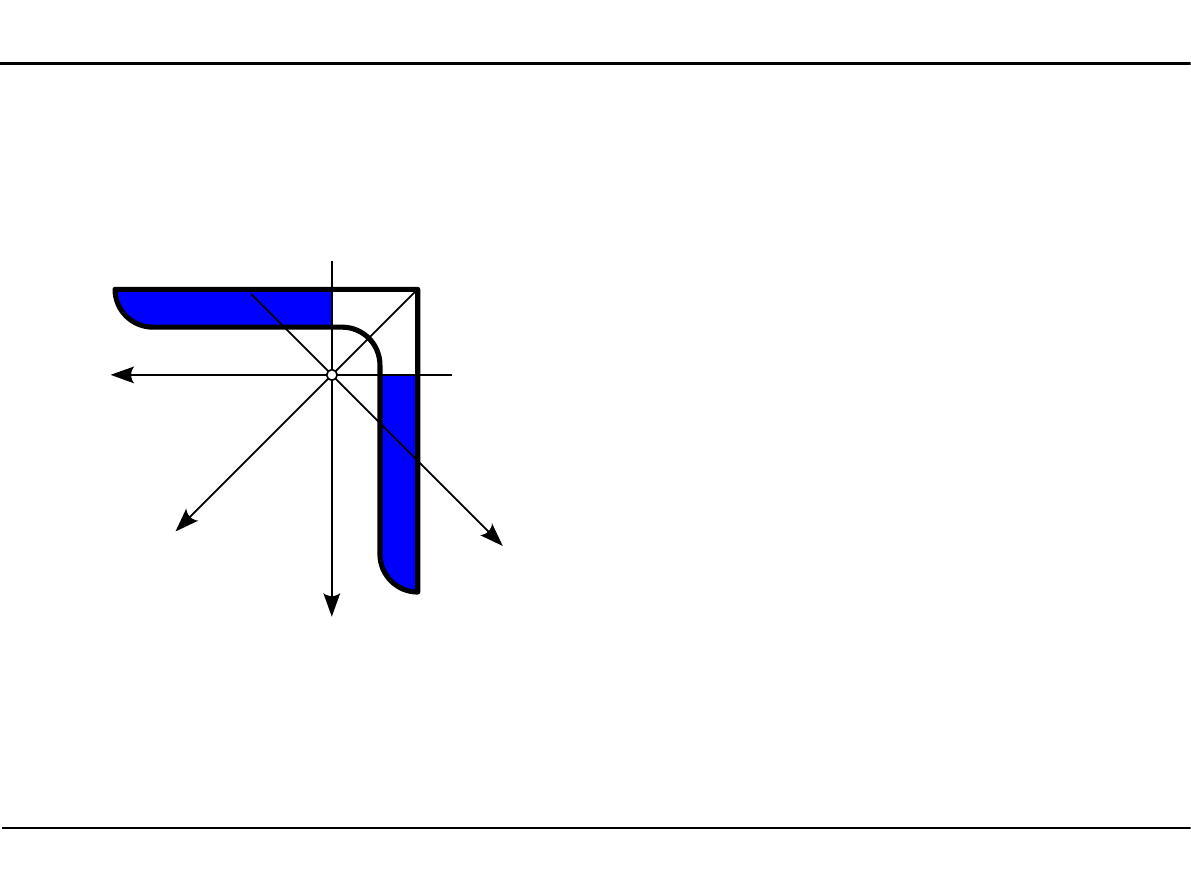
2.11. Charakterystyki geometryczne kształtowników walcowanych
Dewiacyjny moment bezwładności kątownika
J
Y03
=
J
Z03
=
11,0 cm
4
J
1
=
17,4 cm
4
J
2
=
4,59cm
4
I
2
=
17,4⋅4,59=79,87 cm
8
I
2
=
11,0⋅11,0−J
Y03Z03
2
=
79,87 cm
8
∣
J
Y03Z03
∣
=
6,413cm
4
J
Y03Z03
=−
6,413 cm
4
sc
3
Y
03
Z
03

2. Charakterystyki geometryczne przekroju pręta
96
Dr inż. Justyna Grzymisławska
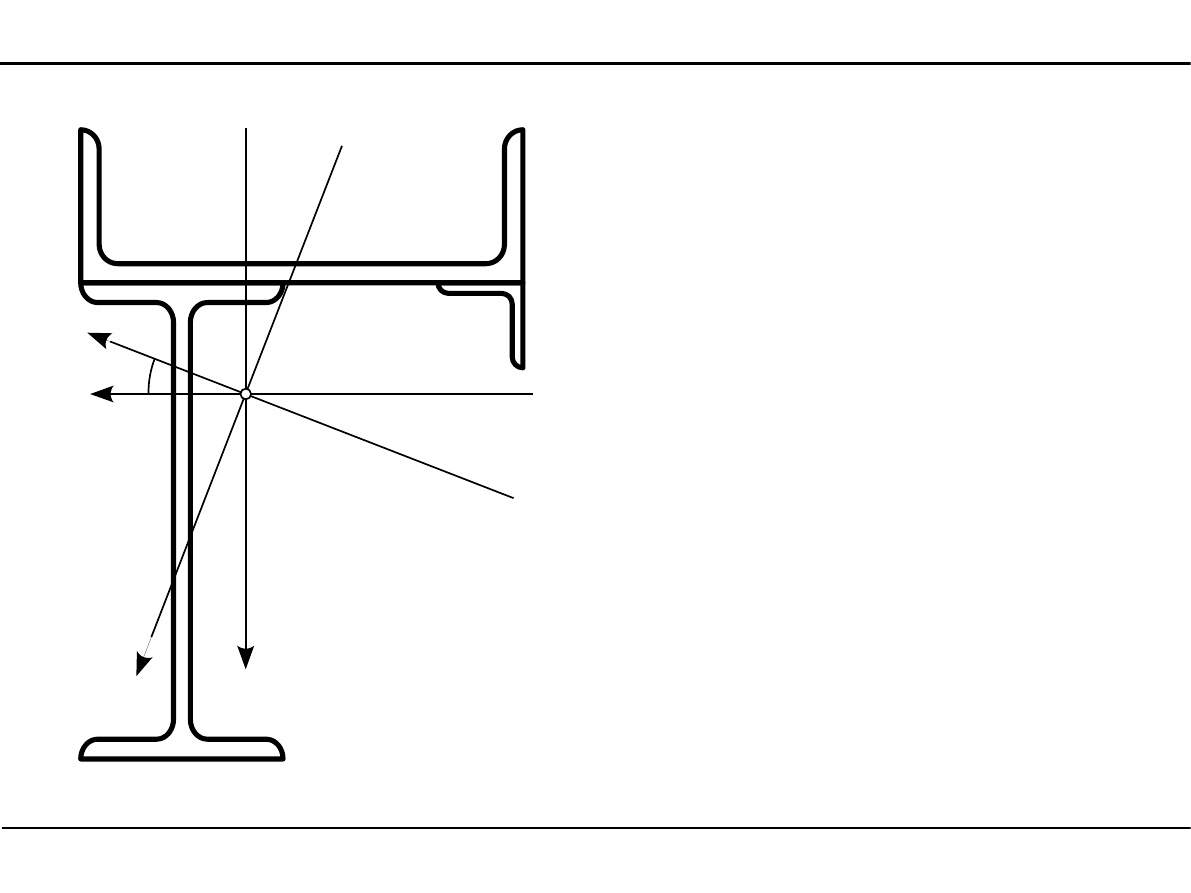
2.11. Charakterystyki geometryczne kształtowników walcowanych
Dewiacyjny moment bezwładności przekroju
y
01
=−
3,280cm
y
02
=
3,770 cm
y
03
=−
14,88 cm
z
01
=−
8,910cm
z
02
=
7,450 cm
z
03
=−
5,150cm
J
Y0Z0
=
0,0
−
3,280
⋅
−
8,910
⋅
48,30,03,770⋅7,450⋅61,1−6,413
−
14,88
⋅
−
5,150
⋅
4,80=
=
3489 cm
4
2. Charakterystyki geometryczne przekroju pręta
97
Dr inż. Justyna Grzymisławska
Y
gl
=1
Z
gl
=2
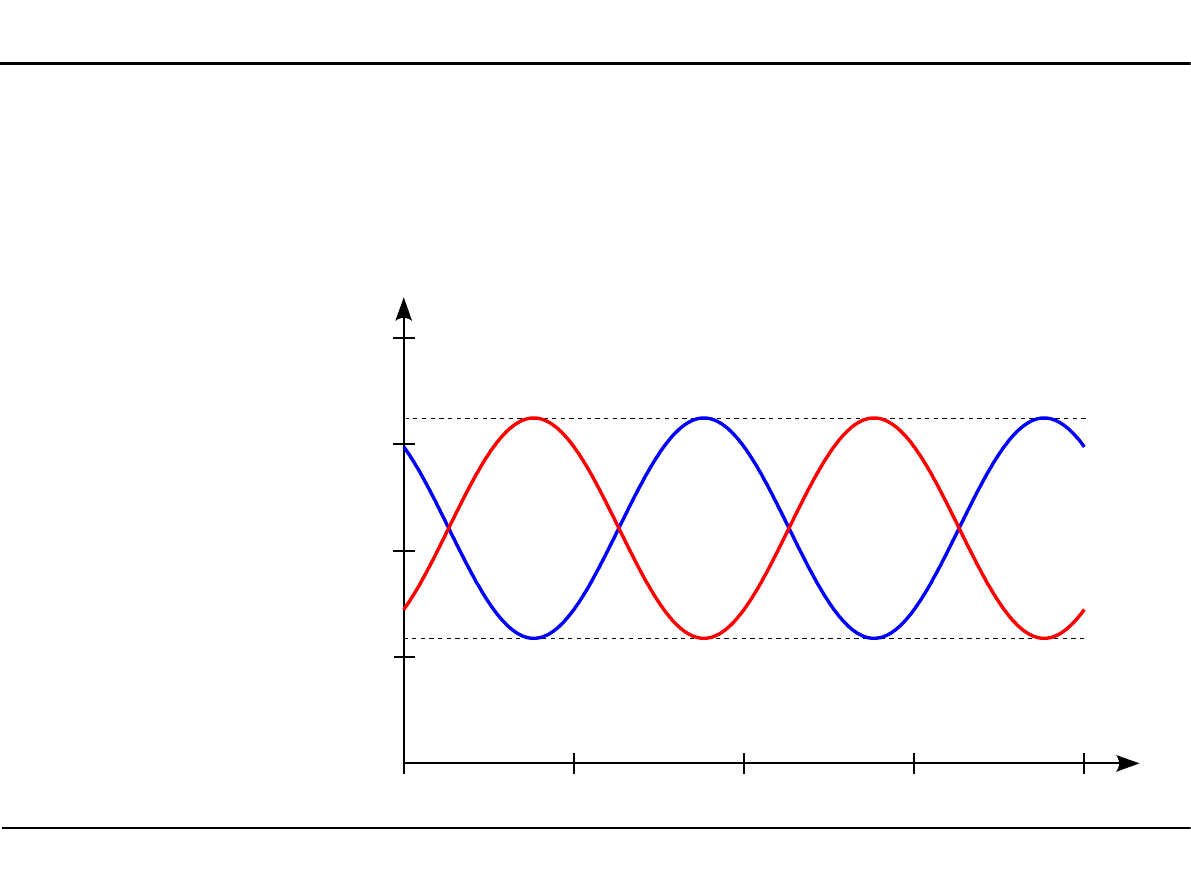
2.11. Charakterystyki geometryczne
kształtowników walcowanych
Główne momenty bezwładności
przekroju
gl
=−
21,23 °
J
Ygl
=
J
1
=
16630cm
4
J
Zgl
=
J
2
=
6290 cm
4
sc
Y
0
Z
0
21
,2
3
0
2. Charakterystyki geometryczne przekroju pręta
98
Dr inż. Justyna Grzymisławska
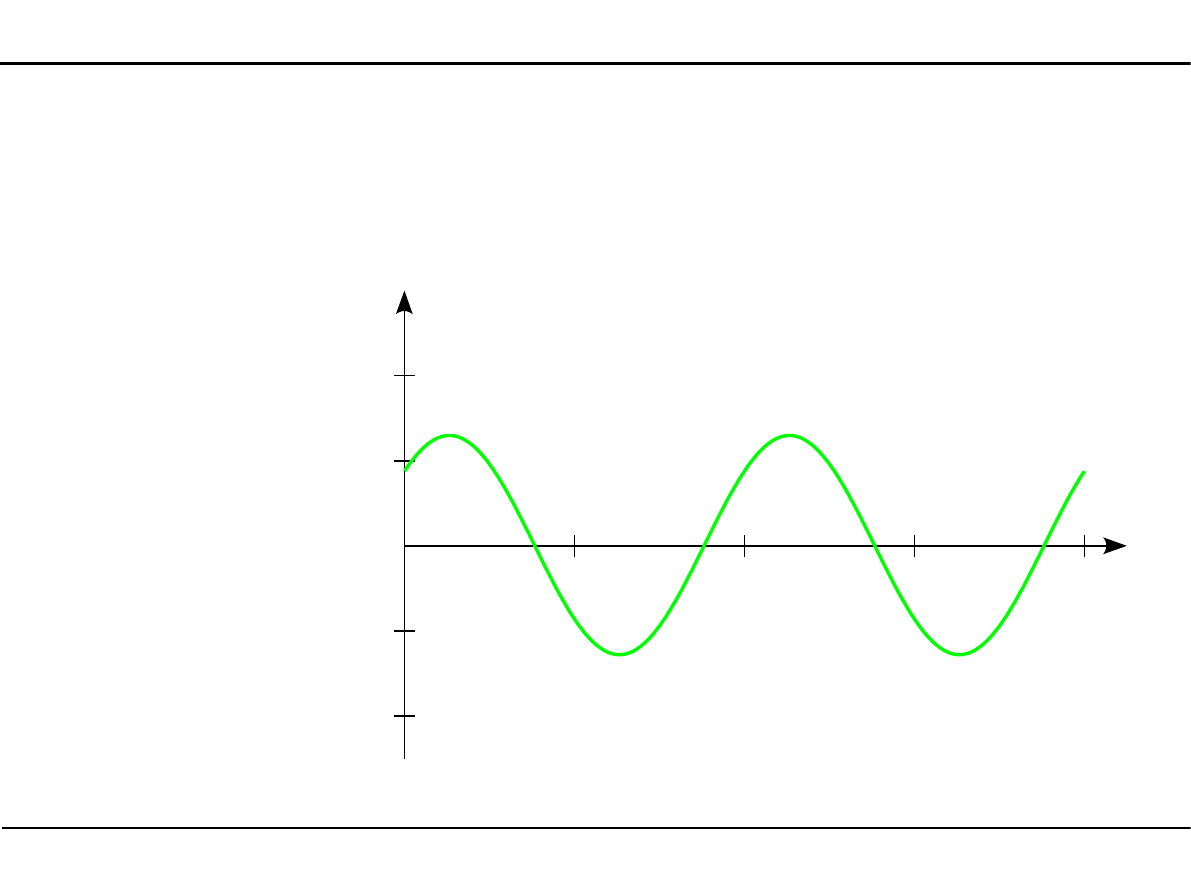
2.11. Charakterystyki geometryczne kształtowników walcowanych
Wykresy funkcji momentów bezwładności
J
Y0
=
15270cm
4
J
Z0
=
7646 cm
4
J
1
=
16630 cm
4
J
2
=
6290 cm
4
α
[
0
]
J
Y
, J
Z
×
1000
[cm
4
]
0
90
180
270
360
5
10
15
20
6296
16620
J
Y
J
Z
2. Charakterystyki geometryczne przekroju pręta
99
Dr inż. Justyna Grzymisławska
2.11. Charakterystyki geometryczne kształtowników walcowanych
J
Y0Z0
=
3489 cm
4
α
[
0
]
J
YZ
×
1000
[cm
4
]
0
180
360
−8
−4
4
8
90
270
Wykresy funkcji momentów bezwładności
2. Charakterystyki geometryczne przekroju pręta
100
Dr inż. Justyna Grzymisławska
180
180
2.11. Charakterystyki geometryczne kształtowników walcowanych
Zadanie 2
Dany jest przekrój złożony z dwóch ceowników 180 przedstawiony na poniższym
rysunku. Wyznaczyć dla jakiej odległości a główne momenty bezwładności mają
jednakowe wartości.
a
2. Charakterystyki geometryczne przekroju pręta
101
Dr inż. Justyna Grzymisławska
Dane ceownika 260
s
h
g
X
X
Y
Y
sc
h
2
h
2
e
2.11. Charakterystyki geometryczne kształtowników walcowanych
J
X
=
1350 cm
4
A=28,0 cm
2
e=1,92 cm
J
Y
=
114,0cm
4
2. Charakterystyki geometryczne przekroju pręta
102
Dr inż. Justyna Grzymisławska
2.11. Charakterystyki geometryczne kształtowników walcowanych
Położenie środka
ciężkości przekroju
[cm]
a
a
2
a
2
Y
0
=Y
gl
Z
0
=Z
gl
sc
18
,0
9,
0
9,
0
2. Charakterystyki geometryczne przekroju pręta
103
Dr inż. Justyna Grzymisławska
sc
2
=Y
02
Z
02
2.11. Charakterystyki geometryczne kształtowników walcowanych
Główne momenty bezwładności
sc
Y
0
=Y
gl
Z
0
=Z
gl
sc
1
Y
01
Z
01
z
01
=
0,0 cm
J
Y01
=
1350 cm
4
z
02
=
0,0 cm
J
Y02
=
1350 cm
4
J
Y0
=
J
Ygl
=
13500,0
2
⋅
28,0
13500,0
2
⋅
28,0=2700 cm
4
2. Charakterystyki geometryczne przekroju pręta
104
Dr inż. Justyna Grzymisławska
sc
2
=Y
02
Z
02
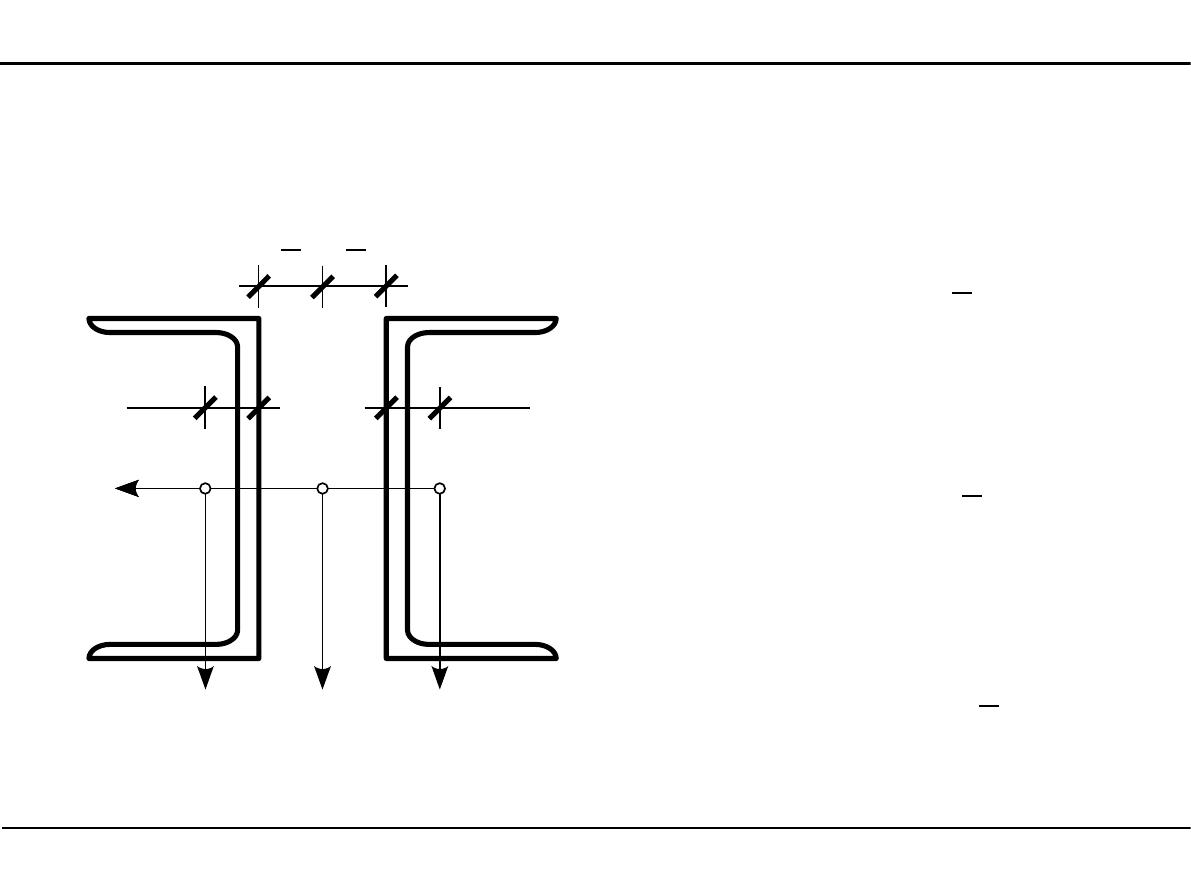
2.11. Charakterystyki geometryczne kształtowników walcowanych
Główne momenty bezwładności
[cm]
sc
Y
0
=Y
gl
Z
0
=Z
gl
sc
1
Y
01
Z
01
a
2
a
2
y
01
=
1,92
a
2
J
Z01
=
114,0 cm
4
y
02
=−
1,92
a
2
J
Z02
=
114,0 cm
4
y
01
2
=
y
02
2
=
1,92
a
2
2
1,92
1,92

2. Charakterystyki geometryczne przekroju pręta
105
Dr inż. Justyna Grzymisławska
2.11. Charakterystyki geometryczne kształtowników walcowanych
Główne momenty bezwładności
J
Z0
=
J
Zgl
=
114,0
1,92
a
2
2
⋅
28,0114,0
1,92
a
2
2
⋅
28,0=2700 cm
4
J
Z01
=
114,0 cm
4
J
Z02
=
114,0 cm
4
y
01
2
=
y
02
2
=
1,92
a
2
2
1,92
a
2
2
=
44,14cm
2
a=9,448cm

2. Charakterystyki geometryczne przekroju pręta
106
Dr inż. Justyna Grzymisławska
Wyznaczanie momentów bezwładności przekroju pręta w zadanym układzie
współrzędnych
J
Y
=
∑
i=1
i=n
J
Y0i
z
i
2
⋅
A
i
J
Z
=
∑
i=1
i=n
J
Z0i
y
i
2
⋅
A
i
J
YZ
=
∑
i=1
i=n
J
Y0iZ0i
y
i
⋅
z
i
⋅
A
i
J
Y0i
, J
Z0i
, J
Y0iZ0i
- momenty bezwładności
względem osi środkowych i-tej figury.
y
i
, z
i
- współrzędne środka ciężkości
i-tej figury w układzie YZ.
A
i
- pole powierzchni i-tej figury.
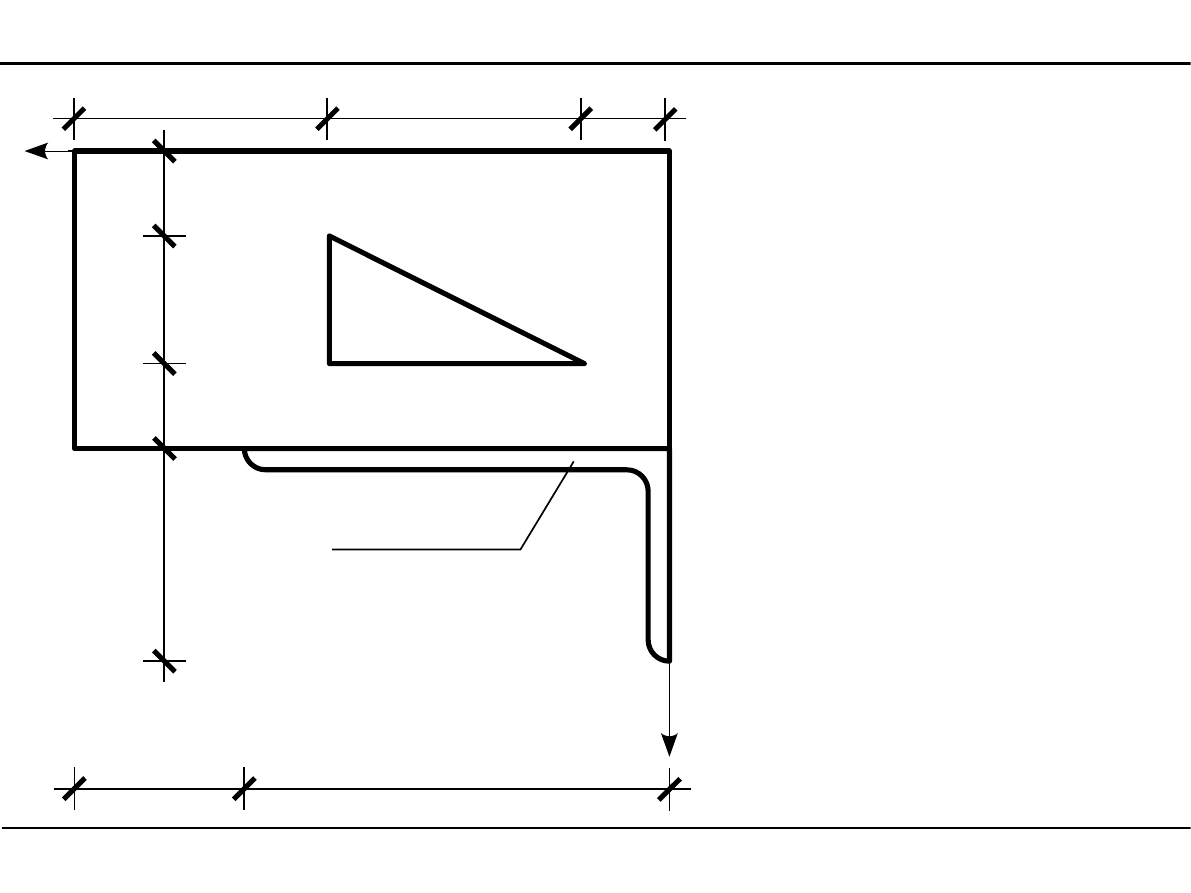
2.12. Charakterystyki geometryczne przekroju pręta w zadanym
układzie współrzędnych
2. Charakterystyki geometryczne przekroju pręta
107
Dr inż. Justyna Grzymisławska
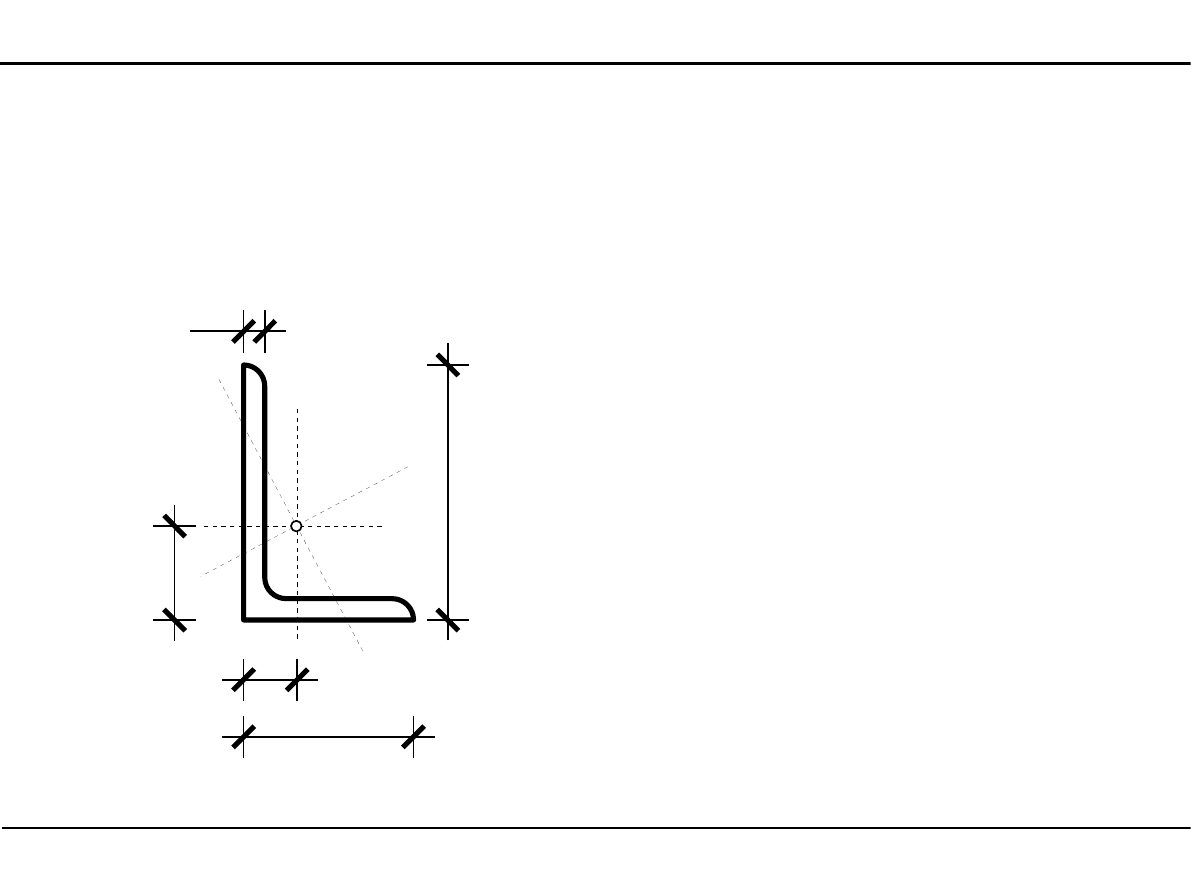
2.12. Charakterystyki
geometryczne przekroju
pręta w zadanym układzie
współrzędnych
Zadanie 1
Wyznaczyć momenty
bezwładności w zadanym
układzie współrzędnych
przekroju przedstawio-
nego na poniższym
rysunku.
100
×
50
×
8
[cm]
10,0
4,0
6,0
2,0
6,0
2,
0
3,
0
5,
0
2,
0
Y
Z
2. Charakterystyki geometryczne przekroju pręta
108
Dr inż. Justyna Grzymisławska
1
1
2
2
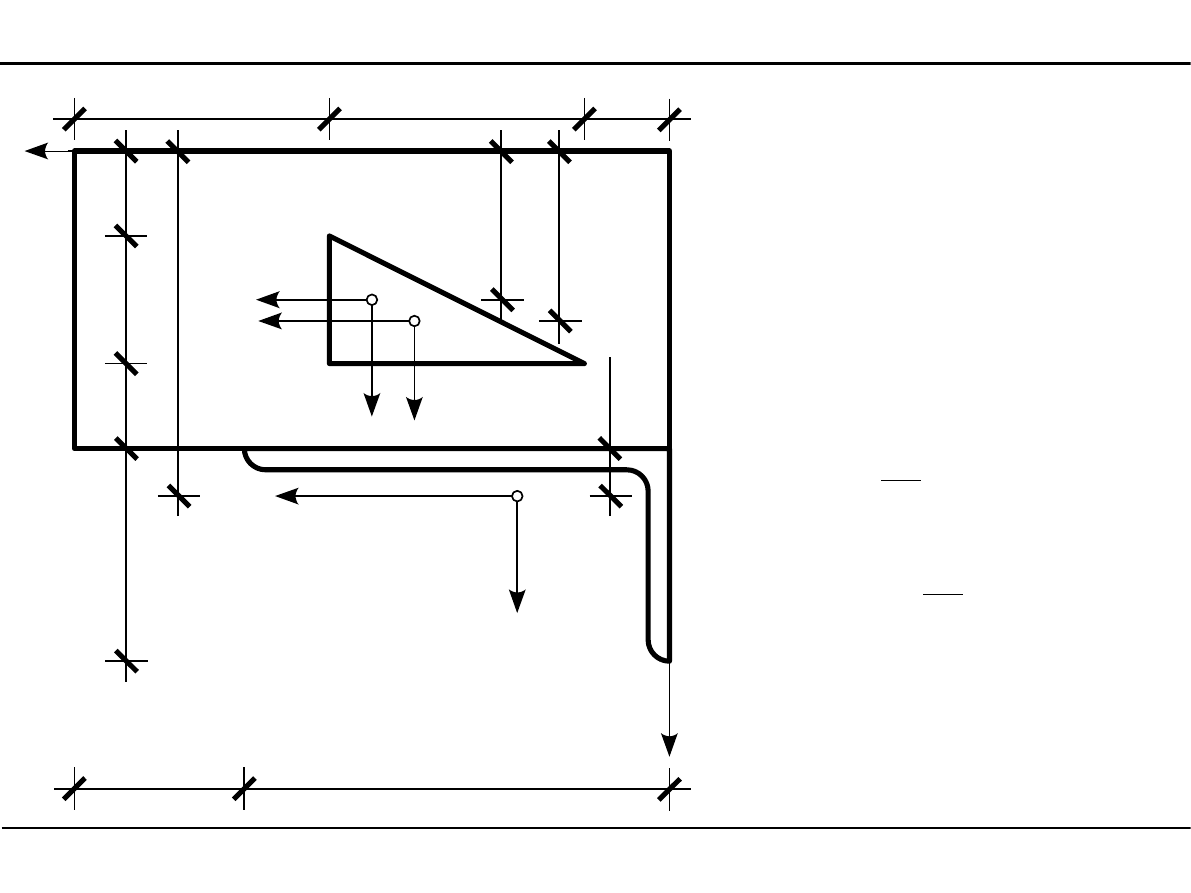
Dane kątownika nierównoramiennego
a
b
g
X
X
Y
Y
sc
e
X
e
Y
2.12. Charakterystyki geometryczne przekroju pręta w zadanym
układzie współrzędnych
J
X
=
116,0cm
4
A=11,4 cm
2
e
X
=
3,59 cm
J
Y
=
19,5 cm
4
e
Y
=
1,12 cm
J
2
=
12,7cm
4
2. Charakterystyki geometryczne przekroju pręta
109
Dr inż. Justyna Grzymisławska
Momenty
bezwładności
w układzie YZ
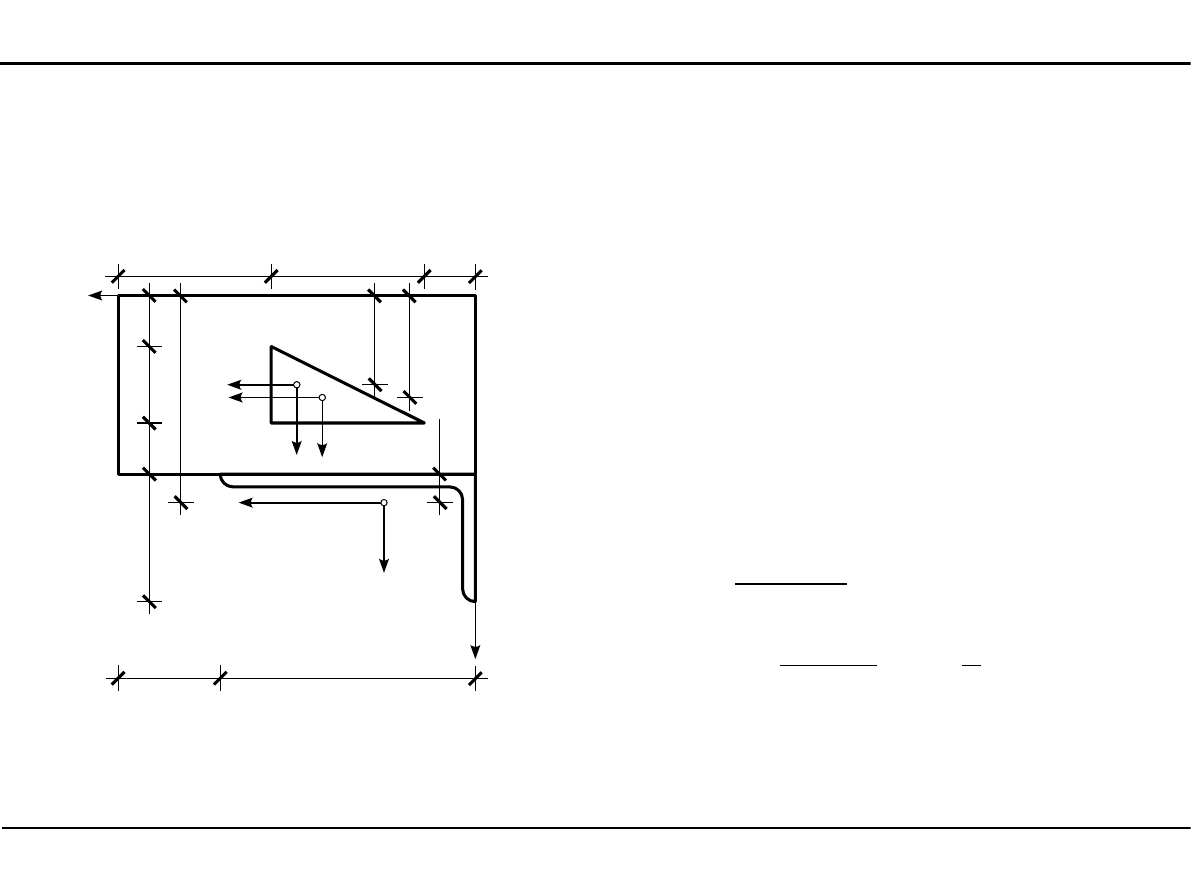
z
1
=
7,0
2
=
3,50cm
z
2
=
5,0−
3,0
3
=
4,0 cm
z
3
=
7,01,12=8,12cm
2.12. Charakterystyki
geometryczne przekroju
pręta w zadanym układzie
współrzędnych
[cm]
6,0
2,0
10,0
2,
0
6,0
3,
0
5,
0
4,0
2,
0
sc
1
Y
01
Z
01
3,
50
sc
2
Y
02
Z
02
4,
0
sc
3
Y
03
Z
03
1,
12
8,
12
Y
Z
2. Charakterystyki geometryczne przekroju pręta
110
Dr inż. Justyna Grzymisławska
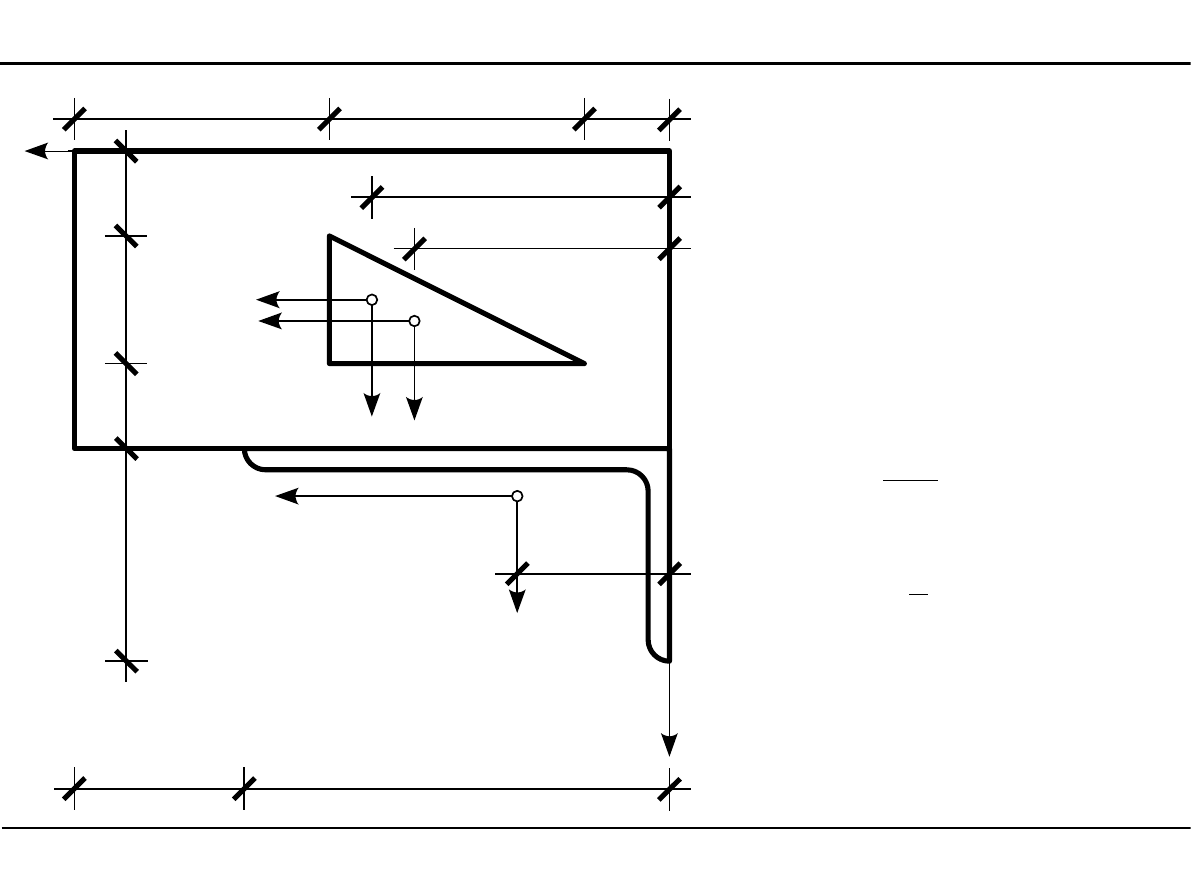
Momenty bezwładności w układzie YZ
2.12. Charakterystyki geometryczne przekroju pręta w zadanym
układzie współrzędnych
z
1
=
3,50 cm
z
2
=
4,0 cm
z
3
=
8,12 cm
J
Y
=
14,0⋅7,0
3
12
3,50
2
⋅
14,0⋅7,0−
−
6,0⋅3,0
3
36,0
4,0
2
⋅
1
2
⋅
6,0⋅3,0
−
19,58,12
2
⋅
11,4=2223 cm
4
Y
Z
6,0
2,0
10,0
[cm]
2,
0
6,0
3,
0
5,
0
4,0
2,
0
sc
1
sc
2
sc
3
Y
01
Z
01
Y
02
Z
02
Y
03
Z
03
4,
0
3,
50
8,
12
1,
12
2. Charakterystyki geometryczne przekroju pręta
111
Dr inż. Justyna Grzymisławska
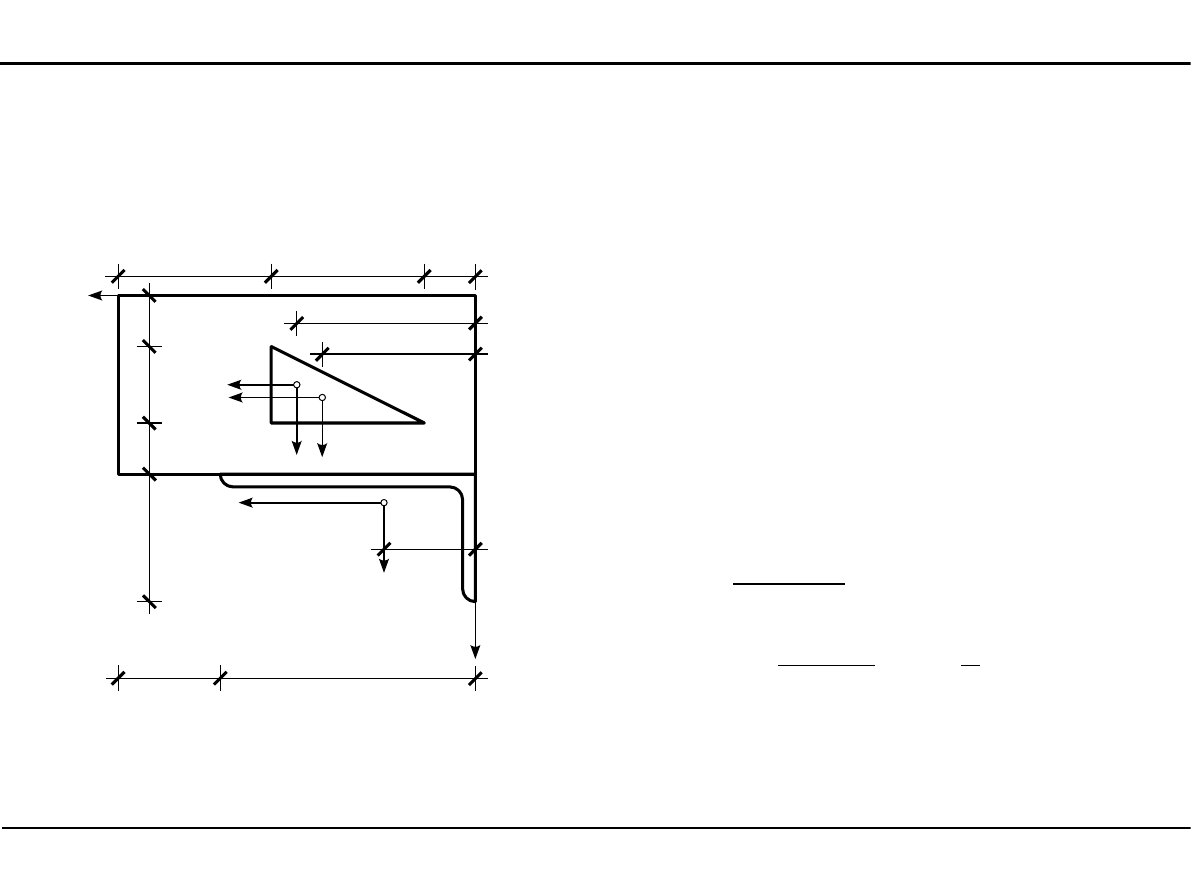
Momenty
bezwładności
w układzie YZ
y
1
=
14,0
2
=
7,0 cm
y
2
=
2,0
2
3
⋅
6,0=6,0 cm
z
3
=
3,59 cm
2.12. Charakterystyki
geometryczne przekroju
pręta w zadanym układzie
współrzędnych
[cm]
6,0
2,0
10,0
2,
0
6,0
3,
0
5,
0
4,0
2,
0
Y
Z
sc
1
Y
01
Z
01
7,0
sc
2
Y
02
Z
02
6,0
sc
3
Y
03
Z
03
3,59
2. Charakterystyki geometryczne przekroju pręta
112
Dr inż. Justyna Grzymisławska
Momenty bezwładności w układzie YZ
2.12. Charakterystyki geometryczne przekroju pręta w zadanym
układzie współrzędnych
y
1
=
7,0 cm
y
2
=
6,0cm
y
3
=
3,59 cm
J
Z
=
7,0⋅14,0
3
12
7,0
2
⋅
14,0⋅7,0−
−
3,0⋅6,0
3
36,0
6,0
2
⋅
1
2
⋅
6,0⋅3,0
−
116,03,59
2
⋅
11,4=6324 cm
4
Y
Z
6,0
2,0
10,0
[cm]
2,
0
6,0
3,
0
5,
0
4,0
2,
0
sc
1
sc
2
sc
3
Y
01
Z
01
Y
02
Z
02
Y
03
Z
03
6,0
7,0
3,59
2. Charakterystyki geometryczne przekroju pręta
113
Dr inż. Justyna Grzymisławska
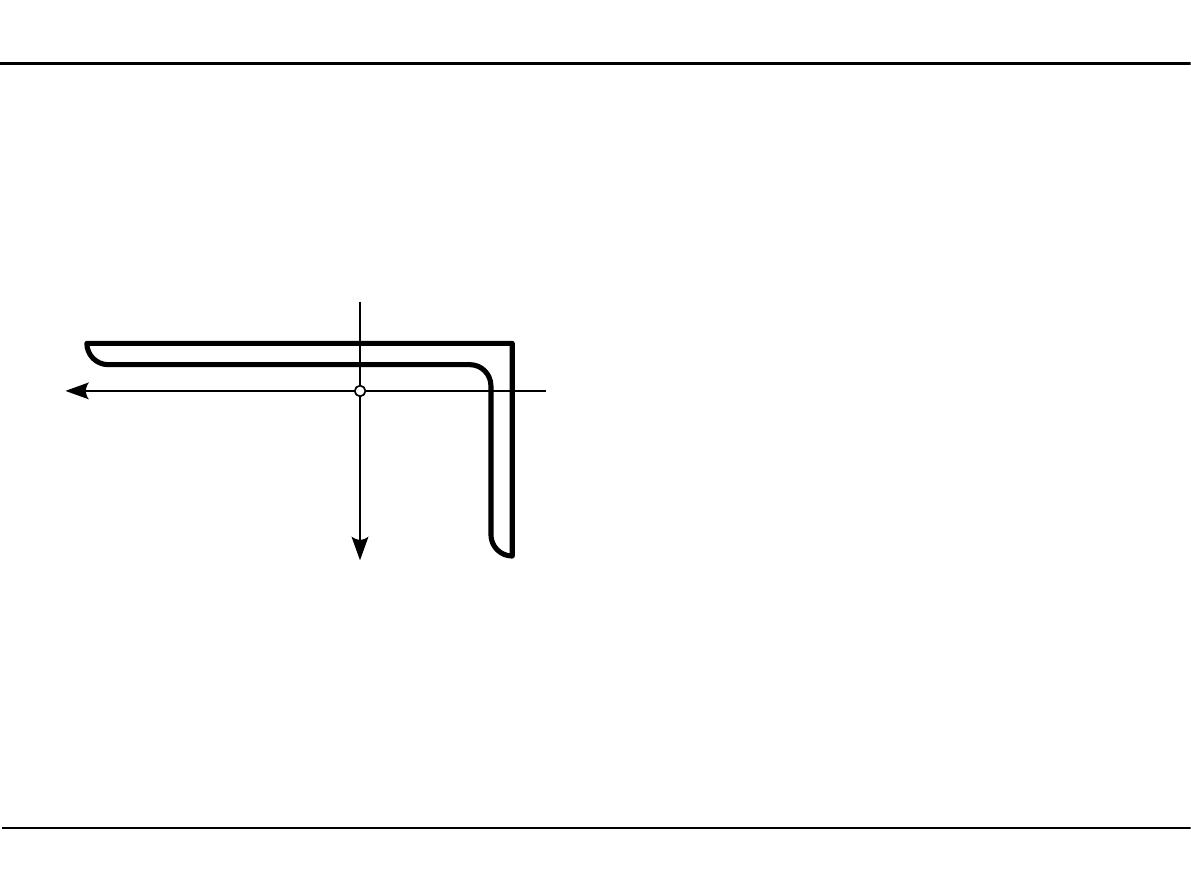
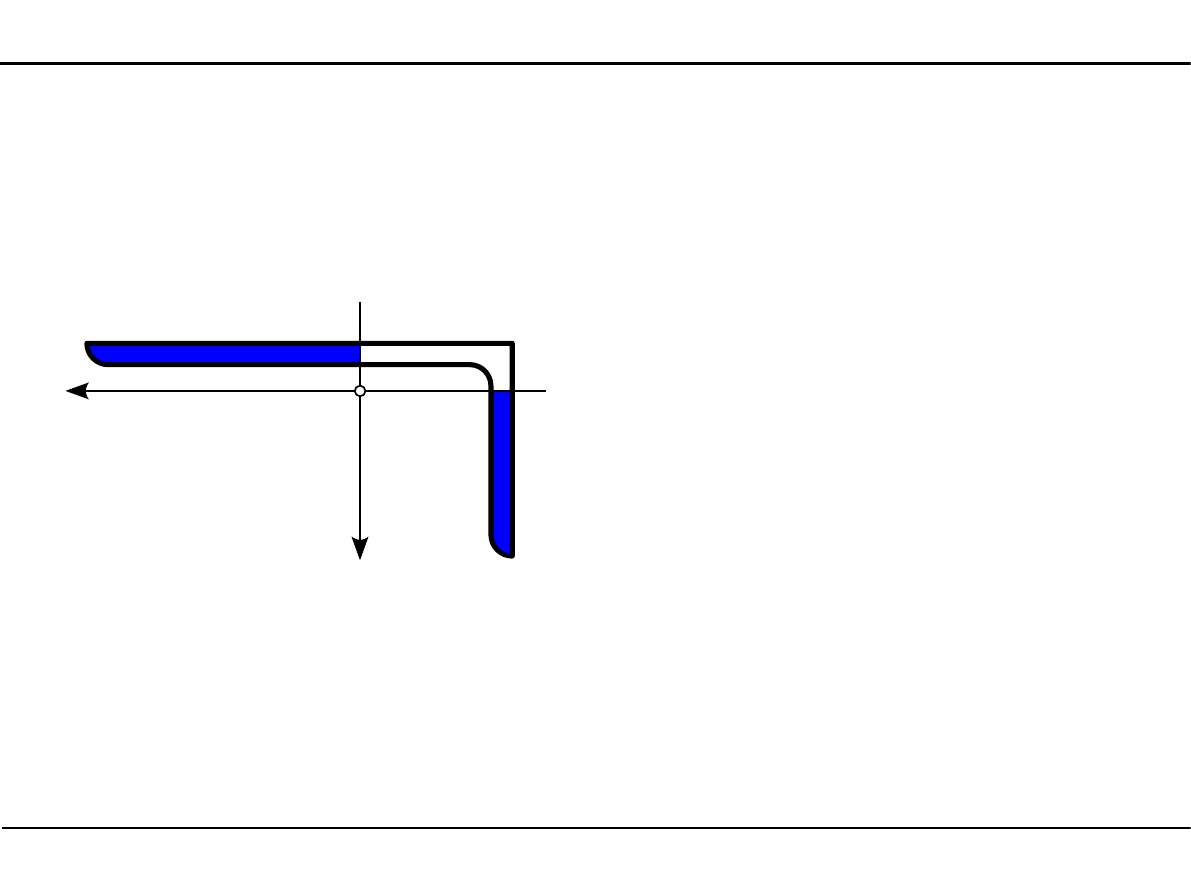
Dewiacyjny moment bezwładności kątownika nierównoramiennego
2.12. Charakterystyki geometryczne przekroju pręta w zadanym
układzie współrzędnych
sc
3
Y
03
Z
03
J
Y03
=
19,5 cm
4
J
2
=
12,7 cm
4
J
Z03
=
116,0 cm
4
I
1
=
19,5116,0=125,5cm
4
I
1
=
J
1
12,7=125,5cm
4
J
1
=
112,8 cm
4
2. Charakterystyki geometryczne przekroju pręta
114
Dr inż. Justyna Grzymisławska
I
2
=
112,8⋅12,7=1433cm
8
I
2
=
19,5⋅116,0−J
Y03Z03
2
=
1433 cm
8
∣
J
Y03Z03
∣
=
26,50 cm
4
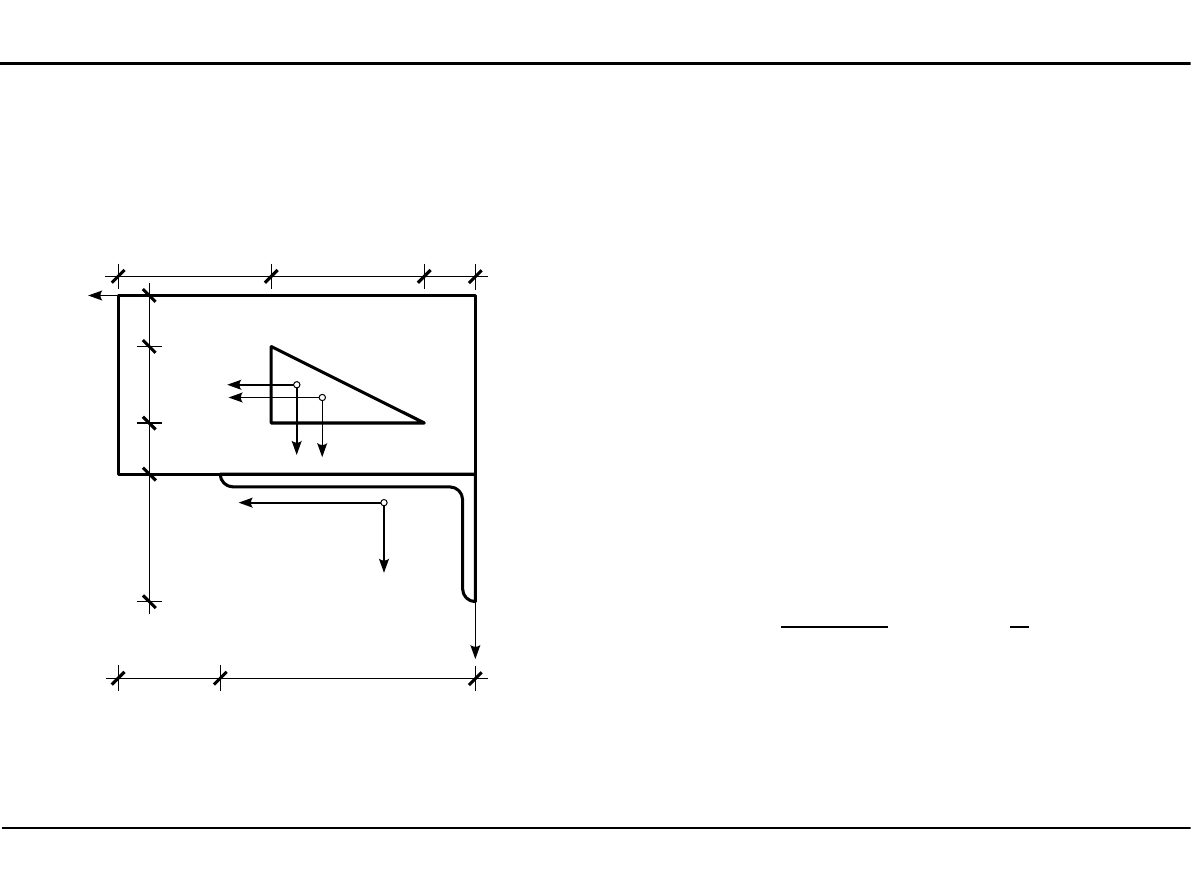
Dewiacyjny moment bezwładności kątownika nierównoramiennego
2.12. Charakterystyki geometryczne przekroju pręta w zadanym
układzie współrzędnych
J
2
=
12,7 cm
4
J
1
=
112,8 cm
4
sc
3
Y
03
Z
03
J
Y03
=
19,5 cm
4
J
Z03
=
116,0 cm
4
J
Y03Z03
=−
26,50cm
4
2. Charakterystyki geometryczne przekroju pręta
115
Dr inż. Justyna Grzymisławska
Momenty bezwładności w układzie YZ
2.12. Charakterystyki geometryczne przekroju pręta w zadanym
układzie współrzędnych
y
1
=
7,0 cm
y
2
=
6,0cm
y
3
=
3,59 cm
z
1
=
3,50 cm
z
2
=
4,0 cm
z
3
=
8,12 cm
J
YZ
=
0,07,0⋅3,50⋅14,0⋅7,0−
−
−
6,0
2
⋅
3,0
2
72
6,0⋅4,0⋅
1
2
⋅
3,0⋅6,0
−
−
26,503,59⋅8,12⋅11,4=2495 cm
4
Y
Z
6,0
2,0
10,0
[cm]
2,
0
6,0
3,
0
5,
0
4,0
2,
0
sc
1
sc
2
sc
3
Y
01
Z
01
Y
02
Z
02
Y
03
Z
03
Document Outline
- Slajd 1
- Slajd 2
- Slajd 3
- Slajd 4
- Slajd 5
- Slajd 6
- Slajd 7
- Slajd 8
- Slajd 9
- Slajd 10
- Slajd 11
- Slajd 12
- Slajd 13
- Slajd 14
- Slajd 15
- Slajd 16
- Slajd 17
- Slajd 18
- Slajd 19
- Slajd 20
- Slajd 21
- Slajd 22
- Slajd 23
- Slajd 24
- Slajd 25
- Slajd 26
- Slajd 27
- Slajd 28
- Slajd 29
- Slajd 30
- Slajd 31
- Slajd 32
- Slajd 33
- Slajd 34
- Slajd 35
- Slajd 36
- Slajd 37
- Slajd 38
- Slajd 39
- Slajd 40
- Slajd 41
- Slajd 42
- Slajd 43
- Slajd 44
- Slajd 45
- Slajd 46
- Slajd 47
- Slajd 48
- Slajd 49
- Slajd 50
- Slajd 51
- Slajd 52
- Slajd 53
- Slajd 54
- Slajd 55
- Slajd 56
- Slajd 57
- Slajd 58
- Slajd 59
- Slajd 60
- Slajd 61
- Slajd 62
- Slajd 63
- Slajd 64
- Slajd 65
- Slajd 66
- Slajd 67
- Slajd 68
- Slajd 69
- Slajd 70
- Slajd 71
- Slajd 72
- Slajd 73
- Slajd 74
- Slajd 75
- Slajd 76
- Slajd 77
- Slajd 78
- Slajd 79
- Slajd 80
- Slajd 81
- Slajd 82
- Slajd 83
- Slajd 84
- Slajd 85
- Slajd 86
- Slajd 87
- Slajd 88
- Slajd 89
- Slajd 90
- Slajd 91
- Slajd 92
- Slajd 93
- Slajd 94
- Slajd 95
- Slajd 96
- Slajd 97
- Slajd 98
- Slajd 99
- Slajd 100
- Slajd 101
- Slajd 102
- Slajd 103
- Slajd 104
- Slajd 105
- Slajd 106
- Slajd 107
- Slajd 108
- Slajd 109
- Slajd 110
- Slajd 111
- Slajd 112
- Slajd 113
- Slajd 114
- Slajd 115
Wyszukiwarka
Podobne podstrony:
Charakterystyki geometryczne przekroju
Obliczanie charakterystyk geometrycznych przekrojow(1)
Charakterystyki geometryczne przekroju
Charakterystyki geometryczne przekroju
Charakterystyki geometryczne przekrojów 2008
charaktrystyki geometryczne
01 Z Charakterystyki geometrycz Nieznany (2)
Charakterystyki geometryczne kadłuba statku
Charakterystyki geometryczne
20. Charakterystyka badania przekrojowego-przykłady badań przekrojowych, licencjat(1)
01-charakterystyki geometryczne
Czym jest święta geometria, Przekroczyć Horyzont Zdarzeń - Wszystko Jest Czarną Całością, Święta Geo
charakterystyki geometryczne figur plaskich czesc I
charakterystyki geometryczne figur plaskich czesc II (1)
Charakterystyki geometryczne figur płaskich
GEOMETRIA PRZEKROJU
Poprawa Charakterystyki geometryczne
więcej podobnych podstron