Podstawowe operacje arytmetyczne i logiczne w
systemie dwójkowym
Politechnika Opolska, Instytut Inżynierii Produkcji
mgr inż. Bogdan Ruszczak ©
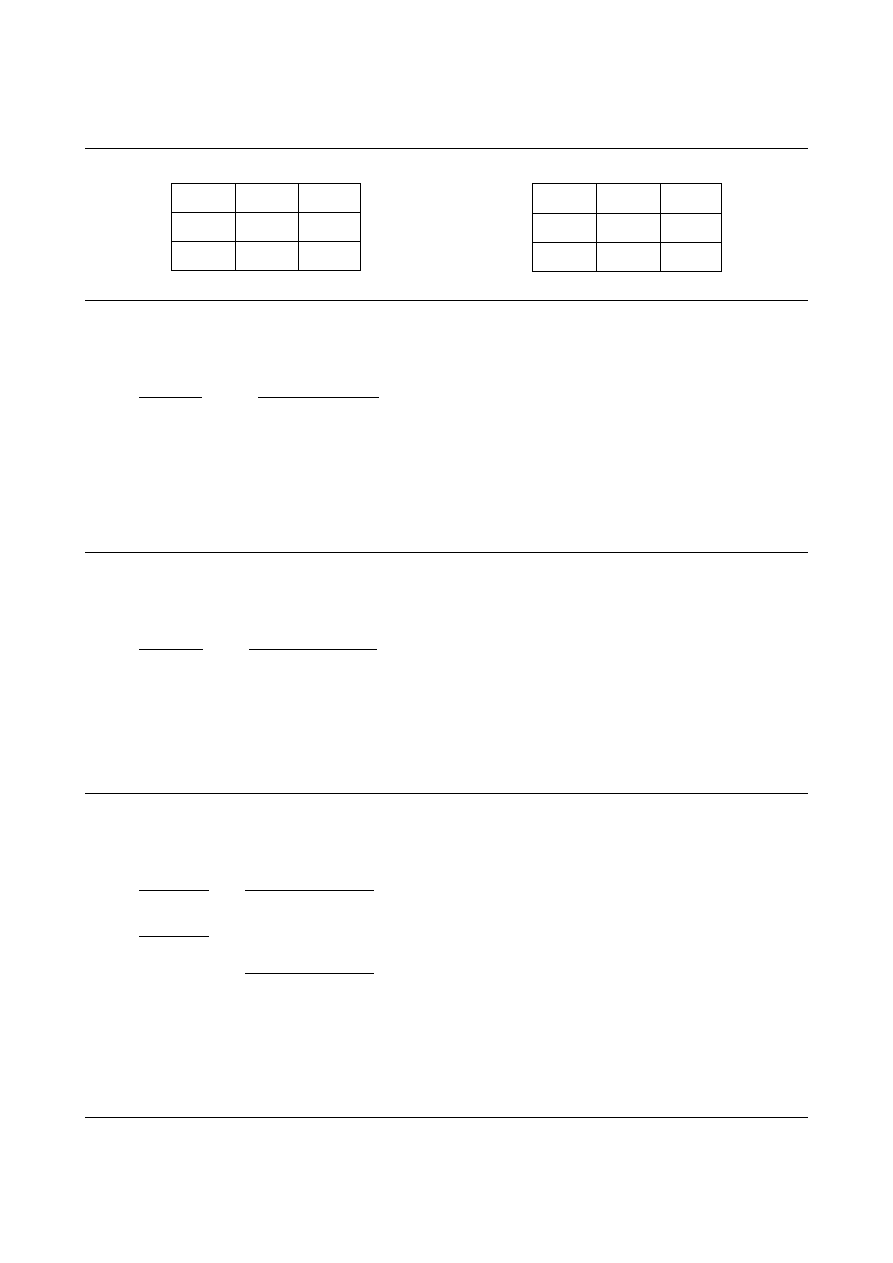
Tabliczka dodawania systemu dwójkowego
+
0
1
0
0
1
1
1
1 0
Tabliczka mnożenia systemu dwójkowego
x
0
1
0
0
0
1
0
1
Zadanie 1: 323
(10)
+ 287
(10)
= 101000011
(2)
+ 10001111
(2)
= ?
323
+ 287
101000011
+ 100011111
610
1001100010
323
(10)
+ 287
(10)
=610
(10)
101000011
(2)
+ 10001111
(2)
= 1001100010
(2)
sprawdzenie:
1001100010
(2)
= 1
·2
9
+ 1·2
6
+ 0·2
5
+ 1·2
1
= 512 + 64 + 32 + 1 =
610
(10)
Zadanie 2: 323
(10)
- 287
(10)
= 101000011
(2)
- 100011111
(2)
= ?
323
- 287
101000011
- 100011111
36
000100100
323
(10)
- 287
(10)
=36
(10)
101000011
(2)
- 10001111
(2)
= 100100
(2)
sprawdzenie:
100100
(2)
= 1
·2
5
+ 1·2
2
= 32 + 4 = 3
6
(10)
Zadanie 3: 39
(10)
·
11
(10)
= 100111
(2)
·
1011
(2)
= ?
39
x 11
100111
x 1011
39
+ 39
429
100111
100111
000000
+ 100111
110101101
39
(10)
·
11
(10)
= 429
(10)
100111
(2)
·
1011
(2)
= 110101101
(2)
sprawdzenie:
110101101
(2)
= 1
·2
8
+
1
·2
7
+
1
·2
5
+
1
·2
3
+
1
·2
2
+ 1·2
0
= 256 + 128 + 32 + 8 + 4 + 1= 429
(10)
www.ruszczak.po.opole.pl
Podstawowe operacje logiczne – różne rodzaje zapisu:
–
Suma logiczna: A
∪
B , A lub B, A
OR
B
–
Iloczyn logiczny: A
∩
B, A i B, A
AND
B
–
Negacja logiczna – zaprzeczenie:
┐
A, A', ~A, nie A,
NOT
A
A
B
A
∪
B
0
1
0
1
0
0
1
1
0
1
1
1
A
B
A
∩
B
0
1
0
1
0
0
1
1
0
0
0
1
A
A'
0
1
1
0
Zadanie 4:
A
∪
B, A
∩
B, A', B'.
A=
1110101011001011
B= 1010110101101001
A
∪
B
A
∩
B
A'
B'
1110101011001011
1010110101101001
1110101011001011
1010110101101001
1110101011001011
1010110101101001
1110111111101011
1010100001001001
0001010100110100
0101001010010110
A
∪
B = 1110111111101011
A
∩
B = 1010100001001001
A' = 1010100110100
B' = 101001010010110
Niektóre twierdzenia algebry Bool'a:
A
∪Α=Α
A
∩Α
=A
(A')'=A
(A
∪Β
)'=A'
∩Β
'
(A
∩Β
)'=A'
∪Β
'
Zadanie 4:
A
∪
B, A
∩
B, A', B'.
A=
1110 1010 1100 1011
B= 1010 1101 0110 1001
C= 1010 1101 0110 1001
W=A
∩((
A
∩
C
)∪Β
')
A= 1110 1010 1100 1011
C= 1010 1101 0110 1001
A
∩
C =1010 1000 0100 1001
www.ruszczak.po.opole.pl
B= 1010 1101 0110 1001
Β
'= 0101 0010 1001 0110
A
∩
C =1010 1000 0100 1001
Β
'= 0101 0010 1001 0110
(
A
∩
C
)∪Β
'= 1111 1010 1101 1111
A= 1110 1010 1100 1011
(
A
∩
C
)∪Β
'= 1111 1010 1101 1111
Zadania do samodzielnego wykonania:
1) 134
(10)
+
145
(10)
= ?
(2)
2) 456
(10)
+
764
(10)
= ?
(2)
3) 127
(10)
+ 255
(10)
= ?
(2)
4) 256
(10)
+
64
(10)
= ?
(2)
5) 328
(10)
– 134
(10)
= ?
(2)
6) 255
(10)
–
127
(10)
= ?
(2)
7) 256
(10)
–
127
(10)
= ?
(2)
8) 172
(10)
–
344
(10)
= ?
(2)
(*)
9) 122
(10)
–
224
(10)
= ?
(2)
(*)
10) 127
(10)
·
11
(10)
= ?
(2)
11) 138
(10)
·
12
(10)
= ?
(2)
12) 118
(10)
·
33
(10)
= ?
(2)
13) 27
(10)
·
24
(10)
= ?
(2)
14) 228
(10)
·
67
(10)
= ?
(2)
15) A
∪
B, A
∩
B, A', B'
a) A=
1001 0110 1100 1011
B= 1011 1111 0110 1101
b) A=
11
11 1111 1111 1111
B= 1111 0000 0000 1111
c) A=
1111 1110 1101 1100
B= 1011 1000 0100 1001
d) A=
1000 0010 1100 1001
B= 1110 0001 0010 1111
(*) A -B dla B>A można rozwiązać: B – A i zmienić znak; A-B=-(B-A)
Rozwiązania:
1) 1 0001 0111
(2)
; 2) 100 1100 0100
(2)
; 3) 1 0111 1110
(2)
; 4) 1 0100 0000
(2)
; 5) 1100 0010
(2)
;
6) 1000 0000
(2)
; 7) 1000 0001
(2)
; 8) 1010 1100
(2)
;9) 110 0110
(2)
; 10) 101 0111 0101
(2)
11) 110 0111 1000
(2)
; 12) 1111 0011 0110
(2)
13) 10 1000 1000
(2)
; 14) 11 1011 1010 1100
(2)
;.
POMOC: Windows - Programy/Akcesoria/Kalkulator - Widok/Naukowy - możliwość przeliczeń binarnych, ósemkowych i szesnastkowych.
www.ruszczak.po.opole.pl