STOPA PROCENTOWA

Realna stopa dochodu/koszt kapitału – jest to nominalna stopa skorygowana o inflację. Wyznaczamy ją na
podstawie wzoru Fishera:

1

1

1









i

re

r

r

r

,

gdzie:

re

r

- realna stopa dochodu,

r

- nominalna stopa dochodu,

i

r

- stopa inflacji.

Często stosuje się przybliżony wzór (wynik nieznacznie różni się od uzyskanego z wzoru Fishera):

i

re

r

r

r





.

Stopa procentowa spot (stopa procentowa natychmiastowa) – stopa procentowa obowiązująca od danego
momentu przez okres, którego dotyczy.

Stopa procentowa forward (stopa procentowa terminowa) – stopa procentowa obowiązująca od pewnego
momentu w przyszłości przez okres, którego dotyczy.





















1

1

1

1

,

s

m

v

s

sr

mr

v

r

,

gdzie:

v

s

r

,

- stopa forward;

v

- ilość okresów stopy forward;

m

r

- m okresowa stopa spot;

m

- ilość okresów stopy

m

r

;

s

r

- s okresowa stopa spot;

s

- ilość okresów stopy

s

r

.

Stopa forward. Horyzont do roku, kapitalizacja prosta.





























1

360

1

360

1

360

,

s

r

m

r

v

r

s

m

v

s

.

Stopa forward. Horyzont powyżej roku, kapitalizacja złożona.









1

1

1

1

,





















v

s

s

m

m

v

s

r

r

r

.

Stopa forward. Dowolny horyzont, kapitalizacja ciągła.





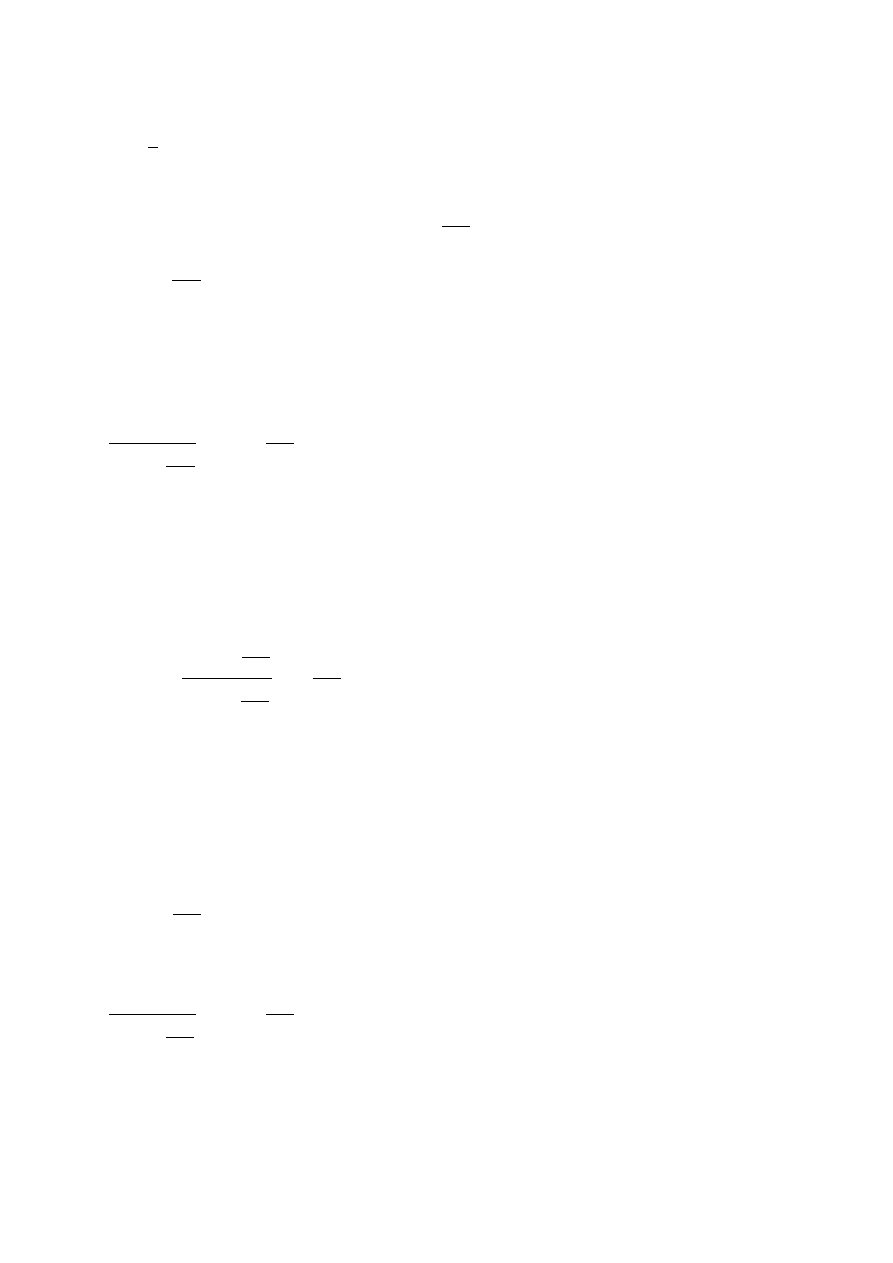
s

m

v

s

sr

mr

v

r





1

,

.

Stopa forward depozytu – jest to stopa depozytu, w który można zainwestować w pewnym momencie w
przyszłości na pewien okres.

Kwota otrzymana z depozytu na v dni po m dniach:

360

1

,

,

v

r

v

s

bid



.

gdzie:

v

s

bid

r

,

,

- v-dniowa stopa forward depozytu za s dni.

Kwota otrzymana z transakcji syntetycznej po m dniach:











 



360

1

360

1

1

,

,

m

r

s

r

m

bid

s

ask

,

gdzie:

s

ask

r

,

- stopa spot kredytu s-dniowego;

m

bid

r

,

- stopa spot depozytu m dniowego.

Syntetyczna stopa forward depozytu (synthetic forward bid rate):

v

s

r

m

r

rs

s

ask

m

bid

v

s

bid

360

1

360

1

360

1

,

,

,

,































,

v

s

bid

rs

,

,

- syntetyczna stopa depozytu v-dniowego za s dni.

Stopa forward kredytu – określa stopę kredytu, który będzie udzielony w pewnym momencie w przyszłości na
pewien okres.

Kwota płacona w kredycie na v dni po m dniach:

360

1

,

,

v

r

v

s

ask



.

Kwota płacona z transakcji syntetycznej po m dniach:











 



360

1

360

1

1

,

,

m

r

s

r

m

ask

s

bid

.

Syntetyczna stopa forward kredytu (synthetic forward ask rate):

360

1

,

,

v

r

v

s

bid



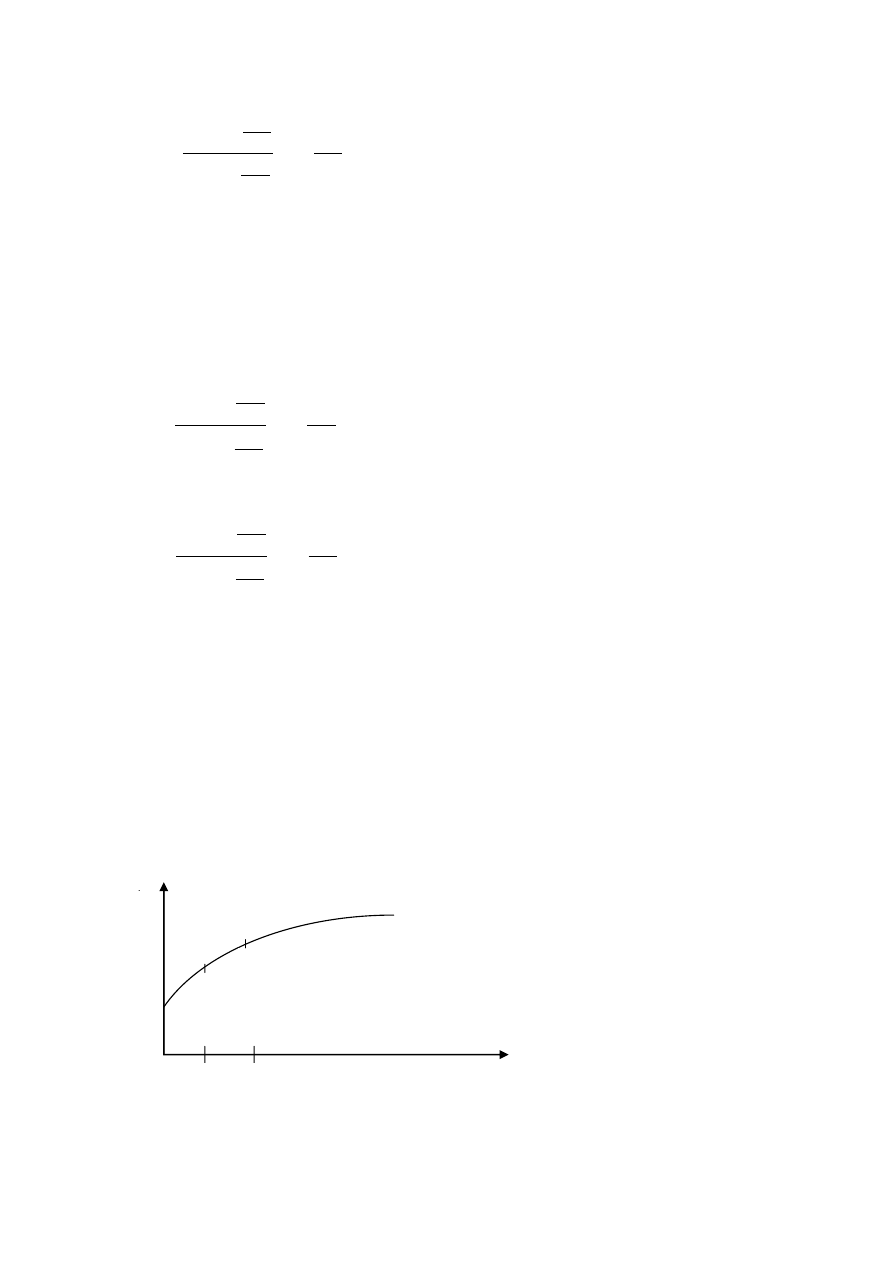
v

s

r

m

r

rs

s

bid

m

ask

v

s

ask

360

1

360

1

360

1

,

,

,

,































.

Warunki, które muszą spełniać stopy terminowe:

v

s

ask

v

s

bid

rs

r

,

,

,

,



v

s

bid

v

s

ask

rs

r

,

,

,

,



Przybliżenia stóp syntetycznych forward depozytu oraz kredytu:

v

s

r

m

r

r

s

bid

m

bid

v

s

bid

360

1

360

1

360

1

,

,

,

,



































,

v

s

r

m

r

r

s

ask

m

ask

v

s

ask

360

1

360

1

360

1

,

,

,

,



































.

Struktura terminowa stóp procentowych

Na podstawie stóp procentowych spot dotyczących różnych okresów, można wyznaczyć stopę terminową. W
pewnym uproszczeniu informuje ona o tym, jakich stóp można się spodziewać w pewnym okresie w przyszłości.
Fakty te wskazują na to, iż określenie stóp dotyczących różnych okresów ma ważne znaczenie praktyczne. W
tym podrozdziale odniesiemy się do teorii związanych ze stopami procentowymi dotyczącymi różnych okresów.
Zagadnienie to nosi nazwę struktura terminowa stóp procentowych (term structure of interest rates).
Stosowana jest również uproszczona nazwa krzywa dochodowości lub krzywa stopy dochodu (yield curve), co
ma uzasadnienie z powodu graficznej prezentacji zagadnienia.

Krzywa dochodowości

Na rysunku przedstawiona jest zależność stopy procentowej (na przykład stopy dochodu) od długości okresu,
którego ta stopa dotyczy. Zależność ta przedstawiona jest w postaci krzywej, składającej się z punktów,

A

Stopa dochodu

B

0,5

1

Liczba lat

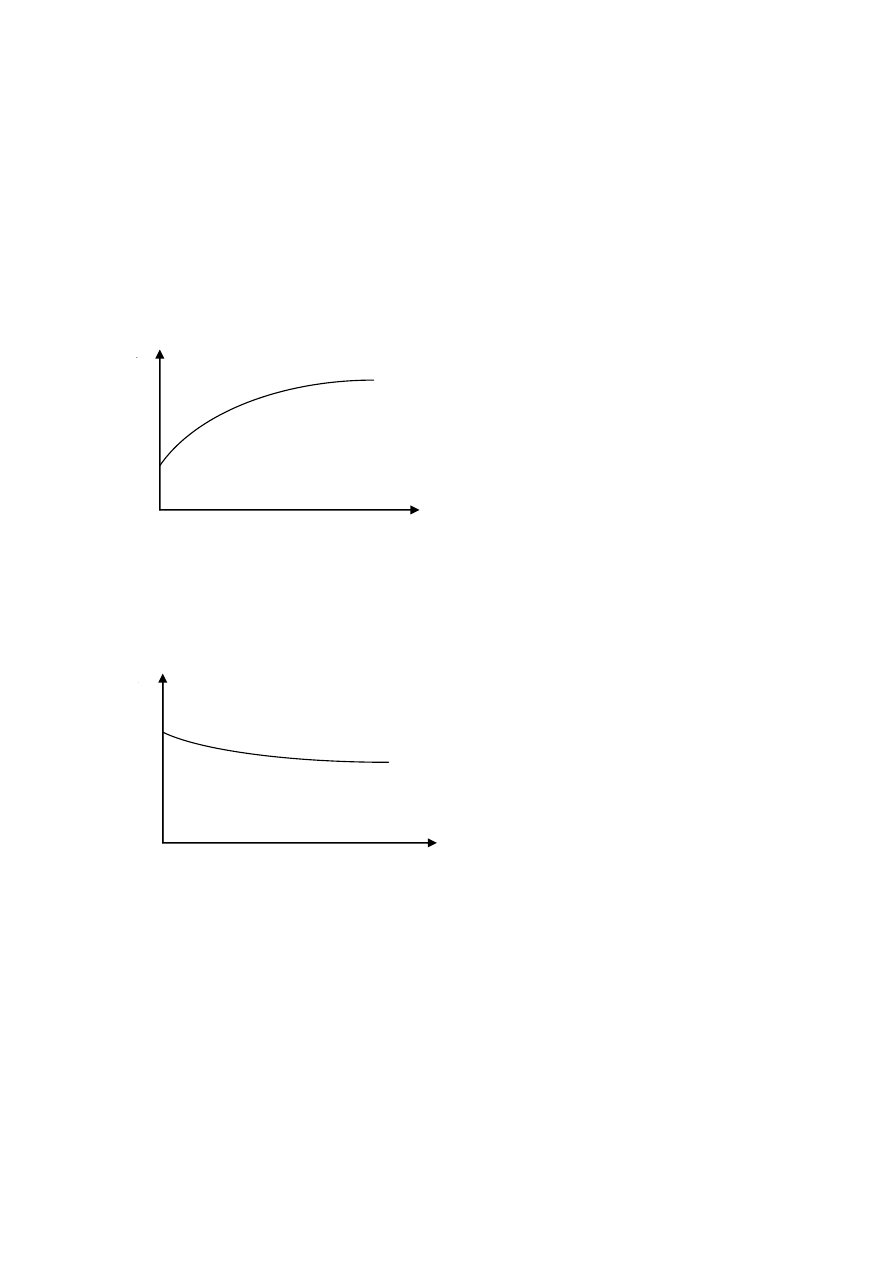
odpowiadających stopom procentowym dotyczącym poszczególnych okresów. Na przykład punkt A odpowiada
stopie półrocznej, zaś punkt B stopie rocznej. W tym przypadku stopa roczna jest wyższa od stopy półrocznej,
ale w praktyce może się zdarzyć odwrotnie. To oznacza, że krzywa dochodowości, będąca ilustracją struktury
terminowej stóp procentowych może mieć różny kształt. Typowe kształty tej krzywej przedstawione są na
rysunkach 3.5, 3.6, 3.7 i 3.8, przy czym:
- na rysunku 3.5 jest krzywa normalna (normal curve);
- na rysunku 3.6 jest krzywa odwrócona (inverted curve);
- na rysunku 3.7 jest krzywa płaska (flat curve);
- na rysunku 3.8 jest krzywa łukowata (humped curve).

Rysunek 3.5. Normalna krzywa dochodowości

Rysunek 3.6. Odwrócona krzywa dochodowości

Rysunek 3.7. Płaska krzywa dochodowości

Stopa dochodu

Liczba lat

Stopa dochodu

Liczba lat

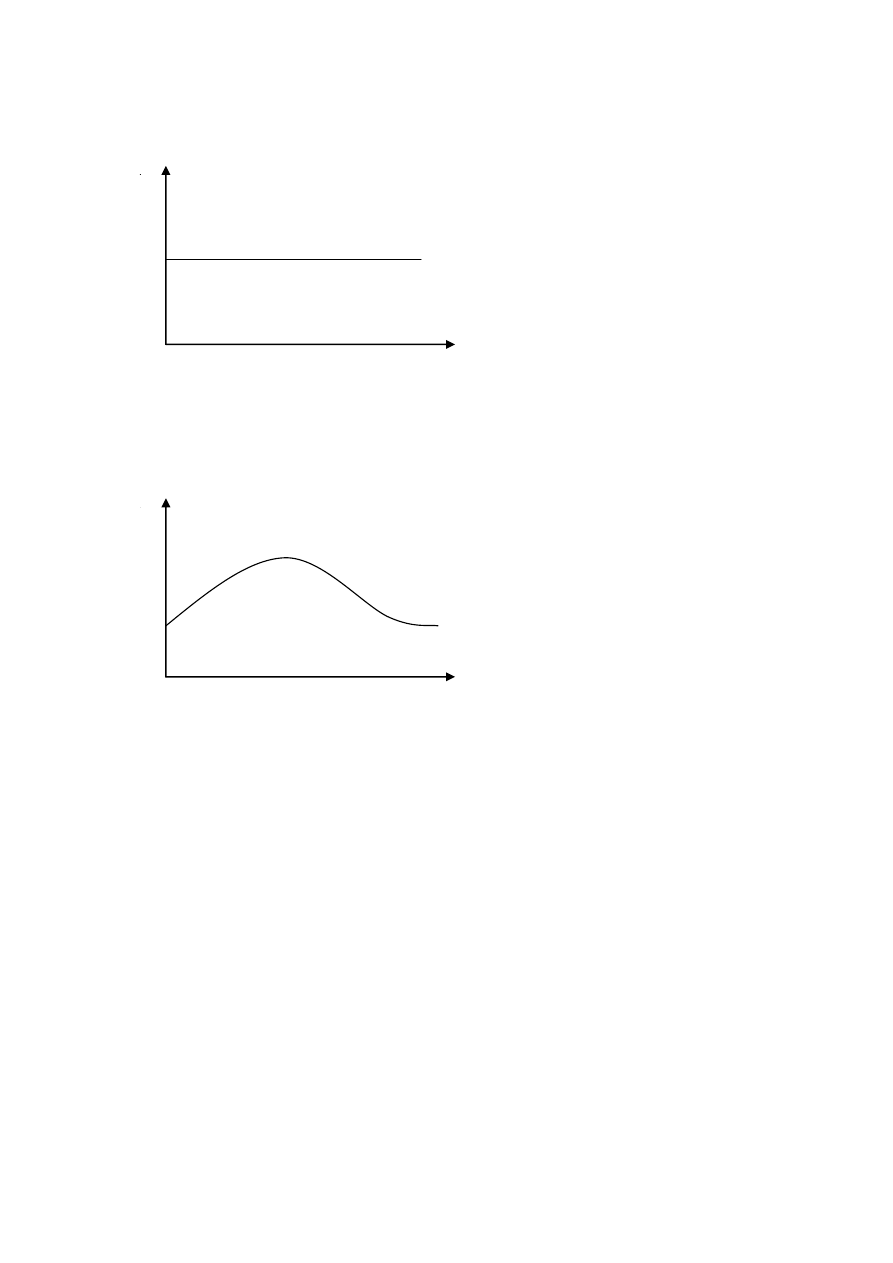
Rysunek 3.8. Łukowata krzywa dochodowości

W praktyce najczęściej spotykana jest krzywa normalna (wyjaśnia to jej nazwę), zaś w teorii najprostsza do
analiz jest krzywa płaska, w której stopy dotyczące różnych okresów są (przynajmniej w przybliżeniu) takie
same.


Obecnie przedstawimy kilka teorii, które mają na celu wyjaśnienie kształtowania się struktury terminowej stóp
procentowych, co oznacza też wyjaśnienie kształtu krzywej dochodowości. Ma to również znaczenie praktyczne.
Na przykład, jeśli wiemy, iż w danym momencie krzywa dochodowości jest malejąca, oznacza to, iż warto
pozyskać kapitał na dłuższy okres (w przypadku którego cena tego kapitału jest niższa). Powoduje to również
określone implikacje dla stóp terminowych.

Traktując rzecz w pewnym uproszczeniu, podstawowe teorie struktury terminowej stóp procentowych są
następujące:
- teoria segmentacji rynku (market segmentation theory);
- teoria oczekiwań (expectations theory);
- teoria preferencji płynności (liquidity preference theory);
- teoria preferowanego habitatu (preferred habitat theory).

Teoria segmentacji rynku jest chyba najprostsza spośród wymienionych podejść. Wychodzi z podstawowego
prawa ekonomii, mówiącego, że o cenie decyduje popyt i podaż. Teoria ta zakłada, że na rynku transferu
kapitału występują segmenty odpowiadające różnym okresom udostępniania kapitału, np. segment dzienny,
półroczny, roczny itp. Stopa procentowa w danym segmencie, czyli stopa procentowa odpowiadająca danemu
okresowi udostępnienia kapitału, zależy od podaży kapitału i popytu na kapitał. Jeśli wzrasta popyt na kapitał
udostępniony na dany okres, w stosunku do podaży kapitału, wówczas stopa procentowa rośnie, odwrotnie jest

Stopa dochodu

Liczba lat

Stopa dochodu

Liczba lat

w przypadku wzrostu podaży w stosunku do popytu. Teoria segmentacji rynku w pewnym sensie nawiązuje do
realnej stopy procentowej będącej składnikiem stopy procentowej we wzorze (3.1).
W zasadzie teoria ta może wyjaśnić każdą z czterech postaci krzywej dochodowości, przedstawionych na
rysunkach 3.5-3.8.
Pewną wadą tej teorii jest upraszczające założenie, iż każdy segment rynku transferu kapitału rozpatrywany jest
odrębnie, bez wskazania zależności z innymi segmentami. Oznaczałoby to na przykład, że stopa półroczna nie
ma żadnego związku ze stopą roczną, co w praktyce może nie być słuszne.

Teoria oczekiwań jest chyba najpopularniejszą spośród wymienionych powyżej teorii. Główna teza tej teorii
mówi, że stopy długoterminowe zależą od stóp krótkoterminowych – tych, które są teraz i tych, których rynek
oczekuje w przyszłości. To właśnie zależność stopy długoterminowej od oczekiwanych stóp krótkoterminowych
uzasadnia nazwę tej teorii. Podstawową tezę teorii oczekiwań zilustrujemy na przykładzie. Podobny przykład
wykorzystaliśmy już przy ilustracji zagadnienia stopy terminowej.
Rozpatrzymy dwie inwestycje o horyzoncie dwuletnim:
- inwestycja dwuletnia, po stopie spot dwuletniej (przyjmujemy tu kapitalizację roczną);
- inwestycja złożona z dwóch części: najpierw inwestycja roczna po stopie spot rocznej, a potem reinwestycja
przychodów po stopie spot rocznej, która będzie za rok.
Podstawowa idea, która jest tu wykorzystana, jest to idea równości stóp dochodu z rozpatrywanych dwóch
inwestycji. Ilustruje to następujący wzór:

)

15

.

3

(

))

(

1

)(

1

(

)

1

(

1

1

1

2

2

r

E

r

r









gdzie:

)

(

1

1

r

E

- oczekiwana stopa spot roczna za rok.

Oznacza to, iż stopa procentowa dwuletnia zależy od dwóch stóp procentowych rocznych, aktualnej i
oczekiwanej za rok. Zauważmy, że ta sama idea była wykorzystana przy wyznaczaniu stopy terminowej, jednak
jest podstawowa koncepcyjna różnica między tymi dwoma podejściami:
- przy WYZNACZANIU stopy terminowej, na przykład stopy rocznej za rok, wykorzystane są znane stopy spot,
roczna i dwuletnia;
- przy WYJAŚNIANIU zależności między stopami spot, na przykład roczną i dwuletnią, wykorzystana jest stopa
spot roczna i oczekiwana stopa spot roczna za rok.
Jest natomiast łącznik między tymi dwoma podejściami, mianowicie:
Stopa terminowa może być (w uproszczeniu) interpretowana jako oczekiwana stopa spot.

Przedstawiony powyżej przykład może być uogólniony. W tym celu rozpatrzmy długoterminową,
m-letnią inwestycję, w przypadku której stopa procentowa (jest to stopa dochodu) jest wyjaśniana za pomocą m
krótkoterminowych, rocznych stóp procentowych. Wówczas otrzymujemy ogólny wzór:

)

16

.

3

(

))

(

1

(

...

))

(

1

))(

(

1

)(

1

(

)

1

(

1

1

1

2

1

1

1

r

E

r

E

r

E

r

r

m

m

m



















Kształtowanie się oczekiwanych stóp krótkoterminowych w relacji do aktualnych stóp krótkoterminowych niesie
pewne informacje, jeśli chodzi o kształt krzywej dochodowości. W szczególności, wyjaśnimy to na przykładzie
dwóch stóp, gdzie relacje są następujące:
- jeśli oczekiwana stopa krótkoterminowa jest wyższa od aktualnej stopy krótkoterminowej, to stopa
długoterminowa jest wyższa od stopy krótkoterminowej – sugeruje to normalną krzywą dochodowości;
- jeśli oczekiwana stopa krótkoterminowa jest niższa od aktualnej stopy krótkoterminowej, to stopa
długoterminowa jest niższa od stopy krótkoterminowej – sugeruje to odwróconą krzywą dochodowości;
- jeśli oczekiwana stopa krótkoterminowa jest równa aktualnej stopie krótkoterminowej, to stopa
długoterminowa jest równa stopie krótkoterminowej – sugeruje to płaską krzywą dochodowości.
Te prawidłowości ilustrują dwa przykłady.

Przykład. Zadanie nr 8 dla studentów.

Jak widać, obserwuje się rosnące stopy spot, aż do piątego roku, w przypadku którego stopa jest niższa, gdyż
oczekiwana stopa krótkoterminowa po czwartym roku jest niższa.

W praktyce wyznaczenie stóp spot przy bardzo długich terminach w podany sposób nie jest proste, gdyż
wymaga znajomości oczekiwań w zakresie stóp krótkoterminowych w dalszej przyszłości.

Teoria preferencji płynności pozostaje w pewnej opozycji do teorii oczekiwań, przynajmniej w tej sytuacji,
gdy teoria oczekiwań wyjaśnia płaską i odwróconą krzywą dochodowości. Teoria ta w pewnym sensie skłania
się do podejścia zawartego we wzorze (3.1), w którym jednym ze składników stopy procentowej jest premia
płynności, która rośnie w miarę wzrostu horyzontu inwestycji. Tutaj warto dodać, iż czasem łączy się tę premię
z premią za ryzyko, twierdząc, że premia płynności jest premią za większą niepewność związaną z długim
horyzontem. My jednak zdecydowaliśmy się dokonać rozdziału tych dwóch składników.
Teoria preferencji płynności najczęściej jest traktowana jako koncepcja wyjaśniająca normalną krzywą
dochodowości. Jest to jednak duże uproszczenie. Dla wyjaśnienia tej kwestii rozpatrzmy dwie inwestycje,
dwuletnią i trzyletnią i przyjmijmy dla uproszczenia, że są one wolne od ryzyka, a także, że realna stopa
procentowa w obu przypadkach jest taka sama i wynosi 2%. Oznacza to, iż stopa procentowa dekomponowana
na składniki i dana wzorem (3.1), w tym wypadku jest równa:

lp

r

r

i







%

2

Przyjmijmy teraz, że oczekiwana stopa inflacji za następne 2 lata wynosi 4%, zaś za następne trzy lata wynosi
2,5% (obie stopy wyrażone są w skali rocznej). Oznacza to, że spodziewany jest spadek stopy inflacji w trzecim
roku.
Przyjmijmy, że stopy spot wynoszą: dwuletnia: 7%, trzyletnia: 6%. Oznacza to (w tym przedziale czasowym)
odwróconą krzywą dochodowości. Jednak po wyznaczeniu premii płynności otrzymujemy:
- dla inwestycji dwuletniej: 1% (bo 7%=4%+2%+1%);
- dla inwestycji trzyletniej: 1,5% (bo 6%=2,5%+2%+1,5%).
Jak widać, premia płynności rośnie, ale krzywa dochodowości jest odwrócona, bo działa silniejszy efekt spadku
oczekiwanej inflacji.

Teoria preferowanego habitatu jest trochę podobna do teorii segmentacji rynku i czasem jest z nią
utożsamiana. Jest jednak pewna różnica między tymi teoriami. Habitat jest pojęciem z biologii i oznacza
środowisko, w którym osobniki danego gatunku znajdują najdogodniejsze warunki życia. W tym przypadku
habitat można utożsamiać z segmentem rynku transferu kapitału, preferowanym przez podmioty udostępniające i
pozyskujące kapitał. W tym zatem sensie teoria preferowanego habitatu sprowadza się do segmentacji rynku,
lecz wyjaśnia, że segmentacja rynku występuje z powodu preferencji podmiotów. Ta teoria może wyjaśnić na
przykład łukowatą krzywą dochodowości, która pojawia się wtedy, gdy występują zwiększone preferencje w
zakresie podaży kapitału krótkoterminowego (zgłaszane przez banki) i kapitału długoterminowego (zgłaszane
przez fundusze emerytalne), w stosunku do kapitału średnioterminowego.

Na zakończenie rozważań o strukturze terminowej stóp procentowych, kilka słów poświęcimy czwartemu
składnikowi stopy procentowej, tzn. premii za ryzyko. Co prawda problem ryzyka jest omawiany szeroko w
dalszej części, jednak tutaj przedstawimy pewne wprowadzające rozważania właśnie w kontekście struktury
terminowej stóp procentowych.
Weźmy pod uwagę wzór (3.1), zawierający dekompozycję stopy procentowej na cztery składniki. Zauważmy, że
trzy spośród nich, tzn. oczekiwana stopa inflacji, realna stopa procentowa i premia płynności mogą być
traktowane jako ustalone dla dowolnego okresu (np. dla dwóch lat, czterech tygodni itp.). Jednak jest jeszcze
czwarty składnik, tzn. premia za ryzyko i ten składnik dla danego okresu może być różny, w zależności od tego,
jakim ryzykiem obarczony jest kapitał, który jest transferowany i któremu właśnie odpowiada stopa procentowa.
Oznacza to, że mogą występować różne krzywe dochodowości, osobno dla każdego poziomu ryzyka.
Zjawisko to nazywa się strukturą terminową ryzyka (term structure of risk). Problem ten zilustrujemy
rozpatrując dwie inwestycje, z których jedna jest wolna od ryzyka, zaś druga obarczona ryzykiem.
Charakteryzują się one różnymi krzywymi dochodowości, czyli różna jest struktura terminowa stóp
procentowych w tych dwóch inwestycjach. Oznaczmy:
- stopy procentowe (dochodu) inwestycji wolnej od ryzyka odpowiadające kolejnym n okresom jako:

fn

f

f

r

r

r

,...,

,

2

1

- stopy procentowe (dochodu) inwestycji ryzykownej odpowiadające kolejnym n okresom jako:

en

e

e

r

r

r

,...,

,

2

1

Ponieważ premia za ryzyko jest – w świetle wzoru (3.1) – nadwyżką stopy dochodu ponad stopę wolną od
ryzyka, możemy łatwo obliczyć premie za ryzyko odpowiadające kolejnym okresom. Są one równe:

fn

en

f

e

f

e

r

r

r

r

r

r







,...,

,

2

2

1

1

W ten sposób otrzymuje się ciąg stóp procentowych, nazywany strukturą terminową ryzyka. Ilustracja zawarta
jest na rysunku 3.9

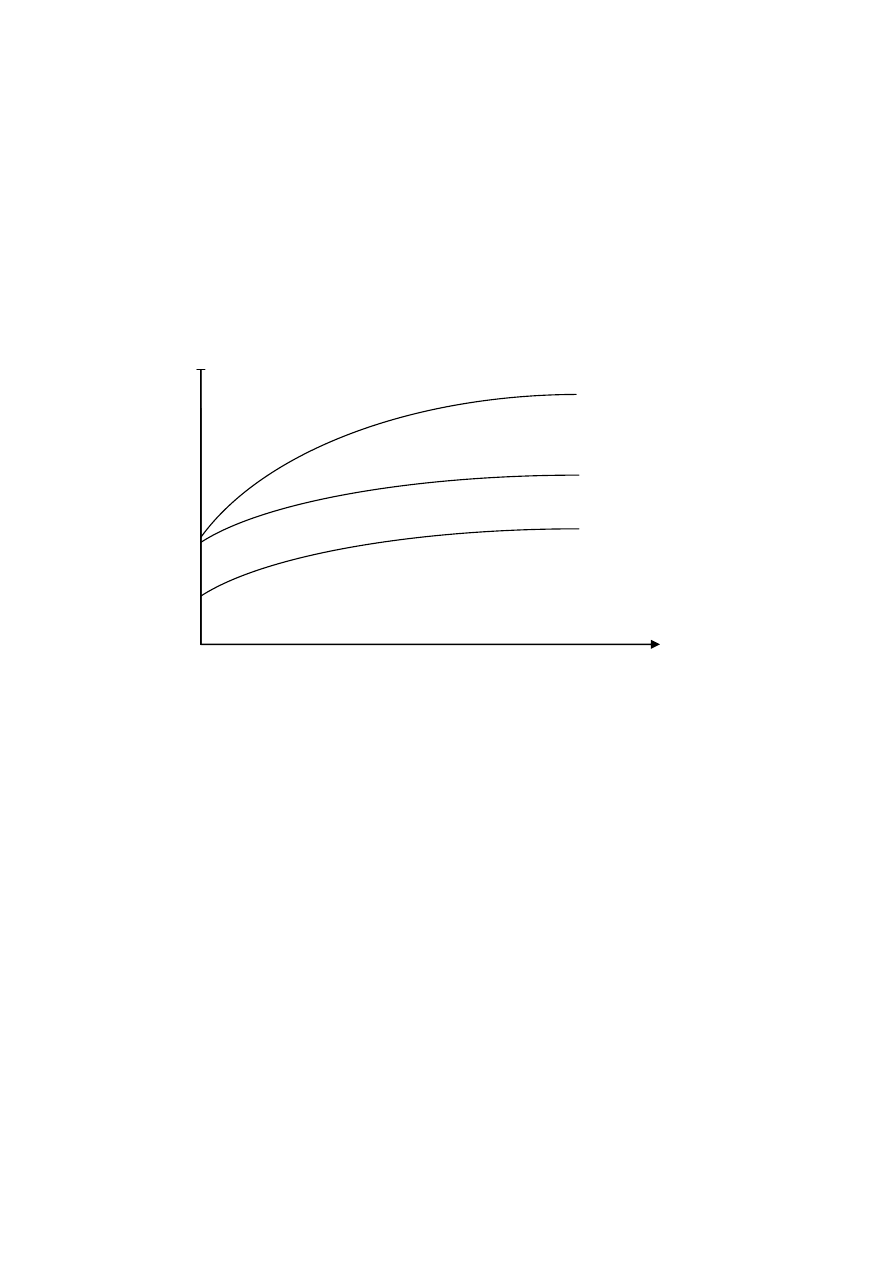
Rysunek 3.9. Struktura terminowa ryzyka

























Na rysunku przedstawione są dwie krzywe dochodowości. Krzywa A odpowiada inwestycji wolnej od ryzyka,
zaś krzywa B odpowiada inwestycji ryzykownej. Różnica między tymi krzywymi to właśnie struktura
terminowa ryzyka. Została ona dodatkowo zaznaczona w postaci krzywej C. Jak widać krzywa A i krzywa C
„sumują się” dając w efekcie krzywą B.
Rozważania te podsumowane są w poniższym przykładzie.

Przykład. Zadanie nr 9 dla studentów.

Liczba lat

A

C

B

Stopa dochodu

ZADANIA

ZAD 1.
Oblicz realną stopę dochodu z lokaty wiedząc że oprocentowanie wynosi

a) 10% a inflacja 3%,
b) 15% a inflacja 1,5%,
c) 6,5% a inflacja 0,5%.

ZAD 2.
Ile powinna wynosić sześćdziesięcio dniowa stopa terminowa (forward) po 30 dniach, jeśli
rynkowa stopa WIBOR 30-dniowa wynosi 5,28% oraz WIBOR 90-dniowa wynosi: 5,55%.

Wszystkie stopy podano w skali rocznej. Kapitalizacja prosta.

ZAD 3.

Na rynku dostępne są następujące stopy spot LIBOR dla kredytów udzielanych w USD
wyrażone w skali rocznej (dane z 11 marca 2009):

a) jednomiesięczna r

1

= 0,52%;

b) trzymiesięczna r

3

= 1,28%;

c) sześciomiesięczna r

6

= 1,82%;

Wszystkie stopy podano w skali rocznej. Przyjąć, że kapitalizacja jest prosta. Oblicz
wszystkie możliwe stopy forward.


ZAD 4.
Ile powinna wynosić roczna stopa terminowa (forward) po roku, jeśli rynkowe stopy
natychmiastowe (spot) – roczna r

1

i dwuletnia r

2

wynoszą:

a) r

1

= 10%, r

2

= 10%,

b) r

1

= 8%, r

2

= 11%,

c) r

1

= 7%, r

2

= 6%.

Wszystkie stopy podano w skali rocznej. Przyjąć, że kapitalizacja jest złożona, roczna.

ZAD 5.
Na rynku dostępne są następujące stopy spot wyrażone w skali rocznej:

a) półroczna r

0,5

= 7%,

b) dziewięciomiesięczna r

0,75

= 7,5%,

c) roczna r

1

= 8%.

Kapitalizacja jest złożona, kwartalna. Jakie stopy forward można obliczyć na podstawie tych
stóp spot? Oblicz te stopy.

ZAD 6.
Dostępne są stopy spot:

a) 180-dniowa równa 5,5%;
b) 270-dniowa równa 6,5%;

wyznacz 90-dniową stopę forward za 180 dni (3 miesięczna stopa za 6 miesięcy) zakładając
że mamy do czynienia z kapitalizacją ciągłą.

ZAD 7.

Dostępne są następujące stopy spot depozytu oraz kredytu:

a) stopy spot depozytu: 30-dniowa – 5,5% oraz 60-dniowa – 6,2%;
b) stopy spot kredytu: 30- dniowa – 5,9% oraz 60-dniowa – 6,5%;

Oblicz 30-dniowe syntetyczne stopy forward depozytu oraz kredytu za 30 dni oraz ich
przybliżenia. Sprawdź czy otrzymane wyniki odpowiadają podstawowym nierównością dla
stóp syntetycznych.

ZAD 8.

Roczna stopa spot wynosi 5%. Oczekiwane roczne stopy spot w kolejnych pięciu latach
wynoszą odpowiednio: 5,3%; 5,6%; 5,7%; 6%; 6,5%. Na tej podstawie wyznacz stopy spot
od dwuletniej do sześcioletniej.


ZAD 9.

Mamy odpowiednie stopy dochodu (spot) z inwestycji wolnej od ryzyka:

a) miesięczna 2,1%;
b) trzymiesięczna 2,5%;
c) półroczna 2,69%;
d) roczna 2,81%;
e) dwuletnia 2,95%;

oraz odpowiednie stopy dochodu (spot) z inwestycji ryzykownej:

a) miesięczna 3%;
b) trzymiesięczna 3,8%;
c) półroczna 4,1%;
d) roczna 5,3%;
e) dwuletnia 6,4%.

Obliczyć strukturę terminową ryzyka, oraz ją wykreślić.

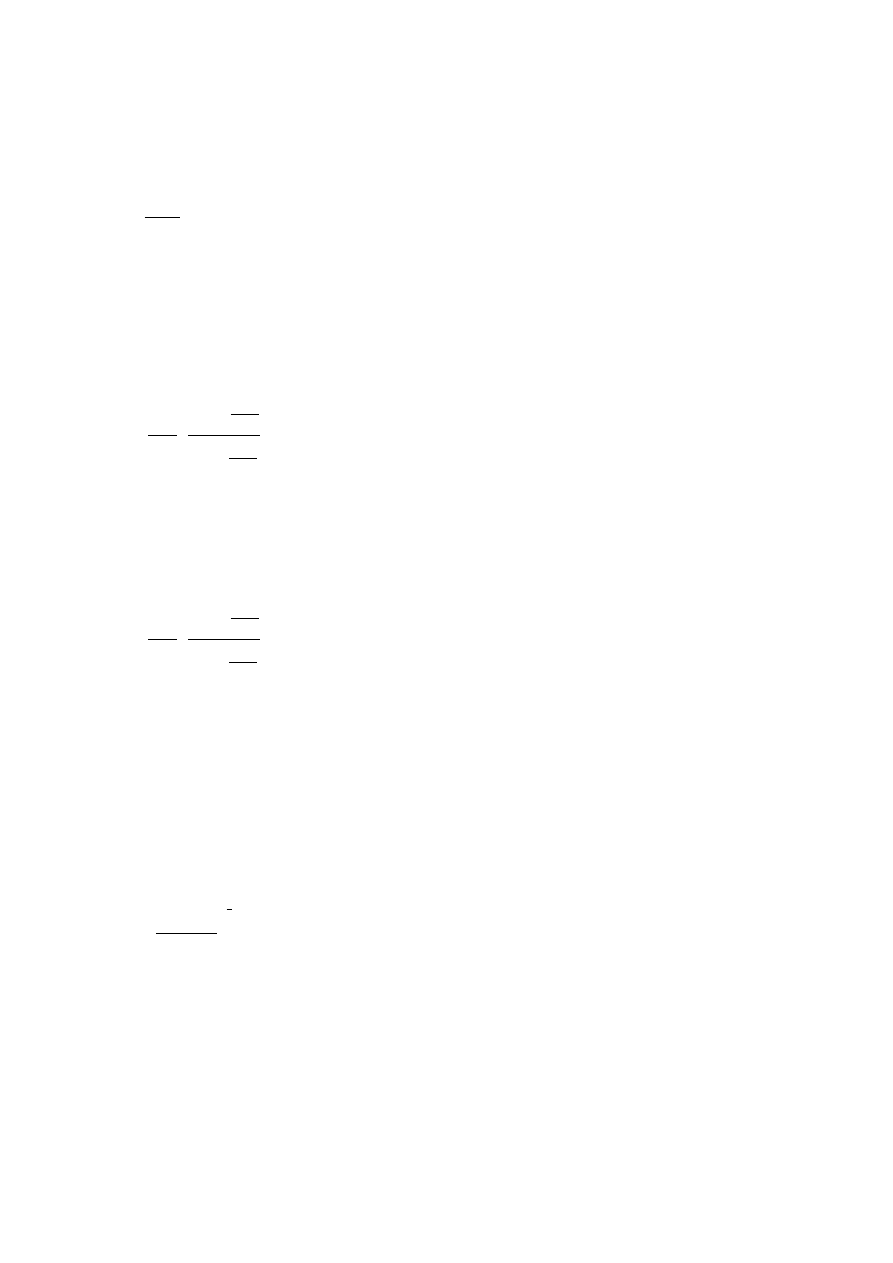
ODPOWIEDZI:

ZAD 1.

1

1

1









i

re

r

r

r

a) 0,068;
b) 0,133;
c) 0,060

ZAD 2.





























1

360

1

360

1

360

,

s

r

m

r

v

r

s

m

v

s

0566

,

0

2

,

1



r

ZAD 3.





























1

360

1

360

1

360

,

s

r

m

r

v

r

s

m

v

s

r

1

= 0,52%, r

3

= 1,28%, r

6

= 1,82%

a) r

1,5

= 0,021;

b) r

3,3

= 0,024;

c) r

1,2

= 0,017.

ZAD 4.









1

1

1

1

,





















v

s

s

m

m

v

s

r

r

r

s = 1, v = 1, m=2

a)

r

1

= 10 %, r

2

= 10 %

1

,

0

1

,

1



r

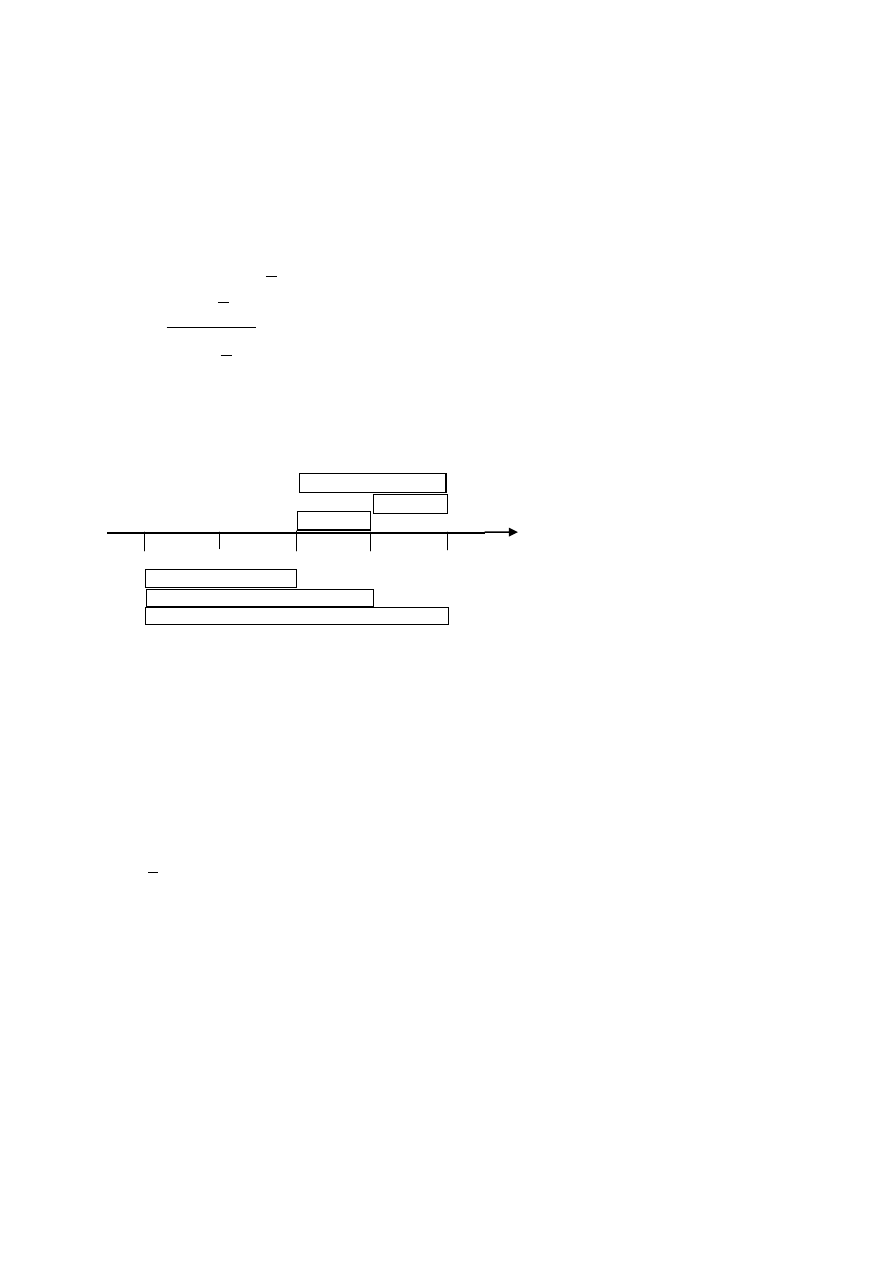
b)

r

1

= 8 %, r

2

= 11 %

140833

,

0

1

,

1



r

c)

r

1

= 7 %, r

2

= 6 %

050093

,

0

1

,

1



r

ZAD 5.

Ze względu na to że kapitalizacja złożona stosujemy wzory na horyzont dłuższy niż rok.

n

n

r

n

r

r

vn

s

s

mn

m

v

s











































































 











 



1

1

1

1

1

1

,

r

0,5

= 7 %, r

0,75

= 7,5 %, r

1

= 8 %, n = 4

0

3 m-ce

6 m-cy

9 m-cy

12 m-cy

r [0,5]

r [0,75]

r [1]

r [0,5;0,25]

r [0,75;0,25]

r [0,5;0,5]

%

9

5

,

0

;

5

,

0



r

5

,

9

25

,

0

;

75

,

0



r

%

%

5

,

8

25

,

0

;

5

,

0



r

ZAD 6.

r

180

= 5,5%, r

270

= 6,5%





s

m

v

s

sr

mr

v

r





1

,

r

180,90

= 0,085

ZAD 7.

r

bid, s

= 5,5% oraz r

bid, m

= 6,2%;

r

ask, s

= 5,9% oraz r

ask, m

= 6,5%;

syntetyczne stopy:

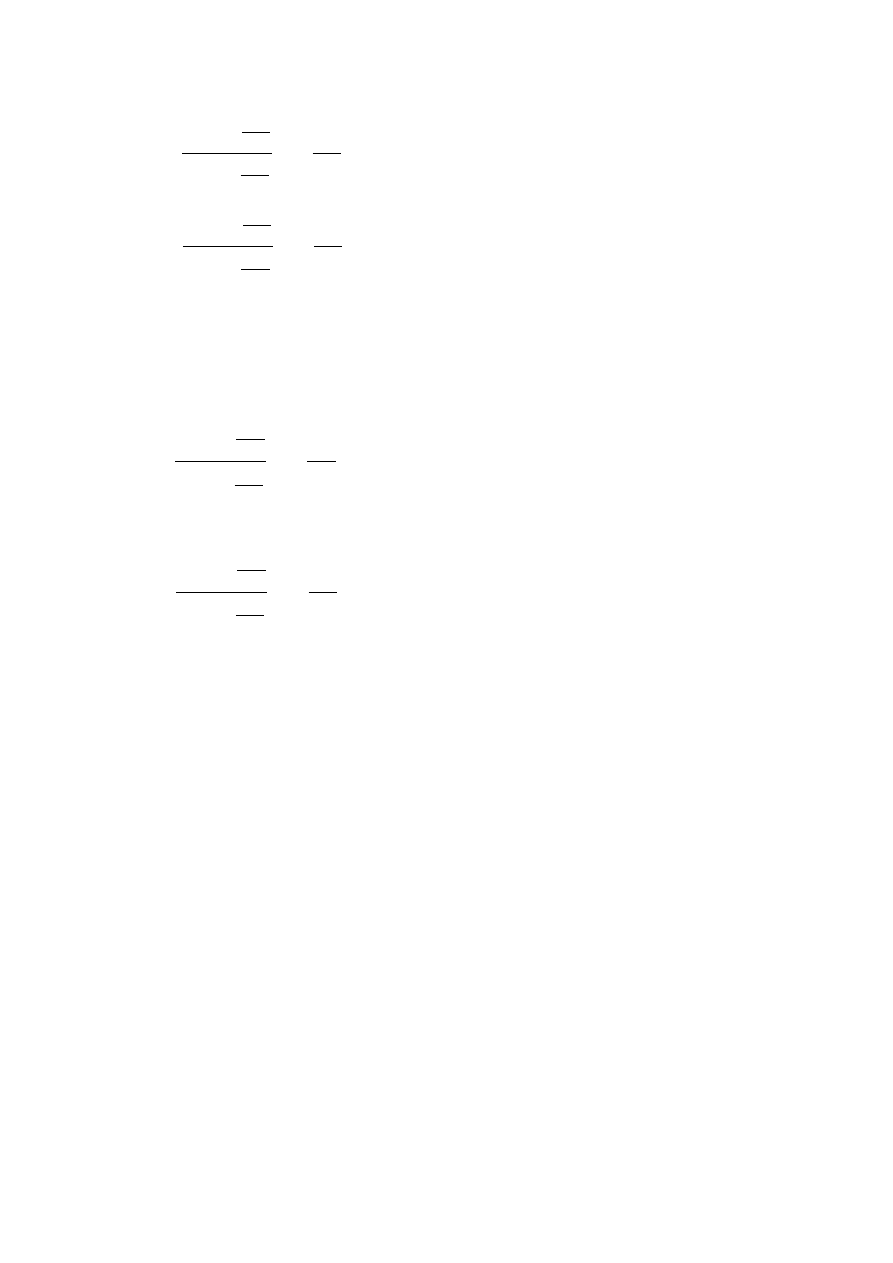
v

s

r

m

r

rs

s

ask

m

bid

v

s

bid

360

1

360

1

360

1

,

,

,

,































v

s

r

m

r

rs

s

bid

m

ask

v

s

ask

360

1

360

1

360

1

,

,

,

,































rs

bid, 30, 30

= 0,06424;

rs

ask, 30, 30

= 0,0743;

przybliżenia:

v

s

r

m

r

r

s

bid

m

bid

v

s

bid

360

1

360

1

360

1

,

,

,

,



































,

v

s

r

m

r

r

s

ask

m

ask

v

s

ask

360

1

360

1

360

1

,

,

,

,



































.

rs

bid, 30, 30

= 0,0681;

rs

ask, 30, 30

= 0,0705.

ZAD 8

.

1

r

= 5%;

 

1

1

r

E

= 5,3%;

 

2

2

r

E

= 5,6%;

 

3

3

r

E

= 5,7%;

 

4

4

r

E

= 6%;

 

5

5

r

E

= 6,5%.



 



 





1

1

1

2

2

1

1

1

r

E

r

r









a)



 





0515

,

0

053

,

0

1

05

,

0

1

1

2

2

2













r

r

;

b)



 







053

,

0

056

,

0

1

053

,

0

1

05

,

0

1

1

3

3

3















r

r

;

c)



 









054

,

0

057

,

0

1

056

,

0

1

053

,

0

1

05

,

0

1

1

4

4

4

















r

r

;

d)



 











0552

,

0

06

,

0

1

057

,

0

1

056

,

0

1

053

,

0

1

05

,

0

1

1

5

5

5



















r

r

;

e)



 













0568

,

0

065

,

0

1

06

,

0

1

057

,

0

1

056

,

0

1

053

,

0

1

05

,

0

1

1

6

6

6





















r

r

.

ZAD 9.

Elementy struktury terminowej:

r1 = 3,00% - 2,10% = 0,90%
r2 = 3,80% - 2,50% = 1,30%
r3 = 4,10% - 2,69% = 1,41%
r4 = 4,30% - 2,81% = 1,49%
r5 = 4,40% - 2,95% = 1,45%

Struktura terminowa ryzyka

Czas

Sto

p

a

d

o

c

h

o

d

u

Stopa dochodu (spot)
z inw estycji
ryzykow nej
Stopa dochodu (spot)
z inw estycji w olnej od
ryzyka
Struktura terminow a
ryzyka.

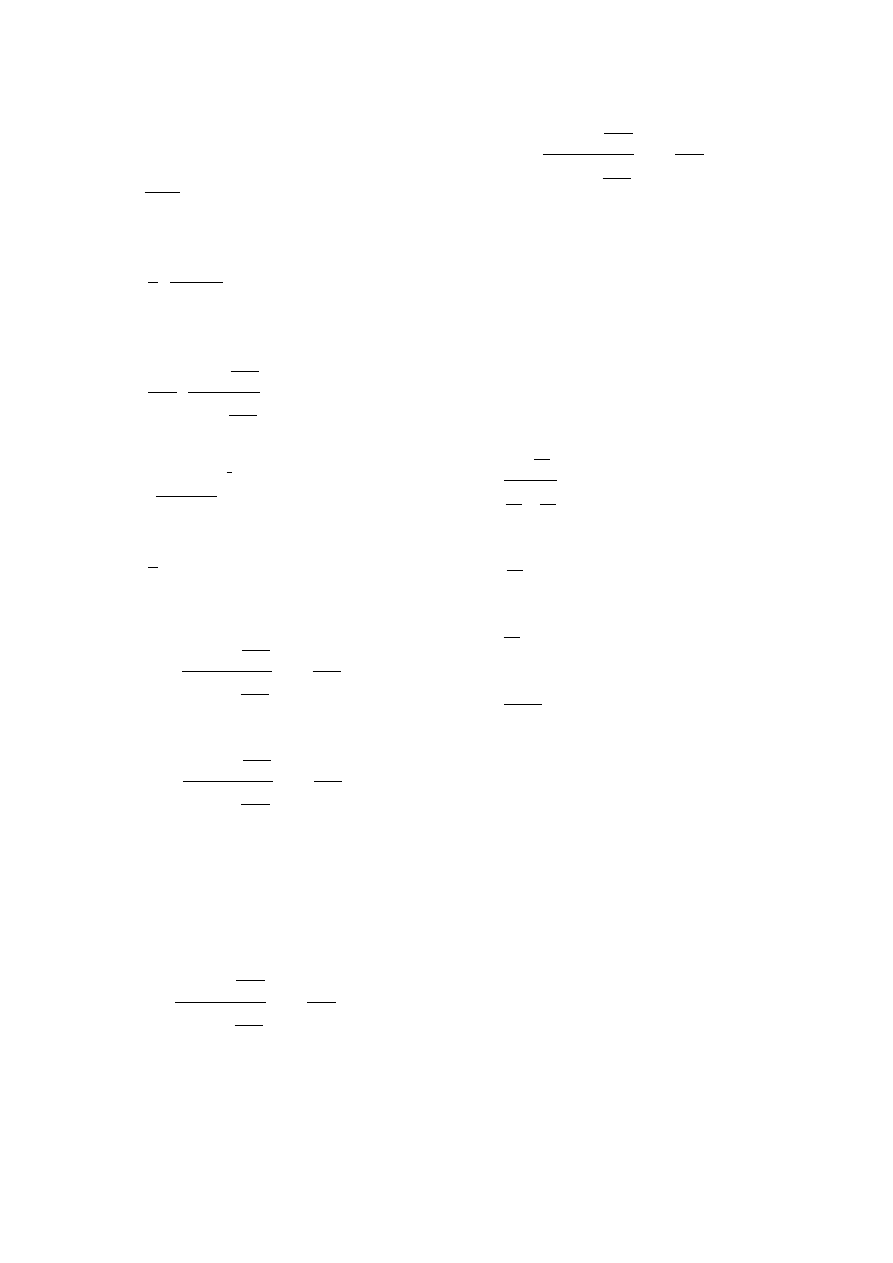
WZORNIK:

1

1

1









i

re

r

r

r





















1

1

1

1

,

s

m

v

s

sr

mr

v

r





























1

360

1

360

1

360

,

s

r

m

r

v

r

s

m

v

s









1

1

1

1

,





















v

s

s

m

m

v

s

r

r

r





s

m

v

s

sr

mr

v

r





1

,

.

v

s

r

m

r

rs

s

ask

m

bid

v

s

bid

360

1

360

1

360

1

,

,

,

,































v

s

r

m

r

rs

s

bid

m

ask

v

s

ask

360

1

360

1

360

1

,

,

,

,































v

s

ask

v

s

bid

rs

r

,

,

,

,



v

s

bid

v

s

ask

rs

r

,

,

,

,



v

s

r

m

r

r

s

bid

m

bid

v

s

bid

360

1

360

1

360

1

,

,

,

,



































v

s

r

m

r

r

s

ask

m

ask

v

s

ask

360

1

360

1

360

1

,

,

,

,





































 



 





1

1

1

2

2

1

1

1

r

E

r

r









R

G

M





0

0

M

b

M





D

G

M





D

G

D

R

D

G

b







1

D

G

g



D

R

r



g

r

g

b







1