
RACIOCÍNIO LÓGICO QUANTITATIVO PARA AFRFB
PROFESSOR: GUILHERME NEVES
Prof. Guilherme Neves www.pontodosconcursos.com.br
1
Aula 15 – Parte 2
ANÁLISE DE VARIÂNCIA ....................................................................................................................................... 2
Hipóteses do modelo ...................................................................................................................................................... 6
Somas de quadrados ...................................................................................................................................................... 7
Graus de liberdade ......................................................................................................................................................... 8
Distribuição de qui-quadrado e soma de quadrados ................................................................................................... 14
Quadrados médios ....................................................................................................................................................... 17
Distribuição F ............................................................................................................................................................... 17
ANÁLISE DE VARIÂNCIA DA REGRESSÃO ...................................................................................................................... 26
Somas de quadrados .................................................................................................................................................... 26
Quadrados médios e estatística F ................................................................................................................................ 29
Coeficiente de determinação ....................................................................................................................................... 31

RACIOCÍNIO LÓGICO QUANTITATIVO PARA AFRFB
PROFESSOR: GUILHERME NEVES
Prof. Guilherme Neves www.pontodosconcursos.com.br
2
ANÁLISE DE VARIÂNCIA
1.
Introdução
A análise de variância serve para testarmos a hipótese de que as médias de
diferentes populações são todas iguais entre si.
Para termos uma primeira ideia do raciocínio empregado nesta ferramenta,
vamos trabalhar com um exemplo simplificado.
Estamos estudando óleos de motor para um determinado modelo de carro. No
mercado há disponíveis 4 marcas diferentes de óleos. O intuito é verificar se as
4 marcas de óleo permitem que os carros rodem, em média, a mesma
quilometragem, antes de ser necessária a próxima troca de óleo.
Obtivemos amostras para cada uma das quatro marcas. Os resultados dos
estudos estão na tabela abaixo (valores em mil quilômetros):
observações
marca A
marca B
marca C
marca D
1ª
4,9
5,3
4,7
4,4
2ª
4,7
5,2
4,2
5,0
3ª
5,3
4,9
4,3
5,1
4ª
4,7
4,9
4,9
4,8
5ª
4,8
4,6
4,8
4,7
Média
4,88
4,98
4,58
4,8
A média geral, de todas as 20 observações acima, independente de marca, é
igual a 4,81.
81
,
4
=
X
Queremos saber se, para as quatro marcas, a média de quilometragem é a
mesma. As hipóteses que vamos testar são:
4
3
2
1
0
:
µ
µ
µ
µ
=
=
=
H
H
A
: pelo menos uma das médias é diferente das demais
Observem que, de acordo com as amostras acima, as médias não são
exatamente iguais. A questão é: as diferenças entre as médias são devidas
apenas a fatores aleatórios? Ou as diferenças são significativas, de modo que é
possível apontar que há pelo menos uma marca diferente das demais?
São estas perguntas que a análise de variância tenta responder.
Bom, como queremos só ter uma primeira idia, fizemos uma simplificação:
todas as amostras têm tamanho 5 (num caso geral, cada amostra pode ter
tamanho diferente das demais).
Uma outra suposição é necessária. Vamos supor que todas as populações de
onde foram extraídas as amostras apresentam a mesma variância
2
σ . Por fim,
vamos supor que todas as populações apresentam distribuição normal.
Vamos calcular a variância dentro de cada grupo.

RACIOCÍNIO LÓGICO QUANTITATIVO PARA AFRFB
PROFESSOR: GUILHERME NEVES
Prof. Guilherme Neves www.pontodosconcursos.com.br
3
Cada observação do quadro acima pode ser representada por:
ij
X
onde i indica varia de 1 até 4 (indicando as marcas A, B, C, D) e j varia de 1
até 5 (indicando as observações feitas dentro de cada marca).
A variância dentro de uma dada marca é dada por:
(
)
1
5
5
1
2
2
−
−
=
∑
=
j
i
ij
i
X
X
s
Como exemplo, vamos detalhar o cálculo da variância dentro da marca C (ou
seja, para o caso de
)
3
=
i
:
(
)
4
)
58
,
4
8
,
4
(
)
58
,
4
9
,
4
(
)
58
,
4
3
,
4
(
)
58
,
4
2
,
4
(
)
58
,
4
7
,
4
(
1
5
2
2
2
2
2
5
1
2
3
3
2
3
−
+
−
+
−
+
−
+
−
=
−
−
=
∑
=
j
j
X
X
s
=
0,097
Fazendo cálculos semelhantes para as demais marcas, temos:
Marca
A
B
C
D
Variância
0,062
0,077
0,097
0,075
Caso todas as marcas apresentem a mesma média, então temos:
- todas elas têm distribuição normal
- todas elas têm mesma variância
2
σ
- todas elas têm mesma média µ
Isto equivale a dizer que todas elas apresentam distribuição idêntica. É como
se todas as observações tivessem sido extraídas de uma única população,
normal, de média µ e variância
2
σ .
Deste modo, temos, na verdade, 4 amostras da mesma população. São 4
amostras de tamanho 5. Vimos na aula de estimadores que a variância da
amostra (com
1
−
n
no denominador) é um estimador não-viciado da variância
da população. Portanto, se tivermos várias amostras, a média de todas as
variâncias amostrais deve ser bem próxima da variância da população.
Assim, uma primeira estimativa da variância da população seria:
=
+
+
+
=
+
+
+
4
075
,
0
097
,
0
077
,
0
062
,
0
4
2
4
2
3
2
2
2
1
s
s
s
s
0,078
Continuando.
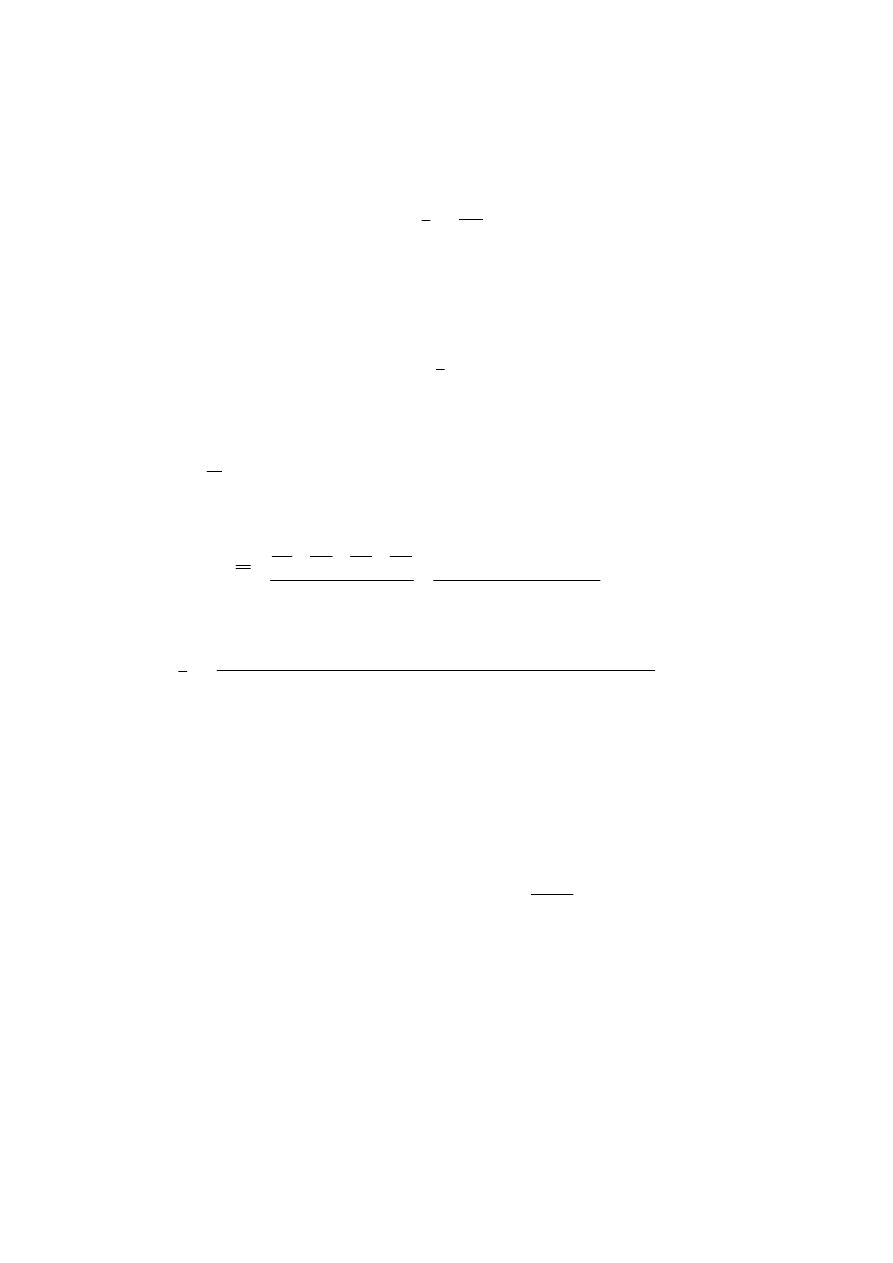
RACIOCÍNIO LÓGICO QUANTITATIVO PARA AFRFB
PROFESSOR: GUILHERME NEVES
Prof. Guilherme Neves www.pontodosconcursos.com.br
4
Ainda supondo que todas as marcas apresentam a mesma média, podemos
achar outra estimativa para a variância da população. Como já estudamos na
aula de estimadores, a média amostral tem variância dada por:
2
X
σ
=
n
2
σ
Ou seja, as médias amostrais apresentam dispersão bem pequena, quando
comparada com a dispersão da população. Se pegarmos a dispersão da
população e dividirmos por n, aí obtemos a dispersão das médias amostrais. As
médias amostrais estão bem concentradas.
2
X
n
σ
×
=
2
σ
Se multiplicarmos a variância das médias amostrais por n, aí obtemos uma
estimativa para a variância populacional.
Assim, podemos usar os diversos valores da média amostral para estimar a
variância de
X
. Feito isso, multiplicamos por “n”, e obtemos outra estimativa
da variância populacional.
A média das médias amostrais é:
=
+
+
+
=
+
+
+
=
4
8
,
4
58
,
4
98
,
4
88
,
4
4
4
3
2
1
X
X
X
X
X
4,81
Temos:
=
2
X
s
=
−
−
+
−
+
−
+
−
1
4
)
81
,
4
8
,
4
(
)
81
,
4
58
,
4
(
)
81
,
4
98
,
4
(
)
81
,
4
88
,
4
(
2
2
2
2
0,029
Esta é a chamada variância entre as marcas.
Como o tamanho das amostras é 5 (
5
=
n
), a nova estimativa da variância da
população é:
144
,
0
029
,
0
5
=
×
Obtidas estas duas estimativas da variância da população, nós dividimos uma
pela outra.
Razão entre as estimativas:
85
,
1
078
,
0
144
,
0
=
E este número acima é que vai nos permitir decidir se as médias são todas
iguais entre si ou não.
Caso as médias sejam, efetivamente, todas iguais entre si, a razão entre as
duas estimativas deveria ser bem próxima de 1. As duas estimativas deveriam
coincidir (ou serem muito próximas uma da outra).
Caso as estimativas não coincidam (e a razão entre elas seja bem diferente de
1), isto é um sinal de que as médias das marcas de óleo são diferentes entre si
(ou seja, há pelo menos uma marca diferente das demais).
Por quê?
RACIOCÍNIO LÓGICO QUANTITATIVO PARA AFRFB
PROFESSOR: GUILHERME NEVES
Prof. Guilherme Neves www.pontodosconcursos.com.br
5
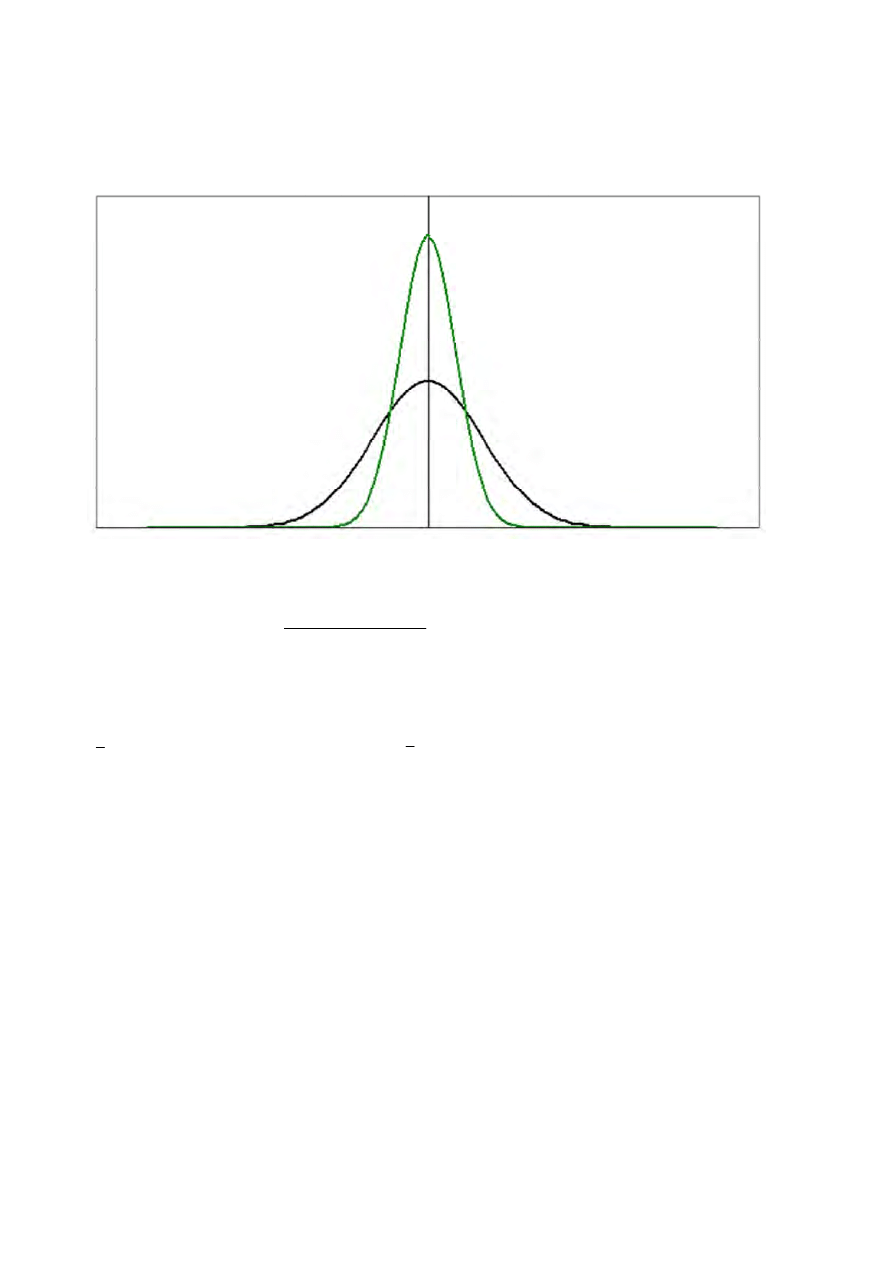
Se todas as marcas tiverem a mesma média, suas funções densidade de
probabilidade se sobreporão (estão todas representadas pela curva em preto
no gráfico abaixo).
No fundo, todas as amostras podem ser consideradas como extraídas da
mesma população.
Com isso, o cálculo
4
2
4
2
3
2
2
2
1
s
s
s
s
+
+
+
(decorrente das variâncias dentro das
marcas) realmente vai gerar uma boa estimativa da variância da população.
Já a segunda estimativa, ela é derivada da variância entre as marcas. Como
as médias amostrais são pouco dispersas (ver curva verde do gráfico acima),
2
X
s
é pequeno. Multiplicando
2
X
s
n ×
, obteremos uma boa estimativa para a
variância da população. As duas estimativas serão bem próximas. A razão
entre elas será quase igual a 1.
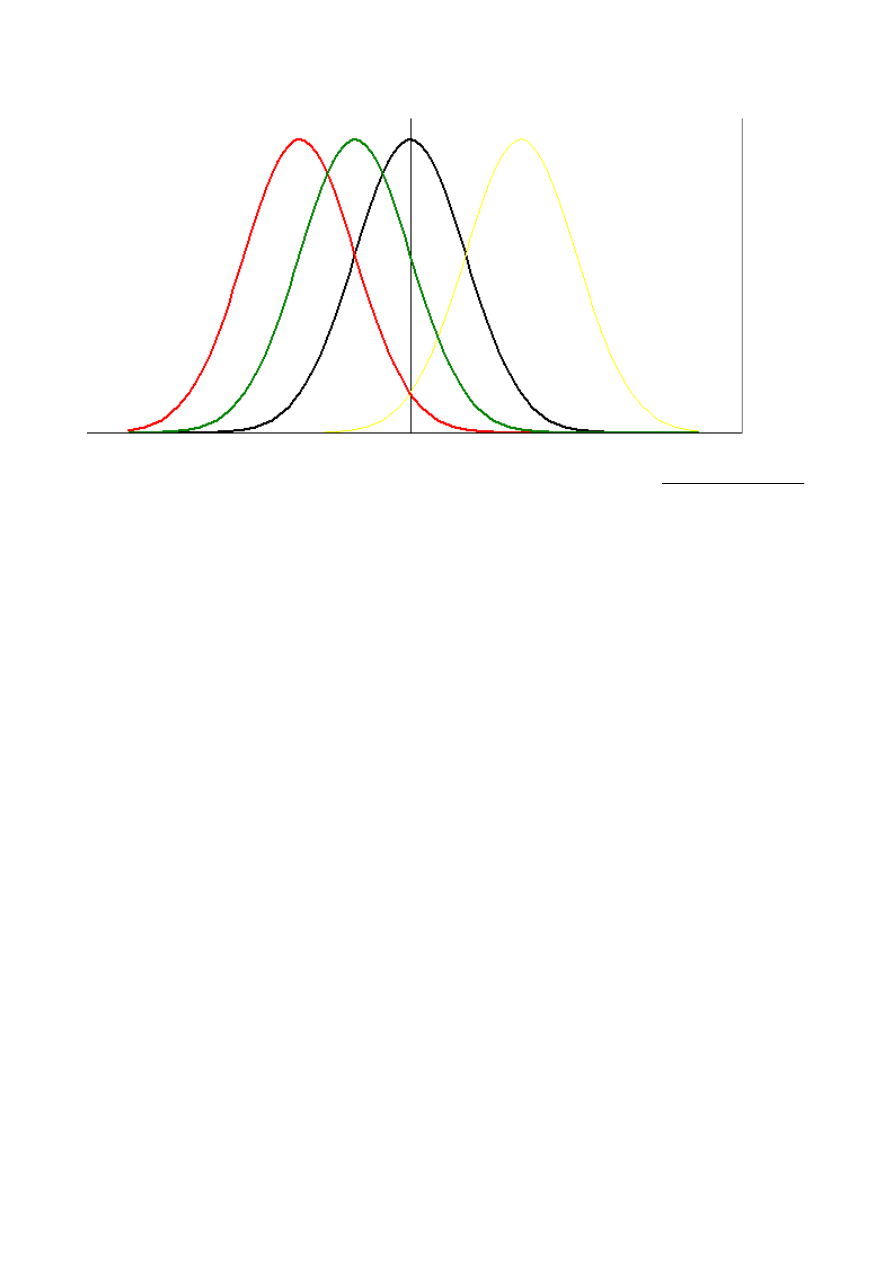
Agora vamos pensar em outro caso.
Se todas as marcas tiverem a mesma variância, mas tiverem médias
diferentes, elas poderiam ser representadas pelo gráfico abaixo:
RACIOCÍNIO LÓGICO QUANTITATIVO PARA AFRFB
PROFESSOR: GUILHERME NEVES
Prof. Guilherme Neves www.pontodosconcursos.com.br
6
Como todas elas apresentam a mesma variância, o cálculo
4
2
4
2
3
2
2
2
1
s
s
s
s
+
+
+
(decorrente das variâncias dentro das marcas) realmente vai gerar uma boa
estimativa da variância da população.
Já a segunda estimativa, baseada na variância entre as médias amostrais, ela
será problemática. As médias amostrais estarão mais dispersas do que
estariam caso as médias populacionais fossem todas iguais entre si. Isto fará
com que a segunda estimativa, derivada da variância entre as marcas, resulte
num estimador maior que aquele decorrente da variância dentro das marcas.
Com isso, a razão entre as duas estimativas será bem maior que 1.
Agora vamos começar a estudar a análise de variância com os nomes que
geralmente aparecem nas questões. Veremos que a “razão entre as
estimativas” vai corresponder, na verdade, a uma razão entre os chamados
quadrados médios.
Hipóteses do modelo
Vamos trabalhar com um modelo mais simples (embora a análise de variância
possa ser aplicada para modelos mais complexos).
Temos k populações em estudo (no exemplo dado na seção anterior,
4
=
k
,
pois eram 4 marcas diferentes). De cada população, são extraídas amostras de
tamanho
i
n (no exemplo anterior,
5
5
4
3
2
1
=
=
=
=
=
n
n
n
n
n
- todas as amostras
tinham tamanho 5).
O número total de extrações feitas (incluindo todos os grupos em estudo) é N .
No nosso exemplo,
20
=
N
(5 extrações para cada uma das 4 marcas de óleo).
Uma dada observação
ij
X
pode ser representada assim:

RACIOCÍNIO LÓGICO QUANTITATIVO PARA AFRFB
PROFESSOR: GUILHERME NEVES
Prof. Guilherme Neves www.pontodosconcursos.com.br
7
ij
i
ij
u
X
+
=
µ
Cada observação é igual à média da população de onde ela foi extraída, mais
um erro aleatório (
ij
u
). As hipóteses são:
·
os erros são variáveis aleatórias com média zero;
·
os erros são independentes entre si;
·
os erros têm variância constante, ou seja,
2
)
(
σ
=
ij
u
V
, para qualquer i e
qualquer j.
·
os erros têm distribuição normal
Na verdade, vocês não precisam se preocupar em decorar as hipóteses acima.
Elas sempre estarão implícitas na questão. O motivo pelo qual eu as mencionei
é o seguinte. Pode acontecer de a questão indicar expressamente tais
hipóteses. Aí o aluno poderia se assustar, pensando que a questão está
pedindo alguma coisa que ele não estudou. Então, se a questão trouxer as
hipóteses acima, não precisa entrar em pânico, achando que é uma coisa de
outro mundo. É só fazer a análise de variância normalmente, como veremos
nos tópicos a seguir.
Somas de quadrados
Como vimos no exemplo inicial (com as 4 marcas de óleo), o teste se baseia
em cálculo da variância (entre e dentro). E a variância é resultado de uma
soma de quadrados de desvios. Então, por hora, vamos focar nestas somas de
quadrados de desvios.
Há três somas importantes: a soma de quadrados total; a soma de quadrados
dentro dos grupos (ou ainda: soma de quadrados dos resíduos); a soma de
quadrados entre grupos (ou ainda: soma de quadrados de tratamentos).
Seja n
i
o número de termos do iésimo grupo. No exemplo das marcas de óleo,
para cada grupo nós tínhamos 5 observações. Ou seja:
5
4
3
2
1
=
=
=
=
n
n
n
n
A soma dos quadrados dos resíduos (ou ainda, dentro dos grupos) é definida
por:
∑∑
=
=
−
=
k
i
ni
j
i
ij
X
X
s
SQ
1
1
2
)
(
Re
Ou seja, tomamos todas as observações e subtraímos da média do respectivo
grupo. Elevamos ao quadrado. Depois somamos tudo.
Para o exemplo das marcas de óleo, ficaríamos com:

RACIOCÍNIO LÓGICO QUANTITATIVO PARA AFRFB
PROFESSOR: GUILHERME NEVES
Prof. Guilherme Neves www.pontodosconcursos.com.br
8
+
+
−
+
−
+
−
+
−
+
−
=
...
)
88
,
4
8
,
4
(
)
88
,
4
7
,
4
(
)
88
,
4
3
,
5
(
)
88
,
4
7
,
4
(
)
88
,
4
9
,
4
(
Re
2
2
2
2
2
s
SQ
2
2
2
2
2
)
8
,
4
7
,
4
(
)
8
,
4
8
,
4
(
)
8
,
4
1
,
5
(
)
8
,
4
5
(
)
8
,
4
4
,
4
(
−
+
−
+
−
+
−
+
−
+
244
,
1
Re =
s
SQ
A soma dos quadrados de tratamentos (ou ainda, entre os grupos) é dada
por:
i
ni
i
i
n
X
X
SQTrat
×
−
=
∑
=
2
1
)
(
Lembrando que
i
X é a média de cada uma das 5 amostras (para
1
=
i
, por
exemplo, temos
88
,
4
1
=
X
, que é a média para a amostra da marca A).
E
X
é a média de todos os valores, é a média geral de todas as observações,
independente de marca. No exemplo das marcas de óleo,
81
,
4
=
X
.
O cálculo da soma de quadrados de tratamentos é dado por:
5
)
81
,
4
8
,
4
(
5
)
81
,
4
58
,
4
(
5
)
81
,
4
98
,
4
(
5
)
81
,
4
88
,
4
(
2
2
2
2
×
−
+
×
−
+
×
−
+
×
−
=
SQTrat
434
,
0
=
SQTrat
A soma de quadrados total é dada por:
∑∑
=
=
−
=
k
i
ni
j
ij
X
X
SQTotal
1
1
2
)
(
Tomamos cada observação e subtraímos da média geral. Elevamos ao
quadrado e somamos tudo. Para o exemplo que temos trabalhado, ficamos
com:
2
2
2
2
)
81
,
4
7
,
4
(
)
81
,
4
8
,
4
(
...
)
81
,
4
7
,
4
(
)
81
,
4
9
,
4
(
−
+
−
+
+
−
+
−
=
SQTotal
= 1,678
Observem que:
SQTrat
s
SQ
SQTotal
+
=
Re
Isto sempre acontece.
Graus de liberdade
Vamos interromper um pouco a matéria que estamos estudando (análise de
variância). Vamos falar um pouco sobre graus de liberdade. Utilizamos esta
expressão em aulas anteriores, sem falar exatamente do que se trata.
Bem, o grau de liberdade nada mais é que um parâmetro que entra no cálculo
da função gama. É uma função importante. A partir dela é que são construídas
as funções densidade de probabilidade para diversas distribuições de
probabilidade importantes (como T, qui-quadrado, F).

RACIOCÍNIO LÓGICO QUANTITATIVO PARA AFRFB
PROFESSOR: GUILHERME NEVES
Prof. Guilherme Neves www.pontodosconcursos.com.br
9
Só que indicar para vocês qual é a função gama e, dentro dela, qual é o
parâmetro que corresponde ao número de graus de liberdade, não vai ajudar
em nada a entender melhor o que é esse grau de liberdade.
Creio eu, deve haver alguma explicação “geométrica” para o número de graus
de liberdade. Para quem já estudou cálculo, estou pensando em alguma coisa
análoga à explicação de derivada e integral por meio de inclinações de reta e
áreas abaixo da curva. Explicações utilizando geometria são mais fáceis para
assimilarmos.
Em todas as vezes que vimos os graus de liberdade, havia uma soma de
quadrados de desvios. A quantidade de graus de liberdade será igual à
quantidade de termos independentes que estamos somando.
A primeira vez que vimos o grau de liberdade foi com a distribuição T. Vimos
que
X
tem média µ e desvio padrão
n
σ
.
Quando desconhecemos o desvio-padrão da população, substituímos
σ
por s
(desvio padrão da amostra).
Para cálculo de s
2
, fazemos assim:
(
)
1
1
2
2
−
−
=
∑
=
n
X
X
s
n
i
i
No denominador temos um número, uma constante, algo que não varia. No
numerador, temos uma soma de n quadrados de desvios, que podem variar de
uma amostra para outra. É este fator que é aleatório. Vamos nos concentrar
nele.
Numerador:
2
2
1
2
3
2
2
2
1
)
)
(
...
)
(
)
(
)
(
X
X
X
X
X
X
X
X
X
X
n
n
−
+
−
+
+
−
+
−
+
−
−
Qual a referência para o cálculo dos desvios? É a média aritmética.
Pois bem, vamos supor que a gente conhece justamente a média aritmética.
Conhecemos a média aritmética da amostra, mas não conhecemos os valores
observados. Ou ainda: a média da amostra é dada.
Quanto aos valores de cada uma das observações, este nós não conhecemos.
Fixada a média da amostra, vamos considerar que a gente é livre para
estabelecer quaisquer valores para as observações e, com isso, calcular o valor
do desvio ao quadrado, que entra na fórmula do numerador.
Assim, nós somos livres para escolher o valor de X
1
(e, com isso, determinar o
valor de
2
1
)
(
X
X −
). Nós também somos livres para escolher o valor de X
2
. E
assim por diante.
Neste processo, nós seríamos livres para escolher os valores de
1
−
n
observações. Nós seríamos livres para escolher os valores de
1
X ,
2
X , ...,
1
−
n
X
.

RACIOCÍNIO LÓGICO QUANTITATIVO PARA AFRFB
PROFESSOR: GUILHERME NEVES
Prof. Guilherme Neves www.pontodosconcursos.com.br
10
Já o valor de X
n
, este nós não temos liberdade para escolher. Escolhidas todas
as demais observações (
1
X ,
2
X , ...,
1
−
n
X
), só existe um único valor de X
n
que
faz com que a média da amostra seja igual ao valor fixado para
X
.
Ou seja, nossa liberdade se restringiu a
1
−
n
desvios ao quadrado. O último
desvio ao quadrado não pode ser livremente escolhido. Portanto, são
1
−
n
graus de liberdade.
A segunda vez que vimos os graus de liberdade foi com a distribuição de qui-
quadrado. Ela é dada por:
=
2
χ
2
2
)
1
(
σ
s
n −
No denominador, temos a variância da população. Ela é um número, uma
constante, algo fixo, que não varia.
No numerador, temos duas parcelas. A primeira é
)
1
( −
n
, que também é um
número fixo (é o tamanho da amostra menos 1).
O outro fator, ele sim varia. Trata-se da variância amostral. É a variância de
uma determinada amostra. Se pensarmos em todas as amostras possíveis, em
cada uma delas
2
s
assume um valor diferente. É este fator que torna
2
2
)
1
(
σ
s
n −
uma variável aleatória, que faz esta expressão variar. Vamos portanto, nos
concentrar neste termo.
Novamente, temos a variância amostral (s
2
), que advém da soma de n desvios
ao quadrado.
Fixada uma determinada média amostral, poderemos escolher livremente o
valor de
1
−
n
desvios. O último desvio, este não pode ser livremente escolhido.
Só há um valor possível para ele, de tal modo que a média das observações
seja igual a uma dada média amostral. Temos, novamente,
1
−
n
graus de
liberdade.
A terceira vez que estudamos graus de liberdade foi no teste de qui-quadrado
para várias proporções.
A estatística teste era dada pela soma de todos os valores de
i
i
i
E
E
O
2
)
(
−
. Agora
os desvios são calculados em relação às freqüências esperadas.
Pergunta: qual a referência para cálculo dos desvios?
A referência são as frequências esperadas. Pois então vamos supor que as
frequências esperadas são dadas e que nós somos livres para escolher as
frequências observadas (determinando, assim, o valor do desvio). Quantas
frequências observadas nós podemos escolher livremente?
RACIOCÍNIO LÓGICO QUANTITATIVO PARA AFRFB
PROFESSOR: GUILHERME NEVES
Prof. Guilherme Neves www.pontodosconcursos.com.br
11
Vejamos um exemplo:
No curso A, havia 100 candidatos inscritos em um concurso. No curso B
também havia 100 candidatos inscritos neste concurso. Foram aprovados 140
candidatos destes 200 alunos. Os 60 restantes foram reprovados. Calcule a
estatística teste para testar a hipótese de que a proporção de aprovados nos
dois cursos é a mesma.
Este problema não tem resposta. Isto porque não foram fornecidas as
freqüências observadas dentro de cada curso. Mas não tem problema. Nosso
interesse aqui não será achar exatamente o valor da estatística teste; sim
determinar o número de graus de liberdade.
Agora nós só conhecemos os totais da amostra.
Do total de alunos (incluindo tanto o curso A quanto B), 140 foram aprovados
e 60 foram reprovados. Sabemos ainda que há 100 alunos em cada curso.
Sabendo apenas os totais (ou seja, o total de aprovados, o total de
reprovados, e o total de alunos em cada curso), podemos determinar as
freqüências esperadas, caso a hipótese nula seja verdadeira:
curso A
curso B
Freqüênci
a
esperada
Freqüência
esperada
Total
Aprovados
70
70
140
Reprovados
30
30
60
Total
100
100
200
Os números em vermelho indicam os totais. São esses números que a gente
conhece.
Se a hipótese nula for verdadeira, esperamos que a proporção de aprovados e
reprovados, em cada curso, seja igual à proporção geral, tomando os dois
cursos em conjunto.
Ou seja, conhecer os valores totais é o mesmo que conhecer as frequências
esperadas. E vice-versa.
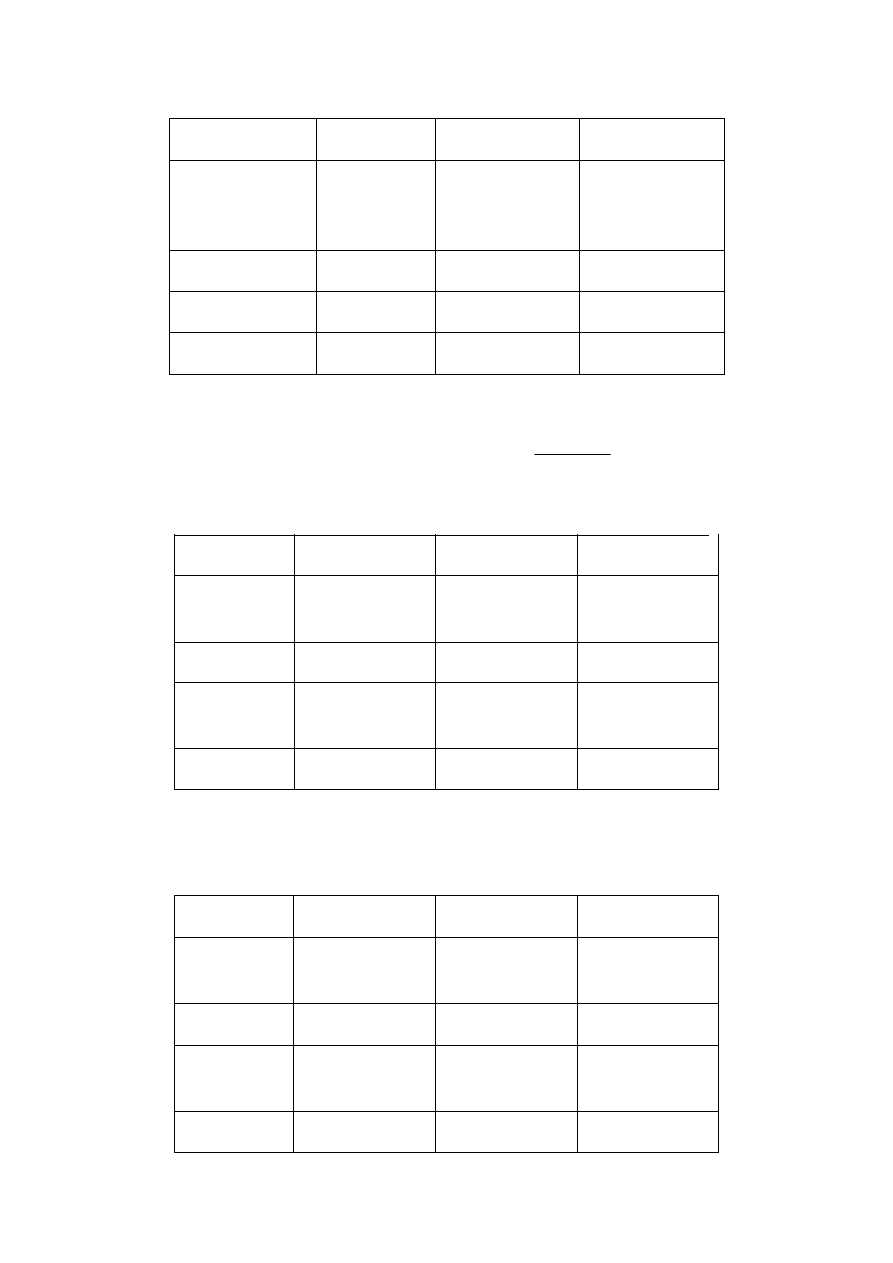
Agora vamos para as freqüências observadas.
RACIOCÍNIO LÓGICO QUANTITATIVO PARA AFRFB
PROFESSOR: GUILHERME NEVES
Prof. Guilherme Neves www.pontodosconcursos.com.br
12
curso A
curso B
Freqüência
observada
Freqüência
observada
Total
Aprovados
?
?
140
Reprovados
?
?
60
Total
100
100
200
As freqüências observadas não foram informadas. Vamos considerar que
somos livres para preenchê-las. Ou seja, no fundo estamos considerando que
somos livres para determinar os valores de cada
i
i
i
E
E
O
2
)
(
−
.
Vamos preencher a primeira célula com o número 80. Por quê? Porque somos
livres para escolher qualquer número, então vamos escolher o número 80.
curso A
curso B
Freqüência
observada
Freqüência
observada
Total
Aprovados
80
?
140
Reprovados
?
?
60
Total
100
100
200
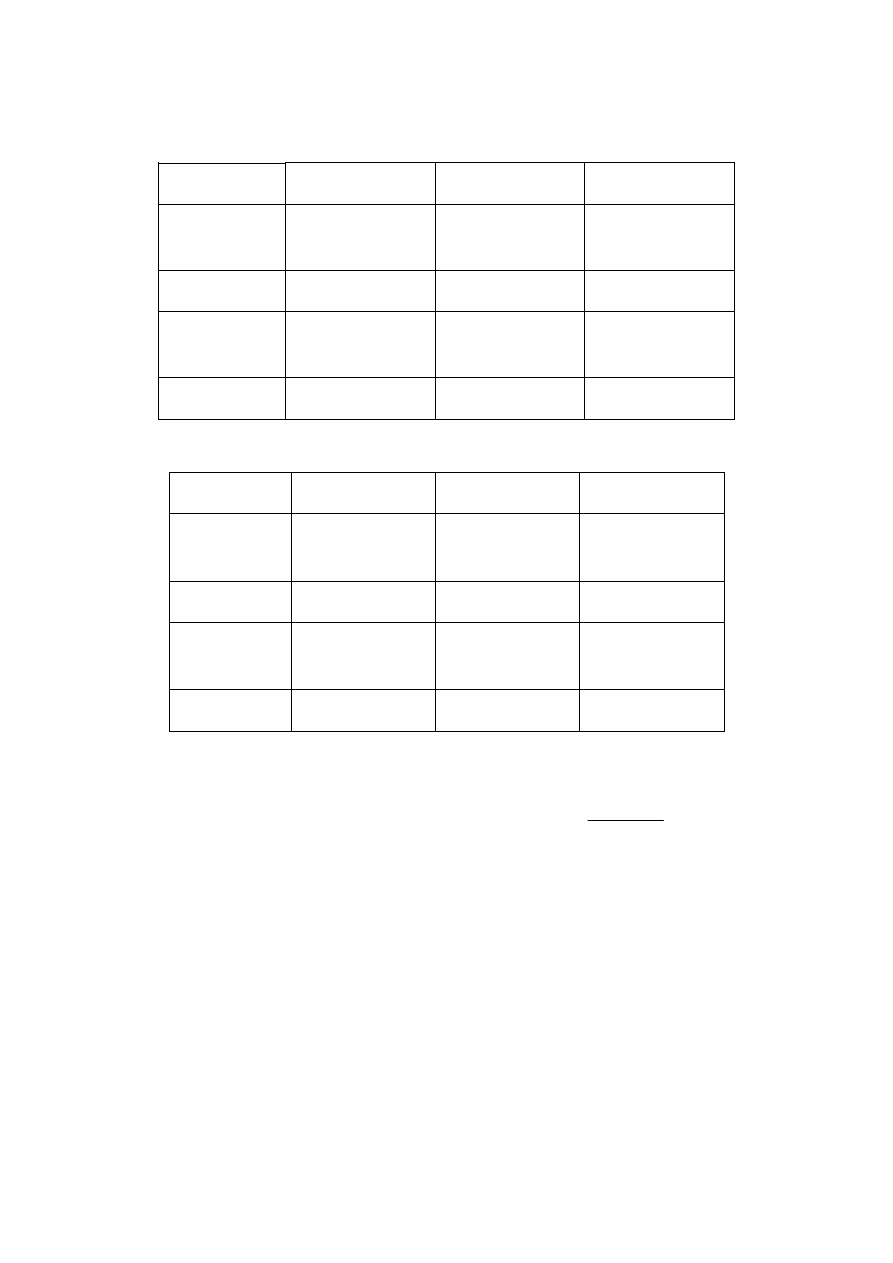
E esta foi a única célula que poderíamos preencher livremente. As demais não
podem mais ser preenchidas livremente.
Para que o total de alunos aprovados seja de 140, a segunda célula deve ser
igual a 60.
curso A
curso B
Freqüência
observada
Freqüência
observada
Total
Aprovados
80
60
140
Reprovados
?
?
60
Total
100
100
200
RACIOCÍNIO LÓGICO QUANTITATIVO PARA AFRFB
PROFESSOR: GUILHERME NEVES
Prof. Guilherme Neves www.pontodosconcursos.com.br
13
Para que o total de alunos do curso A seja igual a 100, a terceira célula deve
ser preenchida com 20.
curso A
curso B
Freqüência
observada
Freqüência
observada
Total
Aprovados
80
60
140
Reprovados
20
?
60
Total
100
100
200
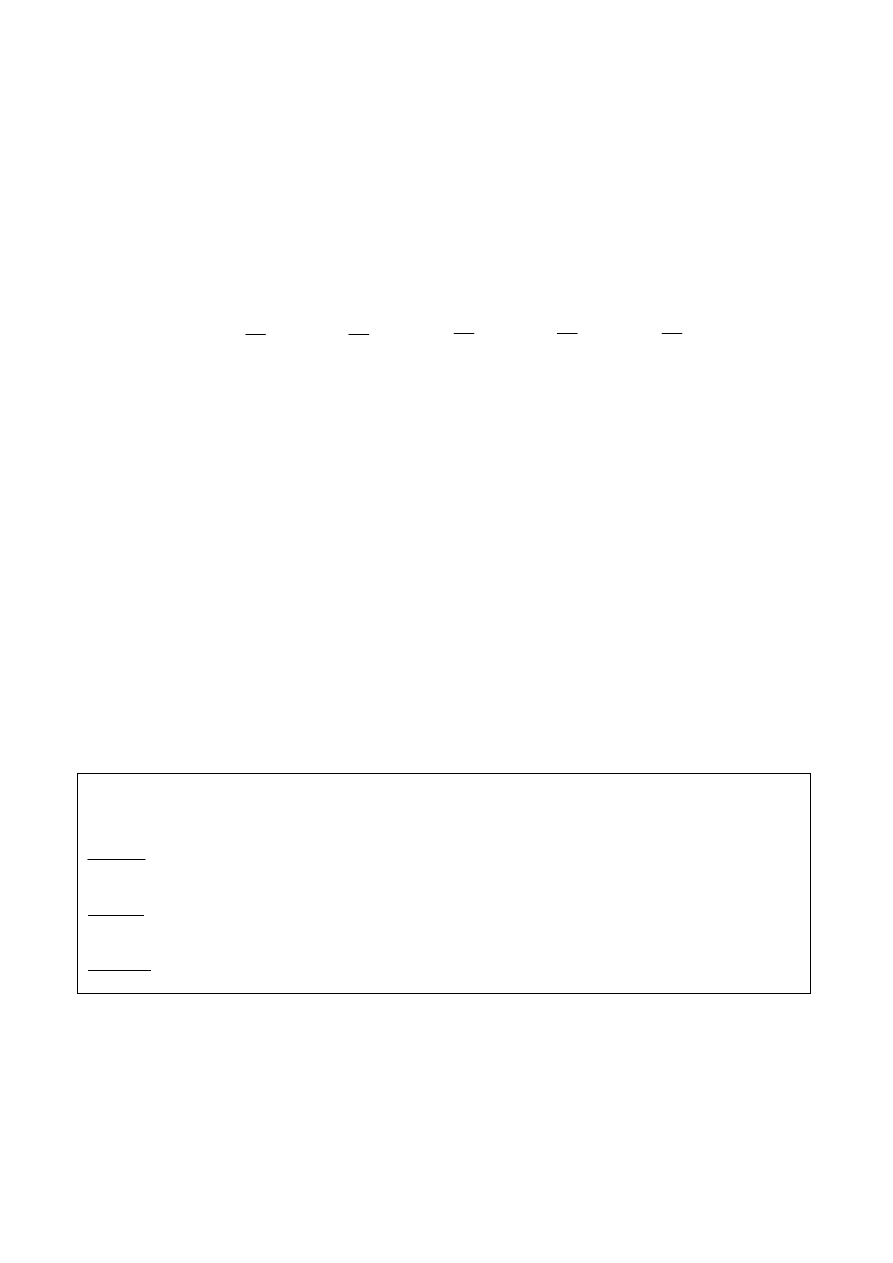
Para que o total do curso B seja igual a 100 e o total de reprovados seja 60, a
quarta célula deve ser igual a 40.
curso A
curso B
Freqüência
observada
Freqüência
observada
Total
Aprovados
80
60
140
Reprovados
20
40
60
Total
100
100
200
Nós só fomos livres para preencher 1 célula. Por isso, temos 1 grau de
liberdade.
Assim, quando formos calcular a soma dos valores
i
i
i
E
E
O
2
)
(
−
, nós podemos
escolher livremente 1 deles. Os demais, estes não serão livremente escolhidos.
Generalizando, para um caso qualquer com várias proporções, o número de
graus de liberdade será sempre igual a
)
1
(
)
1
(
−
×
−
C
L
.
Nos problemas em que o número de linhas ou de colunas for igual a 1, aí a
gente não faz a subtração por 1.
Resumindo tudo: o que fica da “história” é que os graus de liberdade têm
relação com a quantidade de termos que podemos escolher livremente.

RACIOCÍNIO LÓGICO QUANTITATIVO PARA AFRFB
PROFESSOR: GUILHERME NEVES
Prof. Guilherme Neves www.pontodosconcursos.com.br
14
Distribuição de qui-quadrado e soma de quadrados
Seja
X
uma variável aleatória, com média µ e variância
2
σ . Seja
2
s
o
estimador da variância populacional, baseado em uma amostra aleatória de
tamanho n. Vimos que
2
2
)
1
(
σ
s
n −
tem distribuição de qui-quadrado com
1
−
n
graus de liberdade.
Vamos analisar com calma esta expressão.
=
2
χ
2
2
)
1
(
σ
s
n −
E como é que se calcula uma variância amostral? Bom, o primeiro passo é
calcular a soma dos quadrados dos desvios em relação à média da amostra.
Fica assim:
(
)
1
1
2
2
−
−
=
∑
=
n
X
X
s
n
i
i
Voltemos à variável de qui-quadrado em estudo. Ela é dada por:
=
2
χ
2
2
)
1
(
σ
s
n −
Substituindo o valor de s
2
:
=
2
χ
(
)
2
1
2
σ
∑
=
−
n
i
i
X
X
No numerador temos uma soma de quadrados dos desvios.
Então é isso que eu queria chamar a atenção, para facilitar a memorização.
Somas de quadrados de desvios podem ser usadas para gerar distribuições de
qui-quadrado. Basta dividir a soma de quadrado dos desvios pela variância da
população.
Finalmente, voltemos para a matéria de hoje (análise de variância). Se a
hipótese nula for verdadeira (ou seja, se todas as marcas de óleo tiverem a
mesma média), então todas as somas de quadrados de desvios que estudamos
nesta aula podem ser usadas para gerar distribuições de qui-quadrado. Assim:
·
2
Re
σ
s
SQ
tem distribuição de qui-quadrado.
·
2
σ
SQTrat
tem distribuição de qui-quadrado.
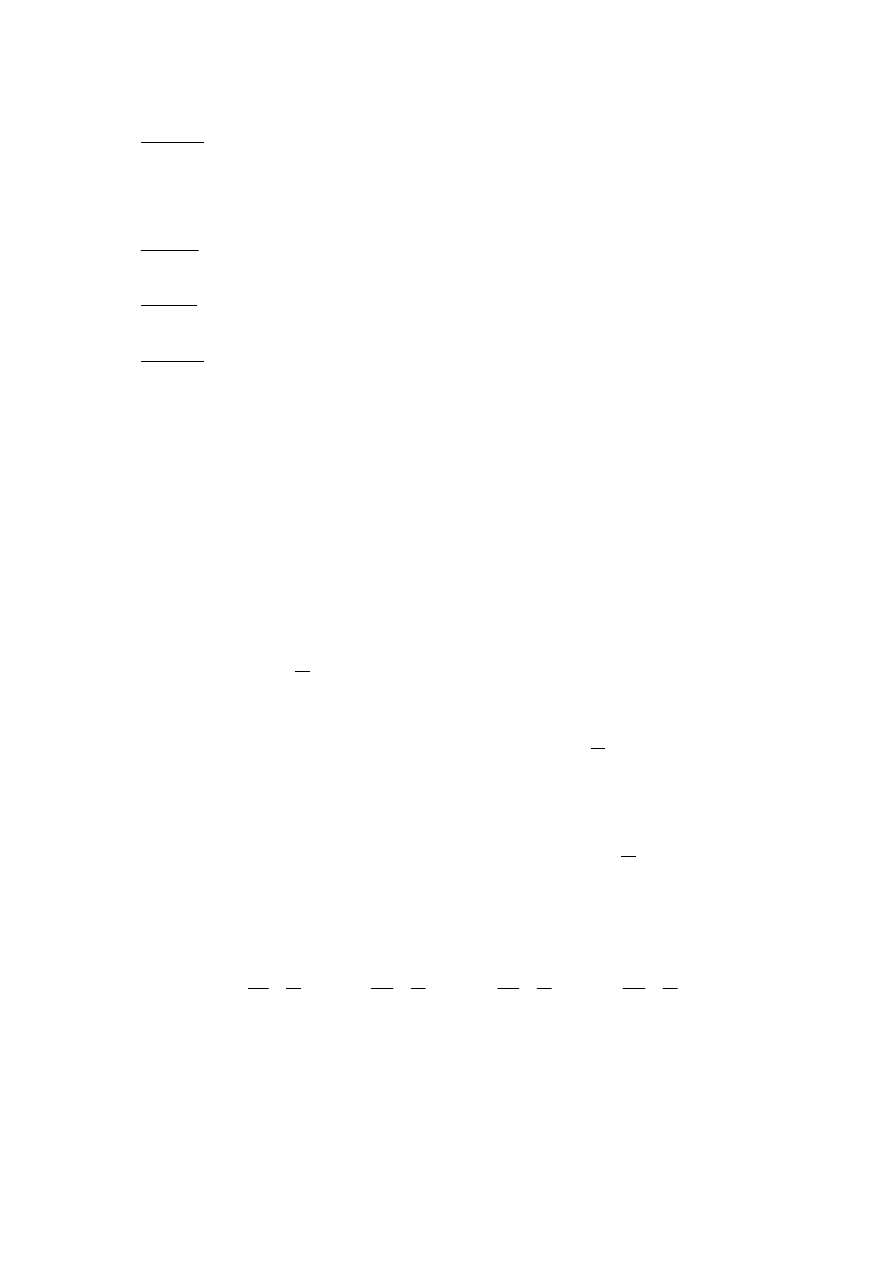
RACIOCÍNIO LÓGICO QUANTITATIVO PARA AFRFB
PROFESSOR: GUILHERME NEVES
Prof. Guilherme Neves www.pontodosconcursos.com.br
15
·
2
σ
SQTotal
tem distribuição de qui-quadrado.
Cada uma destas distribuições tem um certo grau de liberdade. Os graus de
liberdade são:
·
2
Re
σ
s
SQ
:
k
N −
·
2
σ
SQTrat
:
1
−
k
·
2
σ
SQTotal
:
1
−
N
Observem que:
1
)
1
(
)
(
−
=
−
+
−
N
k
k
N
Ou seja, se somarmos os graus de liberdade para os resíduos e para os
tratamentos, chegamos ao grau de liberdade total.
Vamos tentar memorizar os graus de liberdade. Para tanto, vamos lembrar da
“história” que contamos lá na fl. 8.
No cálculo da soma de quadrados total, pegamos cada observação e
subtraímos da média geral. Depois elevamos ao quadrado. Como são N
observações, são N desvios ao quadrado.
Vamos considerar que
X
é dado.
Podemos escolher livremente
1
−
N
desvios. O último, este não pode ser
livremente escolhido. Só há um valor possível para ele, de tal modo que a
média geral da amostra seja igual ao valor fixado para
X
No cálculo da soma de quadrados de tratamentos, pegamos a média de cada
grupo (no nosso exemplo, seria a média de cada uma das 4 marcas de óleo) e
subtraímos da média geral. Novamente, vamos supor que
X
é dado.
São k desvios ao quadrado (neste exemplo,
4
=
k
). Veja:
5
)
81
,
4
8
,
4
(
5
)
81
,
4
58
,
4
(
5
)
81
,
4
98
,
4
(
5
)
81
,
4
88
,
4
(
2
2
2
2
×
−
+
×
−
+
×
−
+
×
−
=
SQTrat
Em símbolos:
4
2
4
3
2
3
2
2
2
1
2
1
)
(
)
(
)
(
)
(
n
X
X
n
X
X
n
X
X
n
X
X
SQTrat
×
−
+
×
−
+
×
−
+
×
−
=
Se não conhecêssemos as médias de cada grupo (só soubéssemos a média
geral das 4 marcas), poderíamos escolher livremente 3 desvios. O último, este
não poderia ser escolhido. Para ele só haveria um valor possível, de tal forma
que a média das 4 marcas seja igual à média geral fixada. Temos, portanto,
1
−
k
graus de liberdade.
RACIOCÍNIO LÓGICO QUANTITATIVO PARA AFRFB
PROFESSOR: GUILHERME NEVES
Prof. Guilherme Neves www.pontodosconcursos.com.br
16
Por fim, no cálculo da soma de quadrados dos resíduos, tomamos cada
observação e subtraímos da média do respectivo grupo. São N desvios ao
quadrado.
Se soubéssemos apenas as médias de cada grupo (ou seja, as médias de cada
marca), e não conhecêssemos o valor de cada observação, poderíamos
escolher livremente diversos desvios.
Para a marca A, teríamos:
+
−
+
−
2
1
12
2
1
11
)
(
)
(
X
X
X
X
+
−
+
−
2
1
14
2
1
13
)
(
)
(
X
X
X
X
2
1
15
)
(
X
X
−
Se não conhecemos as observações, apenas a média da marca A, poderíamos
escolher livremente 4 desvios. O quinto não pode escolher livremente. Só há
um valor possível para ele, de tal modo que a média da marca A seja igual ao
valor estabelecido.
O mesmo ocorre para todas as demais marcas. Em cada uma delas, 1 dos
desvios não pode ser livremente escolhido.
Assim, o número de graus de liberdade é igual a
k
N − . São N desvios ao todo.
Para cada grupo, 1 desvio não pode ser livremente escolhido. Como temos k
grupos, temos k desvios que não podem ser livremente escolhidos.
Todo esse blá blá blá que temos visto desde a fl. 8 (a historinha dos graus de
liberdade e das somas de quadrado sendo relacionadas com distribuições de
qui-quadrado), tudo isso era para facilitar na memorização do resumo abaixo.
Se você não gostou de toda essa conversa, pelo menos decore o quadro a
seguir:
Caso a hipótese nula seja verdadeira (ou seja, todos os grupos
apresentem a mesma média), então:
2
Re
σ
s
SQ
tem distribuição de qui-quadrado com
k
N − graus de liberdade
2
σ
SQTrat
tem distribuição de qui-quadrado com
1
−
k
graus de liberdade
2
σ
SQTotal
tem distribuição de qui-quadrado com
1
−
N
graus de liberdade

RACIOCÍNIO LÓGICO QUANTITATIVO PARA AFRFB
PROFESSOR: GUILHERME NEVES
Prof. Guilherme Neves www.pontodosconcursos.com.br
17
Quadrados médios
Quando dividimos uma soma de quadrados pelo respectivo número de graus
de liberdade, obtemos os chamados “quadrados médios”.
O quadrado médio dos resíduos fica:
k
N
s
SQ
s
QM
−
=
Re
Re
Analogamente, os quadrados médios de tratamento e total ficam:
1
−
=
k
SQTrat
QMTrat
1
−
=
N
SQTotal
QMTotal
Distribuição F
Seja
2
1
χ uma variável aleatória com distribuição de qui-quadrado com g
1
graus
de liberdade. Seja
2
2
χ uma variável aleatória com distribuição de qui-quadrado
com g
2
graus de liberdade.
Vamos criar a seguinte variável:
2
2
2
1
2
1
/
/
g
g
W
χ
χ
=
No numerador temos uma variável de qui-quadrado dividida pelo seu número
de graus de liberdade.
No denominador, temos uma variável de qui-quadrado dividida pelo seu
número de graus de liberdade.
Essa divisão gera uma terceira variável, com distribuição F (ou ainda: F de
Snedecor). Esta variável W possui g
1
graus de liberdade associados ao seu
numerador e g
2
graus de liberdade associados ao seu denominador.
Portanto, a razão:
s
QM
QMTrat
F
Re
=
Tem distribuição F de Snedecor, com
1
−
k
graus de liberdade no numerador e
k
N − graus de liberdade no denominador. Esta razão é utilizada para testar a
hipótese nula, de que todas as populações têm a mesma média (no nosso
exemplo, de que todas as marcas de óleo permitem a mesma quilometragem
média).
Caso a hipótese nula seja verdadeira, os dois quadrados médios serão
próximos, e a razão será próxima de 1.
Caso a hipótese nula seja falsa, os dois quadrados médios serão bem
diferentes entre si, e a razão acima será bem maior que 1.
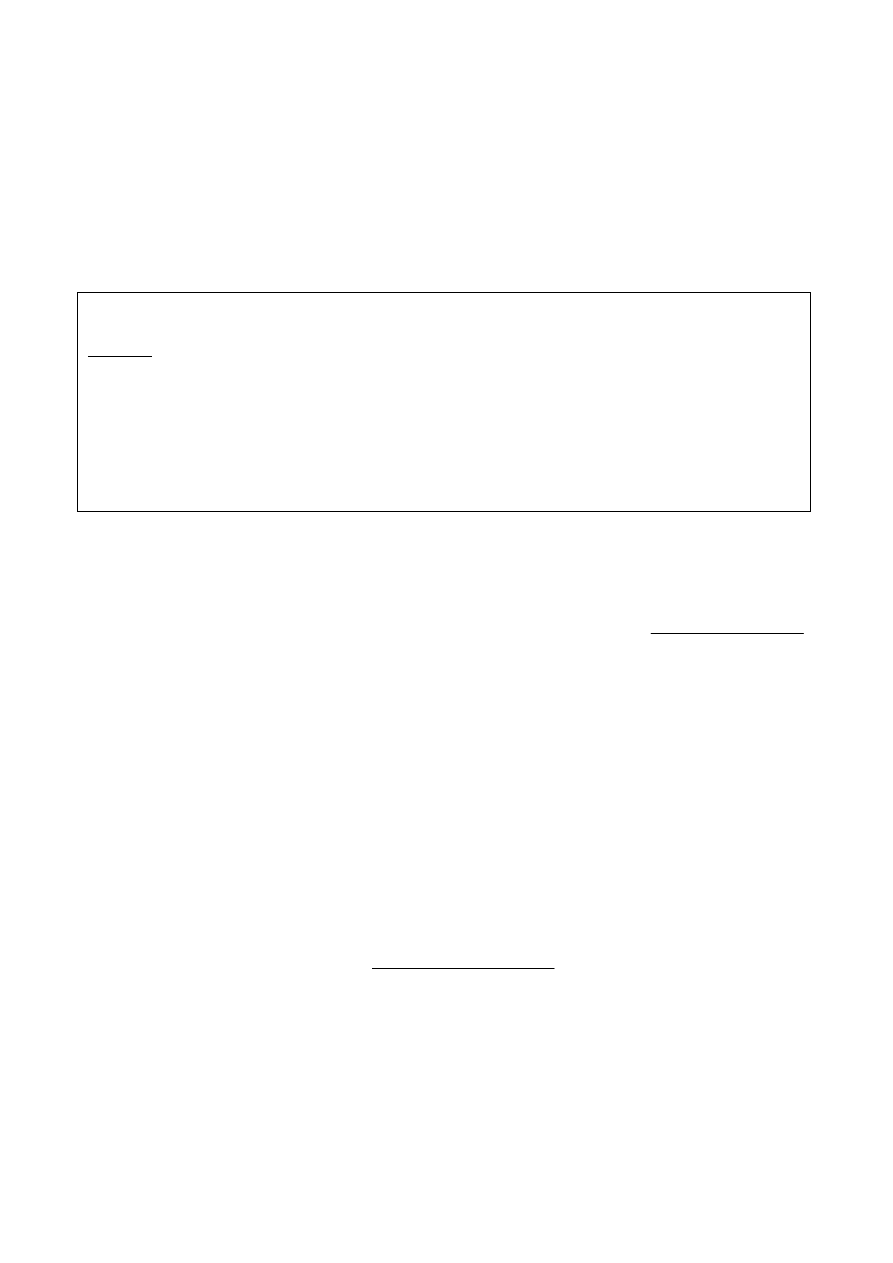
RACIOCÍNIO LÓGICO QUANTITATIVO PARA AFRFB
PROFESSOR: GUILHERME NEVES
Prof. Guilherme Neves www.pontodosconcursos.com.br
18
Então o teste é apenas isso. Basta calcular os valores de
QMTrat
e
s
QM Re
,
específicos para o experimento feito, o que vai gerar a estatística teste (
teste
F _
, ou seja, o valor de F para o experimento feito).
Depois consultamos a tabela da distribuição F (obtendo
crítico
F _
). Depois,
basta comparar a estatística teste com o valor crítico. Se a estatística teste for
maior que o valor crítico, rejeitamos a hipótese nula. Se for menor, aceitamos
a hipótese nula.
Teste F:
s
QM
QMTrat
Re
tem distribuição F (caso a hipótese nula seja verdadeira).
Fazemos o experimento, obtendo valores específicos para
QMTrat
e
s
QM Re
,
o que vai gerar a estatística teste (
teste
F _
).
Se
critico
F
teste
F
_
_
>
, rejeitamos a hipótese nula.
Se
critico
F
teste
F
_
_
<
, aceitamos a hipótese nula.
1. MP RO 2005 [CESGRANRIO]
Se X
1
, X
2
, ... X
n
, Y
1
, Y
2
, ... Y
n
são variáveis aleatórias independentes e com
distribuição normal reduzida, então a variável aleatória
2
2
2
2
1
2
2
2
2
1
...
...
n
n
Y
Y
Y
X
X
X
W
+
+
+
+
+
+
=
tem distribuição:
(A) normal.
(B) qui-quadrado com n - 1 graus de liberdade.
(C) t de Student com n graus de liberdade.
(D) F com (n -1, n -1) graus de liberdade.
(E) F com (n, n) graus de liberdade.
Resolução.
Podemos reescrever a variável W deste modo:
(
)
(
)
n
Y
Y
Y
n
X
X
X
W
n
n
/
...
/
...
2
2
2
2
1
2
2
2
2
1
+
+
+
+
+
+
=
No numerador temos uma distribuição de qui-quadrado com n graus de
liberdade, dividida por n. Idem para o denominador.
Logo, W tem distribuição F com (n, n) graus de liberdade.
Gabarito: E
RACIOCÍNIO LÓGICO QUANTITATIVO PARA AFRFB
PROFESSOR: GUILHERME NEVES
Prof. Guilherme Neves www.pontodosconcursos.com.br
19
2. TCE RO 2007 [CESGRANRIO]
Se X1, X2, ..., Xn, Y1, Y2, ..., Yn são variáveis aleatórias independentes e com
distribuição normal reduzida, então a variável aleatória
2
2
2
2
1
2
2
2
2
1
...
...
n
n
Y
Y
Y
X
X
X
W
+
+
+
+
+
+
=
tem distribuição:
(A) normal.
(B) qui-quadrado com n - 1 graus de liberdade.
(C) t de Student com n graus de liberdade.
(D) F com (n - 1, n - 1) graus de liberdade.
(E) F com (n, n) graus de liberdade.
Resolução.
Questão idêntica à anterior.
Gabarito: E
Exemplo 1.
Para o exemplo das quatro marcas de óleo, trabalhadas
durante a aula, teste a hipótese de que as médias são iguais, contra a
hipótese alternativa de que há pelo menos uma média diferente das
demais. Utilize um nível de significância de 10%.
Resolução.
Podemos juntar todos os cálculos já realizados durante a aula em uma tabela,
assim:
Fonte
da
variação
Graus
de
liberdade
Soma
de
quadrados
Quadrado
médio
teste
F _
Tratamentos
(entre)
3
0,434
0,145
1,858974
Resíduos
(dentro)
16
1,244
0,078
Total
19
1,678
Os quadrados médios foram obtidos pela divisão entre a soma de quadrados e
o número de graus de liberdade.

RACIOCÍNIO LÓGICO QUANTITATIVO PARA AFRFB
PROFESSOR: GUILHERME NEVES
Prof. Guilherme Neves www.pontodosconcursos.com.br
20
Ou seja:
145
,
0
3
434
,
0
=
=
QMTrat
Em vez de utilizar a expressão “tratamento”, o exercício pode se referir à
variação entre tratamentos. Ou seja, o símbolo seria
entre
QM _
145
,
0
_
=
=
entre
QM
QMTrat
Para o quadrado médio de resídulos (dentro), a conta é análoga:
078
,
0
16
244
,
1
_
Re
=
=
=
dentro
QM
s
QM
Estes dois quadrados médios são utilizados para fazer o teste F.
=
=
=
=
078
,
0
145
,
0
_
_
Re
_
dentro
QM
entre
QM
s
QM
QMTrat
teste
F
1,8589
A razão entre os quadrados foi de 1,8589. Foi diferente de 1.
Caso a razão seja bem próxima de 1, aceitamos a hipótese nula. Caso a razão
seja bem afastada de 1, rejeitamos a hipótese nula.
E agora?
O número 1,8589 é próximo ou afastado de 1?
Bem, o que vai nos responder isso é a tabela da distribuição F. Abaixo segue
um trechinho da Tabela F para nível de confiança de 10%.
Fornece valores críticos (F
0
), tal que
%
10
)
(
0
=
> F
F
P
Número de GL do numerador
Número GL
denominador
2
3
4
5
15
2,695172932 2,489787735 2,361433116 2,273022447
16
2,668171457
2,461810755
2,332744869 2,243757603
17
2,644638468 2,437433917 2,307747133 2,218252647
18
2,623946985 2,416005381 2,285771772 2,195827465
19
2,605612364 2,397021508 2,266302568 2,175956494
20
2,589254118 2,380087057 2,248934402 2,158227217
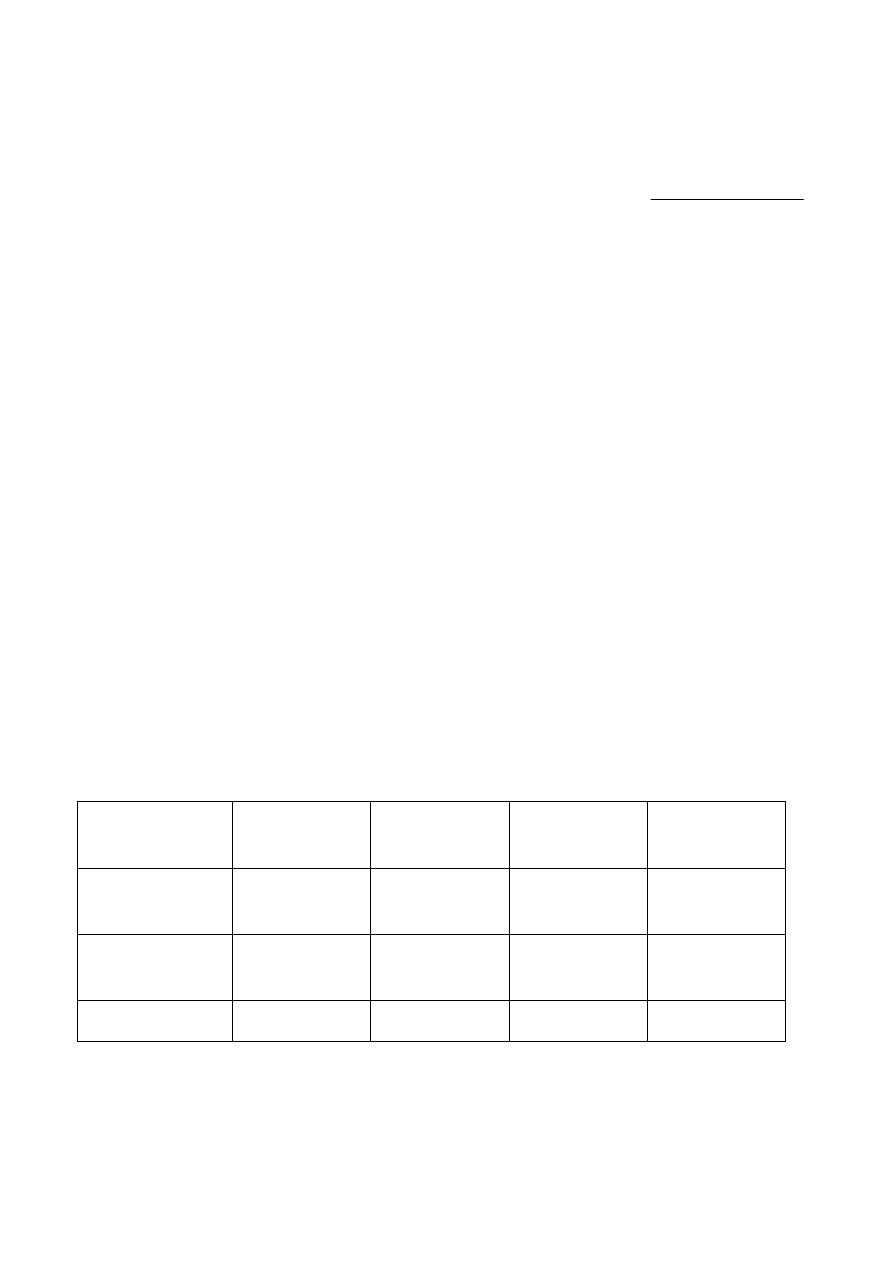
A estatística teste (1,8589) é menor que o valor crítico (2,46). Aceitamos a
hipótese nula.
Para melhor visualização, segue desenho da função densidade de
probabilidade, para (3, 16) graus de liberdade.
RACIOCÍNIO LÓGICO QUANTITATIVO PARA AFRFB
PROFESSOR: GUILHERME NEVES
Prof. Guilherme Neves www.pontodosconcursos.com.br
21
De acordo com a tabela para a distribuição F, temos que a área amarela da
figura abaixo é de 10%.
Que é a região crítica. A estatística teste não caiu na região crítica. Portanto,
aceitamos a hipótese nula.
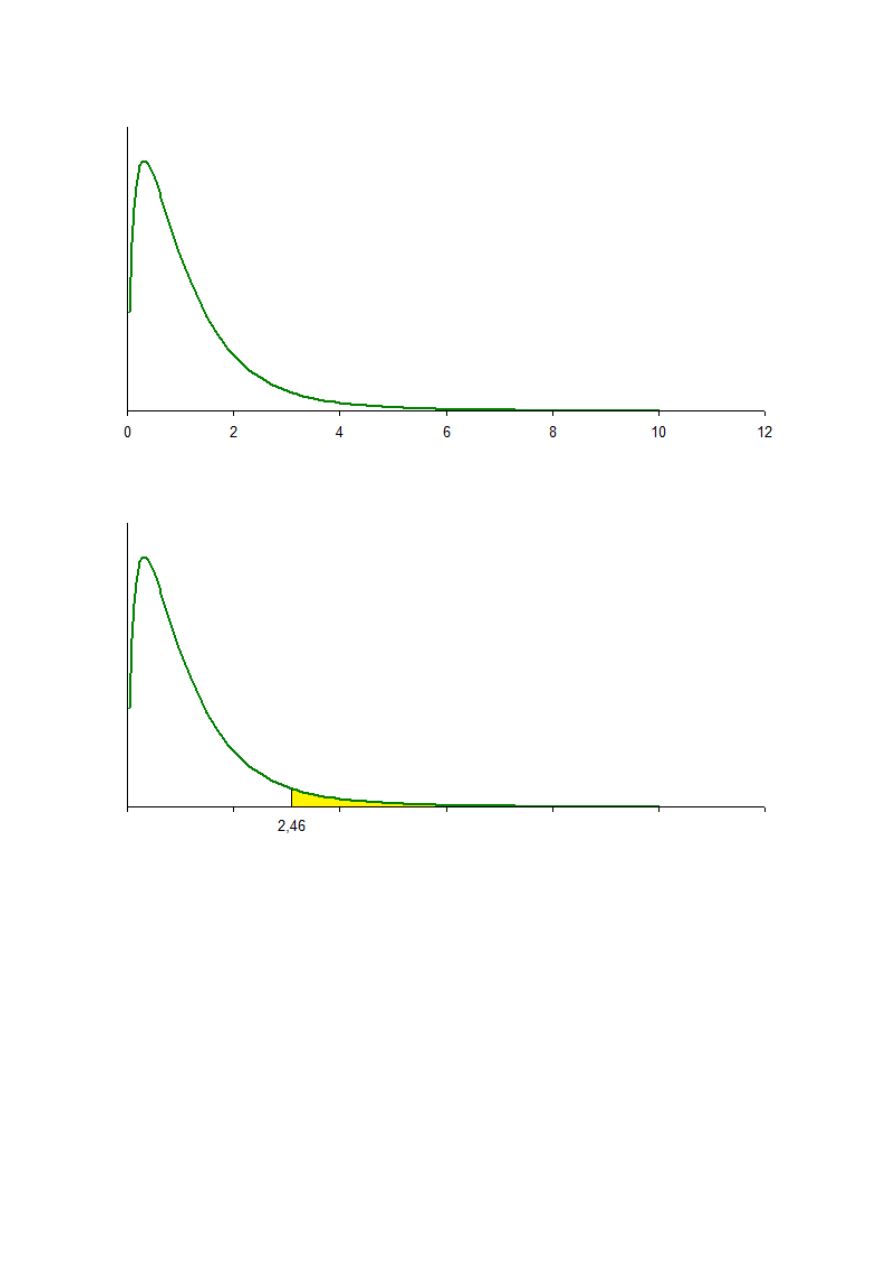
3. PETROBRAS 2008/2 [CESGRANRIO]
Dividem-se aleatoriamente 12 lotes de terra em três grupos.
O primeiro é mantido como grupo de controle (C), enquanto os outros dois
recebem os fertilizantes A e B. A tabela abaixo apresenta a ANOVA parcial do
experimento.
RACIOCÍNIO LÓGICO QUANTITATIVO PARA AFRFB
PROFESSOR: GUILHERME NEVES
Prof. Guilherme Neves www.pontodosconcursos.com.br
22
Então, as constantes a, b e c são, respectiva e aproximadamente, iguais a
(A) 1, 11 e 4,5
(B) 1, 11 e 9
(C) 2, 11 e 9
(D) 2, 12 e 2
(E) 3, 12 e 3
Resolução.
O exercício forneceu direto a tabela da análise de variância, já com todas as
contas prontas.
SQ indica “soma de quadrados”. GL indica “graus de liberdade”. EQM indica
“erro quadrático médio” (que é sinônimo de quadrado médio).
Queremos testar se os três tipos de produção (com fertilizantes A e B, mais o
grupo de controle, C) apresentam os mesmos resultados. O exercício não
indicou exatamente o que se está comparando. Poderia, por exemplo, ser a
quantidade de toneladas produzidas por determinada área plantada.
Ao todo, são 12 observações (uma para cada lote de terra). Portanto:
11
1
12
=
−
⇒
=
N
N
A soma de quadrados total tem
1
−
N
graus de liberdade. Logo, a constante b
da tabela é igual a 11.
11
=
b
O número de graus de liberdade associado à soma de quadrados total é igual à
soma dos demais graus de liberdade.
b
a
=
+ 9
11
9 =
+
a
2
=
a
Com isso, já dá para marcar letra C.
Por fim, a estatística teste fica:
=
=
=
3
,
17
156
_
c
teste
F
9,02
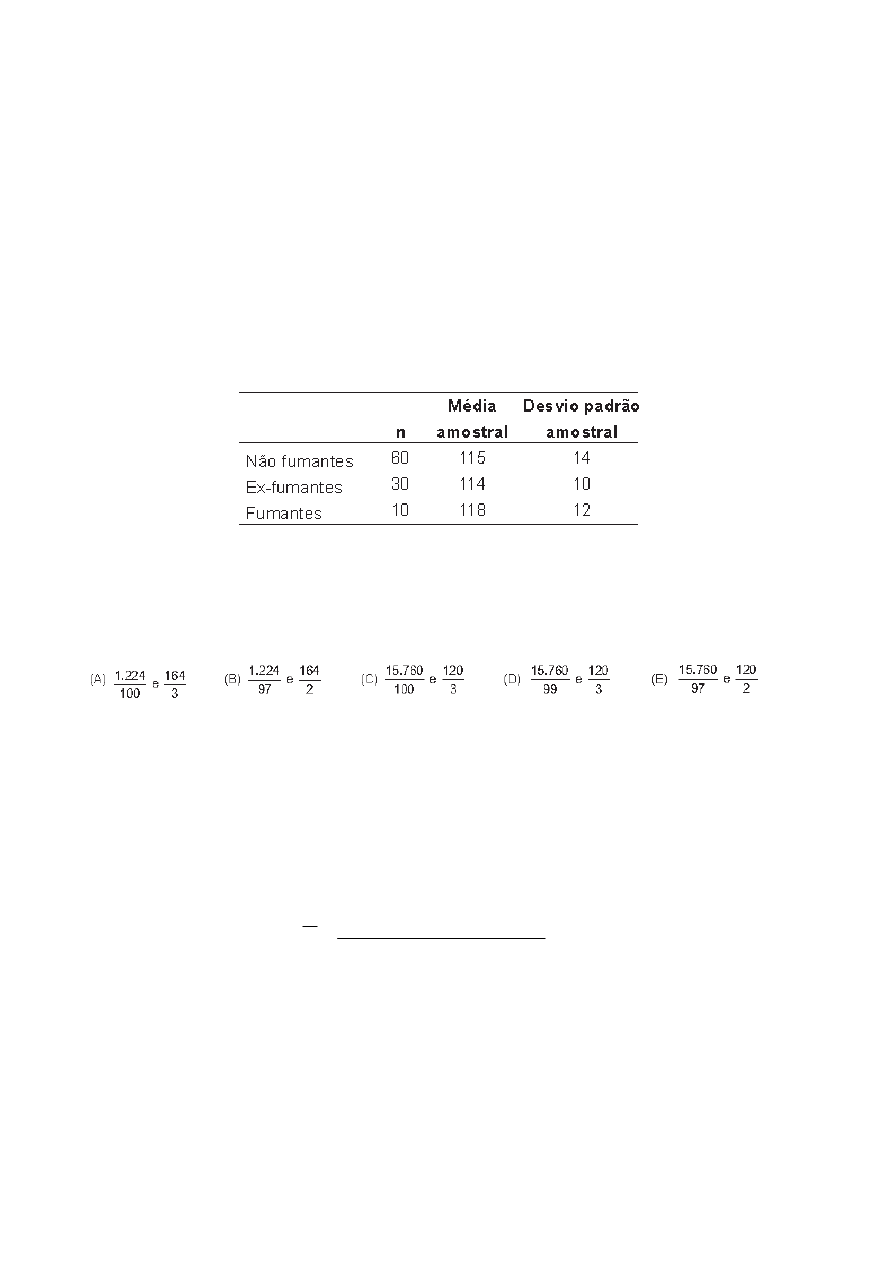
RACIOCÍNIO LÓGICO QUANTITATIVO PARA AFRFB
PROFESSOR: GUILHERME NEVES
Prof. Guilherme Neves www.pontodosconcursos.com.br
23
Gabarito: C
Considere a descrição abaixo para responder as próximas questões.
Um estudo pretende comparar as medidas de pressão sanguínea sistólica de
três grupos: não fumantes, ex-fumantes e fumantes. Uma amostra é
selecionada de cada grupo, sendo os dados relevantes apresentados abaixo.
Supõe-se que as variâncias populacionais sejam iguais, e que a pressão
sanguínea sistólica seja normalmente distribuída. As médias e os desvios
padrões estão expressos em mmHg.
4. FUNASA 2009 [CESGRANRIO]
As estimativas da variância dentro dos grupos e entre os grupos, são,
respectivamente,
Resolução
Temos um total de 100 observações (
100
=
N
), referentes a três grupos
pesquisados (
3
=
k
)
A média geral dos três grupos é dada por:
115
100
10
118
30
114
60
115
=
×
+
×
+
×
=
X
A soma de quadrados entre os grupos é dada por:
120
)
115
118
(
10
)
115
114
(
30
)
115
115
(
60
_
2
2
2
=
−
×
+
−
×
+
−
×
=
entre
SQ
Esta soma de quadrados possui
1
−
k
graus de liberdade.
2
1
3
1
=
−
=
−
k

RACIOCÍNIO LÓGICO QUANTITATIVO PARA AFRFB
PROFESSOR: GUILHERME NEVES
Prof. Guilherme Neves www.pontodosconcursos.com.br
24
Logo, o quadrado médio fica:
2
120
_
=
entre
QM
Vamos agora calcular a soma de quadrados dentro dos grupos. Para tanto,
precisamos, em cada grupo, calcular a soma dos quadrados dos desvios em
relação à média do grupo.
Para os não-fumantes, sabemos que a variância é igual a 14
2
. E como foi
calculada esta variância? Ela foi calculada somando os quadrados dos desvios e
dividindo por 59. Logo, a soma dos quadrados dos desvios, para o grupo dos
não-fumantes, é igual a
59
14
2
×
.
Como o mesmo raciocínio, podemos achar as somas dos quadrados dos
desvios para os demais grupos. Com isso, temos:
15760
9
12
29
10
59
14
_
2
2
2
=
×
+
×
+
×
=
dentro
SQ
Esta soma de quadrados tem
k
N − graus de liberdade.
97
3
100
=
−
=
− k
N
Logo:
97
15760
_
=
dentro
QM
Gabarito: E
5. FUNASA 2009 [CESGRANRIO]
Utilizando um nível de significância de 5%, a Estatística F, as pressões
sanguíneas médias nos três grupos e o valor crítico são, respectivamente,
Resolução.

RACIOCÍNIO LÓGICO QUANTITATIVO PARA AFRFB
PROFESSOR: GUILHERME NEVES
Prof. Guilherme Neves www.pontodosconcursos.com.br
25
Estatística teste:
=
×
=
=
=
15760
97
60
97
/
15760
2
/
120
_
_
_
dentro
QM
entre
QM
teste
F
0,37
Consultando a tabela colocada ao final do arquivo (para um nível de
significância de 5%), temos um pequeno problema. Há uma coluna para 2
graus de liberdade no numerador. Mas não há uma linha para 97 graus de
liberdade no denominador.
O valor mais próximo é 120 graus de liberdade. Logo, o valor crítico deve estar
próximo de 3,07. A própria questão faz esta aproximação, pois traz, em todas
as alternativas, o valor 3,07.
Assim, concluímos que a região crítica corresponde ao intervalo de 3,07 até
infinito.
A estatística teste cai na região de aceitação. Aceitamos a hipótese de que as
médias nos três grupos são iguais entre si.
Gabarito: A

RACIOCÍNIO LÓGICO QUANTITATIVO PARA AFRFB
PROFESSOR: GUILHERME NEVES
Prof. Guilherme Neves www.pontodosconcursos.com.br
26
ANÁLISE DE VARIÂNCIA DA REGRESSÃO
Um teste de hipóteses muito comum é aquele que testa a hipótese nula de que
o coeficiente β da reta de regressão é nulo. Caso a hipótese nula seja
verdadeira, temos que a reta de regressão é horizontal.
Relembrando o significado da reta de regressão. Para cada valor de X nós
temos uma sub-população de valores de Y, com média dada pela reta de
regressão e variância
2
σ .
Se a reta é horizontal, então todas as sub-populações terão a mesma média.
Nós vimos uma ferramenta para testar se a média de diferentes populações
são iguais entre si. Esta ferramenta era a análise de variância.
Como testar a hipótese de β ser igual a zero equivale a testar a hipótese de as
varais populações têm a mesma média, então podemos usar a análise de
variância para isso. Vamos ver como fica.
Somas de quadrados
Quando utilizamos a regressão linear, obtemos
i
Yˆ , que é uma estimativa para
Y
. A diferença entre estas duas grandezas é o desvio.
i
i
i
Y
Y
e
ˆ
−
=
Rearranjando os termos:
i
i
i
Y
e
Y
ˆ
+
=
Subtraindo
Y
dos dois lados:
Y
Y
e
Y
Y
i
i
i
−
+
=
−
ˆ
Elevando ao quadrado:
(
)
(
)
2
2
ˆ
Y
Y
e
Y
Y
i
i
i
−
+
=
−
(
)
(
)
(
)
Y
Y
e
Y
Y
e
Y
Y
i
i
i
i
i
−
×
×
+
−
+
=
−
ˆ
2
ˆ
2
2
2
Somando as parcelas acima para todos os valores de i:
(
)
(
)
(
)
[
]
∑
∑
∑
∑
−
×
×
+
−
+
=
−
Y
Y
e
Y
Y
e
Y
Y
i
i
i
i
i
ˆ
2
ˆ
2
2
2

RACIOCÍNIO LÓGICO QUANTITATIVO PARA AFRFB
PROFESSOR: GUILHERME NEVES
Prof. Guilherme Neves www.pontodosconcursos.com.br
27
É possível demonstrar que
(
)
0
]
ˆ
[
=
−
×
∑
Y
Y
e
i
i
.
Portanto:
(
)
(
)
∑
∑
∑
−
+
=
−
2
2
2
ˆ
Y
Y
e
Y
Y
i
i
i
E o que é que temos aí em cima? Temos somas de quadrados.
Cada uma destas parcelas recebe um nome especial:
(
)
⇒
−
∑
2
Y
Y
i
soma de quadrados total (S.Q.Total)
⇒
∑
2
i
e
soma de quadrados dos resíduos (S.Q.Resíduos)
(
)
⇒
−
∑
2
ˆ
Y
Y
i
soma de quadrados do modelo de regressão (S.Q.Regressão) –
corresponde à Soma de quadrado de tratamentos.
Portanto:
siduos
SQ
gressao
SQ
SQTotal
Re
Re
+
=
É possível demonstrar que:
(
)(
)
[
]
∑
−
−
×
=
Y
Y
X
X
b
gressao
SQ Re
Onde b é a estimativa do coeficiente angular da reta de regressão.
Resumo das somas de quadrados
siduos
SQ
gressao
SQ
SQTotal
Re
Re
+
=
(
)(
)
[
]
∑
−
−
×
=
Y
Y
X
X
b
gressao
SQ Re
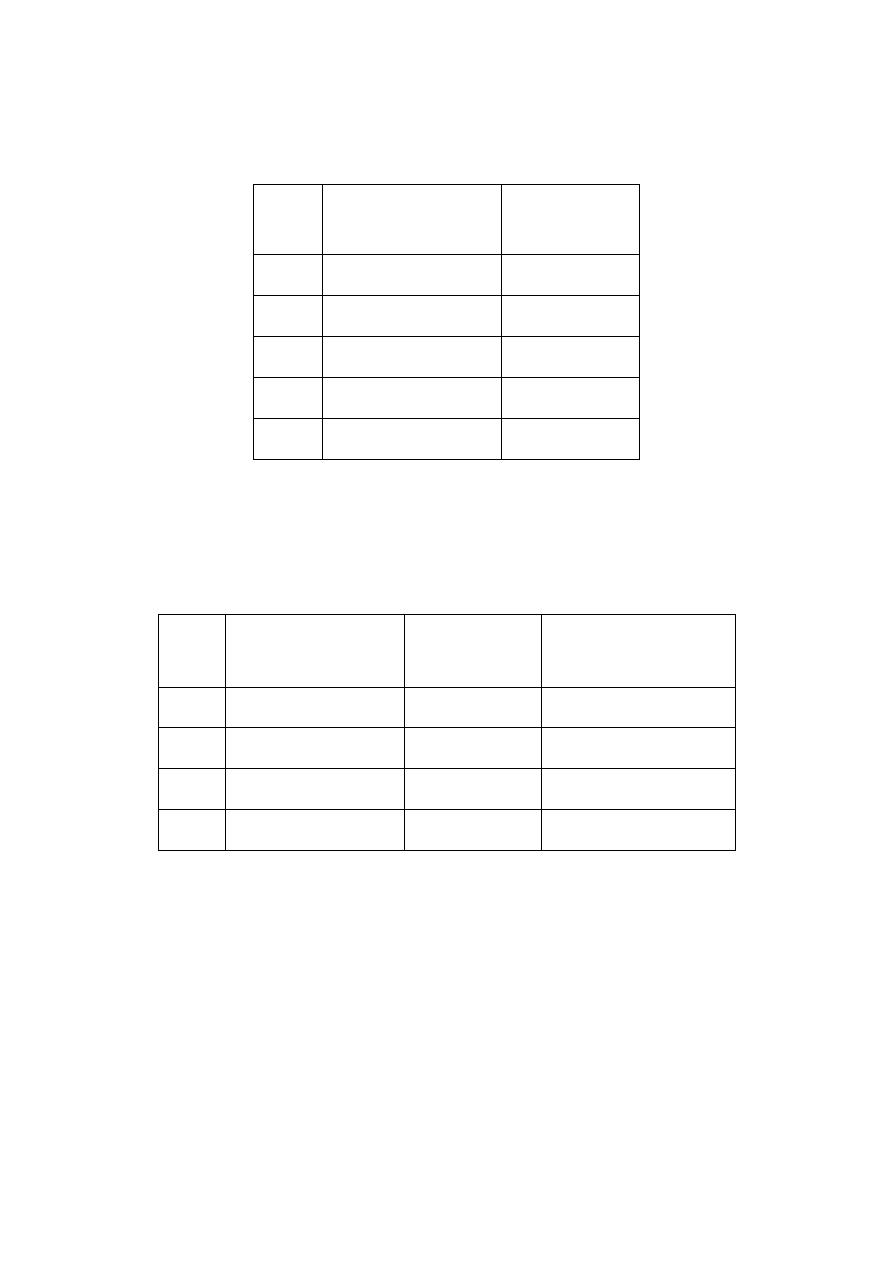
RACIOCÍNIO LÓGICO QUANTITATIVO PARA AFRFB
PROFESSOR: GUILHERME NEVES
Prof. Guilherme Neves www.pontodosconcursos.com.br
28
Vamos calcular cada um destes valores para aqueles 4 alunos que fizeram as
provas de física e matemática.
Aluno
Nota de
matemática
( )
X
Nota de
física
( )
Y
1
2
6
2
6
7
3
8
7
4
10
8
Média
6,5
7
Já fizemos o modelo de regressão linear para, a partir das notas de
matemática, estimar as notas de física. O resultado foi:
Aluno
Nota de
matemática
( )
X
Nota de
física
( )
Y
Nota de física
estimada
( )
Yˆ
1
2
6
5,97
2
6
7
6,89
3
8
7
7,34
4
10
8
7,80
A partir dos valores acima, podemos montar o quadro abaixo:
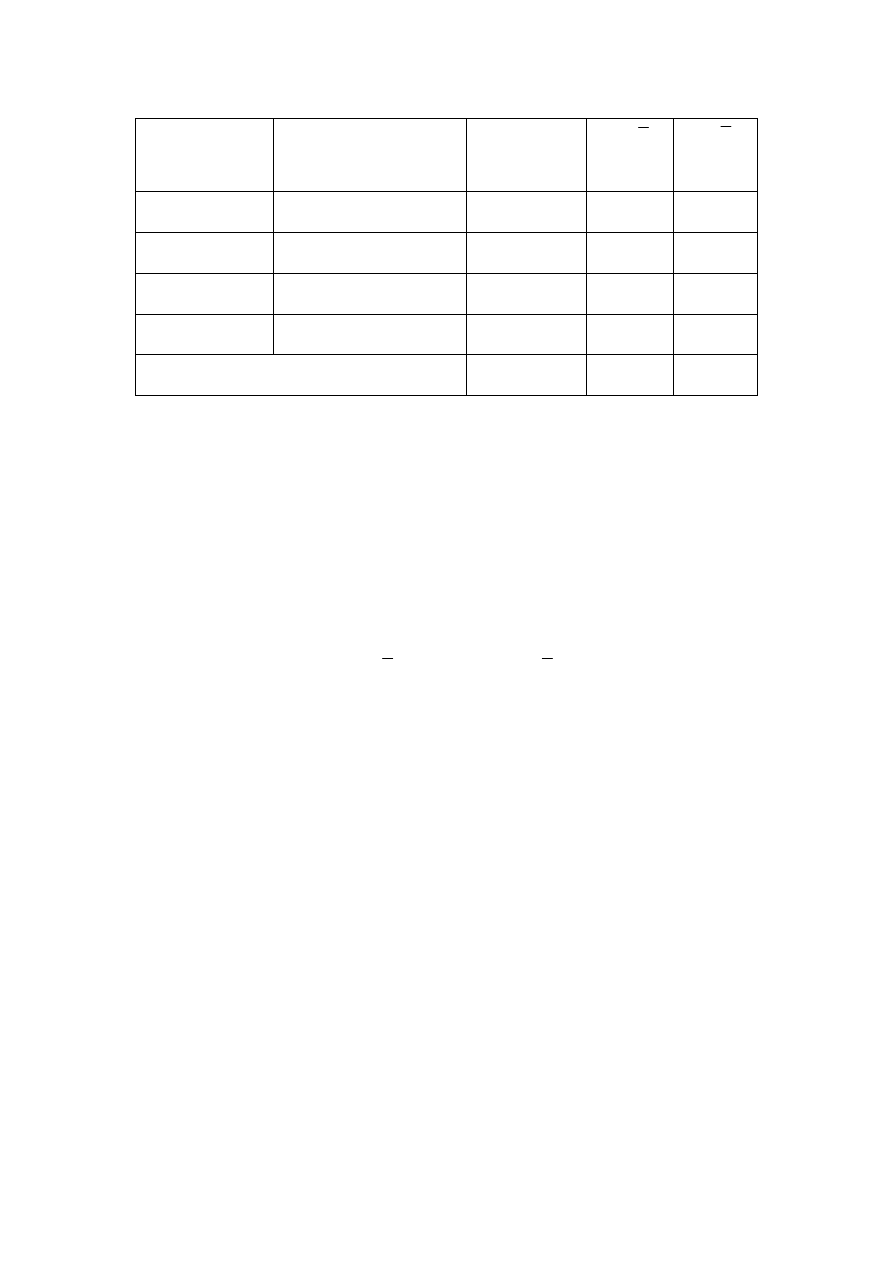
RACIOCÍNIO LÓGICO QUANTITATIVO PARA AFRFB
PROFESSOR: GUILHERME NEVES
Prof. Guilherme Neves www.pontodosconcursos.com.br
29
Nota de
física
( )
Y
Nota de física
estimada
( )
Yˆ
(
)
2
2
ˆ
Y
Y
e
−
=
(
)
2
ˆ
Y
Y −
(
)
2
Y
Y −
6
5,97
0,0009
1,0609
1
7
6,89
0,0121
0,0121
0
7
7,34
0,1156
0,1156
0
8
7,80
0,04
0,64
1
TOTAL
0,1686
1,8286
2
Da última linha da tabela, temos:
2
=
SQTotal
8286
,
1
Re
=
gressao
SQ
1686
,
0
Re
=
siduos
SQ
Note que:
(
)
(
)
∑
∑
∑
−
+
=
−
2
2
2
ˆ
Y
Y
e
Y
Y
i
i
i
Ou ainda:
siduos
SQ
gressao
SQ
SQTotal
Re
Re
+
=
Na verdade, substituindo os valores, obtemos:
9972
,
1
2 =
A diferença se deve aos arredondamentos (os valores apresentados para as
notas de física estimada estão arredondados).
Quadrados médios e estatística F
A análise de variância, aplicada à reta de regressão, serve para testar a
hipótese de que β é igual a zero.
Vimos que, para cada valor de X, nós temos uma população de valores de Y
que gira em torno da reta de regressão. Caso a reta seja horizontal, todas as

RACIOCÍNIO LÓGICO QUANTITATIVO PARA AFRFB
PROFESSOR: GUILHERME NEVES
Prof. Guilherme Neves www.pontodosconcursos.com.br
30
populações de valores de Y girarão em torno do mesmo valor. Todas elas terão
a mesma média.
Logo, as somas de quadrados de desvios, acima definidas, podem ser usadas
para testar a hipótese de que o coeficiente β é igual a zero.
A hipótese nula (
0
=
β
) nada mais é que supor que a reta de regressão é
horizontal. Ou seja, é a hipótese de que todas as sub-populações de Y provém,
na verdade, de uma única população (ou seja, apresentam mesma média e
mesma variância). E vimos que a análise de variância pode ser utilizada
justamente para isso. Basta calcular a estatística F, com base nos quadrados
médios.
No caso da regressão linear, temos:
(
)
⇒
−
∑
2
Y
Y
i
⇒
SQTotal
1
−
n
graus de liberdade
⇒
∑
2
i
e
⇒
siduos
SQ Re
2
−
n
graus de liberdade
(
)
⇒
−
∑
2
ˆ
Y
Y
i
⇒
gressao
SQ Re
1
grau de liberdade
E os quadrados médios ficam assim.
Quadrado médio total:
1
−
=
n
SQTotal
QMTotal
Quadrado médio dos desvios:
2
Re
Re
−
=
n
siduos
SQ
siduos
QM
Quadrado médio do modelo de regressão:
1
Re
Re
gressao
SQ
gressão
QM
=
Para o caso dos alunos que fizeram as provas de física e matemática, temos:
3
2
1
4
2
=
−
=
QMTotal
=
−
=
2
4
1686
,
0
Re
siduos
QM
0,0843
8286
,
1
1
8286
,
1
Re
=
=
gressao
QM

RACIOCÍNIO LÓGICO QUANTITATIVO PARA AFRFB
PROFESSOR: GUILHERME NEVES
Prof. Guilherme Neves www.pontodosconcursos.com.br
31
E a estatística F fica:
=
=
=
0842
,
0
8286
,
1
Re
Re
_
siduos
QM
gressao
QM
teste
F
21,71
Coeficiente de determinação
As somas de quadrados servem para definir uma grandeza conhecida como
coeficiente de determinação da regressão linear.
Ele é dado por:
SQTotal
gressao
SQ
r
Re
2
=
Esta grandeza, no caso do modelo
i
i
i
X
Y
ε
β
α
+
+
=
, é igual ao quadrado do
coeficiente de correlação linear.
Se a soma dos quadrados dos resíduos for pequena, de tal forma que
2
r
se
aproxime de 1, isto significa que as diferenças entre os valores observados (
i
Y )
e a média (
Y
) são quase totalmente explicados pela reta de regressão.
Se a soma dos quadrados dos resíduos for grande, de tal forma que
2
r
se
aproxime de zero, isto significa que a reta de regressão pouco explica sobre as
diferenças entre os valores observados e a média. Ou seja, é perca de tempo
ficar calculando reta de regressão se ela é um estimador ruim.
Como o coeficiente de correlação (r) assume valores entre -1 e 1, então o
coeficiente de determinação (r
2
) assume valores entre 0 e 1.
6. BACEN 2006 [FCC]
Uma empresa, com finalidade de determinar a relação entre gastos anuais com
propaganda (X), em R$ 1.000,00 e o lucro bruto anual (Y), em R$ 1.000,00,
optou por utilizar o modelo linear simples
i
i
i
X
Y
ε
β
α
+
+
=
, em que
i
Y é o valor
do lucro bruto auferido no ano i e
i
ε
o erro aleatório com as respectivas
hipóteses consideradas para a regressão linear simples (
α
e β são parâmetros
desconhecidos). Considerou, para o estudo, as seguintes informações
referentes às observações nos últimos 10 anos da empresa:
100
10
1
=
∑
=
i
i
Y
;
60
10
1
=
∑
=
i
i
X
;
650
=
×
∑
i
i
Y
X
;
( )
400
10
1
2
=
∑
=
i
i
X
;
( )
1080
10
1
2
=
∑
=
i
i
Y

RACIOCÍNIO LÓGICO QUANTITATIVO PARA AFRFB
PROFESSOR: GUILHERME NEVES
Prof. Guilherme Neves www.pontodosconcursos.com.br
32
Montando o quadro de análise de variância, tem-se que:
a) a variação explicada, fonte de variação devido à regressão, apresenta um
valor igual a 80;
b) dividindo a variação residual pela variação total, obtemos o correspondente
coeficiente de determinação;
c) o valor da estatística F necessária para o teste da existência de regressão é
igual ao coeficiente da divisão da variação explicada pela variação residual
d) a variação residual apresenta um valor igual a 17,5
e) a variação total apresenta um valor igual a 62,5.
[Observação: considere que você já sabe que os coeficientes a e b são dados
por:
5
,
2
=
a
;
25
,
1
=
b
, conforme cálculos do Erro! Fonte de referência não
encontrada.]
Resolução.
Em vez de utilizar o termo “soma de quadrados”, a questão está utilizando
“variação”. Assim, fazendo a correspondência dos termos da questão com
aqueles que nós vimos:
- Soma de quadrados total: variação total
- Soma de quadrados dos resíduos: variação residual
- Soma de quadrados da regressão: variação explicada (ou seja, é a parte da
variação total que é explicada pelo modelo de regressão).
A variação total fica:
(
)
∑
−
=
2
Y
Y
SQTotal
i
Utilizando a transformação que vimos:
(
)
2
2
2
Y
n
Y
Y
Y
SQTotal
i
i
−
=
−
=
∑
∑
80
10
10
080
.
1
2
=
×
−
=
SQTotal
Portanto a letra E está errada.
A variação explicada (=variação do modelo = Soma de Quadrados da
Regressão) fica:
(
)(
)
[
]
∑
−
−
×
=
Y
Y
X
X
b
gressao
SQ Re
Utilizando as transformações vistas:

RACIOCÍNIO LÓGICO QUANTITATIVO PARA AFRFB
PROFESSOR: GUILHERME NEVES
Prof. Guilherme Neves www.pontodosconcursos.com.br
33
(
)
(
)
Y
X
n
XY
b
gressao
S
−
×
=
∑
Re
(
)
(
)
∑
−
×
=
Y
X
n
XY
b
gressao
S Re
(
)
5
,
62
50
25
,
1
10
6
10
650
25
,
1
Re
=
×
=
×
×
−
×
=
gressao
SQ
Deste modo, a letra A está errada.
A variância residual (=Soma de Quadrados de Resíduos) é igual a:
5
,
17
5
,
62
80
Re
Re
=
−
=
−
=
gressão
SQ
SQTotal
siduos
SQ
E a letra D está correta.
Vamos checar a alternativa B.
Vimos que:
SQTotal
gressao
SQ
r
Re
2
=
A letra B pretende dizer que
SQTotal
siduos
SQ
r
Re
2
=
, o que está errado.
Por fim, vejamos a letra C. A estatística F é dada por:
)
2
/(
Re
1
/
Re
Re
Re
_
−
=
=
n
siduos
SQ
gressao
SQ
siduos
QM
gressao
QM
teste
F
A alternativa C está errada, pois afirma que a estatística F é dada por
siduos
SQ
gressao
SQ
Re
Re
, ignorando as divisões pelos graus de liberdade.
Gabarito: D.
7. SEAD/PM SANTOS 2005 [FCC]
Para resolver à questão seguinte, considere que foi realizado um estudo em
um país com a finalidade de se determinar a relação entre a Renda Disponível
(Y), em milhões de dólares, e o consumo (C), também em milhões de dólares.
Sabe-se que foi utilizado o modelo linear simples
i
i
i
e
bY
a
C
+
+
=
, em que C
i
é o
consumo no ano i, Y
i
é a renda disponível no ano ‘i’ e
i
e o erro aleatório com as
respectivas hipóteses consideradas para a regressão linear simples.
Este estudo apresentou as seguintes informações colhidas através da
observação nos últimos 10 anos:
800
10
1
=
∑
=
i
i
C
000
.
1
10
1
=
∑
=
i
i
Y
600
.
83
10
1
=
∑
=
i
i
i
C
Y
000
.
105
10
1
2
=
∑
=
i
i
Y
240
.
67
10
1
2
=
∑
=
i
i
C

RACIOCÍNIO LÓGICO QUANTITATIVO PARA AFRFB
PROFESSOR: GUILHERME NEVES
Prof. Guilherme Neves www.pontodosconcursos.com.br
34
O coeficiente de correlação
r
de Pearson entre as variáveis Y e C é obtido pela
fórmula:
)
(
)
(
)
,
cov(
C
DP
Y
DP
Y
C
r
×
=
em que:
Cov(C,Y) é a covariância entre C e Y;
DP(Y) é o desvio padrão de Y
DP(C) é o desvio padrão de C.
Tem-se que o valor do correspondente de determinação
2
r
é igual a:
a) 60%
b) 72%
c) 76%
d) 80%
e) 90%
Resolução:
Nós temos representado os parâmetros do modelo por
α
e β . E
representamos suas estimativas por a e b .
Pois bem, neste exercício os parâmetros estão sendo chamados de a e b .
Vamos chamar suas estimativas de aˆ e bˆ .
(
)
∑
−
=
2
C
C
SQTotal
i
=
( )
2
1
2
C
n
C
n
i
i
−
∑
=
Portanto:
=
SQTotal
( )
240
.
3
80
10
240
.
67
2
2
1
2
=
×
−
=
−
∑
=
C
n
C
n
i
i
( )
(
)
∑
×
×
−
×
=
C
Y
n
YC
b
gressao
SQ
ˆ
Re
(
)
80
100
10
600
.
83
ˆ
Re
×
×
−
×
= b
gressao
SQ
Lá no Erro! Fonte de referência não encontrada. nós vimos que
72
,
0
ˆ =
b
Logo:
(
)
592
.
2
80
100
10
600
.
83
72
,
0
Re
=
×
×
−
×
=
gressao
SQ
Por fim, chegamos a:
RACIOCÍNIO LÓGICO QUANTITATIVO PARA AFRFB
PROFESSOR: GUILHERME NEVES
Prof. Guilherme Neves www.pontodosconcursos.com.br
35
SQTotal
gressao
SQ
r
Re
2
=
80
,
0
240
.
3
592
.
2
2
=
=
r
Gabarito: D
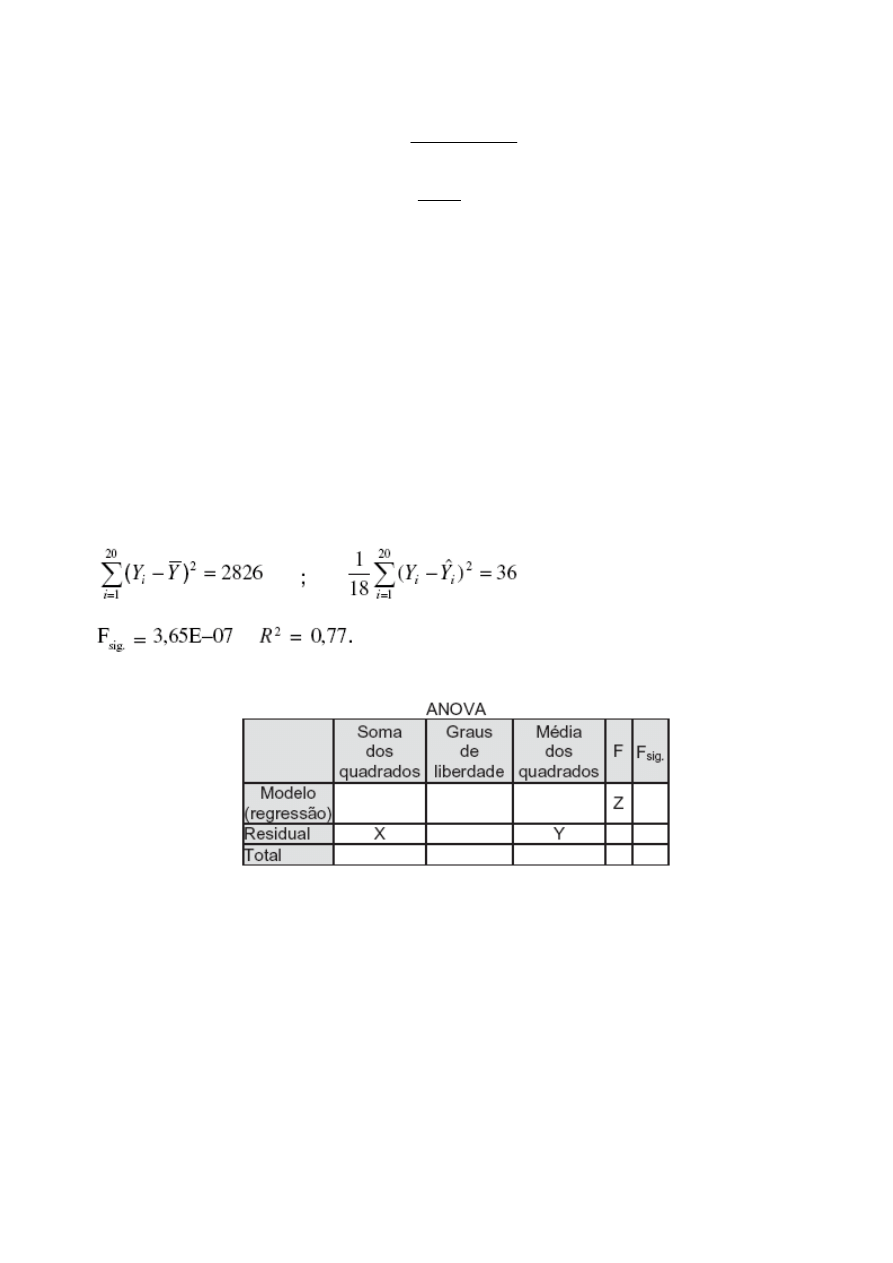
8. TCE RO 2005 [CESGRANRIO]
Avaliações de terrenos baseiam-se, geralmente, em modelos de regressão
linear nos quais o preço de venda é uma função de algumas variáveis tais
como o tamanho do terreno, suas condições e localização. Uma amostra de
terrenos comercializados no último mês coletou dados sobre o preço da venda,
em R$ 1 000,00, o tamanho do terreno, em m2, e a distância ao centro da
cidade, em km. Primeiramente obteve-se o modelo com apenas a variável
tamanho do terreno, X
1
, como explicativa do preço de venda. Os principais
quantitativos relativos a esse modelo foram calculados como:
Considerando o quadro acima, os valores de X, Y e Z, respectivamente, são:
(A) 2826, 121 e 3,65E-07
(B) 2178, 121 e 0,77
(C) 2178, 36 e 0,77
(D) 648, 36 e 60,5
(E) 32,4, 18 e 34,1
RACIOCÍNIO LÓGICO QUANTITATIVO PARA AFRFB
PROFESSOR: GUILHERME NEVES
Prof. Guilherme Neves www.pontodosconcursos.com.br
36
Resolução.
O quadrado médio dos resíduos é igual a 36 (dado no enunciado).
36
18
Re
Re
=
=
siduos
SQ
siduos
QM
=
×
=
36
18
Re siduos
SQ
648
Logo:
648
=
X
Com isso já podemos marcar a letra D.
O quadrado médio dos resíduos é 36 (dado no enunciado). Portanto, Y = 36.
A soma de quadrados total é de 2826 (dado enunciado). Portanto, a soma de
quadrados da regressão é:
siduos
SQ
SQTotal
gressao
SQ
Re
Re
−
=
=
−
=
648
2826
Re gressao
SQ
2178
A estatística F fica:
=
=
=
=
36
2178
36
1
/
Re
Re
Re
_
gressao
SQ
siduos
QM
gressao
QM
teste
F
60,5
Gabarito: D
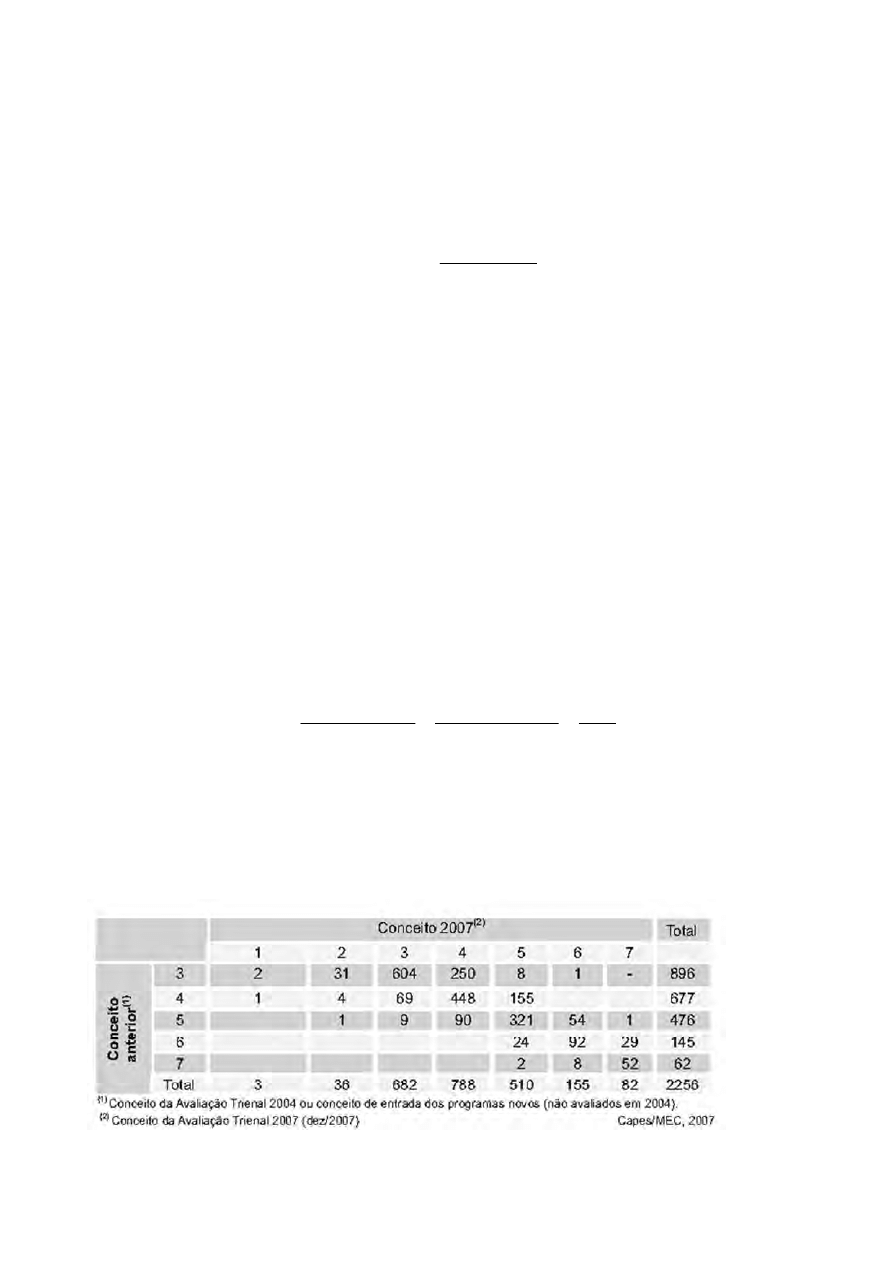
9. CAPES 2008 [CESGRANRIO]

RACIOCÍNIO LÓGICO QUANTITATIVO PARA AFRFB
PROFESSOR: GUILHERME NEVES
Prof. Guilherme Neves www.pontodosconcursos.com.br
37
O Coeficiente de Correlação Linear de Pearson entre os desempenhos de
determinados alunos em duas avaliações nacionais é igual a 0,844. Nesse
caso, conclui-se que a proporção da variabilidade nos resultados de uma das
avaliações explicada pela relação linear entre elas é
(A) 15,6%
(B) 39,4%
(C) 71,2%
(D) 84,4%
(E) 91,8%
Resolução.
O coeficiente de determinação é o quadrado do coeficiente de correlação.
=
=
2
2
844
,
0
r
0,712
Gabarito: C
10. PETROBRAS 2008 [CESGRANRIO]
Um modelo de regressão linear simples de Y em X, com uma variável
explicativa e o termo constante, foi estimado com 32 observações, gerando um
r
2
de 0,25. No teste de validade do modelo, o F-calculado ou F-observado é
igual a
(A) 10
(B) 11
(C) 12
(D) 13
(E) 14
Resolução.
SQTotal
gressao
SQ
r
Re
2
=

RACIOCÍNIO LÓGICO QUANTITATIVO PARA AFRFB
PROFESSOR: GUILHERME NEVES
Prof. Guilherme Neves www.pontodosconcursos.com.br
38
SQTotal
gressao
SQ Re
25
,
0
=
25
,
0
Re
×
= SQtotal
gressao
SQ
Lembrando que:
siduos
SQ
gressao
SQ
SQTotal
Re
Re
+
=
Logo:
SQTotal
siduos
SQ
×
=
75
,
0
Re
A estatística F fica:
10
30
/
75
,
0
25
,
0
)
2
32
/(
Re
1
/
Re
Re
Re
_
=
×
×
=
−
=
=
SQTotal
SQtotal
siduos
SQ
gressao
SQ
siduos
QM
gressao
QM
teste
F
Gabarito: A
11. BNDES 2008/2 [CESGRANRIO – questão adaptada]
Um experimento foi realizado com o objetivo de estimar o preço de uma ação,
dado o seu valor patrimonial, ambos em reais.
Uma amostra de ações negociadas recentemente forneceu dados sobre o preço
e o valor patrimonial por ação. Aplicou-se o modelo de regressão linear simples
ε
β
α
+
+
=
X
Y
. Alguns resultados da tabela da análise da variância, obtida a
partir dos dados dessa amostra, estão apresentados a seguir.
Julgue os itens abaixo:
I – O coeficiente de determinação mostra que o modelo proposto explica
aproximadamente 63% da variabilidade total.
II – O valor da estatística Fcalculado é 100, e a conclusão do teste é que a
variável valor patrimonial é significativa, isto é, deve-se rejeitar a hipótese
nula
0
:
0
=
β
H
.

RACIOCÍNIO LÓGICO QUANTITATIVO PARA AFRFB
PROFESSOR: GUILHERME NEVES
Prof. Guilherme Neves www.pontodosconcursos.com.br
39
Resolução.
Primeiro item.
1
/
Re
Re
gressao
QM
gressao
SQ
=
000
.
56
Re
=
gressao
SQ
O coeficiente de determinação fica:
480
.
88
000
.
56
Re
2
=
=
SQTotal
gressao
SQ
r
= 0,63
Portanto, 63% da variação é explicada pela reta de regressão. Ou seja, o
modelo de regressão explica 63% da variabilidade total. O primeiro item está
certo.
Segundo item.
gressao
SQ
SQTotal
siduos
SQ
Re
Re
−
=
480
.
32
000
.
56
480
.
88
Re
=
−
=
siduos
SQ
A estatística F fica:
=
=
−
=
=
58
/
480
.
32
000
.
56
)
2
60
/(
Re
1
/
Re
Re
Re
_
siduos
SQ
gressao
SQ
siduos
QM
gressao
QM
teste
F
100
O segundo item também está certo.
Gabarito: Certo, certo
Embora esta informação não tenha sido necessária para resolver a questão,
vamos falar sobre o Fsig, que aparece na tabela.
O valor de Fsig nada mais é que o valor descritivo do teste de hipóteses para
0
=
β
. Ou seja, é a probabilidade de uma variável com distribuição F, com 1
grau de liberdade no numerador e 58 no denominador, assumir valores
maiores que 100 (que é a estatística teste).
12. SEFAZ SP 2009 [ESAF]
Uma amostra aleatória simples (X
1
, Y
1
), (X
2
, Y
2
), ..., (X
n
, Y
n
) de duas variáveis
aleatórias X e Y forneceu as seguintes quantidades:

RACIOCÍNIO LÓGICO QUANTITATIVO PARA AFRFB
PROFESSOR: GUILHERME NEVES
Prof. Guilherme Neves www.pontodosconcursos.com.br
40
(
)
∑
=
=
−
n
i
i
X
X
1
2
414
(
)
∑
=
=
−
n
i
i
Y
Y
1
2
359
(
)
∑
=
=
×
−
n
i
i
i
Y
X
X
1
345
Calcule o valor mais próximo do coeficiente de determinação da regressão
linear de Y em X.
a) 0,88
b) 0,92
c) 0,85
d) 0,80
e) 0,83
Resolução:
No caso do modelo usual de regressão linear, o coeficiente de determinação é
igual ao quadrado do coeficiente de correlação.
Aqui a questão explora outra igualdade envolvendo somatórios.
O numerador da fórmula do coeficiente de correlação é:
(
) (
)
[
]
∑
=
−
×
−
n
i
i
i
Y
Y
X
X
1
Fazendo a multiplicação, ficamos com:
(
)
(
)
[
]
∑
=
×
−
−
×
−
n
i
i
i
i
Y
X
X
Y
X
X
1
Separando o somatório da diferença em diferença de somatórios:
=
(
)
[
]
(
)
[
]
∑
∑
=
=
×
−
−
×
−
n
i
i
n
i
i
i
Y
X
X
Y
X
X
1
1
A média de Y é constante e pode “sair” do somatório:
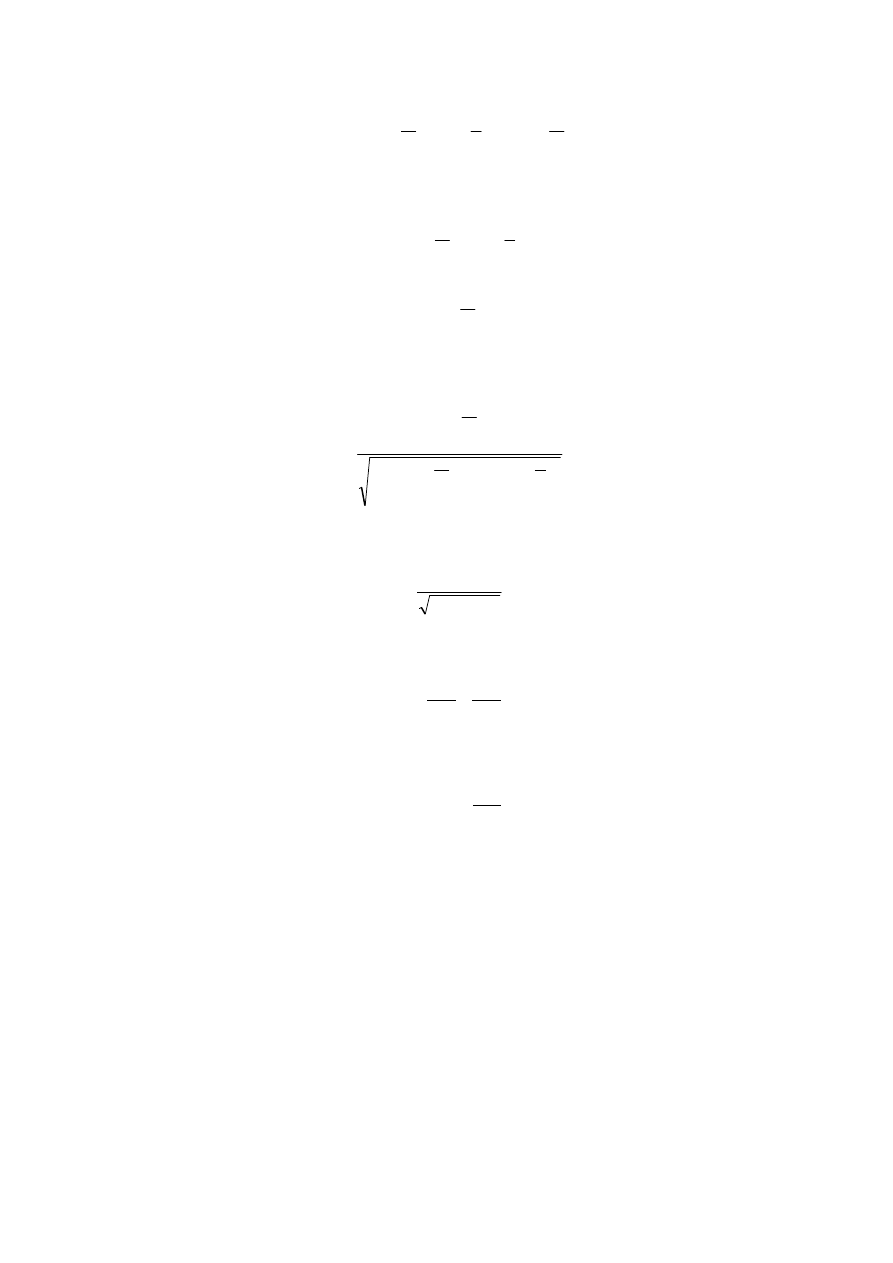
RACIOCÍNIO LÓGICO QUANTITATIVO PARA AFRFB
PROFESSOR: GUILHERME NEVES
Prof. Guilherme Neves www.pontodosconcursos.com.br
41
=
(
)
[
]
(
)
[
]
∑
∑
=
=
−
−
×
−
n
i
i
n
i
i
i
X
X
Y
Y
X
X
1
1
A soma dos desvios em relação à média de X é igual a zero:
=
(
)
[
]
0
1
×
−
×
−
∑
=
Y
Y
X
X
n
i
i
i
=
(
)
[
]
∑
=
×
−
n
i
i
i
Y
X
X
1
Logo, outra fórmula para o coeficiente de correlação seria:
(
)
( )
[
]
(
)
(
)
∑
∑
∑
=
=
=
−
×
−
×
−
=
n
i
n
i
i
i
n
i
i
i
Y
Y
X
X
Y
X
X
r
1
1
2
2
1
E, para esta fórmula, o enunciado já deu todas as contas prontas:
359
414
345
×
=
r
Elevando o coeficiente ao quadrado:
359
345
414
345
2
×
=
r
Fazendo a primeira divisão, temos:
359
345
83
,
0
2
×
=
r
O “0,83” está sendo multiplicado por um número menor que 1. Toda vez que
multiplicamos um número por outro que seja menor que 1, o número original
diminui. Logo, a resposta procurada será menor que 0,83. A única opção é a
letra D.
Gabarito: D
Wyszukiwarka
Podobne podstrony:
Aula 15 Parte 02
Aula 07 Parte 02
Aula 05 Parte 02
Aula 09 Parte 02
Aula 14 Parte 02
Aula 10 Parte 02
Aula 07 Parte 02
Aula 06 Parte 02
Aula 12 Parte 02
Aula 08 Parte 02
Aula 15 Parte 01
Aula 07 Parte 02
Aula 05 Parte 02
Aula 08 Parte 02
Aula 07 Parte 02
Aula 09 Parte 02
Aula 10 Parte 02
więcej podobnych podstron