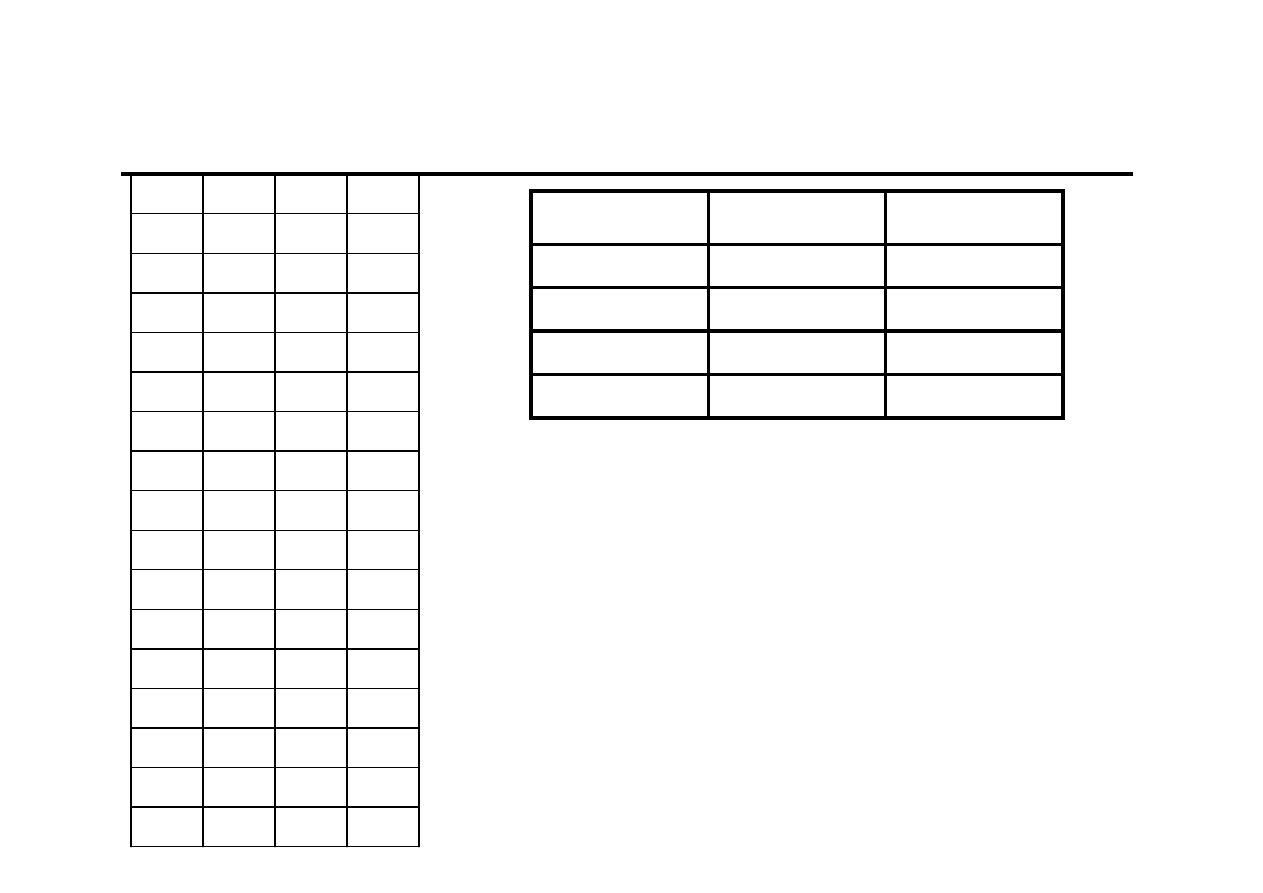
Prognozowanie i symulacje

Ramowy plan wykładu

1. Wprowadzenie w przedmiot

2. Trafność, dopuszczalność i błąd prognozy

3. Prognozowanie na podstawie szeregów

czasowych

4. Prognozowanie na podstawie modelu

ekonometrycznego

5. Heurystyczne modele prognostyczne

6. Symulacje

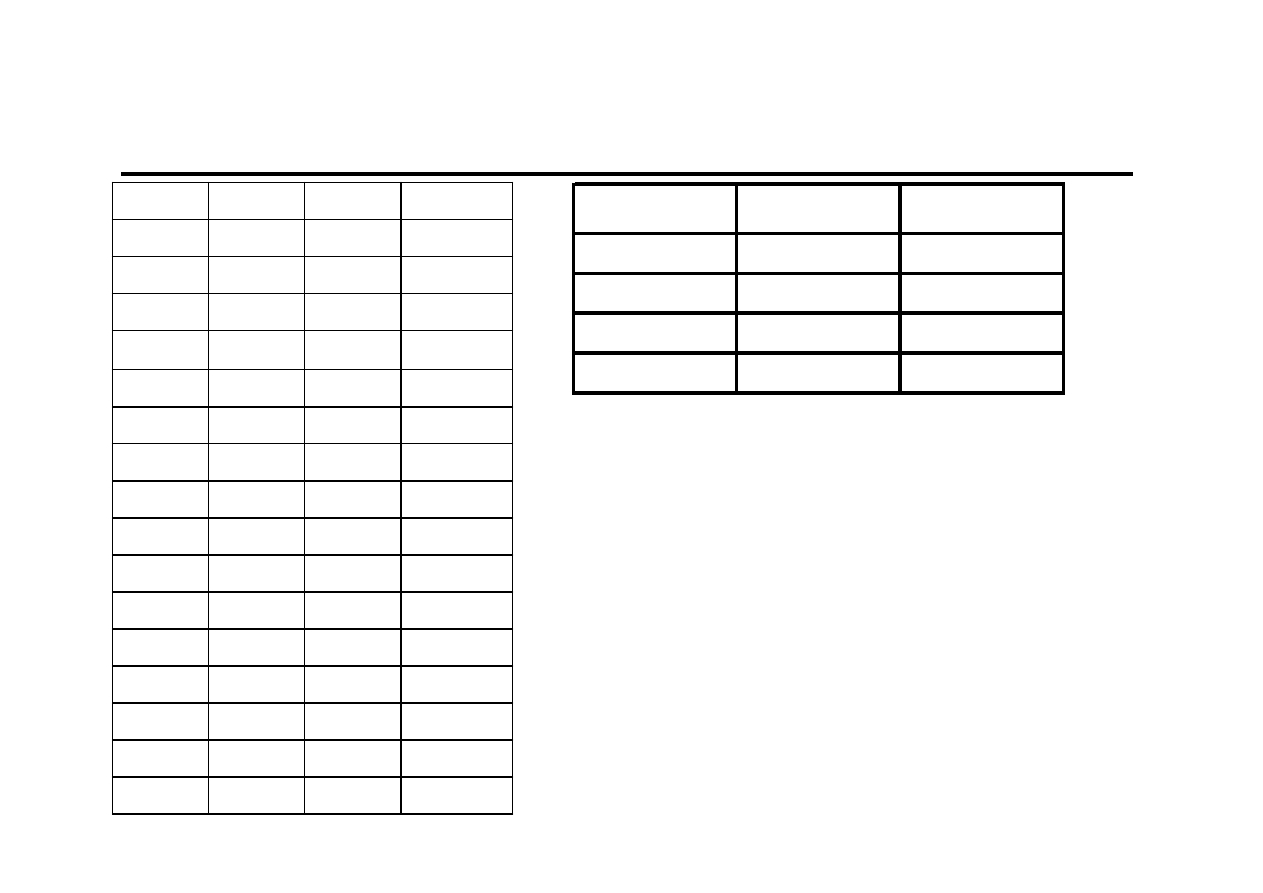
Wybrana literatura

1. Prognozowanie gospodarcze. Metody i zastosowanie,

red. M. Cieślak, PWN, Warszawa 2001

2. Zeliaś A., Pawełek B., Wanat S., Prognozowanie

ekonomiczne. Teoria, przykłady, zadania, PWN,
Warszawa 2003

3. Gajda J., Prognozowanie i symulacja a decyzje

gospodarcze, Wyd. C.H. Beck, Warszawa 2001

4. Prognozowanie gospodarcze, red. E. Nowak, AW Placet,

Warszawa 1998

5. Prognozowanie i symulacja, red. W. Milo, Wyd. UŁ, Łódź

2002

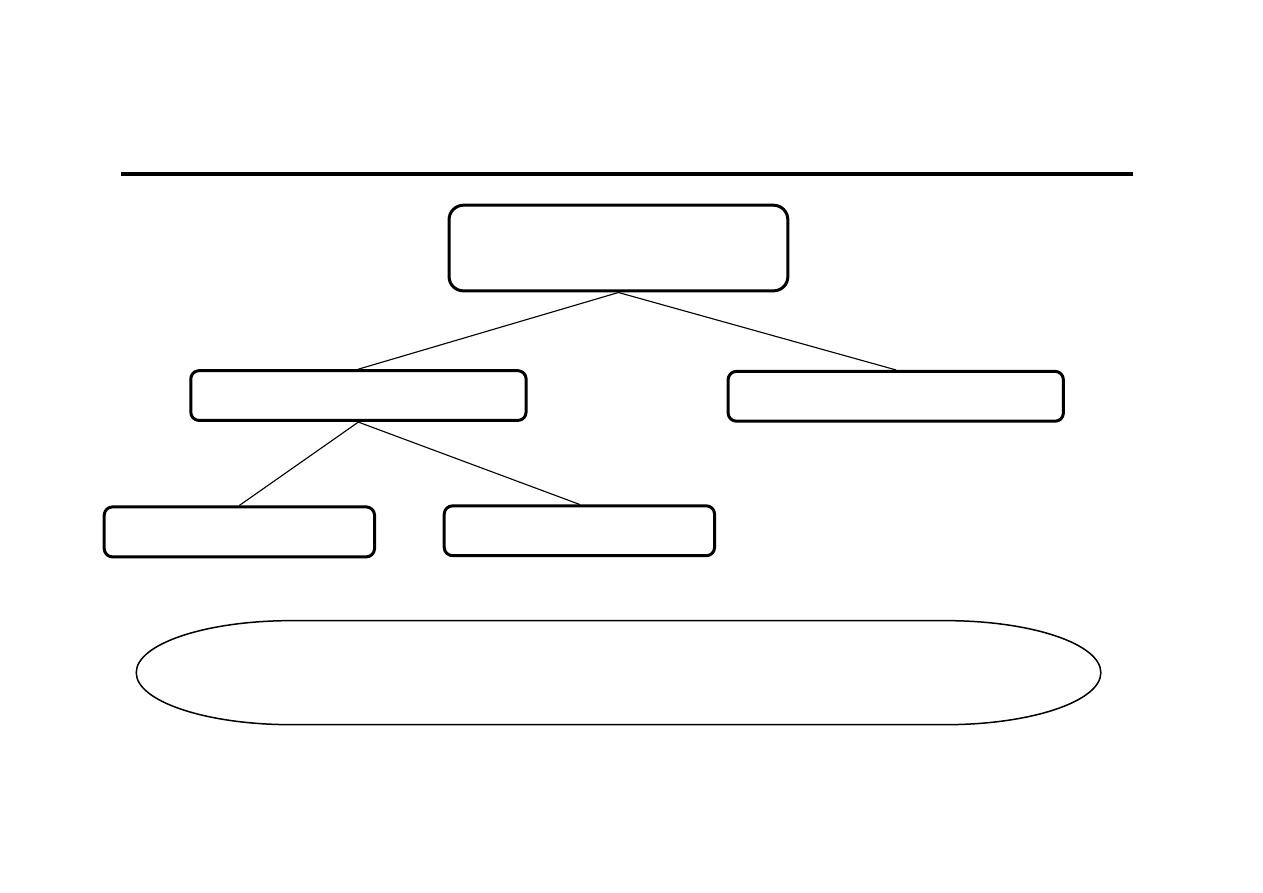
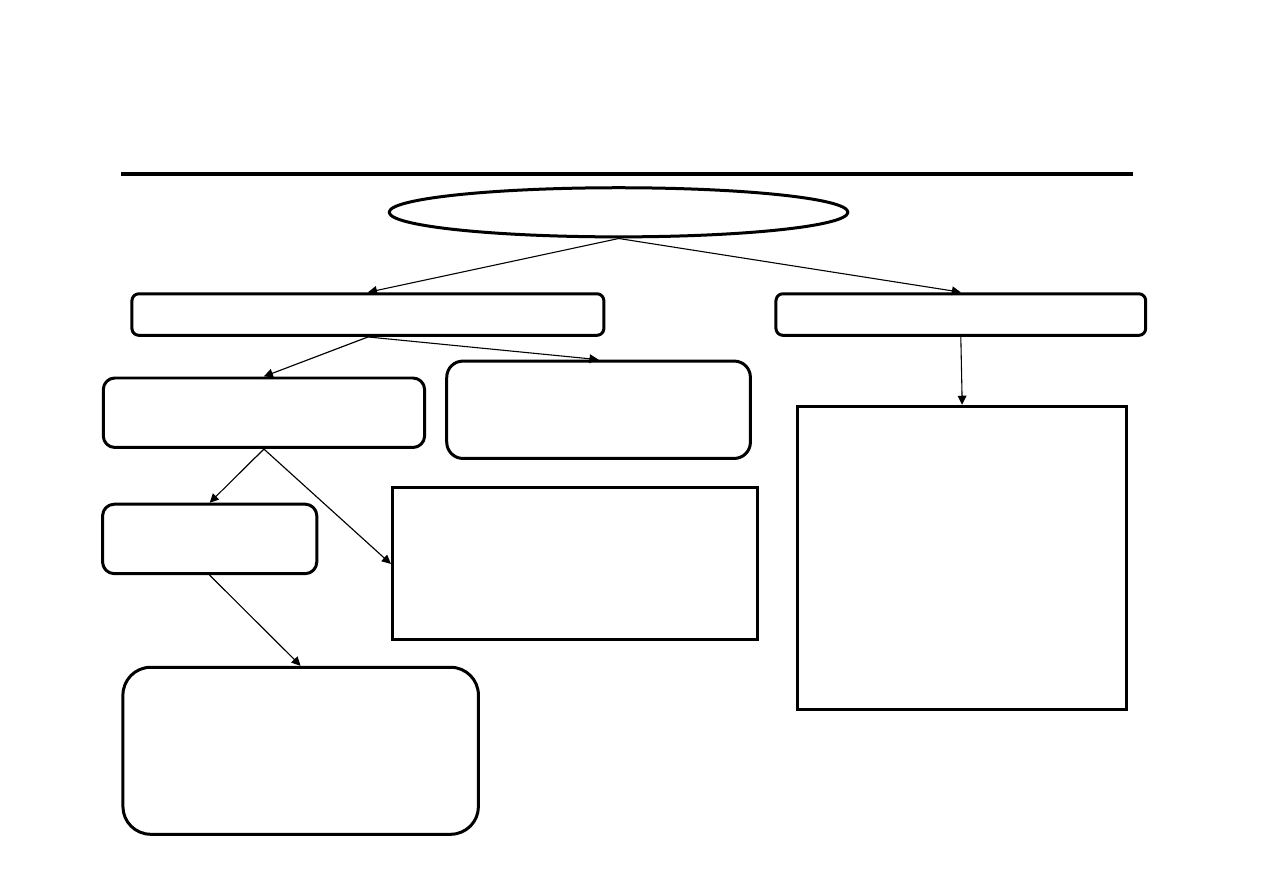
Przewidywanie przyszłości

Przewidywanie

przyszłości

Nieracjonalne

Racjonalne

Zdroworozsądkowe

Naukowe

PROGNOZOWANIE to przewidywanie przyszłości w sposób racjonalny
z wykorzystaniem metod naukowych

PREDYKCJA to prognozowanie na podstawie modelu ekonometrycznego

Prognoza jako wynik prognozowania

PROGNOZA to sąd sformułowany z wykorzystaniem dorobku
nauki odnoszący się do określonej przyszłości, weryfikowalny
empirycznie, niepewny (ale akceptowalny)

Etapy prognozowania:

I.

Sformułowanie zadania prognostycznego

II.

Podanie przesłanek prognostycznych

III. Wybór metody prognozowania

IV. Ocena dokładności lub dopuszczalności prognozy

V. Weryfikacja prognozy

Wyróżnia się trzy podstawowe funkcje prognoz:

I.

PREPARACYJNA (do podejmowania decyzji, stwarza

dodatkowe przesłanki do podejmowania racjonalnych
decyzji)

II.

AKTYWIZUJĄCA (pobudzenie do działań

sprzyjających realizacji korzystnej prognozy,
przeciwdziałających prognozie niekorzystnej)

III. INFORMACYJNA (dostarcza informacji o badanym

zjawisku)

Funkcje prognoz

Metoda prognozowania

METODA PROGNOZOWANIA to sposób przetworzenia danych
z przeszłości wraz ze sposobem przejścia od przetworzonych
danych do prognozy.

Istnieją więc dwie fazy:

• faza diagnozowania przeszłości - odbywa się przez budowę
modelu formalnego (model ekonometryczny) lub myślowego
(w umyśle eksperta)

• faza określania przyszłości – polega na zastosowaniu
odpowiedniej reguły prognozy

Reguły prognozy

• reguła podstawowa – prognoza postawiona na podstawie modelu,
przy założeniu, że będzie on aktualny w prognozowanym okresie

• reguła podstawowe z poprawką – prognoza postawiona na podstawie
modelu z poprawką uwzględniającą, że ostatnio zaobserwowane
odchylenia od modelu utrzymają się w przyszłości

• reguła największego prawdopodobieństwa (dla zmiennych losowych,
których rozkład prawdopodobieństwa jest znany) – prognozą jest
wartość zmiennej, której odpowiada największe prawdopodobieństwo
dla zmiennych skokowych lub maksymalna wartość funkcji gęstości
prawdopodobieństwa dla zmiennych ciągłych

• reguła minimalnej straty – przyjmuje się, że wielkość straty jest funkcją
błędu prognozy i poszukuje się minimum tej funkcji. Prognozą jest
wartość dla której ta funkcja przyjmuje minimum.

Metody prognozowania

Metody prognozowania

Metody niematematyczne

Metody matematyczno-statystyczne

Metody oparte na modelach

ekonometrycznych

Metody oparte na

modelach

deterministycznych

•Metody ankietowe

•Metody intuicyjne

•Metody kolejnych przybliżeń

•Metoda ekspertyz

•Metoda delficka

•Metoda refleksji

•Metody analogowe

•Inne

Modele wielorównaniowe:

•prosty

•rekurencyjny

•o równaniach współzależnych

Modele

jednorównaniowe

•Klasyczne modele trendu

•Adaptacyjne modele trendu

•Modele przyczynowo-opisowe

•Modele autoregresyjne

Metody prognozowania

Prognozowanie na podstawie modelu matematyczno-statystycznego
to prognozowanie ilościowe

Prognozowanie na podstawie modeli niematematycznych, to zwykle
prognozowanie jakościowe

Prognozy ilościowe dzielimy na:

• punktowe, gdzie dla zmiennej prognozowanej wyznacza się jedną
wartość dla T>n,

• przedziałowe, w których wyznacza się przedział, w którym znajdzie
się rzeczywista wartość zmiennej prognozowanej w prognozowanym
okresie T>n.

Prognozowanie

Bazą danych do modelu zmiennej prognozowanej
(1) y

t

=F(t,

ε

t

)

lub (2) y

t

=F(x

1t

, x

2t

,...,x

kt

,

ε

t

)

jest szereg czasowy w postaci:

y

n

n

...

...

y

2

2

y

1

1

y

t

t

x

kn

...

x

2n

x

1n

y

n

n

...

...

...

...

...

...

x

k2

...

x

22

x

12

y

2

2

x

k1

...

x

21

x

11

y

1

1

x

kt

...

x

2t

x

1t

y

t

t

Prognozy zmiennej prognozowanej y

t

wyznaczamy na okres T > n

Prognozę na okres T będziemy oznaczać Y

T

*

Prognoza krótkookresowa to prognoza na taki przedział czasowy, w którym
zakłada się istnienie tylko zmian ilościowych. Prognozy takie wyznacza się
przez ekstrapolację dotychczasowych związków (na podstawie modeli
ekonometrycznych lub trendów)

Horyzont czasowy prognoz

Prognoza średniookresowa dotyczy okresów czasu, w których oczekuje się
zmian ilościowych oraz ewentualnie niewielkich zmian jakościowych.
Prognoza musi uwzględniać oba typy zmian, musi przynajmniej
umiarkowanie odchodzić od ekstrapolacji

Prognoza długookresowa dotyczy przedziału czasu, w którym mogą
występować zmiany ilościowe oraz znaczące zmiany jakościowe

Modele ilościowe

Prognozę na okres T > n można postawić wykorzystując model F (1)

lub(2) jeśli spełnione są następujące założenia:

1. funkcja F wyraża pewną prawidłowość ekonomiczną, która jest

stabilna w czasie (nie spodziewamy się żadnych zmian
jakościowych),

2. składnik losowy

ε

t

jest stabilny,

3. w przypadku modelu ekonometrycznego znane są wartości

zmiennych objaśniających w okresie T > n, czyli znane są wartości
prognoz X

1T

*,X

2T

*,...,X

kT

*,

4. dopuszczalna jest ekstrapolacja modelu poza próbę, czyli poza

obszar zmienności zmiennych objaśniających, jak i zmiennej
(zmiennych) objaśnianej.

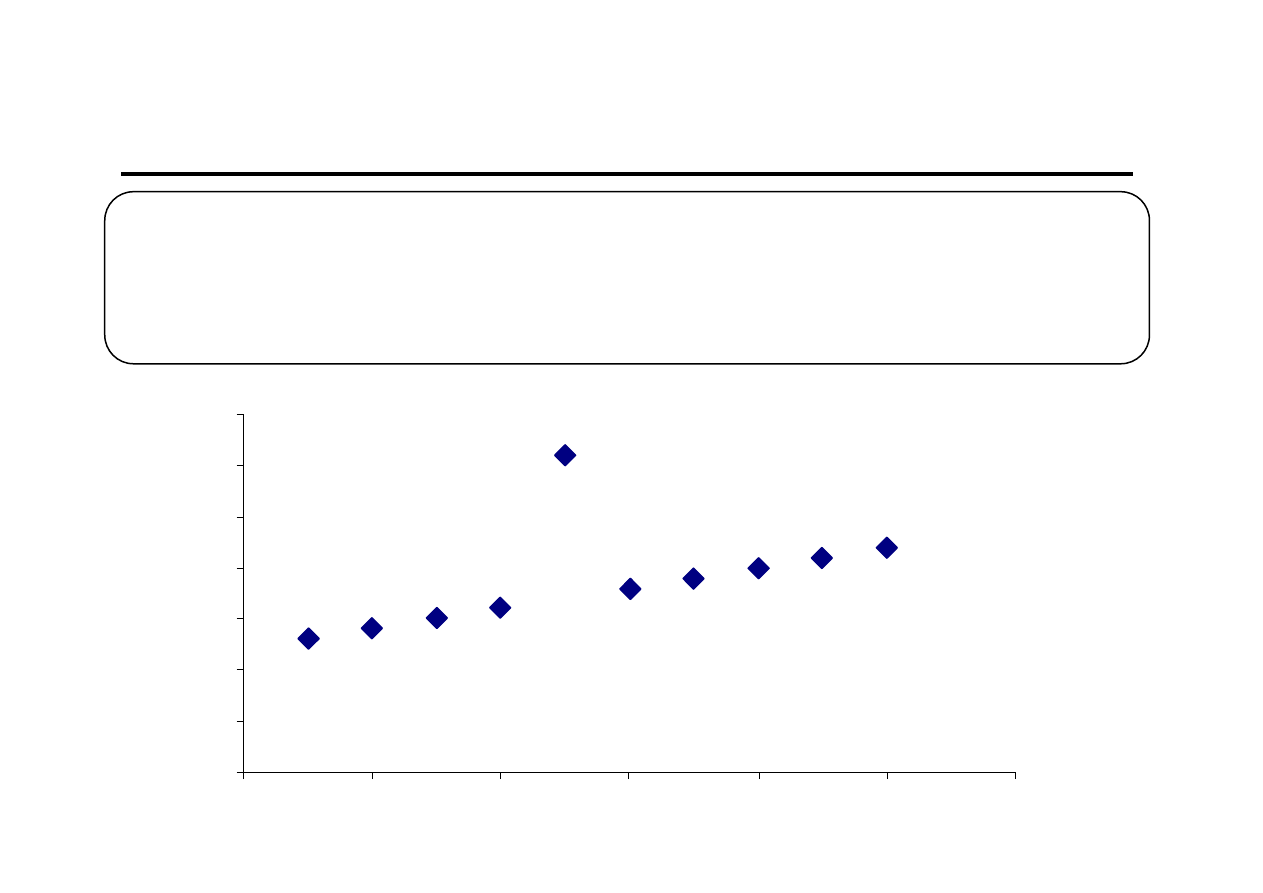
Analiza danych w szeregu czasowym

Analiza danych polega na:

1. Wyodrębnieniu obserwacji odstających

2. Stwierdzeniu braku lub istnienia trendu

0

5

10

15

20

25

30

35

0

2

4

6

8

10

12

A

Y

t

Obserwacje odstające

Po wyodrębnieniu obserwacji odstających należy ustalić:

1. Czy dana obserwacja pojawiła się w skutek błędu rejestracji danych,

2. Czy obserwacja pojawiła się w skutek jednokrotnego zjawiska

zewnętrznego wpływu (np. realizacja pewnego dużego jednokrotnego
zamówienia, o którym wiemy, że nie nastąpi już w przyszłości),

3. Czy obserwacja pojawiła się jako normalne wahanie losowe

(przypadkowe) w próbie.

W przypadku 1. oraz 2. obserwację A można pominąć, a brakującą wartość
uzupełnić średnią arytmetyczną z obserwacji poprzedniej i następnej. W
przypadku 3. obserwacja powinna pozostać w bazie danych
statystycznych.

Błąd prognozy

Po wyborze modelu prognostycznego F można wyznaczyć prognozy dla T>n:

(1) Y

T

* =F(T)

lub (2) Y

T

*=F(x

1T

*, x

2T

*,...,x

kT

*)

wraz z prognozą Y

T

* należy wyznaczyć miernik dokładności prognozy

Przy wyborze modelu prognostycznego należy dążyć do osiągnięcia
zadowalającego poziomu miernika dokładności

Wyróżniamy dwa typy mierników:

1. błąd ex post

2. błąd ex ante

Błąd prognozy można zapisać jako

B

t

= y

t

– Y

t

*

gdzie Y

t

* to wartość prognozy zmiennej Y na okres t, wyznaczona na

podstawie modelu F, a y

t

to rzeczywista wartość zmiennej prognozowanej w

okresie t.

Dopuszczalność prognozy: błąd ex ante

Błąd ex ante wyznacza się dla modeli liniowych, których parametry
oszacowano Metodą Najmniejszych Kwadratów (MNK). Niech model
ma postać:

dla t = 1, 2, 3n

.

to po oszacowaniu MNK jego parametrów model teoretyczny
przyjmuje postać:

dla t = 1, 2, 3n.

w zapisie macierzowym:

t

kt

k

t

t

t

X

X

X

y

ε

α

α

α

α

+

+

+

+

+

=

...

2

2

1

1

0

kt

k

t

2

2

t

1

1

0

t

X

a

...

X

a

X

a

a

Yˆ

+

+

+

+

=

Xa

Yˆ =

Dopuszczalność prognozy (2)

Gdzie w zapisie macierzowym:

oraz

























=

























=

kn

n

n

k

k

n

X

X

X

X

X

X

X

X

X

X

y

y

y

Y

...

1

...

...

...

...

...

1

...

1

,

...

2

1

2

22

12

1

21

11

2

1

Xa

Yˆ =

Y

X

)

X

X

(

a

...

a

a

a

T

1

T

k

1

0

−

=

























=

Dopuszczalność prognozy (3)

Prognozę na okres T > n można wyznaczyć ze wzoru:

gdzie: X*

1T,

X*

2T

,…X*

kT

to prognozy zmiennych objaśniających X

1

, X

2

,…X

k

w okresie T>n co w zapisie macierzowym:

gdzie:

kT

k

T

2

2

T

1

1

0

T

*

X

...

*

X

*

X

*

Y

α

α

α

α

+

+

+

+

=

































=

kT

T

2

T

1

T

*

X

...

*

X

*

X

1

*

X

a

)

*

X

(

*

Y

T

T

T

=

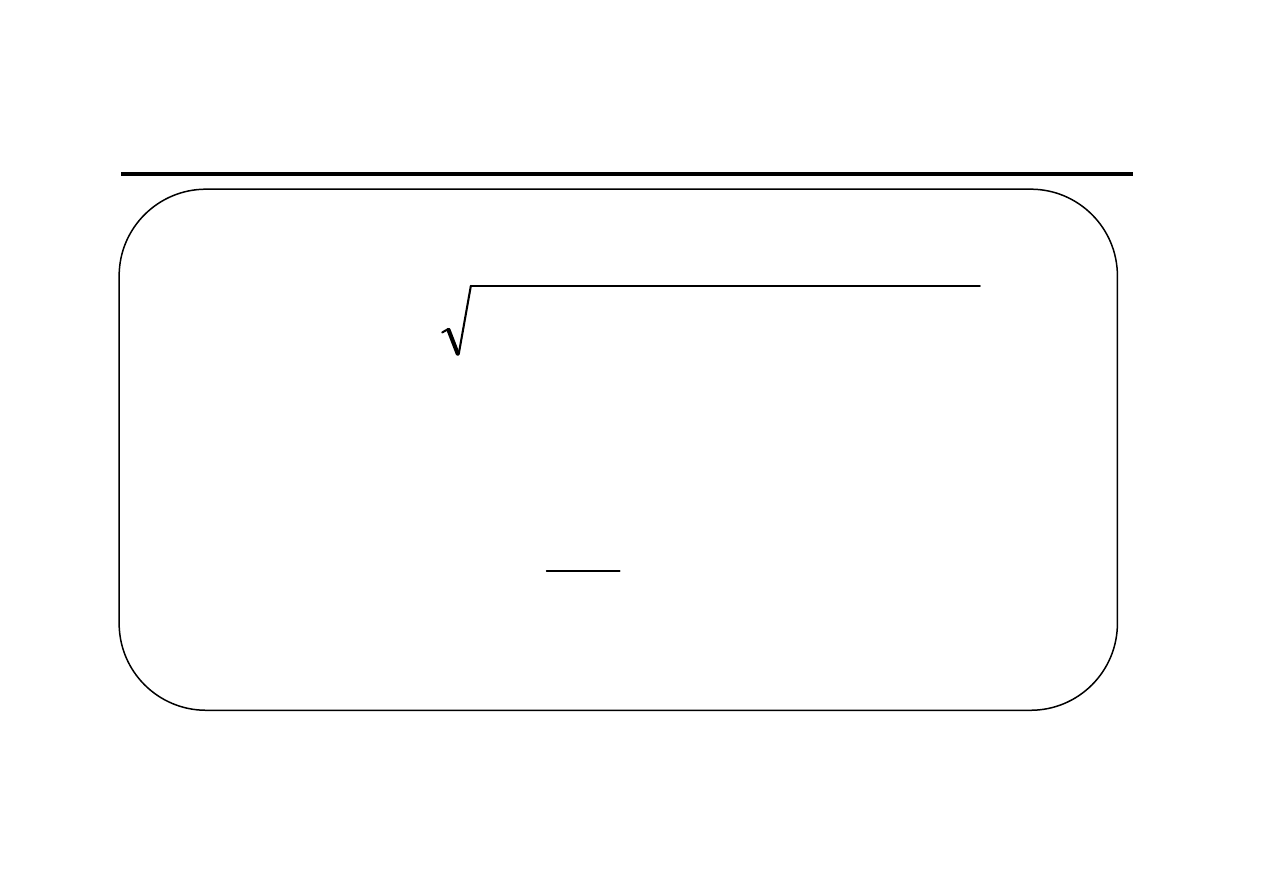
Błąd ex ante to odchylenie standardowe błędu B

T

prognozy Y*

T

na

okres T. Błąd ex ante oznacza się przez V*

T

:

gdzie

S

e

to odchylenie standardowe reszt modelu liniowego.

Względny błąd ex ante prognozy

Y*

T

:

który informuje jaką część prognozy stanowi błąd ex ante

1

*

)

(

)

*

(

*

1

+

=

−

T

T

T

T

e

T

X

X

X

X

S

V

%),

100

(

*

Y

*

V

*

W

T

T

T

⋅

=

Błąd ex ante

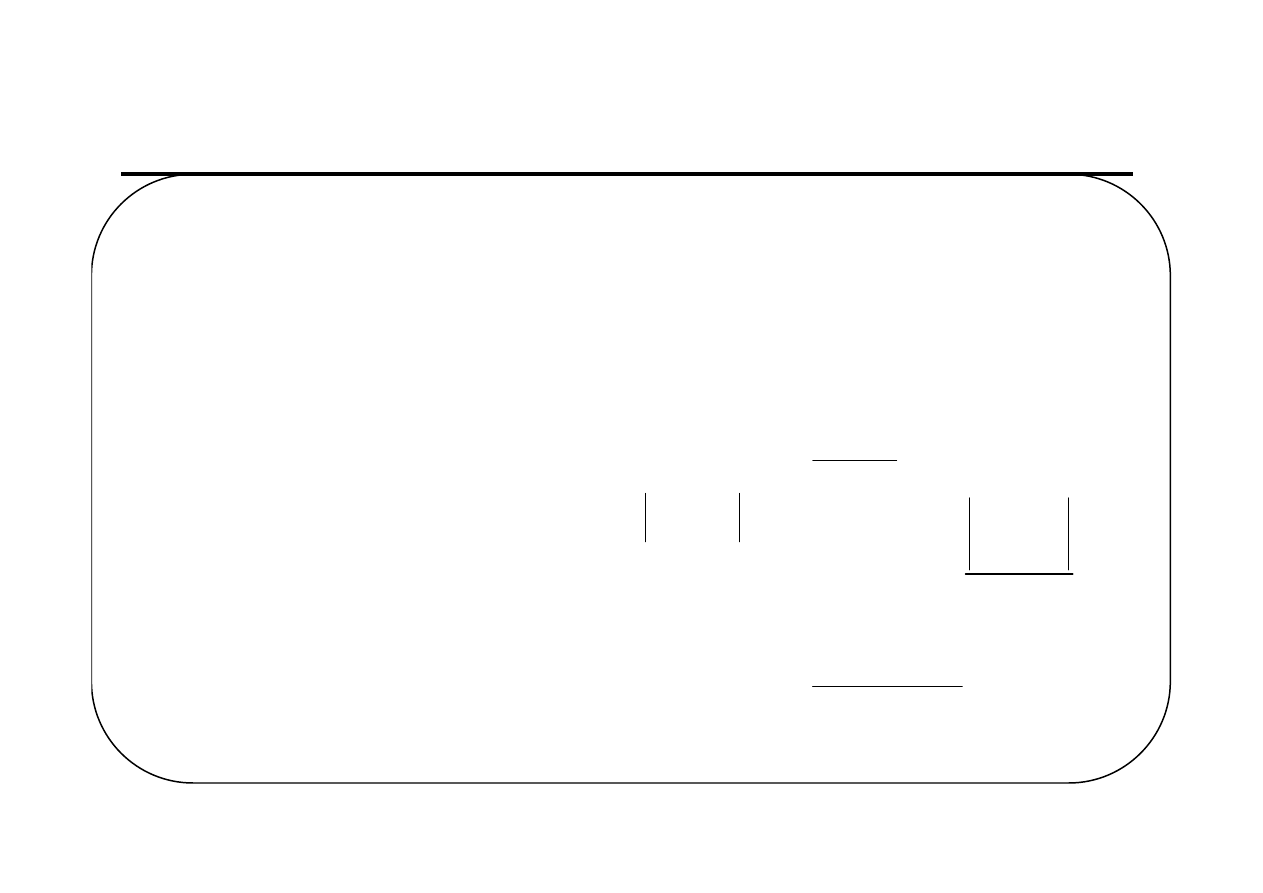
Trafność prognozy – błąd ex post (1)

Błąd ex post może być wyznaczony dla wszystkich modeli ilościowych.
Jeśli t będzie okresem, na który postawiono prognozę Y*

t

i okres ten już

minął, to znana jest wartość rzeczywista Y

t

zmiennej prognozowanej.

Taką prognozę Y*

t

nazywać będziemy prognozą wygasłą. Dla prognoz

wygasłych można wyznaczyć błąd ex post.

Rozróżniamy:

1. względny błąd prognozy (procentowy):

2. absolutny błąd prognozy:

3. względny absolutny błąd prognozy (procentowy):

4. kwadratowy błąd prognozy:

5. względny kwadratowy błąd prognozy:

%)

100

(

*

⋅

−

=

t

t

t

y

y

y

t

PE

*

t

t

t

y

y −

=

AE

%)

100

(

*

⋅

−

=

t

y

t

y

t

y

t

APE

2

*

)

(

t

t

t

y

y −

=

SE

t

t

t

t

y

y

y

2

*

)

(

−

=

PSE

Trafność prognozy – błąd ex post (2)

Do oceny trafności prognoz wygasłych (a a więc dopasowania modelu
prognostycznego F do danych o zmiennej prognozowanej Y można
wykorzystać następujące błędy:

1. średni absolutny błąd ex post prognoz wygasłych

2. średni względny absolutny błąd ex post prognoz wygasłych

3. średni błąd ex post prognoz wygasłych

4. średni względny błąd ex post prognoz wygasłych

5. średni kwadratowy błąd ex post prognoz wygasłych

6. pierwiastek średniego kwadratowego błędu ex post prognoz wygasłych

7. współczynnik Theila

Do badania aktualności modelu prognostycznego –

możemy użyć współczynnika Janusowego

Oznaczmy przez

• M

zbiór numerów

okresów/momentów, w których weryfikujemy
trafność prognoz wygasłych wyznaczonych za
pomocą modelu

• card M – liczebność zbioru M.

}

,...,

2

,

1

{

n

∈

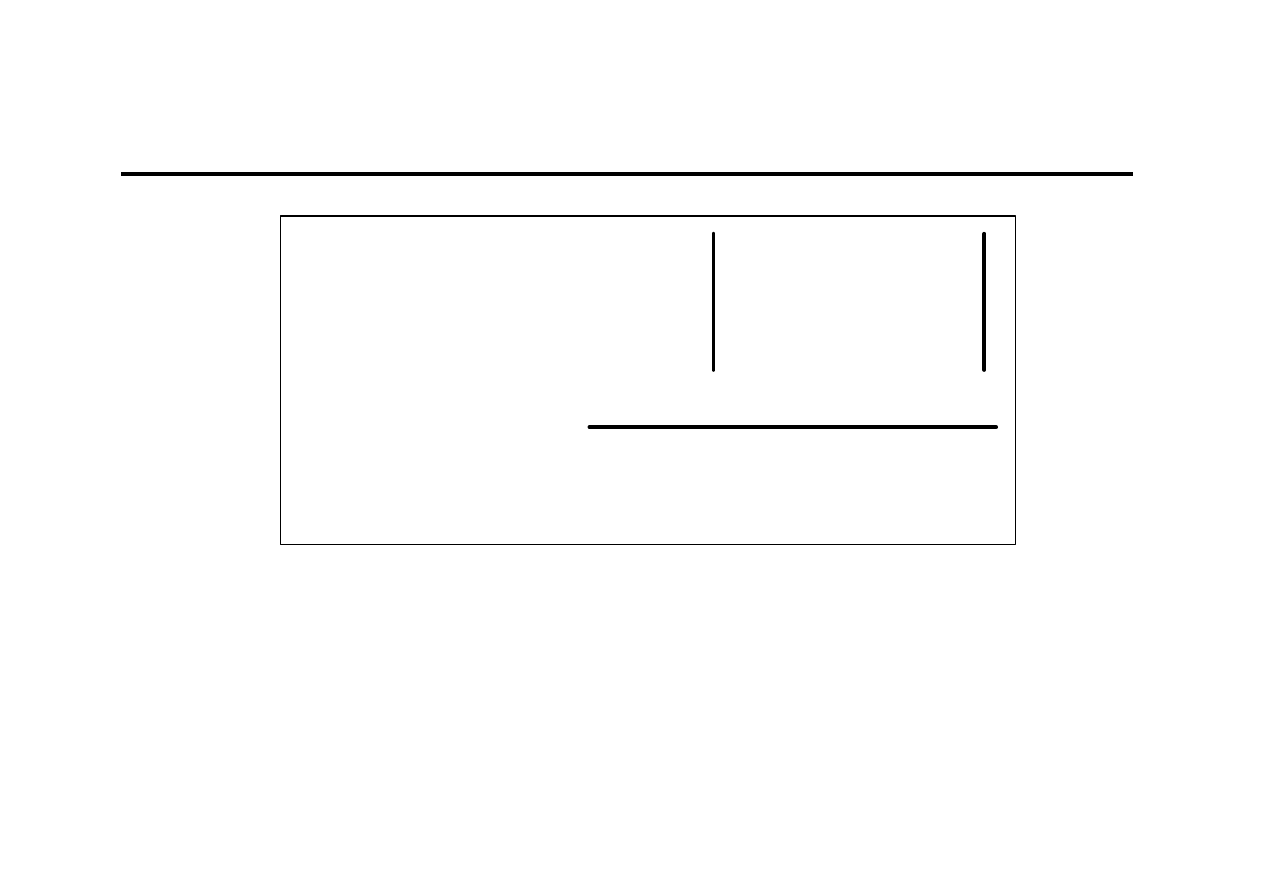
Średni absolutny błąd ex post prognoz

wygasłych MAE

M

card

Y

y

MAE

t

t

M

t

*

∑

∈

−

=

Średni względny absolutny błąd ex post

prognoz wygasłych MAPE(procentowy)

%)

100

(

M

t

*

⋅

−

=

∑

∈

M

card

y

Y

y

MAPE

t

t

t

Średni błąd ex post prognoz wygasłych ME

M

card

Y

y

ME

t

t

)

(

M

t

*

∑

∈

−

=

Średni względny błąd ex post prognoz

wygasłych MPE

M

card

y

y

y

MPE

t

t

t

M

t

*

∑

∈

−

=

Średni kwadratowy błąd ex post prognoz

wygasłych MSE

M

card

y

Y

MSE

t

t

)

(

M

t

2

*

∑

∈

−

=

Pierwiastek średniego

kwadratowego błędu ex post

prognoz wygasłych RMSE

MSE

RMSE =

Współczynnik Theila (1)

∑

∑

∈

∈

−

=

M

t

t

M

t

t

t

y

Y

y

I

2

2

*

2

)

(

2

3

2
2

2

1

2

I

I

I

I

+

+

=

Współczynnik Theila (2)

M

card

Y

Y

I

M

t

t

y

∑

∈

−

=

2

2

2

1

)

*

(

Wyraża wielkość błędu z powodu nieodgadnięcia średniej wartości zmiennej

prognozowanej (nieobciążoności prognozy).

Wartości średnie wyznaczane są dla wartości y

t

takich, że

,

%

100

ˆ

2

2

1

2

1

⋅

=

I

I

I

*

,Y

Y

M

t ∈

Współczynnik Theila (3)

M

card

y

S

S

I

M

t

t

Y

Y

∑

∈

−

=

2

2

*

2

2

)

(

Wyraża wielkość błędu z powodu nieodgadnięcia wahań zmiennej

prognozowanej (niedostatecznej elastyczności)

%

100

ˆ

2

2

2

2

2

⋅

=

I

I

I

M

card

Y

y

S

M

t

t

Y

∑

∈

−

=

2

)

(

M

card

Y

Y

S

M

t

t

Y

∑

∈

−

=

2

*

*

)

*

(

Współczynnik Theila (4)

M

card

y

r

S

S

I

M

t

t

Y

Y

Y

Y

∑

∈

−

⋅

⋅

⋅

=

2

*

,

*

2

3

)

1

(

2

Wyraża wielkość błędu z powodu nieodgadnięcia kierunku tendencji

rozwojowej zmiennej prognozowanej (niedostatecznej zgodności

prognoz z rzeczywistym kierunkiem zmian zmiennej prognozowanej)

to współczynnik korelacji pomiędzy wartościami y

t

i Y

t

* dla

%

100

ˆ

2

2

1

2

3

⋅

=

I

I

I

*

,Y

Y

r

M

t

∈

Współczynnik Janusowy

K

)

(

P

)

(

2

*

2

*

2

card

Y

y

card

Y

y

J

K

t

t

t

P

t

t

t

∑

∑

∈

∈

−

−

=

P – zbiór numerów okresów/momentów, dla których postawiono

prognozy za pomocą modelu i stały się one prognozami
wygasłymi,

card P – liczebność zbioru P,

K to zbiór numerów okresów/momentów dla których

zbudowano model i wyznaczono prognozy wygasłe,

Card K – liczebność zbioru K

Jeżeli J

2

≤ 1, to model jest nadal aktualny i może być

użyty do prognozowania na następne okresy.

}

,...,

2

,

1

{

n

∈

Prognozowanie na podstawie szeregów

czasowych

Składowe szeregu czasowego:

I.

Składowa systematyczna

II.

Składowa przypadkowa

Składowa systematyczna:

1.

Trend (tendencja rozwojowa) – długookresowa skłonność do
jednokierunkowych zmian wartości badanej zmiennej,

2.

Stały przeciętny poziom prognozowanej zmiennej – wartości oscylują
wokół stałego poziomu,

3.

Wahania cykliczne – długookresowe, powtarzające się rytmicznie w
przedziałach czasu dłuższych niż rok, wahania wartości zmiennej
wokół trendu lub stałego poziomu,

4.

Wahania sezonowe – wahania wartości zmiennej wokół trendu lub
stałego poziomu w przedziałach czasu nie przekraczających roku.

Dekompozycja szeregu czasowego

Proces wyodrębniania poszczególnych składowych szeregu czasowego

Ocena wzrokowa sporządzonego wykresu

Identyfikacja poszczególnych składowych szeregu czasowego na
podstawie wykresów szeregu czasowego

Analiza autokorelacji

Oblicza się wartości współczynników korelacji między y

t

oraz y

t-i

(dla

i=1,2,...,k), czyli współczynniki autokorelacji różnych rzędów. Bada się
statystyczną istotność tych współczynników. Jeśli współczynniki dla kilku
pierwszych rzędów są duże i statystycznie istotne, to wskazuje to na
występowanie trendu. Jeśli występuje statystycznie istotny współczynnik
autokorelacji rzędu równego liczbie faz cyklu sezonowego, to wskazuje to
na występowanie wahań sezonowych.

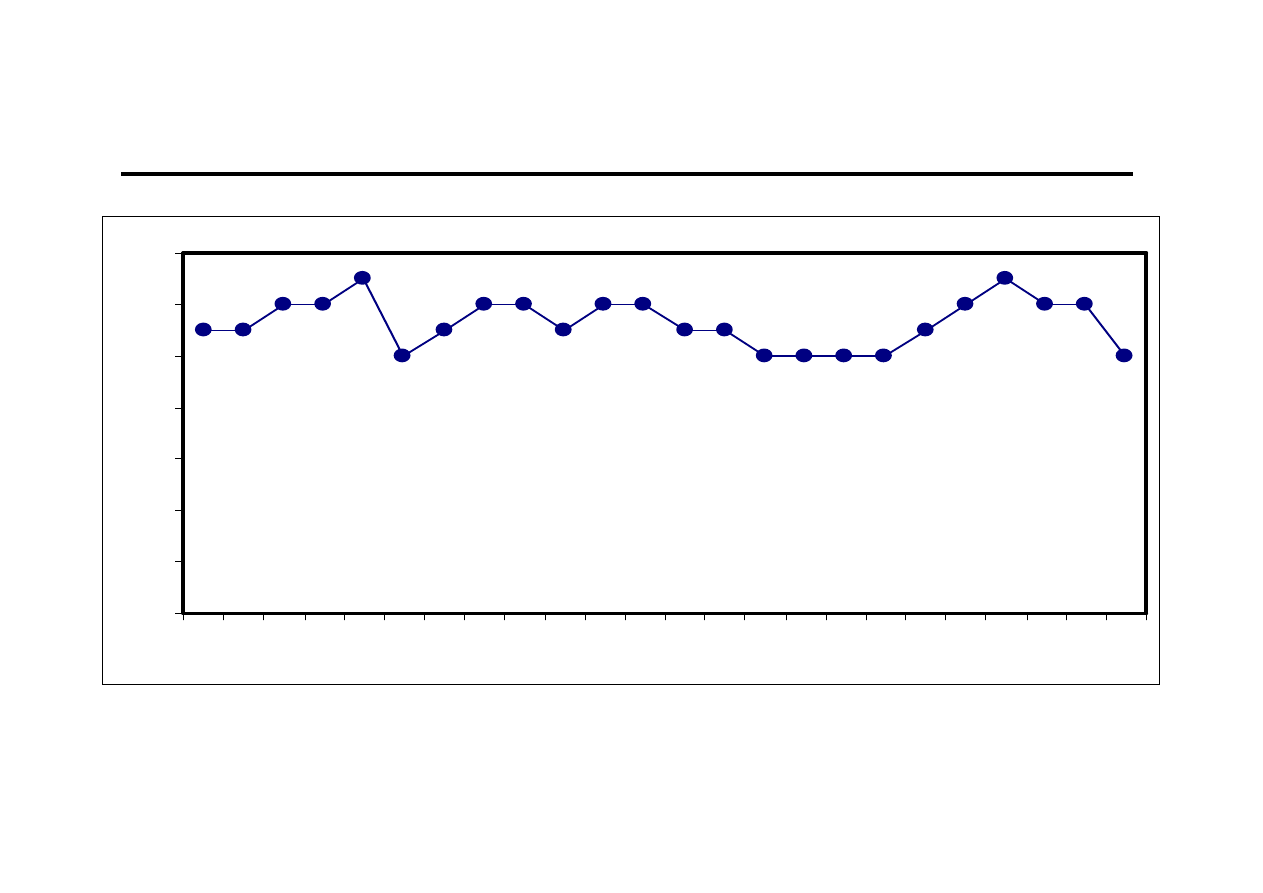
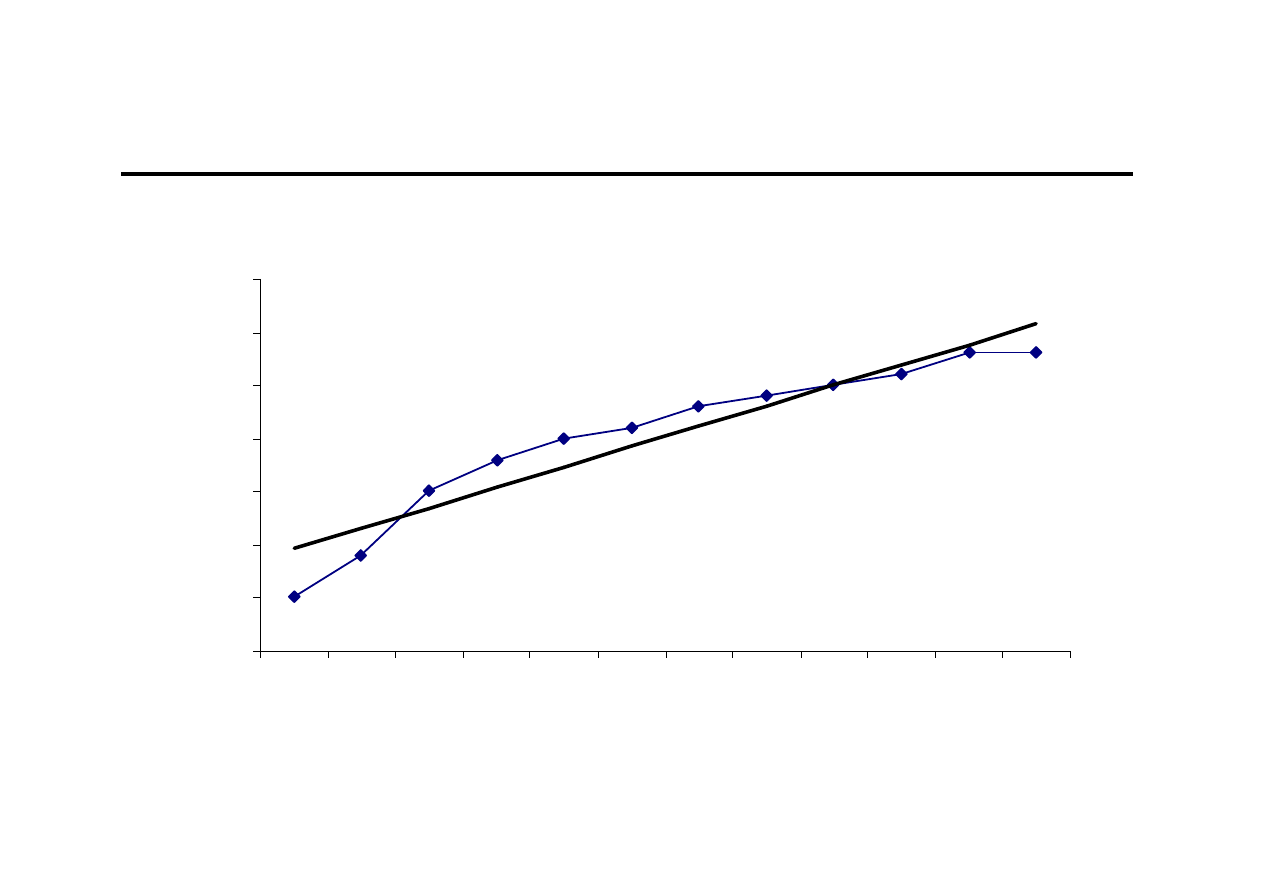
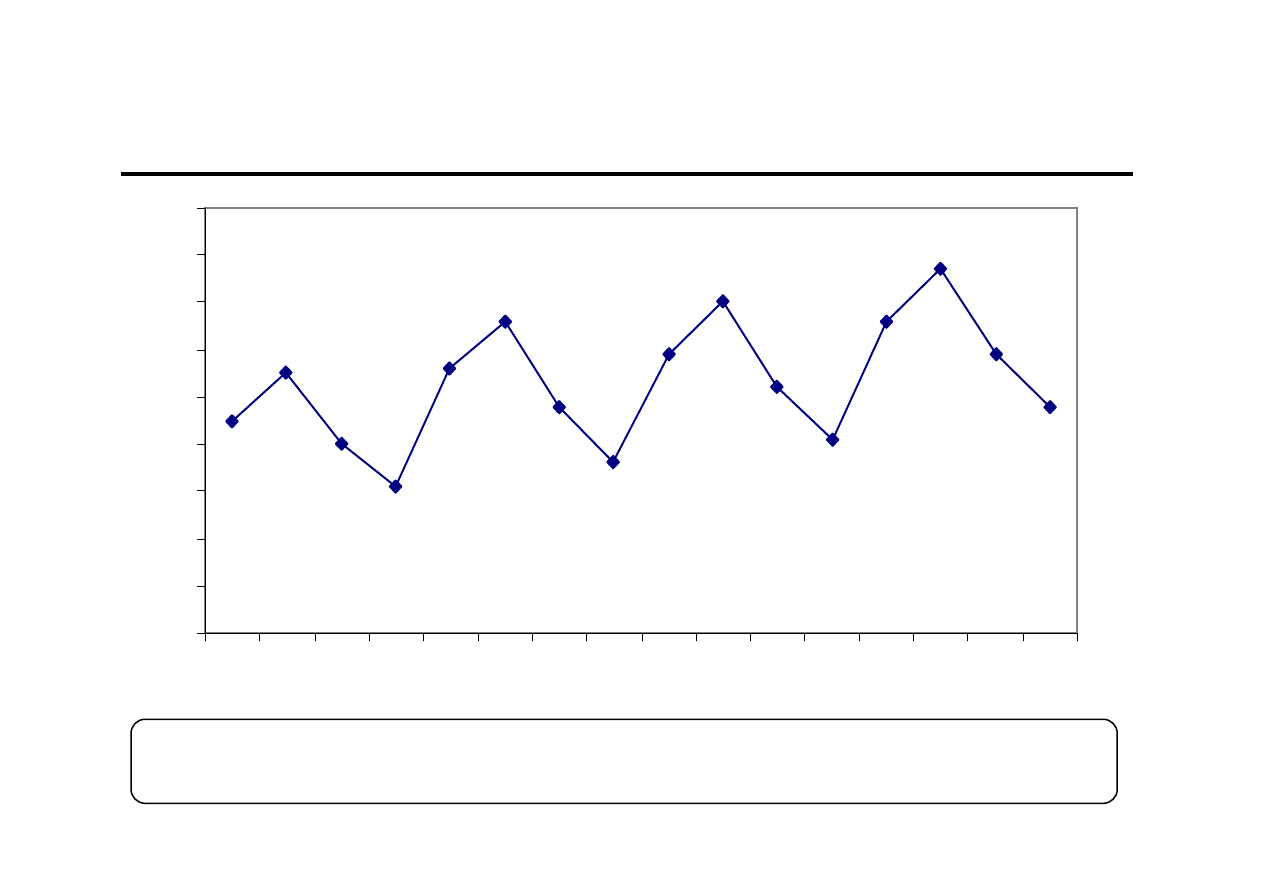
Ocena wzrokowa (1)

0

2

4

6

8

10

12

14

1

2

3

4

5

6

7

8

9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24

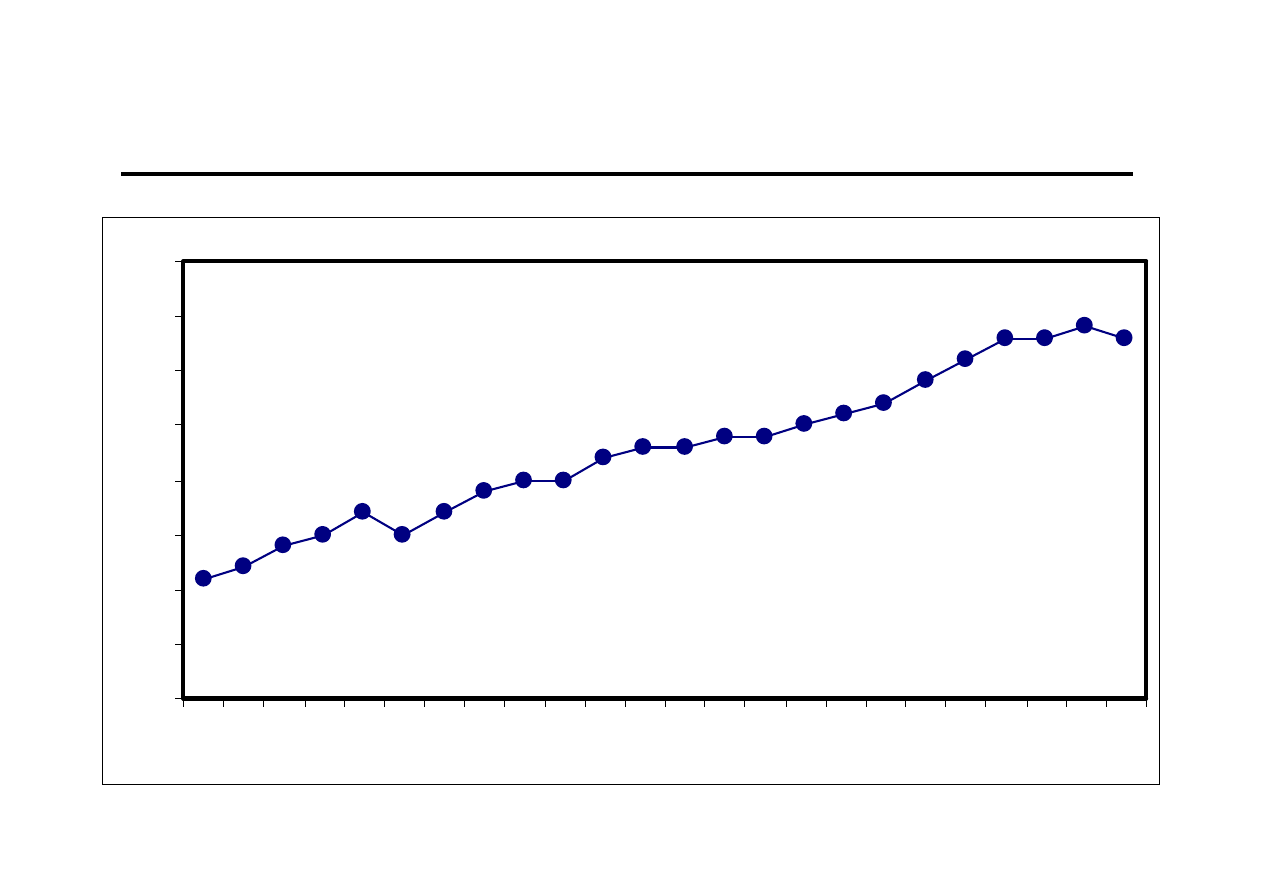
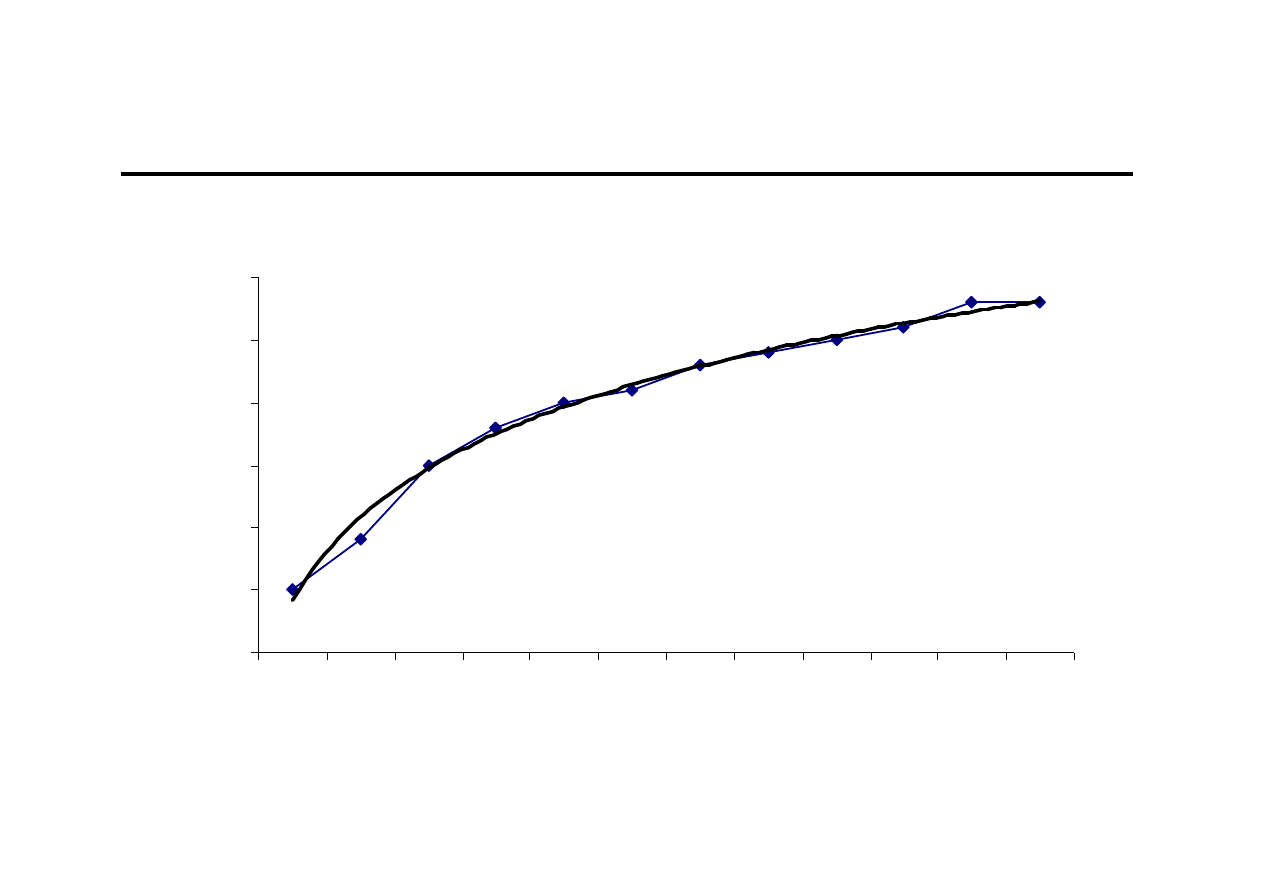
Ocena wzrokowa (2)

0

5

10

15

20

25

30

35

40

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24

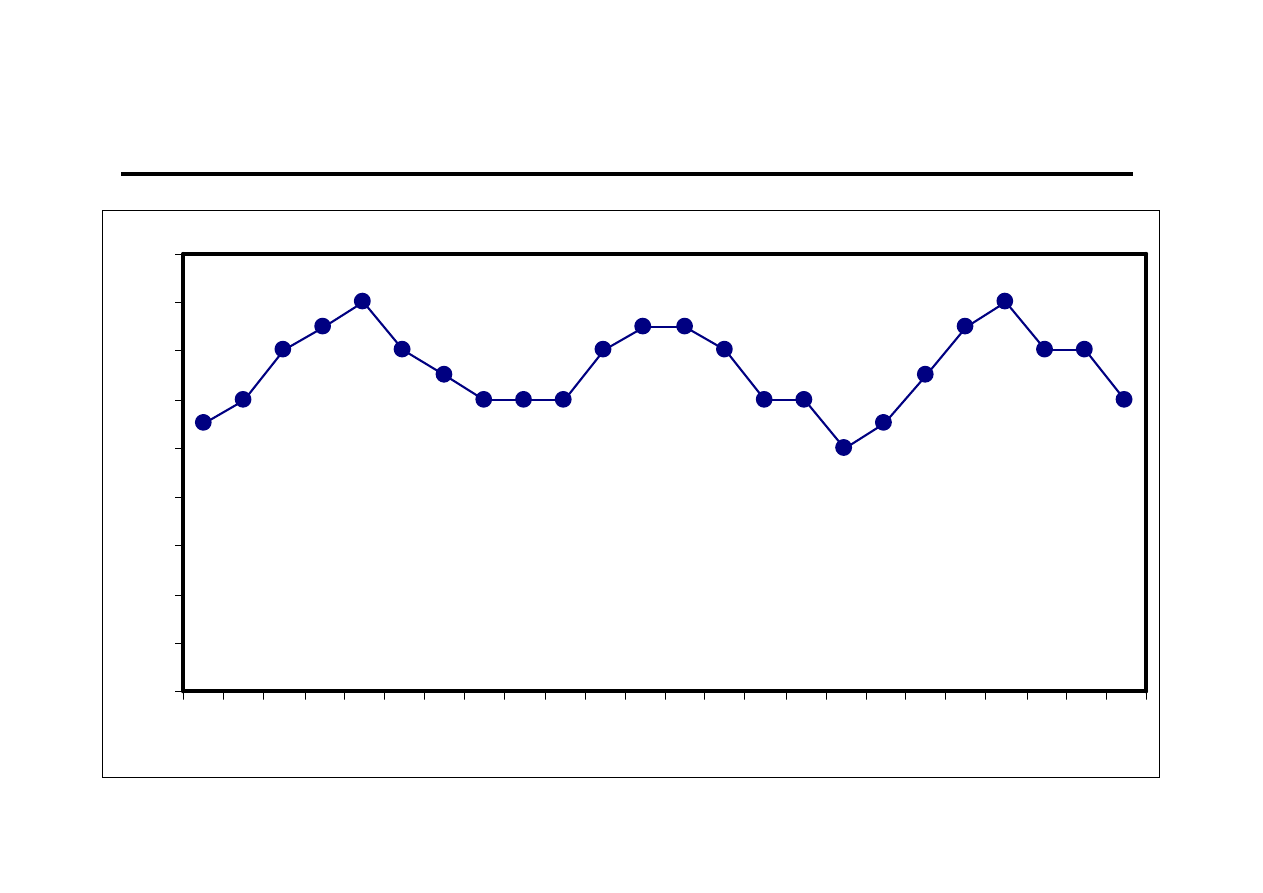
Ocena wzrokowa (3)

0

2

4

6

8

10

12

14

16

18

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24

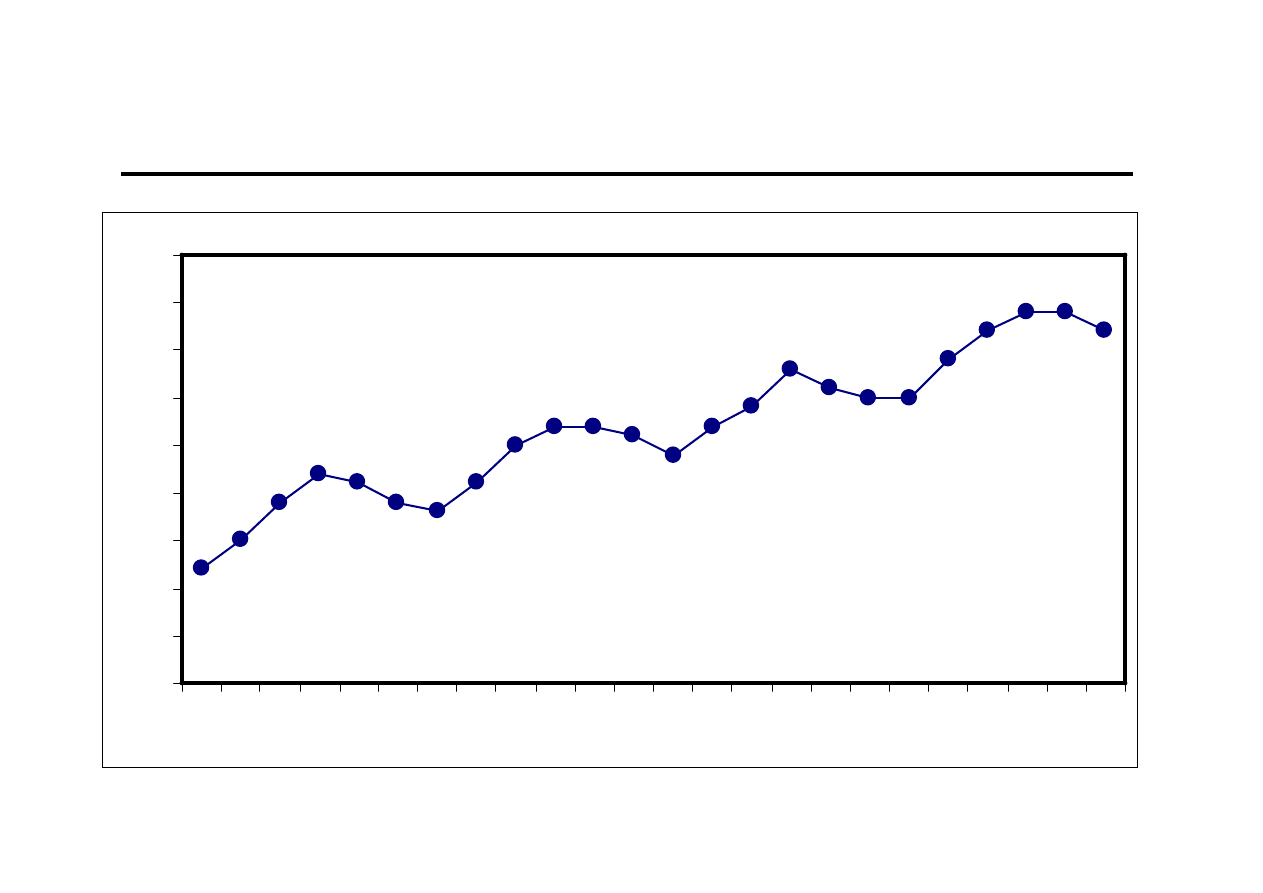
Ocena wzrokowa (4)

0

5

10

15

20

25

30

35

40

45

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24

Modele szeregów czasowych ze stałym

poziomem zmiennej prognozowanej bez

wahań okresowych (1)

Metoda naiwna

metodę można stosować w przypadku niskiej zmienności zmiennej
prognozowanej – zazwyczaj, w sytuacjach, gdy współczynnik zmienności nie
przekracza 10%

Metoda średniej ruchomej ważonej k-elementowej

Stałą wygładzania k ustala się na podstawie najmniejszego błędu prognoz

wygasłych, wagi w

i

ustala prognosta na podstawie wiedzy o zmiennej

prognozowanej Y. Jeśli przyjmie się

to metodę nazywamy metodą

średniej ruchomej k-elementowej.

1

*

−

=

t

t

y

Y

.

,...,

2

,

1

0

,

1

,

1

1

1

*

k

i

dla

w

w

w

y

Y

i

k

i

i

t

k

t

i

k

t

i

i

t

=

>

=

⋅

=

∑

∑

=

−

−

=

+

+

−

k

w

i

1

=

Modele szeregów czasowych ze stałym
poziomem zmiennej prognozowanej (2)

Prosty model wygładzania wykładniczego

dla t =2, 3,3n.

model można stosować jeśli szereg nie cechuje zbyt silna zmienność
(wahania przypadkowe nie są zbyt duże). Stałą wygładzania

α

α

α

α wyznacza

się eksperymentalnie na podstawie wybranego kryterium, jakie powinny
spełniać prognozy wygasłe.

].

1

,

0

(

,

)

1

(

*

1

1

*

∈

⋅

−

+

⋅

=

−

−

α

α

α

t

t

t

Y

y

Y

Do wyboru modelu prognostycznego (prognozy) można wykorzystać

analizę błędów ex post prognoz wygasłych

Modele szeregów czasowych z tendencją

rozwojową zmiennej prognozowanej bez

wahań okresowych(1)

Modele analityczne

stosuje się do prognozowana zjawisk, które charakteryzowały się w przeszłości
regularnymi zmianami, które można opisać za pomocą funkcji czasu i wobec
których zakłada się niezmienność kierunku trendu.

)

(

*

t

f

Y

t

=

Wybór postaci analitycznej modelu dokonuje się na podstawie:

• przesłanek teoretycznych dotyczących mechanizmu rozwojowego
prognozowanego zjawiska,

• oceny wzrokowej wykresu przeszłych wartości zmiennej,

• dopasowania modelu do wartości rzeczywistych zmiennej prognozowanej.

Modele szeregów czasowych z tendencją

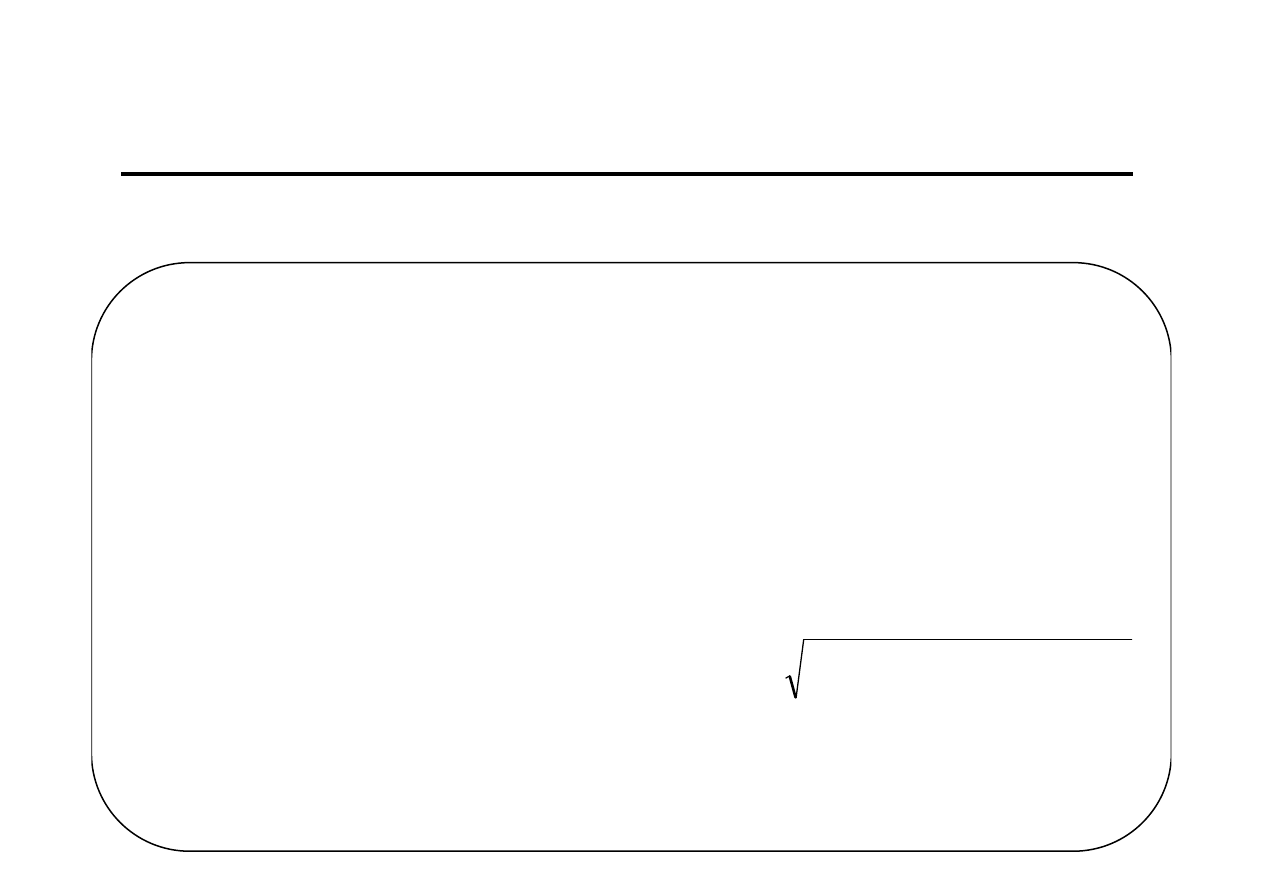
rozwojową zmiennej prognozowanej (2)

Do oceny dopasowania modelu liniowego, którego parametry oszacowano

MNK, do wartości empirycznych można się posłużyć:

a) współczynnikiem determinacji:

b) standardowym błędem szacunku modelu (odchyleniem standardowym reszt):

gdzie: k– oznacza liczbę zmiennych objaśniających w modelu

[ ]

1

,

0

,

)

(

)

ˆ

(

)

ˆ

(

1

1

2

2

1

2

1

2

2

1

2

2

∈

−

−

=

−

−

=

−

=

∑

∑

∑

=

=

=

R

y

y

y

y

nS

y

y

R

n

t

t

n

t

t

Y

n

t

t

ϕ

∑

=

−

−

−

=

n

t

t

t

e

y

y

k

n

S

1

2

)

ˆ

(

1

1

Modele szeregów czasowych z tendencją

rozwojową zmiennej prognozowanej (3)

Model trendu liniowego (lub zlinearyzowanego) przedstawia się w następujący
sposób:

Parametry strukturalne modelu można oszacować metodą najmniejszych kwadratów :

Prognozę na okres T>n wyznacza się z wzoru:

t

a

a

Y

t

⋅

+

=

1

0

t

a

y

a

n

t

t

t

n

t

y

t

y

t

t

t

S

t

t

Y

a

⋅

−

=

∑

=

−

∑

=

−

⋅

−

=

=

1

0

,

1

2

)

(

1

)

(

)

(

2

)

,

cov(

1

T

a

a

Y

T

•

+

=

1

0

*

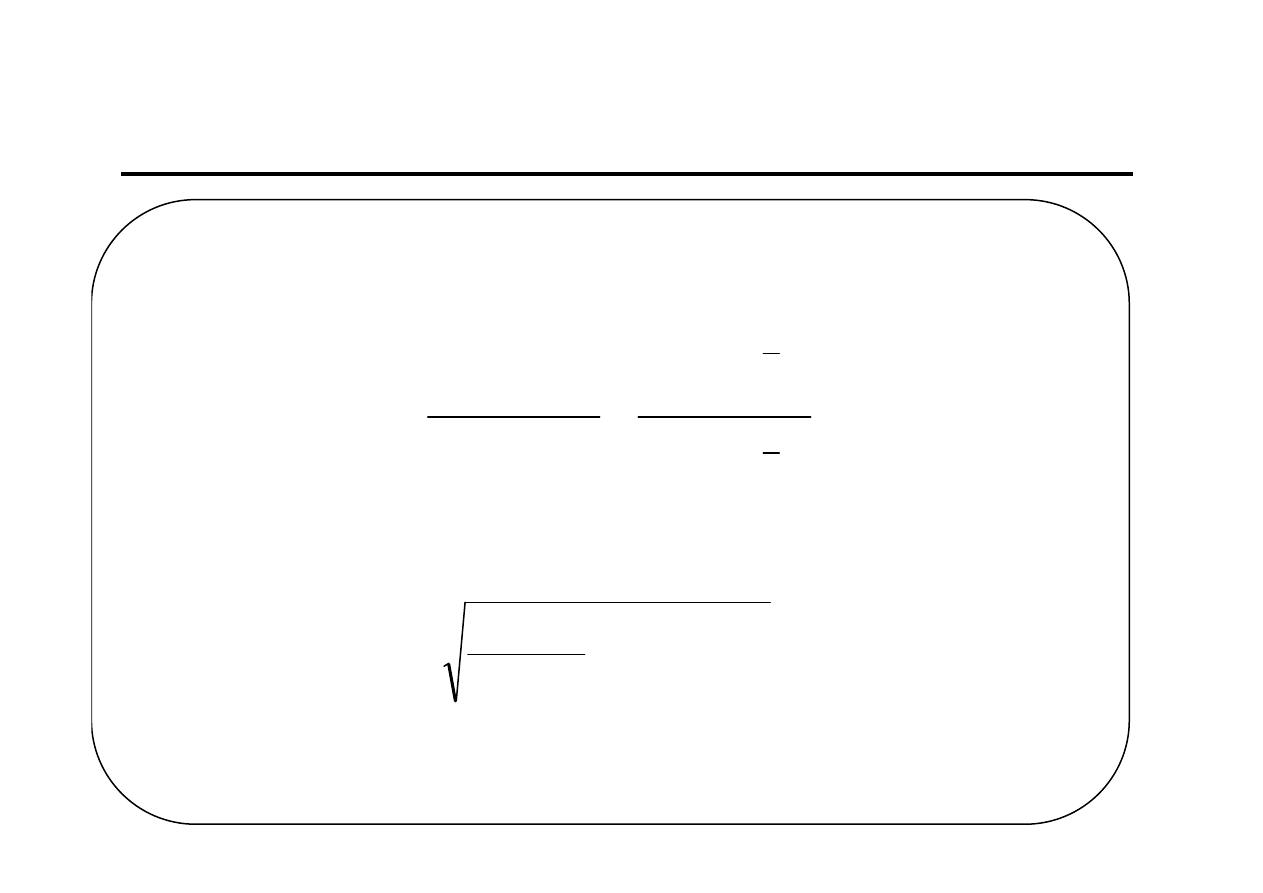
Modele szeregów czasowych z tendencją

rozwojową zmiennej prognozowanej (4)

Do oceny dopuszczalności zbudowanych prognoz używa się błędów ex ante:

a)

dla modelu liniowego

:

b)

dla modeli nieliniowych sprowadzalnych do liniowych poprzez transformację g:

– zmienna określona transformacją liniową

= g(y), to błąd ex ante

prognozy zmiennej na okres T, a pochodna jest liczona w punkcie y*

T

1

1

)

(

)

(

*

1

2

2

+

+

−

−

⋅

=

∑

=

n

t

t

t

T

S

V

n

t

e

T

2

2

*

~

~

*













=

dy

y

d

V

V

T

T

y

~

*

~

T

V

y

~

y

~

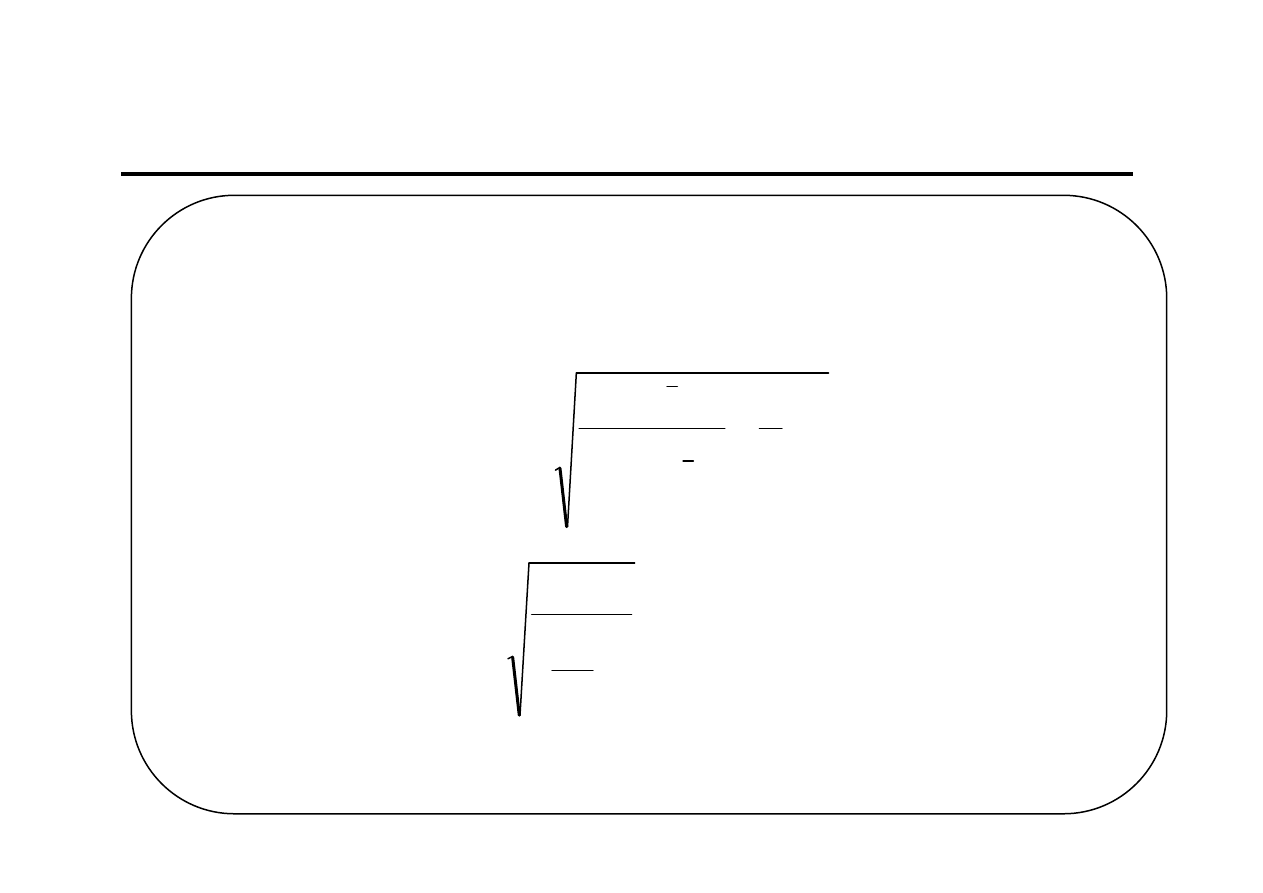
Modele szeregów czasowych z tendencją

rozwojową zmiennej prognozowanej (5)

k

kT

T

t

T

X

T

X

T

X

=

=

=

*

2

2

*

1

*

,...,

,

Model trendu wielomianowego:

Przekształcenie do postaci liniowej: podstawienie:

Prognoza:

k

k

2

2

1

0

*

T

T

a

...

T

a

T

a

a

y

⋅

+

+

⋅

+

⋅

+

=

kT

k

T

T

T

X

a

X

a

X

a

a

Y

*

2

*

2

1

*

1

0

*

...

⋅

+

+

⋅

+

⋅

+

=

1

*

1

)

(

)

*

(

*

,

2

1

*

,

2

1

2

4

2

1

1

1

1

1

+

−

⋅

=

=

=













































T

X

X

T

X

T

T

X

e

S

T

V

k

T

T

T

T

X

k

n

n

n

k

X

M

L

M

O

M

M

M

L

L

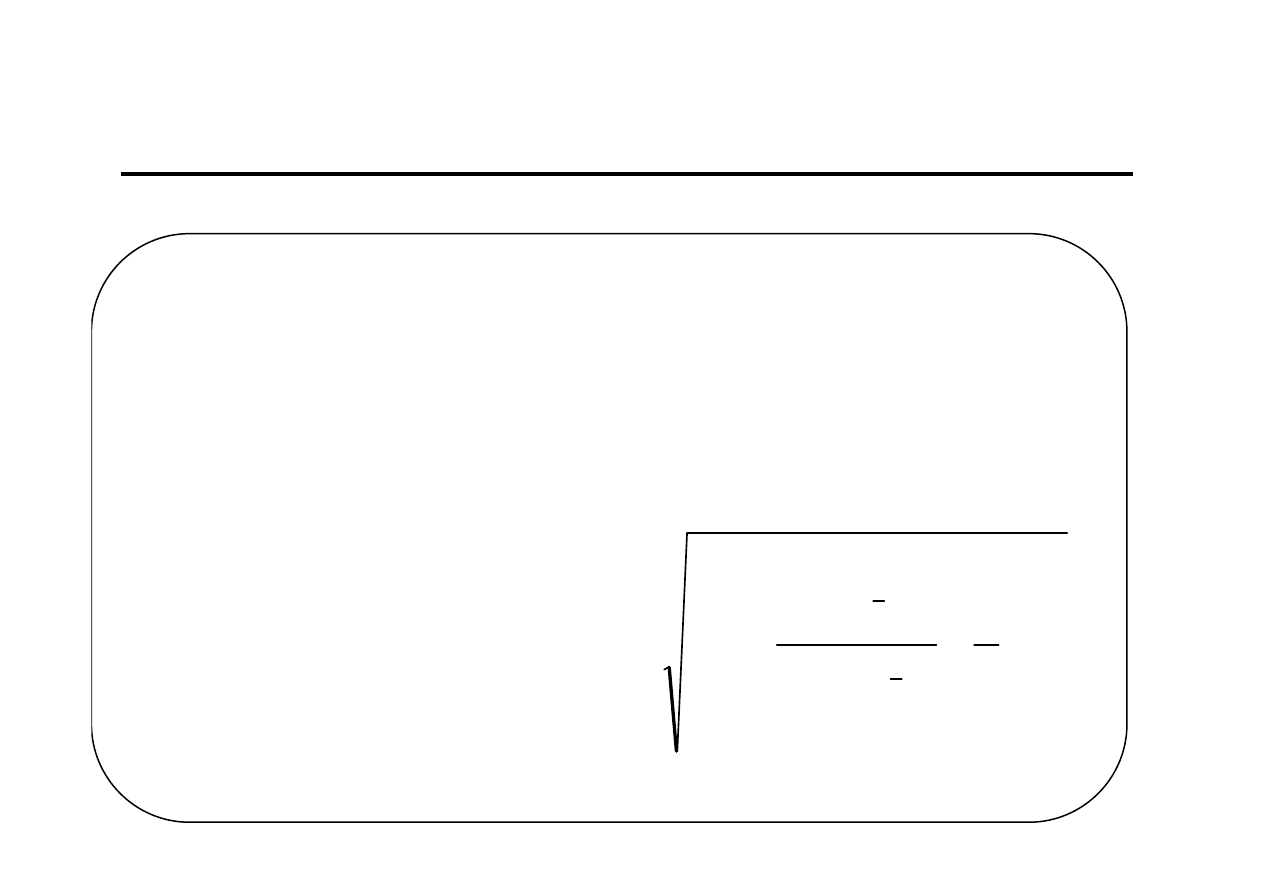
Modele szeregów czasowych z tendencją

rozwojową zmiennej prognozowanej (6)

Model trendu wykładniczego:

Przekształcenie do postaci liniowej:

t

e

a

a

y

T

1

0

*

T

ξ

⋅

⋅

=

*

~

*

T

1

0

*

~

T

Y

T

e

Y

T

b

b

Y

=

∧

⋅

+

=

1

1

0

0

t

t

a

ln

b

,

a

ln

b

,

y

ln

y

~

=

=

=

























+

+

−

−

⋅

⋅

=

























=

































=

∑

=

1

1

)

(

)

(

~

,

ln

ln

ln

~

,

1

3

1

2

1

1

1

1

2

2

2

*

*

2

1

n

t

t

t

T

S

Y

V

y

y

y

y

n

X

n

t

e

T

T

n

M

M

M

Modele szeregów czasowych z tendencją

rozwojową zmiennej prognozowanej (7)

Model trendu potęgowego:

Przekształcenie do postaci liniowej:

t

1

e

T

a

y

a

0

*

T

ξ

⋅

⋅

=

*

~

*

1

0

*

~

~

T

Y

T

T

e

Y

T

b

b

Y

=

⇒

⋅

+

=

1

1

0

0

a

b

,

a

ln

b

,

t

ln

t

~

,

y

ln

y

~

=

=

=

=

]

1

~

)

~

~

(

)

~

[(

~

,

ln

ln

ln

ln

~

,

ln

1

3

ln

1

2

ln

1

1

ln

1

~

*

1

*

2

*

*

3

2

1

+

⋅

⋅

=

































=

































=

−

T

T

T

T

e

T

T

n

X

X

X

X

S

Y

V

y

y

y

y

y

n

X

M

M

M

Modele szeregów czasowych z tendencją

rozwojową zmiennej prognozowanej (8)

Model trendu logarytmicznego:

Przekształcenie do postaci liniowej:

T

a

a

Y

T

ln

1

0

*

⋅

+

=

T

a

a

Y

T

~

1

0

*

⋅

+

=

t

ln

t

~ =

]

1

~

)

~

~

(

)

~

[(

,

,

ln

1

3

ln

1

2

ln

1

1

ln

1

~

*

1

*

2

*

3

2

1

+

⋅

=

































=

































=

−

T

T

T

T

e

T

n

X

X

X

X

S

V

y

y

y

y

y

n

X

M

M

M

Modele szeregów czasowych z tendencją

rozwojową zmiennej prognozowanej (9)

Model trendu hiperbolicznego:

Przekształcenie do postaci liniowej:

t

1

t

~ =

T

1

a

a

y

1

0

*

T

⋅

+

=

T

~

a

a

y

1

0

*

T

⋅

+

=

]

1

~

)

~

~

(

)

~

[(

,

,

1

1

3

1

1

2

1

1

1

1

~

*

1

*

2

*

3

2

1

+

⋅

=

































=









































=

−

T

T

T

T

e

T

n

X

X

X

X

S

V

y

y

y

y

y

n

X

M

M

M

Przykład obliczeniowy (1)

Wielkość sprzedaży rowerów stacjonarnych firmy Wettler u przedstawiciela na

Górny Śląsk w ostatnich kwartałach przedstawiała się następująco [w szt.]:

Przyjmując, że czynniki kształtujące sprzedaż nie ulegną zmianie:

a) postawić prognozę sprzedaży na kolejny kwartał (T=13)

128

128

126

125

124

123

121

120

118

115

109

105

100

105

110

115

120

125

130

1

2

3

4

5

6

7

8

9

10

11

12

Przykład obliczeniowy (trend liniowy) (2)

y = 1,9231x + 107,67

R

2

= 0,8969

100

105

110

115

120

125

130

135

1

2

3

4

5

6

7

8

9

10

11

12

Przykład obliczeniowy (trend logarytmiczny) (3)

y = 9,6416Ln(x) + 104,11

R

2

= 0,9907

100

105

110

115

120

125

130

1

2

3

4

5

6

7

8

9

10

11

12

Przykład obliczeniowy (4)

129

2,5649

13

128

2,4849

128

12

127

2,3979

128

11

126

2,3026

126

10

125

2,1972

125

9

124

2,0794

124

8

123

1,9459

123

7

121

1,7918

121

6

120

1,6094

120

5

117

1,3863

118

4

115

1,0986

115

3

111

0,6931

109

2

104

0,0000

105

1

Y

t

*=9,641648 ln t + 104,1075

ln t

y

t

t

W kolejnym kwartale prognozowana sprzedaż wynosi 129 sztuk rowerów.

Przykład obliczeniowy (błąd ex ante) (5)

b) przyjmując, że błąd prognozy nie może stanowić więcej niż 1% jej wartości

zbadaj dopuszczalność prognozy

5,4808

129

2,5649

13

0,0044

128

2,4849

128

12

0,5972

127

2,3979

128

11

0,0950

126

2,3026

126

10

0,0855

125

2,1972

125

9

0,0246

124

2,0794

124

8

0,0171

123

1,9459

123

7

0,1467

121

1,7918

121

6

0,1405

120

1,6094

120

5

0,2770

117

1,3863

118

4

0,0900

115

1,0986

115

3

3,2063

111

0,6931

109

2

0,7965

104

0,0000

105

1

(y

t

-Y

t

*)

2

Y

t

*=9,641648 ln t + 104,1075

ln t

y

t

t

Przykład obliczeniowy (błąd ex ante) (6)

0,5481

5,4808

1

1

12

1

)

(

1

1

1

2

*

2

≈

⋅

−

−

=

−

−

−

=

∑

=

n

t

t

t

e

Y

y

k

n

S

=

X

~













=

2,5649

1

X

~

*

T

2,4849

1

2,3979

1

2,3026

1

2,1972

1

2,0794

1

1,9459

1

1,7918

1

1,6094

1

1,3863

1

1,0986

1

0,6931

1

0,0000

1

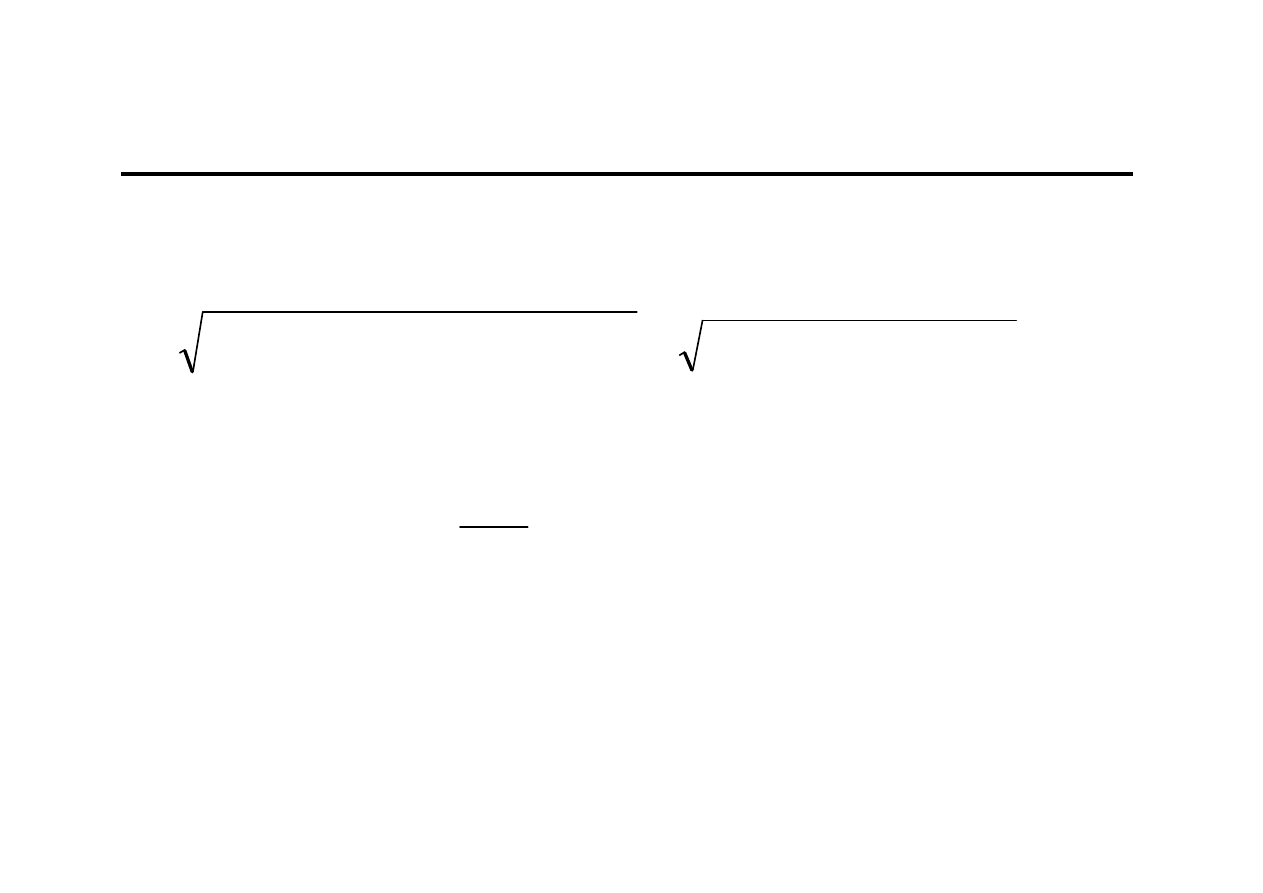
Przykład obliczeniowy (błąd ex ante) (7)

0,8150

1)

0,2120

(

0,5481

]

1

~

)

~

~

(

)

~

[(

*

1

*

2

*

=

+

⋅

=

+

⋅

=

−

T

T

T

T

e

T

X

X

X

X

S

V

0,633%

%

100

y

V

*

T

*

T

*

T

=

⋅

=

η

Prognozę na kolejny kwartał (T=13) można uznać za

dopuszczalną.

Przykład obliczeniowy (8)

c) postaw prognozy na następne dwa kwartały (14 i 15) oraz oceń ich dopuszczalność

130

2,7081

15

130

2,6391

14

129

2,5649

13

128

2,4849

128

12

127

2,3979

128

11

126

2,3026

126

10

125

2,1972

125

9

124

2,0794

124

8

123

1,9459

123

7

121

1,7918

121

6

120

1,6094

120

5

117

1,3863

118

4

115

1,0986

115

3

111

0,6931

109

2

104

0,0000

105

1

Y

t

*=9,641648 ln t + 104,1075

ln t

y

t

t

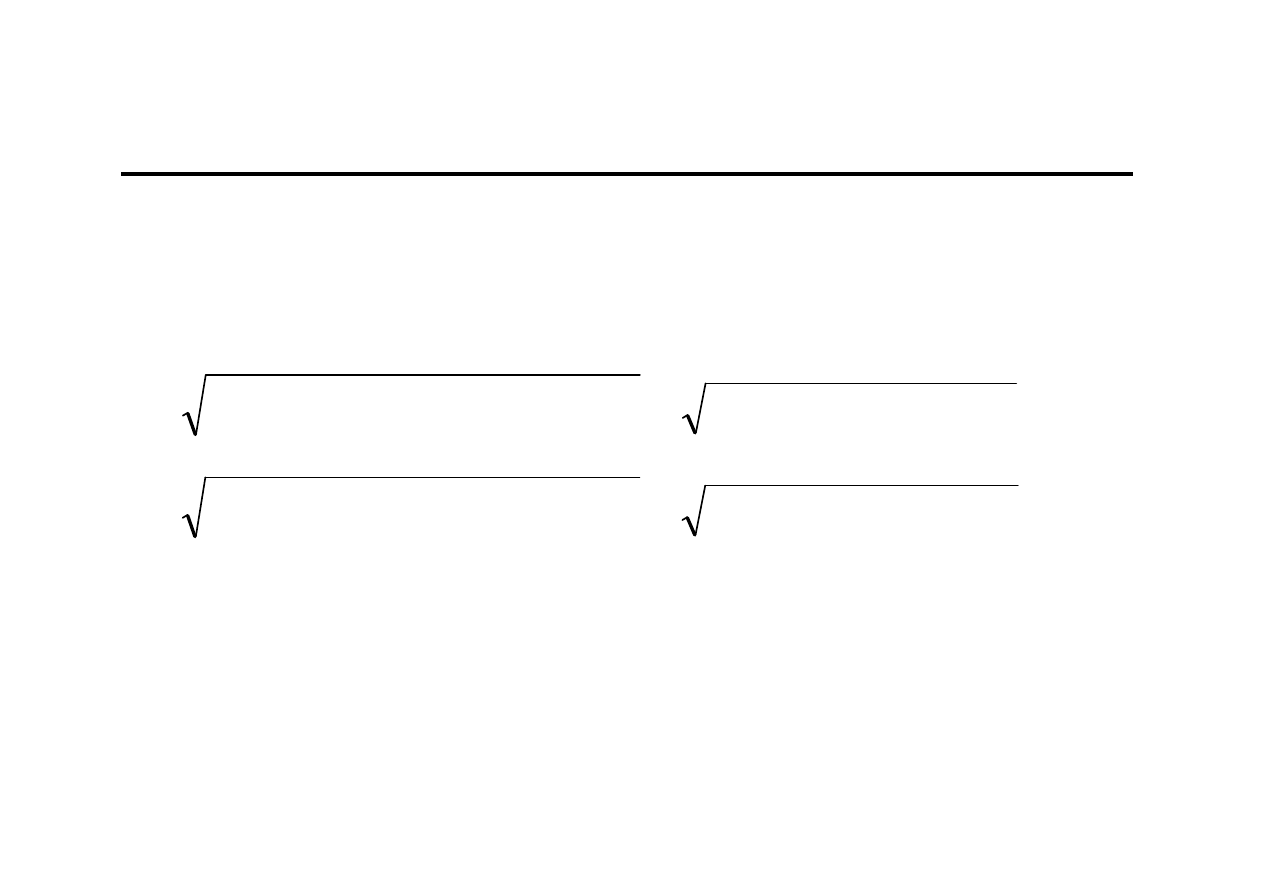
Przykład obliczeniowy (9)

0,8224

1)

0,2341

(

0,5481

]

1

~

)

~

~

(

)

~

[(

*

1

*

2

*

14

=

+

⋅

=

+

⋅

=

−

T

T

T

T

e

X

X

X

X

S

V













=

2,6391

1

X

~

*

14













=

2,7081

1

X

~

*

15

0,8298

1)

0,2563

(

0,5481

]

1

~

)

~

~

(

)

~

[(

*

1

*

2

*

15

=

+

⋅

=

+

⋅

=

−

T

T

T

T

e

X

X

X

X

S

V

0,635%

*

14

=

η

0,637%

*

15

=

η

Obie prognozy (na kwartał 14 oraz 15) można uznać za dopuszczalne.

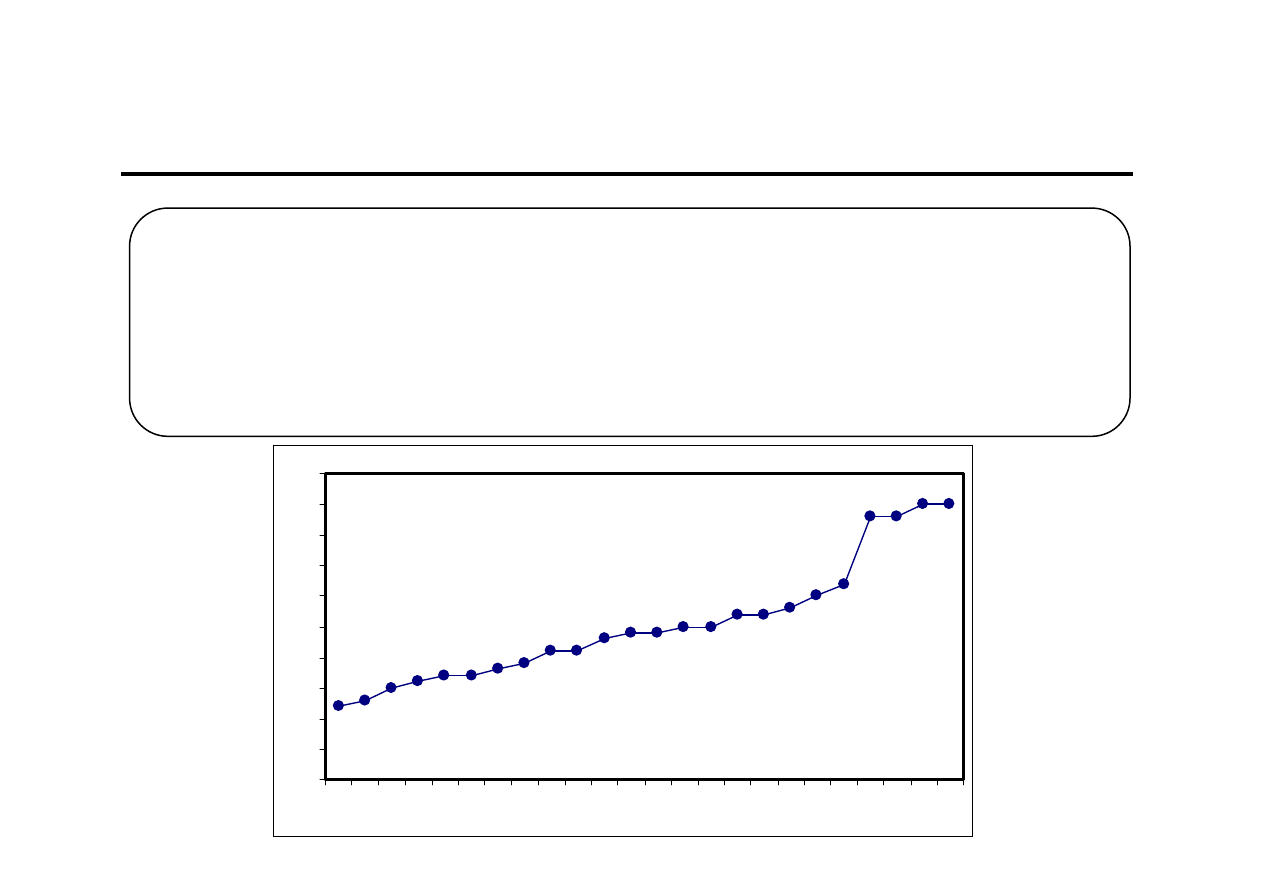
Modele szeregów czasowych z tendencją

rozwojową zmiennej prognozowanej (10)

Jeżeli zaobserwuje się odchodzenie wartości zmiennej prognozowanej od
dotychczasowej tendencji rozwojowej (spowodowane zmianą jakościową), to
można wykorzystać prognozę w formie reguły podstawowej z poprawką:

p

Y

Y

w

T

T

+

=

)

*(

*

0

5

10

15

20

25

30

35

40

45

50

1 2 3 4 5

6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24

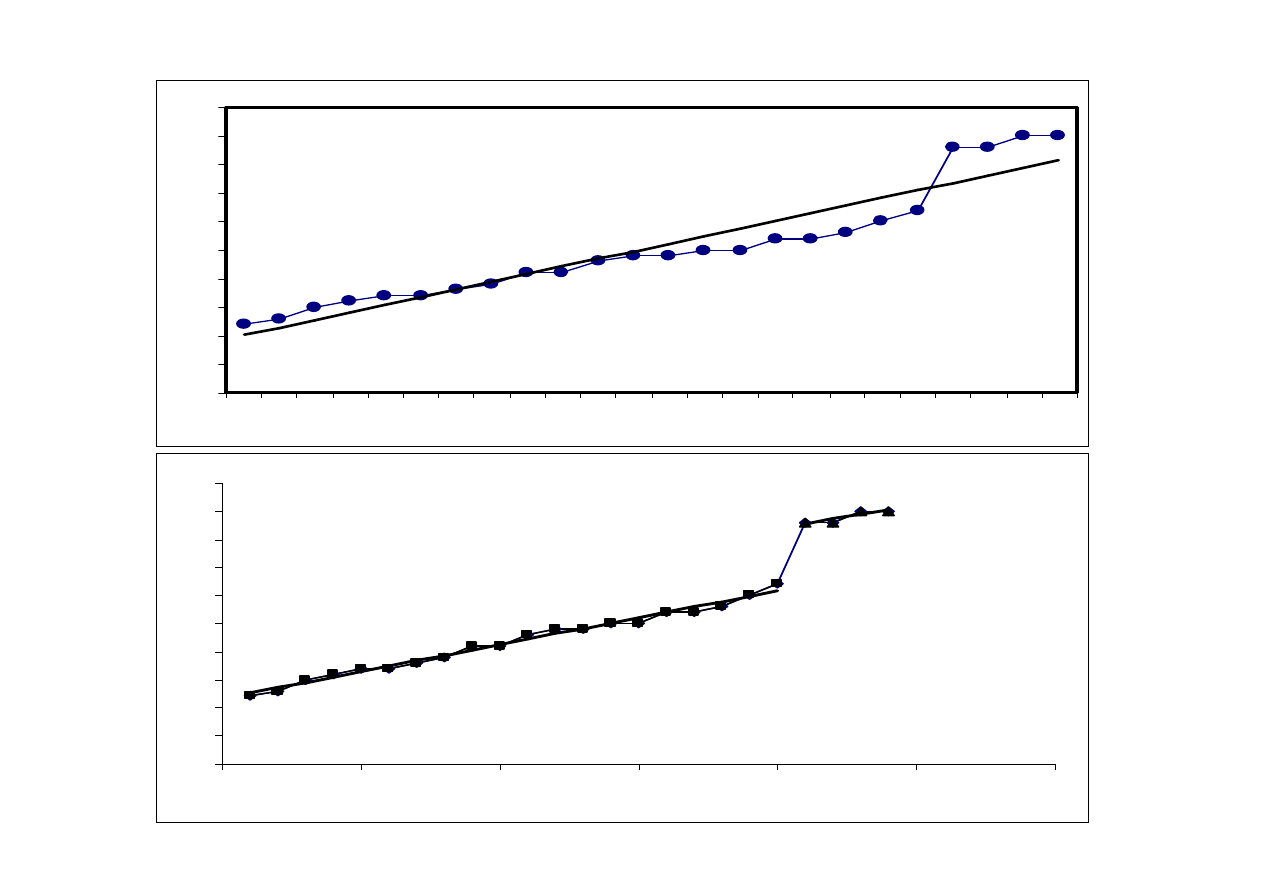
y = 0,9579x + 11,642

R

2

= 0,987

y = 0,8x + 26

R

2

= 0,8

0

5

10

15

20

25

30

35

40

45

50

0

5

10

15

20

25

30

y = 1,333x + 8,7536

R

2

= 0,8964

0

5

10

15

20

25

30

35

40

45

50

1

2

3

4

5

6

7

8

9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24

46,3995

10,7625

średnia:

25

45,4397

10,3228

34,6772

45

24

44,4799

11,2826

33,7174

45

23

43,5201

10,2424

32,7576

43

22

42,5603

11,2022

31,7978

43

21

30,838

30,838

32

20

29,8782

29,8782

30

19

28,9184

28,9184

28

18

27,9586

27,9586

27

17

26,9988

26,9988

27

16

26,039

26,039

25

15

25,0792

25,0792

25

14

24,1194

24,1194

24

13

23,1596

23,1596

24

12

22,1998

22,1998

23

11

21,24

21,24

21

10

20,2802

20,2802

21

9

19,3204

19,3204

19

8

18,3606

18,3606

18

7

17,4008

17,4008

17

6

16,441

16,441

17

5

15,4812

15,4812

16

4

14,5214

14,5214

15

3

13,5616

13,5616

13

2

12,6018

12,6018

12

1

z poprawką

y

t

-y

t

*

y

t

*=0,9598t+11,642

y

t

t

y = 0,9579x + 11,642

R

2

= 0,987

y = 0,8x + 26

R

2

= 0,8

0

5

10

15

20

25

30

35

40

45

50

0

5

10

15

20

25

30

0

5

10

15

20

25

30

35

40

45

50

0

5

10

15

20

25

30

Modele szeregów czasowych z tendencją

rozwojową zmiennej prognozowanej (11)

Prognozę przedziałową dla z góry zadanej wiarygodności p (dla z góry zadanego

prawdopodobieństwa, że wartość rzeczywista zmiennej prognozowanej w okresie T>n

znajdzie się w danym przedziale) konstruuje się w następujący sposób

:

u – współczynnik związany z wiarygodnością prognozy p, rozkładem reszt modelu
oraz długością szeregu czasowego.

Jeśli rozkład reszt modelu nie jest zgodny z rozkładem normalnym lub hipoteza o
normalności nie była weryfikowana, to u zależy wyłącznie od wiarygodności
prognozy, a obliczając u korzysta się z nierówności Czebyszewa:

Jeśli rozkład reszt modelu jest zgodny z rozkładem normalnym, to u odczytuje się z
tablic rozkładu normalnego dla dużej próby dla prawdopodobieństwa
lub z tablic rozkładu t-Studenta dla małej próby (n<30) dla prawdopodobieństwa

(1-p) oraz n-k-1 stopni swobody.

{

}

p

V

u

Y

y

V

u

Y

P

T

T

T

T

T

=

⋅

+

≤

≤

⋅

−

*

*

*

*

p

u

−

=

1

1

2

1

p

+

Przykład obliczeniowy (1)

Wielkość sprzedaży rowerów stacjonarnych firmy Wettler u przedstawiciela na
Górny Śląsk w ostatnich kwartałach przedstawiała się następująco [w szt.]:

Przyjmując, że czynniki kształtujące sprzedaż nie ulegną zmianie, postawić
prognozę przedziałową na kolejny kwartał na poziomie wiarygodności 0,95.

128

128

126

125

124

123

121

120

118

115

109

105

a) rozkład reszt modelu nie jest badany lub nie jest zgodny z rozkładem

normalnym

b) jeśli rozkład reszt jest zgodny z rozkładem normalnym, to

47

4

95

0

1

1

,

,

u

=

−

=

23

2,

u =

Przykład obliczeniowy (2)

a) rozkład reszt modelu nie jest badany lub nie jest zgodny z rozkładem

normalnym wtedy

b) jeśli rozkład reszt jest zgodny z rozkładem normalnym, to

z prawdopodobieństwem p=0.95.

]

133

;

125

[

]

8150

,

0

47

,

4

129

;

8150

,

0

47

,

4

129

[

13

13

∈

⋅

+

⋅

−

∈

y

y

]

131

;

127

[

]

8150

,

0

23

,

2

129

;

8150

,

0

23

,

2

129

[

13

13

∈

⋅

+

⋅

−

∈

y

y

Modele szeregów czasowych z tendencją

rozwojową zmiennej prognozowanej (12)

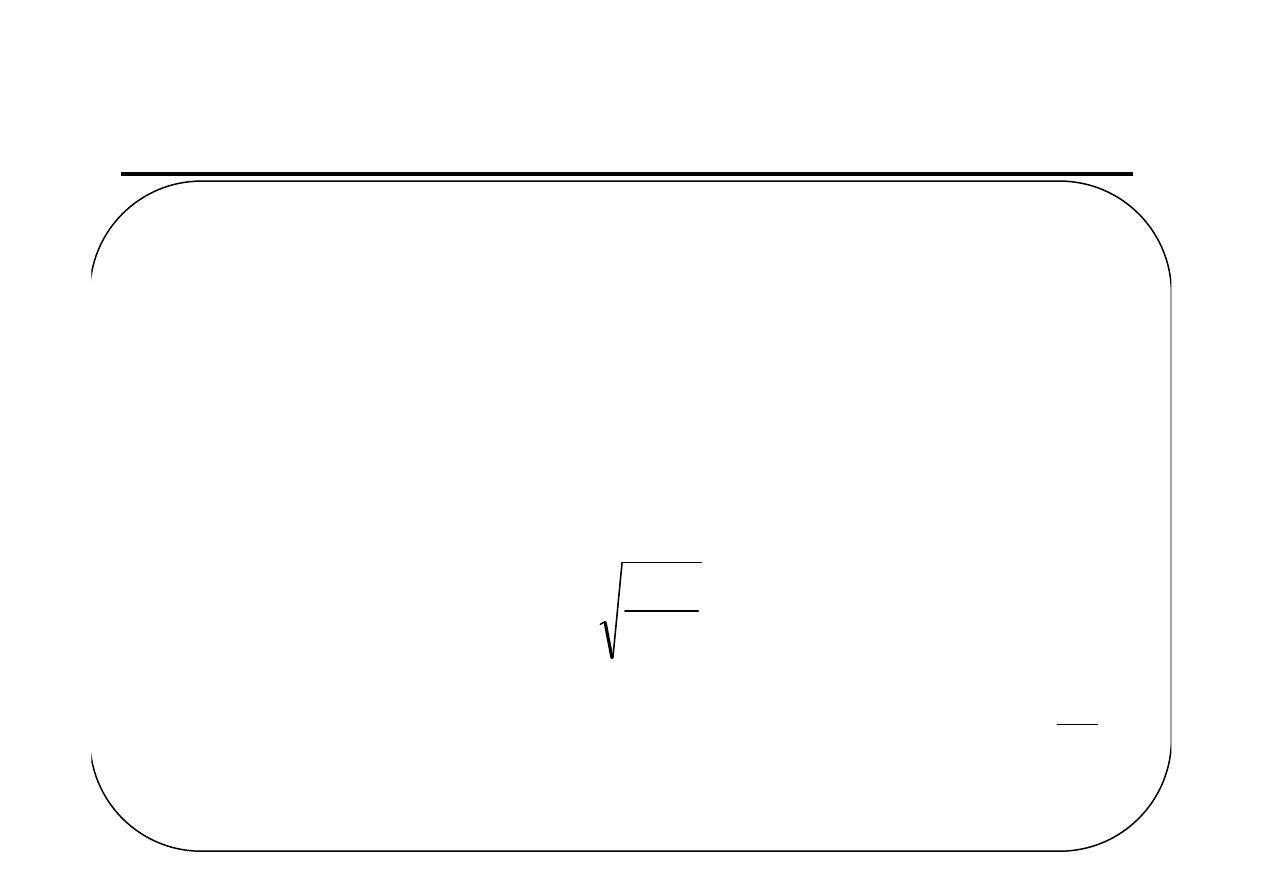
Model liniowy Holta

gdzie

dla t=2, 3,Z,n.

Parametry wygładzania

α i β dobiera się eksperymentalnie na podstawie

wybranego kryterium, które powinny spełniać prognozy wygasłe. Ponadto

α i β

należą do przedziału [0;1].

Model wymaga wartości początkowych F

1

oraz S

1 .

Można przyjąć:

n

n

*

t

S

)

n

T

(

F

y

⋅

−

+

=

)

S

F

(

)

(

y

F

t

t

t

t

1

1

1

−

−

+

⋅

−

+

⋅

=

α

α

1

t

1

t

t

t

S

)

1

(

)

F

F

(

S

−

−

⋅

β

−

+

−

⋅

β

=

liniowego

modelu

z

,

lub

,

lub

0

,

1

1

0

1

1

2

1

1

1

1

1

1

a

S

a

F

y

y

S

y

F

S

y

F

=

=

−

=

=

=

=

0

10

20

30

40

50

60

70

80

90

100

1

2

3

4

5

6

7

8

9

10

11

12

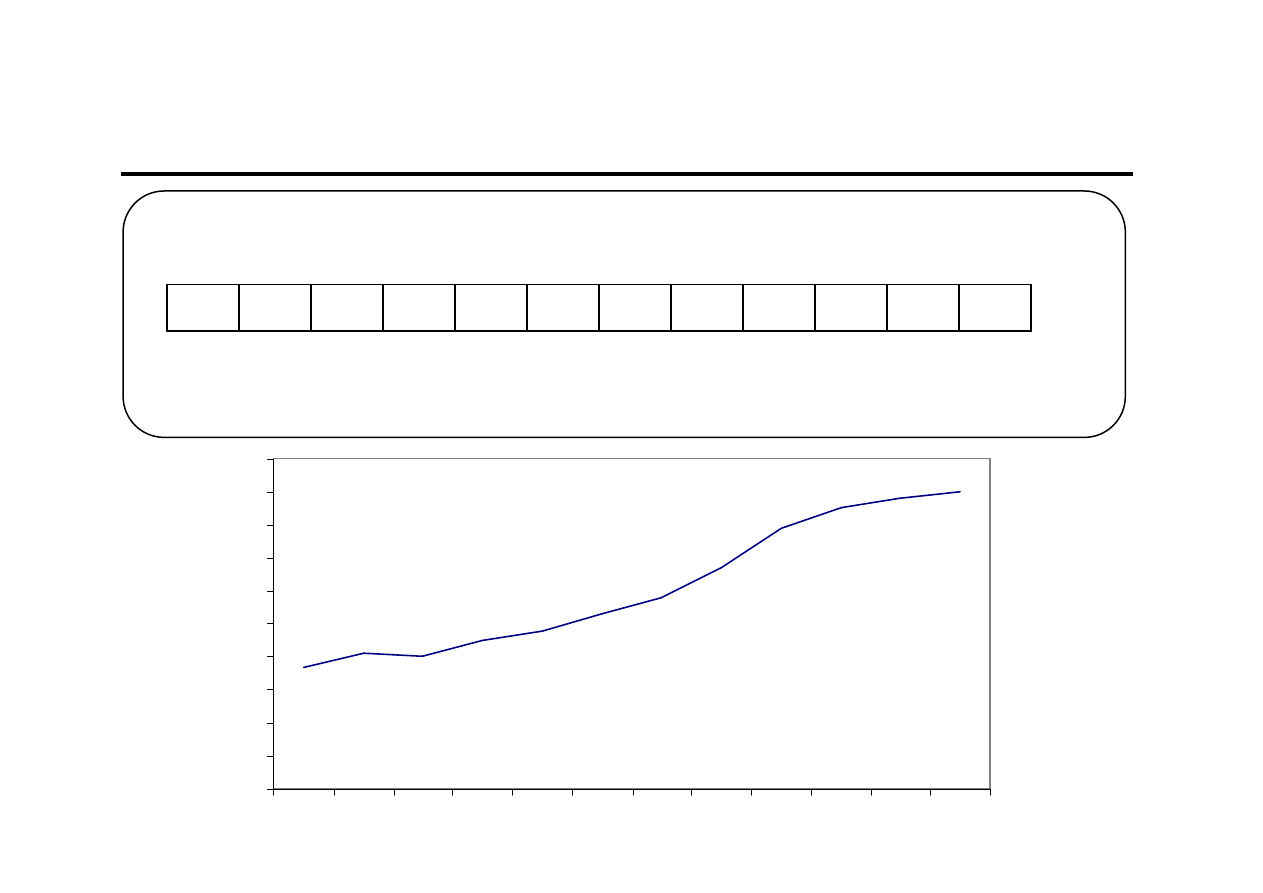
Przykład obliczeniowy (1)

Wielkość sprzedaży pralek automatycznych firmy „Kolar” u jednego
z przedstawicieli w ostatnich miesiącach przedstawiała się następująco [w szt.]:

Przyjmując, że czynniki kształtujące sprzedaż nie ulegną zmianie:

a) postaw prognozę na następny miesiąc

90

88

85

79

67

58

53

48

45

40

41

37

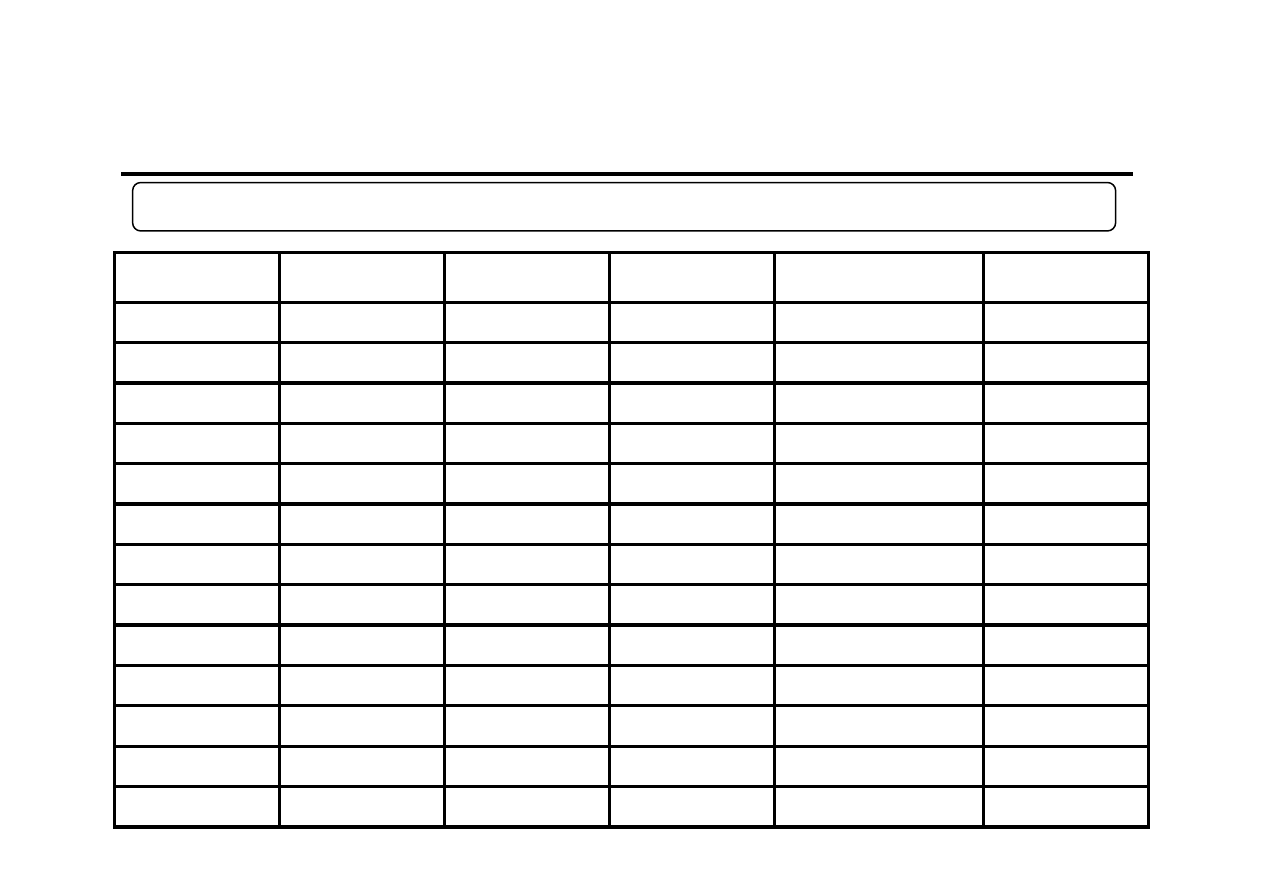
Przykład obliczeniowy (2)

Początkowe rozwiązanie dla

α=0,5 oraz β=0,5

t

y

t

F

t

S

t

y*

t

=F

t-1

+S

t-1

(y

t

-y*

t

)

2

1

37

37

0

-

-

2

41

39

1

37

16

3

40

40

1

40

0

4

45

43

2

41

16

5

48

46,5

2,75

45

9

6

53

51,125

3,6875

49

14,0625

7

58

56,40625 4,484375

55

10,16016

8

67

63,94531 6,011719

61

37,32446

9

79

74,47852 8,272461

70

81,77528

10

85

83,87549 8,834717

83

5,058106

11

88

90,3551

7,657166

93

22,18603

12

90

94,00613 5,654099

98

64,19644

13

100

25,06936

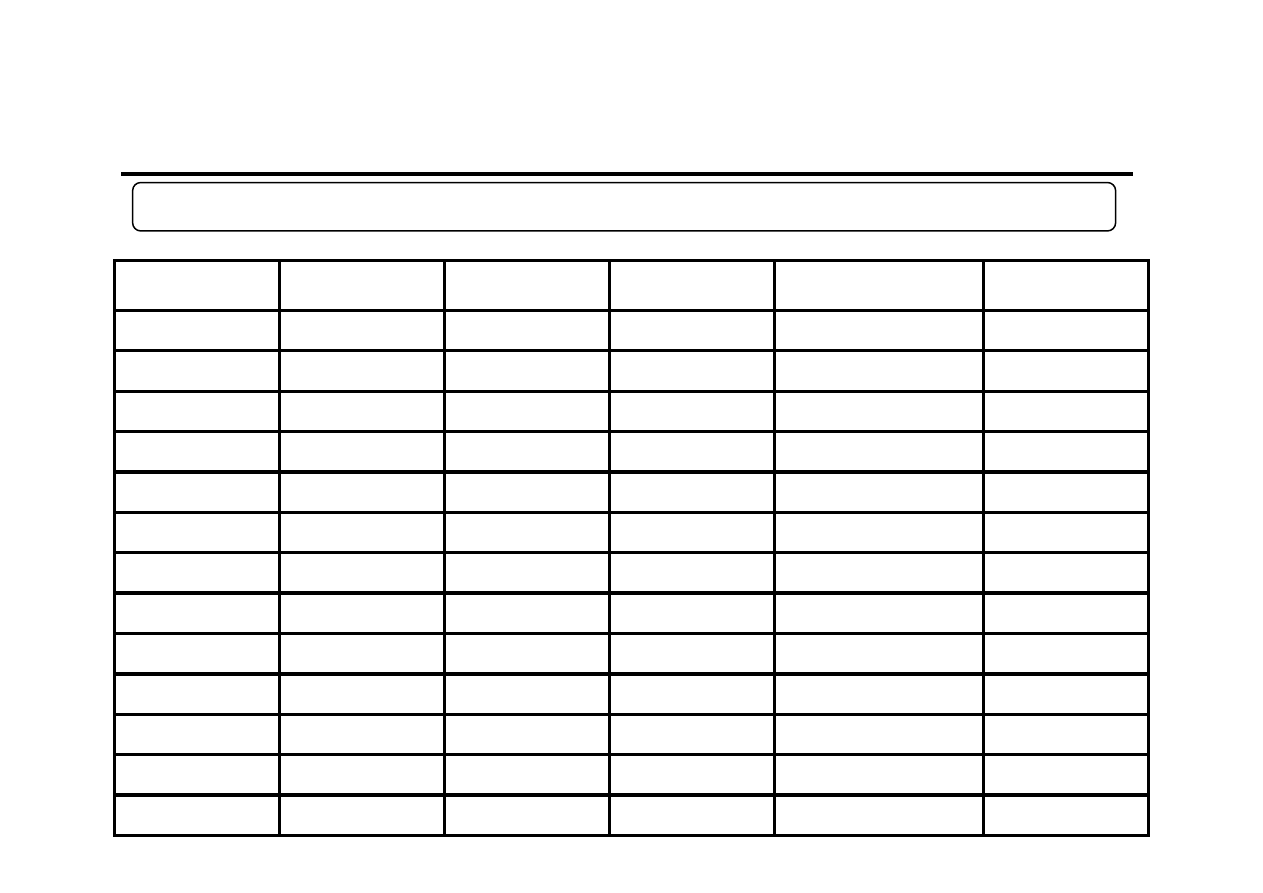
Przykład obliczeniowy (3)

t

y

t

F

t

S

t

y*

t

=F

t-1

+S

t-1

(y

t

-y*

t

)

2

1

37

37

0

-

-

2

41

40,9264

2,758843

37

16

3

40

40,06781 0,217095

44

13,58098

4

45

44,91324 3,469144

40

22,23209

5

48

48,00704 3,205412

48

0,146215

6

53

52,96711 4,438306

51

3,19534

7

58

57,98906 4,848399

57

0,353534

8

67

66,9234

7,719349

63

17,32676

9

79

78,91982 10,72459

75

18,9856

10

85

85,08546

7,52129

90

21,57054

11

88

88,08477 4,343963

93

21,22217

12

90

90,04469

2,66884

92

5,898745

13

93

12,77382

α=0,981598763552985 oraz β=0,702640116555618

Przykład obliczeniowy (4)

α=1 oraz β=0,701813393637758

t

y

t

F

t

S

t

y*

t

=F

t-1

+S

t-1

(y

t

-y*

t

)

2

1

37

37

4

-

-

2

41

41

4

41

0

3

40

40

0,490933

45

25

4

45

45

3,655457

40

20,33168

5

48

48

3,195448

49

0,429623

6

53

53

4,461907

51

3,256407

7

58

58

4,839548

57

0,289544

8

67

67

7,759409

63

17,30936

9

79

79

10,73551

75

17,98261

10

85

85

7,412066

90

22,42508

11

88

88

4,315619

92

19,46633

12

90

90

2,690487

92

5,362092

13

93

11,98661

Przykład obliczeniowy (5)

α=0,820035105981983 oraz β=0

F

1

=a

0

oraz S

1

=a

1

na podstawie wszystkich obserwacji

t

y

t

F

t

S

t

y*

t

=F

t-1

+S

t-1

(y

t

-y*

t

)

2

1

37

25,62121

5,43007

-

-

2

41

39,20958

5,43007

31

98,97699

3

40

40,83497

5,43007

45

21,52635

4

45

45,22766

5,43007

46

1,600336

5

48

48,4783

5,43007

51

7,063547

6

53

53,16347

5,43007

54

0,825134

7

58

58,10682

5,43007

59

0,352295

8

67

66,37676

5,43007

64

11,99315

9

79

77,70548

5,43007

72

51,74168

10

85

84,66446

5,43007

83

3,476166

11

88

88,37694

5,43007

90

4,387076

12

90

90,68513

5,43007

94

14,49335

13

96

19,67601

Przykład obliczeniowy (6)

α=1 oraz β=0,596147803853797

F

1

=a

0

oraz S

1

=a

1

na podstawie 3 pierwszych obserwacji

t

y

t

F

t

S

t

y*

t

=F

t-1

+S

t-1

(y

t

-y*

t

)

2

1

37

36,33333

1,5

-

-

2

41

41

3,387801

38

10,02778

3

40

40

0,772023

44

19,2528

4

45

45

3,292522

41

17,87579

5

48

48

3,118136

48

0,085569

6

53

53

4,240005

51

3,541413

7

58

58

4,693074

57

0,577592

8

67

67

7,260639

63

18,54961

9

79

79

10,086

74

22,46155

10

85

85

7,650139

89

16,69538

11

88

88

4,877969

93

21,6238

12

90

90

3,162274

93

8,282706

13

93

12,634

Przykład obliczeniowy (7)

α=1 oraz β=0,951541620905999

F

1

oraz S

1

na podstawie najmniejszego błędu prognoz wygasłych

t

y

t

F

t

S

t

y*

t

=F

t-1

+S

t-1

(y

t

-y*

t

)

2

1

37

41,35685

0

-

-

2

41

41

-0,339554

41

0,127339

3

40

40

-0,967996

41

0,436189

4

45

45

4,710801

39

35,61697

5

48

48

3,082903

50

2,926839

6

53

53

4,907101

51

3,675262

7

58

58

4,995498

58

0,00863

8

67

67

8,805948

63

16,03603

9

79

79

11,84522

76

10,20197

10

85

85

6,28325

91

34,16661

11

88

88

3,159101

91

10,77973

12

90

90

2,056168

91

1,343515

13

92

10,48355

Model trendu pełzającego z wagami harmonicznymi

Procedura metody jest następująca:

I.

Ustalenie stałej wygładzania k < n;

II.

Oszacowanie na podstawie kolejnych fragmentów szeregu o długości k
liniowych funkcji trendu

III.

Obliczenie wartości teoretycznych wynikających z poszczególnych funkcji
trendu;

IV. Obliczenie wartości trendu pełzającego dla każdego okresu t (średnia

arytmetyczna z wartości teoretycznych adekwatnych funkcji trendu dla danego
okresu);

V.

Obliczenie przyrostów funkcji trendu:

VI. Nadanie wag poszczególnym przyrostom:

VII. Określenie średniego przyrostu trendu jako średniej ważonej wszystkich

obliczonych przyrostów

VIII. Wyznaczenie prognozy punktowej na okres T:

∑

−

=

+

+

⋅

=

1

n

1

t

1

t

n

1

t

w

C

w

∑

=

+

−

−

=

t

1

i

n

1

t

i

n

1

1

n

1

C

1

−

−

=

t

w

t

w

t

y

y

w

w

n

T

y

Y

n

w

T

⋅

−

+

=

)

(

*

Przykład obliczeniowy (1)

Na podstawie danych z poprzedniego przykładu (sprzedaż pralek firmy „Wolar”)
postaw prognozę na następny miesiąc przy zastosowaniu modelu trendu
pełzającego z wagami harmonicznymi.

I.

Niech k=3, im wyższa wartość stałej k, tym większe wygładzenie szeregu i
tym słabsze reagowanie na zmiany zachodzące w szeregu czasowym

t

a1

a0

1

"1-3"

1,5

36,33333

2

"2-4"

2

36

3

"3-5"

4

28,33333

4

"4-6"

4

28,66667

5

"5-7"

5

23

6

"6-8"

7

10,33333

7

"7-9"

10,5

-16

8

"8-10"

9

-4

9

"9-11"

4,5

39

10

"10-12"

2,5

60,16667

Przykład obliczeniowy (2)

Wartości teoretyczne

1

2

3

4

5

6

7

8

9

10

1 37,83
2 39,33 40,00
3 40,83 42,00 40,33
4

44,00 44,33 44,67

5

48,33 48,67 48,00

6

52,67 53,00 52,33

7

58,00 59,33 57,50

8

66,33 68,00 68,00

9

78,50 77,00 79,50

10

86,00 84,00 85,17

11

88,50 87,67

12

90,17

Przykład obliczeniowy (3)

Wartości wygładzone- trend pełzający

średnie wartoście teoretyczne

1

37,83

2

39,67

3

41,06

4

44,33

5

48,33

6

52,67

7

58,28

8

67,44

9

78,33

10

85,06

11

88,08

12

90,17

Przykład obliczeniowy (4)

Przyrosty funkcji trendu pełzającego

przyrosty

1
2

1,83

3

1,39

4

3,28

5

4,00

6

4,33

7

5,61

8

9,17

9

10,89

10

6,72

11

3,03

12

2,08

Przykład obliczeniowy (5)

Nadanie wag przyrostom

Wagi realizują postulat postarzania informacji – najnowsze przyrosty mają
największe znaczenia. Suma wag wynosi 1.

wagi

1
2

0,008264463

3

0,017355372

4

0,027456382

5

0,038820018

6

0,051807031

7

0,066958547

8

0,085140365

9

0,107867637

10

0,138170668

11

0,183625213

12

0,274534304

Przykład obliczeniowy (6)

wagi

przyrosty

iloczyn

1
2

0,008264463

1,83 0,015152

3

0,017355372

1,39 0,024105

4

0,027456382

3,28 0,089996

5

0,038820018

4,00

0,15528

6

0,051807031

4,33 0,224497

7

0,066958547

5,61 0,375712

8

0,085140365

9,17 0,780453

9

0,107867637

10,89 1,174559

10

0,138170668

6,72 0,928814

11

0,183625213

3,03 0,555976

12

0,274534304

2,08 0,571946

4,89649

95

89649

4

)

12

13

(

17

,

90

*

13

≈

⋅

−

+

=

,

Y

Modele szeregów czasowych z wahaniami

okresowymi zmiennej prognozowanej (1)

Metoda wskaźników

•

gdy występują wahania sezonowe wraz z tendencją rozwojową lub

stałym przeciętnym poziomem

• prognozę wyznacza się na podstawie wartości funkcji trendu
skorygowanej o wskaźnik sezonowości

• przy wahaniach bezwzględnie stałych (gdy amplitudy wahań, w
analogicznych okresach są stałe) może być model addytywny:

• przy wahaniach względnie stałych (wielkości amplitud zmieniają się
mniej więcej w tym samym stosunku) może być model multiplikatywny:

•gdzie to wielkość prognozy wyznaczona z funkcji trendu lub
stałego przeciętnego poziomu

i

w

T

Ti

c

y

y

+

=

)

*(

*

i

w

T

Ti

c

y

y

⋅

=

)

*(

*

)

*(w

T

y

Modele szeregów czasowych z wahaniami

okresowymi zmiennej prognozowanej (2)

1.Oblicza się następujące wartości (eliminacja trendu):

2.Oblicza się „surowe wskaźniki sezonowości” (eliminacja oddziaływania
składnika losowego):

k – liczba jednoimiennych faz w szeregu; r – liczba faz w cyklu

3.Wyznacza się „czyste wskaźniki sezonowości” (informują o natężeniu
wahań sezonowych):

4.Wyznacza się wartość prognozy:

t

ti

ti

t

ti

ti

y

ˆ

y

z

y

ˆ

y

z

=

−

=

lub

∑

−

=

×

+

=

1

0

1

k

j

i

,

r

j

i

i

z

k

z

∑

=

=

=

−

=

r

i

i

i

i

i

i

z

r

q

q

z

c

q

z

c

1

1

gdzie

,

lub

i

w

t

ti

i

w

t

ti

c

y

y

c

y

y

⋅

=

+

=

)

*(

*

)

*(

*

lub

Przykład obliczeniowy (1)

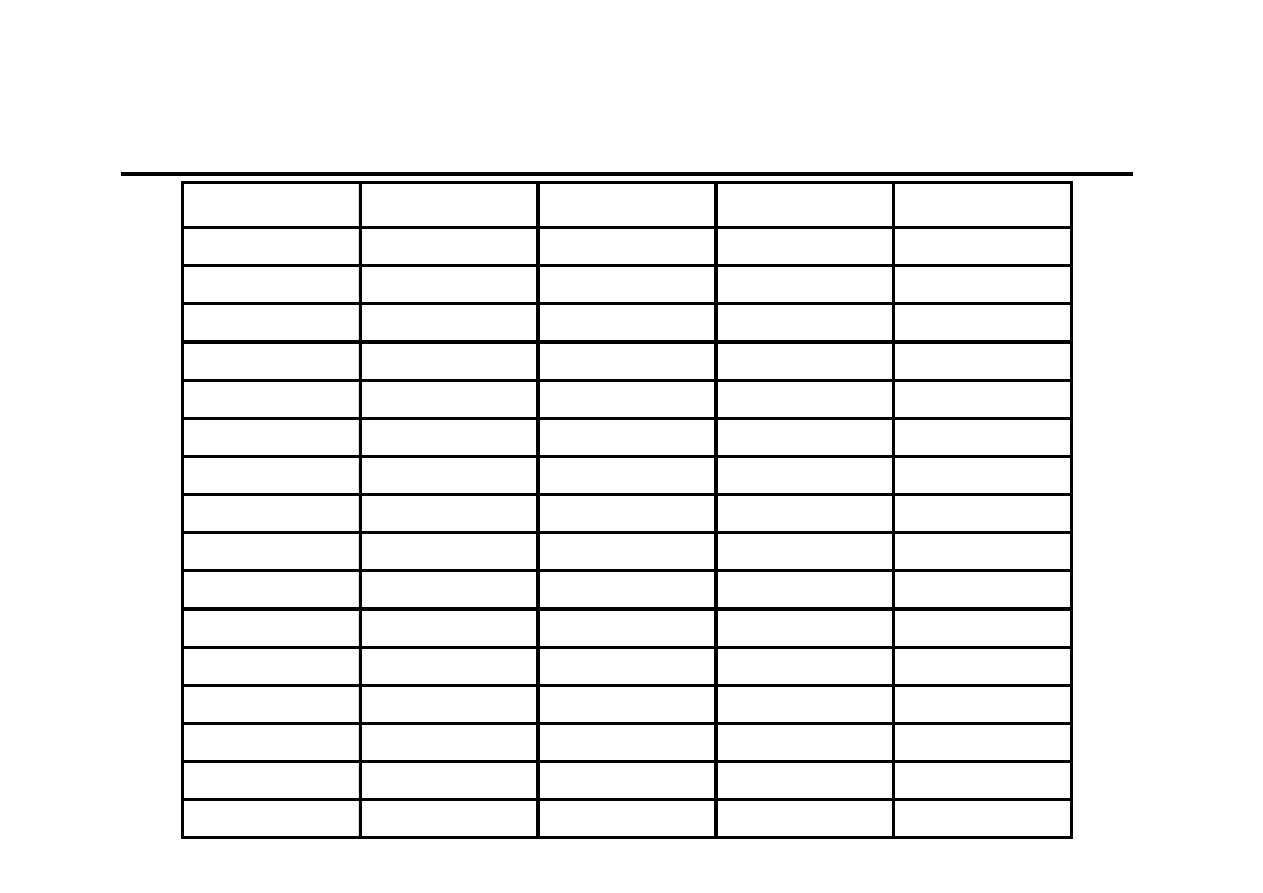
Firma „Czarny diament” prowadzi sprzedaż paliwa
opałowego klientom indywidualnym. Dochody firmy zależą
praktycznie od wielkości sprzedaży miału opałowego. Dane
dotyczące kwartalnej wielkości sprzedaży miału [t]
z ostatnich lat przedstawiono w poniższej tabeli. Należy
wyznaczyć prognozę na kolejne kwartały.

480

590

770

660

410

520

700

590

360

480

660

560

310

400

550

450

0

100

200

300

400

500

600

700

800

900

1

2

3

4

5

6

7

8

9

10 11

12 13 14

15 16

Przykład obliczeniowy (2)

Analiza amplitud wahań dopuszcza stosowanie modelu addytywnego,
jak i multiplikatywnego.

Przykład obliczeniowy (3)

Model addytywny

-131

611

480

16

-11

601

590

15

180

590

770

14

81

579

660

13

-158

568

410

12

-38

558

520

11

153

547

700

10

54

536

590

9

-165

525

360

8

-34

514

480

7

156

504

660

6

67

493

560

5

-172

482

310

4

-71

471

400

3

89

461

550

2

0

450

450

1

y

t

-y

^

t

y

^

t

y

t

t

i

z

i

c

i

1

50,54

50,54

2

144,76

144,76

3

-38,51

-38,51

4

-156,79

-156,79

0

80

497

79

156

59

654

30

605

51

38

81

643

79

777

76

144

633,03

79

672

54

50

25

622

4

20

3

19

2

18

1

17

,

)

,

(

,

y

,

)

,

(

,

y

,

,

y

,

,

,

y

*

,

*

,

*

,

*

,

=

−

+

=

=

−

+

=

=

+

=

=

+

=

Przykład obliczeniowy (4)

Model multiplikatywny

0,784993

611

480

16

0,982202

601

590

15

1,30528

590

770

14

1,139636

579

660

13

0,721383

568

410

12

0,932612

558

520

11

1,280189

547

700

10

1,100716

536

590

9

0,685407

525

360

8

0,933025

514

480

7

1,310365

504

660

6

1,13614

493

560

5

0,642997

482

310

4

0,848647

471

400

3

1,194201

461

550

2

1,00049

450

450

1

y

t

/y

^

t

y

^

t

y

t

t

i

z

i

c

i

1

1,09

1,09

2

1,27

1,27

3

0,92

0,92

4

0,71

0,71

0,9999

95

463

71

0

59

654

02

595

92

0

81

643

62

805

27

1

633,03

97

680

09

1

25

622

4

20

3

19

2

18

1

17

,

,

,

y

,

,

,

y

,

,

y

,

,

,

y

*

,

*

,

*

,

*

,

=

⋅

=

=

⋅

=

=

⋅

=

=

⋅

=

Modele szeregów czasowych z wahaniami

okresowymi zmiennej prognozowanej (3)

Metoda trendów jednoimiennych okresów

• gdy występują wahania sezonowe wraz z tendencją rozwojową lub
stałym przeciętnym poziomem

• polega na szacowaniu parametrów analitycznej funkcji trendu
oddzielnie dla poszczególnych faz cyklu

• prognozę stawia się przez ekstrapolację odpowiedniej funkcji trendu

Przykład obliczeniowy

Należy wyznaczyć prognozę sprzedaży miału przez firmę
„Czarny diament” na kolejne kwartały metodą trendów
jednoimiennych okresów.

I

II

III

IV

450

550

400

310

560

660

480

360

590

700

520

410

660

770

590

480

t

y

t

,

,

y

t

,

y

t

,

,

y

*

,

t

*

,

t

*

,

t

*

,

t

14

250

25

15

25

360

5

17

530

5

16

5

449

4

3

2

1

+

=

+

=

+

=

+

=

530

20

14

250

650

19

25

15

25

360

845

18

5

17

530

730

17

5

16

5

449

4

20

3

19

2

18

1

17

=

⋅

+

=

=

⋅

+

=

=

⋅

+

=

=

⋅

+

=

*

,

*

,

*

,

*

,

y

,

,

y

,

y

,

,

y

Modele szeregów czasowych z wahaniami

okresowymi zmiennej prognozowanej (4)

Model Wintersa

• gdy występują wahania sezonowe wraz z tendencją rozwojową lub
stałym przeciętnym poziomem

• jest modelem z trzema równaniami

• może być multiplikatywny, wtedy prognoza wynosi:

• może być addytywny, wtedy prognoza wynosi:

r

T

n

n

*

T

C

)]

n

T

(

S

F

[

y

−

⋅

−

+

=

r

T

n

n

*

T

C

)

n

T

(

S

F

y

−

+

−

+

=

Modele szeregów czasowych z wahaniami

okresowymi zmiennej prognozowanej (5)

Model Wintersa multiplikatywny

]

;

[

,

,

C

)

(

F

y

C

,

S

)

(

)

F

F

(

S

),

S

F

)(

(

C

y

F

r

t

t

t

t

t

t

t

t

t

t

r

t

t

t

1

0

1

1

1

1

1

1

1

∈

−

+

=

−

+

−

=

+

−

+

=

−

−

−

−

−

−

γ

β

α

γ

γ

β

β

α

α

Modele szeregów czasowych z wahaniami

okresowymi zmiennej prognozowanej (6)

Model Wintersa addytywny

]

;

[

,

,

C

)

(

)

F

y

(

C

,

S

)

(

)

F

F

(

S

),

S

F

)(

(

)

C

y

(

F

r

t

t

t

t

t

t

t

t

t

t

r

t

t

t

1

0

1

1

1

1

1

1

1

∈

−

+

−

=

−

+

−

=

+

−

+

−

=

−

−

−

−

−

−

γ

β

α

γ

γ

β

β

α

α

Dowolne kombinacje

1

0

Średnia wartość

zmiennej

prognozowanej

z pierwszego cyklu

II

Ilorazy wartości

rzeczywistych do wartości

średniej (w pierwszym cyklu)

Różnica średnich

wartości z drugiego

i pierwszego cyklu

Wartość zmiennej

z pierwszej fazy

drugiego cyklu

I

C

1

(w pierwszym cyklu)

S

2

F

2

Modele szeregów czasowych z wahaniami

okresowymi zmiennej prognozowanej (7)

Propozycje wartości początkowych

Przykład obliczeniowy (1)

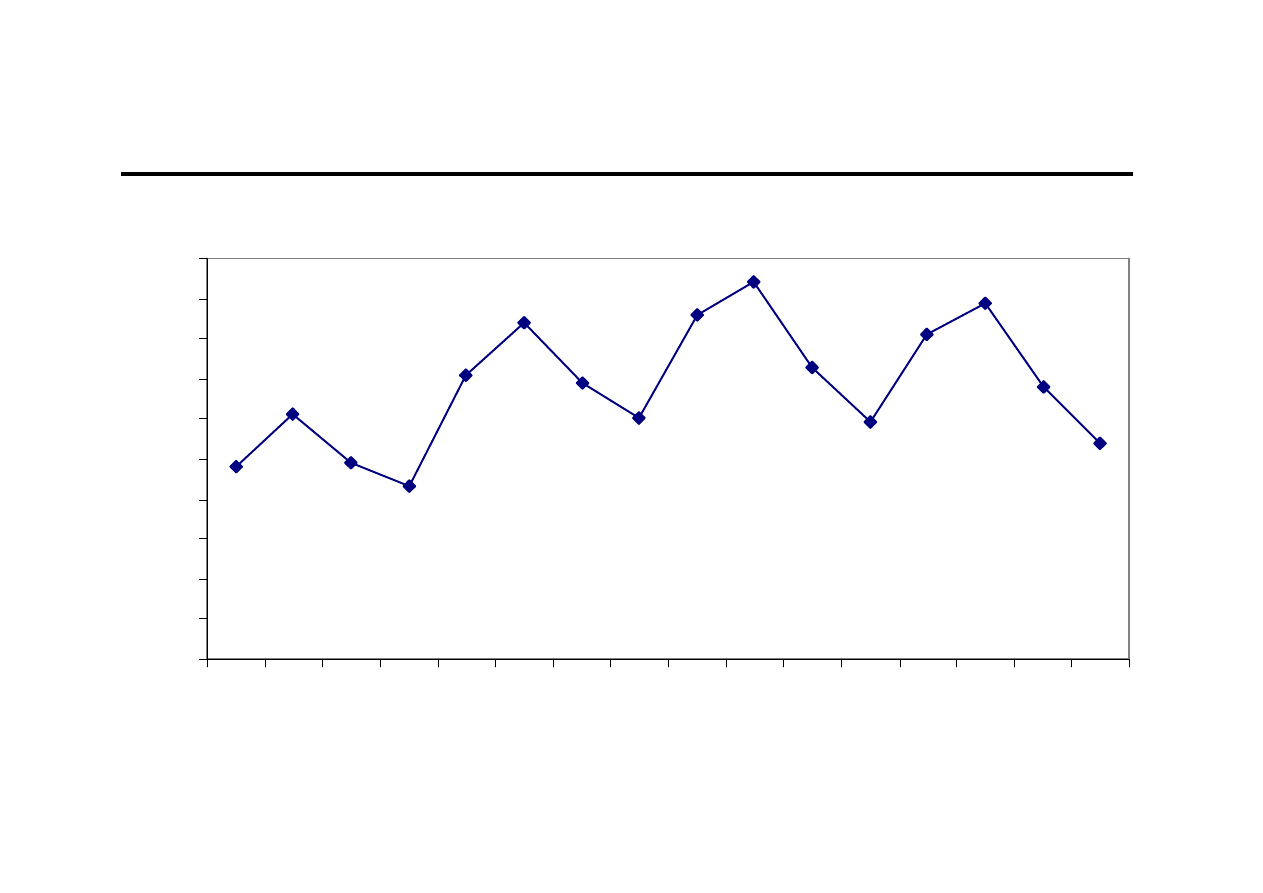
Firma „Save Lock” prowadzi sprzedaż wkładek
bębenkowych wysokiej klasy bezpieczeństwa. Dane
dotyczące miesięcznej wielkości sprzedaży [j.p.]
z ostatnich lat przedstawiono w poniższej tabeli. Należy
wyznaczyć prognozę na kolejne kwartały.

540

680

890

810

590

730

940

860

600

690

840

710

430

490

610

480

0

100

200

300

400

500

600

700

800

900

1000

1

2

3

4

5

6

7

8

9

10

11

12

13

14

15

16

Przykład obliczeniowy (2)

Przykład obliczeniowy (3)

• szereg cechuje sezonowość

• ostatnie obserwacje wskazują na zmianę tendencji

• najlepiej wykorzystać model adaptacyjny

• można wykorzystać model Wintersa

Zostanie wykorzystany multiplikatywny model Wintersa

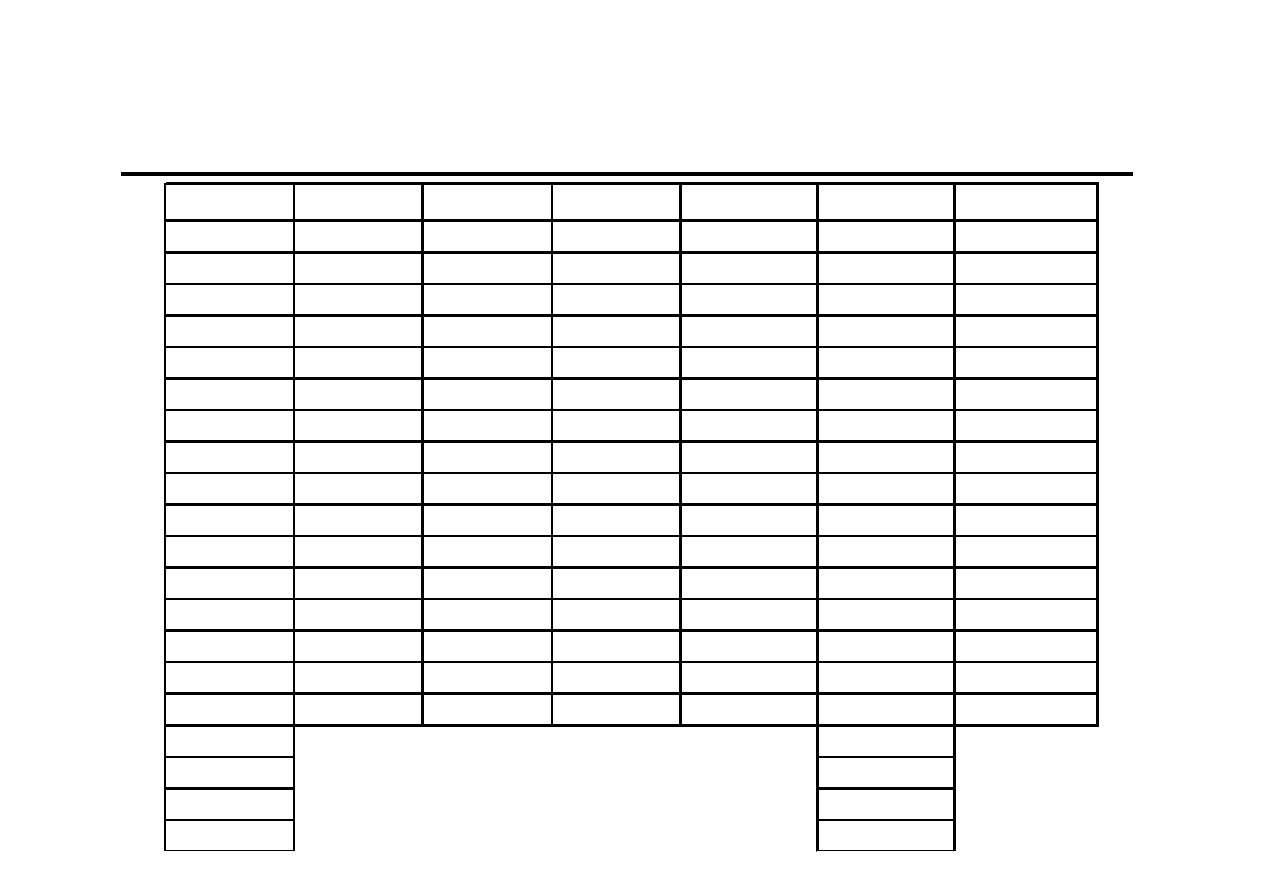
Przykład obliczeniowy (4)

Rozwiązanie początkowe dla

α

α

α

α=ββββ=γγγγ=0,5

t

y

t

F

t

S

t

C

t

y*

t

(y

t

-y

^

t

)

2

1

480

0,955

2

610

1,214

3

490

0,975

4

430

0,856

5

710

710

230

0,9776119

6

840

815,9836

168

1,1216814

1141

90657,914

7

690

845,7887

99

0,8954655

959

72629,393

8

600

822,925

38

0,792414

808

43425,99

9

860

870,3185

43

0,982878

842

336,07975

10

940

875,5258

24

1,097661

1024

7076,506

11

730

857,3503

3

0,873463

805

5693,4881

12

590

802,4005

-26

0,7638538

682

8402,8008

13

810

800,2407

-14

0,9975367

763

2201,6908

14

890

798,4804

-8

1,1061391

863

733,23613

15

680

784,5316

-11

0,8701111

691

110,6448

16

540

740,2675

-28

0,7466599

591

2592,0659

17

711

21259,983

18

758

19

572

20

470

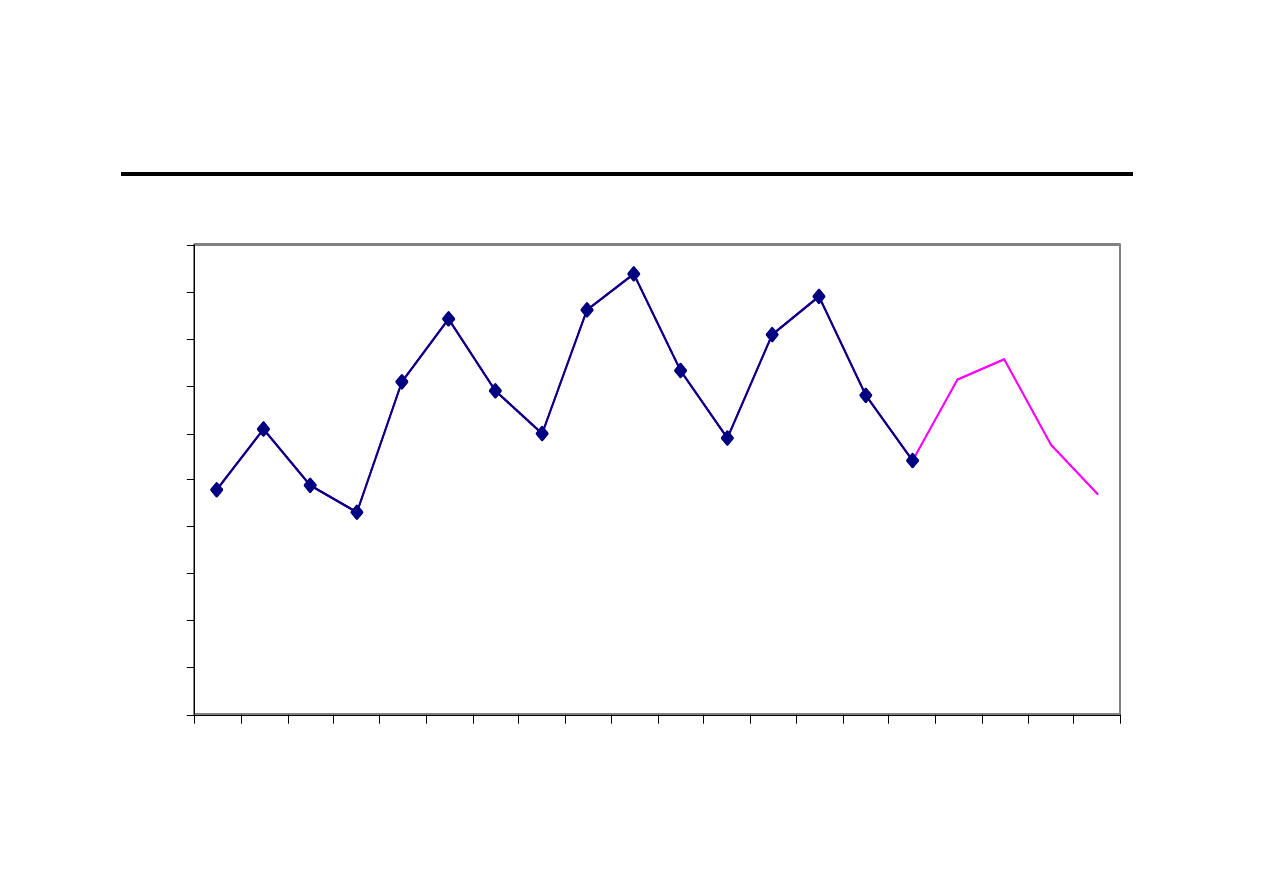
Przykład obliczeniowy (5)

0

100

200

300

400

500

600

700

800

900

1000

1

2

3

4

5

6

7

8

9 10 11 12 13 14 15 16 17 18 19 20

Przykład obliczeniowy (6)

α

α

α

α=0,82; ββββ=0,53; γγγγ=1,00

t

y

t

F

t

S

t

C

t

y*

t

(y

t

-y

^

t

)

2

1

480

0,955

2

610

1,214

3

490

0,975

4

430

0,856

5

710

710

230

1

6

840

736,4025

122

1,1406806

1141

90657,914

7

690

734,7055

57

0,9391518

838

21763,691

8

600

717,3676

18

0,8363912

677

5991,2408

9

860

837,6188

72

1,02672

735

15607,336

10

940

839,3696

35

1,119888

1037

9490,4107

11

730

794,6583

-7

0,9186338

821

8283,0782

12

590

720,1156

-43

0,8193129

659

4712,5909

13

810

768,9355

6

1,0534043

695

13117,563

14

890

791,1069

14

1,125006

867

510,77176

15

680

751,9158

-14

0,9043566

740

3590,787

16

540

673,2249

-48

0,8021094

605

4179,413

17

658

16173,163

18

649

19

478

20

386

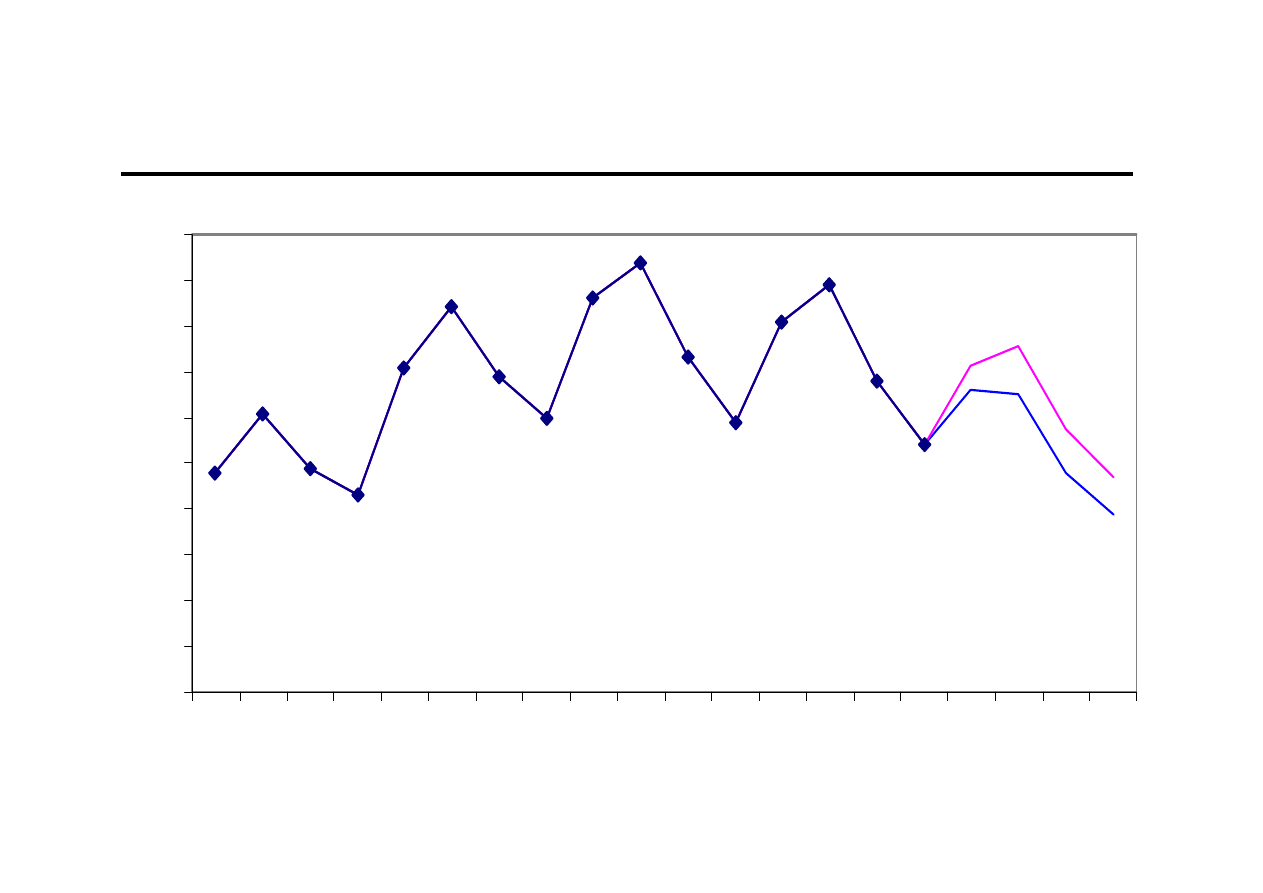
Przykład obliczeniowy (7)

0

100

200

300

400

500

600

700

800

900

1000

1

2

3

4

5

6

7

8

9 10 11 12 13 14 15 16 17 18 19 20

Modele szeregów czasowych z wahaniami

okresowymi zmiennej prognozowanej (8)

Analiza harmoniczna

• gdy występują wahania sezonowe wraz z tendencją rozwojową lub
stałym przeciętnym poziomem

• model buduje się w postaci sumy tzw. harmonik – funkcji
sinusoidalnych lub cosinusoidalnych o danym okresie

• pierwsza harmonika ma okres równy n, druga n/2, trzecia n/3, itd..

• liczba wszystkich harmonik wynosi n/2

• prognozę stawia się na podstawie modelu:

∑

=

























⋅

⋅

+













⋅

⋅

+

=

2

1

2

2

/

n

i

i

i

)

w

(

*

T

*

T

t

i

n

cos

t

i

n

sin

y

y

π

β

π

α

Modele szeregów czasowych z wahaniami

okresowymi zmiennej prognozowanej (9)

1. Jeśli występuje trend, to oblicza się następujące wartości (eliminacja
trendu):

2. Szacuje się parametry

α

0

,

α

i

,

β

i

modelu:

korzystając z zależności:

t

t

t

y

ˆ

y

'

y

−

=

,

n

,...,

i

,

t

i

n

cos

'

y

n

b

,

n

,...,

i

,

t

i

n

sin

'

y

n

a

,

'

y

n

a

n

t

t

i

n

t

t

i

n

t

t

1

2

1

dla

2

2

1

2

1

dla

2

2

1

1

1

1

0

−

=













⋅

⋅

⋅

=

−

=













⋅

⋅

⋅

=

=

∑

∑

∑

=

=

=

π

π

∑

=

























⋅

⋅

+













⋅

⋅

+

=

2

1

0

2

2

/

n

i

i

i

*

T

t

i

n

cos

t

i

n

sin

'

y

π

β

π

α

α

Modele szeregów czasowych z wahaniami
okresowymi zmiennej prognozowanej (10)

3. Z modelu można wyeliminować harmoniki, których udział

w wyjaśnianiu wariancji rozpatrywanej zmiennej jest najmniejszy.
Udział w wariancji zmiennej prognozowanej dla wszystkich oprócz
ostatniej harmoniki wynosi:

natomiast dla ostatniej:

gdzie:

s

2

jest szacunkiem wariancji zmiennej prognozowanej

2

2

2s

c

i

i

=

ω

2

2

s

c

i

i

=

ω

2

2

2

i

i

i

b

a

c

+

=

Przykład obliczeniowy (1)

Firma „Save Lock” prowadzi sprzedaż wkładek
bębenkowych wysokiej klasy bezpieczeństwa. Dane
dotyczące miesięcznej wielkości sprzedaży [j.p.]
z ostatnich lat przedstawiono w poniższej tabeli. Należy
wyznaczyć prognozę na kolejne kwartały za pomocą analizy
harmonicznej.

540

680

890

810

590

730

940

860

600

690

840

710

430

490

610

480

Przykład obliczeniowy (2)

0

100

200

300

400

500

600

700

800

900

1000

1

2

3

4

5

6

7

8

9

10

11

12

13

14

15

16

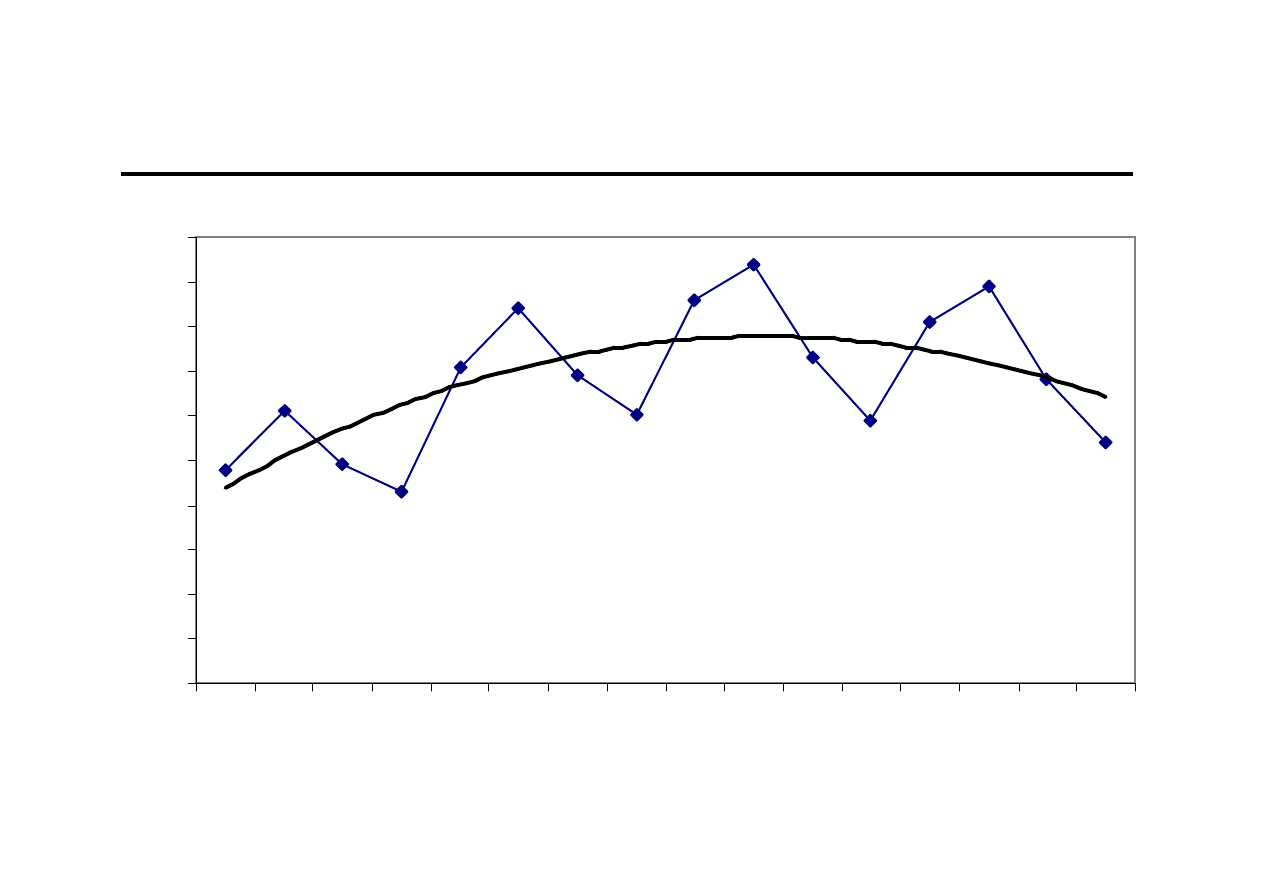
Występuje trend wielomianowy

Przykład obliczeniowy (3)

eliminacja trendu

y

t

t

t

2

y

^

t

y'=(y

t

-y

^

t

)

450

1

1

432,9289

17,07108

550

2

4

450,4485

99,55147

400

3

9

467,0053

-67,00525

310

4

16

482,5991

-172,5991

560

5

25

497,23

62,76996

660

6

36

510,8981

149,1019

480

7

49

523,6033

-43,60329

360

8

64

535,3456

-175,3456

590

9

81

546,125

43,875

700

10

100

555,9415

144,0585

520

11

121

564,7952

-44,79517

410

12

144

572,6859

-162,6859

660

13

169

579,6138

80,3862

770

14

196

585,5788

184,4212

590

15

225

590,5809

-0,580882

480

16

256

594,6201

-114,6201

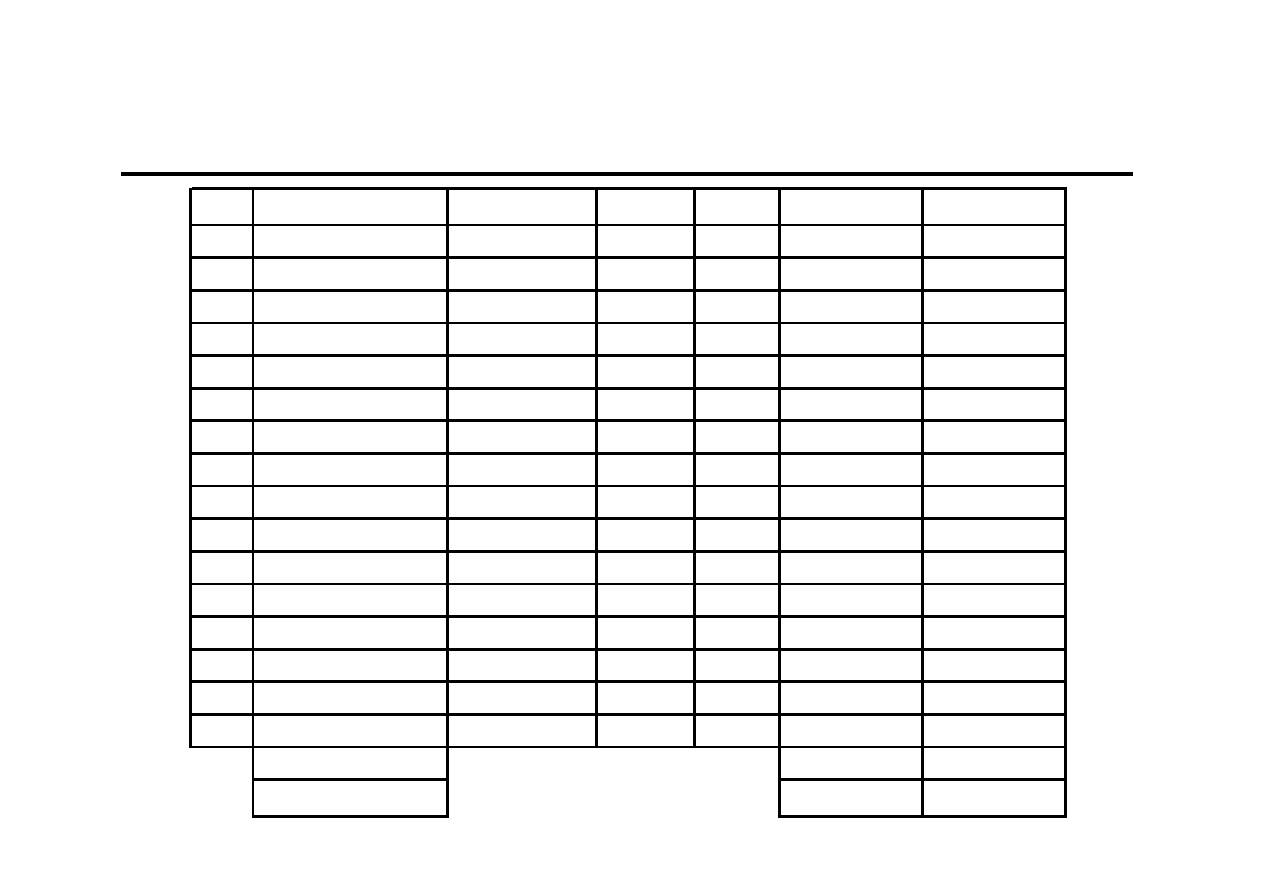
Przykład obliczeniowy (4)

Szacowanie wartości parametrów

α

α

α

α

0

,

α

α

α

α

1

,

ββββ

1

t

y'=(yt-y^t)

x=(2p/16)t

sinx

cosx

y

t

sin x

y

t

cos x

1

17,07107843 0,3926991 0,383

0,92

6,532819

15,77162

2

99,55147059 0,7853982 0,707

0,71

70,39352

70,39352

3

-67,0052521

1,1780972 0,924

0,38 -61,90478 -25,6418

4

-172,5990896 1,5707963

1

0

-172,5991 -1,06E-14

5

62,76995798 1,9634954 0,924 -0,38 57,99188 -24,02102

6

149,1018908 2,3561945 0,707 -0,71

105,431

-105,431

7

-43,60329132 2,7488936 0,383 -0,92 -16,68626 40,28419

8

-175,3455882 3,1415927 1E-16

-1

-2,15E-14 175,3456

9

43,875

3,5342917 -0,383 -0,92 -16,79024 -40,53521

10

144,0584734 3,9269908 -0,707 -0,71 -101,8647 -101,8647

11

-44,79516807 4,3196899 -0,924 -0,38 41,38534

17,14237

12

-162,6859244

4,712389

-1

-0

162,6859

2,99E-14

13

80,38620448 5,1050881 -0,924 0,38 -74,26717 30,76247

14

184,4212185 5,4977871 -0,707 0,71 -130,4055 130,4055

15

-0,580882353 5,8904862 -0,383 0,92

0,222294 -0,536665

16

-114,620098

6,2831853 -2E-16

1

2,81E-14 -114,6201

Σ

Σ

Σ

Σ 2,27374E-13

Σ

Σ

Σ

Σ -129,875 67,45477

α

α

α

α

0000

1,42109E-14

α

α

α

α

1111

-16,23438 8,431846

β

β

β

β

1111

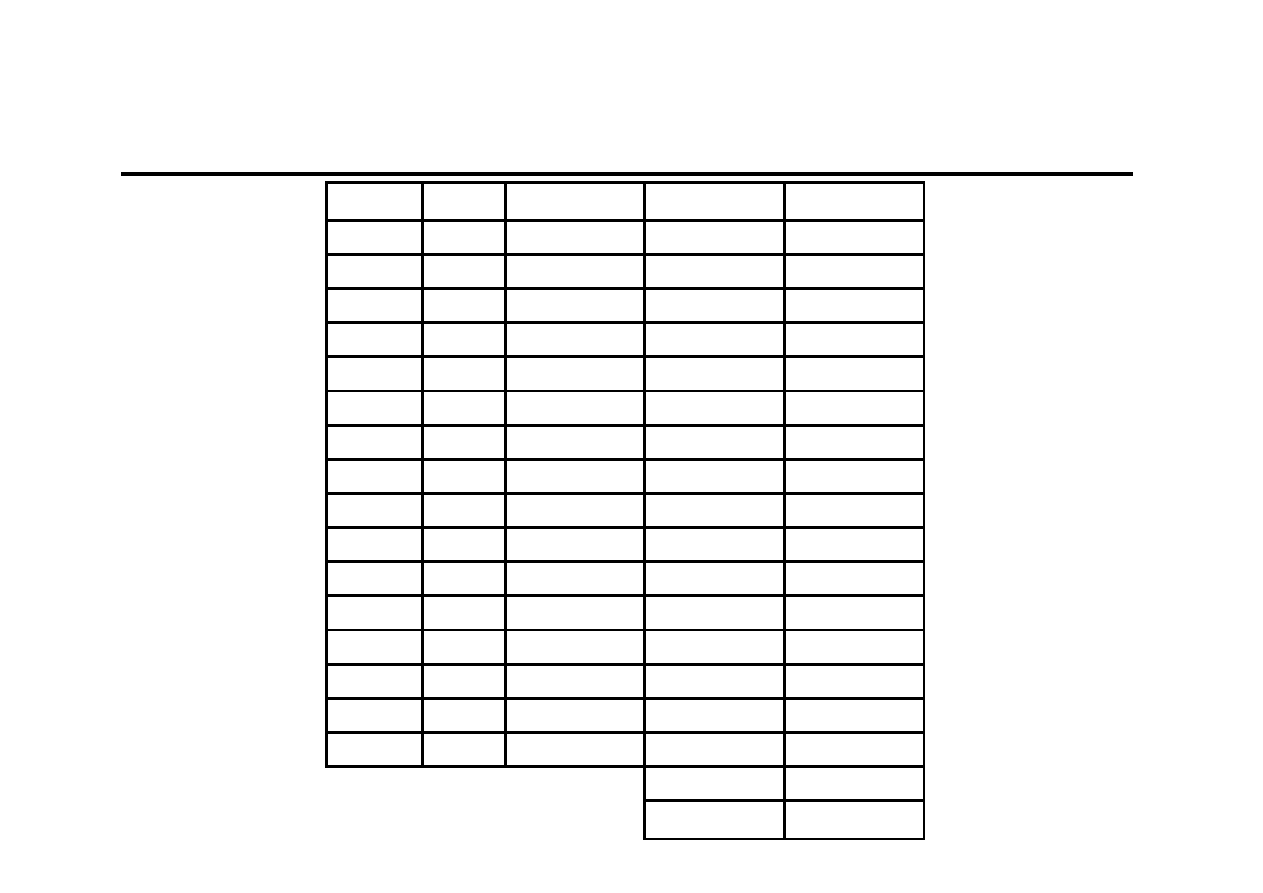
Przykład obliczeniowy (5)

Szacowanie wartości parametrów

α

α

α

α

2

,

ββββ

2

2x

sinx

cosx

y

t

sin x

y

t

cos x

0,785

0,71

0,707107 12,07108 12,07108

1,571

1

6,13E-17

99,55147

6,1E-15

2,356

0,71 -0,707107 -47,37987 47,37987

3,142

0

-1

-2,11E-14 172,5991

3,927 -0,71 -0,707107 -44,38506 -44,38506
4,712

-1

-1,84E-16 -149,1019 -2,74E-14

5,498 -0,71 0,707107 30,83218 -30,83218
6,283

-0

1

4,3E-14

-175,3456

7,069

0,71

0,707107 31,02431 31,02431

7,854

1

3,06E-16

144,0585

4,41E-14

8,639

0,71 -0,707107 -31,67497 31,67497

9,425

0

-1

-5,98E-14 162,6859

10,21 -0,71 -0,707107 -56,84163 -56,84163

11

-1

-4,29E-16 -184,4212 -7,91E-14

11,78 -0,71 0,707107 0,410746 -0,410746
12,57

-0

1

5,62E-14 -114,6201

Σ

Σ

Σ

Σ -195,8564 34,99993

α

α

α

α

2222

-24,48205 4,374991

ββββ

2222

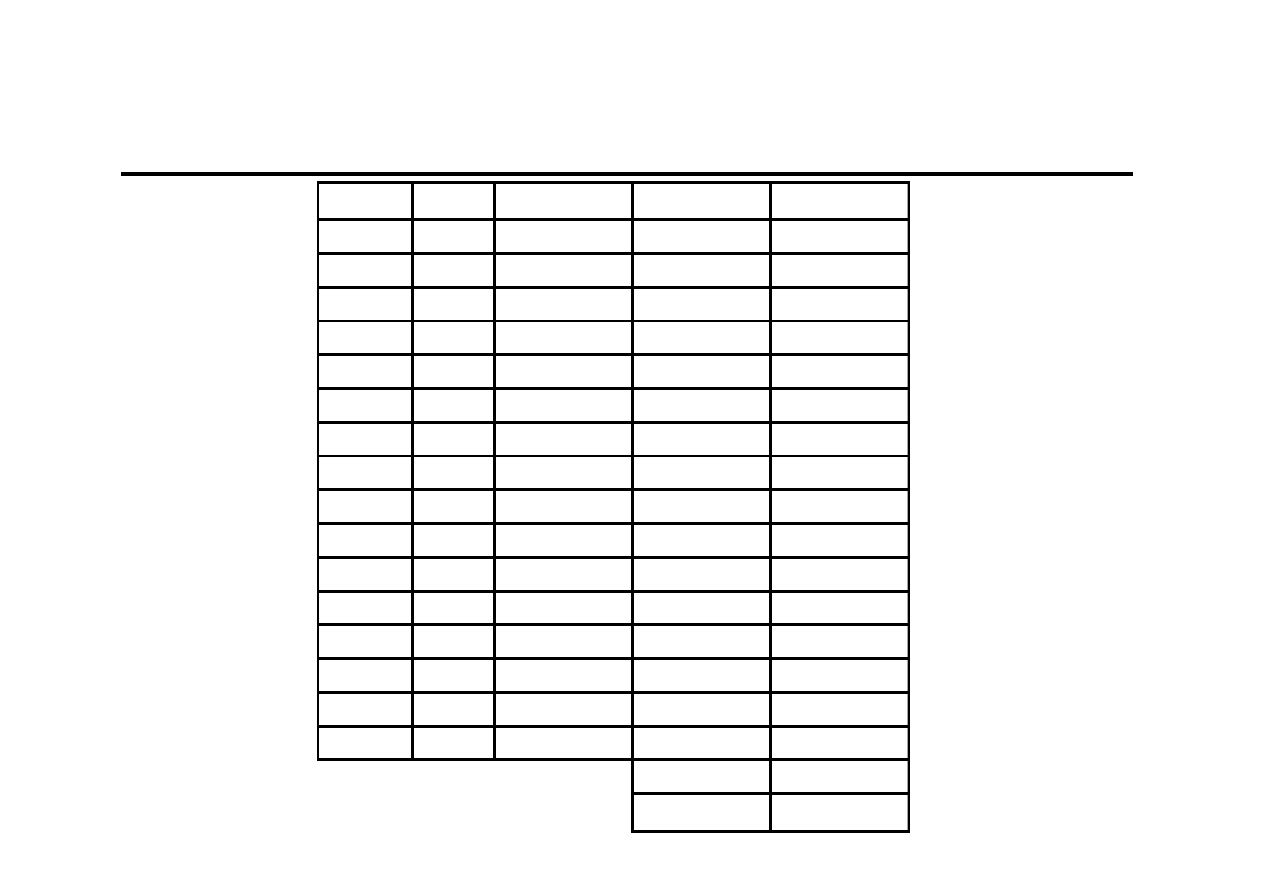
Przykład obliczeniowy (6)

Szacowanie wartości parametrów

α

α

α

α

3

,

ββββ

3

3x

sinx

cosx

y

t

sin x

y

t

cos x

1,178

0,92

0,382683 15,77162 6,532819

2,356

0,71 -0,707107 70,39352 -70,39352

3,534 -0,38

-0,92388

25,6418

61,90478

4,712

-1

-1,84E-16 172,5991

3,17E-14

5,89

-0,38

0,92388

-24,02102 57,99188

7,069

0,71

0,707107

105,431

105,431

8,247

0,92 -0,382683 -40,28419 16,68626

9,425

0

-1

-6,44E-14 175,3456

10,6

-0,92 -0,382683 -40,53521 -16,79024

11,78 -0,71 0,707107 -101,8647 101,8647
12,96

0,38

0,92388

-17,14237 -41,38534

14,14

1

5,51E-16 -162,6859 -8,97E-14

15,32

0,38

-0,92388

30,76247 -74,26717

16,49 -0,71 -0,707107 -130,4055 -130,4055
17,67 -0,92 0,382683 0,536665 -0,222294
18,85

-0

1

8,43E-14 -114,6201

Σ

Σ

Σ

Σ -95,80282 77,67286

α

α

α

α

3333

-11,97535 9,709107

ββββ

3333

Przykład obliczeniowy (7)

Szacowanie wartości parametrów

α

α

α

α

4

,

ββββ

4

4x

sinx

cosx

y

t

sin x

y

t

cos x

1,571

1

6,13E-17

17,07108

1,05E-15

3,142

0

-1

1,22E-14 -99,55147

4,712

-1

-1,84E-16 67,00525

1,23E-14

6,283

-0

1

4,23E-14 -172,5991

7,854

1

3,06E-16

62,76996

1,92E-14

9,425

0

-1

5,48E-14 -149,1019

11

-1

-4,29E-16 43,60329

1,87E-14

12,57

-0

1

8,59E-14 -175,3456

14,14

1

5,51E-16

43,875

2,42E-14

15,71

0

-1

8,82E-14 -144,0585

17,28

-1

-2,45E-15 44,79517

1,1E-13

18,85

-0

1

1,2E-13

-162,6859

20,42

1

-9,8E-16

80,3862

-7,88E-14

21,99

0

-1

1,58E-13 -184,4212

23,56

-1

-2,7E-15

0,580882

1,57E-15

25,13

-0

1

1,12E-13 -114,6201

Σ

Σ

Σ

Σ 360,0868 -1202,384

α

α

α

α

4444

45,01085

-150,298

ββββ

4444

Przykład obliczeniowy (8)

Szacowanie wartości parametrów

α

α

α

α

5

,

ββββ

5

5x

sinx

cosx

y

t

sin x

y

t

cos x

1,963

0,92 -0,382683 15,77162 -6,532819

3,927 -0,71 -0,707107 -70,39352 -70,39352

5,89

-0,38

0,92388

25,6418

-61,90478

7,854

1

3,06E-16 -172,5991 -5,29E-14

9,817 -0,38 -0,92388 -24,02102 -57,99188
11,78 -0,71 0,707107

-105,431

105,431

13,74

0,92

0,382683 -40,28419 -16,68626

15,71

0

-1

-1,07E-13 175,3456

17,67 -0,92 0,382683 -40,53521 16,79024
19,63

0,71

0,707107 101,8647 101,8647

21,6

0,38

-0,92388 -17,14237 41,38534

23,56

-1

-2,7E-15

162,6859

4,38E-13

25,53

0,38

0,92388

30,76247 74,26717

27,49

0,71 -0,707107 130,4055 -130,4055

29,45 -0,92 -0,382683 0,536665 0,222294
31,42

-0

1

1,4E-13

-114,6201

Σ

Σ

Σ

Σ -2,737666 56,77146

α

α

α

α

5555

-0,342208 7,096432

ββββ

5555

Przykład obliczeniowy (9)

Szacowanie wartości parametrów

α

α

α

α

6

,

ββββ

6

6x

sinx

cosx

y

t

sin x

y

t

cos x

2,356

0,71 -0,707107 12,07108 -12,07108

4,712

-1

-1,84E-16 -99,55147 -1,83E-14

7,069

0,71

0,707107 -47,37987 -47,37987

9,425

0

-1

-6,34E-14 172,5991

11,78 -0,71 0,707107 -44,38506 44,38506
14,14

1

5,51E-16

149,1019

8,22E-14

16,49 -0,71 -0,707107 30,83218 30,83218
18,85

-0

1

1,29E-13 -175,3456

21,21

0,71 -0,707107 31,02431 -31,02431

23,56

-1

-2,7E-15 -144,0585 -3,88E-13

25,92

0,71

0,707107 -31,67497 -31,67497

28,27

0

-1

-1,79E-13 162,6859

30,63 -0,71 0,707107 -56,84163 56,84163
32,99

1

-4,9E-16

184,4212 -9,04E-14

35,34 -0,71 -0,707107 0,410746 0,410746

37,7

-0

1

1,69E-13 -114,6201

Σ

Σ

Σ

Σ -16,03005 55,63873

α

α

α

α

6666

-2,003756 6,954841

ββββ

6666

Przykład obliczeniowy (10)

Szacowanie wartości parametrów

α

α

α

α

7

,

ββββ

7

7x

sinx

cosx

y

t

sin x

y

t

cos x

2,749

0,38

-0,92388

6,532819 -15,77162

5,498 -0,71 0,707107 -70,39352 70,39352
8,247

0,92 -0,382683 -61,90478

25,6418

11

-1

-4,29E-16 172,5991

7,4E-14

13,74

0,92

0,382683 57,99188 24,02102

16,49 -0,71 -0,707107 -105,431

-105,431

19,24

0,38

0,92388

-16,68626 -40,28419

21,99

0

-1

-1,5E-13

175,3456

24,74 -0,38

0,92388

-16,79024 40,53521

27,49

0,71 -0,707107 101,8647 -101,8647

30,24 -0,92 0,382683 41,38534 -17,14237
32,99

1

-4,9E-16 -162,6859 7,97E-14

35,74 -0,92 -0,382683 -74,26717 -30,76247
38,48

0,71

0,707107 130,4055 130,4055

41,23 -0,38

-0,92388

0,222294 0,536665

43,98

-0

1

1,97E-13 -114,6201

Σ

Σ

Σ

Σ 2,842793 41,00288

α

α

α

α

7777

0,355349

5,12536

ββββ

7777

Przykład obliczeniowy (11)

Szacowanie wartości parametrów

α

α

α

α

8

,

ββββ

8

8x

sinx

cosx

y

t

sin x

y

t

cos x

3,142

0

-1

2,09E-15 -17,07108

6,283

-0

1

-2,44E-14 99,55147

9,425

0

-1

-2,46E-14 67,00525

12,57

-0

1

8,46E-14 -172,5991

15,71

0

-1

3,85E-14 -62,76996

18,85

-0

1

-1,1E-13

149,1019

21,99

0

-1

-3,74E-14 43,60329

25,13

-0

1

1,72E-13 -175,3456

28,27

0

-1

4,84E-14

-43,875

31,42

-0

1

-1,76E-13 144,0585

34,56

0

-1

-2,2E-13

44,79517

37,7

-0

1

2,39E-13 -162,6859

40,84

-0

-1

-1,58E-13 -80,3862

43,98

-0

1

-3,16E-13 184,4212

47,12

0

-1

-3,13E-15 0,580882

50,27

-0

1

2,25E-13 -114,6201

Σ

Σ

Σ

Σ -2,6E-13 -96,23529

α

α

α

α

8888

-3,25E-14 -12,02941

ββββ

8888

Przykład obliczeniowy (12)

Udział harmonik w wariancji

Nr harmoniki

a

i

b

i

c

i

c

i

2

ω

ω

ω

ω

i

[%]

1

-16,23438

8,431846

18,29347

334,651

1,28%

2

-24,48205

4,374991

24,86989

618,5112

2,36%

3

-11,97535

9,709107

15,41674

237,6758

0,91%

4

45,01085

-150,298

156,8931

24615,46

93,86%

5

-0,342208

7,096432

7,104679

50,47646

0,19%

6

-2,003756

6,954841

7,237738

52,38485

0,20%

7

0,355349

5,12536

5,137664

26,39559

0,10%

8

-3,25E-14 -12,02941

12,02941

144,7067

1,10%

144,7067

100,00%

Σ

Σ

Σ

Σ 26224,96

s

2

13112,48

Ponieważ harmonika 4 wyjaśnia
prawie 94% zmienności zmiennej
prognozowanej, to do
prognozowania wykorzystany
będzie model tylko z tą harmoniką

Przykład obliczeniowy (13)

Model prognostyczny

Postać analityczna funkcji trendu

2

48

0

96

18

45

414

t

,

t

,

,

)

t

(

f

y

)

w

*(

T

−

+

=

=

Postać modelu

t

cos

,

t

sin

,

t

,

t

,

,

y

ˆ

t

2

30

150

2

01

45

48

0

96

18

45

414

2

π

π

−

+

−

+

=

20

2

30

150

20

2

01

45

20

48

0

20

96

18

45

414

19

2

30

150

19

2

01

45

19

48

0

19

96

18

45

414

18

2

30

150

18

2

01

45

18

48

0

18

96

18

45

414

17

2

30

150

17

2

01

45

17

48

0

17

96

18

45

414

2

20

2

19

2

18

2

17

π

π

π

π

π

π

π

π

cos

,

sin

,

,

,

,

y

cos

,

sin

,

,

,

,

y

cos

,

sin

,

,

,

,

y

cos

,

sin

,

,

,

,

y

*

*

*

*

−

+

⋅

−

⋅

+

=

−

+

⋅

−

⋅

+

=

−

+

⋅

−

⋅

+

=

−

+

⋅

−

⋅

+

=

Przykład obliczeniowy (14)

Prognoza

451

556

750

643

20

19

18

17

=

=

=

=

*

*

*

*

y

y

y

y

Prognozowanie na podstawie modelu

ekonometrycznego WIELORÓWNANIOWEGO

1. Model prosty: każde równanie można potraktować jako oddzielny

model – prognozowanie jak w przypadku modelu jednorównaniowego.

2. Model rekurencyjny: występują jednokierunkowe powiązania między

nie opóźnionymi zmiennymi endogenicznymi.

Stosuje się prognozowanie łańcuchowe, które polega na określeniu
wartości prognozy pierwszej zmiennej endogenicznej i obliczeniu przy
jej wykorzystaniu prognoz następnych zmiennych w kolejności
zgodnej z uporządkowaniem przyczynowym.

Błędy ex ante wyznacza się dla każdego równania oddzielnie
analogicznie jak w modelu jednorównaniowym.

Rozwiązanie. Wielkość produkcji (Y

1

) oraz zatrudnienia (Y

2

) opisano

modelem:

gdzie X

1

oznacza wielkość sprzedaży z poprzedniego roku

Przykład obliczeniowy (1)

Przedsiębiorstwo „Urban” produkujące sprzęt wędkarski zleciło
wyznaczenie wielkości produkcji i zatrudnienia na następny okres.
Prognozy te będą służyły wspomaganiu decyzji dotyczącej
przyjmowanej strategii marketingowej w najbliższym czasie.
Przyjęto, że prognozy będą użyteczne, jeśli nie będą obarczone
błędem większym niż 5%.

t

t

t

t

t

t

Y

Y

X

Y

2

1

1

0

2

1

1

1

1

0

1

ξ

β

β

ξ

α

α

+

+

=

+

+

=

−

Przykład obliczeniowy (2)

348

10

343

297

1574

9

326

274

1520

8

297

235

1430

7

292

229

1415

6

289

225

1405

5

284

218

1389

4

266

194

1334

3

255

179

1300

2

234

151

1234

1

x

1t-1

y

2t

y

1t

t

Przykład obliczeniowy (3)

1,780510219

87857,11

7

345406,5

0,504339769

0,99998

1,531043267

0,005296

505,7380532

3,112667

REGLINP dla pierwszego równania:

t

t

t

X

Y

1

1

1

1

112667

,

3

7380532

,

505

ξ

+

⋅

+

=

−

Przykład obliczeniowy (4)

Obliczanie wartość teoretycznych Y

1

, które będą

wykorzystane do szacowania drugiego równania:

1

1

1

112667

,

3

7380532

,

505

*

−

⋅

+

=

t

t

X

Y

348

10

1573,383

343

297

1574

9

1520,468

326

274

1520

8

1430,2

297

235

1430

7

1414,637

292

229

1415

6

1405,299

289

225

1405

5

1389,736

284

218

1389

4

1333,708

266

194

1334

3

1299,468

255

179

1300

2

1234,102

234

151

1234

1

y*

1t

x

1t-1

y

2t

y

1t

t

Przykład obliczeniowy (5)

REGLINP dla drugiego równania:

t

2

t

1

t

2

Y

429987

,

0

585000

,

379

Y

ξ

+

⋅

+

−

=

0,433319

16243,79

7

262408,6

0,248802

0,999973

1,178168

0,000839

-379,585

0,429987

Przykład obliczeniowy (6)

Macierze wariancji i kowariancji:













−

−

=

+

⋅

+

−

=

000001

,

0

000986

,

0

000986

,

0

388081

,

1

)

(

429987

,

0

585000

,

379

2

2

1

2

a

D

Y

Y

t

t

t

ξ













=

+

⋅

+

=

−

000028

,

0

0,008060

-

0,008060

-

2,344093

)

(

112667

,

3

7380532

,

505

2

1

1

1

1

a

D

X

Y

t

t

t

ξ

Przykład obliczeniowy (7)

Wartości prognoz i błędy ex ante:

304

946

,

1588

429987

,

0

585000

,

379

*

Y

946

,

1588

348

112667

,

3

7380532

,

505

*

Y

10

,

2

10

,

1

≈

⋅

+

−

=

=

⋅

+

=

306440

,

0

*

621174

,

0

*

10

,

2

10

,

1

=

=

V

V

%

100922

,

0

*

%

039093

,

0

*

10

,

2

10

,

1

=

=

η

η

Prognozowana wielkość produkcji wynosi 1588,946 , jest

obarczona błędem względnym 0,039093%, natomiast

prognozowane zatrudnienie wynosi 304, jest obarczone błędem

względnym 0,100922%. W obu przypadkach prognozy są

dopuszczalne.

• Analogie historyczne

• Polegają na przenoszeniu prawidłowości historycznych wykrytych
w jednych zmiennych (wiodących, wyprzedzających – służące do
budowy prognozy) na inne zmienne (opóźnione, naśladujące –
prognozowane) dotyczące tego samego obiektu prognostycznego
• Dotyczą prognoz średnio- i długookresowych. Prognosta
przyjmuje postawę aktywną

• Analogie przestrzenno-czasowe

• Polegają na przenoszeniu prawidłowości historycznych wykrytych
w jednych obiektach na inne obiekty
• Dotyczą prognoz średnio- i długookresowych. Prognosta
przyjmuje postawę aktywną

Prognozowanie przez analogie (1)

Analogie historyczne

Przykład

Przedsiębiorstwo „Podwiązka” sp. z o.o. produkuje
dwa rodzaje pończoch: wzorzyste i ażurowe.
Wzorzyste są sprzedawane od kilku lat, a ażurowe
od kilku miesięcy. Wielkość sprzedaży obu
rodzajów pończoch podano
w kolejnej tabeli. Należy wyznaczyć przewidywaną
wielkość sprzedaży pończoch ażurowych na
najbliższe miesiące, wiedząc, że wymagania
menedżerów zostaną spełnione, gdy względny
błąd ex ante nie przekroczy 5%.

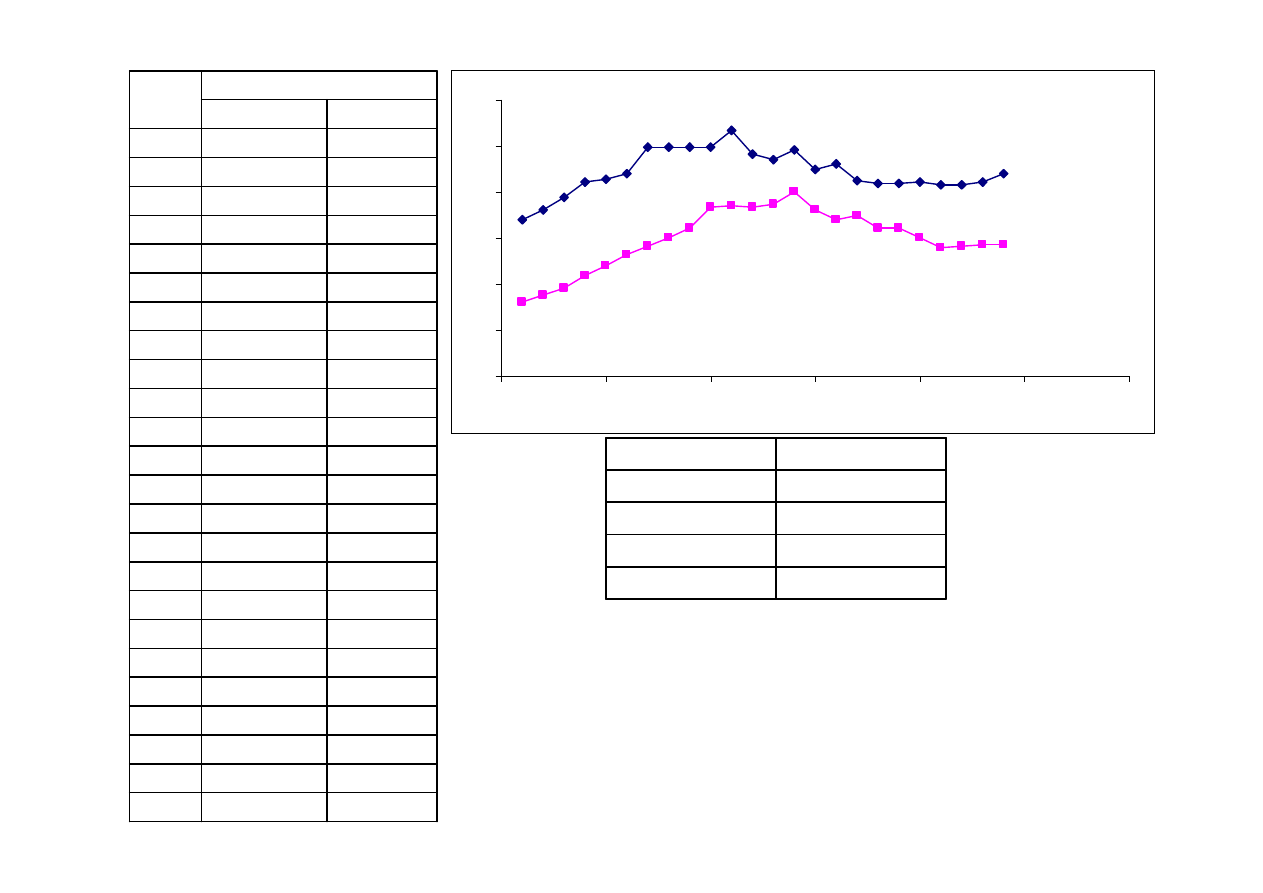
22

14,3

24

21

14,2

23

20,8

14,1

22

20,7

14

21

21,1

15

20

20,9

16,1

19

20,9

16

18

21,2

17,5

17

23

17

16

22,5

18,1

15

24,5

20

14

23,5

18,7

13

24,1

18,4

12

26,6

18,5

11

24,9

18,3

10

24,8

16

9

24,9

15

8

24,8

14,1

7

22

13,2

6

21,4

12

5

21,1

10,9

4

19,4

9,5

3

18,1

8,8

2

17

8

1

Ażurowe

Wzorzyste

Sprzedaż w tysiącach sztuk

t

0

5

10

15

20

25

30

0

5

10

15

20

25

30

376

,

6

006

,

1

3

+

⋅

=

−

t

t

x

y

y

t

– wlk sprzedaży pończoch ażurowych w

okresie t [tys. szt.]

X

t-3

– wlk sprzedaży pończoch wzorzystych w

okresie nr t-3 [tys. szt.]

2,193387

117,938

19

1021,627

0,339767

0,981742

0,502368

0,031485

6,375845

1,006359

6

,

20

376

,

6

1

,

14

006

,

1

376

,

6

006

,

1

22

*

25

≈

+

⋅

=

+

⋅

=

x

y

7

,

20

376

,

6

2

,

14

006

,

1

376

,

6

006

,

1

23

*

26

≈

+

⋅

=

+

⋅

=

x

y

8

,

20

376

,

6

3

,

14

006

,

1

376

,

6

006

,

1

24

*

27

≈

+

⋅

=

+

⋅

=

x

y

Prognozowana wielkość sprzedaży pończoch

ażurowych na kolejne 3 okresy:

25

0,452980819

2,203%

26

0,473773119

2,293%

27

0,495694413

2,387%

Bezwględny

błąd ex ante

Wględny błąd

ex ante

T

Heurystyczne metody prognozowania

METODA DELFICKA

Do prognozowania zjawisk nowych, dla których ilość informacji
historycznych jest niewielka. Polega na badaniu opinii niezależnych i
kompetentnych ekspertów na określony, prognostyczny temat.
Opinie te najczęściej dotyczą prawdopodobieństwa lub czasu
zaistnienia przyszłych zdarzeń, którą wyznacza się przez
zastosowananie reguły największego prawdopodobieństwa

•Heurystyka (grec. heurisko – znajduję, odkrywam) – umiejętność
wykrywania nowych faktów i związków między faktami, prowadząca
do poznania nowych prawd.

•Heurystyczne metody prognozowania – to metody
wykorzystujące do budowy prognozy opinie ekspertów, czyli osób
wybranych ze względu na ich wiedzę, doświadczenie, autorytet.

•Opinie ekspertów są oparte na ich intuicji i doświadczeniu

SYMULACJA (1)

similis (łac.) - podobieństwo, podobny

similo (łac.) - podobny

simulare (łac.) - udawać, upodabniać się

mimeisthai (grec.) - naśladować, grać rolę

imitatio (łac.) - naśladowanie

SYMULACJA (2)

Symulacja -

eksperyment

prowadzony na pewnego rodzaju

modelu

- matematycznym, informatycznym lub rzeczywistym,

celem określenia znaczenia zmian wartości parametrów lub

wartości zmiennych objaśniających dla wartości zmiennych

prognozowanych.

Wikipedia (

http://pl.wikipedia.org

):

Symulacja komputerowa to technika polegająca na sprawdzaniu, jak
zachowuje się dany

system

w różnych okolicznościach, a więc jaka jest

wartość

zmiennej

wyjściowej, przy założeniu różnych wartości

zmiennych

wejściowych.

Symulacje komputerowe

polegają na zbudowaniu

odpowiedniego

modelu

matematycznego zapisanego w komputerze (np. w

arkuszu kalkulacyjnym lub w dowolnym

języku programowania

), który

zawiera powiązania między zmiennymi wejściowymi a interesującą nas
zmienną wyjściową. Techniki symulacyjne są szczególnie przydatne tam,
gdzie analityczne wyznaczenie rozwiązania byłoby bardzo pracochłonne, a
niekiedy nawet niemożliwe.

SYMULACJA DETERMINISTYCZNA

Symulacja z wykorzystaniem metody iteracyjnej Gaussa-Seidela

jako narzędzie do rozwiązywania (prognozowania) modeli

ekonometrycznych liniowych i nieliniowych

Metoda iteracyjna Gaussa-Seidela na przykładzie prognozowania

na podstawie ekonometrycznego modelu wielorównaniowego

o równaniach współzależnych

)

,

,

,

,

(

)

,

,

(

)

,

,

(

3

2

1

2

1

3

3

3

1

1

2

2

2

1

3

1

1

x

x

x

y

y

f

y

x

x

y

f

y

x

x

y

f

y

=

=

=

y

1

y

2

y

3

Metoda Gaussa-Seidela (1)

Znane są postaci analityczne: f

1

, f

2

, f

3

, wartości parametrów

strukturalnych oraz prognozowane wartości zmiennych

egzogenicznych.

1

0

Przyjmuje się y

3

=y

3

0

jako wartość początkową (może być

wartością historyczną lub wysymulowaną wcześniej)

)

,

,

,

,

(

)

,

,

(

)

,

,

(

3

2

1

1

2

1

1

3

1
3

3

1

1

1

2

1

2

2

1

0

3

1

1

1

x

x

x

y

y

f

y

x

x

y

f

y

x

x

y

f

y

=

=

=

2

0

Metoda Gaussa-Seidela (2)

)

,

,

,

,

(

)

,

,

(

)

,

,

(

3

2

1

2

2

2

1

3

2

3

3

1

2

1

2

2

2

2

1

1
3

1

2

1

x

x

x

y

y

f

y

x

x

y

f

y

x

x

y

f

y

=

=

=

3

0

)

,

,

,

,

(

)

,

,

(

)

,

,

(

3

2

1

2

1

3

3

3

1

1

2

2

2

1

1

3

1

1

x

x

x

y

y

f

y

x

x

y

f

y

x

x

y

f

y

r

r

r

r

r

r

r

=

=

=

−

(r+1)

0

3

Metoda Gaussa-Seidela (3)

Proces iteracyjny jest kontynuowany do momentu, gdy wartości
zmiennych endogenicznych (y

1

,y

2

,y

3

) między kolejnymi iteracjami

nie różnią się w sposób znaczący.

Najczęściej w celu stwierdzenia czy proces można zakończyć
stosuje się kryterium różnic względnych:

lub kryterium różnic bezwzględnych:

ε

≤

−

−

−

1

1

r

i

r

i

r

i

y

y

y

ε

≤

−

−1

r

i

r

i

y

y

Wystarczająco

(arbitralnie) mała liczba

np. 0,0001; 0,000001; 3

PRZYKŁAD

Wyznaczenie przybliżonej wartości

π

π

π

π (1)

a

a

X

Y

a

2

1

2

o

2

kw

a

4

1

P

a

P

⋅

⋅

=

=

π

kw

o

kw

o

P

P

4

4

1

P

P

⋅

=

⇒

⋅

=

π

π

1. Wybrać losowo punkt

2. Czy wybrany punkt (x,y) należy do okręgu?

Jeżeli TAK, to zwróć wartość 1,

w przeciwnym wypadku 0

3. Punkty 1,2 powtórzyć n razy

4. Wartość p wynosi

=4*suma(ile razy TAK w punkcie 2)/n

[ ]

[ ]

a

;

0

y

,

a

;

0

x

|

)

y

,

x

(

2

∈

∈

ℜ

∈

2

2

2

a

)

a

2

1

y

(

)

a

2

1

x

(

≤

−

+

−













a

2

1

,

a

2

1

generator

Obliczanie powierzchni figury

a

a

Y

1. Wybrać losowo punkt

2. Czy wybrany punkt (x,y) należy do

figury?
Jeżeli TAK, to zwróć wartość 1,
w przeciwnym wypadku 0

3. Punkty 1,2 powtórzyć n razy

4. Pole figury wynosi

=

a

2

*suma(ile razy TAK w punkcie 2)/n