
1
Wykład drugi

2
Metody iteracyjne
przybliżonego rozwiązywania
układów równań liniowych
EiT, sem. 2, 2014/2015
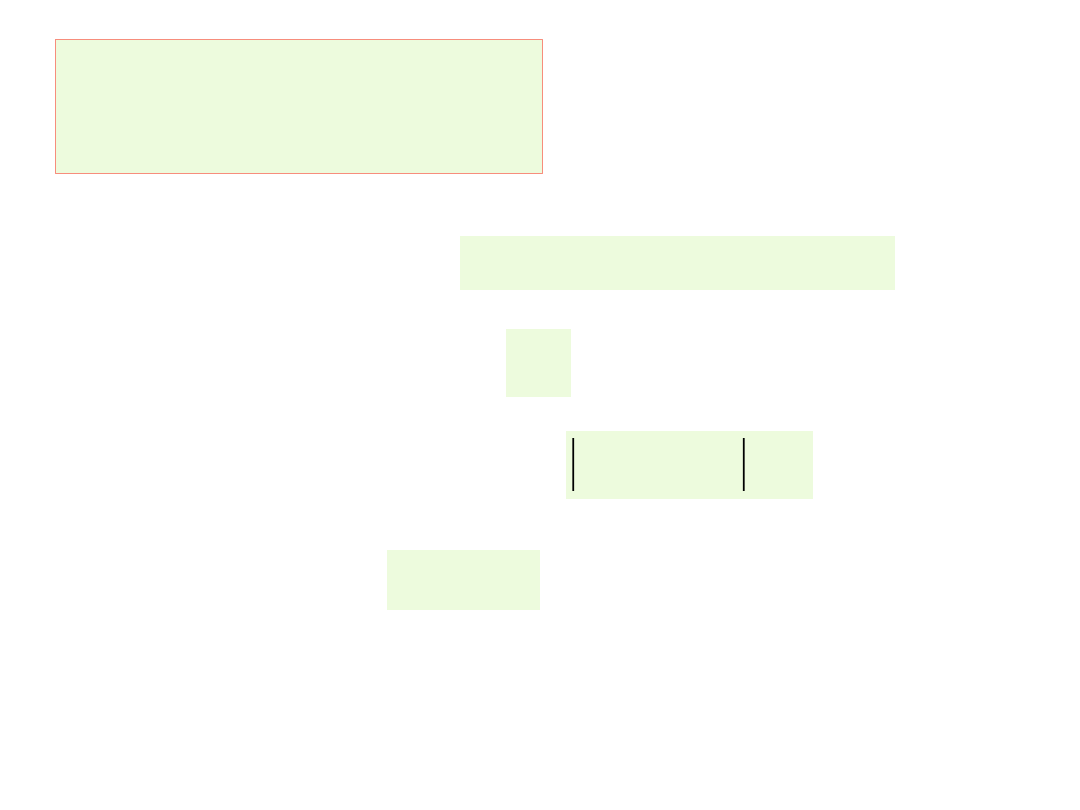
3
Metody iteracji prostej:
-
metoda Jacobiego,
- metoda Gaussa-Seidla
1. Wzór rekurencyjny -
2. Warunki początkowe -
)
(o
x
3. Warunki zakończenia obliczeń -
)
(
)
1
(
k
k
x
x
4. Rozwiązanie -
*
)
1
(
x
x
k
5. Warunki zbieżności algorytmu
....
,
2
,
1
,
0
)
(
)
(
)
1
(
k
x
f
x
k
k
A x + b = 0

4
Metody iteracji prostej
Dane jest równanie liniowe
n
R
x
b
x
A
,
(1)
A
– macierz nieosobliwa n x n wymiarowa,
b
– wektor wyrazów wolnych
Równanie (1) przekształcamy do postaci:
c
x
G
x
(2)
G
– macierz n x n wymiarowa, c – wyrazy wolne
,
2
,
1
,
0
dla
,
,
1
0
k
k
k
n
c
x
G
x
x
R
(3)

5
,
2
,
1
,
0
dla
,
,
1
0
k
k
k
n
c
x
G
x
x
R
(3)
Ciąg zdefiniowany formułą rekurencyjną algorytmu iteracji prostej
Jeżeli ciąg
jest zbieżny, to jego granicą jest wektor będący
rozwiązaniem równania (2)
*
)
1
(
x
x
k
...
,
2
,
1
,
0
)
1
(
k
x
k
...
,
2
,
1
,
0
)
1
(
k
x
k

6
Metoda Jacobiego
n
R
x
b
x
A
,
c
x
G
x
,
2
,
1
,
0
dla
,
,
1
0
k
k
k
n
c
x
G
x
x
R
n
n
nn
n
n
n
n
b
b
b
x
x
x
a
a
a
a
a
a
a
a
a
2
1
2
1
2
1
2
22
21
1
12
11
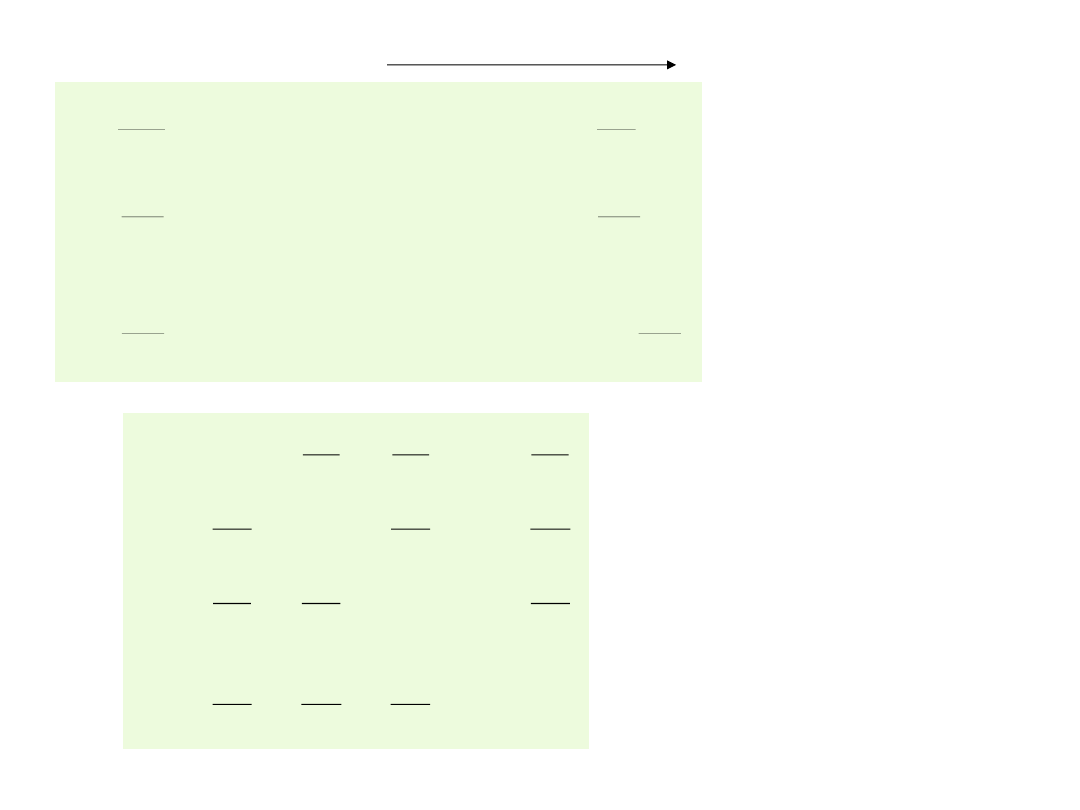
7
nn
n
n
n
n
n
n
nn
n
n
n
n
n
a
b
x
a
x
a
x
a
a
x
a
b
x
a
x
a
x
a
a
x
a
b
x
a
x
a
x
a
a
x
1
1
,
2
2
1
1
22
2
2
3
23
1
21
22
2
11
1
1
3
13
2
12
11
1
1
.
.
..
.
.
.
..
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
1
1
(4)
(5)
0
0
0
0
3
2
1
33
3
33
32
33
31
22
2
22
23
22
21
11
1
11
13
11
12
nn
n
nn
n
nn
n
n
n
n
a
a
a
a
a
a
a
a
a
a
a
a
a
a
a
a
a
a
a
a
a
a
a
a
G
b
x
A
c
x
G
x
8
nn
n
k
n
n
n
k
n
k
n
nn
k
n
k
n
n
k
k
k
k
n
n
k
k
k
i
a
b
x
a
x
a
x
a
a
x
a
b
x
a
x
a
x
a
a
x
a
b
x
a
x
a
x
a
a
x
n
i
x
,
1
1
,
,
2
2
,
1
1
1
,
22
2
,
2
,
3
23
,
1
21
22
1
,
2
11
1
,
1
,
3
13
,
2
12
11
1
,
1
0
,
1
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
..
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
1
1
,
,
,
2
,
1
dla
,
R
,
2
,
1
,
0
k
nn
n
n
a
b
c
a
b
c
a
b
c
22
2
2
11
1
1
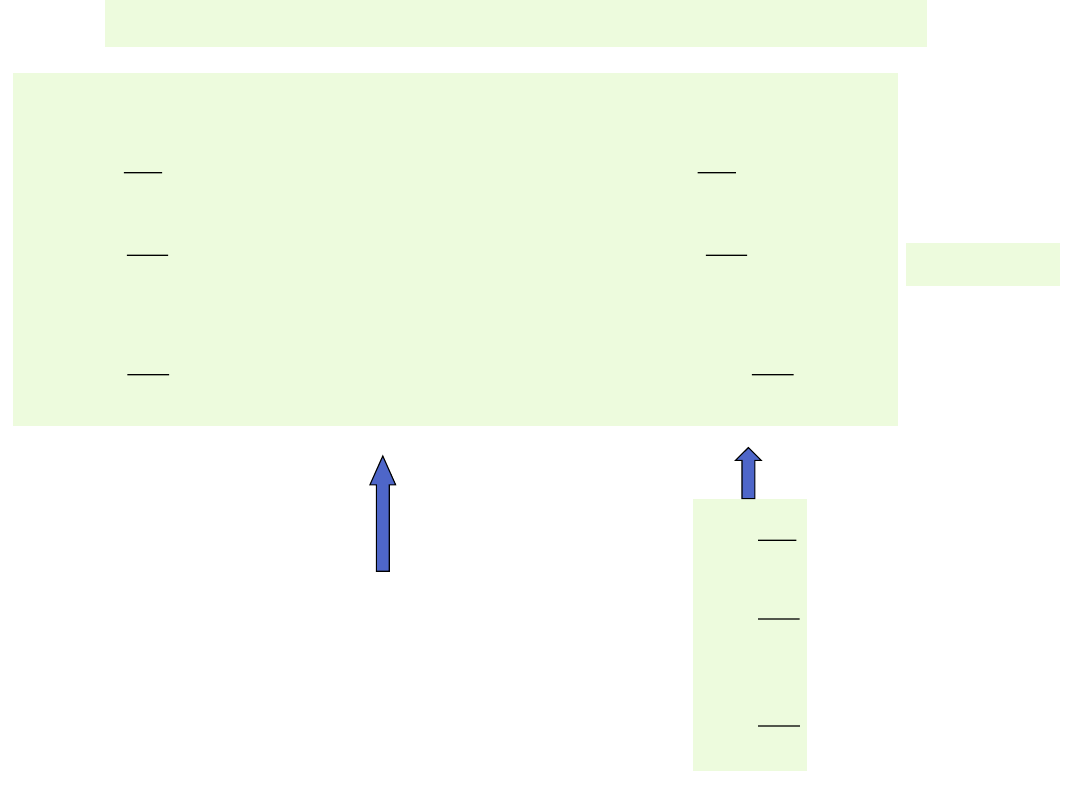
macierz G
Formuła rekurencyjna algorytmu w metodzie Jacobiego

9
Zaczynamy obliczenia od przyjęcia, że
c
x
)
0
(
Kończymy obliczenia, gdy
)
(
)
1
(
k
k
x
x
Rozwiązanie
*
)
1
(
x
x
k
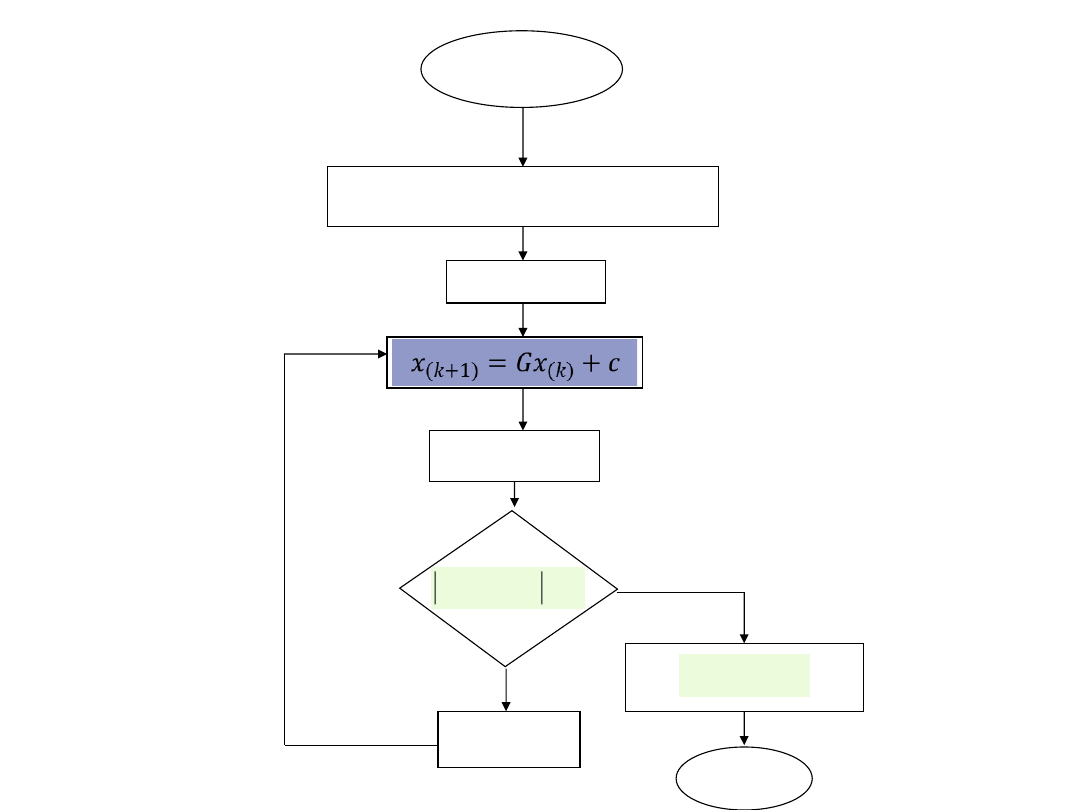
10
START
DANE: G, c, x
(0)
,
ε
k = 0
obliczenia
x
(k+1)
SPRAWDZENIE
x
(k+1)
= x*
STOP
TAK
NIE
k = k + 1
)
(
)
1
(
k
k
x
x

11
Czy warto zaczynać obliczenia ????
Trzeba sprawdzić warunki zbieżności !!!!
12
nn
n
n
n
n
g
g
g
g
g
g
g
g
g
G
2
1
2
22
21
1
12
11
Warunki zbieżności
n
i
g
n
j
g
n
j
ij
n
i
ij
,...,
2
,
1
1
...,
,
2
,
1
1
1
1
Wyszukiwarka
Podobne podstrony:
Czwarty wykład 2014 bez tła
Pierwszy wyklad 2014 bez tła
Szósty wykład 2014 bez tła
Czwarty wykład 2014 bez tła
Czwarty wykład cd 2014 bez tła
Biochemia 13 2014, drugi wykład z lipidów
wykład z cholestazy (bez zdjęć)
MOO wyklad 2 ekstrema bez ograniczen
Pestycydy wykłady 2014
podstawy rachunkowosci we dzienne wyklad 2014
ppmy wyklad 2014 KasiaB
ANTROPOLOGIA NOTATKI Z WYKŁADÓW (2014)
Rezerwa z tytułu odrocznego podatku - materiały do wykładu 2014, UE KATOWICE ROND, I stopień, VI sem
Rezerwy na świadczenia pracownicze - materiały do wykladu 2014, UE KATOWICE ROND, I stopień, VI seme
Liturgika drugi wykład
ANALITYCZNA, Kripke -, Drugi wykład Kripke poświęca w dalszym ciągu tematowi deskrypcji, którą chc
więcej podobnych podstron