
Wykład pierwszy

2
Metody
rozwiązywania
układów równań liniowych
Sem. 2 EiT, 2014/2015
3
Metody dokładne:
Cramera, Gaussa-Jordana, eliminacji Gaussa, dekompozycji LU
Metody iteracyjne (przybliżone):
Jacobiego, Gaussa-Seidla
Otrzymujemy rozwiązanie po określonej liczbie działań arytmetycznych,
która zależy od liczby równań w układzie równań - n
Poszukujemy rozwiązania układu równań liniowych A·x = b det A ≠ 0
Rozwiązaniem jest wektor
*
x
b
x
A
x
x
x
x
n
*
*
*
2
*
1
*
Nie potrafimy określić ile kolejnych iteracji k należy wykonać, żeby oszacować
wektor
zbliżony do wektora
*
x
,....
2
,
1
,
0
)
(
)
(
)
1
(
k
x
f
x
k
k
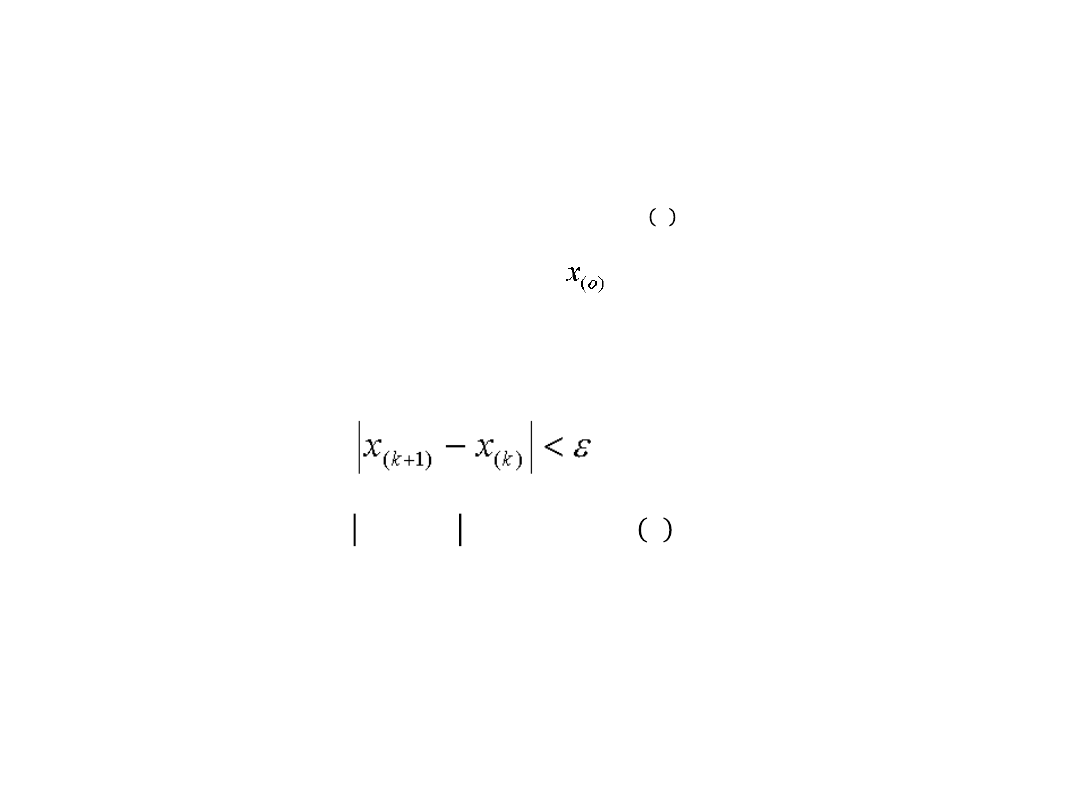
4
Metody iteracyjne (przybliżone)
- operacje do wykonania
-
wartość wektora początkowego
-
warunki zakończenia obliczeń, np.
Problem
– zbieżność algorytmu
𝑥
(𝑘+1)
= 𝐺𝑥
𝑘
+ 𝑐 𝑘 = 0, 1, 2, 3, …
𝐴 𝑥 + 𝑏 = 0
𝑓(𝑥
(𝑘+1)
< 𝛿 𝑑𝑙𝑎 𝑓 𝑥 = 0
STOP dla k = M
Algorytm

5
Algorytm
Algorytm
to przepis postępowania, zbiór pewnych reguł,
-
wszystkie czynności,
-
kolejność ich wykonywania.
Realizacja algorytmu
– wykonanie wszystkich czynności
z zachowaniem ich kolejności.
Algorytm
w matematyce oraz informatyce to:
skończony, uporządkowany zbiór jasno zdefiniowanych czynności,
koniecznych do wykonania pewnego zadania.
Słowo "algorytm" pochodzi od nazwiska Muhammed ibn Musa Alchwarizmi
(
يمزراوخلا ىسوم نب دمحم الله دبع وبأ)
matematyka perskiego z IX wieku i początkowo oznaczało w Europie sposób
obliczeń oparty na dziesiętnym systemie liczbowym.
Zadanie:
Algorytm ma przeprowadzić system z pewnego stanu początkowego
do pożądanego stanu końcowego.
Realizacja:
Algorytm może zostać zaimplementowany w postaci programu
komputerowego lub innego urządzenia.
P
rzykład stosowanego w życiu codziennym algorytmu
6
7
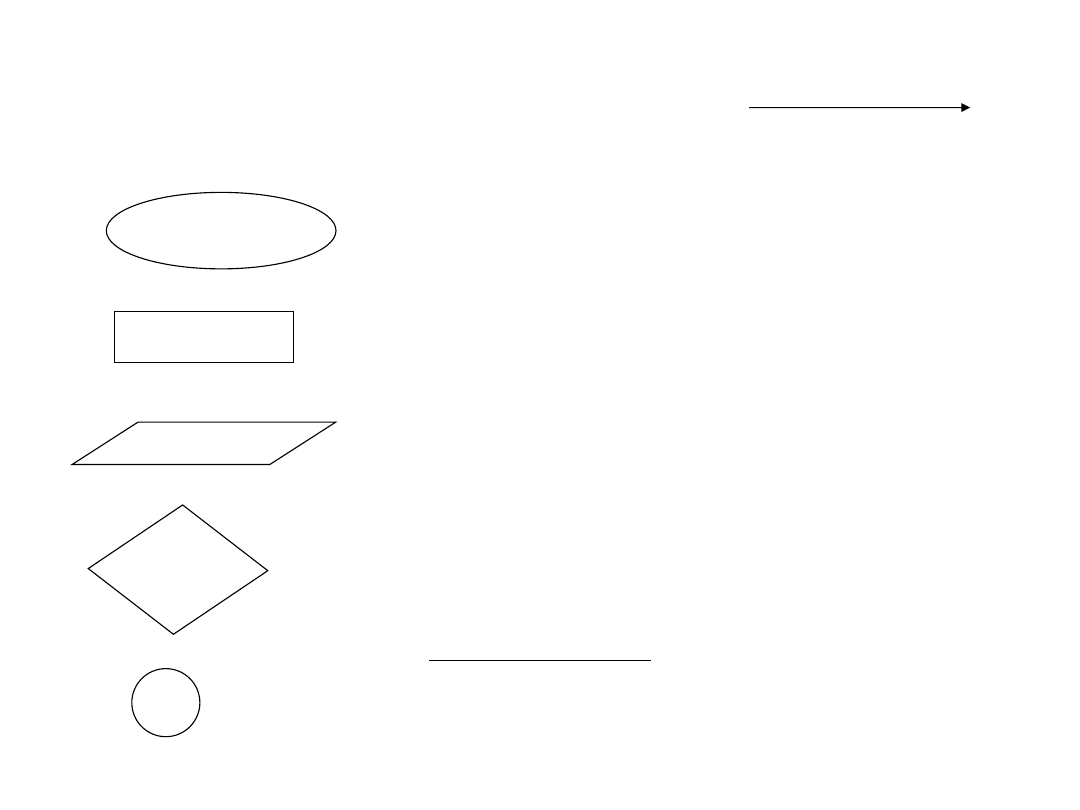
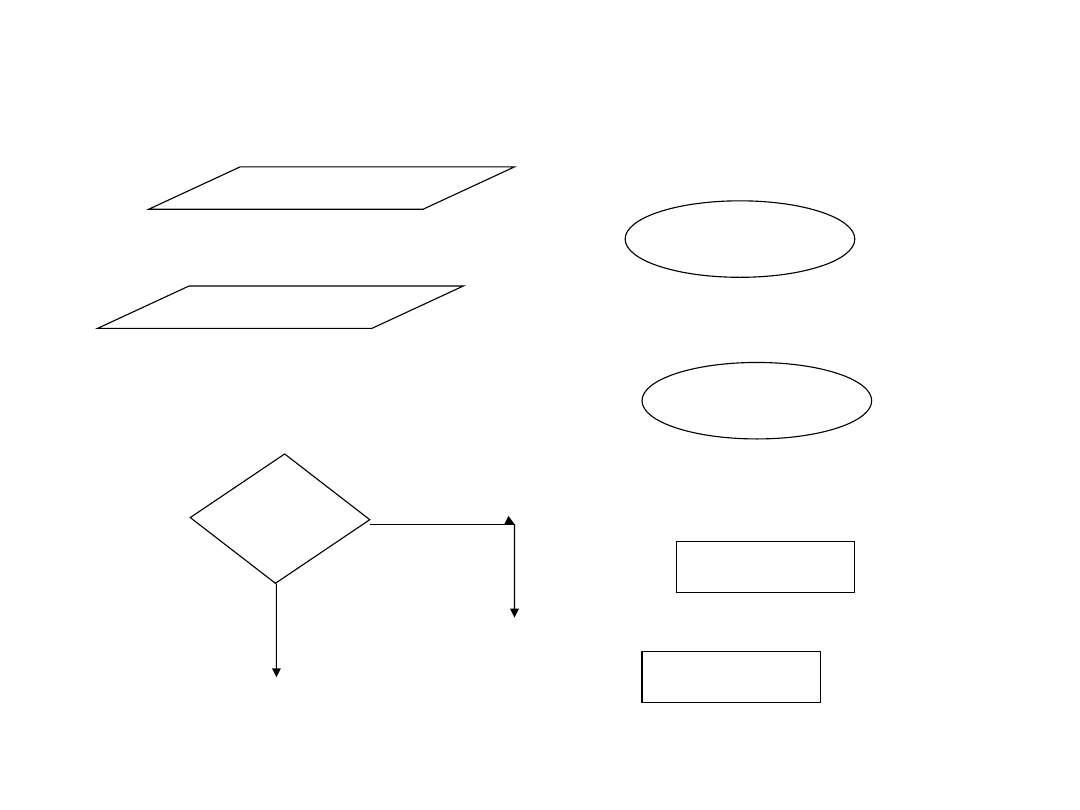
Zapis algorytmu
– karta następstw, sieć działań
Symbole:
początek, koniec
operator, operacja do wykonania
operator wejścia, wyjścia, np. wprowadzanie danych
do pamięci, wyprowadzanie danych z pamięci
element decyzyjny
łącznik
połączenia poszczególnych
symboli
kierunek działania
8
CZYTAJ a, b, c
DRUKUJ x, y
A > B
TAK
NIE
START
STOP
k= k + 1
x (k+1) = f (x (k))
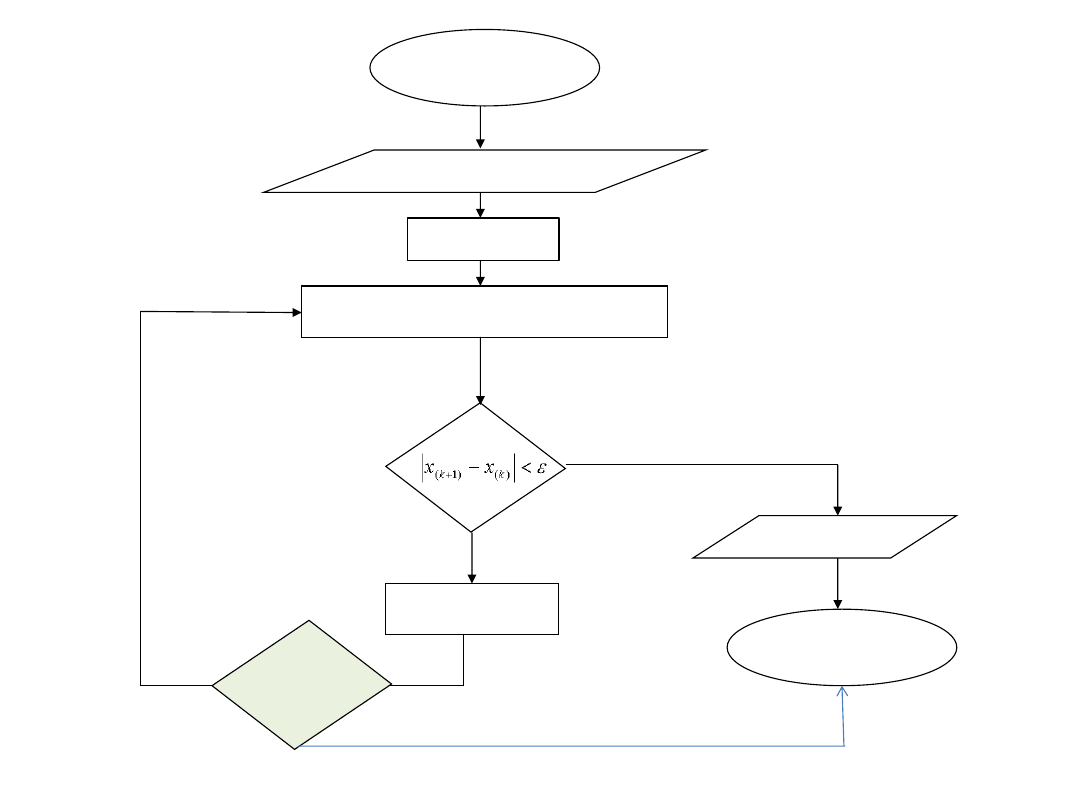
9
Sieć działań
Karta następstw
START
Dane wejściowe: x
0
, a, b,
ε
Obliczenia: x
k+1
= f (x
k
)
TAK
Drukuj x
k+1
STOP
NIE
k = k + 1
k = 0
k = M
NIE
TAK
Ax + b = 0
M - liczba

10
Metoda dekompozycji LU
metoda dokładna rozwiązywania
układów równań liniowych
11
Metoda dekompozycji LU
A x = b
det
A ≠ 0
A x = b
[L U] x = b
A = L U
L
– macierz trójkątna dolna, otrzymana z macierzy A,
U
– macierz trójkątna górna, otrzymana z macierzy A
L y = b
U x = y
Najpierw musimy obliczyć macierz L i macierz U
(1)
wyznaczamy y
(2)
wyznaczamy x

12
Macierz U
1
0
0
0
1
0
0
1
0
1
3
3
2
2
2
23
1
1
1
13
1
12
n
n
n
a
a
a
a
a
a
U
Macierz L
n
nn
n
n
n
a
a
a
a
a
a
a
a
a
a
3
3
2
2
1
1
3
33
2
32
1
31
2
22
1
21
1
11
0
0
0
0
0
0
L
(3)
(4)

13
44
43
42
41
34
33
32
31
24
23
22
21
14
13
12
11
34
24
23
14
13
12
44
43
42
41
33
32
31
22
21
11
1
0
0
0
1
0
0
1
0
1
0
0
0
0
0
0
a
a
a
a
a
a
a
a
a
a
a
a
a
a
a
a
u
u
u
u
u
u
l
l
l
l
l
l
l
l
l
l
Algorytm Crouta
Przykład dla n = 4
Pomocnicza macierz Q
44
43
42
41
34
33
32
31
24
23
22
21
14
13
12
11
l
l
l
l
u
l
l
l
u
u
l
l
u
u
u
l
Q
(5)
(6)
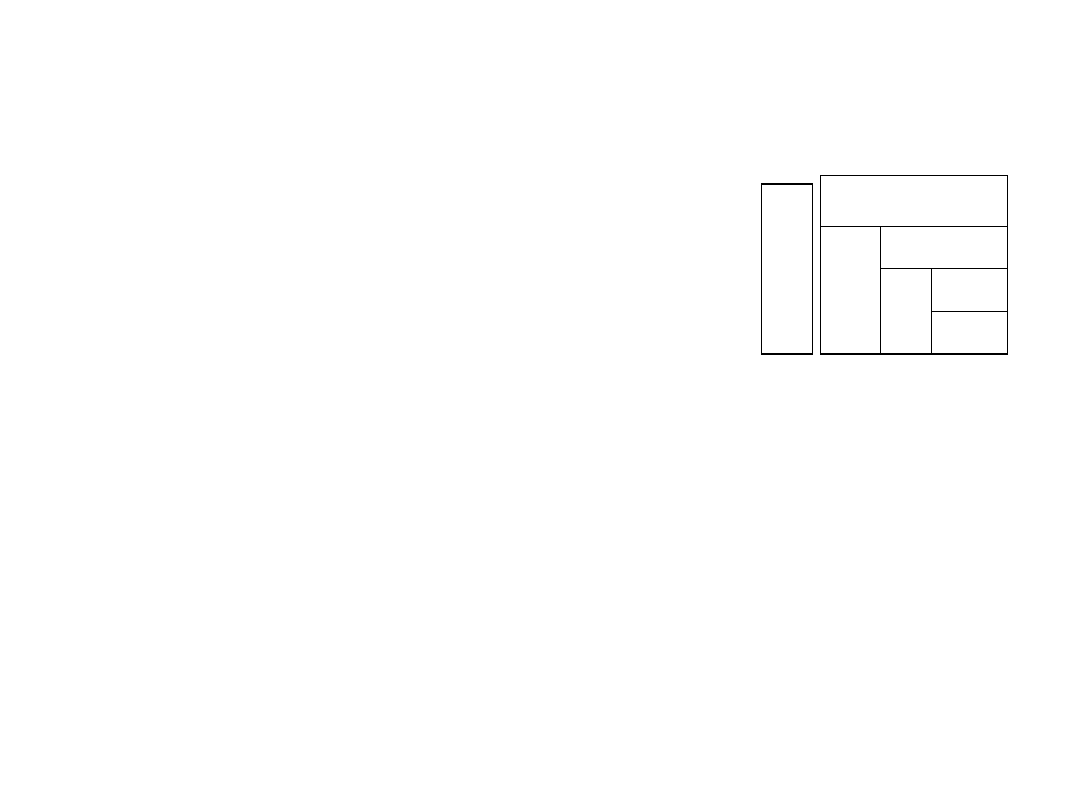
14
16
14
10
4
15
13
9
3
12
11
8
2
7
6
5
1
Elementy macierzy Q, dla n = 4, są obliczane w kolejności zaznaczonej
w poniższej tablicy
Numer oznacza kolejność obliczania elementów.
Najpierw obliczamy elementy macierzy L (pierwsza kolumna),
potem elementy macierzy U (pierwszy wiersz, bez pierwszego elementu
m
acierzy U, który jest równy 1),
potem elementy macierzy L (druga kolumna, bez pierwszego elementu,
k
tóry jest równy 0),
potem elementy macierzy U (drugi wiersz, ale bez pierwszego i drugiego
e
lementu macierzy U, które są odpowiednio równe 0 i 1),
potem elementy macierzy L, itd.
44
43
42
41
34
33
32
31
24
23
22
21
14
13
12
11
l
l
l
l
u
l
l
l
u
u
l
l
u
u
u
l
Q
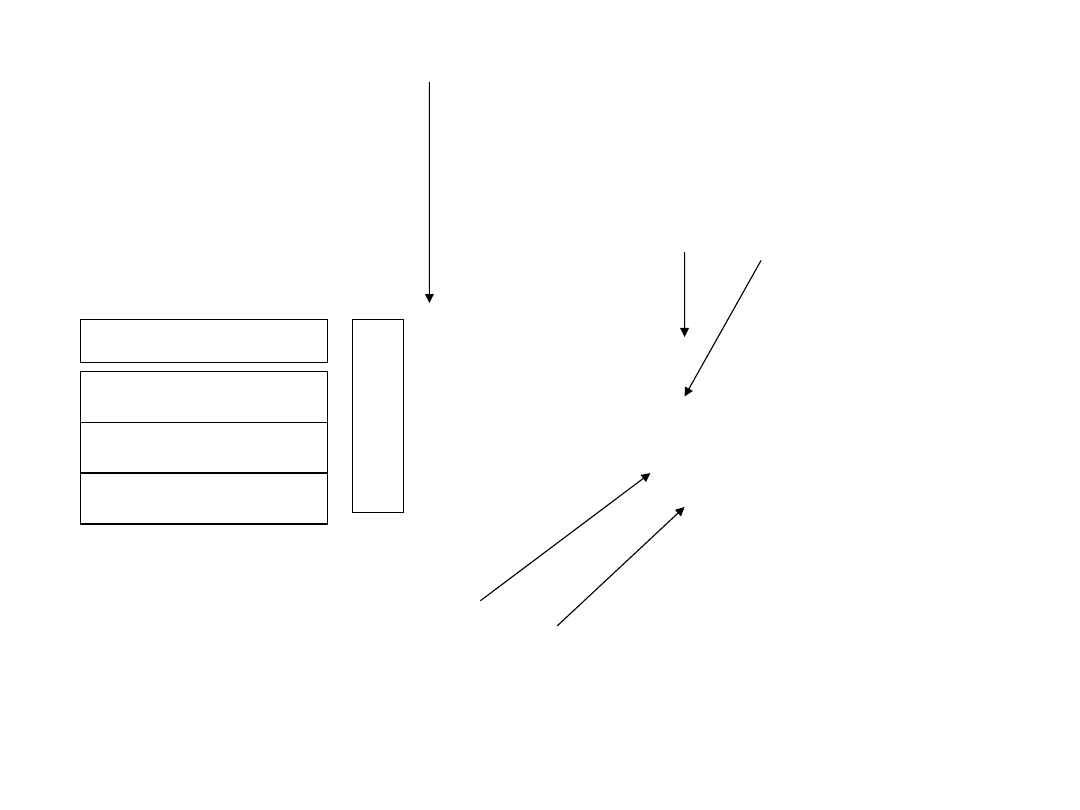
15
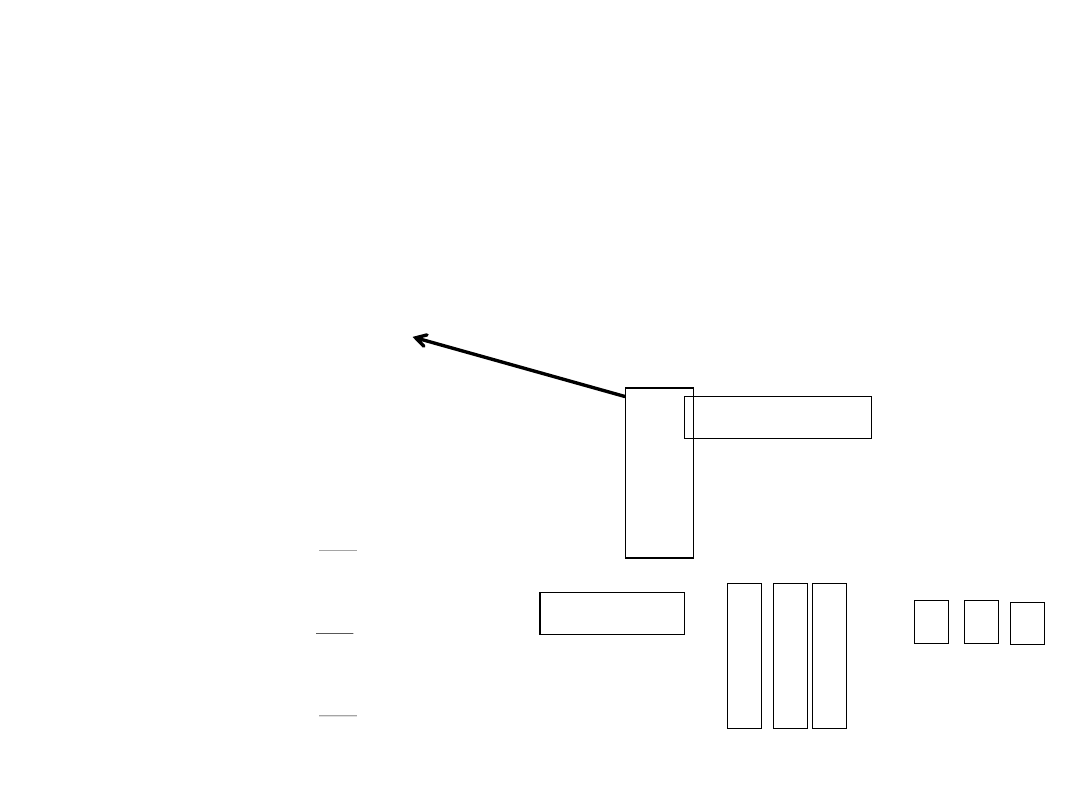
Biorąc pod uwagę zależność (5), wykonujemy obliczenia
dla kolejnego elementu
ij
a
w postaci iloczynu i-tego wiersza macierzy L i j-tej kolumny macierzy U
44
43
42
41
34
33
32
31
24
23
22
21
14
13
12
11
l
l
l
l
u
l
l
l
u
u
l
l
u
u
u
l
Q
44
43
42
41
34
33
32
31
24
23
22
21
14
13
12
11
34
24
23
14
13
12
44
43
42
41
33
32
31
22
21
11
1
0
0
0
1
0
0
1
0
1
0
0
0
0
0
0
a
a
a
a
a
a
a
a
a
a
a
a
a
a
a
a
u
u
u
u
u
u
l
l
l
l
l
l
l
l
l
l
16
Biorąc pod uwagę zależność (5), wykonujemy obliczenia
dla kolejnego elementu
ij
a
w postaci iloczynu i-tego wiersza macierzy L i j-tej kolumny macierzy U
1
11
11
l
a
11
11
a
l
,
1
21
21
l
a
21
21
a
l
,
1
31
31
l
a
31
31
a
l
,
1
41
41
l
a
41
41
a
l
,
12
11
12
u
l
a
11
12
12
l
a
u
,
13
11
13
u
l
a
11
13
13
l
a
u
,
14
11
14
u
l
a
11
14
14
l
a
u
,
44
43
42
41
34
33
32
31
24
23
22
21
14
13
12
11
l
l
l
l
u
l
l
l
u
u
l
l
u
u
u
l
Q
44
43
42
41
34
33
32
31
24
23
22
21
14
13
12
11
34
24
23
14
13
12
44
43
42
41
33
32
31
22
21
11
1
0
0
0
1
0
0
1
0
1
0
0
0
0
0
0
a
a
a
a
a
a
a
a
a
a
a
a
a
a
a
a
u
u
u
u
u
u
l
l
l
l
l
l
l
l
l
l

17
22
12
21
22
l
u
l
a
12
21
22
22
u
l
a
l
,
32
12
31
32
l
u
l
a
12
31
32
32
u
l
a
l
,
42
12
41
42
l
u
l
a
12
41
42
42
u
l
a
l
,
23
22
13
21
23
u
l
u
l
a
22
13
21
23
23
l
u
l
a
u
,
24
22
14
21
24
u
l
u
l
a
22
14
21
24
24
l
u
l
a
u
,
44
43
42
41
34
33
32
31
24
23
22
21
14
13
12
11
l
l
l
l
u
l
l
l
u
u
l
l
u
u
u
l
Q

18
33
23
32
13
31
33
l
u
l
u
l
a
23
32
13
31
33
33
u
l
u
l
a
l
,
43
23
42
13
41
43
l
u
l
u
l
a
23
42
13
41
43
43
u
l
u
l
a
l
,
34
33
24
32
14
31
34
u
l
u
l
u
l
a
33
24
32
14
31
34
34
l
u
l
u
l
a
u
,
44
34
43
24
42
14
41
44
l
u
l
u
l
u
l
a
34
43
24
42
14
41
44
44
u
l
u
l
u
l
a
l
.
44
43
42
41
34
33
32
31
24
23
22
21
14
13
12
11
l
l
l
l
u
l
l
l
u
u
l
l
u
u
u
l
Q

19
L y = b
→ y
U x = y
→ x
Przykład dla n = 3
3
2
1
3
2
1
33
32
31
22
21
11
0
0
0
b
b
b
y
y
y
l
l
l
l
l
l
3
2
1
3
2
1
23
13
12
1
0
0
1
0
1
y
y
y
x
x
x
u
u
u
33
32
31
23
22
21
13
12
11
l
l
l
u
l
l
u
u
l
Q

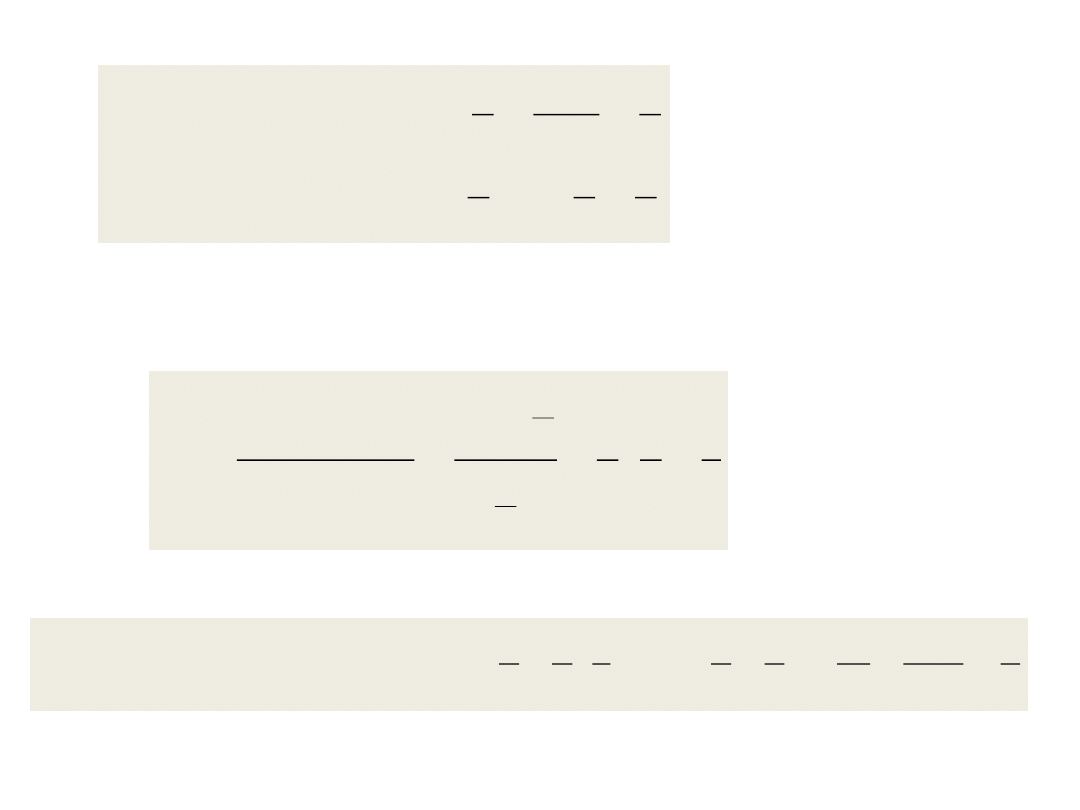
Metoda dekompozycji LU -
przykład
5
2
1
1
6
1
2
1
5
1
1
2
3
2
1
3
2
1
3
2
1
x
x
x
x
x
x
x
x
x
A
·x = b A = L·U
L
·U·x = b
L
·y = b
U
·x = y
33
32
31
22
21
11
0
0
0
l
l
l
l
l
l
L
1
0
0
1
0
1
23
13
12
u
u
u
U
33
32
31
23
22
21
13
12
11
l
l
l
u
l
l
u
u
l
Q
9
7
3
8
6
2
5
4
1
1
1
2
31
31
21
21
11
11
a
l
a
l
a
l
2
1
2
1
11
13
13
11
12
12
l
a
u
l
a
u
2
1
2
1
1
2
1
1
1
2
3
2
1
4
2
1
1
2
12
31
32
32
12
21
22
22
u
l
a
l
u
l
a
l
3
1
3
2
2
1
2
3
2
1
1
1
22
13
21
23
23
l
u
l
a
u
6
8
6
1
3
6
12
6
1
2
1
2
3
1
2
1
2
1
1
2
23
32
13
31
33
33
u
l
u
l
a
l

6
8
2
1
1
0
2
3
1
0
0
2
L
1
0
0
3
1
1
0
2
1
2
1
1
U
6
8
2
1
1
3
1
2
3
1
2
1
2
1
2
Q
L
·y = b
5
6
8
2
1
1
6
2
3
1
5
2
3
2
1
2
1
1
y
y
y
y
y
y
2
5
1
y
6
2
3
2
5
1
2
y
3
7
2
5
6
2
3
2
2
y
y
1
6
8
6
7
6
15
6
30
6
8
5
6
8
3
7
2
1
2
5
1
3
3
3
y
y
y
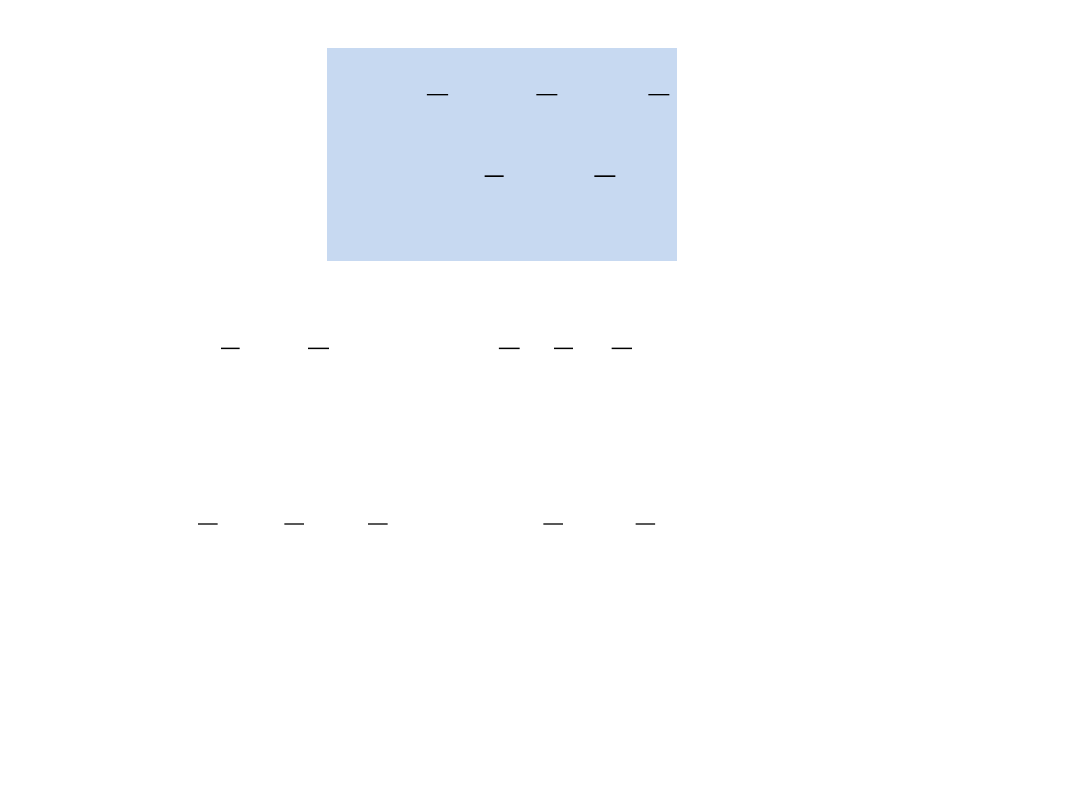
U
·x = y
1
1
3
7
3
1
1
2
5
2
1
2
1
1
3
3
2
3
2
1
x
x
x
x
x
x
1
3
x
2
2
3
6
3
1
3
7
3
7
1
3
1
2
2
2
x
x
x
1
1
2
1
1
2
5
2
5
1
2
1
2
2
1
1
1
1
1
x
x
x

2x
1
+ x
2
+ x
3
= 5
x
1
+ 2x
2
- x
3
= 4
x
1
+x
2
+ 2x
3
= 5
Zadania do rozwiązania
2x
1
+ x
2
+ x
3
= 5
x
1
+ x
2
+ 2x
3
= 6
2x
1
+2x
2
+ x
3
= 6

Wyszukiwarka
Podobne podstrony:
Czwarty wykład 2014 bez tła
Drugi wykład 2014 bez tła
Szósty wykład 2014 bez tła
Czwarty wykład 2014 bez tła
Czwarty wykład cd 2014 bez tła
PRODUKTY UBEZEPIECZENIOWE - PIERWSZY WYKŁAD, WZR UG ZARZĄDZANIE - ZMP I STOPIEŃ, V SEMESTR (zimowy)
Biochemia 13 2014, pierwszy wykład z lipidów
wykład z cholestazy (bez zdjęć)
pierwszy wykład jakość
MOO wyklad 2 ekstrema bez ograniczen
pierwsze 2 wykłady
Pytania testowe z pierwszego wykladu
Pestycydy wykłady 2014
podstawy rachunkowosci we dzienne wyklad 2014
ppmy wyklad 2014 KasiaB
więcej podobnych podstron