Zad. 1.

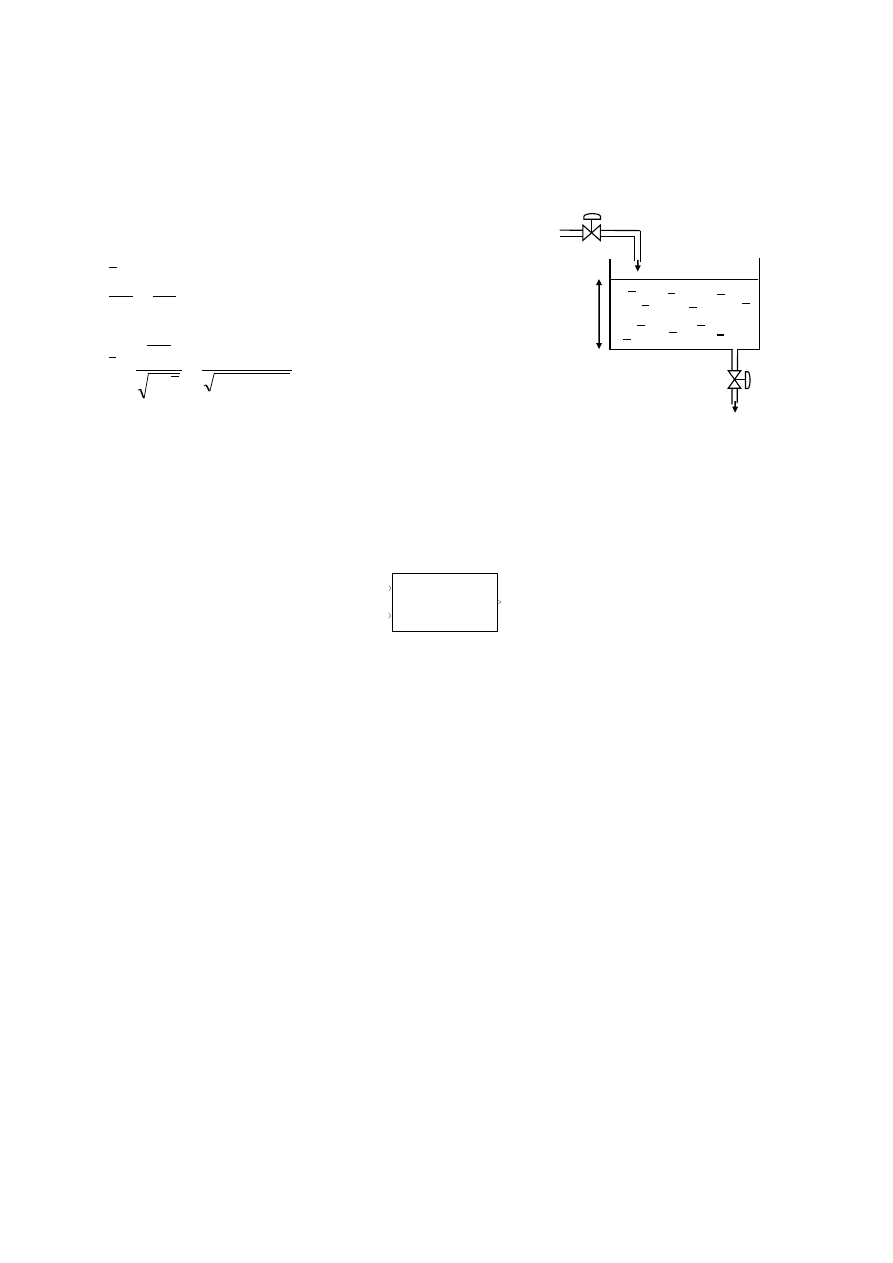
Zaprojektuj układ regulacji poziomu cieczy w zbiorniku przedstawionym na poniższym rysunku. Zastosuj
regulator typu PID. Nominalny poziom cieczy w zbiorniku wynosi 10 m.

Specyfikacja

/s

m

03

.

0

/h

m

108

m

10

m

5

=

3

3

2









wy

we

q

q

h

A

2

m

00214

.

0

10

81

.

9

2

03

.

0

2











h

g

q

s

we

Sygnał sterujący generowany przez regulator [zakres <0,1>] odpowiada liniowo przepływowi q

we

[zakres <0, 1>

m

3

/s]. Instalacja jest wyposażona w ciągły sygnał (y) pomiaru wysokości cieczy w zbiorniku [zakres <0,10> V ]

odpowiadający liniowo wysokości cieczy (h) [zakres <0, 20> m]. Zawór wyjściowy może być sterowany w
trybie ręcznym za pomocą sygnału s [zakres <0,1>] odpowiadającemu liniowo polu przekroju otwarcia zaworu
w zakresie <0,1> m

2

. Projektowany regulator nie ma wpływu na stopień otwarcia zaworu wyjściowego. Układ

pomiarowo-sterujący pracuje z cyklem 1 s. Eksperymenty dla obiektu mogą być przeprowadzone za pomocą
poniższego bloku Simulink (zbiornik całkowicie opróżniony).

Wyznaczenia parametrów modelu transmitancyjnego należy dokonać za pomocą 2 punktów pomiarowych.

Należy zastosować „typowy” regulator stosowany dla uzyskanego modelu obiektu (wykład).

Na prośbę egzaminującego należy przedstawić następujące wyniki prac:

- projekt Simulink umożliwiający przeprowadzenie eksperymentu identyfikacyjnego w punkcie pracy – 10%

zmiana sterowania w stosunku do stanu nominalnego

- wykres dla przetworzonych danych pomiarowych wykorzystywanych do bezpośredniej identyfikacji modelu

transmitancyjnego – Matlab

- wzór ogólny dla przyjętego modelu transmitancyjnego oraz uzyskane wartości liczbowe jego parametrów

- wykres obrazujący porównanie wyników odpowiedzi obiektu i przyjętego modelu

- typ i wzór przyjętego regulatora

- wartości nastaw regulatora wyznaczone z metody tabelarycznej oraz przeliczone wartości nastaw dla bloku

regulatora stosowanego w Simulink

- projekt Simulink umożliwiający przeprowadzenie eksperymentu skoku wartości zadanej dla modelu obiektu

- projekt Simulink umożliwiający przeprowadzenie eksperymentu skoku wartości zadanej dla obiektu w

punkcie pracy - zwiększenie wartości zadanej o 10% w stosunku do wartości nominalnej

- projekt Simulink umożliwiający przeprowadzenie eksperymentu wprowadzenia zakłócenia skokowego w

układzie dla punktu pracy za pomocą otwarcia zaworu wyjściowego w zakresie o 20% większym niż w
stanie nominalnym

- fragmenty programów Matlab realizujące poszczególne punkty zadania: przetwarzanie danych, identyfikacja

parametrów modelu obiektu, symulacje, wykresy, wyliczenie nastaw regulatorów

Obiekt

qwe

s

y

A

h

q

we

q

wy

s

Otwieramy plik Zad4.mdl

Zapisujemy plik mat jak i mdl pod swoją nazwą

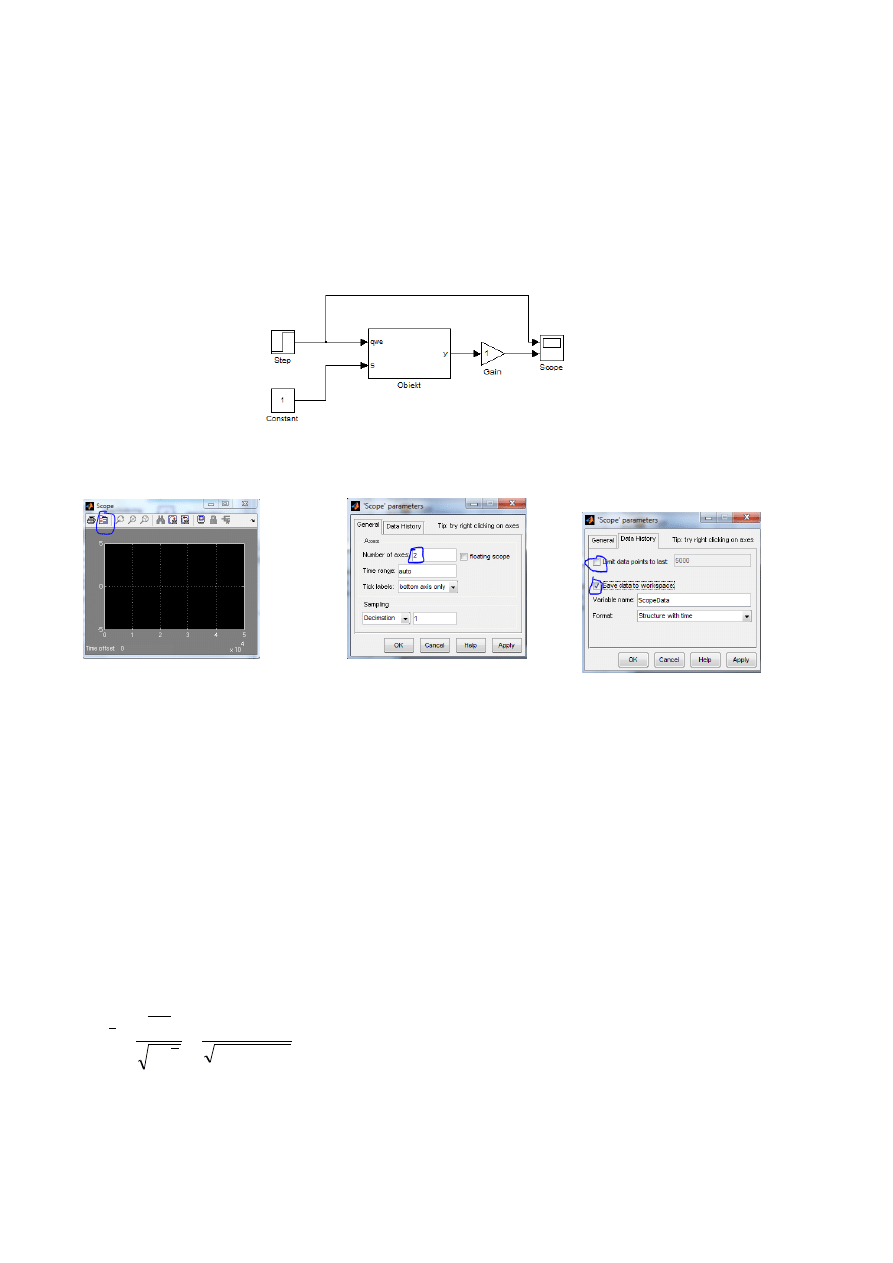
Tworzymy schemat do identyfikacji-wpisujemy w matlabie polecenie ‘simulink’

Ustawienia Scope:

Scope parameters

Liczba wejść; 2

wyłączenie limitu czasu i zapis danych do

określonej zmiennej ‘ScopeData’

Ustawienie Gain:

W zadaniu jest napisane: „Sygnał sterujący generowany przez regulator [zakres <0,1>] odpowiada liniowo
przepływowi q

we

[zakres <0, 1> m

3

/s]. Instalacja jest wyposażona w ciągły sygnał (y) pomiaru wysokości

cieczy w zbiorniku [zakres <0,10> V ] odpowiadający liniowo wysokości cieczy (h) [zakres <0, 20> m].”

Oznacza to że wyjście nie może być podpięte bezpośrednio tak jak wejście lecz trzeba sygnał wymnożyć przez
2, więc do gain wpisujemy 2

Ustawienie constant:

Do bloku constant wpisujemy wartość stałej

2

m

00214

.

0

10

81

.

9

2

03

.

0

2











h

g

q

s

we

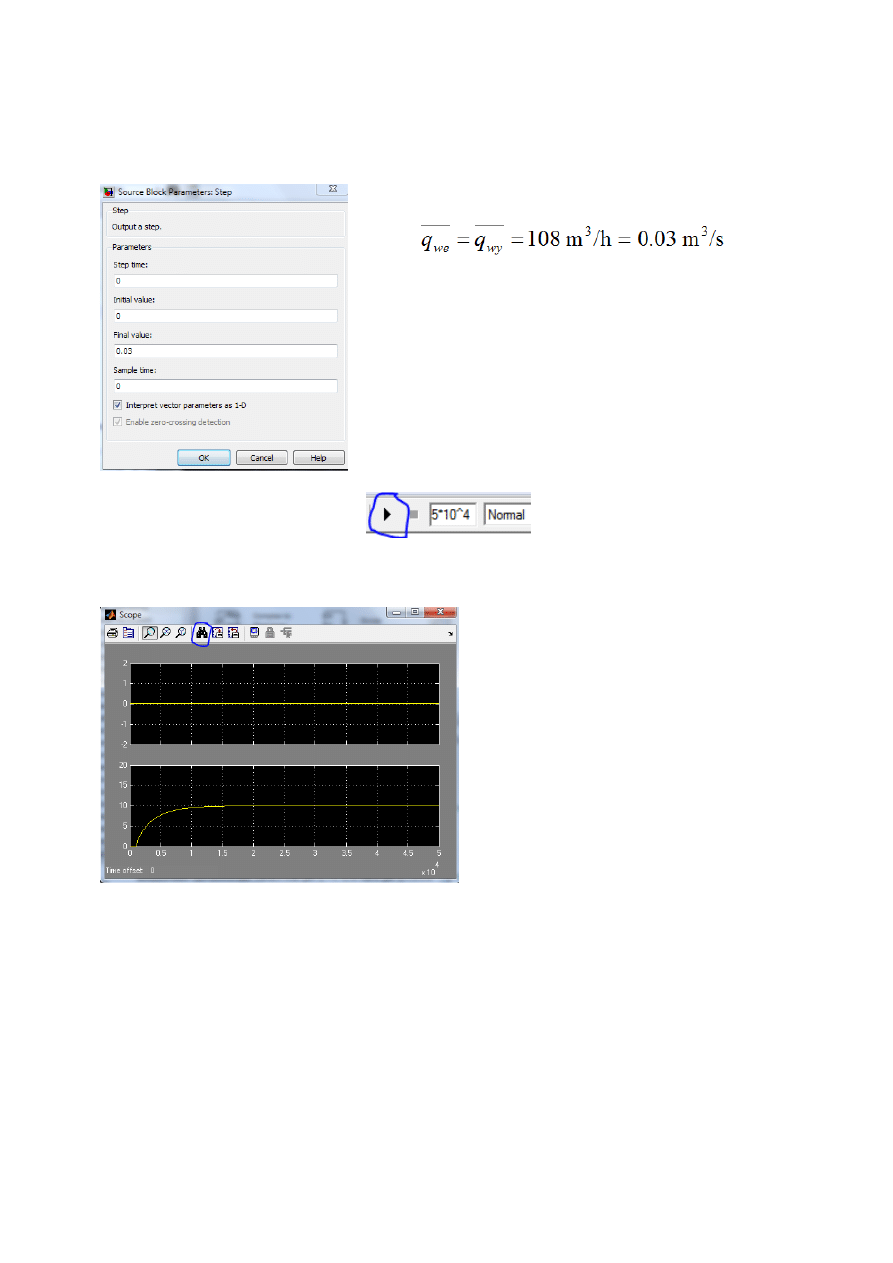
Ustawienie Step:

Pierwszym krokiem jest zidentyfikowanie obiektu (jaka będzie odpowiedź skokowa) i sprawdzenie przy
maksymalnym przepływie czasu po którym zbiornik się napełni.

W wierszu ‘final value’ wpisujemy 0.03, ponieważ mamy dane w

zadaniu:

Teraz możemy przeprowadzić symulację

Po symulacji od razu wciskamy ‘Autoscale’ ozn. lornetką

Po powiększeniu wykresu widać, że dolny przebieg
(wyjście) stabilizuje się przy wartości ok. 2.5*10^4. I
napełnił się do nominalnej wartości h=10m.

Ponad to pierwszą rzeczą którą powinniśmy zrobić
to identyfikacja czyli określenie jaki jest to rodzaj
odpowiedzi skokowej. Z wykresu widać, że jest to
inercja z opóźnieniem (rodzaje odpowiedzi
skokowych znajdują się w wykładzie 9). Wiedza ta
przyda nam się później przy aproksymacji przebiegu
i liczeniu transmitancji.

Kolejny punkt zadania to ‘projekt Simulink umożliwiający przeprowadzenie eksperymentu identyfikacyjnego w
punkcie pracy – 10% zmiana sterowania w stosunku do stanu nominalnego’

Sterowanie zmieniamy po czasie po którym przebieg się już ustabilizuje czyli u nas jest to 2.5*10^4. Wartość
nominalna przepływu to 0.03 a o 10% więcej to 0.033

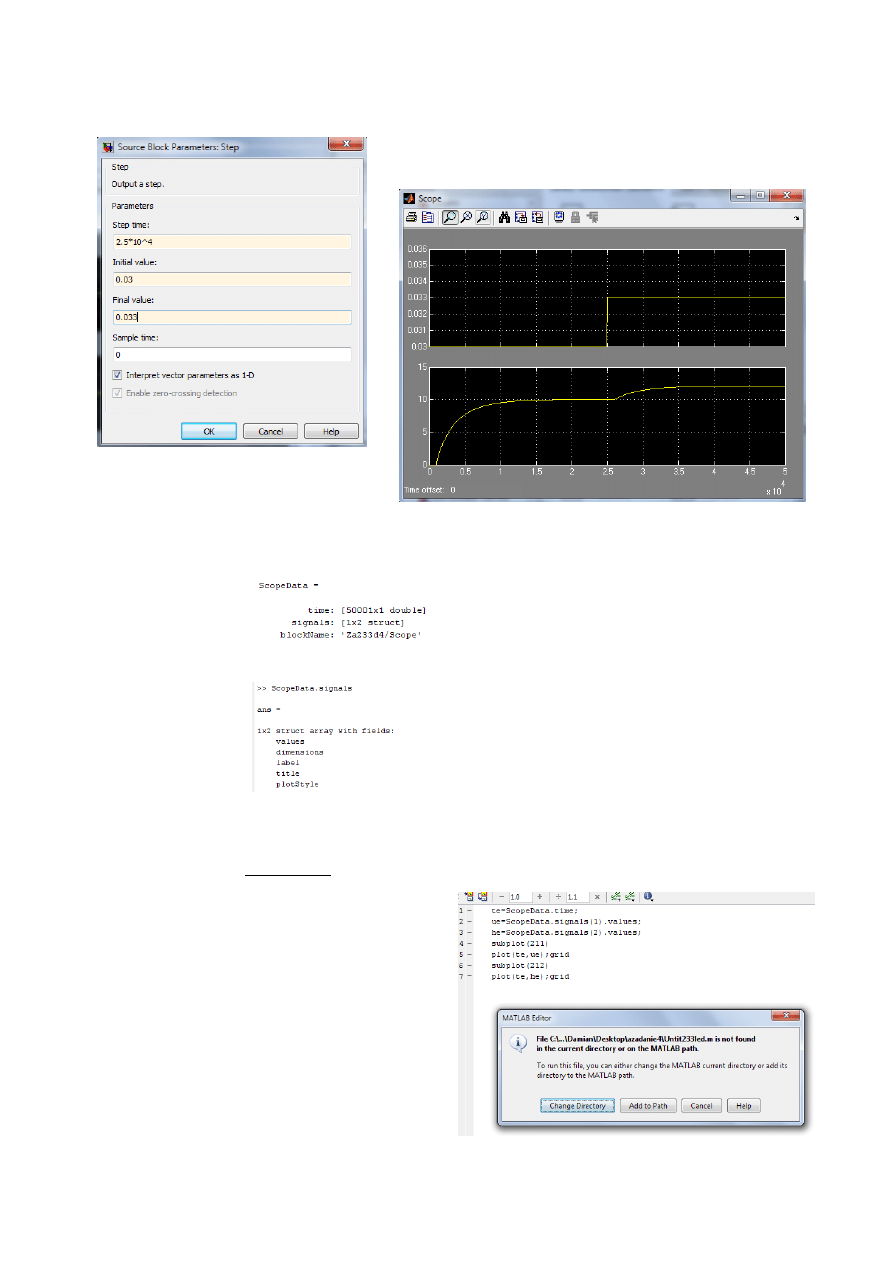
Więc zmieniamy ustawienia w bloku ‘Step’ i włączamy symulacje

Powinien nam się pokazać przebieg z ustalonym przez nas skokiem
o czasie 2.5*10^4 z opóźnieniem:

Teraz wprowadzamy dwie komendy do matlaba:

ScopeData

ScopeData.signals

Następnie otwieramy w matlabie file->new->blank M-file

Pojawi nam się editor, zapisujemy go. Teraz wszystkie komendy będziemy wprowadzać do niego

te=ScopeData.time;
ue=ScopeData.signals(1).values;
he=ScopeData.signals(2).values;
subplot(211)
plot(te,ue);grid

subplot(212)
plot(te,he);grid

Po tej komendzie klikamy F5 I klikamy Add to Path

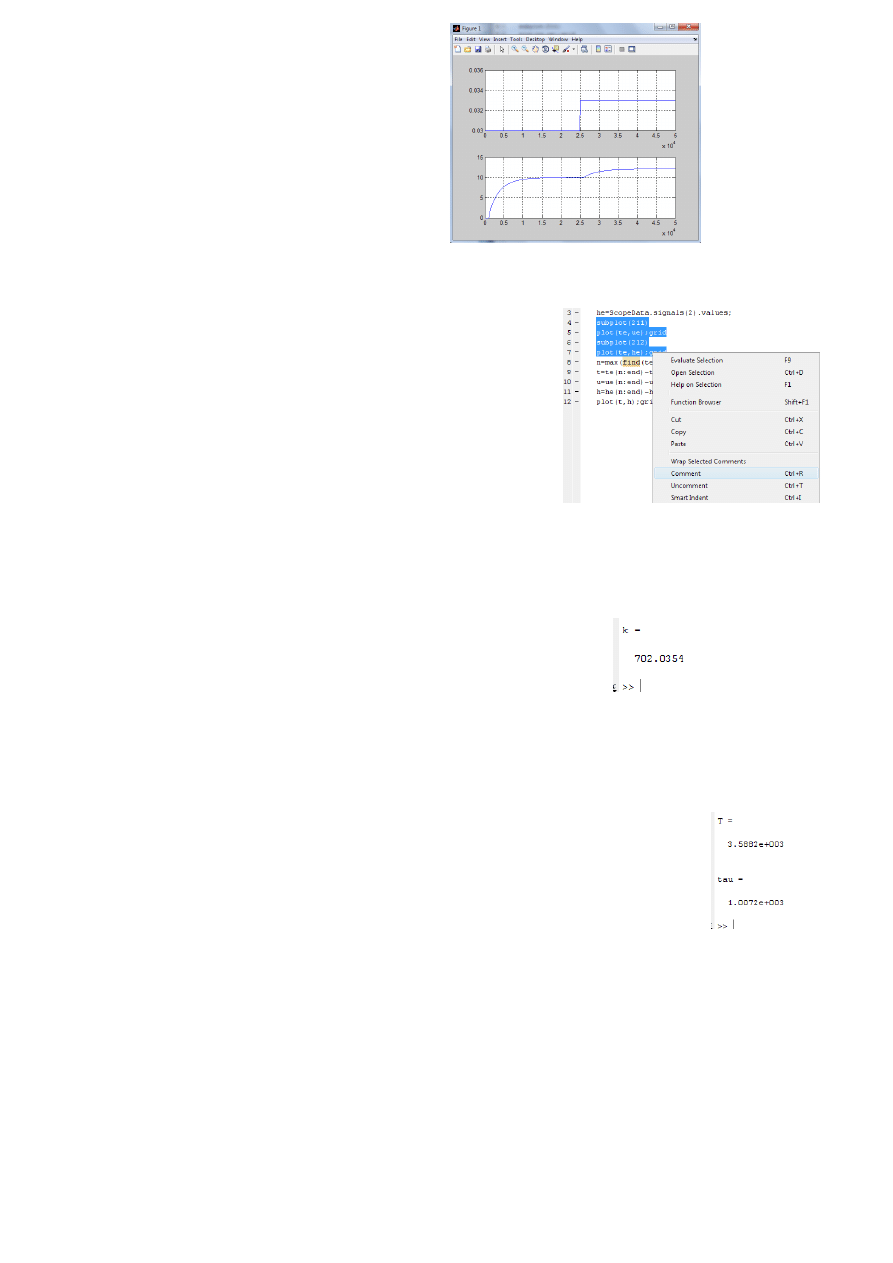
Powinno się nam pojawić okno z wykresami

Piszemy dalej:

n=max(find(te<=2.5*10^4)); -wartość czasu jest zmienna, zależy
t=te(n:end)-te(n);

jak odczytamy z wykresu

u=ue(n:end)-ue(n-1);
h=he(n:end)-he(n);

plot(t,h);grid

Po tej komendzie enter i zaznaczamy cztery wiersze i dajemy comment
tak żeby pojawiły się procenty po lewej %






Piszemy dalej:


hu=h(end);
U=u(end);
k=hu/U -klikamy F5 i w oknie matlaba powinno pojawić się obliczone ‘k’

Piszemy dalej:

n10=max(find(h<=0.1*hu));
h10=h(n10);
t10=t(n10);
n90=max(find(h<=0.9*hu));
h90=h(n90);
t90=t(n90);
T=(t90-t10)/2.2
tau=t10-0.1*T - klikamy F5 i w oknie matlaba powinno pojawić się obliczone ‘T i tau’

Wzory na T i tau odczytujemy z materiałów pomocniczych dla inercji z opóźnieniem

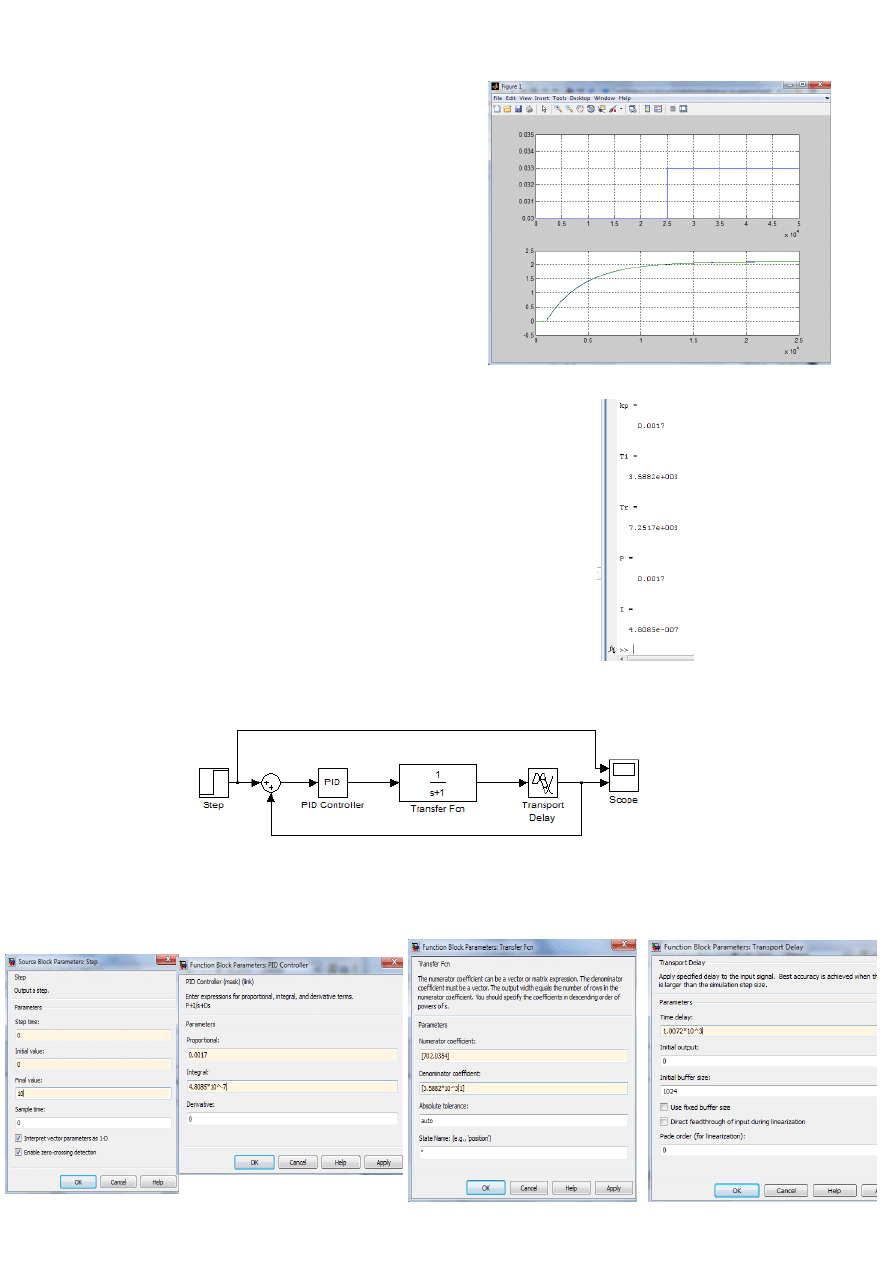
Piszemy dalej: aproksymacja i transmitancja (jakoś tak )

[Lp Mp]=pade(tau,12);
L=k*Lp;
M=[T 1];
M1=conv(M,Mp);
hm=lsim(L,M1,u,t);
plot(t,h,t,hm);grid -klikamy F5

i w oknie Figure1 przebiegi

na wyjściu powinny nam sie nałożyć na siebie









Piszemy dalej:

kp=0.34*T/(k*tau)

-odczytujemy z tabeli

Ti=T

-odczytujemy z tabeli

Tr=7.2*tau

-odczytujemy z tabeli bądź dany w zadaniu

P=kp
I=kp/Ti -klikamy F5 i wynik w matlabie







W oknie modelu tworzymy nowy model (drugi) file->new->model

Wprowadzamy dane do bloczków wg wyników z matlaba.

W sumatorze ustawiamy dolny + na -

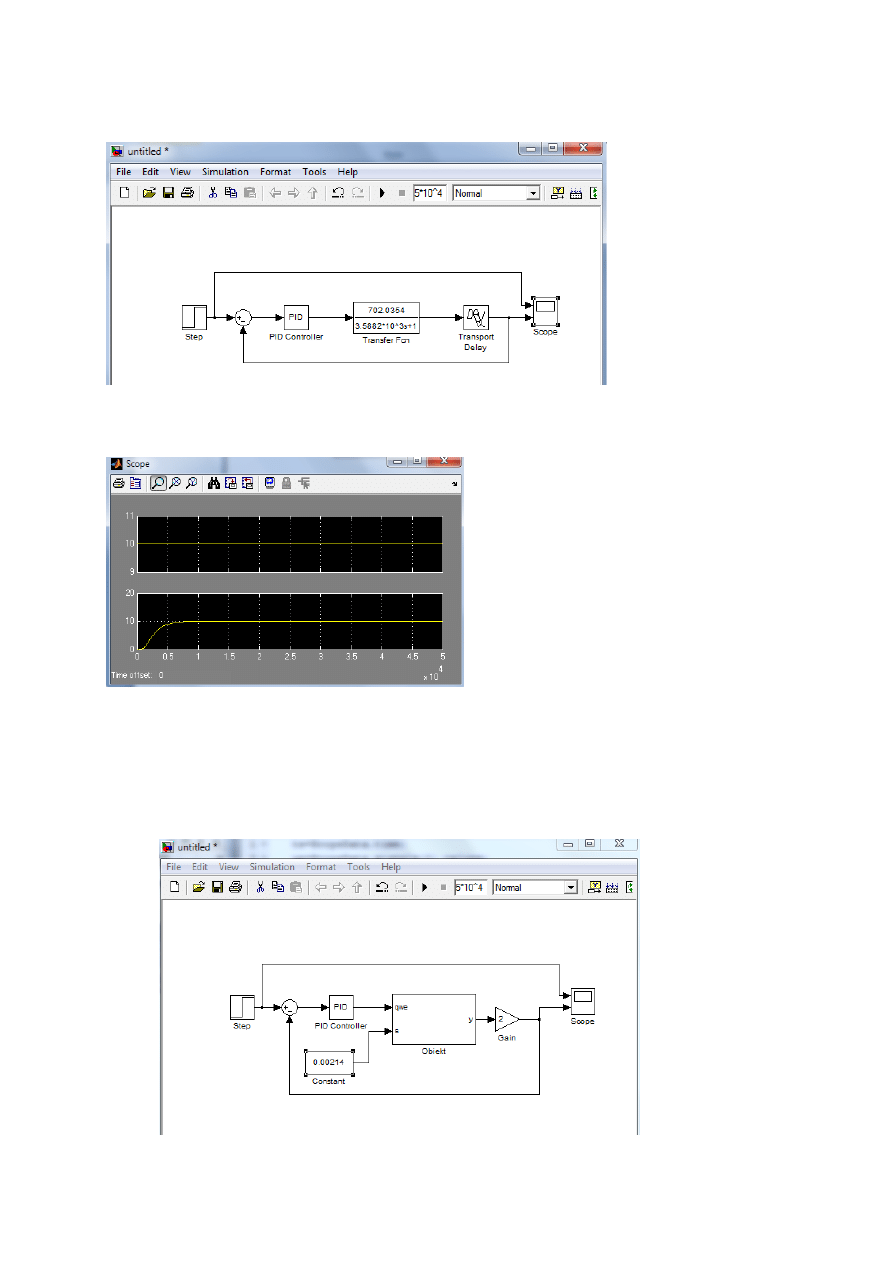
Schemat po wprowadzeniu parametrów:

Zwiększamy także czas
symulacji z 10.0 na np.
5*10^4 aby cały przebieg
był widoczny.

Puszczamy symulacje i powinno wyjść:

Teraz wyrzucamy z drugiego modelu bloki transfer FCN i transport delay i kopiujemy do niego nasz

obiekt, gain i constant z pierwszego modelu.

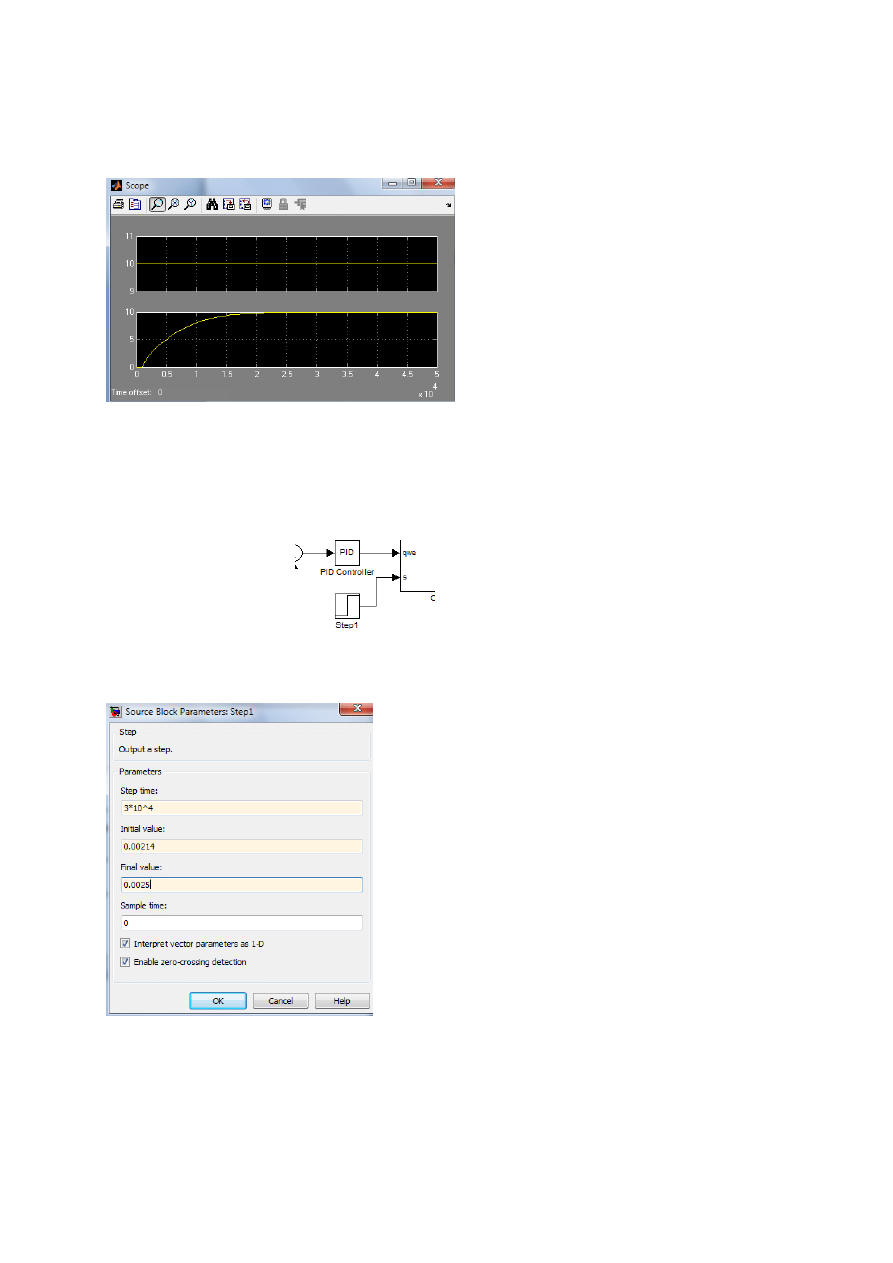
Symulujemy i powinno wyjść:

Następnie podmieniamy blok constant na blok step1 żeby sprawdzić jak, już nasz gotowy układ, reaguje na
wprowadzenie zakłócenia

Wprowadzamy do bloku step1 parametry naszego zakłócenia

3*10^4 – jest to czas w jakim wprowadzamy zakłócenie. Może
być inny, byle już po ustabilizowaniu przebiegu

0.00214 –nominalny stan otwarcia zaworu

0.0025- otwarcie zaworu o ok 20% (powiedziane w zadaniu)
większe od nominalnego w czasie 3*10^4 potrzebne do
sprawdzenia czy przebieg się ustabilizuje czyli poziom wody ustali
na h=10m

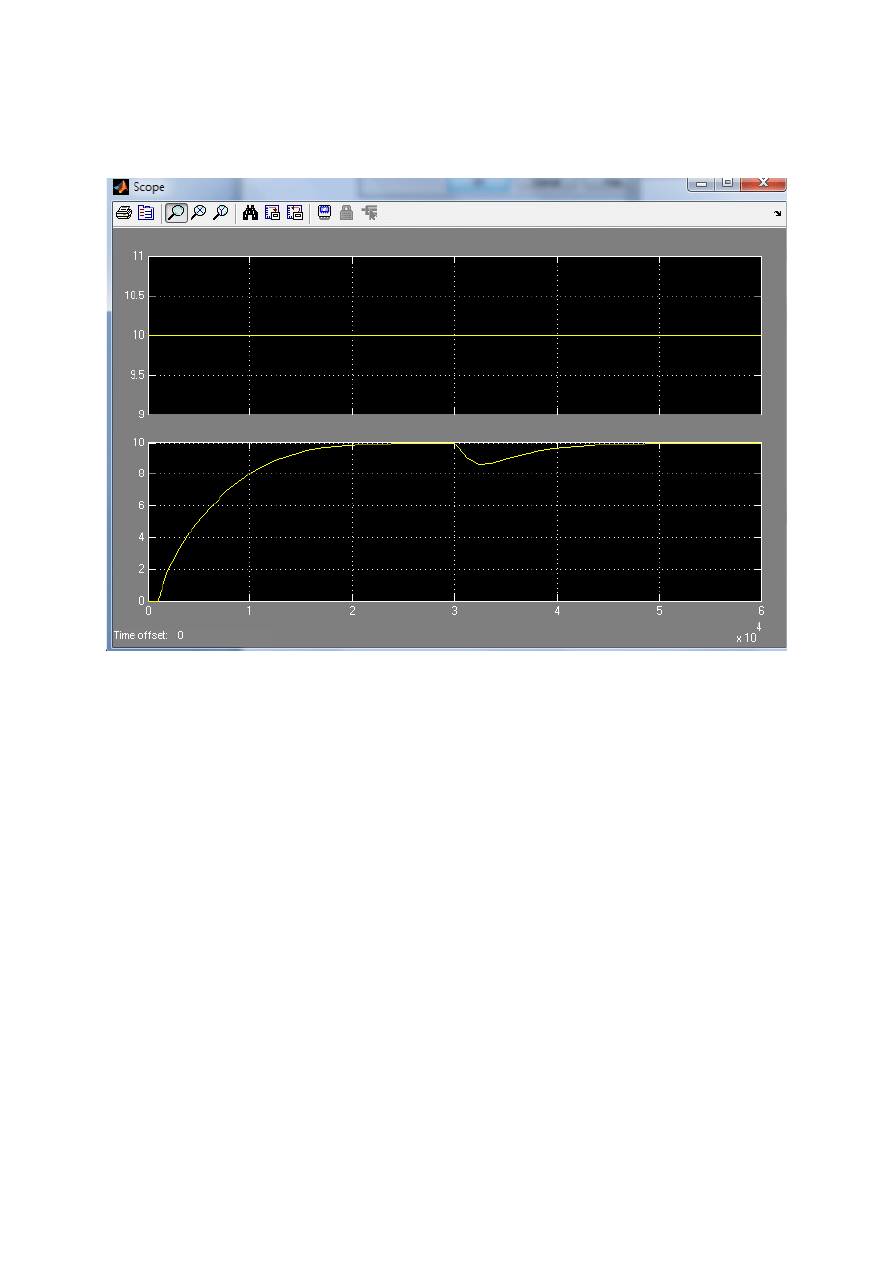
Wynik symulacji:

Jak widać poziom wody ustalił się powtórnie od nalewania (po zakłóceniu) na określonym na wejściu poziomie
10m

Pełny kod

Z opuźnieniem
ScopeData
ScopeData.signals
te=ScopeData.time;
ue=ScopeData.signals(1).values;
he=ScopeData.signals(2).values;
% subplot(211)

% plot(te,ue);grid
% subplot(212)
% plot(te,he);grid F5
n=max(find(te<=2*10^4));
t=te(n:end)-te(n);
u=ue(n:end)-ue(n-1);
h=he(n:end)-he(n);
plot(t,h);grid -procenty
hu=h(end);
U=u(end);
k=hu/U F5
n10=max(find(h<=0.1*hu));
h10=h(n10);
t10=t(n10);
n90=max(find(h<=0.9*hu));
h90=h(n90);
t90=t(n90);
T=(t90-t10)/2.2
tau=t10-0.1*T F5
[Lp Mp]=pade(tau,12);
L=k*Lp;
M=[T 1];
M1=conv(M,Mp);
hm=lsim(L,M1,u,t);
plot(t,h,t,hm);grid F5
kp=0.34*T/(k*tau)
Ti=T
Tr=7.2*tau
P=kp
I=kp/Ti F5

Bez opóźnienia

. przepisujemy początek

.

.

.

.

.

T=(t90-t10)/2.2

-odczytujemy z tabeli

tau=t10-0.1*T F5

-wyrzucamy cały wiersz

[Lp Mp]=pade(tau,12);

-wyrzucamy cały wiersz

L=k*Lp;

-wyrzucamy Lp

M=[T 1];
M1=conv(M,Mp);

-wyrzucamy cały wiersz

hm=lsim(L,M1,u,t);

-zamiast M1 samo M

plot(t,h,t,hm);grid F5
kp=0.34*T/(k*tau)

-odczytujemy z tabelki

Ti=T
Tr=7.2*tau F5

-dany bądź z tabeli

P=kp
I=kp/Ti F5
W przypadku PID należy podać wzór na D i z tabeli odczytać Td

Gdy nie ma opóźnienia to nie wstawiamy bloku transport delay