w w w . c h o m i k u j . p l / M a r W a g 9 8 7
STATYSTYKA – EGZAMIN:
1.
Statystyka – to zbiór metod służących do: pozyskiwania, prezentacji i analizie danych.
Proces pozyskiwania danych, to badanie statystyczne polegające na obserwacji
statystycznej.
2.
Podstawowe zadania statystyki to:
-
analiza (sprowadzająca się do sumarycznego opisu zbioru danych), przy
wykorzystaniu metod i opisu statystycznego;
-
interpretacja danych.
3.
Statystyka matematyczna – W wielu rzeczywistych sytuacjach zebranie wszystkich
potencjalnych danych nie jest możliwe, a analizy dokonuje się na podstawie
odpowiednio zebranych danych częściowych o badanym zjawisku. Jest to analiza
wykorzystująca metody rachunku prawdopodobieństwa.
4.
Populacja generalna – Badanie statystyczne dotyczy zawsze pewnej zbiorowości,
której elementami są obiekty materialne lub zjawiska. Badana zbiorowość
statystyczna to „populacja generalna” lub „zbiorowość generalna”.
5.
Cecha statystyczna – Elementy populacji generalnej mogą mieć różne właściwości
które podlegają obserwacji i które pozwalają na rozróżnianie elementów
w populacji. Właściwości te to „cechy statystyczne”.
6.
Rozkład cechy – Jeżeli elementy populacji różnią się między sobą wartościami
analizowanej cechy, to mówi się o rozkładzie cechy w populacji. Celem badania
statystycznego na ogół jest poznanie rozkładu interesującej nas cechy w populacji
generalnej oraz uzyskanie informacji o wartościach syntetycznych charakterystyk
tego rozkładu.
7.
Badania:
-
b. pełne – obejmują wszystkie elementy zbiorowości generalnej;
-
b. częściowe – obejmują część elementów populacji generalnej.
8.
Próba – podzbiór elementów populacji generalnej podlegających badaniu.
9.
Próba losowa – to próba otrzymana w wyniku doboru losowego.
10.
Warunki dla zapewnienia losowego doboru próby:
-
każdy
element
populacji
generalnej
ma
dodatnie,
znane
prawdopodobieństwo znalezienia się w próbie losowej;
-
istnieje możliwość ustalenia prawdopodobieństwa znalezienia się w próbie
dla każdego zespołu elementów populacji.
11.
Wnioskowanie statystyczne – Podstawowym zagadnieniem pojawiającym się
w badaniach częściowych jest możliwość uogólnienia uzyskanych na podstawie próby
wyników na całą populację oraz oszacowanie popełnionych przy tym błędów. Jest
to „wnioskowanie statystyczne”. Wyróżnia się:
-
estymację (szacowanie) nieznanych wartości parametrów rozkładu cechy;
-
sprawdzanie (weryfikację) hipotez dotyczących wartości parametrów rozkładu
lub postaci samego rozkładu.
12.
Cechy skokowe (dyskretne) – cechy statystyczne (mierzalne), które przyjmują
wartości całkowite.
13.
Cechy ciągłe – to cechy statystyczne przyjmujące wartości rzeczywiste.
14.
Szereg pozycyjny – Jeżeli próba dotycząca jednej cechy mierzalnej nie jest zbyt liczna,
tzn. dotyczy
≤
30 jednostek, to wstępne jej opracowanie polega na uszeregowaniu w
porządku rosnącym danych liczb. Jest to „szereg pozycyjny”.
w w w . c h o m i k u j . p l / M a r W a g 9 8 7
- wyniki surowe:
4 5 0 1 2 4 0 9 4 5
- po uporządkowaniu: 0 0 1 2 4 4 4 5 5 9
15.
Szereg rozdzielczy - jeżeli liczebność próby jest duża (orientacyjnie > 30), to drugim
etapem jej opracowania jest dokonanie grupowania (klasyfikacji). Grupowanie polega
na podziale próby na podzbiory zwane grupami lub klasami. Wartościami
reprezentującymi poszczególne klasy są ich środki oraz ich liczebności, czyli liczby
jednostek próby należących do danej klasy. Tworzą one razem „szereg rozdzielczy
(histogram)”.
16.
Zmienna losowa - jest to taka zmienna, która w wyniku doświadczenia przybiera
jedną i tylko jedną wartość ze zbioru tych wszystkich wartości, jakie ta zmienna może
przyjąć. Wartości zmienne losowej to inaczej realizacje zmiennej losowej. Zmienna
losowa przybiera różne wartości z różnym prawdopodobieństwem.
P(X=x
i
) = p
i
– funkcja rozkładu prawdopodobieństwa
∑
=
=
n
i
p
1
1
1
17.
Rodzaje zmiennych losowych:
-
skokowe, to takie , które mają skończony lub przeliczalny zbiór wartości;
-
ciągłe, to takie, które mogą przybierać dowolne wartości liczbowe z pewnego
przedziału liczbowego.
18.
Rozkład zmiennej losowej:
Niech X jest zmienną losową dyskretną, która może przyjmować wartości x
1
, x
2
, ...
odpowiednio z prawdopodobieństwem p
1
, p
2
, ... Każdej realizacji zmiennej losowej X
przyporządkowane jest więc pewne prawdopodobieństwo. Rozkładem skokowej
(dyskretnej) zmiennej losowej X nazywa się prawdopodobieństwo tego, że zmienn X
przybiera wartości x
i
(i=1,2,...):
P(X=x
i
) = p
i
∑
=
=
n
i
p
1
1
1
19.
Dystrybuanta zmiennej losowej – (skumulowane prawdopodobieństwo), to funkcja
oznaczona przez F(x), określona:
F(x) = P(X<x)
Określa ona prawdopodobieństwo tego, że zmienna losowa X przyjmuje jakąkolwiek
wartość mniejszą od z góry przyjętej danej wartości x.
20.
Rozkład Normalny Gaussa:
Zmienna losowa ciągła X ma rozkład normalny o wartości średniej M i odchyleniu
standardowym
σ
,
co
zapisujemy
M(m;
σ
),
jeśli
jej
funkcja
gęstości
prawdopodobieństwa wyraża się wzorem:
]
2
)
(
[
2
2
2
1
)
(
π
π
σ
⋅
−
−
⋅
⋅
⋅
=
m
x
e
x
f
21.
Rozkład Bernoulli’ego:
To rozkład dwumianowy, dotyczący zmiennej losowej dyskretnej, w którym wykonuje
się serię n niezależnych doświadczeń w takich samych warunkach, gdzie
w wyniku pojedynczego doświadczenia może zrealizować się pewne zdarzenie A
z prawdopodobieństwem P(A) = p lub zdarzenie przeciwne A z prawd. P(A) = 1-p = q.
Prawd., że wśród przeprowadzonych n doświadczeń zrealizuje się k razy zdarzenie A
jest określone wzorem:
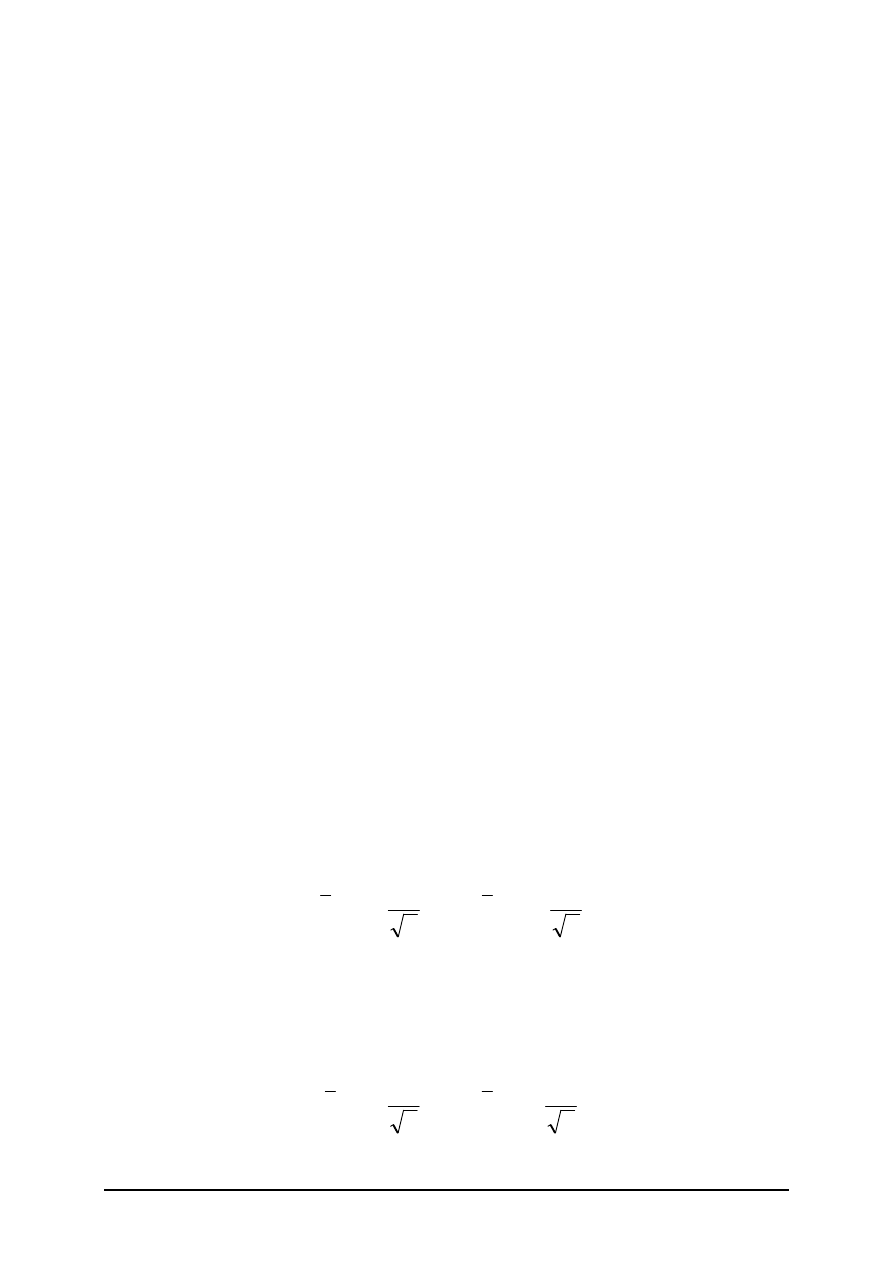
w w w . c h o m i k u j . p l / M a r W a g 9 8 7
k
n
k
p
p
k
n
k
X
P
−
−
⋅
⋅
=
=
)
1
(
)
(
)
(
gdzie x = 0,1,2,...n
22.
Rozkład Poisson’a:
To rozkład dwumianowy, dotyczący zmiennej losowej dyskretnej, w którym liczba
doświadczeń jest wystarczająco duża (n>50) natomiast prawdopodobieństwo jest
bliskie zeru (p<0,1). Rozkład jest określony wzorem:
x
n
x
p
p
x
n
k
X
P
−
−
⋅
⋅
=
=
)
1
(
)
(
)
(
gdzie: x = 0,1,2,...n
23.
Reguła trzech
σσσσ
:
Jeżeli x jest zmienną losową ciągłą o rozkładzie N(
µ
;
σ
), to zachodzi:
P(
µ
-3
σ
≤
x
≤
µ
+3
σ
) = 0,9973
Tzn., takie jest prawdopodobieństwo, że zmienna losowa przyjmuje takie wartości,
które różnią się od wartości oczekiwanej
µ
nie więcej niż o
±
3 odchylenia
standardowe
σ
.
24.
Rozkład wykładniczy:
Zmienna losowa X ma wykładniczy rozkład prawdopodobieństwa, jeśli jej funkcja
gęstości wyraża się wzorem:
0
,
0
0
;
0
{
)
(
>
>
≤
=
−
λ
λ
λ
x
x
dla
e
x
f
x
Parametr
λ
jest związany z wartością oczekiwaną i wariancją:
E(x) = 1/
λ
D
2
(x) = 1/
λ
2
25.
Estymacja przedziałowa funkcji:
To szacowanie parametru w postaci przedziału ufności, który z dużym prawdopod.
obejmuje prawdziwą wartość parametru.
MODEL 1:
Badana cecha w populacji generalnej ma rozkład normalny N(
µ
;
σ
). Gdzie
µ
jest
nieznane, natomiast
σ
jest znana. Z populacji tej wylosowano niezależnie próbę
o liczebności n elementów. Przedział ufności dla średniej
µ
populacji:
α
σ
µ
σ
α
α
−
=
⋅
+
<
<
⋅
−
1
{
n
u
x
n
u
x
P
gdzie 1-
α
to współczynnik ufności przyjęty z góry; u
α
to kwantyl rozkładu normalnego
odczytany z tablicy.
MODEL 2:
Badana cecha w populacji generalnej ma rozkład normalny N(
µ
;
σ
). Gdzie
µ
oraz
σ
są
nieznane. Z populacji tej wylosowano niezależnie małą próbę o liczebności n (n<30)
elementów. Przedział ufności dla średniej
µ
populacji:
α
µ
α
α
−
=
⋅
+
<
<
⋅
−
1
{
n
s
t
x
n
s
t
x
P
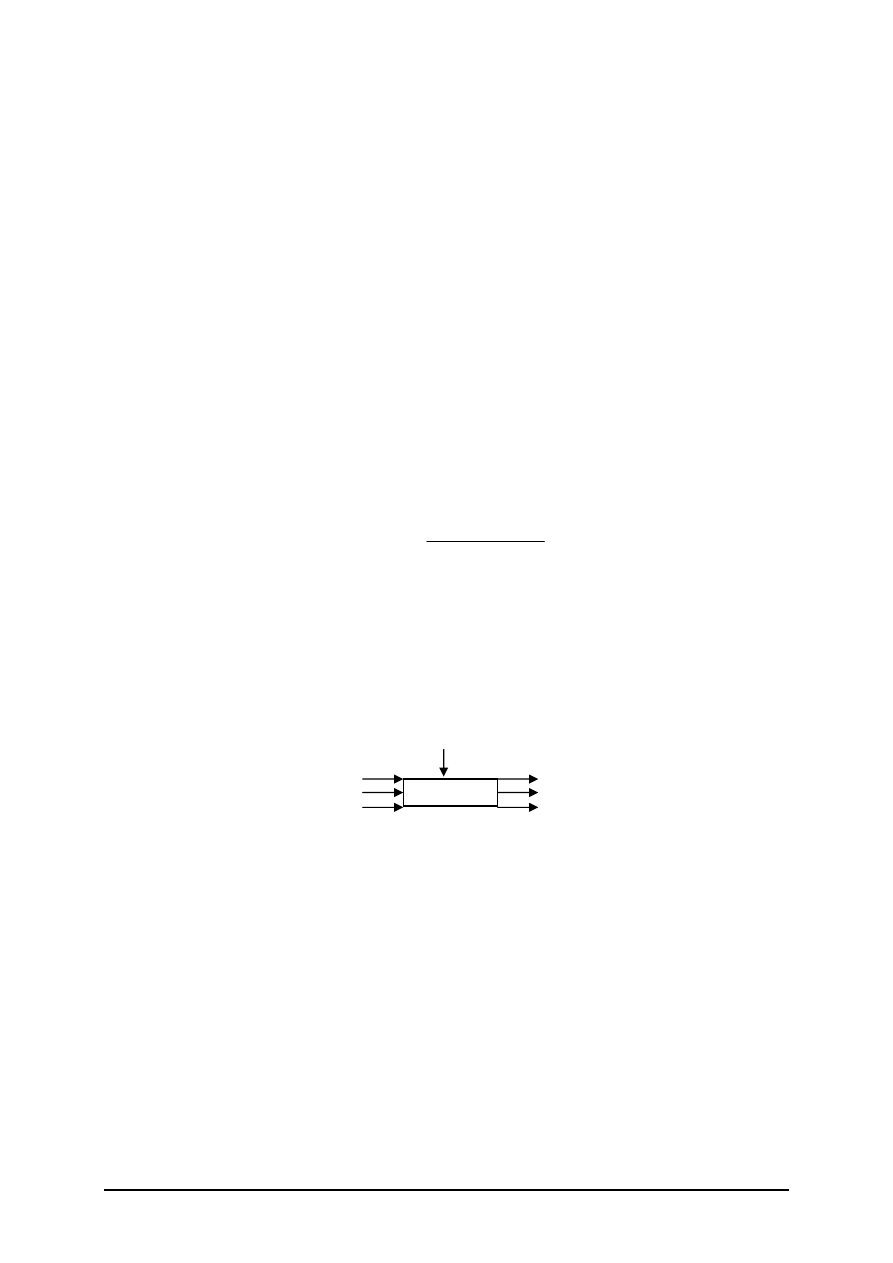
w w w . c h o m i k u j . p l / M a r W a g 9 8 7
gdzie 1-
α
to współczynnik ufności przyjęty z góry; u
α
to kwantyl rozkładu t-Studenta
odczytany z tablicy.
26.
Weryfikacja (testowanie) hipotez statystycznych – to drugi obok estymacji
podstawowy rodzaj wnioskowania statystycznego.
27.
Hipoteza statystyczna – to każde przypuszczenie dotyczące wielkości parametru
rozkładu zmiennej losowej w populacji generalnej lub próbnej, albo też postaci tego
rozkładu, uzyskane na podstawie próby losowej.
28.
Hipotezy statystyczne:
-
parametryczne, związane z wartościami parametrów;
-
nieparametryczne, związane z postacią rozkładów.
29.
Hipoteza zerowa – to hipoteza głosząca że różnica pomiędzy parametrem
Θ
a jego
oceną T jest statystycznie nieistotna (jest na poziomie zerowym): H
0
:
Θ
= T
Hipoteza alternatywna – to hipoteza określająca dla hipotezy zerowej zależność:
H
1
:
Θ
≠
T
lub
H
1
:
Θ
> T
lub
H
1
:
Θ
< T
Hipotezę zerową weryfikuje się za pomocą określonego testu, po czym określa obszar
krytyczny odrzuceń hip. zerowej dla danego poziomu istotności
α
.
30.
Test zgodności – Wprowadza się charakterystykę, będącą miarą odległości między
dystrybuantą rozkładu empirycznego, a dystrybuantą rozkładu hipotetycznego:
∑
=
⋅
⋅
−
=
r
i
i
p
n
p
r
n
1
2
1
1
2
)
(
χ
gdzie: n
i
– liczebność empiryczna i-tego przedziału klasowego (>10); r – liczba
przedziałów klasowych; p
i
– prawdopodobieństwo odpowiadające wartości badanej
cechy w i-tej klasie.
31.
Eksperyment – seria doświadczeń.
Cel planowania eksperymentu – wyznaczanie opisu matematycznego obiektu badań
lub zjawiska, tzw. modelu matematycznego, umożliwiającego analizę jego
zachowania i ustalenia czynników wpływających na zachowanie obiektu.
32.
Obiekt badań – można go przedstawić jako czarną skrzynkę:
x
1
, x
2
, x
n
– zmienne wejściowe (czynniki);
y
1
, y
2
, y
n
– zmienne wyjściowe, charakteryzujące stan obiektu w zależności od
zmiennych wejściowych (zmienne stanu);
z – zmienna przypadkowa o nieokreślonym rozkładzie, niekontrolowana (zakłócenie).
33.
Eksperyment wstępny – przeprowadza się w przypadku, gdy brak jakiejkolwiek
informacji o obiekcie badań. Jego celem jest uzyskanie wstępnych informacji o
obiekcie niezbędnych do przeprowadzenia eksperymentu podstawowego.
Zadaniem „eksperymentu podstawowego” jest uzyskanie modelu badanego
obiektu, który wykorzystuje się dla optymalizacji obiektu (lub procesu) lub jako opis
matematyczny służący do badania jego
zachowa
ń
.