
Michał Kowalski - GiBS
Ś
cianki szczelne
Rozwi
ą
zanie ogólne pojedynczo zakotwionej
ś
cianki szczelnej w jednorodnym, idealnie
sypkim gruncie zawodnionym
Michał Kowalski - GiBS
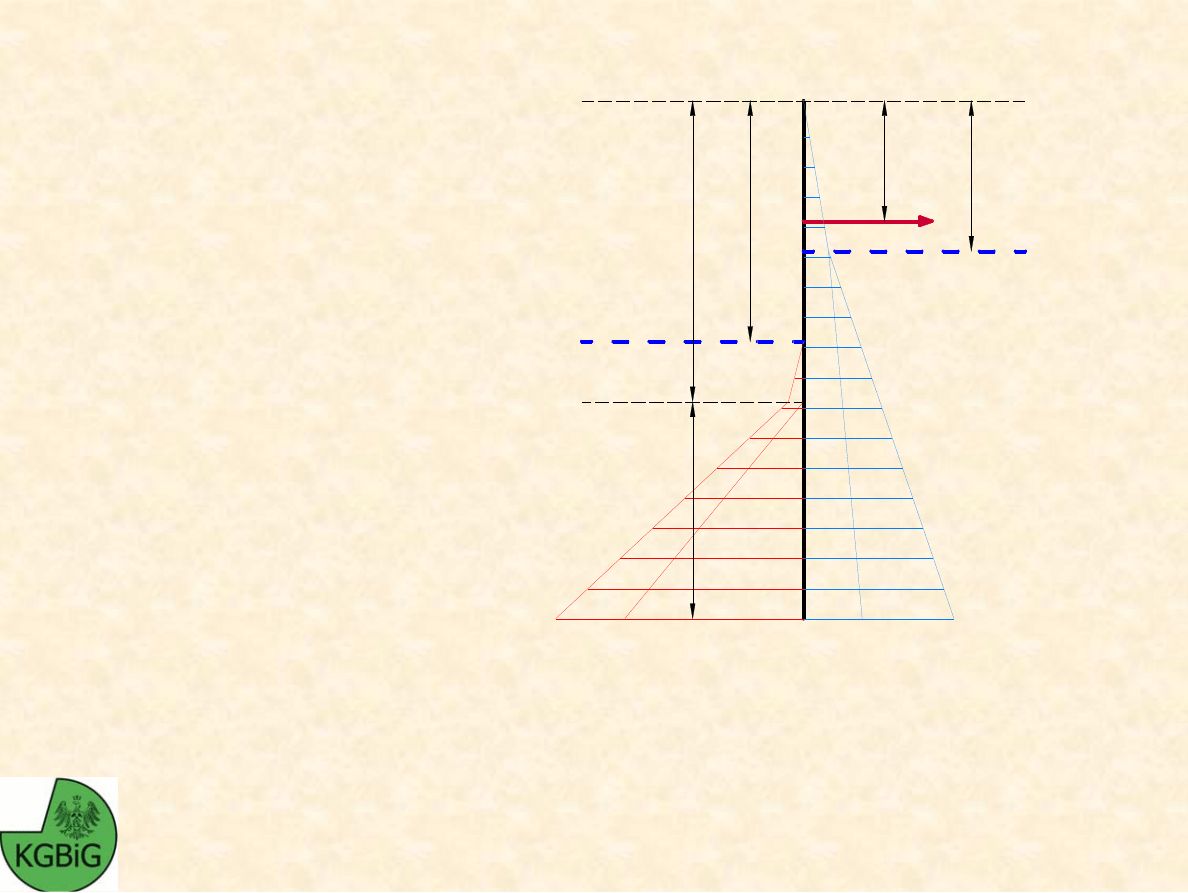
Rozpatrzmy siły działaj
ą
ce na
ś
ciank
ę
szczeln
ą
umieszczon
ą
w jednorodnym, idealnie sypkim,
zawodnionym gruncie. Załó
ż
my,
ż
e
dla utrzymania stateczno
ś
ci wykopu o
gł
ę
boko
ś
ci h została ona zabita w
grunt na gł
ę
boko
ść
d. Zwierciadło wód
gruntowych po stronie wykopu
znajduje si
ę
na gł
ę
boko
ś
ci h
l
, po
stronie naziomu na gł
ę
boko
ś
ci h
r
.
W odległo
ś
ci a od naziomu wykopu
ś
cianka została zakotwiona kotwi
ą
oddziałuj
ą
c
ą
z sił
ą
T.
Ś
cianka szczelna w jednorodnym gruncie zawodnionym
a
h
h
h
l
r
ZWG
ZWG
r
l
d
T
WPROWADZENIE

Michał Kowalski - GiBS
Ś
cianka szczelna w jednorodnym gruncie zawodnionym
Ze wzgl
ę
du na ci
ś
nienie spływowe przyj
ę
to:
(
)
(
)
(
)
(
)
(
)
r
r
w
r
l
a
r
w
r
l
p
h
d
h
d
h
d
h
h
h
d
h
d
h
d
h
h
−
+
+
−
+
γ
−
+
γ′
=
γ′
−
+
+
γ
−
−
γ′
=
γ′
7
.
0
7
.
0
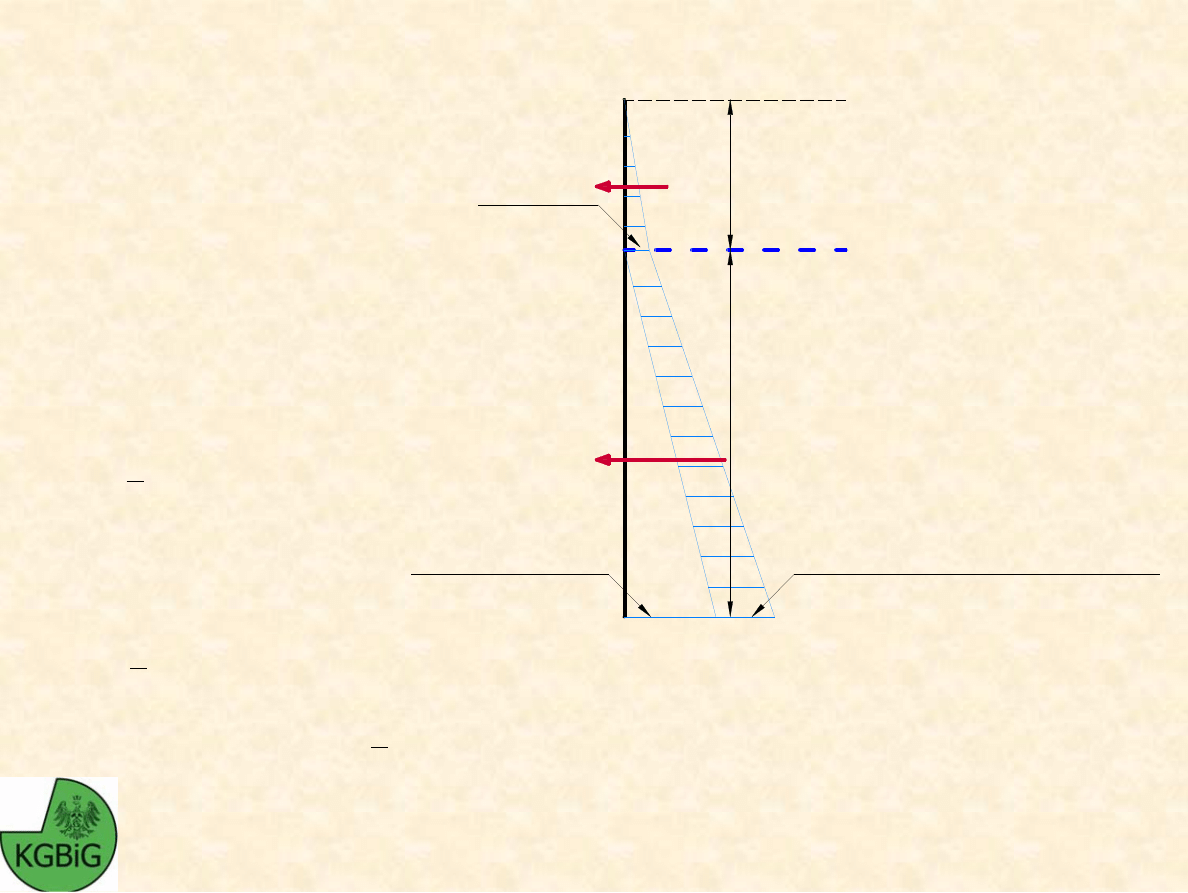
Michał Kowalski - GiBS
ZWG r
r
h
h+d-h
r
E
a1
SIŁY PARCIA – strona prawa:
Ś
cianka szczelna w jednorodnym gruncie zawodnionym
(
)
(
)
[
]
(
)
(
) (
)(
)
2
2
1
2
1
:
2
2
r
w
a
a
r
r
a
a
r
r
w
r
a
a
r
a
r
a
a
r
h
d
h
K
h
d
h
h
K
E
h
d
h
h
d
h
h
d
h
K
h
K
h
K
E
d
h
z
h
−
+
γ
+
γ′
+
−
+
γ
=
−
+
−
+
γ
+
−
+
γ′
+
γ
+
γ
=
+
<
≤
r
a
h
K
γ
(
)
r
a
a
r
a
h
d
h
K
h
K
−
+
γ′
+
γ
(
)
r
w
h
d
h
−
+
γ
2
2
1
:
0
1
r
a
a
r
h
K
E
h
z
γ
=
<
<
a2
E
Michał Kowalski - GiBS
d
l
h
h
ZWGl
l
Ś
cianka szczelna w jednorodnym gruncie zawodnionym
(
)
(
)
[
]
(
)
2
2
2
1
2
1
2
1
:
2
2
d
d
K
d
h
h
E
d
d
d
K
h
h
h
h
E
d
h
z
h
w
p
p
l
w
p
w
p
p
l
w
l
w
p
γ
+
γ′
+
−
γ
=
⋅
γ
+
γ′
+
−
γ
+
−
γ
=
+
<
≤
(
)
l
w
h
h
−
γ
d
K
p
p
γ′
(
)
d
h
h
l
w
+
−
γ
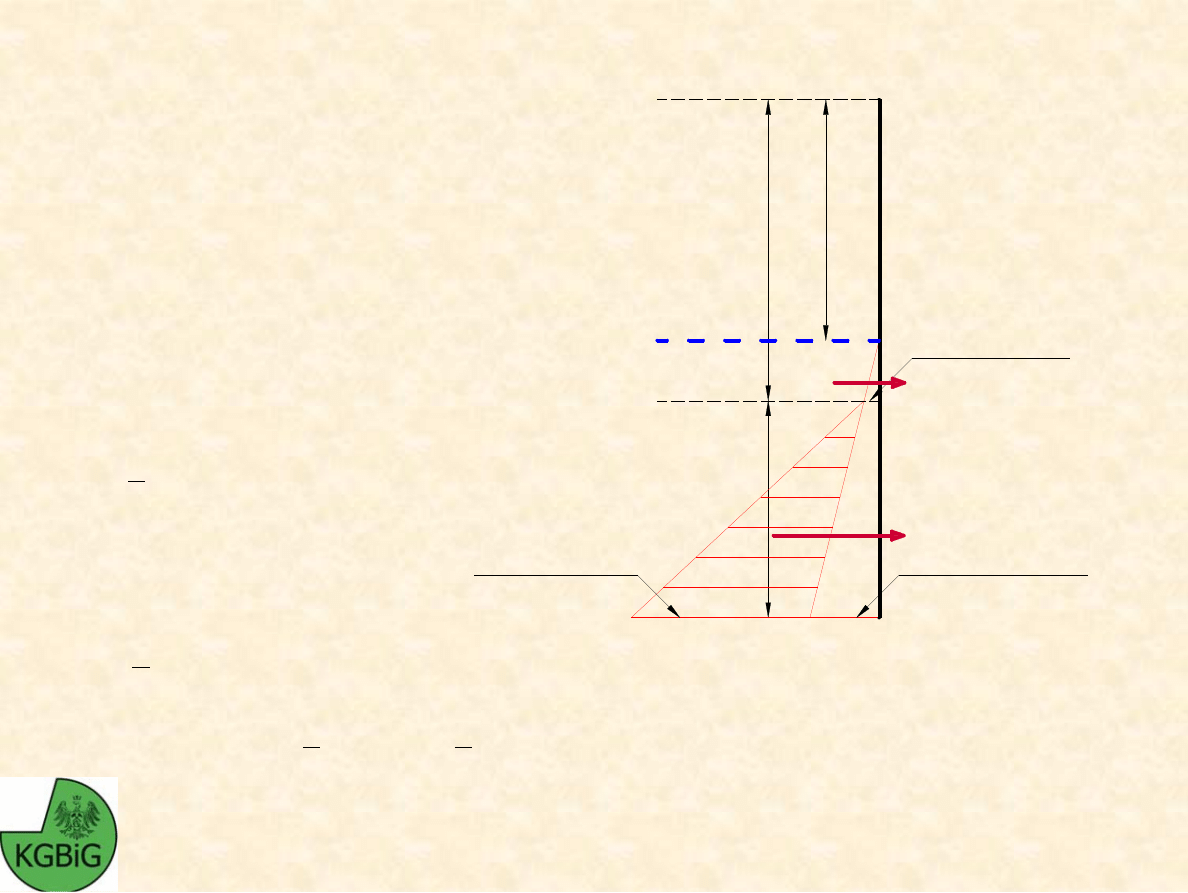
SIŁY PARCIA – strona lewa:
(
)
2
2
1
:
1
l
w
p
l
h
h
E
h
z
h
−
γ
=
<
<
p1
E
p2
E
Michał Kowalski - GiBS
Ś
cianka szczelna w jednorodnym gruncie zawodnionym
(
)
(
)
(
)(
)
(
)(
)
(
)(
)
r
w
a
a
r
a
r
w
a
a
r
a
r
r
r
w
a
a
r
a
r
a
r
w
r
a
a
r
a
r
a
r
r
h
d
h
K
h
K
h
d
h
K
h
K
h
d
h
R
h
d
h
K
h
K
h
K
h
d
h
h
d
h
K
h
K
h
K
h
d
h
R
−
+
γ
+
γ′
+
γ
−
+
γ
+
γ′
+
γ
⋅
−
+
=
−
+
γ
+
γ′
+
γ
+
γ
−
+
γ
+
−
+
γ′
+
γ
+
γ
⋅
−
+
=
2
3
3
2
3
2
a
E
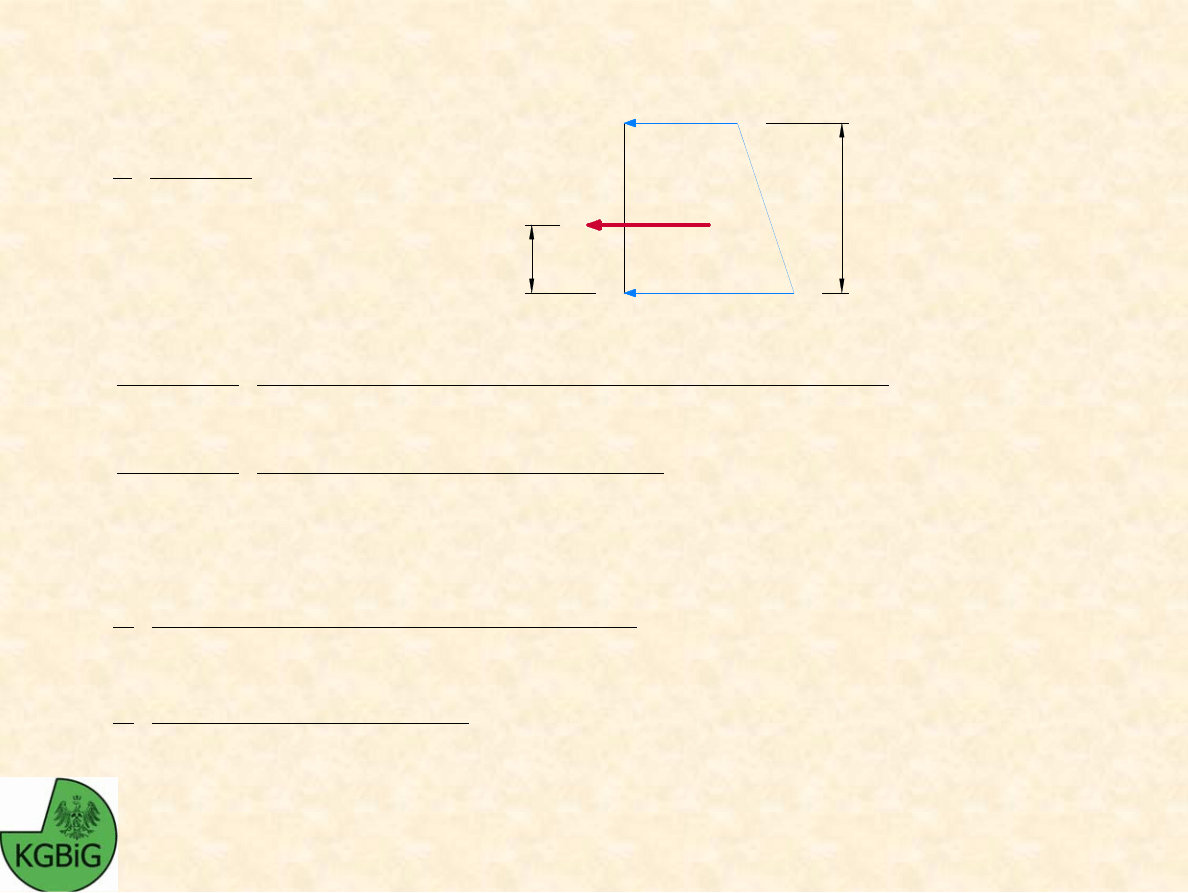
Okre
ś
lenie ramienia siły
2
p
E
Okre
ś
lenie ramienia siły
(
)
(
)
(
) (
)
(
)
(
)
d
K
d
h
h
d
K
d
h
h
d
R
d
d
K
h
h
h
h
d
d
K
h
h
h
h
d
R
p
p
l
w
p
p
l
w
l
w
p
p
l
l
w
w
p
p
l
w
l
w
l
γ′
+
+
−
γ
γ′
+
+
−
γ
⋅
=
γ
+
γ′
+
−
γ
+
−
γ
γ
+
γ′
+
−
γ
+
−
γ
⋅
=
2
2
3
3
3
2
3
2
1
2
1
2
3
e
e
e
e
h
h
e
+
+
⋅
=
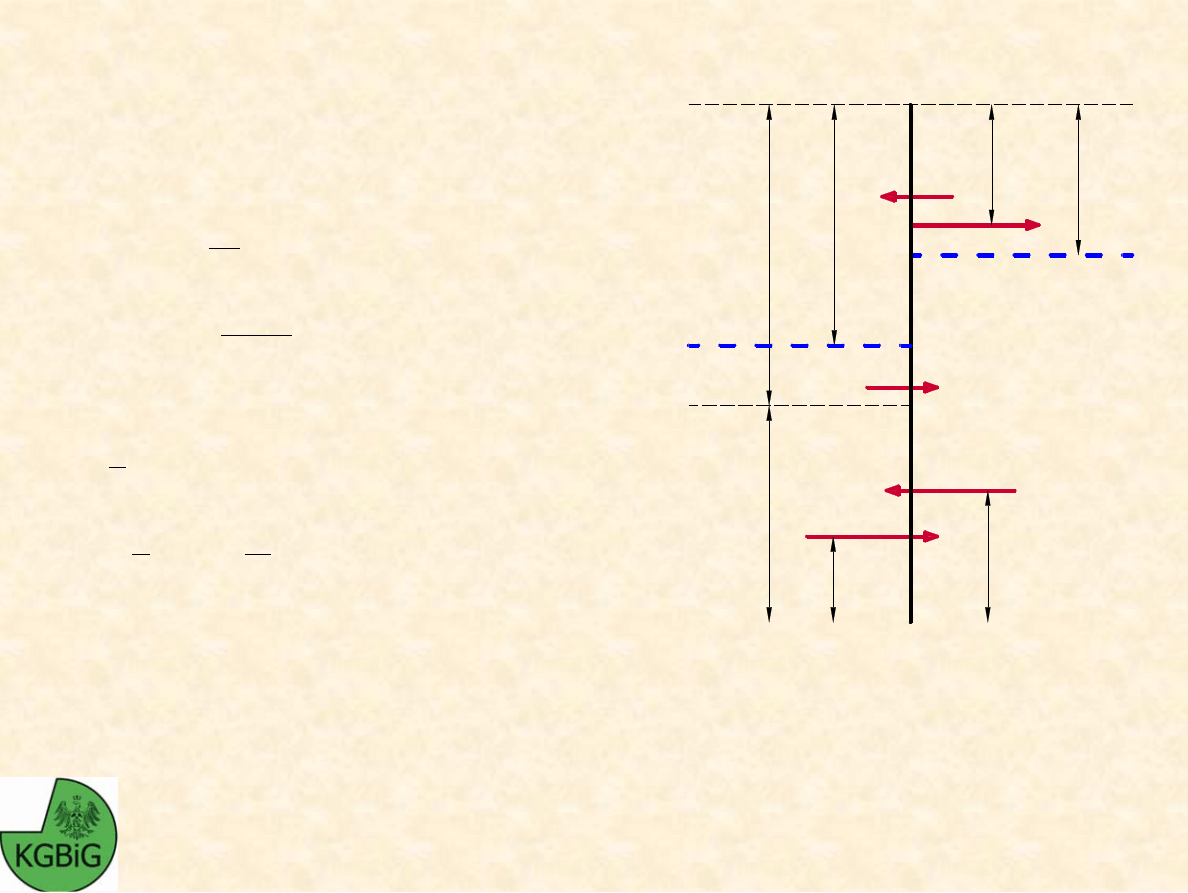
RAMIONA DZIAŁANIA SIŁ:
e
1
2
e
h
E
h
e
Michał Kowalski - GiBS
Ś
cianka szczelna w jednorodnym gruncie zawodnionym
(
)
(
)
(
)
(
)
0
3
3
2
3
2
0
3
3
2
1
2
1
2
1
2
1
=
−
−
+
−
−
−
−
+
−
−
+
+
−
=
−
−
+
−
−
−
−
−
+
−
−
+
+
−
−
l
p
l
p
r
a
r
a
l
p
l
p
r
a
r
r
a
R
a
d
h
E
h
a
h
E
R
a
d
h
E
a
h
E
R
a
d
h
E
h
h
a
h
E
R
a
d
h
E
h
a
h
E
Z powy
ż
szego równania nale
ż
y iteracyjnie okre
ś
li
ć
gł
ę
boko
ść
zakotwienia
d.
Po okre
ś
leniu warto
ś
ci d nale
ż
y sprawdzi
ć
, czy nie jest ona mniejsza ni
ż
wynika
z warunku na przebicie hydrauliczne.
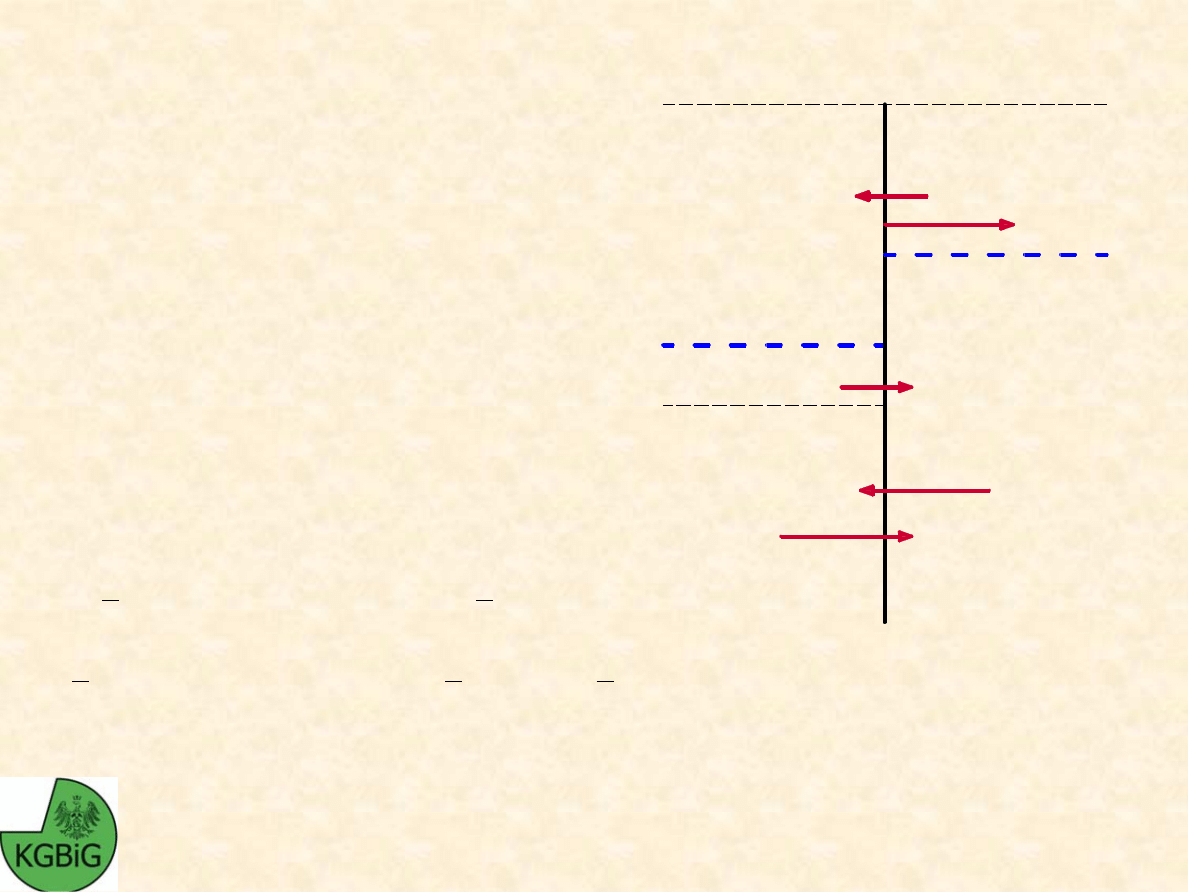
SUMA MOMENTÓW WZGL
Ę
DEM
PUNKTU ZAKOTWIENIA:
p1
E
p2
E
E
a1
a2
E
T
a
h
r
h
l
l
R
R
r
h
d

Michał Kowalski - GiBS
Ś
cianka szczelna w jednorodnym gruncie zawodnionym
WARUNEK NA PRZEBICIE HYDRAULICZNE:
– spadek hydrauliczny
– ci
ś
nienie spływowe
– wska
ź
nik bezpiecze
ń
stwa
d
h
h
h
h
i
r
r
l
2
)
(
+
−
−
=
w
r
r
l
w
d
h
h
h
h
i
j
γ
+
−
−
=
γ
=
2
)
(
5
.
2
'
≥
=
j
γ
F
(
)
(
) (
)
(
)
2
1
2
2
1
2
h
Fh
F
h
d
h
h
h
h
F
d
d
h
h
h
h
F
F
d
h
h
h
h
l
r
r
r
l
r
r
l
r
r
l
−
+
−
=
−
−
−
=
+
−
=
−
⇒
=
+
−
−
Michał Kowalski - GiBS
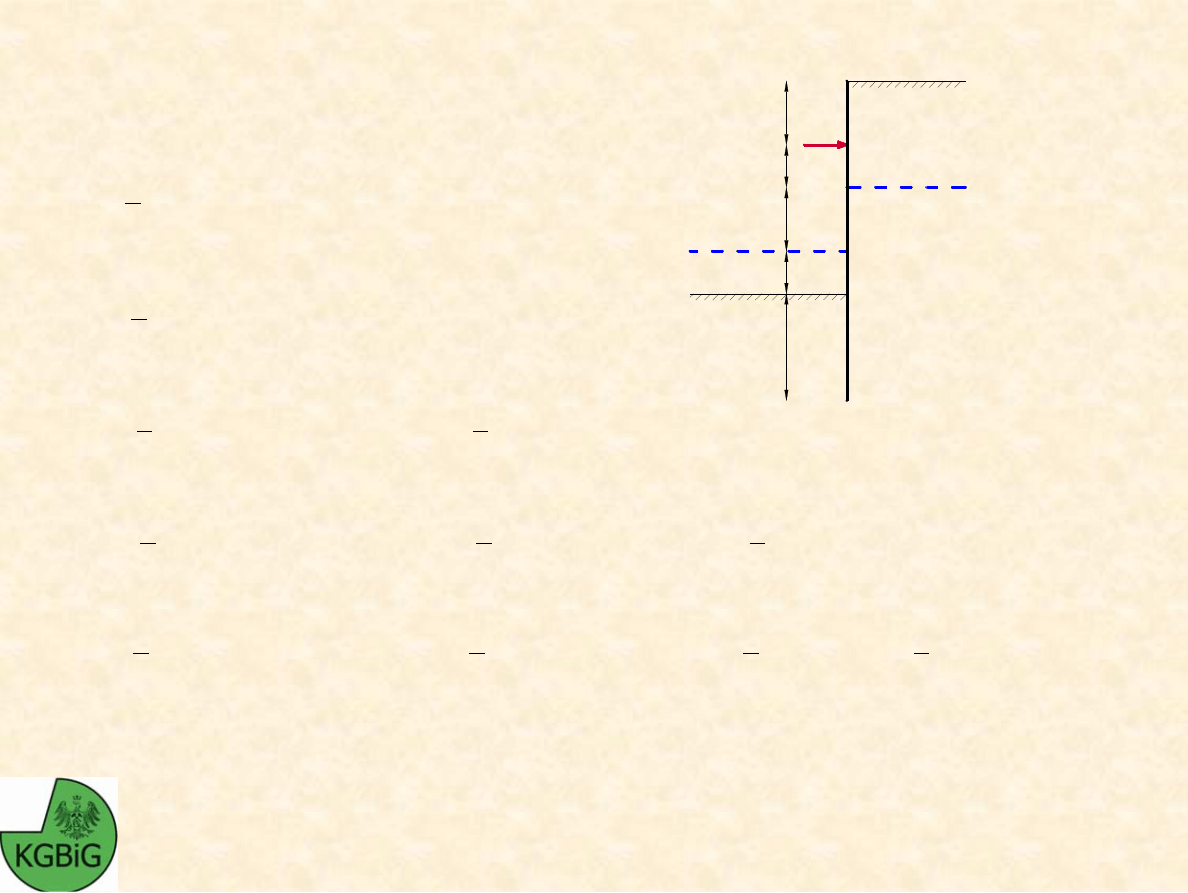
OKRE
Ś
LENIE SIŁY T W KOTWI:
Ś
cianka szczelna w jednorodnym gruncie zawodnionym
2
1
2
1
2
1
2
1
0
1
p
p
a
a
p
p
a
a
n
i
ix
E
E
E
E
T
E
E
E
E
T
P
−
−
+
=
⇒
=
+
+
−
−
=
∑
=
l
ZWG
r
ZWG
T
E
a2
a1
E
E
p2
E
p1
(
) (
)(
)
(
)
(
)
γ
+
γ′
+
−
γ
−
−
γ
−
+
−
+
γ
+
γ′
+
−
+
γ
+
γ
=
2
2
2
2
2
2
1
2
1
2
1
2
1
2
1
d
d
K
d
h
h
h
h
h
d
h
K
h
d
h
h
K
h
K
T
w
p
p
l
w
l
w
r
w
a
a
r
r
a
r
a
Michał Kowalski - GiBS
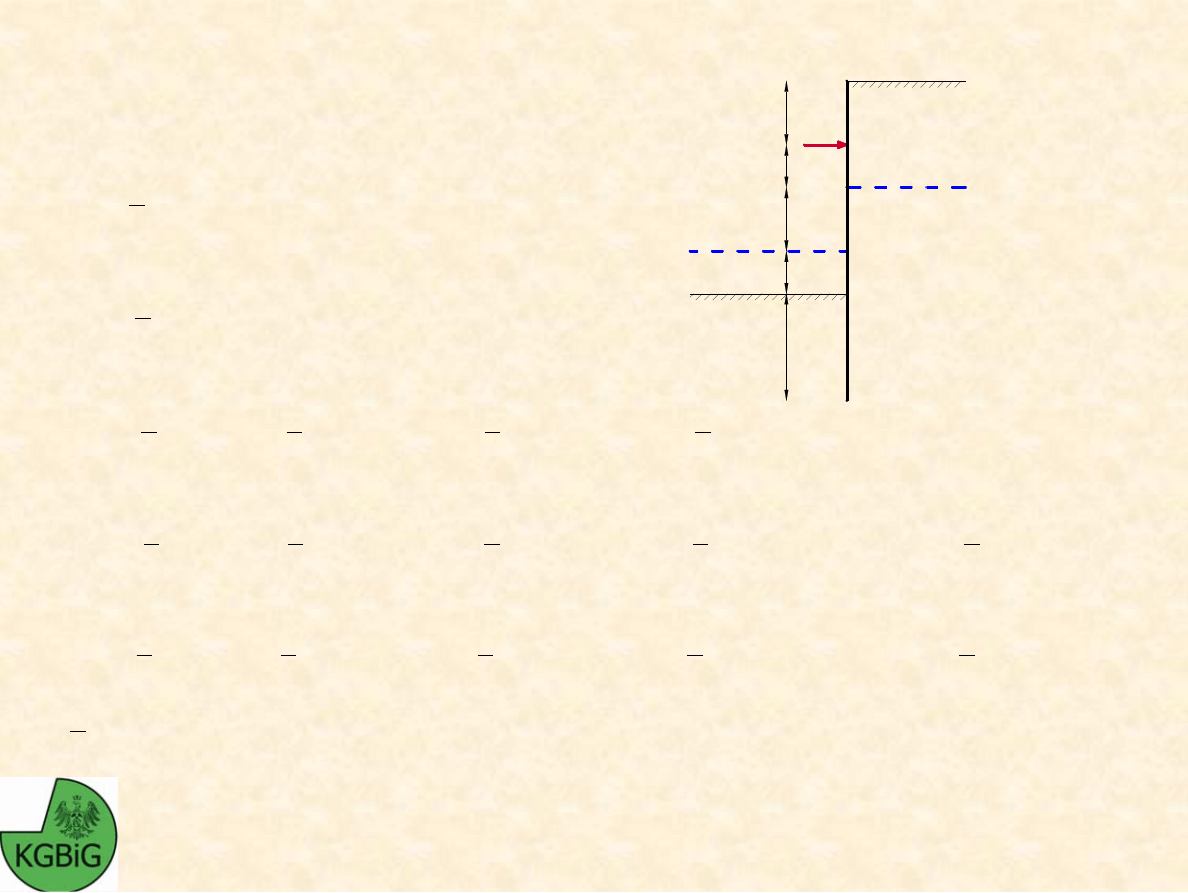
SIŁY TN
Ą
CE W PRZEDZIAŁACH:
Ś
cianka szczelna w jednorodnym gruncie zawodnionym
2
2
1
0
z
K
Q
a
z
przedział
I
a
I
γ
−
=
<
≤
IV
III
II
I
V
(
) (
)(
)
(
)
(
)
2
2
2
2
2
1
2
1
2
1
2
1
h
z
K
h
z
h
z
K
h
z
h
K
T
h
K
Q
d
h
z
h
przedział
V
p
p
l
w
r
w
a
a
r
r
a
r
a
V
−
γ′
+
−
γ
+
−
γ
+
γ′
−
−
γ
−
+
γ
−
=
+
≤
≤
(
) (
)(
)
(
)
2
2
2
2
1
2
1
2
1
l
w
r
w
a
a
r
r
a
r
a
IV
l
h
z
h
z
K
h
z
h
K
T
h
K
Q
h
z
h
przedział
IV
−
γ
+
−
γ
+
γ′
−
−
γ
−
+
γ
−
=
<
≤
(
) (
)(
)
2
2
2
1
2
1
r
w
a
a
r
r
a
r
a
III
l
r
h
z
K
h
z
h
K
T
h
K
Q
h
z
h
przedział
III
−
γ
+
γ′
−
−
γ
−
+
γ
−
=
<
≤
T
z
K
Q
h
z
a
przedział
II
a
II
r
+
γ
−
=
<
≤
2
2
1
Michał Kowalski - GiBS
MOMENTY ZGINAJ
Ą
CE W PRZEDZIAŁACH:
Ś
cianka szczelna w jednorodnym gruncie zawodnionym
3
6
1
0
z
K
M
a
z
przedział
I
a
I
γ
−
=
<
≤
IV
III
II
I
V
(
)
(
)
(
)(
)
(
)
(
)
3
3
3
2
2
6
1
6
1
6
1
2
1
3
2
2
1
h
z
K
h
z
h
z
K
h
z
h
K
a
z
T
h
z
h
K
M
d
h
z
h
przedział
V
p
p
l
w
r
w
a
a
r
r
a
r
r
a
V
−
γ′
+
+
−
γ
+
−
γ
+
γ′
−
−
γ
−
−
+
−
γ
−
=
+
≤
≤
(
)
(
)
(
)(
)
(
)
3
3
2
2
6
1
6
1
2
1
3
2
2
1
l
w
r
w
a
a
r
r
a
r
r
a
IV
l
h
z
h
z
K
h
z
h
K
a
z
T
h
z
h
K
M
h
z
h
przedział
IV
−
γ
+
−
γ
+
γ′
−
−
γ
−
−
+
−
γ
−
=
<
≤
(
)
(
)
(
)(
)
3
2
2
6
1
2
1
3
2
2
1
r
w
a
a
r
r
a
r
r
a
III
l
r
h
z
K
h
z
h
K
a
z
T
h
z
h
K
M
h
z
h
przedział
III
−
γ
+
γ′
−
−
γ
−
−
+
−
γ
−
=
<
≤
(
)
a
z
T
z
K
M
h
z
a
przedział
II
a
II
r
−
+
γ
−
=
<
≤
3
6
1

Michał Kowalski - GiBS
Ś
cianka szczelna w jednorodnym gruncie zawodnionym
PRZYKŁAD:
Rozpatrzmy konstrukcj
ę ś
cianki szczelnej dla wykopu o wysoko
ś
ci h = 5m,
wykonanego w gruncie o ci
ęż
arze obj
ę
to
ś
ciowym
γ
= 20kN/m
3
i k
ą
cie tarcia
wewn
ę
trznego równym
φ
= 30º. Ci
ęż
ar obj
ę
to
ś
ciowy gruntu z uwzgl
ę
dnieniem
wyporu wody wynosi
γ
’ = 11kN/m
3
. Załó
ż
my, zakotwienie w odległo
ś
ci a = 2m od
naziomu. Zwierciadło wód gruntowych znajduje si
ę
na gł
ę
boko
ś
ci h
r
= 2.5m po
stronie naziomu i na gł
ę
boko
ś
ci h
l
= 4m po stronie wykopu.
Okre
ś
li
ć
zagł
ę
bienie
ś
cianki szczelnej (d) i sił
ę
naci
ą
gu kotwi (T). Narysowa
ć
wykres
sił tn
ą
cych oraz momentów zginaj
ą
cych wzdłu
ż ś
cianki. Znale
źć
maksymalny
moment zginaj
ą
cy.
Zagł
ę
bienie
ś
cianki okre
ś
lamy stosuj
ą
c procedur
ę
iteracyjn
ą
podstawiaj
ą
c kolejno
warto
ś
ci d a
ż
do uzyskania wymaganej zbie
ż
no
ś
ci obu stron równania.
Otrzymujemy:
m
d
558
.
3
=

Michał Kowalski - GiBS
Ś
cianka szczelna w jednorodnym gruncie zawodnionym
Dla takiej warto
ś
ci zabicia siła T w kotwi jest równa:
(
) (
)(
)
(
)
(
)
kN
d
d
K
d
h
h
h
h
h
d
h
K
h
d
h
h
K
h
K
T
w
p
p
l
w
l
w
r
w
a
a
r
r
a
r
a
15
.
90
2
1
2
1
2
1
2
1
2
1
2
2
2
2
2
=
γ
+
γ′
+
−
γ
−
−
γ
−
+
−
+
γ
+
γ′
+
−
+
γ
+
γ
=
Z warunku na przebicie hydrauliczne przyjmuj
ą
c F = 3 otrzymujemy:
(
)
m
d
0
.
1
2
5
.
2
5
3
5
.
2
4
min
=
+
−
⋅
−
=
Do dalszych oblicze
ń
przyj
ę
to gł
ę
boko
ść
zabicia
ś
cianki obliczon
ą
z sumy
momentów wzgl
ę
dem punktu zakotwienia.
m
d
558
.
3
=
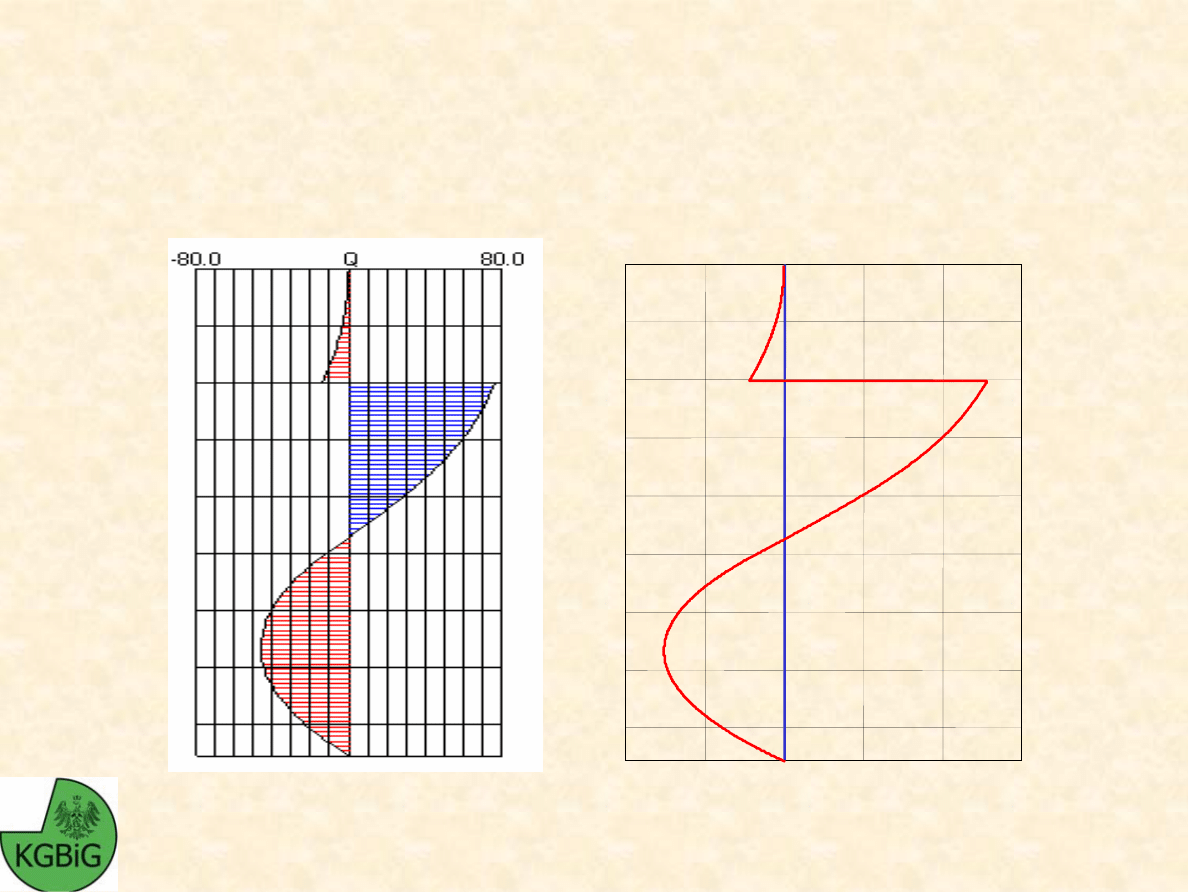
Michał Kowalski - GiBS
WYKRES SIŁ TN
Ą
CYCH
WZDŁU
ś Ś
CIANKI
Ś
cianka szczelna w jednorodnym gruncie zawodnionym
0
1
2
3
4
5
6
7
8
0
G
ł
ę
b
o
k
o
ś
ć
,
m
Siła tn
ą
ca, kN
-60
-30
30
60
90
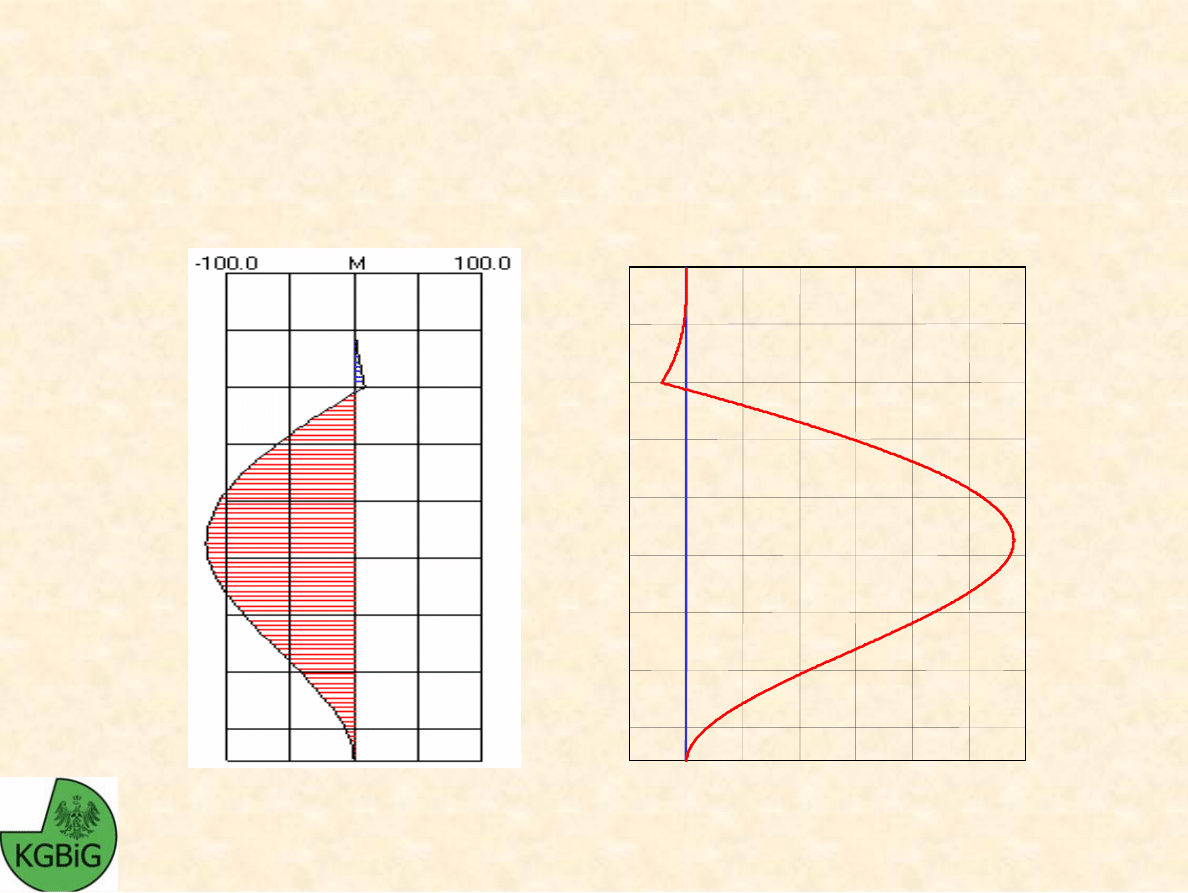
Michał Kowalski - GiBS
WYKRES MOMENTÓW ZGINAJ
Ą
CYCH
WZDŁU
ś Ś
CIANKI
Ś
cianka szczelna w jednorodnym gruncie zawodnionym
0
1
2
3
4
5
6
7
8
0
G
ł
ę
b
o
k
o
ś
ć
,
m
Momenty zginaj
ą
ce, kNm
-20
20
40
60
80
100
120
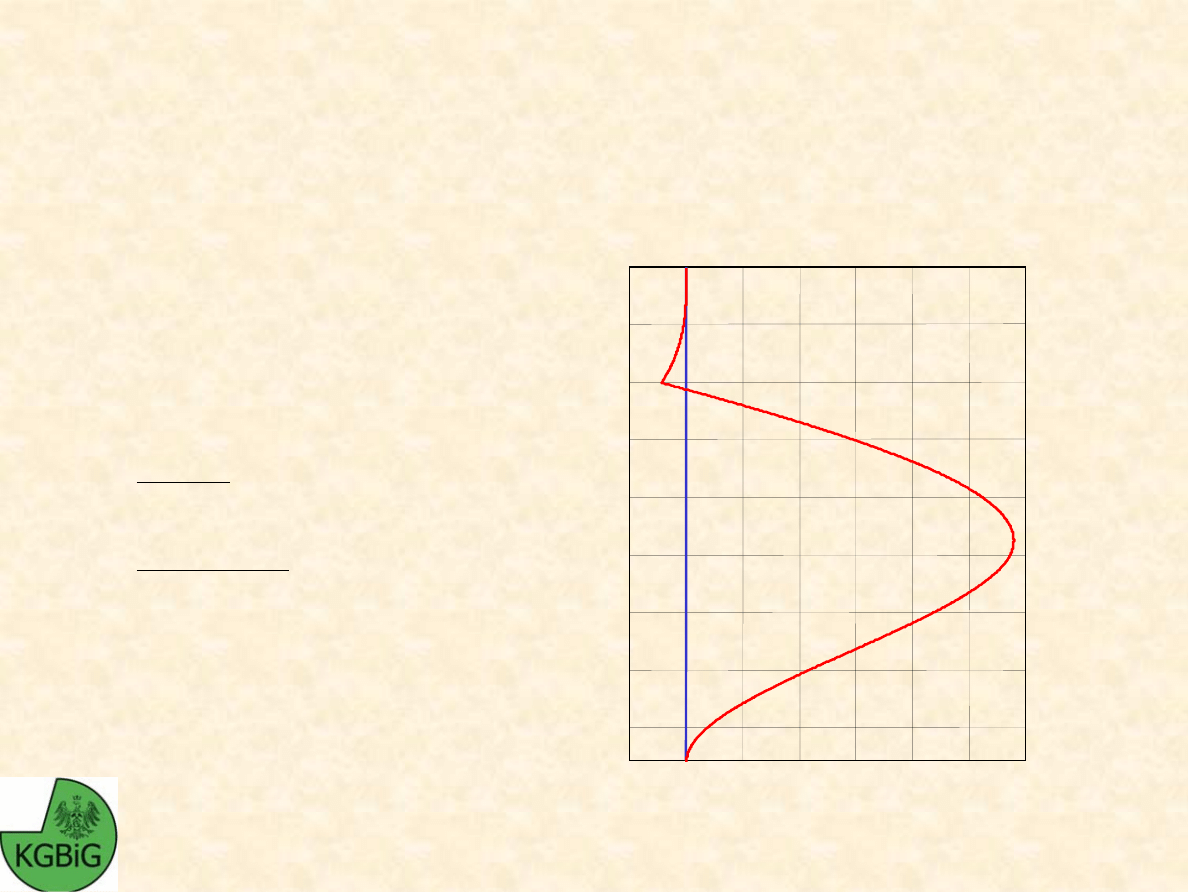
Michał Kowalski - GiBS
DOBÓR PROFILU
Ś
CIANKI
Ś
cianka szczelna w jednorodnym gruncie zawodnionym
0
1
2
3
4
5
6
7
8
0
G
ł
ę
b
o
k
o
ś
ć
,
m
Momenty zginaj
ą
ce, kNm
-20
20
40
60
80
100
120
Maksymalny moment zginaj
ą
cy
jest równy:
Wska
ź
nik wytrzymało
ś
ci
przekroju:
k
d
– napr
ęż
enie dopuszczalne
dla stali
kNm
M
g
64
.
115
max
,
=
3
max
,
771
150
64
.
115
cm
MPa
kNm
W
k
M
W
gx
d
g
gx
=
=
=
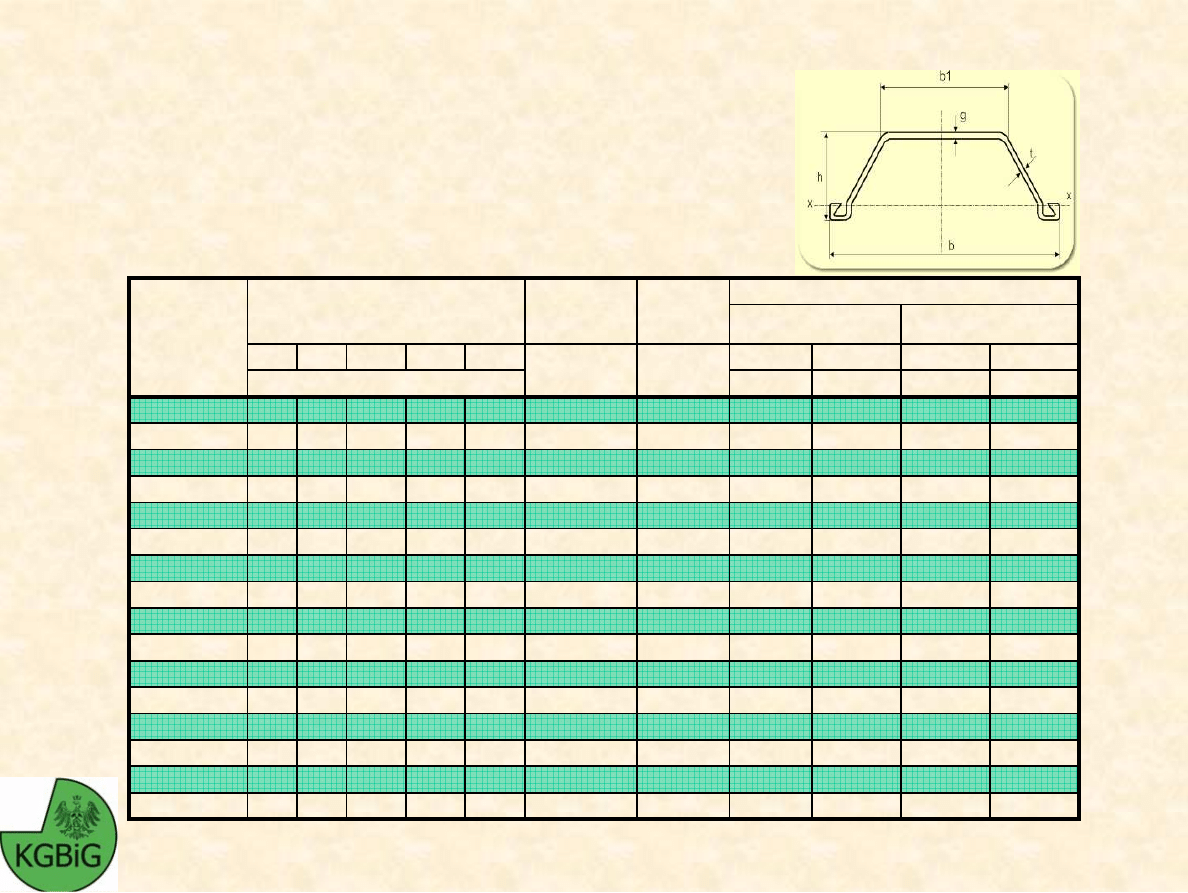
Michał Kowalski - GiBS
Ś
cianka szczelna w jednorodnym gruncie zawodnionym
1777.6
25953.0
288.1
3282.3
68.9
87.8
15.0
9.7
170.0
320
436
*G 62/P2
1680.2
24362.7
284.3
3182.5
66.6
84.8
14.0
9.6
169.0
320
436
*G 62/P1
1492.5
21641.9
258.6
2830.2
59.8
76.2
12.0
9.4
167.0
320
436
*G 62/C1
1600.0
23200.0
282.0
3106.0
62.0
78.9
13.0
9.5
168.0
320
436
G 62
1487.1
25210.0
370.4
4380.7
71.4
91.0
12.0
11.0
193.0
285
538
*G 61/P2.2
1460.5
24903.7
368.7
4386.5
69.0
87.9
12.0
10.0
194.0
285
538
*G 61/P2.1
1387.8
23525.7
364.8
4245.1
68.0
86.6
11.0
10.5
193.0
285
538
*G 61/P1.2
1366.0
23131.0
362.0
4188.0
66.8
85.0
11.0
10.0
192.0
285
538
*G 61/P1.1
1360.6
23200.4
350.6
4116.3
64.8
82.6
11.0
9.5
193.0
285
538
*G 61/P1
1283.0
21753.0
258.0
4067.0
64.6
82.3
10.0
10.0
192.0
285
538
*G 61/P1.0
1156.8
19726.0
313.8
3570.3
56.4
71.9
9.0
8.5
191.0
285
538
*G 61/C1
1275.0
21900.0
335.0
3870.0
61.0
77.5
10.0
9.0
192.0
285
538
G 61
961.3
14977.1
268.1
2974.3
59.0
75.2
10.0
8.3
178.5
275
632
*G 46/P3
920.2
14336.9
260.0
2863.9
56.7
72.3
9.5
7.9
177.5
275
632
*G 46/P2
821.0
12690.0
246.0
2066.0
51.8
66.0
8.5
7.1
176.5
275
632
*G 46/P1
735.0
11352.0
233.0
2462.0
47.0
58.6
7.5
6.4
175.5
275
632
G 46
cm
3
cm
4
cm
3
cm
4
mm
W
x
I
x
W
x
I
x
kg
cm
2
G
t
h
b1
b
Dla przekroju
ś
ciany
d
ł
. 1 m
Dla przekroju
grodzicy
Wielko
ś
ci statyczne
Masa 1 m
Powierzchnia
przekroju
Wymiary
Wyró
ż
nik
oznaczenia
WYBRANE PROFILE
Ś
CIANEK SZCZELNYCH
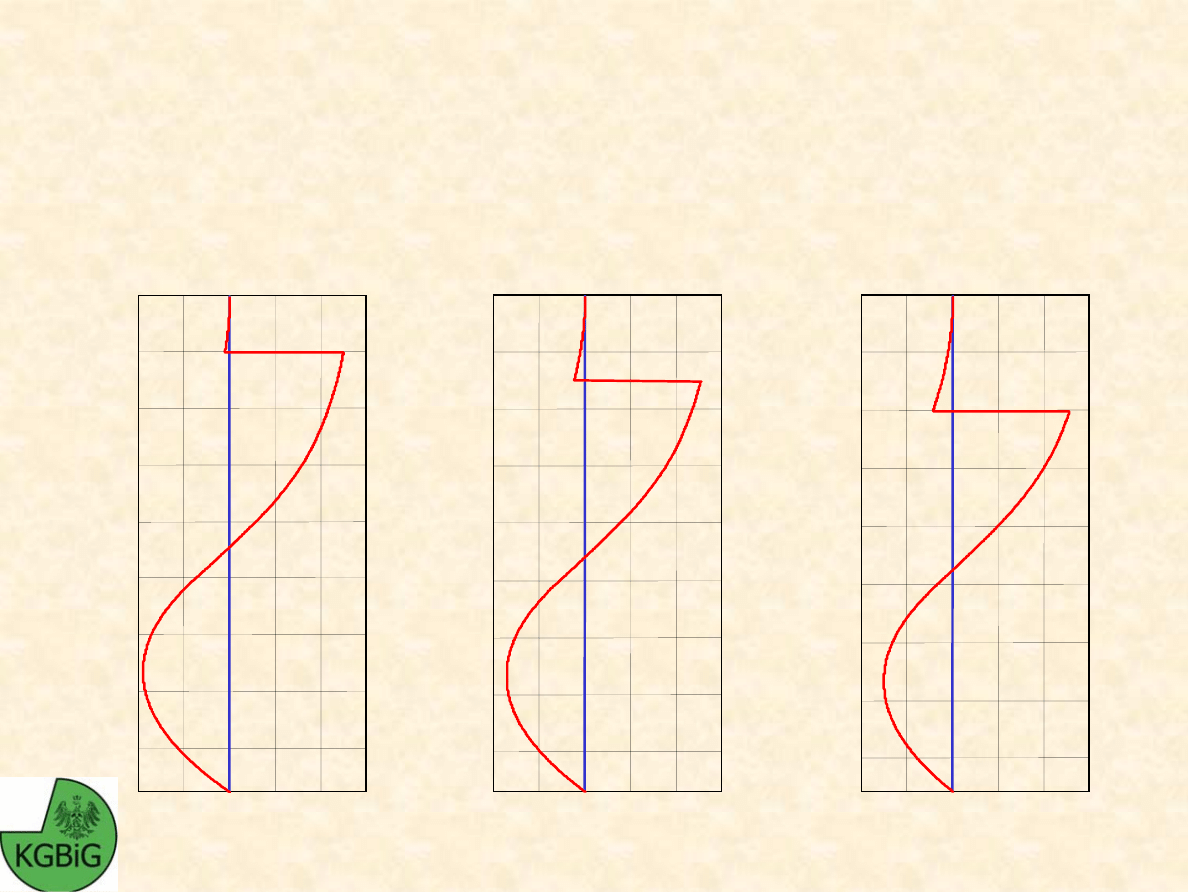
Michał Kowalski - GiBS
Ś
cianka szczelna w jednorodnym gruncie zawodnionym
WPŁYW GŁ
Ę
BOKO
Ś
CI ZAKOTWIENIA
NA SIŁY TN
Ą
CE
m
a
0
.
1
=
0
1
2
3
4
5
6
7
8
0
G
ł
ę
b
o
k
o
ś
ć
,
m
Siła tn
ą
ca, kN
-60 -30
30
60
90
m
a
5
.
1
=
0
1
2
3
4
5
6
7
8
0
G
ł
ę
b
o
k
o
ś
ć
,
m
Siła tn
ą
ca, kN
-60 -30
30
60
90
m
a
0
.
2
=
0
1
2
3
4
5
6
7
8
0
G
ł
ę
b
o
k
o
ś
ć
,
m
Siła tn
ą
ca, kN
-60 -30
30
60
90
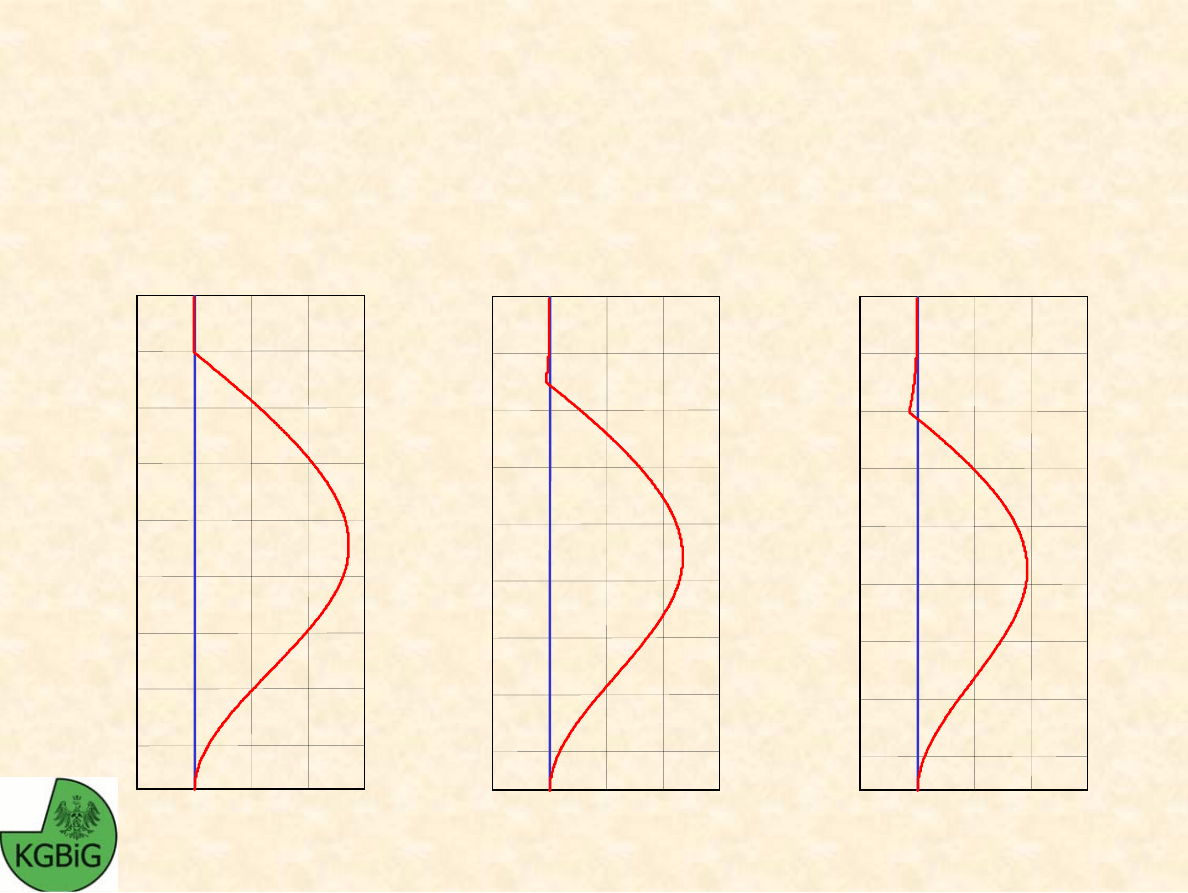
Michał Kowalski - GiBS
Ś
cianka szczelna w jednorodnym gruncie zawodnionym
WPŁYW GŁ
Ę
BOKO
Ś
CI ZAKOTWIENIA
NA MOMENTY ZGINAJ
Ą
CE
0
1
2
3
4
5
6
7
8
0
G
ł
ę
b
o
k
o
ś
ć
,
m
Moment zginaj
ą
cy, kNm
-60
60
120
180
m
a
0
.
1
=
0
1
2
3
4
5
6
7
8
0
G
ł
ę
b
o
k
o
ś
ć
,
m
Moment zginaj
ą
cy, kNm
-60
60
120
180
m
a
0
.
2
=
0
1
2
3
4
5
6
7
8
0
G
ł
ę
b
o
k
o
ś
ć
,
m
Moment zginaj
ą
cy, kNm
-60
60
120
180
m
a
5
.
1
=

Michał Kowalski - GiBS
Ś
cianka szczelna w jednorodnym gruncie zawodnionym
m
a
0
.
1
=
3
max
max
1085
76
.
162
79
.
74
76
.
3
12
.
78
cm
W
kNm
M
kN
T
m
d
kN
T
gx
kotwi
=
=
=
=
=
m
a
5
.
1
=
3
max
max
935
30
.
140
16
.
76
67
.
3
66
.
83
cm
W
kNm
M
kN
T
m
d
kN
T
gx
kotwi
=
=
=
=
=
m
a
0
.
2
=
3
max
max
771
64
.
115
82
.
76
56
.
3
15
.
90
cm
W
kNm
M
kN
T
m
d
kN
T
gx
kotwi
=
=
=
=
=
Przy zmianie gł
ę
boko
ś
ci zakotwienia
ś
cianki z a = 1.0m na a = 2.0m nast
ę
puje
zmniejszenie maksymalnego momentu zginaj
ą
cego działaj
ą
cego na
ś
ciank
ę
o
29%.
WPŁYW GŁ
Ę
BOKO
Ś
CI ZAKOTWIENIA
NA OTRZYMANE WYNIKI
Wyszukiwarka
Podobne podstrony:
projekty szkolen(1) id 401146 Nieznany
Projekt nr2 id 399211 Nieznany
Projekt2 poprawiony id 400268 Nieznany
Projekt z ekologii id 399851 Nieznany
3 Projektowanie betonu id 34011 Nieznany (2)
Projektowanie przekladnie id 40 Nieznany
Projekt z budownictwa id 399843 Nieznany
Projektowanie raportow id 40062 Nieznany
Projektowanie betonu id 400490 Nieznany
Projekt 10 id 397717 Nieznany
karta oceny projektu 2010 id 23 Nieznany
Projekt 7 (najnowszy) id 398366 Nieznany
projekt 212 id 398203 Nieznany
projekt pale id 399321 Nieznany
PROJEKT WZOR 2 id 399817 Nieznany
projekt 14 id 397725 Nieznany
projekt zewo id 399982 Nieznany
Projekty domow id 401015 Nieznany
Projekt nr 2 id 399188 Nieznany
więcej podobnych podstron