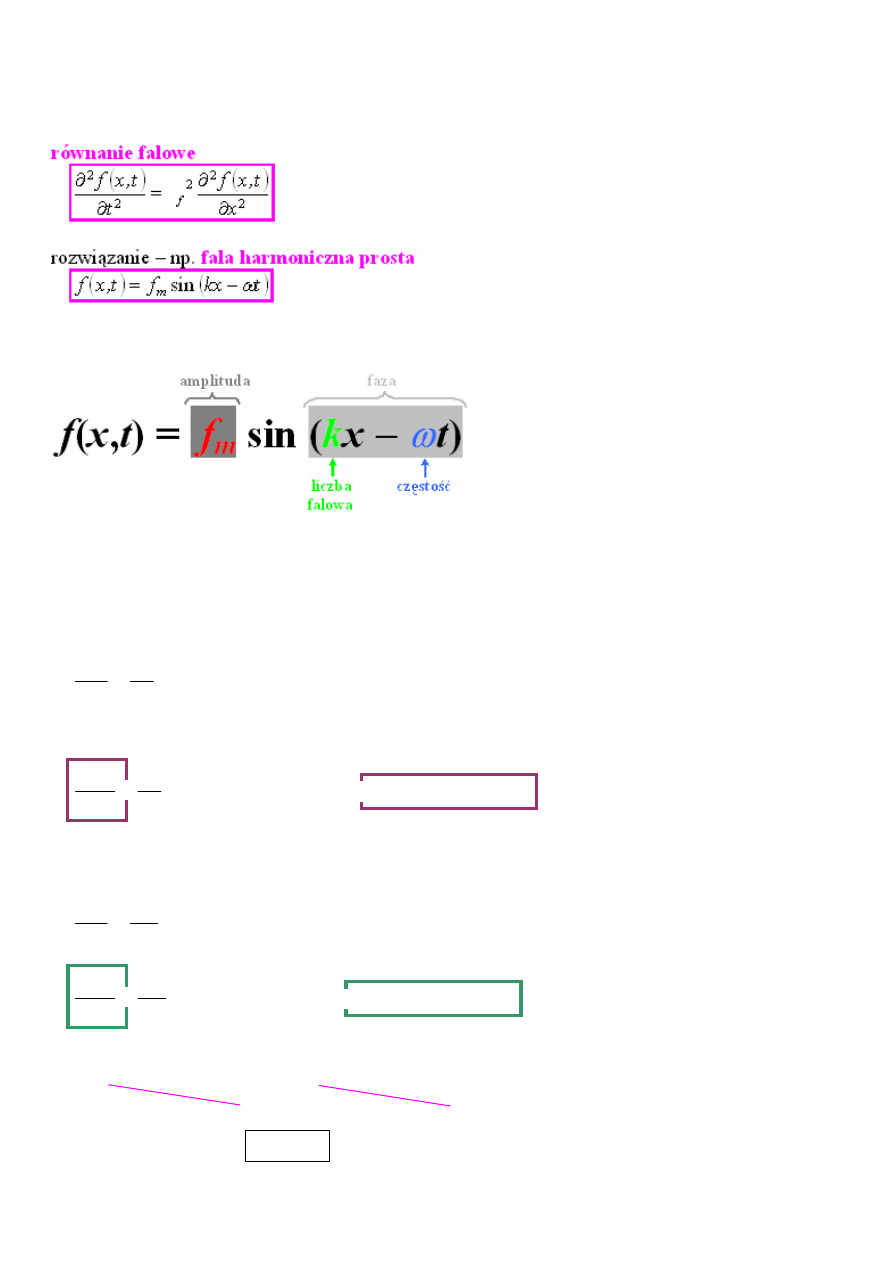
Fala harmoniczna prosta jako rozwiązanie równania falowego

opis formalny:

struktura rozwiązania:

należy podstawić rozwiązanie (równanie fali harmonicznej prostej) do równania falowego

obliczamy pierwszą pochodną cząstkową względem czasu

∂

f/

∂

t (wyłączamy czynnik stały

przed znak pochodnej, korzystamy ze wzoru na pochodną funkcji złożonej

'

f

f

'

u

'

f

u

⋅

=

)

(

))

(

(

):

[

]

)

cos(

)

sin(

t

x

k

f

t

x

k

f

t

t

f

m

m

ω

ω

ω

−

−

=

−

∂

∂

=

∂

∂

obliczamy drugą pochodną cząstkową względem czasu

∂

2

f/

∂

t

2

(zasady j.w.)

[

]

)

sin(

)

cos(

2

2

2

t

x

k

f

t

x

k

f

t

t

f

m

m

ω

ω

ω

ω

−

=

−

−

∂

∂

=

∂

∂

analogicznie obliczamy pierwszą i drugą pochodną cząstkową względem położenia

∂

f/

∂

x

i

∂

2

f/

∂

x

2

[

]

)

cos(

)

sin(

t

x

k

f

k

t

x

k

f

x

x

f

m

m

ω

ω

−

=

−

∂

∂

=

∂

∂

[

]

)

sin(

)

cos(

2

2

2

t

x

k

f

k

t

x

k

f

k

x

x

f

m

m

ω

ω

−

=

−

∂

∂

=

∂

∂

podstawiamy drugie pochodne cząstkowe względem czasu i położenia do równania falowego:

)

sin(

)

sin(

2

2

2

t

x

k

f

k

t

x

k

f

m

f

m

ω

υ

ω

ω

−

=

−

k

k

f

f

υ

ω

υ

ω

=

→

=

2

2

2

(1)

υ

ponieważ dla fali harmonicznej prostej prędkość fazowa wyraża się wzorem:

k

f

ω

υ

=

równanie (1) jest tożsamością – tzn. fala harmoniczna prosta jest rozwiązaniem równania
falowego