od czasu do czasu lubię się trochę zrelaksować

podczas różniczkowania i całkowania

dr inż. Jacek JACKIEWICZ

L I T E R A T U R A

Literatura podstawowa

[1] Gutowski R.: Mechanika analityczna. PWN, Warszawa, 1971.
[2]

Jarzębowska E.: Mechanika analityczna. Oficyna Wydawnicza

Politechniki Warszawskiej, Warszawa, 2003.

[3]

Sawiak S., Wittbrodt E.: Mechanika ogólna, Wybrane zagadnienia -

teoria i zadania. Wydawnictwo Politechniki Gdańskiej, Gdańsk,

2007.

[4]

Nizioł J.: Metodyka rozwiązywania zadań z mechaniki, Część III:

Dynamika. WNT, Warszawa, 2009.

2

L I T E R A T U R A

Literatura uzupełniająca

[1]

Gelfand I. M., Fomin S. W.: Rachunek wariacyjny. PWN, Warszawa,

1975.

[2]

Borkowski Sz.: Mechanika ogólna, Tom 3: Dynamika Lagrange’a i

Hamiltona. Wydawnictwo Politechniki Śląskiej, Gliwice, 1998.

[3]

Leyko J.: Mechanika ogólna, Tom 2: Dynamika. Wydawnictwo

Naukowe PWN, Warszawa, 2010.

[4]

Jakowluk A.: Mechanika analityczna - Dynamika maszyn i robotów,

Tom III: Mechanika teoretyczna i podstawy teorii mechanizmów i

robotów. Wydawnictwo Politechniki Białostockiej, Białystok, 1994.

[5]

Szcześniak W.E.: Dynamika analityczna i "MATHEMATICA" w

zadaniach i przykładach obliczeniowych. Oficyna Wydawnicza

Politechniki Warszawskiej, Warszawa, 2010.

3

WPROWADZENIE

4

Celem nauczania przedmiotu mechanika analityczna jest nabycie umiejętności

Celem nauczania przedmiotu mechanika analityczna jest nabycie umiejętności
korzystania z metod rachunku wariacyjnego, które mogą być z powodzeniem

korzystania z metod rachunku wariacyjnego, które mogą być z powodzeniem
stosowane do opisu modeli ciągłych. W podręcznikach z mechaniki klasycznej,

stosowane do opisu modeli ciągłych. W podręcznikach z mechaniki klasycznej,
wykorzystywanych podczas studiów pierwszego stopnia, układ rzeczywisty jest

wykorzystywanych podczas studiów pierwszego stopnia, układ rzeczywisty jest
reprezentowany tylko za pomocą modeli dyskretnych, tj. punktu materialnego, bryły

reprezentowany tylko za pomocą modeli dyskretnych, tj. punktu materialnego, bryły
sztywnej lub skończonej kombinacji punktów materialnych i/lub brył sztywnych, co

sztywnej lub skończonej kombinacji punktów materialnych i/lub brył sztywnych, co
stanowi istotne ograniczenie możliwości przeprowadzania odpowiednich analiz

stanowi istotne ograniczenie możliwości przeprowadzania odpowiednich analiz
wytrzymałościowych i dynamicznych elementów konstrukcji maszyn, gdy powinny

wytrzymałościowych i dynamicznych elementów konstrukcji maszyn, gdy powinny
być one rozpatrywane jako układy ciągłe, a nie jako układy prętowe.

być one rozpatrywane jako układy ciągłe, a nie jako układy prętowe.

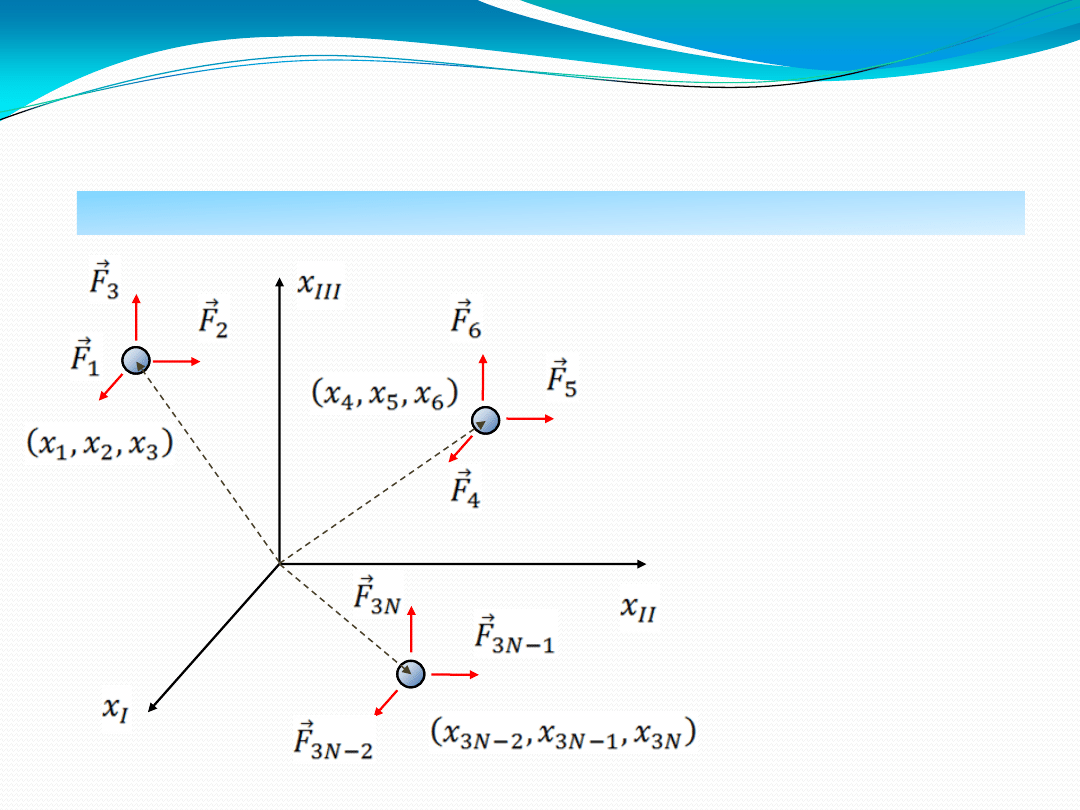
WPROWADZENIE – PODSTAWOWE POJĘCIA

ZASADA PRAC PRZYGOTOWANYCH

5

układ N punktów materialnych,

których położenie jest określone

za pomocą współrzędnych

na każdy punkt działa siła zewnętrzna

o 3 składowych

6

WPROWADZENIE – PODSTAWOWE POJĘCIA

ZASADA PRAC PRZYGOTOWANYCH

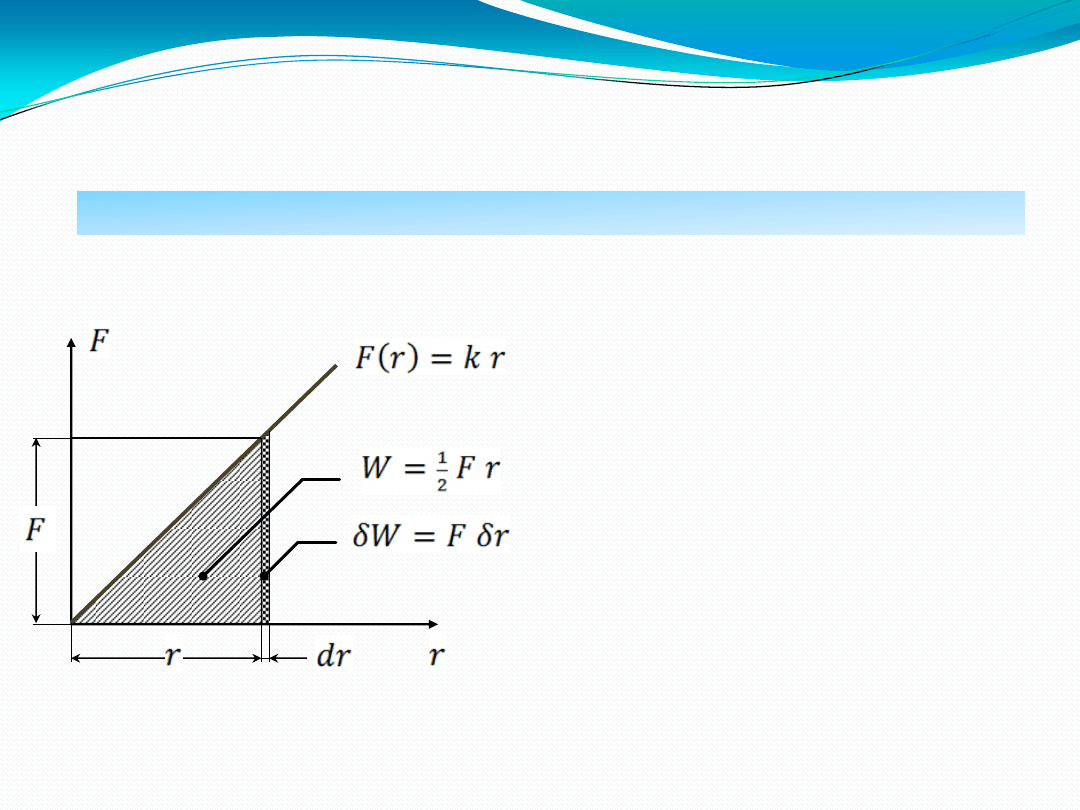
7

WPROWADZENIE – PODSTAWOWE POJĘCIA

ZASADA PRAC PRZYGOTOWANYCH

Układ Clapeyrona charakteryzuje się tym,

że zależności dla sił są liniowe.

Zachodzi to wtedy, gdy materiał jest

liniowo-sprężysty.

W trakcie odkształcania tego układu nie

zmieniają się warunki podparcia, gdy nie

ma naprężeń i odkształceń wstępnych

oraz zmian temperatury.

8

WPROWADZENIE – PODSTAWOWE POJĘCIA

ZASADA PRAC PRZYGOTOWANYCH





PRZEMIESZCZENIE WIRTUALNE

PRZEMIESZCZENIE WIRTUALNE

Przyjmujemy dowolnie małe przemieszczenia,
nazywane przemieszczeniami wirtualnymi.

Przemieszczenia wirtualne nie są zależne od czasu.

Na drodze przemieszczeń wirtualnych siły zewnętrzne
nie zmieniają swojej wartości.

Przyjęto następujące oznaczenie przemieszczenia wirtualnego:

( a nie ).

9

WPROWADZENIE – PODSTAWOWE POJĘCIA

ZASADA PRAC PRZYGOTOWANYCH





PRACA WIRTUALNA

PRACA WIRTUALNA





postać skalarna

postać skalarna::

praca wykonana przez wszystkie siły zewnętrzne danego układu:

praca wykonana przez wszystkie siły zewnętrzne danego układu:





postać wektorowa

postać wektorowa::

10

WPROWADZENIE – PODSTAWOWE POJĘCIA





przemieszczenie wirtualne

przemieszczenie wirtualne

• pomyślane,
• możliwe (kinematycznie dopuszczalne),
• niezależne od czynników zewnętrznych (np. obciążeń),
• bardzo małe w porównaniu z wymiarami ciała,
• niezależne od czasu,
• ciągłe (co najmniej raz różniczkowalne).

11

WPROWADZENIE – PODSTAWOWE POJĘCIA





obciążenie wirtualne

obciążenie wirtualne

• pomyślane,
• możliwe,
• niezależne od czynników zewnętrznych,
• bardzo małe w odniesieniu do obciążeń zewnętrznych,
• niezależne od czasu,
• nie musi być ciągłe.

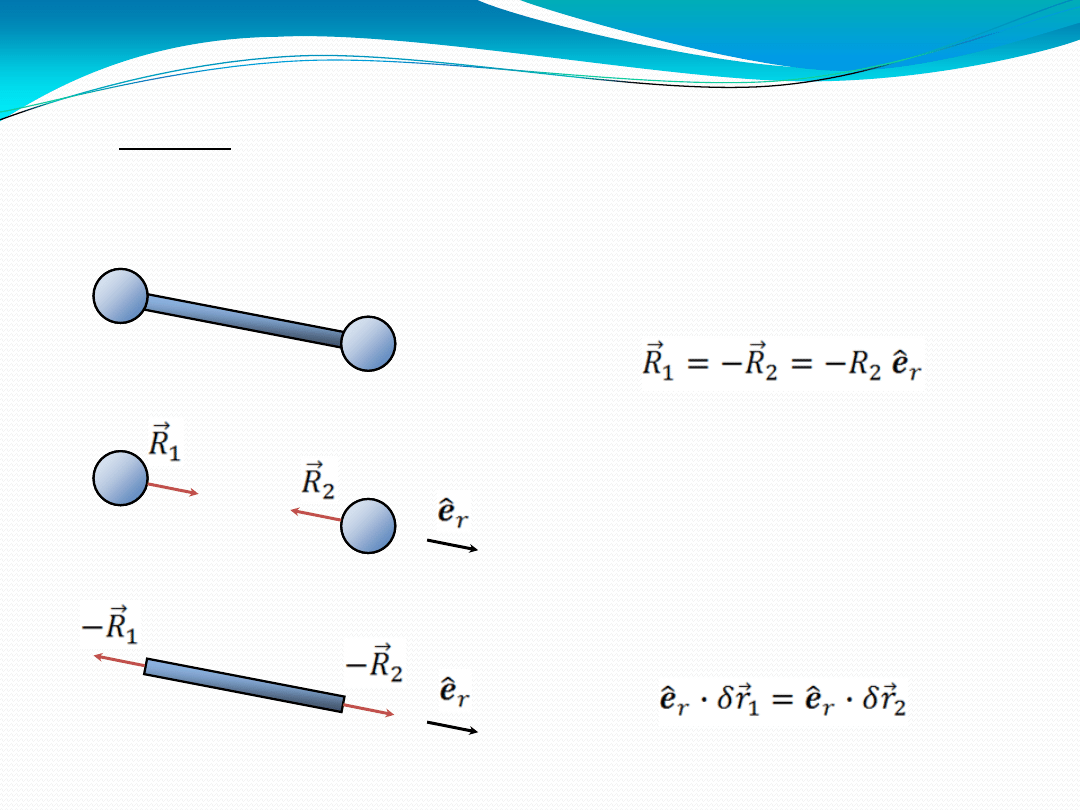
12





Przykład

Przykład::

Dwie masy połączone za pomocą sztywnego pręta

Dwie masy połączone za pomocą sztywnego pręta
(więź elementarna)

(więź elementarna)

1 aksjomat statyki, reakcje więzów:

1 aksjomat statyki, reakcje więzów:

Ponieważ wartości sił

Ponieważ wartości sił RR

11

i i RR

22

są równe,

są równe,

to

to

odpowiadające

odpowiadające

tym siłom

tym siłom

składowe przemieszczeń wirtualnych

składowe przemieszczeń wirtualnych
też muszą być odpowiednio równe:

też muszą być odpowiednio równe:

13





Przykład

Przykład::

Dwie masy połączone za pomocą sztywnego pręta

Dwie masy połączone za pomocą sztywnego pręta
(więź elementarna)

(więź elementarna)





praca wirtualna reakcji więzów więzi elementarnej

praca wirtualna reakcji więzów więzi elementarnej

Ciało sztywne jest zbiorem punktów materialnych obdarzonych masą, które są

Ciało sztywne jest zbiorem punktów materialnych obdarzonych masą, które są
utrzymywane w ustalonych (niezmiennych) odległościach pomiędzy sobą.

utrzymywane w ustalonych (niezmiennych) odległościach pomiędzy sobą.





wniosek

wniosek

Praca wirtualna wykonana przez siły wewnętrzne ciała sztywnego jest równa zeru.

Praca wirtualna wykonana przez siły wewnętrzne ciała sztywnego jest równa zeru.

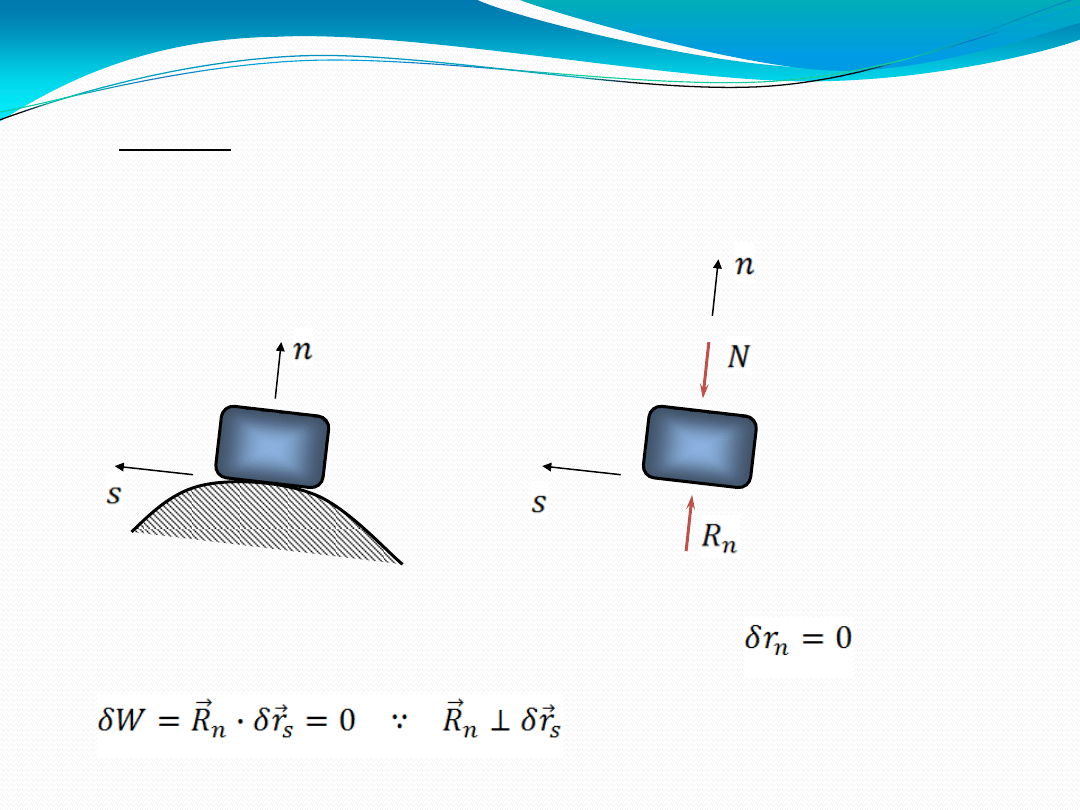
14





Przykład

Przykład::

Ciało ślizgające się po gładkiej, sztywnej powierzchni

Ciało ślizgające się po gładkiej, sztywnej powierzchni
(bez tarcia)

(bez tarcia)

powierzchnia zewnętrzna jest sztywna i ustalona:

przemieszczenie spełniające warunki

utwierdzeń jest prostopadłe do reakcji

więzów

15

WPROWADZENIE – PODSTAWOWE POJĘCIA

Przemieszczenia wirtualne mszą spełniać warunki więzów.

W układach idealnych (bez tarcia) reakcje nie wykonują pracy.

Więzy geometryczne nakładają ograniczenia na współrzędne położenia
poszczególnych elementów danego układu.





więzy geometryczne

więzy geometryczne

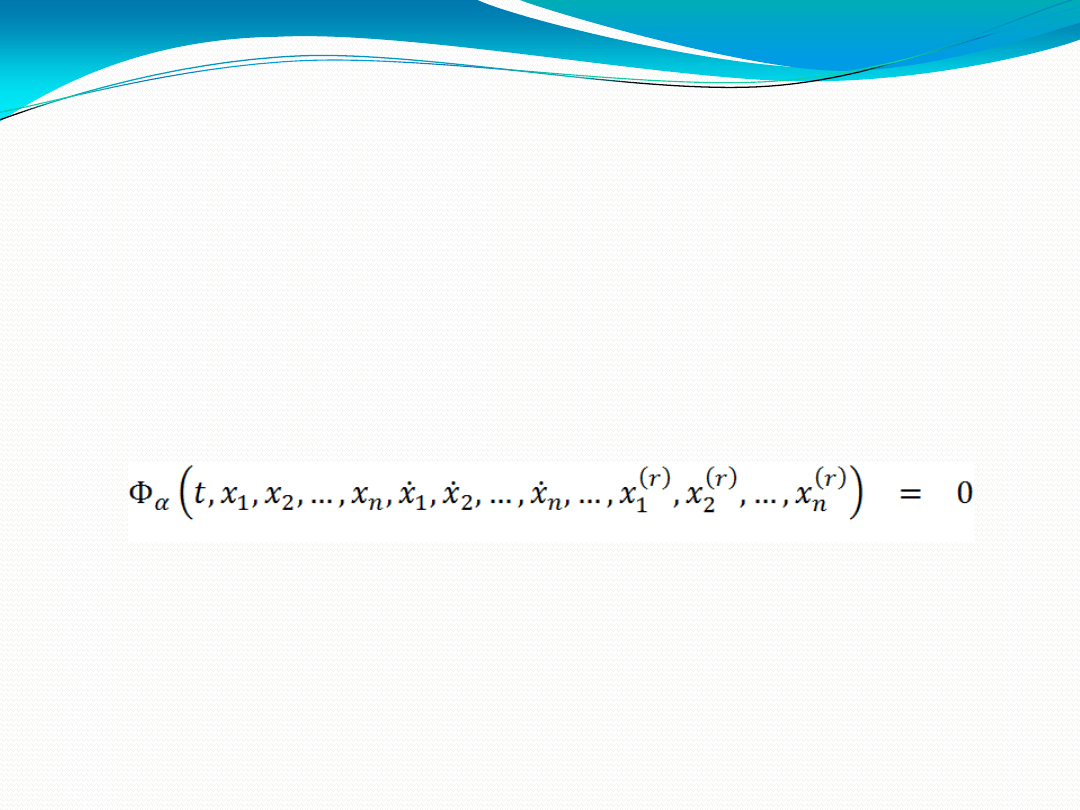
16

WPROWADZENIE – PODSTAWOWE POJĘCIA

Więzy kinematyczne nakładają ograniczenia na składowe prędkości i/lub
przyspieszeń, a także ograniczenia na rodzaj zmian prędkości i/lub
przyspieszeń.





więzy kinematyczne

więzy kinematyczne

Jeżeli równania różniczkowe tego typu więzów można efektywnie scałkować
to nazywamy je holonomicznymi, gdy nie - to wówczas nieholonomicznymi.

17

WPROWADZENIE – PODSTAWOWE POJĘCIA





podział więzów

podział więzów

skleronomiczne – nie zależą jawnie od czasu,

reonomiczne – jawnie zależą od czasu.





oznaczenia

oznaczenia

wypadkowa zewnętrznych sił biernych działających na i-ty punkt

materialny układu

wypadkowa zewnętrznych sił czynnych działających na i-ty punkt

materialny układu

WPROWADZENIE – PODSTAWOWE POJĘCIA

ZASADA PRAC PRZYGOTOWANYCH

18

równowaga statyczna

równowaga statyczna

WPROWADZENIE – PODSTAWOWE POJĘCIA

ZASADA PRAC PRZYGOTOWANYCH

19

Warunkiem koniecznym i wystarczającym równowagi skleronomicznego układu
punktów materialnych (który w stanie początkowym znajduje się w bezruchu i
jest poddany działaniu wzajemnych, obustronnych oddziaływań w postaci sił
wewnętrznych tego układu nie wykonujących pracy) jest zerowa praca wirtualna
sił zewnętrznych (czynnych i biernych), działających na rozpatrywany układ,
wzdłuż drogi dowolnych przemieszczeń wirtualnych spełniających warunki
więzów.

WPROWADZENIE – PODSTAWOWE POJĘCIA

ZASADA PRAC PRZYGOTOWANYCH

20

Odwołując się do zasady d’Alemberta:

która sprowadza zagadnienia dynamiki do szczególnych problemów statyki
otrzymujemy

WPROWADZENIE – PODSTAWOWE POJĘCIA

ZASADA PRAC PRZYGOTOWANYCH

21

Warunkiem koniecznym i wystarczającym równowagi układu materialnego jest,
aby suma prac wirtualnych wszystkich sił czynnych i reakcji więzów przy
dowolnym przemieszczeniu wirtualnym układu była równa zeru.

Warunkiem koniecznym i wystarczającym równowagi układu materialnego o
więzach idealnych jest, aby suma prac wirtualnych wszystkich sił czynnych przy
dowolnym przemieszczeniu wirtualnym układu była równa zeru.

22





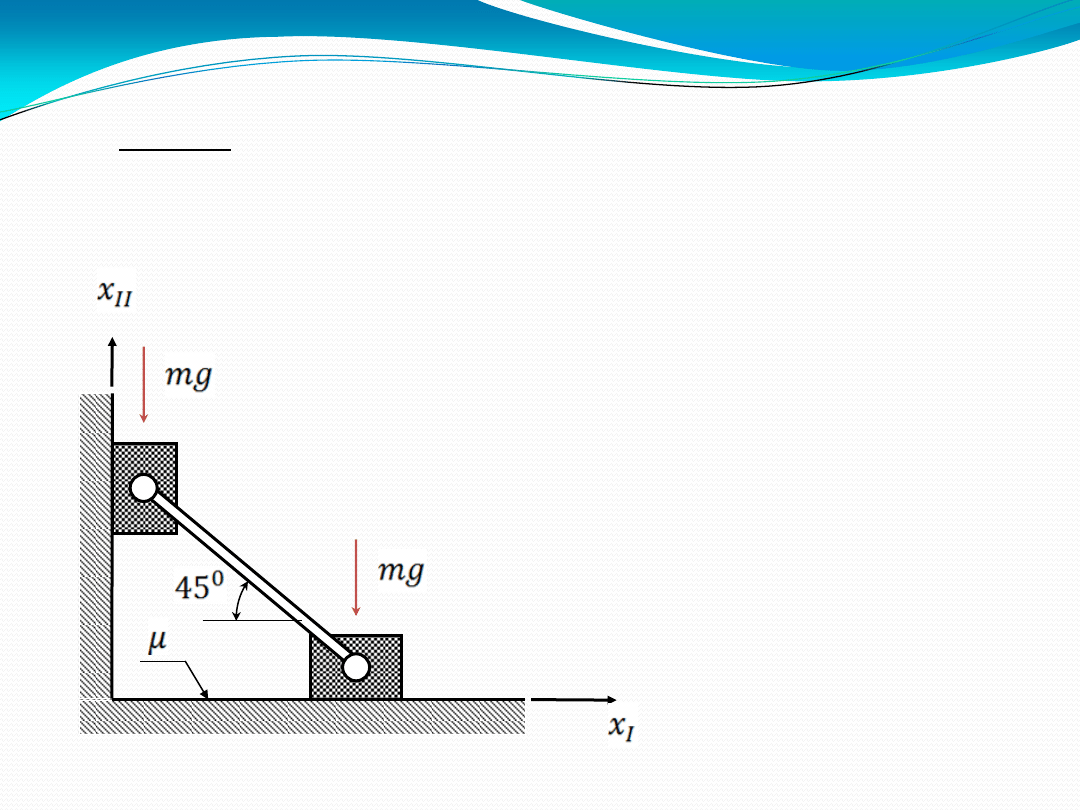
Przykład

Przykład::

Znajdujący się w równowadze układ mechaniczny

Znajdujący się w równowadze układ mechaniczny
składa się z dwóch mas połączonych ze sobą za

składa się z dwóch mas połączonych ze sobą za
pomocą sztywnego, nieważkiego pręta. Należy

pomocą sztywnego, nieważkiego pręta. Należy
określić współczynnik tarcia dolnej masy o

określić współczynnik tarcia dolnej masy o
chropowatą podłogę (pionowa ściana jest gładka).

chropowatą podłogę (pionowa ściana jest gładka).