Prof. Edmund Wittbrodt

ELEMENTY MECHANIKI ANALITYCZNEJ

Rozpatrujemy układ o wielu stopniach swobody, np. układ złożony z p punktów materialnych. Na układ mogą być
nałożone więzy.

Układ swobodny składający się z p punktów materialnych

Współrzędne dowolne:

np.: wektorowe

]

,

,

[

i

i

i

i

z

y

x

r

,

p

i

,...,

2

,

1

=

kartezjańskie (prostokątne)

i

i

i

z

y

x

,

,

p

i

,...,

2

,

1

=

Współrzędne uogólnione:

i

q , gdzie

s

i

,...,

2

,

1

=

, przy czym:

w

n

s

−

=

- liczba stopni swobody

w - liczba więzi

n - liczba współrzędnych

Współrzędne uogólnione są to współrzędne niezależne od siebie,
opisujące jednoznacznie położenie układu w przestrzeni
(jest to minimalna liczba współrzędnych potrzebnych do opisu położenia układu)

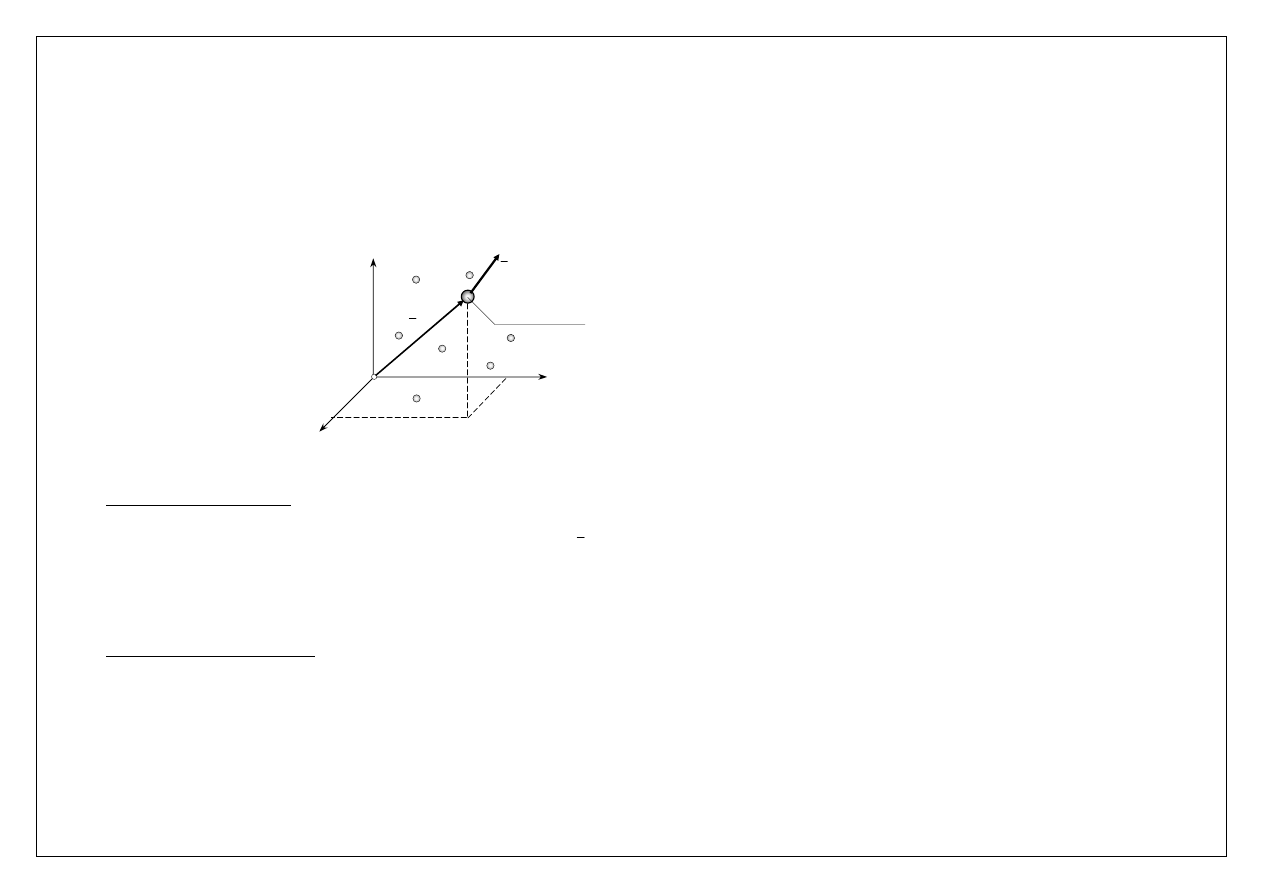
O

x

y

z

i

r

i

P

punkt materialny
o masie m

i

x

i

y

i

z

i

Prof. Edmund Wittbrodt

Więzy

Więzami są ograniczenia nałożone na ruch układu (na współrzędne lub prędkości punktów lub brył układu). Można je
wyrazić w postaci zależności analitycznych nazywanych równaniami więzów.

Rodzaje więzi:

geometryczne i kinematyczne

holonomiczne i nieholonomiczne

skleronomiczne i reonomiczne

dwustronne i jednostronne

idealne i rzeczywiste

Więzy geometryczne dwustronne są więzami, których równania więzów w zapisie wektorowym mają postać

0

)

,.....,

,

,

(

2

1

=

p

j

r

r

r

t

f

,

w

j

,.....,

2

,

1

=

,

a w zapisie skalarnym

0

)

,

,

,

,.........

,

,

,

,

,

,

(

2

2

2

1

1

1

=

p

p

p

j

z

y

x

z

y

x

z

y

x

t

f

,

w

j

,.....,

2

,

1

=

,

gdzie w

−

liczba nałożonych na układ więzi (odebranych stopni swobody).

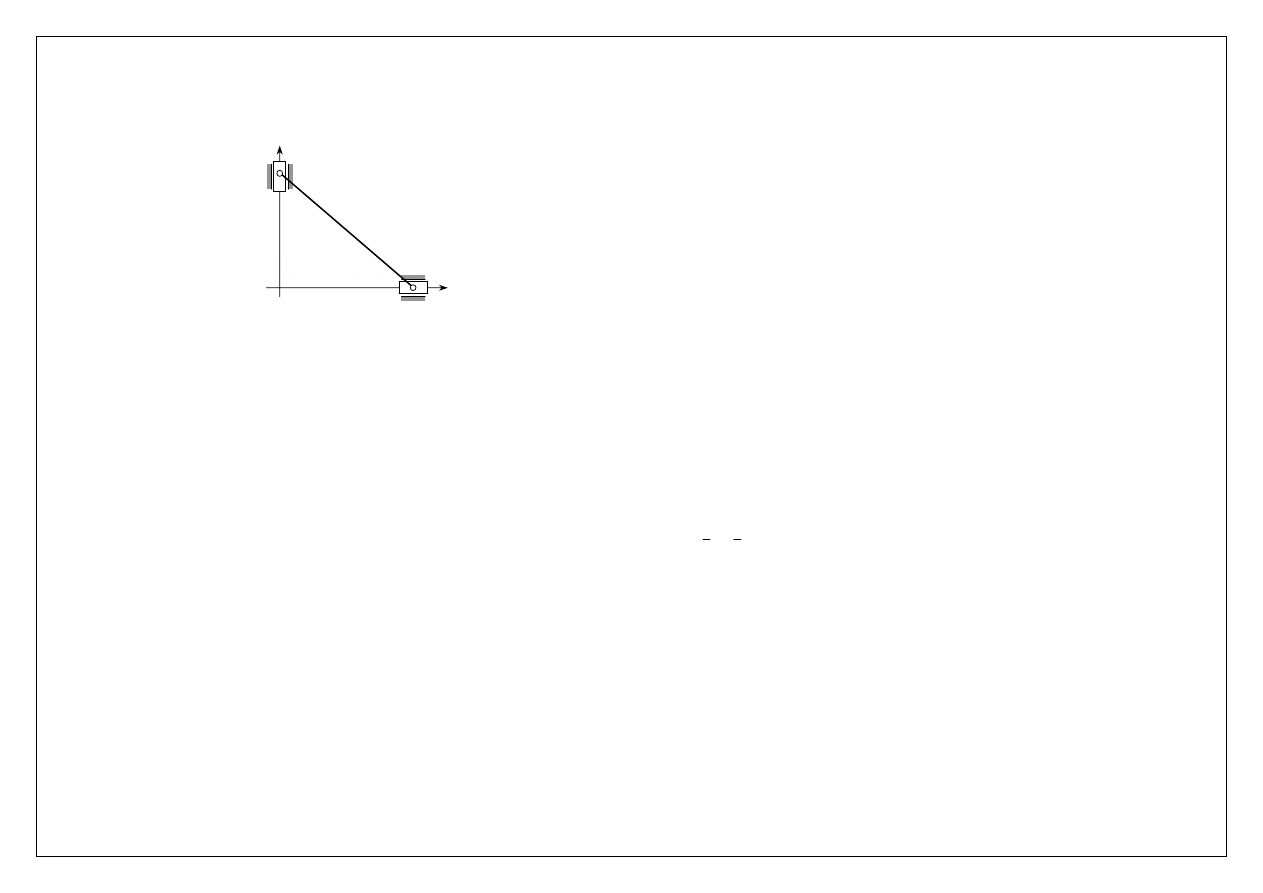
Prof. Edmund Wittbrodt

Przykład układu z więziami geometrycznymi (punkt B związany z A za pomocą sztywnego
łącznika) o jednym stopniu swobody

Zależności pomiędzy współrzędnymi dowolnymi, a współrzędnymi uogólnionymi dla układu z więzami holonomicznymi
i reonomicznymi

)

,

,.......,

,

(

2

1

t

q

q

q

x

x

s

i

i

=

)

,

,.......,

,

(

2

1

t

q

q

q

y

y

s

i

i

=

lub w zapisie wektorowym

)

,

,.......,

,

(

2

1

t

q

q

q

r

r

s

i

i

=

p

i

,...,

1

=

)

,

,.......,

,

(

2

1

t

q

q

q

z

z

s

i

i

=

gdzie: s

−

liczba stopni swobody układu, p

−

liczba punktów materialnych.

f(x,y)= x

2

+y

2

-l

2

=0

y

x

l

y

x

O

A

B

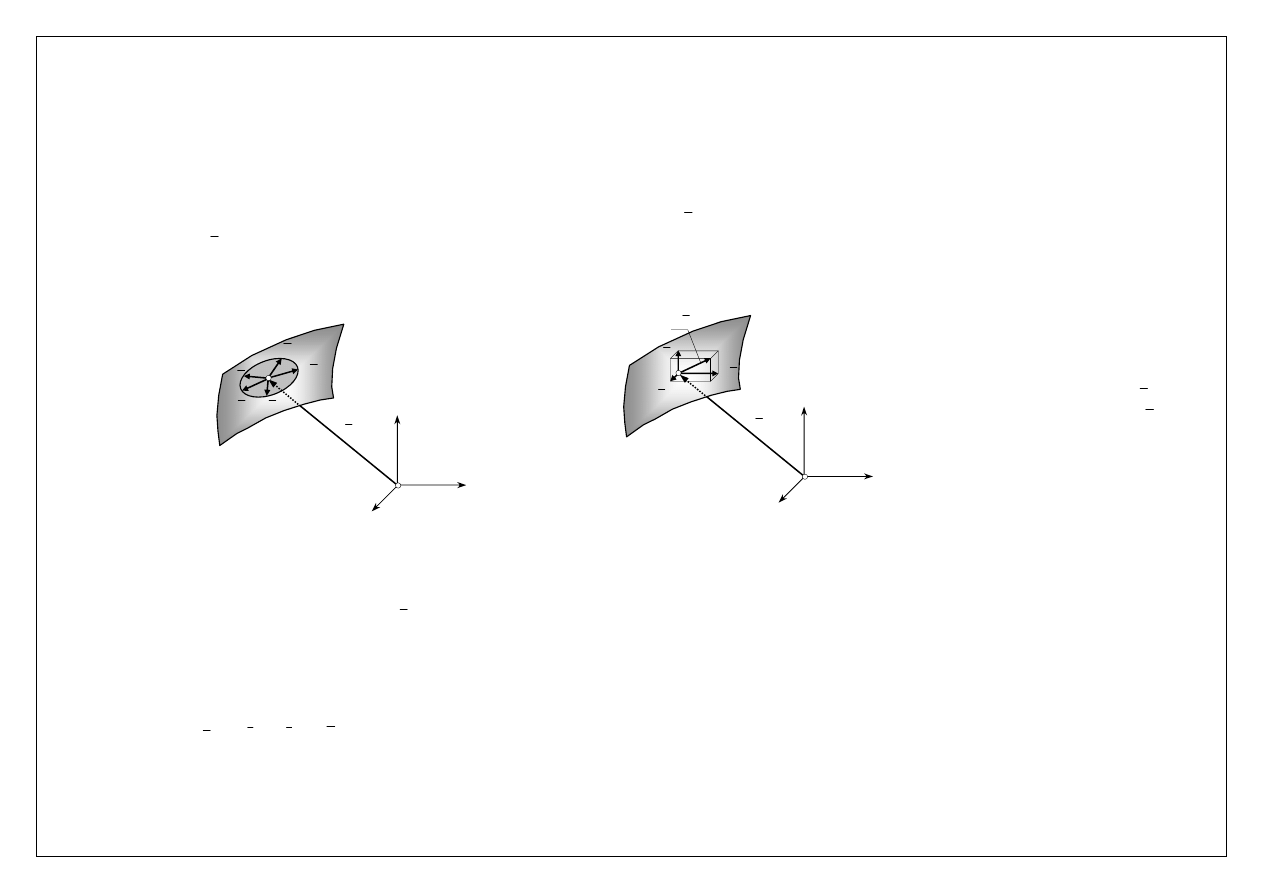
Prof. Edmund Wittbrodt

Przemieszczenia przygotowane

Przemieszczenie (przesunięcie) przygotowane (wirtualne) jest to każde dowolne, możliwe przemieszczenie punktu, zgodne z
więzami. Jeżeli położenie punktu określone jest za pomocą wektora

r

, to przemieszczenie przygotowane oznaczamy

symbolem

r

δ

.

Przemieszczenia: a) przygotowane

r

δ

,

b) rzeczywiste

dr

Przemieszczenie przygotowane

r

δ

jest to pomyślane (wyobrażalne) przesuniecie punktu, o kierunku zgodnym

z kierunkiem możliwej prędkości tego punktu.

Przemieszczenie przygotowane jest wektorem, który możemy przedstawić w postaci

k

z

j

y

i

x

r

δ

δ

δ

δ

+

+

=

.

P

O

x

z

P

a)

r

δ

r

δ

r

δ

r

δ

r

δ

r

y

P

O

x

y

z

r

b)

dr

dx

dy

dz

Prof. Edmund Wittbrodt

Jeżeli dane jest równanie więzów w postaci

0

)

,

,

(

=

z

y

x

f

, przedstawiające równanie powierzchni, na której znajduje się

rozpatrywany punkt, to dla przesunięcia przygotowanego zachodzi związek

0

=

∂

∂

+

∂

∂

+

∂

∂

z

z

f

y

y

f

x

x

f

δ

δ

δ

, co można zapisać

0

=

⋅

∂

r

f

grad

r

δ

.

Jeżeli mamy do czynienia z układem p punktów materialnych, poddanych w więzom, to zachodzą następujące związki

0

1

=













⋅

∂

∂

+

⋅

∂

∂

+

⋅

∂

∂

∑

=

p

i

i

i

j

i

i

j

i

i

j

z

z

f

y

y

f

x

x

f

δ

δ

δ

,

w

j

,.....,

2

,

1

=

, lub w postaci wektorowej

0

1

=

⋅

∑

=

∂

i

p

i

j

r

r

f

grad

i

δ

,

w

j

,.....,

2

,

1

=

.

Przyrosty elementarne współrzędnych prostokątnych dowolnego i-tego punktu są równe:

∑

=

∂

∂

=

s

j

j

j

i

i

q

q

x

x

1

δ

δ

,

∑

=

∂

∂

=

s

j

j

j

i

i

q

q

y

y

1

δ

δ

,

p

i

,.....,

2

,

1

=

lub w zapisie wektorowym

∑

=

∂

∂

=

s

j

j

j

i

i

q

q

r

r

1

δ

δ

,

p

i

,.....,

2

,

1

=

∑

=

∂

∂

=

s

j

j

j

i

i

q

q

z

z

1

δ

δ

,

gdzie s

−

liczba stopni swobody.

Prof. Edmund Wittbrodt

Zasada prac przygotowanych (wirtualnych)

Praca przygotowana jest to elementarna praca siły

,

,

i

xi

yi

zi

P P

P

P









na przemieszczeniu przygotowanym

[

]

,

,

i

i

i

i

r

x

y

z

δ δ

δ

δ

i

zi

i

yi

i

xi

i

i

z

P

y

P

x

P

r

P

L

δ

δ

δ

δ

δ

+

+

=

⋅

=

.

Jeżeli na układ p punktów materialnych, na które działają siły

i

P

, poddano przesunięciom przygotowanym

i

r

δ

, to praca

przygotowana tych sił jest równa

∑

∑

=

=

+

+

=

⋅

=

p

i

i

zi

i

yi

i

xi

p

i

i

i

z

P

y

P

x

P

r

P

L

1

1

)

(

δ

δ

δ

δ

δ

gdzie:

i

i

i

z

y

x

δ

δ

δ

,

,

−

przyrosty elementarne współrzędnych i-tego punktu w układzie x,y,z,

zi

yi

xi

P

P

P

,

,

−

składowe siły działającej na i-ty punkt w układzie x,y,z.

Prof. Edmund Wittbrodt

Zasada prac przygotowanych: Warunkiem koniecznym i wystarczającym równowagi dowolnego układu punktów jest, aby
suma prac przygotowanych wszystkich sił czynnych i sił reakcji więzów, przy dowolnym przemieszczeniu przygotowanym,
była równa zeru

0

)

(

1

=

⋅

+

⋅

=

∑

=

i

i

p

i

i

i

r

R

r

P

L

δ

δ

δ

,

gdzie:

i

P

−

siła czynna działająca na i-ty punkt,

i

R

−

reakcja

więzów działających na i-ty punkt,

i

R

i

r

δ

−

przesunięcie

przygotowane i-tego punktu.

Praca przygotowana więzów idealnych jest zawsze równa zeru

0

=

⋅

i

i

r

R

δ

,

p

i

,.....

2

,

1

=

,

gdyż są to wektory prostopadłe.

Zasada prac przygotowanych dla układów o więzach idealnych: Warunkiem koniecznym i wystarczającym równowagi
dowolnego układu punktów o więzach idealnych jest, aby suma prac przygotowanych wszystkich sił czynnych działających
na ten układ, przy dowolnym przemieszczeniu przygotowanym, była równa zeru

0

1

=

⋅

=

∑

=

p

i

i

i

r

P

L

δ

δ

.

Prof. Edmund Wittbrodt

Siły uogólnione

Siły uogólnione

j

Q

są to wielkości spełniające równanie

∑

=

=

s

j

j

j

q

Q

L

1

δ

δ

, j=1,2,...s,

gdzie:

L

δ

– praca przygotowana układu,

j

q

δ

– przesunięcie przygotowane, zgodne z j-tą współrzędną uogólnioną,

j

Q

– j-ta

siła uogólniona, zgodna z j-tą współrzędną uogólnioną, s – liczba stopni swobody (współrzędnych uogólnionych).


Siłę uogólnioną możemy wyznaczyć z następującej zależności

∑

=

∂

∂

+

∂

∂

+

∂

∂

=

p

i

j

i

zi

j

i

yi

j

i

xi

j

q

z

P

q

y

P

q

x

P

Q

1

)

(

, j=1,2,...s,

gdzie:

zi

yi

xi

P

P

P

,

,

– rzuty siły działającej na i-ty punkt,

i

i

i

z

y

x

,

,

– współrzędne prostokątne i-tego punktu,

j

q

– j-ta

współrzędna uogólniona, s – liczba stopni swobody układu, p – liczba punktów układu.


Siła uogólniona w zachowawczym polu sił jest równa

j

j

q

V

Q

∂

∂

−

=

, j=1,2,...s

gdzie: V – energia potencjalna układu, podawana jako funkcja współrzędnych uogólnionych.

Prof. Edmund Wittbrodt

Równowaga w zachowawczym polu sił

Jeżeli na układ materialny o więzach idealnych działa zachowawcze pole sił, to jest on w równowadze wtedy, gdy jego
energia potencjalna przyjmuje wartość ekstremalną

0

=

∂

∂

j

q

V

, j=1,2,...s

gdzie: V – energia potencjalna układu, podawana jako funkcja współrzędnych uogólnionych, s – liczba stopni swobody
układu.



Zasada Dirichleta:

Jeżeli na nieswobodny układ materialny działa zachowawcze pole sił, wówczas położenie, w którym energia potencjalna
tego układu osiąga minimum, jest położeniem równowagi stałej.

Prof. Edmund Wittbrodt

Ogólne równanie dynamiki analitycznej

Równania dynamiki, z uwzględnieniem sił reakcji więzów, w postaci

i

i

i

i

R

P

r

m

+

=

&

&

,

p

i

,.....,

2

,

1

=

lub:

xi

xi

i

i

R

P

x

m

+

=

&

&

,

yi

yi

i

i

R

P

y

m

+

=

&

&

zxi

zi

i

i

R

P

z

m

+

=

&

&

,

p

i

,.....,

2

,

1

=

pomnożymy skalarnie przez

i

r

δ

, lub odpowiednio przez

,

,

δ

δ

δ

i

i

i

x

y

z

oraz zsumujemy stronami. Wtedy otrzymujemy

0

)

(

1

=

⋅

−

+

∑

=

p

i

i

i

i

i

r

r

m

R

P

δ

&

&

lub

0

]

)

(

)

(

)

[(

1

=

−

+

+

−

+

+

−

+

∑

=

p

i

i

i

i

zi

zi

i

i

i

yi

yi

i

i

i

xi

xi

z

z

m

R

P

y

y

m

R

P

x

x

m

R

P

δ

δ

δ

&

&

&

&

&

&

.

Natomiast dla układów z więzami holonomicznymi, idealnymi i dwustronnymi, zachodzą związki:

0

)

(

1

=

⋅

−

∑

=

p

i

i

i

i

i

r

r

m

P

δ

&

&

lub

0

]

)

(

)

(

)

[(

1

=

−

+

−

+

−

∑

=

p

i

i

i

i

zi

i

i

i

yi

i

i

i

xi

z

z

m

P

y

y

m

P

x

x

m

P

δ

δ

δ

&

&

&

&

&

&

,

gdzie:

]

,

,

[

zi

yi

xi

i

P

P

P

P

– siła działająca na i-ty punkt,

]

,

,

[

i

i

i

i

z

y

x

r

δ

δ

δ

δ

– przesunięcie przygotowane i-tego punktu,

i

i

a

r

=

&

&

–

przyspieszenie i-tego punktu, p – liczba punktów materialnych.

Równania te, sformułowane przez Lagrange’a, przedstawiają zasadę d’Alemberta dla układu punktów materialnych o
więzach idealnych, holonomicznych i dwustronnych w układzie inercjalnym. Noszą one również nazwę ogólnych równań
dynamiki analitycznej.

Prof. Edmund Wittbrodt

Równania Lagrange’a II rodzaju

Równania Lagrange’a II rodzaju mają postać

j

j

j

j

j

Q

q

V

q

D

q

E

q

E

dt

d

=

∂

∂

+

∂

∂

+

∂

∂

−

∂

∂

&

&

,

s

j

,.....,

2

,

1

=

gdzie: E – energia kinetyczna układu,

D – funkcja dyssypacji energii układu (prędkość rozpraszania energii mechanicznej),

V – energia potencjalna układu,

Q

j

– siła uogólniona (niepotencjalna i niedyssypatywna część siły czynnej) działająca w kierunku j-tej współrzędnej

uogólnionej,

j

q

– j-ta współrzędna uogólniona,

j

q

&

– j-ta prędkość uogólniona (zgodna z j-tą współrzędną uogólnioną),

s – liczba stopni swobody układu.