Zadanie 2

Z wykorzystaniem metody Hamiltona 1

m1I1 r1

x2

m2

m3

x3

dane są warunki:

zapisanie poszczególnych energii:

szukamy warunków geometrycznych:

upraszczamy równania energii:

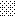
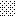
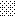
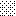
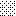
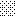
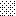
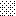
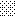
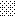
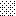
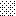
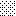
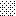
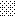
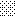
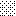
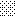
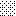
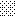
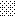
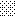
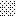
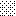
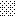
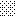
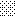
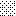
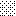
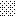
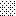
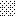
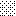
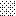
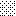
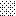
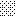
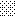
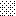
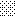
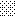
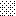
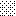
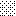
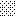
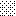
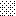
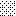
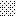
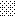
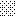
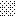
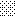
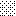
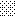
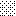
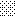
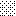
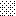
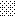
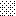
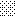
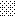
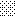
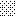
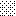
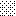
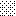
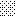
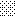
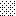
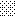
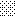
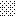
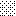
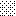
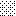
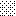
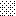
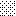
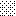
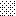
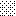
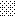
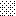
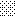
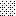
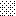
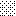
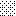
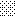
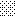
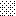
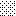
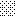
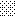
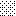
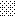
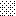
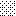
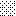
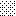
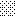
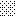
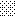
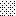
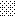
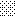
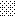
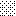
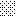
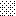
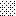
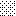
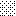
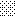
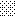
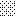
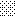
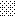
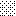
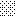
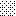
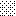
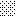
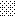
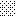
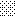
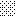
następnie obliczamy:

!

"

"

równanie Hamiltona:

#

"

#

"

&

#

' ( )* ( (

,

%

$

' +

(

+

+ ( -

przyjmujemy dane w celu wykreślenia wykresów:

-./

-.0

01

5000

]d 4500

[ra 1 4000

łao 3500

kew 3000

toą 2500

kie 2000

n

"40'

2'3

1500

szczeie 1000

m

500

rzep

0

0

5

10

15

20

25

30

35

40

45

czas t [s]

250

200

/s]d

[ra 1 150

łao kawtoą

100

ść kokd

544-'

ręp

2'3

50

0

0

5

10

15

20

25

30

35

40

45

czas t [s]

7

6

]2

/s^d 5

[ra

544-

1

+2'3

ła

o

4

kewtoą k 3ien

szeie 2

sp

rzyp

1

0

0

5

10

15

20

25

30

35

40

45

czas t [s]