ZADANIA Z TEORII STEROWANIA

1. Ciało o masie m może poruszać się ruchem postępowym pozostając na uwięzi w postaci sprężyny o sztywności k i poruszając się w ośrodku stawiającym opór proporcjonalny do prędkości (współczynnik proporcjonalności wynosi b). Napisać funkcję Hamiltona - Pontriagina oraz równania sprzężone dla następującego zagadnienia sterowania: doprowadzić to ciało w minimalnym czasie do stanu zerowego za pomocą siły zewnętrznej ograniczonej co do modułu.

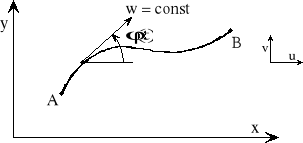
2. Statek płynie w płaszczyźnie xy przez obszar z silnymi prądami. Prąd ma składowe prędkości u(x, y) w kierunku x oraz v(x,y) w kierunku y. Prędkość statku względem wody ma stałą wartość w, zaś kierunek prędkości względnej zadany jest przez kąt φ między wektorem tej prędkości i osią x (rys.). Traktując statek jako punkt materialny, a kąt φ jako sterowanie, sformułować warunki potrzebne do wyznaczenia takiego prawa sterowania, aby czas przepływu z punktu A do punktu B (z góry danych) był minimalny. Następnie przy założeniu, że składowe prędkości nie zależą od współrzędnej y, wyznaczyć konkretne prawo sterowania statkiem.
   Wskazówki:
   1. w zadaniu tym równanie stanu można uzyskać wyłącznie na podstawie relacji kinematycznych.
   2. zastosować ZMP w wersji bez ograniczenia na sterowanie; wówczas dla sterowania optymalnego można przyjąć, że
   .
   
   
   

3. Samolot pionowego startu o masie m zaczyna manewr lądowania na wysokości h_A gdzie ma prędkość v_A (pionowo w dół), a kończy manewr na zadanej wysokości h_B gdzie ma mieć prędkość v_B. Zakładając, że:
   - opór aerodynamiczy wynosi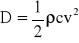
   , c = const >0
   - ciąg silnika hamującego nie zależy od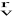
   i ρ przy czym 0≤ F ≤F_max
   Na podstawie ZMP sformułować model matematyczny potrzebny do zaprojektowania manewru w taki sposób aby odbył się on w minimalnym czasie.
   Uwaga: Model matematyczny tzn. równania stanu, wskaźniki jakości, hamiltonian itd.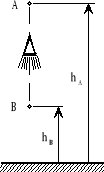
   
   

4. Dla pewnego układu, którego równanie stanu ma postać
, wyznaczyć sterowanie minimalizujące wskaźnik jakości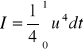
i przeprowadzające układ z położenia
do
w czasie
.

5. Wyznaczyć strategię sterowania, które przeprowadzi układ opisany równaniem


ze stanu x(0) = x₀ do stanu x(1) = 0 i zminimalizuje przy tym wskaźnik jakości

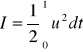
6. Ruch pewnego obiektu opisany jest równaniami

,

Obiekt ten ma tak przejść w zadanym czasie T ze stanu zerowego do dowolnego stanu końcowego, aby zminimalizować całkę


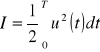
Zbudować algorytm wyznaczenia tego sterowania.