Opracowała: K. Sokołowska
43
13. RACHUNEK CAŁKOWY
13.1.
Całka nieoznaczona
•
Poszukiwanie funkcji F(x), gdy znana jest jej pochodna
( ) ( )
x
f
x
F
=
′
, czyli działanie
odwrotne do różniczkowania nazywa się całkowaniem, a funkcję szukaną F(x) nazywa
się funkcją pierwotną funkcji f(x).
Np. Funkcją pierwotną funkcji
1
)
(
=
x
f
jest funkcja
( )
x
x
F
=
, bo
( )
1
=
′
x
, ale też
( )
45
+
=
x
x
F
,
( )
2
1
3
−
=
x
x
F
,
( )
C
x
x
F
+
=
•
Tw.
Jeżeli F(x) jest funkcją pierwotną funkcji f(x), czyli
( ) ( )
x
f
x
F
=
′
, to F(x)+C, gdzie C
jest dowolną stałą, też jest funkcją pierwotną funkcji f(x)
•
Def.
Zbiór wszystkich funkcji pierwotnych danej funkcji f(x), tzn. takich, że ich pochodna jest
równa funkcji podcałkowej
(
)
)
(
)
(
x
f
C
x
F
=
′
+
nazywamy całką nieoznaczoną funkcji
f(x) i oznaczamy:
( )
∫
+
=
C
x
F
dx
x
f
)
(
,
gdzie f(x)dx nazywamy wyrażeniem podcałkowym, f(x) – funkcją podcałkową, a x-
zmienną całkowania
13.2.
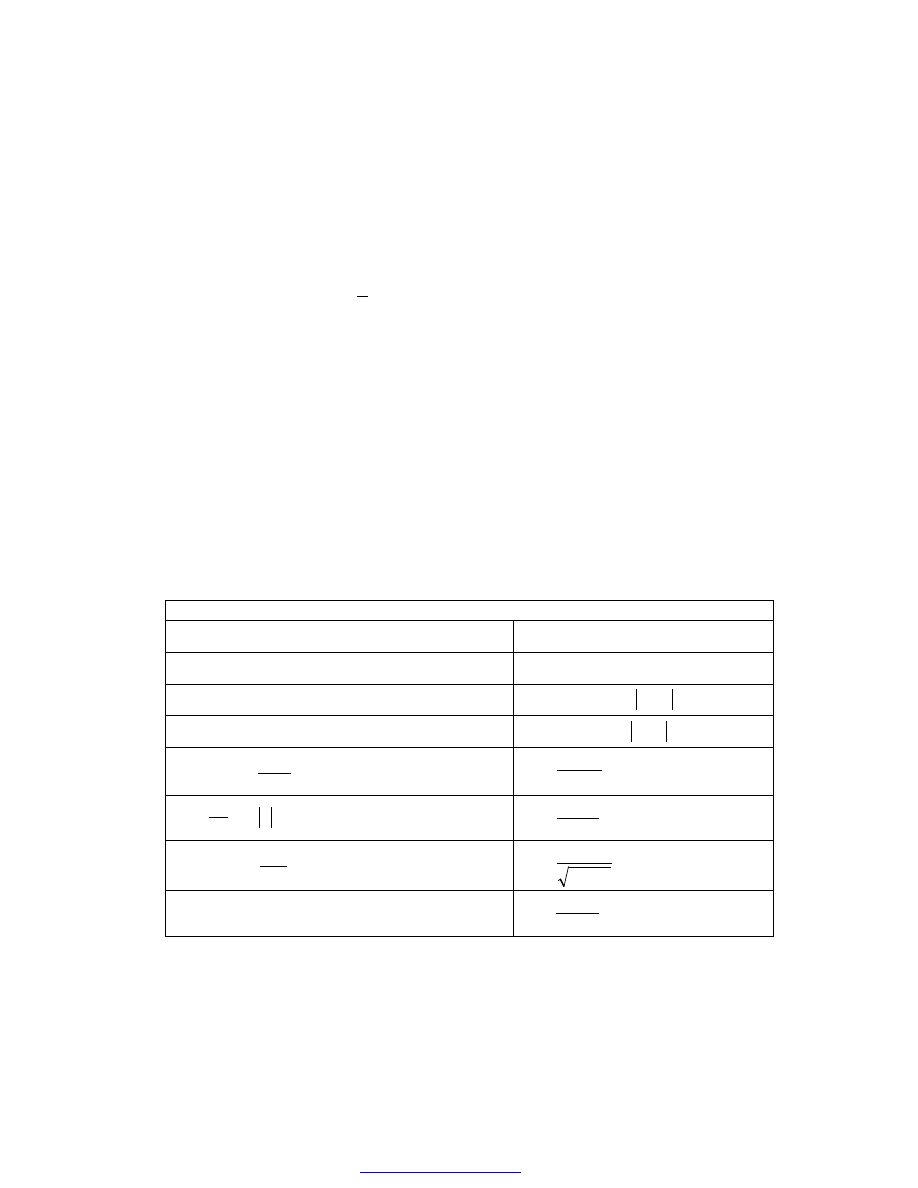
Podstawowe wzory rachunku całkowego
PODSTAWOWE WZORY RACHUNKU CAŁKOWEGO
a)
∫
∫
∈
=
,
,
)
(
)
(
R
a
gdzie
dx
x
f
a
dx
x
af
a-stała
7.
∫
+
−
=
C
x
xdx
cos
sin
b)
[
]
∫
∫
∫
±
=
±
dx
x
g
dx
x
f
dx
x
g
x
f
)
(
)
(
)
(
)
(
8.
∫
+
=
C
x
xdx
sin
cos
1.
∫
+
=
C
x
dx
9.
∫
+
−
=
C
x
tgxdx
cos
ln
2.
∫
+
=
C
ax
adx
10.
∫
+
=
C
x
ctgxdx
sin
ln
3.
1
,
1
1
−
≠
+
+
=
∫
+
n
C
n
x
dx
x
n
n
11.
0
cos
,
cos
1
2
≠
+
=
∫
x
C
tgx
dx
x
4.
∫
+
=
C
x
x
dx
ln
12.
0
sin
,
sin
1
2
≠
+
−
=
∫
x
C
ctgx
dx
x
5.
∫
+
=
C
a
a
dx
a
x
x
ln
13.
C
x
dx
x
+
=
−
∫
arcsin
1
1
2
6.
∫
+
=
C
e
dx
e
x
x
14.
C
arctgx
dx
x
+
=
+
∫
2
1
1
13.3.
Podstawowe reguły całkowania
1. Całka nieoznaczona z iloczynu funkcji przez stałą:
( )
( )
R
a
gdzie
dx
x
f
a
dx
x
af
∈
=
∫
∫
,
PDF created with pdfFactory trial version

Opracowała: K. Sokołowska
44
2. Całka nieoznaczona z sumy (różnicy) funkcji
( ) ( )
[
]
( )
( )
,
dx
x
g
dx
x
f
dx
x
g
x
f
∫
∫
∫
±
=
±
PRZYKŁAD 34
(
)
=
−
+
=
−
+
=
−
+
∫
∫
∫
∫
∫
∫
∫
dx
x
xdx
dx
x
dx
x
xdx
dx
x
dx
x
x
x
2
1
3
3
3
2
5
2
5
2
5
C
x
x
x
C
x
C
x
C
x
+
−
+
=
+
−
+
+
+
2
3
2
4
3
2
3
2
3
2
2
1
4
3
4
2
5
4
1
2
2
5
4
3. Całkowanie przez podstawienie (przez zamianę zmiennej)
W wielu przypadkach obliczenie całki z funkcji f(x) może być zastąpione obliczeniem
innej całki, która powstała z poprzedniej przez znalezienie nowej zmiennej t, takiej, że
)
(x
w
t
=
, co powoduje, że wyrażenie podcałkowe może być zapisane w postaci
dt
t
g )
(
,
gdzie g(t) jest funkcją łatwiejszą do scałkowania, niż f(x). Wówczas mamy:
[
]
∫
∫
∫
′
⋅
=
=
dx
x
w
x
w
g
dt
t
g
dx
x
f
)
(
)
(
)
(
)
(
, gdzie
)
(x
w
t
=
,
dx
x
w
dt
)
(
′
=
PRZYKŁAD 34
Obliczyć całkę
xdx
x cos
sin
6
∫
Wykonujemy podstawienie
,
sin
t
x
=
skąd różniczkując obie strony mamy:
,
cos
dt
xdx
=
czyli
,
cos x
dt
dx
=
, a więc:
C
x
C
t
dt
t
x
dt
x
t
x
dt
dx
dt
xdx
t
x
xdx
x
+
=
+
=
=
=
=
=
=
=
∫
∫
∫
7
sin
7
cos
cos
cos
cos
sin
cos
sin
7
7
6
6
6
4. Całkowanie przez części:
Niech funkcje f(x) i g(x) mają w pewnym przedziale ciągłe pochodne pierwszego rzędu.
Wzór na całkowanie przez części łatwo wyprowadzić z reguły różniczkowania iloczynu
funkcji. Zauważmy, że:
[
]
[
]
)
(
)
(
)
(
)
(
)
(
)
(
)
(
)
(
)
(
)
(
)
(
)
(
)
(
)
(
)
(
)
(
)
(
)
(
∫
∫
∫
′
⋅
+
⋅
′
=
⋅
⇔
′
⋅
+
⋅
′
=
⋅
⇔
′
⋅
+
⋅
′
=
′
⋅
dx
x
g
x
f
dx
x
g
x
f
x
g
x
f
dx
x
g
x
f
x
g
x
f
x
g
x
f
x
g
x
f
x
g
x
f
x
g
x
f
Stąd
∫
∫
′
⋅
−
=
′
⋅
dx
x
f
x
g
x
g
x
f
dx
x
g
x
f
)
(
)
(
)
(
)
(
)
(
)
(
Niech :
dv
dx
x
g
v
x
g
du
dx
x
f
u
x
f
=
′
⇒
=
=
′
⇒
=
)
(
)
(
)
(
)
(
∫
∫
−
=
vdu
uv
udv
lub
∫
∫
′
−
=
′
u
v
uv
v
u
PDF created with pdfFactory trial version

Opracowała: K. Sokołowska
45
PRZYKŁAD 35
Obliczyć całkę :
xdx
x ln
5
∫
Zakładamy, że x>0 i całkujemy przez części przyjmując:
6
,
1
,
ln
6
5
x
V
x
u
x
V
x
u
=
=
′
=
′
=
Korzystając ze wzoru:
∫
∫
′
−
=
′
u
v
uv
v
u
otrzymujemy:
C
x
x
x
dx
x
x
x
dx
x
x
x
x
xdx
x
+
−
=
−
=
−
=
∫
∫
∫
36
ln
6
6
ln
6
1
6
ln
6
ln
6
6
5
6
6
6
5
5. Całkowanie niektórych funkcji wymiernych
Funkcją wymierną nazywamy iloraz dwóch wielomianów. Całka z funkcji wymiernej
będzie więc miała postać:
( )
( )
dx
x
W
x
W
∫
2
1
.
Przy obliczaniu całki należy postępować w następujący sposób:
1} Jeżeli stopień wielomianu znajdującego się w liczniku
( )
x
W
1
jest wyższy od stopnia
wielomianu znajdującego się w mianowniku
( )
x
W
2
, to licznik
( )
x
W
1
dzielimy przez
mianownik
( )
x
W
2
i funkcję podcałkową przedstawiamy jako sumę wielomianu
( )
x
P
oraz
funkcji wymiernej
( )
( )
x
W
x
M
2
, w której już stopień licznika jest mniejszy niż stopień
mianownika:
( )
( ) ( )
( )
( )
x
W
x
M
x
P
x
W
x
W
2
2
1
+
=
2) Jeżeli stopień wielomianu znajdującego się w liczniku jest niższy od stopnia
wielomianu znajdującego się w mianowniku, to funkcję podcałkową rozkładamy na tzw.
ułamki proste, tj. na sumę wyrażeń postaci:
(
) (
)
(
)
,
...,
,
,
,
3
2
k
b
ax
A
b
ax
A
b
ax
A
b
ax
A
+
+
+
+
oraz
(
) (
)
(
)
,
...,
,
,
,
2
3
2
2
2
2
k
c
bx
ax
C
Bx
c
bx
ax
C
Bx
c
bx
ax
C
Bx
c
bx
ax
C
Bx
+
+
+
+
+
+
+
+
+
+
+
+
gdzie
0
4
2
<
−
ac
b
METODY CAŁKOWANIA
a) Jeżeli licznik funkcji wymiernej jest pochodną mianownika np.
∫
+
+
+
dx
c
bx
ax
b
ax
2
2
, to całkę obliczamy dokonując podstawienia:
(
)
b
ax
dt
dx
dt
dx
b
ax
t
c
bx
ax
+
=
=
+
=
+
+
2
2
2
.
Wówczas mamy:
PDF created with pdfFactory trial version

Opracowała: K. Sokołowska
46
C
c
bx
ax
C
t
t
dt
b
ax
dt
t
b
ax
dx
c
bx
ax
b
ax
+
+
+
=
+
=
=
+
⋅
+
=
+
+
+
∫
∫
∫
2
2
ln
ln
2
2
2
Podobnie postępujemy, gdy pochodna mianownika jest proporcjonalna do licznika.
PRZYKŁAD 36
Obliczyć całkę:
dx
x
x
x
∫
+
−
−
10
7
14
4
2
.
Obliczamy
∆
trójmianu znajdującego się w mianowniku, aby wyznaczyć dziedzinę:
5
,
2
,
9
1
1
=
=
=
∆
x
x
, stąd wniosek, że
{ }
5
,
2
\
R
D
=
. Stosujemy podstawienie:
t
x
x
=
+
−
10
7
2
,
gdyż
zauważamy,
że
(
)
,
7
2
10
7
2
−
=
′
+
−
x
x
x
oraz,
że
)
7
2
(
2
14
4
−
=
−
x
x
. Mamy więc:
dx
x
x
x
∫
+
−
−
10
7
14
4
2
=
(
)
=
−
=
=
−
=
+
−
7
2
7
2
10
7
2
x
dt
dx
dt
dx
x
t
x
x
(
)
C
x
x
C
t
t
dt
x
dt
t
x
+
+
−
=
+
=
=
−
−
∫
∫
10
7
ln
2
ln
2
2
7
2
7
2
2
2
b) Jeżeli licznik funkcji wymiernej nie jest pochodną mianownika (ani nie jest do niej
proporcjonalny), to sposób obliczania całek zależy od znaku
∆
trójmianu kwadratowego
znajdującego się w mianowniku funkcji podcałkowej. Rozpatrzymy dwa przypadki
(gdy
0
,
0
=
∆
>
∆
). Przypadek
∆
<0 pominiemy:
-
∆
>0
PRZYKŁAD 37
Obliczyć całkę:
dx
x
x
x
∫
+
−
−
3
7
2
11
12
2
Obliczamy
∆
trójmianu znajdującego się w mianowniku, aby wyznaczyć dziedzinę:
3
,
2
1
,
25
2
1
=
=
=
∆
x
x
, stąd wniosek, że
=
3
,
2
1
\
R
D
. Następnie przedstawiamy
mianownik
w
postaci
iloczynu
czynników:
(
) (
)(
)
3
1
2
3
2
1
2
3
7
2
2
−
−
=
−
−
=
+
−
x
x
x
x
x
x
i rozkładamy funkcję podcałkową na
ułamki proste:
(
)(
) (
) (
)
3
1
2
3
1
2
11
12
−
+
−
=
−
−
−
x
B
x
A
x
x
x
Doprowadzając prawą stronę do wspólnego mianownika, otrzymujemy:
(
)(
)
(
) (
)
(
)(
)
3
1
2
1
2
3
3
1
2
11
12
−
−
−
+
−
=
−
−
−
x
x
x
B
x
A
x
x
x
,
stąd
(
) (
)
1
2
3
11
12
−
+
−
=
−
x
B
x
A
x
(
) (
)
B
A
x
B
A
x
−
−
+
+
=
−
3
2
11
12
PDF created with pdfFactory trial version
Opracowała: K. Sokołowska
47
Z powyższej tożsamości (czyli związku, który jest prawdziwy dla każdego x) po
przyrównaniu współczynników przy tych samych potęgach x dostajemy:
12=A+2B -11=-3A-B,
stąd po rozwiązaniu tego układu równań mamy, że:
A=2, B=5.
Zatem ułamek
(
)(
)
3
1
2
11
12
−
−
−
x
x
x
rozłożony na ułamki proste ma postać:
(
)(
) (
) (
)
3
5
1
2
2
3
1
2
11
12
−
+
−
=
−
−
−
x
x
x
x
x
.
Obliczenie całki
dx
x
x
x
∫
+
−
−
3
7
2
11
12
2
sprowadza się więc do obliczenia całki z sumy
ułamków prostych:
(
) (
)
(
)
(
)
C
x
x
dx
x
dx
x
dx
x
x
+
−
+
−
⋅
=
−
+
−
=
−
+
−
∫
∫
∫
3
ln
5
1
2
ln
2
1
2
3
5
1
2
2
3
5
1
2
2
-
∆
=0
PRZYKŁAD 38
Obliczyć całkę:
dx
x
x
x
∫
+
−
−
9
12
4
2
7
2
Obliczamy
∆
trójmianu znajdującego się w mianowniku, aby wyznaczyć dziedzinę:
2
3
8
12
,
0
0
=
=
=
∆
x
, stąd wniosek, że
=
2
3
\
R
D
. Następnie przedstawiamy mianownik
w postaci iloczynu czynników:
(
)
2
2
2
3
2
2
3
4
9
12
4
−
=
−
=
+
−
x
x
x
x
i rozkładamy
funkcję podcałkową na ułamki proste:
(
) (
)
3
2
3
2
9
12
4
2
7
2
2
−
+
−
=
+
−
−
x
B
x
A
x
x
x
Doprowadzając prawą stronę do wspólnego mianownika, otrzymujemy:
(
)
(
)
2
2
3
2
3
2
9
12
4
2
7
−
−
+
=
+
−
−
x
x
B
A
x
x
x
,
stąd
(
)
3
2
2
7
−
+
=
−
x
B
A
x
(
)
B
A
Bx
x
3
2
2
7
−
+
=
−
Z powyższej tożsamości po przyrównaniu współczynników przy tych samych potęgach x
dostajemy:
7=A-3B -2=2B,
stąd po rozwiązaniu tego układu równań mamy, że:
A=4, B=-1.
Zatem:
(
) (
)
3
2
1
3
2
4
9
12
4
2
7
2
2
−
−
+
−
=
+
−
−
x
x
x
x
x
.
PDF created with pdfFactory trial version

Opracowała: K. Sokołowska
48
Obliczenie całki
dx
x
x
x
∫
+
−
−
3
7
2
11
12
2
sprowadza się więc do obliczenia całki z sumy
ułamków prostych:
(
) (
)
(
)
(
)
(
)
C
x
x
dx
x
dx
x
dx
x
x
+
−
−
−
−
⋅
=
−
−
−
=
−
−
+
−
∫
∫
∫
3
2
ln
2
1
3
2
1
2
1
4
3
2
1
3
2
4
3
2
1
3
2
4
2
2
13.4.
Całka oznaczona
•
Def
Niech dana będzie funkcja f(x) określona i ciągła w przedziale
b
a,
. Całką oznaczoną
funkcji f(x) w przedziale
b
a,
nazywamy wyrażenie
( ) ( )
a
F
b
F
−
, gdzie F(x) jest jedną z
pierwotnych funkcji f(x), co zapisujemy:
( )
( )
[
]
( ) ( )
a
F
b
F
x
F
dx
x
f
b
a
b
a
−
=
=
∫
,
gdzie liczbę a nazywamy dolna granicą całkowania, a liczbę b nazywamy górną granicą
całkowania.
•
Własności całki oznaczonej:
1. Gdy granice całkowania są równe, całka oznaczona jest równa zeru:
( )
( ) ( )
∫
=
−
=
a
a
a
F
a
F
dx
x
f
0
2. Przestawienie granic całkowania zmienia znak całki na przeciwny:
( )
( )
∫
∫
−
=
b
a
a
b
dx
x
f
dx
x
f
3. Całka sumy (różnicy) równa się sumie (różnicy) całek, tzn.
∫
∫
∫
±
=
±
b
a
b
a
b
a
dx
x
g
dx
x
f
dx
x
g
x
f
)
(
)
(
)]
(
)
(
[
4. Stały czynnik można wyznaczyć przed znak całki oznaczonej
∫
∫
=
b
a
b
a
dx
x
f
k
dx
x
kf
)
(
)
(
5. Jeżeli
c
b
a
≤
≤
, to
∫
∫
∫
+
=
b
a
c
b
c
a
dx
x
f
dx
x
f
dx
x
f
)
(
)
(
)
(
•
Metody całkowania omówione wyżej dla całek nieoznaczonych są również obowiązujące
dla całek oznaczonych.
PDF created with pdfFactory trial version
Opracowała: K. Sokołowska
49
PRZYKŁAD 39
Oblicz całkę
dx
xe
x
∫
3
0
2
.
W tym celu wyznaczymy najpierw funkcję pierwotną funkcji podcałkowej (dla wygody
zwykle przyjmujemy C=0):
2
2
2
1
2
1
2
1
2
2
2
2
x
t
t
t
x
e
e
dt
e
x
dt
xe
x
dt
dx
dt
xdx
t
x
dx
xe
=
=
=
=
=
=
=
=
∫
∫
∫
Mamy więc:
2
1
2
1
2
1
2
1
2
1
9
0
3
3
0
3
0
2
2
2
2
−
=
−
=
=
∫
e
e
e
e
dx
xe
x
x
13.5.
Interpretacja geometryczna całki oznaczonej
•
Jeżeli funkcja f jest ciągła w przedziale
b
a,
i dla każdego
b
a
x
,
∈
przyjmuje wartości
nieujemne (
( )
0
≥
x
f
dla
b
a
x
,
∈
), to całka oznaczona:
( )
dx
x
f
b
a
∫
jest równa polu obszaru ograniczonego wykresem funkcji
( )
x
f
y
=
, prostymi x=a, x=b
oraz osią OX.
•
Jeżeli zaś w przedziale
b
a,
jest
( )
0
≤
x
f
, to analogiczne pole równa się -
( )
dx
x
f
b
a
∫
.
•
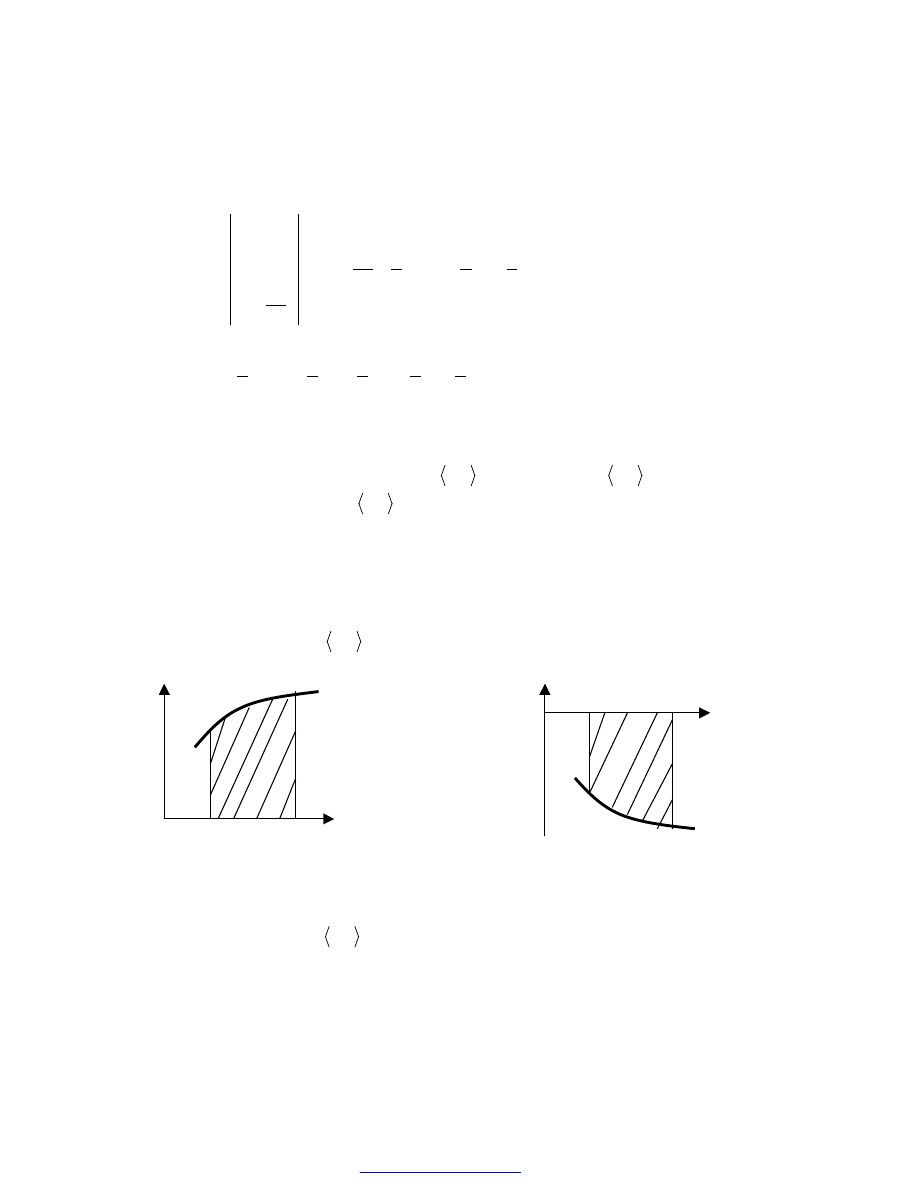
Ogólnie:
Pole obszaru ograniczonego wykresami dwóch funkcji całkowalnych f(x) i g(x), przy
czym dla każdego
b
a
x
,
∈
( ) ( )
x
g
x
f
≤
oraz prostymi x=a i x=b (które w szczególnym
przypadku mogą redukować się do punktów przecięcia się wykresów funkcji), jest równe:
( ) ( )
[
]
dx
x
f
x
g
b
a
∫
−
P
a
b
x
y
y=f(x)
P
a
b
x
y
y=f(x)
PDF created with pdfFactory trial version
Opracowała: K. Sokołowska
50
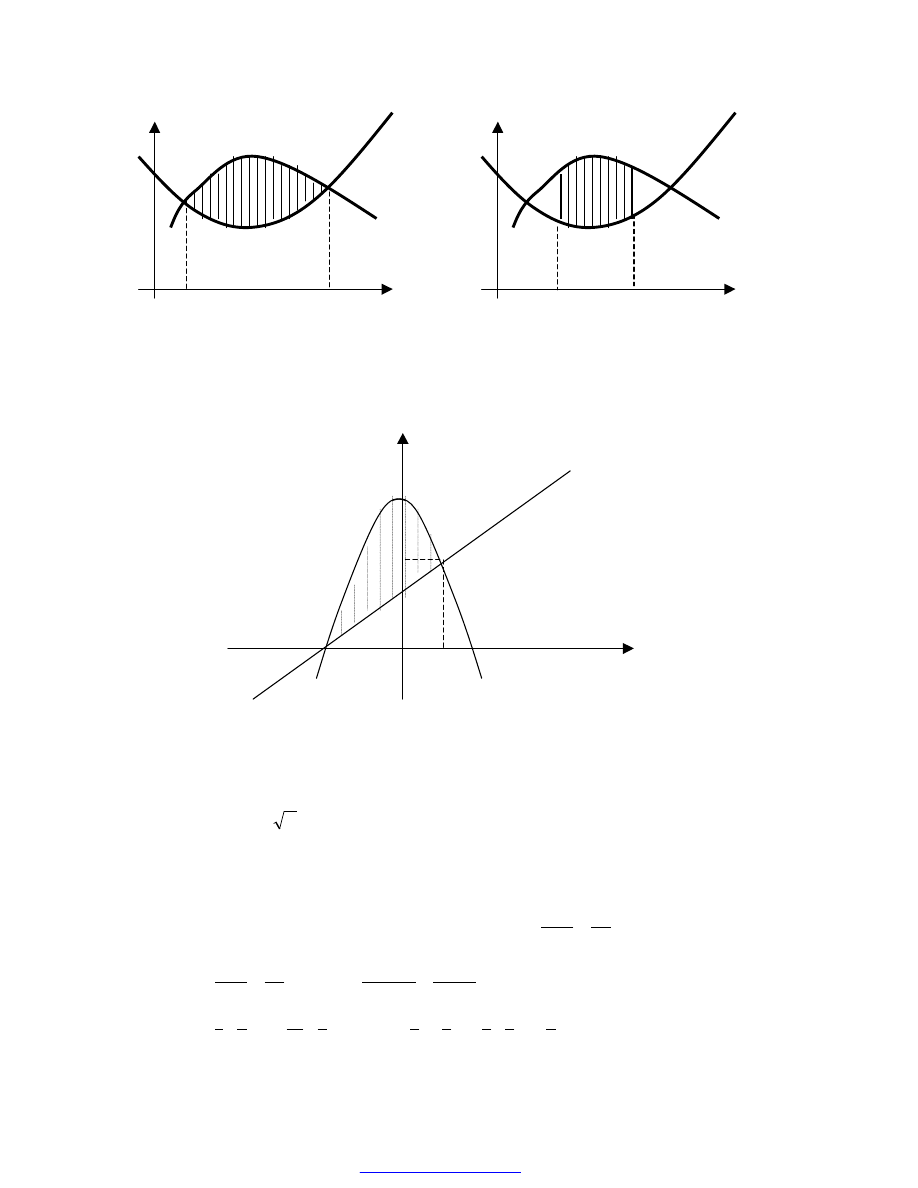
PRZYKŁAD 40
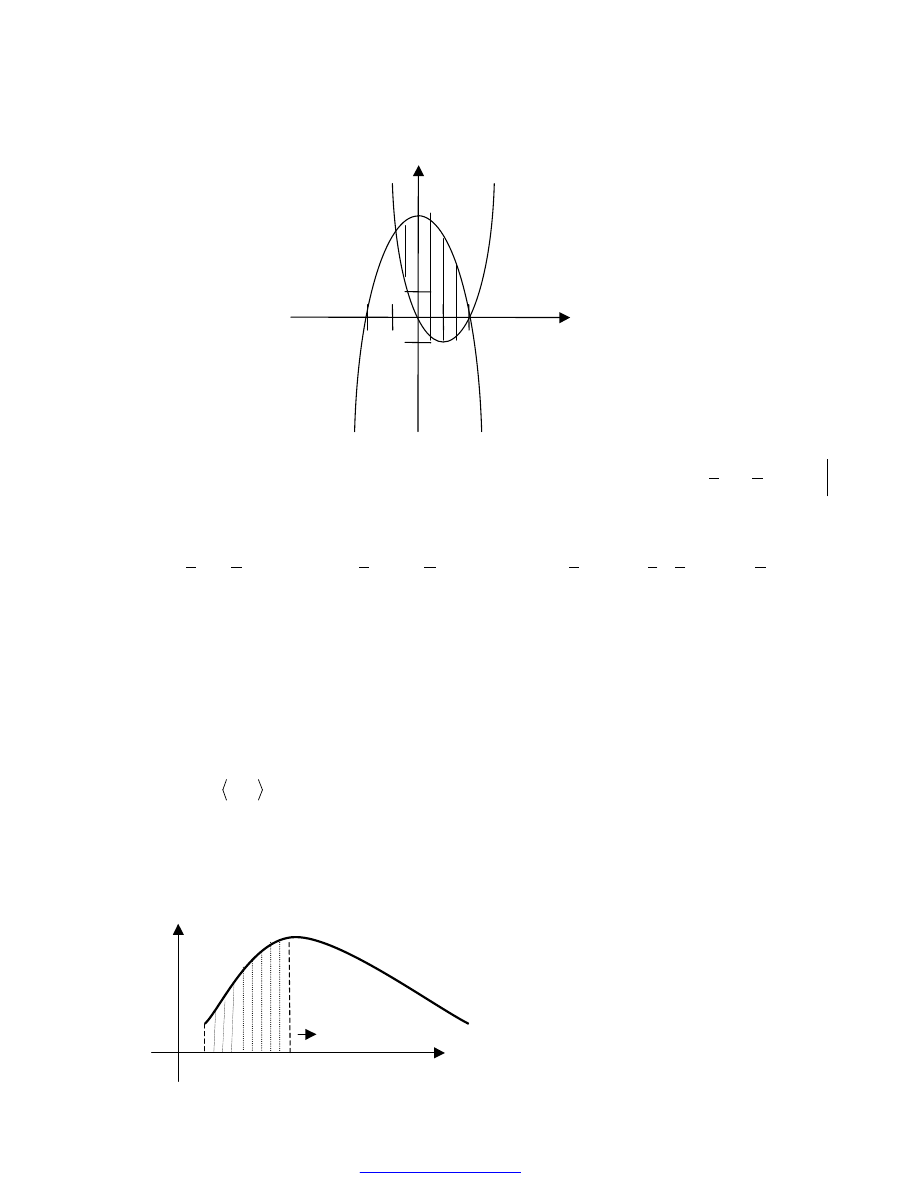
Oblicz pole obszaru ograniczonego wykresami funkcji:
( )
9
2
+
−
=
x
x
f
oraz
( )
3
+
=
x
x
f
Wykonujemy rysunek (wykresy funkcji) oraz zaznaczmy pole, które mamy obliczyć:
Znajdujemy punkty wspólne wykresów tych funkcji rozwiązując równanie:
0
6
3
9
2
2
=
−
+
⇔
+
=
+
−
x
x
x
x
jest to równanie kwadratowe, zatem:
5
,
25
=
∆
=
∆
2
,
3
2
1
=
−
=
x
x
, stąd
0
3
3
1
=
+
−
=
y
,
5
3
2
2
=
+
=
y
.
Otrzymaliśmy dwa punkty przecięcia wykresów funkcji:
(
)
( )
5
,
2
,
0
,
3
2
1
=
−
=
P
P
Szukane pole wynosi:
(
)
(
)
[
]
(
)
=
+
−
−
=
+
−
−
=
+
−
+
−
=
−
−
−
∫
∫
2
3
2
3
2
3
2
2
3
2
6
2
3
6
3
9
x
x
x
dx
x
x
dx
x
x
P
( ) ( )
( )
=
−
⋅
+
−
−
−
−
−
⋅
+
−
−
=
3
6
2
3
3
3
2
6
2
2
3
2
2
3
2
3
[ ]
2
6
5
20
6
4
6
3
21
2
1
4
3
2
11
28
18
2
9
3
27
12
2
4
3
8
j
=
−
=
+
−
=
+
+
−
+
−
−
=
y=g(x)
y=f(x)
b
a
y=g(x)
y=f(x)
b
a
-3
3
2
0
9
5
y=x+3
9
2
+
−
=
x
y
PDF created with pdfFactory trial version
Opracowała: K. Sokołowska
51
PRZYKŁAD 41
Oblicz pole obszaru ograniczonego krzywymi y
1
=4-x
2
, y
2
=x
2
-2x.
y
1
x
-2 0 2
∫
∫
∫
∫
∫
=
+
+
−
=
+
+
−
=
+
−
−
=
−
=
−
=
−
−
−
b
a
b
a
b
a
x
x
x
dx
x
x
dx
x
x
x
dx
y
y
dx
y
dx
y
P
2
1
2
1
2
3
2
1
2
2
2
2
1
2
1
)
2
2
1
3
1
(
2
)
2
(
2
)
2
4
(
)
(
]
[
9
2
9
2
2
2
1
3
1
4
2
3
8
2
)
1
(
2
1
2
1
)
1
(
3
1
2
2
2
4
2
1
8
3
1
2
2
j
=
⋅
=
+
−
−
+
+
−
=
−
⋅
+
⋅
+
−
⋅
−
−
⋅
+
⋅
+
⋅
−
=
13.6.
Całki niewłaściwe
CAŁKA NIEWŁAŚCIWA I RODZAJU - występuje wtedy, gdy mamy do czynienia z
nieskończonymi przedziałami całkowania np.
(
)
+∞
∞
−
+∞
<
>
−∞
,
),
,
;
,
(
α
β
•
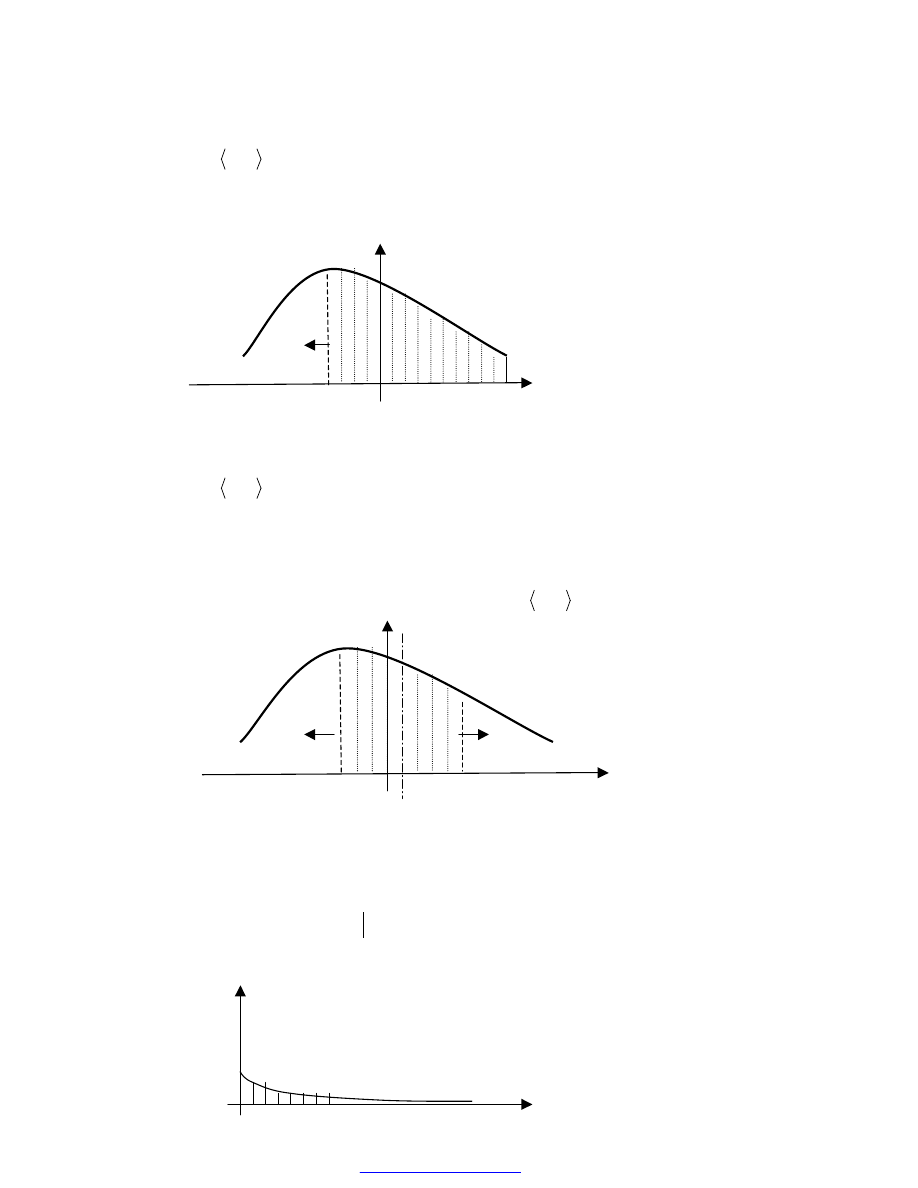
Def
Jeżeli funkcja f(x) jest określona na przedziale
)
,
+∞
<
α
i całkowalna na każdym
przedziale
)
,
,
+∞
⊂<
α
β
α
, to jej całkę niewłaściwą na przedziale
)
,
+∞
<
α
określamy
następująco:
( )
∫
∫
+∞
→
+∞
=
β
β
a
a
dx
x
f
dx
x
f
lim
)
(
,
2
1
4
x
y
−
=
x
x
y
2
2
2
−
=
a
y=f(x)
+∞
→
b
PDF created with pdfFactory trial version
Opracowała: K. Sokołowska
52
•
Def
Jeżeli funkcja f(x) jest określona na przedziale
>
−∞
β
,
(
i całkowalna na każdym
przedziale
>
−∞
⊂
β
β
α
,
(
,
, to jej całkę niewłaściwą na przedziale
>
−∞
β
,
(
określamy
następująco:
( )
∫
∫
−∞
→
∞
−
=
β
β
a
a
dx
x
f
dx
x
f
lim
)
(
.
•
Def
Jeżeli funkcja f(x) jest określona na przedziale
)
,
(
+∞
−∞
i całkowalna na każdym
przedziale
)
,
(
,
+∞
−∞
⊂
β
α
, to jej całkę niewłaściwą na przedziale
)
,
(
+∞
−∞
określamy
następująco:
( )
( )
∫
∫
∫
+∞
→
−∞
→
+∞
∞
−
+
=
β
γ
β
γ
dx
x
f
dx
x
f
dx
x
f
a
a
lim
lim
)
(
,
gdzie
γ jest dowolnym, ustalonym punktem z przedziału
β
α,
PRZYKŁAD 42
Obliczyć całkę niewłaściwą:
dx
e
x
∫
∞
−
0
.
( )
(
)
1
1
lim
lim
lim
0
0
0
=
+
−
=
−
=
=
−
∞
→
−
∞
→
−
∞
→
∞
−
∫
∫
β
β
β
β
β
β
e
e
dx
e
dx
e
x
x
x
Interpretacja geometryczna powyższej całki:
b
y=f(x)
−∞
→
a
y=f(x)
−∞
→
α
+∞
→
β
γ
1
x
e
y
−
=
PDF created with pdfFactory trial version
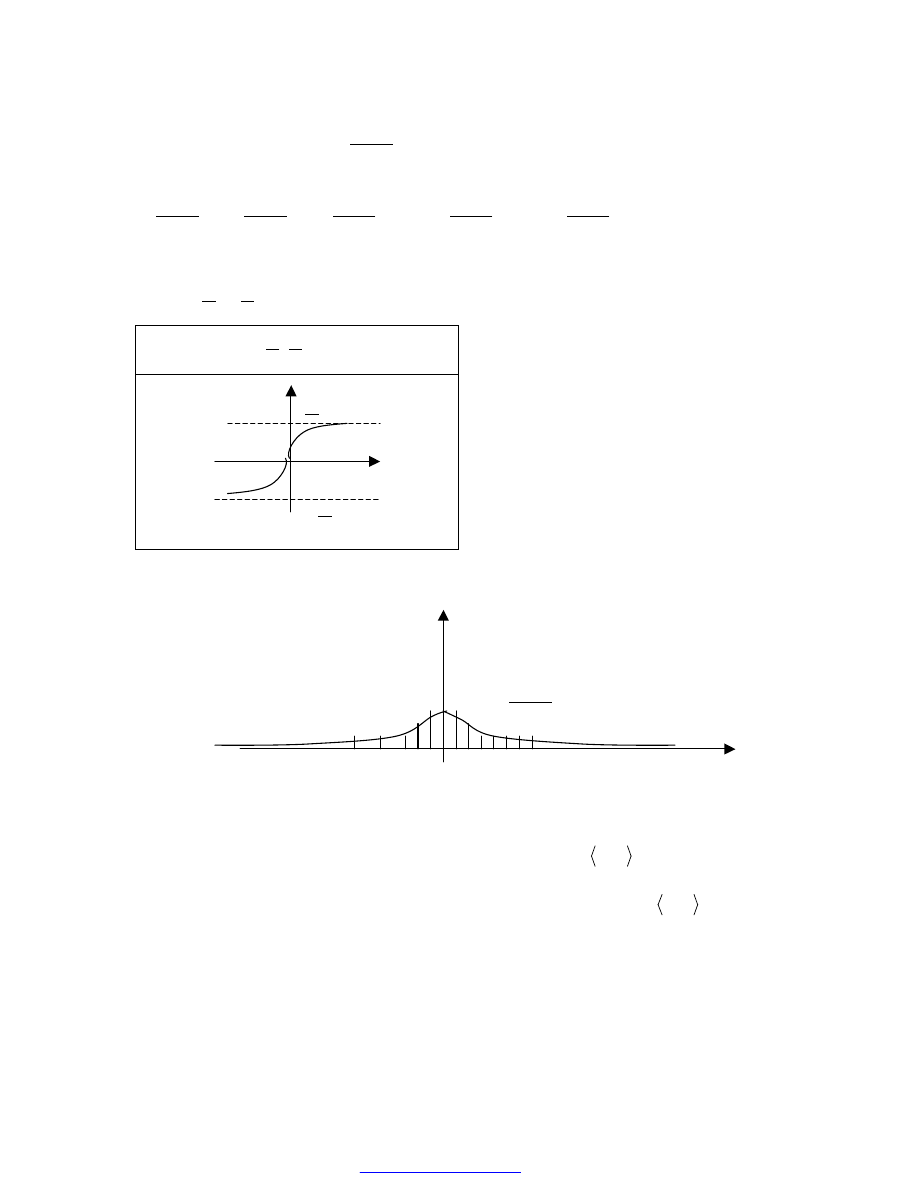
Opracowała: K. Sokołowska
53
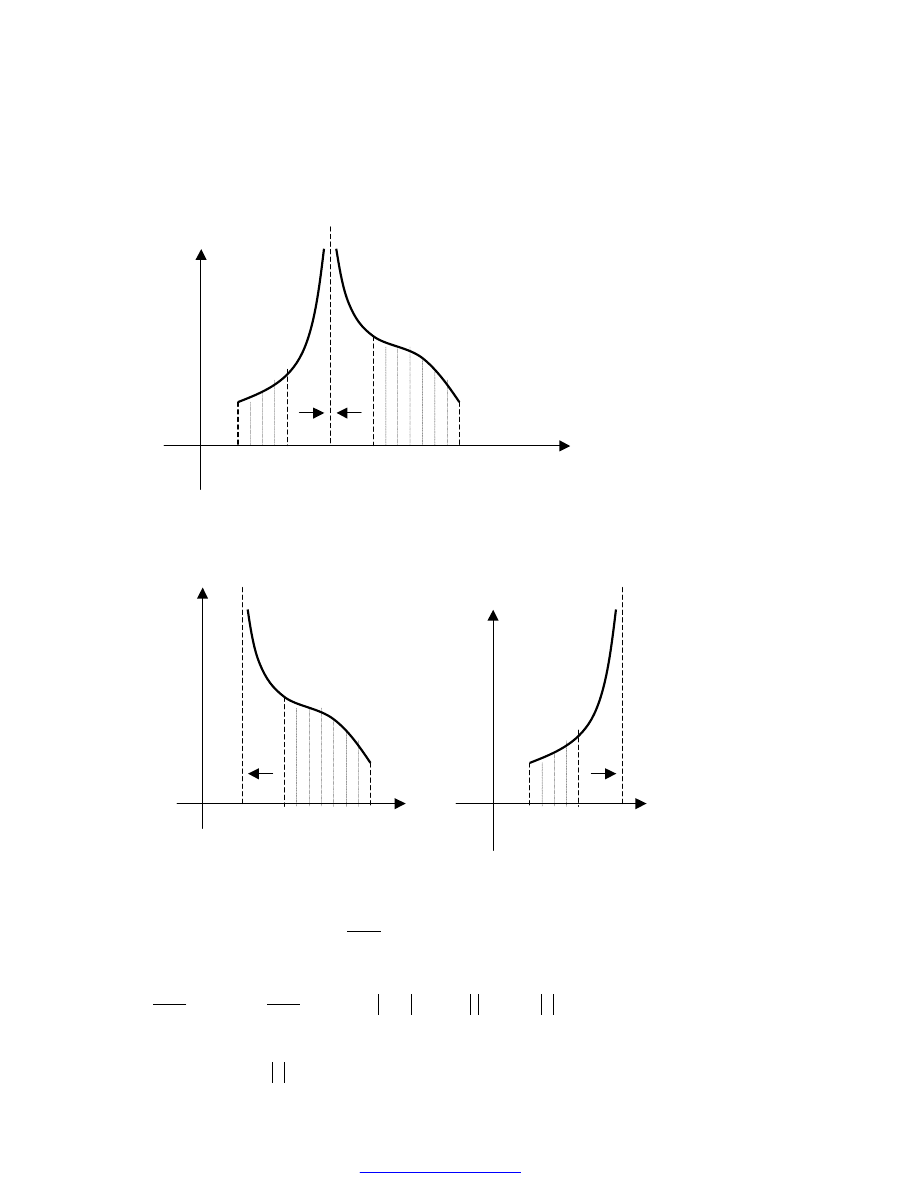
PRZYKŁAD 43
Obliczyć całkę niewłaściwą:
dx
x
∫
+∞
∞
−
+
2
1
1
.
=
+
+
+
=
+
+
+
=
+
∫
∫
∫
∫
∫
+∞
→
−∞
→
+∞
∞
−
+∞
∞
−
dx
x
dx
x
dx
x
dx
x
dx
x
b
b
a
a
0
2
0
2
0
2
0
2
2
1
1
lim
1
1
lim
1
1
1
1
1
1
[
]
[
]
(
)
(
)
=
−
+
−
=
+
+∞
→
−∞
→
+∞
→
−∞
→
0
lim
0
lim
lim
lim
0
0
arctg
arctgb
arctga
arctg
arctgx
arctgx
b
a
b
b
a
a
π
π
π
=
−
+
−
−
=
0
2
2
0
y=arctgx:
−
→
2
,
2
π
π
R
Interpretacja geometryczna powyższej całki:
CAŁKA NIEWŁAŚCIWA II RODZAJU - występuje wtedy, gdy funkcja podcałkowa
jest nieograniczona w skończonym przedziale całkowania. np.
β
α,
.
•
Def.
Jeżeli funkcja f(x) jest nieograniczona w pewnym otoczeniu punktu
β
α
γ
,
∈
i ciągła w
każdym punkcie tego przedziału z wyjątkiem punktu x=c, to jej całkę niewłaściwą na
przedziale <a,b> określamy następująco
( )
( )
∫
∫
∫
+
→
−
→
+
+
+
=
b
c
c
a
b
a
dx
x
f
dx
x
f
dx
x
f
2
2
1
1
0
0
lim
lim
)
(
ε
ε
ε
ε
Gdy c=a lub c=b, mamy:
1
2
1
1
x
y
+
=
2
π
−
2
π
0
PDF created with pdfFactory trial version
Opracowała: K. Sokołowska
54
( )
( )
∫
∫
∫
∫
−
→
+
→
+
+
=
=
ε
ε
ε
ε
b
a
b
a
b
a
b
a
dx
x
f
dx
x
f
dx
x
f
dx
x
f
0
0
lim
)
(
lub
lim
)
(
•
Jeśli granica w powyższych definicjach jest skończona, to mówimy, że całka jest zbieżna.
Jeśli granica jest nieskończona, bądź w ogóle nie istnieje, to mówimy, że całka jest
rozbieżna.
c=a
c=b
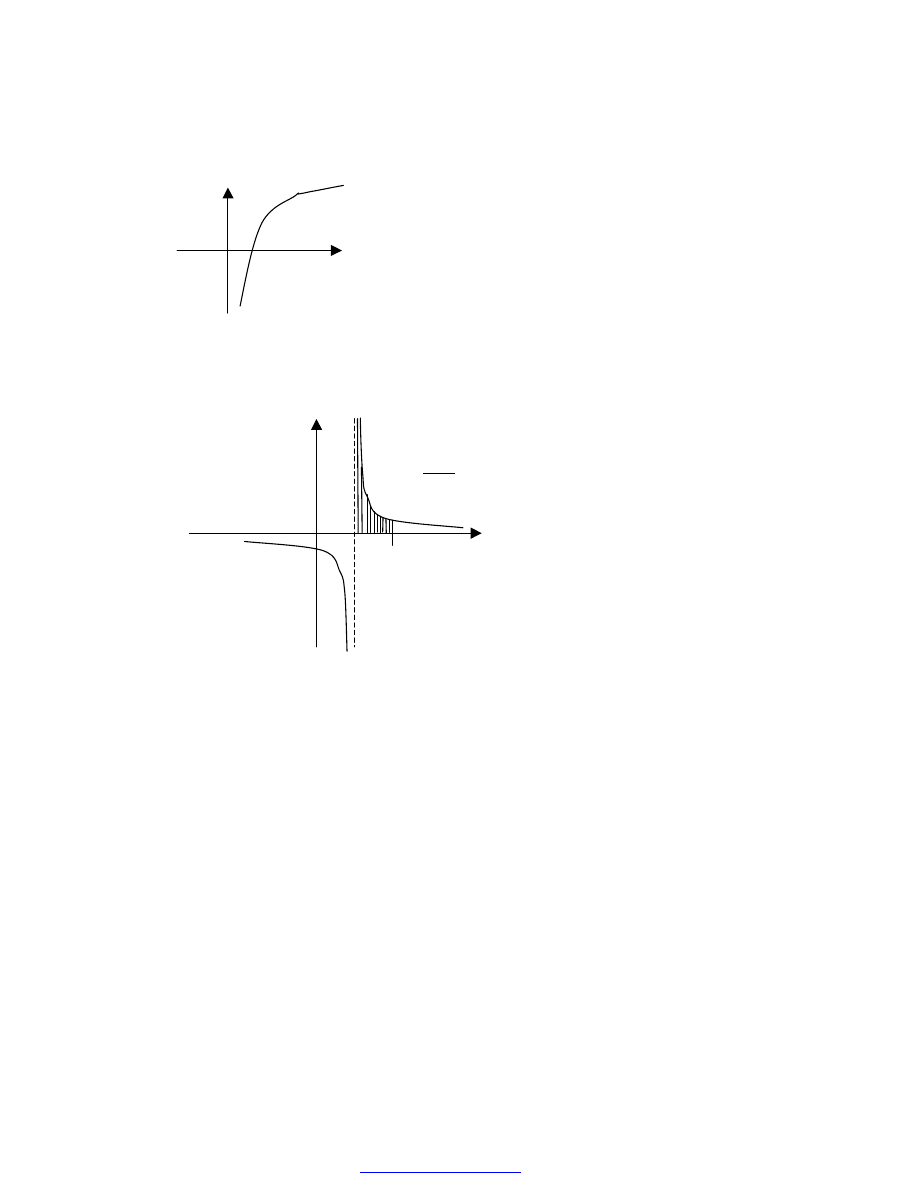
PRZYKŁAD 44
Obliczyć całkę niewłaściwą:
dx
x
∫
−
1
0
1
1
.
W tym przypadku funkcja podcałkowa jest nieograniczona w otoczeniu punktu x=1 l
[
]
[
]
( )
∞
=
∞
−
−
=
−
=
−
=
−
=
−
+
+
+
→
+
→
+
→
∫
∫
0
ln
lim
1
ln
1
ln
lim
1
1
lim
1
1
0
2
1
0
2
1
0
2
1
ε
ε
ε
ε
ε
ε
x
dx
x
dx
x
,
czyli całka jest rozbieżna, więc pole obszaru zaznaczonego na rysunku jest nieskończone.
Gdy
+
→
0
ε
, to
−∞
→
ε
ln
, co wynika z poniższego wykresu funkcji y=lnx:
a
c-
1
ε
y=f(x)
c
b
y=f(x)
c+
2
ε
0
1
→
ε
2
0
ε
←
a
b-
ε
y=f(x)
b
0
→
ε
a
b
y=f(x)
a+
ε
ε
←
0
PDF created with pdfFactory trial version
Opracowała: K. Sokołowska
55
Interpretacja geometryczna powyższej całki:
13.7.
Zastosowanie rachunku całkowego w ekonomii
•
Znajdowanie wielkości pierwotnych, mając dane wielkości krańcowe
PRZYKŁAD 45
Znaleźć funkcję kosztu całkowitego, jeżeli koszt krańcowy dla pewnej firmy jest następującą
funkcją wielkości produkcji (x):
( )
4
3
8
2
3
+
−
=
′
x
x
x
K
i jeżeli koszt stały jest równy 5 tys. zł.
Obliczamy:
-
całkę funkcji K’(x):
( )
(
)
C
x
x
x
dx
x
x
dx
x
K
+
+
−
=
+
−
=
′
∫
∫
4
2
4
3
8
3
4
2
3
-
otrzymaliśmy,
że
funkcja
kosztu
całkowitego
ma
postać:
( )
C
x
x
x
x
K
+
+
−
=
4
2
3
4
-
aby znaleźć wartość stałej C, wykorzystamy informację, że koszt stały jest
równy 5 tys. zł.
-
Mamy stąd
( )
5
5
0
4
0
0
2
5
0
3
4
=
⇒
=
+
⋅
+
−
⋅
⇔
=
C
C
K
-
Funkcja kosztu całkowitego przyjmuje więc postać:
( )
5
4
2
3
4
+
+
−
=
x
x
x
x
K
1
1 2
1
1
−
=
x
y
PDF created with pdfFactory trial version
Wyszukiwarka
Podobne podstrony:
Odpowiedzi calki biegunowe id Nieznany
LISTA 14 Całki krzywoliniowe
pochodne i całki
CALKI teoria
całki, szeregi zadania z kolosa wykład 21 03 2009
Calki i zakres 2012
CAŁKI
calki teoria zadania
Calki wzory podstawowe zadania
Całki Nieoznaczone
Matematyka Sem 2 Wykład Całki Powierzchniowe
Definicja całki nieoznaczonej i funkcji pierwotnej
Calki, IB i IS, 2011 12 id 1073 Nieznany
cw 13 Analiza Matematyczna (calki) id
BOM calki
4 calki
więcej podobnych podstron