WEKTORY

Współrzędne punktu w przestrzeni

W przestrzeni dany jest układ współrzędnych. Każdemu
punktowi odpowiada trójka liczb zwanych współrzędnymi
tego punktu.

Współrzędne punktu zapisujemy w nawiasach okrągłych
np.

)

4

,

3

,

5

(





P

.

Współrzędne wektora w przestrzeni

W przestrzeni dane są dwa punkty:

)

,

,

(

1

1

1

1

z

y

x

P



oraz

)

,

,

(

2

2

2

2

z

y

x

P



Wektor

]

,

,

[

1

2

1

2

1

2

2

1

z

z

y

y

x

x

P

P











Przykład 1. Dane są punkty:

)

3

,

2

,

4

(

1



P

,

)

2

,

5

,

1

(

2



P

Napisz współrzędne wektora



2

1

P

P

.

Rozwiązanie.

]

1

,

3

,

3

[

]

3

2

,

2

5

,

4

1

[

2

1

















P

P

Przykład 2. Dany jest punkt

)

5

,

0

,

4

(

2





P

i wektor

]

3

,

1

,

2

[

2

1







P

P

. Wyznacz punkt

1

P

.

Rozwiązanie. Oznaczmy:

)

,

,

(

1

z

y

x

P



.

Wówczas:

]

5

,

0

,

4

[

2

1

z

y

x

P

P













.

Zatem:

3

5

,

1

,

2

4

















z

y

x

Stąd:

8

,

1

,

6











z

y

x

Odpowiedź.

)

8

,

1

,

6

(

1







P

Długość wektora

Dany jest wektor

]

,

,

[

z

y

x

u

u

u

u





. Długość tego wektora

oznaczamy:

|

|



u

. Wyraża się ona wzorem:

2

2

2

|

|

z

y

x

u

u

u

u









Przykład 3. Dane są punkty:

)

1

,

0

,

2

(

1



P

,

)

2

,

3

,

4

(

2



P

Wyznacz długość wektora



2

1

P

P

.

Rozwiązanie. Napiszmy współrzędne wektora



2

1

P

P

:

]

1

,

3

,

2

[

]

1

2

,

0

3

,

2

4

[

2

1













P

P

Teraz obliczymy jego długość:

74

,

3

14

1

3

2

|

|

2

2

2

2

1













P

P

Dodawanie i odejmowanie wektorów, mnożenie wektora
przez liczbę

Działania te wykonujemy tak jak na macierzach (zapis
wektora traktujemy jak macierz jednowierszową).

Przykład 4. Dane są wektory:

]

2

,

1

,

3

[







u

,

]

0

,

2

,

1

[







v

Wyznacz wektor







v

u

3

2

.

Rozwiązanie.

]

4

,

4

,

3

[

]

0

,

6

,

3

[

]

4

,

2

,

6

[

]

0

,

2

,

1

[

3

]

2

,

1

,

3

[

2

3

2































v

u

Iloczyn skalarny wektorów

Dane są wektory:

]

,

,

[

z

y

x

u

u

u

u





,

]

,

,

[

z

y

x

v

v

v

v





Iloczyn skalarny tych wektorów jest to liczba





v

u 

z

z

y

y

x

x

v

u

v

u

v

u







Kąt między wektorami

Dane są wektory niezerowe



u

oraz



v

.

Cosinus kąta między nimi wyraża się wzorem:

|

|

|

|

)

,

(

cos



















v

u

v

u

v

u



Przykład 5. Oblicz cosinus kąta między wektorami

]

4

,

1

,

2

[







u

,

]

0

,

2

,

1

[







v

.

Rozwiązanie. Kolejno obliczamy:

8

1

4

2

)

1

(

3

2





















v

u 

21

4

)

1

(

2

|

|

2

2

2













u

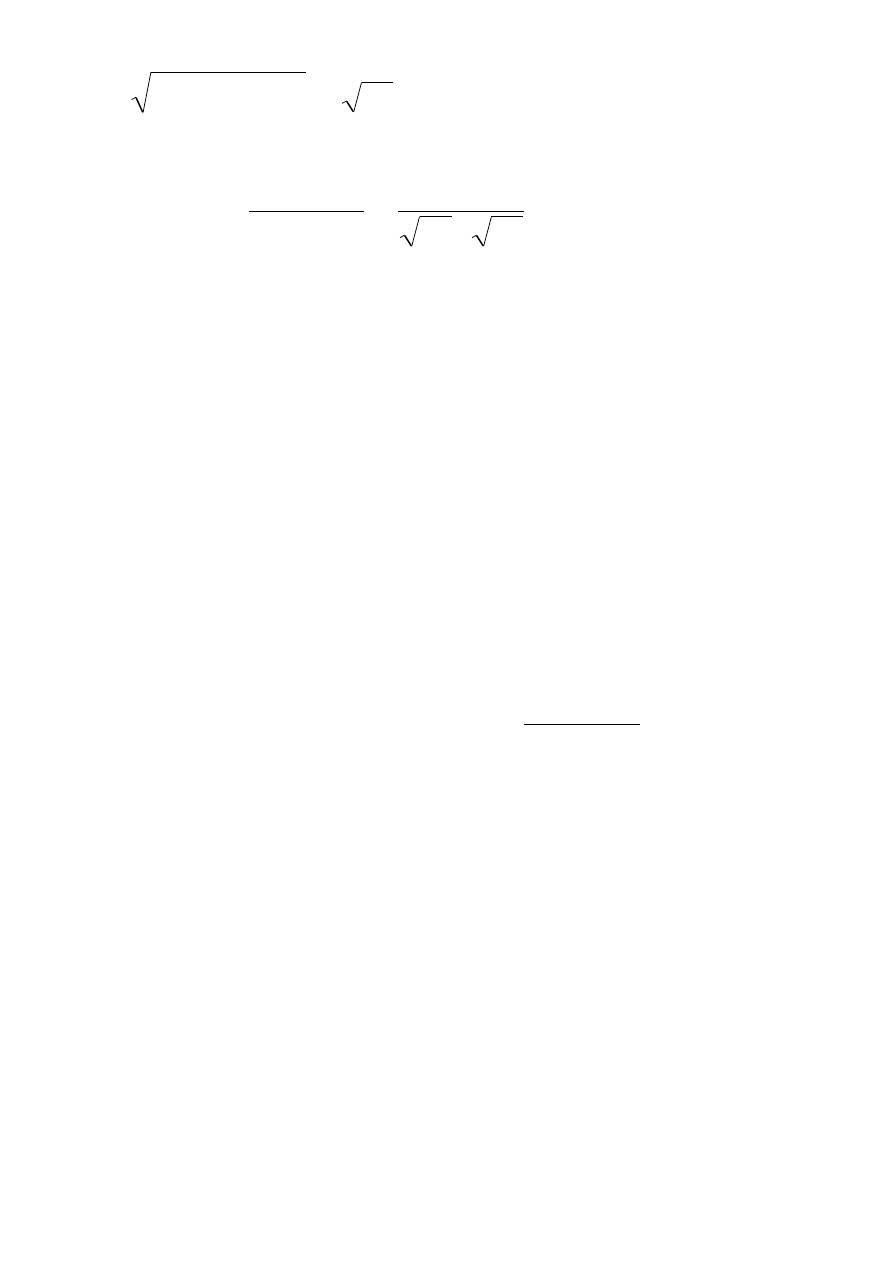
14

1

2

3

|

|

2

2

2











v

467

,

0

14

21

8

|

|

|

|

)

,

(

cos

























v

u

v

u

v

u



Za pomocą tablic lub kalkulatora możemy odczytać, że ten
kąt ma około 62 stopnie.

Twierdzenie. Wektory niezerowe



u

oraz



v

są

prostopadłe wtedy i tylko wtedy gdy

0







v

u 

Uzasadnienie. Wektory prostopadłe tworzą kąt 90

0

.

Cosinus 90

0

jest równy 0. Ułamek

|

|

|

|











v

u

v

u 

jest równy

zero gdy jego licznik jest równy zero, tzn. gdy

0







v

u 

.

Przykład 6. Dla jakich wartości k wektory

]

4

,

2

,

3

[







u

oraz

]

1

,

5

,

[k

v





są prostopadłe?

Rozwiązanie. Obliczamy iloczyn skalarny tych wektorów:

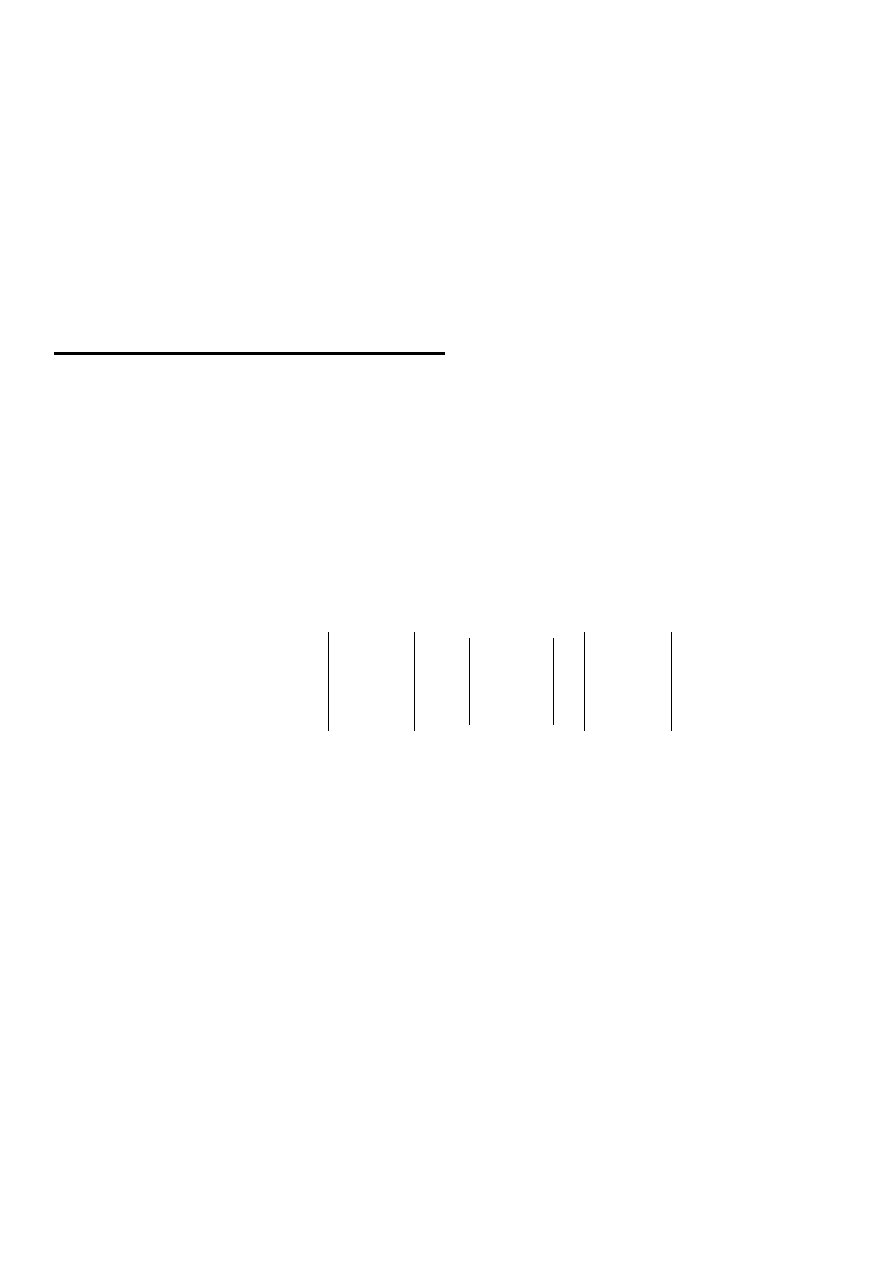
6

3

1

)

4

(

5

2

3























k

k

v

u 

i przyrównujemy go do zera:

0

6

3





k

.

Stąd:

2





k

.

Iloczyn wektorowy wektorów

Dane są wektory:

]

,

,

[

z

y

x

u

u

u

u





]

,

,

[

z

y

x

v

v

v

v





Iloczyn wektorowy tych wektorów jest to wektor



























y

x

y

x

z

x

z

x

z

y

z

y

v

v

u

u

v

v

u

u

v

v

u

u

v

u

,

,

Przykład 7. Wyznacz iloczyn wektorowy wektorów

]

4

,

1

,

2

[







u

,

]

0

,

2

,

1

[







v

.

Rozwiązanie. Dla wygody rachunkowej dobrze jest
zapisać te wektory jeden pod drugim:

]

4

,

1

,

2

[







u

]

0

,

2

,

1

[







v































2

1

1

2

,

0

1

4

2

,

0

2

4

1

v

u

=

]

3

,

4

,

8

[





Przykład 8. Oblicz iloczyn skalarny:

a) wektora



u

i wektora







v

u

z poprzedniego przykładu

b) wektora



v

i wektora







v

u

z poprzedniego

przykładu

Rozwiązanie.

a)

]

4

,

1

,

2

[







u

,









v

u

]

3

,

4

,

8

[









u

0

3

4

)

4

(

)

1

(

)

8

(

2

)

(



























v

u

Oznacza to, że wektory



u

oraz







v

u

są prostopadłe.

b)

]

0

,

2

,

1

[







v

,









v

u

]

3

,

4

,

8

[









v

0

3

0

)

4

(

2

)

8

(

)

1

(

)

(



























v

u

Oznacza to, że wektory



v

oraz







v

u

są prostopadłe.

Wynik tego przykładu nie jest przypadkowy. Prawdziwe
jest bowiem twierdzenie:

Wektor







v

u

jest prostopadły zarówno do wektora



u

jak i do wektora



v

.

Równanie płaszczyzny

Równanie postaci

0









D

Cz

By

Ax

, w którym

D

C

B

A

,

,

,

są liczbami, przedstawia płaszczyznę

(przynajmniej jedna z tych liczb musi być różna od zera).

Przykład 9. Sprawdź, czy punkt (4, -1, 2) należy do
płaszczyzny

0

2

3

2









z

y

x

.

Rozwiązanie. Do równania płaszczyzny wstawiamy

2

,

1

,

4









z

y

x

.

Dostajemy:

0

5

2

2

)

1

(

3

4

2

















, co oznacza, że

punkt nie należy do płaszczyzny.

Twierdzenie. Wektor

]

,

,

[

C

B

A

N





jest prostopadły do

płaszczyzny o równaniu

0









D

Cz

By

Ax

.

Przykład 10. Napisać równanie płaszczyzny prostopadłej

do wektora

]

1

,

3

,

2

[







N

i przechodzącej przez punkt

(3,5,0).

Rozwiązanie. Do równania płaszczyzny

0









D

Cz

By

Ax

wstawiamy

1

,

3

,

2









C

B

A

.

Dostajemy równanie

0

3

2









D

z

y

x

. Trzeba znaleźć

D. Ponieważ punkt (3, 5, 0) ma leżeć na tej płaszczyźnie,
więc musi spełniać jej równanie. Wstawiamy

0

,

5

,

3







z

y

x

i mamy:

0

0

5

3

3

2













D

, stąd

9



D

.

Odpowiedź:

0

9

3

2









z

y

x

.

Przykład 11. Napisz równanie płaszczyzny przechodzącej
przez punkty

)

2

,

2

,

2

(

),

4

,

1

,

3

(

),

0

,

1

,

2

(







C

B

A

.

Rozwiązanie. Wyznaczymy wektor



N

prostopadły do

szukanej płaszczyzny. W tym celu najpierw napiszemy
współrzędne wektorów:

]

4

,

0

,

1

[

]

0

4

,

1

1

,

2

3

[













AB

]

2

,

1

,

0

[

]

0

2

,

1

2

,

2

2

[













AC

.

Jak wiemy iloczyn wektorowy tych wektorów jest do nich
obu prostopadły. Zatem:

]

1

,

2

,

4

[

1

0

0

1

,

2

0

4

1

,

2

1

4

0

































AC

AB

N

Szukana płaszczyzna ma więc równanie postaci:

0

2

4











D

z

y

x

. Wstawimy do tego równania

współrzędne jednego z danych punktów, np. punktu A.
Dostaniemy:

0

0

1

2

2

4















D

, stąd

10



D

.

Odpowiedź:

0

10

2

4











z

y

x

.

Ćwiczenie. Sprawdź samodzielnie, że punkty A, B, C
istotnie należą do wyznaczonej płaszczyzny.