Politechnika Śląska
Wydział Mechaniczny-Technologiczny
Mechanika i Budowa Maszyn
Rok akademicki 2013/2014
DRGANIA W UKŁADACH FIZYCZNYCH
Sprawozdanie z tematu:
Analiza układu o wielu stopniach swobody
Opracowali:
1. Robert Drewniok
2. Paweł Imiołczyk
3. Andrzej Jałowiecki
4. Michał Sierżant
5. Jakub Szafrański
6. Łukasz Zub
Strona 2 z 10
Spis treści
Strona 3 z 10
1. Wstęp teoretyczny
Układ o skończonej liczbie stopni swobody przedstawiany jest, jako zbiór punktów materialnych
połączonych bez masowymi sprężynami i tłumikami. Rozważane układy liniowe w praktyce
inżynierskiej to najczęściej takie, w których siły sprężyste i tłumienia są liniowymi funkcjami
przemieszczeń i prędkości punktów materialnych. Są to układy holonomiczne, a liczba stopni swobody
równa się liczbie współrzędnych uogólnionych. Współrzędne uogólnione są przesunięciami lub kątami
obrotu mas.
Analiza częstości własnych
Równanie ruchu drgań własnych otrzymuje się z równania ruchu po pominięciu członu
zawierającego macierz tłumienia oraz wektor obciążeń zewnętrznych. Wówczas otrzymuje się:
[𝑀] ∙ [𝐴] + [𝐶] ∙ [𝑋] = 0 (1.1)
gdzie:
[M] – macierz mas układu
[A] – macierz przyśpieszeń
[C] – macierz sztywności
[X] – macierz przemieszczeń
0 – macierz zerowa
Rozwiązanie dla zadanego zagadnienia początkowego polega na podaniu warunków, dla których
jest możliwy ruch rozpatrywanego układu. Przez analogię z układem o jednym stopniu swobody
założymy, że drgania własne są ruchem harmonicznym i rozwiązania poszukujemy w postaci funkcji
harmonicznych o częstościowości ω i fazie początkowej ϕ.
𝑥(𝑡) = 𝑞⃗𝑠𝑖𝑛(𝜔𝑡 + 𝜑)
(1.2)
gdzie: 𝑞⃗ – jest wektorem amplitud drgań własnych.
Po podstawieniu wyrażenia (1.2) i jego drugiej pochodnej do równania (1.1) otrzymujemy:
(−𝜔
2
∙ [𝑀] + [𝐶]) ∙ 𝑞⃗ ∙ sin(𝜔𝑡 + 𝜑) = 0
Jest to układ liniowych jednorodnych równań algebraicznych, który ma rozwiązania niezerowe tylko
wówczas, gdy:
det([𝐶] − 𝜔
2
[𝑀]) = 0
Strona 4 z 10
Po rozwinięciu tego wyznacznika otrzymuje się wielomian n-tego stopnia względem ω
2
(dla układu
mającego n dynamicznych stopni swobody). Równanie to nazywa się równaniem charakterystycznym
zagadnienia własnego lub równaniem częstości. Pierwiastki tego równania są częstościami drgań
własnych elementów układu.
Strona 5 z 10
2. Obliczenia
DANE:
m
1
= 1kg
m
2
= 2kg
m
3
= 3kg
C
1
= 10N*m
C
2
= 20N*m
C
3
= 30N*m
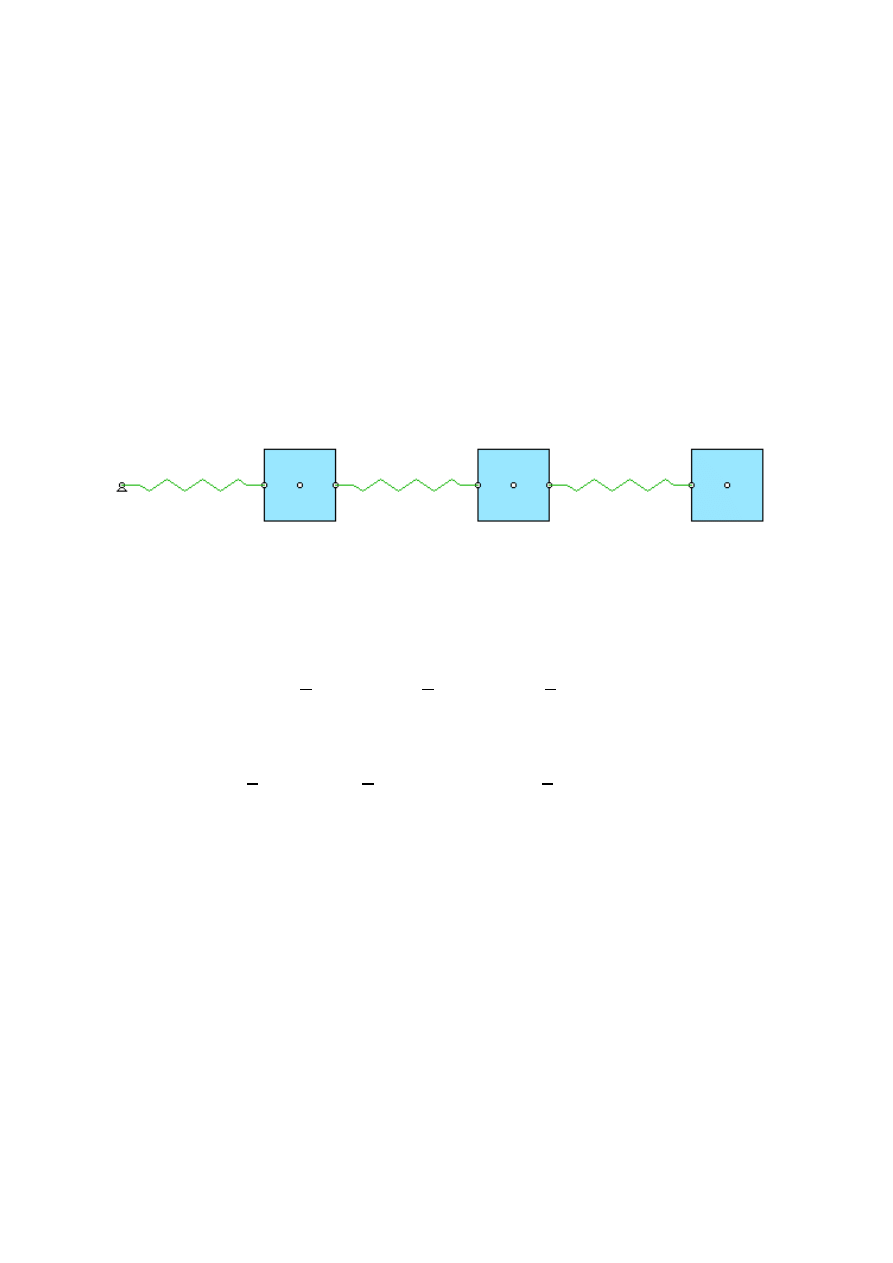
Rys 1. Analizowany układ
𝐸
𝑘
=
1
2
∙ 𝑚
1
∙ 𝑥
1
2
̈ +
1
2
∙ 𝑚
2
∙ 𝑥
2
2
̈ +
1
2
∙ 𝑚
3
∙ 𝑥
3
2
̈
𝐸
𝑝
=
1
2
∙ 𝐶
1
∙ 𝑥
1
2
+
1
2
∙ 𝐶
2
∙ (𝑥
1
− 𝑥
2
)
2
+
1
2
∙ 𝐶
3
∙ (𝑥
2
− 𝑥
3
)
2
Równania Lagrange’a II stopnia:
𝑚
1
∙ 𝑥
1
+
̈
𝐶
1
∙ 𝑥
1
+ 𝐶
2
∙ (𝑥
1
− 𝑥
2
) = 0
𝑚
2
∙ 𝑥
2
−
̈
𝐶
2
∙ (𝑥
1
− 𝑥
2
) + 𝐶
3
∙ (𝑥
2
− 𝑥
3
) = 0
𝑚
3
∙ 𝑥
3
−
̈
𝐶
3
∙ (𝑥
2
− 𝑥
3
) = 0
W zapisie macierzowym:
[
𝑚
1
0
0
0
𝑚
2
0
0
0
𝑚
3
] ∙ [
𝑥
1
̈
𝑥̈
2
𝑥̈
3
] + [
(𝐶
1
+ 𝐶
2
)
−𝐶
2
0
−𝐶
2
(𝐶
2
+ 𝐶
3
) −𝐶
3
0
−𝐶
3
𝐶
3
] ∙ [
𝑥
1
𝑥
2
𝑥
3
] = [
0
0
0
]
m
1
m
2
m
3
C
1
C
2
C
3
Strona 6 z 10
Lub w skrócie:
[𝑀] ∙ [𝐴] + [𝐶] ∙ [𝑋] = 0
Po podstawieniu wartości otrzymujemy:
[
1 0 0
0 2 0
0 0 3
] ∙ [
𝑥
1
̈
𝑥̈
2
𝑥̈
3
] + [
30
−20
0
−20
50
−30
0
−30
30
] ∙ [
𝑥
1
𝑥
2
𝑥
3
] = [
0
0
0
]
Następie tworzymy macierz dynamiczną H:
[𝐻] = [𝑀]
−1
∙ [𝐶]
Po podstawieniu
[𝐻] = [
30
−20
0
−10
25
−15
0
−10
10
]
Następnie tworzymy wyznacznik i przyrównujemy go do 0
𝑑𝑒𝑡 = [
ℎ
11
∙ 𝜔
2
ℎ
12
ℎ
13
ℎ
21
ℎ
22
∙ 𝜔
2
ℎ
23
ℎ
31
ℎ
32
ℎ
33
∙ 𝜔
2
] = 0
Po wstawieniu wartości otrzymujemy:
𝑑𝑒𝑡 = [
30 ∙ 𝜔
2
−20
0
−10
25 ∙ 𝜔
2
−15
0
−10
10 ∙ 𝜔
2
] = 0
Po rozpisaniu wyznacznika otrzymujemy:
(30𝜔
2
∙ 25𝜔
2
∙ 10𝜔
2
) − (30𝜔
2
∙ −15 ∙ −10) − (−20 ∙ −10 ∙ 10𝜔
2
) = 0
7500𝜔
6
− 6500𝜔
2
= 0
𝜔
6
−
15
13
𝜔
2
= 0
Strona 7 z 10
Pierwiastki tego równania są szukanymi częstościami drgań własnych
𝜔 = [
−1,036
0
1,036
]
Jak można zauważyć układ posiada tak naprawdę tylko jedną częstość drgań własnych
równą 1,036 rad/s.
Strona 8 z 10
3. Symulacja układu
Mając obliczoną częstość drgań własnych układu zamodelowano układ tak ja na Rys 1. i wprowadzono
wymuszenie o częstotliwości rezonansowej i otrzymano następujące wykresy przemieszczeń mas:
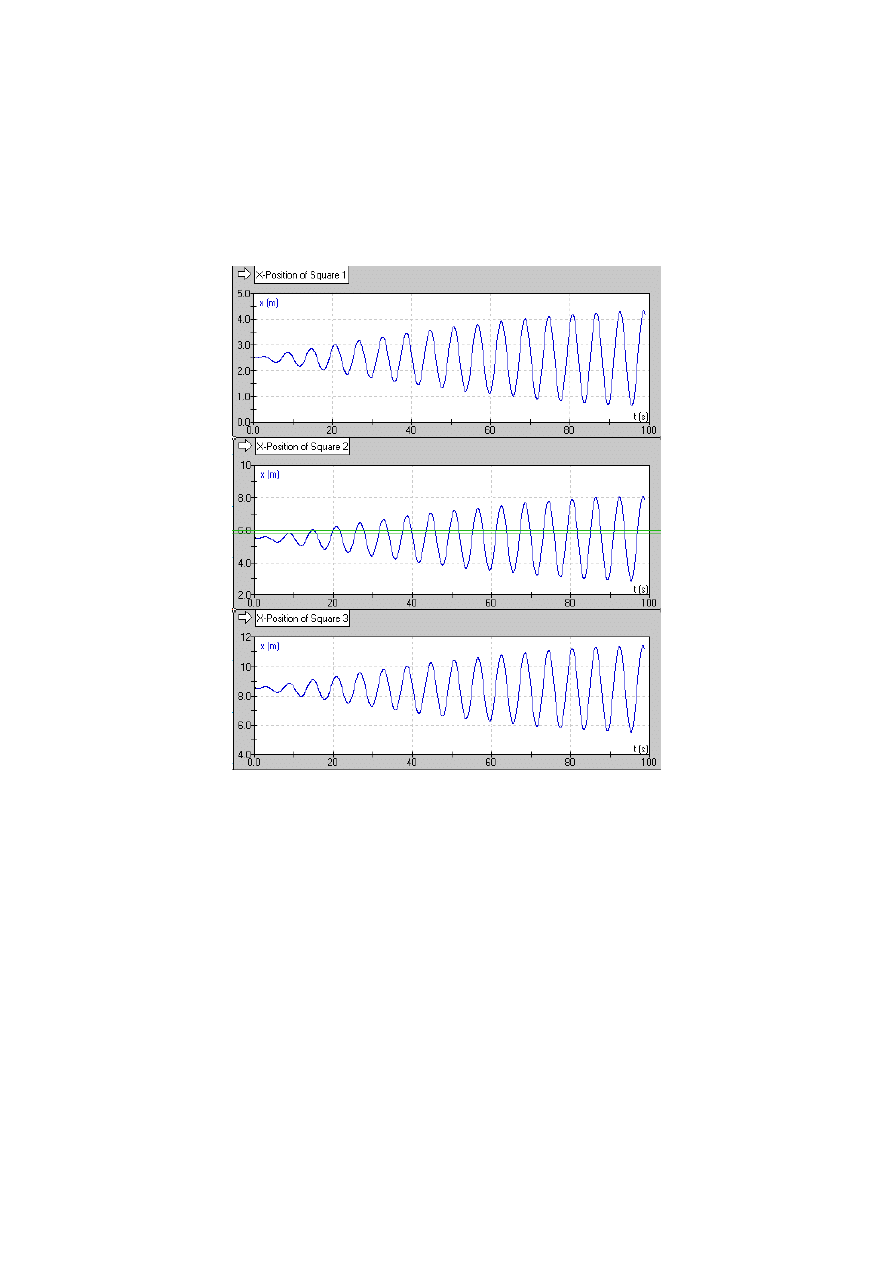
Rys 2. Wykresy przemieszczeń mas. Od góry masa 1, masa 2, masa 3
Jak widać dla wyliczonej częstości drgań własnych układ wpada w rezonans. Amplituda wychylenia dla
każdej masy stopniowo wzrasta. Niezależnie od miejsca przyłożenia wymuszenia układ zachowuje się
identycznie tj.: wszystkie masy drgają w tym samym kierunku (drgania współbieżne).
Strona 9 z 10
Następnie w układzie zastąpiono sprężynę 3 modelem Kelwina-Fojta i ponownie poddano symulacji.
Otrzymane wykresy zamieszczono poniżej:
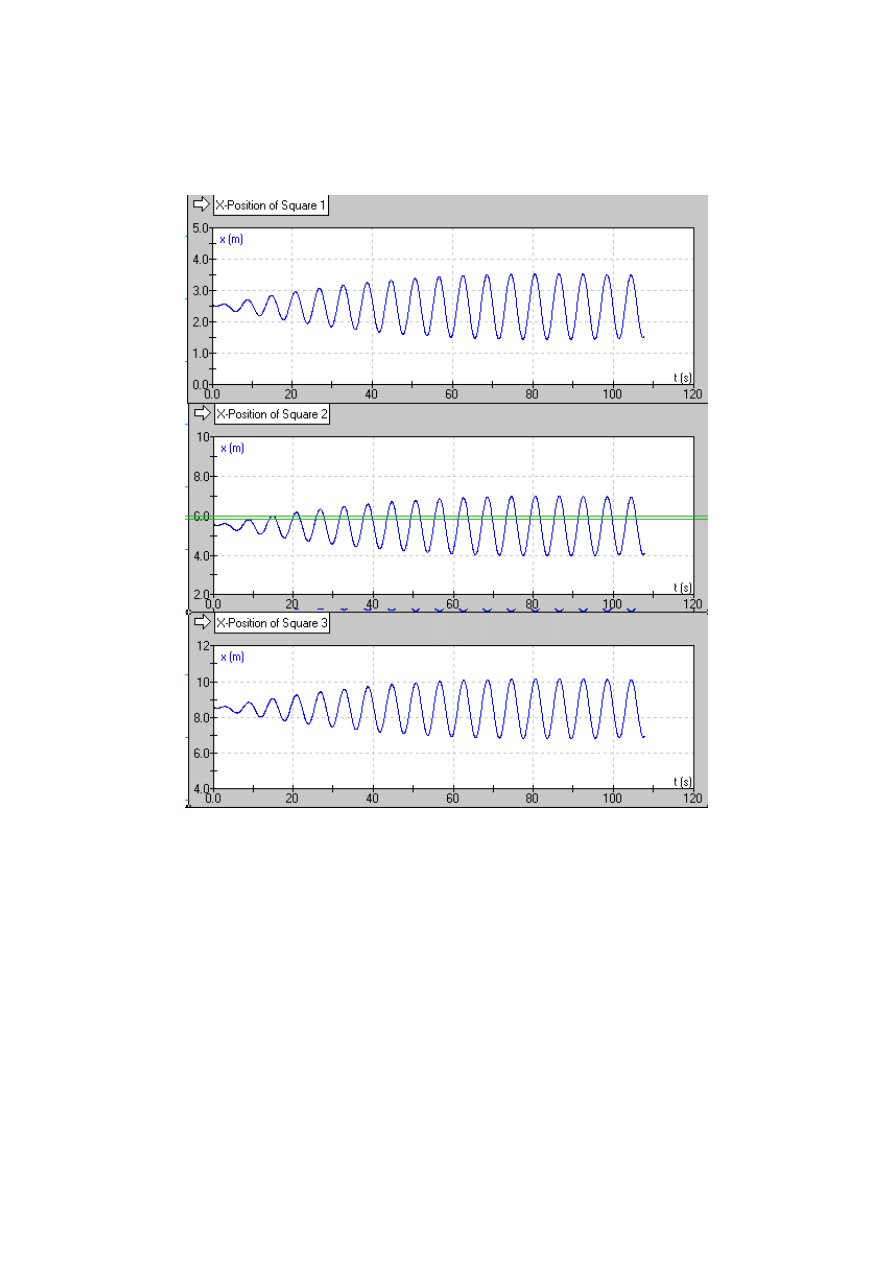
Rys 3. Wykresy przemieszczeń mas po wprowadzeniu tłumienia. Od góry masa 1, masa 2, masa 3.
Jak można zauważyć wprowadzenie do układu elementu tłumiącego powoduje ustabilizowanie się
drgań po pewnym czasie i nie wpadanie układu w rezonans. W tym przypadku zastosowano tłumienie
wiskotyczne, lecz równie dobrze można by zastosować tłumienie tarciem suchym, które dało by ten
sam efekt.
Strona 10 z 10
4. Wnioski końcowe
Analiza układów o wielu stopniach swobody sprowadza się głównie do wyznaczenia równania
charakterystycznego za pomocą, którego jesteśmy w stanie określić częstości drgań własnych
poszczególnych elementów masowych układu. Zagadnienie to staje się coraz bardziej złożone w raz ze
wzrostem stopni swobody i bez stosowania metod numerycznych i komputerów do wspomagania się
w obliczeniach jest to praktycznie nie wykonalne, aby przeprowadzić takową analizę.
Podsumowując przeprowadzone rozważania na temat układów o wielu stopniach swobody można
zauważyć, że w przypadku układu o trzech stopniach swobody mamy do czynienie tylko z jedną
częstością drgań wlanych. Ponadto stosując w układzie jakikolwiek rodzaj tłumienia czy to
wiskotycznego czy suchego stabilizujemy drgania i nie dopuszczamy do sytuacji, w której układ wpada
w niebezpieczny rezonans.