2011-10-05

Z.Kasperski, wykłady, t2.

1

Z.Kasperski- wyklady, t.2

1

Z.Kasperski- wyklady, t.2

Historia liczb

30 000 p.n.e.

Obecność nacięć numerycznych

3300 p.n.e

Pierwsze cyfry w Sumerze i Elamie. Pojawienie hieroglifów egipskich -

pierwsza numeracja pisma

2700 p.n.e

Sumeryjckie cyfry klinowe

2600 p.n.e

Pojawienie się cyfr egipskich

2000 p.n.e

Pojawienie się bazy dziesiętnej

1800 p.n.e

Numeracja babilońska - pierwsza numeracja pozycyjna

1300 p.n.e

Pojawienie się cyfr chińskich

VI w. p.n.e

Odkrycie wartości niewymiernych. Pitagoras

III w. p.n.e

Grecka numeracja alfabetyczna

Pojawienie się zera w numeracji babilońskiej

II w. p.n.e

Chińska numeracja pozycyjna bez zera

Pojawienie się cyfr brahmi - indyjskich

IV w. n.e

Indyjska numeracja pozycyjna. Numeracja dziesiętna z zerem.

V w. n.e

Numeracja pozycyjna Majów z zerem

VIII w. n.e

Wprowadzenie indyjskiej dziesiętnej numeracji pozycyjnej i zera na ziemiach

islamu.

XII w.

Wprowadzenie znaku zero na Zachodzie

XIII w.

Pojawia się pojęcie ciągu. Fibonacci

XV w.

Cyfry indyjsko-arabskie uzyskują formę graficzną i rozpowszechniają się na

Zachodzie

XVI w.

Początki używania ułamków okresowych. Bombelli.

Bombelli i Cardan formuują pojęcie liczb zespolonych

Z.Kasperski- wyklady, t.2

2

LICZBY ZESPOLONE

HISTORIA

I.

-

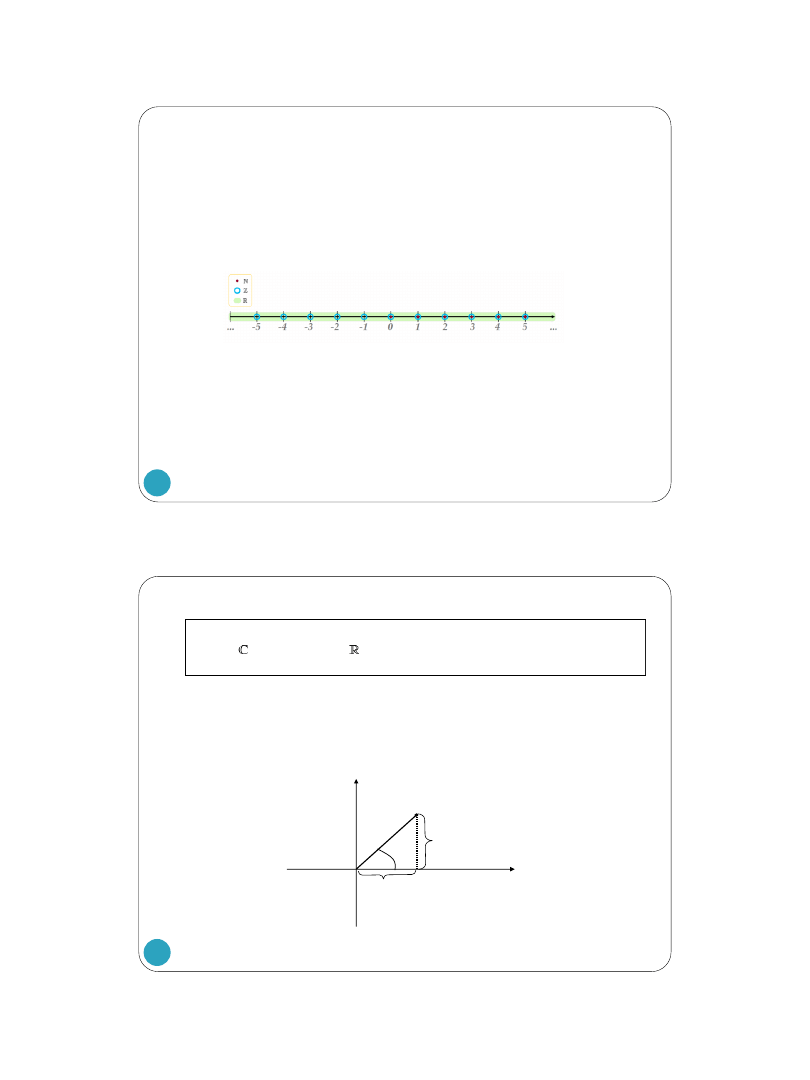
zbiór liczb naturalnych (z ang. natural, naturalny): {1, 2, 3 … },

II.

-

zbiór liczb całkowitych (z niem. Zahlen, liczby): {…, -2, -1, 0,

1, 2,…},

III.

-

zbiór liczb wymiernych (z ang. quotient, iloraz) :

= {𝑥: 𝑥 =

𝑝
𝑞

, 𝑝, 𝑞 ∈ 𝑍},

IV.

-

zbiór liczb niewymiernych, np. 2, 3, π=3,141592654…,

V.

-

zbiór liczb rzeczywistych (z ang. real, rzeczywisty): =

∪

,

VI.

oraz nowo poznawany

– - zbiór liczb zespolonych (z ang.

complex

, złożenie),

2011-10-05

Z.Kasperski, wykłady, t2.

2

ILUSTRACJA GRAFICZNA

Z.Kasperski- wyklady, t.2

3

Z.Kasperski- wyklady, t.2

4

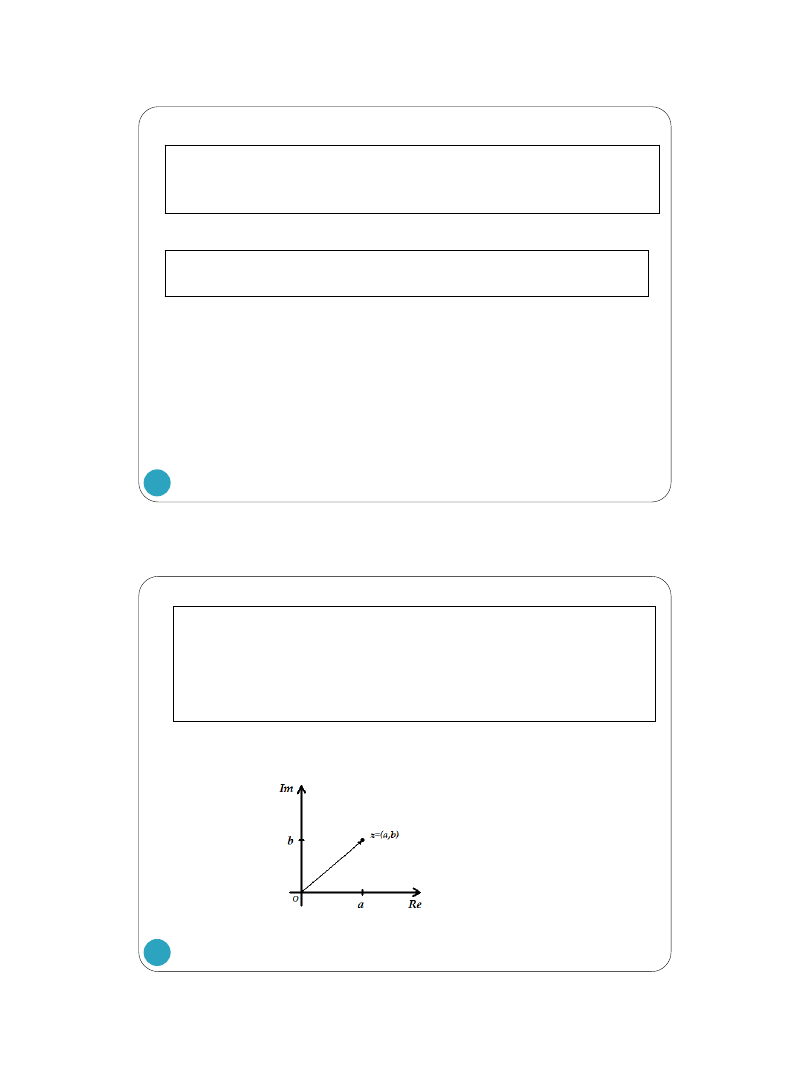
Def.1. Liczbą zespoloną nazywamy uporządkowaną parę liczb rzeczywistych (a, b), czyli

=

𝑧 =

𝑎, 𝑏

: 𝑎, 𝑏 ∈

.

INTERPRETACJA GEOMETRYCZNA

y

x

a

b

M(a,b)

2011-10-05

Z.Kasperski, wykłady, t2.

3

Z.Kasperski- wyklady, t.2

5

PRZYKŁAD 1. Narysować na płaszczyźnie liczby z

1

= (3, 2); z

2

= (-3, 1).

Def.2. Niech

𝑧

1

= (𝑎

1

, 𝑏

1

), 𝑧

2

= (𝑎

2

, 𝑏

2

).

W

ówczas

𝑧

1

= 𝑧

2

⟺ (

𝑎

1

= 𝑎

2

) ∧ (𝑏

1

= 𝑏

2

)

𝑧

1

+

𝑧

2

= 𝑎

1

+ 𝑎

2

, 𝑏

1

+ 𝑏

2

𝑧

1

∙

𝑧

2

= 𝑎

1

𝑎

2

− 𝑏

1

𝑏

2

, 𝑎

1

𝑏

2

+ 𝑎

2

𝑏

1

𝑧 ∙ 𝑧 … ∙ 𝑧 = 𝑧

𝑛

.

n razy

PRZYKŁAD 2. Niech

𝑧

1

= 0, 1 , 𝑧

2

= (3, −4).

Znaleźć

𝑧

1

+

𝑧

2

, 𝑧

1

∙ 𝑧

2

, 𝑧

2

2

.

Z.Kasperski- wyklady, t.2

6

WŁASNOŚCI:

1)

𝑧

1

+

𝑧

2

= 𝑧

2

+ 𝑧

1

,

2) 𝑧

2

= 𝑧

2

∙ 𝑧

1

,

3) 𝑧

1

+ 𝑧

2

+ 𝑧

3

= 𝑧

1

+ 𝑧

2

+ 𝑧

3

4) 𝑧

1

∙ (𝑧

2

∙ 𝑧

3

) = (𝑧

1

∙ 𝑧

2

)

∙ 𝑧

3

,

5) 𝑧

1

∙

𝑧

2

+ 𝑧

3

= 𝑧

1

∙ 𝑧

2

+ 𝑧

1

𝑧

3

.

Def.3. Dla dowolnych

𝑧

1

, 𝑧

2

∈ 𝐶 𝑧

1

− 𝑧

2

= 𝑧 ⟺ 𝑧

1

= 𝑧 + 𝑧

2

,

𝑧

1

𝑧

2

= 𝑧 ⟺ 𝑧

2

∙ 𝑧 = 𝑧

1

2011-10-05

Z.Kasperski, wykłady, t2.

4

Z.Kasperski- wyklady, t.2

7

Oznaczmy:

0

=(0, 0);

1

= (1, 0)

– odpowiednio zero i jedynka. Wówczas

Dla dowolnego z,

z+

0

= z; z

.

1

= z; z

.

0

=

0

.

Tw.1. Niech

𝑧

1

= (𝑎

1

, 𝑏

1

), 𝑧

2

= (𝑎

2

, 𝑏

2

).

Wówczas

𝑧

1

− 𝑧

2

= 𝑎

1

− 𝑎

2

, 𝑏

1

− 𝑏

2

,

𝑧

1

𝑧

2

=

𝑎

1

𝑎

2

+𝑏

1

𝑏

2

𝑎

2

2

+𝑏

2

2

,

𝑎

2

𝑏

1

−𝑎

1

𝑏

2

𝑎

2

2

+𝑏

2

2

,

dla

𝑧

2

≠

0

.

PRZYKŁAD 3. Niech z

1

=(3, 2), z

2

= (-

3, 1). Znależć z

1

- z

2

oraz

𝑧

1

𝑧

2

𝑧

1

∙

𝑧

2

= 𝑎

1

𝑎

2

− 𝑏

1

𝑏

2

, 𝑎

1

𝑏

2

+ 𝑎

2

𝑏

1

SZKIC DOWODU

Tu proszę poprawić!!!

Z.Kasperski- wyklady, t.2

8

Niech

𝐾 = 𝑧 = 𝑥, 0 ; 𝑥 ∈ 𝑅 . Z def.3 i tw.1 wynika:

(

𝑥

1

, 0) + 𝑥

2

, 0 = 𝑥

1

+ 𝑥

2

, 0 ,

(

𝑥

1

, 0) ∙ 𝑥

2

, 0 = 𝑥

1

∙ 𝑥

2

, 0 ,

(

𝑥

1

, 0) − 𝑥

2

, 0 = 𝑥

1

− 𝑥

2

, 0 ,

(𝑥

1

,0)

(𝑥

2

,0)

=

𝑥

1

𝑥

2

, 0 ,

dla

𝑥

2

≠ 0.

WNIOSEK: K = R, czyli z =(x, 0) = x

∈ 𝑅

2011-10-05

Z.Kasperski, wykłady, t2.

5

Z.Kasperski- wyklady, t.2

9

Def.4. Liczbę zespoloną (0, 1) nazywamy jednostką urojoną i oznaczamy przez i,
czyli

i = (0, 1).

WŁASNOŚD:

i

2

= -1

– dowód z def. iloczynu

Tw.2. Każdą liczbę zespoloną z = (a, b) można jednoznacznie zapisad w tzw.
postaci algebraicznej

z = a + ib.

D-d. . . . . . . .

Z.Kasperski- wyklady, t.2

10

Def.5. Niech z = a + ib. Wówczas :

a= Re z (częśd rzeczywista: realis),

b = Im z (częśd urojona : imaginalis),

Liczby postaci z= (0, b) = ib noszą nazwę czysto urojonych, a osie Ox i Oy układu
współrzędnych nazywamy odpowiednio osią rzeczywistą i urojoną.

2011-10-05

Z.Kasperski, wykłady, t2.

6

Z.Kasperski- wyklady, t.2

11

OPERACJE NA LICZBACH W POSTACI ALGEBRAICZNEJ.

PRZYKŁAD 4. Niech z

1

= 1 + 2i ; z

2

= -3 + 4i.

Znaleźć z

1

+ z2; z1- z

2

;

z

1

.

z

2

;

𝑧

1

𝑧

2

.

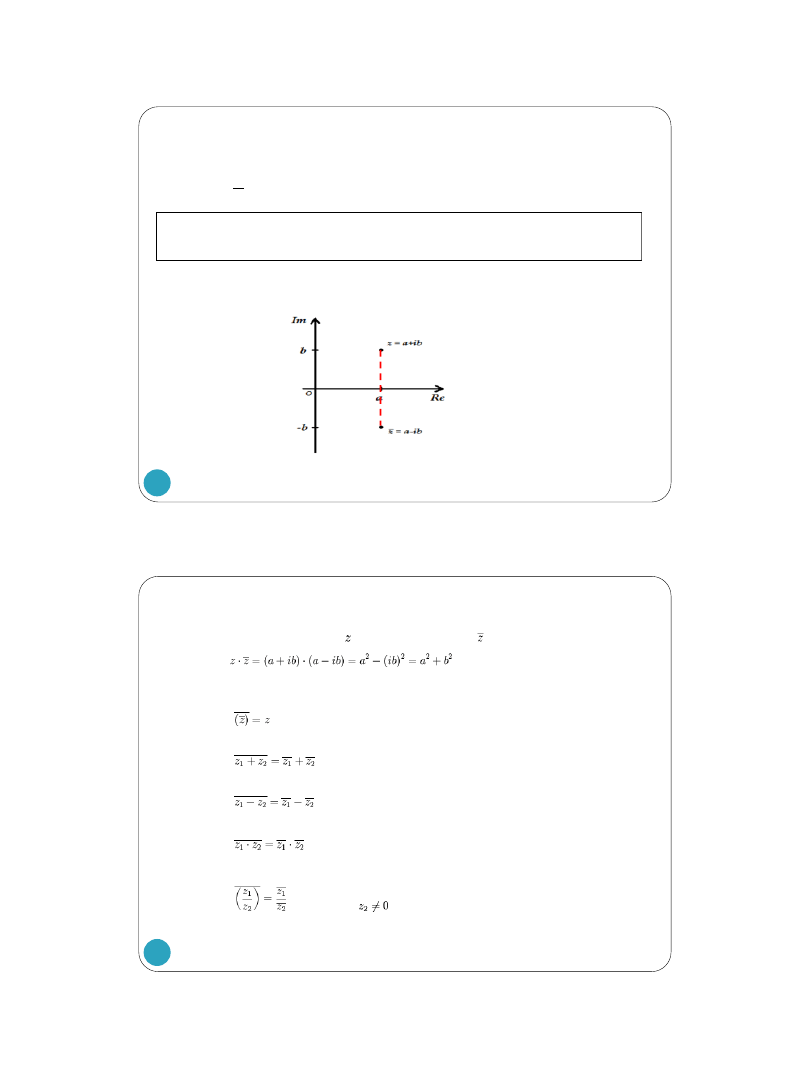
Def.6. Sprzężeniem liczby zespolonej z = a + ib nazywamy liczbę

𝑧 = a – ib.

INTERPRETACJA GEOMETRYCZNA ( symetria względem osi Re ).

Z.Kasperski- wyklady, t.2

12

WŁASNOŚCI

1. Iloczyn liczby zespolonej i liczby do niej

sprzężonej :

,

2.

Sprzężenie liczby sprzężonej:

,

4.

Sprzężenie różnicy jest różnicą sprzężeń:

,

5.

Sprzężenie iloczynu jest iloczynem sprzężeń:

,

6.

Sprzężenie ilorazu jest ilorazem sprzężeń:

, zakładając że

,

3.

Sprzężenie sumy jest sumą sprzężeń:

,

2011-10-05

Z.Kasperski, wykłady, t2.

7

Z.Kasperski- wyklady, t.2

13

Def.7. Modułem liczby zespolonej z = a + ib nazywamy liczbę rzeczywistą

r

=

.

WŁASNOŚCI:

1.

Moduł liczby zespolonej , sprzężonej , i przeciwnej

:

,

2.

Kwadrat modułu liczby zespolonej:

,

3.

Moduł iloczynu liczb zespolonych:

,

4.

Moduł ilorazu liczb zespolonych:

, o ile

.

Z.Kasperski- wyklady, t.2

14

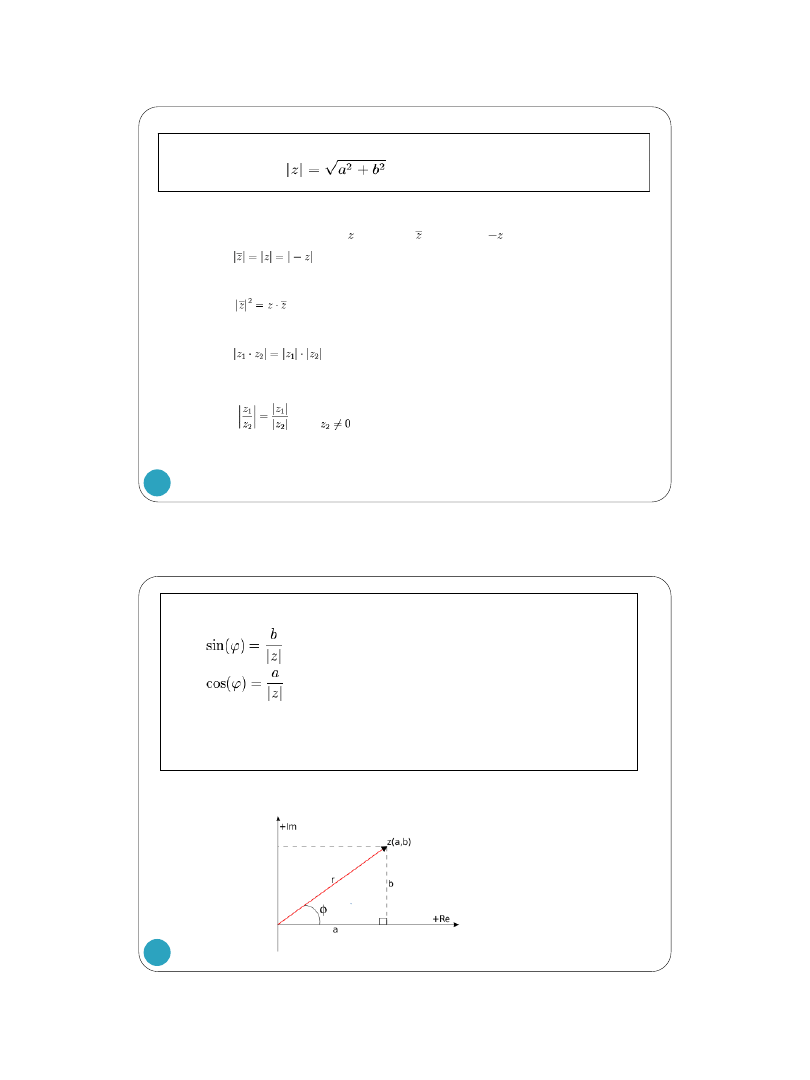
Def.8. Argumentem liczby zespolonej z = a + ib nazywamy liczbę (miarę kąta)

𝜑 taką, że

Argumentem głównym nazywa się ten z argumentów, który spełnia warunek 0 ≤ 𝜙 < 2𝜋.
Argument główny oznaczamy przez arg z.

(dodatkowo przyjmujemy, że dla z =0,

𝜑=0).

|z|

2011-10-05

Z.Kasperski, wykłady, t2.

8

Z.Kasperski- wyklady, t.2

15

PRZYKŁAD 5. Znaleźć argument główny liczby z= 3 – 3i.

Tw.3. Każdą liczbę zespoloną możemy przedstawić w postaci
trygonometrycznej:

𝑧 = 𝑧 𝑐𝑜𝑠𝜑 + 𝑖𝑠𝑖𝑛𝜙 .

D-

d……..

PRZYKŁAD 6. Liczbę zespoloną z = 1 + i przedstawić w postaci
trygonometrycznej.

Z.Kasperski- wyklady, t.2

16

Własności postaci trygonometrycznej



Dwie liczby zespolone są równe, jeśli ich moduły są równe:

oraz argument jednej jes

t wielokrotnością drugiej,

postaci:

.



Mnożenie liczb zespolonych

oraz

ma postać:

(

przy mnożeniu liczb zespolonych ich moduły mnożymy, a

argumenty dodajemy)



Dzielenie liczb zespolonych

oraz

ma postać:

(przy dzieleniu liczb zesp

olonych ich moduły dzielimy, a argumenty

odejmujemy )

2011-10-05

Z.Kasperski, wykłady, t2.

9

Z.Kasperski- wyklady, t.2

17

Tw.4. (wzór de Moivre’a). Jeżeli

𝑧 = 𝑧 𝑐𝑜𝑠𝜑 + 𝑖𝑠𝑖𝑛𝜙 , to

))

sin(

)

(cos(





n

i

n

z

z

n

n





.

PRZYKŁAD 7. Obliczyć ( 1 + i )

10

.

Z.Kasperski- wyklady, t.2

18

Def.9. Pierwiastkiem stopnia n z liczby zespolonej z nazywamy liczbę zespoloną x
spełniającą równanie x

n

= z.

Tw.5. Każda liczba zespolona

=

𝑧 = 𝑧 𝑐𝑜𝑠𝜑 + 𝑖𝑠𝑖𝑛𝜑

ma dokładnie n pierwiastków stopnia n. Zbiór tych pierwiastków ma postad

𝑧

𝑛

= {𝑥

0

, 𝑥

1

, … , 𝑥

𝑛−1

},

gdzie

.

1

,

...

,

1

,

0

,

2

sin

2

cos



























n

k

n

k

i

n

k

z

x

n

k









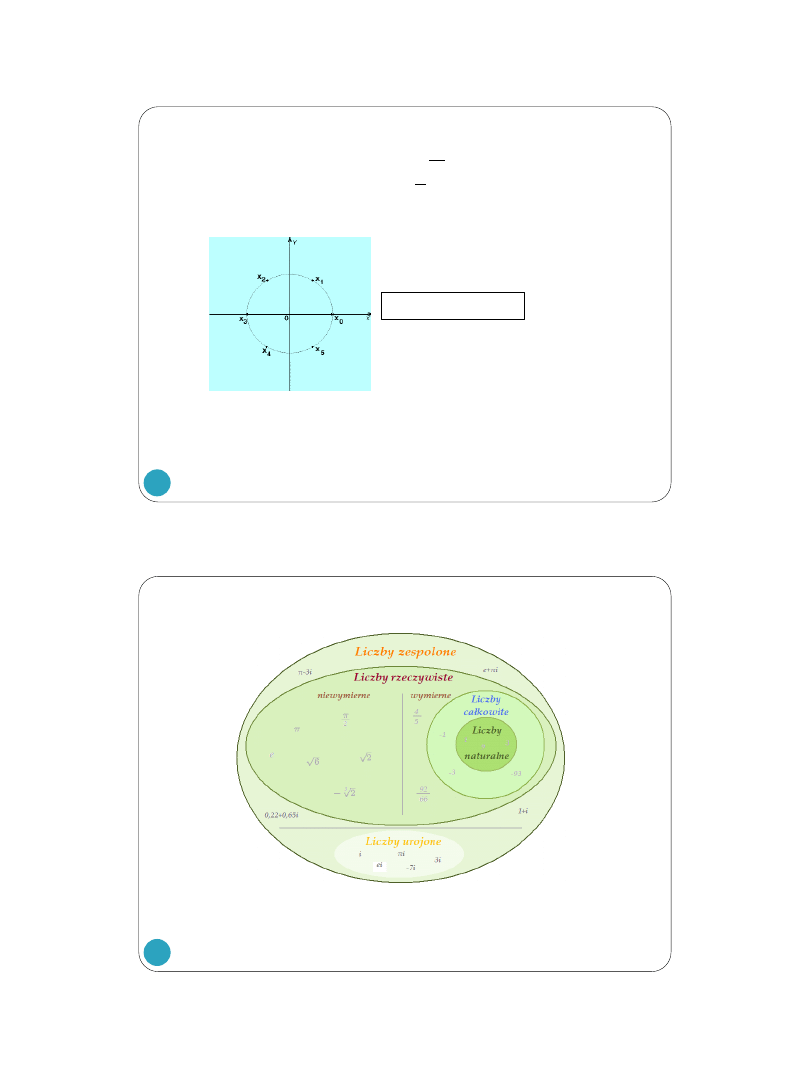
PRZYKŁAD 8. Obliczyć i narysować na płaszczyźnie

𝑎) 8𝑖

3

, 𝑏) −

1
2

+

3

2

𝑖

4

.

2011-10-05

Z.Kasperski, wykłady, t2.

10

Z.Kasperski- wyklady, t.2

19

WNIOSEK:

ZBIÓR PIERWIASTKÓW STOPNIA 𝑛 ≥ 3 JEST ZBIOREM WIERZCHOŁKÓW n-KĄTA

FOREMNEGO WPISANEGO W OKRĄG O PROMIENIU

|𝑧|

𝑛

I ŚRODKU W PUNKCIE (0, 0). KĄT MIĘDZY

SĄSIEDNIMI RAMIONAMI WODZĄCYMI JEST RÓWNY

2𝜋

𝑛

.

Pierwiastki szóstego stopnia z 1.

Z.Kasperski- wyklady, t.2

20

PODSUMOWANIE