1
LICZBY ZESPOLONE
Definicja
Liczbą zespoloną nazywamy uporządkowaną parę liczb rzeczywistych, np.
,
x y .
Zbiór wszystkich liczb zespolonych oznaczamy przez
C
:
R
y
x
y
x
z
C
,
:
,
Geometrycznie: Liczbę zespoloną
,
z
x y
przedstawiamy na płaszczyźnie w postaci punktu
o współrzędnych
,
x y lub w postaci wektora o początku w punkcie
0, 0 i końcu w punkcie
,
x y . Zbiór wszystkich liczb zespolonych nazywamy wtedy płaszczyzną zespoloną.
Definicja
Liczbę zespoloną
0,1 nazywamy jednostką urojoną i oznaczamy ją przez i :
0,1
i
Jednostka urojona spełnia równanie:
1
2
i
P
OSTAĆ ALGEBRAICZNA LICZBY ZESPOLONEJ
Każdą liczbę zespoloną można jednoznacznie zapisać w postaci:
z
x iy
, gdzie
R
y
x
,
Definicja
Niech x iy
będzie postacią algebraiczną liczby zespolonej
z
. Wówczas:
liczbę x nazywamy częścią rzeczywistą liczby zespolonej
z
, co zapisujemy:
Re z
x
liczbę
y
nazywamy częścią urojoną liczby zespolonej
z
, co zapisujemy:
Im z
y
Własność liczb zespolonych w postaci algebraicznej
Dwie liczby zespolone są równe wtedy i tylko wtedy, gdy ich części rzeczywiste i urojone są
równe, tzn.
1
2
1
2
1
2
Re
Re
Im
Im
z
z
z
z
z
z
Definicja
Sprzężeniem liczby zespolonej z x iy
, gdzie
R
y
x
,
, nazywamy liczbę zespoloną z
określoną wzorem
z
x iy
x
x
y
y
,
z
x y
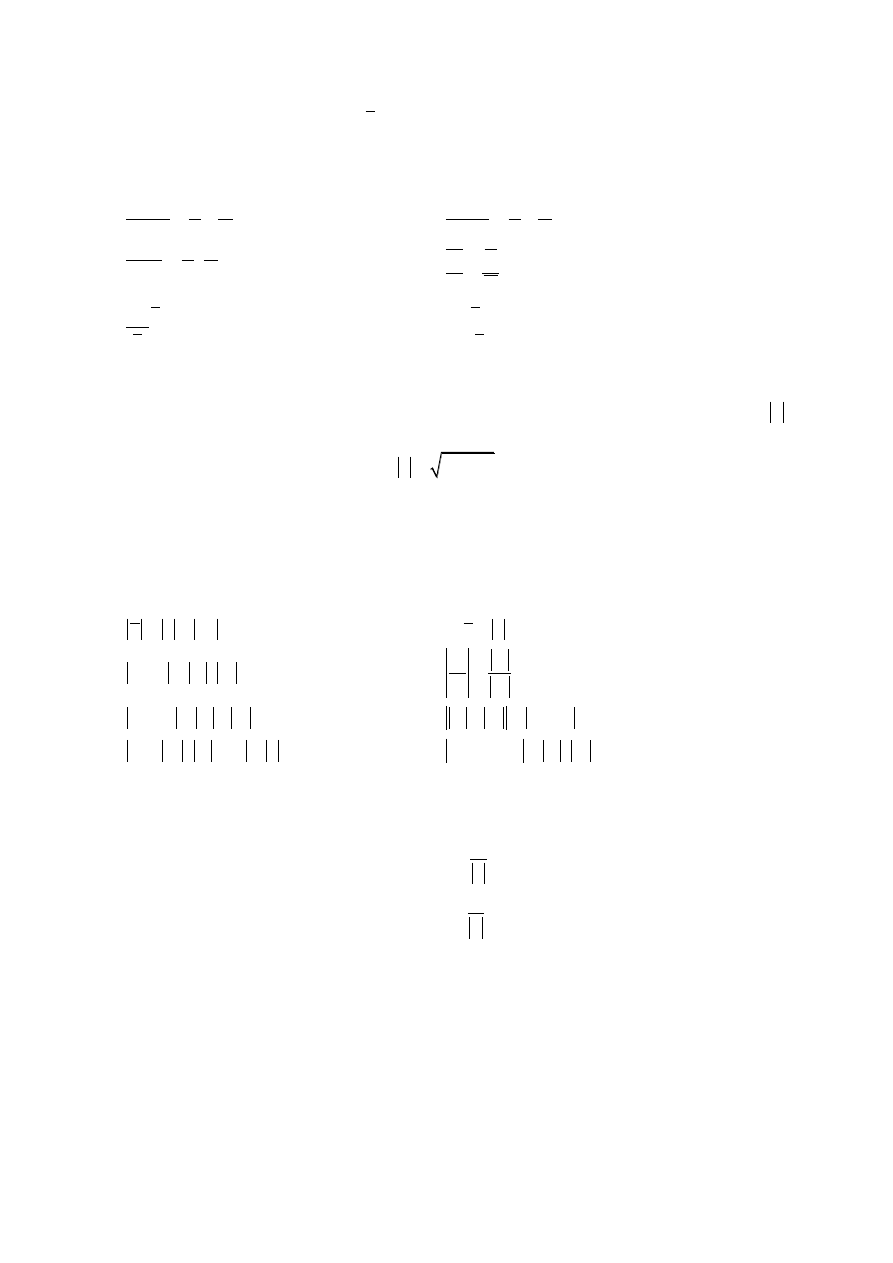
2
Geometrycznie: Liczba sprzężona z do liczby z jest jej obrazem w symetrii względem osi
rzeczywistej (Re z).
Własności sprzężenia liczb zespolonych
Niech
C
z
z
z
2
1
,
,
. Wtedy:
1.
1
2
1
2
z
z
z
z
2.
1
2
1
2
z
z
z
z
3.
1
2
1
2
z z
z z
4.
1
1
2
2
z
z
z
z
, o ile
2
0
z
5.
2 Re
z
z
z
6.
2 Im
z
z
i
z
7.
z
z
8.
Im
Im
z
z
Definicja
Modułem liczby zespolonej z x iy
, gdzie
R
y
x
,
, nazywamy liczbę rzeczywistą z
określoną wzorem:
2
2
z
x
y
Geometrycznie moduł liczby zespolonej
z
jest odległością punktu
z
od początku układu
współrzędnych.
Własności modułu liczby zespolonej
Niech
C
z
z
z
2
1
,
,
. Wtedy:
1. z
z
z
2.
2
z z
z
3.
1
2
1
2
z z
z
z
4.
1
1
2
2
z
z
z
z
, o ile
2
0
z
5.
1
2
1
2
z
z
z
z
6.
1
2
1
2
z
z
z
z
7. Re z
z
, Im z
z
8.
1
2
1
2
Re z z
z
z
Definicja
Każdą liczbę
R
spełniającą układ równań:
cos
sin
x
z
y
z
nazywamy argumentem liczby zespolonej
0
z
x iy
, gdzie
R
y
x
,
.
Argumentem głównym liczby zespolonej
0
z
nazywamy argument
tej liczby spełniający
nierówność
0
2
. Argument główny liczby zespolonej
z
oznaczamy przez
arg z
.
Każdy argument
liczby zespolonej
0
z
ma postać
arg
2
z
k
, gdzie
Z
k
Geometrycznie: Argument liczby zespolonej z jest miarą kąta zorientowanego utworzonego
przez dodatnią część osi rzeczywistej (Re z) i wektor wodzący liczby z.
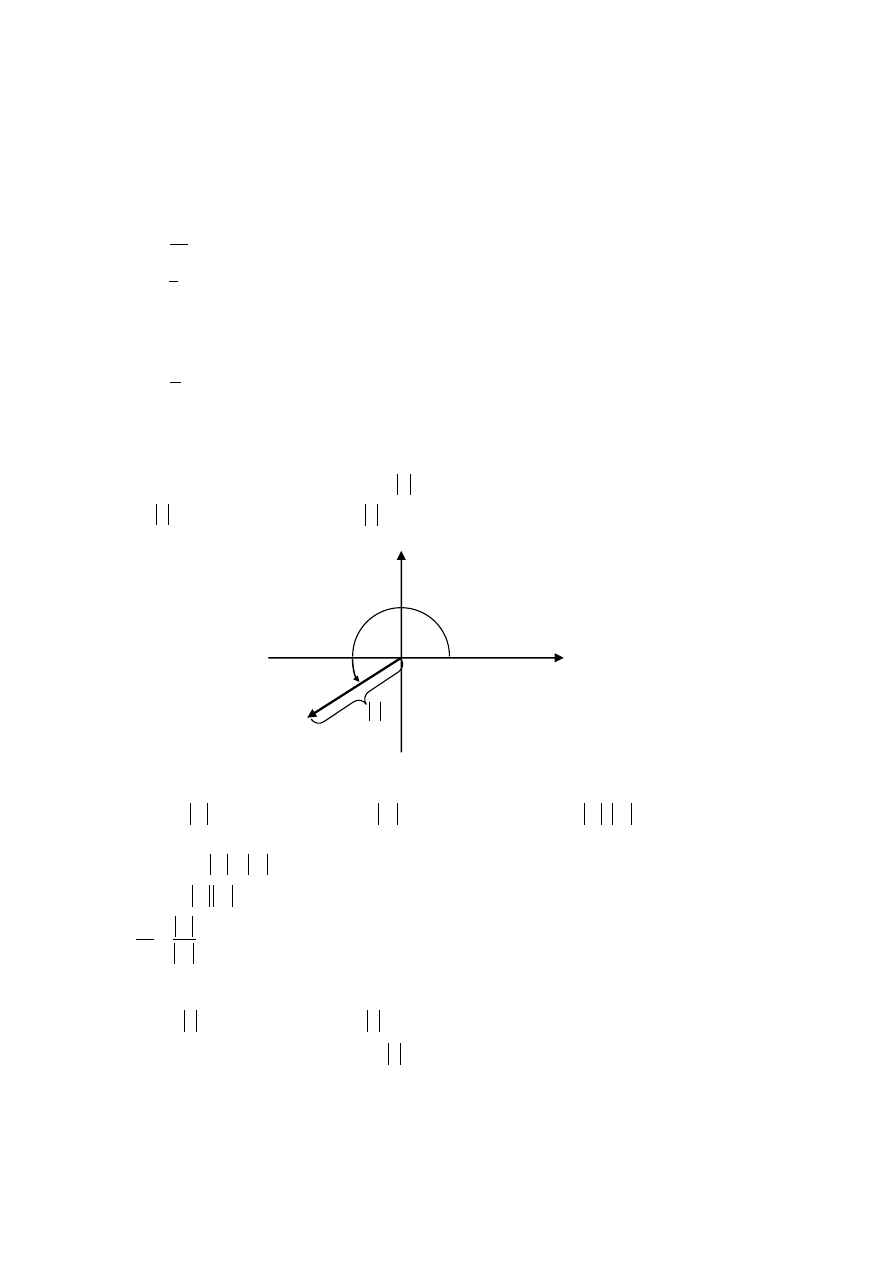
3
Własności argumentu liczby zespolonej
Niech
C
z
z
z
2
1
,
,
oraz niech
N
n
. Wtedy:
1.
1
2
1
2
arg
arg
arg
2
z z
z
z
k
dla pewnego
Z
k
2.
arg
arg
2
n
z
n
z
k
dla pewnego
Z
k
3.
1
1
2
2
arg
arg
arg
2
z
z
z
k
z
dla pewnego
Z
k
, o ile
2
0
z
4.
arg
2
arg
z
z
5.
arg
, gdy 0
arg
arg
arg
, gdy
arg
2
z
z
z
z
z
6.
1
arg
2
arg z
z
, o ile
0
z
P
OSTAĆ TRYGONOMETRYCZNA LICZBY ZESPOLONEJ
Każdą liczbę zespoloną
z
można przedstawić w postaci:
cos
sin
z
z
i
gdzie
0
z
oraz
R
. Liczba
z jest wówczas modułem liczby
z
, a
jednym z jej
argumentów.
Własności liczb zespolonych w postaci trygonometrycznej
Niech
1
1
1
1
cos
sin
z
z
i
,
2
2
2
2
cos
sin
z
z
i
, gdzie
1
2
,
0
z
z
oraz
R
2
1
,
,
będą liczbami zespolonymi. Wtedy:
1.
1
2
1
2
1
2
2
z
z
z
z
k
, dla pewnego
Z
k
2.
1
2
1
2
1
2
1
2
cos
sin
z z
z z
i
3.
1
1
1
2
1
2
2
2
cos
sin
z
z
i
z
z
, o ile
2
0
z
Wzór de Moivre’a
Niech
cos
sin
z
z
i
, gdzie
0
z
oraz
R
, oraz niech
N
n
. Wtedy:
cos
sin
n
n
z
z
n
i
n
Literatura
1. T. Jurlewicz, Z. Skoczylas: Algebra liniowa 1. Definicje, twierdzenia, wzory.
2. T. Jurlewicz, Z. Skoczylas: Algebra liniowa 1. Przykłady i zadania.
Re z
Im z
z
z